Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of Néel and Brownian relaxations on dynamic magnetization empirically characterized in single-core and multicore structures of magnetic nanoparticles†
Haruki
Goto
a,
Masato
Futagawa
b,
Yasushi
Takemura
 c and
Satoshi
Ota
c and
Satoshi
Ota
 *b
*b
aDepartment of Optoelectronics and Nanostructure Science, Graduate School of Science and Technology, Shizuoka University, Hamamatsu 432-8561, Japan
bDepartment of Electrical and Electronic Engineering, Shizuoka University, Hamamatsu 432-8561, Japan. E-mail: ota.s@shizuoka.ac.jp
cDepartment of Electrical and Computer Engineering, Yokohama National University, Yokohama 240-8501, Japan
First published on 24th April 2025
Abstract
This study takes a novel approach toward understanding the diagnostic and therapeutic efficacy of magnetic nanoparticles for cancer theranostics. We focused on the parameters influencing the dynamic magnetization response, such as particle core size and magnetic anisotropy. Our experimental investigation on the relationship between magnetic relaxation and these particle parameters provides fresh insights for developing biomedical applications. The magnetic relaxation time was estimated from the magnetic relaxation process and measured by applying a pulsed magnetic field over a wide time range of 20 ns to 200 ms. Magnetic nanoparticles with single-core and multicore structures under viscous fluid and solid conditions were investigated to evaluate the Néel and Brownian relaxations, respectively, associated with the magnetization and physical particle rotations. We observed a distinct magnetization response associated with the complex magnetic relaxation mechanisms, which challenged the concept described by the conventional theory of effective relaxation time. Moreover, we clarified the relationship between the effective magnetic anisotropy energy and attempt time for controlling the magnetization dynamics dependent on particle structures. Our novel measurement technique and investigation of the magnetic relaxation time provide guidance for significantly optimizing material design and determining the magnetic field conditions for the biomedical applications of magnetic nanoparticles, particularly in cancer theranostics.
1 Introduction
The sensitivity and resolution in magnetic particle imaging (MPI)1 and heating performance in hyperthermia treatment2 depend on the magnetic properties of magnetic nanoparticles (MNPs). MNP parameters, such as size and the anisotropy constant associated with particle structure, have been evaluated,3–8 and the relationship between these parameters and performance in biomedical applications has been discussed.9–13 The core size and anisotropy constant of MNPs were estimated using a measured magnetization curve in a static magnetic field.9 The dependence of shape and size on the anisotropy constant was determined by analyzing the blocking temperature.10 The size, shape, and structure of MNPs influenced the signal intensity of MPI11–15 and hyperthermia performance.16–27Magnetic relaxation is an important magnetization characteristic for biomedical applications. The tumor microscopic structure has been assessed by measuring the magnetic relaxation of MNPs injected into tumors in vivo.28 The Néel and Brownian relaxations are two relaxation types associated with magnetization and particle physical rotation, respectively. The relaxation times τN and τB for the Néel and Brownian types are represented, respectively, by the following equations:
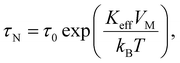 | (1) |
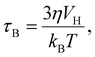 | (2) |
 | (3) |
Under zero-field conditions, the magnetic relaxation time is given by eqn (1) and (2). The dependence of the Néel and Brownian relaxation times on the applied magnetic field strength has been observed using numerical simulations.30
Magnetic relaxation has been evaluated using magnetic susceptibility measurements under an alternating current (AC) magnetic field, and the magnetic relaxation time has been calculated based on the Debye model.31 In addition, magnetic relaxation processes have been observed using a pulsed magnetic field.32–34
In this study, we prepared electrical circuits to measure the magnetic relaxation process over a considerably wide measurement period with relatively low concentrations compared to in our previous studies,32,33 to decrease the effects of the dipole interactions. Measurements were conducted by changing the solvent, and the effect of the relaxation mechanisms on the net magnetization dynamics was thus investigated. The distribution of the magnetic relaxation time, including the Néel and Brownian relaxation mechanisms, was estimated from the measured magnetic relaxation process. It is known that the magnetic relaxation mechanism can be affected by several parameters, such as the particle volume, anisotropy constant and attempt time, based on the particle structure and material composition. While the dominance of the relaxation mechanism based on the effective relaxation time theory has been previously discussed,35–37 the effective parameters affecting the relaxation mechanism dependent on particle structure have not been confirmed empirically.
An empirical model of the magnetic relaxation in multicore MNPs would be useful for hyperthermia treatment and MPI owing to the large hysteresis26 and strong nonlinear magnetization of such MNPs,3 respectively, which could be characterized by comparison with the relaxation in single-core particles. This comparison could contribute to the design of MNPs for future biomedical applications. Generally, MNPs formed by clustered core particles as effective particles are referred to as multicore-structured MNPs.38 It was previously reported that under a magnetic field, the magnetic moments in single-crystalline core particles were rotated in multicore particles, which was different from the domain-wall displacement in the multidomain structures.31
2 Experimental section
2.1 Sample preparation
Various commercially dispersed iron oxide nanoparticles were obtained, namely SHA-20 (Ocean NanoTech Ltd, San Diego, CA, USA), Synomag®-D (Micromod Partikeltechnologie GmbH, Rostock, Germany), and Resovist® (PDR Pharma Ltd, Tokyo, Japan), each with a concentration of 20 mg-Fe per mL. SHA-2039 and Resovist®40 consisted of Fe3O4 and γ-Fe2O3, respectively, while Synomag®-D26 consisted of γ-Fe2O3. As the liquid samples, MNPs were dispersed in diluted water with viscosity η of 0.89 mPa s and diluted water mixed with glycerol (FUJIFILM Wako Pure Chemical Corp., Tokyo, Japan) to adjust η = 5.4 and 12.4 mPa s. η were measured using a viscometer (VM-10A; Sekonic Corp., Tokyo, Japan). Additionally, the MNPs were embedded in epoxy resin to form solid samples. The structure and diameter of the MNPs were observed by transmission electron microscopy (TEM) at the Hanaichi UltraStructure Research Institute (Okazaki, Japan). Details regarding the analysis of the diameters of the MNPs are provided in ESI Note S1.†2.2 Measurement of the DC magnetization
The DC magnetization of the MNPs was measured using a vibrating sample magnetometer (VSM) system (Riken Denshi Co., Tokyo, Japan), which primarily comprised an electromagnet, sample vibrator, and pick-up coils. Electric current was supplied to the electromagnet using a bipolar power supply (Kudo Electric Co. Ltd, Sendai, Japan), controlled by a function generator (WF1983; NF Corp., Yokohama, Japan). The strength of the applied magnetic field was measured using a Tesla meter (F41; Lake Shore Cryotronics Inc., Ohio, USA). The magnetization signal detected by the pick-up coils was measured using a lock-in amplifier (LI5645; NF Corporation, Japan) and recorded using a Memory HiCorder unit (MR6000-01) with a digital voltmeter (MR8990) purchased from Hioki EE Corporation, Ueda, Japan. The method for estimating the effective core diameters is detailed in ESI Note S2.†2.3 Measurement of the magnetic relaxation process
The magnetic relaxation process in the prepared samples was measured using various types of pick-up and excitation coils. The pick-up coils measured the induced voltage (Volt) according to Faraday's law, represented by Volt = −dΦ/dt, where Φ is the magnetic flux. A high number of turns in the pick-up coil is required to achieve sufficiently high sensitivity to measure the slow magnetization response. By contrast, when the magnetization response is fast, the number of turns should be small, because the time constant of the coil is proportional to the inductance. Designing different electric circuits was thus necessary, including coil sets, such as circuits (i)–(v), as shown in Fig. S4 and Table S1,† for each measurement period. The magnetization response was measured using circuits (i)–(iii) in η = 0.89 and 5.4 mPa s, circuits (i)–(iv) in η = 12.4 mPa s, and circuits (i)–(v) in the solid. A cancel coil was used in circuits (ii)–(v) to reduce the voltage derived from the applied magnetic field together with the differential amplifier SA-440F5 driven by the DC voltage source LP5392 (NF Corp., Yokohama, Japan). The function generators AFG3022C (Tektronix Inc., Beaverton, OR, USA) and WF1974 (NF Corp., Yokohama, Japan) were used as the pulse waveform generators in circuits (i)–(iii) and (iv)–(v), respectively. The output waveform was measured using the MSO64 6-BW-1000 oscilloscope (Tektronix Inc., Beaverton, OR, USA). The cut-off frequencies of the low pass filters included in each circuit were adjusted with negligible interruption to the measured signal of MNPs to remove white noise.The specific measurement periods were determined by the time constant and sensitivity of the electric circuits, and the magnetization in each measured MNP, as shown in Table S2.† When measuring the solid sample in circuit (i), the two measurement periods were set by adjusting the rise time of the pulsed magnetic field. High resolution in the vertical range of the oscilloscope was required for measuring the relatively slow magnetization response. A wide vertical range of the oscilloscope was thus required to also measure the fast response, owing to Faraday's law, but this reduced the resolution for measuring the low voltage induced by the slow response.
The maximum intensity of the pulsed excitation magnetic fields was 0.1 mT, with the rise time defined as 90% of the maximum value reached in 12.2 ns. Details on connecting the magnetic relaxation processes measured across the different circuits and the normalization of the magnetization values per unit weight are provided in ESI Note S3.† The method for estimating the magnetic relaxation time is described in ESI Note S4.†
2.4 Measurement of AC susceptibility
AC susceptibilities were measured at frequencies ranging from 100 Hz to 1 MHz at an amplitude of 0.1 mT. Circuits (iii), (vi), and (vii), shown in Fig. S4c, S9a, and S9b,† were used in the 100 Hz to 10 kHz, 10–100 kHz, and 100 kHz to 1 MHz frequency ranges, respectively. The measured AC susceptibilities of the different circuits were normalized at 10 kHz and 100 kHz of the frequency, dividing the measurement range into smaller ranges to treat the AC susceptibilities continuously in the 100 Hz to 1 MHz frequency range. The function generator AFG3022C (Tektronix Inc., Beaverton, OR, USA) was used as the AC waveform generator. Regarding the differential amplifier and oscilloscope, systems similar to those used to measure the magnetic relaxation process were used.The real and imaginary parts of the susceptibility, χ′ and χ′′, were calculated as follows:
 | (4) |
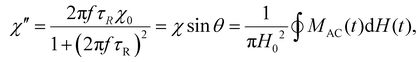 | (5) |
3 Results and discussion
3.1 DC magnetization curve
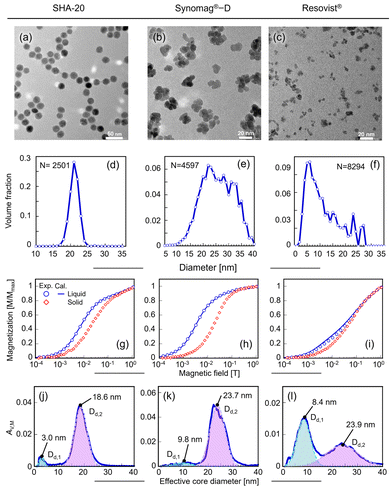
Fig. 1a–c show the core structures of the measured MNPs. SHA-20 exhibited a single-core structure, whereas Synomag®-D primarily exhibited a multicore structure with a few particles displaying single cores. The Resovist® particles were mainly single-core particles, with some multicore ones. Fig. 1d–f present the volume fraction, as analyzed from Fig. 1a–c, where aggregated particles were counted as effectively large multicore particles in Synomag®-D. A histogram of the number of counted particles is also shown in Fig. S10.†Fig. 1g–i show the measured magnetization curves under DC magnetization fields of 0–1.5 T. The coercivities of Synomag®-D and Resovist® were marginal in the solid samples, indicating that the MNPs behaved superparamagnetically. The coercivity of SHA-20 in the solid sample was 0.65 mT, which was relatively large compared to that of Synomag®-D and Resovist®.
The maximum magnetizations in the solid and liquid samples were similar for all the MNPs tested. The magnetization in the solid sample was lower than that in the liquid sample at the magnetic field strength where magnetization did not achieve saturation because the magnetic anisotropy energy bound the magnetization to the easy axis. Fig. 1j–l show the effective core diameter dC distribution, estimated from the DC magnetization curves for the liquid samples. Furthermore, the distribution was fitted by a normal distribution. Table 1 shows the mean ± SD values for the dC distribution. SHA-20 exhibited a diameter of approximately 20 nm without an organic coating layer.39 This aligned with the second peak of the dC distribution shown in Fig. 1j. For Synomag®-D, the effective dC of the core particles included in the multicore structure was approximately 10 nm, whereas that of the multicore particles was approximately 20 nm.42,43 These aligned with the first and second peaks of the dC distribution, Dd,1 and Dd,2, shown in Fig. 1k. In Resovist®, the averaged values of the dC distribution were 8.4 and 23.9 nm, as shown in Table 1. In particular, the distribution of Dd,2 in Resovist® was broader than that for SHA-20 and Synomag®-D, consistent with the trends reported in previous studies.9,38,42,43
| SHA-20 | Synomag®-D | Resovist® | ||
|---|---|---|---|---|
| d C [nm] | D d,1 | 3.0 ± 1.0 | 9.8 ± 3.6 | 8.4 ± 2.7 |
| D d,2 | 18.6 ± 2.5 | 23.7 ± 2.9 | 23.9 ± 6.5 | |
| Saturation magnetization [emu per g-Fe] | 111.5 | 110.6 | 96.3 | |
While Fig. 1j–l generally aligned with Fig. 1d–f, the distribution peaks calculated from the TEM images were higher than those derived from the DC magnetization curves, particularly in Synomag®-D. With respect to SHA-20, the distribution of Dd,1 was not observed in the TEM image (Fig. 1d and j). The saturation magnetization shown in Table 1 showed higher values for bulk γ-Fe2O3 (60–80 emu per g-Fe) and Fe3O4 (92–100 emu per g-Fe).39 The differences in the dC distribution and saturation magnetization were due to gradually increasing the magnetization toward saturation by the dipole–dipole interactions and the inhibition of magnetization by the demagnetizing field, which led to magnetic polarization.
3.2 Magnetic relaxation dependent on the particle structure
Fig. 2 shows the time evolution of the magnetization response measured by applying a pulsed magnetic field to the liquid and solid samples. The percentages of Mpulse at 200 ms in uncompleted magnetic relaxation for SHA-20 and Resovist® were 94% and 96%, respectively. Regarding SHA-20 and Resovist®, the magnetic relaxation time increased with η because τB was proportional to η, as shown in eqn (2). By contrast, the relaxation process was almost unaffected by η in Synomag®-D. Hence, the process was slightly faster for η = 5.4 and 12.4 mPa s compared with that in η = 0.89 mPa s. | ||
| Fig. 2 Magnetic relaxation process measured by applying a pulsed magnetic field to the liquid and solid samples, as shown by the plots, which were fitted using eqn (S3)† as represented by the curves with respect to (a) SHA-20, (b) Synomag®-D, and (c) Resovist®. The viscosity in the liquid sample was adjusted to 0.89, 5.4, and 12.4 mPa s. | ||
The magnetic relaxation time was fitted by a lognormal distribution from 100 ns to 1 s (see Fig. 3). Because the magnetization response up to approximately 20 ns was affected by the transitional response of the applied magnetic field limited by the time constant of the measurement circuit due to the inductance of the excitation coil, a relaxation time distribution larger than 100 ns was fitted with a lognormal distribution. A relaxation time shorter than 20 ns insufficiently illustrated the magnetization response owing to the transitional response of the applied magnetic field, whereas the magnetic relaxation occurred faster than 20 ns.
 | ||
| Fig. 3 Distribution of the magnetic relaxation time estimated from the magnetic relaxation process shown in Fig. 2 using eqn (S3),† as represented by the solid curves, which were fitted to a lognormal distribution from 100 ns to 1s at each characteristic peak, as shown by the dotted curves for (a) SHA-20, (b) Synomag®-D, and (c) Resovist®. | ||
The peak values of the relaxation time distribution, τpeak, fitted using the lognormal distribution (see Fig. 3) are shown in Fig. 4. The plots and dotted lines represent the liquid and solid samples, respectively, for each measured MNP. The theoretical curves of τB calculated using eqn (2) are shown as dotted curves in Fig. 4. Notably, the mean hydrodynamic diameters measured using dynamic light scattering (DLS), dH,DLS, were 60.3, 45.5, and 53.8 nm (PDI = 0.160, 0.070, and 0.199) for SHA-20, Synomag®-D, and Resovist®, respectively. The distributions shown for the solid samples were derived from Néel relaxation because particle rotation was inhibited.
 | ||
| Fig. 4 Peak values of the relaxation time distributions determined in liquid and solid samples using the lognormal distribution in Fig. 3, shown by plots and dotted lines, respectively, with respect to (a) SHA-20, (b) Synomag®-D, and (c) Resovist®. The theoretical τB calculated using eqn (2), is shown by the dotted curves. | ||
In SHA-20, the relaxation time distribution was divided into two distributions of Dτ,1 and Dτ,2 in the liquid samples, and four distributions of Dτ,1, Dτ,2, Dτ,3, and Dτ,4 in the solid sample by fitting them to the lognormal distribution, as shown in Fig. 3a. In the liquid samples, τpeak in Dτ,2 increased with η. By contrast, τpeak in Dτ,1 was not affected by η. The theoretical curve was close to the approximated curve of τpeak in Dτ,2 in the liquid samples, as shown in Fig. 4a (R2 = 0.946). Furthermore, the estimated hydrodynamic diameter dH,est was 62.9 nm, which was close to the measured dH,DLS.
These observations indicated that Dτ,2 in the liquid samples was derived from Brownian relaxation. τpeak in Dτ,1 in the liquid samples, which was approximately identical to τpeak in Dτ,1 in the solid sample, was derived from Néel relaxation. In addition, these were longer than those in the solid samples owing to the influence of particle rotation as the initial response in the Brownian relaxation. The relaxation time distribution in the solid samples exhibited multiple peaks, despite the sharp diameter distribution observed in the TEM images (see Fig. 1d) and in the DC magnetization curves (see Fig. 1j). This suggests that the magnetic anisotropy in SHA-20 could vary, possibly owing to the heterogeneous particle aggregation impacted by surface modification. The distribution density of aggregated particle counts, as analyzed from the TEM image and as shown in Fig. S11,† supports this hypothesis.
In Synomag®-D, the relaxation time distribution was divided into Dτ,1 and Dτ,2 with η = 0.89 mPa s; Dτ,1, Dτ,2, and Dτ,3 with η = 5.4 mPa s and η = 12.4 mPa s; and Dτ,1, Dτ,2, Dτ,3, and Dτ,4 in the solid sample by fitting using the lognormal distribution (see Fig. 3b).
τ peak in Dτ,2 with η = 0.89 mPa s and τpeak in Dτ,3 with η = 5.4 and 12.4 mPa s were close to τpeak in Dτ,3 in the solid sample. Also, τpeak in Dτ,1 with η = 0.89 mPa s and τpeak in Dτ,2 with η = 5.4 and 12.4 mPa s were close to τpeak in Dτ,2 in the solid sample. Again, τpeak in Dτ,1 with η = 5.4 and 12.4 mPa s were close to τpeak in Dτ,1 in the solid sample. These peaks were considered to be dominantly derived from Néel relaxation. In addition, τpeak in the liquid samples was not proportional to the viscosity, despite Mmax in the liquid being sufficiently larger than that in the solid (see Fig. 2), presumably due to the particle rotation, which is conventionally affected by the viscosity. This contradiction was due to the specific magnetic relaxation mechanism discussed in Section 3.4. In the solid samples, τN was typically shorter than ∼10 ns. However, the distributions from the TEM images (see Fig. 1e) and DC magnetization curves (see Fig. 1k) indicated particle diameters of predominantly 20–30 nm, with τN exceeding 10 ns. This finding suggests that the magnetization of core particles (10–15 nm) in multicore particles may occur primarily with τN shorter than 10 ns.
In Resovist®, the τpeak values in Dτ,2, Dτ,4, and Dτ,3 with η = 0.89, 5.4, and 12.4 mPa s were longer than the theoretical τB calculated at dH,DLS = 53.8 nm. Furthermore, the τpeak values were proportional to η, as shown in Fig. 4c, indicating their association with Brownian relaxation at dH,est = 96.9 nm (R2 = 0.998).
By contrast, the Brownian relaxation derived from dH,DLS = 53.8 nm presumably occurred because the magnetization distribution MmaxAM,τ at the theoretical τB was sufficiently large. Considering the Brownian relaxation derived from dH,DLS and dH,est, the distribution of dH in Resovist® was relatively more comprehensive than in both SHA-20 and Synomag®-D, which indicates the limitation of the spherical approximation for hydrodynamic structures.
τ peak in Dτ,1 in the liquid was close to τpeak in Dτ,1 in the solid, owing to the dominance of Néel relaxation, which indicates that the particles in Dd,1 in Fig. 1l dominantly rotated with Néel relaxation. Because the τpeak values in Dτ,2 with η = 0.89 mPa s, Dτ,4 with η = 5.4 mPa s, and Dτ,3 with η = 12.4 mPa s were proportional to the viscosity, the relatively large particles in Dd,2 in Fig. 1l dominantly rotated with Brownian relaxation. The dominance of Néel relaxation in smaller particles and that of Brownian relaxation in larger particles in Resovist® particles was also observed in ref. 44. On the other hand, it is also worth noting that it is difficult to determine the threshold of the core particle size when the dominant relaxation mechanisms changes. Here, τpeak in Dτ,3 with η = 5.4 mPa s was close to both the theoretical τB and τpeak in Dτ,2 in the solid, demonstrating the contribution of both Néel and Brownian relaxations. By contrast, τpeak in Dτ,2 with η = 12.4 mPa s was close to only τpeak in Dτ,2 in the solid, because only Néel relaxation occurred when τB increased with a high η. Néel relaxation was more significant with increasing η because τB was long compared to τN, in accordance with the conventional theory of the effective relaxation time shown by eqn (3). The MNPs with a relaxation time corresponding to Dτ,2 in η = 5.4 mPa s were presumably distributed in the broad Dτ,1 at η = 0.89 mPa s and Dτ,2 at η = 12.4 mPa s.
3.3 Magnetization dynamics under AC magnetic fields dependent on the particle structure
Fig. 5 shows the real and imaginary parts of the susceptibility, χ′ and χ′′, respectively, measured under AC magnetic fields in η = 0.89 and 5.4 mPa s and solid samples. In addition, χ′ and χ′′ were calculated from the magnetic relaxation time distribution (see Fig. 3) based on the Debye model given by eqn (4) and (5). | ||
| Fig. 5 AC susceptibility calculated from the magnetic relaxation time distribution shown in Fig. 3 using eqn (4) and (5), as represented by the solid curves, with respect to (a) SHA-20, (b) Synomag®-D, and (c) Resovist®. The plots show the measured AC susceptibility from 100 Hz to 1 MHz for η = 0.89 and 5.4 mPa s in the solid samples. | ||
The measured and calculated χ′ and χ′′ agreed at η = 0.89 and 5.4 mPa s. In addition, the frequency in the local maximum peaks of χ′′ observed in the 100 Hz to 10 kHz range was proportional to η in SHA-20 and Resovist®, but was not proportional to η in Synomag®-D. These results corresponded to the magnetic relaxation time distribution trend shown in Fig. 3 and 4.
In the solid, particularly with respect to Resovist®, although the measured and computed χ′ agreed with each other, the measured χ′′ was smaller than the calculated χ′′. The magnetic relaxation time for the small dc components included in Dd,1 (see Fig. 1l), which was shorter than the transition time of the applied magnetic field, was estimated as a longer relaxation time compared to the actual value in Resovist®. This limitation decreased the peak frequency of the calculated χ′′ compared to the measured χ′′, increasing the χ′′ calculated using eqn (5).
In SHA-20, 94% of the magnetic relaxation process in the solid occurred at 200 ms. Some uncertain components derived from the remaining 6% magnetization caused the slight disagreement between the measured and calculated χ′′ in the solid.
3.4 Model of the complex magnetic relaxation dependent on the particle structure
Under a zero magnetic field, the easy axis inherent in the particle body and magnetization were simultaneously disturbed by the thermal energy in the liquid. In SHA-20, the magnetization was rotated along the easy axis under the applied magnetic field (see Fig. 6a). Magnetic relaxation in the liquid samples was derived from the physical rotation of the particles defined as Brownian relaxation when τB ≪ τN, where the dynamic magnetization response was controlled by dH and η. In addition, the magnetic torque acting on the magnetization was transmitted to the particle body owing to the large braking torque.45In the solid or liquid samples with an extremely high η, the magnetization rotation was limited owing to Keff. By contrast, the magnetization rotation constraint of the easy axis was relatively weak in Synomag®-D owing to the behavior of the core particles in the multicore structure under the case of a zero magnetic field. The thermal energy in the liquid disturbed the easy axis and magnetization almost independently. When the magnetic field was applied, the magnetization was first rotated by Néel relaxation. The easy axis was rotated second (see Fig. 6b) owing to the significant MNP components with a considerable anisotropy energy KeffVM, which was sufficient to transmit the magnetic torque acting on the magnetization to the particle body when τN ≤ τB. This two-step motion, determined by balancing the friction and braking torques, was repeated by promoting the magnetization occurring at τN ≤ τB, as shown in Fig. 3 and 4; in particular τpeak in Dτ,1 in SHA-20 and τpeak in Dτ,1 and Dτ,2 in Synomag®-D in the liquid sample.
It is challenging to represent this phenomenon using the conventional theory of the effective relaxation time. However, it could be observed that the dynamic orientation of the easy axis towards the applied magnetic field gradually promoted magnetization, owing to the effective decrease in KeffVM.46 Moreover, decreasing the MmaxAM,τ when the relaxation time was long with increasing η reflected the reduced contribution of particle rotation to magnetization as the gap between τN and τB increased under the case of τN < τB.
3.5 Mechanism of the Néel relaxation process dependent on the anisotropy energy and attempt time
With respect to all the tested MNPs, τpeak in the solid samples, as shown in Fig. 4, was assumed to be associated with the relatively large dC included in Dd,2, as shown in Fig. 1. Meanwhile, Keff was obtained by dividing the component of VM calculated from the peak value of dC, dC,peak in Dd,2 by applying the spherical approximation from KeffVM calculated from the τpeak values in the solid shown in Fig. 4 using eqn (1), because only Néel relaxation occurred in the solid. Fig. 7 shows the Keff values estimated using eqn (1) at various τ0 for each particle, indicating the significant impact of τ0 for estimating Keff.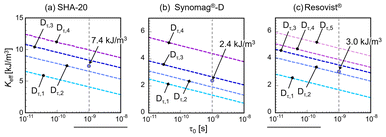 | ||
| Fig. 7 Effective anisotropy constant Keff estimated at various τ0 using eqn (1) for each relaxation time distribution in (a) SHA-20, (b) Synomag®-D, and (c) Resovist®. | ||
When τ0 = 10−9 s, for SHA-20, the averaged Keff, Keff,τ, in all the peaks of 7.4 kJ m−3 (see Fig. 7a) was similar to that as analyzed from the blocking temperature in ref. 7. The Keff,τ in SHA-20 was relatively large compared to the 2.4 kJ m−3 and 3.0 kJ m−3 values estimated for Synomag®-D and Resovist® (see Fig. 7b and c), respectively.
By contrast, in Synomag®-D, the area enclosed by the DC magnetization curves in the liquid and solid samples as 0.015 was larger than that in SHA-20 as 0.013 (see Fig. 8a), which indicates that KeffVM in Synomag®-D was larger than that in SHA-20, as shown by Brownian relaxation occurring owing to the magnetization being pinned to the easy axis.
 | ||
| Fig. 8 (a) Phase diagram of the particle structures illustrated by τN dependent on KeffVM and τ0 calculated from eqn (1). The areas enclosed by the DC magnetization curves in the liquid and solid samples were 0.013 in SHA-20 and 0.015 in Synomag®-D. The magnetic field H and magnetization M were normalized by their maximum values, Hmax and Mmax, respectively. (b) Transition of the magnetization state of the core particles included in a multicore particle, dependent on the applied magnetic field strength in Synomag®-D. | ||
The dependence of KeffVM on the particle structure estimated from the static magnetization response contradicted that calculated from the magnetic relaxation time based on the dynamic magnetization response at constant τ0. This indicates that τ0 was dependent on the particle structure, as shown in Fig. 8a. For Synomag®-D, τ0 was relatively short with a large KeffVM because τN was dominantly distributed below ∼10−9 s, which is a shorter timescale compared with that of SHA-20, as shown in Fig. 3.
Besides, the coercivity of the DC magnetization curves in Synomag®-D was comparatively small under the case of a zero magnetic field (see Fig. S12†), although KeffVM in Synomag®-D was larger than that in SHA-20. In Synomag®-D, the core particles included in the multicore structure were first magnetized by τN of approximately less than 10 ns. The magnetization of the effective core particles that were thermally disturbed under a zero magnetic field was generated by the partial alignment of the core particles (see Fig. 8b). The KeffVM value for Synomag®-D increased after the formation of effective anisotropy within the multicore structure, which occurred during magnetic relaxation, as shown by the complex τN distribution over the wide time range (see Fig. 3b in solid).
Further estimation of τ0 in future studies will provide more insights into the magnetization mechanisms within multicore structures, particularly in relation to the behavior of the core particles.
4 Conclusion
The widely distributed magnetic relaxation time of MNPs was empirically estimated from a magnetic relaxation process to be substantially fast compared to an applied pulsed magnetic field in the 20 ns to 200 ms range.With respect to the single-core MNPs of SHA-20, a relaxation time proportional to the viscosity in accordance with the conventional theory of Brownian relaxation was dominantly observed in the liquid. When the Brownian relaxation time was substantially shorter than the Néel relaxation time, owing to the large anisotropy energy, Brownian relaxation dominantly occurred in the liquid in accordance with the conventional theory of the effective relaxation time.
By contrast, in the multicore MNPs of Synomag®-D, the distribution of the magnetic relaxation time associated with particle physical rotation without proportionality to the viscosity was confirmed in a fluid system. This phenomenon, which is difficult to explain using the theory of the effective relaxation time, was caused by repeating the two-step motion due to the balance between the friction and braking torques when the Néel relaxation time was shorter than the Brownian relaxation time. In addition, the conflicted phenomenon of a relatively large anisotropy energy and small coercivity in the DC magnetization curve was observed, which could be explained by the two different magnetization responses in individual core particles around the zero magnetic field and in the effective core particles formed by the core particles aligning under the magnetic field. The measurement based on static and dynamic magnetization responses indicated a shorter attempt time and larger anisotropy energy in Synomag®-D compared to those in SHA-20.
This indicated that the magnetization response could be universally determined by the effective magnetization parameters associated with the particle structure. On the other hand, the relationship between the effective magnetization parameters and particle structure was unrevealed, which is one of key factors for improving the performance when designing MNPs for use in biomedical applications, such as cancer theranostics.
In future work, it is necessary to enlarge the measurement period limited by the transition time of the applied magnetic field and the sensitivity of the detection coil to investigate specific magnetic relaxation mechanisms influenced by the structure of MNPs.
Author contributions
Haruki Goto: conceptualization, methodology, validation, formal analysis, investigation, software, data curation, writing – original draft, visualization. Masato Futagawa: validation, writing – review & editing. Yasushi Takemura: writing – review & editing, funding acquisition. Satoshi Ota: conceptualization, methodology, validation, formal analysis, software, data curation, writing – review & editing, supervision, project administration, funding acquisition.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was partially supported by JSPS KAKENHI grant numbers 20H02163, 20H05652, and 23K26114, and JST ACT-X grant number JPMJAX21A5, JST SPRING, Japan Grant Number JPMJSP2167.References
- B. Gleich and J. Weizenecker, Nature, 2005, 435, 1214–1217 CrossRef CAS PubMed.
- A. Jordan, P. Wust, H. Fähling, W. John, A. Hinz and R. Felix, Int. J. Hyperthermia, 1993, 9, 51–68 CrossRef CAS PubMed.
- T. Yoshida, N. B. Othman and K. Enpuku, J. Appl. Phys., 2013, 114, 173908 CrossRef.
- P. Ilg, Phys. Rev. B, 2017, 95, 214427 CrossRef.
- S. Ota and Y. Takemura, J. Magn. Soc. Jpn., 2019, 43, 34–41 CrossRef.
- R. Moreno, S. Poyser, D. Meilak, A. Meo, S. Jenkins, V. K. Lazarov, G. Vallejo-Fernandez, S. Majetich and R. F. L. Evans, Sci. Rep., 2020, 10, 2722 CrossRef CAS PubMed.
- T. Kahmann, E. L. Rösch, K. Enpuku, T. Yoshida and F. Ludwig, J. Magn. Magn. Mater., 2021, 519, 167402 CrossRef CAS.
- E. Sasaoka, C. Yang, S. B. Trisnanto, Z. Song, S. Ota and Y. Takemura, J. Magn. Soc. Jpn., 2023, 47, 115–117 CrossRef.
- S. Ota, S. B. Trisnanto, S. Takeuchi, J. Wu, Y. Cheng and Y. Takemura, J. Magn. Magn. Mater., 2021, 538, 168313 CrossRef CAS.
- H. Mamiya, H. Fukumoto, J. L. Cuya Huaman, K. Suzuki, H. Miyamura and J. Balachandran, ACS Nano, 2020, 14, 8421–8432 CrossRef CAS PubMed.
- S. Ota, Y. Matsugi, T. Nakamura, R. Takeda, Y. Takemura, I. Kato, S. Nohara, T. Sasayama, T. Yoshida and K. Enpuku, J. Magn. Magn. Mater., 2019, 474, 311–318 CrossRef CAS.
- Z. W. Tay, S. Savliwala, D. W. Hensley, K. L. B. Fung, C. Colson, B. D. Fellows, X. Zhou, Q. Huynh, Y. Lu, B. Zheng, P. Chandrasekharan, S. M. Rivera-Jimenez, C. M. Rinaldi-Ramos and S. M. Conolly, Small Methods, 2021, 5, 2100796 CrossRef CAS PubMed.
- Q. Wang, X. Ma, H. Liao, Z. Liang, F. Li, J. Tian and D. Ling, ACS Nano, 2020, 14, 2053–2062 CrossRef CAS PubMed.
- R. M. Ferguson, K. R. Minard, A. P. Khandhar and K. M. Krishnan, Med. Phys., 2011, 38, 1619–1626 CrossRef PubMed.
- A. Tomitaka, R. M. Ferguson, A. P. Khandhar, S. J. Kemp, S. Ota, K. Nakamura, Y. Takemura and K. M. Krishnan, IEEE Trans. Magn., 2015, 51, 6100504 Search PubMed.
- J. P. Fortin, C. Wilhelm, J. Servais, C. Ménager, J. C. Bacri and F. Gazeau, J. Am. Chem. Soc., 2007, 129, 2628–2635 CrossRef CAS PubMed.
- D. E. Bordelon, C. Cornejo, C. Grüttner, F. Westphal, T. L. DeWeese and R. Ivkov, J. Appl. Phys., 2011, 109, 124904 CrossRef.
- P. Guardia, R. D. Di Corato, L. Lartigue, C. Wilhelm, A. Espinosa, M. Garcia-Hernandez, F. Gazeau, L. Manna and T. Pellegrino, ACS Nano, 2012, 6, 3080–3091 CrossRef CAS PubMed.
- P. Hugounenq, M. Levy, D. Alloyeau, L. Lartigue, E. Dubois, V. Cabuil, C. Ricolleau, S. Roux, C. Wilhelm, F. Gazeau and R. Bazzi, J. Phys. Chem., 2012, 116, 15702–15712 CAS.
- E. Lima, T. E. Torres, L. M. Rossi, H. R. Rechenberg, T. S. Berquo, A. Ibarra, C. Marquina, M. R. Ibarra and G. F. Goya, J. Nanopart. Res., 2013, 15, 1654 CrossRef.
- R. Ludwig, M. Stapf, S. Dutz, R. Müller, U. Teichgräber and I. Hilger, Nanoscale Res. Lett., 2014, 9, 602 CrossRef PubMed.
- R. D. Di Corato, A. Espinosa, L. Lartigue, M. Tharaud, S. Chat, T. Pellegrino, C. Ménager, F. Gazeau and C. Wilhelm, Biomaterials, 2014, 35, 6400–6411 CrossRef CAS PubMed.
- C. L. Dennis, K. L. Krycka, J. A. Borchers, R. D. Desautels, J. van Lierop, N. F. Huls, A. J. Jackson, C. Gruettner and R. Ivkov, Adv. Funct. Mater., 2015, 25, 4300–4311 CrossRef CAS.
- M. Vasilakaki, C. Binns and K. N. Trohidou, Nanoscale, 2015, 7, 7753–7762 RSC.
- C. Blanco-Andujar, D. Ortega, P. Southern, Q. A. Pankhurst and N. T. K. Thanh, Nanoscale, 2015, 7, 1768–1775 RSC.
- P. Bender, J. Fock, C. Frandsen, M. F. Hansen, C. Balceris, F. Ludwig, O. Posth, E. Wetterskog, L. K. Bogart, P. Southern, W. Szczerba, L. Zeng, K. Witte, C. Grüttner, F. Westphal, D. Honecker, D. González-Alonso, L. Fernández Barquín and C. Johansson, J. Phys. Chem. C, 2018, 122, 3068–3077 CrossRef CAS.
- H. Gavilán, K. Simeonidis, E. Myrovali, E. Mazarío, O. Chubykalo-Fesenko, R. Chantrell, Ll. Balcells, M. Angelakeris, M. P. Morales and D. Serantes, Nanoscale, 2021, 13, 15631–15646 RSC.
- S. Ota, H. Kosaka, K. Honda, K. Hoshino, H. Goto, M. Futagawa, Y. Takemura and K. Shimizu, Adv. Mater., 2024, 36, 2404766 CrossRef CAS PubMed.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- A. L. Elrefai, T. Yoshida and K. Enpuku, J. Magn. Magn. Mater., 2020, 507, 166809 CrossRef CAS.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 083921 CrossRef.
- S. B. Trisnanto, S. Ota and Y. Takemura, Appl. Phys. Express, 2018, 11, 075001 CrossRef.
- S. Ota and Y. Takemura, J. Phys. Chem. C, 2019, 123, 28859–28866 CrossRef CAS.
- T. Q. Bui, A. J. Biacchi, C. L. Dennis, W. L. Tew, A. R. H. Walker and S. I. Woods, Appl. Phys. Lett., 2022, 120, 012407 CrossRef CAS PubMed.
- S. Purushotham and R. V. Ramanujan, J. Appl. Phys., 2010, 107, 114701 CrossRef.
- L. Maldonado-Camargo, I. Torres-Díaz, A. Chiu-Lam, M. Hernández and C. Rinaldi, J. Magn. Magn. Mater., 2016, 412, 223–233 CrossRef CAS.
- P. T. Phong, L. H. Nguten, D. H. Manh, I. J. Lee and N. X. Phuc, J. Electron. Mater., 2017, 46, 2393–2405 CrossRef CAS.
- D. Eberbeck, F. Wiekhorst, S. Wagner and L. Trahms, Appl. Phys. Lett., 2011, 98, 182502 CrossRef.
- K. Wu, J. Liu, R. Saha, C. Peng, D. Su, Y. A. Wang and J. P. Wang, ACS Omega, 2021, 6, 6274–6283 CrossRef CAS PubMed.
- R. Lawaczeck, H. Bauer, T. Frenzel, M. Hasegawa, Y. Ito, K. Kito, N. Miwa, H. Tsutsui, H. Vogler and H. J. Weinmann, Acta Radiol., 1997, 38, 584–597 CAS.
- T. Yamaminami, S. Ota, S. B. Trisnanto, M. Ishikawa, T. Yamada, T. Yoshida, K. Enpuku and Y. Takemura, J. Magn. Magn. Mater., 2021, 517, 167401 CrossRef CAS.
- S. Liu, A. Chiu-Lam, A. Rivera-Rodriguez, R. DeGroff, S. Savliwala, N. Sarna and C. M. Rinaldi-Ramos, Nanotheranostics, 2021, 5, 348–361 CrossRef PubMed.
- K. Enpuku, S. Draack, F. Ludwig and T. Yoshida, J. Appl. Phys., 2021, 130, 183901 CrossRef CAS.
- T. Yoshida, T. Nakamura, O. Higashi and K. Enpuku, Jpn. J. Appl. Phys., 2018, 57, 080302 CrossRef.
- Y. L. Raĭkher and M. I. Shliomis, Adv. Chem. Phys., 1994, 87, 595–751 CrossRef.
- S. Ota, S. Ohkawara, H. Hirano, M. Futagawa and Y. Takemura, J. Magn. Magn. Mater., 2021, 539, 168354 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00722d |
| This journal is © The Royal Society of Chemistry 2025 |