Combined in- and out-of-plane chemical ordering in super-ordered MAX phases (s-MAX)

Abstract

The challenge of synthesizing stable super-ordered MAX phases (s-MAX), with both in-plane and out-of-plane chemical ordering, lies in the combination of five different elements and the inherent order of them. A plethora of compositions is thus possible for these quinary phases, however finding the most promising ones and their suitable synthesis methods remains challenging. In this study, we address this issue by employing density functional theory (DFT) to investigate the phase stability of s-MAX phases with the general formulae M1₄M2₂M3₆Al₃C₉ (413 MAX) and M1₄M2₂M3₃Al₃C₆ (312 MAX). We identified 26 stable s-MAX phases, with in-plane order of M1 and M2 in the outer layer next to Al and out-of-plane order with M1 + M2 in the outer layer and M3 in the inner layers. An additional 14 s-MAX phases with partial disorder, i.e., M2 with in-plane order in the outer layer whereas disorder of M1 and M3 across outer and inner layers, were also found to be thermodynamically stable. Ideal super-ordered s-MAX is favoured over s-MAX with partial disorder when, among other things, the atomic size of M2 and M3 is larger than M1. These findings provide a framework for designing compositionally tuned s-MAX phases with enhanced functionality, contributing to the development of advanced materials and MXene precursors.

---

1. Introduction

MAX phases are a family of atomically laminated materials with the general formula M_n+1AX_n, where M is a transition metal, A is an A-group element, X is typically C or N, and n = 1–4. They exhibit a unique combination of metallic and ceramic properties owing to their layered structure with a mixture of covalent, ionic, and metallic bonds.^1–3 MAX phases are also the primary precursors used for conversion into their two-dimensional derivative, MXene.^4,5

Originally discovered as ternary compounds in the 1960s,^6–10 MAX phases have expanded into more complex compositions through alloying on the M,^11,12 A,^13,14 or X^15,16 sites, being referred to as solid-solution MAX phases, offering enhanced control of their properties. Recent advancements have also shown that introducing chemical order within MAX phases can significantly influence their performance. This includes the discovery of two primary types of ordering: (i) in-plane (i-MAX),^17,18 schematically shown in Fig. 1a, where atoms are chemically ordered within the metal basal planes, and (ii) out-of-plane (o-MAX), illustrated in Fig. 1b,^19,20 where metal layers are chemically ordered in a sandwich-like structure. Both types of ordering have the potential to allow for precise compositional tuning which, in turn, will impact their properties while also affecting the potential for MAX to MXene conversion.

Fig. 1 Schematic illustration of (a) in-plane chemical order of two metals, M1 and M2, in a 211 MAX phase denoted as i-MAX, (b) out-of-plane chemical order of two metals, M1 and M3, in a 413 MAX phase denoted as o-MAX, and (c) combined in- and out-of-plane chemical order of three metals, M1, M2 and M3, in a 413 phase denoted as s-MAX.

The formation of these chemically ordered structures, however, requires careful selection of metals, as an improper combination may lead to disorder on the metal sites (a solid solution) or the preferred formation of competing phases beyond MAX phases.^21,22 In i-MAX phases, achieving in-plane chemical order requires a significant size difference of the transition metals, e.g., by combining smaller Mo, W, or Cr with larger Sc, Y, or a rare-earth (RE) element.^{17,18,22–24} Similarly, o-MAX phases rely on the elemental layering of different metal components, promoted by out-of-plane separation through the preferred occupation of different Wyckoff sites. This is typically achieved when two metals have similar sizes and when the metal in the outer layer (red atoms in Fig. 1b) does not form a corresponding binary rock-salt structure with fcc-stacking and has a large electronegativity difference with respect to the A-element.^20,21,25 It should be noted that o-MAX phases have shown tendencies for interlayer intermixing between metals in outer and inner layers.^20,26–29

A most recent breakthrough has experimentally demonstrated that it is possible to combine in-plane and out-of-plane ordering into a single, more complex structure referred to as super-ordered MAX phases (s-MAX).³⁰ These quinary s-MAX phases are composed of three metals where the careful selection of metals allows for the simultaneous control of in-plane and out-of-plane order, shown for Mo_4/3RE_2/3Nb₂AlC₃, where RE = Y, Gd, Tb, Dy, Ho, Er, Tm, and Lu. The latter (RE) is chemically ordered in-plane at the outer metal layer in ideal stoichiometry, whereas Mo and Nb maintain the out-of-plane ordered occupation.³⁰ Furthermore, s-MAX can also be delaminated into the s-MXene with topochemically ordered vacancies in Mo_4/3Nb₂C₃T_z. Notably, the s-MXene shows enhanced capacitance as compared to the Mo₂Nb₂C₃T_z o-MXene.³⁰ This super-ordering thus shows potential to further enhance the functional properties of the material, providing additional ways to enhance the compositional and structural space and related properties of both MAX phases and MXenes.

In this work, we use first-principles calculations to systematically investigate the stability of new s-MAX phases by predicting stable metal combinations that simultaneously support both in-plane and out-of-plane chemical ordering. To clarify the inherent chemical order present in 413 s-MAX phases compared to the original M1_4/3M2_2/3M3₂AX₃ composition, we introduce an alternative integer notation M1₄M2₂M3₆A₃X₉ with the corresponding notation for 312 s-MAX being M1₄M2₂M3₃A₃X₆. The studied compositions include M1 and M3 = {Sc, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe}, M2 = {Sc, Y}, A = Al, and X = C. The choice of M2 = Sc and Y is motivated by their large atomic size, which promotes in-plane ordering, as previously observed for i-MAX phases.^22,30 Meanwhile, A = Al and X = C are selected due to their prevalence in experimentally known MAX phases with Al being a commonly etched element during MXene synthesis.^3,31–34 This choice ensures relevance to experimentally viable MAX compositions and their 2D derivatives.

The predicted stability of these phases provides valuable guidance for synthesis experiments. The precise ordering of multiple elements across different layers opens new possibilities for tuning M–A (outer layer) and M–X (inner layer) bonding separately, enabling the design of materials with tailored properties. Our goal is to identify novel super-ordered s-MAX phases that expand the functionality of traditional MAX phases, provide a platform for designing advanced materials, and allow for novel parent precursor materials for the derivation of future MXenes.

2. Methods

2.1. Computational details

All calculations were performed within the framework of density functional theory (DFT) as implemented in Vienna Ab initio Software Package (VASP) version 5.4.4,^35–37 with the projector augmented wave (PAW) method^38–40 and a plane wave basis set expanded to a kinetic energy cutoff of 520 eV. The Perdew–Burke–Ernzerhof (PBE) functional⁴⁰ was used to describe the electron exchange–correlation effects, and all PBE potentials used are listed in Table S1.† We used a Γ-centered k-point sampling, with a density of 0.1 Å⁻¹.⁴¹ All calculations were spin-polarized with an initial magnetic moment of three for the metal sites in a ferromagnetic (FM) spin configuration. Anti-ferromagnetic (AFM) spin configurations were also considered for selected s-MAX phases. Structures were fully relaxed in terms of volume, shape, and atomic positions using an energy convergence of 10⁻⁷ eV per atom and a force convergence of 0.001 eV Å⁻¹.

Phonon dispersion spectra were calculated using the finite displacement method as implemented in Phonopy,⁴² with atomic displacements of 0.01 Å, for supercells corresponding to a 2 × 2 × 1 expansion of the primitive cells (e.g., 192 atoms for the 413 s-MAX phase). Resulting forces were computed using VASP with the aforementioned settings and Phonopy was then used to calculate the force constants and phonon dispersion relations along high-symmetry paths.

For thermodynamic phase stability predictions of a targeted phase (composition), the set of most competing phases, known as equilibrium simplex, is identified among all competing phases using a linear optimization procedure.^43,44 This approach has been proven successful in confirming already experimentally synthesized materials as well as predicting the existence of new ones.^3,17,20–22 The stability of an s-MAX phase is quantified in terms of the formation enthalpy, ΔH_cp, by comparing its energy, E[s-MAX], to the energy of the equilibrium simplex, E(equilibrium simplex), at a given composition according to the following equation:

ΔH_cp = E[s-MAX] − E(equilibrium simplex). (1)

A phase is considered stable if ΔH_cp < 0, indicating a phase being energetically favored as compared to decomposition into its competing phases, whereas ΔH_cp > 0 indicates that decomposition is more energetically favourable. The complete set of competing phases considered herein encompass those found in the Materials Project database (v2021.05.13),⁴⁵ as well as ternary M_n+1AX_n phases (n = 1–3)³ and quaternary MAX phases with in-plane order (n = 1), out-of-plane order (n = 2 and 3) and solid solution disorder (n = 1, 2, and 3).^21,22 In addition, different metal carbides with disorder on the metal site and hypothetical quinary 312 and 413 s-MAX phases considered in this work have also been accounted for as competing phases; see Fig. S1c† for a schematic illustration of the 312 s-MAX phase.

Furthermore, to model configurational disorder on the M1 and M3 sites in s-MAX (Fig. 1c) and on all M-sites in quinary traditional 312 and 413 MAX phases, we herein use the special quasi-random structures (SQS) method⁴⁶ to generate supercells with metals distributed in a disordered fashion. The SQS approach compares the correlation functions of a finite unit cell to those of an infinite, ideal random system, providing structures that closely approximate near-random arrangements of metals. When T ≠ 0 K, the contribution from configurational entropy for a disordered distribution of M1 + M3 (s-MAX phase with partial disorder) and M1 + M2 + M3 (MAX phase with disorder) will decrease the Gibbs free energy, ΔG^disorder_cp, as approximated by

ΔG^disorder_cp[T] = ΔH^disorder_cp − TΔS, (2)

where T is the temperature and ΔS is the entropic contribution. The configurational entropy when assuming an ideal solid solution of metals i on the M-sites is given bywhere k_B is the Boltzmann constant (in eV K⁻¹), w is the fraction of sites with respect to the entire supercell on which disorder is modelled upon, index m represents the sublattice, a_m is the number of sites of sublattice m, N_m is the total number of different metals in sublattice m, and x^m_i is the concentration of metal i being randomly distributed on sublattice m. For a 413 s-MAX phase with partial disorder of M1 and M3 in a 2 : 3 ratio in a 240-atom supercell, w = 0.417, a_M1 = 40, a_M3 = 60, x₁^M1 = 0.4, and x₁^M3 = 0.6. A 413 MAX phase with disorder of three metals (M1, M2 and M3) with a 4 : 2 : 6 ratio in a 192 atom supercell has w = 0.5, a_M1 = 32, a_M2 = 16, a_M3 = 48, x₁^M1 = 0.333, x₁^M2 = 0.167, and x₁^M3 = 0.5.

3. Results and discussion

The super-ordered MAX phase (s-MAX) synthesized to date is composed of three metals (M1, M2, and M3) in a 4 : 2 : 6 ratio. This corresponds to an M1_4/3M2_2/3M3₂AX₃ composition, alternatively denoted M1₄M2₂M3₆A₃X₉ in the integer form, due to its inherent chemical order. The ground state crystal structure is composed of four metal layers, resembling an i-MAX phase with an in-plane order of M1 and M2 in the outer metal layers next to the A-layers and an o-MAX phase with an out-of-plane order of M1 + M2 and M3 metals in its outer and inner metal layers, respectively. Also note that the in-plane order in the outer metal layer also has an impact on the structure of the A-layer. M2, which has a larger atomic size than M1, is shifted towards the A-layer, resulting in a Kagomé-like arrangement of the A-layer. This has previously been demonstrated for i-MAX phases.¹⁸ The space group symmetry for the 413 s-MAX is P6₃/mcm (no. 193).

From a computational perspective, it is not possible to a priori know how the mixing of three metals (M1, M2, and M3) will be distributed in the MAX phase. Examples thereof include the super-ordered structure (Fig. 2a) or having the metals completely mixed and randomly distributed across all metal sites in a 413 MAX phase (Fig. 2c). Considering the large number of known solid solution MAX phases,³ an intermediate hybrid with in-plane order of M2 in the outer layer while M1 and M3 form a solid solution is also a potential configuration (Fig. 2b). These three structures have the same composition, but have a different distribution of M1, M2, and M3.

Fig. 2 Different distributions of metals M1, M2, and M3 in a 413 MAX phase. (a) Combined in- and out-of-plane order in a 413 s-MAX with the space group symmetry P6₃/mcm, (b) s-MAX with in-plane order of M2 in the metal layer next to A and with disorder of M1 + M3 on the other metal sites with the space group symmetry P6₃/mcm, and (c) complete disorder of M1, M2, and M3 on metal sites in a 413 MAX phase with the space group symmetry P6₃/mmc.

The thermodynamic stability has been systematically investigated for the three models depicted in Fig. 2 with M1 and M3 = {Sc, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe}, M2 = {Sc, Y}, A = Al, and X = C. The choice of M2 = Sc and Y is motivated by their large atomic size needed to promote in-plane order as exemplified in i-MAX phases,^22,30 while A = Al and X = C are motivated by their prevalence in experimentally known MAX phases. Aluminium is one of the most common A-site elements in MAX phases and is frequently etched during the synthesis of MXenes, making Al-based s-MAX phases a well-established starting point for both theoretical and experimental investigations.^31–34 Similarly, carbon is the dominant X-site element in known MAX phases, leading to the prevailing study of carbide-based MAX phases and MXenes.³ While alternative A-site elements (such as Si or Ga) and X-site elements (such as N, O or B) exist, our focus on Al and C ensures direct relevance to experimentally viable MAX compositions and their 2D derivatives.

We choose to evaluate the stability at a temperature of 2000 K motivated by the typical temperature used for powder synthesis of MAX phase materials. Since the synthesis is performed at T > 0 K, typically in the range from 1000 to 1800 °C (1273 to 2073 K) for MAX phases, the impact from configurational entropy to the Gibbs free energy needs to be considered for all structures modelled with a disordered distribution. This has been considered for a solid-solution of M1 + M3 while having M2 ordered in-plane in outer layers s-MAX with partial disorder as shown in Fig. 2b and M1 + M2 + M3 (MAX phase with disorder as shown in Fig. 2c) as well as for competing solid-solution MAX phases such as (M1_0.67M3_0.33)₂AlC, (M1_0.67M3_0.33)₃AlC₂, and (M1_0.5M3_0.5)₄AlC₃. Accounting for configurational entropy at finite temperature allows for the prediction of whether an ordered or disordered distribution of metals is to be expected upon synthesis. This has previously been demonstrated as a most valid approach, used to confirm experimental observations of chemical order and disorder for a range of MAX phases.^21,22

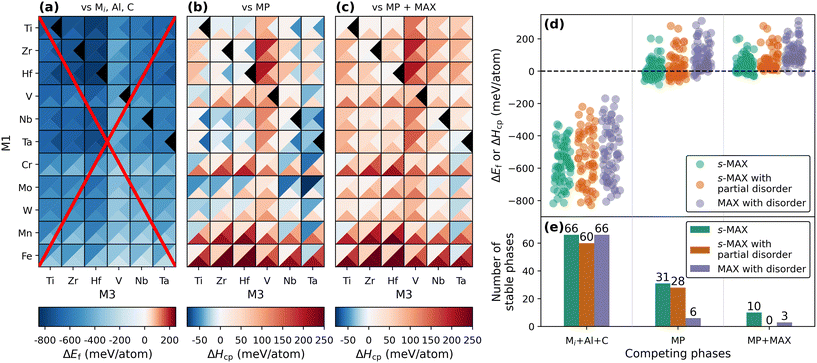
The stability heatmap in Fig. 3 shows the calculated stability for both s-MAX (upper left triangle) and s-MAX with partial disorder (lower right triangles) at 2000 K, having M2 = Sc (panel a) or Y (panel b). Note that the stability analysis performed includes all possible competing phases other than the composition in focus. This means that for a given composition, s-MAX, s-MAX with partial disorder, and MAX with disorder can appear to be stable in the figure, though the one of lowest energy is the one we predict to be possible to synthesize. Tables S2 and S3† include data used for the preparation of Fig. 3, along with complementary data for corresponding solid solution MAX phases (Fig. 2c). Blue indicates stable phases (ΔH_cp or ΔG^disorder_cp < 0). The identified competing phases for each composition can be found in Tables S2 (M2 = Y) and S3 (M2 = Sc).† Note that the stability for s-MAX has been evaluated for all combinations of M1 and M3 whereas s-MAX with partial disorder and MAX phase with disorder has only been considered for a subset of combinations of M1 and M3. This is motivated by the observation that whenever ΔH_cp is well above zero (the phase is far from stable) for s-MAX, the evaluated corresponding stability for disordered structures is not much more stable. Combinations not considered with respect to (partial) disorder are indicated by tringles coloured in black.

Fig. 3 Stability heatmap evaluated at 2000 K for 413 MAX phases upon mixing metals M1, M2, and M3 in a 2 : 1 : 3 ratio with (a) M2 = Sc and (b) M2 = Y. For a given combination of M1 and M3, the upper left triangles indicate the stability for combined in- and out-of-plane ordered s-MAX, the right triangles indicate the stability for s-MAX with partial disorder, having in-plane order of M2 in the outer metal layer combined with disorder of M1 + M3, and the bottom triangles indicate the stability for MAX with disorder of M1, M2, and M3. Black triangles represent combinations of M1, M2 and M3 not considered.

The predicted stability for s-MAX phases is similar for both M2 = Sc and Y. There are 10(1) stable s-MAX phases for M2 = Y(Sc), typically for M1 = Cr, Mo, W, and Mn combined with M3 = Ti, Nb, and Ta. Among these, we find the recently synthesized s-MAX phase Mo₄Y₂Nb₆Al₃C₉ (M1 = Mo, M3 = Nb) at ΔH_cp = −9 meV per atom, predicted to be stable when compared to the identified set of most competing phases Mo₄Y₂Nb₃Al₃C₆ (312 s-MAX phase, see further details below), Nb₆C₅, and C. This is in contrast to M3 = Sc, Y, Cr, Mo, W, Mn, or Fe, for which all phases are found far from stable. Note that the inner metal layers in the 413 MAX phase structure are fcc stacked with carbon, and common for these M3 metals is that neither of them forms a stable binary rock-salt MC structure, indicating a lack of preference for residing within the MAX phase. This observation aligns with what has been found for o-MAX phases.^20,21,25 Detailed structural information for stable s-MAX with M2 = Y or Sc is found in Tables S4† (M2 = Sc) and S5† (M2 = Y). In addition, only one stable s-MAX phase with partial disorder (order of M2 and disorder of M1 and M3, see the schematic in Fig. 2b) is identified for Sc₄Y₂Nb₆Al₃C₉. Stable MAX phases with full M-site disorder are found in 3(13) systems. The number of stated stable phases provided in the text above does not take into consideration whether multiple configurations of the same composition are found stable or not, since they are mutually excluded as competing phases (as discussed above). Only accounting for the configurations being the most stable reduces the number of stable phases to 9(1) s-MAX phases, 1(0) s-MAX phases with partial disorder, and 3(13) MAX phases with disorder for M2 = Y(Sc).

A closer look at the identified set of most competing phases in Tables S2 and S3† reveals that many sets include i- and o-MAX phases, MAX phases with disorder on the metal site, and s-MAX and s-MAX phases with partial disorder of M1 and M3. This is notable, considering that many of the quaternary MAX phases considered competing phases are found stable under the constraint of their corresponding stoichiometry (see Fig. S2–S4†) and have been synthesized, e.g., Mo_4/3Y_2/3AlC (Mo₄Y₂Al₃C₃ in integer notation) with reported theoretical stability of −101 meV per atom.¹⁸

Although this work primarily considers ferromagnetic (FM) ordering on a large scale, anti-ferromagnetic (AFM) ordering may, in fact, have a lower energy. To test the impact from different magnetic ordering, we selected s-MAX phases with M1 = Cr, Mn or Fe, M2 = Y, also fulfilling ΔH_cp < 25 meV per atom. Seven different collinear AFM spin configurations within the unit cell were applied; see Fig. S5† for details and Table S6† for corresponding results. Seven out of nine s-MAX phases were found with an AFM of lower energy than FM. However, the decrease in energy for various AFM configurations ranged between 0.1 and 1.4 meV per atom, which is small and considered close to degenerate. Based on this, we conclude that magnetic ordering has a minimal impact on energy and, in turn, stability.

Dynamic stability has been investigated for 12 s-MAX phases with M2 = Y. This choice is motivated by Y having a larger atom size compared to Sc, which in turn may have a larger impact on the structure and stability with respect to lattice vibrations. Fig. S6–S11† shows the calculated phonon dispersion spectra for s-MAX phases that are non-magnetic. All six are concluded to be dynamically stable, as indicated by the absence of imaginary frequencies. For the six s-MAX phases with a magnetic element on M1 (Cr, Mn or Fe), considering only FM ordering would have led to multiple s-MAX phases being dynamically unstable. However, when also accounting for the two magnetic ordering of lowest energy in Table S6,† at least one magnetic order per composition was found to be dynamically stable, as shown in Fig. S12–S28.† From this, we conclude that all 12 s-MAX phases are dynamically stable and that magnetic ordering has an impact on the dynamical stability.

The effect from entropic considerations shown in Fig. 3 is demonstrated when comparing to the phase stability evaluated at 0 K, i.e., without any configurational entropy considered for s-MAX with partial disorder and competing solid-solution MAX phases with metal site disorder, shown in Fig. S29.† Noteworthy is that at 0 K, most stable phases are s-MAX, 16 for M2 = Y and 11 for M2 = Sc. There are only 2 additional stable phases with either partial disorder or complete disorder.

Similar to the super-ordered 413 s-MAX phases, in-plane and out-of-plane order can be achieved for the 312 MAX phase structure. This is illustrated in Fig. S1c† where the three metals (M1, M2, and M3) have a 4 : 2 : 3 ratio that leads to a M1_4/3M2_2/3M3AX₂ composition (M1₄M2₂M3₃A₃X₆ in the integer form), due to its inherent chemical order. Its ground state crystal structure is composed of three metal layers, like an i-MAX phase with in-plane order of M1 and M2 in the outer metal layers next to the A-layers and like an o-MAX phase with M1 + M2 in the outer metal layers and M3 in the inner metal layer. Relaxation of the 312 s-MAX phase results in a Cmcm (no. 63) space group symmetry. Also note that the in-plane order in the outer metal layer impacts the structure of the A-layer, which is no longer hexagonal, like in traditional MAX phases, but more Kagomé-like.

Thermodynamic stability for 312 s-MAX, s-MAX with partial disorder (disorder of M1 and M3), and MAX with disorder has been systematically investigated for M1 and M3 = {Sc, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe}, M2 = {Sc, Y}, A = Al, and X = C. Again, the stability analysis performed includes all possible competing phases other than the specific composition in focus. This means that s-MAX, s-MAX with partial disorder, and MAX with disorder can all appear to be stable in the figure, though the one with the lowest energy is the one predicted to be synthesizable. Calculated energies and identified competing phases are provided in Tables S7 and S8.† The stability for 312 s-MAX has been evaluated for all combinations of M1 and M3 whereas s-MAX with partial disorder and MAX with disorder has only been considered for a subset of combination of M1 and M3, in line with the approach used for 413 s-MAX (above) This is motivated by the observation that when ΔH_cp is well above zero for s-MAX, the corresponding stability for disordered MAX phase structures are not significantly different. Combinations not considered with respect to disorder are indicated by tringles coloured in black.

Fig. 4 shows the calculated stability for both s-MAX (upper left triangles) and s-MAX with partial disorder (lower right triangles) at 2000 K, for M2 = Sc (panel a) or Y (panel b). Stable phases are indicated by blue colours (ΔH_cp or ΔG_cp^disorder < 0). There are 14(4) stable s-MAX phases with M2 = Y(Sc) and an additional 7(6) stable s-MAX phases with partial disorder and 0(25) stable MAX phases with disorder. The stability for 312 s-MAX shows both similar and different outcomes when compared to 413 s-MAX as shown in Fig. 3. Like 413, it is favourable to have M3 from Group 4 (Ti, Zr, Hf) or Group 5 (V, Nb, Ta). In addition, having Sc in the inner metal layer (M3) is also found favourable when combined with M1 from Group 5 (V, Nb, Ta) or Group 6 (Cr, Mo, W). This aligns with the predicted stable and synthesized Mo₂ScAlC₂ o-MAX phase with Sc in the inner layer (Fig. S1b†).⁴⁷ Another difference compared to the 413 system is that many 312 s-MAX phases with partial disorder are found stable, most notable for M2 = Y (Fig. 4b). It is also worth noting the presence of many stable MAX phases with disorder for M2 = Sc. Accounting for the configuration being most stable at a given composition M1, M3 and M2 = Y(Sc), the number of stable phases is reduced to 14(2) s-MAX phases, 5(3) s-MAX phases with partial disorder, and 0(24) stable MAX phases with disorder (again taking into account that they are mutually excluded as competing phases in their respective evaluation in Fig. 4, as discussed above). It should once again be noted that many 312 s-MAX phases are found stable despite having i- and o-MAX phases, quaternary MAX phases with metal site disorder, and 413 s-MAX and 413 s-MAX phases with partial disorder as competing phases (see Tables S7 and S8†). Noteworthy is that many of these 312 s-MAX phases also turn out as highly competing phases for the 413 s-MAX phases as seen in Tables S1 and S2.† Detailed structural information for stable 312 s-MAX with M2 = Y and Sc are provided in Tables S9† (M2 = Sc) and S10† (M2 = Y).

Fig. 4 Stability heatmap evaluated at 2000 K for 312 MAX phases upon mixing metals M1, M2, and M3 in a 4 : 2 : 3 ratio with (a) M2 = Sc and (b) M2 = Y. For a given combination of M1 and M3, the upper left triangles indicate the stability for combined in- and out-of-plane ordered s-MAX, the right triangles indicate the stability for s-MAX with partial disorder, having in-plane order of M2 in the outer metal layer combined with disorder of M1 + M3, and the bottom triangles indicate the stability for MAX with disorder of M1, M2, and M3. Black triangles represent combinations of M1, M2 and M3 not considered.

A closer look at the outcome of the stability shown in Fig. 3 and 4 reveals that there are qualitative differences between which combinations of M1, M2, and M3 lead to stable phases. Among the 26 stable s-MAX phases, 23 have M2 = Y. Also common for stable s-MAX is that M1 is typically from Group 6 (16 phases) or 5 (6 phases) combined with M3 from Group 4 (7 phases) or 5 (14 phases). Here, we note that this combination of metals is in line with observations and explanations reported for o-MAX phases, i.e., having a metal in the inner layer (M3) that can form a stable binary rock-salt MC structure while the outer layer (M1) has a metal with small electronegativity.^20,21,25 This can be compared with stable s-MAX phases with partial disorder, where 13 out of 14 have M2 = Sc, whereas, for MAX phases with full disorder, 25 of 41 have M2 = Sc. The major difference in elemental combinations when compared to ideal s-MAX is that M1 and M3 are typically a combination of metals from Group 4 (Ti, Zr, Hf) and 5 (V, Nb, Ta). Here, the disorder of metals is thus favoured when the metals have similar atomic size and electronegativity. The reason why M2 = Y dominates s-MAX phases with partial disorder whereas M2 = Sc dominate MAX with disorder is related to their atomic sizes. Since Sc is smaller than Y (1.62 compared to 1.80 Å), it can more easily mix with M1 and M3 without imposing too much internal stress on the structure. This is also the argument for the many Y-based s-MAX phases with partial disorder where the large Y atom maintains the in-plane order in the outer layers while M1 and M3 are mixed.

One purpose for calculating the stability of novel and yet-to-be-synthesized compounds, as shown in Fig. 3 and 4, is to narrow down the set of possible elemental combinations and guide synthesis attempts towards compositions and structures being likely to be achieved experimentally. However, the selection of competing phases when performing stability analysis does play a major role in the correlation between predicted phase stability and the outcome of the experiments. In Fig. 5, we demonstrate this for 413 s-MAX phases with M2 = Y when choosing three different sets of competing phases. In total, 66 unique compositions have been considered; 66 s-MAX phases, 60 s-MAX phases with partial disorder (M1 ≠ M3), and 66 MAX phases with disorder.

Fig. 5 Predicted phase stability depending on the choice of competing phases. (a) Formation energy ΔE_f including only single element competing phases, and formation enthalpy ΔH_cp with competing phases from (b) Materials Project and (c) Materials Project and additional MAX phase structures/compositions not currently present in the database. Data evaluated for 413 MAX phases upon mixing metals M1, M2 = Y, and M3 in a 4 : 2 : 3 ratio, with contribution from configurational entropy at 2000 K. Upper left triangles show stability for s-MAX phases, the right triangles indicate the stability for s-MAX with partial disorder, having in-plane order of M2 in the outer metal layer combined with disorder of M1 + M3, and the bottom triangles indicate the stability for MAX with disorder of M1, M2, and M3. Black triangles represent combinations of M1, M2 and M3 not considered. Comparison of (d) calculated stability and (e) the number of predicted stable phases for different sets of competing phases.

In the first case, illustrated in Fig. 5a, we only consider the single elements as competing phases. This gives the formation energy, ΔE_f. Note that all compositions and distributions of M1, M2, and M3 turn out to be stable (ΔE_f < 0), as indicated by the blue colour, when compared to the respective elements in their ground state crystal structure. The most stable s-MAX phases have ΔE_f < −800 meV per atom, whereas the least stable phases, but still stable, are found around ΔE_f ≈ −200 meV per atom. Obviously, the result of these predictions is far from realistic and thus a poor guiding indicator for synthesizable materials.

Next, we consider competing phases from the Materials Project database alone, resulting in a formation enthalpy ΔH_cp (see Fig. 5b). The number of stable phases with ΔH_cp < 0 is not only drastically reduced to less than 50% of the compositions and configurations investigated, 31 s-MAX phases, 28 s-MAX phases with partial disorder, and six MAX phases with full disorder, but the predicted range of ΔH_cp goes from −82 meV per atom for Mo₄Y₂Ta₆Al₃C₉ s-MAX to +310 meV per atom for the (Hf_0.5Y_0.167Fe_0.33)₂AlC MAX phase with full M-site disorder. Among the identified set of most competing phases, we find, e.g., intermetallics, perovskites, and ternary MAX phases (those being included in Materials Project). Calculating ΔH_cp with competing phases from Materials Project is a far more valid approach than ΔE_f, but be aware that it may still result in an overestimation of the calculated stability due to relevant competing phases being missing in the database.

In the final comparison, competing phases from the Materials Project and additional MAX phase-related structures not currently listed in Materials Project are considered, such as all ternary MAX phases, quaternary MAX phases with chemical order and disorder, and quinary 312 s-MAX phases. Corresponding formation enthalpy ΔH_cp, shown in Fig. 5c, reveals that the number of identified stable phases has decreased further to 10 s-MAX phases, no s-MAX phases with partial disorder, and three MAX phases with disorder. The most stable phase is Mo₄Y₂Ta₆Al₃C₉ at −27 meV per atom. The main difference in stability when comparing Fig. 5b and c originates from the inclusion of additional competing phases, such as i-MAX, o-MAX, and s-MAX as well as MAX, s-MAX and metal carbides with full disorder on the metal site. This is particularly apparent when looking at compositions with ΔH_cp < 0 in Fig. 5b and comparing these to the same compositions in Fig. 5c. Note that the scale of the colourbar is the same for ΔH_cp in panels b and c.

With Fig. 5, we want to demonstrate that formation energy is a very poor indicator of phase stability and not useful for the identification of the most promising materials for synthesis. In the example presented above, this is particularly evident, as all phases investigated were predicted stable based on this approach. This is further supported by previous work where 81.8% (or 2210 compositions) out of 2702 quaternary 211 MAX phases fulfilled ΔE_f < 0,²² a number reduced to merely 189 compositions when compared to all identified competing phases (ΔH_cp < 0). Note that among these 189 stable MAX phase compositions, we find 13 synthesized i-MAX phases as well as more than 30 synthesized M₂AX phases with metal site disorder. This further supports the argument of performing phase stability calculations by considering, as far as possible, a complete set of competing phases, as this will not only provide valuable insights into strong competing phases but also act as a filter to identify those phases being most promising for experimental verification. This challenge becomes particularly relevant when evaluating the stability of s-MAX phases, as their formation enthalpy is inherently linked to the stability of their competing phases.

The s-MAX phases predicted as stable in Fig. 3, 4, and 5c exhibit calculated formation enthalpies in the range −27 ≤ ΔH_cp < 0, including the synthesized Mo₄Y₂Nb₆Al₃C₉ (ΔH_cp = −9 meV per atom). These values may initially seem to indicate only marginal stability, especially when compared to i- and o-MAX phases in Fig. S2–S4† and in Ref. 22,48,49. However, it is crucial to examine the context of their competing phases (Tables S2, S3, S7 and S8†) that often include highly stable, experimentally known i-MAX and o-MAX phases (summarized in Tables S12–S14†), such as Mo₄Y₂Al₃C₃ (ΔH_cp = −99 meV per atom), Cr₄Sc₂Al₃C₃ (ΔH_cp = −98 meV per atom), V₄Zr₂Al₃C₃ (ΔH_cp = −48 meV per atom), Mo₂ScAlC₂ (ΔH_cp = −13 meV per atom), and Mo₂Ti₂AlC₃ (ΔH_cp = −18 meV per atom).

Since the formation enthalpy of a phase is determined relative to its competing phases, the stability of s-MAX phases is inherently influenced by the presence of their highly stable, lower-order MAX phases. As the number of elements in a compound increases, the number and stability of its potential decomposition products (competing phases) also increase. Consequently, the ΔH_cp of a complex compound like s-MAX is determined relative to a baseline set by these often very stable, simpler competing phases. Therefore, a direct comparison between the ΔH_cp values of compositionally simpler i- and o-MAX phases and the more complex s-MAX phases is problematic. This is a fundamental limitation because the formation enthalpy is always evaluated relative to the most stable competing phases, which often contain fewer elements and therefore appear to be more stable. Thus, rather than directly comparing formation enthalpy values between different MAX phase types, the stability of a given s-MAX phase should be assessed by carefully analysing its specific set of competing phases, as identified in Tables S2, S3, S7 and S8.†

4. Conclusion

This study systematically explores the stability of combined in-plane (M1 and M2 in a 2 : 1 ratio in outer metal layers) and out-of-plane ordering (M3 in inner metal layers) in super-ordered s-MAX phases, uncovering critical trends that influence their formation. A total of 26 s-MAX phases have been identified as stable, including the recently reported Mo₄Y₂Nb₆Al₃C₉. Remarkably, these phases remain stable despite strong competition from highly stable and well-known i-MAX, o-MAX, and traditional MAX phases and metal carbides with chemical disorder. Additionally, 9 s-MAX phases with partial disorder, i.e., with M1 and M3 atoms exhibiting disorder, have also been identified as stable. Noteworthy is that 29 out of 25 stable phases have M2 = Y. The findings reveal that ordered s-MAX phases, M1₄M2₂M3₃Al₃C₆ (312) and M1₄M2₂M3₆Al₃C₉ (413), are favoured when M3 in the inner layer is a metal with a corresponding stable binary rock-salt MC structure while M1 in the outer layer is a metal with small electronegativity and a significantly smaller atomic size than M2. s-MAX with partial disorder, that is, with M2 in-plane order in the outer layer combined with disorder of M1 and M3 across all metal layers, is found favoured for combinations when M1 and M3 are from Group 4 (Ti, Zr, Hf) and 5 (V, Nb, Ta). These insights pave the way for designing s-MAX phases with tuneable properties, enabling precise control over their composition and structure. Moreover, the stability of these phases highlights their potential as precursor materials for conversion into high-performance MXenes from an enhanced elemental playground, thus opening new opportunities in advanced material development.

Data availability

The data supporting this article have been included in the paper or as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Knut and Alice Wallenberg (KAW) Foundation through a scholar grant (2019.0433) and project funding (2020.0033), and the Swedish Government Strategic Research Area in Materials Science on Advanced Functional Materials at Linköping University, Faculty Grant SFOMat-LiU 2009-00971. The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at the National Supercomputer Centre (NSC) partially funded by the Swedish Research Council through grant agreement no. 2022-06725.

References

1. M. W. Barsoum, The MN+1AXN phases: A new class of solids; Thermodynamically stable nanolaminates, Prog. Solid State Chem., 2000, 28(1–4), 201–281.
2. N. Kubitza, et al., Extending the Chemistry of Layered Solids and Nanosheets: Chemistry and Structure of MAX Phases, MAB Phases and MXenes, ChemPlusChem, 2023, 88(8), e202300214.
3. M. Dahlqvist, M. W. Barsoum and J. Rosen, MAX phases – Past, present, and future, Mater. Today, 2024, 72, 1–24.
4. M. Naguib, et al., Two-dimensional nanocrystals produced by exfoliation of Ti3AlC2, Adv. Mater., 2011, 23(37), 4248–4253.
5. A. VahidMohammadi, J. Rosen and Y. Gogotsi, The world of two-dimensional carbides and nitrides (MXenes), Science, 2021, 372(6547), eabf1581.
6. H. Rohde and H. Kudielka, Strukturuntersuchungen an Carbosulfiden von Titan und Zirkon, Z. Kristallogr., 1960, 114(1–6), 447–456.
7. W. Jeitschko, H. Nowotny and F. Benesovsky, Kohlenstoffhaltige ternäre Verbindungen (V-Ge-C, Nb-Ga-C, Ta-Ga-C, Ta-Ge-C, Cr-Ga-C und Cr-Ge-C), Monatsh. Chem., 1963, 94(5), 844–850.
8. W. Jeitschko, H. Nowotny and F. Benesovsky, Die H-Phasen Ti2InC, Zr2InC, Hf2InC und Ti2GeC, Monatsh. Chem., 1963, 94(6), 1201–1205.
9. W. Jeitschko, H. Nowotny and F. Benesovsky, Carbides of formula T2MC, J. Less-Common Met., 1964, 7(2), 133–138.
10. W. Jeitschko, H. Nowotny and F. Benesovsky, Ternäre Carbide und Nitride in Systemen: Übergangsmetall-Metametall-Kohlenstoff (Stickstoff), Monatsh. Chem. Verw. Teile Anderer Wiss, 1964, 95(1), 156–157.
11. M. Naguib, et al., New Solid Solution MAX Phases: (Ti0.5,V0.5)3AlC2, (Nb0.5,V0.5)2AlC, (Nb0.5,V0.5)4AlC3 and (Nb0.8,Zr0.2)2AlC, Mater. Res. Lett., 2014, 2(4), 233–240.
12. M. Han, et al., Tailoring Electronic and Optical Properties of MXenes through Forming Solid Solutions, J. Am. Chem. Soc., 2020, 142(45), 19110–19118.
13. T. Cabioch, et al., Tailoring of the thermal expansion of Cr2(Alx,Ge1−x)C phases, J. Eur. Ceram. Soc., 2013, 33(4), 897–904.
14. Y. Li, et al., A-site alloying-guided universal design of noble metal-based MAX phases, Matter, 2024, 7(2), 523–538.
15. T. Scabarozi, et al., Electronic and thermal properties of Ti3Al(C0.5,N0.5)2, Ti2Al(C0.5,N0.5) and Ti2AlN, J. Appl. Phys., 2008, 104(7), 073713 1–6.
16. T. Zhang, et al., Synthesis of Three Families of Titanium Carbonitride MXenes, J. Am. Chem. Soc., 2023, 145(41), 22374–22383.
17. Q. Tao, et al., Two-dimensional Mo1.33C MXene with divacancy ordering prepared from parent 3D laminate with in-plane chemical ordering, Nat. Commun., 2017, 8, 14949.
18. M. Dahlqvist, et al., Prediction and synthesis of a family of atomic laminate phases with Kagomé-like and in-plane chemical ordering, Sci. Adv., 2017, 3(7), e1700642.
19. Z. Liu, et al., Crystal structure and formation mechanism of (Cr2/3Ti1/3)3AlC2 MAX phase, Acta Mater., 2014, 73, 186–193.
20. B. Anasori, et al., Experimental and theoretical characterization of ordered MAX phases Mo2TiAlC2 and Mo2Ti2AlC3, J. Appl. Phys., 2015, 118(9), 094304.
21. M. Dahlqvist and J. Rosen, Predictive theoretical screening of phase stability for chemical order and disorder in quaternary 312 and 413 MAX phases, Nanoscale, 2020, 12(2), 785–794.
22. M. Dahlqvist and J. Rosen, The rise of MAX phase alloys – large-scale theoretical screening for the prediction of chemical order and disorder, Nanoscale, 2022, 14(30), 10958–10971.
23. J. Yang, et al., Novel W-based in-plane chemically ordered (W2/3R1/3)2AlC (R = Gd, Tb, Dy, Ho, Er, Tm and Lu) MAX phases and their 2D W1.33C MXene derivatives, Carbon, 2021, 183, 76–83.
24. Q. Tao, et al., Atomically Layered and Ordered Rare-Earth i-MAX Phases: A New Class of Magnetic Quaternary Compounds, Chem. Mater., 2019, 31(7), 2476–2485.
25. B. Anasori, et al., Two-dimensional, ordered, double transition metals carbides (MXenes), ACS Nano, 2015, 9(10), 9507–9516.
26. E. N. Caspi, et al., Ordering of (Cr,V) layers in nanolamellar (Cr0.5V0.5)n+1AlCn compounds, Mater. Res. Lett., 2015, 3(2), 100–106.
27. M. Dahlqvist and J. Rosen, Order and disorder in quaternary atomic laminates from first-principles calculations, Phys. Chem. Chem. Phys., 2015, 17, 31810–31821.
28. B. C. Wyatt, et al., Design of Atomic Ordering in Mo2Nb2C3Tx MXenes for Hydrogen Evolution Electrocatalysis, Nano Lett., 2023, 23(3), 931–938.
29. B. Ratzker, et al., Synthesis of Ti1−xWx Solid Solution MAX Phases and Derived MXenes for Sodium-Ion Battery Anodes, Adv. Funct. Mater., 2024, 2406499.
30. H. Guo, et al., Rare-Earth (R) In-Plane Ordering in Novel (Mo, R, Nb)4AlC3 Quinary o-MAX Nanolaminates and their 2D Derivatives, Adv. Mater., 2024, 36(36), 2404466.
31. X. Li, et al., MXene chemistry, electrochemistry and energy storage applications, Nat. Rev. Chem., 2022, 6(6), 389–404.
32. B. Anasori and M. Naguib, Two-dimensional MXenes, MRS Bull., 2023, 48, 238–244.
33. J. Zhou, et al., Atomic Scale Design of MXenes and Their Parent Materials — From Theoretical and Experimental Perspectives, Chem. Rev., 2023, 123(23), 13291–13322.
34. A. Lakmal, P. B. Thombre and C. E. Shuck, Solid-Solution MXenes: Synthesis, Properties, and Applications, Acc. Chem. Res., 2024, 57(20), 3007–3019.
35. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B, 1993, 47(1), 558–561.
36. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50.
37. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54(16), 11169–11186.
38. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994, 50(24), 17953–17979.
39. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59(3), 1758–1775.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
41. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13(12), 5188–5192.
42. A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B, 2008, 78(13), 134106.
43. M. Dahlqvist, et al., Phase stability of Ti2AlC upon oxygen incorporation: A first-principles investigation, Phys. Rev. B, 2010, 81(2), 024111.
44. M. Dahlqvist, B. Alling and J. Rosén, Stability trends of MAX phases from first principles, Phys. Rev. B, 2010, 81(22), 220102.
45. A. Jain, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002.
46. A. Zunger, et al., Special quasirandom structures, Phys. Rev. Lett., 1990, 65(3), 353–356.
47. R. Meshkian, et al., Theoretical stability and materials synthesis of a chemically ordered MAX phase, Mo2ScAlC2, and its two-dimensional derivate Mo2ScC2 MXene, Acta Mater., 2017, 125, 476–480.
48. M. Dahlqvist and J. Rosen, Chemical order or disorder – a theoretical stability expose for expanding the compositional space of quaternary metal borides, Mater. Adv., 2022, 3, 2908–2917.
49. A. M. Malik, J. Rohrer and K. Albe, Theoretical study of thermodynamic and magnetic properties of transition metal carbide and nitride MAX phases, Phys. Rev. Mater., 2023, 7(4), 044408.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00672d

---