Simulation of the crystallization process of Ge₂Sb₂Te₅ nanoconfined in superlattice geometries for phase change memories

Abstract

Phase change materials are the most promising candidates for the realization of artificial synapses for neuromorphic computing. Different resistance levels corresponding to analogic values of the synapsis conductance can be achieved by modulating the size of an amorphous region embedded in its crystalline matrix. Recently, it has been proposed that a superlattice made of alternating layers of the phase change compound Sb₂Te₃ and of the TiTe₂ confining material allows for a better control of multiple intermediate resistance states and for a lower drift with time of the electrical resistance of the amorphous phase. In this work, we consider the substitution of Sb₂Te₃ with the Ge₂Sb₂Te₅ prototypical phase change compound that should feature better data retention. By exploiting molecular dynamics simulations with a machine learning interatomic potential, we have investigated the crystallization kinetics of Ge₂Sb₂Te₅ nanoconfined in geometries mimicking Ge₂Sb₂Te₅/TiTe₂ superlattices. It turns out that nanoconfinement induces a slight reduction in the crystal growth velocities with respect to the bulk, but also an enhancement of the nucleation rate due to heterogeneous nucleation. The results support the idea of investigating Ge₂Sb₂Te₅/TiTe₂ superlattices for applications in neuromorphic devices with improved data retention. The effect on the crystallization kinetics of the addition of van der Waals interaction to the interatomic potential is also discussed.

---

1 Introduction

The Ge₂Sb₂Te₅ (GST) compound is the prototypical material for applications in phase change memories (PCMs) in which binary information is encoded by the crystalline and amorphous phases of GST.^1,2 Joule heating through the material or via local heaters leads to either amorphization via crystal melting (reset operation) or to recrystallization of the amorphous phase (set operation), while read out of the memory consists of a measurement of the resistance at low bias that differs by three order of magnitude between the two phases. Phase change alloys are also among the most promising materials for the realization of artificial neurons and synapses for neuromorphic computing.³ In these applications, one exploits the different resistivity levels of the material that can be achieved either by partial crystallization of the amorphous phase in the set process or by varying the size of the amorphous region during reset.

In a recent work,⁴ it was proposed that a superlattice (SL) geometry made of alternating layers of the phase change material Sb₂Te₃ and more thermally stable confining layers of TiTe₂ exhibits superior properties for neuromorphic computing. Progressive amorphization or recrystallization of several Sb₂Te₃ slabs allows better control of the different resistance states for neuromorphic applications. Moreover, the read out of the different resistance states in PCMs is typically hampered by a drift with time of the resistivity of the amorphous phase induced by structural relaxations (aging).⁵ This drift can be reduced by nanoconfinement as was also shown in ref. 4 for the Sb₂Te₃/TiTe₂ SL. In the PCM device made of this SL, the TiTe₂ slabs act as a thermal and diffusion barrier that keeps the crystalline form during cycling due to its high melting temperature, while Sb₂Te₃ undergoes the phase change.⁴ This mechanism of the operation of the memory has been, however, questioned in a recent work⁶ in which the TiTe₂ slabs were shown to disappear after cycling in the active region of a mushroom cell made of a Sb₂Te₃/TiTe₂ SL. Anyway, pure Sb₂Te₃ has a relatively low crystallization temperature that would limit data retention in the memories. Therefore, it has been proposed to substitute Sb₂Te₃ with a phase change material with a higher crystallization temperature such as GST or GeTe.^7,8 Sb₂Te₃ and GeTe are actually the parent compounds of GST that can be seen as a pseudobinary compound along the GeTe–Sb₂Te₃ tie-line. However, we should consider that nanoconfinement could slow down the crystallization kinetics,⁹ as is the case for elemental Sb, for instance, whose amorphous phase crystallizes explosively at 300 K in the bulk, but it is dramatically stabilized in ultrathin films 3–10 nm thick capped by insulating layers.^10,11 In a previous work,⁷ we have shown by molecular dynamics (MD) simulations that nanoconfinement only slightly reduces the crystallization speed of GeTe that could then be used for memory applications in the superlattice GeTe/TiTe₂ geometry with a foreseen superior data retention with respect to Sb₂Te₃/TiTe₂. Therefore, it is of interest to investigate whether the flagship GST phase change compound could also be used in GST/TiTe₂ SLs. The structural properties of GST/TiTe₂ SLs in the crystalline and partially liquid/amorphous phases have actually been studied in a recent work by atomistic simulations based on density functional theory (DFT),⁸ where it was shown that the interaction between TiTe₂ and GST is weak and mainly due to van der Waals (vdW) forces. The stress on the GST film induced by the TiTe₂ capping should then be small as well, as opposed to the situations with other capping layers. For example, a capping layer of Al₂O₃ was shown to strongly increase the crystallization time for film thickness below 10 nm.¹² Capping by W was also shown to strongly hinder crystallization in thin (7 nm) GST films at temperatures below about 500 K, while the crystallization speed is only slightly affected at higher temperatures.¹³ In several papers,^14,15 it was proposed that less facile crystallization at lower temperatures arises through different possible mechanisms related to the stress induced by the capping layer. At higher temperatures, the density change upon crystallization can be easily accommodated by viscous flow, and then the interface with the capping layer has the opposite effect of enhancing heterogeneous crystal nucleation¹⁴ (see ref. 9 for a review and a thorough discussion on crystallization in thin GST films).

On these premises, in this article we report on MD simulations of the crystallization of GST in a nanoconfined geometry mimicking the superlattice made of alternating layers of GST and TiTe₂, similarly to the Sb₂Te₃/TiTe₂ superlattices of ref. 4. To this aim, we have exploited the neural network (NN) interatomic potential¹⁶ for GST¹⁷ that we have recently developed by fitting a large DFT database of energy and forces within the NN framework implemented in the DeePMD code.^18–20 In the present work, the NN potential fitted on the DFT database is supplemented by the semiempirical van der Waals (vdW) correction due to Grimme (D2).²¹ Therefore, for the sake of comparison to the SL, we also repeated the simulation of crystallization in the bulk with vdW corrections, which were not included in our previous work.¹⁷

2 Computational details

Molecular dynamics simulations were performed by using the NN interatomic potential for GST developed in our previous work¹⁷ using the DeePMD package.^18–20 The NN was trained on a DFT database of energies and forces of about 180 000 configurations of small supercells (57–108 atoms) computed by employing the Perdew–Burke–Ernzerhof (PBE) exchange and correlation functional²² and norm conserving pseudopotentials.²³ The potential was validated on the structural and dynamical properties of the liquid, amorphous and crystalline phases and used to study the crystallization kinetics in the bulk.¹⁷

At normal conditions, the thermodynamically stable form of GST is a hexagonal crystal (space group P3̄m1)^24–26 with nine atoms in the primitive unit cell arranged along the c direction with an ABCABC stacking. Each formula unit forms a lamella separated from the others by a so-called vdW gap, although the interlamellar interaction is not just a vdW contact as discussed in ref. 27. Three different models of hexagonal GST have been proposed in literature differing in the distribution of Sb/Ge atoms in the cationic sublattices.^24–26 Here, we considered the Kooi stacking²⁵ with Sb atoms occupying the cationic planes close to the vdW gap and without disorder in the cationic sublattice. It was shown that GST features phonon instabilities in the Kooi stacking when the DFT-PBE scheme is applied.²⁸ These instabilities at the PBE level are removed²⁸ by including the semiempirical vdW correction due to Grimme (D2).²¹ In the crystallization process, the amorphous (supercooled liquid) phase transforms into the cubic phase which is instead stable at the PBE level. Therefore, in our previous work on the crystallization of bulk GST,¹⁷ vdW interactions were not included. In the present work, we will instead start from the hexagonal phase of GST to model the superlattice geometry. Moreover, vdW interactions are expected to control the interplanar distance between the GST slab and the TiTe₂ slabs. Therefore, in the present simulations we have added the vdW-D2 interactions. In the next section, we will briefly summarize results on the crystallization kinetics in the bulk by including vdW interactions, before moving to the discussion of the crystallization of GST in nanoconfined geometry.

We have simulated the effect of confinement on GST crystallization by considering a slab made of two quintuple layers of GST (18 atomic planes with a thickness of about 3 nm), encapsulated by capping layers aiming at mimicking the confining slabs of TiTe₂ in GST/TiTe₂ SLs. As we did in a previous work on nanoconfined GeTe,⁷ the capping layer mimicking TiTe₂ on each side is made by a frozen bilayer of crystalline GeTe itself constrained at the lattice parameter of TiTe₂ as shown in Fig. 1a. In fact, TiTe₂ is a layered hexagonal crystal (space group P3̄m1) made of trilayer Te–Ti–Te blocks stacked along the c axis and separated by vdW gaps.²⁹ The geometry of the hexagonal Te layers is the same in TiTe₂ and GST albeit with different lattice parameters. The a and c lattice parameters of hexagonal GST computed with and without vdW corrections are compared in Table 1 with experimental data.²⁶ The experimental in-plane lattice parameter of TiTe₂ is instead a = 3.7795 Å.²⁹ A good commensuration between a trilayer of TiTe₂ and GST in the hexagonal xy plane is obtained by considering multiples of the orthorhombic supercells with edges a and , namely 16 × 8 orthorhombic cells of TiTe₂ and 14 × 7 orthorhombic cells of GST. The misfit is only 2% along both x and y. We finally set the in-plane lattice parameters of the supercell to those of GST which means that the bilayers mimicking TiTe₂ are slightly strained by the amount given above. The model thus contains 14 × 7 × 2 = 196 atoms per atomic layer of GST and 16 × 8 × 4 = 512 atoms in each of the bilayers mimicking TiTe₂, for a total amount of 4552 atoms of which 3528 are mobile. Periodic boundary conditions are applied along the three Cartesian axes (see Fig. 1). The TiTe₂-like bilayers are oriented in such a way to expose the Te layer to the GST slabs on both sides as would occur for a TiTe₂ slab. The distance between the outermost Te plane of the capping layer and of hexagonal GST is fixed to the value of 3.55 Å, obtained from geometry optimization at the PBE-D3 level of a GST/TiTe₂ SL in ref. 8. Since TiTe₂ has a melting temperature much higher than that of GST, we mimicked the confinement by TiTe₂ by freezing the atoms of the crystalline GeTe-like capping bilayers during the thermal cycle.

Fig. 1 (a) Crystalline and (b) amorphous phase of the slab made of two quintuple layers of GST encapsulated by capping layers. The capping layer is made by a frozen bilayer of crystalline GeTe at the lattice constant of TiTe₂, aiming at mimicking the confining slabs of TiTe₂ in GST/TiTe₂ SLs. Color code for atomic spheres: Ge (gray), Te (orange), Sb (pink), Ge atoms in the capping layers have a different color (red) to highlight the fact that these are fake structures. The same color is kept for Te in GST and in the capping layers. The Ovito³⁰ tool was used for the visualization and the generation of all atomic snapshots in this article.

Table 1 Theoretical equilibrium lattice parameters a and c (Å) and equilibrium density ρ (atoms per ų) of hexagonal GST computed with (NN+vdW) and without (NN) van der Waals corrections, compared with experimental data from ref. 26. Note that there was a misprint in the NN equilibrium volume in Table 3 of ref. 17. The correct value was actually equal to the DFT result, as can be inferred from Supplementary Fig. 8 of ref. 17

	NN+vdW	NN	Expt
a (Å)	4.235	4.30	4.2247
c (Å)	17.15	17.64	17.2391
ρ (atoms per Å^3)	0.03379	0.03182	0.03378

---

MD simulations were performed with the DeePMD code by using the LAMMPS code as MD driver,³¹ a time step of 2 fs, and a Nosé–Hoover thermostat.^32,33

The GST slab was amorphized by first equilibrating the system at 1500 K for 200 ps and then at 1000 K for 100 ps. The liquid-like slab was then quenched to 300 K in 150 ps. Structural properties of the resulting amorphous slab were computed over 70 ps simulation at 300 K. The amorphous model was then heated at different target temperatures to study the crystallization process in simulations about 1–3 ns long at each temperature at constant volume.

To identify the crystalline nuclei we used the local order parameter Q^dot₄,^34,35 that we considered in our previous work on the crystallization of bulk GST.¹⁷

3 Results and discussion

3.1 Structural properties of the bulk

The structure of bulk amorphous GST (a-GST) is discussed in previous DFT works^36,37 and in our previous work on the development of the NN potential.¹⁷ Te atoms are mostly three-fold coordinated in a pyramidal geometry (three bonding angles of 90°), Sb atoms are both three-fold coordinated in a pyramidal geometry and four- or five-fold coordinated in a defective octahedral environment (octahedral bonding angles but coordination lower than six), Ge atoms are mostly in pyramidal or defective octahedral geometry with a minority fraction in tetrahedral geometries.

A comparison of the structural properties of a-GST with and without vdW interaction at the experimental density of the amorphous phase (0.0309 atoms per ų)³⁸ is shown in Fig. 2. We name this model a low density configuration (bulk-LD) to distinguish it from other models at higher density that we will discuss later on. The data with no vdW interaction are taken from our previous work,¹⁷ while the data with vdW interaction are obtained from the simulation of a 3996-atom cubic model generated by quenching from 1000 K to 300 K in 100 ps. Pair correlation functions, angle distribution functions and the distribution of coordination numbers are shown in Fig. 2. The coordination numbers are obtained by integrating the partial pair correlation functions up to the bonding cutoff of 3.2 Å (Ge–Ge, Ge–Sb, Ge–Te, Sb–Te and Te–Te) and 3.4 Å (Sb–Te). The position of the first peak of the partial pair correlation functions and the average partial coordination numbers are compared in Table S1 and S2 in the ESI,† with experimental data from anomalous X-ray scattering,³⁹ extended X-ray absorption spectroscopy (EXAFS),⁴⁰ and reverse Monte-Carlo analysis of combined X-ray and neutron diffraction and EXAFS.⁴¹ A more comprehensive comparison of experimental data with previous DFT calculations with PBE and other functionals is reported in a very recent work (see Table 5 in ref. 42). As discussed in ref. 42, the PBE functional typically overestimates the bond lengths in amorphous GST with respect to experiments, as reported in several previous works,^36,37 with a notable exception due to the use of a particular pseudopotential for Ge.⁴³ Despite the overestimation of the bond lengths in the amorphous phase, the PBE functional reproduces well vibrational spectra and thermal conductivity of the amorphous as well as crystalline phases.^28,44–46 A quantitative measure of the fraction of tetrahedral environments can be obtained from the local order parameter q introduced in ref. 47. It is defined as , where the sum runs over the pairs of atoms bonded to a central atom j and forming a bonding angle θ_ijk. The order parameter evaluates to q = 1 for the ideal tetrahedral geometry, to q = 0 for the 6-fold coordinated octahedral site, to q = 5/8 for a 4-fold coordinated defective octahedral site, and q = 7/8 for a pyramidal geometry. The distribution of the local order parameter q for tetrahedricity for four-coordinated Ge atoms is also reported in Fig. 2d. The bimodal shape corresponds to tetrahedral and defective octahedral geometries. We quantified the fraction of Ge atoms in a tetrahedral environment by integrating the q parameter between 0.8 and 1 as discussed in previous works.⁴⁸ The fraction of Ge atoms in a tetrahedral geometry is almost equal in simulations with (33%) and without (30%) vdW corrections.

Fig. 2 Structural properties at 300 K of models of amorphous GST generated with (red lines) and without (blue lines from ref. 17) vdW corrections, both at the experimental density of the amorphous phase of 0.0309 atoms per ų (bulk-LD). (a) Partial pair correlation functions. (b) Bond angle distribution function resolved per central atomic species. The data are normalized to the number of triplets in each model. (c) Distribution of coordination numbers resolved per chemical species. (d) Distribution of the q order parameter for tetrahedricity of the fourfold coordinated Ge atoms.

The addition of vdW interactions leads to a slightly better defined first minimum (first coordination shell) of the pair correlation functions both in the amorphous and in the liquid phases (not shown here), as was already observed for GeTe.^50,51 On the other hand, vdW corrections have a strong impact on the atomic mobility, as already found in previous works on GeTe as well.⁵² Indeed, the diffusion coefficient D in the supercooled liquid is around a factor three lower with the addition of vdW corrections. The diffusion coefficients with and without vdW interactions are compared in Fig. 3a. The diffusion coefficient was obtained from the mean square displacement (MSD) and the Einstein relation MSD = 6Dt from equilibrated trajectories at constant energy (NVE simulations). The MSD as a function of time at different temperatures is shown in Fig. 3b. As was the case for GeTe,⁵² the addition of the vdW interaction leads to a better agreement with experiments on the viscosity above melting. In GeTe, vdW interactions actually overcorrect the underestimation of the viscosity yielded by the DFT-PBE framework. Similarly, the viscosity of GST at 900 K computed by NN+vdW of 2.3 ± 0.2 mPa s is about 15% larger than the experimental value of 2.0 mPa s from ref. 53. The viscosity was computed from the Green–Kubo formula as shown in Fig. S1 in the ESI.† Results on the viscosity in a wide temperature range above and below melting will be discussed in a forthcoming publication in relation with the breakdown of the Stokes–Einstein relation.

Fig. 3 (a) Diffusion coefficient D as a function of temperature from bulk NN simulations with and without vdW interactions at the experimental density of the amorphous phase (0.0309 atoms per ų). The data (points) are fitted by the Cohen–Grest (CG) formula⁴⁹ as log₁₀(D(T)) = A − 2B/(T − T₀ + [(T − T₀)² + 4CT]^1/2), which yields A = −2.45, B = 602 K, C = 17.3 K and T₀ = 330.6 K without vdW (see ref. 17) and A = −3.76, B = 433 K, C = 0.76 K and T₀ = 384.5 K with vdW (dashed lines). (b) Mean square displacement (MSD) of bulk GST as a function of time at different temperatures (K) from NVE simulations (NN+vdW) in the supercooled liquid.

3.2 Structural properties of the superlattice

The a-GST slab encapsulated by frozen capping bilayers mimicking TiTe₂ (superlattice configuration) is shown in Fig. 1b. We observed a small expansion of the amorphous slab that leads to a density of about 0.0329 atoms per ų (estimated in spheres of 10 Å radius in the inner part of the slab) to be compared to the initial density of 0.0338 atoms per ų of the slab in the crystalline phase. We remark that the experimental density of the amorphous phase is 0.0309 atoms per ų.³⁸

The structural properties of the a-GST slab are compared in Fig. 4 to those of a bulk model quenched from the melt at the density fixed to the theoretical density of hexagonal GST with vdW (see Table 1). This high density bulk model (bulk-HD) was generated by quenching from 1000 K to 300 K in 150 ps a 3528-atom orthorhombic cell with lattice parameters a = 59.29 Å, b = 51.34 Å, and c = 34.30 Å. Partial pair correlation functions, bond angle distribution functions, distribution of the coordination numbers, and the distribution of order parameter q for tetrahedricity are shown in Fig. 4a–d. The bonding cutoffs are the same as those used for the bulk in the previous section. The average partial coordination numbers of the slab and the bulk are compared in Table 2.

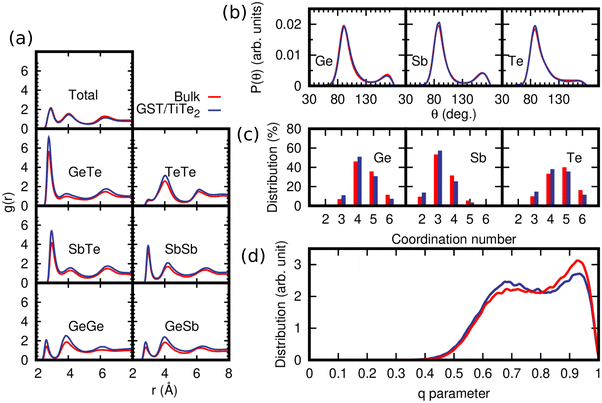Fig. 4 Structural properties at 300 K of the slab of amorphous GST confined by the TiTe₂-like capping layers in SL (blue lines, SL, see Fig. 1b) compared to those of a bulk model of amorphous GST at the density of the hexagonal phase generated by quenching from the melt (bulk-HD, red lines). (a) Partial pair correlation functions. (b) Bond angle distribution function resolved per central atomic species. (c) Distribution of coordination numbers resolved per chemical species. The data are normalized to the number of triplets in each model. (d) Distribution of the q order parameter for tetrahedricity of the fourfold coordinated Ge atoms.

Table 2 Average coordination number for different pairs of atoms computed from the partial pair correlation functions for the amorphous slab confined by the capping layers (GST/TiTe₂-like SL), compared with the data of a bulk amorphous model at the density of the hexagonal phase of GST (bulk-HD, see text)

		Bulk-HD	GST/TiTe2-like SL
Ge	With Ge	0.36	0.38
	With Sb	0.39	0.38
	With Te	3.76	3.58
	Total	4.52	4.34
Sb	With Ge	0.39	0.38
	With Sb	0.74	0.65
	With Te	3.51	3.41
	Total	4.63	4.44
Te	With Ge	1.50	1.43
	With Sb	1.40	1.36
	With Te	0.43	0.39
	Total	3.33	3.18

---

The coordination numbers are lower in the superlattice than in the bulk in part because of the slightly lower density (0.0329 vs. 0.0338 atoms per ų) and because of the presence of the two surfaces. We observed a slight enrichment of Te (66% instead of 56%) at the two surfaces of the amorphous slab facing the Te planes of the capping layers. The resulting fraction of Ge atoms in tetrahedral geometry (with respect to the total number of Ge atoms) is 24.5% in the slab and 20.1% in the amorphous model of the bulk at the density of the hexagonal crystal.

3.3 Crystallization kinetics in bulk Ge₂Sb₂Te₅

The kinetics of crystallization in the bulk were analyzed in our previous work¹⁷ from simulations without vdW corrections. To study crystallization with vdW interaction, we generated a 3996-atom cubic model at the experimental density of the amorphous phase (see above). The model was first equilibrated at 1200 K for 40 ps, then quenched to 900 K in 40 ps and further equilibrated for 60 ps. The system was then brought to the target temperature in 160 ps to study nucleation and growth. The reduction of the self-diffusion coefficient upon addition of the vdW interactions mentioned above leads to an increase in the nucleation time and a decrease in the crystal growth velocity. The potential energy as a function of time for NN+vdW simulations at different temperatures, shown in Fig. 5a, reveals the onset of crystallization with a nucleation time that increases with temperature. Overcritical nucleus/nuclei form on a time scale of 4–12 ns in the temperature range 550–590 K. Nucleation was not observed at and above 600 K in simulations lasting over 12 ns. The nucleation times of 2–10 ns (see Fig. 5a) are in same range of the width of set pulses for crystallization in memory cells 20–60 nm large,⁵⁴ although heterogeneous nucleation is likely in the devices.

Fig. 5 (a) Potential energy as a function of time in NN+vdW simulations of the homogeneous crystallization of the supercooled liquid phase at different temperatures and at the experimental density of a-GST (bulk-LD). Only temperatures at which we see the formation of overcritical nuclei are shown. (b) Crystal growth velocities from simulations with (blue dots) and without (red dots from ref. 17) vdW corrections. The error bars when present refer to data extracted from more than two nuclei. For temperatures where nucleation was not observed after a few nanoseconds, i.e. below 550 K and above 590 K in the NN+vdW simulations, the crystal growth velocities were estimated by heating (cooling) at the target temperature a configuration with an overcritical nucleus generated at a lower (higher) temperature. Experimental data from ultrafast differential scanning calorimetry (green curve)⁵⁵ and the fitting of the NN+vdW data with the WF formula (2) (blue dashed line) are also shown.

The crystal growth velocity was computed as v_g = dR(t)/dt by assuming a spherical overcritical nucleus with radius R given by R(t) = (3N(t)/(4πρ_cubic))^⅓, where N is the number of atoms in the nucleus, ρ_cubic is the theoretical density of the cubic crystal (0.0331 atoms per ų). The evolution in time of the radius of overcritical nuclei at different temperatures is shown in Fig. S2 in the ESI.† Crystal growth velocities with and without vdW interactions for bulk a-GST at the experimental density (bulk-LD) are compared in Fig. 5b. For temperatures where nucleation was not observed after a few nanoseconds, i.e. below 550 K and above 590 K in the NN+vdW simulations, the crystal growth velocities were estimated by heating (cooling) at the target temperature a configuration with an overcritical nucleus generated at a lower (higher) temperature. The results with vdW corrections are in an overall better agreement with experimental data from ultrafast differential scanning calorimetry of ref. 55. The reduction of v_g due to the vdW correction mirrors the reduction of the diffusion coefficient reported in Fig. 3. We also computed v_g with a more general method that does not make any assumption on the shape of the crystallite with very similar results, as will be discussed in the next section.

The theoretical v_g was fitted by the Wilson–Frenkel (WF) formula as we did in our previous work¹⁷ for the simulations without vdW corrections. Namely, we used the WF formula v_g(T) = 6D(T)d/λ²(1 − e^{(−Δμ(T)/k_BT)})e^{−ΔS(T)/k_B}, where d is a geometric factor that we will define later, λ is a typical jump distance that is used as fitting parameter, and D(T) is the temperature-dependent diffusion coefficient extracted from the simulations. ΔS is the (positive) entropy difference between the liquid and the crystal which is calculated from the specific heat (with vdW), as discussed in our previous work¹⁷ to which we refer to for further details. The factor e^−ΔS/k_B in the WF formula, which was first introduced by Jackson,⁵⁶ turned out to be necessary to reproduce the theoretical v_g(T) without vdW corrections in our previous work.¹⁷ Δμ(T) is the difference in free energy between the liquid and the crystal given by the Thompson–Spaepen approximation 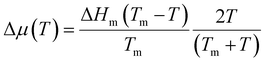,⁵⁷ where ΔH_m is the enthalpy jump at the melting temperature T_m. We set ΔH_m = 166 meV per atom and T_m = 940 K as estimated in our previous work from NN+vdW simulations.¹⁷ Due to the sensitivity of the results on the choice of T_m, we have also further checked for possible finite size effects in the estimate of T_m from the phase coexistence method in the slab geometry used in our previous work.¹⁷ By increasing the c axis of the slab model from the value of 11 nm of ref. 17 to 30 nm, the resulting T_m of 940 K does not change. At the highest temperatures, Δμ(T) becomes very small and therefore the corrections due to the surface energy of the crystalline nucleus become important. In fact, the change in free energy due to the addition of an atom to a spherical nucleus is given by −Δμ(T) + 2σ/(ρ_cubicR) where σ is the crystal–liquid interfacial energy. Indeed, at the highest temperatures above 700 K, R(t) changes slope with time due to the interfacial term, as shown in Fig. S2 in the ESI.† Since v_g was calculated from R in the range 15–20 Å at all temperatures, in the lack of a reliable estimate of σ, we considered the term 2σ/(ρ_cubicR) = Δμ_S as a constant offset to −Δμ(T) which was used as an additional fitting parameter in the WF formula.

Coming now to the geometric factor, for a spherical nucleus d = 2/3(vol_site3/(4π))^1/3, where vol_site is the volume associated with an adsorption site on the crystalline nucleus.⁵⁸ If we take vol_site = 4π/3(λ/2)³, the WF formula reads v_g = 4D/λ(1 − e^−Δμ/k_BT)e^{−ΔS(T)/k_B}. As we did in our previous work,¹⁷ we here use the more general and complete formula

v_g = u_kin(1 − e^{(−Δμ+Δμ_S)/k_BT})e^{−ΔS(T)/k_B}, with (1)

u_kin = 8(vol_site3/(4π))^1/3D/λ² (2)

where vol_site^1/3 is about half the lattice parameter of the cubic cell, i.e. 3 Å. The resulting fit is shown in Fig. 5b with λ = 2.04 Å, which is a reasonable jump distance, and Δμ_S = 0.0098 eV which corresponds to σ = 0.052 J m⁻² for R = 20 Å. This value is similar to those used previously in numerical simulations (0.060–0.075 J m⁻²).^59,60

3.4 Crystallization kinetics in the superlattice

Turning now to SL geometry, the crystallization kinetics were studied by heating the system at six different target temperatures of 500, 550, 600, 650, 700, and 750 K in constant volume simulations, 1–3 ns long each. Albeit there is a large mismatch between the lattice parameters of GST and of the capping layers, crystal nucleation always starts at the surfaces as was observed in our previous works on nanoconfined GeTe⁷ and GeTe nanoparticles.⁵¹ Within the classical nucleation theory of heterogeneous nucleation, the crystallites preferentially form at the surface when σ > σ_c − σ_a where σ_c and σ_a are surface energy of the crystal and amorphous (supercooled liquid) phases.^61,62 As discussed in Sections 2 and 3.2, the density of GST in the SL is close to the theoretical equilibrium density of the hexagonal phase. We call SL-HD the high density model discussed so far to distinguish it from another model at lower density that we will introduce later on.

The onset of crystallization is visible from the evolution in time of the potential energy and of the number of crystalline atoms, shown in Fig. 6. The nucleation time of about 0.5 ns at 650–750 K is much shorter than in the bulk (see Fig. 5) due to heterogeneous nucleation. At 550 K just one nucleus forms at one surface on a longer time scale of 2.2 ns (not shown in Fig. 6), while at all other temperatures we see the formation of an overcritical nucleus at both surfaces. At 700 K, up to four overcritical nuclei form. At the highest temperature of 750 K, the crystallization of the slab is nearly complete in 2 ns.

Fig. 6 Crystallization of amorphous GST capped by bilayers mimicking confinement by TiTe₂ in GST/TiTe₂-like SL at different temperatures (SL-HD). (a) Potential energy and (b) number of crystalline atoms as a function of time. At 550 K crystal nucleation occurs after 2.2 ns, i.e. on a longer timescale not shown in the figure.

Snapshots of the crystallization process at 750 K are shown in Fig. 7; similar snapshots for the simulations at 650 and 700 K are given in Fig. S3 and S4 in the ESI.† Note that beside the overcritical nuclei, several small undercritical nuclei form and disappear at both surfaces. The crystallites formed at the surface mostly expose the (001) plane of the cubic phase. For the single temperature of 700 K, we repeated the simulations of crystallization for two other independent amorphized models. In just one case, we also see the formation of a nucleus exposing the (111) plane at the surface.

Fig. 7 Simulation of the crystallization of a 3528-atom slab of amorphous GST capped by bilayers mimicking confinement by TiTe₂ in GST/TiTe₂-like SL (SL-HD). Snapshots at different times at 750 K are shown for (a) 0.5 ns, (b) 1 ns, and (c) 1.5 ns. Crystallization starts at the surfaces of the amorphous slab, albeit the capping layers do not act as nucleation centers. Only crystalline atoms, identified by the Q^dot₄ order parameter (see Section 2), are shown. Different crystalline nuclei have different colors. (d) Final configuration after 2 ns. The color code for panel (d) is the same as Fig. 1.

To further analyze the orientation of the crystallites, we repeated a simulation for a SL model generated by amorphizing a hexagonal phase with a slightly lower density corresponding to the equilibrium lattice parameters obtained without the vdW correction (see Table 1). We name this model at lower density SL-LD′, where the prime is meant to distinguish this low density from the bulk model at the experimental density of the amorphous phase (bulk-LD). Snapshots of the crystallization process of the SL-LD′ model at 750 K are shown in Fig. 8. The evolution in time of the potential energy and of the number of crystalline atoms for this second set of simulations of the SL-LD′ model are shown in Fig. S5 in the ESI.† At 750 and 600 K, we see the formation of an overcritical nucleus just at one surface, while at 700 and 650 K a single overcritical nucleus forms at both surfaces. During the crystallization process, we first observed an enrichment in Te in the outermost layers of the amorphous slab which leads to the nucleation at the surface of cubic crystallites all exposing the (111) plane. This occurs at both surfaces of the amorphous slab. At 700 K, we repeated the simulations for another two independent models with very similar results. This preferential orientation of the crystallites is in agreement with experimental findings on surface nucleation in thick GST films,⁶³ albeit at temperatures lower than those simulated here.

Fig. 8 Simulation of the crystallization of a 3528-atom slab of amorphous GST capped by bilayers mimicking confinement by TiTe₂ in GST/TiTe₂ superlattices at a lower density of the GST slab (SL-LD′, see text). Snapshots at different times at 750 K are shown for (a) 0.5 ns, (b) 0.75 ns, and (c) 1 ns. Crystallization starts at the surfaces of the amorphous slab, albeit the capping layers do not act as nucleation centers. Only crystalline atoms, identified by the Q^dot₄ order parameter (see Section 2), are shown. Different crystalline nuclei have different colors. (d) Final configuration after 1.2 ns. The color code is the same as Fig. 1.

We speculate that the different orientation of the crystallites formed in the two sets of simulations at slightly different densities arise from the requirement of minimizing the surface energy of the crystallites nucleated at the surface of the amorphous slab and at the same time of maximizing the vdW attraction energy with the capping layers. In fact, the surface energy is only very slightly higher for the (111) than for the (001) plane. The theoretical surface energy of the (001) face calculated within our framework is 20 meV Å⁻², which is higher than the previous estimate by DFT calculations (10.2 meV Å⁻²)⁶⁴ because of the inclusion of vdW interactions. The calculation of the surface energy of the (111) face of the cubic crystal is problematic because a slab with both surfaces terminated by Te is non-stoichiometric. As a reasonable approximation, we can assume that the surface energy of the (111) face of the cubic crystal exposing Te atoms is close to the surface energy of the (0001) face of the hexagonal crystal which can be easily computed from a stoichiometric slab model yielding 16 meV Å⁻², which is very close to previous DFT+vdW calculations (14 meV Å⁻²).⁶⁵ The small difference between the surface energy of the two faces (4 meV Å⁻²) might be compensated by the adhesion energy with the capping layers which depends in turn on the surface atomic density, higher for the (001) than for the (111) face. We can then envisage that a small change in density might favor one orientation over the other which also means that the preferential orientation of the crystallites forming at the interface might depend on the type of capping layer and it might then change by using, for instance, metal selenides instead of metal tellurides as spacers in the SLs.

In the SL at the lower density (SL-LD′), the fully crystallized slab in the simulation at 750 K consists of ten Te layers, as in the original hexagonal crystalline slab, and nine cationic layers with, as expected, no vdW gap and a Te outermost plane on both sides of the slab. This geometry implies that the fraction of vacancies in the cationic sublattice is equal to 1/9, to be compared with the value of 1/5 in the bulk cubic phase. Therefore, in the slab about half of the stoichiometric vacancies of the cubic phase are filled. In the real material, the cubic phase should have a larger concentration of vacancies as a result of self-doping which turns the system into a degenerate p-type semiconductor. Even in the presence of additional non-stoichiometric vacancies responsible for about 2.73 × 10²⁰ holes per cm³ as measured experimentally,⁶⁶ we expect in the slab a fraction of vacancies lower than the stoichiometric value which should imply a switch to an n-type conductivity.⁶⁷

Coming now to the crystal growth velocity, due to the presence of a heterogeneous and complex nucleation process, we cannot compute v_g by using the same scheme reported in Section 3.2 for crystallization in the bulk in which nuclei were assumed to have a spherical shape. Therefore, for the SL we used the scheme adopted in our previous work on nanoconfined GeTe,⁷ namely v_g has been computed from the time derivative of the crystalline volume V_c according to the scheme proposed in ref. 68 as v_g(t) = S_ac⁻¹dV_c/dt where S_ac is the area of the crystal–amorphous interface. The crystalline volume V_c is obtained by summing up the volumes of the Voronoi polyhedra of each crystalline-like atom (excluding the volume of isolated atoms or clusters of less than 28 crystalline-like atoms). S_ac is computed as the total area of the faces that are shared by Voronoi polyhedra of amorphous-like and crystalline-like atoms. We used the Voro++ code.⁶⁹ The data of volumes V_c and areas S_ac were smoothed using a Savitzky–Golay filter with a time window of 10–50 ps for the calculation of growth velocity, similarly to ref. 70. The instantaneous v_g, V_c and S_ac as a function of time at the different temperatures is shown in Fig. 9. The average crystal growth velocities in the SL at high density (SL-HD) are obtained by averaging the instantaneous crystal growth velocity in a time interval of a few hundreds of ps as shown in Fig. S6 in the ESI.† We excluded the initial part of the growth when the nuclei are not overcritical and the final part when the nuclei interact with other overcritical nuclei, with their periodic images or hit the other surface of the slab. The resulting v_g are compared in Table 3 with those of reference calculations for the bulk at the density of the crystalline hexagonal phase (bulk-HD) and at the experimental density of a-GST (bulk-LD).

Fig. 9 (a) Instantaneous crystal growth velocity v_g, (b) volume occupied by the crystalline atoms V_c and (c) area of the crystal–amorphous interface S_ac as a function of time at the different temperatures in the crystallization of the superlattice configuration (SL-HD). The crystal growth velocity is computed as v_g = dV_c/dtS_ac⁻¹ as described in ref. 70. The v_g reported in Table 3 are obtained by averaging the instantaneous v_g over the time intervals highlighted in Fig. S6 in the ESI.†

Table 3 Crystal growth velocities v_g (m s⁻¹) for the superlattice with GST slabs confined by the TiTe₂-like capping layers at two different densities, namely the equilibrium density of hexagonal GST with vdW (SL-HD) and the lower equilibrium density without vdW (SL-LD′). The data at 700 K are average with error bars over three independent models. The data for the orthorhombic bulk model at the density of the crystalline hexagonal phase with vdW (bulk-HD) and at the experimental density of a-GST (bulk-LD) are also reported. The data refer to the calculations with the Voronoi polyhedra (see text). Data in parenthesis for the crystallization in the bulk have been obtained instead from the analysis of the radius of the growing nuclei (see text). In the case of bulk-HD, two values are reported, the first refers to the orthorhombic cell and the second to the larger cubic cell (see text)

	vg (m s^−1)
Temperature (K)	SL-HD	SL-LD′	Bulk-HD	Bulk-LD
550	0.15	—	0.29 (0.35–0.67)	0.70 (0.61)
600	0.53	0.75	0.70 (1.00–0.98)	1.63 (1.76)
650	1.03	1.30	1.40 (2.00–2.40)	(2.45)
700	1.45 ± 0.15	2.00 ± 0.3	2.50 (2.75–2.90)	(2.98)
750	2.10	2.6	2.20 (2.50–2.40)	(2.72)

---

The crystallization in bulk-HD was studied with two models at the same density, namely the 3528-atom orthorhombic cell introduced in Section 3.2 and a second 4536-atom cubic cell. The amorphous models were generated by quenching from the melt in 150 ps. The models were then heated and equilibrated at the target temperature. Crystal nucleation in the bulk-HD models was observed on a short time scale at 550 K in our model and at 600 K in the other. The crystal growth velocity at the higher (lower) temperature was computed by heating (cooling) at the target temperature a configuration from the simulation with a crystalline nucleus grown up to about 160–170 atoms. This choice is made to ensure that the nucleus remains overcritical at the higher temperatures. The crystal growth velocities for the SL simulations at lower density (SL-LD′) are also shown in Table 3. The equivalent of Fig. 9 and of Fig. S6† for SL-LD′, bulk-HD and bulk-LD models are given in Fig. S7–S12 in the ESI.†

The crystal growth velocity for SL-HD is lower than in the bulk at the same density (see Table 3). We note that the atomic mobility in the xy plane (perpendicular to the z axis of the SL) is very similar in the SL and in the bulk at the same density, as shown by the diffusion coefficient D in Fig. S13 and Table S3 in the ESI,† and therefore the difference in v_g cannot be ascribed to a change in D in the kinetic prefactor u_kin of the WF formula (eqn (2)). D is computed from the Einstein relation and the MSD reported in Fig. S14 in the ESI.† Moreover, we note that the pressure is 1.70 GPa in bulk-HD (at the density of hexagonal GST) and is slightly tensile (−0.45 GPa) at the experimental density. On the other hand, the stress tensor in the SL-HD model is nearly isotropic with diagonal components of σ_xx = 1.01 GPa, σ_yy = 1.05 GPa, and σ_zz = 1.15 GPa and very small off-diagonal components (<0.035 GPa). The average pressure of 1.07 GPa is in between those of bulk-HD and bulk-LD, which is consistent with a weak coupling between GST and the capping layers and with a density slightly lower than that of bulk-HD (see Section 3.2). Therefore, the capping layer does not exert a stress on the GST slab suitable for modifying the atomic mobility, which is, in fact, very similar to that of bulk-HD. We note that the stress in the SL-HD model was computed from the virial theorem and the forces acting on the GST atoms only. The same lowering of v_g was found for GeTe/TiTe₂-like SLs in our previous work⁷ and it was ascribed to the interaction between the growing overcritical nuclei and the undercritical nuclei that, although they form and disappear, can hinder the growth of the overcritical ones. Since in the SL geometry nucleation takes place at the surface, the different nucleation centers are on average closer in the slab than in the bulk. The same explanation can hold here for the SL-HD model, especially at the lowest temperatures, although this is a rather tentative interpretation at the moment, as this effect is difficult to be addressed quantitatively. The SL-LD′ and bulk-LD do not have the same density and therefore a direct comparison is not possible, but it is confirmed that v_g increases with decreasing density because of a higher diffusion coefficient.

Regarding crystallization of GST in confined geometry, a fragile-to-strong crossover (FSC) was inferred in ref. 13 from differential scanning calorimetry (DSC) on a 7 nm film of GST confined by W capping layers. The DSC traces were fitted by the Johnson–Mehl–Avrami model for the growth process of already formed nuclei,¹³ which implies that the FSC should arise from the kinetic prefactor u_kin of the WF formula (eqn (2)) for v_g. In ref. 13, u_kin was shown to follow a super-Arrhenius behavior above the strong-fragile crossover temperature T_fs and a simple Arrhenius behavior below T_fs, which was estimated as 1.25T_g = 473 K for the 7 nm film capped by W.¹³ This value of T_fs is below the temperature at which we see nucleation and growth on our simulation time scale. Indeed, we do not see any clear sign of a fragile-to-strong crossover in u_kin down to 500 K, neither for the bulk at the experimental density (bulk-LD) nor for the SL-HD system (3 nm thick GST) as shown in Fig. 10. u_kin is extracted from our v_g and the application of the WF formula (eqn (2)). We note that a recent measurement of the crystal growth velocity below about 475 K by nanocalorimetry in GST films 10–40 nm thick⁷¹ revealed a strong behavior as well; extrapolation of this data at high temperatures led the authors to estimate T_fs at about 680 K which is not consistent with our findings (see also Fig. 3). The lower value of u_kin of the SL relative to the bulk is due in part to the different density and in part to the fact that u_kin for the SL should also embody the effect of the interaction with undercritical nuclei at the surface of the slab, mentioned above, via an effective diffusion coefficient D_eff in eqn (2).

Fig. 10 u_kin (eqn (2)) as a function of temperature for the superlattice SL-HD, and for the bulk at the experimental density of the amorphous phase (bulk-LD, see text). u_kin is extracted from v_g and the application of the WF formula (eqn (2)). The term Δμ_S is included for the bulk only.

Overall, we conclude that the confinement does not have a dramatic effect on the crystallization kinetics of our models of GST/TiTe₂-like SLs. In fact, v_g of the confined GST slab at the temperature of maximal crystallization speed is comparable (within a factor of two at most) to that of the bulk. This feature makes GST/TiTe₂ SLs a viable candidate for applications in neuromorphic computing with improved data retention.

4 Conclusions

In summary, we have exploited a recently devised NN potential for GST to study the effect of nanoconfinement on the crystallization kinetics of its amorphous phase. We considered ultrathin (3.14 nm) slabs of GST confined by capping layers aimed at mimicking the TiTe₂ spacers in GST/TiTe₂ superlattices, analog to the Sb₂Te₃/TiTe₂ heterostructure proposed in ref. 4 for applications in neuromorphic devices. The replacement of Sb₂Te₃ by GST would improve the data retention of the device thanks to the higher crystallization temperature of GST compared to Sb₂Te₃. The simulations show that nanoconfinement leads to a decrease in the crystal growth velocity with respect to the bulk amorphous phase which is, however, rather minor for the prospective application in neuromorphic devices. On the other hand, we also observed an increase in the nucleation rate with respect to the bulk due to heterogeneous nucleation. In conclusion, MD simulations support the idea of investigating GST/TiTe₂ superlattices for applications in neuromorphic devices with improved data retention as also proposed in ref. 8.

Author contributions

M.B. conceptualized the work and wrote the original draft of the paper. The simulations were performed by D.A. and S.M. All authors contributed to the analysis of the data and approved the final version of the paper.

Data availability

LAMMPS, and DeePMD are free and open source codes available at https://lammps.sandia.gov and https://deepmodeling.com/space/DeePMD-kit, respectively. The trajectories of the crystallization process of the different models are available in the Materials Cloud repository at https://doi.org/10.24435/materialsclous:t4-kf. The neural network potential generated in O. Abou El Kheir et al., npj Comput. Mater., 2024, 10, 33, is available in the Materials Cloud repository at https://doi.org/10.24435/materialscloud:a8-45.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge financial support from the PRIN 2020 project “Neuromorphic devices based on chalcogenide heterostructures” No. 20203K2T7F funded by the Italian Ministry for University and Research (MUR). The project has received funding also from European Union Next-Generation-EU through the Italian Ministry of University and Research under PNRR M4C2I1.4 ICSC 371 Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum 372 Computing (Grant No. CN00000013). We acknowledge the CINECA award under the ISCRA initiative for the availability of high-performance computing resources and support. We gratefully thank R. Mazzarello for discussions and information.

References

1. M. Wuttig and N. Yamada, Nat. Mater., 2007, 6, 824–832.
2. W. Zhang, R. Mazzarello, M. Wuttig and E. Ma, Nat. Rev. Mater., 2019, 4, 150–168.
3. A. Sebastian, M. Le Gallo, R. Khaddam-Aljameh and E. Eleftheriou, Nat. Nanotechnol., 2020, 15, 529–544.
4. K. Ding, J. Wang, Y. Zhou, H. Tian, L. Lu, R. Mazzarello, C. Jia, W. Zhang, F. Rao and E. Ma, Science, 2019, 366, 210–215.
5. D. Ielmini, A. L. Lacaita and D. Mantegazza, IEEE Trans. Electron Devices, 2007, 54, 308–315.
6. G. M. Cohen, A. Majumdar, C.-W. Cheng, A. Ray, D. Piatek, L. Gignac, C. Lavoie, A. Grun, H.-Y. Cheng, Z.-L. Liu, H.-L. Lung, H. Miyazoe, R. L. Bruce and M. BrightSky, Phys. Status Solidi RRL, 2024, 18, 2300426.
7. D. Acharya, O. Abou El Kheir, D. Campi and M. Bernasconi, Sci. Rep., 2024, 14, 3224.
8. R. Piombo, S. Ritarossi and R. Mazzarello, Adv. Sci., 2024, 11, 2402375.
9. B. J. Kooi and M. Wuttig, Adv. Mater., 2020, 32, 1908302.
10. M. Salinga, B. Kersting, I. Ronneberger, V. P. Jonnalagadda, X. T. Vu, M. Le Gallo, I. Giannopoulos, O. Cojocaru-Mirédin, R. Mazzarello and A. Sebastian, Nat. Mater., 2018, 17, 681–685.
11. D. Dragoni, J. Behler and M. Bernasconi, Nanoscale, 2021, 13, 16146–16155.
12. H.-Y. Cheng, S. Raoux and Y.-C. Chen, J. Appl. Phys., 2010, 107, 074308.
13. Y. Chen, N. Han, F. Kong, J.-Q. Wang, G. Wang and X. Shen, Appl. Phys. Lett., 2022, 121, 061904.
14. J. Orava, A. L. Greer, B. Gholipour, D. W. Hewak and C. E. Smith, Appl. Phys. Lett., 2012, 101, 091906.
15. R. E. Simpson, M. Krbal, P. Fons, A. V. Kolobov, J. Tominaga, T. Uruga and H. Tanida, Nano Lett., 2010, 10, 414–419.
16. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
17. O. Abou El Kheir, L. Bonati, M. Parrinello and M. Bernasconi, npj Comput. Mater., 2024, 10, 33.
18. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001.
19. J. Zeng, D. Zhang, D. Lu and P. Mo, et al., J. Chem. Phys., 2023, 159, 054801.
20. H. Wang, L. Zhang, J. Han and W. E, Comput. Phys. Commun., 2018, 228, 178.
21. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
22. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
23. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 1703.
24. I. Petrov, R. Imamov and Z. Pinsker, Sov. Phys. Crystallogr., 1968, 13, 339.
25. B. Kooi and J. T. M. De Hosson, J. Appl. Phys., 2002, 92, 3584–3590.
26. T. Matsunaga, N. Yamada and Y. Kubota, Acta Crystallogr., Sect. B:Struct. Sci., 2004, 60, 685–691.
27. J.-Y. Raty, M. Schumacher, P. Golub, V. L. Deringer, C. Gatti and M. Wuttig, Adv. Mater., 2004, 32, 1806280.
28. D. Campi, L. Paulatto, G. Fugallo, F. Mauri and M. Bernasconi, Phys. Rev. B, 2017, 95, 024311.
29. D. L. Greenaway and R. Nitsche, J. Phys. Chem. Solids, 1965, 26, 1445–1458.
30. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
31. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ‘t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
32. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
33. W. J. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
34. P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B:Condens. Matter Mater. Phys., 1983, 28, 784.
35. P. Rein ten Wolde, M. J. Ruiz-Montero and D. Frenkel, J. Chem. Phys., 1996, 104, 9932–9947.
36. S. Caravati, M. Bernasconi, T. D. Kuehne, M. Krack and M. Parrinello, Appl. Phys. Lett., 2007, 91, 171906.
37. J. Akola and R. O. Jones, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 235201.
38. W. K. Njoroge, H.-W. Woltgens and M. Wuttig, J. Vac. Sci. Technol., A, 2002, 20, 230–233.
39. J. R. Stellhorn, S. Hosokawa and S. Kohara, Anal. Sci., 2020, 36, 5–9.
40. D. A. Baker, M. A. Paesler, G. Lucovsky, S. C. Agarwal and P. C. Taylor, Phys. Rev. Lett., 2006, 96, 255501.
41. P. Jóvári, L. Kaban, J. Steiner, B. Beuneu, A. Schöps and A. Webb, J. Phys.:Condens. Matter, 2007, 19, 335212.
42. I. Pethes, A. Piarristeguy, A. Pradel, R. Escalier, M. Micoulaut, S. Michalik, J. Darpentigny, A Zitolo and P. Jóvári, J. Am. Ceram. Soc., 2025, 108, e20258.
43. A. Bouzid, G. Ori, M. Boero, E. Lampin and C. Massobrio, Phys. Rev. B, 2017, 96, 224204.
44. G. C. Sosso, S. Caravati, R. Mazzarello and M. Bernasconi, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 134201.
45. G. Sosso, S. Caravati, C. Gatti, S. Assoni and M. Bernasconi, J. Phys.:Condens. Matter, 2009, 21, 245401.
46. L. Yang and B.-Y. Cao, J. Phys. D: Appl. Phys., 2021, 54, 505302.
47. J. R. Errington and P. G. Debenedetti, Nature, 2001, 409, 318.
48. E. Spreafico, S. Caravati and M. Bernasconi, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 144205.
49. M. H. Cohen and G. Grest, Phys. Rev. B:Condens. Matter Mater. Phys., 1979, 20, 1077.
50. M. Micoulaut, A. Piarristeguy, H. Flores-Ruiz and A. Pradel, Phys. Rev. B, 2017, 96, 184204.
51. D. Acharya, O. Abou El Kheir, S. Perego, D. Campi and M. Bernasconi, J. Phys. Chem. C, 2024, 128, 19380–19391.
52. H. Weber, M. Schumacher, P. Jóvári, Y. Tsuchiya, W. Skrotzki, R. Mazzarello and I. Kaban, Phys. Rev. B, 2017, 96, 054204.
53. M. Schumacher, H. Weber, P. Jóvári, Y. Tsuchiya, T. G. Youngs, I. Kaban and R. Mazzarello, Sci. Rep., 2016, 6, 27434.
54. W. J. Wang, L. P. Shi, R. Zhao, K. G. Lim, H. K. Lee, T. C. Chong and Y. H. Wu, Appl. Phys. Lett., 2008, 93, 043121.
55. J. Orava, A. L. Greer, B. Gholipour, D. W. Hewak and C. E. Smith, Nat. Mater., 2012, 11, 279.
56. K. A. Jackson, Interface Sci., 2002, 10, 159–169.
57. C. V. Thompson and F. Spaepen, Acta Metall., 1979, 27, 1855–1859.
58. S. Raoux, W. Welnic and D. Ielmini, Chem. Rev., 2010, 110, 240–267.
59. J. Orava and A. L. Greer, Acta Mater., 2017, 139, 226.
60. G. W. Burr, P. Tchoulfian, T. Topuria, C. Nyffeler, K. Virwani, A. Padilla, R. M. Shelby, M. Eskandari, B. Jackson and B.-S. Lee, J. Appl. Phys., 2012, 111, 104308.
61. D. Turnbull and J. J. Fisher, J. Chem. Phys., 1949, 17, 71–73.
62. S. Raoux, W. Welnic and D. Ielmini, Chem. Rev., 2010, 110, 240–267.
63. B. Kooi, W. M. G. Groot and J. T. M. De Hosson, J. Appl. Phys., 2004, 95, 924–932.
64. D. Mandelli, S. Caravati and M. Bernasconi, Phys. Status Solidi B, 2012, 249, 2140–2144.
65. V. Deringer and R. Dronskowski, J. Phys. Chem. C, 2013, 117, 15075–15089.
66. B.-S. Lee, J. R. Abelson, S. G. Bishop, D.-H. Kang, B.-K. Cheong and K.-B. Kim, J. Appl. Phys., 2005, 97, 093509.
67. S. Caravati, M. Bernasconi, T. D. Kuhene, M. Krack and M. Parrinello, J. Phys.:Condens. Matter, 2009, 21, 255501.
68. I. Ronneberger, W. Zhang and R. Mazzarello, MRS Commun., 2018, 8, 1018–1023.
69. C. Rycroft, Chaos, 2009, 19, 041111.
70. Y. Xu, Y. Zhou, X.-D. Wang, W. Zhang, E. Ma, V. L. Deringer and R. Mazzarello, Adv. Mater., 2022, 34, 2109139.
71. J. Zhao, J. Hui, Z. Ye, T. Lai, M. Y. Efremov, H. Wang and L. H. Allen, Adv. Mater. Interfaces, 2022, 9, 2200429.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00283d

---