Open Access Article
Open Access ArticleStable antiparallel domains in 3D corrugated magnetic thin films†
Rafael
Delgado-García
 *a,
Ruben
Guerrero
*a,
Ruben
Guerrero
 a,
Gabriel
Rodríguez-Rodríguez
a,
Gabriel
Rodríguez-Rodríguez
 a,
Fernando
Gálvez
a,
Fernando
Gálvez
 a,
Miguel Ángel
Arranz
a,
Miguel Ángel
Arranz
 ab and
Jose Miguel
Colino
ab and
Jose Miguel
Colino
 a
a
aInstituto de Nanociencia, Nanotecnología y Materiales Moleculares – INAMOL, Universidad de Castilla-La Mancha, Avenida Carlos III s/n, Toledo, 45071, Spain. E-mail: rafael.delgado@uclm.es
bFacultad de Ciencias Químicas, Universidad de Castilla-La Mancha, Avenida Camilo J. Cela 10, Ciudad Real, 13071, Spain
First published on 17th February 2025
Abstract
Magnetic nanostructured materials are of great interest in fields such as non-conventional computing or magnetic field sensing due to the possibilities that 3D magnetic textures embedded on metamaterials offer. We present a novel study on the magnetization and magneto-optical properties of a ferromagnetic (permalloy), continuous thin film that is highly corrugated by its deposition on the surface of a triangular silicon nanograting with a low periodicity (250 nm) and a quite large amplitude (180 nm), which leads to the formation of an unusual magnetic texture. This grating profile activates several optical phenomena and thus hinders magnetic characterization, which usually requires the analysis of the magneto-optical Kerr effect (MOKE); however, in this paper we unveil the magnetization and disclose magnetic features sized smaller than the light wavelength. Not only does the optical activity include rotation of the polarization plane upon reflection but also, when using violet light (diffraction regime), there is excitation of surface plasmon polaritons at the metal film and consequently, a strong effect on the magneto-optical activity: the transverse Kerr signal is enhanced up to one order of magnitude and the longitudinal Kerr signal changes sign, in comparison with the values of red light (subwavelength regime). Optical modelling led us to understand that features of the field-cycled MOKE are associated with the non-uniform spatial distribution of magneto-optical activity in the film whereby, firstly, the Kerr effect with red light arises at the lower half of the grating and, secondly, the use of violet light focuses the effect at the film ridges and valleys. The surface-MOKE measured with an in-plane field cycled at different angles indicates a distinctive feature: there is only one magnetic easy axis (groove direction) but two directions symmetrically about the hard axis where the coercive field vanishes. This dependence, in agreement with the micromagnetic simulations, is consistent with the formation of a pattern of antiparallel magnetic domains with nanometric periodicity at the remanent magnetization. We have verified the existence of the magnetic pattern with magnetic force microscopy. Our findings offer a novel way to disentangle the magnetization reversal of 3D corrugated materials by performing Kerr magnetometry at different optical regimes.
1 Introduction
Nanostructuration offers unique possibilities for magnetic materials as the macroscopic magnetic properties can be changed by tuning the relevant length scales.1 Linear nanostructuration of the material surface can be achieved e.g. by ion erosion procedures,1–5 which form periodic patterns that can modify the dipolar stray fields of the magnetic structures. These patterns imbue magnetic anisotropy to isotropic materials like polycrystalline NiFe (permalloy, Py) thin films.6 However, since the mean ion penetration depth depends on the primary energy of ions, the resulting structures have a low amplitude-to-periodicity aspect ratio of around 10%, limiting anisotropy engineering to films of low corrugation that offers a small effect on the anisotropy.3,7 Thermal annealing procedures6 or laser induced periodic surface structures (LIPSSs)8,9 can produce patterns of a higher corrugation aspect ratio as compared to those obtained with ion erosion, although pattern defects are still usually observed.10 This issue hinders the design of shape-engineered nanostructured magnetic materials due to the role of pattern defects and rugosity in the magnetic anisotropy contribution.7 These limitations can be overcome by using laser interference lithography11 as it can produce a regular periodic structure with a high corrugation aspect ratio (up to 180 nm height for 250 nm periodicity). Depositing magnetic thin films on these structures provides not only a workbench for anisotropy design for a wide range of film thicknesses, but also may induce a magnetic texture appropriate for applications.12,13Linear nanostructuration of magnetic materials modifies their behavior through the enhancement of dipolar magnetic interactions,7,14e.g. favoring a distribution of magnetic moments aligned with the pattern direction in a uniaxial anisotropy.15 This interaction may yield either parallel1–6,8,12,15 or antiparallel1,16 arrangement of magnetic domains along the anisotropy axis. Only a few reports present antiparallel alignment of magnetic domains1,16 in quasi periodic magnetic nanostructures. However, they lack irregular magnetic distributions which may make their implementation difficult in applications.17,18 We also previously studied a corrugated magnetic film with a large thickness12 where the moments of the upper and lower film interfaces are oriented antiparallel to each other, although the middle region remains uniformly magnetized. The formation of antiparallel domains in a very regular nanopattern throughout the film could be advantageous in non-conventional computing applications such as neural networks or racetrack memory.19–21 Device operation based on domain wall movement could benefit from an array of magnetization pinning sites associated with the nanopattern. We foresee an improvement of device reproducibility and, in the case of racetrack memory, a higher storage density as well.
Moreover, since the magnetic properties of these 3D systems depend strongly on spatial features,8,9 the obtention of ferromagnetic thin films with coherent morphology and amplitude ratios eases the reproduction of these magnetic configurations and the exploration of feasible candidates for applications. In this work we have studied a highly corrugated (180 nm in height, 250 nm in periodicity) permalloy-based thin film with a coherent triangular morphology, aiming for the formation of well-defined magnetic structures during the magnetization reversal process that could be used to develop optical magnetic field sensors.22
Besides the interesting magnetic properties that can be achieved by surface modification, it can also induce anisotropic magneto-optical properties23,24 that allow the implementation of magnetic field sensors. These sensors are based on surface plasmon-polariton (SPP) excitations25 that increase in a notable way the magneto-optical effects due to the enhancement of the near-field electric field.26,27 The key parameter in these sensors is the transverse Kerr effect amplitude enhancement when the SPP excitation is active. This behavior offers a wide range of possibilities for these sensors in chemical sensing.28,29 As recent works have shown, enhancement of the Kerr signal can be achieved in many magnetoplasmonic systems based on grating structures.23,24,30,31 However, these nanostructured metamaterials may present other optical phenomena such as wavelength-dependent high extinction ratios11,32 or rotation of polarization by reflection.33 This hampers the characterization of the magnetization reversal via the Kerr effect because the changes in light wavelength and grating orientation result in optical performance variations qualitatively equal to those induced by magnetization textures. To separate the film magnetization from the magneto-optical features, we perform a combination of Kerr effect measurements at different in-plane field angles and different wavelengths, namely: red (λ = 633 nm) and violet (λ = 405 nm).
2 Experimental methods
2.1 Film growth, patterning and microscopy
The materials system is comprised of a 27 nm thick permalloy (Ni80Fe20) thin film grown by normal-incidence DC sputtering onto a nanostructured silicon(100) wafer, which was fabricated using a procedure reported elsewhere.11,12 Briefly, the silicon(100) surface is prepared by laser interference lithography and then wet etched, yielding the triangular profile shown using lateral SEM in Fig. 1a. The optical interference determines the periodicity of the silicon substrate that, in our case, is 250 ± 10 nm. On top of the Si substrate a thin permalloy layer is sputtered at normal incidence with a rate of 3 Å s−1 under an argon atmosphere (PAr = 1 × 10−2 mbar, Pbase = 2 × 10−7 mbar). The deposition is conformal to the substrate at this film thickness12 as verified by AFM topography [Fig. 1b]. Using this procedure, we obtained a corrugated thin film that follows a triangular profile with a periodicity (Λ) of 250 nm and a symmetric elevation angle of 55°, topped by a 20 nm width plateau. The obtained material is hereafter referred to as PyST. The geometry defines two main directions: the groove axis, parallel to the grooves, and the grating axis, which is parallel to the grating vector, (see Fig. 1a). Control samples were grown on flat silicon substrates in the same deposition run. Permalloy film thickness was estimated from X-ray reflectometry (see the ESI†). Other permalloy films of similar thickness were deposited on identical silicon gratings to check the results reported in this work.
(see Fig. 1a). Control samples were grown on flat silicon substrates in the same deposition run. Permalloy film thickness was estimated from X-ray reflectometry (see the ESI†). Other permalloy films of similar thickness were deposited on identical silicon gratings to check the results reported in this work.
We have performed magnetic force microscopy (MFM) with a Nanosurf Naio AFM equipped with cobalt alloy coated AFM tips. MFM has been performed at remanence (zero applied field) after in-plane magnetic saturation (300 mT) along either the groove axis or the grating axis. Measurements have been carried out in the dual scan mode, with the first scan following the morphology and the second scan following a plane lifted 15 nm from the upper plateau of the nanostructured PyST sample.
2.2 Optical and magneto-optical experiments
The optical performance of the PyST system has been first characterized with the reflectance dependence on the azimuthal angle with the optical setup shown in Fig. 2, at an angle of incidence Θ = 45°, using violet (λ = 405 nm, λ < 2Λ) or red (λ = 633 nm, λ > 2Λ) laser sources. The incident beam is polarized with a Glan–Thompson prism in the TM (transverse magnetic) mode, i.e. the electric field is contained within the optical plane. The reflected beam is divided into its TM and TE (transverse electric) components using a Wollaston prism and both component intensities are recorded using photodiodes, yielding Rpp and Rsp for TM and TE polarization components, respectively. We can modify the azimuthal angle (α in Fig. 2) by rotating the sample 180° in steps of 0.9°, with α = 0° for , the grating vector, parallel to
, the grating vector, parallel to  , where
, where  is the normal to the optical plane (see Fig. 2). Besides the reflected beam, we observe another beam corresponding to the m = −1 diffraction order, as expected from the grating equation34
is the normal to the optical plane (see Fig. 2). Besides the reflected beam, we observe another beam corresponding to the m = −1 diffraction order, as expected from the grating equation34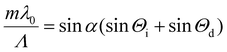 | (1) |
 , i.e. Θd = 90°. This phenomenon is known as the Rayleigh anomaly.35
, i.e. Θd = 90°. This phenomenon is known as the Rayleigh anomaly.35
Diffraction couples the incident light momentum with surface plasmon evanescent waves in metal–air interfaces yielding the Wood anomaly,36,37 reducing the reflectivity and increasing the magneto-optical effects26,38,39 due to the near-field electric field enhancement.40 The Wood anomaly occurs for a rotating diffraction grating, i.e. α as a variable, according to the following equation:36,38
kSPP2 = K2 + k20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θi + m2Kk0 Θi + m2Kk0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θi Θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α | (2) |
 | (3) |
 is the real part of the electric permittivity of the permalloy41 at a given wavelength λ0, and K = 2π/Λ is the modulus of the grating vector momentum. Rayleigh and Wood anomalies as a function of light wavelength and α are shown in the ESI† for the case of Θi = 45°.
is the real part of the electric permittivity of the permalloy41 at a given wavelength λ0, and K = 2π/Λ is the modulus of the grating vector momentum. Rayleigh and Wood anomalies as a function of light wavelength and α are shown in the ESI† for the case of Θi = 45°.
The optical setup [Fig. 2] is also used to measure the magneto-optical response with the sample placed in an electromagnet's bore whereby a magnetic field  is applied in the optical plane parallel to the sample surface, namely the longitudinal Kerr geometry.42 Test experiments to evaluate the Kerr reflectivity amplitude at magnetic saturation were also performed, with the magnetic field applied perpendicular to the optical plane, namely the transverse Kerr geometry. A wavelength-specific halfwave plate is added so the reflected beam polarization can be rotated prior to the Wollaston prism, maintaining the consistency of the Kerr signal components all over the angular range measurement. Kerr rotation and Kerr reflectivity responses of the ferromagnetic sample were recorded by applying an alternating magnetic field with an amplitude up to 90 mT and a low frequency (11 Hz). The experiment was carried out independently with violet (λ = 405 nm), blue (α = 450 nm) and red (λ = 633 nm) laser sources. We neglect the magneto-optical signal from the diamagnetic Si substrate because the Py thickness is more than twice the light penetration depth, i.e. δp ∼ 12 nm, according to reference data.41
is applied in the optical plane parallel to the sample surface, namely the longitudinal Kerr geometry.42 Test experiments to evaluate the Kerr reflectivity amplitude at magnetic saturation were also performed, with the magnetic field applied perpendicular to the optical plane, namely the transverse Kerr geometry. A wavelength-specific halfwave plate is added so the reflected beam polarization can be rotated prior to the Wollaston prism, maintaining the consistency of the Kerr signal components all over the angular range measurement. Kerr rotation and Kerr reflectivity responses of the ferromagnetic sample were recorded by applying an alternating magnetic field with an amplitude up to 90 mT and a low frequency (11 Hz). The experiment was carried out independently with violet (λ = 405 nm), blue (α = 450 nm) and red (λ = 633 nm) laser sources. We neglect the magneto-optical signal from the diamagnetic Si substrate because the Py thickness is more than twice the light penetration depth, i.e. δp ∼ 12 nm, according to reference data.41
The difference between the TE and TM intensities is related to the Kerr rotation angle θKerr, which is proportional to the magnetization of the system parallel to the direction of the applied field, namely longitudinal magnetization ML. The intensity of such an effect is defined by the magneto-optical rotation coefficient given as
 | (4) |
 | (5) |
 | (6) |
2.3 Optical modelling and micromagnetics
We have performed optical simulations using Rigorous Coupled-Wave Analysis GD-Calc® software.43 The model structure comprises a nanostructured silicon substrate44 with the same dimensions as those of our patterned wafer, topped by a continuous layer of 30 nm thick permalloy41 and vacuum (air) as the superstrate. We have simulated the reflectivity in the TM mode with an incidence angle of Θi = 45°. From the results of the electric field components within the Py film, we can estimate the local magneto-optical activity of the transverse MOKE as it is proportional to the product of the TM electric field components.45,46Finally, we have performed micromagnetic simulations to understand not only the macroscopic magnetic behavior obtained from the magneto-optical measurements but also the micromagnetic behavior and the magnetization reversal. To this purpose, a corrugated 27 nm thick magneto-crystalline isotropic permalloy thin film (Ms = 8.6 × 105 A m−1, Aex = 13.0 × 10−12 J m−1, data from ref. 47) with the same geometric features as those of PyST has been simulated using Mumax.48 The simulation environment comprised 8 full periodicities with periodic boundary conditions of 10 times the simulation environment in the X and Y directions, which correspond to the grating and groove axes of the triangular geometry depicted in Fig. 1. The cell size has been set at 0.97 nm, far below the theoretical exchange length of 5.3 nm. Hysteresis loops have been calculated for this structure starting from a maximum applied field of 4000 mT and a field step size of 1 mT.
3 Results and discussion
Fig. 3 depicts the dependence of reflectivity on the azimuthal angle α of PyST with red [Fig. 3a] and violet light [Fig. 3b] when the incident light is transverse magnetic (TM). In both figures, black dots represent total reflectivity, red dots represent TM reflected light (Rpp) and blue dots represent TE reflected light (Rsp). The experiments reveal a strong dependence on angle α for the three curves. For red light [Fig. 3a], at α = 0° (groove axis), we find maximum reflectivity (black curve) as the system works as a reflective mirror since the impinging light wavefronts are parallel to the pattern. On the other hand, at α = 90° (grating axis), destructive interference between reflected wavefronts49,50 decreases the total reflectivity, as was similarly reported by Brundrett et al.32 for a triangular silicon grating (Λ = 280 nm) in the visible range. From our reflectivity data, the extinction ratio between parallel (α = 0°) and perpendicular (α = 90°) cases is 2.7 for red light while it is 6.0 for violet light due to losses related to diffraction. The reflected light polarization state strongly depends on the angle, as seen by an increasing TE component (blue curve, Rsp) for angles between the groove and grating axes, as the metallic grating acts as a rotated reflective polarizer due to waveguiding effects.33,51 | ||
| Fig. 3 (a and b) Angular reflectivity of the PyST sample as a function of the azimuthal angle α, defined as shown in panel (e), for (a) red (λ = 633 nm) and (b) violet (λ = 405 nm) TM polarized light. Incidence angle was set at 45°. Red and blue curves correspond to TM (Rpp) and TE polarized (Rsp) reflected components, respectively, while black curves correspond to total reflected light from the sample (Rpp + Rsp). (c and d) Angular Kerr signal amplitude at saturation for (c) red and (d) violet light. Kerr rotation θKerr (blue) and Kerr reflectivity RKerr (black) amplitudes are derived from eqn (4) and (5). Rayleigh (α = 70°) and Wood (α = 55°) anomalies calculated from eqn (1) and (2) for λ = 405 nm and Θi = 45° are shown in red and green dotted lines, respectively. (e) AFM image of the nanostructure grooves.12 | ||
For the violet wavelength [Fig. 3b], Wood and Rayleigh anomalies modify the reflectivity dependence on the azimuthal angle. When the diffraction condition sets in at an α value between 70° and 110°, the TM intensity (red curve, Rpp) shows a peak corresponding to the Rayleigh anomaly. This is followed by a strong TM intensity decrease at α = 55° and α = 125° due to the absorption by the coupling of the impinging light with the surface plasmon – Wood anomaly – resembling a Fano-type resonance.52,53 The excitation of SPP is known to modify the magneto-optical Kerr effect in the transverse geometry with a large increase in Kerr reflectivity.36 Our measurements in longitudinal geometry are displayed in Fig. 3c and d for the Kerr rotation (θSatKerr) and Kerr reflectivity (RSatKerr), with red or violet light, respectively. Similarly to reports by Grunin and other authors,28,36 we note an enhanced Kerr reflectivity, RSatKerr, when the plane of incidence lies along the groove axis (α = 0°) up to 1550% for violet light as compared to red light (either value included in Table 1). This is a huge change of magnitude. On the other hand, the behavior of the Kerr rotation upon excitation of SPP is relevant. Whereas θSatKerr is negative at all azimuthal angles with red light, being maximum at the grating axis (α = 90°), it is positive for the violet light or nearly null at the angles between Wood and Rayleigh anomalies. Thus, a sign change is observed when the light wavelength crosses the plasmon resonance. Besides, a comparison of θSatKerr when the plane of incidence lies along the grating axis shows an enhanced rotation for the violet light by as much as 87.5% over the value of red light (Table 1). Again, the use of violet light – near the SPP resonance – eases the magneto-optical effect sensing.
| λ (nm) | ΔθSatKerr/R (α = 0°) | ΔθSatKerr/R (α = 90°) | ΔRSatKerr/R (α = 0°) | ΔRSatKerr/R (α = 90°) |
|---|---|---|---|---|
| 633 | −0.012% | −0.088% | 0.037% | −0.341% |
| 405 | 0.045% | 0.165% | 0.613% | 0.260% |
We would like to point out that the qualitative dependence of the intensity ratios on the azimuthal angle is the opposite. In fact, the grating axis (α = 90°) to groove axis (α = 0°) Kerr reflectivity ratio is as large as 9.3 for red light and just 0.42 for violet light but, in contrast, the total reflectivity – extinction ratio – for red light (2.7) is less than that for violet light (6.0). So, we can infer that the intensity of the magneto-optical signal is not directly dependent on the total reflectivity. We associate the observed changes in the Kerr effect coefficient dependence on the wavelength and angle with optical anomalies35,37 that lead to abrupt changes in media permittivity.50,54 Our results, summarized in Table 1, show that it is possible to increase the Kerr effect by one order of magnitude by decreasing the light wavelength from red to violet as well as by rotating the nanostructured sample from the groove axis, where no optical anomalies are expected to occur, to the grating axis. Furthermore, the ratio of ΔRSatKerr/R and ΔθSatKerr/R for the same azimuthal angle and wavelength yields the quantitative relation between transverse (MT/MS) and longitudinal (ML/MS) reduced magnetizations, respectively, which makes clear how to infer the surface magnetization from the Kerr measurement.
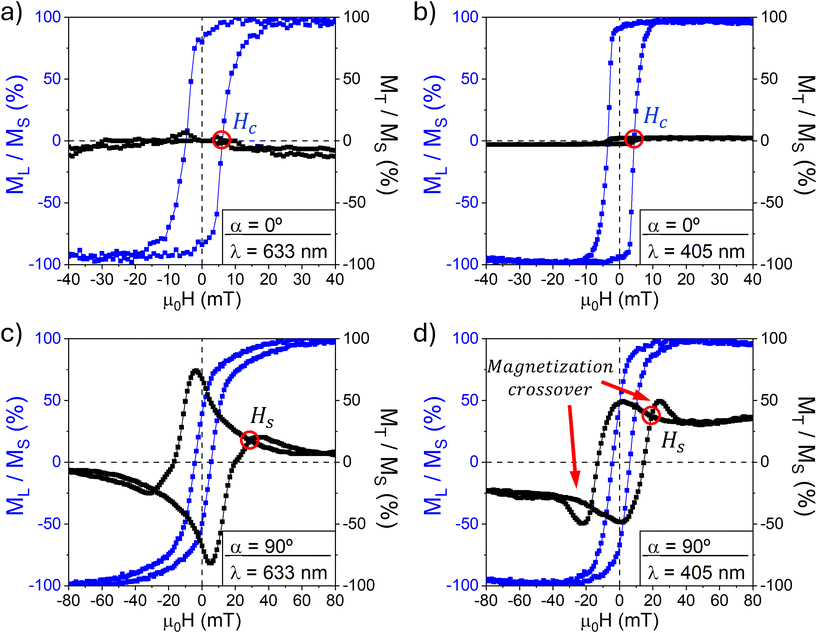
Magnetization reversal curves measured with longitudinal Kerr magnetometry using red and violet light lasers and the electromagnetic field parallel to the groove axis (α = 0°) [Fig. 4a and b] show square-like hysteresis loops in the longitudinal magnetization (ML, blue) that resemble that of easy axes in uniaxial anisotropic systems. The coercive field Hc of 5 mT is moderate and the longitudinal remanence of about 90–95% of the saturation magnetization is high. For this configuration, the transverse magnetization (MT, black) is negligible at all fields, showing that the magnetization tends to point parallel to the grooves of the pattern in a single domain as it minimizes the energy of the system.
Magnetization reversal curves with the applied field parallel to the grating axis (α = 90°) [Fig. 4c and d] show hysteretic behavior in the longitudinal magnetization (ML) with a remanent magnetization of 50% of the saturation value. The transverse magnetization, MT, proportional to Kerr reflectivity RKerr, measured with red light [Fig. 4c] resembles the behavior of hard axes of uniaxial systems with a coherent rotation reversal. The maximum transverse magnetization occurs at the coercive field (Hc, defined as the magnetic field where the longitudinal magnetization is reversed). This fact together with the hysteretic longitudinal magnetization indicates that the mechanism of magnetization reversal in our PyST system comprises both domain nucleation and coherent rotation. For the violet light [Fig. 4d], the transverse magnetization loop qualitatively deviates from the case of red light, showing a substantial magnetization crossover and a switching field value of 18 mT apparently lower than that of 28 mT with red light. These magnetic features will be discussed later regarding the estimates of magneto-optical activity. For now, the observed magnetic features at both the groove and grating axis loops indicate that the magnetization reversal is driven by domain nucleation rather than coherent rotation. We also note that transverse magnetization with violet light is not null at magnetic saturation, contrary to the expected behavior. This might be due to second order (quadratic) magneto-optical effects42 that could be emphasized at this wavelength.
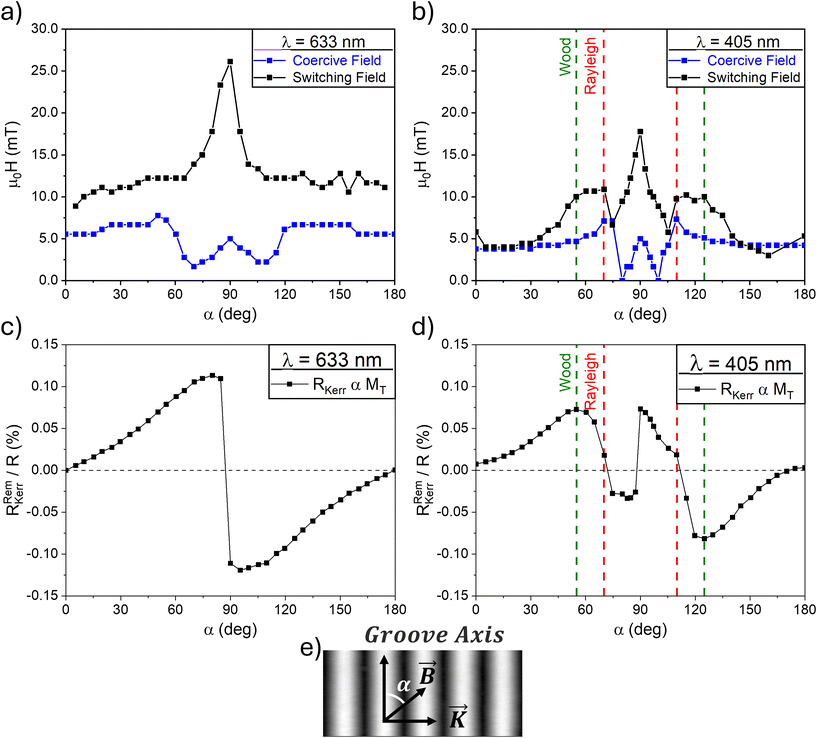
The standard approach to study the magnetic anisotropy and reversal mechanisms of magnetic plane systems is the measurement of hysteresis loops at the whole set of different angles α between the in-plane applied field and the main axis. Nano-corrugated ferromagnetic systems exhibit magnetic anisotropy due to shape-induced demagnetizing fields.3,7,8,12 Our previous studies12 proved that demagnetizing fields modify magnetization reversal in a non-straightforward way. To understand the reversal pathway, we have extracted the critical fields, i.e. coercive and switching fields, from the hysteresis loops measured at different angles α. The results for red and violet light are shown in Fig. 5a and b. We define the switching field, Hs, as the applied magnetic field at which the two branches of the transverse magnetization merge (see Fig. 4). This field provides an estimation of the anisotropy field out of its hard axis8,9 as it is proportional to the field needed to saturate the magnetization when it rotates.
 | ||
| Fig. 5 (a and b) Dependence on the angle α (as defined in panel (e)) of magnetization reversal fields of PyST: coercive field Hc (blue) and switching field Hs (black) for (a) red light and (b) violet light. (c and d) Angular dependence on angle α of the remanent Kerr reflectivity RRemKerr/R (proportional to transverse magnetization MT) calculated from eqn (6) for (c) red light and (d) violet light. Switching field and remanent transverse magnetization distributions from red light measurements resemble that from a uniaxial magnetic system, while the data from violet light differ due to the role of optical anomalies in magneto-optical measurements. Rayleigh (α = 55°) and Wood (α = 68°) anomalies are shown in red and green dotted lines, respectively. (e) AFM image of the substrate as shown in Fig. 3. | ||
Fig. 5(a) presents the switching field determined from loops measured with different in-plane field angles, Hs(α) – black curve – whose dependence matches the prediction of the simple Stoner–Wolfarth model and therefore indicates a single hard axis at the grating axis (α = 90°) where the switching field is maximum. This resembles a conventional uniaxial magnetization behavior with the anisotropy (easy) axis being the groove axis. The magnitude of the anisotropy field is μ0Hk ≈ 26 mT and the uniaxial anisotropy energy density can be estimated Ku = ½HkMs = 0.76 × 104 J m−3 as a comparatively moderate value. Besides, the remanent transverse magnetization dependence on the field angle MT(α) – proportional to reflectivity data in Fig. 5c – agrees well with the Stoner–Wolfarth prediction for the uniaxial system. In fact, with red light, RRemKerr increases from a negligible value at the groove axis to its maximum at α ≈ 90° and changes sign at the grating axis; this is expected for the uniaxial system when crossing the hard axis.42
The experiments of Hs(α) measured with violet light [Fig. 5b] again show a maximum at the grating axis and confirm the uniaxial anisotropy; however, other features are present in the two ranges of angles where optical anomalies set in, symmetrically placed at both sides of the grating axis; the switching field values are clearly enhanced for angles near and between those corresponding to the Wood and Rayleigh anomalies. The complex relation between magnetization and the magneto-optical coefficients is also observed with the remanence Kerr reflectivity, RRemKerr – proportional to transverse magnetization MT in the absence of the applied field – dependence on the field angle [Fig. 5d]. For violet light, the angular behavior follows partially the trend observed for red light, but with significant deviations in the angle range from α = 55° to α = 125°. Since the transverse remanence is measured with the Kerr reflectivity, the excitation of SPP in the Wood anomaly is expected to interplay. Additionally, RRemKerr reverses its sign at α = 70° and α = 110° as the sample enters the diffraction condition at the Rayleigh anomaly, changing the response of the magneto-optical signal in relation to the magnetization state of the sample.
More interesting is the unique dependence of the coercive field on the applied field angle [blue curves in Fig. 5a and b]. It is remarkable that the coercive field, Hc(α), measured with either red or violet light does not show the uniaxial behavior with a vanishing coercive field at the hard axis. Instead, the Hc(α) curve includes two small dips at α = 70° and 110° for red light, and similarly at α = 80° and 100° for violet light. The coercive force thus vanishes or nearly vanishes at both directions symmetrically about the hard axis but not coinciding with it. The fact that these occur with both wavelengths is evidence of the intrinsic magnetization effect. To our knowledge, this is the first time that such an unfold of the coercive field has been reported.
The hysteretic longitudinal magnetization in the hard axis [Fig. 4c and d] suggested the role of domain wall propagation and magnetization rotation in the reversal. We may argue there must be a non-colinear domain structure in the hard axis, a remanent state that evolves to a single domain by domain wall propagation and annihilation whereas part of the structure rotates. Thus, only if a sufficient field is applied along the groove axis the domain walls completely disappear, i.e. a threshold longitudinal field is required to break the remanent state. In the angular dependence of Fig. 5a and b, this threshold point corresponds to the two angles of the dips close to the grating axis.
We shed light on the remanent domain structure by performing micromagnetic simulations of the magnetization reversal with the field along the grating axis (α = 90°). To avoid spurious solutions related to local minima in the minimization process, we need to introduce a small deviation (0.6°) of the applied field direction from the grating axis. The small deviation leads to different magnetization loops depending on whether the field is considered slightly towards the groove axis i.e. the strictly in-plane field [Fig. 6a] or slightly towards the normal i.e. off-plane [Fig. 6b]. With a small in-plane deviation, the hard axis loop in Fig. 6a shows that the magnetization rotates coherently when magnetization reverses in a way similar to the single domain model.55,56 The magnetic domain distribution that corresponds to the labeled points in the hysteresis loop is shown in Fig. 7A–D, revealing that the ridges and valleys are magnetized collinearly along the groove axis (Fig. 7A), respectively, also in the remanent state (Fig. 7B), where MT is maximum in a single domain parallel to the groove axis. As the field is increasingly reversed, the magnetization follows partially the applied field direction (Fig. 7C), but the domain walls remain pinned up to 340 mT (Fig. 7D), at which MT reduces to zero and the magnetization follows the cross-section profile. The simulated hysteresis loop has qualitatively the same features as that obtained from red Kerr measurements [Fig. 4c].
 | ||
| Fig. 6 (a) Simulated magnetization loop with the applied field along the grating axis for a model having the same pattern dimensions and thickness as the PyST film, considering a small in-plane deviation of the applied field (α = 90.6°). Reduced longitudinal ML (blue) and transverse MT (black) magnetizations are plotted. (b) The same components calculated with the field along the grating axis considering a small off-plane deviation (α = 90° and α = 0.6°). Micromagnetic distributions of magnetic states (A–D) and states (E–H) are shown in Fig. 7. | ||
 | ||
| Fig. 7 Simulated micromagnetic distribution during the magnetization reversal process of a PyST film with a magnetic field applied along the grating axis as shown in the image below. Panels (A–D) correspond to states indicated in Fig. 6a for the hysteresis loops calculated with a strictly in-plane field i.e. including a small in-plane deviation, while panels (E–H) correspond to states indicated in Fig. 6b for the hysteresis loops calculated with an in-plane field including a small off-plane deviation. See the text for details. | ||
Next, we considered the case of a small off-plane deviation i.e. a hard axis field just 0.6° towards the plane normal. We must point out that this small deviation used for the calculations lies within the angle uncertainty of our optical setup; this case can thus be taken as unavoidable. The calculated magnetization curve in Fig. 6b shows some features that may resemble the crossover in the Kerr loops measured with violet light [Fig. 4d]. In this case, the small deviation induces a completely different domain structure as shown in Fig. 7E–H: the magnetization reversal is driven by nucleation and propagation of domain walls with the magnetic moments of ridges and valleys being parallel and antiparallel to the groove axis, respectively [Fig. 7E]. The domain walls move uphill as the magnetic field is reversed, as can be clearly seen in Fig. 7F and G which correspond to the remanent state of 0 mT and to a reversed field of 60 mT, respectively. This domain wall movement results in an annihilation of the upper magnetic domain, which translates into an increase in the transverse magnetization as seen in the measured loop [Fig. 6b]. This increase would be the cause of the observed transverse magnetization crossover in violet light Kerr measurements [Fig. 4d]. The antiparallel domain structure put forward in the micromagnetic simulations is consistent with the measurements of critical fields and the evidence of a vanishing coercive field at two angles symmetrically about the anisotropy axis. We have further explored the stability of the antiparallel domain structure at different in-plane angles, as well as a prediction of behavior with different grating dimensions, in the ESI.†
To validate our hypothesis, we have used magnetic force microscopy to compare the domain structure with the simulations of the remanent state. Because of the surface corrugation, the following measuring approach has been used: the magnetic force probe is scanned in a fixed plane above the hills and the magnetic phase contrast is recorded, for two different remanent states either after the magnetic saturation along the grooves or after magnetic saturation across the grooves. This allows us to validate the hypothesis of the formation of dipoles at transverse remanence as is the case from the calculations with a slight off-plane field deviation.
For the remanence state after saturation in the groove axis [Fig. 8a], phase contrast shows narrow bands (90 nm wide) at the ridges of the PyST film. In this direction, the remanent distribution is expected to correspond to a single domain structure as in Fig. 7B like in a canonical magnetic easy axis. Therefore, phase contrast bands would correspond only to the topography of the sample with no magnetic interaction between the ferromagnetic film and MFM tip. For the remanence state after saturation in the grating axis [Fig. 8b], phase contrast splits into two adjacent bands of opposite signs with the positive band coinciding with the peak of the structure and a side band with a negative sign at its side, enlarging the MFM span range from 90 to 150 nm wide. This splitting of the MFM phase contrast bands is caused by the interaction between the MFM tip and the upwards and downwards magnetic domain walls that enclose antiparallel domains at the ridges of the nanostructure, as in Fig. 7F. We can see from both microscopy images and Kerr loops that the micromagnetic distribution as calculated with slight off-plane field deviation is more likely to appear during magnetization reversal in the grating axis because the antiparallel domain pattern possesses greater stability.
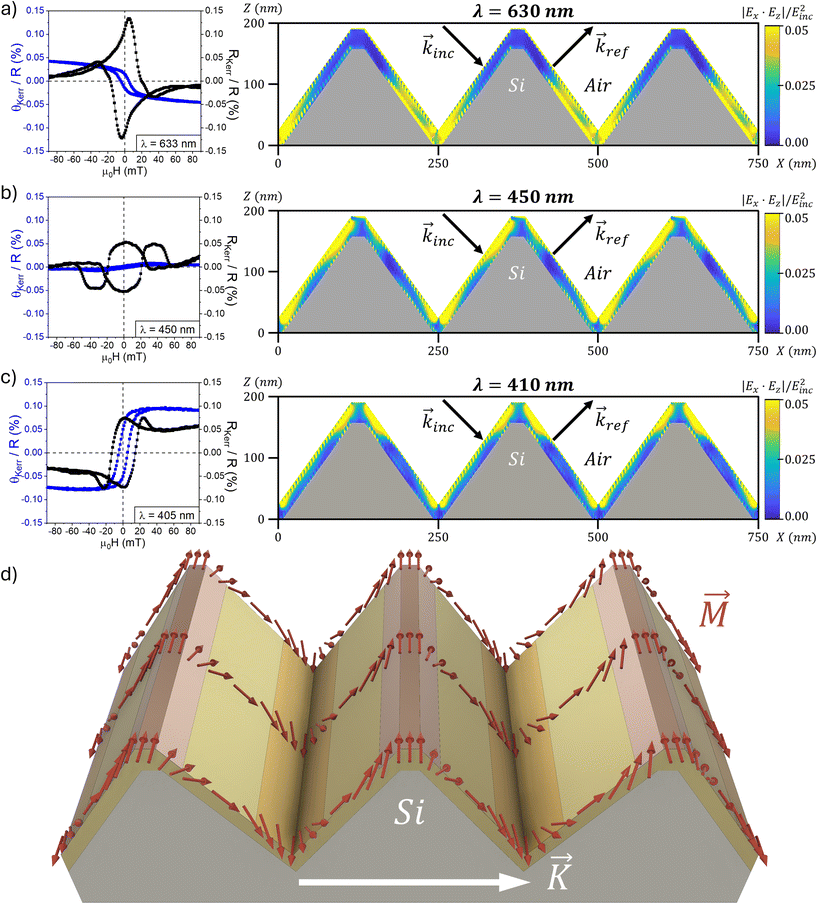
To disclose how the interaction of light with the metallic grating affects the measurement of Kerr loops, we have calculated the spatial distribution of transverse magneto-optical activity45,46 (RKerr) with the grating axis in the optical plane, which is proportional to the product of the two TM electric field components |Ex·Ez| [Fig. 9]. When no SPP are active, with red light [Fig. 9a], the magneto-optical activity of the thin film is almost uniform on the lower half of the nanostructure, while negligible in the upper half. We can observe from micromagnetic simulations [Fig. 9d and 7E–H] that the antiparallel magnetic domains formed in the transverse remanence split onto the top and the bottom of the nanostructure. Thus, the transverse Kerr signal with red light would arise from only the bottom part. The Kerr signal would carry information only from one type of domain i.e. a given moment direction, and the transverse hysteresis loop must therefore resemble that of a single domain, as observed in Fig. 4c.
For blue light [Fig. 9b], and due to the excitation of SPP in the metal–air interface,46 the magneto-optical activity is more intense in the top and bottom parts of the metal film. In this configuration, the longitudinal Kerr effect nearly vanishes while Kerr reflectivity is largely enhanced due to the change in the plasmon resonance frequency with the sample transverse magnetization.57 The enhanced magneto-optical activity in the film ridges and valleys is responsible for the magnetization crossover notably observed in the Kerr reflectivity loop branches (black curve in Fig. 9b). This would correspond to the reversal of the asymmetric plateau of the nanostructure pinpointed in Fig. 7G and H.
Similarly, with violet light [Fig. 9c], the magneto-optical activity redistributes around the film ridges and valleys. It just turns out slightly more focused at these locations in comparison with the case of blue light. A possible explanation is a sub-diffraction focusing of the electromagnetic field thanks to the combination of evanescent and propagating waves of the Rayleigh and Wood anomalies.40 The Kerr reflectivity loop (black curve) still shows a magnetization crossover that is comparatively less than the corresponding loop with blue light due to the same mechanisms. The Kerr rotation loop (blue curve) shows that the sign of the Kerr angle at saturation is opposite to that measured with red light. Chen et al.58 explained this effect in terms of a dipole oscillator model for the action of free electrons in response to an external magnetic field. In this model, the phase delay of the oscillation relative to the Lorentz force changes sign at light frequencies above a resonant frequency. The enhancement of Kerr reflectivity by one order of magnitude with violet light [Fig. 3c and d] and the dependence of the total reflectivity [Fig. 3b] prove that we can excite surface plasmon resonances in our system for wavelengths of the Wood anomaly. Hence, we can understand the sign change of the Kerr rotation with wavelength as a change of the phase delay between the light wave and the induced Lorentz force arising from the plasmon resonance. This effect has also been reported in Ag/Co composite nanogratings59 in either TM or TE modes where, especially in the TM mode, the Kerr rotation angle becomes small for wavelengths away from the resonance. This is in qualitative agreement with the reduced saturation value of Kerr rotation we measure with red light in Fig. 9a.
The combination of the macroscopic probe of magnetization – the MOKE at different wavelengths – the micromagnetics and the modelling of the microscopic MOKE activity is thus the successful analysis of the magnetic structure with spatial resolution that we summarize in Fig. 9d. The width of the ridge domains has been estimated to be ∼65 nm from the phase-contrast MFM scans [Fig. 8b], and the valley domains are assumed to be of equal lateral size. The type of domain wall in a Py film of a low thickness of ∼27 nm could be either Néel or cross-tie.14
4 Conclusions
In summary, we have fabricated a magnetic metamaterial based on a ferromagnetic thin film grown onto a silicon wafer with a nanometric triangular surface profile. Our material system polarizes light upon reflection and exhibits angle-tunable magneto-optical activity that can be further enhanced with the excitation of surface plasmon polaritons with light wavelengths close to the Wood and Rayleigh anomalies. We have characterized magnetization reversal by combining Kerr magnetometry measured with monochromatic light of different optical regimes – red or violet light for the subwavelength and diffraction regimes, respectively – which clearly influence the recorded hysteresis loops. The magnetization loops, the critical fields and the micromagnetic distribution reveal a uniaxial magnetic material that forms unusual antiparallel magnetic domains in the remnant state that follows a transverse magnetization cycle. We have confirmed the occurrence of the latter by magnetic force microscopy measurements and found that this antiparallel domain pattern only appears in transverse magnetization reversal. The antiparallel domain pattern is stable after the field is turned off, also in a sense that it only converts to a single domain when the in-plane field is cycled at least ∼10 degrees off the hard axis. Distributions of the magneto-optical activity in the nanograting are calculated and explain which parts of the film are active and influence the Kerr loop measurements. In this way, we have learned that red diode laser light (subwavelength regime) serves to probe the magnetization of the lower half of the grating profile and is appropriate to clarify the magnetic anisotropy and reversal mechanisms. Complementarily, the violet diode laser light (diffraction regime) focuses the magneto-optical activity especially on the grating ridges and valleys due to the excitation of surface plasmon polaritons and serves to enhance the detection of magnetization crossover.The occurrence of such 3D magnetic states in addition to the large magneto-optical activity of the system makes it a promising material for optical magnetic sensing or computing applications, where the tunability and improved magnetic stability of nanopatterns are of great interest.
Author contributions
Rafael Delgado-Garcia: conceptualization, investigation, methodology, formal analysis, writing – original draft, writing – review & editing, visualization, and funding acquisition. Ruben Guerrero: investigation, methodology, formal analysis, writing – original draft, writing – review & editing, and visualization. Gabriel Rodriguez-Rodriguez: investigation, writing – review & editing, and supervision. Fernando Galvez: investigation, writing – review & editing, and visualization. Miguel Angel Arranz: investigation and writing – review & editing. Jose M. Colino: conceptualization, investigation, validation, writing – original draft, writing – review & editing, project administration, funding acquisition, and supervision.Data availability
Data for this article are available at the Open Science Framework,60 including the following: SEM image from Fig. 1. Nanosurf AFM-MFM raw data from Fig. 1 and 8. We analyzed these data using Gwyddion software.61 Data from the figures in the text. Code from optical simulations done using GDCalc.62 Simulation results from optical simulations done using GDCalc.62 Code from micromagnetic simulations done using Mumax.48 The results from micromagnetic simulations using Mumax.48 We visualized these data using Muview software.63Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
This work has been funded by the Universidad de Castilla-La Mancha (grant reference 2022-GRIN-34151). Rafael Delgado-Garcia thanks the UCLM and Diputación de Toledo for his research grant with reference 2021-REGIONA-10488, as well as the UCLM with the FSE+ for his predoctoral contract with reference 2021-UNIVERS-10626. We thank Dr Carlos Pecharromán for his valuable discussions on optical characterization.References
- J. Fassbender, T. Strache, M. O. Liedke, D. Markó, S. Wintz, K. Lenz, A. Keller, S. Facsko, I. Mönch and J. McCord, New J. Phys., 2009, 11, 125002 CrossRef.
- M. A. Arranz, J. M. Colino and F. J. Palomares, J. Appl. Phys., 2014, 115, 183906 CrossRef.
- M. O. Liedke, M. Körner, K. Lenz, M. Fritzsche, M. Ranjan, A. Keller, E. Čižmár, S. A. Zvyagin, S. Facsko, K. Potzger, J. Lindner and J. Fassbender, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024424 CrossRef.
- S. Koyiloth Vayalil, A. Koorikkat, A. K. Gopi, S. V. Roth and P. S. Anil Kumar, J. Phys.: Condens. Matter, 2020, 32, 185804 CrossRef PubMed.
- J. M. Colino, M. A. Arranz, A. J. Barbero, A. Bollero and J. Camarero, J. Phys. D: Appl. Phys., 2016, 49, 135002 CrossRef.
- S. Ki and J. Dho, Appl. Phys. Lett., 2015, 106, 212404 CrossRef.
- E. Schlömann, J. Appl. Phys., 1970, 41, 1617–1622 CrossRef.
- E. H. Sánchez, G. Rodriguez-Rodriguez, R. Aragón, M. A. Arranz, E. Rebollar, M. Castillejo and J. M. Colino, J. Magn. Magn. Mater., 2020, 514, 167149 CrossRef.
- M. A. Arranz, E. H. Sánchez, E. Rebollar, M. Castillejo and J. M. Colino, Opt. Express, 2019, 27, 21285–21294 CrossRef CAS PubMed.
- Y. Fuentes-Edfuf, J. A. Sánchez-Gil, C. Florian, V. Giannini, J. Solis and J. Siegel, ACS Omega, 2019, 4, 6939–6946 CrossRef CAS.
- S. Domínguez, O. García, M. Ezquer, M. J. Rodríguez, A. R. Lagunas, J. Pérez-Conde and J. Bravo, Photonics Nanostruct., 2012, 10, 46–53 CrossRef.
- R. Delgado-Garcia, G. Rodriguez-Rodriguez, R. Guerrero, F. Galvez and J. M. Colino, J. Appl. Phys., 2023, 133, 053901 CrossRef CAS.
- A. Hierro-Rodriguez, G. Rodríguez-Rodríguez, J. M. Teixeira, G. N. Kakazei, J. B. Sousa, M. Vélez, J. I. Martín, L. M. Alvarez-Prado and J. M. Alameda, J. Phys. D: Appl. Phys., 2013, 46, 345001 CrossRef.
- A. Hubert and R. Schäfer, Magnetic Domains, Springer Berlin Heidelberg, Berlin, Heidelberg, 1998 Search PubMed.
- K. Chen, R. Frömter, S. Rössler, N. Mikuszeit and H. P. Oepen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 064432 CrossRef.
- K. I. Fukunaga and A. Sugawara, J. Appl. Phys., 2008, 103, 053909 CrossRef.
- I. V. Shvets, H. C. Wu, V. Usov, F. Cuccureddu, S. K. Arora and S. Murphy, Appl. Phys. Lett., 2008, 92, 023107 CrossRef.
- J. Wang, F. Cuccureddu, R. Ramos, C. Ó. Coileáin, I. V. Shvets and H.-C. Wu, SPIN, 2019, 09, 1950004 CrossRef CAS.
- A. Sengupta, Y. Shim and K. Roy, IEEE Trans. Biomed. Circuits Syst., 2016, 10, 1152–1160 Search PubMed.
- S. S. P. Parkin, M. Hayashi and L. Thomas, Science, 2008, 320, 190–194 CrossRef CAS PubMed.
- J.-C. Jeon, A. Migliorini, L. Fischer, J. Yoon and S. S. P. Parkin, ACS Nano, 2024, 18, 14507–14513 CrossRef CAS PubMed.
- T. Haider, Int. J. Electromagn. Appl., 2017, 7, 17–24 Search PubMed.
- D. V. Murzin, V. K. Belyaev, F. Groß, J. Gräfe, M. Rivas and V. V. Rodionova, Jpn. J. Appl. Phys., 2020, 59, SEEA04 CrossRef CAS.
- D. Murzin, V. Belyaev, J. Kern, C. Kaspar, W. H. Pernice, R. Bratschitsch and V. Rodionova, Photonics, 2022, 9, 989 CrossRef.
- M. A. Haque, R. Rahad, Md. O. Faruque, M. S. Mobassir and R. H. Sagor, Sens. Biosens. Res., 2024, 43, 100618 Search PubMed.
- V. K. Belyaev, V. V. Rodionova, A. A. Grunin, M. Inoue and A. A. Fedyanin, Sci. Rep., 2020, 10, 7133 CrossRef CAS PubMed.
- F. Usman, K. H. Ghazali, R. Muda, N. H. Johari, J. O. Dennis, N. Tamam, A. Sulieman and Y. Ji, Sens. Actuators Rep., 2023, 6, 100172 CrossRef.
- Q. Wang, H. Yao, Y. Feng, X. Deng, B. Yang, D. Xiong, M. He and W. Zhang, Opt. Express, 2021, 29, 10546 CrossRef CAS PubMed.
- H. Chai, Y. Lu and W. Zhang, Results Phys., 2021, 31, 105049 CrossRef.
- V. K. Belyaev, D. V. Murzin, N. N. Perova, A. A. Grunin, A. A. Fedyanin and V. V. Rodionova, J. Magn. Magn. Mater., 2019, 482, 292–295 CrossRef CAS.
- G. Du, Y. Zuo, N. Liu, Z. Liu, L. Zhang and W. Zhang, ACS Appl. Mater. Interfaces, 2023, 15, 31087–31091 CrossRef CAS PubMed.
- D. L. Brundrett, T. K. Gaylord and E. N. Glytsis, Appl. Opt., 1998, 37, 2534–2541 CrossRef CAS PubMed.
- M. Xu, H. P. Urbach, D. K. G. de Boer and H. J. Cornelissen, Opt. Express, 2005, 13, 2303 CrossRef CAS PubMed.
- M. Born, E. Wolf, A. B. Bhatia, P. C. Clemmow, D. Gabor, A. R. Stokes, A. M. Taylor, P. A. Wayman and W. L. Wilcock, Principles of Optics, Cambridge University Press, 1999 Search PubMed.
- A. A. Darweesh, S. J. Bauman, D. T. Debu and J. B. Herzog, Nanomaterials, 2018, 8, 809 CrossRef PubMed.
- A. A. Grunin, A. G. Zhdanov, A. A. Ezhov, E. A. Ganshina and A. A. Fedyanin, Appl. Phys. Lett., 2010, 97, 261908 CrossRef.
- A. A. Maradudin, I. Simonsen, J. Polanco and R. M. Fitzgerald, J. Opt. (U. K.), 2016, 18, 024004 CrossRef.
- A. A. Grunin, A. V. Chetvertukhin, T. V. Dolgova, A. A. Ezhov and A. A. Fedyanin, J. Appl. Phys., 2013, 113, 17A946 CrossRef.
- G. A. Knyazev, P. O. Kapralov, N. A. Gusev, A. N. Kalish, P. M. Vetoshko, S. A. Dagesyan, A. N. Shaposhnikov, A. R. Prokopov, V. N. Berzhansky, A. K. Zvezdin and V. I. Belotelov, ACS Photonics, 2018, 5, 4951–4959 CrossRef CAS.
- A. Sentenac and P. C. Chaumet, Phys. Rev. Lett., 2008, 101, 013901 CrossRef PubMed.
- K. K. Tikuišis, L. Beran, P. Cejpek, K. Uhlířová, J. Hamrle, M. Vaňatka, M. Urbánek and M. Veis, Mater. Des., 2017, 114, 31–39 CrossRef.
- E. Jiménez, N. Mikuszeit, J. L. F. Cuñado, P. Perna, J. Pedrosa, D. Maccariello, C. Rodrigo, M. A. Niño, A. Bollero, J. Camarero and R. Miranda, Rev. Sci. Instrum., 2014, 85, 053904 CrossRef PubMed.
- C. Kenneth, Johnson, Grating Diffraction Calculator (GD-Calc ®), DOI:10.24433/CO.7479617.v4.
- M. A. Green, Sol. Energy Mater. Sol. Cells, 2008, 92, 1305–1310 CrossRef CAS.
- P. Bertrand, C. Hermann, G. Lampel, J. Peretti and V. Safarov, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 64, 235421 CrossRef.
- C. Clavero, K. Yang, J. R. Skuza and R. A. Lukaszew, Opt. Express, 2010, 18, 7743 CrossRef CAS PubMed.
- J. Wang, X. Zhang, X. Lu, J. Zhang, Y. Yan, H. Ling, J. Wu, Y. Zhou and Y. Xu, Appl. Phys. Lett., 2017, 111, 072401 CrossRef.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, AIP Adv., 2014, 4, 107133 CrossRef.
- N. I. Petrov, V. A. Danilov, V. V. Popov and B. A. Usievich, Quantum Electron., 2018, 48, 537–544 CrossRef CAS.
- P. Cheben, R. Halir, J. H. Schmid, H. A. Atwater and D. R. Smith, Nature, 2018, 560, 565–572 CrossRef CAS PubMed.
- D. Kim, Appl. Opt., 2005, 44, 1366 CrossRef PubMed.
- U. Fano, J. Opt. Soc. Am., 1941, 31, 213 CrossRef.
- B. Luk'Yanchuk, N. I. Zheludev, S. A. Maier, N. J. Halas, P. Nordlander, H. Giessen and C. T. Chong, Nat. Mater., 2010, 9, 707–715 CrossRef PubMed.
- Z. Q. Qiu and S. D. Bader, J. Magn. Magn. Mater., 1999, 200, 664–678 CrossRef CAS.
- C. Tannous and J. Gieraltowski, Eur. J. Phys., 2008, 29, 475–487 CrossRef CAS.
- J. L. F. Cuñado, A. Bollero, T. Pérez-Castañeda, P. Perna, F. Ajejas, J. Pedrosa, A. Gudín, A. Maldonado, M. A. Niño, R. Guerrero, D. Cabrera, F. J. Terán, R. Miranda and J. Camarero, Sci. Rep., 2017, 7, 13474 CrossRef PubMed.
- M. S. Kushwaha and P. Halevi, Phys. Rev. B:Condens. Matter Mater. Phys., 1987, 36, 5960–5967 CrossRef PubMed.
- L. Chen, J. Gao, W. Xia, S. Zhang, S. Tang, W. Zhang, D. Li, X. Wu and Y. Du, Phys. Rev. B, 2016, 93, 214411 CrossRef.
- R. Zhu, L. Chen, S. Tang and Y. Du, Appl. Phys. Express, 2021, 14, 092007 CrossRef CAS.
- R. Delgado-Garcia, R. Guerrero, G. Rodriguez-Rodriguez, F. Galvez, M. A. Arranz and J. M. Colino, 2024, Supporting Data from Stable Antiparallel Domains in 3D Corrugated Magnetic Thin Films, Open Science Framework, https://osf.io/6a9u3/?view_only=6b2c670bb87b409789d8505def1adc07.
- P. Klapetek, D. Nečas and C. Anderson, 2023, Gwyddion user guide, https://gwyddion.net/documentation/user-guide-en/.
- K. C. Johnson, 2022, Grating Diffraction Calculator, Code Ocean, https://codeocean.com/capsule/8614002/tree/v4.
- G. Rowlands, MuView2, GitHub, 2018, https://github.com/grahamrow/Muview2 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr05263c |
| This journal is © The Royal Society of Chemistry 2025 |