Hydride-containing Ag- and Au-rich 8-electron superatomic icosahedral cores: a DFT investigation

Abstract

Following several reports on ligand-protected atom-precise nanoclusters which encapsulate hydrides as interstitial dopants within their icosahedral core, the stability, structure and bonding of MH_x@Ag₁₂ and MH_x@Au₁₂ (M = Mo–Ag; W–Au) 8-electron cores is investigated through DFT calculations. The encapsulation of up to x = 3 hydrides appears to be possible but at the cost of substantial structural distortions. In most of the computed models, the hydrides are found nearly free to move inside their icosahedral cages. Systems with one (nido-type) or two (arachno-type) missing vertices on the icosahedron are also predicted to be viable. In general, the MH_x@Au₁₂ species appear to be of lower stability than their MH_x@Ag₁₂ homologs. We believe that this the work will provide some new directions for the synthesis of hydride-encapsulating superatoms.

---

1. Introduction

The chemistry of atom-precise noble metal nanoclusters has become increasingly topical since the turn of the century. The major reason lies in their numerous potential applications in various fields such as photonics, health sciences, or catalysis.^1–4 Moreover, their atom-precise nature makes them accurate molecular models for less well-defined nanoparticles of larger size. In recent years, researches have turned to the fine-tuning of the noble metal nanocluster properties by their controlled doping with another metal. Designing nanoclusters for their optimized properties requires in the first-place stability. This stability is ordinarily ensured through the presence of ligands such as chalcogenolates, alkynyl, phosphines, or halogenides. These ligands not only “protect” the metallic core, but also in many cases counterbalance its formal positive charge. Indeed, in most cases the structure and electron count of a nanocluster metal core can be described within the superatom model,^5–9 in which they are described as having spherical electronic structures related to those of atoms, with 1S, 1P, 1D, 2S, 1F… shell ordering, and with stability ensured by a closed-shell electron configuration corresponding to one of the “magic” electron numbers of 2, 8, 18, 20, 34… In the case of noble metal nanoclusters, the electrons to be considered are those provided by their (n + 1)s valence AOs and the requirement for a “magic” number generally leads to a formally cationic [M_n]^p+ core.

Hydride is one of the many ligands commonly encountered in this chemistry.^10–16 This monoatomic monoanionic ligand is to some extent related to halides, with which they can sometimes be exchanged. Hydrides have however unique intrinsic characteristics, of which one is their particularly small size. Whereas ordinary ligands protect the [M_n]^p+ inner core from the outside by forming a peripheral outer shell around it, it has been shown very recently that the smaller hydrides can, in some cases, get encapsulated inside the metal core.^17–29 The most striking structurally characterized examples concern 8-electron superatoms, the metal core of which describes a centered icosahedron, which in addition contains one^19,21,22,28 or even two^23,24 hydrogen atom(s). These nanoclusters are gathered in Table 1. Note that all of them are doped silver species. Indeed, no (MH_x)@Au₁₂ relative has been isolated so far, although such species have been predicted to exist on the basis of DFT calculations.¹¹ The encapsulated hydrides are mainly bonded to the central metal atom so that the whole cluster core is better viewed as describing a distorted (MH_x)@M₁₂ (x = 1, 2) icosahedron.

Table 1 Structurally characterized nanoclusters containing an MHx (x = 1,2) unit encapsulated within an Ag₁₂ icosahedral cage and their 8-electron superatomic cores

Compound	Superatomic core	Ref.
[(RhH)Ag24(SPhMe2)18]^2−	[(RhH)@Ag12]^4+	19
[(RhH)Ag20{S2P(O^nPr)2}12]	[(RhH)@Ag12]^4+	24
[(RhH)2Ag33[S2P(O^nPr)2]17]	[(RhH)@Ag12]^4+	29
[(IrH)Ag24(SPhMe2)18]^2−	[(IrH)@Ag12]^4+	23
[(PdH)Ag19{E2P(O^iPr)2}12] (E = S, Se)	[(PdH)@Ag12]^5+	22 and 27
[(PdH)Ag20{E2P(O^iPr)2}12]^+ (E = S, Se)	[(PdH)@Ag12]^5+	22 and 27
[(PtH)Ag19{S2P(O^nPr)2}12]	[(PtH)@Ag12]^5+	21
[(PtH)Ag19{Se2P(O^iPr)2}12]	[(PtH)@Ag12]^5+	21
[PtHPtAg32[S2P(O^nPr)2]17]	[(PtH)@Ag12]^5+	29
[(RuH2)Ag24(SPhMe2)18]^2−	[(RuH2)@Ag12]^4+	23
[(OsH2)Ag24(SPhMe2)18]^2−	[(OsH2)@Ag12]^4+	23
[(RhH2)Ag19{S2P(O^nPr)2}12]	[(RhH2)@Ag12]^5+	24

---

It has been shown that the 1s electron of an encapsulated hydride is to be considered as one of the eight superatomic electrons, contrary to the case where hydrides behave as ordinary outer ligands.^11–29 In other words, if one assumes that a [M_n]^p+ metal core possesses a given “magic” number of (n–p) electrons providing it with closed-shell stability, inserting x hydrogen atoms into it would increase its electron count by x. To maintain stability, the “magic” (n–p) electron count should be preserved, so the inserted hydrogen(s) should be, from the electron counting point of view, considered as formal proton(s), thus increasing the formal core charge to [MnH_x]^(p+x)+. In the case the hydrides are regular external H⁻ ligands, then the metal core should retain its p + charge, resulting in the {[M_n]H_x}^(p−x)+ assembly. Of course, in both cases, the p ± x cationic charge will be, in real life, compensated by the presence of various additional peripheral anionic ligands to reach (or approach) neutrality for the whole nanocluster.

Thus, encapsulated hydrides should be considered as inclusion dopants rather than ligands, i.e., somewhat behaving as metal dopants. Because of this metal parentage, they are sometimes named “metallic hydrogens”,^11,12,15,16 a designation that should not be confused with the meaning of an electron-conducting material. As any metal dopant in nanoclusters, hydrides play a crucial role in their properties. In particular, it has been shown that Au and Ag nanoclusters containing encapsulated hydrides are efficient electrocatalysts in the hydrogen evolution reaction (HER).^{11,12,16,23,24}

Herein we report a comprehensive computational investigation on the encapsulation of one and several hydrides within the M@Ag₁₂ and M@Au₁₂ (M = Mo–Ag and W–Au) centered icosahedral cores, assuming the “magic” 8-electron count to be maintained. We have restricted this study to the superatomic icosahedral cores. Indeed, it has been shown previously that computing the only superatomic core of a nanocluster in its actual oxidation state, i.e. without considering its passivating shell, allows rationalizing its stability, bonding and superatomic electronic structure.^30–32 On the other hand, as far as one is interested in bonding analysis only, this simplification also allows to highlight variations across the periodic table, without the blurring caused by the variation of the ligand and outer metal nature.

2. Results and discussion

2.1 The hydrogen-free 8-electron M@Ag12 and M@Au12 cores

Before investigating hydrogen encapsulation into M@Ag₁₂ and M@Au₁₂ cages, we first briefly review the trends within the icosahedral hydride-free 8-electron [M@Ag₁₂]^x+ and [M@Au₁₂]^x+ clusters when the second- and third-row transition-metal M varies from Group 6 to Group 11. All the optimized geometries were found to be of I_h symmetry. Corresponding selected computed data are provided in Table 2. The [Pd@Ag₁₂]⁴⁺ example is shown in Fig. 1.

Fig. 1 The optimized geometries of [Pd@Ag₁₂]⁴⁺ (I_h), [PdH@Ag₁₂]⁵⁺ (C_3v), and [RuH₂@Ag₁₂]⁴⁺ (C_2v).

Table 2 Selected computed data for the icosahedral 8-electron superatomic cores [M@Ag₁₂]^x+ and [M@Au₁₂]^x+ (M = Mo–Ag, W–Au). Interatomic distances are given in Å. WBI = Wiberg bond index; ΔE_H/L = HOMO–LUMO gap; q_M, q_Ag and q_Au are atomic natural charges

[M@Ag12]^x+							[M@Au12]^x+
M	Mo	Tc	Ru	Rh	Pd	Ag	M	Mo	Tc	Ru	Rh	Pd	Ag
x	0	1	2	3	4	5	x	0	1	2	3	4	5
ΔEH/L (eV)	1.37	1.92	1.46	1.73	2.06	2.64	ΔEH/L (eV)	1.09	1.46	1.04	1.73	2.05	1.95
M–Ag	2.761	2.753	2.760	2.783	2.824	2.899	M–Au	2.757	2.752	2.757	2.772	2.797	2.882
WBI	0.447	0.397	0.340	0.262	0.230	0.230	WBI	0.482	0.422	0.351	0.258	0.205	0.191
Ag–Ag	2.803	2.895	2.903	2.926	2.969	3.048	Au–Au	2.899	2.894	2.899	2.918	2.942	3.030
WBI	0.084	0.085	0.086	0.090	0.089	0.084	WBI	0.087	0.092	0.099	0.110	0.118	0.121
qM	−2.50	−2.22	−2.05	−1.95	−1.56	−1.30	q M	−2.23	−1.93	−1.69	−1.54	−1.09	−0.69
qAg	0.21	0.27	0.34	0.41	0.46	0.53	q Au	0.19	0.24	0.31	0.38	0.42	0.47

---

M	W	Re	Os	Ir	Pt	Au	M	W	Re	Os	Ir	Pt	Au
x	0	1	2	3	4	5	x	0	1	2	3	4	5
ΔEH/L (eV)	1.68	2.04	1.61	1.88	2.17	2.76	ΔEH/L (eV)	1.26	1.14	1.16	1.32	2.07	2.05
M–Ag	2.761	2.756	2.765	2.786	2.826	2.895	M–Au	2.756	2.753	2.762	2.778	2.805	2.849
WBI	0.417	0.364	0.314	0.268	0.231	0.232	WBI	0.462	0.404	0.338	0.281	0.226	0.205
Ag–Ag	2.904	2.897	2.908	2.929	2.971	3.044	Au–Au	2.897	2.895	2.905	2.921	2.949	2.996
WBI	0.084	0.085	0086	0.086	0.086	0.082	WBI	0.089	0.092	0.097	0.104	0.112	0.119
q M	−3.20	−2.84	−2.56	−2.16	−1.76	−1.22	q M	−2.86	−2.54	−2.24	−1.84	−1.41	−0.81
q Ag	0.27	0.32	0.38	0.43	0.48	0.52	q Au	0.24	0.30	0.35	0.40	0.45	0.48

---

It is known from both experimental and computational investigations that the doping of 8-electron centered Ag and Au icosahedral nanoclusters by a transition metal atom from the second and third row and situated on the left side of Ag and Au results in the occupation of the central position by this atom.^33–35 The main reason for this situation originates from a stronger participation of the central atom valence nd orbitals to the nanocluster bonding. This is why in the case of the most left-sided M atoms, their significantly bonding nd shell is sometimes considered as constituting the occupied superatomic 1D level, leading such species to be described as 18-rather than 8-electron superatoms.^35–37 Likewise, when both metals are from the same group 11 column, the [Au@Ag₁₂]⁵⁺ core is observed whereas [Ag@Au₁₂]⁵⁺ is unrealistic.^34,35 Note that only the (n + 1)s electrons are considered in the 8-electron count, the M contribution being negative (M = Groups 6–9) or nul (M = Pd, Pt). All the computed models have an 1S² 1P⁶ closed-shell configuration secured by a significant HOMO–LUMO gap. Although this gap decreases when going from Group 11 to Group 6, it should be noted that the bare [Mo@Au₁₂] and [W@Au₁₂] clusters have been experimentally observed,³⁶ right after the theoretical prediction of [W@Au₁₂].³⁷ This suggests that any of the cations listed in Table 2 (except [Ag@Au₁₂]⁵⁺, see above)^33,34 is likely to be stable, at least as the ligand-protected superatomic core of a larger species.

Both M–M′ (M′ = Ag, Au) and M′–M′ distances increase when M goes from Group 6 to Group to 11. Consistently, the M–M′ Wiberg bond indices (WBIs) decreases, but their variation is more marked than that of the corresponding distances. The stronger bonding for the left-sided M metals has been shown to originate from the larger participation of their nd valence orbitals to superatomic bonding, in such a way that one can include the electrons occupying this somewhat bonding nd(M) shell into the superatomic electron count, allowing [Mo@Au₁₂] or [W@Au₁₂], for example, to be considered as 18-electrons superatoms with 1S² 1P⁶ 1D¹⁰ configuration.^35,37 Contrarily to the M–M′ WBIs, the M′–M′ ones vary little, especially in the M′ = Ag case and they are always smaller than their M–M′ homologues.

2.2 Monohydride systems

Inserting a hydrogen atom as a dopant inside an 8-electron M@Ag₁₂ or M@Au₁₂ system, requires to formally add it as a proton if one wants to maintain the 8-electron count, i.e. the closed-shell stability of the whole architecture. It turns out that we were unable to converge the [(MH)@Ag₁₂]⁶⁺ and [(MH)@Au₁₂]⁶⁺ (M = Ag, Au) models. This may be the consequence of their large cationic charge. We note however that no example of such (AgH)- or (AuH)-centered icosahedral architecture has been reported so far. Relevant computed data of the converged monohydride models are given in Table 3. Only three of them, namely [RhHAu₁₂]⁴⁺ and [MHAu₁₂]⁵⁺ (M = Pd, Pt), have lost their icosahedral parentage, with the MH unit sitting inside a smaller cage (see Fig. S1†). These three models will not be discussed further in this paper.

Table 3 Selected (averaged) computed data for the 8-electron cores [(MH)@Ag₁₂]^x+ and [(MH)@Au₁₂]^x+ (M = Mo–Pd, W–Pt). Interatomic distances are given in Å. WBI = Wiberg bond index; q_M, q_Ag and q_Au are atomic natural charges. See also Table S1† for HOMO–LUMO gaps and metal–metal distances

[(MH)@Ag12]^x+						[(MH)@Au12]^x+
M	Mo	Tc	Ru	Rh	Pd	M	Mo	Tc	Ru	Rh^a	Pd^a
x	1	2	3	4	5	x	1	2	3	4	5
CSM	0.62	0.57	0.52	0.44	0.31	CSM	1.03	1.09	1.09	n/a	n/a
M–H	1.837	1.742	1.679	1.658	1.703	M–H	1.821	1.719	1.657	1.637	1.692
WBI	0.471	0.428	0.371	0.297	0.206	WBI	0.487	0.460	0.417	0.424	0.344
Ag–H	2.085	2.084	2.090	2.099	2.089	Au–H	2.168	2.191	2.211	2.137	1.717
WBI	0.102	0.105	0.109	0.116	0.123	WBI	0.099	0.099	0.107	0.171	0.418
q M	−2.42	−2.13	−1.94	−1.78	−1.38	q M	−1.05	−1.54	−1.80	−2.11	−0.36
q Ag	0.30	0.35	0.43	0.50	0.56	q Au	0.27	0.32	0.38	0.42	0.45
q H	−0.20	−0.20	−0.21	−0.27	−0.38	q H	−0.07	−0.05	−0.05	0.01	0.02

---

M	W	Re	Os	Ir	Pt	M	W	Re	Os	Ir	Pt^a
x	1	2	3	4	5	x	1	2	3	4	5
a Optimized structure having lost its icosahedral parentage.
CSM	0.69	0.67	0.64	0.63	0.66	CSM	1.10	1.28	1.39	1.79	n/a
M–H	1.843	1.754	1.694	1.655	1.651	M–H	1.833	1.729	1.665	1.615	1.561
WBI	0.490	0.457	0.403	0.356	0.306	WBI	0.504	0.489	0.451	0.438	0.584
Ag–H	2.106	2.114	2.133	2.168	2.234	Au–H	2.184	2.233	2.278	2.376	3.085
WBI	0.092	0.092	0.088	0.094	0.090	WBI	0.091	0.085	0.087	0.083	0.030
q M	−3.00	−2.64	−2.36	−1.94	−1.49	q M	−2.59	−2.26	−1.96	−1.51	−0.66
q Ag	0.35	0.40	0.46	0.51	0.57	q Au	0.31	0.36	0.42	0.46	0.46
q H	−0.22	−0.20	−0.21	−0.24	−0.31	q H	−0.11	−0.07	−0.04	−0.02	0.18

---

All the other structures adopt a distorted icosahedral arrangement of C_3v symmetry (see the [(PdH)Ag₁₂]⁵⁺ example in Fig. 1), with M lying approximately at its center and the hydride inside a tetrahedron made of M and an Ag₃ or Au₃ triangular face of the icosahedron. As a result, this face is expanded, leading to significant distortion of the whole icosahedral architecture. The amount of distortion away from ideal I_h symmetry can be evaluated with the continuous symmetry measure³⁸ (CSM, see Tables 3 and S1†). Within the silver series, it tends to decrease when M varies from left to right, whereas a more or less opposite trend is found for the gold series. The CSM values found for the gold series are much larger than their silver counterparts, which might indicate lower stability of the (MH)-centered icosahedral Au₁₂ architecture. Overall our results are in good qualitative agreement with the experimentally known nanoclusters that contain [(MH)@Ag₁₂]⁴⁺ (M = Rh, Ir)^{19,23,24,28,29} and [(MH)@Ag₁₂]⁵⁺ (M = Pd, Pt).^21,22,28 The fact that the computed CSM values are larger than the experimental ones^19,23,24 can be explained by the absence in our models of any templating outer shell that would oppose distortion.

In previous investigations on nanoclusters containing an [(MH)@Ag₁₂]⁵⁺ (M = Pd, Pt) core,^{21,22,25,26,28} it was found that the 1s(H) AO interacts principally with the d_z²(M) orbital, creating an M–H 2-electron bond and leaving the (n + 1)s AO of M almost unperturbed and containing one electron (see Fig. 2). The superatomic orbitals being principally combinations of metallic valence s-type AOs, it follows that the 1s(H) AO is not significantly involved in their composition. From the superatomic point of view, the interstitial hydrogen provides one electron to the 5s(Pd/Pt) AO, which in turn allows the electron count to achieve the closed-shell count of eight. When M varies from Group 11 to Group 6, the participation of its nd orbitals (thus the nd_z² one) to the superatomic orbitals building increases.^35,37 Moreover, the 1s(H) AO tends to interact in a somewhat larger extend with the (n + 1)s AO of M. It results that the contribution of the 1s(H) orbital to the composition of the superatomic orbitals increases. This is exemplified by the substantial increase of the M–H WBIs when going from Group 11 to Group 6 (Table 3), whereas the variation of the Ag–H WBIs is much more modest and mainly reflects the variation of the M radius. Consistently, the hydridic character of H decreases from Group 11 to Group 6.

Fig. 2 Simplified sketch illustrating the major orbital interaction (in black) resulting from the formal inclusion of a hydrogen atom within an electron-deficient [Pd@Ag₁₂]⁵⁺ superatomic entity, to generate the stable [(PdH)@Ag₁₂]⁵⁺ closed-shell superatom. Only one 4d(Pd) orbital is shown for clarity, the other four remaining non-bonding (and occupied) in the process.

2.3 Dihydride systems

As for the monohydride series discussed just above, inserting two hydrogen atoms as dopants inside an 8-electron M@Ag₁₂ or M@Au₁₂ system, requires to formally add them as protons in order to maintain the closed-shell 8-electron count. In the same way as illustrated in Fig. 2 for a monohydride species, the two encapsulated hydrogen atoms interact principally with two valence d-type orbitals, leaving the superatomic orbitals little perturbed. Likely because of their large cationic charges, the models [(MH₂)@Ag₁₂]⁷⁺ and [(MH₂)@Au₁₂]⁷⁺ (M = Ag, Au) as well as [(MH₂)@Ag₁₂]⁶⁺ and [(MH₂)@Au₁₂]⁶⁺ (M = Pd, Pt) could not be converged. Relevant computed data of the converged dihydride models are given in Tables 4 and S2.†

Table 4 Selected (averaged) computed data for the icosahedral 8-electron superatomic cores [(MH₂)@Ag₁₂]^x+ (M = Mo–Rh, W–Ir) and [(MH₂)@Au₁₂]^x+ (M = Mo–Ru, W–Os). Interatomic distances are given in Å. WBI = Wiberg bond index; q_M, q_Ag and q_Au are atomic natural charges. See also Table S2† for HOMO–LUMO gaps and metal–metal distances

[(MH2)@Ag12]^x+					[(MH2)@Au12]^x+
M	Mo	Tc	Ru	Rh	M	Mo	Tc	Ru
x	2	3	4	5	x	2	3	4
CSM	1.58	1.55	1.43	1.37	CSM	1.67	2.11	2.68
M–H	1.809	1.718	1.663	1.658	M–H	1.990	1.750	1.686
WBI	0.483	0.440	0.377	0.296	WBI	0.384	0.432	0.396
Ag–H	2.151	2.164	2.669	2.050	Au–H	1.871	2.036	1.890
WBI	0.092	0.093	0.097	0.123	WBI	0.198	0.145	0.221
H–M–H (°)	70	71	75	84	H–M–H (°)	69	68	70
q M	−2.36	−2.05	−1.81	−1.53	q M	−2.12	−1.71	−1.36
q Ag	0.39	0.45	0.51	0.59	q Au	0.36	0.40	0.45
q H	−0.16	−0.15	−0.18	−0.26	q H	−0.08	−0.03	−0.02

---

M	W	Re	Os	Ir	M	W	Re	Os
x	2	3	4	5	x	2	3	4
CSM	1.71	1.74	1.69	1.72	CSM	3.41	2.37	2.83
M–H	1.818	1.733	1.677	1.651	M–H	1.837	1.722	1.677
WBI	0.503	0.469	0.413	0.358	WBI	0.463	0.483	0.449
Ag–H	2.175	2.198	2.225	2.138	Au–H	1.998	1.957	2.084
WBI	0.082	0.081	0.082	0.095	WBI	0.148	0.156	0.137
H–M–H (°)	69	70	73	80	H–M–H (°)	51	57	69
q M	−2.81	−2.45	−2.15	−1.67	q M	−2.42	−2.02	−1.70
q Ag	0.43	0.48	0.54	0.59	q Au	0.37	0.42	0.48
q H	−0.18	−0.16	−0.17	−0.22	q H	−0.03	0.00	0.00

---

It is of note that only one energy minimum was found for every computed model and all the energy minima adopt the same C_2v configuration, shown in Fig. 1 for the [(RuH₂)@Ag₁₂]⁵⁺ model. In this structure, the two hydrides are approximately lying below two distant edges belonging to two edge-sharing triangular faces, as sketched in Scheme 1.

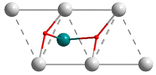Scheme 1 A simplified 2-dimensional representation of the hydride positions in the (MH₂)@M′₁₂ (M′ = Ag, Au) computed models. Dotted lines indicate elongated M′–M′ edges.

Being in addition bonded to the central M atom, the hydrides are only tricoordinated, as opposed to the tetracoordination found in the monohydride models (see above). As a result of this double hydride insertion, several edges are elongated (dotted lines in Scheme 1), resulting in a substantial distortion of the icosahedral architecture, as exemplified by the large CSM values (Table 4). The H–M–H angles in Table 4 lie in the range ∼70–80°. The reported experimental values are a somewhat larger (∼90–100°).^{19,23,24,28,29} The discrepancy can be attributed to the effect of the peripheral shell on the superatomic core it passivates in the real compounds. Indeed, the potential energy surface associated with a variation of the H–M–H angle in our models is rather flat around its minimum. In any case, the linear H–M–H arrangement inside the Ag₁₂ or Au₁₂ icosahedron, as reported for other types of nanocluster^{19,23,24,28,29} is by far not favored.

2.4 More than two hydrides

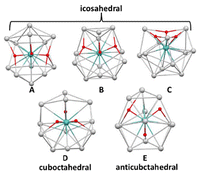
The encapsulating ability of a metal-centered icosahedral cage is obviously limited and inserting more than two hydrides in such M@Ag₁₂ or M@Au₁₂ templates resulted most often in extreme distortion, dismantling, or in non-converged models. This is why we also considered the possibility for hydride encapsulation in centered 12-vertex cuboctahedral and anticuboctahedral cages which have a somewhat larger volume than their icosahedral relative, while maintaining sufficient connectivity within its surface atoms (see Fig. 3). Whereas no reasonable structure could be found with four or more hydrides encapsulated within a centered 12-vertex polyhedron, with only three hydrides several (MH₃)@Ag₁₂ and (MH₃)@Au₁₂ structures could be identified.

Fig. 3 Ideal centered 12-vertex cages.

Looking firstly at the silver-rich series, five M@Ag₁₂ structures, labelled A, B, C, D and E, were characterized as true minima in the cases of M = Mo–Ru and W–Os. They are shown in Fig. 4 for the M = Mo example. In the cases of M = Tc and Re, additional secondary minima were obtained in which the hydrides are embedded within an open Ag₁₁ cage capped by one Ag atom. These fairly distorted structures are not commented further on. In the cases of M = Ru and Os, a unique minimum of type B was found. Structures A, B, C, D and E have only approximate C_s, C_s, C₃, C₂ and C_s symmetry, respectively. As indicated by their large CSM values calculated with respect to the closest ideal polyhedron (Tables 5 and S3†), their Ag₁₂ polyhedral envelope adopts configurations resulting from severe distortions away from ideal icosahedron, cuboctahedron and/or anticuboctahedron.

Fig. 4 The five (MH₃)@Ag₁₂ isomers exemplified in the case of [(MoH₃)@Ag₁₂]³⁺.

Table 5 Selected (averaged) computed data for the 8-electron superatomic cores [(MH₃)@Ag₁₂]^x+ (M = Mo–Ru, W–Os). Interatomic distances are given in Å. WBI = Wiberg bond index; ΔE = isomer relative energy; q_M, q_Ag and q_Au are atomic natural charges. See also Table S3† for HOMO–LUMO gaps and metal–metal distances

M	Mo					Tc					Ru
x	3					4					5
Structure type	A	B	C	D	E	A	B	C	D	E	B
ΔE (kcal mol^−1)	0.0	2.9	3.1	7.4	11.5	0.0	2.1	2.1	8.0	10.5
CSM	2.32	2.41	1.88	6.40	4.91	2.55	2.37	1.93	6.49	6.95	2.25
M–H	1.791	1.798	1.797	1.794	1.808	1.703	1.707	1.717	1.733	1.711	1.659
WBI	0.492	0.481	0.481	0.494	0.489	0.442	0.436	0.446	0.435	0.434	0.615
Ag–H	2.074	2.085	2.153	2.055	2.168	2.065	2.214	2.167	2.148	2.067	2.138
WBI	0.097	0.098	0.091	0.113	0.091	0.098	0.082	0.096	0.100	0.093	0.301
q M	−2.27	−2.30	−2.18	−2.30	−2.27	−1.97	−1.99	−1.93	−1.92	−1.97	−1.70
q Ag	0.47	0.48	0.48	0.46	0.48	0.52	0.53	0.52	0.54	0.53	0.60
q H	−0.12	−0.15	−0.15	−0.13	−0.16	−0.10	−0.13	−0.13	−0.17	−0.13	−0.15

---

M	W					Re					Os
x	3					4					5
Structure type	A	B	C	D	E	A	B	C	D	E	B
ΔE (kcal mol^−1)	0.0	2.8	3.3	7.2	11.3	0.0	1.9	2.1	7.7	10.4
CSM	2.43	2.66	2.17	6.49	5.28	2.54	2.75	2.44	6.64	5.27	2.98
M–H	1.804	1.801	1.807	1.809	1.809	1.724	1.718	1.734	1.739	1.726	1.671
WBI	0.516	0.508	0.519	0.508	0.508	0.473	0.477	0.478	0.481	0.471	0.420
Ag–H	2.063	2.103	2.146	2.060	2.103	2.121	2.203	2.196	2.194	2.225	2.220
WBI	0.091	0.085	0.086	0.089	0.086	0.085	0.085	0.097	0.085	0.071	0.074
q M	−2.61	−2.59	−2.51	−2.59	−2.59	−2.27	−2.27	−2.18	−2.23	−2.26	−1.94
q Ag	0.50	0.51	0.50	0.51	0.51	0.55	0.55	0.55	0.56	0.56	0.61
q H	−0.14	−0.17	−0.16	−0.17	−0.17	−0.12	−0.13	−0.14	−0.18	−0.14	−0.12

---

With respect to the gold-rich series, only M = Mo, W, Tc and Re provided converged systems with M@Au₁₂ architectures and again structure-types A, B, C, D, and E were found (Table 6), but the number of isomers per M element does not exceed two.

Table 6 Selected (averaged) computed data for the 8-electron superatomic cores [(MH₃)@Au₁₂]^x+ (M = Mo, W, Tc, Re). Interatomic distances are given in Å. WBI = Wiberg bond index; ΔE_H/L = HOMO–LUMO gap; ΔE = isomer relative energy; q_M, q_Ag and q_Au are atomic natural charges

M	Mo		W		Tc		Re
x	3		3		4		4
Structure type	B	C	A	C	C	E	C
CSM	3.60	3.34	2.25	3.33	3.81	3.22	4.19
ΔEH/L (eV)	1.85	1.71	1.98	1.78	1.54	1.24	1.64
ΔE (kcal mol^−1)	2.9	0.0	1.6	0.0	0.0	17.4
M–Au	2.977	3.004	2.924	2.999	3.039	2.934	3.031
WBI	0.347	0.343	0.354	0.345	0.296	0.307	0.301
Au–Au	2.823	2.816	2.852	2.816	2.827	2.873	2.829
WBI	0.135	0.137	0.113	0.133	0.143	0.123	0.138
M–H	1.824	1.791	1.927	1.806	1.719	1.846	1.728
WBI	0.475	0.494	0.439	0.526	0.454	0.357	0.491
Au–H	1.847	1.831	1.897	1.858	1.830	1.852	1.907
WBI	0.198	0.211	0.167	0.179	0.236	0.212	0.180
q M	−1.87	−1.81	−2.43	−2.10	−1.45	−1.69	−1.75
q Au	0.41	0.40	0.47	0.43	0.46	0.49	0.48
q H	−0.02	0.01	−0.06	−0.03	0.03	−0.08	0.01

---

The bonding within these 8-electron superatomic models is related to that of their mono- and di-hydride relatives. Although more hypothetical (no such system experimentally reported to date), the lowest energy structures A, B and C, all of icosahedral parentage, are likely to constitute superatomic cores of viable ligand-protected nanoclusters. It is of note that, as this manuscript was under revision, an 8-electron copper-rich cluster with a (PtH₃)@Cu₁₂ core having a structure more or less related to the E anticuboctahedral arrangement was just published.³⁹

2.5 The dynamics of the hydrides inside their icosahedral cages

There are experimental NMR data on both mono-^{19,21,22,28,29} and di-hydride^23,24 species indicating that the embedded hydrides move nearly freely inside their icosahedral envelopes. We have calculated the activation barrier for the hydride in (MH)@Ag₁₂ species moving from one tetrahedral site to the next tetrahedron. This pathway is illustrated in Fig. 5 and selected computed data associated with the transition states are given in Table 7. Unsurprisingly, these transition states are of C₂ symmetry, with the hydride connected to the two Ag atoms common to its starting and final tetrahedral sites. They were fully characterized as having one unique imaginary “vibrational frequency” of b₁ symmetry. Owing to the flatness of the explored potential energy surfaces, some of these transition states were not easy to identify. Consistently, the energy barriers are very small (varying between 2 and 6 kcal mol⁻¹). We have tested our results on a realistic ligand-protected nanocluster with complete outer sphere, namely the reported [(PtH)Ag₁₉{S₂P(OⁿPr)₂}₁₂],²¹ simplified in [(PtH)Ag₁₉(S₂PH₂)₁₂] for the sake of computational cost. Owing to the symmetry of this cluster (C₃), there are three slightly different pathways for the hydride moving from one tetrahedral site to the next one. The one we tested has a barrier of 0.2 kcal mol⁻¹, a value even lower than that found for the bare [PtH@Ag₁₂]⁵⁺ core, indicating that modeling only the bare core provides results that can be safely projected on real ligand-protected species, at least at a semi-quantitative level.

Fig. 5 The pathway of the hydride movement in [(RuH)Ag₁₂]³⁺.(Ag_aro: Ag atoms around the H atom in the starting structure. Ag_ico: Ag atoms not around the H atom in the starting structure.).

Table 7 Selected computed data for the (MH)@Ag₁₂ (M = Mo–Pd, W–Pt) transition states. Interatomic averaged distances are given in Å. ΔE is its relative energy with respect to the energy minimum

M	ΔE (kcal mol^−1)	M–H	Ag–H	Ag–H–Ag (°)	H–M–Ag (°)
Mo	5.6	1.823	1.830	161	99
Tc	4.6	1.740	1.844	155	103
Ru	4.3	1.669	1.871	149	106
Rh	3.4	1.648	1.889	145	108
Pd	2.0	1.693	1.883	143	109
W	1.8	1.840	1.791	162	99
Re	5.2	1.743	1.868	156	102
Os	4.2	1.686	1.898	151	104
Ir	3.3	1.655	1.938	148	106
Pt	1.7	1.644	2.005	145	108

---

We also tested the hydride dynamics on the dihydride series (MH₂)@Ag₁₂. With two hydrides moving either sequentially or in a concerted fashion, several pathways are a priori possible. The concerted least-motion pathway illustrated in Fig. 6 was investigated. Selected computed data associated with the transition state are given in Table 8. The activation barriers remain lower than 3 kcal mol⁻¹, except for M = Ir and Rh, with barriers of 5.1 and 7.2 kcal mol⁻¹, respectively.

Fig. 6 The pathway of the hydride movement in [(RuH₂)Ag₁₂]³⁺.

Table 8 Selected computed data for the (MH₂)@Ag₁₂ (M = Mo–Pd, W–Pt) transition states. Interatomic averaged distances are given in Å. ΔE is its relative energy with respect to the energy minimum

M	ΔE (kcal mol^−1)	M–H	Ag–H	Ag–H–Ag (°)
Mo	2.8	1.794	1.932	60
Tc	2.6	1.706	1.946	62
Ru	2.4	1.650	1.943	65
Rh	7.2	1.659	2.067	80
W	2.8	1.808	1.948	60
Re	2.5	1.724	1.971	62
Os	2.2	1.668	1.984	65
Ir	5.1	1.645	2.192	73

---

2.6 Incomplete icosahedral cages: the nido case and beyond

Whereas the hydride-containing 8-electron superatom [HAu₂₅(SMe)₁₈] has been theoretically predicted to exist,¹¹ as far as we know no gold nanocluster possessing a [(AuH)@Au₁₂]⁶⁺ core has been structurally characterized so far. However, gold and gold-rich superatoms containing hydrides embedded in polyhedral cages having some open faces are known,^{12–18,40–42} although the hydride location in some of these structures remains to be clarified. This is the case of one of these species, which exhibits a Pt@(Au₈Ag₂) metal kernel, of which the Au₈Ag₂ cage can be described as an icosahedron with two unoccupied neighboring vertices.⁴¹ With respect to copper-rich superatom chemistry, hydride-containing 2-electron superatoms possessing a [(MH)@Cu₁₁]¹⁰⁺ (M = Pd, Pt) core are known.^25,26 In these species, the MH unit is embedded within a copper cuboctahedral cage of which one vertex is unoccupied. From the examples cited above, it appears that the same number of “magic” electrons could characterize species with complete polyhedral cages as well as incomplete cages having at least one or two unoccupied vertices. This is reminiscent to the closo, nido, arachno… parentage existing in the chemistry of the so-called Wade-Mingos-type clusters.⁴³

Below we first investigate the 8-electron monohydride series [(MH)@Ag₁₁]^x+ and [(MH)@Au₁₁]^x+ (M = Mo–Pd, W–Pt), in which the Ag₁₁ or Au₁₁ cages can be viewed as incomplete icosahedra having a missing vertex. The search for energy minima was conducted starting from a M@(Ag₁₁□) (□ = vacancy) skeleton, where the (Ag₁₁□) shape is that of a regular icosahedron (nido-type structure). The hydride was then placed in any of the tetrahedral sites of the centered icosahedron, including those involving the □ vacancy and all these generated starting geometries where fully optimized. It turns out that the same global energy minimum of C_5v symmetry was found for all the computed models, but [(PdH)@Ag₁₁]⁴⁺. In this C_5v structure, exemplified by those of [(RhH)@Ag₁₁]³⁺ and [(PtH)@Ag₁₁]⁴⁺ shown in Fig. 7, the hydride atom sits on the same side as (and close to) the missing vertex of the icosahedron. In the global minimum of [(PdH)@Ag₁₁]⁴⁺ (Fig. 7), the hydride sits also on the same open side of the defective icosahedron, but it is now shifted towards an edge of the pentagonal face, leading to C_s symmetry. A secondary minimum, of C_s symmetry, was found for [(PdH)@Ag₁₁]⁴⁺ (Fig. 7), where the hydride sits on the other side of the vacancy and is bonded to an icosahedron edge, forcing this part of the structure to distort.

Fig. 7 The computed isomers of [(RhH)Ag₁₁]³⁺, [(PdH)Ag₁₁]⁴⁺, and [(PtH)Ag₁₁]⁴⁺ with corresponding relative energies in kcal mol⁻¹.

In fact, the C_5v structure was found to be the unique minimum for all M dopants, except for M = Rh and Pt, for which one secondary minimum was also found (Fig. 7). The secondary minimum of [(RhH)@Ag₁₁]³⁺ resembles somewhat the C_2v isomer of [(PdH)@Ag₁₁]⁴⁺, whereas that of [(PtH)@Ag₁₁]⁴⁺ has lost its icosahedral parentage with one Ag atom capping an Ag₁₀ cage. Selected computed data are provided in Table 9.

Table 9 Selected (averaged) computed data for the nido-type 8-electron superatomic cores [(MH)@Ag₁₁]^x+ (M = Mo–Pd, W–Pt), of C_5v structure except for [(PdH)@Ag₁₁]⁴⁺ (C_s symmetry). Interatomic distances are given in Å. WBI = Wiberg bond index; ΔE_H/L = HOMO–LUMO gap; q_M, q_Ag and q_Au are atomic natural charges

M	Mo	Tc	Ru	Rh	Pd	W	Re	Os	Ir	Pt
x	0	1	2	3	4	0	1	2	3	4
ΔEH/L (eV)	1.01	1.06	1.24	1.62	1.93	1.65	1.16	1.37	1.73	2.04
M–Ag	2.765	2.758	2.765	2.791	2.840	2.770	2.765	2.775	2.801	2.850
WBI	0.435	0.376	0.308	0.231	0.198	0.417	0.359	0.298	0.250	0.214
Ag–Ag	2.892	2.886	2.894	2.920	2.977	2.894	2.890	2.900	2.924	2.971
WBI	0.092	0.093	0.093	0.094	0.092	0.090	0.091	0.091	0.090	0.087
M–H	1.740	1.669	1.617	1.592	1.669	1.756	1.693	1.643	1.611	1.605
WBI	0.575	0.529	0.471	0.400	0.255	0.592	0.548	0.482	0.430	0.379
Ag–H	2.569	2.541	2.536	2.555	2.031	2.585	2.562	2.562	2.585	2.644
WBI	0.051	0.059	0.067	0.075	0.170	0.047	0.054	0.061	0.064	0.063
q M	−2.28	−2.03	−1.82	−1.63	−1.12	−2.78	−2.49	−2.22	−1.83	−1.41
q Ag	0.21	0.278	0.35	0.43	0.49	0.26	0.33	0.39	0.45	0.51
q H	−0.08	−0.05	−0.06	−0.09	−0.27	−0.13	−0.09	−0.07	−0.09	−0.15

---

In all the structures of Fig. 7, the hydride is strongly bonded to M and weakly to Ag. In the C_5v structure, the M–Ag distances are particularly long and the associated WBIs particularly weak (Table 9). Nevertheless, this is the dominant low-energy structure in the [(MH)@Ag₁₁]^x+ series. It is somewhat reminiscent to that of the 8-electron [HAu₉(PMe₃)]²⁺ cluster, where the hydride sits over an open face of the Au@Au₈ metal kernel.¹² Conversely, it is at variance with the 2-electron nido-type nanoclusters [MHCu₁₁{S₂P(OⁱPr)₂}₆(CCPh)₄] (M = Pd, Pt) of cuboctahedral parentage, where the hydride sits at a tetrahedral site opposite to the vacancy.^23,24 It is also noteworthy that in the C_5v structure the hydride contribution to the superatomic orbitals becomes nonnegligible. In the case of [(PtH)@Ag₁₁]⁴⁺ it contributes 35% and 5% to the 1S and 1P_z orbitals respectively. By comparison, in the C_s minimum of [(PdH)@Ag₁₁]⁴⁺ (Fig. 7), its contributions are only 2% and 1%, respectively. Thus, in the C_5v structure, the hydride tends to some extend to replace the missing Ag atom on the icosahedron and play the role of a superatom constituent, whereas in the other structures it behaves similarly as in the closo-type relatives, i.e. as an inserted dopant.²³

Switching from the Ag-rich species to their gold relatives yielded fairly different results. The global minima found for the 8-electron models [(MH)@Au₁₁]^x+ (M = Mo–Pd, W–Pt) are shown in Fig. 8. Only five of them have retained their icosahedral parentage, of which only two (corresponding to M = Tc and Re) are of C_5v symmetry. Those corresponding to M = Mo, W and Ru derive from the C_5v structure by the opening of one edge of the open pentagonal face. The potential energy surfaces of these species were found more complex that in the case of the Ag-rich series, leading to a larger number of isomers. In addition, their lower HOMO–LUMO gaps suggest lower stability, at least in their considered form of unligated superatomic cores. This is why this series will not be discussed further on. In any case, as already found in the other investigated series, gold-rich clusters are more flexible than their silver homologues, leading to a more complex and less predictable structural chemistry.

Fig. 8 The lowest energy isomers of the 8-electron models [(MH)@Au₁₁]^x+ (M = Mo–Pd, W–Pt) with their HOMO–LUMO gap (eV) below.

Unfortunately, exploring the possibility for 8-electron arachno-type systems with (MH)@Ag₁₀ or (MH)@Au₁₀ architectures was not possible, owing to the huge number of potential isomeric structures to be considered. However, there is one example of such a species, which has been structurally characterized (except with respect to the hydride location) namely [PtH(AgNO₃)₂(AuPPh₃)₈]⁺.⁴¹ Its Ag₂Au₈ polyhedron can be viewed as an icosahedron having two neighboring vertices unoccupied. We thus simplified the superatomic core of this nanocluster into the corresponding bimetallic arachno model [PtHAu₁₀]³⁺. Only one energy minimum (of C_2v symmetry) was found, with the hydride located at the open side of the uncomplete icosahedron, (Fig. 9). Again, the Pt–H bond is strong (1.569 Å, WBI = 0.509), whereas the two shortest Ag–H contacts are fairly long (2.632 Å, WBI = 0.083). The participation of the hydride in the 1S and 1P_z orbitals is non-negligible (10% and 6%, respectively). Very similar results were also found for [PdHAg₁₀]³⁺. These results suggest that hydride-encapsulating arachno species are also potentially viable cores for ligand-protected superatoms susceptible to be isolated.

Fig. 9 The optimized geometry the 8-electron arachno model [PtHAu₁₀]³⁺.

3. Conclusion

Our calculations indicate that (MH_x)Ag₁₂ (M = Group 6 to (at least) Group 10; x = 1–3) architectures are viable as constituting the superatomic core of ligand-protected 8-electron nanoclusters. Such entities are expected to more or less retain the icosahedral arrangement of their non-hydridic parents, with some cuboctahedral and/or anticuboctahedral features in the case of x = 3. In all these species, the hydrides are much strongly bonded to the central M atom than to their nearest Ag neighbors. This is why the encapsulated hydrides are relatively free to move inside the Ag₁₂ cage, at least in most of the mono- and di-hydride cases for which particularly small activations barriers are computed. Thus, it is not excluded that the hydride hopping from one tetrahedral site to a next one is accompanied by tunnelling effect through the small barrier. Nido-type monohydride species, i.e. MH units encapsulated within an uncomplete Ag₁₁ icosahedron, are also expected to be stable for the 8-electron count. Interestingly, in most of the computed models, the hydride prefers to be located on the vacancy side, tending to replace the missing Ag atom(s) on the icosahedron, including in the participation of its 1s AO to the superatomic orbitals. In general, the (MH_x)Au₁₂ species exhibit similar structural features as their isoelectronic (MH_x)Ag₁₂ homologues, but with smaller HOMO–LUMO gaps and more complicated potential energy hypersurfaces, suggesting lower stability and/or more complex structural chemistry. Moreover, for the most right-sided M elements, the Au₁₂ cage tends to get unstable with respect to smaller Au_n (n < 12) cages capped by 12 − n Au atoms.

Computational details

Calculations were performed at the Density Functional Theory (DFT) level using the Gaussian (R) 16 program.⁴⁴ The BP86 functional was used^45,46 together with the valence triple-zeta polarization functions (def2-TZVP) basis set.^47,48 All the structures were optimized without any symmetry constraint and confirmed as true minima on their potential energy surface by analytical vibration frequency calculations. Natural atomic orbital (NAO) populations and Wiberg bond indices (the sum of quadratic non-diagonal elements of the density matrix between two atoms) were computed with the natural bond orbital NBO 6.0 program⁴⁹ implemented in the Gaussian (R) 16 package. The compositions of the molecular orbitals were calculated using Multiwfn software.^50,51 In this paper, the meaning of non-convergence during geometry optimization refers to a geometry evolution which leads to dissociation/fragmentation of the considered cluster.

Data availability

The data supporting the findings of this study are available within the article and its ESI.† Complementary raw data are available from the corresponding authors, upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Dr J. Wei (Ningxia University) is acknowledged for inspiring discussions. H. L. thanks the China Scholarship Council for a Ph.D. grant.

References

1. C. M. Aikens, R. Jin, X. Roy and T. Tsukuda, J. Chem. Phys., 2022, 156, 170401.
2. J. Yang, F. Yang, C. Zhang, X. He and R. Jin, ACS Mater. Lett., 2022, 4, 1279.
3. X. Kang, Y. Li, M. Zhu and R. Jin, Chem. Soc. Rev., 2020, 49, 6443.
4. M. F. Matus and H. Häkkinen, Nat. Rev. Mater., 2023, 8, 372.
5. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Gronbeck and H. Hakkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157.
6. H. Häkkinen, Chem. Soc. Rev., 2008, 37, 1847.
7. H. Häkkinen, Adv. Phys.: X, 2016, 1, 467.
8. F. Gam, J. Wei, S. Kahlal, J.-Y. Saillard and J.-F. Halet, Struct. Bonding, 2021, 188, 69.
9. Z. Lin, Chin. J. Struct. Chem., 2024, 43, 100254.
10. R. S. Dhayal, W. E. van Zyl and C. W. Liu, Acc. Chem. Res., 2016, 49, 86.
11. G. Hu, Q. Tang, D. Lee, Z. Wu and D.-e Jiang, Chem. Mater., 2017, 29, 4840.
12. S. Takano, H. Hirai, S. Muramatsu and T. Tsukuda, J. Am. Chem. Soc., 2018, 140, 8380.
13. S. Takano, S. Hasegawa, M. Suyama and T. Tsukuda, Acc. Chem. Res., 2018, 51, 3074.
14. W. E. van Zyl and C. W. Liu, Chem. – Eur. J., 2022, 28, e202104241.
15. S. Maity, S. Takano, S. Masuda and T. Tsukuda, J. Phys. Chem. C, 2024, 128, 19.
16. T.-H. Chiu, J.-H. Liao, R. P. B. Silalahi, M. N. Pilla and C. W. Liu, Nanoscale Horiz., 2024, 9, 675.
17. S. Takano, H. Hirai, S. Muramatsu and T. Tsukuda, J. Am. Chem. Soc., 2018, 140, 12314.
18. H. Hirai, S. Takano and T. Tsukuda, ACS Omega, 2019, 4, 7070.
19. H. Yi, S. M. Han, S. Song, M. Kim, E. Sim and D. Lee, Angew. Chem., Int. Ed., 2021, 60, 22293.
20. C. Zhu, T. Duan, H. Li, X. Wei, X. Kang, Y. Pei and M. Zhu, Inorg. Chem. Front., 2021, 8, 4407.
21. T.-H. Chiu, J.-H. Liao, F. Gam, Y.-Y. Wu, X. Wang, S. Kahlal, J.-Y. Saillard and C. W. Liu, J. Am. Chem. Soc., 2022, 144, 10599.
22. Y.-R. Ni, M. N. Pillay, T.-H. Chiu, Y.-Y. Wu, S. Kahlal, J.-Y. Saillard and C. W. Liu, Chem. – Eur. J., 2023, 29, e202300730.
23. H. Yi, S. Song, S. M. Han, J. Lee, W. Kim, E. Sim and D. Lee, Angew. Chem., Int. Ed., 2023, 62, e202302591.
24. T.-H. Chiu, J.-H. Liao, Y.-Y. Wu, J.-Y. Chen, Y.-J. Chen, W. Wang, S. Kahlal, J.-Y. Saillard and C. W. Liu, J. Am. Chem. Soc., 2023, 145, 16739.
25. R. P. B. Silalahi, Y. Jo, J.-H. Liao, T.-H. Chiu, E. Park, W. Choi, H. Liang, S. Kahlal, J.-Y. Saillard, D. Lee and C. W. Liu, Angew. Chem., Int. Ed., 2023, 62, e202301272.
26. R. P. B. Silalahi, H. Liang, Y. Jo, J.-H. Liao, T.-H. Chiu, Y.-Y. Wu, X. Wang, S. Kahlal, J.-Y. Saillard, Q. Wang, W. Choi, D. Lee, J.-Y. Saillard and C. W. Liu, Chem. – Eur. J., 2024, 30, e202303755.
27. Y.-R. Ni, M. N. Pillay, T.-H. Chiu, J. Rajaram, Y.-Y. Wu, S. Kahlal, J.-Y. Saillard and C. W. Liu, Inorg. Chem., 2024, 63, 2766.
28. S. M. Han, S. Song, H. Yi, E. Sim and D. Lee, Nanoscale, 2024, 16, 4851.
29. T.-H. Chiu, M. N. Pillay, Y.-Y. Wu, Y. Niihori, Y. Negishi, J.-Y. Chen, Y. J. Chen, S. Kahlal, J.-Y. Saillard and C. W. Liu, Chem. Sci., 2024, 15, 14660.
30. R. S. Dhayal, J.-H. Liao, Y.-C. Liu, M.-H. Chiang, S. Kahlal, J.-Y. Saillard and C. W. Liu, Angew. Chem., Int. Ed., 2015, 54, 3702.
31. T.-H. Chiu, J.-H. Liao, F. Gam, I. Chantrenne, S. Kahlal, J.-Y. Saillard and C. W. Liu, J. Am. Chem. Soc., 2019, 141, 12957.
32. F. Gam, C. W. Liu, S. Kahlal and J.-Y. Saillard, Nanoscale, 2020, 12, 20308.
33. F. Alkan, P. Pandeya and C. M. Aikens, J. Phys. Chem. C, 2019, 123, 9516.
34. F. Gam, I. Chantrenne, S. Kahlal, T.-H. Chiu, J.-H. Liao, C. W. Liu and J.-Y. Saillard, Nanoscale, 2022, 14, 196.
35. J. Wei, D. MacLeod Carey, J.-F. Halet, S. Kahlal, J.-Y. Saillard and A. Muñoz-Castro, Inorg. Chem., 2023, 62, 3047.
36. X. Li, B. Kiran, J. Li, H.-J. Zhai and L.-S. Wang, Angew. Chem., Int. Ed., 2002, 41, 4786.
37. P. Pyykkö and N. Runeberg, Angew. Chem., Int. Ed., 2002, 41, 2174.
38. H. Zabrodsky, S. Peleg and D. Avnir, J. Am. Chem. Soc., 1992, 114, 7843.
39. A. He, D. Zuo, G. Jiang, X. Tang, L. Wang, L. Feng, Z. Zhao, J. Wei, N. Zheng and H. Shen, Sci. Adv., 2025, 11, eads4488.
40. J. J. Bour, P. P. J. Schlebos, R. P. E. Kanters, M. F. J. Schoondergang, H. Addens, A. Overweg and J. J. Steggerda, Inorg. Chim. Acta, 1991, 181, 195.
41. T. G. M. M. Kappen, P. P. J. Schlebos, J. J. Bour, W. P. Bosman, G. Beurskens, J. M. M. Smits, P. T. Beurskens and J. J. Steggerda, Inorg. Chem., 1995, 34, 2121.
42. T. G. M. M. Kappen, J. G. M. Van der Linden, A. M. Roelofsen, J. J. Bour, P. P. J. Schlebos and J. J. Steggerda, Inorg. Chim. Acta, 1996, 245, 133.
43. D. M. P. Mingos and D. J. Wales, Introduction to Cluster Chemistry, Prentice Hall, Englewood Cliffs, NJ, 1990.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell Jr., J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
45. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
46. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
47. A. Schaefer, H. Horn and R. J. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
48. A. Schaefer, C. Huber and R. J. Ahlrichs, J. Chem. Phys., 1994, 100, 5829.
49. J. E. Carpenter and F. Weinhold, J. Mol. Struct.: THEOCHEM, 1988, 169, 41.
50. T. Lu and F. Chen, Acta Chim. Sin., 2011, 69, 2393.
51. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04862h

---