Kinetics of ion-mediated directed self-assembly of one-dimensional chains of metal nanoparticles in solution

Abstract

The synergistic optical, electronic, and chemical properties of metal nanoparticles present in close proximity have potential applications in energy, medicine, and sustainability. Fundamental studies and application development based on spontaneous self-assembly of one-dimensional (1D) chains of metal nanoparticles without external organization agencies have been pursued for over four decades. The spontaneous formation of 1D chains in a solution of stabilized spherical nanoparticles may be driven by the emergence of local anisotropy due to dipolar interaction, representing a trapped non-equilibrium state. Here, the kinetics of this broken symmetry in the “directed” self-assembly of spherical particles is studied to form a 1D chain. The 1D chain assembly of 10 nm Au particles that had been stabilized by electrostatic repulsion is initiated by adding a small amount of divalent cation salt. A phenomenological model is presented to explain the transition state controlling the kinetics of the 1D self-assembly. Experimental and simulation studies were combined to measure the kinetics of the chain growth over time which revealed a sharp transition between two growth processes that were analogous to addition and condensation polymerization.

---

Introduction

Exotic properties are exhibited by one-dimensional (1D) chains of spherical metal nanoparticles assembled in close proximity of a few nanometres due to the synergy of the individual optical and electronic behaviour of their localized surface plasmon resonance (LSPR)¹ and Coulomb blockade (CB),^2,3 respectively. Optically, the light is squeezed below the diffraction limit in small gaps between nanoparticles^4,5 to form a plasmonic waveguide,⁶ where enhancement of several orders of magnitude in the optical electric field can lead to sensitive optoelectronic devices.^7–9 In addition, the plasmonic “hot-electron” generation and transport in the chain enhances photocatalysis for a variety of reactions.^10–12 Electronically, multiple electron tunnelling junctions in the chain lead to a conduction gap at room temperature,^13,14 which is otherwise observed at cryogenic temperatures for a single particle.^15,16 The room temperature conduction gap in 1D chains is leveraged to build a highly sensitive all-metal “living transistor” that is gated by the cell's membrane potential to measure biochemical activity in real-time.^17,18 Such 1D chains have some unique features compared to the 2D structures. For example, the excitation wavelength linewidth for LSPR of the 1D chain is significantly sharper than that of the 2D array.¹⁹ Additionally, the conduction gap in the 1D chain occurs at a significantly higher temperature than in the 2D chain.^20,21

The intuitive approach to breaking the symmetry to form 1D chains of spherical nanoparticles is to invoke an external driver. There is a plethora of approaches based on magnetic, electrical and flow fields²² and molecular templates^23–27 to assemble 1D chains of metal nanoparticles in close proximity. A more subtle approach is to tailor the local inter-particle interaction of spherical metal particles to coax them to self-assemble in 1D chains. Local small-distance interactions are especially significant in the self-assembly of nanoparticles below about 25 nm.²⁸ The local interaction-driven approach is deceptively simple and was documented well even decades ago in studies on the aggregation of metal nanoparticles (soot) forming large networks of 1D chains.^29,30 Typically, a uniform negative charge appears on the surface of spherical metal nanoparticles during synthesis (for stabilization and size control)³¹ which is “neutralized” to reduce electrostatic repulsion, causing clustering.³⁰ If the amount of neutralization is relatively small, the local interaction becomes anisotropic due to non-uniform charge distribution leading to 1D chains due to dipolar interaction. A dipole can also be produced by metal–S bond,³² which is a pervasive approach to stabilize the nanoparticles of Novel metals by capping them with –SH containing oligomeric hydrophobic or hydrophilic compounds.³³ A consistent Derjaguin–Landau–Verwey–Overbeek (DLVO) model that accounts for the dipolar interaction due to patchiness and metal–S bond explains the emergence of 1D self-assembly; it shows that electrostatic repulsion is reduced by increasing ion strength because the particles prefer to attach at the end of the growing chain, juxtaposing to the side of the chain.³⁴ The surface ligand approach is quite general to control the 1D linear chain shape and branching.³⁵ For completeness, polymer-mediated anisotropic assembly is also a successful approach;³⁶ however, the particles are too far to synergize the optical and electronic properties of individual nanoparticles.

The aggregation process of 1D nanoparticle chains forming large networks was of great interest decades ago because such structures contained fractal objects that grew as diffusion-limited aggregates;³⁰ these structures had characteristic optical properties due to LSPR coupling between adjacent particles.^37,38 Structurally, by simulation, two growth processes have been identified. First, by adding one particle at a time to the chain (i.e., “addition”);³⁹ seconds, aggregation of larger chains to form bigger clusters (i.e., “condensation”).⁴⁰ In both cases the structure has a fractal geometry, however, the latter product was more open with a smaller fractal dimension of ∼1.35 versus ∼1.67 in the 2D space, respectively.^39,40 Image analysis of the electron percolation pathway on the deposited chain network (in 2D) in this study is shown to involve a fractal structure of dimension ∼1.88,⁴¹ which is consistent with a fractal dimension of ∼1.8 at the percolation threshold.⁴² However, in the abovementioned simulation structural studies, the time of formation is arbitrary.

Here, we report the growth kinetics of the 1D chains and their clusters in real-time. In this study, we create local anisotropy during self-assembly by “neutralizing” the negative charge on citrate-capped 10 nm Au particles by adding a small amount of divalent cation salt, which initiates the clustering process. By controlling the amounts of cations, a highly stable growth of 1D chains over a couple of days is obtained. We track the growth of this chain by a shift in the plasmon absorption band in the UV-Vis spectrum due to plasmonic waveguiding. By correlating the spectrum to the average length of the 1D chain using electromagnetic simulation, we obtain the growth as a function of time. Remarkably, both the addition and condensation regimes are distinctly identified.

Experiment and simulation methods

Gold nanoparticles synthesis

Tetrachloroauric(III) acid (HAuCl₄, 99%), sodium citrate, tannic acid, and potassium carbonate (K₂CO₃) were purchased from Sigma Aldrich. The 10 nm citrate-stabilized negatively charged Au nanoparticles were synthesized using the reverse Turkevich method.³¹ All apparatuses were washed in aqua regia and then rinsed with deionized water. A mixture of 150 mL of 2.2 mM sodium citrate, 1 mL of 150 mM K₂CO₃ and 1 mL of 2.5 mM tannic acid was heated until it boiled in a round bottom flask, which was connected to a reflux condenser. Once boiling was achieved, 1 mL of 25 mM HAuCl₄ was quickly injected into the solution, while stirring vigorously. The boiling solution was continuously stirred until it turned wine-red. Once cooled down, the solution was stored in a 4 °C refrigerator for further use. According to stoichiometry, the estimated molar concentration of particles was 3.2 × 10¹² particle per cm³.

Fabrication of 1D gold nanoparticle chains

Aqueous solutions of 5 mM concentration of cadmium perchlorate (Cd(ClO₄)₂), cadmium nitrate (Cd(NO₃)₂), and cadmium chloride (CdCl₂), respectively, were prepared. For each salt, a specific volume was added dropwise to 1 mL of the nanoparticle suspension under continuous stirring. The volume of salt added was carefully adjusted to ensure the formation of stable nanoparticle chains for at least 2 days. The specific amounts of each salt added are mentioned in the text for different studies. The solution was then left in the shaker for 15 to 18 hours to allow the formation of 1D chains. The change in colour from wine-red to purple-blue indicated the formation of the 1D chain.

UV-Vis spectroscopy

The UV-Vis absorbance spectrum of the nanoparticle suspension was measured in a polystyrene cuvette of 1 cm² square cross-section using 1 mL of solution. The absorbance spectra were measured using an Ocean Optics Model QE65000 spectrometer with an Ocean Optics HL-2000 halogen light source.

Scanning electron microscopy (SEM) for imaging

SEM images were acquired using a Helios 660 SEM at magnifications ranging from 65k to 150k, with electron energy of 5 keV and 10 keV and beam current of 0.2 nA. To prepare a sample for SEM, a silica chip was first cleaned with oxygen plasma at 80 W and 100 mTorr for 2 min, as well as spin-coated at 3000 RPM for 1 min using 1 mg mL⁻¹ aqueous solution of poly (allyl amine hydrogen chloride) (PAH); lastly, the chip was washed vigorously with deionized water to remove excess polymer. About 40 μL of Au nanoparticle suspension was sampled at different time points and diluted in 460 μL of deionized water. The chains from diluted suspension were deposited onto the chip by centrifugation¹⁴ (Universal Hettich 320) at 3500 RPM (2013 g) for 10 min. After deposition, the chip was rinsed with water and air-dried before SEM imaging.

Simulation

To evaluate the optical properties of Au nanoparticle chains, we performed numerical modelling using COMSOL Multiphysics 6. A physical 3D model of a box containing spherically shaped Au nanoparticles. The surrounding material was designed as depicted in ESI, section 3, Fig. S4.† To emulate the experimental geometry, most part of the block was filled with water (n = 1.33). Au particles were positioned in the center of the box and surrounded by the refractive index of salt to emulate the electrical double layer (EDL). The complex relative permittivity function for Au was obtained from the literature.⁴³ For the chains with finite lengths, we used perfectly matched layer (PML) boundary conditions to mimic an open and non-reflecting domain (ESI, section 3, Fig. S4(a)†). For the infinite-length chain, the periodic boundary conditions were defined along the chain axis (ESI, section 3, Fig. S4(b)†). To calculate the absorbance spectra, the incident (Source) and the receiving (Detector) components were located at opposite sides of the nanoparticle structure.

Here, the COMSOL module electromagnetic waves and the frequency domain were used for the simulations. An incident electric field that was polarized along the x-axis was incident on the Au nanoparticles chain, and absorbance was calculated at the detector port. The incident field was uniformly distributed, ensuring consistent E-field exposure across the entire chain length for precise interaction with the nanoparticle chains. For the E-field enhancement, the volume maximum function was used from post-processing to calculate the E-field in the close proximity of gold particles. Final E-field enhancement was evaluated using: 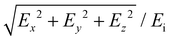, where E_x, E_y, and E_z are the local electric fields in x-, y-, and z-directions, respectively, and E_i is the incident optical electric field.

Results and discussion

Upon the addition of 290 μL of 5 mM Cd(NO₃)₂ solution to 1 mL of 10 nm Au particle suspension with ∼3.2 × 10¹² particles per cm³, a second localized surface plasmon resonance (LSPR) peak begins to appear (Fig. 1(a)). The second LSPR band was correlated to the formation of 1D chains as previously shown by transmission electron microscopy (TEM)¹³ and scanning electron microscopy (SEM).¹⁴ The solution was placed on a shaker to ensure good mixing during the process. Following a procedure described by others for 1D chain self-assembly,⁴⁴ the LSPR band for a single nanoparticle was subtracted to obtain the second peak arising from 1D chains (Fig. 1(b)). (The details of the procedure are described in the ESI, section 1, Fig. S1 and S2.†) The monotonic redshift of the LSPR peak, λ_LSPR (in Fig. 1(b)), is due to a well-known plasmon coupling reaction between adjacent particles as the chain becomes longer. Importantly, note that the peak reaches a stable wavelength, where λ_{LSPR, stable} = 604 nm at ∼30 h. After a longer duration (i.e., 68 h), the invariant stable peak, λ_{LSPR, stable}, begins to diminish, indicating precipitation. Importantly, the redshifted band is a single Gaussian peak with a self-similar shape as evident from the linear relationship between the area of the peak versus its height (Fig. 1(b), inset). Thus, during growth, the overall distribution of the number of particles per chain, i.e., N, remains unchanged. The redshift and its stability at 604 nm is quantitatively attributed to chain growth as shown by the simulation below (Fig. 5). Changing the anion does not have any significant effect on the stable LSPR band (Fig. 1(c)). Also, the λ_{LSPR, stable} is less redshifted for a smaller amount of salt added, which indicates incomplete growth (Fig. 1(d); not shown, but too much salt will precipitate the particles without chain formation). Thus, for this study, the optimum concentration of Cd(NO₃)₂ was added, i.e., 1.1 mM (i.e., 290 μL of 5 mM Cd(NO₃)₂ in 1 mL Au nanoparticle suspension).

Fig. 1 The effect of adding Cd(NO₃)₂ to a suspension of 10 nm Au nanoparticles. (a) UV-Vis absorbance spectra as a function of time. The λ_LSPR redshifts as time increases and the suspension reaches a stable state; λ_{LSPR, stable} at 604 nm after 15 h. The absorbance decreases, but λ_{LSPR, stable} remains unchanged after 68 h. Inset: Nanoparticle suspension changes color from wine-red to blue after 15 h. (b) Single Au nanoparticles-subtracted UV-Vis absorbance spectra. Inset: Linear relationship between the deconvoluted peak area and peak intensity of the subtracted spectra, fitted with equation y = −12.93 + 198.9x with R² = 0.995. (c) The effect of the type of anions on the UV-Vis absorbance spectra of nanoparticle suspension under stable states. (d) The effect of salt concentration on the UV-Vis absorbance spectra of nanoparticle suspension under a stable state.

To qualitatively explain the observations, a simple (mechanistic) phenomenological model is considered (Fig. 2): (i) on adding the salt, the cations (i.e., Cd²⁺ for this study) condense on the Au nanoparticle's diffuse electrical double layer (EDL). The monovalent Na⁺ (from synthesis) and background anions in the EDL are not shown. (ii) As two particles collide due to thermal motion, electrostatic interaction distorts the diffuse EDL, which induces a dipole, μ. (iii) The dipolar interaction leads to binding, followed by rearrangement of the overlapping diffuse EDL of the particles. (iv) The next particle then collides with the doublet, leading to the formation of a triplet. Owing to dipolar interaction due to induced polarization, the particles prefer to be added at the ends, rather than the middle,³⁴ leading to a 1D chain that continues to grow, analogous to addition “polymerization” (not shown further in Fig. 2).

Fig. 2 The mechanism of 1D chain self-assembly. (i) Stabilized nanoparticles with diffuse EDL. (ii) Upon thermal collision, their diffuse EDL deforms leading to an induced dipole moment, μ, that causes attraction (i.e., clustering). (iii) The EDL is rearranged to engulf the new structure to form a bond. (iv) It is energetically more favorable for the third particle to bind at the edge. The 1D self-assembly of chains by addition of particles at the ends continues, which is analogous to a “polymerization” process.

The following inference can be made from the model: (a) the role of the added anion is not significant; this is consistent with the observation in Fig. 1(c). (b) An ionic bridge of the added (multivalent) cation “glues” the particles together. This was shown explicitly by reacting the chains with H₂S (or Na₂S) to form a CdS nano-cement that exhibits electroluminescence,⁴⁵ which was also imaged by high-resolution TEM for Zn²⁺-mediated 1D chains.⁴⁶ (c) If the salt added was below a certain threshold, the amount was not enough for chains to grow sufficiently, which lowered the λ_{LSPR, stable} as observed in Fig. 1(d). (d) As the local environment of the particles in the 1D chains is same (except at the ends), it is reasonable to expect the interparticle spacing, i.e., s, due to the ion bridge in the 1D chain is constant. (e) Consistent with the DLVO analysis,³⁴ the rearrangement of the EDL on binding will be energetically costly for inter-chain binding of “small” chains, thus the growth will primarily be analogous to addition “polymerization”. (f) However, as the chain length increases, the capacitance of the EDL ∼ N will also increase, leading to lower activation energy for rearrangement (∼e²/N, where e is a charge of the electron). As a result, beyond a certain N, chain-chain binding can also occur, analogous to condensation “polymerization”.

According to the above model, the activation barrier dictating the kinetics of the growth of the 1D chain is the energy penalty to rearrange the EDL to form a bond, i.e., the transition state is the superposition of EDL upon collision (Fig. 2). The chain growth for small N should favour “addition” and as chains grow longer, “condensation” should commence, leading to more complex topologies, such as branching. From this rather simplistic phenomenological model and SEM images discussed below (Fig. 3), a transition from addition to condensation polymerization is expected. To find this possible transition, the redshift in UV-Vis peak over time, i.e., t, needs to be related to 〈N〉, to obtain 〈N〉(t).

Fig. 3 SEM images of the self-assembly of 10 nm Au particles at different periods after adding Cd²⁺ salt. SEM images were taken at (a) 2 h, (b) 3 h, (c) 4 h, (d) 7 h, (e) 10 h, (f) 15 h, (g) 20 h, (h) 30 h, and (i) 50 h.

The occurrence of chain growth phenomena in solution can indirectly be visualized by rapid deposition of the chains at different t. This is performed by centrifuge deposition of the chains suspended in the solution onto a Si wafer that is modified with positively charged poly(allyl amine hydrochloride) (PAH).¹⁴ The SEM imaging shows chain growth over time (Fig. 3). In the centrifuge, the angular velocity creates a free-energy gradient that leads to the separation of chains from the suspension, followed by deposition by centrifugal force.¹⁴ It is clear that 1D chains are formed. However, from the appearance of the clusters, it is difficult to discern if the chains are branched or simply entangled because of their enhanced densification and phase separation due to centrifugation just before deposition. However, it is apparent that the chain seems to cluster after 7 h as compared to 4 h; and the clustering progressively grows past 15 h; especially after 20 h, the clusters are large enough that their numbers (per solution volume) begin to decrease (see ESI, section 2, Fig. S3† for magnified views). At 50 h, the clusters appear significantly large, indicating the limited stability of the suspension. Qualitatively, there seems to be a growth spurt past 7 h and between 15 h and 20 h the clustering is large enough so that the number of clusters begins to reduce. Qualitatively, there seems to be a growth spurt between t = 7 h and 20 h with a concomitant decrease in the number of clusters. Thus, there appear to be two regimes of self-assembly.

Next, we simulate the UV-Vis spectrum to quantitatively relate the observations regarding chain growth in Fig. 1 and 2. For the simulations, a linearly polarized (LP) electromagnetic wave is incident on the 1D-chain of Au nanoparticles with an E-field parallel to the chain axis. The incident light is uniformly distributed over the entire chain length. In the simulation, we incrementally increased the number of Au nanoparticles in the chain to mimic chain growth and study the evolution of the λ_LSPR as an increase in N. The material parameters were adjusted as discussed below. The details of the method are in the Experimental section (see Simulation). For a single particle, to obtain the λ_LSPR band at 515 nm for the synthesized 10 nm Au particle, the effective refractive index of the media, n, was 1.42 (ESI, section 4, Fig. S5†). The higher refractive index compared to 1.33 for pure water is due to the high ionic strength in the EDL, typically in the 1 M range, that dictates the boundary conditions at the particle/media interface. The broader experimental band is attributed to the dispersity in size and shape of the particles.

Upon the formation of the doublet, the gap s determines the extent of the inter-particle LSPR coupling. The heat map of the E-field, which is defined as the amplitude of the local optical field, relative to the incident light, intensifies as the s decreases due to stronger inter-particle coupling (Fig. 4(a)). As the calculations are performed with the polarized light in the horizontal direction (ESI, section 3, Fig. S4†), the E-field enhancement is observed only at 0° and 180°. For the near-surface effect, within a few nm, the curvature effects can be neglected, leading to the expected decay of maximum E-field as 1/s² (Fig. 4(b)). For s above 3 nm, the coupling is weak as apparent both from the heat map and 1/s² dependence. Notably, as our simulation is based on classical electromagnetic, an E-field enhancement below s ∼ 1 nm is not very realistic due to strong quantum mechanical effects.

Fig. 4 Electromagnetic simulation of E-field defined as local electric field relative to incident field. (a) Heat map of E-field for different interparticle distances, s. (b) The maximum E-field in the gap, E (i.e., enhancement in the hot spot) for a doublet as a function of their separation distance, s, decreases as inverse square law (1/s²). For the simulation in (a) and (b), index of the media, n = 1.33.

To model the 1D chain, three parameters must be determined: N, n, and s. The s was estimated by the conduction behaviour through a monolayer of the network of the chains, i.e., nanoparticle necklace network (N³) deposited between the two electrodes. Quantitative image analysis that maps the percolation path topology of N³,¹⁴ as well as the electrical measurement of electron tunnelling mediated conduction, showed that s is slightly below 3 nm to explain the observed non-Ohmic behavior⁴¹ and gating properties.⁴⁶ Considering the ∼0.5 nm-thick hydrated perchlorate layer on each particle and the EDL of 2–3 layers in the compensating bridge of the hydrated cations, a reasonable assumption of s = 2.4 nm was made for the ion bridge.

For s = 2.4 nm, as N increases, the λ_LSPR redshifts, as expected, and stabilizes as N → ∞ to λ_{LSPR, stable} (Fig. 5). To model N = ∞, periodic boundary conditions, along the chain growth direction, were applied. These periodic boundaries effectively replicate the conditions of an unending Au nanoparticle chain, which ensures that the E-field solution repeats along the chain axis without any discontinuity. The details of the method are in the Experimental section (see Simulation). Finally, n = 1.73 was chosen, therefore, λ_{LSPR, stable} = 604 nm was consistent with the observation (Fig. 1(b)). The n = 1.73 was determined by an “n-sweep” at fixed s = 2.4 nm and N = ∞ to obtain λ_{LSPR, stable} = 604 nm (ESI, section 5, Fig. S6(a)†). The change in the values of n as s was reduced from 2.4 nm to 2 nm was only −2.89% (ESI, section 5, Fig. S6(b)†). To further confirm that the value of s was reasonable, an “s-sweep” was performed at n = 1.73 to observe that λ_{LSPR, stable} changed only by 604 ± 1.5 nm as s changed from 2.3 nm to 2.5 nm (ESI, section 5, Fig. S7†). Thus, the n = 1.73 and s = 2.4 nm reasonably models the 1D chains bridged by Cd²⁺ ion bridge. The significantly larger effective refractive index of the medium of n = 1.73 for chains, compared to 1.42 for synthesized nanoparticles, is attributed to the large polarizability of Cd²⁺ (due to larger electron screening) as compared to Na⁺.

Fig. 5 Simulated UV-Vis absorbance spectra of Au nanoparticle chains at n = 1.73 and s = 2.4 nm. Increasing the number of particles in the chain, N from 2 to ∞, the absorption spectra strengthens and exhibits a redshift in λ_LSPR. The λ_LSPR stabilizes at λ_{LSPR, stable} = 604 nm for N ∼ 8. However, the absorbance continues to increase beyond N = 8.

To quantify the kinetics, the experimental λ_LSPR(t) (Fig. 1(b)) must be related to simulated λ_LSPR(N) (Fig. 5). The total absorbance is ∼N, and the absorbance cross-section per chain for longer chain is more (see ESI, Fig. S8,† discussed below). Thus, λ_LSPR(t) is dominated by the longest chains, i.e., the front-end of the growth. Thus, λ_LSPR(t) and λ_LSPR(N) correspondence will track the growth of the longest chains. Furthermore, as noted above, the chain distribution remains invariant (from Fig. 1(b) inset), thus, the effect of branching is insignificant. From the experimental (Fig. 1(b)) and simulation (Fig. 5) results, the change in λ_LSPR as a function of t and N, respectively, was determined (Fig. 6). For example, we chose λ_LSPR = 590 nm and determined the corresponding t (from experiment) and N (from simulation) in Fig. 6 to obtain the kinetics curve, 〈N〉 as a function of t, i.e., 〈N(t)〉 (Fig. 7).

Fig. 6 Experimental and simulated λ_LSPR of the self-assembly of Au nanoparticle chain. Experimental result of λ_LSPR as a function of t, where the inset shows a close-up view for t > 1000 min (left). Simulation results of λ_LSPR as a function of N (right).

Fig. 7 Kinetics of the self-assembly of 1D Au nanoparticle chain. From the experimental λ_LSPR(t) and simulated λ_LSPR(N), the kinetics of chain growth 〈N〉(t) exhibits two distinct regimes: 0.0077 min⁻¹ (slow) and 0.0166 min⁻¹ (fast).

There are clearly two distinct regimes in the kinetics curve (Fig. 7). The first regime is slower growth that is primarily attributed to “addition polymerization”, where each particle is added at the end of the chain. As every chain is a growth center, the process continues until most of the particles are consumed. Also, the longer chains will grow slower because of lower mobility, leading to smaller collision rates. Thus, the size distribution should be limited by diffusion. A growth spurt occurs beyond N ∼ 7 (at t ∼ 535 min). In this second regime, condensation polymerization occurs when two long chains join to form a longer chain. Although the geometric growth is rapid, the collision rate is lower. As a result, the rate increases significantly by two-fold. The SEM image (Fig. 3) qualitatively captures the growth process with significantly fewer individual particles, however, the transition is not apparent (see ESI, section 2, Fig. S3† for magnified SEM images). It is nevertheless clear that at some point beyond 7 h, clustering of larger chains occurs.

Lastly, we estimate the number of clusters, N_C(t), as the chain grows over time. Specifically, the expected decrease in N_C is due to chain–chain clustering. For a fixed experimental set-up, I_A ∼ N_Cσ_abs, where, I_A is absorbance and σ_abs is the absorption cross-section. From the simulation, the absorption cross-section, σ_abs,(N) of a chain of length N at λ_LSPR can be calculated (ESI, section 6, Fig. S8(a)†). The absorbance at λ_LSPR measured by UV-Vis spectroscopy (Fig. 1(b)) is I_A(t) (ESI, section 6, Fig. S8(b)†). Since the shape of the respective peaks remains unchanged, the peak height is sufficient to estimate the ratio, I_A/σ_abs ∼ N_C. Similar to the kinetics curve (Fig. 7), the I_A(N) tracks the average chain length, 〈N〉. Thus, for a given time, t₀, (i) the N(t₀) was calculated from Fig. 7; subsequently, (ii) for the N(t₀), the corresponding σ_abs,(N(t₀)) and I_A(t₀) were obtained from ESI, Fig. S8(a) and S8(b),† respectively. This finally led to (iii) N_C(t₀) = I_A(t₀)/σ_abs,(N(t₀)) (Fig. 7). The N_C(t) shows that the number of clusters, N_C, commence to reduce beyond ∼10³ min (Fig. 8). The reduction in N_C is qualitatively consistent with results presented in Fig. 3, where between 15 h and 20 h, the chains noticeably condense to form significantly larger clusters with fewer N_C.

Fig. 8 Normalized number of Au nanoparticle clusters as a function of time. The normalized number of clusters (∼I_A/σ_abs) increases in the slow regime and commences to reduce in the fast regime.

Conclusions

In summary, the growth kinetics of a one-dimensional chain of 10 nm Au nanoparticle in “close proximity” was studied. Based on the experimental observations, simulations, and modelling, the particle–particle contact distance, i.e. (close) proximity was defined as less than 3 nm. Directed self-assembly in the solution was mediated by Cd²⁺ ions. The growth process was tracked in real-time by the redshift in the local surface plasmon resonance (LSPR) spectrum measured by UV-vis spectroscopy. The growth of the 1D self-assembly was confirmed by rapid deposition of the chains at different time points by centrifuge, followed by SEM imaging. Relating the experimentally measured redshift to electromagnetic simulation, the growth of average chain length, 〈N〉, was obtained as a function of time. It is important to highlight that to relate observed and simulated spectrum, robust determination of n and s is needed to estimate growth, N from experimental λ_LSPR(t) shift. This was possible by the occurrence of λ_{LSPR, stable} that is independent of N and bounds on s because the clusters are conducting. The growth kinetics, 〈N(t)〉, showed two sharply defined regimes. The initial slow and later fast growth rate regimes are attributed to addition and condensation processes, respectively. A simple model is described showing the transition state that explains the emergence of broken symmetry to obtain 1D chains of 10 nm spherical particles and the two growth regimes. Although Cd²⁺ has been studied before,^13,20,45 it is used as a model ion for the kinetics study. Other ions, such as Ca²⁺,^14,41,46 Fe³⁺,^17,18,20 and Zn²⁺,²⁰ have been shown to form similar chains and may exhibit similar kinetic behaviour. The understanding of the growth kinetics will potentially lead to approaches to engineer a 2D array of 1D nanoparticle chains for diverse applications by leveraging their electronic and optical properties.

Author contributions

The manuscript was written through the contributions of all authors. J. M. L. and M. A. N. contributed equally to this work. All authors have approved the final version of the manuscript.

Data availability

All the typical raw data from experiments and simulations supporting the article are included in the ESI.†

We will be happy to provide specific data, conditions, and methodology to interested parties if necessary.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

RFS would like to thank the Nebraska Public Power District through the Nebraska Center for Energy Sciences Research at the University of Nebraska-Lincoln and the US Army Research Office (ARO) Grant Number W911NF2310036 for financial support.

References

1. S. K. Ghosh and T. Pal, Chem. Rev., 2007, 107, 4797–4862.
2. K. Elteto, E. G. Antonyan, T. T. Nguyen and H. M. Jaeger, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 064206.
3. A. A. Middleton and N. S. Wingreen, Phys. Rev. Lett., 1993, 71, 3198–3201.
4. C. Ciracì, R. T. Hill, J. J. Mock, Y. Urzhumov, A. I. Fernández-Domínguez, S. A. Maier, J. B. Pendry, A. Chilkoti and D. R. Smith, Science, 2012, 337, 1072–1074.
5. D. A. Iranzo, S. Nanot, E. J. C. Dias, I. Epstein, C. Peng, D. K. Efetov, M. B. Lundeberg, R. Parret, J. Osmond, J. Y. Hong, J. Kong, D. R. Englund, N. M. R. Peres and F. H. L. Koppens, Science, 2018, 360, 291–295.
6. S. A. Maier, P. G. Kik, H. A. Atwater, S. Meltzer, E. Harel, B. E. Koel and A. A. G. Requicha, Nat. Mater., 2003, 2, 229–232.
7. S. Cong, X. H. Liu, Y. X. Jiang, W. Zhang and Z. G. Zhao, Innovation, 2020, 1, 100051.
8. X. Wang, S. C. Huang, S. Hu, S. Yan and B. Ren, Nat. Rev. Phys., 2020, 2, 253–271.
9. V. Shvalya, G. Filipic, J. Zavasnik, I. Abdulhalim and U. Cvelbar, Appl. Phys. Rev., 2020, 7, 031307.
10. J. B. Lee, S. Choi, J. Kim and Y. S. Nam, Nano Today, 2017, 16, 61–81.
11. D. Liu and C. Xue, Adv. Mater., 2021, 33, 2005738.
12. S. C. Warren and E. Thimsen, Energy Environ. Sci., 2012, 5, 5133–5146.
13. V. Maheshwari, J. Kane and R. F. Saraf, Adv. Mater., 2008, 20, 284–287.
14. P. Wilson, J. K. Y. Ong, A. Prasad and R. F. Saraf, J. Phys. Chem. C, 2019, 123, 19999–20005.
15. S. H. Magnus Persson, L. Olofsson and L. Gunnarsson, Appl. Phys. Lett., 1999, 74, 2546–2548.
16. Y. Azuma, Y. Onuma, M. Sakamoto, T. Teranishi and Y. Majima, Nanoscale, 2016, 8, 4720–4726.
17. E. H. Lee, S. W. Lee and R. F. Saraf, ACS Nano, 2014, 8, 780–786.
18. S.-W. Lee, E.-H. Lee, G. Thiel, J. L. Van Etten and R. F. Saraf, ACS Nano, 2016, 10, 5123–5130.
19. S. L. Zou and G. C. Schatz, J. Chem. Phys., 2004, 121, 12606–12612.
20. J. Kane, J. Ong and R. F. Saraf, J. Mater. Chem., 2011, 21, 16846–16858.
21. R. Parthasarathy, X. M. Lin, K. Elteto, T. F. Rosenbaum and H. M. Jaeger, Phys. Rev. Lett., 2004, 92, 076801.
22. H. Y. Wang, H. Li, P. Gu, C. L. Huang, S. B. Chen, C. L. Hu, E. Lee, J. P. Xu and J. T. Zhu, Nanoscale, 2023, 15, 2018–2035.
23. T. X. Chang, H. Y. Huang and T. B. He, Macromol. Rapid Commun., 2016, 37, 161–167.
24. A. Kuzyk, R. Schreiber, Z. Y. Fan, G. Pardatscher, E. M. Roller, A. Högele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311–314.
25. S. Mondal, P. Rehak, N. Ghosh, P. Kral and E. Gazit, ACS Nano, 2022, 16, 18307–18314.
26. N. Sharma, A. Top, K. L. Kiick and D. J. Pochan, Angew. Chem., Int. Ed., 2009, 48, 7078–7082.
27. M. G. Warner and J. E. Hutchison, Nat. Mater., 2003, 2, 272–277.
28. K. J. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630.
29. S. R. Forrest and T. A. Witten, J. Phys. A: Math. Gen., 1979, 12, L109–L117.
30. D. A. Weitz and M. Oliveria, Phys. Rev. Lett., 1984, 52, 1433–1436.
31. J. Piella, N. G. Bastús and V. Puntes, Chem. Mater., 2016, 28, 1066–1075.
32. P. Crespo, R. Litrán, T. C. Rojas, M. Multigner, J. M. de la Fuente, J. C. Sánchez-López, M. A. García, A. Hernando, S. Penadés and A. Fernández, Phys. Rev. Lett., 2004, 93, 087204.
33. Q. B. Yun, Y. Y. Ge, B. Huang, Q. B. Wa and H. Zhang, Acc. Chem. Res., 2023, 56, 1780–1790.
34. H. Zhang and D. Y. Wang, Angew. Chem., Int. Ed., 2008, 47, 3984–3987.
35. X. D. Peng, M. M. Zhang, F. Xue, A. D. Zhang, Y. Xu, Y. Huang, H. Wang and H. Y. Chen, Mater. Chem. Front., 2023, 7, 3073–3081.
36. C. L. Yi, Y. Q. Yang, B. Liu, J. He and Z. H. Nie, Chem. Soc. Rev., 2020, 49, 465–508.
37. M. Moskovits, Rev. Mod. Phys., 1985, 57, 783–826.
38. J. A. Creighton, C. G. Blatchford and M. G. Albrecht, J. Chem. Soc., Faraday Trans. 2, 1979, 75, 790–798.
39. T. A. Witten and L. M. Sander, Phys. Rev. Lett., 1981, 47, 1400–1403.
40. M. Kolb, R. Botet and R. Jullien, Phys. Rev. Lett., 1983, 51, 1123–1126.
41. A. Prasad, M. Stoller and R. F. Saraf, ACS Appl. Nano Mater., 2021, 4, 9044–9051.
42. H. E. Stanley, J. Phys. A: Math. Gen., 1977, 10, L211–L220.
43. P. B. Johnson and R. W. Christy, Phys. Rev. B, 1972, 6, 4370–4379.
44. R. W. Taylor, T.-C. Lee, O. A. Scherman, R. Esteban, J. Aizpurua, F. M. Huang, J. J. Baumberg and S. Mahajan, ACS Nano, 2011, 5, 3878–3887.
45. J. K. Y. Ong, C. V. Nguyen, S. Sayood and R. F. Saraf, ACS Nano, 2013, 7, 7403–7410.
46. A. Prasad, J. M. Lim and R. F. Saraf, Adv. Electron. Mater., 2024, 10, 2300485.

---

Footnotes

† Electronic supplementary information (ESI) available: Details on the UV-spectrum data processing, SEM images, and raw data from simulations. See DOI: https://doi.org/10.1039/d4nr04770b

‡ First authors – equal contribution.

---