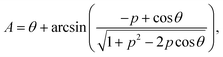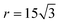Open Access Article
Open Access ArticleUniversal scaling laws on the rotational energy landscape for twisted van der Waals bilayers†
Zichong
Zhang
and
Shuze
Zhu
 *
*
Center for X-Mechanics, Department of Engineering Mechanics, Zhejiang University, Hangzhou 310000, China. E-mail: shuzezhu@zju.edu.cn
First published on 24th February 2025
Abstract
The emerging field of twistronics utilizes the interfacial twist angle between two-dimensional materials to design and explore unconventional electronic properties. However, recent investigations revealed that not every twist angle is stable. Understanding and predicting preferred twist angles are therefore of vital importance and have received considerable attention; however, general analytical theories that can feasibly address the stability of twist angles have not yet been developed. In this work, we reveal the existence of universal analytical scaling laws that delineate the interface rotational energy landscape, enabling the determination of both stable angles and interlayer rotational torque. The universality of our theoretical results is fundamentally based on the evolution of moiré geometry, which is applicable across many material interface systems. Our results not only unify experimental observations and literature atomistic simulations, but also provide new perspectives for the rational design of nanoscale rotation-tunable electronic devices. Our theories can potentially inspire a deeper understanding of moiré-correlated interface mechanics.
Introduction
The field of twistronics, focusing on the utilization of van der Waals layers of two-dimensional (2D) materials, has garnered significant attention in recent years.1–4 The rotational twist angle between these layers plays a crucial role in governing the interlayer coupling, which in turn determines the desirable electronic and other physical properties.5–7 However, recent experimental evidence has highlighted that not all twist angles are inherently advantageous. Investigations utilizing atomic force microscopy have unveiled specific discrete twist angles that exhibit enhanced stability and resistance to interlayer rotation.2 These angles correspond to local minima in the interface energy.8 In the context of magic-angle bilayer graphene, on-tip scanning with a superconducting quantum interference device has detected instances of local twist-angle disorder.9 Furthermore, preferred twist angles often manifest during the growth process of 2D materials through chemical vapor deposition.10 These findings provide strong indications that the instability of twist angles is a prevalent phenomenon within the emerging field of twistronics. This instability may lead to difficulties in achieving the desired targeted twist angles, ultimately resulting in failure to attain the intended state. Therefore, it is important to comprehend and predict the preferred twist angles. Recent investigations10–15 into the instability of twist angles have unveiled a strong correlation between them and moiré patterns. However, general analytical theories that can feasibly address the stability of twist angles have not yet been developed.To address the above challenge, in this work, we show that there are universal analytical scaling laws to account for the interface rotational energy landscape, which lead to a unified understanding of stable twist angles for twisted van der Waals bilayers. Fundamentally based on the evolution of moiré geometry, our theoretical approaches are universally applicable across many material interface systems. To extract general physical insights, we begin with molecular simulations16 for three representative material systems, including twisted bilayer graphene (TBG),17,18 bilayer MoS2,12,19,20 and graphene/h-BN heterobilayers.21,22 Our theories focus on equilateral triangles and hexagons as these shapes are frequently observed in chemical vapor deposition (CVD) growth processes.13,23 Our theoretical approach could also accommodate other shapes (e.g., see results for square shapes in the ESI†). In principle, any initial twisted configurations can be fabricated using the dry-transfer method.23,24 With the understanding of simulation observations, we develop moiré-geometry-based theories, which are capable of analytically accounting for the rotational energy landscape and determining both stable angles and interlayer rotational torque. Such straightforward analytical approaches have clear advantages over atomistic simulations, which may suffer from large model sizes. Our results not only show strong agreement with simulation and literature results, but also can potentially guide the design and deepen the understanding of twistronics.
Results and discussion
Fig. 1 illustrates simulation results on twist angle instability for triangular flakes of TBG, bilayer MoS2, and graphene/h-BN heterobilayers. We study flakes of different sizes in order to show general observations. For each material flake, geometric relaxation is performed after imposing an initial twist angle θ0 (with the rotation axis passing through the flake's symmetric center), from which the final stable angle θ′ is determined. Since our simulation is performed on different materials, it is essential to identify material-specific high-energy (AA/BA) and low-energy AB(3R) stacking configurations.18,25,26 Detailed stacking classifications and simulation methods are provided in the ESI.† In the case of TBG (Fig. 1(b and e)), the flake side length is about 7.3 nm, while the bottom layer is considered infinitely large (Fig. 1(a)). The initially imposed twist angles before relaxation are applied incrementally on two different initial stacking patterns. The initial AA stacking triangles are referred to as “AA triangle” for brevity (similar notation rules apply to other shapes or stacking configurations). The subsequent geometric relaxation reveals three final stable twist angles within the simulated twist angle range. Note that for tiny initial angles imposed on the initial AB(3R) stacking, the final stable angle is always 0° (physically, the flake rotates back to its initial AB(3R) stacking). These discretized final stable angles suggest the presence of rotational energy barriers, with the interface rotational torque driving the flake to rotate towards different final states. On the other hand, the bilayer MoS2 with a side length of 8 nm (Fig. 1(c and f)) and graphene/h-BN heterobilayers (Fig. 1(d and g)) with a side length of 12.4 nm exhibit similar features in discretized final stable angles. We emphasize that these preferred twisted states are also translationally stable (see the ESI†), in agreement with an earlier report.14To understand the twist angle instability, we identify the correlation between moiré patterns and the interface stacking energy landscape (Fig. 2). Despite differences in flake size, TBG and MoS2 exhibit similar moiré patterns at different stable twist angles. For example, the left column in Fig. 2(a and d) shows the top views of the atomistic structure for three stable angles of TBG as shown in Fig. 1(b and e). The lighter region corresponds to the high-energy AA stacking domain, where atoms visually overlap, whereas the darker region represents the low-energy AB stacking.17 The distribution of these domains in MoS2 (Fig. 2(b and e)) is similar, although the stacking definition (i.e., AA and 3R) is different (see the ESI 1†). A more intricate moiré pattern is observed in the graphene/h-BN system (Fig. 2(c and f)), because both AA stacking and BA stacking possess the highest interface energy, with almost equal magnitudes, while the AB stacking still has the lowest interface energy.26 This intricacy can be ascribed to the existence of lattice mismatch.27 Given such complex observations of similarities and discrepancies across different materials, is there a unified theoretical framework to account for stable twist angles?
 | ||
| Fig. 2 The moiré patterns corresponding to the three stable angles from Fig. 1. The local stacking energies of the visual moiré patterns (left column) of different material flakes can be captured by the moiré periodic potential (right column). (a and d) TBG, (b and e) bilayer MoS2, and (c and f) graphene/h-BN heterostructure with initial AA and AB(3R) stacking configurations, where the actual stacking domains are labeled. In the left column of each panel, colors are selected to distinguish different layers. | ||
This work answers the above question. We find that the left-column moiré patterns can be universally described by a moiré periodic potential (the right column of Fig. 2), from which an analytical energy landscape can be elegantly derived. We utilized a general form of  to characterize the moiré potential of TBG and MoS2,28 where
to characterize the moiré potential of TBG and MoS2,28 where  represents the reciprocal lattice vector that accounts for the planar periodicity of the moiré pattern. However, for graphene/h-BN, because AA and BA stackings are considered energetically equivalent,26 the low-energy domains form triangular arrays and each low-energy domain is surrounded by six high-energy domains.21,22,26,29–31 Such an energy distribution can be conveniently represented by
represents the reciprocal lattice vector that accounts for the planar periodicity of the moiré pattern. However, for graphene/h-BN, because AA and BA stackings are considered energetically equivalent,26 the low-energy domains form triangular arrays and each low-energy domain is surrounded by six high-energy domains.21,22,26,29–31 Such an energy distribution can be conveniently represented by 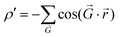 .32,33 The essence of this theoretical treatment is that the symmetric, geometric and energetic characteristics of the moiré pattern in twisted van der Waals bilayers are satisfied.
.32,33 The essence of this theoretical treatment is that the symmetric, geometric and energetic characteristics of the moiré pattern in twisted van der Waals bilayers are satisfied.
Our theories use the following notations. The mismatch parameter p represents the ratio of the lattice constants between the top layer (Rt) and the substrate layer (Rs). For graphene/h-BN heterostructures, p = 0.98,2,27 while for TBG and bilayer MoS2, p = 1. The dimensionless size parameter  is used to denote the normalized flake size, where a is the lattice constant of the top layer and R is the radius of the circumcircle for an equilateral triangle or hexagon. For example, in Fig. 1, the size parameter r is
is used to denote the normalized flake size, where a is the lattice constant of the top layer and R is the radius of the circumcircle for an equilateral triangle or hexagon. For example, in Fig. 1, the size parameter r is  for TBG and
for TBG and 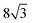 for bilayer MoS2, while for a graphene/h-BN heterostructure,
for bilayer MoS2, while for a graphene/h-BN heterostructure,  .
.
Our theories establish an analytical scaling mapping from the dimensionless twist angle θ, size parameter r, and lattice mismatch parameter p to interlayer rotational energy. The reciprocal lattice vector 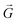 carries information about the moiré wavelength λ and the orientation of the moiré pattern.34 The key step is to describe the evolution of
carries information about the moiré wavelength λ and the orientation of the moiré pattern.34 The key step is to describe the evolution of  as a function of p, r, and θ. When the initial stacking configuration is AA, the center stacking after twisting remains close to AA; therefore, the moiré potential function35 is
as a function of p, r, and θ. When the initial stacking configuration is AA, the center stacking after twisting remains close to AA; therefore, the moiré potential function35 is  . However, if the initial stacking is in the AB(3R) configuration, the center stacking after twisting remains close to AB(3R), and the moiré potential function should be modified35 to
. However, if the initial stacking is in the AB(3R) configuration, the center stacking after twisting remains close to AB(3R), and the moiré potential function should be modified35 to  . In our methodology, it is important to ensure that the mathematical description of the initial orientation and the subsequent rotation of moiré potential function are both consistent with the observed moiré patterns in real materials. Then, λ(θ, p) should be substituted34 as
. In our methodology, it is important to ensure that the mathematical description of the initial orientation and the subsequent rotation of moiré potential function are both consistent with the observed moiré patterns in real materials. Then, λ(θ, p) should be substituted34 as 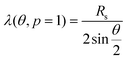 and
and  . Furthermore, because the moiré pattern rotates with the flake, it is necessary to impose a rotation34 to the above moiré potential function. Finally, an analytical expression can be obtained by integrating the moiré energy function over the entire shape of the flake,32,35 denoted as
. Furthermore, because the moiré pattern rotates with the flake, it is necessary to impose a rotation34 to the above moiré potential function. Finally, an analytical expression can be obtained by integrating the moiré energy function over the entire shape of the flake,32,35 denoted as  , where Ω(x, y, r) represents the corresponding shape of the flake. After normalization through division by the flake area, a dimensionless total energy landscape function
, where Ω(x, y, r) represents the corresponding shape of the flake. After normalization through division by the flake area, a dimensionless total energy landscape function  is obtained. The stable twist angles can then be readily extracted from its energy local minima.
is obtained. The stable twist angles can then be readily extracted from its energy local minima.
We first present the elegant and concise rotational total energy function for triangular identical (p = 1) bilayer materials (based on  ).
).
For initial AA stacking:
 | (1) |
For initial AB(3R) stacking:
 | (2) |
Also, the total energy functions for initial AA and AB(3R) stacking configurations of the hexagonal flake (based on  ) are:
) are:
 | (3) |
 | (4) |
Note that for p = 1, the angle34 between the moiré vector and the lattice vector of the substrate is 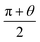 , so for a small twist angle θ, we can assume that the moiré vector and the lattice vector are perpendicular. Exact formulas that fully considering moiré pattern rotation are presented in the ESI,† along with a three-dimensional plot of the energy function S(θ, r, p = 1). The troughs on the surface correspond to energy local minima for stable twist states.
, so for a small twist angle θ, we can assume that the moiré vector and the lattice vector are perpendicular. Exact formulas that fully considering moiré pattern rotation are presented in the ESI,† along with a three-dimensional plot of the energy function S(θ, r, p = 1). The troughs on the surface correspond to energy local minima for stable twist states.
The most general case (p ≠ 1), which can arise from inherent lattice mismatch or strain engineering,18,36 also has an analytical expression.
The total energy function for a triangular flake with the initial AA stacking (based on  as in the case of the Gra/h-BN system32,33) is:
as in the case of the Gra/h-BN system32,33) is:
 | (5) |
The definitions of the symbols in the above equations are listed as follows.
D = 8π2r2(1 + p2 − 2p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)(3 − 9cot2 θ)(3 − 9cot2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A). A). |
The total energy function for a triangular flake with the initial AB stacking (based on  ) is:
) is:
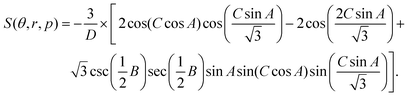 | (6) |
The definitions of the symbols in the above equations are listed as follows.
D = 4π2r2(1 + p2 − 2p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)(1 − 2 θ)(1 − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2A)). cos(2A)). |
The other forms of the analytical total energy function (i.e., based on 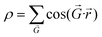 , or hexagonal shapes) and results for the moiré interface caused by lattice mismatch without rotation can be found in the ESI.†
, or hexagonal shapes) and results for the moiré interface caused by lattice mismatch without rotation can be found in the ESI.†
Over a wide range of normalized sizes, we demonstrate a satisfactory agreement between the first three local energy minima extracted from these analytical energy functions and large-scale molecular simulations, as shown in Fig. 3. Results for TBG and bilayer MoS2 (p = 1) are illustrated in Fig. 3(a and b), while results for Gra/h-BN (p ≠ 1) are presented in Fig. 3(c). We observe that for homobilayers (p = 1), the stable final angles are the same for different materials given the same normalized size r, and they differ from those of heterobilayers (p ≠ 1). Note that for small twist angles, local relaxation, which shrinks the AA region and expands the AB region, would appear. This effect is discussed in the ESI,† with the conclusion that local relaxation does not practically affect the angles of local energy extrema, in agreement with an earlier report.35
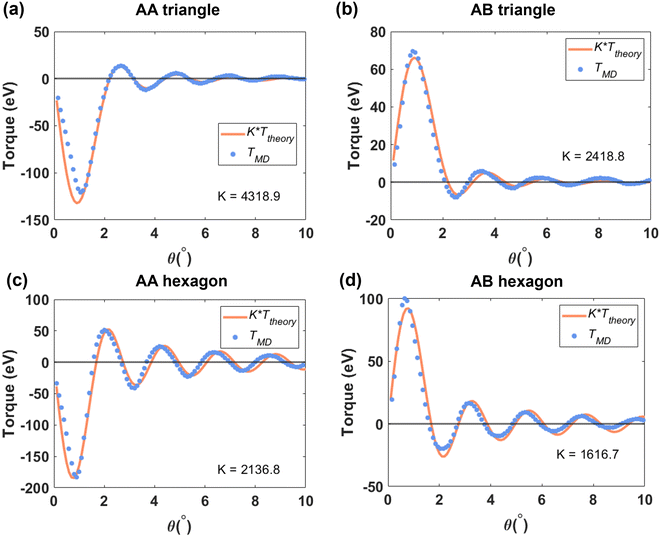
The interlayer rotational torque is a vital concept for interface twist engineering using 2D nano materials.13,37,38 In this work, we show that there are universal scaling laws that account for such interlayer rotational torque, which is the driving force for spontaneous rotation. By using an appropriate scaling factor, the interlayer rotational torque obtained from real material simulations can be reconstructed. Specifically, we demonstrate that the dimensionless theoretical torque Ttheory multiplied by certain coefficient K can match the simulated torque TMD. That is, 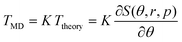 , where S(θ, r, p) is our dimensionless energy function for specific twist angles and flake sizes. The value of K is determined by minimizing the sum of the absolute values of discrepancies between the MD results and the theoretical scaled result (i.e., the L1 norm). In Fig. 4, we use TBG
, where S(θ, r, p) is our dimensionless energy function for specific twist angles and flake sizes. The value of K is determined by minimizing the sum of the absolute values of discrepancies between the MD results and the theoretical scaled result (i.e., the L1 norm). In Fig. 4, we use TBG  to demonstrate the agreement across a continuous range of twist angles. The simulated torque TMD is calculated by numerically differentiating the simulated configuration energy with respect to twist angles. Fig. 4 shows that there is excellent scaling agreement for both triangular and hexagonal TBG flakes with initial AA and AB stacking configurations at a fixed r. Additional calculations in the ESI† indicate that the coefficient K remains almost unchanged for the same geometric shape with varying r. All these comparisons demonstrate satisfactory scaling performance. The zero-torque points correspond to the preferred twisted states or the saddle point on the rotational energy landscape. Our theoretical approach thus not only provides accurate predictions of stable twist angles but also offers significant convenience in interpreting interlayer torque in twisted bilayer systems.
to demonstrate the agreement across a continuous range of twist angles. The simulated torque TMD is calculated by numerically differentiating the simulated configuration energy with respect to twist angles. Fig. 4 shows that there is excellent scaling agreement for both triangular and hexagonal TBG flakes with initial AA and AB stacking configurations at a fixed r. Additional calculations in the ESI† indicate that the coefficient K remains almost unchanged for the same geometric shape with varying r. All these comparisons demonstrate satisfactory scaling performance. The zero-torque points correspond to the preferred twisted states or the saddle point on the rotational energy landscape. Our theoretical approach thus not only provides accurate predictions of stable twist angles but also offers significant convenience in interpreting interlayer torque in twisted bilayer systems.
Finally, Fig. 5 illustrates certain aspects of the immediate application of our theory. First, our theory can readily reproduce literature insights from extensive MD simulation results. For example, the dynamic twisting of graphene/h-BN bilayers has been studied in MD simulations by modulating heterostrain,23 where a hexagonal graphene flake with a width of 13.7 nm is placed on an h-BN monolayer, and then the energy-angle curves for the initial AA stacking are simulated. In this case, to apply our theory, the size parameter  , and eqn (S5)† is directly used for predictions. The satisfactory comparisons of the energy landscape with the original ref. 23 are shown in Fig. 5(a) for zero biaxial strain, Fig. 5(b) for 4% biaxial strain (εb), and Fig. 5(c) in the space of rotation angle and biaxial strain. Second, our theory can help interpret experimental measurements (Fig. 5(d)). For example, the distribution of rotation angles is experimentally measured for a triangular MoSe2 layer grown on a graphene surface,39 where the average size of the as-grown triangle domains is found to be about 8 nm2, so the averaged side length of the equilateral triangle flake is 4.3 nm. Given that the lattice constant for MoSe2 is 0.33 nm40 while that for graphene is 0.246 nm, we get
, and eqn (S5)† is directly used for predictions. The satisfactory comparisons of the energy landscape with the original ref. 23 are shown in Fig. 5(a) for zero biaxial strain, Fig. 5(b) for 4% biaxial strain (εb), and Fig. 5(c) in the space of rotation angle and biaxial strain. Second, our theory can help interpret experimental measurements (Fig. 5(d)). For example, the distribution of rotation angles is experimentally measured for a triangular MoSe2 layer grown on a graphene surface,39 where the average size of the as-grown triangle domains is found to be about 8 nm2, so the averaged side length of the equilateral triangle flake is 4.3 nm. Given that the lattice constant for MoSe2 is 0.33 nm40 while that for graphene is 0.246 nm, we get  , and the normalized size
, and the normalized size  . The analytical energy landscape (eqn (S8)†) is then plotted as the red curve in Fig. 5(d), while the bar graph replots the frequency count on rotation angles in the experiment. It is anticipated that angles with higher energy are unfavorable, resulting in a lower frequency count. Notably, the use of the average flake size in our theory already produces a satisfactory interpretation of why certain angles have higher occurrence. The high energy barrier after the third preferred angle (about 17°) may explain the low count in the vicinity of the fourth preferred angle (about 21°). Third, our theory can guide the design of twistronics structures, where certain angles of interest are intrinsically coupled to certain flake sizes, alleviating the difficulty of experimental synthesis. For example, theoretical investigations41 show that there is actually a set of magic angles for TBG (i.e., 1.1°, 0.5°, 0.35°, and so on); however, the tiny magic angles of TBG smaller than 1° are not easily accessible in experiments.42 Nevertheless, our theory allows one to quickly scan the flake sizes whose preferred twisted states coincide with these peculiar angles. Fig. 5(e) shows a range of triangular flakes whose sizes correspond to θ = 1.1°, 0.5°, and 0.35°. Eqn (2) is directly used for predictions. Given these large sizes, computational searching for these states using conventional atomistic simulations is prohibitive, thus highlighting the advantages of our scaling laws.
. The analytical energy landscape (eqn (S8)†) is then plotted as the red curve in Fig. 5(d), while the bar graph replots the frequency count on rotation angles in the experiment. It is anticipated that angles with higher energy are unfavorable, resulting in a lower frequency count. Notably, the use of the average flake size in our theory already produces a satisfactory interpretation of why certain angles have higher occurrence. The high energy barrier after the third preferred angle (about 17°) may explain the low count in the vicinity of the fourth preferred angle (about 21°). Third, our theory can guide the design of twistronics structures, where certain angles of interest are intrinsically coupled to certain flake sizes, alleviating the difficulty of experimental synthesis. For example, theoretical investigations41 show that there is actually a set of magic angles for TBG (i.e., 1.1°, 0.5°, 0.35°, and so on); however, the tiny magic angles of TBG smaller than 1° are not easily accessible in experiments.42 Nevertheless, our theory allows one to quickly scan the flake sizes whose preferred twisted states coincide with these peculiar angles. Fig. 5(e) shows a range of triangular flakes whose sizes correspond to θ = 1.1°, 0.5°, and 0.35°. Eqn (2) is directly used for predictions. Given these large sizes, computational searching for these states using conventional atomistic simulations is prohibitive, thus highlighting the advantages of our scaling laws.
 | ||
| Fig. 5 Using our analytical theories to (a–c) interpret simulated energy landscape from ref. 23, (d) understand the occurrence of angles from experiments,39 and (e) rationally design flake geometries intrinsically coupled to an array of magic angles of TBG (θ = 1.1°, 0.5°, and 0.35°). | ||
Conclusions
In summary, we show that there are geometry-based universal analytical scaling laws on the rotational energy landscape of twisted van der Waals bilayers, the understanding of which is crucial for twistronics. The universality of our theory is rooted in the fact that the moiré geometry can be material-independent and only couples to three primary dimensionless parameters, namely lattice mismatch, twist angle, and normalized flake size. More importantly, the integrated dimensionless moiré energies possess elegant analytical forms, conveniently revealing the preferred twisted states for triangular or hexagonal flakes. Furthermore, the entire evolution of the actual rotational torque can be accurately reconstructed using an appropriate scaling factor. Our results not only unify experimental observations and literature atomistic simulations, but also potentially inspire a deeper understanding of moiré-correlated interface mechanics. Our findings provide new perspectives for the rational design of nanoscale rotation-tunable electronic devices.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interests.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 12272337 and 12002304) and the Distinguished Young Scientists Fund from the Zhejiang Provincial Natural Science Foundation of China under Grant No. LR23A020001. The authors also acknowledge funding support from Zhejiang University, and Fundamental Research Funds for the Central Universities.References
- A. K. Geim and I. V. Grigorieva, van der Waals heterostructures, Nature, 2013, 499(7459), 419–425, DOI:10.1038/nature12385.
- R. Ribeiro-Palau, C. Zhang, K. Watanabe, T. Taniguchi, J. Hone and C. R. Dean, Twistable electronics with dynamically rotatable heterostructures, Science, 2018, 361(6403), 690–693, DOI:10.1126/science.aat6981.
- M. Yankowitz, Q. Ma, P. Jarillo-Herrero and B. J. LeRoy, van der Waals heterostructures combining graphene and hexagonal boron nitride, Nat. Rev. Phys., 2019, 1(2), 112–125, DOI:10.1038/s42254-018-0016-0.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, 2D materials and van der Waals heterostructures, Science, 2016, 353(6298), aac9439, DOI:10.1126/science.aac9439.
- S. X. Huang, X. Ling, L. B. Liang, J. Kong, H. Terrones, V. Meunier and M. S. Dresselhaus, Probing the Interlayer Coupling of Twisted Bilayer MoS2 Using Photoluminescence Spectroscopy, Nano Lett., 2014, 14(10), 5500–5508, DOI:10.1021/nl5014597.
- S. Carr, D. Massatt, S. Fang, P. Cazeaux, M. Luskin and E. Kaxiras, Twistronics: Manipulating the electronic properties of two-dimensional layered structures through their twist angle, Phys. Rev. B, 2017, 95(7), 075420, DOI:10.1103/PhysRevB.95.075420.
- M. Brzhezinskaya, O. Kononenko, V. Matveev, A. Zotov, I. I. Khodos, V. Levashov, V. Volkov, S. I. Bozhko, S. V. Chekmazov and D. Roshchupkin, Engineering of Numerous Moiré Superlattices in Twisted Multilayer Graphene for Twistronics and Straintronics Applications, ACS Nano, 2021, 15(7), 12358–12366, DOI:10.1021/acsnano.1c04286.
- E. Koren and U. Duerig, Moiré scaling of the sliding force in twisted bilayer graphene, Phys. Rev. B, 2016, 94(4), 045401, DOI:10.1103/PhysRevB.94.045401.
- A. Uri, S. Grover, Y. Cao, J. A. Crosse, K. Bagani, D. Rodan-Legrain, Y. Myasoedov, K. Watanabe, T. Taniguchi and P. Moon, et al., Mapping the twist-angle disorder and Landau levels in magic-angle graphene, Nature, 2020, 581(7806), 47–52, DOI:10.1038/s41586-020-2255-3.
- K. Liu, L. Zhang, T. Cao, C. Jin, D. Qiu, Q. Zhou, A. Zettl, P. Yang, S. G. Louie and F. Wang, Evolution of interlayer coupling in twisted molybdenum disulfide bilayers, Nat. Commun., 2014, 5(1), 4966, DOI:10.1038/ncomms5966.
- A. Silva, V. E. P. Claerbout, T. Polcar, D. Kramer and P. Nicolini, Exploring the Stability of Twisted van der Waals Heterostructures, ACS Appl. Mater. Interfaces, 2020, 12(40), 45214–45221, DOI:10.1021/acsami.0c13971.
- S. Zhu, P. Pochet and H. T. Johnson, Controlling Rotation of Two-Dimensional Material Flakes, ACS Nano, 2019, 13(6), 6925–6931, DOI:10.1021/acsnano.9b01794.
- M. Z. Liao, A. Silva, L. J. Du, P. Nicolini, V. E. P. Claerbout, D. Kramer, R. Yang, D. X. Shi, T. Polcar and G. Y. Zhang, Twisting Dynamics of Large Lattice-Mismatch van der Waals Heterostructures, ACS Appl. Mater. Interfaces, 2023, 15(15), 19616–19623, DOI:10.1021/acsami.3c00558.
- S. Bagchi, H. T. Johnson and H. B. Chew, Rotational stability of twisted bilayer graphene, Phys. Rev. B, 2020, 101(5), 054109, DOI:10.1103/PhysRevB.101.054109.
- V. Morovati, Z. Xue, K. M. Liechti and R. Huang, Interlayer coupling and strain localization in small-twist-angle graphene flakes, Extreme Mech. Lett., 2022, 55, 101829, DOI:10.1016/j.eml.2022.101829.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al., LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171, DOI:10.1016/j.cpc.2021.108171.
- E. Y. Andrei and A. H. MacDonald, Graphene bilayers with a twist, Nat. Mater., 2020, 19(12), 1265–1275, DOI:10.1038/s41563-020-00840-0.
- F. Mesple, N. R. Walet, G. Trambly de Laissardiere, F. Guinea, D. Dosenovic, H. Okuno, C. Paillet, A. Michon, C. Chapelier and V. T. Renard, Giant Atomic Swirl in Graphene Bilayers with Biaxial Heterostrain, Adv. Mater., 2023, 35(41), 2306312, DOI:10.1002/adma.202306312.
- M. Liao, Z. Wei, L. Du, Q. Wang, J. Tang, H. Yu, F. Wu, J. Zhao, X. Xu and B. Han, et al., Precise control of the interlayer twist angle in large scale MoS2 homostructures, Nat. Commun., 2020, 11(1), 2153, DOI:10.1038/s41467-020-16056-4.
- W. Ouyang, R. Sofer, X. Gao, J. Hermann, A. Tkatchenko, L. Kronik, M. Urbakh and O. Hod, Anisotropic Interlayer Force Field for Transition Metal Dichalcogenides: The Case of Molybdenum Disulfide, J. Chem. Theory Comput., 2021, 17(11), 7237–7245, DOI:10.1021/acs.jctc.1c00782.
- C. R. Woods, L. Britnell, A. Eckmann, R. S. Ma, J. C. Lu, H. M. Guo, X. Lin, G. L. Yu, Y. Cao and R. V. Gorbachev, et al., Commensurate-incommensurate transition in graphene on hexagonal boron nitride, Nat. Phys., 2014, 10(6), 451–456, DOI:10.1038/nphys2954.
- M. Neek-Amal and F. M. Peeters, Graphene on boron-nitride: Moiré pattern in the van der Waals energy, Appl. Phys. Lett., 2014, 104(4), 041909, DOI:10.1063/1.4863661.
- X. Yang and B. Zhang, Heterostrain and temperature-tuned twist between graphene/h-BN bilayers, Sci. Rep., 2023, 13(1), 4364, DOI:10.1038/s41598-023-31233-3.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Unconventional superconductivity in magic-angle graphene superlattices, Nature, 2018, 556(7699), 43–50, DOI:10.1038/nature26160.
- S. Huang, L. Liang, X. Ling, A. A. Puretzky, D. B. Geohegan, B. G. Sumpter, J. Kong, V. Meunier and M. S. Dresselhaus, Low-Frequency Interlayer Raman Modes to Probe Interface of Twisted Bilayer MoS2, Nano Lett., 2016, 16(2), 1435–1444, DOI:10.1021/acs.nanolett.5b05015.
- M. M. van Wijk, A. Schuring, M. I. Katsnelson and A. Fasolino, Moiré Patterns as a Probe of Interplanar Interactions for Graphene on h-BN, Phys. Rev. Lett., 2014, 113(13), 135504, DOI:10.1103/PhysRevLett.113.135504.
- R. Guerra, M. van Wijk, A. Vanossi, A. Fasolino and E. Tosatti, Graphene on h-BN: to align or not to align?, Nanoscale, 2017, 9(25), 8799–8804, 10.1039/C7NR02352A.
- Y. Dong, A. Vadakkepatt and A. Martini, Analytical Models for Atomic Friction, Tribol. Lett., 2011, 44(3), 367, DOI:10.1007/s11249-011-9850-2.
- I. Leven, T. Maaravi, I. Azuri, L. Kronik and O. Hod, Interlayer Potential for Graphene/h-BN Heterostructures, J. Chem. Theory Comput., 2016, 12(6), 2896–2905, DOI:10.1021/acs.jctc.6b00147.
- R. Decker, Y. Wang, V. W. Brar, W. Regan, H.-Z. Tsai, Q. Wu, W. Gannett, A. Zettl and M. F. Crommie, Local Electronic Properties of Graphene on a BN Substrate via Scanning Tunneling Microscopy, Nano Lett., 2011, 11(6), 2291–2295, DOI:10.1021/nl2005115.
- W. Yang, G. Chen, Z. Shi, C.-C. Liu, L. Zhang, G. Xie, M. Cheng, D. Wang, R. Yang and D. Shi, et al., Epitaxial growth of single-domain graphene on hexagonal boron nitride, Nat. Mater., 2013, 12(9), 792–797, DOI:10.1038/nmat3695.
- W. Yan, X. Gao, W. Ouyang, Z. Liu, O. Hod and M. Urbakh, Shape-dependent friction scaling laws in twisted layered material interfaces, J. Mech. Phys. Solids, 2024, 185, 105555, DOI:10.1016/j.jmps.2024.105555.
- K. Huang, H. Qin, S. Zhang, Q. Li, W. Ouyang and Y. Liu, The origin of moiré–level stick–slip behavior on graphene/h–BN heterostructures, Adv. Funct. Mater., 2022, 32(35), 2204209, DOI:10.1002/adfm.202204209.
- K. Hermann, Periodic overlayers and moiré patterns: theoretical studies of geometric properties, J. Phys.: Condens. Matter, 2012, 24(31), 314210, DOI:10.1088/0953-8984/24/31/314210.
- S. Z. Zhu, E. Annevelink, P. Pochet and H. T. Johnson, Selection rules of twistronic angles in two-dimensional material flakes via dislocation theory, Phys. Rev. B, 2021, 103(11), 115427, DOI:10.1103/PhysRevB.103.115427.
- J. Feng, X. F. Qian, C. W. Huang and J. Li, Strain-engineered artificial atom as a broad-spectrum solar energy funnel, Nat. Photonics, 2012, 6(12), 865–871, DOI:10.1038/nphoton.2012.285.
- W. Yan, W. Ouyang and Z. Liu, Origin of frictional scaling law in circular twist layered interfaces: Simulations and theory, J. Mech. Phys. Solids, 2023, 170, 105114, DOI:10.1016/j.jmps.2022.105114.
- X. Yang and B. Zhang, Rotational Friction Correlated with Moiré Patterns in Strained Bilayer Graphene: Implications for Nanoscale Lubrication, ACS Appl. Nano Mater., 2021, 4(9), 8880–8887, DOI:10.1021/acsanm.1c01540.
- C. J. Alvarez, M. Tuan Dau, A. Marty, C. Vergnaud, H. Le Poche, P. Pochet, M. Jamet and H. Okuno, Impact of a van der Waals interface on intrinsic and extrinsic defects in an MoSe2 monolayer, Nanotechnology, 2018, 29(42), 425706, DOI:10.1088/1361-6528/aad66f.
- D. S. Koda, F. Bechstedt, M. Marques and L. K. Teles, Coincidence Lattices of 2D Crystals: Heterostructure Predictions and Applications, J. Phys. Chem. C, 2016, 120(20), 10895–10908, DOI:10.1021/acs.jpcc.6b01496.
- R. Bistritzer and A. H. MacDonald, Moiré bands in twisted double-layer graphene, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(30), 12233–12237, DOI:10.1073/pnas.1108174108.
- C. R. Woods, F. Withers, M. J. Zhu, Y. Cao, G. Yu, A. Kozikov, M. Ben Shalom, S. V. Morozov, M. M. van Wijk and A. Fasolino, et al., Macroscopic self-reorientation of interacting two-dimensional crystals, Nat. Commun., 2016, 7(1), 10800, DOI:10.1038/ncomms10800.
Footnote |
| † Electronic supplementary information (ESI) available: Details for atomistic simulations, stability of preferred twisted states against translation, more details on dimensionless rotational energy landscape and theoretical interlayer torque. See DOI: https://doi.org/10.1039/d4nr04493b |
| This journal is © The Royal Society of Chemistry 2025 |