N-/Si-co-doped nanocrystalline diamonds as highly sensitive luminescent thermometers

Abstract

Diamonds can host a variety of luminescent point defects, such as nitrogen vacancies and silicon vacancies, making them remarkably promising materials for luminescence nanothermometry. They also exhibit desirable characteristics, including low cytotoxicity, good biocompatibility and the benefits of carbon chemistry for tuneable surface functionalization with target molecules. In this work, N-/Si co-doped nanocrystalline diamonds were synthesized via microwave plasma-enhanced chemical vapor deposition under varying methane flow and temperature conditions, aiming for maximum photoluminescence intensity. In-depth analysis of the luminescence characteristics of NV⁻ and SiV⁻ emitting point defects with temperature, based on both experiments and ab initio calculations, suggested the existence of thermal coupling between their states. This coupling enabled ratiometric approaches to be exploited for more sensitive luminescent thermometry. A maximum thermal relative sensitivity of 5.5% K⁻¹ was achieved. This is remarkable for in vitro temperature measurements of biological tissues.

---

Introduction

Luminescent nanothermometry is a non-contact technique for determining temperature at the nanoscale. This technique requires materials whose luminescence exhibits strong temperature-dependent characteristics (lifetime, intensity, bandwidth, band position or polarization anisotropy) in the physiological temperature range (299–323 K).¹ Materials commonly used as luminescent nanothermometers include organic–inorganic hybrids, organic dyes, nanogels, polymers, biopolymers, metal–organic frameworks, semiconductor quantum dots, lanthanide-based up-conversion nanoparticles and nanodiamonds. Nevertheless, these materials present some disadvantages, and further research is necessary to identify the best candidate for their application as luminescent nanothermometers.

The organic–inorganic hybrids, organic dyes and nanogels allow temperature determination with a high thermal sensitivity.^2,3 Nevertheless, these materials present a common limitation: their excitation and emission wavelengths fall outside the biological windows, and thus, the penetration depth of light in biological tissues is low.^2,3 Other particular drawbacks are the limited temperature range in which the nanogels can work (300–335 K)² and the fact that if their viscosity is high, their diffusion to reach the target cell would probably be difficult. Moreover, the low photostability of organic gels and their susceptibility to local environmental conditions (for instance, pH or the viscosity of the cytoplasm), which make the thermal sensitivity values vary according to the medium,⁴ make them unsuitable for in vivo applications.

Polymers and biopolymers have been used for both thermal imaging and sensing, although their performance has been particularly outstanding for the former.⁴ Among them, green fluorescent proteins stand out due to the fact that they can act as markers for different functions such as gene expression and due to their high stability and quantum yield.⁴ However, they emit in the visible range, and the gene encoding process, which is usually necessary to improve their thermal sensitivity, is a time-consuming process.⁴

In the case of metal organic frameworks (MOFs) and semiconductor QDs such as perovskite QDs, their photoluminescence can be tuned to fall within the biological windows.^5,6 Nevertheless, they are unstable in physiological environments. The perovskite structure and MOFs degrade in aqueous medium, making it necessary to encapsulate them, for instance, by means of a silica shell.^7–9

The lanthanide-based up-conversion nanoparticles also have emission and excitation wavelengths that fall within the biological windows, and their emission is environment-independent.¹⁰ However, a disadvantage is the low absorption cross-section of the f–f transitions in comparison to the d–d transitions.¹¹ The higher the absorption cross-section, the brighter the luminescence, which ultimately leads to higher sensitivity, which is crucial for their application in luminescent nanothermometry.¹¹

On the other hand, nanodiamonds exhibit low cytotoxicity in cells such as HeLa, good biocompatibility (the highest among all-carbon compounds) and can be functionalized with different molecules to target specific cells due to their high surface-to-volume ratio and charged surface. In addition, the crystal lattice of nanodiamonds can host different defects, such as nitrogen-vacancies or silicon-vacancies. Diamonds containing nitrogen-vacancy defects have been proven useful for temperature determination; nevertheless, their emission falls within the visible range (575 nm for NV⁰ and 637 nm for NV⁻).¹² However, the zero-phonon line (ZPL) of negatively charged silicon-vacancy defects (SiV⁻) is located at 738 nm, which falls within the first biological window, making Si-doped nanodiamonds a promising candidate for luminescent nanothermometry.^13–15 For example, Choi et al. reported an ultrasensitive and ultrafast thermometer using nanodiamonds (∼250 nm) with SiV⁻ centres.¹⁶ Additionally, a dual role for Si-doped nanodiamonds as both heater and thermometer has also been reported.¹⁷ In addition, the size of the nanodiamonds is of interest, with an optimized size typically around 100 nm. Smaller sizes have also been reported, such as nanodiamonds with SiV⁻ centres around 20 nm, prepared via a detonation process.¹⁸ Finally, the analysis of nanodiamonds containing both NV⁻ and SiV⁻ centres, which is the focus of our work, has not been widely reported previously. So et al. have reported multimodal thermometry using multicolour centres in detonation nanodiamonds, which is of great interest in this area. However, further enhancements in sensitivity are needed for living-cell measurements.¹⁹

For all the above reasons, in this work, the growth of N-/Si-co-doped nanocrystalline diamonds on a Si substrate was carried out using microwave plasma-enhanced chemical vapor deposition (MPECVD). The samples were grown under different conditions to analyse the effect of growth temperature and methane flow on the photoluminescence properties of the nanocrystalline diamonds (NCD), as well as to determine the conditions that lead to the highest photoluminescence intensity. The dependence of photoluminescence characteristics, including intensity, full-width at half-maximum (FWHM) and area of the ZPL of NV⁻ and SiV⁻ centres, on temperature was analysed in the physiological temperature range (299–323 K) to assess their potential application as in vitro ratiometric nanothermometers. This approach offers several advantages, such as the ability to determine temperature independently of the environment. The relative sensitivity of temperature determination was also calculated.

Methodology

Nanocrystalline diamond growth

Diamond growth was performed following three steps: (i) cleaning, and (ii) seeding of the Si substrates, and (iii) growth of NCD films. A detailed description of these steps is shown below.

The 4′′ silicon wafers, provided by Ted Pella Inc., were diced into 10 × 10 mm² pieces. The Si substrates had an orientation 〈100〉 and a thickness of 460–530 μm. The Si substrates were used as seeded substrates for NCD growth and as non-seeded substrates for the dopant source (sacrificial silicon) placed next to the former. Both types of substrates were degreased by wet cleaning and additionally cleaned with oxygen gas discharge plasma. For that purpose, they were immersed first in acetone and kept in an ultrasonic bath (Elma Transonic Tl-H-5, 80 kHz, 150 W) for 15 min, and then in isopropyl alcohol and kept in the ultrasonic bath for 15 min. Next, they were dried under nitrogen gas flow. Once they were degreased, they underwent cleaning by an O₂ gas discharge plasma to oxidize possible hydrocarbons contamination on the Si surface. The O₂ cleaning was carried out for 2 min in a home-build vacuum system, in which samples were placed on a stage that acted as a cathode for plasma discharge. The following conditions were used: 50 sccm of O₂ flow, working pressure of 5 mTorr and power of 150 W. This step is key for getting a good ND seeding density.²⁰

The seeding of the Si substrate is an important step for diamond growth. This is due to the fact that the incubation time to get the supersaturated nucleus is too long if no previous treatment of the Si substrate, such as seeding with an ND colloid, is carried out.²¹ By treating the substrate with an ND colloid, a high density of seeds is achieved (∼10¹¹ seeds per cm²), which is necessary to obtain smooth NCD.²¹ The seeding of the Si substrate was carried out as follows: first, the substrate was placed in a spin coater and the ND colloid was added on top of it. This ND colloid was obtained by diluting detonation ND (particle size ∼7 nm) slurry provided by the NanoCarbon Institute Co., Ltd, in water to the concentration of 0.33 g L⁻¹. Next, deionized water was dropped onto the Si substrate for 25 s to rinse it and finally, the seeded substrate was dried by spinning for 40 s at 4000 rpm.

Finally, N-/Si-co-doped NCD films have been grown on the seeded Si substrates in an ASTeX 6500 series MPECVD system. The sacrificial silicon was used as a source for Si doping, whereas N doping was obtained due to the presence of residual N₂ in the reactor chamber. The seeded sample was placed in the centre of the holder inside the reactor chamber and non-seeded sacrificial Si substrates were placed around to dope the diamond as it grows. The desired temperature was reached by changing the pressure, as the microwave power was 4500 W for all the samples. The temperature was monitored by a Williamson Pro92 dual wavelength pyrometer. The thickness of the NCD was determined in situ through laser interferometry, using a 405 nm laser with a power of 20 mW provided by Altechna, a silicon photodiode and an amperemeter. The growth conditions of each sample are detailed in Table 1.

Table 1 Growth conditions of the NCD

Samples	%C/H	Pressure/Torr	Temperature/K	Thickness/nm	Deposition time
S1	0.37	50	973	1450	42 h 35 min
S2	0.74	50	973	1900	18 h 37 min
S3	1.11	50	923	1480	7 h 16 min
S4	1.48	50	923	1475	4 h 30 min
S5	1.85	50	1023	1470	3 h 32 min
S6	1.11	40	1023	1450	6 h 15 min
S7	1.11	55	1053	1000	7 h 3 min
S8	1.11	60	1123	1460	6 h 8 min
S9	1.11	70	1223	1200	9 h 31 min

---

Characterization of the N-/Si-co-doped NCD

First, the NCD films were characterized to observe whether the diamond structure was formed under the different growth conditions. For this purpose, the grazing incidence X-ray diffraction (GIXRD) patterns of the NCD films were obtained using a D8 Advance A-25 diffractometer with a LynxEye detector supplied by Bruker, with a Cu-Kα X-ray source. The patterns were recorded from 40° to 80° with a resolution of 0.020°, at 40 kV and 40 mA. The X-ray beam was directed onto the sample at a grazing incident angle of 5°. By using a low angle of incidence, the Si peak of the substrates shows low or no intensity, or it does not appear, allowing us to observe the diamond peaks with higher intensity.

Raman spectra were acquired to analyse the possible presence of different carbon allotropes, and steady-state photoluminescence spectra were recorded at room temperature to check the Si-doping of the diamonds and study the emission features of the samples. All spectra were recorded with a Horiba LabRAM HR Evolution modular spectrometer, which is suited for both Raman analysis and photoluminescence, and is equipped with a Symphony II IR detector and a Sincerity visible detector, supplied by Horiba as well. As the excitation source, a 473 nm two diode pumped solid state (DPSS) laser was employed, with a power output of 100 mW supplied by Quantum Models©.

The defects present in the sample which showed the most promising photoluminescence characteristics were also analysed through cathodoluminescence (CL) spectroscopy, by exciting the specimen with the electron beam of a scanning electron microscope (SEM). SEM-CL experiments were performed in a focus-ion-beam/field-emission-SEM dual-beam microscope, model TESCAN Solaris coupled to a Horiba iHR320 spectrometer. The luminescence was conducted to the spectrometer entrance slit through a retractable parabolic mirror. The spectra were recorded using a monochromator with a grating of 600 grooves per mm, with a Synapse CCD-detector. The specimen temperature was controlled between 80 and 300 K using a liquid N2-cooled stage (QuorumTechnologies model PP-3005). The SEM beam energy was set to 30 keV and beam current to 50 nA for low temperature measurements and 10 nA for the measurements at room temperature.

To demonstrate the suitability of N-/Si-co-doped diamonds for their application in luminescent nanothermometry, photoluminescence spectra were recorded at different temperatures using the Horiba LabRAM HR evolution modular Raman spectrometer, coupled to a temperature controller supplied by LakeShore model 335, which is adapted to a Cryotherm cryostat, working under vacuum.

DFT calculations

Computational chemistry tools have become increasingly important during recent years to improve our understanding of new materials. NV- and SiV- defects in diamond, particularly the former, have been the subject of for many ab initio studies regarding their formation, electronic structure, and optoelectronic properties. There is no paper or series of papers available throughout the literature focusing on the photoluminescent emission of these two defects in comparable diamond matrices, as a function of temperature, and at the same level of theory. Our aim for this part of the paper is to simulate, using density functional theory (DFT) calculations, the temperature-resolved photoluminescent emission of NV- and SiV- defects, and use the computed results to support part of the discussion of the experimental findings in this work.

The ab initio study of point defects is generally approached with either periodic supercells^22–25 or molecular clusters modelling strategies.^23,26–29 Ádám Gali has previously reviewed and summarized the basic ab initio methods used together with these strategies for the study of NV-defects, which are extensible to SiV-defects, and we will not be repeated here.³⁰ Since the purpose of DFT calculations in our work is to study the photoluminescent emission of these defects, rather than replicating the experimental spectrum of diamond or diamond with NV⁻ or SiV⁻, we approached the problem using a molecular cluster modelling strategy and exploiting the Gaussian 16 program suite of capabilities.³¹ This is not unprecedented.²⁹ We proceeded as follows. First, we built a H-terminated diamondoid, C44H42, and submitted it for a symmetry constrained optimization within the D3d point group at the DFT/B3LYP/6-311+g(d,p) level. This is a sufficiently large cluster to provide a qualitatively correct description of the electronic structure of the defective diamond.²⁷ A H-terminated surface is consistent with our experimental samples. We then created, in separate clusters, the NV-defect, by generating a C vacancy in the centre of the cluster and substituting an adjacent C atom for a N atom, and the SiV-defect, by generating two vacancies in the centre of the cluster and placing a Si atom between them. Each defect lies within a diamond-like matrix with only C atoms as the first and second nearest-neighbouring species, and H atoms as the third nearest-neighbouring species. These defects can be negatively charged by accepting an electron from the environment, typically donated by a substitutional N atom in a tetravalent position of the diamond lattice. As we are using a nonperiodic model system, the negative charge can be included without need for a compensating jellium charge or explicitly modelling of this positively charged substitutional N atom. Both model systems, which we will respectively refer to as C₃₆[C₆NV⁻]H₄₂ and C₃₆[C₆SiV⁻]H₄₂, were submitted for optimization at the DFT/B3LYP/6-311+g(d,p) level as well. We imposed symmetry constraints within the C_3v and D_3d point groups, respectively, for geometry optimizations at the ground states, but not at the excited states. Time-dependent DFT calculations were performed using the Tamm-Dancoff approximation (TDDFT). The vibrational frequencies of C₃₆[C₆NV⁻]H₄₂ and C₃₆[C₆SiV⁻]H₄₂ models were computed at the relevant stationary points. Temperature-resolved photoluminescence (vibronic) spectra were computed using the Franck–Condon–Herzberg–Teller (FCHT) method, using a vertical gradient representation for the electronic transitions.

Further details, such as the charge and multiplicity specifications, the internal coordinates variables definition, along with other relevant keywords and options selection, can be found in the Gaussian 16 input files for these calculations, available in the ESI† for reproduction and learning purposes. Overall, the use of cluster models for qualitative purposes is justified, as it benefits from the possibility of modelling charged defects without the need for compensating charges, a well consolidated TD-DFT formalism for ES calculation, and implementations of the FCHT method for the simulation of PL spectra with readily available outputs in Gaussian 16.

Results and discussion

Characterization of NCDs

The crystalline configuration of NCD films was analysed by GIXRD. Fig. 1a shows the diffractograms of the obtained samples. In all samples, two peaks were observed at 2θ values of 43.8° and 75.2°, corresponding to the (111) and (220) diffraction planes, respectively, in the cubic diamond phase.^32,33 In addition to these peaks, one more peak appeared at approximately 61° in samples S8 and S9, which was assigned to the (220) diffraction plane of SiC.³⁴ This signal appeared slightly shifted for both samples, probably due to differences in crystallinity and stoichiometry of the SiC formed.³⁵ Typical peaks for amorphous carbon at 26.3° and 68.9°, and for graphite at 29.3° and 47.3°, were not observed in any sample.²⁶ In addition, the typical peak assigned to the (004) plane of Si 〈100〉, which usually appears at 68.8°,³⁴ was not observed in our samples, despite using Si substrates.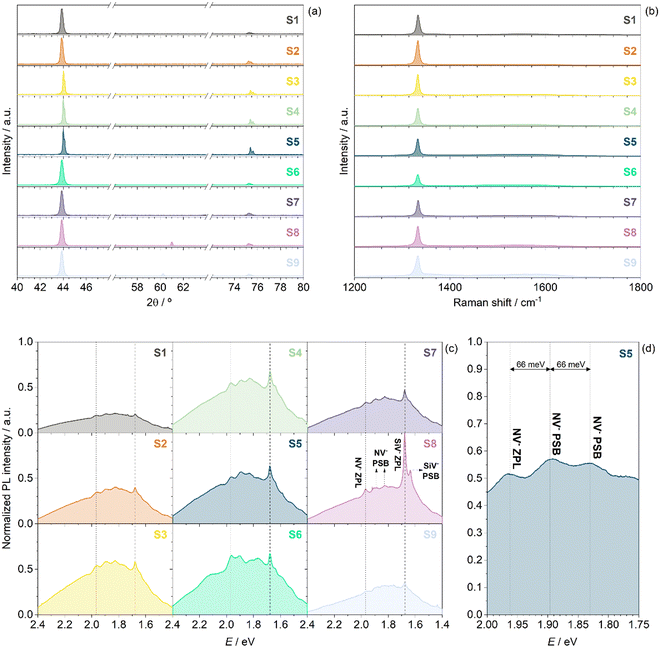

Fig. 1 (a) Diffrctograms obtained from CIXRD, (b) Raman spectra, (c) steady-state PL spectra of nine samples of N-/Si-co-doped NCD, and (d) detail of steady-state spectrum for sample S5.

To confirm that diamonds were obtained and to analyse whether any other carbon allotrope was present in the sample, the Raman spectra of the samples were recorded. Fig. 1b shows the Raman spectra of the N-/Si-co-doped NCD films. All the samples showed the typical signal for crystalline diamonds at approximately 1331 cm⁻¹, corresponding to the optical phonon mode T_2g.³⁶ This signal was shifted from the typical value of 1332.5 cm⁻¹, indicating that the lattice was slightly strained. The Si signal, despite also having a tetrahedral structure, appeared at lower vibrational frequencies due to its higher atomic mass. The band at 930–1030 cm⁻¹ corresponded to multi-phonon scattering originating from the Si substrate.³⁷

The presence of other carbon allotropes, such as graphite, could also be identified by Raman spectroscopy. To simplify the study of the physical properties of graphite, it is often considered as graphene owing to the weak interaction between the graphite sheets.³⁸ Out of the six phonon modes that graphene has at the Brillouin zone centre, only the E_2g optical phonon mode is active in Raman.³⁸ The so-called G band in the Raman spectra of graphite, located at 1583 cm⁻¹, arises from the E_2g mode, which involves in-plane vibrations of the carbon atoms.³⁸ In some of the spectra we obtained, a weak shoulder was observed near the diamond peak at 1370 cm⁻¹, which was assigned to the disorder-induced (D) band.³⁹

In addition, the FWHM of the diamond Raman peak was calculated to analyse the crystallinity of the samples and compare them with the sizes of the NCDs observed in SEM. While lower CH₄ flow rates and lower temperatures typically result in better crystallinity, all the samples studied here exhibited similar crystallinity, as proven by a very narrow range of differences in the FWHM of the diamond Raman signal, between 6.3 and 9.2 cm⁻¹, as shown in Fig. S1 in the ESI.†

The emission features of the samples were analysed through photoluminescence spectroscopy. All spectra were recorded at room temperature using a 473 nm excitation laser under the following conditions: 10 s acquisition time, 5 accumulations and a 25% ND filter. Since all spectra were recorded under the same conditions, the photoluminescence intensities of the samples could be compared once normalized to the thickness of the sample. This allowed for the analysis of which growth conditions led to the best photoluminescence characteristics. Fig. 1c shows the photoluminescence spectra of the samples normalized to the sample thickness. In the spectra, a sharp peak at 738.5 nm (1.679 eV) and a shallow peak at about 757.5 nm (1.637 eV) were clearly observed, which were assigned to the ZPL and the phonon sideband (PSB) of the SiV⁻ centres, respectively.⁴⁰ In addition, three other luminescent signals were observed at about 631, 653 and 676 nm (1.965, 1.899 and 1.834 eV). The first corresponded to the ZPL of the NV⁻ centres, while the others were assigned to the PSB of these centres. Typically, the ZPL of NV⁻ centres is reported at 637 nm, but in polycrystalline NDs, this can be shifted due to several factors, such as crystal size or interactions with the surroundings, including other colour centres. Nevertheless, the configuration of the signals—the presence of the ZPL and two PSBs between 650 and 680 nm—was clear evidence of the presence of NV⁻ centres, as has been reported previously,⁴¹ and is clearly observed in Fig. 1d. Also, the maximum displacement energy of phonons in diamond has been reported as 165 meV.⁴² In addition, the separation between the ZPL and the first PSB signals has been reported previously to be about 0.063 eV.⁴³ In our case, we observed that the separation between these two signals was about 0.066 eV (Fig. 3c), which was in good agreement with the reported values. As a result, these phonon sidebands were within 165 meV of the corresponding ZPLs. Furthermore, we also observed Raman peaks in the spectra. The peak at about 505 nm (2.455 eV) was assigned to the diamond Raman peak, and the weak peak at about 645.0 nm (1.922 eV), observed in some samples, was assigned to the diamond second-order Raman peak.

From Fig. 1c, it could be concluded that the sample exhibiting the highest photoluminescence intensity was sample S8. Therefore, this sample was further analysed for its potential in vitro luminescent nanothermometry. Sample S8 was grown using an intermediate CH₄ flow rate to obtain good diamond crystallinity. Also, the microwave temperature for this sample was high (1123 K), which was counterproductive for diamond crystallinity but facilitated the diffusion of Si atoms from the substrate into the diamond structure, thereby generating a large number of luminescence-active SiV⁻ centres. However, sample S9 was obtained at a higher temperature, but the deposition time was longer than for S8. It is well-known that longer deposition times are counterproductive for Si content, leading to lower Si concentration in the diamonds.⁴⁴

Sample S8 was characterized and assessed for in vitro luminescent nanothermometry. The morphology of sample S8 was analyzed through SEM. In Fig. S2 in the ESI,† the SEM image of sample S8 was compared to that of sample S5, illustrating that despite the different growth conditions, well-faceted NCD crystals were obtained in both cases. The micrographs presented in Fig. S3 in the ESI† correspond to different points of the sample and show that well-faceted crystals were obtained.

The identification of defects was carried out through CL spectroscopy. CL was excited in the specimen by the electron beam of the SEM. CL spectra were recorded at room temperature and 83 K, close to the temperature at which N₂ becomes a liquid under atmospheric pressure. The analysis at room temperature was performed at four different points of the NCD film to study the homogeneity of sample S8. Fig. 2 shows a representative SEM image of one of the relevant points, and its CL spectra at room temperature and at 83 K are presented. SEM images and CL spectra recorded at different points of sample S8 are shown in Fig. S3 in the ESI† and confirmed that well-faceted crystals were obtained. The CL spectrum at room temperature showed two broad bands at 2.95–2.76 eV (440–420 nm), typically referred to as the A band, and at 2.4–2.3 eV (540–515 nm). The origins of both bands are still not clear, but they are usually ascribed to electron–hole recombination in dislocations or planar defects.⁴⁵ The peak at 2.98 eV (416.7 nm) was ascribed to the N3 centre,⁴⁶ which comprises three substitutional N atoms associated with a C vacancy. The peak at 2.59 eV (478.6 nm) was previously observed in the CL spectra of slightly doped homoepitaxial diamond films,⁴⁶ and was typically associated with B atoms. The presence of boron in our samples was unexpected, as there was no boron dopant source in the process. Hence, its origin is unclear. Since boron easily incorporates into diamond, it is very difficult to track its source. In addition, a shoulder was observed at about 1.97 eV (630 nm), which was assigned to the ZPL of NV⁻ centres. Finally, a band at 738.4 nm (1.68 eV) was found and assigned to the ZPL of SiV⁻ centres.⁴⁷ CL spectra shown in Fig. S3 in the ESI,† recorded at different zones of sample S8 at room temperature, are all similar to that shown in Fig. 2, indicating that the sample is homogeneous.

Fig. 2 SEM images and CL spectra obtained at room temperature and at 83 K for the NCD sample S8.

As the homogeneity of the sample was verified at room temperature, the analysis at 83 K was performed at a single point of the sample. The SEM image and CL spectrum obtained at 83 K for this point are shown in Fig. 2. At low temperature, some bands were better resolved, and changes could be observed. In the 1.75–3.50 eV (∼700–350 nm) region, the band at about 2.98 eV (416.7 nm), assigned to N3 centres, was clearer. New bands appeared at 2.47 eV (501.5 nm) and 2.4 eV (516.4 nm),^45,48 which were assigned to the ZPL of H3 colour centres and their sub-bands. The H3 colour centre consists of one or two vacancies and two substitutional nitrogen atoms in C_2v symmetry.⁴⁵ Another band appeared at 2.33 eV (532.1 nm), which was typically related to the lack of crystallinity in the surface region of diamonds.⁴⁶ Finally, in the 1.60–1.75 eV (∼775–700 nm) region, the ZPL of SiV⁻ was observed again. However, at low temperature, the PSB of SiV⁻ was also visible at 1.64 eV (756.0 nm), in agreement with the PL spectra. At room temperature, unexpectedly, the PSB of SiV⁻ centres was not observed. This could be due to differences in measurement spots. It is well-known that SiV⁻ colour centres exhibit a prominent ZPL and weak phonon sidebands.⁴⁹ Typically, the emission of the ZPL can be between 70% and 90% of the total emission. Therefore, in some cases, the PSB intensity is very low and not easily observed. Thus, SEM and CL measurements showed the expected results for N-/Si-co-doped nanocrystalline diamonds.

Overall, the wide physicochemical characterization presented here indicated that N-/Si-co-doped NCDs were successfully grown by MPECVD with good crystallinity and promising emission features for applications in luminescent nanothermometry.

Luminescent nanothermometry

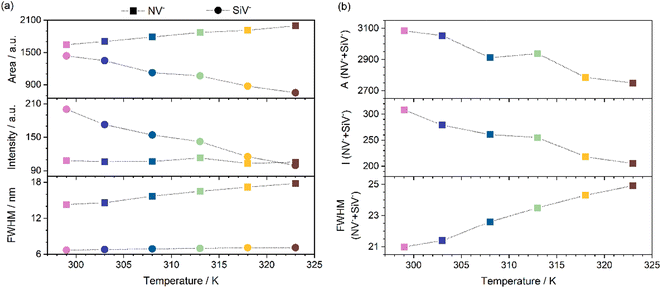
N-/Si-co-doped nanodiamonds were tested as luminescent nanothermometers. The photoluminescence spectra of sample S8 were acquired using a 473 nm laser as the excitation source and recorded at different temperatures within the physiological range, between 299 and 323 K. Specifically, three measurements were performed for each temperature to assess the reproducibility of the method. Each measurement consisted of the average of 100 spectra, as shown in the inset of Fig. 3a. Deconvoluting these photoluminescence spectra is a formidable task, as seven peaks appear along with a notable background (as observed in Fig. 3a). This background arose from all other point-defect luminescent emissions in as-grown defective diamonds, as thoroughly discussed with CL measurements. It was also temperature-sensitive, involving defects whose states may or may not be thermally coupled with those of NV⁻ or SiV⁻ defects. It was therefore difficult to define a common baseline and perform peak fitting for all seven peaks in the spectra. We approached the luminescence thermometry analysis using single-band (ZPL) peak fitting with flat baselines defined between the same endpoints for all spectra. Luminescence descriptors were thus extracted from the baseline-subtracted fitted Gaussian functions, as shown in Fig. 3b. We found this approach to be more robust upon analyzing all probed photoluminescence maps.

Fig. 3 (a) Temperature-resolved PL spectra, each spectrum resulting from the average of 100 spectra acquired in a single spatial scan at a target temperature. (b) Example of the Gaussian fitting of the ZPL emissions of NV⁻ and SiV⁻ centers, from which luminescence descriptors are extracted.

The relevant luminescence descriptors extracted were the area, intensity and full width at half maximum (FWHM) of the ZPL of NV⁻ and SiV⁻ emission centres. These were calculated for each of the eighteen averaged spectra (three averaged spectra per target temperature), such that three values per ZPL peak were obtained for each descriptor at a given temperature. Fig. 4 shows the mean of these values for the three descriptors for both NV⁻ and SiV⁻ emission centres as a function of temperature.

Fig. 4 (a) Evolution of the luminescence descriptors—area, intensity and FWHM—extracted from ZPL peaks of the NV⁻ and SiV⁻ centers and (b) the sum of each descriptor for both emission centres as a function of temperature.

In general, it can be expected that the intensity and area of the photoluminescence peak decrease as the temperature increases, as thermal energy excites the electrons to nonradiative sites.⁵⁰ Regardless of the mechanism involved in the former process, the FWHM is expected to increase due to the population of higher vibrational states as temperature increases. Alternatively, the increase in the population of higher vibrational states leads to a decrease in the intensity and area of the ZPL emissions. Thus, in Fig. 4, we can observe that the FWHMs of NV⁻ and SiV⁻ ZPL peaks indeed increased with increasing temperatures, with this trend being more significant for NV⁻ centres. Also, as expected, the intensity and area for SiV⁻ centres decreased with increasing temperature. Interestingly, however, the intensity for the NV⁻ ZPL remained practically constant with increasing temperature, while its area increased with temperature, as did its FWHM. This behaviour suggested the existence of thermally coupled states between the NV⁻ and SiV⁻ centres. But we cannot forget that PL and CL signals are complex; thus, several defects are present in the samples, and different energy transfer processes can occur. However, evidence of energy transfer between NV⁻ and SiV⁻ centres was observed. In addition, we could support this phenomenon by considering the sum of the luminescence properties of both centres. Fig. 4b shows the evolution of the sum of the area, intensity and FWHM of the luminescence of NV⁻ and SiV⁻ ZPL peaks with temperature. A decrease in the area and intensity within the temperature range was observed, as expected for thermally coupled states. An increase in FWHM with temperature was also observed. These trends provided new evidence of the thermal coupling between both types of centres.

DFT simulations of the temperature-resolved photoluminescent emissions of the NV⁻ and SiV⁻ defects are depicted in Fig. 5. The spectral features were in good agreement with the experiments, particularly in terms of the qualitative shape of the spectra, the relative intensities of their ZPL with respect to their PSB and the extension of the latter towards lower energies (as shown by conveniently plotting the calculated intensities as a function of E-EZPL in Fig. 5). By modelling both defects separately, ensuring their photoluminescence emissions were undoubtedly decoupled, and calculating their emission intensities within the same neighbouring environment and under the same level of theory, we ensured that the comparison remained unbiased. This allowed us to demonstrate that the temperature dependence of their emission intensities followed the previously described ordinary behaviour: decreasing emission intensities with increasing temperature. Therefore, our experimental observation of an increasing intensity of NV⁻ emissions with increasing temperature required the existence of an additional mechanism, such as a strong coupling regime of states in NV⁻ defects to those of SiV⁻ defects. This was likely, considering that closely spaced vibrational states existed for these two emitting colour centres, given their similar neighbouring environments.

Fig. 5 Temperature-resolved photoluminescence spectra of C₃₆[C₆NV⁻]H₄₂ and C₃₆[C₆SiV⁻]H₄₂ model systems, simulated using the FCHT method on optimized geometries and vibrational frequencies from calculations at the DFT/B3LYP/6-311+g(d,p) level with Gaussian 16. Visualizations were performed using OVITO.⁴⁹

This thermal coupling, evidenced by the contrast between our experimental and theoretical results, enabled a new method for luminescent nanothermometry based on the paired thermoresponsive spectral descriptors of NV⁻ and SiV⁻ emitting centres, typically referred to as a ratiometric method. It is expected that the sensitivity of the luminescent nanothermometers will increase by using this method, as discussed below.

Ratiometric luminescent nanothermometry. Given the evidence of thermally coupled states between NV⁻ and SiV⁻ centres, we studied the possible exploitation of the ratiometric approach with N-/Si-co-doped diamonds in luminescent nanothermometry. The ratiometric definition of the thermometric descriptors allows analysis of changes in photoluminescence with temperature independently of detection fluctuations and optoelectronic shifts.^51,52 The ratiometric approach is described by the Boltzmann distribution law:where I₁ and I₂ are typically the fluorescence intensities from the coupled energy levels (E₁ and E₂) to the ground level (E), but this also applies to other thermometric descriptors from the PL emission, i.e. the area or the FWHM; B is a constant that depends on the radiative transition rate, the degeneracy of the energy levels, the emission cross-section and the angular frequency of the two levels; ΔE is the energy difference between the two thermally coupled levels; k_B is the Boltzmann constant and T is the temperature.⁵³ The calibration curves, i.e. the evolution of the thermometric descriptor vs. temperature, are key to assessing the behaviour of our N-/Si-co-doped NCD samples as luminescent nanothermometers. More specifically, the thermometric descriptors defined here are the ratio (R) of the areas (A) of the transitions corresponding to NV⁻ and SiV⁻ centres, R(A) = A_NV/A_SiV, the ratio of their intensities, R(I) = I_NV/I_SiV and the ratio of their FWHM, R(FWHM) = FWHM_NV/FWHM_SiV. The ultimate goal was to determine which of these luminescence characteristics offered the highest sensitivity, for which the relative thermal sensitivities (S_r) were calculated as a performance parameter according to:

Fig. 6 shows the calibration curves and the relative thermal sensitivities for each thermometric descriptor previously defined through the ratiometric approach. Fig. 6a shows the ratiometric descriptors, and a nearly linear dependence on temperature was observed, indicating that they followed Boltzmann's distribution law as discussed above. A linear fit to these datasets provided the thermal models that allowed us to measure temperature from PL measurements. Fig. 6b shows the relative thermal sensitivity ranges between 2.5–5.5% K⁻¹ for the ratio of the areas, 2.0–4.0% K⁻¹ for the ratio of the intensities, and 0.6–0.7% K⁻¹ for the ratio of the FWHMs. From these values, it could be concluded that the ratio of the areas of the ZPL emissions of the NV⁻ and SiV⁻ centres offered the highest relative sensitivity compared to the other descriptors and should be preferentially considered for luminescent nanothermometry.

Fig. 6 (a) Plots of the ratiometric luminescence descriptors vs. temperature. (b) Relative thermal sensitivity values obtained for the thermometric descriptors—area, intensity and FWHM—using the ratiometric approach.

As discussed previously, it is well-known that the ratiometric approach is more reliable than a single-peak approach for temperature determination based on photoluminescence emissions, as the former is not affected by detection fluctuations or optoelectronic shifts. To illustrate this, the relative thermal sensitivities for the area, intensity and FWHM of the NV⁻ and SiV⁻ ZPL, analysed separately as a single signal, were calculated and are shown in Fig. S4 in the ESI.† The relative thermal sensitivity was highest for the analysis of the intensity of the SiV⁻ emission centres, ranging from 2.1 to 4.2% K⁻¹. This sensitivity was acceptable, but it was clearly lower than the best relative thermal sensitivity obtained with the ratiometric approach, in the range 2.5–5.5% K⁻¹ for the ratio of the areas. Therefore, the ratiometric approach increased the relative thermal sensitivity by approximately 19%–30% and validated the use of N-/Si-co-doped NCDs as luminescent nanothermometers with high thermal sensitivity, thanks to the thermally coupled states between NV⁻ and SiV⁻ emitting point defects.

Conclusions

N-/Si co-doped nanocrystalline diamonds were successfully synthesized via microwave plasma-enhanced chemical vapor deposition using different methane flow and temperature conditions, aiming for maximum photoluminescence intensity. The presence of diamond was confirmed by GIXRD and Raman spectroscopy, and the presence of other crystalline species was excluded. The presence of NV⁻ and SiV⁻ emitting centres was confirmed by photoluminescence and CL measurements. The sample with the highest photoluminescence intensity was selected for further luminescent nanothermometry performance analysis. Several thermometric descriptors, namely the area, intensity and FWHM of the ZPL of these point defects, were analysed. We found experimental and theoretical evidence of the presence of thermally coupled states between NV⁻ and SiV⁻ centres. This enabled the use of N-/Si-co-doped nanocrystalline diamonds as luminescent nanothermometers using the ratiometric approach. A high thermal sensitivity, up to 5.5% K⁻¹, was found for the ratio of the areas of the ZPL peaks of the NV⁻ and SiV⁻ emission centres. This value is promising and supports the use of these N-/Si-co-doped nanodiamonds as in vitro luminescent nanothermometers in biological tissues.

Author contributions

M. R.-F.: investigation, methodology, writing – original draft; M. G.: investigation, methodology; I. C.-B.: investigation, methodology, supervision, visualization, writing – original draft; R. A.: investigation, methodology; P. P.: investigation, methodology, supervision, writing – review and editing; K. H.: supervision, writing – review and editing; G. A.: investigation, methodology; D. Z.: methodology; J. N.: funding acquisition, project administration, supervision, writing – review and editing.

Data availability

All relevant data are within the manuscript and the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by MCIN/AEI/10.13039/501100011033 and the European Union “NextGenerationEU”/PRTR” [grant number TED2021-132518B-I00]; by the Ministerio de Universidades del Gobierno de España., which funds M. R.-F.'s PhD position [FPU19/02336]. M. G.-G. acknowledges support under fellowship no. FPU23/01837, funded by MICIU/AEI/10.13039/501100011033, Ministerio de Ciencia, Innovación y Universidades, Agencia Estatal de Investigación, del Gobierno de España. P. P. and K. H. acknowledge funding from the UHasselt Special Research Fund (BOF) via the Methusalem NANO network, IBOF project IBOF-23-065, and the Grand Challenge project BOF21GP05. This work used the University of Cadiz's high-performance computing service for research.

References

1. B. del Rosal, E. Ximendes, U. Rocha and D. Jaque, Adv. Opt. Mater., 2017, 5, 1600508.
2. D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301.
3. Y. Takei, S. Arai, A. Murata, M. Takabayashi, K. Oyama, S. Ishiwata, S. Takeoka and M. Suzuki, ACS Nano, 2014, 8, 198.
4. D. Jaque, B. del Rosal, E. M. Rodríguez, L. M. Maestro, P. Haro-González and J. G. Solé, Nanomedicine, 2014, 9, 1047.
5. A. Cadiau, C. D. S. Brites, P. M. F. J. Costa, R. A. S. Ferreira, J. Rocha and L. D. Carlos, ACS Nano, 2013, 7, 7213.
6. M. Rodríguez-Fernandez, J. C. Piñero, R. Alcantara, J. J. Gallardo and J. Navas, Heliyon, 2023, 9, e16775.
7. A. Das and D. T. Debnath, Chem. – Eur. J., 2023, 29, e202202475.
8. C.-Y. Zhong, L. Xiao, J. Zhou, Z. Chen, Y. Chen, Z.-Q. Liu and J. Z. Zhang, Chem. Eng. J., 2022, 431, 134110.
9. J. D. Rocca, D. Liu and W. Lin, Acc. Chem. Res., 2011, 44, 957.
10. A. Benayas, B. del Rosal, A. Pérez-Delgado, K. Santacruz-Gómez, D. Jaque, G. A. Hirata and F. Vetrone, Adv. Opt. Mater., 2015, 3, 687.
11. W. Piotrowski, M. Kuchowicz, M. Dramićanin and L. Marciniak, Chem. Eng. J., 2022, 428, 131165.
12. F. Pedroza-Montero, K. Santacruz-Gómez, M. Acosta-Elías, E. Silva-Campa, D. Meza-Figueroa, D. Soto-Puebla, B. Castaneda, E. Urrutia-Bañuelos, O. Álvarez-Bajo, S. Navarro-Espinoza, R. Riera and M. Pedroza-Montero, Appl. Sci., 2021, 11, 4065.
13. S. Sotoma, C. P. Epperla and H.-C. Chang, ChemNanoMat, 2018, 2, 15.
14. W. Liu, M. N. A. Alam, Y. Liu, V. N. Agafonov, H. Qi, K. Koynov, V. A. Davydov, R. Uzbekov, U. Kaiser, T. Lasser, F. Jelezko, A. Ermakova and T. Weil, Nano Lett., 2022, 22, 2881.
15. A. M. Romshin, V. Zeeb, A. K. Martyanov, O. S. Kudryavtsev, D. G. Pasternak, V. S. Sedov, V. G. Ralchenko, A. G. Sinogeykin and I. I. Vlasov, Sci. Rep., 2021, 11, 14228.
16. S. Choi, V. N. Agafonov, V. A. Davydov and T. Plakhotnik, ACS Photonics, 2019, 6, 1387.
17. A. M. Romshin, V. Zeeb, E. Glushkov, A. Radenovic, A. G. Sinogeikin and I. I. Vlasov, Sci. Rep., 2023, 13, 8546.
18. M. Fujiwara, G. Uchida, I. Ohki, M. Liu, A. Tsurui, T. Yoshikawa, M. Nishikawa and N. Mizuochi, Carbon, 2022, 198, 57.
19. F. T.-K. So, N. Hariki, M. Nemoto, A. I. Shames, M. Liu, A. Tsurui, T. Yoshikawa, Y. Makino, M. Ohori, M. Fujiwara, E. D. Herbschleb, N. Morioka, I. Ohki, M. Shirakawa, R. Igarashi, M. Nishikawa and N. Mizuochi, APL Mater., 2024, 12, 051102.
20. P. Pobedinskas, G. Degutis, W. Dexters, J. D'Haen, M. K. Van Bael and K. Haenen, Appl. Surf. Sci., 2021, 538, 148016.
21. G. Degutis, P. Pobedinskas, H.-G. Boyen, W. Dexters, W. Janssen, S. Drijkoningen, A. Hardy, K. Haenen and M. K. V. Baela, Chem. Phys. Lett., 2015, 640, 50.
22. A. Gali, J. Mater. Res., 2012, 27, 897.
23. I. I. Vlasov, A. A. Shiryaev, T. Rendler, S. Steinert, S.-Y. Lee, D. Antonov, M. Vörös, F. Jelezko, A. V. Fisenko, L. F. Semjonova, J. Biskupek, U. Kaiser, O. I. Lebedev, I. Sildos, P. R. Hemmer, V. I. Konov, A. Gali and J. Wrachtrup, Nat. Nanotechnol., 2014, 9, 54.
24. Y. Jin, M. Govoni, G. Wolfowicz, S. E. Sullivan, F. J. Heremans, D. D. Awschalom and G. Galli, Phys. Rev. Mater., 2021, 5, 084603.
25. S. A. Tawfik and S. P. Russo, Comput. Phys. Commun., 2022, 273, 108222.
26. R. Richter, M. I. S. Röhr, T. Zimmermann, J. Petersen, C. Heidrich, R. Rahner, T. Möller, J. E. Dahl, R. M. K. Carlson, R. Mitric, T. Randera and A. Merlia, Phys. Chem. Chem. Phys., 2015, 17, 4739.
27. S. Salustro, A. M. Ferrari, R. Orlando and R. Dovesi, Theor. Chem. Acc., 2017, 136, 42.
28. A. Karim, I. Lyskov, S. P. Russo and A. Peruzzo, J. Appl. Phys., 2020, 128, 233102.
29. Y. Makino, T. Yoshikawa, A. Tsurui, M. Liu, G. Yamagishi, M. Nishikawa, T. Mahiko, M. Ohno, M. Ashida and N. Okuyama, Diamond Relat. Mater., 2022, 130, 109493.
30. Á. Gali, Nanophotonics, 2019, 8, 1907.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. P. F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
32. Y.-X. Cui, J.-G. Zhang, F.-H. Sun and Z.-M. Zhang, Trans. Nonferrous Met. Soc. China, 2013, 23, 2962.
33. B. Yang, J. Li, L. Guo, N. Huang, L. Liu, Z. Zhai, W. Long and X. Jiang, CrystEngComm, 2018, 20, 1158.
34. T. Yeghoyan, K. Alassaad, V. Soulière, G. Ferro, M. Gutierrez and D. Araujo, Phys. Status Solidi A, 2019, 216, 1800588–1800597.
35. S. Chowdhury, M. T. Laugier and J. Henry, Int. J. Refract. Met. Hard Mater., 2007, 25, 39.
36. S. Drijkoningen, S. D. Janssens, P. Pobedinskas, S. Koizumi, M. K. Van Bael and K. Haenen, Sci. Rep., 2016, 6, 35667.
37. P. Borowicz, M. Latek, W. Rzodkiewicz, A. Łaszcz, A. Czerwinski and J. Ratajczak, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2012, 3, 45003.
38. S. Reich and C. Thomsen, Phys. Eng. Sci., 2004, 362, 2271.
39. V. Zólyomi, J. Koltai and J. Kürti, Phys. Status Solidi B, 2011, 248, 2435.
40. J. Riedrich-Möller, C. Arend, C. Pauly, F. Mücklich, M. Fischer, S. Gsell, M. Schreck and C. Becher, Nano Lett., 2014, 14, 5281.
41. R. Dhankhar, N. Singh and R. V. Nair, Optik, 2024, 315, 172038.
42. R. Guo, K. Wang, Y. Tian and H. Wang, J. Alloys Compd., 2022, 924, 166507.
43. C. Liu, T. Zhu, J. Jia, Y. Zhu, Q. Chen, W. Zhang, W. Zhang, H. Song, Y. Wang and N. Jiang, Diamond Relat. Mater., 2025, 151, 111789.
44. L. Wang, X. Lv, Q. Wang, L. Li and G. Zou, Mater. Sci. Semicond. Process., 2024, 180, 108554.
45. L.-T. S. Lin, G. Popovici, Y. Mori, A. Hiraki, M. A. Prelas, B. V. Spitsyn, S. Khasawinah and T. Sung, Diamond Relat. Mater., 1996, 5, 1236.
46. C. L. Wang, A. Hatta, N. Jiang, J. H. Won, T. Ito, A. Hiraki, Z. S. Jin and G. T. Zou, Diamond Relat. Mater., 1998, 7, 748.
47. Y. L. Khong, A. T. Collins and L. Allers, Diamond Relat. Mater., 1994, 3, 1023.
48. H. Watanabe, T. Kitamura, S. Nakashima and S. Shikata, J. Appl. Phys., 2009, 105, 093529.
49. Y. Makino, T. Mahiko, M. Liu, A. Tsurui, T. Yoshikawa, S. Nagamachi, S. Tanaka, K. Hokamoto, M. Ashida, M. Fujiwara, N. Mizuopchi and M. Nishiwaka, Diamond Relat. Mater., 2021, 112, 108248.
50. S. J. Ikhmayies and R. N. Ahmad-Bitar, J. Lumin., 2013, 142, 40.
51. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012.
52. P. Martínez-Merino, M. A. Hernández-Rodríguez, J. C. Piñero, C. D. S. Brites, R. Alcántara and J. Navas, Nanoscale, 2024, 16, 8470.
53. F. Qin, H. Zhao, W. Cai, Z. Zhang and W. Cao, Europhys. Lett., 2016, 116, 60008.

---

Footnote

† Electronic supplementary information (ESI) available: (S1) Input files for vibronic spectra simulations in Gaussian 16. (S2) Analysis of the full width at half maximum from Raman spectra. (S3) Scanning electron microscopy. (S4) SEM and cathodoluminescence (CL). See DOI: https://doi.org/10.1039/d4nr04132a

---