 Open Access Article
Open Access ArticleAxial electrokinetic trapping of label-free nanoparticles using evanescent field scattering†
Yera
Ussembayev‡
 ab,
Farshad
Rezakhanloo‡
ab,
Kristiaan
Neyts
ab,
Farshad
Rezakhanloo‡
ab,
Kristiaan
Neyts
 abc and
Filip
Strubbe
*ab
abc and
Filip
Strubbe
*ab
aLCP research group, Ghent University, Technologiepark 126, 9052 Gent, Belgium. E-mail: filip.strubbe@ugent.be
bCenter for Nano and Biophotonics, Ghent University, Technologiepark 126, 9052 Gent, Belgium
cHong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
First published on 13th February 2025
Abstract
Anti-Brownian electrokinetic trapping enables the confinement of individual nanoparticles in liquids by applying electric fields. This technique facilitates the long-term observation of nanoscopic objects, allowing for detailed studies of their physical, chemical, and biomolecular properties. However, this method has been largely restricted to nanoparticles that can be visualized by photoluminescence. While some techniques avoid fluorescent labeling by using dark-field or interferometric scattering microscopy, they are limited to two-dimensional particle trapping and lack control over the axial direction. Here, we demonstrate the axial electrokinetic trapping of fluorescence-free nanoparticles that scatter the evanescent field induced by total internal reflection. The distance between the particle and the glass surface is directly related to the intensity of scattered light, and controlled by an applied electric field. Consequently, nanoparticles can be trapped and monitored in response to applied voltages at kilohertz rates without the need for fluorescent labeling. In addition, we utilize this approach to investigate how surface proximity impacts the diffusion and mobility of the trapped nanoparticles. Our method paves a new way to study a broad range of nano-objects that can be trapped at the single-particle level, relying solely on their light-scattering properties, which offers significant potential for advancing research in surface chemistry, single-molecule biophysics, and cell membrane biology.
Introduction
Anti-Brownian electrokinetic (ABEL) trapping represents a pioneering advancement in the manipulation and confinement of individual nanoparticles and molecules in liquid environments.1,2 Similar to electrostatic3 and optical4 traps, ABEL trapping achieves stable localization of nanoscopic entities by feedback electric forces to neutralize the stochastic motion induced by Brownian dynamics.1,5–7 This capability has unlocked new avenues for in-depth analysis of the physicochemical and biomolecular properties of nanoparticles and molecules over extended durations. For instance, ABEL trapping has been employed to study single-enzyme kinetics, providing insights into the dynamic processes of enzymatic reactions at the single-molecule level.5,6 It has also been used to investigate the mechanical properties of DNA and RNA molecules, revealing details about their folding and interaction mechanisms.7 Furthermore, ABEL trapping has found applications in fundamental physics and information theory.8–10 For example, it has been utilized to experimentally verify Landau's principle,10 which relates to the minimum amount of energy required to perform a logical operation, thus bridging theoretical and practical aspects of thermodynamic computation at the nanoscale. Therefore, the versatility and precision of ABEL trapping make it a powerful tool to explore and manipulate nano-objects for a wide range of applications.Different realizations of ABEL trapping have been developed, including those based on epi-fluorescence1,2,8–11 and laser-scanning5–7,12,13 microscopy, but they have a common limitation of relying on fluorescence-labeled particles or molecules. They use fluorescence signals to track the position of the nanoparticle or molecule in real-time, allowing for precise feedback adjustments to counteract Brownian motion. This dependence on fluorescent labeling restricts the range of particles that can be studied, as not all nanoparticles or molecules can be easily tagged with fluorescent markers.14 Furthermore, even if labeling is successful, it may alter the native properties of the molecules, potentially influencing the outcomes of experiments.14 Another significant drawback is fluorescence bleaching,15 which limits the duration of observation as fluorescent signals diminish over time. Additionally, some fluorescent nanoparticles, including quantum dots and semiconductor nanocrystals,16 often suffer from photoluminescence blinking,17–19 which causes intermittent emission and results in fluctuations in signal intensity. This blinking can complicate the particle position analysis and hinder accurate feedback for ABEL trapping. Consequently, the reliance on fluorescence for nanoparticle detection introduces limitations in both the duration and quality of observations, emphasizing the need for alternative methods that can provide stable and continuous monitoring of nanoparticles without the drawbacks associated with fluorescence.
To date, several ABEL trapping techniques have been developed to avoid the use of fluorescence in particle visualization, based on bright-field microscopy20 (BFM), dark-field microscopy21 (DFM) or interferometric scattering (iSCAT) microscopy.22 BFM offers a simple particle tracking setup20,23 by directly illuminating the sample and detecting 3D particle position changes using real-time Fourier-Bessel decomposition method,20 but it lacks the sensitivity required to resolve small sub-micrometer particles against a bright background. DFM enhances the visibility of nanoparticles by illuminating the sample with light that does not enter the objective lens directly.24 Instead, only light scattered by the particles is collected, creating a bright image of the particles against a dark background. While this method effectively visualizes non-fluorescent particles,21 it requires precise alignment and specialized optics, which can be complex and costly.24 In addition, DFM is less sensitive compared to fluorescence methods, potentially limiting its ability to detect very small or weakly scattering nanoparticles.24 Another method is iSCAT, which utilizes the interference between scattered light from the nanoparticle and a reference beam to enhance detection sensitivity.15 This technique allows for the visualization of very small particles, including proteins25 and quantum dots,22 without the need for fluorescent labeling. iSCAT can achieve high resolution, making it a powerful tool for studying dynamic processes at the nanoscale.22 However, iSCAT setups are not commonly found in standard microscopy laboratories due to their complex instrumentation. Despite these drawbacks, BFM, DFM, and iSCAT provide valuable alternatives to fluorescence-based methods, broadening the scope of nanoparticle research.
In this work, we aim to develop an alternative method to visualize fluorescence-free nanoparticles integrated with ABEL trapping. Our approach leverages evanescent field scattering using total internal reflection (TIR) microscopy26–28 to circumvent the need for fluorescent labeling in nanoparticle visualization as exemplified in Fig. 1. TIR microscopy creates an evanescent field at the interface between the glass surface and the aqueous solution, which decays exponentially with distance from the surface27 (right graph in Fig. 1). Nanoparticles within this field scatter the evanescent light, producing detectable signals without the need for fluorescent markers. Feedback trapping combined with this technique benefits from simplicity and accessibility of TIR microscopy, which is widely available in biological laboratories.28 Moreover, the use of evanescent field scattering will also enable electrokinetic trapping of particles in close proximity to the glass surface. In contrast to previous studies1,5,7,10–13,22 where particles are trapped laterally (in xy-plane) with strong confinement along the z-axis (achieved by using channel heights below one micron), our proposed approach facilitates a full control in the axial direction within the evanescent field and quantitative analysis of how surface interactions, including hydrodynamic drag and electrostatic forces, influence the mobility and diffusion of nanoparticles. This capability is particularly attractive for research in surface chemistry, single-molecule biophysics, and cell membrane biology. The technique may provide detailed insights into the dynamic processes at the single-molecule level, advancing our understanding of many complex biomolecular systems. Additionally, our proposed approach is straightforward and robust, avoiding complex optical setups required by DFM and iSCAT. While some techniques such as dielectrophoresis29 (DEP) and electro-plasmonic trapping,30 offer well-established methods for particle manipulation, our proposed approach presents several notable advantages. Unlike DEP, which requires precise electrode design and relies on the dielectric properties of particles, our method offers visualization without the need for specialized materials or complex setups.29 Moreover, compared to electro-plasmonic trapping, which involves plasmonic enhancement and typically requires the use of metallic surfaces,30,31 our method leverages the simplicity and robustness of evanescent field scattering without light absorption or plasmon-induced heating. By relying solely on light-scattering properties, this technique will offer an alternative route to study a wide range of nanoparticles, providing a versatile and practical tool for researchers exploring nanoscale phenomena.
Results and discussion
The goal of this work is to achieve stable ABEL trapping of fluorescence-free nanoparticles that scatter the evanescent field. As a study model, we consider polystyrene (PS) nanoparticles with a diameter dNP = 190 nm and surface charge q, which are diluted in deionized water as shown in Fig. 1. These nanoparticles are selected for their well-defined physical and chemical properties, making them ideal for controlled experimental studies. The sample is contained within a microfluidic chamber constructed from two glass cover slips, each coated with a thin layer of indium tin oxide (ITO). The ITO-coated glass slides serve as parallel transparent electrodes separated with a channel height of h = 50 μm to generate a uniform electric field E. The nanoparticles are visualized using a custom-built inverted microscope23,32,33 (Methods) combined with TIR laser excitation (ESI Fig. S1†). The laser has a free-space wavelength of λ0 = 532 nm and is focused at an incident angle θTIR ≈ 67° on a right-angle prism mounted on the top glass slide of the flow cell to generate the evanescent field (Fig. 1). The intensity of this field decays exponentially in the axial direction (right graph in Fig. 1) according to the expression:27| I(z) = I0e−z/dEF | (1) |
 | (2) |
In our setup, the penetration depth is approximately 114 nm, which ensures that the interaction of the nanoparticles with the evanescent field is highly localized near the glass surface. For example, Fig. 2a shows a series of video frames where a single light-scattering nanoparticle is freely diffusing within the excited evanescent field. The particle is held near the center of the region of interest (ROI) by manually tracking its lateral diffusive motion. The fluctuating diffraction rings around the particle provide a clear indication of its movement along the z-axis, revealing its random Brownian motion. This visual evidence not only highlights the particle's stochastic behavior but also demonstrates the potential for achieving stable ABEL trapping by leveraging the evanescent field.
Next, we utilize the experimental setup depicted in Fig. 1 to control and monitor the positions of nanoparticles near the glass surface by capturing the photons scattered by individual particles within the evanescent field. By counting the number of scattered photons Imeasured (Fig. 2c and d) within a binning window of Δt = 1 ms, we generate a real-time feedback analogue output (AO) voltage V (Fig. 2e and f) on the FPGA (field-programmable gate array) board (Methods). This system operates at a sampling frequency of fAO = 1 kHz, allowing for rapid adjustments to maintain the nanoparticle within the evanescent field. The generated voltage is applied to the ITO electrodes, creating an external electric field E = V/h along the axial direction. This field counteracts the natural Brownian motion of the diffusing nanoparticle, effectively keeping it confined in a stable trap at the desired target intensity Itarget (represented by the black dotted line in Fig. 2d), as depicted in Fig. 1. The FPGA calculates the trapping voltage using the following equation:1,2,11,20
| V = k(Imeasured − Itarget) | (3) |
The experimentally demonstrated axial ABEL trapping offers a powerful and versatile tool for probing a wide range of nanoparticle properties. This technique is particularly well-suited for examining how proximity to surfaces impacts the mobility, diffusion, and overall stochastic behavior of nanoparticles. In general, the random Brownian motion of a nanoparticle is fundamentally characterized by its diffusion constant, as described by Einstein's relation:
 | (4) |
| γ0 = 6πηR | (5) |
However, when a nanoparticle is near a boundary, such as a glass surface, its friction coefficient and diffusion constant can be modified by the proximity to the surface. This effect is captured by Faxén's law, which provides a correction to the axial diffusion constant based on the distance z from the surface:34,35
 | (6) |
To evaluate the nanoparticles’ response to the feedback electric field, we calculate the intensity variation ΔI = Ii − Ii−1, associated to the particle displacement Δz = zi − zi−1, in relation to the applied voltage Vi−1, as shown in Fig. 3. The diagram in Fig. 3a is based on data derived from the intensity and voltage traces presented in Fig. 2d and e, respectively, while Fig. 3b–e display data obtained from the intensity traces shown in ESI Fig. S3.† The distribution observed in the data reveals several key parameters of the trapped nanoparticles. Specifically, the relative intensity at V = 0 reflects the distribution of intensity increments expected from Brownian motion,20 as depicted in the inset graph of Fig. 3a, because here ΔI arises from the stochastic dynamics of the particle. By fitting a Gaussian distribution (red line) to this histogram (green bars), we determine the standard deviation, or intensity variance, σI, which is related to the position variance σz:
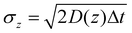 | (7) |
The ratio σz/σI between these two variances provides a conversion factor for the z-position within the linear approximation, expressed as σz/σI = Δz/ΔI. To estimate the electrophoretic mobility of the particles, we apply linear regression to the data (black solid lines in Fig. 3) and use the following formula:20
 | (8) |
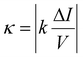 | (9) |
This parameter quantifies the fraction of displacement from the target intensity that is counteracted by drift during each time step Δt, providing a measure of the trap's effectiveness. The calculated trap strength hovers around a mean value of 0.4 across the measured distance range (ESI Fig. S4a†). The obtained values indicate that a relatively strong feedback trap is being generated. Overall, a visual inspection of ΔI vs. V in Fig. 3 reveals several key aspects: the linear proportionality confirms successful trapping, the slope reflects the trapping strength, and the deviation from this linear trend provides insight into the particle's diffusion coefficient.
To highlight the influence of surface proximity on nanoparticle motion in ABEL trapping, we summarize the experimental results in Fig. 4, where the measured diffusion constants of nanoparticles (Methods) are plotted against their distance from the glass surface. The top axis of the graph displays the corresponding target light intensity, which diminishes as the distance from the surface increases, demonstrating the inverse relationship between light intensity and proximity to the surface. The obtained data (green filled dots) reveal a clear trend: the diffusion constant increases as the particles move farther from the surface, aligning well with theoretical predictions shown in the inset graph. This inset graph illustrates the correlation between evanescent field intensity and the diffusion constant calculated according to the eqn (1) and (6), respectively. It highlights the steep decline in intensity near the surface, which corresponds with a rise in the diffusion constant as the particle moves away. By fitting Faxén's law (green solid line) to the averaged data (green open circles), we determine key parameters, including the bulk diffusion constant D0 = 2.4 μm2 s−1 and penetration depth dEF = 102 nm, allowing us to convert the measured data accurately (Methods). The results align well with theoretical predictions, validating our approach. Using these diffusion constants from Fig. 4 in eqn (8), we estimate the electrophoretic mobility of nanoparticles, obtaining values in the range from −1.24 × 10−9 to −2.8 × 10−9 m2 V−1 s−1 for target intensities of 150 and 50 photon counts per millisecond, respectively (ESI Fig. S4c†). These values are more than 10 times lower than the bulk mobility measured by electrophoretic light scattering (Methods), which yields a mobility of μ0 = −4 ± 0.75 × 10−8 m2 V−1 s−1. The reduced mobility observed in the axial ABEL trapping experiments can be attributed to several interrelated factors, primarily the proximity of the nanoparticles to the glass surface. When nanoparticles are near a surface, they experience increased hydrodynamic drag, which significantly reduces their mobility. This proximity also introduces strong electrostatic interactions between the electrode and the surface charge of the particle, further hindering movement. This effect becomes particularly evident when attempting to trap nanoparticles at target intensities above 150 photons per ms, where they tend to adhere to the electrode shortly after feedback is applied. Additionally, the effective electric field may be diminished due to the presence of mobile charge carriers in the water, which screen both the particle surface charge and the applied field, reducing the ability to effectively drive the particles. For deionized water with an electrical conductivity of σ = 0.055 μS cm−1 and an electric permittivity of ε = 700 pF m−1, the characteristic screening time constant36,37 is approximately τ ≅ ε/σ ≈ 0.13 ms. This constant is much lower than the sampling time Δt = 1 ms applied in our experiments, leading to a substantial reduction in the effective field amplitude due to screening effects.20,36,37 This electric field screening, combined with the confinement imposed by the evanescent field, leads to lower observed mobility values compared to those in bulk solutions, where surface-related effects are absent. The observed trends highlight the substantial influence of surface proximity on nanoparticle mobility and diffusion, showcasing the capability of axial ABEL trapping to deliver quantitative insights into nanoscale surface interactions.
 | ||
| Fig. 4 Experimentally estimated diffusion constants of nanoparticles measured via ABEL trapping. The diffusion of nanoparticles is shown as a function of distance z from the surface (bottom axis) and corresponding target intensities (top axis). The green filled dots and open circles represent the measured and averaged data, respectively, while the green solid line shows the fitting to Faxén's law, using eqn (6). The red double arrow indicates the direction of movement, either towards or away from the glass surface. The inset graph illustrates the calculated normalized evanescent field intensity and the normalized diffusion constant as a function of distance from the surface, as predicted by the eqn (1) and (6), respectively. | ||
In conclusion, our work demonstrates the successful implementation of axial ABEL trapping for fluorescence-free nanoparticles that scatter the evanescent field excited by total internal reflection. By combining this advanced trapping technique with TIR microscopy, we achieve precise control and continuous observation of individual nanoparticles near a glass surface. The experimental results reveal a clear dependence of nanoparticle diffusion and mobility on surface proximity, confirming theoretical predictions and providing deeper insights into nanoscale surface interactions. This approach not only overcomes the limitations associated with fluorescent labeling but also paves the way for future studies aimed at understanding and manipulating the behavior of nanoparticles in close proximity to various interfaces. Additionally, coupling this technique with detection capabilities that have single-elementary charge resolution36–38 would enable the exploration of subtle charge-related phenomena at the nanoscale. Integrating the developed method with video-based23 or laser-scanning33 particle tracking systems could further enhance our ability to monitor and analyze the real-time dynamics of nanoparticles over extended durations. Furthermore, our method is versatile and can be applied not only for water-based solvents with varying ionic strengths but also to diverse range of non-polar media.37,38 Moreover, the method holds promise for studying DNA-tethered nanoparticles and molecules,39–41 which could provide invaluable insights into the behavior of biomolecules at single-molecule level. Overall, this work opens up new avenues for exploring the complex interplay of forces at the nanoscale, with broad applications in both fundamental research and technological development.
Methods
Total internal reflection microscopy
The optical setup (ESI Fig. S1†) is based on a custom-built inverted fluorescence microscope.23,32,33 This microscope is integrated with a continuous wave (CW) laser source (L532-050-S, CrystalLaser) with a free-space wavelength of 532 nm, guided and focused onto a right-angle prism (PS615, Thorlabs) at an approximate total internal reflection angle of 67°. The laser power is adjusted using an angle-adjustable half-wave plate (HWP) combined with a polarizing beam splitter (PBS), which splits the power between a direct laser illumination path and a blocked path. The scattered light from the particles is collected by a high numerical aperture (NA 1.3) oil immersion objective lens (CFI Plan Fluor 100× Oil, Nikon) and projected onto both a high-speed CMOS camera (Zyla 4.2 sCMOS, Andor Instruments) and a single-photon counting module (SPCM, SPCM-AQRH-W5, Excelitas Technologies) via a non-polarizing beam-splitter (NPBS) with a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 ratio, respectively. A pinhole (PH) with a diameter of 1 mm is used to define a selected region of interest (ROI), reducing photon counts from the background. The small region of interest (15 μm), defined by the pinhole, ensures a uniform signal from the particles within the applied field of view due to the large laser illumination spot (2 mm), focused on the prism. Samples are secured with a custom-built sample holder mounted on a vertical microstage (MVS010/M, Thorlabs) and 2D horizontal microstages, used to track the particle's lateral diffusive motion manually to keep it centered in the selected field of view. The manual tracking is based on video-imaging of nanoparticle motion in real-time. The sample is positioned on a stage that is controlled to adjust the position dynamically, allowing us to track the nanoparticle's movement within the field of view in xy-plane. By recording high-frame-rate videos (ESI Video V1†), we can identify and manually follow the particle's trajectory under Brownian motion. A combination of a removable mirror (RM) and a dichroic mirror (DM) allows for quick switching between epi-fluorescence and TIR microscopy modes. The laser power for the measurements was set to 1.6 mW (measured at the entrance of the prisms), which results in 400 photons per millisecond for the light scattering by the particle stuck at the surface (ESI Fig. S3a†).
90 ratio, respectively. A pinhole (PH) with a diameter of 1 mm is used to define a selected region of interest (ROI), reducing photon counts from the background. The small region of interest (15 μm), defined by the pinhole, ensures a uniform signal from the particles within the applied field of view due to the large laser illumination spot (2 mm), focused on the prism. Samples are secured with a custom-built sample holder mounted on a vertical microstage (MVS010/M, Thorlabs) and 2D horizontal microstages, used to track the particle's lateral diffusive motion manually to keep it centered in the selected field of view. The manual tracking is based on video-imaging of nanoparticle motion in real-time. The sample is positioned on a stage that is controlled to adjust the position dynamically, allowing us to track the nanoparticle's movement within the field of view in xy-plane. By recording high-frame-rate videos (ESI Video V1†), we can identify and manually follow the particle's trajectory under Brownian motion. A combination of a removable mirror (RM) and a dichroic mirror (DM) allows for quick switching between epi-fluorescence and TIR microscopy modes. The laser power for the measurements was set to 1.6 mW (measured at the entrance of the prisms), which results in 400 photons per millisecond for the light scattering by the particle stuck at the surface (ESI Fig. S3a†).
Microfluidic device fabrication and sample preparation
Microfluidic devices were constructed using two glass substrates: a 0.1 mm thick bottom substrate and a 1 mm thick top substrate, both coated with indium tin oxide (ITO) electrodes. The glass slides were separated by 50 μm spacer beads and assembled using UV-curing glue (Norland Optical Adhesive 68). Prior to assembly, all glass substrates were cleaned with isopropyl alcohol and acetone, followed by rinsing with deionized water. The substrates were then glued together in a rectangular pattern, forming a microchannel approximately 20 mm wide and 50 μm high. The fabricated microfluidic devices were filled with water-based samples containing nanoparticles by capillary forces. As a study model, we selected polystyrene nanoparticles (Magsphere Inc.) with a mean diameter of 190 and 520 nm, which were diluted in deionized water (18 MOhm cm) to achieve a desired concentration of one particle (or fewer) per region of interest, based on the manufacturer's technical datasheet. At least ten nanoparticles were measured for each target intensity to ensure the stability of the results. The flow cells with diluted nanoparticles were sealed to prevent evaporation of the liquid. Samples prepared for ABEL experiments were also analyzed using a Zetasizer Nano (Malvern Instruments) to measure the electrophoretic mobility of the nanoparticles, resulting in a mean value of −4 ± 0.75 × 10−8 m2 V−1 s−1.Data acquisition and analysis
An FPGA (field-programmable gate array, PCIe-7842R, National Instruments) was programmed using the LabVIEW FPGA Module (National Instruments) on a host PC. The FPGA operates two parallel loops: one to count photons based on the digital input (DI) acquired from the SPCM and another to apply a voltage across the microchannel based on the analog output. Separate direct memory access (DMA) FIFO (first-in, first-out) buffers are used to transfer input and output data between the FPGA and the host PC. To calibrate the gathered data, we apply the following analysis. The relative diffusion parameter Drel (left axis in ESI Fig. S5†) is defined based on the standard deviation of the measured intensity, scaled with the target intensity (ESI Fig. S4b†):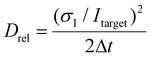 | (10) |
Next, the target intensity (top axis in ESI Fig. S5†) is converted to the distance from the glass surface using eqn (1). The position z, normalized to the penetration depth of the evanescent field dEF, is determined by:
 | (11) |
Here, the zero intensity I0 = 400 photons per ms corresponds to light scattering by a particle immobilized at the surface (ESI Fig. S3a†). The actual penetration depth is challenging to determine precisely as the incident light is not collimated and there is a range of incident angles (with focus at the glass-water interface), which sets up a continuous range of different penetration depths. Therefore, we normalize the calculated distance to the penetration depth since our aim is to calibrate the diffusion constant rather than determine the exact particle position. As a result, the normalized position z/dEF (bottom axis in ESI Fig. S5†) corresponds to increasing distances from the surface, with higher target intensities indicating closer proximity. To obtain the actual diffusion constants and position z, we apply Faxén's law and fit the averaged data to eqn (6), yielding two fitting parameters Dfit = 20.1 s−1 and dfit = 102 nm. Using eqn (4), we calculate the bulk diffusion constant D0 = 2.4 μm2 s−1, and determine a conversion factor α = D0/Dfit. This factor is then applied to convert the measured data to actual diffusion constants D = αDrel (right axis in ESI Fig. S5†) whereas the position is obtained as z = (zdfit)/dEF. All the obtained results are summarized in Fig. 4.
Data availability
The data supporting the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflict of interests.Acknowledgements
This research was supported by a grant from the Flemish Fund for Scientific Research (FWO project G09201N) and Flanders Innovation & Entrepreneurship (VLAIO project VAI.OOB 2023.0001.02). Yera Ussembayev also acknowledges his FWO Postdoc Fellowship (project number 1202225N). PCN and SCRiPTS research groups are acknowledged for providing access to a Zetasizer device. The authors appreciate the fruitful discussions with F. Beunis, L. Oorlynck, and I. Amer Cid.References
- A. E. Cohen and W. E. Moerner, Suppressing Brownian motion of individual biomolecules in solution, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(12), 4362–4365, DOI:10.1073/pnas.0509976103.
- A. E. Cohen and W. E. Moerner, Method for trapping and manipulating nanoscale objects in solution, Appl. Phys. Lett., 2005, 86, 1–3 Search PubMed.
- M. Krishnan, N. Mojarad, P. Kukura and V. Sandoghdar, Geometry-induced electrostatic trapping of nanometric objects in a fluid, Nature, 2010, 467, 692–695, DOI:10.1038/nature09404.
- O. M. Maragò, P. H. Jones, P. G. Gucciardi, G. Volpe and A. C. Ferrari, Optical trapping and manipulation of nanostructures, Nat. Nanotechnol., 2013, 8, 807–819, DOI:10.1038/nnano.2013.208.
- R. H. Goldsmith and W. E. Moerner, Watching conformational- and photodynamics of single fluorescent proteins in solution, Nat. Chem., 2010, 2, 179–186 CrossRef CAS.
- A. H. Squires and W. E. Moerner, Direct single-molecule measurements of phycocyanobilin photophysics in monomeric C-phycocyanin, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 9779–9784 CrossRef CAS.
- Q. Wang and W. E. Moerner, Single-molecule motions enable direct visualization of biomolecular interactions in solution, Nat. Methods, 2014, 11, 555–558 CrossRef CAS.
- K. Proesmans, Y. Dreher, M. Gavrilov, J. Bechhoefer and C. van den Broeck, Brownian Duet: A Novel tale of thermodynamic efficiency, Phys. Rev. X, 2016, 6, 041010, DOI:10.1103/PhysRevX.6.041010.
- M. Gavrilov, R. Chétrite and J. Bechhoefer, Direct measurement of weakly nonequilibrium system entropy is consistent with Gibbs–Shannon form, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11097–11102 CrossRef CAS.
- Y. Jun, M. Gavrilov and J. Bechhoefer, High-precision test of Landauer’s principle in a feedback trap, Phys. Rev. Lett., 2014, 113, 190601, DOI:10.1103/PhysRevLett.113.190601.
- M. Gavrilov, Y. Jun and J. Bechhoefer, Real-time calibration of a feedback trap, Rev. Sci. Instrum., 2014, 85, 095102, DOI:10.1063/1.4894383.
- A. P. Fields and A. E. Cohen, Electrokinetic trapping at the one nanometer limit, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(22), 8937–8942, DOI:10.1073/pnas.1103554108.
- M. Kayci and A. Radenovic, Single fluorescent nanodiamond in a three dimensional ABEL trap, Sci. Rep., 2015, 5, 16669, DOI:10.1038/srep16669.
- D. Jin, et al., Nanoparticles for super-resolution microscopy and single-molecule tracking, Nat. Methods, 2018, 15, 415–423, DOI:10.1038/s41592-018-0012-4.
- G. Young and P. Kukura, Interferometric Scattering Microscopy, Annu. Rev. Phys. Chem., 2019, 70, 301–323 CrossRef CAS.
- Y. Y. Ussembayev, Z. Hens and K. Neyts, Contrasting Anisotropy of Light Absorption and Emission by Semiconductor Nanoparticles, ACS Photonics, 2019, 6, 1146–1152 CrossRef CAS.
- A. L. Efros and D. J. Nesbitt, Origin and control of blinking in quantum dots, Nat. Nanotechnol., 2016, 11, 661–671 CrossRef CAS PubMed.
- C. Rodà, et al., Stimulated Emission through an Electron-Hole Plasma in Colloidal CdSe Quantum Rings, Nano Lett., 2021, 21, 10062–10069 CrossRef.
- I. Tanghe, et al., Broadband Optical Phase Modulation by Colloidal CdSe Quantum Wells, Nano Lett., 2022, 22, 58–64 CrossRef CAS PubMed.
- F. Strubbe, et al., Axial electrokinetic trapping of anisotropic particles, Sci. Rep., 2019, 9, 2806, DOI:10.1038/s41598-019-39224-z.
- M. Gavrilov, J. Koloczek and J. Bechhoefer, Feedback trap with scattering-based illumination, Opt. Life Sci., 2015, JT3A.4 Search PubMed.
- A. H. Squires, A. A. Lavania, P. D. Dahlberg and W. E. Moerner, Interferometric Scattering Enables Fluorescence-Free Electrokinetic Trapping of Single Nanoparticles in Free Solution, Nano Lett., 2019, 19, 4112–4117 CrossRef CAS.
- Í. Amer Cid, Y. Y. Ussembayev, K. Neyts and F. Strubbe, Measurement of the amplitude and phase of the electrophoretic and electroosmotic mobility based on fast single-particle tracking, Electrophoresis, 2021, 42, 1623–1635 CrossRef.
- P. F. Gao, G. Lei and C. Z. Huang, Dark-Field Microscopy: Recent Advances in Accurate Analysis and Emerging Applications, Anal. Chem., 2021, 93, 4707–4726, DOI:10.1021/acs.analchem.0c04390.
- R. W. Taylor, et al., Interferometric scattering microscopy reveals microsecond nanoscopic protein motion on a live cell membrane, Nat. Photonics, 2019, 13, 480–487 CrossRef CAS.
- K. N. Fish, Total internal reflection fluorescence (TIRF) microscopy, Curr. Protoc. Cytom., 2009, 50, 12.18.1–12.18.13, DOI:10.1002/0471142956.cy1218s50.
- M. Oheim, A. Salomon, A. Weissman, M. Brunstein and U. Becherer, Calibrating Evanescent-Wave Penetration Depths for Biological TIRF Microscopy, Biophys. J., 2019, 117, 795–809, DOI:10.1016/j.bpj.2019.07.048.
- D. Axelrod, Total internal reflection fluorescence microscopy in cell biology, Traffic, 2001, 2, 764–774, DOI:10.1034/j.1600-0854.2001.21104.x.
- R. Pethig, Dielectrophoresis: Status of the theory, technology, and applications, Biomicrofluidics, 2010, 4, 022811, DOI:10.1063/1.3456626.
- J. A. Huang, M. Z. Mousavi, Y. Zhao, A. Hubarevich, F. Omeis, G. Giovannini, M. Schütte, D. Garoli and F. De Angelis, SERS discrimination of single DNA bases in single oligonucleotides by electro-plasmonic trapping, Nat. Commun., 2019, 10, 5321, DOI:10.1038/s41467-019-13242-x.
- A. I. Radu, et al., HD DVD substrates for surface enhanced Raman spectroscopy analysis: Fabrication, theoretical predictions and practical performance, RSC Adv., 2016, 6, 44163–44169 RSC.
- Y. Y. Ussembayev, N. K. Zawacka, F. Strubbe, Z. Hens and K. Neyts, Waveguiding of photoluminescence in a layer of semiconductor nanoparticles, Nanomaterials, 2021, 11, 1–13 CrossRef.
- L. Oorlynck, Y. Y. Ussembayev, I. Amer Cid, J. Fraire, C. Hinnekens, K. Braeckmans and F. Strubbe, Laser-Scanning Microscopy for Electrophoretic Mobility Characterization of Single Nanoparticles, Part. Part. Syst. Charact., 2023, 40, 2200152, DOI:10.1002/ppsc.202200152.
- K. C. Neuman and S. M. Block, Optical trapping, Rev. Sci. Instrum., 2004, 75, 2787–2809, DOI:10.1063/1.1785844.
- K. C. Vermeulen, G. J. L. Wuite, G. J. M. Stienen and C. F. Schmidt, Optical trap stiffness in the presence and absence of spherical aberrations, Appl. Opt., 2006, 45, 1812–1819 CrossRef PubMed.
- Y. Ussembayev, et al., Single Elementary Charge Fluctuations on Nanoparticles in Aqueous Solution, ACS Nano, 2023, 17, 22952–22959 CrossRef CAS PubMed.
- F. Beunis, F. Strubbe, K. Neyts and D. Petrov, Beyond Millikan: The dynamics of charging events on individual colloidal particles, Phys. Rev. Lett., 2012, 108, 016101, DOI:10.1103/PhysRevLett.108.016101.
- F. Strubbe, F. Beunis and K. Neyts, Detection of elementary charges on colloidal particles, Phys. Rev. Lett., 2008, 100, 218301, DOI:10.1103/PhysRevLett.100.218301.
- G. Ma, et al., Optical imaging of single-protein size, charge, mobility, and binding, Nat. Commun., 2020, 11, 4768, DOI:10.1038/s41467-020-18547-w.
- S. H. Sternberg, S. Redding, M. Jinek, E. C. Greene and J. A. Doudna, DNA interrogation by the CRISPR RNA-guided endonuclease Cas9, Nature, 2014, 507, 62–67 CrossRef CAS.
- M. L. Visnapuu and E. C. Greene, Single-molecule imaging of DNA curtains reveals intrinsic energy landscapes for nucleosome deposition, Nat. Struct. Mol. Biol., 2009, 16, 1056–1062 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04092a |
| ‡ Equally contributing authors. |
| This journal is © The Royal Society of Chemistry 2025 |



