Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nonlinear memristor model with exact solution allows for ex situ reservoir computing training and in situ inference†
Nicholas
Armendarez
 a,
Md Sakib
Hasan
a,
Md Sakib
Hasan
 *b and
Joseph
Najem
*a
*b and
Joseph
Najem
*a
aDepartment of Mechanical Engineering, The Pennsylvania State University, University Park, PA, USA. E-mail: jsn5211@psu.edu
bDepartment of Electrical and Computer Engineering, The University of Mississippi, University, MS, USA. E-mail: mhasan5@olemiss.edu
First published on 4th December 2024
Abstract
Memristive physical reservoir computing is a promising approach for solving data classification and temporal processing tasks. This method exploits the nonlinear dynamics of physical, low-power devices to achieve high-dimensional mapping of input signals. Ion-channel-based memristors, which operate with similar voltages, currents, and timescales as biological synapses, are promising due to their rich dynamics, especially for use in biological edge settings. Accurate modeling of their dynamics is essential for optimizing network hyperparameters ex situ to save time and energy. Here, a generalized sigmoidal growth model of ion-channel memristor conductance is presented and shown to be more accurate in predicting dynamics than linear or logistic models. Using the exact solution of the proposed sigmoidal model, the MNIST handwritten digit classification task is optimized and trained ex situ, then tested in situ with the same trained weights. This approach achieved an experimental testing accuracy of 90.6%.
1 Introduction
Physical implementations of artificial neural networks (ANNs) have long aimed to replicate the human brain's energy efficiency and computational power.1,34 Conceptually, operating neural networks in hardware allows for massively parallel architectures, bypassing the conventional software Von Neumann bottleneck.34 When models sufficiently capture the dynamics of the analog implementation, it can be advantageous to perform parameter training ex situ, where hyperparameters such as network size can be more easily varied2 at a significantly lower time and energy cost. Critically, models must account for the physical imperfections of the analog implementation; otherwise, the ex situ trained parameters will not translate to in situ inference.3In particular, physical reservoir computing (PRC) has recently been a focus of research, with demonstrations of new ways to realize the reservoir layer using power-efficient dynamic devices.4–13 The basis of these techniques lies in the reservoir computing (RC) paradigm, where recurrent neural network (RNN) training is dramatically simplified by creating a “reservoir layer” of a random, high dimensional, and nonlinear network that has the critical feature of “fading” memory. This property indicates that the current state of the nonlinear reservoir strongly depends on recent inputs and past states, with this dependence decreasing at further time points in the past.14–17 The RC layer is typically connected to a readout layer through fixed, trained weights.14 PRC entails creating this reservoir layer using the physics of excitable materials and devices to generate nonlinear dynamics. Many devices have been utilized as reservoir layers in various configurations;8,18 however, in all cases, input is supplied to the device, and the internal states are some physically measurable quantities, such as voltage or current. These measured states dynamically update based on the device's nonlinear response to present and previous inputs.8 A standard device used to build PRC layers is the volatile memristor, which is typically utilized in a parallel architecture where each device is self-recurrent but uncoupled to adjacent devices.5,6,11,12,19 Memristors are two-terminal electronic components whose resistance is modulated based on past electrical stimulation.20 “Volatile” memristors, in particular, return to some base-level resistance after removing stimulation,5 which helps satisfy the “fading” memory requirement for RC systems.
Many types of devices have been shown to exhibit volatile memristance, including metal–oxide,5–7 spintronic,9 perovskite,21,22 ion-channel,11,23 and nanofluidic pores.24 Among these devices, ion-channel-based memristors are of particular interest due to the similarity in operation to biological synapses,23 which also operate with voltage-gated ion channels. Recent works have established alamethicin and monazamycin as volatile memristive ion channels and demonstrated their use in PRC.11,12,25 The architecture of these memristor PRC systems is shown in Fig. 1a. The dynamics of ion-channel-based memristors appear linear with respect to their state variable update on longer timescales and at near steady-state values but show pronounced nonlinearities on shorter timescales and when far from the steady-state value.25,26 Models for the dynamic update in conductance of these devices range from simple, single-state, linear models23,26 to three11 or even five-state nonlinear models.27 These models have tradeoffs regarding the number of physical phenomena represented versus the ease of solving. Generally, linear models offer exact solutions that scale easily in simulation and have been shown to describe functional reservoir dynamics when deviations from the steady-state are sufficiently small.12 Using a model with an exact solution is advantageous so that the readout weights can be trained ex situ using large datasets and then implemented with the responses from physical devices for inference. The ease of simulation allows hyperparameters, such as input encoding, to be tuned outside physical experiments.
Conversely, nonlinear, multistate models provide increased response accuracy far from the steady state, which can be seen in similar memristor devices using monazamycin peptides.25 Notably, for devices that are initially in a low conductance state subjected to a large voltage step, the experimental increase in conductance follows a sigmoidal rather than an exponential response up to the steady state value for short timescales. Nonlinear models can capture this initial transient, as shown in Fig. 2. Besides more accurately describing the dynamics of the memristors themselves, a nonlinear model is desirable due to the critical role of nonlinearity in RC. Conventional RC characteristically utilizes state nonlinear dynamics at each node,14 and nonlinear dynamics are indeed required when the task to be solved is, itself, highly nonlinear. However, the existing multistate models are not analytically solvable due to the nonlinear coupling of state variables. The lack of an exact solution makes ex situ training and hyperparameter tuning impractical as architectures scale larger. Therefore, it is imperative to model ion channel memristors using a model with explicit nonlinear dynamics and exact solutions, making it better suited for computational purposes.28
Due to the conflicting requirements of state nonlinearity and exact solubility, we investigate which known first-order nonlinear ordinary differential equations (ODEs) might apply to our alamethicin-based memristor.23 Given the biological nature of our memristor, we focus on the logistic ODE and the more generalized Richard's Differential Equation (RDE). These nonlinear models are prevalent in biological systems and have exact solutions.29,30 We demonstrate the effectiveness of using an RDE model to accurately capture the dynamics of alamethicin channels in the transient phase. Furthermore, we use the RDE model's exact solution to train a reservoir layer on the full dataset of MNIST handwritten digits encoded as voltage squarewave trains. We optimize this training by tuning the voltage encoding hyperparameters, achieving higher accuracy in this task than previously reported in the literature.5,11 Finally, to validate the model's accuracy and showcase the efficacy of utilizing the nonlinear dynamics of memristors, we experimentally test the reservoir on the MNIST task using the same readout layer trained ex situ and show that the level of accuracy is largely maintained outside of the simulation environment. Fig. 1 graphically explains the mixed training and inference method. Additionally, a more in-depth flowchart describing the workflow can be found in Fig. S5 ESI.†
2 Results
2.1 Modeling the dynamics of alamethicin-based memristors
The dynamics of ion-channel-forming peptides have been extensively studied,23,26,31,32 and researchers have proposed various models to describe their observed behavior. In the following subsections, we will discuss the existing model for the alamethicin-based memristor,23 which we label as “linear”, as well as the logistic model and highlight their shortcomings in capturing the transient dynamics of the device. We will then describe the proposed Richards’ Differential Equation (RDE) model while discussing its key advantages compared to the other two models. All models are similar in that they model the rate of change of area pore density of alamethicin as a function of transmembrane voltage. Pore density is the preferred state variable because membrane area tends to change between fabricated bilayers (see the Methods section) on a device-to-device basis. Further, the membrane area can increase in the prolonged presence of an electric field via a process known as electrowetting as we describe in the Additional Model Considerations section. The pore density normalization allows us to model the alamethicin dynamics for an arbitrary area and multiply by the measured or predicted area to obtain the total number of pores in the membrane. | (1) |
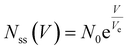 | (2) |
 | (3) |
| Na(t) = Ce−t/τ + Nss | (4) |
| C = Na(t0) − Nss | (5) |
This solution is valid from any positive starting value of Na, assuming that voltage is constant from t0 to t.
As mentioned in the Introduction, while this linear model captures the dynamics of alamethicin near and at steady-state, it fails to capture a significant part of the initial transient response. Fig. 2 shows that the initial response of alamethicin to input voltage is sigmoidal rather than a simple exponential growth. Therefore, an alternative model is required to capture these dynamics. The significant nonlinearity that needs to be accounted for by such a model is the increase in low-state rates of conductance. The conventional linear model of alamethicin does not predict the exponential rise in conductance in the short time immediately after a voltage is applied. To capture this dynamic, we must introduce a nonlinear state equation.
 | (6) |
 | (7) |
While the logistic equation captures a sigmoidal temporal rise in response to a step voltage, it requires symmetry around the inflection point. Experimentally, we observe that the inflection point behaves asymmetrically, typically closer to the beginning of the rise than the middle. We observed this behavior in Fig. 2a, where the transition from concave up to concave down happens closer to the beginning of the response than to the steady state. Therefore, we propose that a more general logistic equation, such as Richard's differential equation, can capture this dynamic.
 | (8) |
 | (9) |
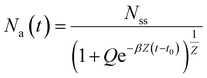 | (10) |
 | (11) |
This solution is valid from any starting value of Na, assuming that voltage is held constant from t0 to t.
Because we are considering only first-order models, we can graphically visualize the differences between the models by examining the phase portrait. The two states of the system are pore density and the rate of change of pore density. We model a single trajectory in the phase space at every input voltage. Fig. 3 demonstrates the differences between the various models.
Alamethicin memristors operated far from the equilibrium state must consider an effect known as electrowetting, which describes that the contact area between lipid monolayers tends to increase with applied voltage.23 Because the models considered here predict the areal density of pores, we must consider that area changes will affect the total number of pores in the memristor, directly affecting the conductance. Electrowetting is well studied, and parameters for the exact solution to the electrowetting equations exist in the literature.23
Furthermore, significant discrepancies between the rates of pore exit in response to sub-threshold and supra-threshold voltages have been modeled conditionally with a different set of rate parameters depending on whether the applied voltage surpasses the threshold of the memristor.12 We also include this two-rate effect in our models and find the parameters for the sub-threshold rates from the literature.12
The steady-state pore density also empirically shows deviations from an exponential voltage function at high activation levels (see Fig. S1 ESI†). We account for this slight difference by fitting the steady-state pore density function to a sigmoidal rather than exponential (Methods). This approach better fits the experimental data but requires an additional fit parameter.
Finally, because experimental data displays stochastic noise due to fluctuations in the number of inserted ion channels, which is proportional to the number of inserted pores,26 we include a white noise term to randomly add between −4% and 4% of the calculated number of pores. The inclusion of a noise term acts not only to better represent the stochasticity in the experimental results but also helps to regularize RC training, increasing testing accuracy at the expense of some amount of training accuracy.16 Furthermore, experimental noise for the conductance of the memristors increases inversely to the level of voltage applied. This relationship is characterized in Fig. S2 (ESI†).
2.2 Ex situ hyperparameter optimization and in situ inference
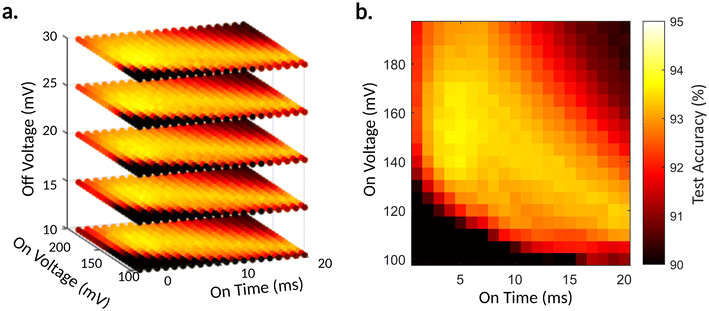
To demonstrate the effectiveness of training a PRC system in simulation and then operating the device for inference, we trained a reservoir of forty memristors on the MNIST handwritten digits database (in simulation) and performed inference on the testing data using physical memristors. The task consists of classifying handwriting digits, digitized into 28 × 28 pixel images, into classes 0 to 9. Typically, portions of the image are scanned (here we crop to 20 × 20 images), and the pixels are binarized so they can easily be converted into voltage waveforms where a pixel value of 1 converts to a high voltage pulse and a pixel value of 0 converts to a low voltage pulse. The MNIST task is a common memristor PRC benchmark because converting spatial data into temporal data allows for temporal coupling in the memristors’ response to that input. Some previous implementations of memristor reservoirs have trained and tested the reservoir response entirely in materia,5,7 while others have done training and testing entirely in simulation.11 Here, we show a hybrid approach, wherein the reservoir is trained in simulation but tested experimentally. However, we note that we performed the readout in software for training and testing. We compare the linear model to the RDE model in this task to determine if the apparent difference in dynamics translates to quantitative differences in task performance.The primary consideration for solving the MNIST task with a memristor reservoir layer is the number and way reservoir states are obtained. Reservoir states are the measured values of the memristors that have changed in response to the voltage waveform input. These state values will be sent to the readout layer for classification. Typically, images are row-scanned to create the voltage waveforms. However, taking only a single state per row is not feasible for accurate prediction, as a memristor could reach too many possible conductances after 20 pulses to distinguish them easily.5,11 Effectively, more states are needed to classify the images, and various methods can create these extra states. One method is to break the rows into shorter segments of only a few pixels, allowing for more states and easily distinguishable conductances.5 Alternatively, the whole row waveform can be sent to the memristor, and multiple states can be sampled throughout the stimulation at regular intervals or “virtual nodes” (VN). The VN technique couples the state of the previous VNs in a row to the presently measured one, which increases the connectivity of the reservoir.4,11 Furthermore, additional memristors can increase the number of states by encoding the row information multiple times with different input parameters such as pulse width and off-time. However, in this work, we consider only single input encoding reservoir formulations to avoid synchronization issues of data streams. Utilizing multiple memristors with different dynamic properties could obtain similar results using a single input encoding, avoiding this synchronization issue.12 To make up for the restriction of only a single input encoding, we encode voltage waveforms from the rows and the columns of the digitized images and extract VNs at each fourth pixel. Utilizing 40 parallel memristors (20 for the rows and 20 for the columns) and sampling a VN at every fourth pixel, we obtain 200 total states for each image. With ten classes of digits (0 to 9) and a linear readout layer with ten additional bias terms, there are 2010 total trained parameters. Four parameters control the input encoding of the pixel sequences into voltage waveforms: Von, Voff, ton, and toff, which represent on-voltage, off-voltage, on-time, and off-time, respectively. These parameters transform the discrete input pixel sequence into a temporal voltage waveform. Each scan generates a sequence that is 20 pixels long. For the kth pixel, the voltage is set to Voff for time toff, followed by either Von or Voff for time ton, conditional on if the kth pixel is a 1 or a 0 respectively. The conversion from pixel sequences to voltage waveforms can be seen in Fig. 4.
We performed a coarse grid search in simulation over these four hyperparameters to find input encoding parameters that would best run in the physical devices. For each point in the grid search, the reservoir was simulated using the new model and trained on the full 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-image MNIST training dataset. The training was a single epoch of stochastic gradient descent utilizing lasso regularization with a regularization parameter of 0.1. The grid search reveals that Von and ton had the most significant effect on the accuracy of the reservoir, while Voff had a lesser effect and toff had the slightest effect. Fig. 5 shows a 3-D cross-section of the 4-D search for the three most effecting parameters and a 2-D cross-section of that 3-D space showing the effect of the two most influencing parameters. The full 4-D space can be seen in Fig. S3 (ESI†). A region of similarly high accuracies was found within the grid search, with the best parameters being Von = 140 mV, Voff = 20 mV, ton = 4.7 ms, and toff = 0.3 ms. This grid search in simulation ran for 4.85 hours on a 48-core server node. This demonstrates the impressive time-saving potential of ex situ optimization of physical reservoir layers, as the equivalent in situ training would have required 293 hours of continuous run time (Note 1 ESI†). This represents an effective 60-times reduction in hyperparameter optimization time.
000-image MNIST training dataset. The training was a single epoch of stochastic gradient descent utilizing lasso regularization with a regularization parameter of 0.1. The grid search reveals that Von and ton had the most significant effect on the accuracy of the reservoir, while Voff had a lesser effect and toff had the slightest effect. Fig. 5 shows a 3-D cross-section of the 4-D search for the three most effecting parameters and a 2-D cross-section of that 3-D space showing the effect of the two most influencing parameters. The full 4-D space can be seen in Fig. S3 (ESI†). A region of similarly high accuracies was found within the grid search, with the best parameters being Von = 140 mV, Voff = 20 mV, ton = 4.7 ms, and toff = 0.3 ms. This grid search in simulation ran for 4.85 hours on a 48-core server node. This demonstrates the impressive time-saving potential of ex situ optimization of physical reservoir layers, as the equivalent in situ training would have required 293 hours of continuous run time (Note 1 ESI†). This represents an effective 60-times reduction in hyperparameter optimization time.
We used the “optimal” parameters obtained from the grid search to train two reservoirs, one with the RDE model and one with the linear one. We experimentally generated inference data in physical memristors using voltage waveforms constructed with the best results we obtained from the input encoding grid search. We use 1000 testing images for inference. Fig. 6 compares the experimental data to the RDE and linear models in response to an example row of input data. This comparison highlights that the nonlinear RDE model better approximates the experimental data in the far-from-steady state encodings required in the MNIST task. Fig. S4 (ESI†) shows the relative error between the model and experimental data for every pixel sequence used.
After every fourth pixel-equivalent pulse, we sampled the memristors and divided the current output by the voltage input to obtain the conductance at that VN. We collected VN conductances for each unique sequence of pixels in the testing dataset. Next, we constructed state matrices for each test image from the VNs, which included 200 states. We then fed these state matrices into the readout layer in software utilizing the trained weights from the simulated reservoir. Fig. 7 highlights the importance of using the RDE model. When the linear model trained weights are used, the classification fails, predicting only the number seven. By comparison, the total accuracy of the testing set using the RDE model obtained weights was 90.6.
3 Methods
3.1 Materials
We prepared the biomolecular memristors used in this study from a stock of alamethicin and lipid solution. This solution was prepared by first creating a 1 M solution of KCl and 10 mM MOPS (Sigma) buffer. The DPhPC lipids (Avanti) were obtained from a commercial source in chloroform. We evaporated this chloroform solution under ambient conditions and then hydrated it with the KCl/MOPS solution so that the concentration of lipids was 2 mg mL−1. Further, the aqueous solution was put through five freeze–thaw cycles and then extruded through a 0.1 μm pore-sized, track-etched membrane (Avanti). Finally, this solution was divided into vials, and alamethicin peptides (Sigma) in chloroform were added to each to have the appropriate alamethicin concentration of 1 μM. For more details on this preparation procedure, we refer the readers to a study by Najem et al.333.2 Experimental setup
We conducted all characterization and inference experiments with the droplet interface bilayer (DIB) technique described by Najem et al.23 Briefly, the aqueous droplets of a solution containing peptides and lipids were deposited by pipette into a reservoir of Hexadecane oil (Sigma). The reservoir was mounted onto an upright microscope (Olympus) which allowed for droplet diameter measurements needed for area normalization. Ag/AgCl wires were prepared by submerging 125 μm diameter silver wire (Goodfellow) into bleach (Chlorox) for 30 minutes. The wires were then connected to external voltage-supplying and current-measuring equipment. Voltages were provided at 10 kHz by a 16-bit digital-to-analog converter (NI 9264, National Instruments), and currents were measured with a custom-built trans-impedance amplifier (TIA) circuit.12 The prepared wires were held on micromanipulators and inserted into the droplets in the oil. Due to the amphiphilic nature of the phospholipids in the aqueous phase, the hydrophobic tails spontaneously orient themselves towards the oil and the hydrophilic heads face the water which forms a lipid monolayer around each droplet. Using the micromanipulators, we bring the droplets into contact and the two lipid monolayers interlace to form a lipid bilayer of approximately 4 nm in width by excluding the oil from between them.12,33 A copper mesh Faraday cage electrically shielded all measurements.3.3 Fitting
While the linear model has been shown to capture the dynamics of alamethicin insertion on long time scales (seconds), examining the initial temporal response to a step voltage input reveals that the dynamics are not perfectly linear. Fig. 2 shows how the linear model does not capture the initial response to step voltage input. The sigmoidal rise in conductance in response to relatively high applied voltage indicates a nonlinear process. Here, we consider the response of alamethicin to remain first-order. We can then examine the two-dimensional state space trajectories where Na and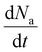 are the two system states. Further, we expect a unique trajectory in this state space for every applied voltage. We empirically extracted the state variables from experimental data and used the extracted state space trajectories to fit phenomenological, nonlinear first-order models to the alamethicin response.
are the two system states. Further, we expect a unique trajectory in this state space for every applied voltage. We empirically extracted the state variables from experimental data and used the extracted state space trajectories to fit phenomenological, nonlinear first-order models to the alamethicin response.
To generate data for phase space extraction, we subjected alamethicin memristors to square waveforms and recorded the current response. At rest, no ion channels existed in the membrane, and upon application of supra-threshold voltage, ion channels formed within the lipid membrane until they reached a steady state. Square waveforms were held constant at the investigation voltage for 100 ms to ensure the memristor had enough time to get a steady state. Data was collected for voltages between 0 and 150 mV in increments of 2 mV; however, only supra-threshold voltages (9–0 mV with the formulation of peptide and salt concentrations used) produced a measurable response that we used for fitting. After each investigation voltage, the memristor was subjected to 0 mV for 10 seconds to ensure it would return to a fully insulating state before the next voltage was applied.
Once we had collected the current data, it was processed using a custom MATLAB script. First, the investigation voltage divided the current response to obtain the conductance. Next, we accounted for the change in the area of the memristor by taking a single measurement of the membrane diameter on the upright microscope. Typically, diameter measurements would be taken continuously over the length of the experiment to obtain real-time data on area change due to electrowetting. However, as the voltage pulses were only 100 ms in these experiments, there was not enough time to obtain adequate data on the area changes as the frame rate of the measurement camera was 30 frames per second. Instead, we measured the area at the beginning of the experiment and used literature values of electrowetting23 to model the relative change in area based on the applied voltages at a 0.1 ms time step. To calculate the pore density of alamethicin, we divided the conductance values by the calculated area at each time point and by the average conductance of a single alamethicin pore, represented by Gu which is found from the literature to be about 5 nS per pore.26
Further, we numerically differentiate this data by dividing the change between points by the timestep (0.1 ms). To minimize the effect of noise, we applied a moving average filter with a window of 50 time steps (5 ms) before numerically differentiating. Pore density and its time derivative are the two states of the system to which we fit the model.
We used a single nonlinear least squares fitting routine for each data set generated by the memristor at the respective investigation voltage. In the case of the logistic model, two parameters (α and Nss) were fit, and in the case of the RDE model, three parameters (β, Nss, and Z) were fit. These parameters were then fit to voltage functions. The parameters α and β were fit to exponential voltage functions, and the parameter Nss was fit to a logistic voltage function of the form:
 | (12) |
4. Conclusions
Accurate modeling of the dynamical systems utilized in a reservoir layer offers increased accuracy in implementing PRC systems. Here, we have demonstrated that careful fitting of an RDE model of ion channel memristor activation can lead to more accurate simulations of device dynamics. More accurate simulations, especially those that can be efficiently run using an exact solution, allow for hyperparameter tunings that may be infeasible to run on physical systems. The importance of exact solutions and ex situ training is exacerbated by the material of the memristors. The lipid and ion-channel composition makes them particularly well-suited to use in biological settings and in biological timescales, where lengthy training and tuning processes may be undesirable. We note the RDE model used here is phenomenological, relying on the fitting routine described herein to obtain accurate parameters. However, the RDE model is generalizable enough to capture the dynamics of many sigmoidal responses, provided the fitting data is available. Further, this study focuses on capturing the initial transient of the step voltage response, as short (∼ms) voltage pulses have been the encoding method for many PRC tasks that utilize memristor reservoirs5,12 beyond the MNIST problem that we discuss in this study. This model may not be well suited to tasks that rely on prolonged high-voltage stimulation of the memristors for data encoding, as other long-term effects may begin to dominate. While we applied the RDE model here due to the biological nature of our devices, we suspect that RDE models may also apply to other memristor types and would be particularly useful in scenarios where the initial rise of memristor conductance is of interest.Author contributions
Nicholas Armendarez modeled the ion-channel-based memristor, performed experiments, analyzed data, fit parameters for the model, and ran all simulations required to complete the reservoir computing tasks, with input from Md Sakib Hasan and Joseph Najem. Nicholas Armendarez also prepared all figures and ESI.† All authors contributed to writing the paper and conceiving the concept. Md Sakib Hasan provided the software frameworks for ex situ training, and both Md Sakib Hasan and Joseph Najem managed, supervised, and funded the project. All authors discussed the results and commented on the manuscript at all stages.Data availability
The data supporting this article have been included in the ESI† document.The data to train and test the network in this study, MNIST handwritten digits, are available at https://yann.lecun.com/exdb/mnist/.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support was provided by the National Science Foundation Grants NSF CCF-2403560 and NSF CCF-2403559.References
- J. Misra and I. Saha, Neurocomputing, 2010, 74, 239–255 CrossRef.
- A. Henderson, C. Yakopcic, S. Harbour, T. Taha, C. Merkel and H. Hazan, Proceedings of the 17th ACM International Symposium on Nanoscale Architectures, 2022, pp. 1–6.
- R. Hasan, C. Yakopcic and T. M. Taha, Analog Integr. Circuits Signal Process., 2019, 99, 1–10 CrossRef.
- L. Appeltant, M. C. Soriano, G. Van der Sande, J. Danckaert, S. Massar, J. Dambre, B. Schrauwen, C. R. Mirasso and I. Fischer, Nat. Commun., 2011, 2, 468 CrossRef CAS PubMed.
- C. Du, F. Cai, M. A. Zidan, W. Ma, S. H. Lee and W. D. Lu, Nat. Commun., 2017, 8, 2204 CrossRef.
- J. Moon, W. Ma, J. H. Shin, F. Cai, C. Du, S. H. Lee and W. D. Lu, Nat. Electron., 2019, 2, 480–487 CrossRef.
- R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084 CrossRef.
- G. Tanaka, T. Yamane, J. B. Héroux, R. Nakane, N. Kanazawa, S. Takeda, H. Numata, D. Nakano and A. Hirose, Neural Networks, 2019, 115, 100–123 Search PubMed.
- T. Taniguchi, A. Ogihara, Y. Utsumi and S. Tsunegi, Sci. Rep., 2022, 12, 10627 CAS.
- J. Cao, X. Zhang, H. Cheng, J. Qiu, X. Liu, M. Wang and Q. Liu, Nanoscale, 2022, 14, 289–298 CAS.
- J. J. Maraj, K. P. Haughn, D. J. Inman and S. A. Sarles, Adv. Intell. Syst., 2023, 2300049 Search PubMed.
- N. X. Armendarez, A. S. Mohamed, A. Dhungel, M. R. Hossain, M. S. Hasan and J. S. Najem, ACS Appl. Mater. Interfaces, 2024, 16(5), 6176–6188 CAS.
- A. S. Mohamed, A. Dhungel, M. S. Hasan and J. S. Najem, ACS Appl. Eng. Mater., 2024, 2(8), 2118–2130 CAS.
- H. Jaeger , Bonn, Germany: German National Research Center for Information Technology GMD Technical Report, 2001, 148, 13.
- W. Maass, T. Natschläger and H. Markram, Neural Comput., 2002, 14, 2531–2560 Search PubMed.
- H. Jaeger, Adv. Neural Inf. Process. Syst., 2002, 15, 609–616 Search PubMed.
- H. Jaeger and H. Haas, science, 2004, 304, 78–80 CrossRef CAS PubMed.
- X. Liang, J. Tang, Y. Zhong, B. Gao, H. Qian and H. Wu, Nat. Electron., 2024, 1–14 Search PubMed.
- N. Ghenzi, T. W. Park, S. S. Kim, H. J. Kim, Y. H. Jang, K. S. Woo and C. S. Hwang, Nanoscale Horiz., 2024, 9, 427–437 Search PubMed.
- L. Chua, IEEE Trans. Circuit Theory, 1971, 18, 507–519 Search PubMed.
- X. Zhu, Q. Wang and W. D. Lu, Nat. Commun., 2020, 11, 2439 CAS.
- R. A. John, Y. Demirağ, Y. Shynkarenko, Y. Berezovska, N. Ohannessian, M. Payvand, P. Zeng, M. I. Bodnarchuk, F. Krumeich and G. Kara, et al. , Nat. Commun., 2022, 13, 2074 CAS.
- J. S. Najem, G. J. Taylor, R. J. Weiss, M. S. Hasan, G. Rose, C. D. Schuman, A. Belianinov, C. P. Collier and S. A. Sarles, ACS Nano, 2018, 12, 4702–4711 Search PubMed.
- P. Robin, T. Emmerich, A. Ismail, A. Niguès, Y. You, G.-H. Nam, A. Keerthi, A. Siria, A. Geim and B. Radha, et al. , Science, 2023, 379, 161–167 CrossRef CAS PubMed.
- J. J. Maraj, J. S. Najem, J. D. Ringley, R. J. Weiss, G. S. Rose and S. A. Sarles, ACS Appl. Electron. Mater., 2021, 3, 4448–4458 CAS.
- M. Eisenberg, J. E. Hall and C. Mead, J. Membr. Biol., 1973, 14, 143–176 CrossRef CAS PubMed.
- I. Vodyanoy, J. Hall and T. Balasubramanian, Biophys. J., 1983, 42, 71–82 CrossRef CAS.
- K. Yang, J. Joshua Yang, R. Huang and Y. Yang, Small Sci., 2022, 2, 2100049 CrossRef CAS.
- F. J. Richards, J. Exp. Bot., 1959, 10, 290–301 CrossRef.
- M. J. Simpson, A. P. Browning, D. J. Warne, O. J. Maclaren and R. E. Baker, J. Theor. Biol., 2022, 535, 110998 CrossRef.
- G. Boheim and H.-A. Kolb, J. Membr. Biol., 1978, 38, 99–150 CrossRef CAS.
- T. Okazaki, M. Sakoh, Y. Nagaoka and K. Asami, Biophys. J., 2003, 85, 267–273 CrossRef CAS.
- J. S. Najem, G. J. Taylor, N. Armendarez, R. J. Weiss, M. S. Hasan, G. S. Rose, C. D. Schuman, A. Belianinov, S. A. Sarles and C. P. Collier, J. Visualized Exp., 2019, e58998 CAS.
- D. Kwon, S. Woo and J. Lee, Journal of Semiconductor Technology and Science, 2022, 22, 115–131 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03439b |
| This journal is © The Royal Society of Chemistry 2025 |