Unveiling magnetic transition-driven lattice thermal conductivity switching in monolayer VS₂

Abstract

Effective thermal management is essential for maintaining the operational stability and data security of magnetic devices across diverse fields, including thermoelectric, sensing, data storage, and spintronics. In this study, density functional theory calculations were conducted to explore the spin-induced modifications in the phonon-mediated thermal properties of H-phase monolayer VS₂, a two-dimensional (2D) ferromagnet. Our investigation revealed that the 2D H-phase of VS₂ exhibits a substantial thermal switching ratio, exceeding four at the Curie temperature, due to the coupling between magnetic order and lattice vibrations. This sensitivity arises from spin-dependent lattice anharmonicity, which results in the stiffening of the V–S bonds, thereby modifying the frequencies of different vibrational modes. Phonon–phonon interaction calculations indicated that phonon–magnon scattering was more predominant in the paramagnetic (PM) phase than in the ferromagnetic (FM) phase, which resulted in a reduced phonon lifetime, mean free path and group velocity. As a result, the lattice thermal conductivity was calculated to drop from 53.98 W m⁻¹ K⁻¹ in the ferromagnetic phase to 12.10 W m⁻¹ K⁻¹ in the paramagnetic phase. By elucidating heat transport in two-dimensional ferromagnets, our study offers valuable insights for manipulating and converting thermal energy.

---

Introduction

The discovery of magnetism in two-dimensional (2D) van der Waals materials offers new possibilities for studying magnetic phenomena at the atomic scale.¹ The presence of magnetic anisotropy in these materials can influence their magnetic ordering and potentially enhance the stability of magnetic phases to thermal fluctuations.² This breakthrough challenges the predictions of the Mermin–Wagner theorem,³ paving the way for advanced magnetic and spintronic applications. Furthermore, magnetism could be tuned by the application of electric fields, improving device efficiency,^4–6 and thereby enhancing the performance stability of nanodevices.⁷

In recent years, 2D transition metal dichalcogenides (TMDCs) have gained significant attention due to their distinctive structural, electrical, magnetic, and mechanical properties.⁸ These materials, composed of covalently bonded transition metals and chalcogenide atoms, have the potential to be exfoliated from their bulk counterparts. 2D TMDCs may exist in various phases (H, T, and T_d), depending on the coordination of metal atoms, each exhibiting distinct electronic structures.⁹ Monolayer VS₂, a prominent ferromagnet from the 2D TMDC family, was recently synthesized.^10,11 Furthermore, H-phase VS₂ was found to be a direct bandgap semiconductor (1.1 eV bandgap¹²). 2D VS₂ is technologically important as it could potentially be used in several applications, such as in lithium-ion batteries as the anode material,¹³ in field-effect transistors,¹⁴ and in spintronics.¹⁵ Additionally, the magnetic moments in 2D VS₂ could also be further tuned with the application of mechanical strain.¹⁶

In semiconductors and insulators, heat transport is predominantly governed by atomic vibrations, and materials with high thermal conductivity are efficient at quickly dissipating heat. Conversely, for thermoelectric devices where maintaining a temperature difference is essential for generating electrical potential, materials with lower lattice thermal conductivity (κ_lat) are desired as they dissipate less heat.¹⁷ In recent years, various methods, such as doping, structural phase transitions,^18,19 electrochemical ion insertion and extraction,²⁰ mechanical deformation,²¹ and redistribution of charge density²² were explored to attain a low κ_lat and a high coefficient of thermoelectric power factor.²³ Conversely, in the realm of electronic cooling for hot-spot thermal management, both active and passive cooling methods were combined, necessitating high power factor and κ_lat.²⁴ Hence, actively and reversibly regulating κ_lat is an innovative pathway for proficient heat management and energy conversion in nanodevices. For example, controlling electron–phonon coupling by factors such as electric fields,²⁵ heat,²⁶ and the application of mechanical strain^27,28 could be used to tune κ_lat in nanomaterials. Also, magnons, the quanta of spin waves in magnetic materials, may couple with phonons, affecting phonon transport and κ_lat.^29,30

This study aims to explore the effect of magnetic phase transition on κ_lat in 2D H-phase VS₂. Recent advancements suggest that 2D ferromagnets may offer a high thermal switching ratio across the Curie temperature (T_c),^31,32 where the thermal switching ratio is the ratio between the κ_lat of the ferromagnetic (FM) and paramagnetic (PM) phase at T_c. However, most 2D ferromagnets are known to have T_c at very high or small temperatures, thereby limiting their room temperature applications. In this context, previous experiments and theoretical calculations suggest that 2D VS₂ undergoes a magnetic phase transition close to room temperature.^12,33,34 Hence, 2D VS₂ may offer exciting prospects for achieving a high thermal switching ratio for device-level applications close to room temperature. Spin–lattice-dependent anharmonicity was explored by examining the stiffness of the V–S bonds, which alters the frequencies of various vibrational modes. Furthermore, phonon–magnon scattering strength was calculated for both the PM and FM phases to interpret phonon mean free paths and phonon lifetimes. In summary, this study examines the potential for achieving a high switching ratio in κ_lat by exploring anharmonicity originating from spin–lattice interactions resulting from the FM to PM transition in monolayer H-VS₂.

Methodology

Density functional theory-based calculations are performed using the Quantum ESPRESSO³⁵ package. The kinetic energy expansions were truncated at 80 Ry, with a charge density cutoff of 640 Ry. The Perdew–Burke–Ernzerhof (PBE)³⁶ exchange–correlation functional, a generalized gradient approximation (GGA),³⁷ was employed alongside the projected augmented wave (PAW)^38,39 pseudopotential method for core and valence electron wave function smoothing. The Vanadium atom's 3s² 3p⁶ 4S² 3d³, while the Sulphur atom's 3s² 3p⁴ valence states were considered. The simulation cell included a 17 Å vacuum to avoid spurious inter-layer interaction effects in periodic models. In addition, we utilized the DFT-D3 method⁴⁰ to account for van der Waals interactions. Furthermore, in the post-geometric optimization of lattice parameters, self-consistent field calculation employed a 13 × 13 × 1 Monkhorst–Pack k-point grid. The Brillouin zone (BZ) was integrated using the tetrahedron method with Blöchl corrections.⁴¹ Herein, the paramagnetic phase of the H phase of VS₂, where individual electron spins are randomly oriented, is approximated as the nonmagnetic state, assuming weak magnetic interactions between the spins. Such approximations were previously used in other 2D TMDCs and 2D materials in general.⁴²

Phonon dispersions were computed using the finite displacement method in a supercell approach implemented in the phonopy package.⁴³ Herein, the displacement amplitude was set as 0.015 Å, and the forces on other atoms in the supercell were calculated under the second-order harmonic approximation. The interatomic force constants (IFCs) are determined using a 3 × 3 × 1 supercell and k mesh of 7 × 7 × 1 with a strict energy convergence criterion of 10⁻⁸ eV in both the FM and PM phases. To examine lattice thermal transport, the phonon-based Boltzmann transport equation (BTE) was solved under the constant relaxation time approximation (CRTA) using the phono3py software.^44,45 This involved calculating both second and third-order IFCs in a 4 × 4 × 1 supercell with 5 × 5 × 1 k-mesh for the FM and PM phase, respectively. A dense 151 × 151 × 1 q-mesh was used for accurate assessments of κ_lat at various temperatures. Furthermore, we employed isotope scattering⁴⁶ without non-analytical term corrections (NAC) in our calculation of κ_lat. As shown in Fig. S4 in the ESI,† the Born effective charges and dielectric constants had minimal impact on the κ_lat value with isotope scattering, even after incorporating NAC into the dynamical matrix.

To examine the stability of the undeformed and the strained (5% uniaxial strain) structures at elevated temperatures, ab initio molecular dynamics (AIMD) simulations^47,48 were conducted using the Born-Oppenheimer Molecular Dynamics (BOMD) approach.^49,50 A supercell containing 36 atoms was constructed to adequately represent the system's properties, and the Brillouin zone was sampled at the Γ point. The equations of motion were integrated using the Verlet algorithm with a time step of 1.25 fs, which was found to be sufficient to capture the high-frequency modes accurately. The FM phase of VS₂ was initially equilibrated at a temperature of 292 K (due to Curie temperature), while the PM phase was equilibrated at 500 K, both using an Anderson thermostat for 10 ps under a canonical ensemble.

Results and discussion

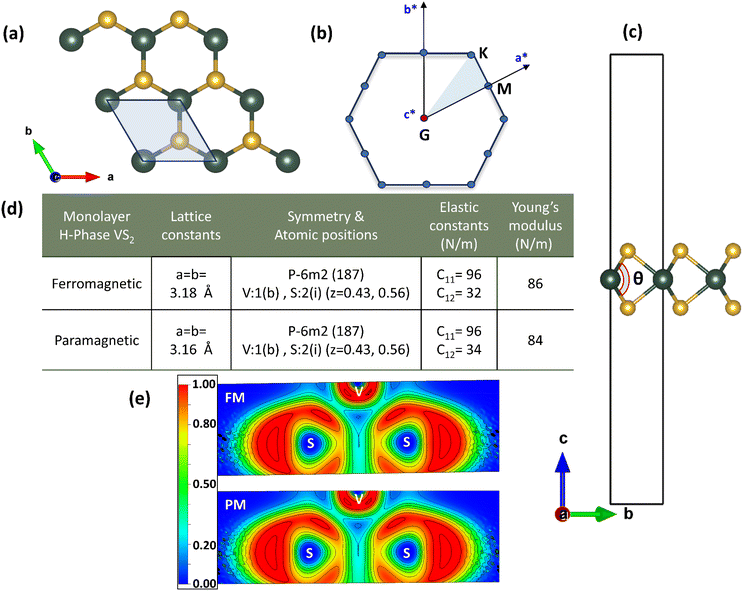
This study focuses on the H-phase VS₂, which, according to previous reports, demonstrates energetic favourability compared to the T-phase when in the monolayer form.⁵¹ The transition metal V atom is centrally located within this structure, surrounded by six chalcogen atoms positioned at the corners of a triangular prism. As shown in Fig. 1(a), the H-phase exhibits mirror symmetry concerning the plane of the metal atom, akin to the D_3h point group and P6̄m2 space group. The impact of FM ordering on VS₂ initially manifests in the structural and energetic properties investigated through the relaxation of structures with and without spin polarization. Furthermore, the lattice constants with geometrically optimized atomic positions are shown in Fig. 1(d) for the FM and PM phases, respectively. It was found that the total energy in the FM phase is lower by 15.3 meV per atom than in the PM phase, suggesting a preference for FM ordering in H-phase VS₂ at the ground state, an observation consistent with experimental findings¹¹ and prior theoretical assessments.^11,33 To analyze the bonding characteristics following the magnetic phase transition, we examined the electron localization function (ELF). The ELF value of 0.24 between vanadium and sulfur was observed in both the FM and PM states of VS₂, as shown in Fig. 1(e). This value indicates that the electron distribution between V and S atoms is not entirely localized. Therefore, the V–S bonds in VS₂ are not purely covalent nor are they purely metallic in nature.^52,53 This observation could be attributed due to the electronegativity difference between V (1.63) and S (2.58), respectively.

Fig. 1 The shaded area within the supercell in (a) represents the unit cell of H-phase VS₂, where the blue and yellow atoms represent vanadium and sulfur, respectively. The first Brillouin zone corresponding to this unit cell is illustrated in (b), * represents reciprocal lattice vectors. A side view of the unit cell, with a thickness of 23.5 angstroms to prevent interlayer interaction, is displayed in (c). In (d), lattice constants and Wyckoff positions are shown in the 2^nd and 3^rd columns, along with the elastic constants and Young's modulus of FM and PM H-phase VS₂. (e) represents the electron localization function (ELF) for the FM and PM states of VS₂.

While strain engineering and doping are established methods for modulating phonon dispersion,⁵⁴ calculations reported here revealed that FM ordering could be another effective, non-invasive approach to controlling the phonon dispersion in 2D magnets. It was found that the magnetic phase change leads to bond length, lattice constant, and bond angle changes, which affect the phonon modes. Particularly, in the FM phase compared to the PM phase, the out-of-plane bond angle (shown in Fig. 1c) between S–V–S decreased to 78° from 78.15°, while the lattice constants increased from 3.16 Å to 3.18 Å. These alterations served as the primary drivers for change in the phonon dispersion behavior and, consequently, the κ_lat. The effect of magnetic ordering on lattice vibrations of H-phase VS₂ is shown in Fig. 2. Additionally, for comparison, the phonon dispersion calculated by density functional perturbation theory is given in ESI in Fig. S1 and Table S1.† In the FM phase, the phonon dispersion exhibited no gap between the acoustic and optical modes, indicating stronger coupling between these vibrational modes. Conversely, a clear gap between the acoustic and optical modes in the PM phase suggested weaker coupling in this state. Furthermore, the phonon partial density of states (PDOS) analysis for both phases showed that the lower-frequency modes, which generally contribute to thermal transport, were mainly due to V atoms. These lower-frequency phonon modes, dominant contributors to κ_lat, highlighted the significant role of V in heat transport compared to S atoms. Notably, the coupling between acoustic and lower-order optical phonons in the FM phase indicates increased scattering than in the PM phase, suggesting increased uninterrupted heat transfer in the PM phase. However, the κ_lat was actually lower in the PM phase (shown in Fig. 3(a)). This discrepancy was likely due to other factors, such as anharmonicity, phonon scattering, and phonon lifetime, which will be discussed next.

Fig. 2 Phonon dispersion and phonon partial density of states (PDOS) for monolayer H-VS₂ for (a) ferromagnetic and (b) paramagnetic configurations.

Fig. 3 (a) Shows the variation of κ_lat with temperature for both the FM phase (up to the Curie temperature) and the PM phase (above the Curie temperature). In Fig. 3(b), the cumulative κ_lat as a function of frequency is depicted for both phases. The lines in blue and red (parallel to the y-axis) illustrate the highest frequency of acoustic modes, which contribute significantly to κ_lat in both the FM and PM phases.

Notably, the PM phase was represented as nonmagnetic for two main reasons. First, simulating a large supercell with random spin orientation is computationally expensive. This type of disordered calculation requires significant resources. Second, the transition to the PM phase increases spin fluctuations due to the random orientation of spins in the PM state. This leads to strong scattering between phonons and spins, resulting in κ_lat.^55–57 Consequently, this effect further lowers the κ_lat, and enhances the switching ratio. Therefore, the reported switching ratio of κ_lat, assuming the nonmagnetic system, represents an upper bound. Several other studies have reported assuming the PM state as nonmagnetic, as considered in the previous literature.^30,58–61

The T_c for any ferromagnetic materials can be estimated using a mean mean-field expression given by, , where k_B is the Boltzmann constant, N is the number of magnetic atoms in the unit cell, and D is the energy difference between the parallel and antiparallel spin alignments. This study used a similar approach and calculated the T_c for monolayer H-phase VS₂ to be 262 K using ultra-soft pseudopotentials. However, when projector augmented-wave (PAW) pseudopotentials were applied, the T_c was found to be 369 K.¹² Therefore, for more rigorous analysis, this study employed a T_c value from Monte Carlo simulations by Fuh et al.,¹² which estimated the T_c to be 292 K. First-principles calculations based on the linearized BTE were used to compute κ_lat of both the FM and PM phases of H-phase VS₂. Given that the FM phase of H-VS₂ is semiconductor in nature,¹² phonons would dominate heat transport. Temperature-dependent values of κ_lat in both FM and PM H-VS₂ are depicted in Fig. 3(a) across T_c (292 K). It can be seen that κ_lat decreased from 53.98 W m⁻¹ K⁻¹ to 12.10 W m⁻¹ K⁻¹ at T_c. Notably, the κ_lat value was optimized with different q-mesh densities and mean free path distances to ensure accuracy, as shown in ESI Fig. S12–14.† Furthermore, it was also observed that in the FM phase, the coupling of acoustic and low-order optical modes to the κ_lat (with the highest frequency being 8.12 THz) accounted for around 95% of the contribution. In contrast, in the PM phase (with the highest frequency being 7.25 THz), the contribution was about 87%. This behavior is depicted in Fig. 3(b), where lines parallel to the y-axis represent the highest frequency of the acoustic modes.

Heat propagation in crystals is generally treated as particle-like, as described by Peierls’ formulation of the BTE. In contrast, the Allen–Feldman equation assumes wavelike tunneling in disordered glass structures.^62,63 In a recent study, these two conduction mechanisms are unified in the Wigner transport equation,^64,65 an extension of the Peierls–Boltzmann and Allen–Feldman formulations for complex crystals, where both wavelike and particle-like propagation of heat carriers coexist. It yields total thermal conductivity (K^αβ_T) in directions α and β, where (K^αβ_T = K^αβ_P + K^αβ_C), and K^αβ_P and K^αβ_C accounts for particle-like and wave-like diffusion of heat in the material, respectively. In this formulation, K^αβ_P is calculated by solving the linearized BTE equation under CRTA. Utilizing the Wigner transport equation, the calculated value showed a nearly negligible contribution in total κ_lat from wave-like propagation mechanism for both the FM and PM phases, as depicted in ESI Fig. S15 and S16,† respectively. This indicates that particle-like phonon wave packets mainly dominate heat transportation in both phases.

The elastic constants were calculated for the FM and PM states to understand the variation in the frequencies of the vibrational modes, which depend on bond stiffness. Upto 5% uniaxial tensile strains were applied along the armchair direction. Thereafter, the second-order elastic constants were calculated from the slope of the stress–strain curve (column 4^th in Fig. 1d). The stress–strain response for FM and PM are shown in ESI Fig. S2 and S3,† respectively. The resulting values (C₁₁, C₁₂) and Young's modulus suggested a slightly stiffer FM state compared to the PM state, which directly translates into a higher κ_lat. Furthermore, in BOMD simulations, the stability of the structure at higher temperatures was assessed. The time history of temperature and total energy showed that both the undeformed and deformed configurations (with 5% strain in the armchair and zigzag directions) of the FM and PM phases remained stable at 292 K and 500 K, respectively, as illustrated in Fig. S6–11 of the ESI.†

Additionally, IFCs are crucial because phonon dispersions are determined by the eigenvalues of the diagonalized dynamical matrix, which is an IFC matrix normalized by atomic masses.⁶⁶ The harmonic IFCs between the FM and PM states exhibited significant differences. Fig. 4(a) and (b) showed the IFCs for the FM and PM phases, respectively, where the FM phase showed a higher value of IFCs than the PM phase. Higher IFCs mean stiffer bonds, leading to a higher κ_lat in the FM phase compared to the PM phase, aligned with the observed behavior of elastic constants.

Fig. 4 The IFCs for FM (a) and PM (b) are illustrated, with red, blue, and green bars representing the force constants in the x, y, and z directions, respectively. The FM configuration exhibited generally higher values compared to the PM configuration.

To comprehend the dependency of phonon frequencies on atomic types and the stability of lattice distortions in relation to the electronic structure of the system,⁶⁷ we calculated cophonicity. When two atoms, let's call them A and B, interact, their vibrations can overlap in a certain range of frequencies. Cophonicity is a measure of how much overlap there is between the individual contributions of atoms A and B to this specific range of vibrational frequencies. In general terms, the cophonocity of species ‘A’ is given by,⁶⁸

where g(ω) represents the total phonon density of states. The center of mass (CM) of the atom-projected phonon, the density of states for A is given by,

The cophonicity of an A–B atomic pair measures the relative position of their centers of mass:⁶⁹

C_ph(A–B) = CM^A − CM^B. (3)

A positive C_ph(A–B) indicates that atom A contributes more to high-frequency modes, while a negative value indicates a higher contribution by atom B.²⁹ Our study found that V atoms’ phonicity in the FM phase was 8.19 and 6.94 in the PM phase. For the S atom, phonicity was 7.84 in the FM phase and 7.85 in the PM phase. These results indicated that V's contribution to phonon states was higher in the FM phase, whereas S's contribution was slightly higher in the PM phase. The transition from the FM to the PM phase led to a significant decrease in V's contribution, which, coupled with a slight increase in S's contribution, resulted in a drop in κ_lat at T_c. Moreover, the increased value of cophonicity indicated a greater mixing of atoms’ phononic states, which resulted in a higher κ_lat.⁷⁰ The cophonicity measurements for V–S pairs were 0.35 in the FM phase and −0.90 in the PM phase, suggesting a higher degree of overlap in the FM phase, thereby leading to an elevated κ_lat.

Kinetic theory suggests κ_lat is dependent on specific heat at constant volume (c_v), the group velocity of a phonon (ν), and relaxation time of phonon (τ) at wave-vector , given by,⁷¹

where κ_αβ is the summation of all the phonon modes and α,β shows arbitrary directions. To analyze the anomalous behavior of κ_lat in the FM phase, this study involved all these mechanisms. In crystals, c_v generally rises with temperature because the excitation of vibrational modes, or phonons, increases in the lattice. In the case of H-VS₂, as the temperature increased and reached T_c, a magnetic phase transition occurred, shifting from the FM state to the PM phase. Consequently, the heat capacity c_v exhibited a slightly high value in the PM phase. Despite higher specific heat (Fig. 5(a)) indicating a greater capacity to store thermal energy in the PM phase, the FM phase surprisingly exhibits a higher κ_lat. This seemingly contradictory behavior stems from the distinct ways heat travels in each phase. As shown in Fig. 5(b), the frequency-dependent Grüneisen parameter (γ) is reported, which quantifies the impact of volume change on vibrational frequencies, given by:⁷², where ‘a’ represents the lattice constant, λ phonon mode at q point. The values of γ revealed a greater spread in the PM configuration, suggesting a higher degree of anharmonicity. This increased anharmonicity likely contributes to the observed value of a lower κ_lat in the PM phase by enhancing phonon scattering and hindering heat transport. Although the γ highlighted the switch in κ_lat from FM to PM due to increased anharmonicity in the PM structure, additional factors like mean free path (MFP) and phonon lifetime also played significant roles. The MFP is the average distance a phonon travels before scattering, while the phonon lifetime is the duration a phonon exists before scattering. As shown in Fig. 6, both MFP and the lifetime of phonons, calculated as a function of temperatures, followed a similar trend to that of κ_lat, exhibiting a sharp drop at the T_c.

Fig. 5 (a) The variation of specific heat with temperature and (b) the plot of Grüneisen parameter versus frequency, where the red color represents the PM phase, and the blue color represents the FM phase of VS₂.

Fig. 6 The mean free path (a) and phonon lifetime (b) variation with temperature, including the FM to PM transition at the Curie temperature.

Longer phonon lifetimes and higher group velocities enable phonons to travel farther and faster, boosting heat flow and resulting in higher κ_lat. Detailed analysis of phonon lifetimes as a function of frequency (Fig. 7(a)) consistently showed higher values in the FM phase, indicating more efficient heat transport. Additionally, the group velocity was higher in the FM phase, particularly for lower-order phonons (up to 8.12 THz), as depicted in Fig. 7(b). This increased phonon lifetime and group velocity in the FM phase, especially for lower-order phonons in monolayer H-VS₂, further enhances heat transport efficiency. Consequently, the combined influence of spin waves and superior phonon characteristics in the FM phase outweighs the PM phase's advantage in specific heat, leading to the observed higher κ_lat in the FM state.

Fig. 7 The lifetime (a) and group velocity (b) variation with frequency for both FM and PM phases of H-phase VS₂.

Unlike nonmagnetic semiconductors, where phonons primarily facilitate heat transport, magnons introduce an additional mechanism in FM semiconductors. While magnons do not directly transport heat, they impact κ_lat through phonon–magnon scattering, involving the emission and absorption of phonons.⁷³ The complexities in the PM phase, such as randomly oriented magnetic moments and spin fluctuations, significantly influence phonon–magnon interactions, causing substantial changes in κ_lat. In this context, the phonon–phonon interaction strength (P_λ) is given by,⁷⁴

where n_a represents the number of atoms in the primitive unit cell and ϕ_{−λλ′λ′′} represents the interaction strength of three phonons (λ′, λ′′, and λ′′′) which involves scattering. The value of P_λ for FM and PM states was calculated (as shown in Fig. 8), indicating that phonon–magnon scattering was predominant in PM states. This predominance caused higher scattering, reduced phonon lifetime, and consequently, lower κ_lat. Conversely, the ferromagnetic ordering in the FM phase allowed enhanced phonon transport by reduced phonon–magnon scattering, resulting in a higher κ_lat. This observation is in agreement with other 2D van der Waals ferromagnets like FeCl₃, RuCl₃, RuBr₃, and RuI₃.⁷⁵

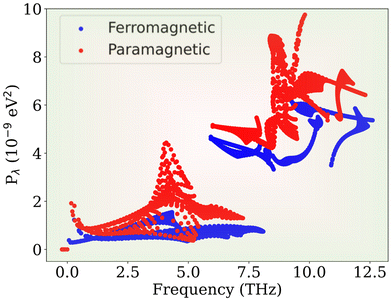Fig. 8 The phonon–phonon interaction strength in FM (blue) and PM (red) states varies with frequency, as illustrated.

Monolayer H-phase VS₂ demonstrated a substantial switching ratio, as illustrated in Fig. 9, comparing temperature-dependent switching ratio values with other nanostructured materials. Previous literature has predicted very high switching ratios, such as 12 for 2D VSe₂ ⁴² and 10² for 2D CrI₃.^29,30 However, these materials have Curie temperatures at very high or very low levels, which somewhat limits the application of the thermal switching effect. For example, the Curie temperatures for 2D VSe₂ and 2D CrI₃ are approximately 420 K and 45 K, respectively. On the other hand, to the best of our knowledge, near room temperature, thermal switching ratios greater than one have been reported for Cu/Co₅₀Fe₅₀ ⁷⁶ multilayer films and bulk FeRh.¹⁸ For instance, the Cu/Co₅₀Fe₅₀ multilayer, which has a Curie temperature of 300 K, was measured to have a switching ratio 2.5. Similarly, bulk FeRh, with a Curie temperature of 340 K, was reported to have a switching ratio of 1.4. In this context, our calculations indicate a large switching ratio of 4.45 at 292 K, the highest reported so far.

Fig. 9 Lattice thermal conductivity and thermal switching ratio at the Curie temperature for various magnetic nanomaterials such as Hydo-graphene,⁵⁸ MnPS₃,⁵⁹ CrI₃,^29,30 RuCl₃, RuBr₃, RuI₃,⁶⁰ VSe₂.⁴² Filled rectangles indicate the range of κ_lat for FM and PM orders. The hollow square shows the switching ratio of κ_lat due to the magnetic phase transition. However, the star revealed the switching ratio of VS₂ (current work).

Conclusions

The thermal switching behavior in monolayer H-phase VS₂, transitioning from the FM to the PM phase, revealed a significant decrease in κ_lat at T_c. Despite the gap in phonon dispersion between the higher and lower order modes in the PM phase, the stiffer FM phase demonstrated higher κ_lat compared to the PM phase. This discrepancy is primarily due to the detailed phonon transport properties, which contribute to the lower κ_lat in the PM phase. The frequency-dependent γ indicated higher anharmonicity in the PM phase, leading to increased phonon scattering and reduced κ_lat. Additionally, the group velocity and phonon lifetimes were higher in the FM phase, further enhancing κ_lat. Furthermore, cophonicity calculations show that vanadium's contribution to phonon states decreases significantly in the PM phase while sulfur's contribution largely remains unchanged. This shift results in reduced κ_lat in the PM phase due to less efficient phonon transport. These findings underscore the complex interplay between phonon dispersion, anharmonicity, and atomic contributions in determining the thermal properties of monolayer H-phase VS₂. In this study, we treated the PM state as nonmagnetic. However, it is possible to accurately simulate the PM state by using a large supercell with randomly distributed local spin moments.⁷⁷ In our case, the supercell required for calculating anharmonic force constants was unrealistically large, so we assumed it to be nonmagnetic. In this context, a recent development is the development of machine learning-based interatomic potentials for studying thermal transport in 2D and 3D materials using classical molecular dynamics.^78,79 While ab initio molecular dynamics simulations, such as those reported here, can provide lattice thermal conductivity predictions at finite temperatures, such calculations are prohibitively costly.^80,81 Machine learning potentials developed using ab initio data can provide a very accurate estimate of thermal properties at a much cheaper cost, however, the development of such potentials for magnetic systems remain challenging.⁸²

Author contributions

Zimmi Singh contributed to the conceptualization, methodology, validation, investigation, visualization, and preparation of the original draft. Abhishek Kumar also contributed to the conceptualization, methodology, validation, investigation, visualization, and drafting of the original manuscript. Sankha Mukherjee was responsible for conceptualization, project management, securing funding, overseeing the work, and reviewing and editing the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Note added after first publication

The volume-dependant output of the Phono3py package have been scaled by the ratio of the simulation cells thickness to the monolayers thickness. As a consequence, the lattice thermal conductivity (Klat) values have been rescaled by a factor of 4.05. Discussion with experts in the field has concluded that the rescaling of values contained within this article does not affect the studies primary scientific conclusions, consequently the findings discussed in this article are maintained.

Acknowledgements

S. M. acknowledges financial support from the SERB SRG project (SRG/2021/002170) and the ISIRD scheme at IIT Kharagpur. The DFT calculations were carried out using resources from the “PARAM Shakti Facility” under the National Supercomputing Mission, Government of India, at IIT Kharagpur. Z. S. is grateful for the research funding provided by the Government of India through the “Prime Minister's Research Fellow” scheme.

References

1. C. Gong, L. Li, Z. Li, H. Ji, A. Stern and Y. Xia, et al., Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature, 2017, 546(7657), 265–269.
2. S. Jenkins, L. Rózsa, U. Atxitia, R. F. L. Evans, K. S. Novoselov and E. J. G. Santos, Breaking through the Mermin-Wagner limit in 2D van der Waals magnets, Nat. Commun., 2022, 13(1), 6917.
3. N. D. Mermin and H. Wagner, Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models, Phys. Rev. Lett., 1966, 17(22), 1133–1136.
4. F. Hellman, A. Hoffmann, Y. Tserkovnyak, G. S. D. Beach, E. E. Fullerton and C. Leighton, et al., Interface-induced phenomena in magnetism, Rev. Mod. Phys., 2017, 89(2), 025006.
5. K. F. Mak, J. Shan and D. C. Ralph, Probing and controlling magnetic states in 2D layered magnetic materials, Nat. Rev. Phys., 2019, 1(11), 646–661.
6. X. Lin, W. Yang, K. L. Wang and W. Zhao, Two-dimensional spintronics for low-power electronics, Nat. Electron., 2019, 2(7), 274–283.
7. H. Song, J. Liu, B. Liu, J. Wu, H. M. Cheng and F. Kang, Two-Dimensional Materials for Thermal Management Applications, Joule, 2018, 2(3), 442–463.
8. J. Zhou, J. Lin, X. Huang, Y. Zhou, Y. Chen and J. Xia, et al., A library of atomically thin metal chalcogenides, Nature, 2018, 556(7701), 355–359.
9. C. Zhang, C. Gong, Y. Nie, K. A. Min, C. Liang and Y. J. Oh, et al., Systematic study of electronic structure and band alignment of monolayer transition metal dichalcogenides in van der Waals heterostructures, 2D Mater., 2016, 4(1), 015026.
10. J. Feng, X. Sun, C. Wu, L. Peng, C. Lin and S. Hu, et al., Metallic Few-Layered VS₂ Ultrathin Nanosheets: High Two-Dimensional Conductivity for In-Plane Supercapacitors, J. Am. Chem. Soc., 2011, 133(44), 17832–17838.
11. D. Gao, Q. Xue, X. Mao, W. Wang, Q. Xu and D. Xue, Ferromagnetism in ultrathin VS₂ nanosheets, J. Mater. Chem. C, 2013, 1(37), 5909–5916.
12. H. R. Fuh, C. R. Chang, Y. K. Wang, R. F. L. Evans, R. W. Chantrell and H. T. Jeng, Newtype single-layer magnetic semiconductor in transition-metal dichalcogenides VX₂ (X = S, Se and Te), Sci. Rep., 2016, 6(1), 32625.
13. Y. Jing, Z. Zhou, C. R. Cabrera and Z. Chen, Metallic VS2 monolayer: A promising 2D anode material for lithium ion batteries, J. Phys. Chem. C, 2013, 117(48), 25409–25413.
14. Q. Ji, C. Li, J. Wang, J. Niu, Y. Gong and Z. Zhang, et al., Metallic vanadium disulfide nanosheets as a platform material for multifunctional electrode applications, Nano Lett., 2017, 17(8), 4908–4916.
15. P. Zhao, J. Li, H. Jin, L. Yu, B. Huang and D. Ying, Designing lateral spintronic devices with giant tunnel magnetoresistance and perfect spin injection efficiency based on transition metal dichalcogenides, Phys. Chem. Chem. Phys., 2018, 20(15), 10286–10291.
16. Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, Evidence of the existence of magnetism in pristine VX₂ monolayers (X = S, Se) and their strain-induced tunable magnetic properties, ACS Nano, 2012, 6(2), 1695–1701.
17. M. S. Dresselhaus, G. Chen, M. Y. Tang, R. Yang, H. Lee and D. Wang, et al., New directions for low-dimensional thermoelectric materials, Adv. Mater., 2007, 19(8), 1043–1053.
18. C. Cazorla and R. Rurali, Dynamical tuning of the thermal conductivity via magnetophononic effects, Phys. Rev. B, 2022, 105(10), 104401.
19. R. Shrestha, Y. Luan, S. Shin, T. Zhang, X. Luo and J. S. Lundh, et al., High-contrast and reversible polymer thermal regulator by structural phase transition, Sci. Adv., 2019, 5(12), eaax3777.
20. J. Shin, J. Sung, M. Kang, X. Xie, B. Lee and K. M. Lee, et al., Light-triggered thermal conductivity switching in azobenzene polymers, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(13), 5973–5978.
21. X. Meng, T. Pandey, J. Jeong, S. Fu, J. Yang and K. Chen, et al., Thermal Conductivity Enhancement in MoS₂ under Extreme Strain, Phys. Rev. Lett., 2019, 122(15), 155901.
22. M. Kan, B. Wang, Y. H. Lee and Q. Sun, A density functional theory study of the tunable structure, magnetism and metal-insulator phase transition in VS₂ monolayers induced by in-plane biaxial strain, Nano Res., 2015, 8(4), 1348–1356.
23. A. Ojha, R. K. Sabat and S. Bathula, Advancement in half-Heusler thermoelectric materials and strategies to enhance the thermoelectric performance, Mater. Sci. Semicond. Process., 2024, 171, 107996.
24. Z. Zhang, X. Wang and Y. Yan, A review of the state-of-the-art in electronic cooling. e-Prime-Advances in Electrical Engineering, Electron. Energy, 2021, 1, 100009.
25. S. Y. Yue, R. Yang and B. Liao, Controlling thermal conductivity of two-dimensional materials via externally induced phonon-electron interaction, Phys. Rev. B, 2019, 100(11), 115408.
26. N. Medvedev, I. Milov and B. Ziaja, Structural stability and electron-phonon coupling in two-dimensional carbon allotropes at high electronic and atomic temperatures, Carbon Trends, 2021, 5, 100121.
27. L. Zhu, T. Zhang, Z. Sun, J. Li, G. Chen and S. A. Yang, Thermal conductivity of biaxial-strained MoS₂: Sensitive strain dependence and size-dependent reduction rate, Nanotechnology, 2015, 26(46), 465707.
28. A. Baski, Z. Singh and S. Mukherjee, Vacancy-mediated inelasticity in two-dimensional vanadium-based dichalcogenides, Phys. Chem. Chem. Phys., 2024, 26(5), 4668–4682.
29. K. Wang, W. X. Zhou, Y. Cheng, M. Zhang, H. Wang and G. Zhang, Magnetic order-dependent phonon properties in 2D magnet CrI₃, Nanoscale, 2021, 13(24), 10882–10890.
30. G. Qin, H. Wang, L. Zhang, Z. Qin and M. Hu, Giant effect of spin-lattice coupling on the thermal transport in two-dimensional ferromagnetic CrI₃, J. Mater. Chem. C, 2020, 8(10), 3520–3526.
31. I. Stolichnov, S. W. E. Riester, E. Mikheev, N. Setter, A. W. Rushforth and K. W. Edmonds, et al., Enhanced Curie temperature and nonvolatile switching of ferromagnetism in ultrathin (Ga,Mn) As channels, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(11), 115203.
32. A. F. Kravets, A. N. Timoshevskii, B. Z. Yanchitsky, M. A. Bergmann, J. Buhler and S. Andersson, et al., Temperature-controlled interlayer exchange coupling in strong/weak ferromagnetic multilayers: A thermomagnetic Curie switch, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(21), 214413.
33. H. J. Wu, Y. L. Wan, Z. Y. Zeng, C. E. Hu, X. R. Chen and H. Y. Geng, Ferromagnetic vanadium disulfide VS₂ monolayers with high Curie temperature and high spin polarization, Phys. Chem. Chem. Phys., 2023, 25(14), 10143–10154.
34. Y. Guo, H. Deng, X. Sun, X. Li, J. Zhao and J. Wu, et al., Modulation of Metal and Insulator States in 2D Ferromagnetic VS₂ by van der Waals Interaction Engineering, Adv. Mater., 2017, 29(29), 1–7.
35. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car and C. Cavazzoni, et al., QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
37. J. P. Perdew and Y. Wang, Erratum: Accurate and simple analytic representation of the electron-gas correlation energy [Phys. Rev. B 45, 13244 (1992)], Phys. Rev. B, 2018, 98(7), 079904.
38. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Pseudopotentials for high-throughput DFT calculations, Comput. Mater. Sci., 2014, 81, 446–452.
39. B. X. Shi, R. J. Nicholls and J. R. Yates, Accurate and efficient structure factors in ultrasoft pseudopotential and projector augmented wave DFT, Phys. Rev. B, 2023, 108(11), 115112.
40. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104.
41. P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B, 1994, 49(23), 16223.
42. C. Wu, Y. Zhao, G. Zhang and C. Liu, Giant thermal switching in ferromagnetic VSe₂ with programmable switching temperature, Nanoscale Horiz., 2022, 8(2), 202–210.
43. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5.
44. A. Togo, First-principles Phonon Calculations with Phonopy and Phono3py, J. Phys. Soc. Jpn., 2023, 92(1), 012001.
45. A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys.: Condens. Matter, 2023, 35(35), 353001.
46. S. I. Tamura, Isotope scattering of dispersive phonons in Ge, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27(2), 858.
47. Modern methods and algorithms of quantum chemistry, ed. Grotendorst J., NIC, 2000.
48. B. Kirchner, P. J. di Dio and J. Hutter, Real-World Predictions from Ab Initio Molecular Dynamics Simulations, in Multiscale Molecular Methods in Applied Chemistry, 2012, pp. 109–153.
49. C. Leforestier, Classical trajectories using the full ab initio potential energy surface H⁻+CH4→CH4 + H⁻, J. Chem. Phys., 1978, 68(10), 4406–4410.
50. A. Warshel and M. Karplus, Semiclassical trajectory approach to photoisomerization, Chem. Phys. Lett., 1975, 32(1), 11–17.
51. H. Zhang, L. M. Liu and W. M. Lau, Dimension-dependent phase transition and magnetic properties of VS₂, J. Mater. Chem. A, 2013, 1(36), 10821–10828.
52. J. Contreras-García and J. M. Recio, Electron delocalization and bond formation under the ELF framework, Theor. Chem. Acc., 2011, 128, 411–418.
53. M. Michalski, A. J. Gordon and S. Berski, Topological analysis of the electron localisation function (ELF) applied to the electronic structure of oxaziridine: the nature of N-O bond, Struct. Chem., 2019, 30, 2181–2189.
54. X. Ma, L. Yin, J. Zou, W. Mi and X. Wang, Strain-Tailored Valley Polarization and Magnetic Anisotropy in Two-Dimensional 2H-VS₂/Cr₂C Heterostructures, J. Phys. Chem. C, 2019, 123(28), 17440–17448.
55. X. Zhao, J. C. Wu, Z. Y. Zhao, Z. Z. He, J. D. Song and J. Y. Zhao, et al., Heat switch effect in an antiferromagnetic insulator Co₃V₂O₈, Appl. Phys. Lett., 2016, 108(24), 242405.
56. Q. J. Li, Z. Y. Zhao, C. Fan, F. B. Zhang, H. D. Zhou and X. Zhao, et al., Phonon-glass-like behavior of magnetic origin in single-crystal Tb₂Ti₂O₇, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(21), 1–6.
57. K. Gofryk, S. Du, C. R. Stanek, J. C. Lashley, X. Y. Liu and R. K. Schulze, et al., Anisotropic thermal conductivity in uranium dioxide, Nat. Commun., 2014, 5, 1–7.
58. H. Li, P. Zhang, T. Ouyang, H. Wang, J. Li and C. He, et al., Notable effect of magnetic order on the phonon transport in semi-hydrogenated graphene, Appl. Phys. Lett., 2022, 120(9), 092403.
59. D. Zhang, K. Wang, S. Chen, L. Zhang, Y. Ni and G. Zhang, Regulating the thermal conductivity of monolayer MnPS₃ by a magnetic phase transition, Nanoscale, 2022, 15(3), 1180–1185.
60. Y. Liu, Q. Liu, Y. Liu, X. Jiang, X. Zhang and J. Zhao, Effects of spin-phonon coupling on two-dimensional ferromagnetic semiconductors: A case study of iron and ruthenium trihalides, Nanoscale, 2021, 13(16), 7714–7722.
61. K. Wang, W. X. Zhou, Y. Cheng, M. Zhang, H. Wang and G. Zhang, Magnetic order-dependent phonon properties in 2D magnet CrI₃, Nanoscale, 2021, 13(24), 10882–10890.
62. P. B. Allen and J. L. Feldman, Thermal conductivity of glasses: Theory and application to amorphous Si, Phys. Rev. Lett., 1989, 62(6), 645.
63. M. Simoncelli, D. Fournier, M. Marangolo, E. Balan, K. Béneut, B. Baptiste, et al., Temperature-invariant heat conductivity from compensating crystalline and glassy transport: from the Steinbach meteorite to furnace bricks, arXiv, 2024, preprint, arXiv:2405.13161,  DOI:10.48550/arXiv.2405.13161.
64. M. Simoncelli, N. Marzari and F. Mauri, Wigner Formulation of Thermal Transport in Solids, Phys. Rev. X., 2022, 12(4), 041011.
65. M. Simoncelli, N. Marzari and F. Mauri, Unified theory of thermal transport in crystals and glasses, Nat. Phys., 2019, 15(8), 809–813.
66. X. Gonze, Interatomic Force Constants in Periodic Solids from Density Functional Perturbation Theory, in Advances in Quantum Chemistry, Academic Press, 1998, vol. 33, pp. 225–239.
67. A. Cammarata and T. Polcar, Tailoring Nanoscale Friction in MX₂ Transition Metal Dichalcogenides, Inorg. Chem., 2015, 54(12), 5739–5744.
68. A. Cammarata and T. Polcar, Layering effects on low frequency modes in n-layered MX₂ transition metal dichalcogenides, Phys. Chem. Chem. Phys., 2016, 18(6), 4807–4813.
69. S. C. Rakesh Roshan, N. Yedukondalu, T. Pandey, L. Kunduru, R. Muthaiah and R. K. Rajaboina, et al., Effect of Atomic Mass Contrast on Lattice Thermal Conductivity: A Case Study for Alkali Halides and Alkaline-Earth Chalcogenides, ACS Appl. Electron. Mater., 2023, 5(11), 5852–5863.
70. A. Cammarata and T. Polcar, Fine control of lattice thermal conductivity in low-dimensional materials, Phys. Rev. B, 2021, 103(3), 1–8.
71. D. A. Broido, A. Ward and N. Mingo, Lattice thermal conductivity of silicon from empirical interatomic potentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(1), 1–8.
72. N. Mounet and N. Marzari, First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(20), 205214.
73. A. S. Borovik-Romanov and S. K. Sinha, Light scattering from spin waves, in Modern Problems in Condensed Matter Sciences, Elsevier, 1988, vol. 22(1), pp. 81–173.
74. A. Togo, L. Chaput and I. Tanaka, Distributions of phonon lifetimes in Brillouin zones, Phys. Rev. B, 2015, 91(9), 094306.
75. Y. Liu, Q. Liu, Y. Liu, X. Jiang, X. Zhang and J. Zhao, Effects of spin-phonon coupling on two-dimensional ferromagnetic semiconductors: A case study of iron and ruthenium trihalides, Nanoscale, 2021, 13(16), 7714–7722.
76. H. Nakayama, B. Xu, S. Iwamoto, K. Yamamoto, R. Iguchi and A. Miura, et al., Above-room-temperature giant thermal conductivity switching in spintronic multilayers, Appl. Phys. Lett., 2021, 118(4), 042409.
77. Y. Zhao, Q. Yao, P. Liu and Q. Liu, Accurate polymorphous description of the paramagnetic phases in MnBi₂Te₄, Comput. Mater. Today, 2024, 2–3, 100007.
78. B. Mortazavi, B. Javvaji, F. Shojaei, T. Rabczuk, A. V. Shapeev and X. Zhuang, Exceptional piezoelectricity, high thermal conductivity and stiffness and promising photocatalysis in two-dimensional MoSi₂N₄ family confirmed by first-principles, Nano Energy, 2021, 82, 105716.
79. Y. Luo, M. Li, H. Yuan, H. Liu and Y. Fang, Predicting lattice thermal conductivity via machine learning: a mini review, npj Comput. Mater., 2023, 9(1), 4.
80. R. Bertossa, F. Grasselli, L. Ercole and S. Baroni, Theory and Numerical Simulation of Heat Transport in Multicomponent Systems, Phys. Rev. Lett., 2019, 122(25), 255901.
81. A. Marcolongo, R. Bertossa, D. Tisi and S. Baroni, QEHeat: An open-source energy flux calculator for the computation of heat-transport coefficients from first principles, Comput. Phys. Commun., 2021, 269, 108090.
82. M. S. Gebre, R. K. Banner, K. Kang, K. Qu, H. Cao and A. Schleife, et al., Magnetic anisotropy in single-crystalline antiferromagnetic Mn₂Au, Phys. Rev. Mater., 2024, 8(8), 084413.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02375g

‡ These authors contributed equally.

---