Structural characterization of water ice condensed on silicate grains by infrared and Raman spectroscopy

Abstract

The sticking and nucleation properties of gas-phase molecular species are influenced by the properties of the substrate, including its chemical and physical characteristics. The chemical reactivity that occurs in ice layers during thermal and irradiation events can also be affected by these properties. The spectroscopic properties of two magnesium silicate minerals, forsterite and enstatite, were investigated by infrared and Raman spectroscopy and Density Functional Theory calculations. The effect of structural properties on the condensation of water ice on top of the mineral grains was analyzed by Raman microscopy. The spectroscopic characterization of the silicates agrees quite well with the computational results, and the modeling of the ice layers on top of the grains describes the spectroscopic signature obtained by Raman microscopy very successfully. The information obtained enhances our understanding of the interface of ice and dust in astrophysical environments.

---

1. Introduction

The chemical and physical properties of a substrate influence the sticking and nucleation properties of gas-phase molecular species and can also influence the chemical reactivity that occurs in ice layers during thermal and irradiation events. These phenomena are of interest in many scientific fields, including atmospheric chemistry, aerospace technology, and astronomy. For example, the chemical and optical properties of dust grains in astronomical objects are affected by the molecular composition of the ice layers deposited on top of the grains, potentially affecting the star formation mechanism. In dense and cold environments, the dust grains are covered by icy mantles, mainly water-based^1–3 and formed by condensation of volatiles from the gas phase. Although silicate minerals can already be identified in astronomical spectra obtained by space telescopes, a detailed understanding of their infrared and Raman signatures remains crucial. Laboratory spectra provide fundamental reference data that enables more accurate band assignments and interpretation of features that are still ambiguous or unresolved in observational data.

The molecular composition of the dust grains in space is far from being exhaustively determined, but infrared (IR) spectra recorded by space telescopes in recent years show clear features that can be assigned to a significant presence of silicates, a fraction of which was identified in their crystalline form,^4–7 which is a tracer of their thermal evolution.⁸

In our experiments, we only considered the crystalline state of the silicates, which traces the occurrence of high-energy processes,^9,10 such as the annealing of amorphous silicates in regions about T ∼ 1000 K, in the inner regions of protoplanetary disks and around evolved stars. Based on the available literature,^8,11 we decided to select for our studies two different magnesium silicate minerals, viz. forsterite and enstatite, which are representative of the average composition of dust grains.

The aim is to investigate from both theoretical and experimental perspectives the effect of different conformations of silicates on the binding properties and thermal processing of ice analogs from a unified theoretical and experimental approach. To this end, a comprehensive spectroscopic characterisation of the vibrational fingerprint was performed on silicate dust samples using IR and Raman spectroscopy.

Due to the high selectivity of Raman spectroscopy for identifying mineral samples, this methodology has been very recently implemented in space mission instruments. Silicate minerals have been recently detected in Martian rocks through SHERLOC Raman measurements collected during the NASA's Mars 2020 mission Perseverance.^12,13 The data collected by the SHERLOC Raman spectrometer revealed a history of aqueous alteration by mapping the mineral composition of another planetary body surface, for the first time.

A theoretical investigation of their structure-related properties was conducted alongside the work, with a particular focus on the role of hydrogen bonding. Once the different silicate materials were characterized, the binding properties and reactivity of water ice samples were investigated.

2. Materials and methods

The structural characterization of the selected samples, forsterite and enstatite, was focused on their interactions with water-based ice samples, focusing on the role of hydrogen bonding in stabilizing different conformations. The spectroscopic features of these systems are unique and can be used to characterize the sample. In this context, laboratory data were recorded in the IR frequency range by using a state-of-the-art IR spectrometer and a Raman microscope. In addition, the morphology of the ice layers deposited on top of the minerals was assessed using the Raman microscope. This instrument was coupled to a cryostat, used to lower the temperature, and a Lakeshore temperature controller for investigation of temperature effects and deposition of ice layers. A theoretical study based on Density Functional Theory (DFT) calculations supported the analysis of spectroscopic measurements.

2.1. Computational details

Geometry and cell optimization, followed by vibrational modes calculations, were carried out for forsterite and enstatite crystals as well as surfaces covered by an ice sheet. The Quantum Espresso package (v7.0)^14,15 was used for that purpose.

The crystal calculations were performed using the experimental unit cells of forsterite¹⁶ and enstatite¹⁷ as the starting point. Simulation boxes of forsterite and enstatite surfaces with an ice layer were prepared by first cleaving the respective unit cells along the (010) plane in the orthorhombic system, which corresponds to the lowest surface energy of these minerals.¹⁸ Subsequently, a 2-molecule-thick layer of water molecules was created on top of the exposed surface by randomly inserting water molecules in the box, at a minimum distance of 3.5 Å from the surface. The vacuum was considered along the direction normal to the surface (z direction), whereas periodic boundary conditions were applied to both x and y directions. The size of the vacuum component was determined by performing a series of single-point energy calculations for various box lengths in the z direction until total energy, total force, and potential difference along the vacuum direction converged. The convergence condition yielded a vacuum of 14 Å and 23 Å for the forsterite + ice and enstatite + ice systems, respectively (see Fig. S1).

The DFT calculations were performed with the PBE exchange and correlation functional,¹⁹ norm-conserving pseudopotentials²⁰ and a plane wave basis set with the following plane wave energy cutoffs: forsterite crystal, 85 Ry; enstatite crystal, 90 Ry; forsterite + ice, 85 Ry; enstatite + ice, 90 Ry. Sampling of reciprocal space was carried out with uniform grids of 2 × 2 × 3, 3 × 1 × 2, 7 × 3 × 1 and 7 × 4 × 1 points for forsterite, enstatite, forsterite + ice and enstatite + ice, respectively, generated by a Monkhorst–Pack scheme.²¹ All these parameters were determined from convergence tests to yield a convergence in total energy values in the order of 1 × 10⁻³ Ry. In the systems containing ice, the discontinuity in the electrostatic potential introduced by the vacuum along the z direction was compensated by applying a dipole correction.²²

Simultaneous geometry and cell optimizations were carried out with convergence thresholds for atomic forces and energies of 10⁻⁵ a.u. and 10⁻⁶ Ry, respectively, and a target pressure of 0 Pa. Vibrational modes, along with IR and Raman responses, were calculated from the equilibrium geometries at the Gamma point. The acoustic sum rule was used to impose a zero value on the acoustic frequencies. A global scaling factor was applied to the theoretical frequencies, calculated by performing a least-squares fit to the frequencies of the main peaks of the experimental spectra within the range 0–1500 cm⁻¹.

2.2. Experimental details

Enstatite and forsterite samples, as naturally occurring minerals, in grains of variable size, were purchased from Alfa Aesar by Thermo Fisher Scientific. The Fourier-transform infrared (FTIR) spectra were recorded on the unprocessed sample at room temperature, using a millimeter-sized grain. Micrometer-sized unprocessed samples dispersed on a commercial silicon optical window, used as substrate, were used to record Raman spectra at room and cryogenic temperatures, using a closed-cycle liquid helium cryostat. The formation of ice layers was achieved by condensation from the gas phase on top of a cold substrate. Further details on each analysis are provided in the following sections.

2.2.1. Infrared spectrometer. The spectrometer located at the Department of Chemical Engineering at the University of Coimbra (Portugal) is a Frontier - PerkinElmer Fourier transform infrared spectrometer (FT-NIR/MIR), equipped with an electrically temperature-stabilized fast recovery deuterated triglycine sulfate (FR-DTGS) detector and a KBr beam splitter. Fig. 1a shows the schematic representation of the configuration of the infrared spectrometer used in this study.

Fig. 1 (a) Schematic representation of the setup of the infrared spectrometer (ATR-FTIR) used in this study. The instrument is a commercial model: Frontier - PerkinElmer®. (b) Main components of the Raman microscope for ice investigation designed and build at the “Center for Astrochemical Studies” at Max Planck Institute for Extraterrestrial Physics.

The FTIR spectra (4000–550 cm⁻¹) were collected with 4 cm⁻¹ spectral resolution and 128 scans. Spectra were obtained using the UATR accessory (Universal Attenuated Total Reflectance) with a Diamond/ZnSe crystal and applying a force of 80 N. The IR spectra were recorded at room temperature, using a millimeter-sized grain (the samples were ground into powder). Background spectra measurements were collected under identical conditions using the empty ATR crystal and automatically subtracted from the corresponding sample spectra.

2.2.2. Raman microscope and cryogenic set-up. The spectroscopic properties of forsterite and enstatite dust grains were also investigated using a WiTec alpha300 R confocal Raman Microscope with a WiTec UHTS 300 spectrometer using a 488 nm Laser, located at the Max Planck Institute for Extraterrestrial Physics in Garching, Germany. The microscope was coupled to a low-vibration Stinger Closed Cycle Flow System He cryostat (ColdEdge Technologies) with a base pressure of 10⁻⁵ mbar at room temperature and a final vacuum of 10⁻⁷ mbar when cold. Fig. 1b outlines the main components of the cryostat and microscope.

This technique enables two-dimensional spatial characterization of samples of different natures. The Raman spectra were collected using a laser power of 1 mW. The maximum lateral resolution achieved was in the order of a few μm. The spectra were recorded in the 4000–0 cm⁻¹ frequency range with a spectral resolution of 4 cm⁻¹ and the signal averaged over 150 scans with an integration time of 0.5 s for each scan. The sample holder can reach a minimum temperature of 5 K. The vacuum chamber is equipped with a quartz optical window, while a silicon window is used as a cold substrate.

The following experimental procedure was applied for the Raman analysis. The spectra of selected dust grains and on the bare silicon substrate were collected at room temperature. The spectra recorded on the silicon surface are used as a reference spectrum to evidence the contribution of the substrate to the Raman spectral features.

Subsequently, the substrate was cooled to the minimum temperature achievable (5 K), and the Raman spectra of the same dust grains were measured. Water ice formation was achieved by condensation of water vapor, at an inlet pressure of 2 mbar, on top of the cold substrate and dust grains for a total time of 3 min for forsterite, and 2 min for enstatite. After the ice was formed, Raman spectra were collected in different positions, on the silicon surface where no grain was present, and on top of the selected dust grains.

The effect of temperature on the water ice phase transition was investigated by annealing the substrate (for a total duration of 3 hours) at 160 K for forsterite and 150 K for enstatite experiments, at which the transition from an amorphous to a crystalline structure is expected to occur.²³ After annealing, Raman spectra were collected on the silicon surface where no grain was present, and on top of the selected dust grains in the same positions as in the 5 K measurements.

3. Results and discussion

3.1. Infrared and Raman spectra of dust grains

Fig. 2–5 compare the experimental and theoretical IR and Raman spectra for the various systems. Tables 1–4 summarize the vibrational mode assignments. Overall, there is a good agreement between the scaled theoretical frequencies and the corresponding experimental values. The calculated frequencies were scaled by different factors for each spectrum, calculated from least-squares linear fits.

Fig. 2 Infrared spectra of solid forsterite, recorded at room temperature. Experimental (red) and calculated (black). Calculated frequencies were scaled by a factor of 1.046.

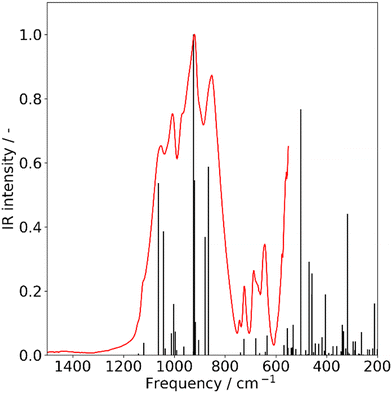Fig. 3 Infrared spectra of solid enstatite, recorded at room temperature. Experimental (red) and calculated (black). Calculated frequencies were scaled by a factor of 1.034.

Fig. 4 Raman spectra of solid forsterite, recorded at 5 K. Experimental (red) and calculated (black). Calculated frequencies were scaled by a factor of 1.048.

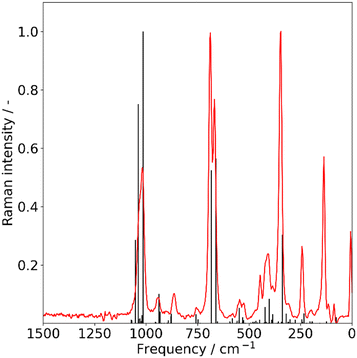Fig. 5 Raman spectra of solid enstatite, recorded at 5 K. Experimental (red) and calculated (black). Calculated frequencies were scaled by a factor of 1.049.

Table 1 Proposed assignments for the IR spectra of the forsterite crystal system

Frequencies/cm^−1			Approximate description
Experimental	Theoretical not scaled	Theoretical scaled^a
a The theoretical frequencies were scaled by 1.046. Abbreviations: ν, bond stretching; δ, bending; w, wagging; s, symmetric; as, anti-symmetric; (sh), shoulder.
980	937	980	ν(Si–O)as
953 (sh)	920	963	ν(Si–O)s
876	840	879	ν(O–Si–O)as + δ(Mg–O)
837	797	834	ν(O–Si–O)s + δ(Mg–O)
604	577	604	δ(Mg–O) + w(Si–O)

---

Table 2 Proposed assignments for the IR spectra of the enstatite crystal system

Frequencies/cm^−1			Approximate description
Experimental	Theoretical not scaled	Theoretical scaled^a
a The theoretical frequencies were scaled by 1.034. Abbreviations: ν, bond stretching; δ, bending; s, symmetric; as, anti-symmetric; (sh), shoulder.
1124	1104	1141	ν(Si–O)as
1055	1028	1063	ν(Si–O)as + δ(O–Mg–O)
1007	970	1003	ν(Si–O)as
970	930	962	ν(Si–O) + δ(O–Mg–O)
922	894	924
906 (sh)	874	904
852	837	866	ν(Si–O)s
742	715	740	ν(Si–O)as
725	702	725	ν(Si–O)
688	657	679	δ(O–Si–O)
673	642	664
644	613	634

---

Table 3 Proposed assignments for the Raman spectra of the forsterite crystal system

Frequencies/cm^−1			Approximate description
Experimental	Theoretical not scaled	Theoretical scaled^a
a The theoretical frequencies were scaled by 1.048. Abbreviations: ν, bond stretching; δ, bending; γ, rocking; tw, twisting; s, symmetric; as, anti-symmetric; (sh), shoulder.
964	925	969	ν(Si–O)
923	884	926	ν(Si–O)as
885	847	888
859	820	860	ν(Si–O)s
827	788	826
629 (sh)	600	629	δ(O–Si–O) + ν(O–Mg–O)s
609	577	605	ν(Mg–O) + δ(O–Si–O)
593	563	590	δ(O–Mg–O) + δ(O–Si–O)
546	520	545	δ(O–Si–O)
436	416	435	ν(Mg–O) + tw(O–Si–O)
423	402	421	tw(O–Si–O) + δ(O–Mg–O)
335	323	339	δ(O–Mg–O)
308	290	304	ν(Mg–O) + δ(O–Mg–O)
229	219	230	δ(O–Mg–O)
153	137	144
108	100	105	γ(Mg–O–Mg)

---

Table 4 Proposed assignments for the Raman spectra of the enstatite crystal system

Frequencies/cm^−1			Approximate description
Experimental	Theoretical not scaled	Theoretical scaled^a
a The theoretical frequencies were scaled by 1.049. Abbreviations: ν, bond stretching; δ, bending; γ, rocking; w, wagging; tw, twisting; s, symmetric; as, anti-symmetric; (sh), shoulder. b Raman feature of the silicon substrate.
1034 (sh)	989	1037	ν(Si–O)
1018	966	1014
942	894	938
866	837	878	ν(Si–O)as
756	723	758	ν(Si–O)s
746 (sh)	713	748
688	652	683	δ(O–Si–O)
668	631	662
556 (sh)	532	558	ν(Mg–O) + δ(O–Si–O)
546	522	548	δ(O–Si–O)
526^b	—	—	—
446	427	448	ν(Mg–O)
419	403	423	tw(O–Si–O)
409	383	402	ν(Mg–O) + δ(O–Si–O)
386	367	385	w(Mg–O–Mg)
345	323	338	γ(O–Si–O)
311	304	319	tw(Mg–O–Mg)
243	223	233	w(O–Mg–O)
205 (sh)	194	204	δ(O–Mg–O)
198	183	192	γ(Mg–O–Mg) + γ(O–Si–O)
157 (sh)	149	156	γ(O–Si–O)
136	118	124

---

The IR spectra for both forsterite and enstatite species are characterized by the most intense feature at ca. 900 cm⁻¹, which appears as a sharp multicomponent band, identified as Si–O symmetric and antisymmetric stretching. The band shape allows for unambiguous assignment to the respective mineralogical species and indicates their physical state (amorphous or crystalline). Our data are in agreement with previous laboratory studies in identifying band shapes that are characteristic of crystalline structures.^11,24–26

The Raman spectral signature of forsterite and enstatite samples differ significantly. The most intense feature for forsterite, assigned to the Si–O symmetric stretching, appears as a doublet at around 850 cm⁻¹. Enstatite sample shows a more complex pattern, with the Si–O stretching band shifted to ca. 1000 and 670 cm⁻¹, and an intense signal observed for the O–Si–O rocking mode at 345 cm⁻¹. The Raman spectra of dust grains have been measured both at room temperature and at 5 K to check for spectral changes owing to the effect of temperature. In all the examined cases, no spectral changes were observed.

To investigate the interaction of the silicate dust grains with water ice, we proceed with the condensation of an ice layer on to the surface of dust samples. The results are discussed in the next section.

3.2. Raman microscopy of ice-covered dust grains

Fig. 6 shows a series of optical images illustrating the visual appearance of the forsterite and enstatite dust grains scattered on the surface of the silicon substrate along with the subsequent formation of water ice, deposited at 5 K and annealed for three hours at 160 and 150 K.

Fig. 6 Overview of dust grains and water ice on top of the silicon substrate, for forsterite at 5 K (a), after H₂O deposition (b), after 3 hours of annealing at 160 K (c), enstatite at 5 K (d), after H₂O deposition (e), after annealing at 150 K (f).

The silicon substrate is visible as a gray background in panels (6a) and (6d), before ice deposition, while the silicate dust grains appear as dark spots due to the high luminosity contrast. When a layer of ice forms on the substrate and grains, the interaction with the camera light produces a false color pattern on the surface, visible in panels (6b) and (6e). The annealing of the ice and the subsequent phase transition to crystalline water are evidenced by the appearance of small discontinuities caused by the formation of cracks in the ice, as shown in panels (6c) and (6f).

The spectra recorded at the position indicated by the crosses in Fig. 6, along with the corresponding calculated spectral signature, are shown in Fig. 7–9. Fig. 7 and 8 show the Raman spectra of ice layers deposited on top of forsterite and enstatite grains, recorded at 5 K, corresponding to panels (b) and (e) in Fig. 6, respectively. Tables 5 and 6 summarize the vibrational mode assignments. The spectra of forsterite and enstatite show no significant changes after the formation of the ice layer. A new feature, assigned to water ice, appears as a broad band around 3300 cm⁻¹. This feature is assigned to the OH stretching of water, and its shape is indicative of the physical state of the ice.

Fig. 7 Raman spectra of forsterite-ice, recorded at 5 K, corresponding on panel (b) in Fig. 6. Experimental (red) and calculated (black). Calculated frequencies were scaled by a factor of 1.007.

Fig. 8 Raman spectra of enstatite-ice, recorded at 5 K corresponding on panel (e) in Fig. 6. Experimental (red) and calculated (black). Calculated frequencies were scaled by a factor of 1.008.

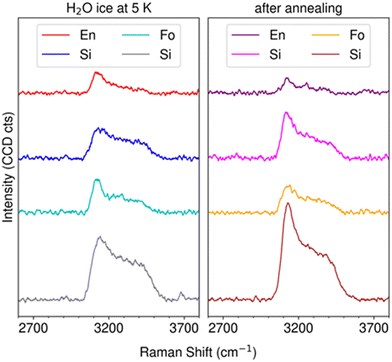Fig. 9 H₂O stretching features of Raman spectra recorded over the surface of dust grains and silicon substrate. The left panel shows the spectra recorded at 5 K, while the right panel shows the spectra recorded after 3 hours of annealing at 160 K for forsterite-ice samples and at 150 K for enstatite-ice samples, respectively. The colors of the spectra are coded to correspond to the optical image positions shown in Fig. 6.

Table 5 Proposed assignments for the Raman spectra of the forsterite-ice system

Frequencies/cm^−1			Approximate description
Experimental	Theoretical not scaled	Theoretical scaled^a
a The theoretical frequencies were scaled by 1.007. Abbreviations: ν, bond stretching; δ, bending; w, wagging; s, symmetric; as, anti-symmetric; HW, hydrogen water; OW, oxygen water; OS, oxygen mineral surface; n.o., not observed.
3329	3408	3432	ν(water)as
3144	3127	3150	ν(water)s
n.o.	2830	2851	ν(OS–HW) + ν(water)
n.o.	2274	2290	ν(OS–HW)H-bond
1586	1573	1585	δ(water)
964	959	966	δ(water) + ν(Si–O)
926	913	919	ν(Si–O)as
859	854	860	ν(Si–O)s
830	827	833	δ(water) + ν(Si–O)
n.o.	755	760	ν(Si–O) + ν(O–Mg)
612	609	613	w(O–Si–O)
596	591	596	δ(water) + δ(O–Si–O)
550	532	536	δ(Si–O–Mg)
530	510	514	δ(O–Si–O)
439	436	439	ν(Mg–O)+ ν(HW–OS)
379	372	374	δ(O–Mg–O) + δ(O–Si–O)
338	339	341	δ(O–Mg–O) + δ(Mg–O–Mg)
229	222	224	δ[(Mg–O–Mg) + waterH-bond]
108	104	105	δ(O–Mg–O)

---

Table 6 Proposed assignments for the Raman spectra for the enstatite-ice system

Frequencies/cm^−1			Approximate description
Experimental	Theoretical not scaled	Theoretical scaled^a
a The theoretical frequencies were scaled by 1.008. Abbreviations: ν, bond stretching; δ, bending; w, wagging; s, symmetric; as, anti-symmetric; HW, hydrogen water; OW, oxygen water; OS, oxygen mineral surface; n.o., not observed. b Raman feature of the silicon substrate.
3280	3240	3265	ν(water)as
3112	3214	3240	ν(water)s
n.o.	2699	2720	ν(OS–HW) + ν(water)
n.o.	2478	2497	ν(OS–HW)H-bond
1034	968	976	δ(Mg–OS–HW) + δ(water) + ν(Si–O)
1018	962	969
1015	951	958	δ(Mg–OS–HW) + δ(water) + ν(Si–O)
974	934	941	ν(Si–O)as
964	927	935	ν(Si–O)s
949	896	903	δ(water) + δ(Mg–OS–HW)
863	833	839	ν(Si–O)
	842	848
	848	855	w(HW–OS) + δ(water)
691	699	705	δ(HW–OS) + δ(water)
668	666	672
530	518	522	δ(water) + δ(O–Si–O)
526^b	517	521
453	458	461	δ(O–Si–O) + ν(Mg–O)
446	445	449
409	415	418	ν(Mg–O) + ν(HW–OS)
389	379	382	δ(Mg–O–Mg)
379	369	372	δ(O–Mg–O) + δ(O–Si–O)
348	340	342
304	306	309
297	297	300	δ(Si–O–Mg)
253	256	258	δ[(Mg–O–Mg) + waterH-bond]
243	239	241
139	146	147

---

Although there is good agreement between the experimental and theoretical spectra in the region below 2500 cm⁻¹, corresponding to the enstatite/forsterite crystal, a significant discrepancy in both frequencies and intensities is observed in the 2500–3500 cm⁻¹ range, where the bands attributable to water appear (Fig. 7 and 8). The main source of this discrepancy is expected to lie in the level of theory employed rather than in the molecular model itself. In particular, generalized gradient approximation (GGA) functionals such as PBE are known to provide a poor description of hydrogen bonding in water, partly due to inherent self-interaction errors and partly due to an inadequate treatment of long-range dispersion forces. The use of exchange–correlation functionals capable of properly addressing these shortcomings—such as range-separated or double-hybrid functionals with dispersion corrections—would make the calculations computationally intractable, while the corresponding gains in accuracy would not be significant for this work.

A close-up of the OH stretching feature in the spectra collected at the points indicated by crosses in Fig. 8 is shown in Fig. 9. The band shape of the water ice is compared at low temperature, recorded at 5 K, and after 3 hours annealing of the ice, at 160 K for forsterite-ice sample, and at 150 K for enstatite-ice samples, for four different positions: on forsterite and enstatite dust grains, and on the silicon substrate near a dust grain, for both samples. The colors of the spectra in Fig. 10 are coded to show the correspondence of each spectrum with the position indicated by the crosses in the optical images shown in Fig. 6.

Fig. 10 Final equilibrium structures of forsterite (a), enstatite (b), forsterite + ice (c) and enstatite + ice (d). Si atoms in blue; Mg atoms in orange; O atoms in red; H atoms in white; hydrogen bonds in dashed green lines. The unit cell box is represented in black.

From the spectra recorded at 5 K, a difference in the shape of the bands can be observed between the positions on the substrate (labeled as Si), which are consistent with an ice structure that can be assigned to low-density amorphous ice (LDA), also known as amorphous solid water (ASW),²⁷ and the positions on top of forsterite and enstatite, which display the characteristic features of a more ordered ice structure and can be assigned to the crystalline ice structure Ih.²⁸ After annealing, the spectra of the ice probed on the substrate shows the shape change that indicates the transition from amorphous to crystalline Ih, as expected. The spectra on the grains may reflect partial desorption as the intensity of the band is slightly reduced, although it is worth noting that Raman spectroscopy does not provide quantitative information, so desorption cannot be confirmed by signal intensity alone.

The data presented support the hypothesis that silicate dust grains promote the formation of an ice layer in the crystalline state due to their physical structure, as confirmed by the computational results. Within this framework, however, the effect of the actual temperature of dust grains cannot be investigated as it is not possible to measure the temperature directly on a single grain. The temperature measurement provides only an average value at the sample holder. Therefore, it should also be considered that crystalline ice formation may be influenced by a temperature gap between the substrate and the dust grain. However, we estimate that these effects are of the order of a few degrees.

3.3. DFT-based unit-cell structural calculations

The structures of all systems after geometry optimization are shown in Fig. 10 (see also Fig. S1), and the corresponding crystal cell parameters for forsterite and enstatite are summarized in Table 7. The dimensions of the optimized unit-cells are in close agreement with the experimental values, with deviations in the range 0.8–1.2% for forsterite and 1.0–1.5% for enstatite. The calculated values are also consistent with other DFT results obtained using generalized gradient approximation or hybrid functional (see Tables S1 and S2). The cell dimensions of the enstatite + ice system in the periodic directions (a–b axis) are very similar to those of the corresponding crystal system. Indeed, the structures remained identical (Fig. 10b and Fig. S1b), although in the case of the forsterite + ice system, one of the dimensions expanded by about 17% to accommodate the ice layer (Fig. 10a and Fig. S1a).

Table 7 Experimental and calculated unit-cell parameters (Å) of forsterite and enstatite crystals

Unit cell parameter/Å	Forsterite		Enstatite
	Experimental^a	Calculated	Experimental^b	Calculated
a Mean and 95% confidence interval of data from ref. 29–31. b Mean and 95% confidence interval of data from ref. 32–34.
a	10.194 ± 0.009	10.315	5.179 ± 0.002	5.244
b	5.981 ± 0.007	6.042	18.223 ± 0.031	18.429
c	4.754 ± 0.007	4.796	8.814 ± 0.008	8.941

---

The structures of forsterite and enstatite crystals did not deviate substantially from their experimental counterparts, with RMSD values of 0.056 Å and 0.076 Å, respectively. Even though the ice layer was initially prepared in a random configuration, it appears to have converged to a crystal-like structure after the optimization of the crystal + ice systems (Fig. 10c and d, and Fig. S1), formed by a hydrogen bond network. This feature is explained by the displacement of water molecules near the surface, in which O atoms occupy the undercoordinated Mg atoms at the exposed (010) surface, leading the O atoms to adopt regularly spaced positions. When observed along the a–b plane (Fig. 10c and d), the structure of the top layer of water displays hexagonal patterns resembling hexagonal crystalline ice (Ih form), although the structure viewed from other perspectives shows some irregularities (Fig. S1). It should, however, be noted that these results only reflect equilibrium geometries. Further exploration of other hypothetical configurations, although possible, would require rather computationally expensive molecular dynamics simulations.

4. Conclusions

In this paper, we report the spectroscopic and theoretical investigation of two silicate species, forsterite and enstatite, which are components of astrophysical dust, and explore the conformational space of water-based ice layers deposited over the surface of dust samples. The spectroscopic characterization of the silicates agrees quite well with the computational results, and the modeling of the ice layers on top of the grains successfully reproduces the spectroscopic signatures obtained by Raman microscopy.

The structure of the water ice on the grains is found to be consistent with a crystalline Ih phase even at low temperature, in contrast to the ice deposited on the silicon substrate, where the ice structure at low temperature is more consistent with the LDA phase. Upon annealing, the ice deposited on top of the substrate undergoes a phase transition to the Ih structure, while the ice on top of the dust grains shows no spectroscopic evidence of a phase change, but instead exhibits signs of possible partial desorption.

The effect of the silicate structure on the physical state of the ice is consistent with the state predicted by theoretical calculations. Future investigations could be conducted on amorphous silicate samples to explore further the effect of silicate morphology on ice layer structure. Although it is not possible to directly measure the temperature of the dust grains, we estimate that the possible temperature gradient between the silicon substrate and the top of the dust grains will not exceed a few degrees, and this rules out the possibility that the different morphology of the ice layer on top of the Si substrate and dust grains is due to thermal effects.

In cold clouds, water ice forms directly on the grain surfaces through the adsorption of atomic oxygen and hydrogen and not from the deposition of H₂O from the gas phase. This formation mechanism could be analyzed to compare the results with the present analysis. In addition, other components of astrophysical dust grains, such as quartz (SiO₂), could be studied.

Author contributions

The manuscript was written through contributions of all authors. Conceptualization and supervision and management of the project: A. Borba and B. M. Giuliano. Infrared spectra of dust grains: A. Borba. Raman spectra of dust grains and Raman spectra of water ice: B. M. Giuliano, F. Kruczkiewicz and B. Müller. Density Functional Theory calculations: T. H. Ferreira, P. Maximiano and P. N. Simões. Formal analysis: A. Borba, B. M. Giuliano, P. N. Simões and P. Caselli. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no competing interests.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5nj03166d.

Acknowledgements

This work within the exchange of researchers within the framework through Bilateral Cooperation between Portugal and Germany 2020/2022, is supported by FCT-Fundação para a Ciência e Tecnologia, Portugal and DAAD-German Academic Exchange Service. CERES research Centre is supported by FCT, within the projects DOI: 10.54499/UIDB/00102/2020 (Base funding) and DOI: 10.54499/UIDP/00102/2020 (Programmatic funding). A. Borba acknowledges FCT financial support for her employment contract DOI:10.54499/DL57/2016/CP1370/CT0003. P. Maximiano and T. H. Ferreira acknowledge FCT for their PhD grants: SFRH/BD/136230/2018 and UI/BD/151294/2021, respectively.

References

1. P. Caselli and C. Ceccarelli, Astron. Astrophys. Rev., 2012, 20, 56.
2. A. C. A. Boogert, P. A. Gerakines and D. C. B. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541.
3. K. Altwegg, H. Balsiger and S. A. Fuselier, Annu. Rev. Astron. Astrophys., 2019, 57, 113.
4. G. Meeus, L. B. F. M. Waters, J. Bouwman, M. E. van den Ancker, C. Waelkens and K. Malfait, Astron. Astrophys., 2001, 365, 476.
5. D. H. Wooden, Earth, Moon, Planets, 2002, 89, 247.
6. C. Waelkens, L. B. F. M. Waters, M. S. de Graauw, E. Huygen, K. Malfait, H. Plets, B. Vandenbussche, D. A. Beintema, D. R. Boxhoorn, H. J. Habing, A. M. Heras, D. I. M. Kester, F. Lahuis, P. W. Morris, P. R. Roelfsema, A. Salama, R. Siebenmorgen, N. R. Trams, N. R. van der Bliek, E. A. Valentijn and P. R. Wesselius, Astron. Astrophys., 1996, 315, L245.
7. L. B. F. M. Waters, F. J. Molster, T. de Jong, D. A. Beintema, C. Waelkens, A. C. A. Boogert, D. R. Boxhoorn, T. de Graauw, S. Drapatz, H. Feuchtgruber, R. Genzel, F. P. Helmich, A. M. Heras, R. Huygen, H. Izumiura, K. Justtanont, D. J. M. Kester, D. Kunze, F. Lahuis, H. J. G. L. M. Lamers, K. J. Leech, C. Loup, D. Lutz, P. W. Morris, S. D. Price, P. R. Roelfsema, A. Salama, S. G. Schaeidt, A. G. G. M. Tielens, N. R. Trams, E. A. Valentijn, B. Vandenbussche, M. E. van den Ancker, E. F. van Dishoeck, H. Van Winckel, P. R. Wesselius and E. T. Young, Astron. Astrophys., 1996, 315, L361.
8. C. A. Poteet, S. T. Megeath, D. M. Watson, N. Calvet, I. S. Remming, M. K. McClure, B. A. Sargent, W. J. Fischer, E. Furlan, L. E. Allen, J. E. Bjorkman, L. Hartmann, J. Muzerolle, J. J. Tobin and B. Ali, Astrophys. J., 2011, 733, L32.
9. F. Molster and C. Kemper, Space Sci. Rev., 2005, 119, 3.
10. H. Jang, L. B. F. M. Waters, I. Kamp and C. P. Dullemond, Astron. Astrophys., 2024, 687, A275.
11. C. Jaeger, F. I. Molster, I. Dorschner, T. Henning, H. Mutschke and L. B. F. M. Waters, Astron. Astrophys., 1998, 339, 904.
12. J. Razzell Hollis, K. R. Moore, S. Sharma, L. Beegle, J. P. Grotzinger, A. Allwood, W. Abbey, R. Bhartia, A. J. Brown, B. Clark, E. Cloutis, A. Corpolongo, J. Henneke, K. Hickman-Lewis, J. A. Hurowitz, M. W. M. Jones, Y. Liu, J. Martinez-Frías, A. Murphy, D. A. K. Pedersen, S. Shkolyar, S. Siljeström, A. Steele, M. Tice, A. Treiman, K. Uckert, S. VanBommel and A. Yanchilina, Icarus, 2022, 387, 115179.
13. A. Corpolongo, R. S. Jakubek, A. S. Burton, A. J. Brown, A. Yanchilina, A. D. Czaja, A. Steele, B. V. Wogsland, C. Lee, D. Flannery, D. Baker, E. A. Cloutis, E. Cardarelli, E. L. Scheller, E. L. Berger, F. M. McCubbin, J. R. Hollis, K. Hickman-Lewis, K. Steadman, K. Uckert, L. DeFlores, L. Kah, L. W. Beegle, M. Fries, M. Minitti, N. C. Haney, P. Conrad, R. V. Morris, R. Bhartia, R. Roppel, S. Siljeström, S. A. Asher, S. V. Bykov, S. Sharma, S. Shkolyar, T. Fornaro and W. Abbey, J. Geophys. Res.: Planets, 2023, 128, e2022JE007455.
14. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
15. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. D. Gironcoli, P. Delugas, F. F. Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105.
16. R. M. Hazen, Am. Mineral., 1976, 61, 1280.
17. D. A. Hugh-Jones and R. J. Angel, Am. Mineral., 1994, 79, 405.
18. M. Bruno, F. R. Massaro, M. Prencipe, R. Demichelis, M. De La Pierre and F. Nestola, J. Phys. Chem. C, 2014, 118, 2498.
19. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
20. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
21. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188.
22. L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301.
23. P. Jenniskens and D. F. Blake, Science, 1994, 265, 753.
24. K. Demyk, L. d'Hendecourt, H. Leroux, A. P. Jones and J. Borg, Astron. Astrophys., 2004, 420, 233.
25. H. Sogawa, C. Koike, H. Chihara, H. Suto, S. Tachibana, A. Tsuchiyama and T. Kozasa, Astron. Astrophys., 2006, 451, 357.
26. C. Koike, Y. Imai, H. Chihara, H. Suto, K. Murata, A. Tsuchiyama, S. Tachibana and S. Ohara, Astrophys. J., 2010, 709, 983.
27. J. J. Shephard, J. S. O. Evans and C. G. Salzmann, J. Phys. Chem. Lett., 2013, 4, 3672.
28. E. Whalley, Can. J. Chem., 1977, 55, 3429.
29. R. T. Downs, C.-S. Zha, T. S. Duffy and L. W. Finger, Am. Mineral., 1996, 81, 51.
30. F. Guyot, Y. Wang, P. Gillet and Y. Ricard, Phys. Earth Planet. Inter., 1996, 98, 17.
31. A. Kirfel, T. Lippmann, P. Blaha, K. Schwarz, D. F. Cox, K. M. Rosso and G. V. Gibbs, Phys. Chem. Miner., 2005, 32, 301–313.
32. S. Ghose, V. Schomaker and R. K. McMullan, Z. Kristallogr. - Cryst. Mater., 1986, 176, 159.
33. N. Morimoto and K. Koto, Z. Kristallogr., 1969, 129, 65.
34. Y. Ohashi, Phys. Chem. Miner., 1984, 10, 217–229.

---