Functionalization of pyrimidine and purine into RNA bases in water/ammonia ices via radical substitution reactions

Abstract

Pyrimidine and purine represent immediate precursors of the four RNA bases, cytosine, uracil, adenine, and guanine. These can be, in principle, synthesized by replacing hydrogen atoms in given positions in pyrimidine and purine with NH₂ and/or OH substituents with subsequent H atom migrations from OH to the neighboring “bare” N atom in the ring creating the carbonyl moiety. Electronic structure ωB97XD/6-311G(d,p) and G3(MP2,CC) calculations of the potential energy profiles for these functionalization reactions show that they are plausible and involve moderate barriers for the radical addition and H atom elimination steps. The OH-for-H substitution reaction steps are the most facile and have lower barriers on purine (submerged by ∼4 kJ mol⁻¹) than on pyrimidine (10–19 kJ mol⁻¹). The NH₂-for-H substitution reactions are more energetically demanding, with their barriers ranging between 33 and 54 kJ mol⁻¹ and no significant differences have been found between pyrimidine and purine. In the gas phase, the critical reaction step is the H shift from O to the neighboring N in the ring following OH-for-H substitution, with barriers as high as 126–154 kJ mol⁻¹. These barriers can be greatly reduced with the direct involvement of 1–2 protic solvent molecules (e.g., H₂O, methanol, and NH₃) in ices, to only ∼30–50 kJ mol⁻¹, thus making H migrations comparable in terms of the energy demands with the NH₂-for-H substitution reaction steps. Minimal barriers have been found with the participation of two solvent molecules in the H transfer process. The barriers with the involvement of only one solvent molecule are slightly higher than those with the involvement of two molecules and the increase in the number of solvent molecules directly taking part in the reaction to three and four raises the barriers significantly. For the reactions in water ice, the H transfer transition state structures prominently involve transient hydronium (H₃O⁺) and Zündel (H₅O₂⁺) ions in the hydrogen migration process. The presence of implicit solvent taken into account through SCRF calculations does not significantly affect the reaction energetics and barrier heights for radical substitutions but slightly reduces the H shift barriers, where this effect is found to be most pronounced (up to ∼20 kJ mol⁻¹) inside ammonia ice.

---

Introduction

One of the long-standing questions that needs to be answered to understand prebiotic chemical evolution is how RNA nucleobases are synthesized naturally, especially under extreme conditions, such as in interstellar molecular clouds. Structurally, the four RNA nucleobases represent functionalized pyrimidine (cytosine and uracil) and purine (adenine and guanine), which are nitrogen heterocycles related to benzene and indene, respectively. It has been shown, both experimentally and theoretically, that benzene (C₆H₆) can be synthesized at extremely low temperatures both in the gas phase, e.g., via the reaction of the ethynyl radical (C₂H) with 1,3-butadiene (C₄H₆),¹ and in the acetylene (C₂H₂) ice irradiated with the cosmic rays proxies.^2,3 Low-temperature gas-phase synthetic routes toward indene have also been found.^4,5 Nitrogen containing heterocycles are generally harder to produce from small acyclic molecules and radicals because each replacement of a CH group with an N atom generally reduces the aromatic stabilization of the ring(s).⁶ This is exemplified by the fact that, contrary to C₂H + C₄H₆, the CN + 1,3-butadiene reaction mostly produces 1-cyano-1,3-butadiene with only trace amounts of pyridine being formed.⁷ Barrierless reaction pathways to synthesize pyridine and pyrimidine under low-temperature conditions have been proposed theoretically only recently^8,9 and they are yet to be verified experimentally. No low-temperature gas-phase routes toward the purine molecule containing four N atoms in place of CH as compared to indene have been discovered so far. Moreover, there is a consensus in the literature that functionalization of pyrimidine and purine into nucleobases, i.e., the replacement of CH with carbonyl (CO) groups and H with amino (NH₂) or methyl (CH₃) substituents can be feasible only in the condensed phase, such as in solution under ambient conditions or in energetically processed ices at low temperatures.

Pyrimidine, purine, and nucleobases which can be derived from them have been found in meteorites^10–15 but not in the interstellar medium, despite extensive searches.^16,17 While simulating the molecular cloud conditions in the laboratory, Oba et al.¹⁸ have recently demonstrated that three out of four RNA nucleobases (except guanine) along with other nucleobases (thymine, xanthine, and hypoxanthine) and their N-heterocyclic precursors (pyrimidine and purine) are produced in mixed ices containing H₂O, CO, NH₃, and CH₃OH irradiated with UV photons at 10 K. Earlier laboratory studies have shown that polycyclic aromatic hydrocarbon (PAH) molecules in ices irradiated with UV light or bombarded by photons can be functionalized forming, e.g., quinones and ethers,^19–22 and similar oxidation/functionalization processes can occur involving their N-containing analogs.^23–27 For example, photoprocessing of purine inside an NH₃:H₂O ice at 15 K showed the formation of identifiable quantities of 2-aminopurine, 6-aminopurine (adenine), 2,6-diaminopurine, hypoxanthine, xanthine, isoguanine, and guanine.²⁸ While the possibility of the formation of both pyrimidinic and purinic nucleobases in energetically processed ices has been now well established, chemical mechanisms underlying these processes are still poorly understood. One school of thought is that molecules in ice are first ionized by radiation and then, ions react with radicals leading to functionalization. Lee's and Head-Gordon's groups have explored various pathways leading to nucleobases via ion–radical reactions theoretically, using electronic structure calculations. For instance, Bera et al.²⁹ found that various isomers of the vinyl cyanine ion C₃H₃N⁺ may contribute to the formation of pyrimidine through their reactions with HCN. A combined experimental and theoretical study by Hamid et al.³⁰ has shown that consecutive reactions of acetylene cations with two HCN molecules lead to the formation of pyrimidine cations in the gas phase. Bera et al.³¹ explored the functionalization pathways of pyrimidine to uracil initiating with pyrimidine cations which react with OH radicals. The first functionalization step forms neutral pyrimidin-4(3H)-one, with the positive charge carried away by the hydronium ion, H₃O⁺. The neutral intermediate is then ionized and reacts with OH again producing uracil + H₃O⁺. The calculations indicated that each reaction step in the sequence is highly exothermic making the overall reaction thermodynamically favorable in the presence of radiation capable of ionizing first pyrimidine and then pyrimidin-4(3H)-one. The authors, however, have not studied the kinetic feasibility of the pyrimidine-to-uracil functionalization process, in particular, for the required H migration steps from OH to N. Similar ion-radical reaction mechanisms were also later investigated for the functionalization of pyrimidine into thymine³² and purine to adenine, guanine, and isoguanine³³ and all of them were found to be highly exothermic in the presence of water molecules which can eventually remove the positive charge in the form of the hydronium ion.

While the ion–radical functionalization mechanism is plausible, it requires the presence of ionizing radiation. Photon energies required for homolytic cleavage of chemical bonds to form radicals are normally lower than those needed for ionization. After radicals are produced, radical–radical reactions are usually highly exothermic and can, in principle, account for the functionalization processes. However, concentrations of radicals are usually significantly lower than the concentration of closed-shell neutral molecules even in irradiated ices. Therefore, it is of interest to explore mechanisms that are based upon molecule–radical reactions introducing functional groups onto the pyrimidine and purine rings. The present work explores such reaction mechanisms using electronic structure calculations of the pertinent potential energy surfaces (PESs) both in the gas phase and inside protic ices (water, ammonia, and methanol) and demonstrates that the critical reaction step can be drastically enhanced with microsolvation of the reacting species by H₂O/NH₃/CH₃OH molecules which directly participate in the H transfer.

Let us first consider possible functionalization mechanisms. As illustrated in Scheme 1, functionalization of pyrimidine into uracil can, in principle, occur through the following steps: (1) radical substitution (S_R) of OH for H via OH addition to pyrimidine followed by H elimination on the carbon between two N atoms in the ring forming pyrimidin-2-ol and H shift from OH to N resulting in pyrimidin-2(1H)-one, and (2) OH-for-H S_R substitution on the C atom next to the bare nitrogen giving rise to 4-hydroxypyrimidin-2(1H)-one followed by the OH-to-N H migration completing the formation of uracil. These reaction steps may also occur in the opposite order: (3) OH-for-H radical substitution in an ortho position with respect to one of the nitrogen atoms in the ring producing pyrimidin-4-ol followed by H migration from the hydroxyl group to the nearest N atom giving pyrimidin-4(3H)-one, and (4) OH-for-H S_R substitution on the C atom between two nitrogens in the ring leading to 2-hydroxypyrimidin-4(3H)-one and H transfer from the newly added OH group to the ‘bare’ N atom in the ring yielding uracil (pyrimidine-2,4(1H,3H)-dione). Cytosine can be also produced from pyrimidin-2(1H)-one – the product of the reaction sequence (1), via (5) NH₂-for-H substitution occurring by NH₂ addition followed by H loss on the carbon atom adjacent to the bare nitrogen. The alternative reaction sequence leading to cytosine includes (6) NH₂-for-H substitution on the C atom in the pyrimidine ring neighboring one of the N atoms producing pyrimidin-4-amine and (7) OH-for-H substitution on the carbon between two N atoms forming 4-aminopyrimidin-2-ol followed by an H shift from OH to N in the para position with respect to the NH₂-substituted C resulting in cytosine.

Scheme 1 Potential mechanistic radical–molecule pathways for functionalization of pyrimidine to uracil and cytosine.

Scheme 2 illustrates similar NH₂-for-H and OH-for-H substitution and H transfer pathways initiated from the two-ring purine molecule producing the other two RNA nucleobases adenine and guanine. For instance, adenine can be formed directly through the radical NH₂-for-H substitution in purine (8). Two alternative sequences can be realized for the formation of guanine: (9) and (10) or (11) and (12). In (9), OH-for-H S_R takes place on the C atom in the six-membered ring of purine in the ortho position with respect to the junction with the five-membered ring. This substitution produces 7H-purin-6-ol and is followed by the H shift from OH to the neighboring N atom giving rise to 1H-purin-6(7H)-one. Then, the sequence continued by the NH₂-for-H substitution on the carbon between two nitrogens in the six-membered ring (10) leading to guanine. The order of the two substitutions can be reversed: in (11), the NH₂-for-H and substitution on the C atom between two N occurs in the six-membered ring of purine forming 7H-purin-2-amine and then, in (12), OH-for-H S_R can lead to 2-amino-7H-purin-6-ol, with the H shift in the former resulting in guanine. Schemes 1 and 2 show that the described functionalization sequences from pyrimidine to uracil and cytosine and from purine to adenine and guanine are mechanistically feasible and the goal of calculations of the pertinent potential energy surfaces (PESs) is to characterize the reaction energetics and the heights of potential barriers to be overcome for the reactions to occur both in the gas phase and inside water/ammonia ices.

Scheme 2 Potential mechanistic radical–molecule pathways for functionalization of purine to adenine and guanine.

Computational methods

The PESs of cytosine, uracil, adenine, and guanine synthesis through the radical substitution OH-for-H and/or NH₂-for-H mechanisms were computationally explored using the long-range corrected hybrid density functional theory (DFT) ωB97X-D method³⁴ with Pople's split-valence 6-311G(d,p) basis set. Since the OH and NH₂ radicals have doublet electronic states, the radical substitution reaction steps feature intermediates and transition states in doublet states, whereas the H migration reactions following H losses occur on singlet PESs. Only the ground electronic state was considered throughout; in particular, an excited electronic state component correlated with the degenerate ground ²Π state of the OH radical was not included in the calculations. Particular electronic states for each calculated structure are given in Fig. 1–5. The stability of the SCF solution for each structure was routinely checked using the “stable = opt” option in the Gaussian 09 package. Single-point calculations for all stationary structures (reactants, intermediates, transition states, and products) using ωB97X-D/6-311G(d,p) optimized geometries were further conducted at the computationally more accurate G3(MP2,CC) model chemistry^35–37 with the final energies obtained as

E[G3(MP2,CC)] = E[CCSD(T)/6-311G(d,p)] + ΔEMP2 + E(ZPE)

where ΔEMP2 = E[MP2/G3large] − E[MP2/6-311G(d,p)] is the basis set correction and E(ZPE) is the zero-point vibrational energy. The ωB97X-D/6-311G(d,p) combination provides sufficiently accurate geometric structures with errors within bond lengths of 0.01–0.02 Å and bond angles of 1–2°, whereas the G3(MP2,CC) scheme normally gives chemically accurate energies with uncertainties of 5–10 kJ mol⁻¹.

Fig. 1 Potential energy profiles for the functionalization reaction of purine to adenine. Relative energies computed at various levels of theory indicated in the figure are shown in kJ mol⁻¹.

Fig. 2 Potential energy profiles for the functionalization reaction of purine to guanine. Relative energies computed at the G3(MP2,CC)//ωB97X-D/6-311G(d,p) levels of theory are shown in kJ mol⁻¹. The numbers in italics in parentheses show barrier heights (in kJ mol⁻¹) for the critical H-transfer steps computed at the ωB97X-D/6-311G(d,p) level.

Fig. 3 Potential energy profiles for the functionalization reaction of pyrimidine to uracil and cytosine. Relative energies computed at the G3(MP2,CC)//ωB97X-D/6-311G(d,p) levels of theory are shown in kJ mol⁻¹. The numbers in italics in parentheses show barrier heights (in kJ mol⁻¹) for the critical H-transfer steps computed at the ωB97X-D/6-311G(d,p) level.

Fig. 4 Optimized structures of transition states for H migration facilitated by extra H₂O molecules. Lengths of breaking and forming O–H and N–H bonds are denoted in Å. Transition states with no H₂O in sequences (1), (2), and (9) are C_s-symmetric with the ¹A′ electronic states and all other structures have only C₁ symmetry with the ¹A electronic state.

Fig. 5 Optimized structures of transition states for H migration in the pyrimidin-2-ol → pyrimidin-2(1H)-one reaction facilitated by extra NH₃ and CH₃OH molecules. Lengths of breaking and forming O–H and N–H bonds are denoted in Å.

In order to explore the condensed phase effects on the reaction mechanisms and energetics in environments comprised of water, ammonia, or methanol ices, we expanded our calculations by using these molecules as implicit solvents (a dipole field) within two implementations of the self-consistent reaction field SCRF approach, PCM^38,39 and SMD.⁴⁰ Generally, single-point SCRF calculations were carried out using the gas phase optimized ωB97X-D/6-311G(d,p) geometries. For selected cases, SCRF-PCM/ωB97X-D/6-311G(d,p) geometry optimization was carried out but its effect on the relative energies and barrier heights appeared to be insignificant, within a few kJ mol⁻¹. The following solvent parameters were used in the SCRF calculations: liquid water – dielectric constant of 78.3553 and a square of the index of refraction of 1.777849 (as default in the Gaussian 09⁴¹ package); water ice – dielectric constant of 3.17 and a square of the index of refraction of 1.7161;⁴² liquid ammonia – dielectric constant of 22.63 and a square of the index of refraction of 1.76;⁴³ ammonia ice – dielectric constant of 3.4 and a square of the index of refraction of 1.96;⁴⁴ liquid methanol – dielectric constant of 32.613 and a square of the index of refraction of 1.765709;⁴¹ and methanol ice – dielectric constant of 3.0⁴⁵ and a square of the index of refraction of 1.5876.⁴⁶ We have tested the sensitivity of the relative energies along the reaction profile with respect to the implicit presence of liquid water vs. water ice solvent for reaction (1) (see Table S3 in the ESI†). Since no significant differences were found, we used the default parameters of liquid water⁴¹ for the other reactions considered. Microsolvation was also considered by explicitly adding up to four H₂O molecules or up to two NH₃ or CH₃OH molecules in the ωB97X-D/6-311G(d,p) and SCRF-ωB97X-D/6-311G(d,p) calculations. Similar theoretical methods have been recently applied by our group to study quantum-tunneling-mediated synthesis of prebiotic chelation agents in interstellar analog ices,⁴⁷ low-temperature synthesis of interstellar hemiacetals,⁴⁸ and keto–enol isomerization of acetone in ices.⁴⁹ These studies have shown that the direct participation of molecules of protic solvents, such as H₂O, NH₃, or CH₃OH in H migration steps can significantly reduce the reaction barriers.

Cartesian coordinates and vibrational frequencies of all optimized structures along with relative Gibbs free energies along calculated reaction profiles (Table S1, ESI†) and spin densities on non-hydrogen atoms for structures in doublet electronic states (Table S2, ESI†) are provided in the ESI.† All electronic structure calculations were carried out using Gaussian 09⁴¹ (ωB97X-D and SCRF) and MOLPRO 2015⁵⁰ (CCSD(T) and MP2) software packages.

Results and discussion

From purine to adenine

Let us begin with the formation of adenine from purine, which requires only one S_R reaction (8). The relevant potential energy diagram is illustrated in Fig. 1. The reaction begins with NH₂ addition to the ortho position in the six-membered ring via an entrance barrier of 33 kJ mol⁻¹ as computed at our most accurate G3(MP2,CC) level in the gas phase. The initial calculations using the density functional ωB97XD/6-311G(d,p) approach give a qualitatively similar result but underestimate the NH₂ addition barrier height by 11 kJ mol⁻¹. SCRF calculations taking into account the dipole field of the implicit water solvent simulating the embedment of the reacting pair in ice increase the barrier by 12 and 9 kJ mol⁻¹ when the PCM and SMD approaches are used, respectively. If the solvent effect correction computed within ωB97XD/6-311G(d,p) is added to the G3(MP2,CC) value, the barrier height inside the ice can be estimated to be in the range of 42–45 kJ mol⁻¹. The addition complex i1 lies 57 kJ mol⁻¹ lower in energy than the initial purine + NH₂ reactants in the gas phase, where the inclusion of the solvent effect correction would place i1's relative energy in the −58 to −45 kJ mol⁻¹ range. Intermediate i1 can then lose a hydrogen atom from the attacked carbon and produce adenine. The H elimination transition state (TS) is positioned 54 kJ mol⁻¹ above the initial reactants in the gas phase and is expected to be slightly shifted from 9 kJ mol⁻¹ down (SMD) to 4 kJ mol⁻¹ upwards (PCM) inside water ice. For the reaction kinetics in bulk, the absolute reaction barrier is a more significant quantity than the relative energy of the transition state with respect to the initial reactants since the chemical activation energy is expected to be rapidly dissipated to the surrounding ice molecules at each elementary reaction step. Taking this consideration into account, the barrier for the i1 → adenine + H reaction evaluated as 111 kJ mol⁻¹ in the gas phase should be slightly reduced to ∼103 kJ mol⁻¹ in the water ice. The overall purine + NH₂ → adenine + H reaction is anticipated to be nearly isoergic; 2 kJ mol⁻¹ endothermic in the gas phase but with the endothermicity reduced by 0.4–0.9 kJ mol⁻¹ in ice.

In summary, the NH₂-for-H S_R reaction making adenine from purine inside irradiated water/ammonia ices can be feasible if the following conditions are satisfied: (1) the irradiation dissociates ammonia molecules into amino radicals in close vicinity from purine; (2) the energy provided by irradiation is sufficient to overcome the barriers for the NH₂ addition (42–45 kJ mol⁻¹) and the subsequent H elimination from i1 (∼103 kJ mol⁻¹). Also, it is unlikely that the reaction can take place in non-irradiated low-temperature ices and the addition–elimination reaction barriers are too high. On one hand, quantum tunneling can enhance the H elimination step which remains significantly endothermic (by ∼50–60 kJ mol⁻¹), but on the other hand, tunneling is not anticipated to be significant for the addition of the heavy NH₂ moiety. Additionally, the amino radicals cannot be produced without an external supply of energy. The calculations for the purine + NH₂ → adenine + H reaction sequence (8) carried out using different theoretical methods both in the gas and ice phases allow us to conclude that the ωB97X-D/6-311G(d,p) results are generally semi-quantitatively consistent with higher level G3(MP2,CC) values (within 10–15 kJ mol⁻¹ or closer) and that the effect of the surrounding ice molecules considered as a dielectric continuum on the reaction energies and barrier height is relatively small, 12–13 kJ mol⁻¹ for the addition step and much lower for the H elimination reactions. The differences between SCRF PCM and SMD are rather small, with PCM providing more consistent values. With these conclusions in mind, we now move to consider more complex functionalization mechanisms toward uracil, cytosine, and guanine. Taking into account the small effect of the implicit solvent on the energetics of the radical substitution reaction, we do not include this effect into consideration for similar reactions discussed below. Moreover, it will be shown that for the formation of uracil, cytosine, and guanine, H migration steps have the highest barriers and thus represent kinetic bottlenecks. Therefore, in further discussion, we focus on the effect of the presence of explicit and implicit solvent molecules for H migrations.

From purine to guanine

Fig. 2 illustrates potential energy diagrams for two alternative reaction sequences leading to the functionalization of purine to guanine, (9) + (10) and (11) + (12). In reaction (9), the OH radical first adds to the C atom in the six-membered ring in the ortho position with respect to its junction with the six-membered ring. The barrier for the new covalent C–O bond formation here is submerged, with the transition state located at 6 kJ mol⁻¹ below the initial reactants. A van der Waals complex i2 between purine and OH stabilized by 11 kJ mol⁻¹ relative to the reactants resides between them and the addition transition state. Once the barrier is cleared, the covalently bound radical intermediate i3 is formed, 88 kJ mol⁻¹ below purine + OH. This is followed by the H atoms loss from i3 producing 7H-purin-6-ol via a barrier of 91 kJ mol⁻¹ with the transition state located only 3 kJ mol⁻¹ above the reactants. 7H-Purin-6-ol then isomerizes to 1H-purin-6(7H)-one by the H migration from O to N overcoming a high 140 kJ mol⁻¹ barrier. Next, reaction (10) leads to guanine from 1H-purin-6(7H)-one by NH₂-for-H substitution on the carbon atom in the meta position in the six-member ring relative to the carbonyl group. Here, the NH₂ addition barrier is 30 kJ mol⁻¹ and the radical intermediate i4 resides in a 74 kJ mol⁻¹-deep well. H elimination from i4 requires a high barrier of 130 kJ mol⁻¹ with the transition state position 56 kJ mol⁻¹ above the 1H-purin-6(7H)-one + NH₂ reactants. The formation of guanine in reaction (10) is found to be slightly endothermic (by 5 kJ mol⁻¹) but the overall (9) + (10) sequence, purine + OH + NH₂ → guanine + 2H, is 61 kJ mol⁻¹ exothermic overall. The second pathway, (11) + (12) initiates with the NH₂-for-H S_R reaction. In this case, NH₂ addition to the C atom in the six-membered ring of purine located between two N atoms proceeds via a barrier of 47 kJ mol⁻¹ and leads to the intermediate i5 which is 30 kJ mol⁻¹ lower in energy than the reactants. i5 loses an H atom via a high barrier of 76 kJ mol⁻¹ and the transition state which is nearly isoergic with the NH₂ addition transition state. The substitution reaction forms 7H-purin-2-amine with the overall slight exothermicity of 3 kJ mol⁻¹. Next, reaction (12) proceeds by OH-for-H substitution via a van der Waals complex i6 (−11 kJ mol⁻¹) and submerged transition state (−9 kJ mol⁻¹) toward the covalently bound intermediate i7 (−92 kJ mol⁻¹) and the H elimination from the latter leads to 2-amino-7H-purin-6-ol through a 94 kJ mol⁻¹ barrier (2 kJ mol⁻¹ above the 7H-purin-2-amine + OH reactants). Finally, the H shift in 2-amino-7H-purin-6-ol requiring a 141 kJ mol⁻¹ barrier completes the formation of guanine. The energetics of reaction (12) appears to be very similar to reaction (9) indicating that the NH₂ substitution (from purine to 7H-purin-2-amine) practically should not affect the mechanism and kinetics of the OH-for-H substitution reaction. Comparing the (9) + (10) and (11) + (12) reaction sequences, we can conclude the functionalization process starting with the NH₂-for-H substitution reaction and followed by the OH-for-H substitution is slightly more favorable than the process in the reverse order because the NH₂-for-H S_R reaction is energetically preferable in unsubstituted purine than in 1H-purin-6(7H)-one. However, the differences in the critical barriers for H loss and the reaction energies for (10) and (11) do not exceed 10 kJ mol⁻¹. The potential energy diagrams for the OH-for-H substitution and H migration reactions (9) and (12) are very similar.

From pyrimidine to uracil and cytosine

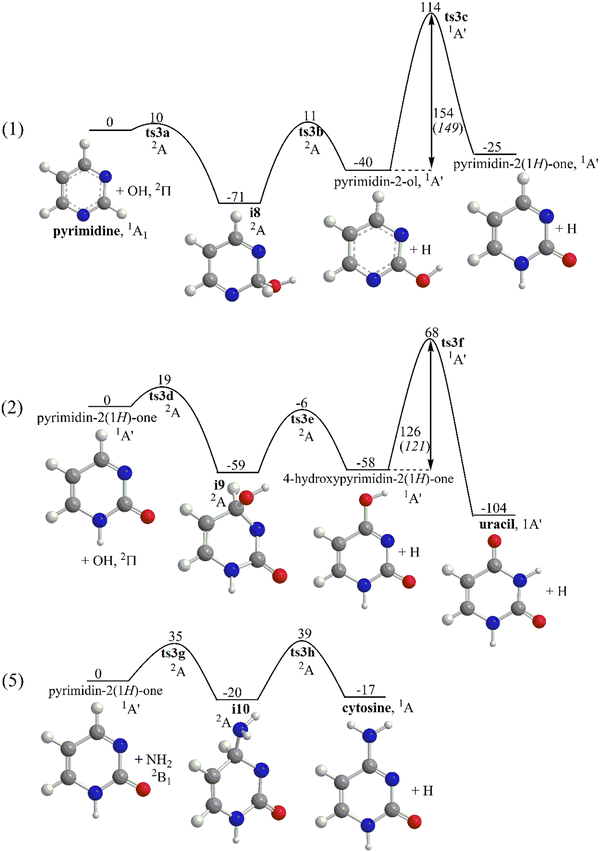
Selected reaction pathways for the functionalization of pyrimidine to uracil (1) + (2) and to cytosine (1) + (5) are illustrated in Fig. 3. The common reaction sequence (1) begins with O addition to the C atom in pyrimidine sandwiched between two N's with a barrier of 10 kJ mol⁻¹ as computed at the G3(MP2,CC) level of theory. The addition complex i8 resides 71 kJ mol⁻¹ below the reactants and can undergo H elimination which requires overcoming a barrier of 82 kJ mol⁻¹ (11 kJ mol⁻¹ above the reactants) to produce pyrimidin-2-ol. The OH-for-H S_R reaction from pyrimidine to pyrimidin-2-ol is 40 kJ mol⁻¹ exothermic. The second reaction step in (1) is H migration from the hydroxyl group to a neighboring nitrogen atom, which exhibits a higher barrier, 154 (149) kJ mol⁻¹ at the G3(MP2,CC) (ωB97X-D/6-311G(d,p)) levels. Note that at temperatures where the rotation of the OH group around the single CO bond in pyrimidin-2-ol is facile, the two N atoms in pyrimidin-2-ol are equivalent and the H migration can occur to any of them. From pyrimidin-2-ol, the functionalization process can proceed to either uracil (2) or cytosine. The reaction toward uracil involves yet another OH-for-H radical substitution reaction, this time on the C atom located in the para position with respect to the NH group. The OH addition step requires a 19 kJ mol⁻¹ barrier to be overcome and the bound species formed, i9, resides 59 kJ mol⁻¹ below the pyrimidin-2(1H)-one + OH reactants. Then, H elimination from i9 produces 4-hydroxypyrimidin-2(1H)-one via a barrier of 65 kJ mol⁻¹ in a nearly isoergic reaction. Finally, H shift from O to N in 4-hydroxypyrimidin-2(1H)-one forms uracil. The H migration step is rate-controlling in the entire reaction sequence (2) because of a high 126 kJ mol⁻¹ barrier. Overall, the pyrimidin-2(1H)-one + OH → uracil + H reaction is computed to be 104 kJ mol⁻¹ exothermic, which is significantly higher than the energy gain in reaction (1). The overall exothermicity of the (1) + (2) functionalization process, pyrimidine + 2OH → uracil + 2H is 129 kJ mol⁻¹.

The formation of cytosine can be also initiated by reaction (1). It is followed by the NH₂-for-H S_R reaction (5) where the amino radical adds to pyrimidin-2(1H)-one to the para C atom (relative to the OH group) via a 35 kJ mol⁻¹ barrier to form i10 stabilized by 20 kJ mol⁻¹. The ensuing H elimination from the attacked carbon requires a barrier of 59 kJ mol⁻¹ (39 kJ mol⁻¹ above the pyrimidin-2(1H)-one + NH₂ reactants) and produces cytosine, with the overall reaction being 17 kJ mol⁻¹ exothermic. The (1) + (5) functionalization process, pyrimidine + OH + NH₂ → cytosine + 2H is 42 kJ mol⁻¹ exothermic. Summarizing the (1) + (2) and (1) + (5) reaction sequences from pyrimidine to uracil and cytosine in the gas phase, one can see that the addition–elimination reactions feature moderate barriers, from 10–20 kJ mol⁻¹ when hydroxyl is involved to 35–40 kJ mol⁻¹ with NH₂ participation. The rate determining step in the reactions introducing the carbonyl function on the pyrimidine ring is the H shift from OH to N following OH-for-H substitution. For instance, in (1) and (2) the corresponding barriers are 154 and 126 kJ mol⁻¹ making this step improbable under low temperature conditions. It should be noted that the mechanistic and energetic similarities of the OH-for-H and NH₂-for-H substitutions and OH to N migrations allow us to anticipate analogous behavior for the (3) + (4) and (6) + (7) reaction sequences leading to the formation of uracil and cytosine, respectively, which are not considered in detail in the present work.

Enhancement of H migrations in protic solvents

Can the H migration barriers be reduced in the condensed phase, in particular, in water ices? To address this question, we considered microsolvation of the reacting molecules with one to four water molecules, which can be directly involved in the H transfer process. The results are illustrated in Table 1 and Fig. 4. The inclusion of one H₂O molecule in the H shift in reaction (1) reduced the barrier by ∼100 kJ mol⁻¹ from 154 (149) to 54 (49) kJ mol⁻¹ as computed at the G3(MP2,CC) (ωB97X-D/6-311G(d,p)) levels of theory. The inclusion of implicit solvent using the SCRF-PCM approach at the ωB97X-D/6-311G(d,p) level results in a further barrier reduction to 43 kJ mol⁻¹ but this change is small and could be within the margins of error of the method. The reason for the drastic barrier decrease can be understood by looking at the transition state structures (Fig. 3). Without extra H₂O participating in the reaction, the transition state features a strained four-member ring rhombic structure. When H₂O is involved, H is transferred via a six-membered ring. Here, one H atom shifts from OH to the water molecule, which in turn donates one of its H atoms to the nitrogen atom. Interestingly, the critical fragment involved in the H migrations is reminiscent of the hydronium ion H₃O⁺, with the two forming/breaking O–H bond lengths of 1.155 and 1.171 Å, i.e., 12–14% elongated as compared to the O–H bond length in hydronium, 1.027 Å. The partial Mulliken charge on the transient H₃O fragment is +0.40 e. With two water molecules participating in the reaction, the H transfer barrier is further reduced to 42 and 36 kJ mol⁻¹ without and with the effect of implicit solvent taken into account, respectively. In this case, the transition state involves an eight-member ring structure featuring a transient Zündel ion H₅O₂⁺ fragment (Fig. 3) with the +0.59 e partial charge. Here, three H atoms are being transferred simultaneously; the initial breaking O–H bond and the ultimately forming N–H bond are stretched to 1.398 and 1.472 Å, respectively, whereas the O–H bonds involving H atoms in transit in the Zündel fragment are 1.06–1.07 Å at the periphery and ∼1.20 Å for the central hydrogen atom. Adding extra water molecules directly partaking in the H transfer results in a noticeable barrier increase, to 48 and 57 kJ mol⁻¹ at the SCRF-PCM ωB97X-D/6-311G(d,p) level of theory for three and four H₂O. This increase in the barrier height, from 54 (42) kJ mol⁻¹ with two H₂O molecules to 70 (66) and 89 (77) kJ mol⁻¹ with three and four water molecules, respectively, as computed at the G3(MP2,CC) (ωB97X-D/6-311G(d,p)) levels of theory, is more pronounced when the implicit solvent is not taken into account. Interestingly, the transition state structure with three waters has a central hydronium ion-like fragment, whereas two other H₂O moieties look like slightly distorted neutral water molecules. The transition state with 4 H₂O features a central transient Zündel H₅O₂⁺ moiety with two neutral waters adjacent to the O and N atoms in the pyrimidin-2-ol skeleton. Thus, the H transfer barrier is minimal with 2 water molecules with the Zündel structure in the transition state, but the barrier with one extra H₂O and with the transition state involving a hydronium structure is only slightly higher, by 7 kJ mol⁻¹.

Table 1 Barrier heights (in kJ mol⁻¹) for the H migration steps in the presence of explicit water molecules in ice directly participating in the reaction calculated at the SCRF-PCM/ωB97X-D/6-311G(d,p) level of theory^a

Reaction	No H2O	1H2O	2H2O	3H2O	4H2O
a Numbers in parentheses show the results computed at the ωB97X-D/6-311G(d,p) and G3(MP2,CC) (in bold) levels without SCRF-PCM.
Sequence (1)	145 (149, 154)	43 (49, 54)	36 (42, 54)	48 (66, 70)	57 (77, 89)
Sequence (2)	127 (121, 126)	31 (32, 36)	29 (30, 37)	40 (45, 52)	48 (60, 70)
Sequence (9)	139 (137, 140)	35 (37, 43)	26 (28, 42)	36 (51, 67)
Sequence (12)	137 (137, 141)	35 (37, 41)	29 (30, 38)	39 (46, 59)

---

Similar trends are observed in the H migration step of the reaction sequence (2). The reaction barrier falls from 126 (121) kJ mol⁻¹ without extra water involvement to 36 (32) and 37 (30) with one and two H₂O molecules and then rises to 52 (45) and 70 (60) kJ mol⁻¹ with three and four H₂O; the values outside and in parentheses are computed at the G3(MP2,CC) and ωB97X-D/6-311G(d,p) levels, respectively. With the effect of the implicit solvent included at the SCRF-PCM ωB97X-D/6-311G(d,p) level, the computed barriers are 127, 31, 29, 40, and 48 kJ mol⁻¹ with zero, one, two, three, and four H₂O molecules involved (Table 1). Minimal barriers are found again with one and two water molecules and they are practically not different within the accuracy of the calculations. The transition state structures with one and three waters contain a central transient hydronium ion, whereas the structures with two and four waters include a Zündel ion moiety. Thus, microsolvation with explicit water molecules is able to dramatically enhance the H migration process, whereas the effect of the implicit solvent on the barrier height is generally small, similar to that computed for the NH₂-for-H radical substitution reaction, exceeding 5 kJ mol⁻¹ only for the barrier with four water molecules. The only subtle difference is that macrosolvation tends to slightly decrease the H shift barriers, whereas the NH₂ addition and H elimination barriers grow a little when implicit solvent interactions are included.

The ability of microsolvation to enhance the H transfer process appears not to be unique for H₂O but general for protic solvents. This is demonstrated by the calculations of the barrier height for the pyrimidin-2-ol → pyrimidin-2(1H)-one reaction in the presence of one or two extra ammonia and methanol molecules (Table 2 and Fig. 5). In particular, the barrier decreases from 149 kJ mol⁻¹ at the ωB97X-D/6-311G(d,p) level to 53 and 48 kJ mol⁻¹ when one and two intermediary NH₃ molecules are involved in the reaction and to 45 and 35 kJ mol⁻¹ with the participation of one and two methanol molecules, respectively. The effect of the macrosolvation evaluated using the SCRF-PCM calculations is relatively small and similar to that for water in the case of methanol. Here, the H migration barrier is further reduced to 42 (39) and 32 (29) kJ mol⁻¹ with one and two extra CH₃OH, respectively, when the solvent parameters of methanol ice (liquid) are employed in PCM. The influence of macrosolvation in ammonia is more significant; the barrier falls to 37 (24) and 26 (13) kJ mol⁻¹ with one and two NH₃ participating in microsolvation when the reaction takes place encapsulated in ammonia ice (liquid ammonia). It can be seen that while the PCM calculations affect the optimized transition state geometries, especially with NH₃, the energy changes are rather small, with the barrier heights obtained with and without SCRF-PCM geometry optimization do not differ by more than 3 kJ mol⁻¹, being within the anticipated accuracy of the theoretical method.

Table 2 Barrier height (in kJ mol⁻¹) for the H migration step in the pyrimidin-2-ol → pyrimidin-2(1H)-one reaction in the presence of one or two explicit ammonia and methanol molecules directly participating in the reaction calculated at the ωB97X-D/6-311G(d,p) and SCRF-PCM/ωB97X-D/6-311G(d,p) levels of theory^a

	Gas phase	1NH3	2NH3	1CH3OH	2CH3OH
a Numbers in parentheses show the single-point results computed at the SCRF-PCM/ωB97X-D/6-311G(d,p) level using ωB97X-D/6-311G(d,p) geometries optimized without SCRF. b PCM calculations were performed using the parameters for liquid ammonia (dielectric constant of 22.63 and a square of the index of refraction at optical frequencies of 1.76) and liquid methanol (dielectric constant of 32.613 and a square of the index of refraction at optical frequencies of 1.765709). c PCM calculations were performed using the parameters for the ammonia ice (dielectric constant of 3.4 and a square of the index of refraction at optical frequencies of 1.96) and the methanol ice (dielectric constant of 3.0 and a square of the index of refraction at optical frequencies of 1.5876).
No PCM	149	53	48	45	35
PCM–liquid^b		24 (27)	13 (15)	39 (39)	29 (28)
PCM–ice^c		37 (36)	26 (26)	42 (42)	32 (31)

---

As in the functionalization reactions of pyrimidine, the critical reaction steps in the functionalization of purine to guanine are H migrations from OH to N featuring the highest barriers of ∼140 kJ mol⁻¹. Similar to the pyrimidine reactions, these barriers can be drastically reduced as a result of the direct involvement of water molecules. For instance, in reaction (9) the barrier falls from 140 (137) kJ mol⁻¹ without extra water participation, to 43 (37), 42 (28), and 67 (51) kJ mol⁻¹ when one, two, or three H₂O molecules, respectively, participate in the H transfer process, as computed at the G3(MP2,CC) (ωB97X-D/6-311G(d,p)) levels of theory. The inclusion of implicit solvent affects the H transfer barrier heights only slightly reducing them by 2 kJ mol⁻¹ with one and two H₂O molecules and by 15 kJ mol⁻¹ with three H₂O. A similar behavior is observed also for reaction (12) where the H transfer barrier falls from 141 (137) kJ mol⁻¹ in the gas phase to 41 (37), 38 (30), and 59 (46) kJ mol⁻¹ with one, two, or three extra waters and the implicit solvent effect is also rather small. The effect of microsolvation on the critical barrier height maximizes with two water molecules. The structures of the transition states are reminiscent of those found in reactions (1) and (2). The transition states with two H₂O molecules feature a transient Zündel ion structure (Fig. 4), and those with one H₂O have a clearly distinguishable hydronium ion moiety.

Conclusions

Ab initio and DFT electronic structure calculations of the potential energy profiles for the functionalization of pyrimidine to cytosine and uracil and purine to adenine and guanine via neutral radical–molecule substitution reactions involving NH₂ and OH radicals show that these reactions are plausible and involve moderate barriers for the radical addition and H atom elimination steps. The OH-for-H substitution reaction steps are the most facile, with barriers varying from submerged to 19 kJ mol⁻¹. The OH-for-H S_R reactions have lower barriers on purine (submerged – ∼4 kJ mol⁻¹) than on pyrimidine (10–19 kJ mol⁻¹). The NH₂-for-H substitution reactions are more energetically demanding, with their barriers ranging between 33 and 54 kJ mol⁻¹. No significant differences have been found in the energetic parameters for the NH₂-for-H substitutions on pyrimidine and purine. In the gas phase, the critical reaction step is the H shift following the OH-for-H substitution with barriers as high as 126–154 kJ mol⁻¹. However, these barriers can be greatly reduced with the direct involvement of 1–2 protic solvent molecules (e.g., H₂O, methanol, and NH₃) in ices, to only ∼30–50 kJ mol⁻¹, thus making the H migrations comparable in terms of the energy demands with the NH₂-for-H substitution reaction steps. Minimal barriers have been found with the participation of two solvent molecules in the H transfer process. The barriers with the involvement of only one solvent molecule are slightly higher than those with two molecules and the increase in the number of solvent molecules directly taking part in the reaction to three and four raises the barriers significantly. For the reactions in water ice, the H transfer transition state structures mainly involve transient hydronium (H₃O⁺) and Zündel (H₅O₂⁺) ions in the hydrogen migration process. The presence of an implicit solvent (dielectric continuum) does not significantly affect the reaction energetics and barrier heights for radical substitutions but slightly reduces the H shift barriers, where this effect is found to be most pronounced (up to ∼20 kJ mol⁻¹) inside ammonia ice.

As compared to the functionalization mechanisms involving ion-neutral radical reactions, the radical–molecule reactions are less exoergic but the input energy requirements to produce radicals via homolytic bond cleavages are generally lower than for ionization of closed shell molecules. The OH-for-H and especially NH₂-for-H substitution steps are hindered by barriers and cannot occur in ices at low temperatures unless the required energy is provided by irradiation. The alternative could be barrierless radical–radical reactions between NH₂/OH and the radicals formed by C–H bond cleavages in pyrimidine or purine. The H migration steps also have barriers too high to be plausible at very low temperatures even with the help of microsolvation, but they can be accomplished via quantum tunneling. Overall, except for the formation of adenine from purine, functionalization of pyrimidine and purine to the RNA nucleobases has been found much more preferable in the condensed phase than in the gas phase owing to the great enhancement of the H transfer from OH to N by microsolvation by protic solvent molecules.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the Supercomputer Center “Sergey Korolev” at Samara National Research University and the Instructional & Research Computing Center (IRCC, web: https://ircc.fiu.edu) at FIU for providing HPC computing resources that have contributed to the research results reported within this paper.

References

1. B. M. Jones, F. Zhang, R. I. Kaiser, A. Jamal, A. M. Mebel, M. A. Cordiner and S. B. Charnley, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 452–457.
2. L. Zhou, W. Zheng, R. I. Kaiser, A. Landera, A. M. Mebel, M.-C. Liang and Y. L. Yung, Astrophys. J., 2010, 718, 1243–1251.
3. N. F. Kleimeier, Y. Liu, A. M. Turner, L. A. Young, C. H. Chin, T. Yang, X. He, J. I. Lo, B. M. Cheng and R. I. Kaiser, Phys. Chem. Chem. Phys., 2022, 24, 1424–1436.
4. A. M. Mebel, A. Landera and R. I. Kaiser, J. Phys. Chem. A, 2017, 121, 901–926.
5. S. Doddipatla, A. M. Thomas, C. He, Z. Yang, R. I. Kaiser, G. R. Galimova, A. N. Morozov and A. M. Mebel, Sci. Adv., 2021, 7, eabd4044.
6. A. Landera and A. M. Mebel, Faraday Discuss., 2010, 147, 479–494.
7. S. B. Morales, C. J. Bennett, S. D. Le Picard, A. Canosa, I. R. Sims, B. J. Sun, P. H. Chen, A. H. H. Chang, V. V. Kislov, A. M. Mebel, X. Gu, F. Zhang and R. I. Kaiser, Astrophys. J., 2011, 742, 26.
8. L. I. Krikunova, A. A. Nikolayev, D. P. Porfiriev and A. M. Mebel, J. Chin. Chem. Soc., 2023, 70, 439–450.
9. Z. Yang, C. He, S. J. Goettl, A. M. Mebel, P. F. G. Velloso, M. O. Alves, B. R. L. Galvão, J.-C. Loison, K. M. Hickson, M. Dobrijevic, X. Li and R. I. Kaiser, Nat. Astron., 2024, 8, 856–864.
10. R. Hayatsu, Science, 1964, 146, 1291–1293.
11. C. E. Folsome, J. Lawless, M. Romiez and C. Ponnamperuma, Nature, 1971, 232, 108–109.
12. P. G. Stoks and A. W. Schwartz, Nature, 1979, 282, 709–710.
13. Z. Martins, O. Botta, M. L. Fogel, M. A. Sephton, D. P. Glavin, J. S. Watson, J. P. Dworkin, A. W. Schwartz and P. Ehrenfreund, Earth Planet. Sci. Lett., 2008, 270, 130–136.
14. M. P. Callahan, K. E. Smith, H. J. Cleaves, II and J. P. Dworkin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13995–13998.
15. Z. Martins, Life, 2018, 8, 28.
16. Y.-J. Kuan, S. B. Charnley, H.-C. Huang, W.-L. Tseng and Z. Kisiel, Mon. Not. R. Astron. Soc., 2003, 345, 650–656.
17. S. B. Charnley, Y.-J. Kuan, H.-C. Huang, O. Botta, H. M. Butner, N. Cox, D. Despois, P. Ehrenfreund, Z. Kisiel, Y.-Y. Lee, A. J. Markwick, Z. Peeters and S. D. Rodgers, Adv. Space Res., 2005, 36, 137–145.
18. Y. Oba, Y. Takano, H. Naraoka, N. Watanabe and A. Kouchi, Nat. Commun., 2019, 10, 4413.
19. M. P. Bernstein, S. A. Sandford, L. J. Allamandola, J. Seb Gillette, S. J. Clemett and R. N. Zare, Science, 1999, 283, 1135–1138.
20. M. P. Bernstein, J. E. Elsila, J. P. Dworkin, S. A. Sandford and L. J. Allamandola, Meteorit. Planet. Sci., 2001, 36, 351–358.
21. M. P. Bernstein, J. E. Elsila, J. P. Dworkin, S. A. Sandford, L. J. Allamandola and R. N. Zare, Astrophys. J., 2002, 576, 1115–1120.
22. M. P. Bernstein, L. P. Moore, J. E. Elsila, S. A. Sandford, L. J. Allamandola and R. N. Zare, Astrophys. J., 2003, 582, L25–L29.
23. M. Nuevo, S. N. Milam, S. A. Sandford, J. E. Elsila and J. P. Dworkin, Astrobiology, 2009, 9, 683–695.
24. J. E. Elsila, M. R. Hammond, M. P. Bernstein, S. A. Sandford and R. N. Zare, Meteorit. Planet. Sci., 2006, 41, 785–796.
25. M. Nuevo, S. N. Milam and S. A. Sandford, Astrobiology, 2012, 12, 295–314.
26. M. Nuevo, C. K. Materese and S. A. Sandford, Astrophys. J., 2014, 793, 125–131.
27. S. A. Sandford, P. P. Bera, T. J. Lee, C. K. Materese and M. Nuevo, Top. Curr. Chem., 2015, 356, 123–164.
28. C. K. Materese, M. Nuevo and S. A. Sandford, Astrobiology, 2017, 17, 761–770.
29. P. P. Bera, T. J. Lee and H. F. Schaefer, III, J. Chem. Phys., 2009, 131, 074303.
30. A. M. Hamid, P. P. Bera, T. J. Lee, S. G. Aziz, A. O. Alyoubi and M. S. El-Shall, J. Phys. Chem. Lett., 2014, 5, 3392–3398.
31. P. P. Bera, M. Nuevo, S. N. Milam, S. A. Sandford and T. J. Lee, J. Chem. Phys., 2010, 133, 104303.
32. P. P. Bera, M. Nuevo, C. K. Materese, S. A. Sandford and T. J. Lee, J. Chem. Phys., 2016, 144, 144308.
33. P. P. Bera, T. Stein, M. Head-Gordon and T. J. Lee, Astrobiology, 2017, 17, 771–785.
34. J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
35. L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764–7776.
36. L. A. Curtiss, K. Raghavachari, P. C. Redfern, A. G. Baboul and J. A. Pople, Chem. Phys. Lett., 1994, 314, 101–107.
37. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650–7657.
38. V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417.
39. F. Lipparini, G. Scalmani, B. Mennucci, E. Cances, M. Caricato and M. J. Frisch, J. Chem. Phys., 2010, 133, 014106.
40. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.1, Gaussian Inc., Wallingford, CT, 2009.
42. S. Evans, J. Glaciol., 2017, 5, 773–792.
43. V. Streitferdt, S. M. Tiefenthaler, I. G. Shenderovich, S. Gärtner, N. Korber and R. M. Gschwind, Eur. J. Inorg. Chem., 2021, 3684–3690.
44. C. P. Smyth and C. S. Hitchcock, J. Am. Chem. Soc., 2002, 56, 1084–1087.
45. D. W. Davidson, Can. J. Chem., 1957, 35, 458–473.
46. R. Luna, G. Molpeceres, J. Ortigoso, M. A. Satorre, M. Domingo and B. Maté, Astron. Astrophys., 2018, 617, A116.
47. J. H. Marks, A. A. Nikolayev, M. M. Evseev, J. Wang, A. M. Turner, N. F. Kleimeier, O. V. Kuznetsov, M. McAnally, A. N. Morozov, I. O. Antonov, A. M. Mebel and R. I. Kaiser, Chem, 2023, 9, 3286–3303.
48. J. Wang, A. A. Nikolayev, J. H. Marks, M. Mcanally, V. N. Azyazov, A. K. Eckhardt, A. M. Mebel and R. I. Kaiser, J. Phys. Chem. Lett., 2023, 14, 6078–6085.
49. J. Wang, A. A. Nikolayev, C. Zhang, J. H. Marks, V. N. Azyazov, A. K. Eckhardt, A. M. Mebel and R. I. Kaiser, Phys. Chem. Chem. Phys., 2023, 25, 17460–17469.
50. H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos and A. Bernhardsson, MOLPRO, Version 2015.1, A Package of Ab Initio Programs, University of Cardiff, Cardiff: UK, 2015.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nj03552f

---