 Open Access Article
Open Access ArticleUnravelling quantum dot–molecule interactions for π-conjugated ligands: insights into binding and anchoring group effects†
Yinon
Deree
,
Adar
Levi
 ,
Xiang
Li
,
Ori
Gidron
,
Xiang
Li
,
Ori
Gidron
 * and
Uri
Banin
* and
Uri
Banin
 *
*
Institute of Chemistry and the Center for Nanoscience and Nanotechnology, The Hebrew University, Jerusalem 91904, Israel. E-mail: ori.gidron@mail.huji.ac.il; uri.banin@mail.huji.ac.il
First published on 19th June 2025
Abstract
Quantum dots (QDs) coated with π-conjugated ligands display triplet energy transfer (TET), which opens the path for photon upconversion via QD photosensitization. Herein we study the effect of the ligand binding and its orientation on the triplet energy transfer efficiency through analysing the quenching of the QD photoluminescence. Comparing anthracene ligands with different anchoring groups, we find that replacing carboxylate with thiol or dithiol groups enhances quenching rates by factors of 3 and 4.5, respectively. To obtain this quantitative information, we devise a modified Stern–Volmer model taking into account the Poisson distribution of the ligand binding on the QDs. To this end, we show that bound anthracene-based ligands exhibit distinct spectral changes in their absorption spectra, including a ligand-dependent bathochromic shift with a modified vibronic progression and broadened spectral width. These changes, related to the deprotonation of the anchoring groups upon binding and the confined environment on the QD surface, enable the distinction of the crossover from bound to free ligands upon ligand addition. This allows us to incorporate accurate ligand binding stoichiometry to extract reliable quenching rates. Consistent with DFT calculations, the improved quenching for the thiolated anthracenes is ascribed to the parallel orientation of the π-system relative to the QD surface enabling larger orbital overlap that leads to faster TET rates via the Dexter mechanism. This work contributes to the design principles for efficient QD–organic hybrid systems towards improved triplet energy transfer.
New conceptsHybrid systems composed of quantum dots (QDs) and π-conjugated organic ligands are widely used in optoelectronic and photochemical applications that rely on triplet energy transfer (TET). However, the design of such systems is hindered by the lack of reliable tools to quantify ligand binding, an essential parameter that governs energy transfer rates. Here, we introduce a novel optical method to quantify ligand binding to QDs, based on distinct and reproducible spectral changes in anthracene-based ligands with different anchoring groups. These changes enable accurate determination of ligand stoichiometry and are used to develop a modified Stern–Volmer analysis that accounts for ligand distribution. We show that thiolated ligands not only bind more effectively but also enhance quenching rates due to their favorable parallel π-system orientation relative to the QD surface, as supported by DFT calculations. This work establishes a new framework for quantitatively analyzing QD–ligand interactions and provides practical design principles for optimizing hybrid systems in photon upconversion and related applications. |
Introduction
Hybrid systems composed of organic molecules and inorganic QDs play a crucial role in triplet energy transfer (TET)1–3 and photoinduced electron transfer (PET),4,5 two fundamental processes in various optoelectronic and photochemical applications. These processes are essential for technologies such as photocatalysis,6,7 photochemistry,6,8 photon upconversion,9,10 and singlet fission,11,12 where efficient energy and electron transfer are crucial for enhancing system performance. In such hybrid systems, π-conjugated ligands such as anthracene and tetracene carboxylic acid are frequently used, as their singlet and triplet energies are aligned with that of the QDs. Specifically, anthracene carboxylic acid (ACA) is considered a benchmark molecule in such hybrid systems.1,3,13–15Along with matching the energy levels, an additional parameter concerns the orientation of the π-system relative to the QD surface that affects the QD–molecule orbital overlap. To this end, we compare anthracene ligands bearing carboxylate, thiol, and dithiol anchoring groups (ACA, TA, and DTA, respectively; Fig. 1a), which all lead to quenching of the QD photoluminescence (PL) upon binding, an indication of their functionality in TET. For analysis of the QD–ligand interaction, it is crucial to determine whether binding has occurred, as well as to quantify the number of bound ligands. Anthracene covalently bound to silicon QDs exhibits a red shift and broadening in its absorption spectrum,16,17 attributed to electronic coupling. However, no spectral changes have been reported for carboxylate or thiol ligands bound to QDs. Therefore, the number of bound ligands is commonly approximated under the assumption that the extinction coefficient of the ligand does not change significantly upon binding, and that the absorbance originates from the bound ligand.3,16–18 Deviations from one of these assumptions would lead to substantial errors in estimating the number of bound ligands per QD, and consequently, to substantial errors in estimating the TET rates.
Here we develop a modified Stern–Volmer (SV) equation that allows for extracting the quenching rate of a single bound ligand, taking into account the Poisson distribution of ligand binding. The analysis is based on our observation that binding the anthracene ligands leads to distinct spectral changes in their absorption spectra, including a ligand-dependent bathochromic shift with a modified vibronic progression and broadened spectral width. These spectral changes arise predominantly from the deprotonation of the anchoring group upon binding, with additional contributions from changes in the surrounding environment. These distinct changes serve as an indicator of ligand binding, enabling accurate quantification of the average number of ligands bound per QD. We find that replacing the carboxylic anchoring group with thiol or dithiol anthracene results in a 3 and 4.5-fold increase in the quenching rate, respectively. The enhanced quenching rate for the thiolated ligands is attributed to the parallel orientation of the π-system relative to the QD surface, enabling optimal orbital overlap, in agreement with DFT calculations. These findings facilitate the direct measurement of the QD ligand energy transfer process, providing further design principles towards the optimization of such hybrid systems.
Results and discussion
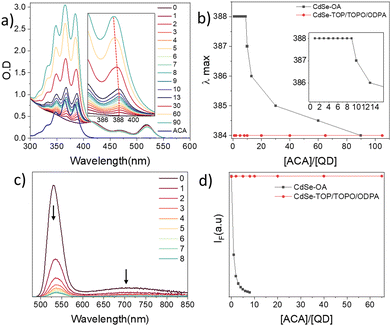
Upon adding 2 equivalents of the ligands to the CdSe QDs solution (2 equivalents correspond to an average of 2 ligands per QD, QD diameter 2.7 nm), significant PL quenching is observed, as reported in prior works for ACA (Fig. 1a). Remarkably, the thiolated ligands manifest a higher degree of quenching compared to the ACA, already pointing out the centrality of binding and ligand orientation in determining the TET efficiency. For quantitative information on the transfer rates, the dependence of the PL quenching on ligand coverage needs to be analysed. To this end, the first step is to quantify the degree of binding of the added ligands. Notably, we observe that the addition of ligands was also accompanied by a distinct shift of the absorption in the region of the ligands (Fig. 1a). This bathochromic shift depends on the ligand type, ranging from 33 meV for carboxylic bound ACA, to 50 meV for the AT that binds via a single thiol, to 63 meV for ADT with the two thiol groups. The bathochromic shift is accompanied by spectral broadening, most pronounced for ADT. The relative intensities of the vibronic peaks also change upon binding, which is related to the difference between ground and excited geometries. This difference is more pronounced for the thiolated ligands AT and ADT, as the 0–0 transition intensifies compared to the 0–1 and 0–2 transitions. This indicates a more rigid structure of the bound ligand compared to the free ligand. The bathochromic shift was also accompanied by a substantial increase in the extinction coefficient, as illustrated by the different intensities of equimolar solutions of free (blue) and bound (green) ligands in Fig. 1a. The increase in molar absorption coefficient is especially pronounced for ACA, with the bound ligand exhibiting nearly double the absorbance of the free ligand.To explain the spectral changes upon binding, we measured the absorbance spectra of the deprotonated ligands using triethylamine and sodium methoxide as bases (Fig. S3–S5, ESI†). The spectral changes upon deprotonation correlate with the changes observed for the bound ligands. However, slight differences indicate that while deprotonation accounts for the major spectral changes observed upon binding, other factors, such as different chemical environments (Fig. S3–S5, ESI†) or electronic coupling, also contribute. Overall, binding affects the absorption spectra and the intensity of both the carboxylate and thiol ligands. An illustration of ACA binding to QD–OA is represented in Fig. 1b, where proton exchange takes place between OA− and ACA.
To extract the quantitative quenching rates, we measured the emission and absorption upon the addition of ligands, as illustrated in Fig. 2 for ACA ligands added to CdSe–OA QDs. The red-shifted absorption, which is ascribed to the bound ligands, does not change upon adding the first 10 equivalents (Fig. 2a). The addition of more ACA ligands (>10 equivalents) results in a blue shift, indicating the presence of both bound and free ligands. This is clearly observed when plotting the lowest energy vibronic peak as a function of the ACA-to-QD ratio (Fig. 2b). Thus, there exists a regime where determining the average number of bound ligands is straightforward, being equal to the ligand-to-QD concentration ratio, as all ligands are bound under these conditions.
The binding also results in the quenching of the QD emission (Fig. 2c). Both the ligand spectral changes and the QD emission quenching were reversible upon the addition of OA, confirming that the binding of the labile ligand ACA is in equilibrium (Fig. S10 and S16, see ESI†). In contrast, starting from TOP/TOPO/ODPA ligands (TOP/O-trioctylphosphine/oxide; ODPA-octadecylphosphonic acid), which bind strongly to CdSe-QDs, no spectral change or emission quenching is observed, even upon addition of >60 equivalents of ACA (Fig. S17, see ESI†).19 This confirms that TET requires direct ligand–QD surface binding, in line with the Dexter mechanism as previously reported.3,18
To understand why these spectral changes were previously overlooked, we need to consider the methods commonly used to prepare such hybrid systems: the most frequently applied preparation methods involve ligand replacement with a significant excess of ACA ligands, followed by the removal of any excess unbound ligands by washing.3,18,20–23 We found that the washing process not only removes free ligands but also a portion of the bound ligands (Fig. S6, ESI†), inhibiting precise control and determination of the ligand coverage. The less commonly applied method is direct mixing, which involves ligand replacement without subsequent removal of free ligands.14,15,24 We found that this method enables better monitoring of the binding process and that the binding occurs almost instantaneously without the need for prolonged heating or sonication used in previous reports. At low ligand concentrations, nearly all the ligand molecules bind to the QD as confirmed by an equilibrium model (Fig. S1, see ESI†). This explains the absence of free ACA molecules below 10 equivalents. Since only 10 equivalents of ligands fully bind, the spectral changes are noticeable only at low ligand concentrations (Fig. 2a), which may explain why this phenomenon was previously overlooked.
Establishing the quantitative determination of the bound ligands allows us to introduce a model for extracting the quenching rates, which provides a measure of the TET processes. The SV equation, which addresses the effect of quenchers on the PL, is traditionally applied to molecules, not QDs, requiring further consideration. For instance, in the SV plot, the x-axis represents the concentration of the quencher, but this concentration is a less relevant variable for QDs. Instead, the average number of ligands bound to the QDs would be a more appropriate variable.
Additionally, SV analysis is typically used for two types of quenching mechanisms: dynamic and static. Dynamic quenching is unlikely, as collisions between the QDs and free molecules in solution do not typically quench the PL as observed above for the CdSe-TOP/TOPO/ODPA case. Instead, the quenching mechanism is static, i.e. between essentially bound anthracene ligands and the QDs.
Moreover, unlike molecules that undergo static quenching by forming a ground-state complex with a single quencher molecule, QDs can bind multiple quencher molecules. Furthermore, the extent to which a single ligand will quench the QD PL needs to be determined. If a single bound molecule were to completely turn off the emission of the QDs, the lifetime of the QDs should remain unaffected upon adding quenchers to the solution. This is because only the QDs without bound molecules would contribute to the signal, being the only ones capable of emitting light. However, as shown in Fig. 3a, the lifetime decreases with an increasing average number of ACA ligands bound to the QDs, indicating that a single molecule is not sufficient to cause complete quenching of the QDs PL.
This motivated us to introduce a modified SV model for hybrid QD–ligand systems. The model differs from previous models as it takes into account the observation that several quenchers are necessary for complete PL quenching in hybrid systems.25,26
To account for an average number of bound ligands, we assume a Poisson distribution of the ligands bound to the QDs (ESI† for further details). The quantum yield ϕ(n) of one QD with n ligands has the form:
 | (1) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) (x), the average quantum yield as a function of the average number of bound ligands
(x), the average quantum yield as a function of the average number of bound ligands 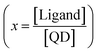 :
: | (2) |
This form assumes that the quenching is additive, meaning that the overall quenching is the sum of the individual contributions of each bound ligand. Using all the above, we get an expression equivalent to the SV equation, for the experimentally determined  (for detailed derivation, see ESI†):
(for detailed derivation, see ESI†):
 | (3) |

We first examine this equation in two extreme limits: For b → 0, which means that one bound ligand is sufficient for the complete quenching of the PL, eqn (3) converges to:
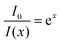 | (4) |
 , where the difference is that KSV depends on the QD concentration
, where the difference is that KSV depends on the QD concentration  :
: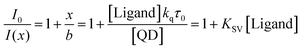 | (5) |
Fig. 3b presents a plot of the model with varying values of b. As b approaches zero, the exponential behavior becomes evident. Additionally, the plot shows convergence to linearity at high b values, or alternatively, as x increases, all the curves (for all b values) tend to linearity (Fig. 3b includes dashed-dot black lines representing the linear asymptote for the high x values). Two key insights can be drawn from this model:
(1) Strong quenchers (small b value) exhibit concave-up behaviour at small x values, and as the quencher strength increases (b approaching zero), the function exhibits full exponential behavior.
(2) The graph becomes linear for all x values in the limit of large b, with near-linear behavior already observed at b = 1. This indicates that when kq ∼ k0 or when kq < k0 the graph is essentially linear.
Applying the model for studying the quenching rates of anthracene with a carboxylic anchoring group (ACA), and with one or two thiol anchoring groups (AT and ADT, respectively, Fig. 3c) reveals clearly the significant differences in their function and efficiency in TET. Since thiols were reported to quench the fluorescence by inducing traps, we also studied the quenching of thiophenol (TP) as a control.27–29 The experiments were performed with ligand quantities ensuring that all ligands were bound to the QDs, as confirmed by the lack of any change in the bound ligand absorption spectrum (the “flat region” in Fig. 2b).
The SV plot in Fig. 3c displays a noticeable difference among the four ligands. The quenching rate of the thiol anthracene AT is 3 times faster than that of its carboxylic acid analogue ACA (0.07 ns−1 and 0.2 ns−1, respectively), and the quenching rate of the dithiol ligand ADT (0.3 ns−1) is 4.5 times faster than ACA. While ACA shows linear behavior, the thiol-anthracene ligands AT and ADT both exhibit exponential behavior, which the model predicts for the limit of strong quenchers (small b values). TP shows significantly slower rates (two orders of magnitude lower), confirming that the observed quenching for the anthracene ligands arises from TET processes, as previously reported for thiol-tetracenes30 and also by upconversion experiments (Fig. S23, see ESI†).
Density functional theory (DFT) calculations can shed light on the observed differences in the quenching rates. While the frontier orbital energies do not differ significantly (Table S3, see ESI†), their orientation shows notable differences (Fig. 4). Since the carboxylate typically forms a bidentate bond on Cd surface sites,31 ACA adopts a nearly orthogonal orientation (Fig. 4b, left), which should minimize the orbital interactions between the π-orbitals of the anthracene and the QDs. In contrast, the bond angles around the sulfur atom (∼90°) are expected to result in a parallel orientation between the π-orbitals of the anthracene and the QD surface (Fig. 4b, middle and right). Since the TET rate is proportional to the orbital overlap between the QDs and ligands, this parallel orientation can explain the faster quenching observed for AT and ADT compared to ACA. The slightly faster quenching observed for the bidentate ADT compared with the monodentate AT could stem from a more stable parallel orientation of the former.
 | ||
| Fig. 4 Optimized structures of bound ligands are shown alongside illustrative binding orientations on the CdSe surface for ACA (left), AT (middle), and ADT (right). (a) Side view. (b) Top view. | ||
Conclusions
This work demonstrates that the binding of π-conjugated ligands to QDs can induce spectral changes, primarily due to the deprotonation of the anchoring group and changes in the surrounding environment. We show that these spectral changes, manifested as a redshift, line broadening and vibronic distortion, can serve as both quantitative and qualitative indicators of ligand binding, allowing us to determine the average number of bound ligands per QD directly. By using the average number of bound ligands, we developed a modified SV equation suitable for hybrid systems and applied it to compare different ligands. We find that while carboxylate ligands account for weaker quenching, corresponding to a linear SV behaviour, thiol anchoring groups account for stronger binding and exponential SV behaviour, explained by increased coupling in their parallel orientation. These findings establish a simple and effective optical approach to probe binding and electronic coupling at the ligand–QD interface to provide design principles for optimizing hybrid upconversion systems.Author contributions
Conceptualization: Y. Deree, U. Banin, O. Gidron; methodology: Y. Deree, U. Banin, O. Gidron; investigation: X. Li, A. Levi (nanocrystal synthesis); Y. Deree (all other experiments); data curation: Y. Deree; writing – original draft: Y. Deree; writing – review & editing: Y. Deree, U. Banin, O. Gidron; supervision: U. Banin, O. Gidron; project administration and funding acquisition: U. Banin, O. Gidron.Conflicts of interest
There are no conflicts to declare.Data availability
All data supporting the findings of this study are included in the article and its ESI.†Acknowledgements
U. B. acknowledges support from the Israel Science Foundation within the MAPATS program (Grant No. 2655/23) and thanks the Alfred & Erica Larisch Memorial Chair. OG acknowledges the European Union's Horizon 2020 research and innovation program (grant agreement no. 850836, ERC Starting Grant “PolyHelix”) and the support of the Israel Science Foundation (grant No. 3085/21). Y. D. acknowledges the support from the Hebrew University Center for Nanoscience and Nanotechnology.Notes and references
- R. Lai, Y. Sang, Y. Zhao and K. Wu, J. Am. Chem. Soc., 2020, 142, 19825–19829 CrossRef CAS PubMed.
- T. Huang, S. He, A. Ni, T. Lian and M. Lee Tang, Chem. Sci., 2024, 15, 4556–4563 RSC.
- C. Mongin, S. Garakyaraghi, N. Razgoniaeva, M. Zamkov and F. N. Castellano, Science, 2016, 351, 369–372 CrossRef CAS PubMed.
- A. J. Morris-Cohen, K. O. Aruda, A. M. Rasmussen, G. Canzi, T. Seideman, C. P. Kubiak and E. A. Weiss, Phys. Chem. Chem. Phys., 2012, 14, 13794–13801 RSC.
- S. Lian, D. J. Weinberg, R. D. Harris, M. S. Kodaimati and E. A. Weiss, ACS Nano, 2016, 10, 6372–6382 CrossRef CAS PubMed.
- Y. Jiang, C. Wang, C. R. Rogers, M. S. Kodaimati and E. A. Weiss, Nat. Chem., 2019, 11, 1034–1040 CrossRef CAS PubMed.
- A. J. Bagnall, N. Eliasson, S. Hansson, M. Chavarot-Kerlidou, V. Artero, H. Tian and L. Hammarström, ACS Catal., 2024, 14, 4186–4201 CrossRef CAS PubMed.
- Y. Yuan, N. Jin, P. Saghy, L. Dube, H. Zhu and O. Chen, J. Phys. Chem. Lett., 2021, 12, 7180–7193 CrossRef CAS PubMed.
- Z. Huang, C.-H. Tung and L.-Z. Wu, Acc. Mater. Res., 2024, 5, 136–145 CrossRef CAS.
- Y. Niihori, T. Kosaka and Y. Negishi, Mater. Horiz., 2024, 11, 2304–2322 RSC.
- J. Zhang, H. Sakai, K. Suzuki, T. Hasobe, N. V. Tkachenko, I.-Y. Chang, K. Hyeon-Deuk, H. Kaji, T. Teranishi and M. Sakamoto, J. Am. Chem. Soc., 2021, 143, 17388–17394 CrossRef CAS PubMed.
- C. Wang, M. S. Kodaimati, S. Lian and E. A. Weiss, Faraday Discuss., 2019, 216, 162–173 RSC.
- Z. Chi, J. Xu, S. Luo, X. Ran, X. Wang, P. Liu, Y. He, Y. Kuang and L. Guo, Phys. Chem. Chem. Phys., 2023, 25, 8913–8920 RSC.
- Z. A. VanOrman, C. R. I. Conti, G. F. Strouse and L. Nienhaus, Chem. Mater., 2021, 33, 452–458 CrossRef CAS.
- Z. A. VanOrman, A. S. Bieber, S. Wieghold and L. Nienhaus, Chem. Mater., 2020, 32, 4734–4742 CrossRef CAS.
- P. Xia, E. K. Raulerson, D. Coleman, C. S. Gerke, L. Mangolini, M. L. Tang and S. T. Roberts, Nat. Chem., 2020, 12, 137–144 CrossRef CAS PubMed.
- K. Wang, R. P. Cline, J. Schwan, J. M. Strain, S. T. Roberts, L. Mangolini, J. D. Eaves and M. L. Tang, Nat. Chem., 2023, 15, 1172–1178 CrossRef CAS PubMed.
- X. Li, Z. Huang, R. Zavala and M. L. Tang, J. Phys. Chem. Lett., 2016, 7, 1955–1959 CrossRef CAS PubMed.
- R. Gomes, A. Hassinen, A. Szczygiel, Q. Zhao, A. Vantomme, J. C. Martins and Z. Hens, J. Phys. Chem. Lett., 2011, 2, 145–152 CrossRef CAS.
- C. Mongin, P. Moroz, M. Zamkov and F. N. Castellano, Nat. Chem., 2018, 10, 225–230 CrossRef CAS PubMed.
- G. B. Piland, Z. Huang, M. Lee Tang and C. J. Bardeen, J. Phys. Chem. C, 2016, 120, 5883–5889 CrossRef CAS.
- Z. Huang, X. Li, M. Mahboub, K. M. Hanson, V. M. Nichols, H. Le, M. L. Tang and C. J. Bardeen, Nano Lett., 2015, 15, 5552–5557 CrossRef CAS PubMed.
- Z. Huang, X. Li, B. D. Yip, J. M. Rubalcava, C. J. Bardeen and M. L. Tang, Chem. Mater., 2015, 27, 7503–7507 CrossRef CAS.
- L. Hou, A. Olesund, S. Thurakkal, X. Zhang and B. Albinsson, Adv. Funct. Mater., 2021, 31, 2106198 CrossRef CAS.
- A. M. Funston, J. J. Jasieniak and P. Mulvaney, Adv. Mater., 2008, 20, 4274–4280 CrossRef CAS.
- Z. A. VanOrman, R. Weiss, A. S. Bieber, B. Chen and L. Nienhaus, Chem. Commun., 2023, 59, 322–325 RSC.
- G. Tang, X.-H. He, M. Liu, H. Hao, Y. Liu and F.-L. Jiang, J. Phys. Chem. C, 2024, 128, 8681–8688 CrossRef CAS.
- G. Kalyuzhny and R. W. Murray, J. Phys. Chem. B, 2005, 109, 7012–7021 CrossRef CAS PubMed.
- C. Bullen and P. Mulvaney, Langmuir, 2006, 22, 3007–3013 CrossRef CAS PubMed.
- V. Gray, Z. Zhang, S. Dowland, J. R. Allardice, A. M. Alvertis, J. Xiao, N. C. Greenham, J. E. Anthony and A. Rao, J. Phys. Chem. Lett., 2020, 11, 7239–7244 CrossRef CAS PubMed.
- O. Voznyy, J. Phys. Chem. C, 2011, 115, 15927–15932 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00319a |
| This journal is © The Royal Society of Chemistry 2025 |




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: