On the utility of complementary analytics for on-surface synthesis

Abstract

On-surface synthesis (OSS) facilitates the coupling of larger molecules on solid surfaces into extended covalent nanostructures that are difficult or impossible to achieve by wet chemistry. Its primary analytical tool is scanning probe microscopy (SPM), which provides submolecular views of reactants, products and sometimes intermediates. However, relevant aspects such as subtle chemical changes and structural details remain inaccessible. In addition, direct monitoring of reaction progress in real time by SPM is challenging. This analytical gap is increasingly being filled by complementary analytics: mass spectrometry can be used not only to detect volatile by-products that are released during the reaction, but also to monitor intermediates and higher oligomers. Surface sensitive vibrational spectroscopy, either with electrons or photons, is advantageous for the identification of perceived reaction products, even in cases where the routine approach based on X-ray photoelectron spectroscopy (XPS) is not very promising. X-ray standing wave (XSW) analysis is a less common technique in OSS but well established in surface science, providing experimental access to adsorption heights with picometre accuracy. Its value for detailed comparison and validation of prevailing density functional theory (DFT) based structure calculations cannot be overstated. Recent examples also show the benefits of XSW for less regular structures, such as those often obtained in OSS. Finally, the assessment of reaction kinetics has considerable potential to provide fundamental insights into elementary processes and hidden reaction partners for the unique coupling of larger molecules on surfaces into extended structures. Real-time XPS has sufficient chemical and temporal resolution to monitor reaction kinetics for coupling on surfaces. Ideally, mechanistic insights can be gained by modelling. However, the typically applied linear temperature profiles have limitations that can be overcome by exploring new temperature profiles. Again, the accurate determination of kinetic reaction parameters, such as activation energies, is of paramount importance for benchmarking DFT calculations. Although spectroscopy is already applied for OSS its broader and more systematic implementation appears highly promising for the advancement of the fundamental understanding of OSS, hence eventually also for optimizing the reaction protocols and outcomes.

---

Markus Lackinger

Markus Lackinger currently heads a research group at the Deutsches Museum, one of Germany's largest research museums and a member of the Leibniz Association. He collaborates closely with the Technical University of Munich, where he is an adjunct professor in the School of Natural Sciences. His scientific background is in surface science, and he has always had a keen interest in molecular systems. In this context, developing protocols and novel approaches for synthesising increasingly extended 2D polymers on solid surfaces, and thoroughly characterising their structures and properties by a comprehensive set of complementary analytical tools, is one of his major research interests and goals.

---

Introduction

On-surface synthesis (OSS) has evolved from molecule based surface science into an independent and highly vibrant field of research that has started to breach out into various other fields, as molecular electronics and catalysis.¹ In the history of surface science, adsorbed organic molecules soon proved to be interesting study objects that endow surfaces with new defined features such as discrete electronic states and quantized excitations for spectroscopy. On the other hand, organic molecules were versatile and instructive model systems for fundamental studies of supramolecular self-assembly on surfaces. The functionalisation of molecules for intermolecular hydrogen bonding,² for example, has opened up a wide field of study with the aim of understanding and ultimately controlling structure formation in two dimensions under the additional influence of a periodic potential exerted by a crystalline support. This research took a clear turn, with reactive molecules on metal surfaces undergoing chemical changes and also coupling with each other, marking the dawn of OSS. In the early days, boronic acids and halogenated precursors were the primary targets,^3–5 but it soon became apparent that many other functional groups also had potential for coupling on surfaces.⁶ OSS is similar to heterogeneous catalysis in some respects with the crucial difference that the typical educts are larger, non-volatile molecules and, accordingly, the even more extended products do not desorb anymore. As a result, product identification no longer relied on desorption techniques such as temperature programmed desorption (TPD), but required alternative techniques. While the initial focus was on understanding chemical changes, there was soon a strong interest in more detailed structure determination and property characterization. Evidently, the mechanisms for chemical reactions on surfaces can be very different from those in solution chemistry,⁷ due to the two-dimensional constraint and the chemical involvement of the surface, sparking a keen interest in elucidating mechanisms. Initially, many relevant research questions could be addressed using conventional scanning tunnelling microscopy (STM),⁸ as discussed in the next section. With the advent of more advanced and powerful scanning probe microscopies (SPM), particularly bond-resolved imaging,⁹ more subtle problems could also be tackled. However, as is often the case in chemical analytics the use of complementary techniques promotes a fuller understanding. The aim of this review is to provide an overview of the different analytical techniques successfully employed in OSS, their specific applications, assets and limitations, and to identify possible future directions. This review is organised around the main themes of product identification, structure determination and kinetic studies. Ideally, it will provide assistance in addressing specific analytical questions in OSS.

Product identification

OSS is often aimed at reticular synthesis, i.e. employing judiciously designed molecular building blocks to materialise a desired product with a defined structure. Accordingly, product verification is the primary objective of the analytics. However, deviations from the intended reaction pathway are not uncommon, with side reactions or defect formation leading to different products or distributions, or to metastable intermediates.^4,10–12

High resolution SPM imaging

A prominent example of intermediates from before the field was called OSS are the organometallic chains formed in surface-assisted Ullmann coupling, originally called “protopolymers” in the pioneering work of Weiss.¹² The linking metals were invisible to the STM, which later turned out to be prototypical. But the bond lengths measured by STM proved sufficiently accurate to exclude covalent bonds, which are approximately 0.25 nm shorter.^5,11 In the end, the appropriate conclusions were arrived at through chemical reasoning combined with consideration of specific surface influences. Yet, conventional STM imaging is not always exhaustive in distinguishing structures that differ only in subtle details. An interesting example is the unique identification of the bond order in carbon–carbon bonds.¹³ In particular for chains and rings of carbon atoms it became important to distinguish between the cumulenic form (double bonds only) and the polyynic form (alternating single and triple bonds).¹⁴ OSS is primarily carried out on metal surfaces where the products are strongly adsorbed and their frontier molecular orbitals hybridized with metal states. The result is often a featureless, uniform STM contrast with little relevant information content other than geometry. Decoupling from the metal surface by a thin insulating layer can bring the unperturbed molecular frontier orbitals to light.¹⁵ This principle was adapted to OSS by lateral manipulation of reaction products onto patches of an insulating NaCl layer.¹⁶ But decoupling on the scale of the entire sample remains intricate. However, for some intramolecular reactions, most notably cyclodehydrogenations, the footprint of the molecule does not change significantly. In most cases this chemical change planarizes an initially non-planar molecule, hence can still be recognized in STM. But the precise chemical structure, for instance the degree of cyclodehydrogenation, can more clearly be deduced from direct imaging of the molecular scaffold by bond-resolved STM (BR-STM) or frequency-modulated atomic force microscopy (FM-AFM) using CO-functionalised tips.⁹ This approach has been particularly fruitful for flat polycyclic hydrocarbons, where the structure elucidation of truly unknown molecules, either from crude oil, combustion or from outer space, has been a particular highlight.¹⁷ However, FM-AFM quickly becomes challenging and reaches its limits with deviations from planarity.¹⁸

Although SPM is an obvious, extremely powerful and reasonable first approach to structure determination, it comes with caveats. In its standard mode of operation STM is sensitive to the electronic states around the Fermi energy, but not directly to the atomic positions. For instance, the structure assignment of the chiral graphene nanoribbons (GNR) synthesized from 10,10′-dibromo-9,9′-bianthryl on Cu(111) based on STM imaging was controversial and gave rise to long-standing discussions.¹⁹ Although BR-STM or FM-AFM in principle allows direct imaging of the atomic scaffold, functionalised tips are required. But wiggling of the typically used CO molecules on the tip causes not only image distortions but also artefacts.²⁰ Nevertheless, the topology of reaction products can be assessed, for instance the number of atoms in a carbon (hetero)cycle can be determined,²¹ while the exact atomic positions remain inaccessible. Although the accuracy can be improved by using probes terminated by tightly bound oxygen,²² this major shortcoming also exacerbates the Achilles heel of SPM, namely the accurate determination of bond and dihedral angles or adsorption heights. The latter, however, contain important information about both the conformation of the nanostructures and the strength of the interactions with the surface, both of which influence the electronic properties.

In summary, despite the unprecedented resolving power of SPM and the new contrasts attained by advanced imaging techniques, using multiple complementary methods is still essential in order to arrive at conclusive structures with fine details resolved.

Scanning tunneling spectroscopy

At the next level, a detailed assessment of the local electronic structure can be helpful when high-resolution imaging does not provide sufficient information. This is particularly useful in cases where a limited number of conceivable products differ greatly in their electronic properties. STM is therefore predestined to measure either the energy dependence of the local density of states or the spatial distribution of distinct electronic states. A particularly intriguing example are open shell structures, where the ground state is not always obvious, i.e. electronic structures can differ even for the same atomic structure.²³ In addition, imaging the spatial distribution of specific electronic states by dI/dV mapping at the appropriate energy and comparison with calculated frontier molecular orbitals can also be the key to successful product confirmation.²⁴

Vibrational spectroscopy

Optical vibrational spectroscopy is the standard in analytical chemistry for the identification of specific chemical groups. The two common variants, infrared (IR) absorption and Raman spectroscopy, can both also provide sub-monolayer sensitivity^25,26 and high spatial resolution on surfaces.

Vibrational spectroscopy can be particularly useful when X-ray photoelectron spectroscopy (XPS), the main complementary analytical technique of OSS, remains inconclusive, because the chemical core level shifts that are associated with the reaction are either too small (e.g. sp³ versus sp² hybridised carbon) or affect only a minor fraction of the respective element. On electrically conductive surfaces, image charges screen the electric dipole parallel to the surface, imposing the selection rule for IR absorption spectroscopy that only vibrations with a dipole component perpendicular to the surface can be detected. This could potentially be limiting for adsorbed structures, if there are too few IR-active vibrations with sufficient oscillator strength. While Raman cross-sections are generally lower, the surface selection rules are more complicated.²⁷ However, of particular relevance to OSS, graphene nanostructures exhibit exceptionally high Raman cross sections, and submonolayer spectra can even be acquired with conventional spectrometers.²⁶ By contrast, IR absorption spectroscopy of (sub)monolayers often requires dedicated instrumentation, such as for polarisation modulation infrared reflection absorption spectroscopy (PM-IRRAS).

Raman spectroscopy is particularly useful for distinguishing sp- from sp²-hybridised carbon. This was convincingly demonstrated in the study by Sedona and co-workers for molecular wires with different sequences of phenyl rings and alkyne linkages.²⁵ Fig. 1a shows the ex situ acquired Raman spectra of different molecular wires synthesised on Au(111) together with their structural models and simulated spectra. The intense peak at 2200 cm⁻¹ is attributed to the stretching mode of the C–C triple bonds and is consequently absent in the spectrum of the para-poly-phenylene wire shown at the bottom. The small peaks at 980 cm⁻¹ and 1340 cm⁻¹ in the top spectrum are assigned to the stretching mode of the C–C single bond between two alkyne moieties and thus allow to distinguish graphyne from graphdiyne wires. In addition, even the minor peaks are well reproduced by the simulations, allowing unambiguous assignment.

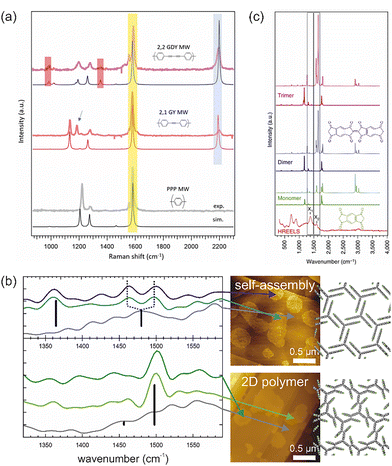Fig. 1 Vibrational spectroscopy in OSS. (a) Raman spectra of molecular wires synthesised on Au(111) with different sequences of phenyl rings and alkyne units: graphdiyne (GDY), graphyne (GY) and para-poly-phenylene (PPP). The almost perfect agreement between experimental (top) and simulated (bottom) spectra convincingly underlines the product confirmation and peak assignment. (b) Nano-FTIR AFM study of the topochemical photopolymerisation of self-assembled fantrip monolayers into 2D polymers. IR absorption spectra were acquired at deliberately selected locations (marked by the arrows) identified in previously acquired AFM images (center). The background spectra (grey) were acquired from the pristine surface between the molecular domains. Characteristic IR absorption bands can be assigned based on calculated modes (black bars) and confirm the polymerisation. The monolayer structures of the initial fantrip self-assembly (top) and the resulting 2D polymer (bottom) are shown on the right. (c) HREELS of molecular wires (bottom) in comparison to both calculated IR (full line) and Raman spectra (dotted line) of monomers (chemical structure shown in green), dimers (chemical structure shown in blue) and trimers. (a) Reproduced from ref. 25 with permission from the Royal Society of Chemistry. (b) Complied from data previously published in ref. 28 (c) Reproduced from ref. 29.

Interestingly, high spatial resolution can be achieved for both IR and Raman spectroscopy by exploiting the enhancement of electric fields under metallized SPM probes by surface plasmon resonances. Dedicated nano-FTIR AFM instruments are commercially available and have already proved useful for OSS as exemplified by the topochemical polymerisation of fluorinated anthracene–triptycene (fantrip) monomers into 2D polymers, summarised in Fig. 1b.²⁸ The locations for acquisition of the IR absorption spectra were chosen in the previously recorded AFM images shown on the right, which also allowed background spectra of the pristine substrate to be obtained. The top part of Fig. 1b shows an IR absorption spectrum of the self-assembled fantrip monolayer prior to photopolymerisation with a characteristic IR absorption band at 1360 cm⁻¹. After complete photopolymerisation, this band vanishes and a new prominent band at 1500 cm⁻¹ indicates the formation of the 2D polymer by [4+4] cycloadditions between fantrip's anthracene blades. The main IR absorption bands are well reproduced by density functional theory (DFT) calculations of free-standing monolayers shown by the black bars with their respective oscillator strengths. Interestingly, the self-assembled monolayer shows two peaks at 1465 cm⁻¹ and 1495 cm⁻¹ (dashed lines in Fig. 1b), whereas DFT predicts a single peak at the central position of 1480 cm⁻¹. More sophisticated calculations could further explore the origin of this peak splitting, which could possibly be caused by adsorption.

The caveat of nano-FTIR AFM is that, although technically feasible, it is not usually implemented in an ultra-high vacuum (UHV) environment, the preferred setting for OSS. This means that air-stable and contamination-insensitive samples are required. By contrast, tip-enhanced Raman spectroscopy (TERS) is now routinely applied in UHV and its potential for submolecular spatial resolution has been first demonstrated impressively on single molecules.³⁰ Consequently, its utility for OSS was soon recognized and unlocked also for photopolymerized 2D structures.³¹ But TERS was also instructive for characterising GNR intermediates and products.³² The use of femtosecond light pulses and pump–probe schemes even allowed time-resolved studies of ultrafast phonon dynamics in GNR to unravel coupling and dephasing.³³

Both IR and Raman spectra can be calculated based on DFT-optimized structures using available tool boxes. Often calculations in free-standing structures can already reproduce the main features,²⁸ so the next level would be to interpret the surface effects caused by the symmetry breaking upon adsorption.

In addition, more traditional surface science offers an electron-based vibrational spectroscopy, namely high resolution electron energy loss spectroscopy (HREELS), albeit typically with lower resolution than optical spectroscopy. Vibrations are excited by three independent scattering mechanisms, namely dipole and impact scattering as well as negative ion resonances. As already the name implies, dipole scattering obeys the same dipole selection rules as IR absorption spectroscopy, while the two other scattering mechanisms can also excite IR-inactive vibrations. Unfortunately, examples are rare but even more so instructive.^29,34–36 Fig. 1c shows the HREELS spectra of molecular wires of polymerized s-indacene-1,3,5,7(2H,6H)-tetrone monomers synthesised on Ag(110) alongside the simulated IR and Raman spectra of the monomer as well as dimers and trimers.²⁹ In particular, the peaks X1 and X2 become prominent after thermal annealing. Although the simulations suggest that both peaks are already present in the monomer, they become more intense upon dimer and trimer formation, and thus serve as an indicator of polymerisation.²⁹

Yet, HREELS offers an additional benefit: electronic interband transitions can similarly be excited providing direct access to the optical gap.

Mass spectrometry

In OSS mass spectrometry can be applied either for direct identification of products and intermediates or alternatively for the detection of volatile by-products as in temperature programmed reaction spectroscopy (TPRS).^{28,35,37–41} An instructive example for the latter is the release of H₂ shown in Fig. 2a to underscore the unexpected coupling of apparently inert alkanes on apparently inert gold surfaces.³⁷ In most cases, standard TPRS is not suitable for direct confirmation of products in OSS because the high molecular weight products in the kilo to megadalton range do not thermally desorb. Aside from that, the mass range limits of conventional quadrupole mass analysers are quickly reached. Time-of-flight secondary ion mass spectrometry (ToF-SIMS) is therefore the method of choice, routinely detecting extremely high masses up to 10 000 amu. This enabled the detection of up to the pentadecamer of the covalently bonded, but not yet planarized, polymer during the growth of chevron GNR.³⁵ A high mass resolution of 1 amu is routinely achieved, allowing the differentiation of reaction states that differ by the presence or absence of a single hydrogen atom. Fig. 2b shows the detection of trimer species, again in the covalent but not yet planar polymer, during the growth of GNRs that were a few amu too light by mass spectrometry.³⁹ This was explained by a premature onset of the cyclodehydrogenation, which was also found to be detrimental to the growth of longer GNRs. In the on-surface photopolymerisation of fantrip on hexacosane-passivated graphite, both the hexacosane and the fantrip monomers could be detected by ToF-SIMS in the positive channel prior illumination with laser light at 365 amu and 770 amu, respectively (Fig. 2c, top).²⁸ In addition, fantrip showed a defined fragment at 522 amu with one anthracene blade missing. After illumination, the monomers were absent in ToF-SIMS, while the hexacosane from the passivation layer could still be observed (Fig. 2c, bottom). However, the absence of the monomer alone is too weak an evidence of successful polymerisation. But the presence of the 2D polymer was further indicated by the continued detection of fluorine by ToF-SIMS in the negative channel.²⁸

Fig. 2 Mass spectrometry in OSS. (a) Detection of the hydrogen that is produced and released by the coupling of alkanes as volatile by-product by TPRS. (b) ToF mass spectrometry to monitor the growth of GNR in a low vacuum of ∼1.5 mbar. Oligomeric species in the initial polymer that are deficient by 1–3 hydrogen atoms indicate premature cyclodehydrogenation, which could counterintuitively be reduced by introducing H₂ gas. (c) ToF-SIMS monitoring the photopolymerisation of fantrip monomers into 2D polymers on hexacosane-passivated graphite. (a) From ref. 37. Reprinted with permission from AAAS. (b) Reprinted with permission from ref. 39. Copyright 2017 American Chemical Society. (c) Complied from data previously published in ref. 28.

For mass spectrometry of larger entities in OSS, the limitations of thermal desorption can be at least partially overcome by inducing desorption with either a particle beam as in ToF-SIMS or a modified matrix assisted laser desorption/ionisation (MALDI).³⁹ This allows the detection of positively or negatively ionized desorbing species, with ionization working best on metal surfaces. Fragmentation, which is common for electron impact ionization also applies here, resulting in the detection of different entities from (sub-)monomeric species to (higher) oligomers, regardless of whether 1D or 2D structures are being probed. Not necessarily, but often in practice samples have to be transferred through the atmosphere because the ToF mass spectrometer is not directly attached to the UHV growth chamber. This poses a serious risk of contamination or further air-induced chemical reactions. Accordingly, exploiting the full potential of in situ mass spectrometry would offer new opportunities, as demonstrated by the direct observation of the gradual hydrogen/deuterium exchange reactions in polycyclic aromatic molecules on hot metal surfaces.⁴¹

For extended nanostructures, especially if they are completely planar like the GNR, desorption appears to remain the main bottleneck for metals,³⁹ urging for more weakly interacting surfaces. Yet, these are often inferior to metals in terms of ionisation, which may be solved by post-synthetic metal deposition as an ionisation agent for purely analytical purposes.

(Electronic) structure determination

Although the general chemical structure is known for verified products, inferring structural details can be instructive to better understand and model other relevant properties. Accurate structures are also important for comparison and benchmarking with calculations. DFT is the most widely used method for this purpose, as it offers the best compromise between accuracy and manageable system sizes for meaningful models. The DFT outcome, however, can dependend on the parameters used, especially the functional,⁴² and should not be taken for granted.

SXRD and LEED

The gold standard for atomic structure determination are surface sensitive diffraction techniques using either X-rays or electrons as implemented in surface X-ray diffraction (SXRD) and low energy electron diffraction (LEED).⁴³ Both techniques offer picometre accuracy in atomic coordinates. Unfortunately, SXRD often requires synchrotron radiation and is therefore less accessible, whereas LEED is available in many laboratories. But recording a single or a few diffraction patterns is not enough as the information about atom positions is contained in the intensity variation of the diffraction peaks with electron energy (voltage), as recorded in so-called I(V) curves.⁴⁴ There are two main limitations to the widespread application of LEED I(V) to OSS, namely the crystallinity requirement and the extensive theory involved. Obtaining highly regular covalent two-dimensional structures remains a challenge and progress is slow but steady,^28,45 whereas one-dimensional structures with their defined sequence have better inherent order. However, to obtain a clear diffraction pattern, the 1D nanostructures must be uniformly oriented. Alignment is often improved on more anisotropic surfaces, e.g. (110) of fcc metals.^29,46,47

The surface sensitivity of LEED originates in the strong scattering of the low energy electrons. Consequently, the analysis of LEED I(V) requires so-called dynamic theories that take full account of multiple scattering. Although various implementations and codes are available, the technique is not as widely used as the benefits would justify. However, apart from graphene,⁴⁸ a complete structure determination of an extended covalent nanostructure has not yet been reported. On the other hand, OSS often results in differently oriented domains that superimpose to form a complex diffraction pattern. A promising strategy to cope with smaller domain sizes could be micro-diffraction as implemented in low energy electron microscopy (LEEM).⁴⁹

ARPES and POT

Once uniform alignment of OSS nanostructures with respect to a single-crystalline support has been accomplished, the sample is suitable not only for LEED, but also for angle-resolved photo emission spectroscopy (ARPES).⁴⁷ Therefore, the effort would be worthwhile. ARPES enables momentum-resolved measurements of occupied electronic states, providing experimental access to 2D electronic band structures and dispersion relations. Accordingly, photoemission spectroscopy can reveal flat bands, which are of particular interest in strongly correlated systems. It can also be used to determine the effective masses of charge carriers, which is an important measure of their mobility. Consequently, ARPES is particularly relevant for conjugated nanostructures intended for electronic applications, with GNR being the prime 1D target.⁵⁰ But, electronic conjugation becomes even more intriguing in 2D, where electronic structures converge more quickly as the network size increases.⁵¹ Pioneering ARPES measurements of these highly promising yet challenging synthetic organic 2D materials have already been reported.^45,52

For future studies photoemission orbital tomography (POT) is an exciting extension of ARPES that promises direct access to orbital wave functions.⁵³ It has already been applied to self-assembled structures of Kekulene,⁵⁴ i.e. large aromatic macrocycles synthesized on Cu(111), and to the orbital mapping of GNR synthesis reaction intermediates.⁵⁵ The application of POT to extended conjugated organic nanostructures is yet to be realised. This exciting prospect provides an additional incentive to strive for highly regular and aligned structures.

XSW and NEXAFS

As discussed in the section on SPM imaging, it is difficult to accurately determine bond angles, lengths and adsorption heights by relying on SPM alone. Fortunately, this gap can be filled by two X-ray absorption techniques, near-edge X-ray absorption fine structure (NEXAFS)^56,57 and X-ray standing wave (XSW).⁵⁸ Both derive their chemical sensitivity from core level binding energies of the respective elements and their chemical shifts analogous to XPS. In other words, if a particular species can be resolved in XPS, there is a good chance that it can also be distinguished in NEXAFS or XSW. Although the highest accuracies are achieved for commensurate adsorbate structures, where each adsorbed molecular entity is an exact replica of the other, even periodicity of the adlayer is not an inherent requirement of either technique. However, some degree of uniformity is certainly helpful. Broadly speaking, NEXAFS can measure tilt angles of molecular moieties with respect to the surface, while XSW allows accurate quantification of adsorption heights.

Albeit synchrotron radiation is required, NEXAFS is fairly well represented in OSS,^59–61 particularly for reactions that planarize sterically hindered, highly non-planar reactants, such as cyclodehydrogenations.⁵⁹ Our group has used NEXAFS to indirectly evaluate the strength of molecule–surface interactions by measuring tilt angles in a polyphenylene honeycomb network (see Fig. 3c for structure).⁶² For σ-bonded phenyl groups, the ortho-hydrogens give rise to a steric hindrance that favours tilting of the phenyl rings relative to each other as evidenced by the ∼44° dihedral angle of biphenyl in the gas phase.⁶³ In the adsorbed state, attractive molecule–surface interactions enforce a more or even completely planar geometry, which is more favourable both in terms of adsorption energy and π-conjugation. The actual dihedral angle results from the interplay of these two counteracting forces and can be used as gauge for the strength of molecule–surface interactions.

Fig. 3 XSW in OSS. (a) Pure phenylene and (b) mixed triazine–phenylene honeycomb networks on Ag(111). (c) Chemical structure of the ideal covalent network: R: C–H pure phenylene versus R: N mixed triazine–phenylene network; in both cases the organometallic intermediate (top row) and the covalent final product (middle row) were studied and gave consistent results. The organometallic carbon atoms bind to Ag adatoms and adsorb significantly lower than the rest of the molecular network. For the mixed triazine–phenylene network, the decoupled stage was additionally studied after intercalation of a chemisorbed iodine monolayer (bottom row). (a) Adapted from ref. 68 and (b) reproduced from ref. 69 with permission from the Royal Society of Chemistry.

On Ag(111) the covalent polyphenylene honeycomb network was not entirely planar, with a NEXAFS-derived average tilt angle of 15° ± 5°. Since direct synthesis of such a C–C bonded network on more weakly interacting, i.e. inert surfaces is, as yet, not possible, we have developed a protocol for post-synthetic decoupling from the metal growth surface by intercalation of an iodine monolayer,^62,64 which has been extended to chlorine.⁶⁵ After decoupling, the NEXAFS measured tilt angle increased significantly to 35° ± 5°, indicating weaker molecule–surface interactions. Supported by characteristic changes in the STM contrast, this provided strong, but indirect evidence of successful intercalation. Particularly insightful was the comparison with DFT-calculated structures in the terphenyl model yielding flat or an energetically equivalent almost flat adsorption directly on Ag(111) versus a significant 19° tilt angle on top of the iodine monolayer.⁶² In both cases the calculated tilt angles are smaller than the experimental ones, suggesting overbinding with the set of DFT parameters used. However, a word of caution seems appropriate for both the experimental and theoretical results. Two-dimensional networks are best modelled with periodic boundary conditions. Yet, the inclusion of the crystalline surface requires commensurability. It is therefore necessary to ensure that the applied strain does not influence the result, ideally by comparing two cases with minimized tensile and compressive stress, while maintaining the experimentally derived azimuthal orientation. On the other hand, NEXAFS is a global technique, averaging over the macroscopic extension of the X-ray beam. For the three-fold symmetric (111) surfaces of fcc metals, the azimuthal dependence averages out.⁵⁶ But in the polyphenylene honeycomb network, not all phenyl rings are equivalent, as 25% are vertices (green in Fig. 3c) and the other 75% (blue in Fig. 3c) form the edges, each with different steric constraints, hence tilt angles. In addition, Ullmann coupling of 2D networks typically results in small rugged domains. Accordingly, the proportion of undercoordinated phenyl rings at the periphery can be significant and their contribution must not be ignored.

More direct evidence for the strength of molecule–surface interactions or the success of decoupling is provided by adsorption heights, i.e. vertical distances of adsorbate to topmost surface atoms. When measured for different defined sites of a molecular nanostructure it is also possible to extract quantitative information about the conformation. Adsorption heights can be accurately measured by XSW.⁵⁸ In OSS this synchrotron-based technique is more commonly applied to surface-grown inorganic 2D materials such as hexagonal boron nitride,⁶⁶ or decoupled individual molecules adsorbed on top,⁶⁷ but rarely to covalent molecular structures.^68,69 But inherent disorder is not an insurmountable obstacle as XSW can deal with non-uniform structures. In favourable cases distributions of adsorption heights can be recognized and, with additional knowledge of the system, also disentangled.

XSW has been applied in OSS to both pure phenylene and mixed triazine–phenylene honeycomb networks on Ag(111) (cf. Fig. 3c for structures).^68,69 The latter was synthesized from a 2,4,6-tris(4-bromophenyl)-1,3,5-triazine (TBPT) precursor. Initially, Saywell et al. measured for the polyphenylene network the adsorption heights of both the organometallic intermediate that emerged after debromination and the covalent final structure that was obtained through additional heating.⁶⁸ The organometallic carbon atoms that directly bind to Ag give rise to a shoulder in C 1s at lower binding energy, hence their adsorption height can be measured separately. Interestingly, XSW yielded a diminished adsorption height of 2.48 Å of the organometallic carbon atoms, while all other carbon atoms reside at an average height of 3.0 Å. This sheds light on the controversially discussed nature of the organometallic bond:⁷⁰ the carbon atoms bind to lower lying Ag adatoms of the surface, resulting in distortion of the network. By contrast, the covalent networks exhibit a rather uniform adsorption height of 3.1 Å with respect to Ag(111). These results are largely consistent with our results obtained for the mixed triazine–phenyl network similarly on Ag(111), as summarized in Fig. 3b. The asset of this system is that the large chemical shift of ∼2.8 eV of the C 1s carbon atoms in the triazine ring to a higher binding energy with respect to phenyl enables spectroscopic discrimination of the triazine vertices and the phenyl edges of the honeycomb network. Accordingly, we observe not only a slightly lower adsorption height of the organometallic carbon atoms of 2.3 Å, but also a slightly larger adsorption height of 3.1 Å for the triazine centres. For the covalent networks the adsorption heights are virtually identical.

In addition, we characterized the covalent network after decoupling from Ag(111) by intercalation of an iodine monolayer. Its adsorption height increased markedly to 5.92 Å above Ag(111), which converts to 3.60 Å above the iodine layer, taking into account the similarly measured iodine adsorption height of 2.32 Å. Moreover, the coherent fraction decreased substantially after iodine intercalation, which in the light of previous NEXAFS results⁶² can be interpreted as a relaxation of the network due to tilting of the phenyl rings on more weakly interacting surfaces. The adsorption heights of the mixed phenyl-triazine network on pristine Ag(111) were well reproduced by DFT calculations, less so on the iodine monolayer for which optimised parameters had not been established.

Reaction kinetics and mechanisms

Accurate kinetic measurements can provide a solid basis for inferring reaction mechanisms or for obtaining kinetic reaction parameters as activation energies for benchmarking DFT calculations.⁷¹ Albeit STM can occasionally be used to assess the kinetics of different elementary processes as nucleation,⁷² in OSS kinetic measurements are primarily performed by XPS, which provides sufficient chemical and temporal resolution for real-time studies.⁷³ Typically, the temperature is ramped linearly and XP spectra are acquired continuously from an element directly involved in the chemical reaction. Technically, this is done either by scanning a small binding energy window on the time scale of a minute per spectrum or in so-called snapshot mode on the time scale of seconds using line detectors. Surface-assisted Ullmann coupling and cyclodehydrogenations were the early primary targets of such studies.^40,59,74,75 Debromination, in particular, is straightforward to measure because the Br 3d core level exhibits a large chemical shift between its molecule- and surface-bound states. In addition, the binding energy region around 70 eV has a virtually flat background, improving the accuracy of quantification. Looking closer at this seemingly simple first step of the Ullmann reaction proved unexpectedly revealing. As summarised in Fig. 4a, the direct comparison of the debromination of 1,3,5-tris(4-bromophenyl)benzene (TBB) on Ag(111) and Au(111) showed clear differences: a higher onset temperature for Au(111), which is expected and well established due to the lower reactivity.⁷⁶ Interestingly, however, while the debromination on Ag(111) was modelled reasonably well by a first-order rate law, the reaction on Au(111) was much more gradual and kinetic fits gave unphysical results. This was resolved by postulating a thermodynamic control on Au(111), which implies a dynamic equilibrium between debromination and rebromination, i.e. reversibility. By interpreting the XPS measured degree of debromination as the equilibrium concentration, the reaction energy was deduced from a thermodynamic model and compared favourably with DFT-calculated values.⁷⁵ The unexpected reversibility of debromination on Au(111) was underscored by subsequent studies.⁷⁷ Speculatively, a possible explanation for the absence of rebromination, and hence reversibility, on Ag(111) is its inhibition by the formation of strong organometallic bonds with Ag adatoms.

Fig. 4 Real-time XPS in OSS. (a) Debromination of TBB on Au(111) (yellow) versus Ag(111) (blue). The solid lines represent fits with a kinetic model for Ag(111) and a thermodynamic model for Au(111). (b) Debromination of TBPT on Ag(111). The solid line shows a fit with an optimized combination of E_a and A as indicated and derived from the fitting map shown in (c). Its colour code shows the root mean square derivation between experimental and simulated traces calculated for all combinations of E_a and A on a fine 1000 × 1000 grid, i.e. for 10⁶ points. (d) Real-time XPS of the second reaction step of Ullmann coupling, i.e. the conversion of organometallic intermediates into covalent products. This comparison nicely illustrates the influence of different heating rates in these kinetic measurements. The chemical structures of the respective precursors are shown alongside the experimental data. (a) and (d) Adapted with permission from ref. 75 and 80. Copyright 2019 & 2016 American Chemical Society. (a) Experimental and simulated debromination traces on both Ag(111) and Au(111), as published in ref. 75, have been complied to enable direct comparison. In ref. 75 the probability P_dehal for the dehalogenated state was originally shown. Here, to be compatible with the debromination trace, the probability for the halogenated state P_hal is shown instead as P_hal = 1 − P_dehal. (b) and (c) Reproduced from ref. 78 with permission from the Royal Society of Chemistry.

However, in-depth analysis of debromination of TBPT on Ag(111) revealed the inadequacy of simple first-order kinetics: fitting with a grid search algorithm in the two-dimensional parameter space of the rate constant k, consisting of activation energy E_a and pre-exponential A, resulted in unexpectedly low values in the order of 10⁷ s⁻¹ for the latter (Fig. 4b and c).⁷⁸ This could indicate either surface diffusion as a rate-determining step⁷⁹ or a second-order rate law. Both interpretations imply that debromination on Ag(111) is not a simple unimolecular reaction. In fact, the fitting quality could be improved by assuming a second-order rate law. Underscored by DFT calculations, we proposed that debromination on Ag(111) is assisted by readily available Ag adatoms.⁷⁸

Also, the kinetics of the second reaction step of Ullmann coupling, i.e. the conversion of the organometallic intermediate to the covalent final state can be monitored in C 1s either by the disappearance of the organometallic shoulder at lower binding energies or by integral peak shifts.^75,80 Again, in combination with modelling, interesting mechanistic insights were derived. For instance, modelling the real-time XPS data shown in Fig. 4d for the conversion of the organometallic intermediate into the covalent product of poly-para-phenylene wires synthesized from 1,4-halogen-substituted benzene precursors revealed a two-step mechanism based on initial nucleation and subsequent growth.⁸⁰ In a follow-up study, it was additionally shown that the co-adsorbed by-products of the Ullmann coupling, i.e. the dissociated halogens, exert a further significant influence on the conversion kinetics.⁸¹

As an approach to explore the accuracies and limitations of real-time XPS for quantitative inference of kinetic reaction parameters, we propose to first simulate temperature traces with exactly known reaction parameters and then reduce the data quality at will by thinning the data point density and superimposing noise. In a second step, these artificial experimental data of arbitrary quality are fitted to recover the original reaction parameters.⁸² This approach emphasised a fitting ambiguity already suggested by the actual experimental data: different linear combinations of activation energy E_a and the logarithm of the pre-exponential ln(A) can result in comparable fitting quality as also evident by the line in Fig. 4c. A possible workaround may be to use alternative temperature profiles that are easy to implement experimentally. For example, isothermal segments allow direct determination of the rate constant k for a given temperature if the rate law is known. If this is not the case, fits with different assumed rate laws can be evaluated comparatively.⁷⁸ An Arrhenius plot of the rate constants k measured for different temperatures T then directly yields both E_a and A.^61,78 Furthermore, it would be instructive in future studies to additionally validate the used models by applying them to experimental data sets acquired at different heating rates.

But real-time XPS is not the only analytical tool that provides a glimpse on reaction kinetics. Also fast STM achieving video frame rates and above can be useful for exploring kinetic aspects on the millisecond time scale.^78,83

Summary and outlook

In summary, the increasing use of complementary surface sensitive analytics has contributed to a more holistic understanding of coupling reactions on solid surfaces. This has led to a greater appreciation of the unique role of the surface as template, catalyst, reaction partner and supplier of additional, non-obvious reactants such as adatoms, adsorbed reaction by-products (e.g. halogens or hydrogen) or (activated) species form the residual gas, most notably atomic hydrogen.⁸⁴ Insights range from increased confidence in product identification, to more detailed knowledge of (electronic) structures, to a better understanding of the specific mechanisms of reactions on surfaces.

Future directions could include the broader or more sophisticated implementation of already applied surface science techniques, or the implementation of hitherto underrepresented techniques. For instance, a wider application of mass spectrometry could benefit from more sophisticated probes, e.g. size-selected gas cluster ions for ToF-SIMS.⁸⁵

Sample homogeneity is a relevant and sometimes crucial aspect of analytics, particularly for OSS, where chemically and structurally distinct products are often obtained. In this context, SPM data capable of resolving individual molecular entities is invaluable, especially considering the attractive prospect of acquiring local vibrational spectra by TERS or nano-FTIR. However, obtaining significant statistics by SPM is cumbersome, whereas this comes naturally with globally averaging techniques. For instance, the averaged chemical state can readily be assessed by XPS on a macroscopic scale, regardless of sample homogeneity. Although NEXAFS and XSW are fairly tolerant, achieving a more uniform sample improves the interpretability and meaningfulness of the results. By contrast, thus far underrepresented techniques such as LEED, SXRD and ARPES, as well as the as yet not widely applied POT, require full crystallinity, i.e. uniform OSS products with a defined epitaxial relationship on single-crystalline supports. Pursuing this holy grail of OSS is extremely rewarding, not least because it allows to harness the full potential of these powerful, high-resolution techniques. Combining the various techniques with SPM ultimately yields a complete picture.

Significantly increased time resolution would be a particularly intriguing new direction. Two-photon photoemission (2PPE) is readily available and was previously used to study the electronic structure of GNR.³⁴ However, 2PPE is highly appropriate to also asses the dynamics of optically excited states, allowing to learn more about optical properties of nanostructures or the surface influence on emerging photochemistry.^28,86 But despite its long history, SPM is still evolving. Particularly inspiring are the advances in ultrafast, light-wave-driven terahertz STM, which is leading to unprecedented time resolution.⁸⁷ Although previously applied to GNRs that were conventionally synthesized on Au(111),⁸⁸ more interesting features and richer physics can be expected on inert supports. However, in order to unearth these spectroscopic treasures, the OSS of study-worthy nanostructures on inert surfaces needs to progress.⁸⁹

Most of the complementary information in OSS comes from X-ray based techniques. For (real-time) XPS, intense synchrotron radiation beneficially increases both time and energy resolution. Maximising the photoionisation cross-sections by tuning the photon energies is an additional, arguably even more important advantage of synchrotron radiation, especially when the risk of beam damage prohibits high intensities. By contrast, synchrotron facilities are mandatory for NEXAFS and XSW. In this context, I would like to emphasise that synchrotron facilities generally encourage beamtime applications from less- to non-proficient users with appropriate, scientifically rewarding questions. Competent beamline scientists will assist throughout the entire process, from proposal writing to data acquisition, analysis and interpretation.

The predestined path of OSS should lead from the identification of suitable applications for the so produced novel nanomaterials to their realisation and would culminate in technological implementation. This journey inevitably heralds a new era of analysis aimed at characterising the unique properties relevant to the intended application. Although it is conceivable that selected properties, such as the electric field effect, may be measured without breaking the UHV, other applications will inevitably require relocation of samples to different environments. Gas permeation through ultrathin membranes can be measured in UHV,⁹⁰ but sample preparation is likely to require transfer, for which fully UHV-compatible protocols have not yet been developed.⁹¹ On the other hand, photocatalytic or electrocatalytic performance will inevitably need to be measured in gas atmospheres or in solution. These very worthwhile objectives will require air-stable samples,⁹² to which inert supports will contribute. In addition, as the field progresses closer to applications, characterisation will require different skills, expertise and instrumentation – the perfect breeding ground for inspiring and fruitful collaborations, an invaluable ingredient for the continued prosperity of OSS.

Conflicts of interest

There are no conflicts to declare.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Acknowledgements

Financial support for the research that contributed to this review article from the Deutsche Forschungsgemeinschaft (grant 415284307) is gratefully acknowledged.

References

1. Q. T. Fan, J. M. Gottfried and J. F. Zhu, Acc. Chem. Res., 2015, 48, 2484–2494; Q. Shen, H. Y. Gao and H. Fuchs, Nano Today, 2017, 13, 77–96; S. Clair and D. G. de Oteyza, Chem. Rev., 2019, 119, 4717–4776; L. Grill and S. Hecht, Nat. Chem., 2020, 12, 115–130.
2. J. A. Theobald, N. S. Oxtoby, M. A. Phillips, N. R. Champness and P. H. Beton, Nature, 2003, 424, 1029–1031; S. Griessl, M. Lackinger, M. Edelwirth, M. Hietschold and W. M. Heckl, Single Mol., 2002, 3, 25–31.
3. L. Grill, M. Dyer, L. Lafferentz, M. Persson, M. V. Peters and S. Hecht, Nat. Nanotechnol., 2007, 2, 687–691.
4. N. A. A. Zwaneveld, R. Pawlak, M. Abel, D. Catalin, D. Gigmes, D. Bertin and L. Porte, J. Am. Chem. Soc., 2008, 130, 6678–6679.
5. R. Gutzler, H. Walch, G. Eder, S. Kloft, W. M. Heckl and M. Lackinger, Chem. Commun., 2009, 4456–4458.
6. S. Weigelt, C. Busse, C. Bombis, M. M. Knudsen, K. V. Gothelf, E. Laegsgaard, F. Besenbacher and T. R. Linderoth, Angew. Chem., Int. Ed., 2008, 47, 4406–4410; S. Weigelt, J. Schnadt, A. K. Tuxen, F. Masini, C. Bombis, C. Busse, C. Isvoranu, E. Ataman, E. Laegsgaard, F. Besenbacher and T. R. Linderoth, J. Am. Chem. Soc., 2008, 130, 5388–5389; A. Gourdon, Angew. Chem., Int. Ed., 2008, 47, 6950–6953; S. Weigelt, C. Bombis, C. Busse, M. M. Knudsen, K. V. Gothelf, E. Laegsgaard, F. Besenbacher and T. R. Linderoth, ACS Nano, 2008, 2, 651–660; J. Eichhorn, W. M. Heckl and M. Lackinger, Chem. Commun., 2013, 49, 2900–2902.
7. T. Wang and J. F. Zhu, Surf. Sci. Rep., 2019, 74, 97–140; Q. G. Zhong, Y. B. Hu, K. F. Niu, H. M. Zhang, B. Yang, D. Ebeling, J. Tschakert, T. Cheng, A. Schirmeisen, A. Narita, K. Müllen and L. F. Chi, J. Am. Chem. Soc., 2019, 141, 7399–7406; J. Deyerling, B. B. Berna, D. Biloborodov, F. Haag, S. Toemekce, M. G. Cuxart, C. H. Li, W. Auwaerter and D. Bonifazi, Angew. Chem., Int. Ed., 2025, 64, e202412978.
8. M. Lackinger and W. M. Heckl, J. Phys. D: Appl. Phys., 2011, 44, 464011.
9. L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, Science, 2009, 325, 1110–1114; G. Kichin, C. Weiss, C. Wagner, F. S. Tautz and R. Temirov, J. Am. Chem. Soc., 2011, 133, 16847–16851.
10. J. Eichhorn, D. Nieckarz, O. Ochs, D. Samanta, M. Schmittel, P. J. Szabelski and M. Lackinger, ACS Nano, 2014, 8, 7880–7889.
11. J. Eichhorn, T. Strunskus, A. Rastgoo-Lahrood, D. Samanta, M. Schmittel and M. Lackinger, Chem. Commun., 2014, 50, 7680–7682.
12. G. S. McCarty and P. S. Weiss, J. Am. Chem. Soc., 2004, 126, 16772–16776.
13. C. H. Shu, M. X. Liu, Z. Q. Zha, J. L. Pan, S. Z. Zhang, Y. L. Xie, J. L. Chen, D. W. Yuan, X. H. Qiu and P. N. Liu, Nat. Commun., 2018, 9, 2322; Q. Sun, X. Yu, M. L. Bao, M. X. Liu, J. L. Pan, Z. Q. Zha, L. L. Cai, H. H. Ma, C. X. Yuan, X. H. Qiu and W. Xu, Angew. Chem., Int. Ed., 2018, 57, 4035–4038.
14. K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299–1301; L. Y. Sun, W. Zheng, W. Z. Gao, F. M. Kang, M. L. Zhao and W. Xu, Nature, 2023, 623, 972–976; L. Y. Sun, W. Zheng, F. M. Kang, W. Z. Gao, T. D. Wang, G. H. Gao and W. Xu, Nat. Commun., 2024, 15, 7649.
15. J. Repp, G. Meyer, S. M. Stojkovic, A. Gourdon and C. Joachim, Phys. Rev. Lett., 2005, 94, 026803.
16. P. Ruffieux, S. Y. Wang, B. Yang, C. Sanchez-Sanchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli, D. Passerone, T. Dumslaff, X. L. Feng, K. Müllen and R. Fasel, Nature, 2016, 531, 489–492.
17. L. A. Lieske, M. Commodo, J. W. Martin, K. Kaiser, V. Benekou, P. Minutolo, A. D'Anna and L. Gross, ACS Nano, 2023, 17, 13563–13574; B. Schuler, G. Meyer, D. Peña, O. C. Mullins and L. Gross, J. Am. Chem. Soc., 2015, 137, 9870–9876; K. Kaiser, F. Schulz, J. F. Maillard, F. Hermann, I. Pozo, D. Peña, H. J. Cleaves, A. S. Burton, G. Danger, C. Afonso, S. Sandford and L. Gross, Meteorit. Planet. Sci., 2022, 57, 644–656.
18. F. Albrecht, F. Bischoff, W. Auwärter, J. V. Barth and J. Repp, Nano Lett., 2016, 16, 7703–7709.
19. D. G. de Oteyza, A. García-Lekue, M. Vilas-Varela, N. Merino-Díez, E. Carbonell-Sanromà, M. Corso, G. Vasseur, C. Rogero, E. Guitián, J. I. Pascual, J. E. Ortega, Y. Wakayama and D. Peña, ACS Nano, 2016, 10, 9000–9008.
20. N. Moll, B. Schuler, S. Kawai, F. Xu, L. F. Peng, A. Orita, J. Otera, A. Curioni, M. Neu, J. Repp, G. Meyer and L. Gross, Nano Lett., 2014, 14, 6127–6131; B. S. Lammers, D. Yesilpinar, A. Timmer, Z. X. Hu, W. Ji, S. Amirjalayer, H. Fuchs and H. Mönig, Nanoscale, 2021, 13, 13617–13623.
21. Q. Fan, D. Martin-Jimenez, D. Ebeling, C. K. Krug, L. Brechmann, C. Kohlmeyer, G. Hilt, W. Hieringer, A. Schirmeisen and J. M. Gottfried, J. Am. Chem. Soc., 2019, 141, 17713–17720; Q. Fan, D. Martin-Jimenez, S. Werner, D. Ebeling, T. Koehler, T. Vollgraff, J. Sundermeyer, W. Hieringer, A. Schirmeisen and J. M. Gottfried, J. Am. Chem. Soc., 2020, 142, 894–899.
22. H. Mönig, S. Amirjalayer, A. Timmer, Z. X. Hu, L. C. Liu, O. D. Arado, M. Cnudde, C. A. Strassert, W. Ji, M. Rohlfing and H. Fuchs, Nat. Nanotechnol., 2018, 13, 371–375.
23. J. C. Li, S. Sanz, J. Castro-Esteban, M. Vilas-Varela, N. Friedrich, T. Frederiksen, D. Peña and J. I. Pascual, Phys. Rev. Lett., 2020, 124, 177201.
24. F. F. Xiang, S. Maisel, S. Beniwal, V. Akhmetov, C. Ruppenstein, M. Devarajulu, A. Dörr, O. Papaianina, A. Görling, K. Y. Amsharov and S. Maier, Nat. Chem., 2022, 14, 871–876.
25. F. De Boni, R. Pilot, A. Milani, V. V. Ivanovskaya, R. J. Abraham, S. Casalini, D. Pedron, C. S. Casari, M. Sambi and F. Sedona, Nanoscale, 2024, 16, 11211–11222.
26. J. M. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. L. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470–473.
27. M. Moskovits, J. Chem. Phys., 1982, 77, 4408–4416.
28. L. Grossmann, B. T. King, S. Reichlmaier, N. Hartmann, J. Rosen, W. M. Heckl, J. Björk and M. Lackinger, Nat. Chem., 2021, 13, 730–736.
29. N. Kalashnyk, K. Mouhat, J. Oh, J. Jung, Y. C. Xie, E. Salomon, T. Angot, F. Dumur, D. Gigmes and S. Clair, Nat. Commun., 2017, 8, 14735.
30. R. Zhang, Y. Zhang, Z. C. Dong, S. Jiang, C. Zhang, L. G. Chen, L. Zhang, Y. Liao, J. Aizpurua, Y. Luo, J. L. Yang and J. G. Hou, Nature, 2013, 498, 82–86.
31. L. Q. Zheng, M. Servalli, A. D. Schlüter and R. Zenobi, Chem. Sci., 2019, 10, 9673–9678; F. Shao, W. Wang, W. M. Yang, Z. L. Yang, Y. Zhang, J. G. Lan, A. D. Schlüter and R. Zenobi, Nat. Commun., 2021, 12, 4557.
32. A. Shiotari, T. Kumagai and M. Wolf, J. Phys. Chem. C, 2014, 118, 11806–11812.
33. Y. Luo, A. Martin-Jimenez, M. Pisarra, F. Martin, M. Garg and K. Kern, Nat. Commun., 2023, 14, 3484.
34. C. Bronner, F. Leyssner, S. Stremlau, M. Utecht, P. Saalfrank, T. Klamroth and P. Tegeder, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085444.
35. Z. P. Chen, W. Zhang, C. A. Palma, A. L. Rizzini, B. L. Liu, A. Abbas, N. Richter, L. Martini, X. Y. Wang, N. Cavani, H. Lu, N. Mishra, C. Coletti, R. Berger, F. Klappenberger, M. Klaui, A. Candini, M. Affronte, C. W. Zhou, V. De Renzi, U. del Pennino, J. V. Barth, H. J. Rader, A. Narita, X. L. Feng and K. Müllen, J. Am. Chem. Soc., 2016, 138, 15488–15496.
36. Y. Y. Sung, H. Vejayan, C. J. Baddeley, N. V. Richardson, F. Grillo and R. Schaub, ACS Nano, 2022, 16, 10281–10291.
37. D. Y. Zhong, J. H. Franke, S. K. Podiyanachari, T. Blömker, H. M. Zhang, G. Kehr, G. Erker, H. Fuchs and L. F. Chi, Science, 2011, 334, 213–216.
38. L. E. Dinca, C. Y. Fu, J. M. MacLeod, J. Lipton-Duffin, J. L. Brusso, C. E. Szakacs, D. L. Ma, D. F. Perepichka and F. Rosei, ACS Nano, 2013, 7, 1652–1657; Q. T. Fan, L. H. Yan, M. W. Tripp, O. Krejci, S. Dimosthenous, S. R. Kachel, M. Y. Chen, A. S. Foster, U. Koert, P. Liljeroth and J. M. Gottfried, Science, 2021, 372, 852–856.
39. W. Zhang, Z. P. Chen, B. Yang, X. Y. Wang, R. Berger, A. Narita, G. B. Barin, P. Ruffieux, R. Fasel, X. L. Peng, H. J. Räder and K. Müllen, Anal. Chem., 2017, 89, 7485–7492.
40. M. Di Giovannantonio, O. Deniz, J. I. Urgel, R. Widmer, T. Dienel, S. Stolz, C. Sanchez-Sanchez, M. Muntwiler, T. Dumslaff, R. Berger, A. Narita, X. L. Feng, K. Müllen, P. Ruffieux and R. Fasel, ACS Nano, 2018, 12, 74–81.
41. C. Wäckerlin, Angew. Chem., Int. Ed., 2021, 60, 8446–8449.
42. D. P. Woodruff, Jpn. J. Appl. Phys., 2019, 58, 100501; A. Michaelides, K. Reuter and M. Scheffler, J. Vac. Sci. Technol., A, 2005, 23, 1487–1497.
43. W. Moritz and M. A. van Hove, Surface Structure Determination by LEED and X-rays, Cambridge University Press, 2022.
44. G. Michalk, W. Moritz, H. Pfnur and D. Menzel, Surf. Sci., 1983, 129, 92–106.
45. G. Galeotti, F. De Marchi, E. Hamzehpoor, O. MacLean, M. R. Rao, Y. Chen, L. V. Besteiro, D. Dettmann, L. Ferrari, F. Frezza, P. M. Sheverdyaeva, R. Liu, A. K. Kundu, P. Moras, M. Ebrahimi, M. C. Gallagher, F. Rosei, D. F. Perepichka and G. Contini, Nat. Mater., 2020, 19, 874–880.
46. J. A. Lipton-Duffin, O. Ivasenko, D. F. Perepichka and F. Rosei, Small, 2009, 5, 592–597; J. A. Lipton-Duffin, J. A. Miwa, M. Kondratenko, F. Cicoira, B. G. Sumpter, V. Meunier, D. F. Perepichka and F. Rosei, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11200–11204.
47. G. Vasseur, Y. Fagot-Revurat, M. Sicot, B. Kierren, L. Moreau, D. Malterre, L. Cardenas, G. Galeotti, J. Lipton-Duffin, F. Rosei, M. Di Giovannantonio, G. Contini, P. Le Fèvre, F. Bertran, L. B. Liang, V. Meunier and D. F. Perepichka, Nat. Commun., 2016, 7, 10235.
48. D. Martoccia, P. R. Willmott, T. Brugger, M. Björck, S. Günther, C. M. Schlepütz, A. Cervellino, S. A. Pauli, B. D. Patterson, S. Marchini, J. Wintterlin, W. Moritz and T. Greber, Phys. Rev. Lett., 2008, 101, 126102; W. Moritz, B. Wang, M. L. Bocquet, T. Brugger, T. Greber, J. Wintterlin and S. Günther, Phys. Rev. Lett., 2010, 104, 136102.
49. J. I. Flege and E. E. Krasovskii, Phys. Status Solidi RRL, 2014, 8, 463–477; M. Petrovic, M. Horn-von Hoegen and F. J. M. Zu Heringdorf, Appl. Surf. Sci., 2018, 455, 1086–1094.
50. L. Talirz, H. Söde, T. Dumslaff, S. Y. Wang, J. R. Sanchez-Valencia, J. Liu, P. Shinde, C. A. Pignedoli, L. B. Liang, V. Meunier, N. C. Plumb, M. Shi, X. L. Feng, A. Narita, K. Müllen, R. Fasel and P. Ruffieux, ACS Nano, 2017, 11, 1380–1388; N. Merino-Díez, J. Lobo-Checa, P. Nita, A. Garcia-Lekue, A. Basagni, G. Vasseur, F. Tiso, F. Sedona, P. K. Das, J. Fujii, I. Vobornik, M. Sambi, J. I. Pascual, J. E. Ortega and D. G. de Oteyza, J. Phys. Chem. Lett., 2018, 9, 2510–2517.
51. R. Gutzler and D. F. Perepichka, J. Am. Chem. Soc., 2013, 135, 16585–16594; A. Badami-Behjat, G. Galeotti, R. Gutzler, D. L. Pastoetter, W. M. Heckl, X. L. Feng and M. Lackinger, Nanoscale Horiz., 2024, 9, 1042–1051.
52. D. Dettmann, P. M. Sheverdyaeva, E. Hamzehpoor, S. Franchi, G. Galeotti, P. Moras, C. Ceccarelli, D. F. Perepichka, F. Rosei and G. Contini, ACS Nano, 2023, 18, 849–857.
53. P. Puschnig, S. Berkebile, A. J. Fleming, G. Koller, K. Emtsev, T. Seyller, J. D. Riley, C. Ambrosch-Draxl, F. P. Netzer and M. G. Ramsey, Science, 2009, 326, 702–706.
54. A. Haags, A. Reichmann, Q. T. Fan, L. Egger, H. Kirschner, T. Naumann, S. Werner, T. Vollgraff, J. Sundermeyer, L. Eschmann, X. S. Yang, D. Brandstetter, F. C. Bocquet, G. Koller, A. Gottwald, M. Richter, M. G. Ramsey, M. Rohlfing, P. Puschnig, J. M. Gottfried, S. Soubatch and F. S. Tautz, ACS Nano, 2020, 14, 15766–15775.
55. D. Dettmann, G. Galeotti, O. MacLean, M. Tomellini, M. Di Giovannantonio, J. Lipton-Duffin, A. Verdini, L. Floreano, Y. Fagot-Revurat, D. F. Perepichka, F. Rosei and G. Contini, Small, 2021, 17, 2103044.
56. G. Hähner, Chem. Soc. Rev., 2006, 35, 1244–1255.
57. T. Breuer, M. Klues and G. Witte, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 102–115.
58. D. P. Woodruff, Rep. Prog. Phys., 2005, 68, 743–798.
59. K. A. Simonov, N. A. Vinogradov, A. S. Vinogradov, A. V. Generalov, E. M. Zagrebina, N. Mårtensson, A. A. Cafolla, T. Carpy, J. P. Cunniffe and A. B. Preobrajenski, J. Phys. Chem. C, 2014, 118, 12532–12540.
60. M. Zugermeier, M. Gruber, M. Schmid, B. P. Klein, L. Ruppenthal, P. Müller, R. Einholz, W. Hieringer, R. Berndt, H. F. Bettinger and J. M. Gottfried, Nanoscale, 2017, 9, 12461–12469; M. Lischka, G. S. Michelitsch, N. Martsinovich, J. Eichhorn, A. Rastgoo-Lahrood, T. Strunskus, R. Breuer, K. Reuter, M. Schmittel and M. Lackinger, Nanoscale, 2018, 10, 12035–12044; M. Lischka, M. Fritton, J. Eichhorn, V. S. Vyas, T. Strunskus, B. V. Lotsch, J. Bjork, W. M. Heckl and M. Lackinger, J. Phys. Chem. C, 2018, 122, 5967–5977; V. V. Ivanovskaya, A. Zobelli, A. Basagni, S. Casalini, L. Colazzo, F. de Boni, D. G. de Oteyza, M. Sambi and F. Sedona, J. Phys. Chem. C, 2023, 127, 393–402.
61. M. Abyazisani, J. Bradford, N. Motta, J. Lipton-Duffin and J. MacLeod, J. Phys. Chem. C, 2018, 122, 17836–17845.
62. A. Rastgoo-Lahrood, J. Björk, M. Lischka, J. Eichhorn, S. Kloft, M. Fritton, T. Strunskus, D. Samanta, M. Schmittel, W. M. Heckl and M. Lackinger, Angew. Chem., Int. Ed., 2016, 55, 7650–7654.
63. A. Almenningen, O. Bastiansen, L. Fernholt, B. N. Cyvin, S. J. Cyvin and S. Samdal, J. Mol. Struct., 1985, 128, 59–76.
64. A. Rastgoo-Lahrood, M. Lischka, J. Eichhorn, D. Samanta, M. Schmittel, W. M. Heckl and M. Lackinger, Nanoscale, 2017, 9, 4995–5001.
65. A. Kinikar, T. G. Englmann, M. Di Giovannantonio, N. Bassi, F. F. Xiang, S. Stolz, R. Widmer, G. B. Barin, E. Turco, K. Eimre, N. M. Díez, A. Ortega-Guerrero, X. L. Feng, O. Gröning, C. A. Pignedoli, R. Fasel and P. Ruffieux, ACS Nano, 2024, 18, 16622–16631.
66. M. Schwarz, A. Riss, M. Garnica, J. Ducke, P. S. Deimel, D. A. Duncan, P. K. Thakur, T. L. Lee, A. P. Seitsonen, J. V. Barth, F. Allegretti and W. Auwärter, ACS Nano, 2017, 11, 9151–9161.
67. M. Schwarz, D. A. Duncan, M. Garnica, J. Ducke, P. S. Deimel, P. K. Thakur, T. L. Lee, F. Allegretti and W. Auwärter, Nanoscale, 2018, 10, 21971–21977; C. Brulke, T. Heepenstrick, I. Krieger, B. Wolff, X. S. Yang, A. Shamsaddinlou, S. Weiss, F. C. Bocquet, F. S. Tautz, S. Soubatch and M. Sokolowski, Phys. Rev. B, 2019, 99, 121404.
68. C. J. Judd, F. L. Q. Junqueira, S. L. Haddow, N. R. Champness, D. A. Duncan, R. G. Jones and A. Saywell, Commun. Chem., 2020, 3, 166.
69. L. Grossmann, D. A. Duncan, S. P. Jarvis, R. G. Jones, S. De, J. Rosen, M. Schmittel, W. M. Heckl, J. Björk and M. Lackinger, Nanoscale Horiz., 2021, 7, 51–62.
70. D. Barton, H. Y. Gao, P. A. Held, A. Studer, H. Fuchs, N. L. Doltsinis and J. Neugebauer, Chem. – Eur. J., 2017, 23, 6190–6197; C. Zhang, E. Kazuma and Y. Kim, Angew. Chem., Int. Ed., 2019, 58, 17736–17744; Z. Z. Zhang, D. F. Perepichka and R. Z. Khaliullin, J. Phys. Chem. Lett., 2021, 12, 11061–11069.
71. L. Chen, J. Rosen and J. Björk, ChemPhysChem, 2025, 26, e202400865.
72. G. L. Zhan, Z. F. Cai, K. Strutynski, L. H. Yu, N. Herrmann, M. Martínez-Abadía, M. Melle-Franco, A. Mateo-Alonso and S. De Feyter, Nature, 2022, 603, 835–840.
73. S. Stolz, M. Di Giovannantonio, O. Groning and R. Widmer, Chimia, 2022, 76, 203–211.
74. A. Batra, D. Cvetko, G. Kladnik, O. Adak, C. Cardoso, A. Ferretti, D. Prezzi, E. Molinari, A. Morgante and L. Venkataraman, Chem. Sci., 2014, 5, 4419–4423; K. A. Simonov, A. V. Generalov, A. S. Vinogradov, G. I. Svirskiy, A. A. Cafolla, C. McGuinness, T. Taketsugu, A. Lyalin, N. Martensson and A. B. Preobrajenski, Sci. Rep., 2018, 8, 3506.
75. M. Fritton, D. A. Duncan, P. S. Deimel, A. Rastgoo-Lahrood, F. Allegretti, J. V. Barth, W. M. Heckl, J. Björk and M. Lackinger, J. Am. Chem. Soc., 2019, 141, 4824–4832.
76. M. Lackinger, Chem. Commun., 2017, 53, 7872–7885; J. Björk, F. Hanke and S. Stafstrom, J. Am. Chem. Soc., 2013, 135, 5768–5775.
77. S. Stolz, M. Di Giovannantonio, J. I. Urgel, Q. Sun, A. Kinikar, G. B. Barin, M. Bommert, R. Fasel and R. Widmer, Angew. Chem., Int. Ed., 2020, 59, 14106–14110.
78. L. Grossmann, M. Hocke, G. Galeotti, G. Contini, L. Floreano, A. Cossaro, A. Ghosh, M. Schmittel, J. Rosen, W. M. Heckl, J. Björk and M. Lackinger, Nanoscale, 2024, 16, 7612–7625.
79. R. C. Baetzold and G. A. Somorjai, J. Catal., 1976, 45, 94–105.
80. M. Di Giovannantonio, M. Tomellini, J. Lipton-Duffin, G. Galeotti, M. Elrahimi, A. Cossaro, A. Verdini, N. Kharche, V. Meunier, G. Vasseur, Y. Fagot-Revurat, D. F. Perepichka, F. Rosei and G. Contini, J. Am. Chem. Soc., 2016, 138, 16696–16702.
81. G. Galeotti, M. Di Giovannantonio, J. Lipton-Duffin, M. Ebrahimi, S. Tebi, A. Verdini, L. Floreano, Y. Fagot-Revurat, D. F. Perepichka, F. Rosei and G. Contini, Faraday Discuss., 2017, 204, 453–469.
82. M. Lackinger, ChemPhysChem, 2024, 25, e202400156.
83. L. L. Patera, F. Bianchini, C. Africh, C. Dri, G. Soldano, M. M. Mariscal, M. Peressi and G. Comelli, Science, 2018, 359, 1243–1246; D. Dettmann, M. Panighel, N. P. Genesh, G. Galeotti, O. MacLean, M. F. Camellone, T. K. Johal, S. Fabris, C. Africh, D. F. Perepichka, F. Rosei and G. Contini, J. Am. Chem. Soc., 2024, 146, 24493–24502.
84. L. Talirz, H. Söde, J. M. Cai, P. Ruffieux, S. Blankenburg, R. Jafaar, R. Berger, X. L. Feng, K. Müllen, D. Passerone, R. Fasel and C. A. Pignedoli, J. Am. Chem. Soc., 2013, 135, 2060–2063.
85. K. Moritani, M. Hashinokuchi, J. Nakagawa, T. Kashiwagi, N. Toyoda and K. Mochiji, Appl. Surf. Sci., 2008, 255, 948–950.
86. A. Basagni, L. Ferrighi, M. Cattelan, L. Nicolas, K. Handrup, L. Vaghi, A. Papagni, F. Sedona, C. Di Valentin, S. Agnoli and M. Sambi, Chem. Commun., 2015, 51, 12593–12596; M. Lackinger and A. D. Schlüter, Eur. J. Org. Chem., 2021, 5478–5490; C. Nacci, M. Schied, D. Civita, E. Magnano, S. Nappini, I. Pis and L. Grill, J. Phys. Chem. C, 2021, 125, 22554–22561; M. Lackinger, Trends Chem., 2022, 4, 471–474.
87. D. Peller, L. Z. Kastner, T. Buchner, C. Roelcke, F. Albrecht, N. Moll, R. Huber and J. Repp, Nature, 2020, 585, 58–62.
88. S. E. Ammerman, V. Jelic, Y. Wei, V. N. Breslin, M. Hassan, N. Everett, S. Lee, Q. Sun, C. A. Pignedoli, P. Ruffieux, R. Fasel and T. L. Cocker, Nat. Commun., 2021, 12, 6794.
89. M. Kittelmann, P. Rahe, M. Nimmrich, C. M. Hauke, A. Gourdon and A. Kühnle, ACS Nano, 2011, 5, 8420–8425; G. Galeotti, M. Fritton and M. Lackinger, Angew. Chem. Int. Ed., 2020, 59, 22785–22789; M. Lackinger, Dalton Trans., 2021, 50, 10020–10027; K. W. Sun, Y. Fang and L. F. Chi, ACS Mater. Lett., 2021, 3, 56–63; L. Grossmann, S. Korn, R. Breuer, M. Schmittel, H. B. Weber, W. M. Heckl and M. Lackinger, Angew. Chem., Int. Ed., 2025, 64, e202422521.
90. D. Naberezhnyi, L. Mai, N. Doudin, I. Ennen, A. Hutten, E. I. Altman, A. Devi and P. Dementyev, Nano Lett., 2022, 22, 1287–1293.
91. A. J. Watson, W. B. Lu, M. H. D. Guimaraes and M. Stöhr, 2D Mater., 2021, 8, 032001; G. B. Barin, A. Fairbrother, L. Rotach, M. Bayle, M. Paillet, L. B. Liang, V. Meunier, R. Hauert, T. Dumslaff, A. Narita, K. Müllen, H. Sahabudeen, R. Berger, X. L. Feng, R. Fasel and P. Ruffieux, ACS Appl. Nano. Mater., 2019, 2, 2184–2192.
92. J. Lawrence, A. Berdonces-Layunta, S. Edalatmanesh, J. Castro-Esteban, T. Wang, A. Jimenez-Martin, B. de la Torre, R. Castrillo-Bodero, P. Angulo-Portugal, M. S. G. Mohammed, A. Matej, M. Vilas-Varela, F. Schiller, M. Corso, P. Jelinek, D. Peña and D. G. de Oteyza, Nat. Chem., 2022, 14, 1451–1458.

---