Advances in computational approaches for bridging theory and experiments in electrocatalyst design

Abstract

The activation of inert molecules such as CO₂, N₂, and O₂ is central to addressing global energy and environmental challenges via electrocatalysis. However, their intrinsic stability and the complex solid–liquid interfacial phenomena present formidable obstacles for catalyst design. Recent advances in computational approaches are beginning to bridge the longstanding gap between idealized theoretical models and experimental realities. In this review, we highlight the progress made in scaling relations and descriptor-based screening methods, which underpin the Sabatier principle and volcano plot frameworks, enabling rapid identification of promising catalytic materials. We further discuss the evolution of thermodynamic and kinetic models—including the computational hydrogen electrode model, constant electrode potential model, and ab initio thermodynamics—that allow for accurate predictions of reaction energetics and catalyst stability under realistic operating conditions. Moreover, the advent of constant potential simulations and explicit solvation models, bolstered by ab initio molecular dynamics and machine learning-accelerated molecular dynamics, has significantly advanced our understanding of the dynamic electrochemical interface. High-throughput computational workflows and data-driven machine learning techniques have further streamlined catalyst discovery by efficiently exploring large material spaces and complex reaction pathways. Together, these computational advances not only provide mechanistic insights into inert molecule activation but also offer a robust platform for guiding experimental efforts. The review concludes with a discussion of remaining challenges and future opportunities to further integrate computational and experimental methodologies for the rational design of next-generation electrocatalysts.

---

1. Introduction

The sustainable conversion of inert molecules such as carbon dioxide (CO₂), nitrogen (N₂), and oxygen (O₂) represents a formidable challenge in the field of electrocatalysis. For example, water electrolysis enables the production of green hydrogen through the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER).¹ In fuel cells, the oxygen reduction reaction (ORR) and hydrogen oxidation reaction (HOR) facilitate the conversion of chemical energy into electricity.^2–4 Carbon dioxide reduction (CO₂R) transforms CO₂, a major greenhouse gas, into valuable chemicals,^5–7 while the nitrogen reduction reaction (NRR) provides an electrochemical route for ammonia synthesis, offering a sustainable alternative to the Haber–Bosch process.^8–10 These small molecules, due to their strong covalent bonds and nonpolar character, are remarkably resistant to activation, yet their efficient transformation is crucial for addressing global energy and environmental issues.^11,12 Traditional experimental approaches to catalyst discovery have largely relied on trial-and-error methods guided by chemical intuition. However, such approaches often fail to capture the complex interplay between surface phenomena, reaction kinetics, and dynamic interfacial effects, leading to suboptimal catalyst performance.¹³

Recent decades have witnessed a paradigm shift with the emergence of advanced computational methods, which provide atomic-level insights into reaction mechanisms and active site behavior. Density functional theory (DFT) has become the cornerstone of computational catalysis, enabling researchers to model electronic structures and predict adsorption energies with considerable accuracy.^14–16 The development of scaling relations and descriptor-based screening methods, based on the Sabatier principle and Brønsted–Evans–Polanyi (BEP) relationships, has allowed for the systematic identification of catalysts that exhibit an optimal balance between reactant adsorption and product desorption.^17–19 Volcano plots derived from these principles succinctly capture the trade-offs inherent in catalyst performance, offering a clear metric for evaluating candidate materials.^18,20

Despite these advances, a significant gap remains between the idealized conditions assumed in computational studies and the complex environments encountered in practical electrocatalytic systems.^21–23 Conventional DFT calculations typically operate under constant charge conditions, neglecting the dynamic nature of the electrochemical interface. In reality, the presence of a solvent, the formation of an electric double layer (EDL), and the influence of applied potential all contribute to the catalytic behavior of materials.^24–26 To address these limitations, constant potential methods and grand canonical DFT have been developed, allowing simulations to more accurately reflect experimental conditions by maintaining a fixed electrode potential during calculations.^27–29 These methods facilitate a more realistic description of the interfacial phenomena that govern reaction kinetics and selectivity.

Another critical aspect of electrocatalysis is the influence of the solid–liquid interface. The interplay between the catalyst surface and the surrounding electrolyte has been shown to significantly affect reaction pathways and the stability of adsorbed intermediates. Explicit solvent models, particularly those implemented via ab initio molecular dynamics (AIMD), have provided valuable insights into the role of hydrogen-bond networks and solvent reorganization in modulating surface reactions.⁸ Such studies have revealed that solvent molecules can actively participate in proton-coupled electron transfer (PCET) processes, thereby altering the reaction mechanism and lowering activation barriers.^30,31 However, AIMD simulations are computationally demanding and often limited to short timescales, which has motivated the development of machine learning (ML) potentials that can extend the accessible simulation window while retaining near ab initio accuracy.^21,32–34

High-throughput computational workflows have further accelerated the discovery of promising catalysts.^35–37 By automating DFT calculations across extensive material databases, researchers can rapidly screen thousands of potential catalysts and identify key descriptors that correlate with high activity and selectivity. The integration of ML techniques into these workflows has enhanced predictive capabilities, enabling the development of data-driven models that can forecast adsorption energies, reaction barriers, and even catalyst stability under varying conditions.^38–41 Methods such as the sure independence screening and sparsifying operator (SISSO) and graph neural networks (GNNs) have proven particularly effective in extracting meaningful features from complex datasets,^42–44 thereby bridging the gap between theoretical predictions and experimental observations.⁴⁵

In addition to facilitating the initial screening and mechanistic understanding, computational approaches play a crucial role in addressing catalyst stability—a key determinant of practical viability. Catalyst degradation or evolution through processes such as dissolution of single-atom catalysts, surface reconstruction of transition metal (TM) oxides, and adsorbate-induced poisoning can significantly diminish performance over time.^46–48 The application of ab initio thermodynamics, combined with Pourbaix diagram analyses, allows researchers to predict the stability of catalyst materials under realistic operating conditions.^49–53 Moreover, ML-assisted long-time-scale molecular dynamics simulations offer a promising route to model the dynamic evolution of catalyst surfaces, providing insights into structural changes that occur during operation and guiding the design of more robust electrocatalysts.^54,55

Ultimately, the convergence of advanced computational methods with experimental techniques is paving the way for a more integrated approach to electrocatalyst design. Computational insights not only guide experimental synthesis and testing but also benefit from experimental feedback, which in turn refines theoretical models. This iterative loop—where theory informs experiment and experimental data enhance computational predictions—is critical for overcoming the complexities associated with inert molecule activation in electrocatalysis.⁵⁶ By leveraging the synergies between high-throughput screening, constant potential simulations, explicit solvation models, and ML-driven dynamics, researchers are steadily narrowing the gap between idealized models and practical applications.^57,58 In this review, we discuss recent advances in computational approaches that have significantly contributed to bridging the theory–experiment gap in electrocatalysis for inert molecule activation (Fig. 1). We begin with a discussion of fundamental catalysis theory and the computational models that underpin modern catalyst screening. We then explore state-of-the-art techniques in identifying activity trends and electrocatalysts design, followed by a detailed examination of catalyst stability and the role of the solid–liquid interface. Finally, we outline the remaining challenges and future opportunities that lie at the intersection of computation and experiment, with the aim of guiding the rational design of next-generation electrocatalysts.

Fig. 1 Schematic illustration of the cutting-edge computational methods and applications in electrocatalysis.

2. Fundamental catalysis theory and computational methods

Recent advances in computational electrocatalysis have enabled the rational design of catalysts by providing atomic-scale insights into reaction mechanisms, activity descriptors, and stability trends. Substantial progress has been made in characterizing electrochemical interfaces and reactions using first-principles methods, offering deeper understanding of electrostatic potential distribution, ion dynamics, and water orientation at the interface. To illustrate how these methods are organized across multiple length and time scales, Fig. 2 and Table 1 present a bottom-up multiscale computational framework, highlighting how different modeling approaches work and probe electrocatalytic processes. This section outlines the fundamental theoretical frameworks and computational methods that underpin modern computational electrocatalysis, focusing on thermodynamic and kinetic modeling, constant potential approaches, and ML-assisted high-throughput calculations.

Fig. 2 Illustration of a bottom-up multiscale computational heterogeneous catalysis study.

Table 1 Summary of common methods in electrocatalysis studies

Method	Typical outputs	Strengths	Limitations	Common software
Density functional theory	Adsorption energies, reaction energies, charge density maps	Accurate quantum-level insight into energetics	Computationally expensive	VASP
				Quantum ESPRESSO
Ab initio molecular dynamics	Atomic trajectories, temperature-dependent structures	Captures thermal motion and dynamic stability	Very costly for long timescales	VASP-AIMD
				CP2K
Microkinetic modeling	TOF, coverage, selectivity, rate-limiting step	Links DFT and catalytic performance	Requires accurate energetics and pre-exponential factors	CatMAP
				PyKinetics
Machine learning methods	Predicted adsorption energies, ΔG, overpotentials, full-surface predictions, energy landscapes	Fast predictions, captures non-linear relations, handles complex systems	Needs large training sets; high complexity; model interpretability and generalization issues	scikit-learn
				PyTorch
				TensorFlow

---

2.1 Fundamental theory

2.1.1 Density functional theory (DFT). DFT has become the foundation of modern computational catalysis, offering a quantum mechanical framework to model the electronic structures and reaction intermediates. Since its formalization by Hohenberg and Kohn, DFT has enabled the approximation of electron density as the fundamental variable governing molecular interactions.^14,59,60 In surface chemistry, DFT allows precise calculation of adsorption energies, reaction pathways, and charge transfer processes on catalytic surfaces.^61,62 DFT is rooted in the Schrödinger equation, which governs the quantum mechanical behavior of electrons in molecules and solids. However, solving the full many-body wavefunction is computationally infeasible due to its exponential complexity. To address this challenge, the Born–Oppenheimer approximation was introduced,⁶³ allowing the decoupling of nuclear and electronic motion, thus simplifying the problem of electron density determination.

Modern DFT is built upon three key theorems. The Hohenberg–Kohn (HK) first theorem establishes a one-to-one correspondence between the external potential and the ground-state electron density, ensuring that all ground-state properties, including energy, are uniquely determined by the electron density ρ(r).⁶⁴ The HK first theorem defines the total energy as a function of electron density, e.g. , including the kinetic energy of the electronic system, the electron–electron interaction potential energy, and the electron-external potential interaction energy. The HK second theorem provides a variational principle, stating the energy functional E[ρ] reaches its minimum at the true ground-state density. This provides the theoretical framework for obtaining ground-state properties through density optimization at the constraint that ρ(r) integrates to the total electron number N.⁶⁴ Finally, Kohn–Sham (KS) theory states that the many-body wave function can be expressed as a single Slater determinant constructed from one-electron orbital φ_i(r). The corresponding energies ε_i of these orbitals can be obtained by solving the Kohn–Sham equation: 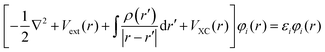. The Hamiltonian of the Kohn–Sham equation introduces an additional exchange–correlation operator, V_XC(r), which treats the many-body electron interactions.⁶⁵ A central challenge in DFT lies in approximating the exchange–correlation functional, which accounts for electron–electron interactions. The generalized gradient approximation (GGA),⁶⁶ widely used in heterogeneous catalysis, improves upon the local density approximation (LDA) by incorporating density gradients. Among GGA functionals, the Perdew–Burke–Ernzerhof (PBE) functional remains the most commonly used due to its balance between accuracy and computational efficiency.^66,67 Modifications such as RPBE refine the exchange enhancement factor to improve adsorption energy predictions,⁶⁸ while revPBE reduces overbinding errors.⁶⁷

Beyond GGA, nonlocal effects such as dispersion interactions are crucial in catalytic systems involving adsorbates and solvents. To account for van der Waals (vdW) interactions, dispersion-corrected functionals such as Grimme's D2 and D3 have been developed.^69,70 More recently, the Bayesian error estimation functional with vdW corrections (BEEF–vdW) has been introduced, leveraging Bayesian inference to estimate computational uncertainties^71,72 and offering a probabilistic approach to error estimation in electronic structure calculations. These advancements have significantly enhanced the predictive power of DFT in electrocatalysis, facilitating the rational design of catalysts by providing reliable adsorption energies, reaction barriers, and stability trends.

2.1.2 Transition states, BEP theory, d-band theory, Sabatier principle, and volcano plot. In heterogeneous electrocatalysis, a wide range of reactions such as CO₂RR, NRR, ORR/OER, and HER play pivotal roles in energy conversion technologies. These reactions proceed through sequences of elementary steps, involving proton–electron transfers and the formation of key surface intermediates (Fig. 3). Understanding the nature of these steps, such as the transformation from *COOH to *CO in CO₂RR, or from *N₂H to *NH₃ in NRR, is essential for identifying catalytic bottlenecks and optimizing performance.

Fig. 3 Schematic illustration of elementary reaction pathways and main surface intermediates for CO₂RR to C1 and C2 products, NRR, OER, ORR, OER, and HER. Each panel highlights key proton–electron transfer steps and adsorbed species involved in the catalytic cycles.

Heterogeneous catalysis relies on interactions between reactant molecules and catalyst surfaces, where adsorption critically influences reaction pathways and overall activity. Over the past century, theoretical models have offered key insights into adsorption, reaction kinetics, and catalyst design. Notably, transition state theory (TST), Brønsted–Evans–Polanyi (BEP) relations, d-band theory, Sabatier's principle, and volcano plots have become essential tools in computational catalysis.

TST, developed in the 1930s by Eyring, Evans, and Polanyi describes reaction kinetics by assuming that reactants are in quasi-equilibrium with a high-energy transition state—the energy maximum along the reaction coordinate.⁷³ By incorporating statistical mechanics, TST enables estimation of reaction rates from energy barriers obtained via DFT, which is widely used to calculate rate constant.^18,19,74 The BEP relationship, closely related to TST, establishes a linear correlation between activation barrier and reaction energy. It reflects that the transition state energy shifts systematically with the thermodynamic driving force. The slope indicates the sensitivity of activation barrier to reaction energy, while the intercept corresponds to the inherent barrier height when the reaction energy is zero. BEP relations have been widely used in catalyst screening, enabling a rapid estimation of reaction barriers from simpler descriptors such as adsorption energies.^18,19

The d-band theory, introduced by Hammer and Nørskov, explains adsorption trends on TM surfaces by describing interactions between adsorbate valence states and metal s- and d-states.^75,76 While s-states contribute uniformly, variations in d-state interactions determine catalytic activity. Bonding strength depends on the position of the d-band center relative to the Fermi level: a higher d-band center leads to stronger adsorption due to higher antibonding states, while a lower d-band center weakens adsorption.^62,77 This theory provides an intuitive way to predict adsorption trends across TMs and has been extensively utilized to design catalysts with optimized adsorption properties.

The Sabatier principle, proposed by Paul Sabatier in the early 20th century, states that an ideal catalyst should bind reactants neither too weakly nor too strongly.^78,79 Weak adsorption leads to insufficient activation, while overly strong adsorption hinders desorption and can cause catalyst poisoning. This trade-off gives rise to volcano plots, which relate catalytic activity to adsorption strength.⁸⁰ These plots typically show activity peaking at an optimal adsorption energy, with lower activity observed on either side due to suboptimal binding.

A classic example is the use of oxide heat of formation in ammonia synthesis,^81,82 where the nitrogen adsorption energy (*N) have been shown to better capture the surface interaction strength. Since nitrogen participates in all intermediates, its adsorption energy serves as a more relevant descriptor than oxygen-related descriptors.

Today, volcano plots are widely used in electrocatalysis, guiding the design of catalysts for the hydroxylamine electrosynthesis,⁸³ ORR,^84,85 and CO₂RR.⁸⁶ These theoretical tools form the foundation for rational catalysts design. BEP relations connect reaction barriers with adsorption energies, d-band theory explains adsorption trends across metals, and the Sabatier principle provides a strategy for balancing adsorption strength and activity. When integrated with modern computational methods, they enable high-throughput screening of large catalyst libraries for energy-related applications.

A major limitation of volcano plots is the presence of linear scaling relations between adsorption energies of key intermediates. For example, in ORR, *OH and *O adsorption energies are strongly correlated, preventing independent optimization of each step.^87,88 Strategies to “break” these scaling relations include: (1) strain engineering, which modifies lattice constants to decouple adsorption behaviors.^89,90 (2) Electronic tuning via alloying or heteroatom doping to disrupt linear correlations.⁹¹ (3) Nanostructuring and confinement, which introduces undercoordinated sites or nanoscale pores to alter intermediate binding.⁹² Recent studies have shown that doped 2D materials (e.g., nitrogen-doped graphene) and single-atom catalysts (SACs) can break these scaling relations by stabilizing intermediates in ways distict from bulk surfaces.^93,94

2.2 Thermodynamic and kinetic modeling

2.2.1 The computational hydrogen electrode (CHE) model. The computational hydrogen electrode (CHE) model, introduced by Nørskov and co-workers,^95,96 provides a practical framework for describing electrochemical thermodynamics using first-principles calculations. By referencing the chemical potential of the proton–electron pair to that of molecular hydrogen, the CHE model avoids the need to explicitly model solvated protons and charge transfer processes. This simplification allows for the direct calculation of reaction free energies at electrode surfaces. The key assumption of the CHE model is that protons and electrons are in equilibrium with gaseous hydrogen via the half-cell reaction:

H⁺ + e⁻ ↔ 1/2H₂, U = 0 V vs. RHE

where U is the applied electrode potential relative to the reversible hydrogen electrode (SHE). When the equation reaches equilibrium at different applied potentials, the chemical potential of the proton–electron pair is expressed as the half of the chemical potential of gaseous H₂ minus eU at any pH.

μ(H⁺ + e⁻) = 1/2μ(H₂) − eU − 0.059pH

The CHE model enables a direct assessment of catalytic activity from computed thermodynamic data, linking atomistic structure to catalytic performance. However, it neglects solvation effects, which can lead to errors when intermediates strongly interact with the solvent. It also does not account for reaction kinetics or activation barriers. Moreover, assuming a fixed electrode potential may oversimplify the system by overlooking changes in electronic structure and work function caused by varying adsorbate coverage.

2.2.2 Implicit and explicit solvation models. Solvent effects play a vital role in electrochemical simulations, influencing reaction energetics and interfacial behavior. Two primary approaches—implicit and explicit solvation—have been developed to incorporate these effects with different levels of computational cost and accuracy.⁹⁷ Implicit solvation model treats the solvent as a continuous dielectric medium, avoiding explicit solvent molecules while capturing key electrostatic interactions. The polarizable continuum model, implemented in VASPsol by Hennig et al.,⁹⁸ employs a linearized Poisson–Boltzmann equation to describe electrolyte response. VASPsol++, introduced by Plaisance et al.,⁹⁹ improves upon this by using a nonlocal cavity definition and a nonlinear Poisson–Boltzmann equation to better simulate highly charged interfaces.

In contrast, explicit solvation models include solvent molecules directly, offering higher accuracy at the cost of computational efficiency.^31,100 Reliable results require a sufficient number of solvent molecules to mimic bulk properties, often making DFT-level simulations expensive.^101–103 The QM/MM approach offers a practical alternative, combining quantum methods (e.g., DFT) for the reactive region with molecular mechanics for the solvent, using electrostatic embedding to couple the two subsystems.^24,104,105 This approach has been implemented in VASP.²⁴

Chan et al.¹⁰⁶ systematically compared implicit and explicit models using AIMD and implicit solvation methods (VASPsol, SCCS in quantum ESPRESSO/environ) for adsorbates (*CO, *CHO, *COH, *OCCHO, *OH, and *OOH) on Cu, Au, and Pt surfaces. Surprisingly, implicit models did not consistently outperform vacuum calculations, and solvation energies were found to be non-transferable across metals. These results highlight the limitations of implicit models in capturing specific solute–solvent interactions, suggesting that explicit solvation remains the method of choice when accuracy is critical.

2.2.3 Kinetic modeling in electrocatalysis. Accurate determination of activation barriers is essential for understanding reaction kinetics in electrocatalysis. Computational methods range from static approaches, such as the NEB method,^107,108 to more advanced dynamic techniques, such as AIMD, offering great advantages in capturing the structural dynamics of the reaction environment.

The NEB method is widely used in computational catalysis for determining minimum energy pathways and reaction barriers by interpolating a series of images between reactant and product states. It efficiently locates the transition state without requiring prior knowledge of the reaction mechanism. However, NEB assumes static initial and final structures and neglects thermal and entropic effects, making it less suitable for systems where solvent dynamics or finite-temperature contributions are significant AIMD offers a dynamic description of reaction pathways by explicitly simulating atomic motion at finite temperatures, capturing thermal fluctuations, solvent effects, and dynamic restructuring of the catalyst surface. It offers a more realistic picture of electrocatalytic environments. Several enhanced sampling techniques have been integrated into AIMD to improve reaction barrier estimations. (1) Blue-moon sampling constrains the reaction coordinate (ξ) at different fixed values and reconstructs the free energy profile through thermodynamic integration, offering a more statistically converged barrier estimation. (2) Umbrella sampling introduces harmonic biases along ξ to enhance sampling near transition states and prevent trapping in local minima. (3) Metadynamics dynamically introduces Gaussian energy penalties around previously visited states, allowing the system to escape local energy wells and explore alternative reaction pathways. Once the biased potential converges, the unbiased free energy profile is reconstructed. These techniques significantly improve the accuracy of activation energy calculations compared to traditional NEB methods, particularly in electrochemical systems where solvent and electrode interactions play a crucial role in reaction mechanisms. Recent developments have focused on integrating AIMD with constant-potential methods and solvation models to better capture realistic electrochemical conditions. By including solvent effects, surface charge variations, and temperature-dependent dynamics, these approaches provide deeper insight into reaction mechanisms under operando conditions, ultimately aiding the rational design of efficient electrocatalysts.

2.2.4 Grand canonical DFT and constant potential methods. Accurately modeling electrochemical reactions requires computational methods that account for variations in electrode potential, charge distribution, and electrolyte effects. Traditional DFT-based approaches operate under a constant charge ensemble, where the total charge of the system is fixed, making it challenging to capture potential-dependent electrochemical processes.^109–112 However, real electrochemical systems operate under constant potential (CP) conditions, where the electrode charge dynamically responds to the applied potential. To address this discrepancy, grand canonical DFT (GC-DFT) and CP-DFT have been developed, providing a more realistic representation of electrochemical environments.^54,113

The electrode potential relative to the SHE can be determined from DFT using U = (−E_f − Φ_SHE)/e, where E_f and Φ_SHE are Fermi energy and the absolute potential of SHE (4.44 V).^29,32,114 The CP method adjusts E_f by modifying the number of electrons within the cell. GC-DFT is a widely used approach that allows charge exchange between the electrode and an electron reservoir to maintain a fixed electrochemical potential (μ). The total free energy of an electrochemical system is determined by optimizing the electron number to match the system's Fermi level to the applied potential.^115,116 The relationship between the system's energy and the applied potential is described by the grand potential formulation, Ω = A + μ_eN_e, where A is the Helmholtz free energy, μ_e is the electrochemical potential, N_e is the number of electrons in the system.^115,116 The implementation of implicit solvation models, such as VASPsol, further enables a continuous variation in electron number by balancing charge with ionic screening in the electrolyte.

Benchmarking studies using GC-DFT have successfully described potential-dependent catalytic pathways. For instance, GC-DFT-based constant-potential MD simulations described CO electrochemical hydrogenation on FeNC at U = −1.5 V, showing trends consistent with experiments.¹¹⁷ However, GC-DFT has intrinsic limitations: the use of fractional charges for tuning work functions can cause unphysical charge delocalization into the electrolyte, undermining double-layer modeling accuracy. Moreover, implicit solvation fails to capture explicit solvation shell interactions essential for accurate reaction energetics.^118,119

An alternative approach to achieving constant potential conditions is constant potential DFT, which directly tunes the Fermi level by adjusting the electron number iteratively until the target potential is reached. Unlike GC-DFT, which relies on a reservoir, CP-DFT self-consistently tunes the system's charge to match the desired potential.¹¹⁹ Liu et al. developed an implementation of CP-DFT in VASP (CP-VASP), integrating it with explicit solvation models and a potential reference scheme to compute electrode potentials relative to SHE.^29,119 Similar implementations have also been reported in recent studies.^53,120,121

Using CP-VASP, they investigated the ORR on Co–N–C catalysts through constant-potential AIMD simulations.²⁹ The electron number was iteratively adjusted during slow-growth simulations to maintain charge balance, with counter charges modeled via VASPsol and an explicit thin water layer incorporated for solvation effects. Their study provided insight into why Co–N–C catalysts exhibit selective H₂O₂ formation despite its thermodynamic instability relative to H₂O.²⁹ By comparing the free energy profiles of competing reaction pathways, they found that while H₂O is the thermodynamically preferred product, the activation energy for H₂O₂ formation is lower, explaining the experimentally observed selectivity trend. Additionally, the evolution of electron number during product formation differed significantly: the system gained approximately one electron in the H₂O pathway, whereas it remained nearly constant in the H₂O₂ pathway, a feature that conventional constant-charge methods fail to capture. Furthermore, their results demonstrated that as the applied potential decreases, H₂O₂ selectivity increases, which they attributed to surface charge effects and enhanced hydrogen bonding interactions.²⁹

In addition to GC-DFT and CP-DFT, several correction schemes, such as cell extrapolation and charge extrapolation,^122,123 have been proposed to approximate constant-potential behavior from constant-charge calculations. Furthermore, recent advancements, such as the eNEB method proposed by Duan et al.,^109,124 have provided novel strategies to compute potential-dependent activation energies more efficiently.

2.2.5 Microkinetic modeling. While thermodynamic models provide insights into reaction energetics, they do not capture reaction rates. Microkinetic modeling addresses this by solving reaction rate equations based on DFT-derived energy barriers, by incorporating elementary step kinetics, surface coverages, and potential-dependent energetics.¹²⁵ This approach bridges DFT calculations with experimentally observable reaction rates, enabling a deeper understanding of rate-determining steps, turnover frequencies (TOF), and product selectivity. Two widely used computational methods for microkinetic modeling are mean-field microkinetic modeling and kinetic Monte Carlo (kMC) simulations.¹³ Microkinetic models integrate elementary reaction steps to determine the overall reaction rate and TOF by solving a set of coupled differential equations that describe surface coverages and reaction fluxes based on transition state theory.

In the case of CO₂RR, microkinetic modeling has revealed that the rate-limiting step varies depending on the metal catalyst. For weak CO-binding metals like Cu, the protonation of *COOH to *CO is the key bottleneck, whereas for strong CO-binding metals like Au, *CO desorption dominates the reaction kinetics.⁸⁶ This differentiation highlights the crucial role of catalyst binding strength in determining CO₂ reduction activity and selectivity, providing valuable insights for rational catalyst design.

Nørskov and co-workers employed DFT calculations combined with mean-field microkinetic modeling to predict the TOF for ammonia synthesis on TM catalysts.¹²⁵ Their study revealed that the catalytic activity is fundamentally constrained by the BEP scaling relationship, which links reaction barriers to adsorption energies, limiting NH₃ production under mild conditions. By examining on-top nitrogen binding sites, they identified improved scaling behavior, leading to enhanced predicted catalytic activity. These findings suggest that stabilizing such active sites could enable more efficient ammonia synthesis under milder conditions, providing design insights beyond traditional scaling constraints.

Recent advances have integrated ML and artificial neural networks into kMC simulations to enhance efficiency. For example, GNNs have been trained on DFT-calculated barrier data, enabling accurate predictions of adsorbate–adsorbate interactions and lateral effects.¹²⁶ Additionally, deep neural networks combined with kMC and stochastic sampling algorithms allow for autonomous reaction network exploration, improving predictions of complex catalytic pathways.¹²⁷ One notable application of ML-enhanced kMC simulations is in Cu-based CO₂RR, where they were used to model surface diffusion and thermodynamic stability of key intermediates on different low-index Cu facets.¹²⁸ These data-driven approaches significantly advance microkinetic modeling by capturing the full complexity of surface reaction dynamics and facilitating the autonomous discovery of elementary reaction pathways.

2.3 High-throughput computation and machine learning

The discovery of efficient electrocatalysts for small molecule activation, such as NRR and CO₂RR, remains a challenging and resource-intensive process. Traditional computational approaches, primarily based on DFT, provide atomic-level insights into reaction mechanisms but are computationally expensive and time-consuming. High-throughput computation (HTC) and ML have emerged as transformative tools to accelerate the catalyst design cycle by enabling large-scale screening and predictive modeling (Fig. 4).

Fig. 4 A simple workflow from high throughput computation to machine learning.

2.3.1 High-throughput computation. HTC involves automating computational workflows to rapidly evaluate a large number of candidate materials. In electrocatalysis, HTC is typically used to compute adsorption energies, reaction barriers, and electronic properties of catalysts across a vast compositional space. A well-designed HTC workflow consists of: (1) generating a diverse library of catalyst structures, including bulk materials, SACs, and doped surfaces. (2) Performing systematic energy calculations to evaluate key descriptors, such as adsorption energies of reactants and intermediates. (3) Collecting and processing computational results to identify trends, correlations, and scaling relationships, such as the BEP principle, to predict promising candidates. A notable application of HTC in NRR screening demonstrated the efficiency of boron-doped SACs by systematically evaluating adsorption energies and free energies using DFT, revealing that CrB₃C₁ exhibits minimal overpotential (0.13 V) and high selectivity over the HER.¹²⁹ Qi et al. employed HTC and artificial intelligence to screen the stability and activity of 3d, 4d, and 5d TM SACs on eight defective metal oxide surfaces for CO₂RR.¹³⁰ Among 232 SAC systems, 100 were stable in vacuum, but only 28 remained stable with adsorbed intermediates. They identified key factors influencing stability, including the electronegativity and outer electrons of SACs, the d-band center of metal oxides, and coordination environments. The study predicted Os/VO-ZrO₂ (111) as the most promising CO₂RR electrocatalyst and Ru/VO-ZrO₂ (111) as highly active in the reverse water–gas shift reaction.

2.3.2 Machine learning. Leveraging large datasets generated from HTC and experimental results,¹³¹ ML has emerged as a powerful tool for accelerating catalyst discovery by predicting material properties, optimizing reaction conditions, identifying high-performance electrocatalysts, and guiding experimental synthesis.^39,132–134 Supervised learning typically employs models such as linear regression, random forests, support vector machines, and neural networks to predict adsorption energies, reaction barriers, and catalytic activity from chemical descriptors. These simpleML models are trained on DFT-calculated datasets and enable high-throughput screening of potential catalysts by learning structure–property relationships.^39,134,135 A comparison of representative machine learning approaches, their application targets, and model characteristics in electrocatalysis is summarized in Table 2, providing a quick reference for commonly used methods and their typical use cases. By incorporating interpretable ML methods, such as feature importance analysis, SHAP value distribution, and dependency plots, researchers have also successfully examined how and why the “black-box” models perform accurately, and how specific features contribute to the overall model prediction. For example, Zhang et al. studied a dataset of 90 graphene-based SACs and predicted Gibbs free energy to assess SACs’ nitrogen reduction reaction activity.¹³⁴ Through feature importance analysis and SHAP evaluation, gradient boosting regression (GBR) was identified as the best-performing model, key descriptors influencing catalytic performance, including TM radius (r_TM), average TM radius (r_TM-ave), d-electron count (N_d), and heat of formation (H_of), were identified, providing valuable insights into the role of the active center and coordination environment in NRR activity.¹³⁴

Table 2 Comparison of representative machine learning approaches for electrocatalysis applications

Model type	Representative methods	Typical outputs	Input format	Strengths/limitations
Traditional ML	Linear regression, random forest, SVM, XGBoost	Adsorption energy, activation energy	Hand-crafted descriptors (e.g., SOAP, magpie)	Fast and interpretable; requires feature engineering; may underperform on complex data
Neural networks	Multilayer perceptron, CNN	Activity, band gap, charge distribution	Grid data, numerical vectors	Handle nonlinear patterns; need large datasets; limited structural awareness
Graph neural networks	GCN, GAT, SchNet, DimeNet, CGCNN, MEGNet	ΔG, adsorption energies, density of states	Atomic graphs (structure as input)	Structure-aware; good generalization; may lack interpretability
Transformer models	MatFormer, graphormer, ChemBERTa, MAT, ViT	Reaction energies, catalyst discovery	Graph or sequence (e.g., SMILES, graphs)	Powerful representation; computationally heavy; large data preferred
Active learning frameworks	Bayesian optimization, uncertainty sampling, CURATE-AI	Data-efficient ML, uncertainty quantification	Works with ML models as wrapper	Reduces data cost; needs uncertainty estimation
Diffusion models	EDM, GeoDiff, graph-diffusion, GDM	Molecule/catalyst structure generation	Graphs or 3D point clouds	Strong in inverse design; training complexity; new and under active development

---

To overcome the limitations posed by the chemo-structural complexity of heterogeneous catalysts and the challenge of generating high-quality training data, deep learning neural networks have emerged as a more advanced approach in ML for electrocatalysis.⁴³ Unlike traditional supervised learning models, which rely on predefined descriptors and feature engineering, deep neural networks (DNNs),¹³⁶ convolutional neural networks (CNNs),⁴² and GNNs can automatically extract complex patterns and nonlinear relationships from raw data,^136–138 making them well-suited for handling large-scale datasets and diverse catalyst structures. Among these, GNNs have proven particularly effective in modeling heterogeneous catalytic systems, as they represent atomic structures as graphs, allowing for spatially aware learning of chemical interactions without requiring manual descriptor selection.⁴² Additionally, CNNs have been applied to analyze surface structures from microscopy and spectroscopic data, facilitating the direct integration of experimental and computational insights.¹³⁹ In this stage, principal component analysis (PCA),^43,44 t-distributed stochastic neighbor embedding (t-SNE),^140,141 and k-means clustering for dimensionality reduction and pattern recognition. This approach helps identify key descriptors governing catalytic performance by analyzing large datasets without predefined labels, revealing hidden trends in reaction energetics and materials properties.

Beyond catalyst screening, ML potentials (MLPs) provide a powerful means to explore reaction dynamics at electrochemical interfaces.^142,143 Unlike classical force fields, MLPs are trained on quantum mechanical data, enabling simulations at DFT accuracy while dramatically extending time and spatial scales. This approach allows for the detailed study of reaction trajectories, charge transfer, and solvation effects around active sites¹⁴⁴ in complex electrocatalytic processes. The continued advancement of GNNs, active learning, and automated reaction network exploration will further enhance the predictive power of ML-driven electrocatalysis, bridging the gap between theoretical modeling and experimental validation.

3. Advances in electrocatalysts screening and design

3.1 Engineering electrocatalysts via scaling relationship and reactive descriptors

Over the past two decades, scaling relationships have been extensively established for key heterogeneous catalytic reactions, providing a fundamental framework for understanding catalytic activity and selectivity (Fig. 5a).⁵⁶ These relationships arise from reactive descriptors, which quantify specific physical or chemical properties of a reaction system and often exhibit linear correlations with catalytic performance. In this section, we examine the role of scaling relationships and reactive descriptors in heterogeneous catalysis, including electronic descriptors derived from d-band theory, structural descriptors directly applicable to catalyst design, and generalized descriptors capturing broader catalytic trends.¹⁴⁵ By leveraging these descriptors, researchers can rationalize activity trends and facilitate high-throughput catalyst screening.

Fig. 5 (a) Typical reactivity descriptors in metallic catalysts.⁵⁶ (b) Scaling relationship between adsorption energies of CH_x and NH_x intermediates against adsorption energies of C and N atoms (crosses: x = 1; circles: x = 2; triangles: x = 3).¹⁴⁶ (c) Active map between adsorption free energy of OH and H versus the universal descriptor φ for all SAC supported on macrocyclic molecules.¹⁴⁷ (d) A universal descriptor Φ for predicting the activity of N₂ dimerization ΔG_L.¹⁴⁸

The development of reactivity descriptors based on scaling relationships has been extensively studied. One of the earliest and most influential electronic descriptors originates from d-band theory,^76,149–151 which establishes a direct correlation between the electronic structure of TMs and their adsorption strength for reaction intermediates. This framework has provided a fundamental basis for understanding catalytic activity and guiding the rational design of transition-metal-based catalysts. Ma et al. employs d-band center theory as a key descriptor to understand and optimize strain-engineered Pt-doped Ti₂CF₂ (Pt-VF-Ti₂CF₂) catalysts for the ORR and OER.⁸⁹ Through first-principles calculations, it reveals that applying compressive (−14%) and tensile (4%) strain shifts the d-band center, modifying adsorption strength and catalytic activity. The optimized strain conditions lower ORR and OER overpotentials to 0.45 V and 0.43 V, respectively, while also suppressing the HER.⁸⁹ Our previous research also demonstrated that the sub-orbitals of d-electrons play different roles in the adsorption of catalytic intermediates.⁹⁰ For example, when surface TM bind with adsorbed molecules, orbital primarily exhibits an attractive effect, while the d_xz/d_yz → 2π* coupling mainly displays a repulsive effect. Consequently, Ti₂CO₂ shows anomalous d-band adsorption characteristics for *N, *NH, *NH₂, and *NH₃ under applied tensile strain.⁹⁰ While the d-band center provides insights into electronic structure modifications, it does not fully capture the influence of d-electron distribution on catalytic mechanisms. Dai et al. employs the d-electron number (N_d) as a key descriptor to rationalize and optimize the NRR performance of Cu-based single-atom alloy (SAA) catalysts. Using DFT calculations, the authors constructed 108 Cu-based SAAs and identified a quintuple degenerate d-electron state that redistributes according to the “acceptance-donation” mechanism. They established a Sabatier principle-like relationship, revealing that a moderate N_d of 5 balances N₂ activation and hydrogenation steps, optimizing catalytic performance. Adopting N_d as a key descriptor to regulate electron transfer enable efficient SAC screening and catalyst design in NRR has also been verified in other studies.^152,153

For most applications, performing exhaustive calculations for all adsorption energies is a highly challenging task. To address this issue, extensive investigations have been conducted on the correlations between different adsorption energies, enabling the accelerated design and screening of electrocatalysts. Numerous studies have demonstrated that reaction barrier and reaction free energy of rate-determining step thermodynamic calculations is closely related to the adsorption strength of key reaction intermediates.^88,154,155 The first scaling relationships were identified between adsorbed species and their hydrogenated counterparts (Fig. 5b),¹⁴⁶ revealing a linear correlation between adsorption energies across different transition-metal surfaces. This study systematically explores adsorption energy trends for CH_x, NH_x, OH_x, and SH_x species using DFT calculations. The results demonstrate that adsorption energy scales with the adsorption strength of the central atom (C, N, O, or S), with scaling constants depending only on the hydrogenation state.¹⁴⁶ They further propose a model based on d-band interactions, showing that valency and surface electronic properties dictate adsorption strength.¹⁵⁶ Adsorption energy-based descriptors, such as ΔE(*OH),⁸⁸ ΔE(*CO),¹⁵⁷ ΔE(*N)¹⁵⁴ and ΔE(*NNH)^158,159 have been widely employed to predict catalytic performance in reactions like the oxygen evolution reaction, CO₂ reduction, and N₂ reduction. Typically, the slope of these relationships is positive and can be determined using electron-counting principles,^146,159 while the intercept is largely dependent on surface structure where undercoordinated sites tend to exhibit more negative offsets than over coordinated ones.¹⁶⁰ Despite these general trends, exceptions have been observed: some scaling relations feature negative slopes,¹⁶¹ structure sensitivity disappears when the slope equals unity,^162,163 covalent interactions can lead to notable deviations from predicted slopes, and non-scalable adsorbates can still exhibit scaling relationships through ligand and coordination effects.¹⁶⁴

To incorporate the geometric structure of optimal active sites into catalyst design, specific active sites can be engineered to enhance catalytic performance.^8,48,165 By counting the coordination number (CN) of atoms at these active sites, one can estimate their binding strength toward reaction intermediates, which can then be linked to adsorption-energy scaling relationships to predict catalytic activity.¹² In face-centered cubic (fcc) metals, CN values typically range from 0 (isolated atoms) to 12 (bulk atoms in a crystalline lattice).¹² Currently, CN is primarily defined for TMs and certain alloys. Notably, SACs have gained widespread attention in electrocatalysis due to their high coordination unsaturation and ability to form well-defined adsorption sites, enhancing catalytic performance.¹⁶⁶ Wang et al. synthesized atomically dispersed Co catalysts with tunable nitrogen coordination numbers to investigate their effect on CO₂ electroreduction performance.¹⁶⁷ Their study demonstrated that decreasing the Co–N coordination number from 4 to 2 enhanced catalytic activity and selectivity, achieving a record CO formation turnover frequency of 18 200 h⁻¹. Both experimental and theoretical analyses revealed that lower coordination numbers increase the number of unoccupied Co 3d orbitals, facilitating CO₂ activation and adsorption. This work confirms that modulating the coordination environment of active sites is an effective strategy for improving electrocatalytic performance, providing insights into rational catalyst design. A more advanced approach involves the generalized CN, accounts for the weighted contributions of neighboring atoms, offering improved predictive accuracy¹⁶⁸ refines this metric by weighting contributions from neighboring atoms. Additionally, advanced descriptors such as orbital-wise coordination number and bond-energy-integrated orbital-wise coordination number have been developed to further enhance adsorption energy and catalytic behavior predictions.^169,170

To extend predictive models beyond specific catalyst classes, researchers have developed universal descriptors that integrate electronic and structural factors. Binary descriptors, such as combined electronic and geometric features, have been applied to diverse catalyst systems. Efforts to generalize reactivity trends across different material classes aim to overcome the limitations of conventional scaling relationships and enable more comprehensive catalyst screening. Cheng et al. developed a universal descriptor for SACs in ORR, OER, and HER by correlating catalytic activity with the local coordination environment and electronegativity of the active site, . The descriptor effectively predicts catalytic performance and was validated experimentally (Fig. 5c).¹⁴⁷ Furthermore, they proposed structural descriptors, including d-band center gap, Fe–O bond length, and valence states, to predict ORR activity in Fe–N–C single-atom catalysts.¹⁷¹ They demonstrated that coordination and environmental heteroatoms modulate electronic properties, optimizing catalytic performance. Other universal descriptors based on electronic properties were proposed. Liu et al. introduced an effective d-electron number as a universal descriptor for electrocatalytic urea synthesis (Fig. 5d).¹⁴⁸ By analyzing TM clusters anchored on carbonitride, they established a structure–activity relationship that enables high-throughput screening of urea synthesis catalysts. Chen et al. developed an integrated descriptor based on spin polarization, crystal orbital Hamilton population,¹⁴⁵ and d-band center gap to screen three-metal cluster catalysts on W₂N₃ for NRR. The descriptor effectively predicts the limiting potential and enables the discovery of highly active catalysts. These studies demonstrate the power of universal descriptors in electrocatalysis, enabling rational catalyst design and high-throughput screening.

3.2 Machine learning accelerated catalyst screening and discovery

The efficient identification of structural motifs with various favorable descriptors is highly desirable but remains challenging due to the significant computational cost of accurately solving the many-electron Schrödinger equation. ML offers a powerful alternative by leveraging large datasets from database, high-throughput DFT calculations, or ab initio calculations to capture complex atomic and molecular interactions with surfaces, narrow down the candidate pool, enabling rapid and accurate predictions of chemical reactivity.⁴³ In recent years, supervised learning methods, such as regression models, have been widely applied to electrocatalyst screening. By leveraging key descriptors such as adsorption energies and reaction barriers, these models establish structure–performance relationships.

Ren et al. utilized GBR models trained on DFT-calculated adsorption energies to screen 90 graphdiyne-based SACs for CO₂ reduction.¹⁷² The study identified key electronic and geometric descriptors, such as d-band center and coordination number, influencing catalytic activity. The GBR model successfully predicted the Gibbs free energy for nitrogen reduction and provided an interpretable framework for electrocatalyst design. The results demonstrated that Mn and Fe-based SACs exhibited optimal CO₂RR performance, providing a guideline for future experimental validation. Wu et al. integrated extreme gradient boosting (XGBoost) with DFT calculations to screen 289 adsorbate–pair combinations on Cu surfaces,¹⁷³ evaluating their impact on methane and C₂₊ product formation. Feature selection reduced the initial 52 descriptors to fewer than 10, significantly enhancing model accuracy (RMSE ∼ 0.082 eV). The study identified 152 adsorbates that improved methane production and 81 that enhanced C₂₊ formation, demonstrating how ML-assisted screening can systematically optimize reaction environments. Niu et al. employed DFT calculations to study the catalytic activity of single-atom Rh embedded in defective g-C₃N₄ (VN-CN).¹⁷⁴ By coupling DFT with ML-based feature importance analysis, the study identified d-band center and electronegativity-weighted d-electron count as key descriptors for OER and ORR. The findings confirmed Rh/VN-CN as an optimal bifunctional catalyst, with overpotentials of 0.32 V (OER) and 0.43 V (ORR), showcasing ML's potential in descriptor-driven catalyst screening.

Wan et al. integrated DFT with various supervised learning models, including GBR, random forest regression (RFR), support vector regression (SVR), k-nearest neighbor regression (KNR), and Gaussian process regression (GPR) (Fig. 6a).¹⁷⁵ The best-performing model achieved a RMSE of 0.24 V for ORR and 0.23 V for OER. Through feature importance analysis, the study identified the d-electron count of the metal center as a key descriptor governing activity. The validated ML model successfully predicted three promising catalysts (RhPc, Co–N–C, and Rh-C₄N₃), showing higher activity than noble metals. The work highlights the potential of ML-DFT hybrid schemes in accelerating electrocatalyst discovery while providing fundamental insights into catalytic activity trends. Zhang et al. developed an interpretable ML model to predict the Gibbs free energy of NRR on SACs without relying on DFT-calculated features.¹³⁴ Using a dataset of 90 graphene-supported SACs, they trained GBR model predicts ΔG(N₂ → *NNH) and ΔG(NH₂ → NH₃) with high accuracy (R² = 0.972 and 0.984, RMSE = 0.051 and 0.085 eV, respectively). Their approach enables efficient catalyst screening without extensive DFT computations, providing a cost-effective strategy for rational catalyst design in electrocatalysis.

Fig. 6 (a) Machine learning workflow for the study on ORR/OER catalytic activity and reaction mechanism of carbon–nitride-related SACs.¹⁷⁵ (b) Machine learning-assisted dual-atom sites design with interpretable descriptors for multiple electrocatalytic reactions (i.e., O₂/CO₂/N₂ reduction and O₂ evolution reactions).¹⁷⁶ It includes four major parts: (i) primitive descriptor (ϕ_xx) for atomic property effects through d-band shape analysis, (ii) screening principle (ϕ_opt) of potential desirable heteronuclear DACs based on reactant effects, (iii) ML-based descriptors (ϕ_xy) for synergistic effects through physically meaningful feature engineering based on ϕ_xx and feature selection/sparsification algorithms, (iv) the final universal descriptor model (Φ) with quantification of coordination effects and corresponding experimental verifications (c) schematics of the high-throughput virtual screening strategy to discover selective CO₂RR catalysts. (d) Parity plots of ML-predicted (ΔE_ML) and DFT-calculated (ΔE_DFT) binding energy of CO* (red), H* (green) and OH* (blue).¹⁷⁷ Two-dimensional (e) activity volcano plot and (f) selectivity plot for CO₂ reduction. (g) t-SNE representation of approximately 4000 adsorption sites (g) and (h) coordination sites on which we performed DFT calculations with Cu-containing alloys.¹⁷⁸

Traditionally, supervised ML algorithms rely on large datasets to identify patterns and establish correlations between input features and catalytic performance. However, achieving generalizable and physically meaningful predictions requires integrating scientific knowledge into ML frameworks. By combining data-driven precision with physics-informed modeling, researchers can develop ML models that not only learn from empirical data but also adhere to fundamental catalytic principles. Recent advancements in deep learning techniques, such as GNNs, CNNs, and theory-infused neural networks (TINNs), have significantly improved predictive capabilities by directly mapping electronic structures, reaction environments, and catalytic activity. At the atomic scale, the emergence of MLPs has transformed MD simulations, enabling the study of catalyst stability, surface restructuring, and reaction pathways over extended time and spatial domains.

Mok et al. proposed a novel high-throughput screening approach that integrates pre-trained ML models with a CO₂RR selectivity map to predict catalyst activity and selectivity for four reaction products (Fig. 6c and d).¹⁷⁷ By evaluating 465 metallic catalysts, they uncovered promising Cu–Ga and Cu–Pd alloy catalysts with experimentally validated CO₂RR performance. Their approach extends beyond conventional databases, allowing broader chemical space exploration. The findings emphasize the importance of motif-based ML in accelerating electrocatalyst discovery by predicting both activity and selectivity. Lin et al. developed an interpretable ML framework to design dual-atom catalysts (DACs) by constructing a universal descriptor, ARSC, which decouples atomic, reactant, synergistic, and coordination effects on d-band shape (Fig. 6b).¹⁷⁶ Using a feature engineering and sparsification method (PFESS), they screened 840 DACs across multiple electrocatalytic reactions, significantly reducing computational costs compared to conventional DFT calculations. The model identified Co–Co/Ir-Qv3 as a highly efficient bifunctional ORR/OER catalyst, validated experimentally. This work provides a universal machine-learning descriptor for catalyst discovery and highlights the potential of interpretable ML in high-dimensional catalytic systems. Kim et al. applied a slab graph convolutional neural network to predict the adsorption energies of key intermediates in the NRR on transition-metal surfaces.⁴² The model was trained on 3040 DFT-calculated adsorption energies for N₂, N₂H, NH, NH₂, and H, achieving a mean absolute error (MAE) of 0.23 eV. By analyzing d-orbital occupation trends, the study revealed that catalysts with 4–6 d-electrons exhibit the lowest limiting potentials for NRR. The ML-guided screening identified four promising catalysts (V₃Ir (111), Tc₃Hf (111), V₃Ni (111), and Tc₃Ta (111)) with superior NRR activity, demonstrating the potential of graph-based deep learning in high-throughput catalyst discovery.

Zhong et al. employed an active ML-accelerated high-throughput screening framework to identify efficient electrocatalysts for CO₂ reduction.¹⁷⁸ They screened 244 Cu-based intermetallic compounds, and 12 229 surfaces and 228 969 adsorption sites were used to predict CO adsorption energies. The active ML approach iteratively refined the model by selecting the most informative data points for additional DFT calculations, significantly improving prediction accuracy while reducing computational cost. Fig. 6e–h present key findings from their screening. The volcano plot (Fig. 6e and f) indicates that an optimal CO adsorption energy (ΔE_CO) of −0.67 eV is required for high catalytic activity. A hydrogen adsorption energy above −0.5 eV is necessary for activity, while a value above −0.2 eV ensures selectivity toward CO₂ reduction rather than hydrogen evolution. A t-SNE analysis (Fig. 6g) mapped approximately 4000 adsorption sites, showing that Cu–Al alloys exhibit a high density of near-optimal ΔE_CO sites, suggesting superior activity across different surface compositions. Further experimental validation confirmed that Cu–Al catalysts achieved a faradaic efficiency of over 80% for ethylene production at 400 mA cm⁻², surpassing pure Cu (66%).¹⁷⁸

Nonetheless, the need for interpretability in ML models often limits the complexity of the algorithms, potentially compromising predictive accuracy. This creates an inherent trade-off between model transparency and performance. A promising strategy is to develop a hybrid ML framework that integrates interpretable models with high-accuracy black-box algorithms. In such case, the new model can provide precise predictions while maintaining interpretable insights. Wang et al. developed a theory-infused neural network (TinNet) that integrates deep learning with d-band theory to predict adsorption properties on transition-metal surfaces for O₂ reduction, CO₂ reduction, and H₂ oxidation.¹⁷⁹ The model was trained on 748 DFT-calculated adsorption energies of OH, achieving high accuracy (error ∼0.1–0.2 eV) while maintaining physical interpretability. Compared to conventional data-driven ML models, TinNet preserved fundamental electronic structure–activity relationships, enabling more reliable catalyst screening. The study demonstrated that hybridizing physics-based descriptors with deep learning can improve both model performance and explainability, facilitating the rational design of electrocatalysts. These two studies collectively demonstrate how advanced ML models, including physics-infused neural networks and graph-based architectures, can enhance the accuracy, interpretability, and efficiency of catalyst screening. The integration of scientific principles with ML models ensures both robust performance and physical consistency, paving the way for more reliable and efficient electrocatalyst design.

4. Dynamic evolution of active sites under operating conditions

4.1 The leaching of the active sites

The long-term stability of single-atom catalysts is a critical bottleneck limiting their wide-spread practical application in electrocatalysis. Unlike nanoparticles, SACs are are intrinsically dynamic under operating conditions, where external potentials and adsorbates can drive structural transformations.¹⁸⁰ Recent experimental and theoretical studies have consistently demonstrated that single metal atoms can undergo migration, leaching, or aggregation into clusters during catalytic processes such as selective hydrogenation, CO oxidation, and propane dehydrogenation, depending heavily on the interplay between metal–support and metal–reactant interactions.^55,180,181 The findings highlight the necessity of real-time structural characterization to accurately determine the active species in catalytic processes.

A growing body of computational work has provided atomic-level insight into these instability mechanisms. For example, Bai et al. investigated the dynamic stability of Cu SACs under working conditions using a constant-potential hybrid-solvation dynamic model (CP-HS-DM) (Fig. 7a–c).²⁹ Their study revealed that hydrogen adsorption at negative potentials weakens Cu–N bonds, facilitating the leaching of Cu atoms from the N-doped graphene support. The energy barrier for Cu leaching was significantly reduced in the presence of adsorbed hydrogen, dropping to 0.70 eV when a single hydrogen atom was adsorbed. Importantly, these findings suggest that electrochemical hydrogen adsorption is a key factor driving the destabilization of Cu SACs and their transformation into catalytically active clusters, challenging the conventional assumption of static SAC stability.

Fig. 7 (a) Schematic of Cu active sites under working potentials. (b) Free energy (ΔG) of the Cu SA leaching process for the formation of Cu²⁺(aq) with xH (x = 1, 2) adsorption under different potentials. (c) Free energy profile and average energy during the Cu SA leaching process under one H atom adsorption at an N atom at U_RHE = −1.2 V.²⁹ (d) Dynamic evolution of Co–C_x (x = 1, 2, 3, 4, 5, and 6) bond length. (e) Free energy diagram of the central Co leaching process. (f) Free energy of H transfer to the coordinated C atom.⁵³ (g) Schematic of Cu migration and (h) its corresponding free energy profile. (i) Bond variation during the leaching process.⁵²

Complementary to this, Liu et al. investigated the leaching behavior and stability of Co ACs supported on γ-graphyne under electrochemical conditions using DFT and AIMD simulations (Fig. 7d–f).⁵³ Their study focused on the evolution of Co–C coordination bonds and the energetics of Co atom dissolution under applied strain. The results showed that the Co–C bond length increased progressively during the leaching process, particularly under 3% tensile strain, indicating weakening interactions between the Co atom and the support. Free energy calculations revealed that the dissolution of the central Co atom is thermodynamically feasible under these conditions, with a notable increase in energy of approximately 1.5 eV as the Co atom moves away from its original position. Additionally, AIMD simulations demonstrated that the transfer of *H species to the coordinated carbon atoms around the Co site significantly affects stability, with free energy variations supporting a strain-dependent leaching mechanism. Together, these findings highlight how both mechanical strain and interfacial proton dynamics can synergistically accelerate single-atom instability—factors often overlooked in conventional catalyst design strategies.

Similarly, Li's group investigated the leaching dynamics and stability of single-atom Cu catalysts (Cu₁) under electrochemical conditions using density functional theory DFT and AIMD simulations (Fig. 7g–i).⁵² Their results support a recurring conclusion: isolated SACs may not be the real active centers during prolonged operation. Instead, small metal clusters formed via leaching and aggregation may dominate catalytic activity, especially for C₂₊ product formation in CO₂RR. Their study revealed that Cu₁ atoms anchored on C₃N₄ are structurally unstable and prone to leaching. AIMD simulations demonstrated that Cu₁ can migrate within the C₃N₄ framework and eventually detach from the substrate, leading to aggregation. Specifically, when the Cu₁ atom moves 0.90 Å from its initial position, two Cu–N bonds break and elongate to 2.39 Å and 2.74 Å, requiring an activation energy (E_a) of 0.89 eV. This indicates a significant tendency for Cu₁ dissolution, explaining its instability under reaction conditions.

A unifying mechanism across these studies points to the role of hydrogen adsorption at negative potentials, which leads to electron accumulation, facilitates H⁺ adsorption, and ultimately weakens metal–support bonds.¹⁸² From an electronic structure perspective, Cu atoms with fully filled 3d orbitals form relatively weak Cu–N bonds, making the Cu and N sites more reactive towards protons. This electronic predisposition, coupled with electrochemical driving forces, provides a compelling explanation for Cu SAC instability and cluster evolution under working conditions.

Taken together, these studies suggest a shift in design paradigm: rather than treating SACs as inherently stable and monodispersed, catalyst design should account for dynamic evolution and deliberately consider cluster formation pathways, potentially embracing them as functional intermediates rather than degradation products.

4.2 Surface reconstruction and adsorbate-induced stability changes

Electrocatalytic reactions occur under dynamic conditions where the catalyst surface is continuously exposed to reactive intermediates, applied potentials, and electrolyte environments. These factors can induce surface reconstruction, leading to changes in atomic arrangements, electronic properties, and catalytic activity.⁴⁶ Unlike the conventional view of catalysts as static structures, recent experimental and theoretical studies have revealed that surface atoms can reorganize during reactions, forming new active sites or stabilizing metastable configurations (Fig. 8a).⁵⁵

Fig. 8 (a) HAADF-STEM images and XPS spectra of Pt-SS (Pt single site) and Pt-NP (Pt nano particle), which indicates the formation of a highly oxidized state of Pt-SS.⁵⁵ (b) In situ STEM images and atomic models reveal reconstruction process of the SnO₂ (110) surface. (c) Schematic energy changes and (d) DFT calculated surface energies of different surface states under different temperatures.¹⁸³ (e) The dynamic reconstruction of SnO₂ and SnS₂ surfaces under electrochemical conditions.¹⁸⁴ (f) The spatial distribution of surface atoms on 1H-covered, unrestructured 6H-covered, and shifted-row 6H-covered Cu (100) surfaces. (g) Snapshots of the of the 12H state within 10 ps. (h) RMSD of top-layer Cu coordinates of different surfaces. (i) Geometries and simulated STM images of the key surface states.⁵⁴

A representative example is the electrochemical reconstruction of the SnO₂ (110) surface studied via in situ aberration-corrected STEM, which demonstrated a temperature-driven transformation from a bulk-truncated (1 × 1) surface to a Sn₂O-added reconstruction at temperatures above 800 °C (Fig. 8b–d).¹⁸³ This rearrangement is energetically favorable, as Sn atoms migrate to interstitial positions, enhancing stability. DFT calculations confirm that such reconstructed surfaces introduce positively charged Sn^δ+ sites, which exhibit enhanced O₂ activation abilities. These results highlight that even classical oxide catalysts possess rich dynamic behavior, and their active forms may differ significantly from their as-synthesized state.

Following this concept, Wang et al. extends this understanding to electrocatalysis (Fig. 8e),¹⁸⁴ demonstrating that Sn-based catalysts undergo significant structural evolution under CO₂RR conditions. Using a combination of large-scale data mining, DFT, and ML-force field accelerated molecular dynamics, the study shows that SnO_x surfaces dynamically transform into metallic Sn-covered structures. This reconstruction alters the electronic environment and adsorption properties, impacting catalytic activity. The study also reveals that single-atom Sn catalysts and polyatomic Sn species exhibit opposite pH-dependent activity trends, emphasizing the need to consider dynamic reconstruction when designing Sn-based CO₂RR catalysts. These insights point to a paradigm shift that instead of treating structural stability as a virtue, controlled and beneficial reconstruction may be intentionally utilized as a catalytic design principle.

Similarly, Zhang et al. studied investigates the hydrogen-induced restructuring of Cu (100) under electroreduction conditions using a combination of grand canonical DFT and AIMD (Fig. 8f–i).⁵⁴ They discovered that hydrogen adsorption drives a “shifted-row” reconstruction, which stabilizes at one-third monolayer coverage where H atoms fill newly formed three-fold hollow sites. This process originates from the weakening of Cu–Cu bonds due to strong Cu–H interactions. Simulated STM images closely matched experimental observations, and a detailed potential- and pH-dependent stability map revealed that kinetic factors significantly delay the onset of restructuring compared to thermodynamic predictions. This suggests that kinetics, not just energetics, play a decisive role in when and how reconstruction occurs.⁵⁴ Fig. 8f further supports these findings by analyzing the dynamics of hydrogen-covered Cu (100) surfaces, showing that surface restructuring is strongly influenced by hydrogen coverage and local kinetic barriers.

In the context of SACs, dynamic reconstruction is equally critical. A study on transition-metal-supported SACs (dv-g/TM systems) demonstrated that single atoms anchored in graphene divacancies can undergo adsorbate-assisted vacancy migration, dynamically changing their coordination environments during electrochemical reactions.¹⁸⁵ This reversible evolution allows the system to bypass conventional scaling relations, enabling improved catalytic performance. These results offer a compelling case for designing structurally adaptive SACs that respond intelligently to reaction conditions.

During CO electro-oxidation in alkaline electrolyte, the Cu (111) surface undergoes dynamic restructuring.¹⁸⁶ Initially, the surface consists of flat terraces with smooth step edges. Upon applying a potential, the surface transforms into threadlike Cu nanostructures and small Cu adatom islands due to mass transport and structural reorganization. This restructuring is attributed to OH adsorption, which induces Cu atom ejection, while CO preferentially stabilizes undercoordinated Cu adatoms, preventing their agglomeration. This dynamic self-activation process enhances catalytic activity by continuously generating new active sites. Upon reversing the potential, the original smooth Cu (111) structure is largely restored, demonstrating the reversible nature of this activation. This reversible reactivation suggests that dynamic structural transformations may not only be tolerated but can be exploited to maintain catalytic performance over extended operation.

These studies collectively underscore that surface reconstruction is not merely a degradation pathway but often a prerequisite for high activity and selectivity. However, a key design challenge remains how to distinguish between beneficial, self-regulating reconstruction (e.g., Sn or Cu-based systems) and irreversible degradation (e.g., leaching in SACs)? Moreover, the interplay between reaction conditions (e.g., potential, pH, coverage) and dynamic behavior points to the necessity of integrating in situ characterization, ab initio thermodynamics, and machine-learning-accelerated simulations into catalyst discovery.

5. Dynamics and structures of electrochemical interface

The electrochemical interface is highly dynamic, with complex interactions between the catalyst, solvent, and electrolyte species governing reaction mechanisms.^{27,114,187,188} Unlike gas-phase catalysis, electrocatalytic processes involve explicit solvation, electric fields, and electrolyte effects, which significantly influence reaction pathways and energy barriers. Understanding these dynamic factors is crucial for accurately modeling electrocatalytic performance and designing more efficient catalysts. This section explores explicit solvation effects and the role of cations and anions in shaping reaction pathways at the electrochemical interface.

5.1 Explicit solvation effects on reaction pathway

Solvent molecules play an essential role in electrocatalysis, not only stabilizing intermediates but also modifying reaction barriers through hydrogen bonding, dielectric screening, and solvation-induced charge redistribution. Traditional implicit solvation models fail to capture these effects accurately, necessitating explicit solvation models and AIMD simulations. This subsection discusses the impact of explicitly modeled solvent molecules on reaction energetics, transition states, and overall catalytic activity, providing insights into how solvation effects can be leveraged for catalyst design. Explicit solvent models provide crucial insight into the atomistic structure and dynamics of the electrochemical interface, thereby revealing solvent-mediated pathways and enabling more realistic predictions of catalytic performance.

In NRR systems, the inclusion of explicit water molecules and constant-potential conditions has revealed new mechanistic insights. For example, simulations have identified NH₂–NH₂ as a key intermediate, with N–N bond cleavage as the rate-determining step. The orientation of this intermediate is strongly influenced by the local electric field, which can facilitate bond dissociation on certain active sites (e.g., Fe₁@MoS₂), while bimetallic configurations such as Fe₂ and Fe₃ exhibit synergistic activation effects that further lower the energy barrier.¹⁸⁹

Explicit solvation also plays a pivotal role in determining product selectivity. In CO₂ and CO reduction systems, the solvation environment influences whether intermediates undergo surface-coupled or solvent-mediated hydrogenation. For instance, the key intermediate *CH–COH can lead to ethanol via direct surface hydrogenation, or to ethylene through a solvent-driven pathway. The balance between these routes is sensitive to the presence of active surface hydrogen atoms, which are in turn modulated by the arrangement of guest metal atoms on the catalyst surface.¹⁹⁰ This demonstrates that engineering the catalyst–solvent interface, particularly through control over hydrophilicity and atomic structure, offers a powerful lever for tuning selectivity in complex electrocatalytic reactions. Beyond thermodynamics and pathways, the incorporation of explicit solvent models enhances the accuracy of kinetic predictions. For instance, in studies of the ORR on FeNi-based dual-atom catalysts, the computed Tafel slope (281 mV dec⁻¹) from grand canonical simulations closely matched the experimental value (169 mV dec⁻¹), validating the fidelity of the model.¹¹¹ Such quantitative agreement highlights the necessity of capturing the correct solvent-electrode coupling in theoretical electrochemical models.

At the molecular level, the structure of interfacial water itself is highly potential-dependent and has profound effects on reaction dynamics. AIMD simulations have shown that water molecules undergo a sequence of orientation transitions—from “two O–H down” to “two O–H parallel” and eventually to “two O–H up” configurations—as the electrode potential shifts (Fig. 9a–e).¹⁹¹ This results in a non-monotonic, M-shaped distribution of hydrogen bonding at the interface. These findings reveal that solvent reorganization under applied bias is not passive but actively dictates the nature of the electric double layer and the accessibility of proton-coupled reaction pathways. In some cases, the solvent environment enables non-traditional interaction modes. For example, during ORR on single-atom catalysts, AIMD simulations have shown that *OOH intermediates can dissociate to form a pseudo-adsorbed OH⁻ species that resides not on the catalyst surface, but within the hydration layer (∼10 Å away), interacting via long-range redox coupling (Fig. 9i–k).¹⁹² This observation challenges the conventional definition of an “active site” and suggests that catalysis can extend into the solvent environment, mediated by dynamic solvent–intermediate coupling.

Fig. 9 (a) Probability distribution profiles for angle α between the bisector of interface water and the surface normal and the angle β between the O–H bond of water and the surface normal with applied potentials. Potential-dependent (b) water orientation, (c) H-bond number and interfacial water. Potential-dependent population (d) and H-bond N_P (e) of interfacial water with different orientations.¹⁹¹ (f) Snapshots of N₂ first hydrogenation. Free energy profiles of (g) N₂ adsorption and (h) first hydrogenation. (i) Formation of pseudo-adsorption state.³¹ (j) Evolution of distance between single Fe site and the pseudo-adsorbed state OH^δ−. (k) Coordination number of O by H (CN_O) versus R.¹⁹²

Finally, combining static first-principles calculations with constrained MD under explicit solvation has been used to bridge the gap between theoretical and experimental observations in NRR. Such simulations have shown that interfacial water plays a crucial role in promoting N₂ adsorption and modulating hydrogenation barriers under specific electrode potentials. Notably, at −0.68 V, the first hydrogenation step becomes exothermic, aligning closely with experimental trends (Fig. 9f–h).³⁰ This reinforces the idea that accurate modeling of electrocatalysis must simultaneously incorporate solvent effects, interfacial charge distributions, and electrode potential, especially when aiming to interpret or predict experimental results.

5.2 Cation and anion effects on reaction pathways

Electrolyte composition profoundly influences electrocatalytic reactivity by modulating the electric double layer, altering adsorption energies, and stabilizing charged intermediates. Cations can influence reaction kinetics through electrostatic stabilization and specific ion–surface interactions, while anions can modify PCET steps and change selectivity patterns.¹⁹³ Here, key advances in understanding cation and anion effects and their implications for optimizing electrocatalytic reactions are highlighted. Recently, Monteiro et al. demonstrated that CO₂ electroreduction didn’t proceed on Cu (Fig. 10a–c), Au, or Ag electrodes in the absence of metal cations,¹⁹⁴ but CO formation only occurred when metal cations were added. Their results also show that the *CO₂⁻ intermediate can be stabilized by partially the de-solvated cations via a short range electrostatic interaction. The solvation shell of metal cations can be modulated by the electrolyte molecules. Ni et al. introduced aprotic organic molecules into the first solvation shell of K⁺.¹⁸⁷ They modulated the electric double layer, reducing free water concentration and suppressing HER in CO₂ electroreduction. Ringe et al. investigated the influence of cation identity on CO₂ electroreduction using a multi-scale modeling approach that combined size-modified Poisson–Boltzmann theory with DFT simulations.¹⁹⁵ The study demonstrated that cation size strongly affects the interfacial electric field, thereby modulating CO₂ reduction activity. The model quantitatively explained experimental trends, showing that larger cations (Cs⁺) enhance CO₂ conversion to CO on Ag and C₂ products on Cu, in contrast to smaller cations (Li⁺). Resasco et al. also demonstrated that the hydrocarbon intermediates can be stabilized by ions in electrolyte.¹⁹⁶ Using alkaline metal cations to suppress the competition reactions has also been reported in enhancing nitrogen reduction reaction (Fig. 10d and e) on bismuth nanocrystals (BiNCs).¹⁹⁷ Hao et al.¹⁹⁷ performed electrochemical and in situ X-ray absorption spectroscopy experiments and found that K⁺ stabilizes key *NNH intermediates, reducing the free energy barrier for N₂ activation (ΔG_NNH decreased from 3.01 to 2.88 eV on Bi (012)). This resulted in a high faradaic efficiency of 66% and NH₃ yield of 200 mmol g⁻¹ h⁻¹.

Fig. 10 (a) Schematic representation of the interaction of the cation with the negatively charged CO₂⁻ intermediate. CV of CO₂ reduction on gold (b) and silver (c).¹⁹⁴ (d) ΔG_*NNH on Bi (012), (110) and (104) facets without (patterned bars) and with (filled bars) K⁺ cations, and (e) illustration of K⁺ promoted eNRR by hindering proton transfer to the catalyst surfaces.¹⁹⁷ (f) Anion's concentration effects on ORR activity.¹⁹⁸ Free energy profile and representative states for CO₂ adsorption in pure water (g) and with different cations (Li⁺, Na⁺, K⁺, and Cs⁺) (h).¹⁹⁹ (i) N₂ dissociation in pure water and with cations.²⁰⁰ (j) Binding energies of CO₂ molecules and (k) the activated parameter of O–C–O in the presence of halide ions.³⁰

In addition to the experimental observations, the complex mechanism and dynamics at the reaction interface can be elucidated by theoretical methods. To answer the question why M–N–C catalysts generally exhibit dramatic activity drop for oxygen reduction when traversing from alkaline to acid, Chen's group examined the microstructure around metal reactive center at alkaline and acid interfaces under ORR conditions by introducing the potassium/hydroxide ions (K⁺/OH⁻) and hydronium/fluoride (H₃O⁺/F⁻) ions into the water film,²⁰¹ respectively. They revealed that interfacial water molecules are disordered in alkaline media to facilitate hydrogen bonding with surface oxygenated intermediates and enhance PCET. In contrast, in acidic media, strong electric field polarization leads to ordered interfacial water. Furthermore, Chen's group¹¹⁴ reported that a depletion region of interfacial water in alkaline media also reduces H-bond connectivity, increasing the proton transfer barrier and slowing reaction kinetics in hydrogen electrocatalysis. Qin et al. used DFT and AIMD to investigate the impact of varying K⁺ concentrations on CO₂RR at Cu surfaces. They attributed the improved selectivity toward C₂ products to the modulated local electric field.²⁰² Zhang et al. analyzed how different alkali cations (Li⁺, Na⁺, K⁺, Cs⁺) (Fig. 10g and h) influence CO₂RR activity on Cu (100).¹⁹⁹ They found a monotonically decreasing CO₂ activation barrier is obtained from Li⁺ to Cs⁺, which is attributed to the different coordination abilities of alkaline metals with CO₂.¹⁹⁹ Specifically, Li⁺ and Na⁺ can only coordinate with one oxygen atom of CO₂, but K⁺ and Cs⁺ can coordinate with both oxygen atoms of CO₂. The promotion effects of alkaline metal cations were elucidated in nitrogen reduction reaction at Fe electrodes.²⁰⁰ Mao et al. identified four key effects of Li⁺ (Fig. 10i): (i) promoting N₂ activation, (ii) stabilizing intermediates, (iii) suppressing HER, and (iv) modulating interfacial charge distribution.²⁰⁰ Their results showed that Li⁺ lowers the *NNH formation barrier to 0.50 eV, compared to 0.81 eV in pure water, leading to an NRR faradaic efficiency of 27.93% at −0.3 V vs. RHE.

Beyond cations, anions in acidic media can either promote or inhibit electrochemical processes. Therefore, a comprehensive understanding of the interfacial mechanisms is urgently needed to clarify the microscopic details. Koper's group investigated the influence of non-specifically adsorbed (NSA) anions on the oxygen reduction reaction kinetics on Pt (111).¹⁹⁸ Their study demonstrated that increasing the concentration of NSA anions, such as ClO₄⁻ and methane sulfonate, reduced the ORR rate (Fig. 10f). The ORR kinetic current at 0.9 V decreased from 1.93 mA cm⁻² in 0.02 M HClO₄ to lower values in more concentrated solutions, indicating that anion concentration directly affects the *O ↔ *OH transition and thus the ORR rate. By recording cyclic voltammograms in different HClO₄ concentrations, they established a kinetic descriptor—the reversibility of the *O ↔ *OH transition.¹⁹⁸ Using AIMD and DFT, Mao et al. investigated the effect of dynamically formed halide ions (F⁻, Cl⁻, Br⁻, I⁻) on CO₂RR at Cu surfaces (Fig. 10j and k).³⁰ They found that halide ions enhance CO₂ adsorption by 0.45 eV and lower the CO–CO coupling barrier by 0.32 eV in the presence of I⁻. The study demonstrated that halide ions modulate charge distribution near the solid–liquid interface, improving CO₂ reduction selectivity while inhibiting HER.³⁰

Together, the presence of alkali metal cations at the reaction interface can significantly alter the electrochemical reactivity and selectivity by directly participating in the reaction, modifying the local solvation structure, tuning the local electric field, or regulating the local pH, thereby modifying the reaction thermodynamics and kinetics. These insights collectively emphasize the significant role of electrolyte cations and anions in tuning electrocatalytic reactions and guide the rational design of electrolyte environments for electrocatalysis.

6. Conclusions and perspectives

This review systematically explores the theoretical and computational advancements in electrocatalysis, emphasizing fundamental catalytic theories, thermodynamic and kinetic modeling, and ML-driven high-throughput screening. We discussed the role of scaling relationships, reactive descriptors, and ML algorithms in accelerating catalyst discovery while also addressing the dynamic evolution of active sites under realistic conditions. The interplay between solvent effects, interfacial ion regulation, and electrochemical environments was analyzed to highlight their crucial influence on reaction mechanisms. By integrating explicit solvation models, constant-potential simulations, and grand canonical DFT, we provided insights into how modern computational methods bridge the gap between theoretical predictions and experimental observations. These efforts not only improve catalyst design strategies but also deepen our mechanistic understanding of electrochemical interfaces. Moving forward, several challenges and opportunities remain in the field of computational electrocatalysis:

Identifying the rate-determining step under operating conditions: despite extensive DFT simulations of free energy profiles for electrochemical reactions such as the O₂ evolution reaction, N₂ reduction reaction, and CO₂ reduction, a major limitation remains: these calculations often neglect activation barriers, providing no direct insight into reaction kinetics. While some studies have attempted transition state searches to determine activation energies, explicitly incorporating solvent molecules remains a formidable challenge. The dynamic nature of the solid–liquid interface further complicates the identification of the rate-determining step under realistic electrochemical conditions. This is particularly critical as solvent reorganization and solvation effects play a key role in stabilizing transition states and modifying reaction barriers. A significant advance in this direction is the integration of enhanced sampling techniques, such as meta-dynamics and constrained AIMD, to explore reaction pathways beyond static DFT calculations. Moreover, ML-accelerated transition state searches, leveraging Gaussian process regression and neural network-based potential energy surface exploration, offer a promising strategy to systematically identify the rate-determining step. Moving forward, a critical challenge lies in establishing a computational framework that integrates constant-potential DFT, explicit solvation, and free-energy barrier calculations to achieve a mechanistic understanding of catalytic reactions at real electrochemical interfaces. Addressing this challenge will be pivotal for designing highly active and selective electrocatalysts, as it directly links theoretical insights to experimentally measurable kinetic parameters.

Toward realistic electrochemical interface models: the accuracy of computational electrochemistry is fundamentally limited by the representation of the solid–liquid interface. Traditional vacuum-based models fail to capture key interfacial phenomena such as electric double-layer effects,^26,203,204 ion adsorption, and solvent-induced stabilization of intermediates. While monolayer solvation models have been used to approximate electrode–electrolyte interactions, their impact on free-energy calculations has been shown to be minimal. More recent efforts incorporating multi-layer explicit solvation have provided a more realistic description, yet they remain computationally prohibitive. A fundamental challenge is bridging the gap between simplified computational models and real electrochemical environments, where factors such as applied potential, electrolyte composition, and pH effects dynamically alter surface reactivity. Current methodologies struggle to incorporate all thermodynamic constraints simultaneously. To address this, novel approaches such as the constant electrode potential method, grand canonical AIMD simulations, and MLPs offer promising strategies to simulate potential-dependent surface dynamics under realistic reaction conditions.^43,143 Notably, the fourth-generation high-dimensional neural network potentials²⁰⁵ are now being developed to describe long-range interactions and charge transfer effects, making them well-suited for modeling electrified interfaces. These techniques will enable the atomistic exploration of solvent-mediated reaction mechanisms under operational conditions, significantly improving the predictive power of computational catalysis. Furthermore, our understanding of catalysis is shifting from the static active-site model to the dynamic active-site model.⁵² In another word, the active sites are dynamically formed and disrupted under reaction conditions, rather than a fixed atomic arrangement dictating catalytic activity while this dynamic behavior may initially seem detrimental, it is, in fact, essential for establishing a steady-state catalytic environment that ensures long-term stability and sustained activity. In electrochemical reactions, the active site structure evolves due to adsorbate-induced reconstruction, ion-induced modifications, and solvation effects, necessitating the development of simulation techniques that accurately capture these transient states.

Advancing physics-informed and interpretable ML for catalysis: the rapid adoption of ML in electrocatalysis has revolutionized materials discovery, yet a major challenge remains: balancing accuracy and interpretability. Most conventional ML models function as “black boxes”, capturing correlations without revealing fundamental causal relationships. This limitation hinders their broader applicability in mechanistic studies and rational catalyst design. Looking ahead, the next frontier lies in physics-inspired ML, where ML models incorporate domain-specific physical constraints and scientific priors to enhance both accuracy and explainability. The integration of data-enhanced multiscale modeling with physics-informed neural networks will be instrumental in bridging electronic-structure calculations with macro-scale catalytic performance metrics. Advancements in feature representation beyond locality approximations, graph neural networks embedded with d-band theory,^138,206 and symbolic regression techniques for descriptor discovery hold great promise for improving the interpretability of ML models.²⁰⁷ Furthermore, uncertainty quantification techniques, such as Bayesian learning and ensemble modeling, will be crucial in systematically assessing the reliability of ML-driven predictions.

Author contributions

Yaqin Zhang: methodology, software, investigation, formal analysis, validation, writing original draft, review & editing. Yu Xiong: validation, formal analysis, review & editing. Yuhang Wang: validation, formal analysis, review & editing. Qianqian Wang: review & editing. Jun Fan: conceptualization, resources, review & editing, supervision, funding acquisition.

Conflicts of interest

The authors declare no competing financial interest.

Data availability

No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.

Acknowledgements

This work was supported by the Hong Kong Research Grant Council Collaborative Research Fund: C1002-21G and C1017-22G, as well as City University of Hong Kong project no. 7006111.

References

1. M. Yu, A. Li, E. Kan and C. Zhan, Substantial Impact of Spin State Evolution in OER/ORR Catalyzed by Fe–N–C, ACS Catal., 2024, 14(9), 6816–6826.
2. Y. R. Ying, K. Fan, X. Luo, J. L. Qiao and H. T. Huang, Unravelling the origin of bifunctional OER/ORR activity for single-atom catalysts supported on CN by DFT and machine learning, J. Mater. Chem. A, 2021, 9(31), 16860–16867.
3. L. Zhang, X. Guo, S. Zhang and S. Huang, Building up the “Genome” of bi-atom catalysts toward efficient HER/OER/ORR, J. Mater. Chem. A, 2022, 10(21), 11600–11612.
4. Y. Zeng, X. Wang, Y. Hu, W. Qi, Z. Wang, M. Xiao, C. Liu, W. Xing and J. Zhu, Research progress of electrocatalysts for hydrogen oxidation reaction in alkaline media, Carbon Neutralization, 2024, 3(4), 710–736.
5. F. Yang, A. O. Elnabawy, R. Schimmenti, P. Song, J. Wang, Z. Peng, S. Yao, R. Deng, S. Song, Y. Lin, M. Mavrikakis and W. Xu, Bismuthene for highly efficient carbon dioxide electroreduction reaction, Nat. Commun., 2020, 11(1), 1088.
6. C. Cao, D. D. Ma, J. F. Gu, X. Xie, G. Zeng, X. Li, S. G. Han, Q. L. Zhu, X. T. Wu and Q. Xu, Metal-Organic Layers Leading to Atomically Thin Bismuthene for Efficient Carbon Dioxide Electroreduction to Liquid Fuel, Angew. Chem., Int. Ed., 2020, 59(35), 15014–15020.
7. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Norskov, How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels, Energy Environ. Sci., 2010, 3(9), 1311–1315.
8. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Catalysts for nitrogen reduction to ammonia, Nat. Catal., 2018, 1(7), 490–500.
9. W. Lin, H. Chen, G. Lin, S. Yao, Z. Zhang, J. Qi, M. Jing, W. Song, J. Li, X. Liu, J. Fu and S. Dai, Creating Frustrated Lewis Pairs in Defective Boron Carbon Nitride for Electrocatalytic Nitrogen Reduction to Ammonia, Angew. Chem., Int. Ed., 2022, 61(36), e202207807.
10. Z. Wang, C. Li, K. Deng, Y. Xu, H. Xue, X. Li, L. Wang and H. Wang, Ambient nitrogen reduction to ammonia electrocatalyzed by bimetallic PdRu porous nanostructures, ACS Sustainable Chem. Eng., 2019, 7(2), 2400–2405.
11. Y. Wang, H. Shao, C. Zhang, F. Liu, J. Zhao, S. Zhu, M. K. H. Leung and J. Hu, Molecular dynamics for electrocatalysis: Mechanism explanation and performance prediction, Energy Rev., 2023, 2(3), 100028.
12. F. Calle-Vallejo, The ABC of Generalized Coordination Numbers and Their Use as a Descriptor in Electrocatalysis, Adv. Sci., 2023, 10(20), e2207644.
13. T. Y. Mou, H. S. Pillai, S. W. Wang, M. Y. Wan, X. Han, N. M. Schweitzer, F. L. Che and H. L. Xin, Bridging the complexity gap in computational heterogeneous catalysis with machine learning, Nat. Catal., 2023, 6(2), 122–136.
14. J. K. Norskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Density functional theory in surface chemistry and catalysis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(3), 937–943.
15. S. Ghosh, P. Verma, C. J. Cramer, L. Gagliardi and D. G. Truhlar, Combining Wave Function Methods with Density Functional Theory for Excited States, Chem. Rev., 2018, 118(15), 7249–7292.
16. M. J. Eslamibidgoli and M. H. Eikerling, Electrochemical Formation of Reactive Oxygen Species at Pt (111)—A Density Functional Theory Study, ACS Catal., 2015, 5(10), 6090–6098.
17. W. Zhou, Y. Chen, L. Tan, Q. Tang, C. Lu and L. Dong, Understanding the C–H activation of methane over single-atom alloy catalysts by density functional theory calculations, AIChE J., 2023, 69(8), e18118.
18. A. Logadottir, T. H. Rod, J. K. Norskov, B. Hammer, S. Dahl and C. J. H. Jacobsen, The Brønsted-Evans-Polanyi relation and the volcano plot for ammonia synthesis over transition metal catalysts, J. Catal., 2001, 197(2), 229–231.
19. T. Bligaard, J. K. Norskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, The Brønsted-Evans-Polanyi relation and the volcano curve in heterogeneous catalysis, J. Catal., 2004, 224(1), 206–217.
20. B. Meyer, B. Sawatlon, S. Heinen, O. A. von Lilienfeld and C. Corminboeuf, Machine learning meets volcano plots: computational discovery of cross-coupling catalysts, Chem. Sci., 2018, 9(35), 7069–7077.
21. J. B. Le, X. H. Yang, Y. B. Zhuang, M. Jia and J. Cheng, Recent Progress toward Ab Initio Modeling of Electrocatalysis, J. Phys. Chem. Lett., 2021, 12(37), 8924–8931.
22. A. E. Russell, Electrocatalysis: theory and experiment at the interface, Phys. Chem. Chem. Phys., 2008, 10(25), 3607–3608.
23. J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Modeling the electrified solid–liquid interface, Chem. Phys. Lett., 2008, 466(1–3), 68–71.
24. S.-J. Shin, D. H. Kim, G. Bae, S. Ringe, H. Choi, H.-K. Lim, C. H. Choi and H. Kim, On the importance of the electric double layer structure in aqueous electrocatalysis, Nat. Commun., 2022, 13(1), 174.
25. P. Sebastián-Pascual, Y. Shao-Horn and M. Escudero-Escribano, Toward understanding the role of the electric double layer structure and electrolyte effects on well-defined interfaces for electrocatalysis, Curr. Opin. Electrochem., 2022, 32, 100918.
26. M. Becker, P. Loche, M. Rezaei, A. Wolde-Kidan, Y. Uematsu, R. R. Netz and D. J. Bonthuis, Multiscale Modeling of Aqueous Electric Double Layers, Chem. Rev., 2024, 124(1), 1–26.
27. J. A. Gauthier, C. F. Dickens, S. Ringe and K. Chan, Practical Considerations for Continuum Models Applied to Surface Electrochemistry, ChemPhysChem, 2019, 20(22), 3074–3080.
28. G. Kastlunger, P. Lindgren and A. A. Peterson, Controlled-Potential Simulation of Elementary Electrochemical Reactions: Proton Discharge on Metal Surfaces, J. Phys. Chem. C, 2018, 122(24), 12771–12781.
29. X. Bai, X. Zhao, Y. Zhang, C. Ling, Y. Zhou, J. Wang and Y. Liu, Dynamic Stability of Copper Single-Atom Catalysts under Working Conditions, J. Am. Chem. Soc., 2022, 144(37), 17140–17148.
30. X. Mao, T. He, G. Kour, H. Yin, C. Ling, G. Gao, Y. Jin, Q. Liu, A. P. O'Mullane and A. Du, Computational electrocatalysis beyond conventional hydrogen electrode model: CO₂ reduction to C₂ species on copper facilitated by dynamically formed solvent halide ions at the solid–liquid interface, Chem. Sci., 2024, 15(9), 3330–3338.
31. S.-J. Qian, H. Cao, J.-W. Chen, J.-C. Chen, Y.-G. Wang and J. Li, Critical Role of Explicit Inclusion of Solvent and Electrode Potential in the Electrochemical Description of Nitrogen Reduction, ACS Catal., 2022, 12(18), 11530–11540.
32. A. Gross and S. Sakong, Ab Initio Simulations of Water/Metal Interfaces, Chem. Rev., 2022, 122(12), 10746–10776.
33. J. B. Le, A. Chen, L. Li, J. F. Xiong, J. G. Lan, Y. P. Liu, M. Iannuzzi and J. Cheng, Modeling Electrified Pt(111)-H_ad/Water Interfaces from Ab Initio Molecular Dynamics, JACS Au, 2021, 1(5), 569–577.
34. G. Piccini, M.-S. Lee, S. F. Yuk, D. Zhang, G. Collinge, L. Kollias, M.-T. Nguyen, V.-A. Glezakou and R. Rousseau, Ab initio molecular dynamics with enhanced sampling in heterogeneous catalysis, Catal. Sci. Technol., 2022, 12(1), 12–37.
35. T. Yang, T. T. Song, J. Zhou, S. Wang, D. Chi, L. Shen, M. Yang and Y. P. Feng, High-throughput screening of transition metal single atom catalysts anchored on molybdenum disulfide for nitrogen fixation, Nano Energy, 2020, 68, 104304.
36. C. Y. Ling, Y. X. Ouyang, Q. Li, X. W. Bai, X. Mao, A. J. Du and J. L. Wang, A general two-step strategy-based high-throughput screening of single atom catalysts for nitrogen fixation, Small Methods, 2019, 3(9), 1800376.
37. X. Guo, S. Lin, J. Gu, S. Zhang, Z. Chen and S. Huang, Establishing a Theoretical Landscape for Identifying Basal Plane Active 2D Metal Borides (MBenes) toward Nitrogen Electroreduction, Adv. Funct. Mater., 2020, 31(6), 2008056.
38. W. J. Murdoch, C. Singh, K. Kumbier, R. Abbasi-Asl and B. Yu, Definitions, methods, and applications in interpretable machine learning, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(44), 22071–22080.
39. H. Xin, T. Mou, H. S. Pillai, S.-H. Wang and Y. Huang, Interpretable Machine Learning for Catalytic Materials Design toward Sustainability, Acc. Mater. Res., 2023, 5(1), 22–34.
40. Y. Wang, J. M. Lamim Ribeiro and P. Tiwary, Machine learning approaches for analyzing and enhancing molecular dynamics simulations, Curr. Opin. Struct. Biol., 2020, 61, 139–145.
41. P. Friederich, F. Hase, J. Proppe and A. Aspuru-Guzik, Machine-learned potentials for next-generation matter simulations, Nat. Mater., 2021, 20(6), 750–761.
42. M. Kim, B. C. Yeo, Y. Park, H. M. Lee, S. S. Han and D. Kim, Artificial intelligence to accelerate the discovery of N₂ electroreduction catalysts, Chem. Mater., 2020, 32(2), 709–720.
43. X. Zhang, Y. Tian, L. T. Chen, X. Hu and Z. Zhou, Machine Learning: A New Paradigm in Computational Electrocatalysis, J. Phys. Chem. Lett., 2022, 13(34), 7920–7930.
44. L. H. Mou, T. T. Han, P. E. S. Smith, E. Sharman and J. Jiang, Machine Learning Descriptors for Data-Driven Catalysis Study, Adv. Sci., 2023, 10(22), 2301020.
45. M. R. Karim, M. Ferrandon, S. Medina, E. Sture, N. Kariuki, D. J. Myers, E. F. Holby, P. Zelenay and T. Ahmed, Coupling High-Throughput Experiments and Regression Algorithms to Optimize PGM-Free ORR Electrocatalyst Synthesis, ACS Appl. Energy Mater., 2020, 3(9), 9083–9088.
46. H. Zhao, X. Lv and Y.-G. Wang, Realistic Modeling of the Electrocatalytic Process at Complex Solid-Liquid Interface, Adv. Sci., 2023, 10(32), 2303677.
47. T. Yang, T. T. Song, M. Callsen, J. Zhou, J. W. Chai, Y. P. Feng, S. J. Wang and M. Yang, Atomically Thin 2D Transition Metal Oxides: Structural Reconstruction, Interaction with Substrates, and Potential Applications, Adv. Mater. Interfaces, 2019, 6(1), 1801160.
48. X. Yang, D. Xia, Y. Kang, H. Du, F. Kang, L. Gan and J. Li, Unveiling the Axial Hydroxyl Ligand on Fe-N₄-C Electrocatalysts and Its Impact on the pH-Dependent Oxygen Reduction Activities and Poisoning Kinetics, Adv. Sci., 2020, 7(12), 2000176.
49. A. S. Dobrota, N. V. Skorodumova, S. V. Mentus and I. A. Pašti, Surface pourbaix plots of M@N4-graphene single-atom electrocatalysts from density functional theory thermodynamic modeling, Electrochim. Acta, 2022, 412, 140155.
50. Z. Wang, X. Guo, J. Montoya and J. K. Nørskov, Predicting aqueous stability of solid with computed Pourbaix diagram using SCAN functional, npj Comput. Mater., 2020, 6(1), 160.
51. O. Vinogradova, D. Krishnamurthy, V. Pande and V. Viswanathan, Quantifying Confidence in DFT-Predicted Surface Pourbaix Diagrams of Transition-Metal Electrode–Electrolyte Interfaces, Langmuir, 2018, 34(41), 12259–12269.
52. J. Zhang, Y. Wang and Y. Li, Not One, Not Two, But at Least Three: Activity Origin of Copper Single-Atom Catalysts toward CO2/CO Electroreduction to C2+ Products, J. Am. Chem. Soc., 2024, 146(22), 14954–14958.
53. T. Y. Liu, T. Z. Xu, T. C. Li and Y. Jing, Selective CO₂ Reduction over γ-Graphyne Supported Single-Atom Catalysts: Crucial Role of Strain Regulation, J. Am. Chem. Soc., 2024, 146(34), 24133–24140.
54. Z. S. Zhang, Z. Y. Wei, P. Sautet and A. N. Alexandrova, Hydrogen-Induced Restructuring of a Cu (100) Electrode in Electroreduction Conditions, J. Am. Chem. Soc., 2022, 144(42), 19284–19293.
55. F. Maurer, J. Jelic, J. J. Wang, A. Gänzler, P. Dolcet, C. Wöll, Y. M. Wang, F. Studt, M. Casapu and J. D. Grunwaldt, Tracking the formation, fate and consequence for catalytic activity of Pt single sites on CeO₂, Nat. Catal., 2020, 3(10), 824–833.
56. Z. J. Zhao, S. H. Liu, S. J. Zha, D. F. Cheng, F. Studt, G. Henkelman and J. L. Gong, Theory-guided design of catalytic materials using scaling relationships and reactivity descriptors, Nat. Rev. Mater., 2019, 4(12), 792–804.
57. G. H. Gu, C. Choi, Y. Lee, A. B. Situmorang, J. Noh, Y.-H. Kim and Y. Jung, Progress in Computational and Machine-Learning Methods for Heterogeneous Small Molecule Activation, Adv. Mater., 2020, 32(35), 1907865.
58. Y. P. Zhou, Y. X. Ouyang, Y. H. Zhang, Q. Li and J. L. Wang, Machine Learning Assisted Simulations of Electrochemical Interfaces: Recent Progress and Challenges, J. Phys. Chem. Lett., 2023, 14(9), 2308–2316.
59. W. Kohn, A. D. Becke and R. G. Parr, Density Functional Theory of Electronic Structure, J. Phys. Chem., 1996, 100(31), 12974–12980.
60. N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115(19), 2315–2372.
61. S. Saini, J. Halldin Stenlid and F. Abild-Pedersen, Electronic structure factors and the importance of adsorbate effects in chemisorption on surface alloys, npj Comput. Mater., 2022, 8(1), 163.
62. B. Hammer and J. K. Nørskov, Theory of Adsorption and Surface Reactions, Chemisorption and Reactivity on Supported Clusters and Thin Films, 1997, pp. 285–351.
63. M. Born and R. Oppenheimer, ON The Quantum Theory of Molecules, Quantum Chemistry, World Scientific, 2000, vol. 8, pp. 1–24.
64. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871.
65. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138.
66. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
67. Y. K. Zhang and W. T. Yang, Comment on “Generalized gradient approximation made simple”, Phys. Rev. Lett., 1998, 80(4), 890.
68. B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59(11), 7413–7421.
69. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104.
70. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799.
71. J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Density functionals for surface science: Exchange-correlation model development with Bayesian error estimation, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85(23), 235149.
72. A. J. R. Hensley, K. Ghale, C. Rieg, T. Dang, E. Anderst, F. Studt, C. T. Campbell, J.-S. McEwen and Y. Xu, DFT-Based Method for More Accurate Adsorption Energies: An Adaptive Sum of Energies from RPBE and vdW Density Functionals, J. Phys. Chem. C, 2017, 121(9), 4937–4945.
73. H. Eyring, The Activated Complex in Chemical Reactions, J. Chem. Phys., 1935, 3(2), 107–115.
74. R. A. van Santen, M. Neurock and S. G. Shetty, Reactivity Theory of Transition-Metal Surfaces: A Brønsted–Evans–Polanyi Linear Activation Energy–Free-Energy Analysis, Chem. Rev., 2010, 110(4), 2005–2048.
75. H. Xin, A. Vojvodic, J. Voss, J. K. Nørskov and F. Abild-Pedersen, Effects of d-band shape on the surface reactivity of transition-metal alloys, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89(11), 115114.
76. H. Xin and S. Linic, Communications: Exceptions to the d-band model of chemisorption on metal surfaces: The dominant role of repulsion between adsorbate states and metal d-states, J. Chem. Phys., 2010, 132(22), 221101.
77. B. Hammer and J. K. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376(6537), 238–240.
78. P. Sabatier, La catalyse en chimie organique, C. Béranger, 1920, vol. 3.
79. M. Che, Nobel Prize in chemistry 1912 to Sabatier: Organic chemistry or catalysis?, Catal. Today, 2013, 218–219, 162–171.
80. A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier principle to a predictive theory of transition-metal heterogeneous catalysis, J. Catal., 2015, 328, 36–42.
81. A. Vojvodic, A. J. Medford, F. Studt, F. Abild-Pedersen, T. S. Khan, T. Bligaard and J. K. Nørskov, Exploring the limits: A low-pressure, low-temperature Haber–Bosch process, Chem. Phys. Lett., 2014, 598, 108–112.
82. S. Dahl, A. Logadottir, C. J. H. Jacobsen and J. K. Nørskov, Electronic factors in catalysis: the volcano curve and the effect of promotion in catalytic ammonia synthesis, Appl. Catal., A, 2001, 222(1), 19–29.
83. R. Yang, Y. Wang, H. Li, J. Zhou, Z. Gao, C. Liu and B. Zhang, Descriptor-Based Volcano Relations Predict Single Atoms for Hydroxylamine Electrosynthesis, Angew. Chem., Int. Ed., 2024, 63(14), e202317167.
84. J. Li, A. Alsudairi, Z.-F. Ma, S. Mukerjee and Q. Jia, Asymmetric Volcano Trend in Oxygen Reduction Activity of Pt and Non-Pt Catalysts: In Situ Identification of the Site-Blocking Effect, J. Am. Chem. Soc., 2017, 139(4), 1384–1387.
85. K. S. Exner, Four Generations of Volcano Plots for the Oxygen Evolution Reaction: Beyond Proton-Coupled Electron Transfer Steps?, Acc. Chem. Res., 2024, 57(9), 1336–1345.
86. S. Ringe, The importance of a charge transfer descriptor for screening potential CO₂ reduction electrocatalysts, Nat. Commun., 2023, 14(1), 2598.
87. N. G. Ma, Y. Q. Zhang, Y. H. Wang, C. X. Huang, J. Zhao, B. C. Liang and J. Fan, Machine learning-assisted exploration of the intrinsic factors affecting the catalytic activity of ORR/OER bifunctional catalysts, Appl. Surf. Sci., 2023, 628, 157225.
88. N. G. Ma, Y. H. Wang, Y. Q. Zhang, B. C. Liang, J. Zhao and J. Fan, First-principles screening of Pt doped Ti₂CNL (N = O, S and Se, L = F, Cl, Br and I) as high-performance catalysts for ORR/OER, Appl. Surf. Sci., 2022, 596, 153574.
89. N. Ma, N. Li, T. Wang, X. Ma and J. Fan, Strain engineering in the oxygen reduction reaction and oxygen evolution reaction catalyzed by Pt-doped Ti₂CF₂, J. Mater. Chem. A, 2022, 10(3), 1390–1401.
90. Y. Zhang, Y. Wang, N. Ma, B. Liang, Y. Xiong and J. Fan, Revealing the Adsorption Behavior of Nitrogen Reduction Reaction on Strained Ti₂CO₂ by a Spin-Polarized d-band Center Model, Small, 2024, 20(9), 2306840.
91. D. L. Gao, D. Yi, C. Sun, Y. G. Yang and X. Wang, Breaking the volcano-shaped relationship for highly efficient electrocatalytic nitrogen reduction: a computational guideline, ACS Appl. Mater. Interfaces, 2022, 14(47), 52806–52814.
92. T. A. Shifa and A. Vomiero, Confined Catalysis: Progress and Prospects in Energy Conversion, Adv. Energy Mater., 2019, 9(40), 1902307.
93. Y. Ouyang, L. Shi, X. Bai, Q. Li and J. Wang, Breaking scaling relations for efficient CO₂ electrochemical reduction through dual-atom catalysts, Chem. Sci., 2020, 11(7), 1807–1813.
94. J. Liu, S. C. Smith, Y. Gu and L. Kou, C–N Coupling Enabled by N–N Bond Breaking for Electrochemical Urea Production, Adv. Funct. Mater., 2023, 33(47), 2305894.
95. J. Rossmeisl, K. Chan, R. Ahmed, V. Tripkovic and M. E. Björketun, pH in atomic scale simulations of electrochemical interfaces, Phys. Chem. Chem. Phys., 2013, 15(25), 10321–10325.
96. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892.
97. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways, J. Chem. Phys., 2014, 140(8), 084106.
98. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit self-consistent electrolyte model in plane-wave density-functional theory, J. Chem. Phys., 2019, 151(23), 234101.
99. S. M. R. Islam, F. Khezeli, S. Ringe and C. Plaisance, An implicit electrolyte model for plane wave density functional theory exhibiting nonlinear response and a nonlocal cavity definition, J. Chem. Phys., 2023, 159(23), 234117.
100. Z. S. Zhang, J. Li and Y. G. Wang, Modeling Interfacial Dynamics on Single Atom Electrocatalysts: Explicit Solvation and Potential Dependence, Acc. Chem. Res., 2024, 57(2), 198–207.
101. P. Yang, H. Liu, Q. Jin, Y. Lai, Y. Zeng, C. Zhang, J. Dong, W. Sun, Q. Guo, D. Cao and J. Guo, Visualizing the Promoting Role of Interfacial Water in the Deprotonation of Formic Acid on Cu (111), J. Am. Chem. Soc., 2023, 146(1), 210–217.
102. X. Chen, X.-T. Wang, J.-B. Le, S.-M. Li, X. Wang, Y.-J. Zhang, P. Radjenovic, Y. Zhao, Y.-H. Wang, X.-M. Lin, J.-C. Dong and J.-F. Li, Revealing the role of interfacial water and key intermediates at ruthenium surfaces in the alkaline hydrogen evolution reaction, Nat. Commun., 2023, 14(1), 5289.
103. L. Agosta, D. Arismendi-Arrieta, M. Dzugutov and K. Hermansson, Origin of the Hydrophobic Behaviour of Hydrophilic CeO₂, Angew. Chem., Int. Ed., 2023, 62(35), e202303910.
104. H.-K. Lim, Y. Kwon, H. S. Kim, J. Jeon, Y.-H. Kim, J.-A. Lim, B.-S. Kim, J. Choi and H. Kim, Insight into the Microenvironments of the Metal–Ionic Liquid Interface during Electrochemical CO₂ Reduction, ACS Catal., 2018, 8(3), 2420–2427.
105. S. Pezeshki and H. Lin, Recent developments in QM/MM methods towards open-boundary multi-scale simulations, Mol. Simul., 2015, 41(1–3), 168–189.
106. H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, Solvation at metal/water interfaces: An ab initio molecular dynamics benchmark of common computational approaches, J. Chem. Phys., 2020, 152(14), 144703.
107. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904.
108. G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113(22), 9978–9985.
109. Z. Y. Duan and P. H. Xiao, Simulation of Potential-Dependent Activation Energies in Electrocatalysis: Mechanism of O–O Bond Formation on RuO₂, J. Phys. Chem. C, 2021, 125(28), 15243–15250.
110. X. P. Qin, T. Vegge and H. A. Hansen, Cation-Coordinated Inner-Sphere CO₂ Electroreduction at Au-Water Interfaces, J. Am. Chem. Soc., 2023, 145, 1897–1905.
111. M. Tamtaji, Y. Y. Li, Y. T. Cai, H. W. Liu, W. Goddard and G. H. Chen, Reaction mechanism and kinetics of oxygen reduction reaction on the iron-nickel dual atom catalyst, J. Mater. Chem. A, 2023, 11(46), 25410–25421.
112. Y. Wang, L. You and K. Zhou, Origin of the N-coordinated single-atom Ni sites in heterogeneous electrocatalysts for CO₂ reduction reaction, Chem. Sci., 2021, 12(42), 14065–14073.
113. S. Tan, Y. Ji and Y. Li, Single-Atom Electrocatalysis for Hydrogen Evolution Based on the Constant Charge and Constant Potential Models, J. Phys. Chem. Lett., 2022, 13(30), 7036–7042.
114. P. Li, Y. Jiang, Y. Hu, Y. Men, Y. Liu, W. Cai and S. Chen, Hydrogen bond network connectivity in the electric double layer dominates the kinetic pH effect in hydrogen electrocatalysis on Pt, Nat. Catal., 2022, 5(10), 900–911.
115. X. Chen, G. Kastlunger and A. A. Peterson, Fundamental Drivers of Electrochemical Barriers, Phys. Rev. Lett., 2023, 131(23), 238003.
116. C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, First principles reaction modeling of the electrochemical interface: Consideration and calculation of a tunable surface potential from atomic and electronic structure, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73(16), 165402.
117. Z. Xia and H. Xiao, Grand Canonical Ensemble Modeling of Electrochemical Interfaces Made Simple, J. Chem. Theory Comput., 2023, 19(15), 5168–5175.
118. X. Hu, S. Chen, L. Chen, Y. Tian, S. Yao, Z. Lu, X. Zhang and Z. Zhou, What is the Real Origin of the Activity of Fe–N–C Electrocatalysts in the O₂ Reduction Reaction? Critical Roles of Coordinating Pyrrolic N and Axially Adsorbing Species, J. Am. Chem. Soc., 2022, 144(39), 18144–18152.
119. S. Yu, Z. Levell, Z. Jiang, X. Zhao and Y. Liu, What Is the Rate-Limiting Step of Oxygen Reduction Reaction on Fe–N–C Catalysts?, J. Am. Chem. Soc., 2023, 145(46), 25352–25356.
120. T. Y. Liu, Y. Wang and Y. F. Li, How pH Affects the Oxygen Reduction Reactivity of Fe-N-C Materials, ACS Catal., 2023, 13(3), 1717–1725.
121. Neha, M. Aggarwal, A. Soni and T. Karmakar, Polymorph-Specific Solubility Prediction of Urea Using Constant Chemical Potential Molecular Dynamics Simulations, J. Phys. Chem. B, 2024, 128(35), 8477–8483.
122. K. Chan and J. K. Nørskov, Potential Dependence of Electrochemical Barriers from ab Initio Calculations, J. Phys. Chem. Lett., 2016, 7(9), 1686–1690.
123. K. Chan and J. K. Nørskov, Electrochemical Barriers Made Simple, J. Phys. Chem. Lett., 2015, 6(14), 2663–2668.
124. Z. Y. Duan and G. Henkelman, Identification of Active Sites of Pure and Nitrogen-Doped Carbon Materials for Oxygen Reduction Reaction Using Constant-Potential Calculations, J. Phys. Chem. C, 2020, 124(22), 12016–12023.
125. A. R. Singh, J. H. Montoya, B. A. Rohr, C. Tsai, A. Vojvodic and J. K. Nørskov, Computational Design of Active Site Structures with Improved Transition-State Scaling for Ammonia Synthesis, ACS Catal., 2018, 8(5), 4017–4024.
126. M. Andersen, C. P. Plaisance and K. Reuter, Assessment of mean-field microkinetic models for CO methanation on stepped metal surfaces using accelerated kinetic Monte Carlo, J. Chem. Phys., 2017, 147(15), 152705.
127. K. Tran and Z. W. Ulissi, Active learning across intermetallics to guide discovery of electrocatalysts for CO₂ reduction and H₂ evolution, Nat. Catal., 2018, 1(9), 696–703.
128. J. Kimari, V. Jansson, S. Vigonski, E. Baibuz, R. Domingos, V. Zadin and F. Djurabekova, Application of artificial neural networks for rigid lattice kinetic Monte Carlo studies of Cu surface diffusion, Comput. Mater. Sci., 2020, 183, 109789.
129. M. Zafari, D. Kumar, M. Umer and K. S. Kim, Machine learning-based high throughput screening for nitrogen fixation on boron-doped single atom catalysts, J. Mater. Chem. A, 2020, 8(10), 5209–5216.
130. R. Qi, B. Zhu, Z. Han and Y. Gao, High-Throughput Screening of Stable Single-Atom Catalysts in CO₂ Reduction Reactions, ACS Catal., 2022, 12(14), 8269–8278.
131. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Computational high-throughput screening of electrocatalytic materials for hydrogen evolution, Nat. Mater., 2006, 5(11), 909–913.
132. Z. Wang, Y. Gong, M. L. Evans, Y. Yan, S. Wang, N. Miao, R. Zheng, G.-M. Rignanese and J. Wang, Machine Learning-Accelerated Discovery of A₂BC₂ Ternary Electrides with Diverse Anionic Electron Densities, J. Am. Chem. Soc., 2023, 145(48), 26412–26424.
133. Y. Wang, X. Cui, J. Zhao, G. Jia, L. Gu, Q. Zhang, L. Meng, Z. Shi, L. Zheng, C. Wang, Z. Zhang and W. Zheng, Rational Design of Fe–N/C Hybrid for Enhanced Nitrogen Reduction Electrocatalysis under Ambient Conditions in Aqueous Solution, ACS Catal., 2018, 9(1), 336–344.
134. Y. Q. Zhang, Y. H. Wang, N. G. Ma and J. Fan, Directly predicting N₂ electroreduction reaction free energy using interpretable machine learning with non-DFT calculated features, J. Energy Chem., 2024, 97, 139–148.
135. Y. H. Wang, Y. Q. Zhang, N. G. Ma, J. Zhao, Y. Xiong, S. Luo and J. Fan, Machine learning accelerated catalysts design for CO reduction: An interpretability and transferability analysis, J. Mater. Sci. Technol., 2025, 213, 14–23.
136. Y. M. Gu, Q. Zhu, Z. T. Liu, C. Fu, J. Y. Wu, Q. Zhu, Q. Q. Jia and J. Ma, Nitrogen reduction reaction energy and pathways in metal-zeolites: deep learning and explainable machine learning with local acidity and hydrogen bonding features, J. Mater. Chem. A, 2022, 10(28), 14976–14988.
137. H. S. Pillai, Y. Li, S. H. Wang, N. Omidvar, Q. Mu, L. E. K. Achenie, F. Abild-Pedersen, J. Yang, G. Wu and H. Xin, Interpretable design of Ir-free trimetallic electrocatalysts for ammonia oxidation with graph neural networks, Nat. Commun., 2023, 14(1), 792.
138. C. C. Price, A. Singh, N. C. Frey and V. B. Shenoy, Efficient catalyst screening using graph neural networks to predict strain effects on adsorption energy, Sci. Adv., 2022, 8(47), eabq5944.
139. J. Acquarelli, T. van Laarhoven, J. Gerretzen, T. N. Tran, L. M. C. Buydens and E. Marchiori, Convolutional neural networks for vibrational spectroscopic data analysis, Anal. Chim. Acta, 2017, 954, 22–31.
140. G. X. Hu, V. Fung, J. S. Huang and P. Ganesh, Work Function Engineering of 2D Materials: The Role of Polar Edge Reconstructions, J. Phys. Chem. Lett., 2021, 12(9), 2320–2326.
141. L. van der Maaten, Accelerating t-SNE using Tree-Based Algorithms, J. Mach. Learn. Res., 2014, 15, 3221–3245.
142. S. Hwang, J. Jung, C. Hong, W. Jeong, S. Kang and S. Han, Stability and Equilibrium Structures of Unknown Ternary Metal Oxides Explored by Machine-Learned Potentials, J. Am. Chem. Soc., 2023, 145(35), 19378–19386.
143. L. Bonati, D. Polino, C. Pizzolitto, P. Biasi, R. Eckert, S. Reitmeier, R. Schlögl and M. Parrinello, The role of dynamics in heterogeneous catalysis: Surface diffusivity and N₂ decomposition on Fe(111), Proc. Natl. Acad. Sci. U. S. A., 2023, 120(50), e2313023120.
144. B. W. J. Chen, B. Wang, M. B. Sullivan, A. Borgna and J. Zhang, Unraveling the Synergistic Effect of Re and Cs Promoters on Ethylene Epoxidation over Silver Catalysts with Machine Learning-Accelerated First-Principles Simulations, ACS Catal., 2022, 12(4), 2540–2551.
145. S. Chen, Y. Gao, W. Wang, O. V. Prezhdo and L. Xu, Prediction of Three-Metal Cluster Catalysts on Two-Dimensional W₂N₃ Support with Integrated Descriptors for Electrocatalytic Nitrogen Reduction, ACS Nano, 2023, 17, 1522–1532.
146. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Scaling properties of adsorption energies for hydrogen-containing molecules on transition-metal surfaces, Phys. Rev. Lett., 2007, 99(1), 016105.
147. H. Xu, D. Cheng, D. Cao and X. C. Zeng, A universal principle for a rational design of single-atom electrocatalysts, Nat. Catal., 2018, 1(5), 339–348.
148. J. Liu, X. Lv, Y. Ma, S. C. Smith, Y. Gu and L. Kou, Electrocatalytic Urea Synthesis via N₂ Dimerization and Universal Descriptor, ACS Nano, 2023, 17, 25667–25678.
149. Q. Zhu, W. Huang, C. Huang, L. Gao, Y. Su and L. Qiao, The d band center as an indicator for the hydrogen solution and diffusion behaviors in transition metals, Int. J. Hydrogen Energy, 2022, 47(90), 38445–38454.
150. S. Bhattacharjee, U. V. Waghmare and S.-C. Lee, An improved d-band model of the catalytic activity of magnetic transition metal surfaces, Sci. Rep., 2016, 6(1), 35916.
151. H. L. Xin, A. Vojvodic, J. Voss, J. K. Norskov and F. Abild-Pedersen, Effects of d-band shape on the surface reactivity of transition-metal alloys, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89(11), 115114.
152. Y. Zhang, N. Ma, Y. Wang, B. Liang and J. Fan, Theoretical design toward highly efficient single-atom catalysts for nitrogen reduction by regulating the “acceptance-donation” mechanism, Appl. Surf. Sci., 2023, 623, 156827.
153. Y. Zhang, Y. Wang, N. Ma, Y. Li, B. Liang, S. Luo and J. Fan, Establishing an orbital-level understanding of active origins of heteroatom-coordinated single-atom catalysts: The case of N₂ reduction, J. Colloid Interface Sci., 2023, 650, 961–971.
154. X. Liu, Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Building up a picture of the electrocatalytic nitrogen reduction activity of transition metal single-atom catalysts, J. Am. Chem. Soc., 2019, 141(24), 9664–9672.
155. H. Jin, C. Guo, X. Liu, J. Liu, A. Vasileff, Y. Jiao, Y. Zheng and S. Z. Qiao, Emerging Two-Dimensional Nanomaterials for Electrocatalysis, Chem. Rev., 2018, 118(13), 6337–6408.
156. C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, An electronic structure descriptor for oxygen reactivity at metal and metal-oxide surfaces, Surf. Sci., 2019, 681, 122–129.
157. Y. Wang, N. Ma, Y. Zhang, B. Liang and J. Fan, Cu₄@C₂N for effective electrochemical CO₂ reduction and intermediates dependent adsorption behaviours: A computational study, Appl. Surf. Sci., 2023, 626, 157126.
158. Y. Chen, X. Zhang, J. Qin and R. Liu, Taming the challenges of activity and selectivity in catalysts for electrochemical N₂ fixation via single metal atom supported on WS₂, Appl. Surf. Sci., 2022, 571, 151357.
159. W. Gao, Y. Chen, B. Li, S.-P. Liu, X. Liu and Q. Jiang, Determining the adsorption energies of small molecules with the intrinsic properties of adsorbates and substrates, Nat. Commun., 2020, 11(1), 1196.
160. F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Physical and Chemical Nature of the Scaling Relations between Adsorption Energies of Atoms on Metal Surfaces, Phys. Rev. Lett., 2012, 108(11), 116103.
161. H.-Y. Su, K. Sun, W.-Q. Wang, Z. Zeng, F. Calle-Vallejo and W.-X. Li, Establishing and Understanding Adsorption–Energy Scaling Relations with Negative Slopes, J. Phys. Chem. Lett., 2016, 7(24), 5302–5306.
162. F. Calle-Vallejo and M. T. M. Koper, Accounting for Bifurcating Pathways in the Screening for CO₂ Reduction Catalysts, ACS Catal., 2017, 7(10), 7346–7351.
163. M. J. Kolb, D. Loffreda, P. Sautet and F. Calle-Vallejo, Structure-sensitive scaling relations among carbon-containing species and their possible impact on CO₂ electroreduction, J. Catal., 2021, 395, 136–142.
164. A. Brito-Ravicini and F. Calle-Vallejo, Interplaying coordination and ligand effects to break or make adsorption-energy scaling relations, Exploration, 2022, 2(2), 20210062.
165. M. Yu, J. Wu, Y. Chen, Y. Du, A. Li, E. Kan and C. Zhan, Strain-controlled spin regulation in Fe–N–C catalysts for enhanced oxygen reduction reaction activity, J. Mater. Chem. A, 2024, 12(36), 24530–24541.
166. X. F. Yang, A. Q. Wang, B. T. Qiao, J. Li, J. Y. Liu and T. Zhang, Single-Atom Catalysts: A New Frontier in Heterogeneous Catalysis, Acc. Chem. Res., 2013, 46(8), 1740–1748.
167. X. Q. Wang, Z. Chen, X. Y. Zhao, T. Yao, W. X. Chen, R. You, C. M. Zhao, G. Wu, J. Wang, W. X. Huang, J. L. Yang, X. Hong, S. Q. Wei, Y. Wu and Y. D. Li, Regulation of coordination number over single Co sites: triggering the efficient electroreduction of CO₂, Angew. Chem., Int. Ed., 2018, 57(7), 1944–1948.
168. F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Finding optimal surface sites on heterogeneous catalysts by counting nearest neighbors, Science, 2015, 350(6257), 185–189.
169. H. B. Tao, L. W. Fang, J. Z. Chen, H. B. Yang, J. J. Gao, J. W. Miao, S. L. Chen and B. Liu, Identification of Surface Reactivity Descriptor for Transition Metal Oxides in Oxygen Evolution Reaction, J. Am. Chem. Soc., 2016, 138(31), 9978–9985.
170. D. Y. Wu, C. K. Dong, H. B. Zhan and X. W. Du, Bond-Energy-Integrated Descriptor for Oxygen Electrocatalysis of Transition Metal Oxides, J. Phys. Chem. Lett., 2018, 9(12), 3387–3391.
171. J. Liu, J. Zhu, H. Xu and D. Cheng, Rational Design of Heteroatom-Doped Fe–N–C Single-Atom Catalysts for Oxygen Reduction Reaction via Simple Descriptor, ACS Catal., 2024, 14(9), 6952–6964.
172. M. Ren, X. Guo, S. Zhang and S. Huang, Design of Graphdiyne and Holey Graphyne-Based Single Atom Catalysts for CO₂ Reduction With Interpretable Machine Learning, Adv. Funct. Mater., 2023, 33(48), 2213543.
173. D. Wu, J. Zhang, M.-J. Cheng, Q. Lu and H. Zhang, Machine Learning Investigation of Supplementary Adsorbate Influence on Copper for Enhanced Electrochemical CO₂ Reduction Performance, J. Phys. Chem. C, 2021, 125(28), 15363–15372.
174. H. Niu, X. Wan, X. Wang, C. Shao, J. Robertson, Z. Zhang and Y. Guo, Single-Atom Rhodium on Defective g-C₃N₄: A Promising Bifunctional Oxygen Electrocatalyst, ACS Sustainable Chem. Eng., 2021, 9(9), 3590–3599.
175. X. Wan, W. Yu, H. Niu, X. Wang, Z. Zhang and Y. Guo, Revealing the oxygen Reduction/Evolution reaction activity origin of Carbon-Nitride-Related Single-Atom catalysts: Quantum chemistry in artificial intelligence, Chem. Eng. J., 2022, 440, 135946.
176. X. Lin, X. Du, S. Wu, S. Zhen, W. Liu, C. Pei, P. Zhang, Z. J. Zhao and J. Gong, Machine learning-assisted dual-atom sites design with interpretable descriptors unifying electrocatalytic reactions, Nat. Commun., 2024, 15(1), 8169.
177. D. H. Mok, H. Li, G. Zhang, C. Lee, K. Jiang and S. Back, Data-driven discovery of electrocatalysts for CO₂ reduction using active motifs-based machine learning, Nat. Commun., 2023, 14(1), 7303.
178. M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C. T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C. S. Tan, M. Askerka, F. Che, M. Liu, A. Seifitokaldani, Y. Pang, S. C. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Accelerated discovery of CO₂ electrocatalysts using active machine learning, Nature, 2020, 581(7807), 178–183.
179. S.-H. Wang, H. S. Pillai, S. Wang, L. E. K. Achenie and H. Xin, Infusing theory into deep learning for interpretable reactivity prediction, Nat. Commun., 2021, 12(1), 5288.
180. L. C. Liu, D. M. Meira, R. Arenal, P. Concepcion, A. V. Puga and A. Corma, Determination of the Evolution of Heterogeneous Single Metal Atoms and Nanoclusters under Reaction Conditions: Which Are the Working Catalytic Sites?, ACS Catal., 2019, 9(12), 10626–10639.
181. V. Muravev, G. Spezzati, Y. Q. Su, A. Parastaev, F. K. Chiang, A. Longo, C. Escudero, N. Kosinov and E. J. M. Hensen, Interface dynamics of Pd-CeO₂ single-atom catalysts during CO oxidation, Nat. Catal., 2021, 4(6), 469–478.
182. A. S. Varela, W. Ju, A. Bagger, P. Franco, J. Rossmeisl and P. Strasser, Electrochemical Reduction of CO₂ on Metal-Nitrogen-Doped Carbon Catalysts, ACS Catal., 2019, 9(8), 7270–7284.
183. G. X. Li, S. D. Li, Z. K. Han, C. Zou, H. L. Wu, W. T. Yuan, B. E. Zhu, Y. Gao, H. S. Yang, Z. Zhang and Y. Wang, In Situ Resolving the Atomic Reconstruction of SnO₂ (110) Surface, Nano Lett., 2021, 21(17), 7309–7316.
184. Y. Wang, D. Zhang, B. Sun, X. Jia, L. Zhang, H. Cheng, J. Fan and H. Li, Divergent Activity Shifts of Tin-Based Catalysts for Electrochemical CO₂ Reduction: pH-Dependent Behavior of Single-Atom Versus Polyatomic Structures, Angew. Chem., Int. Ed., 2025, 64(8), e202418228.
185. X. Yao, L. Huang, E. Halpren, L. Chen, Z. Chen and C. V. Singh, Structural Self-Regulation-Promoted NO Electroreduction on Single Atoms, J. Am. Chem. Soc., 2023, 145(48), 26249–26256.
186. A. Auer, M. Andersen, E.-M. Wernig, N. G. Hörmann, N. Buller, K. Reuter and J. Kunze-Liebhäuser, Self-activation of copper electrodes during CO electro-oxidation in alkaline electrolyte, Nat. Catal., 2020, 3(10), 797–803.
187. W. Ni, Y. Guan, H. Chen, Y. Zhang, S. Wang and S. Zhang, Molecular Engineering of Cation Solvation Structure for Highly Selective Carbon Dioxide Electroreduction, Angew. Chem., Int. Ed., 2023, 62(37), e202303233.
188. J. Gu, S. Liu, W. Ni, W. Ren, S. Haussener and X. Hu, Modulating electric field distribution by alkali cations for CO₂ electroreduction in strongly acidic medium, Nat. Catal., 2022, 5(4), 268–276.
189. K. Xie, F. Wang, F. Wei, J. Zhao and S. Lin, Revealing the Origin of Nitrogen Electroreduction Activity of Molybdenum Disulfide Supported Iron Atoms, J. Phys. Chem. C, 2022, 126(11), 5180–5188.
190. Y. Ouyang, L. Shi, X. Bai, C. Ling, Q. Li and J. Wang, Selectivity of Electrochemical CO₂ Reduction toward Ethanol and Ethylene: The Key Role of Surface-Active Hydrogen, ACS Catal., 2023, 13(23), 15448–15456.
191. Y.-M. Wang, H.-M. Yan, H. Cao, J.-W. Chen, H. Yang, J.-Y. Zhu and J. Sun, Atomic-Scale Understanding of Electrified Interfacial Structures and Dynamics during the Oxygen Reduction Reaction on the Fe–N₄/C Electrocatalyst, ACS Catal., 2023, 13(16), 11080–11090.
192. J. W. Chen, Z. S. Zhang, H. M. Yan, G. J. Xia, H. Cao and Y. G. Wang, Pseudo-adsorption and long-range redox coupling during oxygen reduction reaction on single atom electrocatalyst, Nat. Commun., 2022, 13(1), 1734.
193. C. Zhan, M. R. Cerón, S. A. Hawks, M. Otani, B. C. Woods, T. A. Pham, M. Stadermann and P. G. Campbell, Specific ion effects at graphitic interfaces, Nat. Commun., 2019, 10, 4858.
194. M. C. O. Monteiro, F. Dattila, B. Hagedoorn, R. García-Muelas, N. López and M. T. M. Koper, Absence of CO₂ electroreduction on copper, gold and silver electrodes without metal cations in solution, Nat. Catal., 2021, 4(8), 654–662.
195. S. Ringe, E. L. Clark, J. Resasco, A. Walton, B. Seger, A. T. Bell and K. Chan, Understanding cation effects in electrochemical CO₂ reduction, Energy Environ. Sci., 2019, 12(10), 3001–3014.
196. J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, Promoter Effects of Alkali Metal Cations on the Electrochemical Reduction of Carbon Dioxide, J. Am. Chem. Soc., 2017, 139(32), 11277–11287.
197. Y. C. Hao, Y. Guo, L. W. Chen, M. Shu, X. Y. Wang, T. A. Bu, W. Y. Gao, N. Zhang, X. Su, X. Feng, J. W. Zhou, B. Wang, C. W. Hu, A. X. Yin, R. Si, Y. W. Zhang and C. H. Yan, Promoting nitrogen electroreduction to ammonia with bismuth nanocrystals and potassium cations in water, Nat. Catal., 2019, 2(5), 448–456.
198. M. Luo and M. T. M. Koper, A kinetic descriptor for the electrolyte effect on the oxygen reduction kinetics on Pt(111), Nat. Catal., 2022, 5(7), 615–623.
199. Z. Zhang, H. Li, Y. Shao, L. Gan, F. Kang, W. Duan, H. A. Hansen and J. Li, Molecular understanding of the critical role of alkali metal cations in initiating CO₂ electroreduction on Cu (100) surface, Nat. Commun., 2024, 15(1), 612.
200. X. Mao, X. Bai, G. Wu, Q. Qin, A. P. O'Mullane, Y. Jiao and A. Du, Electrochemical Reduction of N₂ to Ammonia Promoted by Hydrated Cation Ions: Mechanistic Insights from a Combined Computational and Experimental Study, J. Am. Chem. Soc., 2024, 146(27), 18743–18752.
201. P. Li, Y. Jiao, Y. Ruan, H. Fei, Y. Men, C. Guo, Y. Wu and S. Chen, Revealing the role of double-layer microenvironments in pH-dependent oxygen reduction activity over metal-nitrogen-carbon catalysts, Nat. Commun., 2023, 14(1), 6936.
202. X. Qin, T. Vegge and H. A. Hansen, Cation-Coordinated Inner-Sphere CO₂ Electroreduction at Au–Water Interfaces, J. Am. Chem. Soc., 2023, 145(3), 1897–1905.
203. S. Ringe, C. G. Morales-Guio, L. D. Chen, M. Fields, T. F. Jaramillo, C. Hahn and K. Chan, Double layer charging driven carbon dioxide adsorption limits the rate of electrochemical carbon dioxide reduction on Gold, Nat. Commun., 2020, 11(1), 33.
204. P. P. Lopes, D. Strmcnik, J. S. Jirkovsky, J. G. Connell, V. Stamenkovic and N. Markovic, Double layer effects in electrocatalysis: The oxygen reduction reaction and ethanol oxidation reaction on Au(111), Pt(111) and Ir(111) in alkaline media containing Na and Li cations, Catal. Today, 2016, 262, 41–47.
205. T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, A fourth-generation high-dimensional neural network potential with accurate electrostatics including non-local charge transfer, Nat. Commun., 2021, 12(1), 398.
206. S. Gong, K. Q. Yan, T. Xie, Y. Shao-Horn, R. Gomez-Bombarelli, S. W. Ji and J. C. Grossman, Examining graph neural networks for crystal structures: Limitations and opportunities for capturing periodicity, Sci. Adv., 2023, 9(45), eadi3245.
207. C. Cornelio, S. Dash, V. Austel, T. R. Josephson, J. Goncalves, K. L. Clarkson, N. Megiddo, B. El Khadir and L. Horesh, Combining data and theory for derivable scientific discovery with AI-Descartes, Nat. Commun., 2023, 14(1), 1777.

---