Direct quantification of the plasmon dephasing time in ensembles of gold nanorods through two-dimensional electronic spectroscopy

Abstract

In this study, we used two-dimensional electronic spectroscopy to examine the early femtosecond dynamics of suspensions of colloidal gold nanorods with different aspect ratios. In all samples, the signal distribution in the 2D maps at this timescale shows a distinctive dispersive behavior, which can be explained by the interference between the exciting field and the field produced on the nanoparticle's surface by the collective motion of electrons when the plasmon is excited. Studying this interference effect, which is active only until the plasmon has been dephased, allows for a direct estimation of the dephasing time of the plasmon of an ensemble of colloidal particles. Our findings provide insight into the fundamental behavior of plasmonic states and highlight the potential of two-dimensional electronic spectroscopy in uncovering ultrafast and coherent optical phenomena at the nanoscale.

---

1. Introduction

The study and manipulation of the interaction between light and free electrons in metal (nano)structures is the subject of the rapidly expanding field of plasmonics.¹ Plasmon resonances refer to the coherent oscillations of the electron cloud induced by the electromagnetic field at a metal-dielectric interface (surface plasmon polariton) or on a metal nanoparticle (localized surface plasmon).^2–4 These oscillations impart unique optical properties and exceptional versatility to nanostructured metals, allowing for the manipulation of light at the nanoscale and leading to numerous applications in nanoscience, including, among others, surface-enhanced spectroscopy,^5,6 photothermal therapy,⁷ nano-photonics,² nano-sensing^6,8,9 and polariton chemistry.^10,11

One of the most recent frontiers in this field involves exploring the quantum properties of plasmons to develop quantum-controlled plasmonic devices that operate at the quantum level.¹² These developments, sparked by recent experimental observations, have expanded our understanding and opened possibilities for unprecedented applications in the field of quantum technology.^12–16

However, all of these envisioned applications face a major hurdle, plasmonic losses.¹⁷ Plasmonic systems, especially metal nanoparticles, are characterized by extremely fast dephasing times, making it essential to understand the physical mechanisms behind these rapid dephasing dynamics to optimize their performance. Therefore, much work is currently focused on understanding the processes that lead to dephasing and minimizing it. This requires having access to direct and reliable measurements of dephasing times, but this direct quantification is challenged by the short timescales involved, from a few to a few tens of femtoseconds.

When dealing with single nanoparticles, it is possible to directly estimate dephasing times using specific frequency (such as dark field scattering)¹⁸ and time-resolved (interferometric)¹⁹ techniques. Additionally, recently developed time-resolved near-field microscopy (SNOM, PEEM, etc.)^20,21 shows great promise for effectively characterizing large single plasmonic nanostructures. However, these techniques do not apply to the most common case of samples consisting of large ensembles of colloidal metal nanoparticles. These types of samples have recently attracted a lot of interest due to their easy and inexpensive preparation, along with significant field enhancement properties that are important in many applications.²² For these samples, the dephasing time is typically estimated through linewidth analysis despite the significant size and shape inhomogeneity typical of these systems, making it difficult for reliable and accurate quantification. Recently, peta-hertz sampling experiments, which characterized the localized plasmon field in arbitrary nanostructures with subcycle precision by measuring the build-up and dephasing of localized surface plasmons, were also proposed.^23,24

Here, we demonstrate that two-dimensional electronic spectroscopy (2DES) can complementarily contribute to filling this gap as it effectively overcomes the limitations imposed by inhomogeneous broadening in ensemble measurements. The capability of multidimensional techniques to distinguish between homogeneous and inhomogeneous contributions in the linewidth analysis is well-documented^25–27 and has already been exploited to investigate the sub-100 fs dynamics of broad distributions of dimensionally heterogeneous gold nanorods (NRs).²⁸ However, in the linewidth analysis of largely inhomogeneous samples, disentangling inhomogeneous and homogeneous contributions often involves complex approaches, including pulse shape considerations and lineshape models, which can introduce considerable inaccuracies. To overcome this challenge, here we propose to exploit another relevant property of 2DES, i.e., the possibility of tracking the dephasing dynamics directly in the time domain by following the temporal decay of a signal related to the presence of an electric field on the nanoparticles' surface. While the dynamical information determined in the frequency and time domains is formally equivalent, being related through a Fourier transform relationship, the direct measurement of dephasing in the time domain avoids the complications introduced by inhomogeneous broadening, offering a more accurate and practical route to characterizing ultrafast dynamics in ensemble plasmonic systems.

To this purpose, we employed 2DES combined with a simple forced damped harmonic oscillator model to observe and rationalize the initial coherent dynamics occurring within the first tens of femtoseconds in colloidal solutions of gold NRs, during which the plasmonic resonance remains coherent and has not yet undergone dephasing. This work builds on our previous study, where we analyzed ultrafast dynamics in an analog system in the time range >45 fs after ultrafast plasmon dephasing, by synergistically employing pump-probe and 2DES.²⁹ By focusing on the initial coherent dynamics, we aim to complete and generalize the understanding of ultrafast plasmonic behavior in gold NRs.

2. Experimental section

2.1 Samples preparation

The samples under investigation consist of colloidal suspensions of Au NRs with different aspect ratios (ARs) (see also ESI, Fig. S1†). The synthesis consists of three main steps, performed separately: (i) preparation of the seeds (nucleation), (ii) growth, and (iii) oxidation.^30,31 All the solvents and reactants were obtained from Sigma-Aldrich (Merck KGaA, Darmstadt, Germany) and used as received without further purification.

2.1.1 Preparation of the seeds. In a water bath at 27–30 °C, 4.92 μL of gold(III) chloride (HAuCl₄, 253.9 mM) and 4.7 mL of cetyl trimethyl ammonium bromide (CTAB, 100 mM) were added to 20 μL of MilliQ water. The mixture was stirred at 350 rpm until the gold salt dissolved. Then, 300 μL of sodium borohydride (NaBH₄, 10 mM) was quickly injected under vigorous stirring (1200 rpm). After 10–20 seconds, the solution was stirred at 500 rpm and kept at 27–30 °C for 2 hours before use.

2.1.2 Growth. In a water bath at 27–30 °C, 190 μL of hydrochloric acid (HCl, 1 M), 19.7 μL of HAuCl₄ (253.9 mM), and 80 μL of MilliQ water were added to 10 mL of CTAB solution (100 mM) and stirred until the gold salt dissolved. Then, 120 μL of silver nitrate (AgNO₃, 10 mM) was added, followed by 100 μL of ascorbic acid (100 mM). Next, 24 μL of the seed solution was added, and the growth mixture was stirred at 500 rpm for 30 minutes and left overnight. The next day, the solution was centrifuged twice and redispersed in MilliQ water.

2.1.3 Oxidation. To adjust the AR and to blue-shift the longitudinal surface plasmon resonance (LSPR), an oxidizing solution of HAuCl₄ (1 mM) and CTAB (100 mM) was added dropwise into the gold NR solution under magnetic stirring. After 1 hour, the solution was centrifuged twice to remove excess gold salt and redispersed in water and CTAB (15 mM). The amount of oxidizing agent was controlled based on the desired plasmon peak shift, assuming a linear dependence between the peak shift and Au³⁺ concentration.

2.2 2DES experiments

The 2DES experiments were conducted using a 3 KHz Ti:Sapphire Coherent® Libra laser system coupled with a commercial NOPA (Light Conversion® TOPAS White). A compression of about 10 fs at the sample position was achieved through a prism compressor coupled with a Fastlite Dazzler pulse shaper for fine adjustment. The final pulse duration was optimized through FROG measurements (Fig. S2†). In each experiment, the pulse energy at the sample position is reduced to about 7 nJ per pulse by a broadband half-waveplate/polarizer system.

The 2DES experiment relied on the passively phase stabilized setup, where the laser output was split into four identical phase-stable beams (three exciting beams and a fourth beam further used as Local Oscillator, LO) in a BOX-CARS geometry using a suitably designed 2D grating. Time delays between pulses were modulated using pairs of four CaF₂ wedges. Each pair of wedges included one mounted on a translation stage to adjust the medium's thickness crossed by the exciting beam, providing a temporal resolution of 0.07 fs. Delay times t₁ (coherence time between the first and second pulse), t₂ (population time between the second and third pulse), and t₃ (rephasing time between the third pulse and the emitted signal) were defined. The experiment involved defining rephasing and non-rephasing time intervals for recording the signal, which could be achieved by manipulating the pulse sequence. The combination of rephasing and non-rephasing contributions allowed for the generation of purely absorptive maps.²⁶ The experiment resulted in a 3D array of data that describes the evolution of 2D frequency–frequency correlation maps as a function of t₂. In each map, the excitation (ω_exc) and detection (ω_det) frequency axes correspond to the Fourier transform of t₁ and t₃, respectively.²⁶ The so-called 2D maps can be extracted by slicing this signal at fixed values of t₂. These maps can be viewed as frequency–frequency correlation maps that evolve as function of t₂.²⁶

The population time t₂ was scanned from 0 to 200 fs with 3 fs time steps, while the coherence time t₁ was scanned from 0 to 80 fs with steps of 2 fs for the rephasing experiments and from 0 to 64 fs with steps of 2 fs for the non-rephasing experiments. Each experiment was conducted a minimum of five times, and the responses were averaged to ensure reproducibility. For a more detailed description of the setup, see ref. 32.

3. Results and discussion

3.1 2DES characterization

Fig. 1 shows the purely absorptive 2D maps extracted at selected values of t₂ for three representative NR samples that have different AR. The energy of the longitudinal surface plasmon resonance (LSPR) scales linearly with AR, and in our samples, this energy ranges from about 1.99 to 2.13 eV, as shown in panels (a, d, and g). For each sample, the laser spectrum is tuned to cover almost exclusively the LSPR. Additional maps for NRs with different AR are reported in ESI (Fig. S2).†

Fig. 1 Experimental results obtained for three different NR samples with the LSPR located at: (a–c) 1.99 eV; (d–f) 2.07 eV; and (g–i) 2.13 eV. (a, d and g) Extinction spectra of the NRs suspensions (black line) and spectral profiles of the laser spectrum used for 2DES measurements (orange area). (b, e and h) Corresponding purely absorptive 2DES maps (real signal) at selected values of population time t₂. Gray dashed lines serve as a visual guide to emphasize the nodal lines in the dispersive-like signals observed at early times. The signal shape changes significantly from earlier to later times: at later times, the signal is influenced by broadening and redshift caused by electron–electron scattering, while at earlier times the signal is dominated by coherent interactions with the electric field generated on the nanoparticle's surface. This behavior is more evident in plots (c, f and i), which display the projection of the 2D maps onto the detection axis as a function of t₂. The yellow and green boxes indicate the time regions dominated by electron–electron scattering and coherent plasmon effects, respectively.

Fig. 1(b, e and h) reports examples of 2D maps at selected values of population time t₂ for three NRs samples characterized by different LSPR energies. Qualitatively, in all samples, a neat difference in the signal distribution can be identified between early times (t₂ < 45 fs) and longer timescales (t₂ > 45 fs). This is particularly evident in Fig. 1(c, f and i) where the projection of the 2D maps onto the detection axis as a function of t₂ is reported. According to the projection slice theorem, this is equivalent to the pump-probe spectrum obtained under the same experimental conditions.^33,34

For t₂ > 45 fs (yellow box in Fig. 1(i)), we can clearly identify two main features: a positive (red) peak and a negative (blue) peak with the same coordinate on the excitation energy axis and different detection frequencies. Both signals show an increasing amplitude with a time constant of about a hundred femtoseconds. This peculiar signal distribution and its time evolution are attributed to the nonlinear broadening and red-shift induced by the transient electronic temperature that increases as a result of electron–electron scattering, as previously observed.^28,29,35

The behavior is instead completely different at very early times (t₂ < 45 fs, green box), where the maps are dominated by a dispersive shape with an almost horizontal nodal line (dashed lines in Fig. 1(b, e and h)) and with maxima signals having nearly opposite signs with respect to the maps at longer times. This suggests that the early time dynamics is driven by a mechanism completely different from the electron–electron scattering dominating the time behavior at longer timescales. Furthermore, one can notice that, although the coordinates of the signals appearing in the maps strongly depend on the spectral profile of the exciting beam and on its overlap with the extinction spectrum of the sample, the position of the nodal line roughly follows the position of the central frequency of the longitudinal plasmon for the different samples (Fig. 1(b, e and h)).

A first physical insight into the origin of this behavior can be achieved by considering the excitation sequence in a 2DES experiment. The interaction with the first two pulses excites the plasmon resonance; at this point the electrons, and consequently the electron-driven electric field, start to oscillate coherently during t₂. If the third pulse arrives before plasmon dephasing, its interaction with the intense electric field produced by the plasmon must necessarily affect the final response. Recent studies have shown that excited plasmon resonances in plasmonic nanostructures have an intrinsic frequency-dependent phase shift relative to the exciting beam. This phase shift changes from in-phase to out-of-phase near the center resonance frequency.^36–38 Therefore, the interference between the third (probe) exciting field and the excited plasmon resonances when the third pulse interacts before the plasmon has dephased might explain the dispersive lineshape, how the position of the nodal lines depends on the LSPR energy, and why this behavior persists only for the first tens of fs.

3.2 The forced damped harmonic oscillator model

A simple way to support this interpretation is to start from the forced damped harmonic oscillator model recently used to describe the enhanced electric field on the surface of a plasmonic nanoparticle. This model describes the displacement of free charges on the particle surface d(ω,t) by introducing a damped harmonic oscillator with a characteristic frequency ω₀ and a damping coefficient Γ, driven by an external electric field E_ext(ω,t) = E₀(ω)cos(ωt) with frequency ω.^39,40

In the quasistatic approximation,⁴¹ and for damping coefficients much smaller than ω₀, one can derive the equation of motion of displacement as a function of the external field frequency ω:⁴⁰

d(ω,t) = A(ω)E₀(ω)cos(ωt + Φ(ω)) (1)

where the amplitude A and the phase Φ of the periodic displacement depend on ω (Fig. 2):

Fig. 2 Results obtained from the damped harmonic oscillator model. (a) Ratio between the amplitude of the electric field on the nanoparticle's surface E_surf and E₀ (assumed to be constant for each frequency: E₀(ω) = 1). (b) Phase of the displacement Φ(ω) as a function of the frequency ω (eqn (2)). (c) Frequency dependence of the signal S(ω) calculated using eqn (5), assuming E₀(ω) = 1 constant for each frequency. In all the (a–c) panels, traces obtained using different values of dephasing time are reported in different colours. (d) Comparison between the experimental signal (blue dot) and the signal calculated with eqn (5) (solid red line) using the laser profile in Fig. 1(g) to estimate the frequency dependence of E₀(ω). The experimental signal refers to the data shown in Fig. 1(h) and was obtained by integrating the 2D map at t₂ = 6 fs along the excitation axis. The parameters used to generate the graphs are reported in Table S1 of the ESI.†

In eqn (2), K is a constant factor that can be easily evaluated using well-known physical parameters:

where e is the elementary charge, m the mass of the electron, ε_∞ the high-frequency dielectric function of gold,⁴² ε_m the dielectric constant of the medium (water, in our case), ε₀ the vacuum permittivity and n^(x) the depolarization factor along the longitudinal axis (x), which is a geometrical factor depending on the three axes a,b,c of the ellipsoid which approximate the geometry of the NR (Fig. S1†).

One can easily see that in the resonant condition, thus when ω = ω₀, the amplitude of d reaches its maximum and the phase shift Φ between d and E_ext is equal to π/2. When ω ≠ ω₀, i.e. in off-resonance conditions, the oscillator can still be activated but both the phase Φ and the amplitude A show a significant dependence on the detuning.⁴⁰ This dependence must be carefully considered when comparing the model results with the experimental data, as will be discussed below.

Finally, considering the electron density of gold, ρ, the total electric field produced on the nanoparticle's surface E_surf is obtained by summing the electric field from bound and free charges in the ellipsoid:⁴⁰

where the last term on the right, due to free charges, is the dominant contribution.

The relevant aspect of this derivation is that the total electric field generated on the nanoparticle's surface has an amplitude comparable to that of the external field, allowing them to effectively interfere with each other (Fig. 2(a)).

If we excite the nanoparticle with a fs pump pulse, an electric field described by E_surfe^−t/τ will be generated on its surface, with τ = 2h/Γ the dephasing time of the plasmon. In the model mentioned above, the amplitude of this field is predicted to be similar to that of the external exciting field. Therefore, in the 2DES experiment, after the first two pulses have activated the plasmon resonance, it is expected that when the third pulse addresses the nanoparticle before the plasmon dephasing, it will interfere with the electric field generated on its surface. Assuming that this interference effect is the major contribution to the non-linear response of the system before the plasmon dephasing (and thus before the hot electron dynamics start developing) the intensity of the signal S(ω,t) at early times, which is proportional to the square modulus of the field amplitude, can be expressed as follows:

S(ω,t) ∝ (|(E_surf(ω,t) + E_ext(ω,t)|² − |E_ext(ω,t)|²) (5)

This signal basically represents the variation of electric field intensity on the surface due to the interference with respect to the external electric field. The frequency dependence of S(ω,t) calculated with eqn (5) is plotted in Fig. 2(c) where an external field with an amplitude constant for all the frequencies (E₀(ω) = 1) has been used in first approximation. A dispersive shape with a change of sign at ω ∼ω₀ is found, as a result of the phase trend depicted in Fig. 2(b).

For a better comparison with experimental results, the frequency dependence of the exciting external field must be taken into account, since, as already discussed, both the phase and the amplitude in eqn (2) show a significant dependence on the detuning. To this aim, we modelled E₀(ω) with the experimental spectral laser profile. An example of the results obtained is reported in Fig. 2(d) and compared with the experimental data. When looking at the experimental 2DES maps, the signals appear mostly symmetrical along the excitation frequency axis, suggesting that, under the current experimental conditions, there is not a clear dependence on t₁ (and ω_exc). Therefore, for ease of visualization, rather than considering the whole 2D signal, in Fig. 2(d) we report the projection of the real part of the absorptive 2D map onto the detection axis, as in Fig. 1(c, f and i).

The comparison confirms that the model captures the dispersive trend observed in all our experiments exceptionally well. Furthermore, the experimental signal can be reproduced satisfactorily only if a suitable dephasing time is used to estimate the parameters appearing in eqn (5) (in this case, τ = 8 fs), a value in good agreement with the estimate obtained through linewidth analysis of the extinction spectrum. This suggests that, in principle, it should be possible to estimate τ directly by fitting the experimental signal with eqn (5).

However, the signal also strongly depends on the laser profile, and several additional mechanisms can contribute at early times (including coherent artifacts and pulse overlap effects), making the estimation of τ by a direct fitting procedure not fully reliable.

A much more robust procedure is presented in Fig. 3. Let us again consider the projections of the real part of the absorptive 2D maps on the detection axis as a function of t₂ shown in Fig. 1(c, f and i). As already discussed, looking at the time behavior, we can assume that the signal at early times is induced only by coherent effects, i.e. the interference of the third pulse with the plasmon. Instead, the signal at t₂ ≫ τ is induced only by the dynamics of the hot electrons. Therefore, the resulting signal, at each population time, can be fitted as a linear combination of these two limit cases denoted by A (early time signal) and B (long time signal). This was accomplished using the expression: k_a × A + k_b × B, where k_a and k_b are the parameters that quantify the contribution of A and B to the total signal, respectively. In this way, we can estimate the contribution of coherent effects at each t₂ and obtain a dynamic trend that actually reflects the dephasing of the plasmon, as illustrated in Fig. 3(b).

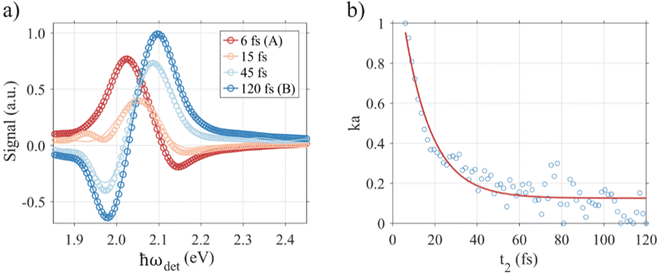Fig. 3 (a) Projections of the signal at selected values of t₂. The trace at t₂ = 6 fs (trace A, dark red) and at t₂ = 120 fs (trace B, dark blue) corresponds to signals assumed to be induced exclusively by plasmon field interference and hot electron dynamics, respectively. (b) Plasmon dephasing's dynamics expressed as k_a vs. t₂, where k_a is estimated by fitting the signal at each t₂ with the equation: k_a × A + k_b × B, with k_a and k_b being the free parameters which quantify the contribution of A and B, respectively. The exponential fit returns a dephasing time of τ = 13.2 fs. Data refer to the sample in Fig. 1(g–i).

To ensure the robustness of this analysis, the same procedure was applied to different samples with varying AR. The results are shown in Fig. 4, where the estimated dephasing times are converted into damping coefficients and plotted against the LSPR energy. In fact, it is anticipated that the damping coefficient (dephasing time) increases (decreases) for NRs with lower AR, as the LSPR energy approaches the interband transitions in gold, whose onset occurs at approximately 1.8 eV. This is a consequence of the contribution of interband scattering to the total damping coefficient Γ.⁴³ The trend illustrated in Fig. 4 for the estimated damping coefficients accurately reflects both qualitatively and quantitatively the behavior previously observed through linewidth measurements of single gold NRs of the same dimensions.⁴³ We want to emphasize that, to our knowledge, this is the first time that 2DES has been used to measure plasmon dephasing time in colloidal solutions of nanoparticles directly in the time domain.

Fig. 4 Estimated damping coefficients Γ as a function of LSPR's energy. Γ values are calculated from the dephasing times τ extracted from the 2DES data. The error bars are estimated from repeated measurements.

In principle, the methodology derived here to extract the dephasing times from 2DES maps could also be applied to (1D) pump-probe measurements. However, because of the peculiar almost colinear excitation geometry and the nonbackground-free signal, pump-probe measurements are often affected by a higher scattering level, making it challenging to observe clear sub-50 fs time dynamics.

4. Conclusion

In conclusion, a simple model based on a damped harmonic oscillator has been adapted to explain the shape of the 2DES maps in the first few tens of femtoseconds, which is directly influenced by the ultrafast dephasing time of the plasmon resonance. According to this model, the electric field on the nanoparticle's surface has an intensity similar to the exciting laser pulses until the plasmon dephases. This allows efficient interference, resulting in a dispersive shape in 2D maps with a characteristic change of sign along the detection frequency axis. To avoid the challenges of directly analyzing the signal's shape at early times, which can be distorted by pulse overlap artifacts, an effective method to estimate the dephasing is to measure the time it takes for the signal to transition from the shape induced by the coherent plasmon to that solely due to the hot electron dynamics, once the plasmon has completely dephased. This method, when applied to different NRs samples, produced results in excellent agreement with theoretical predictions and other indirect measurements. This confirms that 2DES, complemented by the described analysis protocol, represents an exceptionally valuable tool with the unforeseen capability of providing a direct estimate of the dephasing time of plasmon resonances in ensembles of colloidal nanoparticles.

Author contributions

Federico Toffoletti: investigation; formal analysis; validation; visualization; writing – original draft. Elisabetta Collini: conceptualization; validation; supervision; resources; funding acquisition; writing – review and editing.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and in the ESI.†

Conflicts of interest

The authors confirmed that this article has no conflict of interest.

Acknowledgements

This research was funded by the European Union – Next Generation EU, Mission 4 Component 1 CUP C53D23003810006 (PRIN project ‘CHI-EP’) and supported by the P-DiSC#04BIRD2022-UNIPD Grant.

References

1. A. A. Maradudin, J. R. Sambles and W. L. Barnes, Modern Plasmonics, Elsevier, Amsterdam, 2014, vol. 4.
2. M. Kauranen and A. V. Zayats, Nat. Photonics, 2012, 6, 737–748.
3. G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887.
4. V. Amendola, R. Pilot, M. Frasconi, O. M. Maragò and M. A. Iatì, J. Phys.: Condens. Matter, 2017, 29, 203002.
5. M. Moskovits, Rev. Mod. Phys., 1985, 57, 783–826.
6. J. P. Camden, J. A. Dieringer, J. Zhao and R. P. Van Duyne, Acc. Chem. Res., 2008, 41, 1653–1661.
7. X. Huang and M. A. El-Sayed, Alexandria J. Med., 2011, 47, 1–9.
8. M. Li, S. K. Cushing and N. Wu, Analyst, 2015, 140, 386–406.
9. J. Divya, S. Selvendran, A. S. Raja and A. Sivasubramanian, Biosens. Bioelectron.:X, 2022, 11, 100175.
10. T. W. Ebbesen, A. Rubio and G. D. Scholes, Chem. Rev., 2023, 123, 12037–12038.
11. R. Bhuyan, J. Mony, O. Kotov, G. W. Castellanos, J. Gómez Rivas, T. O. Shegai and K. Börjesson, Chem. Rev., 2023, 123, 10877–10919.
12. M. S. Tame, K. R. McEnery, Ş. K. Özdemir, J. Lee, S. A. Maier and M. S. Kim, Nat. Phys., 2013, 9, 329–340.
13. P. Törmä and W. L. Barnes, Rep. Prog. Phys., 2015, 78, 013901.
14. J. Lee, D.-J. Jeon and J.-S. Yeo, Adv. Mater., 2021, 33, 2006606.
15. S. Pres, B. Huber, M. Hensen, D. Fersch, E. Schatz, D. Friedrich, V. Lisinetskii, R. Pompe, B. Hecht, W. Pfeiffer and T. Brixner, Nat. Phys., 2023, 19, 656–662.
16. N. Peruffo, F. Mancin and E. Collini, Adv. Opt. Mater., 2023, 11, 2203010.
17. S. V. Boriskina, T. A. Cooper, L. Zeng, G. Ni, J. K. Tong, Y. Tsurimaki, Y. Huang, L. Meroueh, G. Mahan and G. Chen, Adv. Opt. Photonics, 2017, 9, 775–827.
18. W. Jiang, H. Hu, Q. Deng, S. Zhang and H. Xu, Nanophotonics, 2020, 9, 3347–3356.
19. T. Zhao, J. W. Jarrett, J. S. Johnson, K. Park, R. A. Vaia and K. L. Knappenberger Jr, J. Phys. Chem. C, 2016, 120, 4071–4079.
20. Q. Sun, S. Zu and H. Misawa, J. Chem. Phys., 2020, 153, 120902.
21. Y. Nishiyama, K. Imaeda, K. Imura and H. Okamoto, J. Phys. Chem. C, 2015, 119, 16215–16222.
22. P. Yang, J. Zheng, Y. Xu, Q. Zhang and L. Jiang, Adv. Mater., 2016, 28, 10508–10517.
23. D. A. Zimin, I. Cherniukh, S. C. Böhme, G. Rainò, M. V. Kovalenko and H. J. Wörner, arXiv, 2023, preprint, arXiv:2312.11727,  DOI:10.48550/arXiv.2312.11727.
24. K.-F. Wong, W. Li, Z. Wang, V. Wanie, E. Månsson, D. Hoeing, J. Blöchl, T. Nubbemeyer, A. Azzeer, A. Trabattoni, H. Lange, F. Calegari and M. F. Kling, Nano Lett., 2024, 24, 5506–5512.
25. M. Cho, Two-Dimensional Optical Spectroscopy, CRC Press, Boca Raton, FL, 2009.
26. E. Fresch, F. V. A. Camargo, Q. Shen, C. C. Bellora, T. Pullerits, G. S. Engel, G. Cerullo and E. Collini, Nat. Rev. Methods Primers, 2023, 3, 84.
27. D. M. Jonas, Annu. Rev. Phys. Chem., 2003, 54, 425–463.
28. A. Lietard, C. S. Hsieh, H. Rhee and M. Cho, Nat. Commun., 2018, 9, 891.
29. F. Toffoletti and E. Collini, J. Phys. Chem. Lett., 2024, 15, 339–348.
30. L. Scarabelli, A. Sánchez-Iglesias, J. Pérez-Juste and L. M. Liz-Marzán, J. Phys. Chem. Lett., 2015, 6, 4270–4279.
31. J. Rodríguez-Fernández, J. Pérez-Juste, P. Mulvaney and L. M. Liz-Marzán, J. Phys. Chem. B, 2005, 109, 14257–14261.
32. L. Bolzonello, A. Volpato, E. Meneghin and E. Collini, J. Opt. Soc. Am. B, 2017, 34, 1223–1233.
33. J. D. Hybl, A. A. Ferro and D. M. Jonas, J. Chem. Phys., 2001, 115, 6606–6622.
34. M. Khalil, N. Demirdöven and A. Tokmakoff, Phys. Rev. Lett., 2003, 90, 047401.
35. D. Finkelstein-Shapiro, P.-A. Mante, S. Sarisozen, L. Wittenbecher, I. Minda, S. Balci, T. Pullerits and D. Zigmantas, Chem, 2021, 7, 1092–1107.
36. K. Lodewijks, W. Van Roy, G. Borghs, L. Lagae and P. Van Dorpe, Nano Lett., 2012, 12, 1655–1659.
37. W.-Y. Chen, C.-H. Lin and W.-T. Chen, Nanoscale, 2013, 5, 9950–9956.
38. V. G. Kravets, F. Schedin, A. V. Kabashin and A. N. Grigorenko, Opt. Lett., 2010, 35, 956–958.
39. J. Zuloaga and P. Nordlander, Nano Lett., 2011, 11, 1280–1283.
40. T. Hao and Q. Li, Curr. Opt. Photonics, 2023, 7, 449–456.
41. C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley-VCH, Germany, 1983.
42. M. B. Raschke, S. Berweger and J. M. Atkin, in Plasmonics: Theory and Applications, ed. T. V. Shahbazyan and M. I. Stockman, Springer, Heidelberg, 2013, pp. 237–281.
43. C. Sönnichsen, T. Franzl, T. Wilk, G. von Plessen, J. Feldmann, O. Wilson and P. Mulvaney, Phys. Rev. Lett., 2002, 88, 077402.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00917g

---