Structurally engineered heat loss suppression in nanogap-aligned nanowires for power efficient heating

Abstract

Thermal management at the nanoscale offers potential advancements in power-efficient geometrical design; however, both conduction- and convection-based structural optimization have yet to be fully investigated due to dimensional limitations. In this study, we analytically designed a structured configuration within a regime comparable to the mean free path of heat-transferring carriers. The optimally designed nanowire configuration, featuring aligned nanowires with narrow gaps (∼22 nm), was designed based on the analytic calculation. A tailored nanofabrication technique enabled a reliable geometrical parametric study, experimentally validating the proposed theoretical design. Finally, by engineering both conduction heat loss and air molecular interactions in convective heat loss at the nanoscale, we suggest an optimized heater for atmospheric conditions based on scaling factor-induced thermophysical properties, surpassing the efficiency of traditional film-based heaters.

---

Introduction

Thermal management of heating elements is an important design parameter for energy efficiency in various electronics, such as gas sensors,^1,2 IR emitters,³ and microfluidic systems,^4,5 where low power consumption is essential. With the ongoing miniaturization of electronic devices, the increasing use of nanomaterials-based devices requires tailored heater designs based on their extraordinary heat transfer mechanisms at the nanoscale.^6,7 In particular, thermophysical regimes influenced by geometrical scaling, such as surface scattering^8,9 and molecular collisions,¹⁰ have continuously offered potential advantages in power-efficient geometrical design. However, reported efforts to improve heat transfer paths at the nanoscale have been limited due to experimental constraints at this scale. Specifically, while the suppression of conduction heat loss is widely utilized, convection influenced by the arrangement of nanostructures has not been harnessed effectively in conjunction.

In terms of thermal conduction, when materials are scaled down to the nanoscale, comparable to the mean free path of heat-transferring carriers such as electrons and phonons, the resulting surface scattering effectively suppresses heat loss. Additionally, the inherently small cross-sectional area of nanomaterials further minimizes heat loss, making them highly effective when considered as low-power heating elements. Indeed, the use of nanomaterials in thermal management has facilitated the development of power-efficient heating elements, which successfully demonstrated low-power gas sensing electronics.^11–13 Nevertheless, convection has often been overlooked in these designs, primarily due to concerns about its potential to enlarge the air conductive heat loss.

With respect to thermal convection, as the size decreases, the increased surface-to-volume ratio induces the thinner thermal boundary and greater heat loss path around the exposed surface areas, negatively affecting power-efficient heating. Although heat transfer based on molecular collisions decreases due to the reduced collision frequency in smaller characteristic length regimes,^14,15 these complex molecular interactions have not been effectively applied to heating components in the transition regime (0.1 < Knudsen number (Kn) < 10). In this context, convective heat transfer based on geometrical scaling has been primarily explored for individual nanostructures,^16,17 with experimental studies limited to the sub-micro scale and conditions with an extended air mean free path through pressure control.^10,18–20 Meanwhile, advanced geometrical designs that modify arrangements have been proposed to further suppress molecular collisions for more efficient thermal management.²¹ Specifically, structures arranged with narrow gaps comparable to the air mean free path can significantly suppress molecular diffusion, resulting in reduced effective heat loss in the assembly of structure. However, this arrangement of structures to restrict convective heat transfer has only been explored at the microscale under vacuum conditions, which artificially extend the air mean free path at that scale.¹⁹ These partially explored heating configurations, aimed at suppressing thermal conduction at the nanoscale and convective heat transfer through geometric arrangements, have yet to be fully realized, indicating that engineered design and demonstration are required for optimization.

Here, the optimized efficient heating architecture at the nanoscale is designed to address both thermal conduction and convective heat loss for low-power heating under atmospheric conditions. In pursuit of this goal, a highly aligned arrangement of thin nanowire (<100 nm) with extremely narrow nanogaps (<30 nm), comparable to both electron and air mean free path of heat-transferring carriers, is proposed. An analytic model was established to predict the geometry-dependent conductive and convective heat loss in heating components, and experimental validation was conducted using a reliable fabrication method of platinum (Pt) nanowire array. Ultimately, the optimized heating configuration was successfully demonstrated by parametric study, exhibiting strong agreement with the developed analytic model. The proposed design presents more efficient heating than traditional thin film heater even at the same joule-heating current density.

Result and discussion

The proposed heating structure, nanowire array aligned with nanogap, is schematically shown in Fig. 1a. The structure has a suspended configuration between fixed electrodes on both sides of the nanowires, enabling efficient joule heating by only inducing axial conductive heat loss to the substrate, following a conventional beam-type heating structure. For a fair comparison, the investigation of increased heating efficiency based on geometry was performed at the same current density as the conventional thin-film heating structure. In other words, slicing the same volume of the film into nanosized sections and placing them closer together within narrow gap is expected to enhance heating efficiency. In the joule-heating of structures, convective and conductive heat loss are the main concern, excluding radiative heat loss, as the radiation is negligible at typical microheater application target temperatures of 200–300 °C due to the low emissivity of Pt (∼0.05).²²

Fig. 1 (a) Schematic illustration of the optimal heating configuration for nanogap-aligned nanowires and a conventional film-shaped beam heater (bottom left). (b) Schematic diagram showing changes in thermal conduction based on structural dimensions at the same current density (i) changes in beam conduction for nanosized materials and (ii) changes in air conduction when nanosized materials are aligned with nanogaps (Q_cond: conductive heat transfer, k: thermal conductivity, A_c: cross-sectional area of the beam, T: temperature, Q_conv: convective heat transfer, h: convective heat transfer coefficient, A_s: exposed surface area of the material).

First, conductive heat (Q_cond), or beam conduction, is transferred to the substrate along the axial direction of the beam through the electrodes and is proportional to the thermal conductivity (k) and cross-sectional area of the beam (A_c) (Fig. 1b(i)). As mentioned earlier, in materials smaller than 100 nm in thickness, surface scattering of heat-transferring carriers, electrons in metals, becomes more intense. This increased surface scattering raises electrical resistivity, which is directly proportional to thermal resistivity, thereby reducing beam conduction.

Second, convective heat (Q_conv) is transferred from the material surface to the surrounding air (Fig. 1b(ii)). As the material size decreases, convective heat transfer driven by bulk fluidic motion decreases, while heat transfer due to air molecular interactions increases.^10,18,23 Particularly in the high Knudsen number regime (Kn > 0.1), thinner effective thermal boundaries caused by surface interactions lead to sharp temperature gradients at the surface, enhancing overall heat transfer in nanosized material surfaces.^18,24 However, when nanosized materials are placed close to each other, comparable to the air mean free path (λ_air), molecular interactions within each other's thermal boundaries can be suppressed, reducing the increased convective heat transfer coefficient.²¹ In this regard, designing geometrical configurations with narrow gaps between nanostructures can effectively mitigate beam and air conduction heat loss, resulting in improved thermal management for the optimization of heating efficiency.

In the optimization of joule-heating configuration, consideration of heat loss alongside the heating length is necessary, as both beam conduction and air conduction are significantly influenced by the axial length. Under the steady state condition of fixed room temperature at both ends of the electrodes, the joule-heated beam exhibits a parabolic temperature profile.²³ The temperature along the nanowire's longitudinal direction, depending on the operating power, can be calculated using the steady-state thermal equilibrium equation (eqn (1)).²⁵

Here, Q represents the generated heat, h is the thermal convection coefficient, A_s is the surface area, T is the local temperature along the wire, T₀ is the ambient temperature, k is the thermal conductivity, A_c is the cross-sectional area, and x is the distance away from the film central point in an axial direction. Consequently, the necessary electrical power (hereafter, operating power) to reach an average beam temperature of 100 °C at 760 Torr for a 50 nm-thick Pt thin film is calculated as a function of length (Fig. 2a and ESI Fig. S1†). In shorter lengths, due to rapid temperature changes per unit length, most of the total power loss is attributed to beam conduction. As the length increases, the exposed surface area of the beam grows, making convective heat loss the dominant factor. Ultimately, minimal power consumption for achieving the same temperature is reached by balancing conduction and convection at an optimal heating length.

Fig. 2 (a) Operating power calculation according to Pt film length, with schematics illustrating the dominant heat loss paths in conduction (left) and convection (right) for different lengths. (b) Measured electrical resistivity and thermal conductivity of Pt nanowires compared to films. (c) Calculated convective heat transfer coefficient with respect to characteristic length at 760 Torr. (d) Total convective coefficient ratio of the array depending on the gap between materials. Expected power consumption trends when (e) thermal conduction decreases and (f) thermal convection decreases.

We further established an analytic model to account for the variation in the heat transfer coefficient at the nanoscale. Based on initial experimental data across different dimensions and the two-layer model in high Knudsen number regime,^19,26 the conductive and convective heat transfer coefficients are calculated. First, in terms of conductive heat transfer, thermal conductivity was calculated based on electrical resistivity measurements using the Wiedemann–Franz law²⁷ (Fig. 2b). The reduced thermal conductivity, observed when the thickness of the film and the characteristic length (D) of the nanowire decreased below 100 nm, was implemented. Here, for analytic calculation, the defined characteristic length and the structural parameter are shown in ESI Fig. S2.†

Next, the convective heat transfer coefficient for nanosized materials in the transition regime at atmospheric pressure is expressed as h = Nu·k_air/D. The Nusselt number (Nu) for Pt is calculated in the transition regime, considering both ballistic transport and diffusion, based on an experimentally determined slip length.^18,20 Air conductivity (k_air) is used as 0.0259 W m⁻¹ K⁻¹.^10,28 As a result, for nanosized materials at room temperature, the convective heat transfer coefficient increases as the characteristic length decreases, due to diffusion-dominant molecular interactions within the thinner thermal boundary layer (Fig. 2c). Then, as the gap between the material arrays decreased, the convective heat transfer coefficient was calculated as a ratio compared to arrays spaced far enough apart to avoid mutual influence (Fig. 2d). Based on the two-layer model,^18,19 in the continuum layer outside the material surface, air molecular collisions are dominant. When the continuum layers of adjacent two wires become close enough to overlap, we assumed that heat loss path is blocked due to molecular collisions between them, and the total convective heat transfer coefficient for the array was decreased accordingly (ESI Fig. S3†). Consequently, the total convective heat transfer coefficient decreases sharply as the gap narrows, particularly when it falls below 2λ_air.

Assuming that reduced thermal conductivity of the metal and air conductivity is applied for heating film, power consumption according to the heating length is expected to follow as shown in Fig. 2e and f. As the conductive heat loss through the nanowires axial direction decreases, the dominant beam conduction at shorter lengths is expected to decrease, leading to reduced power consumption (Fig. 2e). On the other hand, as air conduction decreases, resulting in lower convective heat transfer, the heat loss at longer lengths is anticipated to diminish (Fig. 2f). Note that the conductive heat transfer coefficient, influenced by the characteristic length, also affects the exposed heat loss path due to the changed surface area. To achieve an optimized heating component, an analytic model was developed that takes these factors into comprehensive consideration.

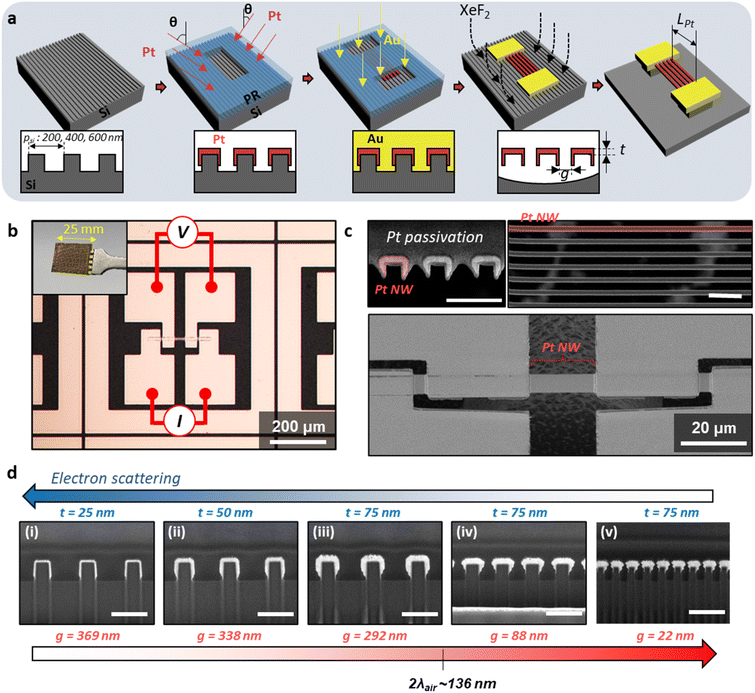
To experimentally validate the developed analytic predictions, we employed a reliable method to fabricate nanowire arrays with precisely controlled gap and size. The fabrication process is based on physical vapor deposition (PVD) on a nanograting film with a predefined period, previously developed to realize a suspended nanowire array, nanolene,²⁹ as schematically shown in Fig. 3a. First, Si nanograting substrates with different periods (200 nm, 400 nm, and 600 nm) were prepared using krypton fluoride (KrF) lithography and a subsequent reactive ion etching (RIE) process. For the 200 nm nanograting substrate, we additionally applied spacer lithography³⁰ and size-reduction method³¹ to achieve a linewidth below 100 nm, as the resolution of KrF lithography is limited to 150 nm. By starting with different periods of Si substrate, the gap between the nanowires was precisely controlled. Next, UV lithography is used for pattering the area where the nanowires would be, and Pt was obliquely deposited onto the substrate resulting in a C-shaped cross-section. Following deposition, a lift-off process was implemented to remove the patterned photoresist, leaving Pt nanowires only in the areas defined by the photoresist. The characteristic length of the nanowires was controlled by adjusting the deposition thickness and angle. Subsequently, using the conventional lift-off process, gold (Au) electrodes with a chromium (Cr) adhesion layer were formed on the patterned areas on both ends of the Pt nanowires. Here, the surface roughness of Pt as-deposited was measured as S_q = 0.431 nm using atomic force microscopy (ESI Fig. S4†), and we conducted experiment under consistent conditions to verify the analytical design without the influence of surface roughness. Finally, the Si substrate was dry-etched using xenon difluoride (XeF₂) gas to make the nanowire array suspended in the air.

Fig. 3 (a) Schematic of the reliable nanowire array fabrication process. (b) Optical microscopic image and photograph of the fabricated nanowire array. (c) SEM images of the suspended Pt nanowires: cross-sectional view (upper left, scale bar: 500 nm), top view (upper right, scale bar: 1 μm), and projected view (bottom). (d) SEM cross-sectional images of nanowires on a Si nanograting substrate, fabricated with varying gaps and sizes for parametric studies (scale bar: 500 nm).

The fabricated nanowire array was visually inspected using an optical microscope (Fig. 3b) and scanning electron microscope (SEM) (Fig. 3c). Four electrodes were configured for each nanowire array to perform 4-point probing, allowing for accurate measurement of the induced electrical power on the nanowires while eliminating the effects of contact resistance. The fabricated nanowire arrays were reliably formed with consistent dimensions over a large area of the Si substrate (inset, Fig. 3b). A cross-sectional image was obtained by cutting the nanowire array cross-section after sputtering an additional Pt layer inside the SEM as a passivation layer to protect against the ion beam (Fig. 3c, upper left). The nanowires, featuring high mechanical bending stiffness due to their inherent C-shaped cross-section, remained perfectly separated, even at spacings of less than 100 nm (Fig. 3c, upper right). Note that this C-shaped configuration of nanowires offers advantages in mechanical stability, ensuring reliable device applications through thermal and mechanical durability tests.^29,32

Using this reliable fabrication method, we realized nanowires with specific sizes and gaps to independently compare beam conduction and air conduction, ultimately optimizing heat loss. The actual cross-sections of the fabricated nanowire arrays, which enable a parametric study, are shown in Fig. 3d. By forming nanowires with different thicknesses on a fixed period of 600 nm, the size-dependent beam conduction, due to surface scattering, can be verified. For gaps larger than 200 nm, the effect of air conduction on the gap size is expected to be negligible. Subsequently, by controlling the gap between nanowires on Si substrates with different periods of Si nanograting substrate, while maintaining the same thickness of Pt, the gap-dependent air conduction effect can be studied under the same current density. By achieving gaps between nanowires smaller than twice the air mean free path (∼136 nm),¹⁵ suppressed air conduction is expected under atmospheric pressure (760 Torr).

The fabricated nanowires were electrically examined, as shown in Fig. 4a and b. For the thinnest nanowires with a thickness of 25 nm, the I–V curve demonstrates reliable electrical performance, even with a length of 100 μm, as resistance increases with length (Fig. 4a). We then compared the electrical resistivity with respect to the nanowire and film thickness (Fig. 4b). The resistivity increased proportionally to the reciprocal of the thickness, following the Fuch–Sondheimer equations,³³ which account for the increased electrical resistivity in thin films due to surface scattering. Even with the same thickness, nanowires exhibited higher electrical resistivity compared to films because of their confinement along multiple sides. We electrically measured the temperature coefficient of resistance by controlling the ambient temperature conditions and used those values to normalize the measured resistance to temperature. To clearly compare the heating efficiency with respect to the dimensions, we compared the nanowire array using the same current density, taking a 50 nm film with a width of 24 μm as the reference. Before making this comparison, we measured the cross-sectional area of the individual nanowire from the SEM images and then normalized to the same cross-sectional area (Fig. 4c). For further calculations based on the nanowire dimensional parameters, the perimeter and cross-sectional area were directly calculated from the SEM images (ESI, Fig. S5†).

Fig. 4 (a) I–V measurement data for different lengths of nanowires with a thickness of 25 nm, as shown in Fig. 3. (b) Electrical resistivity as a function of nanowire and film thickness. (c) Measured cross-sectional areas of nanowires with thicknesses of 25 nm, 50 nm, and 75 nm, along with their corresponding SEM images (measurements from three different nanowires, scale bar = 200 nm). (d) Calculated (dashed line) and measured (dots) operating power required to reach 100 °C for heaters of different lengths, using a 50 nm film with a width of 24 μm as the reference. (e) Operating power extracted from (d) at a length of 10 μm and at the length with minimum operating power.

The experimental results and analytic calculations of the operating power required to reach an average beam temperature of 100 °C as a function of length are shown in Fig. 4d and ESI Fig. S6,† corresponding to the nanowires shown in Fig. 3d(i)–d(iii). As expected in Fig. 2e, due to the increased thermal resistivity of the nanowires, beam conduction decreased, as evident from the power consumption at shorter lengths. However, as the heater length increases, the power consumption of the nanowire array with a thickness of 25 nm surpasses that of the film. This is attributed to the smaller characteristic length of the thin nanowires, which leads to increased air conduction of individual nanowire. The extracted power consumption at a length of 10 μm and at the optimal length is shown in Fig. 4e. At 10 μm-heater length, power consumption decreased in the order of the film, followed by nanowires with smaller thicknesses. However, the minimum power consumption at the optimal length was observed with a thickness of 75 nm. This suggests that simply reducing the size of nanowires to suppress beam conduction does not necessarily lead to lower power consumption, as there is an optimal thickness, compared to films, which balances the increased air conduction.

With the 75 nm thickness nanowires, we further compared the operating power required to reach 100 °C at different gaps, corresponding to the nanowires shown in Fig. 3d(iii)–3d(v). According to our analytic calculations, the effective convective heat transfer coefficient of the nanowire array decreases as the gap becomes smaller, compared to that of a single nanowire (Fig. 5a). The fabricated nanowires with smaller gaps resulted in nanowires having smaller characteristic lengths. Hence, the convective coefficient increases as the individual nanowires are made denser, since it is inversely proportional to the characteristic length. However, when the gap is reduced to below 100 nm, the effective heat transfer coefficient can become even lower. The operating power of these nanowires with a reduced convective heat transfer coefficient was compared across different lengths in both experimental data and analytic calculations (Fig. 5b). The proposed calculations, which account for the reduced convective heat transfer coefficient with respect to characteristic length and gap, exhibited strong agreement with the measurements. As predicted in Fig. 2f, the reduction in power consumption due to decreased air conduction is evidenced in longer heater lengths. This reduction is clearly confirmed in the comparison of power consumption at exceedingly long lengths, such as 500 μm, where air conduction becomes the dominant heat loss path over beam conduction (Fig. 5c and ESI Fig. S7†). The optimal power consumption for the nanowires with the same thickness occurred at a longer optimal length. This extension of the optimal length indicates that the balance point between beam conduction and air conduction has shifted due to the reduced convection. Finally, for the optimally designed nanowire thickness, gap, and length, significant agreement of the proportional increase in temperature with operating power is confirmed in both analytic calculations and experimental measurements (Fig. 5d).

Fig. 5 (a) Calculated convective heat transfer coefficient for nanowire arrays and individual nanowires with varying characteristic lengths and gaps. (b) Calculated (dashed line) and measured (dots) operating power required to reach 100 °C for heaters with different gaps, using a 50 nm film with a width of 24 μm as the reference. (c) Operating power extracted from (b) at a length of 500 μm and at the length with minimum operating power. (d) Calculated (dashed line) and experimentally measured (dots) temperature with the respect to the operating power for a nanowire array with a thickness of 75 nm, a gap of 22 nm, and a length of 100 μm.

Conclusions

In summary, we demonstrated an optimized heating configuration at the nanoscale that effectively addresses both thermal conduction and convective heat loss under atmospheric conditions. By controlling the thickness, gap, and length of the nanowires, we have analytically proposed an efficient thermal management strategy, enabling the design of optimized heating elements. Using a reliable fabrication method to precisely control the nanowire characteristic length and gap on the scale of tens of nanometers, our proposed design was experimentally validated, showing strong agreement with the calculations. This study highlights that simply reducing the size of nanowires is not sufficient for minimizing power consumption; rather, there is an optimal balance between conduction and convection that depends on the structural dimensions and arrangements of nanowires, revealing how nanowire-based heating components surpass traditional thin-film heaters. This work suggests further potential for optimizing nanoscale thermal systems, particularly in the transition regime, and provides valuable guidelines for designing energy-efficient heating structures.

Experimental methods

Experimental details for sample preparation

The Si nanograting substrate was fabricated using KrF lithography followed by RIE. For the 200 nm period Si nanograting, a spacer lithographic technique³⁰ was used with KrF lithography, followed by a cyclic size reduction process using HNO₃ and HF.³¹ The resulting structural specifications of the Si nanograting are as follows: period = 600 nm, line width = 150 nm, height = 300 nm; period = 400 nm, line width = 150 nm, height = 250 nm; period = 200 nm, line width = 60 nm, height = 200 nm. Pt was deposited using an e-beam evaporator with a 10 nm Cr adhesion layer. Oblique deposition was performed by tilting the sample inside a customized loading chamber, with the deposition angle fixed at 60°. DC sputtering (SRN-110, SORONA) was used to deposit Au electrodes (500 nm thickness) with a 10 nm Cr adhesion layer for adhesion. Negative photoresist NR9-3000PY (Futurrex, Inc.) was used for lift-off molds (=2.2 μm thick) for all patterning steps, and an MJB4 mask aligner (SUSS MicroTec) was employed for photolithography. Si substrate etching was performed using a xenon release etcher system (XERIC XeF₂, Memsstar), with the XeF₂ gas exposure time modulated to achieve the desired etch profiles at 9 mTorr pressure.

Measurement set-up

The electrical measurements for all devices were performed using the 4-point probing method to isolate the resistive changes in the nanowires and film, eliminating the influence of contact resistance between the Pt and Au electrodes. The measured resistance was normalized to resistivity using the measured values of the nanowire cross-sectional area and length from the SEM images. For the temperature coefficient of resistance (TCR) measurement, the devices were placed on a hot plate, and the resistivity of five devices was measured at different temperatures. Then, the results were then plotted linearly to extract the TCR.

Data availability

The data supporting this article are included within the manuscript and as part of the ESI.†

Author contributions

M.-S. J. conceived the idea, conducted the experiment, performed data analysis and software development, contributed to visualization, and drafted the manuscript. B.-J. K. was responsible for conducting the experiments, data curation, and formal analysis. M.-K. C. contributed to the conceptualization and experimentation. S.-Y. J. provided resources and contributed to the experimentation. M.-H. S. was responsible for methodology development and validation. J.-Y. Y. contributed to the conceptualization and methodology. J.-S. Y. and S.-H. K. provided resources for the project. J.-B. Y. inspired the research, offered guidance, supervised the project, and contributed to methodology development and manuscript review and editing. The manuscript and all figures were written and drawn through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research Foundation of Korea by the Korean government (MSIT) (NRF-2021R1A2C201071413, RS-2023-00222166).

Notes and references

1. T. Kim, W. Cho, B. Kim, J. Yeom, Y. M. Kwon, J. M. Baik, J. J. Kim and H. Shin, Small, 2022, 2204078.
2. W. Cho, T. Kim and H. Shin, Sens. Actuators, B, 2022, 371, 132541.
3. T. Mori, Y. Yamauchi, S. Honda and H. Maki, Nano Lett., 2014, 14, 3277–3283.
4. V. Miralles, A. Huerre, F. Malloggi and M.-C. Jullien, Diagnostics, 2013, 3, 33–67.
5. N. Qaiser, S. M. Khan, W. Babatain, M. Nour, L. Joharji, S. F. Shaikh, N. Elatab and M. M. Hussain, J. Manuf. Syst., 2023, 33, 035001.
6. T. Dinh, H.-P. Phan and D. V. Dao, J. Heat Transfer, 2018, 140, 072001.
7. J. C. Cuevas, Nat. Commun., 2019, 10, 1–4.
8. C. Y. Jin, Z. Li, R. S. Williams, K.-C. Lee and I. Park, Nano Lett., 2011, 11, 4818–4825.
9. J. P. Mathew, R. Patel, A. Borah, C. B. Maliakkal, T. Abhilash and M. M. Deshmukh, Nano Lett., 2015, 15, 7621–7626.
10. C. Cheng, W. Fan, J. Cao, S.-G. Ryu, J. Ji, C. P. Grigoropoulos and J. Wu, ACS Nano, 2011, 5, 10102–10107.
11. J. Yun, C. Y. Jin, J.-H. Ahn, S. Jeon and I. Park, Nanoscale, 2013, 5, 6851–6856.
12. S. H. Kim, M. S. Jo, K. W. Choi, J. Y. Yoo, B. J. Kim, J. S. Yang, M. K. Chung, T. S. Kim and J. B. Yoon, Small, 2023, 2304555.
13. K. W. Choi, M. S. Jo, J. S. Lee, J. Y. Yoo and J. B. Yoon, Adv. Funct. Mater., 2020, 30, 2004448.
14. D. Wang, Non-diffusive Heat Conduction in Nano-/Microscale Structures, University of California, Merced, 2015.
15. Z. M. Zhang, Nano/Microscale Heat Transfer, McGraw-Hill, 2007.
16. W. Kang, M. Merrill and J. M. Wheeler, Nanoscale, 2017, 9, 2666–2688.
17. N. Gächter, F. Könemann, M. Sistani, M. G. Bartmann, M. Sousa, P. Staudinger, A. Lugstein and B. Gotsmann, Nanoscale, 2020, 12, 20590–20597.
18. J. Gao, D. Xie, Y. Xiong and Y. Yue, Appl. Phys. Express, 2018, 11, 066601.
19. H.-D. Wang, J.-H. Liu, X. Zhang, T.-Y. Li, R.-F. Zhang and F. Wei, J. Nanomater., 2013, 2013, 3.
20. L. Gottesdiener, J. Phys. E Sci. Instrum., 1980, 13, 908.
21. M.-H. Seo, J.-H. Park, K.-W. Choi, M.-S. Jo and J.-B. Yoon, Appl. Phys. Lett., 2019, 115, 131901.
22. C. Xing, C. Jensen, T. Munro, B. White, H. Ban and M. Chirtoc, Appl. Therm. Eng., 2014, 73, 317–324.
23. M. Li, C. Li, J. Wang, X. Xiao and Y. Yue, Appl. Phys. Lett., 2015, 106, 253108.
24. H. Akhlaghi and E. Roohi, Phys. Fluids, 2021, 33, 061701.
25. J. H. Young, Appl. Sci. Res., 1986, 43, 55–65.
26. N. A. Fuchs, Geofis. Pura Appl., 1963, 56, 185–193.
27. F. Völklein, H. Reith, T. Cornelius, M. Rauber and R. Neumann, Nanotechnology, 2009, 20, 325706.
28. J. Strnad and A. Vengar, Eur. J. Phys., 1984, 5, 9.
29. J. S. Lee, K. W. Choi, J. Y. Yoo, M. S. Jo and J. B. Yoon, Small, 2020, 16, 1906845.
30. J. Yeon, Y. J. Lee, D. E. Yoo, K. J. Yoo, J. S. Kim, J. Lee, J. O. Lee, S.-J. Choi, G.-W. Yoon and D. W. Lee, Nano Lett., 2013, 13, 3978–3984.
31. M.-S. Jo, K.-W. Choi, M.-H. Seo and J.-B. Yoon, Micro Nano Syst. Lett., 2017, 5, 1–7.
32. M.-S. Jo, K.-H. Kim, J.-S. Lee, S.-H. Kim, J.-Y. Yoo, K.-W. Choi, B.-J. Kim, D.-S. Kwon, I. Yoo and J.-S. Yang, ACS Nano, 2023, 17, 23649–23658.
33. E. H. Sondheimer, Adv. Phys., 2001, 50, 499–537.

---

Footnote

† Electronic supplementary information (ESI) available: Analytic calculation of power consumption in Pt film heater, geometrical parameters and symbols for structural design, schematic of the air-conduction model, calculated and measured power consumption of the fabricated nanowire heaters. See DOI: https://doi.org/10.1039/d4na00894d

---