A method to predict binary eutectic mixtures for mechanochemical syntheses and cocrystallizations

Abstract

The prediction of the phase behaviour of a mixture of solid components when they come into contact is of high interest in fast growing research fields such as mechanochemistry and deep eutectic solvents (DESs). This paper provides a friendly predictive tool (PoEM, i.e. Predictor of Eutectic Mixtures), along with some guidelines and quantitative references, to quickly estimate the variation in the melting point due to the mixture of reactants for a mechanochemical process. An empirical model that estimates the ideal eutectic point and includes deviation from ideality based on intermolecular interactions is presented here, allowing for the design of synthetic procedures for solvent-less cocrystallization processes. PoEM calculations are validated by comparing the prediction with experimental behaviour of a number of mixtures with a low melting eutectic mixture. Finally, as a working example we consider how to identify coformers for the synthesis of a cocrystal containing thymol such that the cocrystallization would proceed through the formation of a metastable liquid phase.

---

Introduction

The use of mechanochemistry has emerged as an attractive, cost effective and sustainable tool for covalent^1–6 or supramolecular syntheses.^7–11 The most impactful benefit of mechanochemical protocols is the significant reduction of solvent waste; other advantages include different reaction pathways that can sometimes be exploited thus obtaining a specific polymorphic form, in some cases, forbidden via solution chemistry.^12–15 In mechanochemical processes, the jar loaded with the reagents and the milling bodies is accelerated in the mechanochemical setup, triggering the breaking and forming of covalent bonds or supramolecular aggregates as a result of the impacts occurring within the jar. Although many studies appeared in recent literature focusing on the in situ monitoring of different mechanochemical reactions,^16,17 the mechanism of the reaction paths is far from being understood.^18–20 Many variables concur with the outcome of a mechanochemical reaction and even the effect of the mixing of the reagents could have a role in the overall mechanochemical reaction. It has been suggested that proceeding through liquid intermediates may facilitate the activation of the mechanochemical process.^21,22 The a priori knowledge of whether a reaction mixture could give rise to a low melting eutectic mixture would be of great impact for the experimental design of mechanochemical protocols. In this paper we focus on mechanochemical processes driven by the formation of a liquid eutectic phase due to the mixing of the starting materials. The occurrence of a low melting eutectic mixture as an intermediate product may lead to faster conversions towards the final products, since liquid phases can promote mass transport and molecular mobility, which are often critical aspects of mechanochemical reactions both in vibrational milling and resonance acoustic mixing (RAM).^23–25 Indeed, in RAM the intimate mixing between molecular components represents the most critical aspect for the success of the ball-free mechanochemical reaction.^25,26 Additionally, liquid mixtures overcome the limitation posed by surface interactions between solid particles, inherent in solid-state reactions.

Basic thermodynamics tells that the eutectic point of a binary mixture results from the intersection of solidus–liquidus equilibrium curves of the two components, each described by Schroeder-van Laar's equation²⁷ (eqn (1)), which links the actual melting temperature (T_calc.) of the (i) component with its molar fraction (x_i) and activity coefficient (γ_i) in the mixture; the slope and intercept of the curve depend on the enthalpy of fusion (ΔH_i) and melting temperature (T_i) of the pure component (i):

Binary mixtures are usually described assuming an ideal behaviour of the components (γ = 1), observed when the interactions in the mixture are of the same magnitude as the interactions in the separate components, i.e. the enthalpy of mixing is equal to zero. However, when the heteromeric interactions in the mixture are predominant (γ < 1) or weaker (γ > 1) with respect to the homomeric interactions in the separate components, the mixture is not-ideal and the actual molar fraction in eqn (1) is scaled by using the activity coefficient γ, whose values depend on the composition.

The estimation of the effect of intermolecular interactions on modulating the melting point of the eutectic mixtures has been already investigated by computational methods, in particular in the field of deep eutectic solvents (DESs).^28,29 However, these calculations are often considerably time-consuming, with several parameters being refined to predict the lowering of the eutectic melting temperature due to deviation from ideal behaviour of a binary mixture.

We aim at delivering a set of user-friendly guidelines to assess whether two molecular components would give a low-melting eutectic phase when mixed together, in order to quickly understand the characteristics of the starting mixture in the mechanochemical process. We base our approach on the regular solution theory,³⁰ where the intermolecular interactions between components are described through the experimental parameter χ, as an approximation of the activity coefficient³¹ (eqn (2)):

ln γ = χ (1 − x_i)² (2)

The value of χ can be experimentally determined knowing the melting temperature and composition of the eutectic point of the binary mixture.

We provide here a readily usable general approach to predict the melting point for a mixture of reactants in mechanochemical processes, accounting for the divergence from ideal conditions.

Results and discussion

Method outline

The prediction of the eutectic temperature and composition requires the experimental melting data of the two components in eqn (1), and the estimation of the non-ideality parameter χ in eqn (2). The eutectic point is then calculated as the intersection of the two branches of the binary phase diagram (Fig. 1). While χ can be derived from the experimental determination of the eutectic melting point, its value is hard to predict by a computational approach. Our method is outlined in Scheme 1 and aims to correlate the experimental χ value of a training set of binary mixtures with some general indicators, which can be related to non-ideal behaviour through a qualitative estimate of intermolecular interactions between the compounds composing the mixture. This is depicted in the top section of Scheme 1. Once a robust correlation model is developed for this training set, this allows us to derive an operational estimate of χ for new pairs of molecules of interest by simple considerations of their propensity to form heteromeric synthons. This estimated χ allows us in turn to derive a prediction for the eutectic behaviour in terms of the melting point and composition, by elaborating eqn (1). This is represented in the bottom part of Scheme 1, showing the use of the novel tool PoEM. Since χ describes how the chemical species interact when mixed together, we tried to qualitatively correlate the interaction parameter χ with some of the properties of the molecular partners from which the out-of-ideality behaviour of the mixture can be predicted. Starting from a training set of 36 binary mixtures, we determined the experimental χ values at the eutectic points by combining eqn (1) and DSC measurements. For each system the interaction parameter χ has been calculated from the discrepancy gap between the melting temperature experimentally determined at the eutectic point and the melting temperature of the eutectic mixture under the hypothesis of the ideal conditions. The larger the deviation of the eutectic melting point between real and ideal conditions, the larger the contribution of the interaction parameter χ which is, in turn, correlated with the propensity of the chemical species to form heteromeric interactions.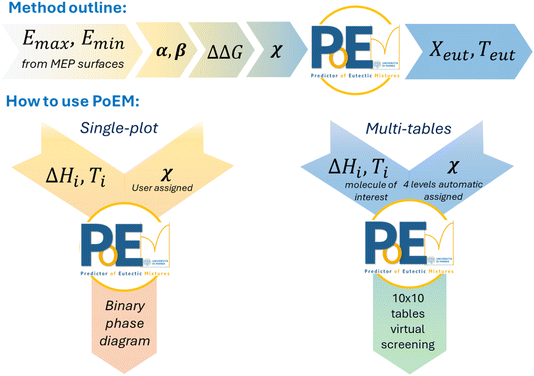

Fig. 1 Schematic representation of the binary phase diagram under the ideal condition (χ = 0, black line), and in the presence of positive (χ < 0, red line) or negative (χ > 0, blue line) deviations from ideality.

Scheme 1 Top: flow chart of the method proposed here for estimating χ values from MEP calculations. Bottom: flow chart of PoEM's calculation modes with corresponding input and output variables.

In parallel, the propensity of these binary mixtures to exhibit non-ideal behaviour was represented through the interaction energies (ΔΔG) between the two components calculated as proposed by Hunter,³² through the elaboration of the MEP values.

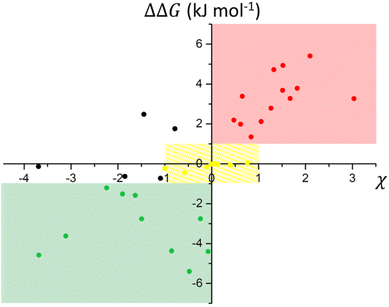
The scatterplot correlating experimental deviations from ideality expressed by χ and the simulated interaction energies of the molecular pairs calculated by Hunter's method, allowed us to identify windows of χ which likely corresponded to ranges of ΔΔG (Fig. 2, and Table 1). Interaction energies may also be associated with the presence of typical supramolecular synthons known in the literature.

Fig. 2 Plot of interaction energies ΔΔG versus χ values for the training set of binary mixtures. Data are divided into three domains, according to less favourable (red), more favourable (green), or ideal interactions observed in the experimental binary mixtures. Data points are depicted with colours corresponding to the respective domains; black dots refer to outlier values.

Table 1 Experimental ranges of interaction energies ΔΔG (kJ mol⁻¹) and corresponding χ values

ΔΔG < −1	−1 < ΔΔG < 1	1 < ΔΔG < 3	ΔΔG > 3
−4 < χ < 0	−4 < χ < 1	−2 < χ < 3	0 < χ < 3

---

Someone wishing to mix two compounds in a mechanochemical process may then (i) estimate the strength of their supramolecular synthons, (ii) make the hypothesis of the corresponding χ value, and finally (iii) evaluate the eutectic melting point and composition from Schroeder-van Laar's equation (Scheme 1).

The overall method mentioned above has been implemented into a ready-to-use predictive software PoEM (i.e. Predictor of Eutectic Mixtures), coded in Python language, to evaluate the eutectic properties (i.e. melting temperature and molar composition) from Schroeder-van Laar's equations as a function of the interaction parameter χ. It also provides a plugin to plot the resulting binary phase diagram. In addition, PoEM can also provide indications of potential molecular partners for a molecule of interest by scanning a landscape of possible compounds characterized by different T_i and ΔH_i. This could help to design mechanochemical synthetic strategies mediated by liquid eutectic intermediates.

Method setup

Calculation of the eutectic point requires the assessment of the extent of deviations from ideality of the mixture. The activity coefficient (γ) in a mixture depends on an interaction parameter (χ) and the composition terms (1 − x_i²), as in eqn (2). Under the ideal conditions (γ = 1) χ = 0, deviations from ideality result in the interaction parameter diverging from zero. In this case, the heteromeric interactions within the binary mixture can be more (χ < 0) or less (χ > 0) prone to occur with respect to the homomeric interactions in the separate components (Fig. 1).³¹ The difference between heteromeric and homomeric interactions can be quantified following Hunter's approach.³³ The ΔΔG of formation for the mixture is calculated considering that chemical species may act as both donors and acceptors in intermolecular interactions (eqn (3)):

ΔΔG/kJ mol⁻¹ = (α₁β₁ + α₂β₂) − (α₁β₂ + α₂β₁) (3)

Hunter's parameters α and β respectively describe the best donor and acceptor functional groups in the two components 1 and 2 (eqn (3)).

The terms (α₁β₁ + α₂β₂) and (α₁β₂ + α₂β₁) account for the free energy of homomeric and heteromeric contributions, respectively. A widely used approach to estimate the magnitude of these intermolecular interactions based on the donor/acceptor contributions considers maxima and minima (E_max and E_min) of molecular electrostatic potential (MEP) surfaces. E_max and E_min values have been used to estimate the strength of hydrogen bond interactions, both in solution and solid states, or even predict the likelihood of cocrystallization.^34–36 Hunter et al.³⁷ showed that the E_max and E_min of the MEP surfaces can be converted in the α and β parameters (eqn (3)) taking into account empirical properties depending on the functional group properties as donor (m_α, c_α) or acceptor groups (m_β, c_β):

α = m_αE_max + c_α (4)

β = m_βE_min + c_β (5)

Considering these assumptions, we built a training set based on 9 molecules (Scheme 2) containing a variety of functional groups found in natural or Generally Recognized As Safe (GRAS) ingredients, for which we have computed the MEP and calculated the α and β parameters according to eqn (4) and (5). The interaction parameter χ was derived from the combination of eqn (1) and (2) and finally correlated with ΔΔG (Fig. 2, and Table 1) in order to obtain a qualitative model to predict the eutectic point of any binary mixture among compounds similar to those considered here.

Scheme 2 Chemical sketches of the individual components used in the training set of binary mixtures.

Training set of binary mixtures

The selection of chemical species in the training set of binary mixtures was based on simple molecular scaffolds, characterized by both hydrogen bond donor and acceptor moieties, thus exploiting the most recurrent and stabilizing intermolecular interactions that might occur upon mixing (Scheme 2).

For all the molecules in the training set, the MEPs were computed (see the ESI†) and α and β parameters were obtained considering the groups with the highest and lowest MEP values (eqn (4) and (5)).

The interaction energies ΔΔG within the mixtures of Scheme 2 were calculated by using eqn (3) (see the ESI for details†). For the same mixtures, the experimental values of χ were obtained by fitting eqn (1) to the actual eutectic data determined by DSC measurements. The interaction energy ΔΔG versus χ values calculated for the experimental binary mixtures are then plotted in Fig. 2.

Three main domains arise from the plot which can be correlated with the interaction energy observed under ideal (yellow area) and not-ideal (green and red areas) conditions. In the range −1 < ΔΔG < 1 (Fig. 2, yellow domain), binary mixtures exhibit close to ideal behaviour, with χ lower than 1 in absolute value.

This range is populated by mixtures in which components present either a similar chemical structure (e.g. PHE-DQUI and BA-HBA) or competitive functional groups (e.g. PHE-BP and DQUI-BP) (details in the ESI†).

In the case of positive deviation from ideality (Fig. 2, red domain), χ values consistently remain positive for ΔΔG > 1, with a tendency to increase as the interaction energies become higher, meaning that the interactions in the mixture are less favourable than in the separate components.

When negative deviations from ideality are observed (Fig. 2, green domain), the interactions in the mixture are more favourable than in the separate components (ΔΔG < 0), and the interaction parameter χ has negative values. The maximum value observed within the training set was χ = 3.08 for the binary mixture of APY-DQUI, while a minimum of χ = −3.69 was reached for the binary mixture HBA-HQUI. Only a few outliers fall outside these areas, involving binary mixtures where the simplifications assumed in Hunters's model only partially account for the thermodynamic properties of the systems, suggesting that other effects might be involved (Fig. 2, black dots) (see the ESI†). The distribution of the binary mixtures of the training set in Fig. 2 leads to the definition of four levels of ΔΔG corresponding to different values of χ (Table 1).

This classification can be used for estimating a window of eutectic conditions for any binary mixture similar to the ones considered here: once the ΔΔG is computed with eqn (3) based on MEP calculations, an estimate of the interaction parameter χ is derived from Table 1, and can be used in eqn (1) and (2). Repeating the calculations for the χ limiting values of the pertinent window provides the borders of the temperature range where the actual melting occurs for the eutectic mixture of the components under examination. In the case of ionic interactions within the binary mixture, which is typically observed in DESs, the eutectic point may largely deviate from the ideal conditions, and the interaction parameter χ results in deeply negative values (χ ≪ −4), so these cases are not considered in our model.³⁸

Predictive tool for calculating binary eutectic mixtures (PoEM)

Based on this estimation of χ, we developed a quick tool to evaluate a likely range for the actual eutectic point of a binary mixture. The ideal eutectic point of a binary mixture can be calculated from enthalpies and temperatures of fusion of the two components, by intersecting the curves derived from eqn (1) based on the Schroeder-van Laar's theory. Prediction of the actual eutectic point requires the correction for non-ideality through eqn (2), within the theory of regular solutions. Eqn (6) combines eqn (1) and (2) and relates the actual composition for component i (x_i) to the melting temperature of the mixture T_calc..

The Schroeder-van Laar's curves (eqn (6)) of the two components intersect at the actual eutectic point, whose calculation requires the value of the non-ideality parameter χ. This can be estimated from Table 1, if the magnitude of intermolecular interactions occurring within the mixture (ΔΔG) is known, or if it issimply qualitatively postulated by comparison of the possible synthons active in the mixture. This routine has been implemented in PoEM (i.e. Predictor of Eutectic Mixtures), a ready-to-use software that predicts the actual eutectic point (T_eut, X_eut) of molecular binary mixtures.

PoEM offers a graphical user interface (GUI) which allows us to perform fast calculations and visualize the results in plots or tables. Two different algorithms are coded in PoEM, namely the single-plot, and multi-tables (see the ESI for details†). In the single-plot algorithm, the ideal binary phase diagram of a mixture is presented by plotting the Schroeder-van Laar's curves calculated from the enthalpies of fusion and melting temperatures of the two components (ΔH₁, T₁, ΔH₂, T₂) set as the input.

The estimated actual binary phase diagram is also reported, based on the interaction parameter χ defined by the user; the actual plot is superimposed with the ideal plot (χ = 0) offering a graphical visualization of the effect of the intermolecular interaction within the mixture (Fig. 3, bottom) (see the ESI†). The characterization of mechanochemical syntheses or cocrystallization that might proceed through the formation of liquid intermediates, such as the low melting eutectic phase, finds a direct application in the use of the single-plot algorithm.

Fig. 3 Top: optical microscopy images at 100× magnification for thymol (THY) : 2,2′ bipyridine (BPY) binary mixture collected under ambient conditions. (a) Separated crystals of the chemical species. (b) A liquid eutectic phase is observed when they are put in contact. (c) The liquid eutectic phase grew until the minor component is still present. (d) Residual solid thymol embedded within the eutectic liquid phase. Bottom: PoEM output from the single-plot plugin: Schroeder-van Laar's curve plotted for THY for χ = 0 (dashed blue line) and χ = −0.96 (solid blue line) and for BPY for χ = 0 (dashed orange line) and χ = −0.96 (solid orange line). Eutectic point calculated under the ideal conditions (grey point, χ = 0) and under real conditions (red point, χ = −0.96).

The second function of PoEM, the multi-table algorithm, can be useful for cocrystal design. In particular, PoEM does not provide hints of the likelihood that two components will form a cocrystal, but facilitates the choice of the properties of coformers if it is desired that cocrystallization might proceed through a liquid precursor. Mechanochemical syntheses of cocrystals may be in fact triggered by a transient liquid eutectic phase, as described by Mazzeo et al.²² The formation of a low melting eutectic intermediate requires suitable thermodynamic properties of the two coformers.

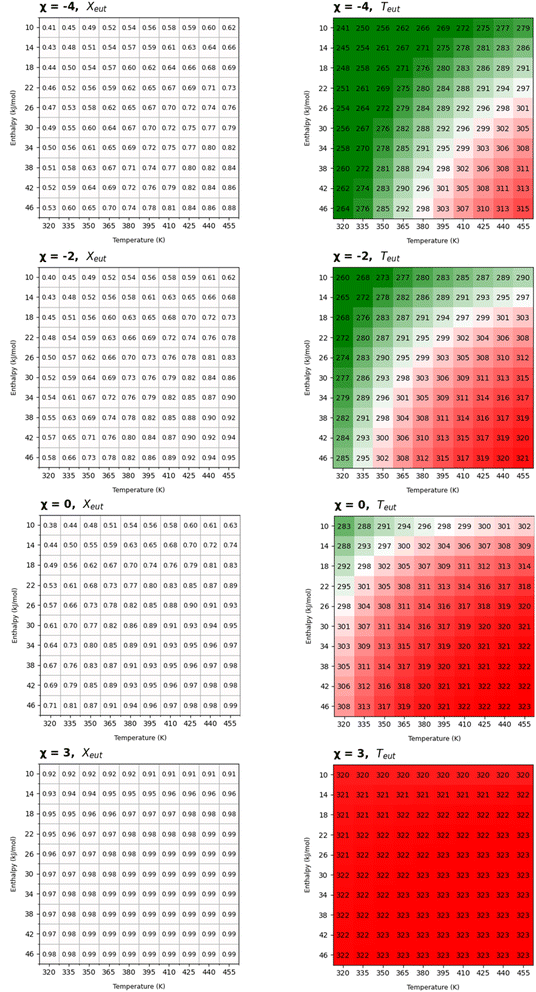
Given a molecule of interest, whose melting temperature and enthalpy are known, PoEM simplifies the selection of coformers by providing predictive tables reporting the hypothetical eutectic points between the molecule of interest and an array of 100 virtual coformers defined by the thermodynamic parameters ΔH_fus and T_fus. The virtual coformers are simulated spanning ranges of enthalpies of fusion and melting temperatures on a 10 × 10 grid, whose combinations cover a significant number of common organic compounds (see the ESI†). Each of these 10 × 10 (ΔH_i, T_i) combinations is regarded as a potential molecular partner of the molecule of interest, overall simulating 100 potential binary mixtures. The algorithm returns four tables calculated at 4 different χ levels (namely −4, −2, 0, and 3), mirroring the χ ranges as reported in Table 1 spanning from the interaction parameter under ideal conditions (χ = −0) to very high (χ = −4) or moderate positive (χ = −2) or negative (χ = +3) deviation from ideality. As an example of the output tables we report the virtual eutectic melting temperatures and compositions for simulated binary mixtures in the hypothesis of the cocrystal syntheses containing thymol as the molecule of interest (Fig. 4). For a quick and easy graphical evaluation of the conditions for which a low melting eutectic intermediate is likely to occur upon mixing of the components in a mechanochemical process, the eutectic temperatures are depicted using a colour gradient centered at around ambient temperature, shifting towards red for T_eut > 298 K, green for T_eut < 298 K and white for T_eut = 298 K.

Fig. 4 Tables generated by PoEM of the eutectic compositions (left) and melting temperature (right) obtained combining thymol (molecule of interest) with 10 × 10 hypothetical coformers at different χ values (−4, −2, 0, and 3). Cells reporting melting temperature are depicted using a colour gradient, shifting towards red for T_eut > 298 K, green for T_eut < 298 K and white for T_eut = 298 K.

Although the usual interest involves finding the conditions for which low melting eutectic mixture can trigger cocrystallization, the opposite need could also occur, trying to avoid the formation of low melting intermediates: in this case coformers showing higher T_eut should be preferred. The combinations which result in eutectic mixtures under ambient conditions can be easily visualised, and the design of cocrystallization proceeding through liquid intermediates (or avoiding it) can be rationally addressed by choosing coformers with melting enthalpy and temperature fitting the green (or red) range of the grid.

Validation of PoEM's calculations

The formation of an intermediate liquid phase upon mixing of solid components has been often underrated in crystal engineering although various examples have been reported in the literature for the synthesis of cocrystals upon the formation of metastable liquid eutectic mixtures under ambient conditions. These observations could have been predicted by using PoEM.

A validation test was run to assess the reliability of PoEM in predicting the eutectic point of binary mixtures for a few cases already reported in the literature known to form a low-melting eutectic mixture (Fig. 5). The melting enthalpies and temperatures of the chemical species of the binary mixtures were experimentally re-determined through DSC measurements to ensure homogeneity of the dataset (see the ESI†). For the systems whose eutectic temperature was not specified, it is assumed to be below 293.15 K, since observation of a liquid intermediate was reported in the original papers. The results of PoEM's calculations are summarised in Table 2.

Fig. 5 Representation of hydrogen bond interactions between components of selected binary mixtures from the literature that give a low melting eutectic mixture. Donor and acceptor groups are depicted in blue and red respectively. BP: benzophenone, CAM: camphor, DPA: diphenylamine, LAU: lauric acid, MEN: menthol, PYR: pyrazine, and THY: thymol.

Table 2 Experimental and calculated T_eut and calculated χ for the binary mixtures with low melting eutectic points reported in the text. Calculated T_eut were obtained by PoEM considering the range of favourable interactions (−4 < χ < 0, Table 1)

Binary mixture	T eut (exp.)	T eut (χ = −4)	T eut (χ = 0)	χ (calc.)
DPA-BP^39	286.43 K	264.64 K	296.56 K	−1.17
THY-PYR^40	<293.15 K	248.14 K	288.03 K	<0.43
THY-MEN^41,42	<260.00 K	249.88 K	286.77 K	< −2.80
MEN-CAM^43	283.20 K	236.12 K	289.72 K	−0.44
MEN-LAU^44	291.64 K	267.45 K	294.11 K	−0.34

---

The agreement between experimental and estimated melting temperatures depends on the value of χ introduced in eqn (6). Since this value cannot be computed with precision, we suggest that some robust upper and lower limiting values of χ are considered, in order to derive a temperature range where the actual eutectic melting occurs.

On a qualitative-based evaluation, we considered all these binary mixtures prone to form favourable heteromeric interactions, and thus we attributed an interaction parameter −4 < χ < 0. PoEM's calculations at χ = −4 and χ = 0 returned a range of eutectic temperatures that include the experimental T_eut (Table 2). For comparison, the actual χ values calculated at the experimental T_eut are also reported in Table 2. As shown in Table 2, binary mixtures whose ideal behaviour (χ = 0) suggests a melting point below room temperature, show a higher chance to observe a liquid eutectic mixture also for experimental non-ideal behaviuor (χ < 0).

The selected systems exemplify low melting eutectic mixtures characterized by moderate interaction parameter χ values, which may represent an alternative approach to design DES systems, generally based on strong interactions between components (typically ionic) and large negative χ values. Chemical mixtures with low melting temperatures and high affinity may help the formation of liquid eutectic mixtures.

As a further proof of concept, we considered the combination of thymol (THY) and 2,2-bipyridine (BPY), where the functional groups of THY and BPY suggest the probable formation of hydrogen bond interactions. For this mixture PoEM predicts a low melting eutectic mixture under ideal conditions (χ = 0, T_eut = 302.03 K) (Fig. 3, bottom), pointing to a promising liquid eutectic mixture if the mixing interactions are favourable. In fact, as predicted, when crystals of THY and BPY are mixed at 293.15 K, a liquid phase is formed at the contact surface (Fig. 3, top). In agreement with favourable hydrogen bonds between the partners, the interaction parameter lowers the eutectic melting point below room temperature. In this case, in fact, χ must be lower than −0.96, which is consistent with the χ values calculated for analogous PHE/THY and DQUI/THY binary mixtures (training set, see ESI†), since both PHE and DQUI present N aromatic sites acting as hydrogen bond acceptors as for BYP.

To ensure PoEM reliability when using datasets collected by different users or using literature thermodynamic data, we also tested a few cases of binary mixtures already reported in the literature, entering melting enthalpies and temperatures provided by the authors or, if missing, by the National Institute of Standards and Technology (NIST).⁴⁵ The first set of the components are not likely to form strong intermolecular interactions upon mixing (Table 3, upper part), thus, for these cases we set the interaction parameter in the range 0 < χ < 2, which are the most popular values for positive interaction energies (ΔΔG) as shown in Fig. 2, assuming that heteromeric interactions are comparable or even less favoured than homomeric ones. The rest of the binary mixtures from the literature here considered are composed of molecules quite likely to interact favourably (Table 3, bottom part), thus for these cases we considered the range 0 < χ < −4, well populated by systems with negative interaction energies as reported in Fig. 2. As shown in Table 3, the experimental T_eut fit in the range of eutectic temperatures calculated at the limiting values both for favourable and non-favourable mixing free energies. One exception is BPH-HB, whose calculated χ = 2.57 at the experimental T_eut evidences a strong destabilization of the binary system, still located at the limit of the 0 < χ < 3 range reported in Table 1 and Fig. 2. This shows that PoEM's results are robust and general and can be applied to any user dataset. It is important to remark that using a sensible and wide χ range ensures a reliable estimate of the actual temperature window comprising the eutectic value.

Table 3 Experimental and calculated T_eut and calculated χ of reported binary mixtures obtained from thermodynamic data provided by authors (^a) or the NIST (^b). Calculated T_eut were obtained by PoEM considering the range of non-favourable interactions (0 < χ < 2, upper part); the range of favourable interactions (−4 < χ < 0, lower part)^a

Binary mixture	T eut (exp.)	T eut (χ = 0)	T eut (χ = 2)	χ (calc.)
a AAP: 4-aminoacetophenone, BB: bibenzyl, BN: benzoin, BNA: 4-bromo-2-nitroaniline, BPH: biphenyl, HB: 3-hydroxybenzaldehyde, MBA: 4-methylbenzoic acid, ORL: ornidazole, PNP: 4-nitrophenol, and RC: resorcinol.
BN-AAP^(a)^46	366.15 K	363.83	377.17 K	0.27
PNP-AAP^(a)^46	353.15 K	343.05 K	370.58 K	0.74
BPH-HB^(a)^47	341.50 K	325.90 K	339.89 K	2.57
BNA-HB^(a)^48	351.15 K	343.55 K	368.12 K	0.63
MBA-ORL^(b)^49	351.15 K	349.61 K	357.16 K	0.24

---

Binary mixture	T eut (exp.)	T eut (χ = −4)	T eut (χ = 0)	χ (calc.)
BN-RC^(a)^48	360.15	335.19	367.69	−0.79
BPH-BB^(b)^50	302.65	272.31	304.45	−0.21

---

Conclusions

Knowing the characteristics of the starting mixture is fundamental for the rational design of a mechanochemical process. In cases where the starting compounds are simple organic neutral molecules, it may be that their mixture gives rise to a low melting eutectic liquid phase, which could either facilitate the mechanochemical process by creating a liquid intermediate or prevent physical mixing by creating a sticky slurry. We here report a simple method to derive the eutectic melting temperature and composition for real mixtures, simulating a reasonable not-ideal behaviour without the need for massive computational effort. The interaction parameter χ between chemical species involved in the binary mixture is evaluated on the basis of the ΔΔG of formation, calculated from the α and β parameters derived from the MEP for each chemical species.

Once χ is known, the eutectic point can be predicted from Schroeder-van Laar's equation for real cases. A limiting value of χ can also be estimated by qualitative considerations, and the borders of a range comprising the eutectic point can be derived. This method has been implemented in the software PoEM (i.e. Predictor of Eutectic Mixtures). PoEM can ideally be used to predict whether two chemical species can give rise to a low melting eutectic phase when mixed together. It also allows us to rationally drive the choice of coformers which form a low melting mixture with a molecule of interest providing tables of potential eutectic mixtures from the combination of 10 × 10 enthalpies of fusion and melting temperatures. It also provides a plugin to plot the final binary phase diagram.

PoEM can be freely downloaded from https://cristallografia.org/software/ and authors welcome feedback on case studies.

Experimental

Materials and methods

All the reagents and solvents were purchased from Sigma-Aldrich Chemical Co. and used with no further purification.

Synthetic procedures

Binary mixtures were prepared at a molar ratio close to their ideal eutectic composition (χ = 0). The two components of the mixture were gently ground until a homogeneous powder was formed, avoiding the occurrence of undesirable events such as phase transitions or cocrystallizations. Binary mixtures of APY-THY, BP-THY, and IMZ-THY formed a liquid phase at 293.15 K, which was assumed to be the melting temperature of their eutectic mixtures.

Differential scanning calorimetry (DSC)

Differential scanning calorimetry analysis was performed with a PerkinElmer Diamond equipped with a model ULSP 90 ultracooler. The measurements were performed in closed 10 μL Al-pans under a constant flow of nitrogen (20 μL min⁻¹), using a temperature gradient of 5 °C min⁻¹.

Pure components were analysed with a heating-cooling-heating firing profile, determining the experimental melting temperatures and enthalpies of fusion (T_i, ΔH_i) used for the estimation of Schroeder-van Laar's equilibrium curves. The firing profiles varied according to the melting temperature of each compound. Binary mixtures were analysed with a single heating ramp aiming at measuring the melting temperature of the eutectic mixtures.

The enthalpy of the endothermic or exothermic events was determined by the integration of the area under the DSC peak, which is reported in J g⁻¹.

Molecular electrostatic potential (MEP) calculations

Interaction energies between the components of binary mixtures were calculated using MEP surface values, introduced into Hunter's parameter (α and β) equations (see the ESI†). MEPs were calculated by Crystal Explorer17 package software at the 6-31G(d) level of theory using either 0.0300 or 0.0104 e bohr⁻³ isodensity surfaces to account for secondary ionic interactions. The highest positive value (E_max) of each MEP surface was used to calculate the α parameter, whilst the lowest negative value (E_min) was used for the β parameter. Interaction energies (ΔΔG) were obtained by the difference of homomeric (α₁β₁ + α₂β₂) and heteromeric (α₁β₂ + α₂β₁) interactions. A detailed description of the method supported by calculated parameters and interaction energies is reported in the ESI.†

MEP calculations were performed on the crystal structure of all components used in the binary mixtures, with normalized hydrogen distances. CSD Refcodes of crystal structures used are reported in the ESI.†

PoEM's calculation methods

PoEM calculates the eutectic point of binary mixtures using the Scipy optimize function⁵¹ that ensures that Schroeder-van Laar's curves of the two components converge at the eutectic point, by varying one (x_eut) or two parameters (x_eut and χ). The eutectic composition of the mixture (x_eut) is constrained within a range from 0 to 1. The optimization process is performed on equations derived from eqn (6) (specifically eqn (S2) and (S3) in the ESI†). Further information is available in the ESI.†

Data availability

The data supporting this article have been included as part of the ESI.† The software PoEM (Predictor of Eutectic Mixtures) is available at the Italian Crystallographic Association software repository at https://cristallografia.org/software/.

Author contributions

Michele Prencipe: software, visualization, validation, methodology, formal analysis, investigation, data curation, writing (original draft preparation). Paolo Pio Mazzeo: validation, investigation, resources, supervision, writing (review and editing), funding. Alessia Bacchi: funding, conceptualization, methodology, formal analysis, writing (review and editing), supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has benefited from the equipment and framework of the COMP-HUB and COMP-R Initiatives, funded by the ‘Departments of Excellence’ program of the Italian Ministry for University and Research (MIUR, 2018–2022 and MUR, 2023–2027). The funding of MIUR within the PRIN2020 project ‘NICE-Nature Inspired Crystal Engineering’ PRIN2020Y2CZJ2 is acknowledged. This work also benefitted from the call – Missione 4 “Istruzione e Ricerca” – Componente 2 – Investimento 1.1 “Fondo per il Programma Nazionale di Ricerca e Progetti di Rilevante Interesse Nazionale (PRIN)” with projects ‘Crystals4Bees’ X4BEES PRIN2022-D53D23010140001 and ‘FLuorInated PePtidEs for Resumption (FLIPPER)’ 202224KAX8. P. P. M. also acknowledges the starting grant from the University of Parma 2023-UNPRCLE-0066646. Dr Andrea Daolio is acknowledged for the fruitful discussion and help in writing the code of PoEM.

Notes and references

1. D. Tan and F. García, Chem. Soc. Rev., 2019, 48, 2274–2292.
2. R. Takahashi, A. Hu, P. Gao, Y. Gao, Y. Pang, T. Seo, J. Jiang, S. Maeda, H. Takaya, K. Kubota and H. Ito, Nat. Commun., 2021, 12, 1–10.
3. A. Porcheddu, R. Mocci, M. Brindisi, F. Cuccu, C. Fattuoni, F. Delogu, E. Colacino and M. V. D'Auria, Green Chem., 2022, 24, 4859–4869.
4. F. Cuccu, L. De Luca, F. Delogu, E. Colacino, N. Solin, R. Mocci and A. Porcheddu, ChemSusChem, 2022, 15, e202200362.
5. T. Seo, K. Kubota and H. Ito, J. Am. Chem. Soc., 2023, 145, 6823–6837.
6. F. Mele, A. M. Constantin, F. Sacchelli, D. Schiroli, P. P. Mazzeo, G. Maestri, E. Motti, R. Maggi, R. Mancuso, B. Gabriele, F. Pancrazzi and N. Della Ca', Green Chem., 2024, 26, 6429–6435.
7. D. Braga, F. Grepioni, L. Maini, P. P. Mazzeo and K. Rubini, Thermochim. Acta, 2010, 507–508, 1–8.
8. D. Capucci, D. Balestri, P. P. Mazzeo, P. Pelagatti, K. Rubini and A. Bacchi, Cryst. Growth Des., 2017, 17, 4958–4964.
9. P. P. Mazzeo, M. Pioli, F. Montisci, A. Bacchi and P. Pelagatti, Cryst. Growth Des., 2021, 21, 5687–5696.
10. F. Montisci, P. P. Mazzeo, C. Carraro, M. Prencipe, P. Pelagatti, F. Fornari, F. Bianchi, M. Careri and A. Bacchi, ACS Sustain. Chem. Eng., 2022, 10, 8388–8399.
11. C. Zuffa, C. Cappuccino, M. Marchini, L. Contini, F. Farinella and L. Maini, Faraday Discuss., 2023, 241, 448–465.
12. A. M. Belenguer, G. I. Lampronti, A. J. Cruz-Cabeza, C. A. Hunter and J. K. M. Sanders, Chem. Sci., 2016, 7, 6617–6627.
13. H. Kulla, S. Greiser, S. Benemann, K. Rademann and F. Emmerling, Cryst. Growth Des., 2017, 17, 1190–1196.
14. D. Tan and T. Friščić, Eur. J. Org. Chem., 2018, 2018, 18–33.
15. K. Linberg, B. Röder, D. Al-Sabbagh, F. Emmerling and A. A. L. Michalchuk, Faraday Discuss., 2023, 241, 178–193.
16. T. Friščić, I. Halasz, P. J. Beldon, A. M. Belenguer, F. Adams, S. A. J. Kimber, V. Honkimäki and R. E. Dinnebier, Nat. Chem., 2012,(5), 66–73.
17. L. Batzdorf, F. Fischer, M. Wilke, K.-J. Wenzel and F. Emmerling, Angew. Chem., 2015, 127, 1819–1822.
18. G. I. Lampronti, A. A. L. Michalchuk, P. P. Mazzeo, A. M. Belenguer, J. K. M. Sanders, A. Bacchi and F. Emmerling, Nat. Commun., 2021, 12, 1–9.
19. A. A. L. Michalchuk and F. Emmerling, Angew. Chem., Int. Ed., 2022, 61, e202117270.
20. P. P. Mazzeo, G. I. Lampronti, A. A. L. Michalchuk, A. M. Belenguer, A. Bacchi and F. Emmerling, Faraday Discuss., 2023, 241, 289–305.
21. N. Biliškov, Cryst. Growth Des., 2021, 21, 1434–1442.
22. P. P. Mazzeo, M. Prencipe, T. Feiler, F. Emmerling and A. Bacchi, Cryst. Growth Des., 2022, 22, 4260–4267.
23. T. Friščić, S. L. Childs, S. A. A. Rizvi and W. Jones, CrystEngComm, 2009, 11, 418–426.
24. A. A. L. Michalchuk, K. S. Hope, S. R. Kennedy, M. V. Blanco, E. V. Boldyreva and C. R. Pulham, Chem. Commun., 2018, 54, 4033–4036.
25. L. Gonnet, T. H. Borchers, C. B. Lennox, J. Vainauskas, Y. Teoh, H. M. Titi, C. J. Barrett, S. G. Koenig, K. Nagapudi and T. Friščić, Faraday Discuss., 2023, 241, 128–149.
26. J. G. Osorio, E. Hernández, R. J. Romañach and F. J. Muzzio, Powder Technol., 2016, 297, 349–356.
27. I. Prigogine and R. Defay, Chemical Thermodynamics, Longmans Green, 1954.
28. A. van den Bruinhorst and M. Costa Gomes, Curr. Opin. Green Sustainable Chem., 2022, 37, 100659.
29. B. D. Like, C. E. Uhlenbrock and M. J. Panzer, Phys. Chem. Chem. Phys., 2023, 25, 7946–7950.
30. J. H. Hildebrand and R. L. Scott, The Solubility of Non-electrolytes, Reinhold Pub. Corp, New York, 3rd edn, 1949.
31. L. J. B. M. Kollau, M. Vis, A. Van Den Bruinhorst, A. C. C. Esteves and R. Tuinier, Chem. Commun., 2018, 54, 13351–13354.
32. C. A. Hunter and C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324.
33. M. C. Storer and C. A. Hunter, Chem. Soc. Rev., 2022, 51, 10064–10082.
34. B. Sandhu, A. McLean, A. S. Sinha, J. Desper, A. A. Sarjeant, S. Vyas, S. M. Reutzel-Edens and C. B. Aakeröy, Cryst. Growth Des., 2018, 18, 466–478.
35. N. Sarkar, N. C. Gonnella, M. Krawiec, D. Xin and C. B. Aakeröy, Cryst. Growth Des., 2020, 20, 7320–7327.
36. M. Đaković, Crystallogr. Rev., 2020, 26, 69–100.
37. M. C. Storer, K. J. Zator, D. P. Reynolds and C. A. Hunter, Chem. Sci., 2023, 15, 160–170.
38. L. J. B. M. Kollau, R. Tuinier, J. Verhaak, J. Den Doelder, I. A. W. Filot and M. Vis, J. Phys. Chem. B, 2020, 124, 5209–5219.
39. K. Chadwick, R. Davey and W. Cross, CrystEngComm, 2007, 9, 732–734.
40. F. Montisci, P. P. Mazzeo, C. Carraro, M. Prencipe, P. Pelagatti, F. Fornari, F. Bianchi, M. Careri and A. Bacchi, ACS Sustain. Chem. Eng., 2022, 10(26), 8388–8399.
41. A. Alhadid, C. Jandl, L. Mokrushina and M. Minceva, Cryst. Growth Des., 2021, 21, 6083–6091.
42. F. Fornari, F. Montisci, F. Bianchi, M. Cocchi, C. Carraro, F. Cavaliere, P. Cozzini, F. Peccati, P. P. Mazzeo, N. Riboni, M. Careri and A. Bacchi, Chemom. Intell. Lab. Syst., 2022, 226, 104580.
43. B. Joos, M. K. Van Bael and A. T. Hardy, J. Chem. Educ., 2020, 97, 2265–2272.
44. J. Chen, F. Zhu, H. Qin, Z. Song, Z. Qi and K. Sundmacher, Chem. Eng. Sci., 2022, 262, 118042.
45. W. E. Acree Jr and J. S. Chickos, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, 2024.
46. S. Kant, U. S. Rai and R. N. Rai, J. Therm. Anal. Calorim., 2012, 110, 551–557.
47. K. P. Sharma and R. N. Rai, Thermochim. Acta, 2012, 535, 66–70.
48. R. S. B. Reddi, V. S. A. K. Satuluri, U. S. Rai and R. N. Rai, J. Therm. Anal. Calorim., 2012, 107, 377–385.
49. K. D. Prasad, S. Cherukuvada, L. Devaraj Stephen and T. N. Guru Row, CrystEngComm, 2014, 16, 9930–9938.
50. H. H. Lee and J. C. Warner, J. Am. Chem. Soc., 1935, 57, 318–321.
51. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. Pietro Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G. L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, Nat. Methods, 2020, 17, 261–272.

---

Footnote

† Electronic supplementary information (ESI) available: Thermal Analysis, MEP calculations, computational, software GUI. See DOI: https://doi.org/10.1039/d4mr00080c

---