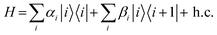Mapping the structure-function landscape of semiconducting polymers

Abstract

The molecular design of semiconducting polymers (SCPs) has been largely guided by varying monomer combinations and sequences by leveraging a robust understanding of charge transport mechanisms. However, the connection between controllable structural features and resulting electronic disorder remains elusive, leaving design rules for next-generation SCPs undefined. Using high-throughput computational methods, we analyse 100+ state-of-the-art p- and n-type polymer models. This exhaustive dataset allows for deriving statistically significant design rules. Our analysis disentangles the impact of key structural features, examining existing hypotheses, and identifying new structure–property relationships. For instance, we show that polymer rigidity has minimal impact on charge transport, while the planarity persistence length, introduced here, is a superior structural characteristic. Additionally, the predictive power of machine learning models trained on our dataset highlights the potential of data-driven approaches to SCP design, laying the groundwork for accelerated discovery of materials with tailored electronic properties.

---

New concepts

We demonstrate that it is finally possible to rationalise the entire class of semiconducting polymers and make predictions on their charge mobility with a known confidence level. A new methodology presented here enables the generation of accurate predictive models for hundreds of polymers, bringing the power of digital discovery into the field of semiconducting polymers. Data analysis of such a large and homogeneous set provides new, statistically significant, structure–property relationships. We find, for instance, that polymer rigidity is not important for its charge transport properties, which are instead dominated by a structural parameter we introduce: the planarity persistence length. We also resolve debates that have long puzzled researchers, such as the relative importance of conformational and electrostatic disorder. Combining our methodology with machine learning techniques we realise the possibility of screening thousands of polymers providing an unprecedented tool for their design and discovery.

Introduction

Semiconducting polymers (SCPs) hold great promise for low-cost, lightweight, flexible, and large-scale electronic devices because of their tuneable electronic and mechanical properties.^1,2 The ability to create a wide range of materials through modular synthesis, simply by varying monomer combinations and sequences within the polymer repeat unit, provides a vast landscape for molecular design.³ Despite this remarkable versatility, clear chemical design rules have yet to emerge. For example, (near)-amorphous polymers have shown record charge carrier mobilities comparable to those of highly ordered ones,⁴ while attempts to manipulate chain rigidity,⁵ side-chains,⁶ or the donor–acceptor nature of the backbone⁷ seem to indicate that there are multiple optima for this class of materials, making the chemical space hard to navigate effectively. Consequently, there is currently no clear target for the next generation high-mobility SCPs. Nonetheless, we have a fairly robust understanding of the charge transport mechanisms and the physical features desirable for high-mobility polymers.^8,9 For instance, the best-performing materials exhibit a narrow tail in the density of states (DOS) at the bandgap, which is associated with a greater degree of carrier delocalisation.^10–12 In contrast, broader tails and greater localisation are known to derive from an increased disorder of the polymer, but establishing a connection between the highly controllable chemical features and the disorder remains elusive. This challenge is ultimately due to (i) the presence of multiple entangled sources of disorder- the conformation of the polymer chain and the electrostatic interaction with the surrounding polymer chains- and (ii) the fact that such disorder is determined by the polymer's microstructure rather than its local chemical topology.

A major opportunity to develop fully predictive models of SCPs lies in the availability of high-quality computational methods, established by various research groups,^13–23 prove to be consistently capable of generating accurate descriptions of the local microstructure and electronic properties of SCPs.^4,6,18,24,25 Until now, these models have been deployed on very few polymers, typically one polymer per investigation, and they are commonly used to complement experimental investigations on benchmark systems.^{4,6,10,18,25,26} In this work, however, we establish that such methods can be used at scale, to create a fairly exhaustive map of the relationship between chemical structure and electronic properties for the entire class of SCPs. The availability of a homogenous (and expandable) dataset also enables the derivation of statistically significant design rules, gradually replacing the traditional approach of formulating research hypotheses tested on a limited number of cases. To this end, we generate more than 100 state-of-the-art models of p- and n-type SCPs, including their microstructure and electronic properties. Through disentangling the structural features and analysing their specific correlations with the calculated electronic properties, we test several existing hypotheses regarding the structure–property relationships and introduce previously unrecognised structural characteristics strongly correlated with intra-chain charge carrier mobility. Additionally, our results illustrate how machine learning (ML) models, built on these computed results, can provide rapid and statistically significant predictions for the design of new polymers.

Results

We selected over 30 commonly used π-conjugated monomers (Fig. 1(a)), combined them into 105 distinct repeat unit (RU) structures, completed with sidechains, and constructed SCPs. The SCPs are named using a standardised convention described in Method, and the list of all (n- and p-type) polymers considered is given in ESI,† Section S1. Note that the n-type polymers are identified by the conduction band edge energy being smaller than −3.6 eV. With a view to representing broadly the many high-performing SCPs that have been reported over the last decade, we included in our monomer selection fully fused polycyclic motifs such as indacenodithiophene (IDT) and its extended derivatives (IDTT and TIF),²⁷ lactam- and lactone-based structures including the popular diketopyrrolopyrrole (DPP) unit²⁸ and a series of isoindigo motifs.²⁹ Naphthalene diimides, such as NDI and NDTI,³⁰ are popular building blocks for constructing high-performing n-type polymers due to their highly electron-deficient character. These larger π-conjugated units are typically coupled with smaller co-monomer units taking advantage of donor–acceptor molecular orbital hybridization to control the frontier molecular orbital energy levels. Such co-monomer units are represented by a variety of electron-deficient motifs – including benzothiadiazole (BT) and benzotriazole (BTZ) – and more electron-rich thiophene-based units (e.g., T, TT, and TVT), providing a large molecular toolbox for manipulating polymer properties. Lastly, a recurring theme in molecular design in recent years has been the pursuit of non-covalent intramolecular interactions³¹ intended to planarize the polymer backbone; this is often accomplished with S–F interactions explaining our inclusion of fluorinated monomers such as BTFF, TFF, BFF, and BFFFF in addition to their ability to tune the donor–acceptor interactions.

Fig. 1 (a) Structures and acronyms of monomers used in this study. CH₃ groups are used to indicate the connection with the alkyl side chain. (b) Schematic representation of the Embedded Chain (“embd”) model used for DOS and LL calculations, as described in ref. 32. (c) Example results for a p-type polymer based on the Embedded Chain model, showing DOS(E) and LL(E) with definitions of key metrics: band-edge (E0.05%), tail-width (W_T = |E0.5% − E0.05%|, highlighted in orange), and bandwidth (W_B = |E50% − E0.5%|, highlighted in green). (d) Correlation graph between W_B/W_T and LL (Spearman's rank correlation coefficient, S = 0.8). (e) Comparison of LL values calculated from the “embd” and “iso” input models.

The methodology for performing simulations across a large number of systems builds on a workflow validated in ref. 32 and reported in the Method section below. Long polymer chains are modelled within an environment containing the corresponding RUs (referred to as the “soup” model) to replicate the bulk electrostatic and steric environment. As shown in the ESI,† Section S3, the quantities described throughout this work accurately reflect bulk properties and remain unaffected by the increase in the number of RUs of the chain beyond the 10-RU SCPs used in this study. Notably, microstructures of several SCPs generated by the bulk models using the same workflow have been previously compared to GIWAXS, showing excellent agreement.^24,25,32 The electronic structure is computed for individual polymer chains embedded within an electrostatic environment (labelled as “embd” in the figures), represented with suitable point charges (Fig. 1(b)). To isolate the effects of the electrostatic environment, we also analyse the electronic structure of isolated chains in the same conformation but without embedding (labelled as “iso”).

The DOS(E), a critical descriptor for SCPs, captures the distribution of electronic states and their accessibility for charge carriers. To analyse 100+ cases we should introduce more concise descriptors of the DOS. Specifically, for p-type SCPs, we compute the energies E0.5%, E5%, and E50%, which correspond to the hole filling of 0.5%, 5%, and 50% of the valence band, respectively. We define the tail-width as W_T = E0.5% − E0.05% and the (half) bandwidth as W_B = E50% − E5% (Fig. 1(c)). An analogous definition is applied for n-type polymers and their conduction band. At each energy, it is possible to define a localisation length LL(E), computable from the electronic structure results.³³ Evaluated at the band edge LL(E0.5%) (see Fig. 1(c)), this quantity expresses the delocalisation of the states more relevant for transport,^34,35 and we refer to it simply as LL in the remainder of this work.

In our work, we employ LL as a proxy for mobility, which is justified by multiple lines of both experimental and computational evidence demonstrating its strong correlation with key electronic properties relevant to charge transport in semiconducting polymers, e.g., mobility. For example, Fig. 1(d) demonstrates the expected strong correlation between W_B/W_T and LL (Spearman's rank correlation coefficient, S = 0.8), highlighting how either DOS tail or localisation characteristics can be linked with charge mobility.³⁵ Furthermore, other modelling studies based on model reduction calculations showed that LL and computed mobility are strongly correlated.³⁶

The comparison of LL values calculated from the “iso”, LL(iso), and “embd”, LL(embd), models (Fig. 1(e)), underscores the impact of the environmental electrostatic effect on charge transport, with the expected trend: LL(iso) > LL(embd). This finding highlights that, while the inter-chain electrostatic environment plays a role, a significant portion of the charge localisation behaviour originates from the chain conformation itself. Note that we distinguish between n-type and p-type polymers in the scatter plot presentations, although we do not find significant differences between the two classes in any of the discussions presented below. On the basis of this hierarchy, the following discussion will first explore the contribution of chain conformation to LL by analysing the “iso” models, followed by the impact of electrostatic environment, whose contribution can be studied in isolation by comparing the “embd” and “iso” results. This approach allows us to directly examine the disorder arising from the intra- and inter-chain effects.

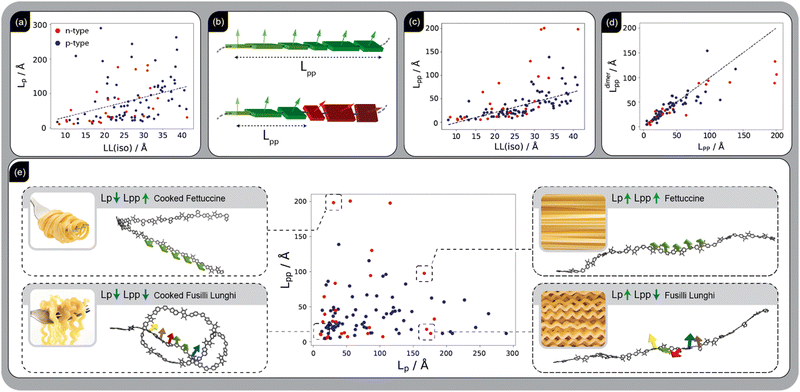
By generating over 100 realistic models and calculating properties correlated with mobility, we gain a unique opportunity to identify SCP structural features that contribute to high mobility. Our focus is on features that can be deliberately engineered to guide the synthesis of new polymers. For example, while polymer rigidity has long been considered a desirable property for SCPs,^37–39 Fig. 2(a) reveals only a weak correlation (S = 0.49) between persistence length (L_p), a proxy for polymer rigidity, and LL. Among the structural properties analysed, the one most strongly correlated with LL (S = 0.75) is the chain planarity persistence length (L_pp), which quantifies how planar a polymer backbone remains along its length (Fig. 2(b)). To determine this, we calculate the angle distribution between monomers along the chain, combining all the relative angles across 200 input chain models per SCP, and identify the length at which the planarity is lost (see Method). Fig. 2(c) shows that L_pp, unlike L_p, exhibits a strong correlation with LL, and it is therefore a superior predictor of charge delocalisation, an idea proposed in more qualitative terms in studies of individual polymers.^10,40,41

Fig. 2 (a) Correlation graph between persistence length, L_p, and localisation length for “iso” models, LL(iso) (S = 0.49). (b) Illustrative side views of polymer chains with relatively large and small planarity persistence length (L_pp). Rectangles represent monomers, with arrows indicating the normal vectors to the monomer planes. (c) Correlation graph between L_pp and LL for “iso” models (S = 0.75). (d) Correlation graph between L_pp and L^dimer_pp, obtained from the convolution of dihedral angle distributions of each neighbouring pair within the repeat units from small MD simulations of dimers (S = 0.95). (e) Correlation between L_pp and L_p (S = 0.17), highlighting their independence. Examples of SCP configurations showcase the relationship between L_pp and L_p with visual analogies to pasta shapes: (i) large L_p and L_pp, resembling uncooked fettuccine (flat and stiff); (ii) large L_p and small L_pp, similar to uncooked fusilli (stiff and twisted); (iii) small L_p and large L_pp, akin to cooked fettuccine (locally flat but soft); and (iv) small L_p and L_pp, resembling cooked fusilli (soft and twisted). The colour of each normal vector is matched to that of the neighbouring monomer if the relative angle is less than 30°.

This can be rationalised by considering the introduction of disorder in a tight-binding Hamiltonian, which leads to localisation of the resulting orbitals that increases with disorder.⁴² A variation in the dihedral angle in a conjugated polymer chain induces changes in both the off-site (inter-monomer coupling) and on-site Hamiltonian elements which, in turn, causes disorder and state localisation. In ESI,† Section S4.6 we employ a tight-binding model Hamiltonian to more quantitatively investigate the dependence of LL and L_pp on the dihedral angle distribution.

A key advantage of L_pp as a descriptor is its rapid computability, making it useful for screening polymers prior to synthesis. As shown in Fig. S4.3.3 in the ESI,† L_pp can be derived almost exactly (S = 0.99) from the dihedral angle distribution of a polymer's conjugated fragments within a single RU, obtained from MD simulation trajectories. Furthermore, as demonstrated in Fig. 2(d), L_pp can be predicted with high accuracy (S = 0.95) using a small MD simulation of dimers (ESI,† Section S4.4), or estimated with reasonable accuracy (S = 0.86) for initial screening through torsional potentials in the gas phase (ESI,† Section S4.5) – a fast and routine calculation, as detailed in Table S4 of the ESI,† which compares the associated computational cost and accuracy. The quantities L_p and L_pp are often mistakenly conflated in discussions of design rules, while they are largely uncorrelated, as explicitly shown in Fig. 2(e). In practice, chain stiffness is not a particularly desirable attribute, whereas long-range planarity is crucial. To illustrate the difference between these two descriptors we visualise selected SCPs across L_p and L_pp ranges, using the common analogy⁴³ with different pasta shapes: (i) SCPs with both large L_p and L_pp, resembling uncooked fettuccine, flat and stiff ribbons; (ii) SCPs with large L_p but small L_pp, comparable to uncooked fusilli; stiff but twisted chains (iii) SCPs with small L_p but large L_pp, similar to cooked fettuccine, locally flat but soft; and (iv) SCPs with both small L_p and L_pp, resembling cooked fusilli pasta, soft and twisted chains.

We now consider an approach to quantify the relative importance of electrostatic disorder, arising from intra- and inter-chain electrostatic interactions, and the electronic coupling disorder, which is caused by disruptions in π-conjugation along the polymer backbone, to the total disorder. To determine the two contributions from the DOS, we fit a model DOS to the computed DOS using a purely electronically disordered Hamiltonian of ten states, with one state |i〉 per site (RU) i and nearest-neighbour coupling

where α_i and β_i are random variables distributed normally around average values α and β with standard deviations σ(α) and σ(β), representing the on-site energies and inter-site couplings (and disorder in each), respectively (see Method for details). Fig. 3(a) (provides an illustrative representation of the model, along with an example) of the simultaneous fitting applied to both “iso” and “embd” models.

Fig. 3 (a) Schematic representation of the reduced model used to quantify electrostatic and coupling disorder, along with an example of the fitting process applied to “iso” and “embd” models. (b) Correlation between the ratio of coupling (β) to the diagonal disorder (σ(α)), and the localisation length (LL) for “embd” models (S = 0.83). (c) Correlation between the difference of on-site disorder of “embd” and “iso” models (representing the energetic effect of the environment) and μ^GAS, which can be rapidly computed from the chemical structure (S = 0.85). The colour-map illustrates the electrostatic potential distribution around two example repeat units, one with relatively low and the other with high environmental electrostatic disorder.

Mapping an extremely complex system into a reduced model with only four physically intuitive parameters offers significant advantages in rationalising the SCP materials class. For instance, it is evident that the on-site disorder, σ(α), is consistently larger than the disorder in the inter-site coupling, σ(β), with an average σ(α)/σ(β) ratio of 5.2 (the distribution is shown in Fig. S6, ESI†). This approach allows us to determine the range of parameters observed across the systems studied and identify the achievable optimum for each.⁴⁴ For example, σ(α) spans from 0.09 to 0.31 eV, while β ranges from 0.02 to 0.21 eV (Fig. S6, ESI†). Since there is a negligible correlation between them (S = 0.05), they can be optimised separately to maximise the ratio β/σ(α), which has a very strong correlation (S = 0.83) with the localisation length shown in Fig. 3(b). It is worth noting that β is a property that can be readily computed for an isolated chain, while σ(α) has an intra-molecular component, driven by the individual chain conformation discussed earlier, and an inter-molecular component which is explored next.

It was noted in Fig. 1(e) that the electrostatic environment has an impact on the LL(embd) ranging from small to considerable, one of the elements complicating the straightforward rationalisation of SCP properties. In the 4-parameter model, this translates into a broad distribution of on-site disorder values, with σ(α)^EMB–σ(α)^ISO ranging from 0.025 to 0.20 eV across the polymers considered, with nearly identical average values for p-type and n-type systems. Interestingly, it is possible to predict the electrostatic effect of the environment based on the electrostatic properties of the isolated RU. As shown in Fig. 3(c), there is a very strong correlation (S = 0.85) between σ(α)^EMB–σ(α)^ISO and the dipole moment of the isolated RU, μ^GAS, a simple indicator of the electrostatic “noise” caused by the environment (ESI,† Section S3.3). This consideration can be integrated into polymer design since also this quantity can be rapidly obtained from the chemical structure of the RU.

The study presented so far shows that better SCPs can be designed to remain planar over a longer distance, have large effective coupling along the chain, and be subject to a smaller electrostatic disorder from the environment. Because of the sizeable dataset, we can derive a machine learning (ML) method to predict LL from easy-to-compute quantities, enabling an ultra-rapid screening of potentially interesting polymers. To estimate the LL, we use three descriptors: (1) coupling (β) computed from a single point electronic structure calculation (ESI,† Section S5), (2) μ^GAS from atomic charges and optimised structure of the RU, and (3) the L_pp computed from a small-scale MD simulation of dimers (ESI,† Section S4). We used the Random Forest algorithm⁴⁵ to predict LL(embd) from these descriptors, selecting one-third of the dataset as a test set to validate the model (see details in Method). Such a simple model based on only three independent input parameters can effectively rank SCPs based on LL(embd) (Fig. 4(left)), with no SCPs from the top third of LL(embd) values being misclassified into the lowest third category. This is a promising outcome for such computationally inexpensive calculations. The ML study serves as a robust coarse-level screening tool, more than an order of magnitude faster than full calculations (an analysis of the computational cost is provided in ESI,† Section S7). It is ideal for screening thousands of SCPs, while full calculations-including MD and QC – can be reserved for the best candidates selected after the initial ML evaluation. Additionally, a Random Forest model also provides the relative importance of its input parameters, which can be translated into the relative strength of each design principle. As shown in Fig. 4(right), while coupling and electrostatic effects of the environment exhibit comparable impacts, the planarity persistence length emerges as the dominant factor due to its strong correlation with LL, as illustrated in Fig. 2(c). Furthermore, the present ML model is developed for undoped linear SCPs and different classes require dedicated alternative data sets. In particular, the highly relevant area of doped SCPs would require the inclusion of additional factors such as the chemical nature of the dopant, their concentration and interaction with the charge carriers.

Fig. 4 (left) Comparison of predicted localisation length from the machine learning model, LL(ML), with the calculated localisation length from the QM/MM method, LL(embd), for a test set comprising one-third of the dataset. The upper half of each circle represents LL(embd), while the lower half shows the ML prediction. The model achieves an average root mean squared error of 3.87 Å, an average cross-validated root mean squared error of 4.02 Å, and an average Spearman rank correlation coefficient of 0.85 across five independent test-set selections. (right) Feature importance analysis in the machine learning study, showing the relative contribution of each input variable to the model's predictive performance, quantifying how much each feature improves the accuracy of the predictions.

While β and μ^GAS are intrinsic molecular properties, L_pp is also primarily governed by the chemical structure of the polymer, as supported by the strong correlation observed across different calculations, including torsional potential calculations (gas phase), “soup” simulations, and melt models (ESI,† Section S4). Nevertheless, L_pp may still be influenced by processing under certain conditions. Although our current analysis focuses on identifying key structure–property relationships under near-equilibrium conditions, processing-induced changes in planarity and charge transport could be a valuable direction for future investigation. The MD-based methods employed here can be extended to explore how conditions such as solvent evaporation or thermal annealing impact L_pp, opening up pathways for experimental control and optimisation. Furthermore, the present ML model is developed for intrinsic, undoped linear SCPs and extension to doped systems, where additional factors such as dopant interactions and concentration must be considered, is an important direction for future work.

Conclusion and outlook

We have used a homogeneous and large set of high-quality polymer models to derive a comprehensive analysis of the key features determining charge transport in semiconducting polymers. Unlike studies focused on one or a few polymers, this approach provides statistically significant insights and can be used to test specific research hypotheses relevant to the design of this material class. For example, we found that the stiffness of the polymer chain does not significantly affect charge transport. In contrast, the primary factor contributing to greater charge delocalisation and a smaller tail in the density of states is the planarity persistence length (L_pp), which is the best measure of intra-chain disorder and easily evaluated in silico. Delocalisation along the chain increases with higher effective coupling between repeat units (β), another property that can be rapidly assessed in the early stages of polymer design. Inter-chain electrostatic interactions vary in importance depending on the polymer, but their relevance can be determined from the electrostatic properties of the isolated repeat units.

This work provides a hierarchy of methodologies that can be used to screen polymers depending on the desired accuracy: descriptors for screening thousands, the atomistic soup model for hundreds, or full atomistic models for tens of SCPs. The throughput and automation of these methods are unprecedented for semiconducting polymers and enable, for the first time, a continuous feedback loop between modelling and experimentation. Theoretical predictions can be now considered much faster than synthesis and characterisation. This throughput also facilitates the adoption of advanced ML methods for result analysis, not only based on patterns in chemical structures but also on the most relevant and easily computable physical properties, advancing in silico design beyond the current paradigm of incremental optimisation of existing material structures.⁴⁶ Finally, there are no inherent limitations in applying these methods to extract various properties (e.g., optical,⁴⁷ thermoelectric,⁴⁸ and mechanical⁴⁹), including electronic processes such as doping⁵⁰ or inter-chain charge transfer.²⁵

Method

The full list of SCPs considered here is provided in ESI,† Section S1. We employed a standardised SCP naming convention: each monomer has a unique abbreviation (mentioned in Fig. 1(a)), with regio-regularity (if relevant) specified as l or r, the monomer sequence matches the repeat unit label, and sidechain details, grouped as linear (a) or branched alkyl (b), are included in brackets. For instance, IDT(a16x4)_lBTF represents a repeat unit of IDT and lBTF, where IDT has four linear sidechains, each 16 carbons long.

Simulation workflow used across 105 SCPs includes four stages: (i) force field development and “soup” model construction, (ii) 1 μs molecular dynamics (MD) simulation at 500 K and 1 bar, (iii) 200 samples taken from the trajectory made in (ii) and cooled down to 300 K in 1 ns to generate input models for quantum chemistry (QC) calculations, and (iv) QC calculations on all input models to obtain average density of states (DOS) and localisation length (LL). A summary of the methods used is provided in ESI,† Section S2, and details in ref. 32. Model validation is explained in ESI,† Section S3.

Polymer persistence length (L_p) is defined as the distance over which correlations in the direction of the tangent are lost. We use a standard way of calculation:⁵¹ the angles, θ, between the tangents of monomers at distances ranging from L₁ to L_N (where N is the total number of monomers in chain) are calculated and averaged over 200 chain models. An exponential decay function, 〈cos(θ)〉 = exp(−L_N/L_p), is then fitted. From this fit, L_p is determined. Details including examples of polymers with relatively low and high L_p are provided in ESI,† Section S4.1.

Polymer planarity persistence length (L_pp) defined as the length along the polymer over which chain planarity is lost. This is quantified by calculating the relative angles between the normal vectors to the monomer planes along the chain. Details of the method are provided in ESI,† Section S4.2. Instead of extracting the actual angles between all monomers along the chain, e.g., θ¹⁻², θ¹⁻³,…, θ^1−N, N = number of monomers in a chain, to create angle distributions, one can also estimate L_pp by convolving the angle distributions of only neighbouring monomers from MD simulation, L^MD_pp, or Boltzmann distribution obtained from torsional potential calculated in gas phase, L^GAS_pp. The details of these methods are provided in ESI,† Sections S4.3–S4.5.

Reduced models of the polymer electronic structure were generated in two stages: (i) finding initial values of parameters α and β by fitting the eigenvalues of a tight-binding disorder-less Hamiltonian to the DFT-computed orbital energies of the periodic, rigid 10-mer, (ii) using a simulated annealing algorithm to fit DOS derived from a 6-parameters tight-binding Hamiltonian including disorder to DOS computed from full QM/MM models. Further details of the above procedure are provided in ESI,† Section S5.

For machine learning (ML) study, we employed a Random forest regressor to predict the LL(embd) of SCPs using a dataset containing three molecular descriptors: β (coupling, calculated by method explained ESI,† Section S5), L_pp (obtained from small MD simulation of dimers explained in ESI,† Section S4.5), and μ^GAS (from single-point calculation on repeat unit in vacuum). The data was subjected to multiple train-test splits using five different randomised splits to ensure robustness in the model's performance evaluation. Each split involved scaling the features using a standard scaler, training the Random Forest model with 100 estimators, and subsequently predicting the target variable on the test set. The model's performance was assessed using mean squared error (MSE), cross-validated MSE (with five folds), and Spearman's rank correlation coefficient.

Data availability

Simulation files, including structure and force field for all 105 SCPs, simulation files of initial and equilibrated “soup” models for 5 SCPs, MD parameter files, and a CSV spreadsheet with all the plotted quantities for each SCP in the paper are available at https://github.com/HMakkiMD/SCP_HT. A README file is also provided, detailing a simple guide to navigate through the steps.

All scripts necessary to reproduce the data presented in the paper, including those for density of states (DOS), localization lengths (LL), descriptors (such as tail and band (half) widths (WT and WB), LL(E), persistence length (L_p), planarity persistence length (L_pp), dipole moments (μ^GAS)), reduced tight-binding models, and machine learning analysis based on random forest, are available at https://github.com/HMakkiMD/SCP_HT. The codes for QC/MD calculations encompassing force field development and model construction, input generation for QC calculations, and codes for density of states and localisation length calculations are available at https://github.com/HMakkiMD/GAMMPS.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the support from the European Research Council (grant no. 101020369).

References

1. Y. Zheng, S. Zhang, J. B.-H. Tok and Z. Bao, Molecular Design of Stretchable Polymer Semiconductors: Current Progress and Future Directions, J. Am. Chem. Soc., 2022, 144(11), 4699–4715,  DOI:10.1021/jacs.2c00072.
2. L. Ding, Z.-D. Yu, X.-Y. Wang, Z.-F. Yao, Y. Lu, C.-Y. Yang, J.-Y. Wang and J. Pei, Polymer Semiconductors: Synthesis, Processing, and Applications, Chem. Rev., 2023, 123(12), 7421–7497,  DOI:10.1021/acs.chemrev.2c00696.
3. H. Bronstein, C. B. Nielsen, B. C. Schroeder and I. McCulloch, The Role of Chemical Design in the Performance of Organic Semiconductors, Nat. Rev. Chem., 2020, 4(2), 66–77,  DOI:10.1038/s41570-019-0152-9.
4. J. F. Coker, S. Moro, A. S. Gertsen, X. Shi, D. Pearce, M. P. Van Der Schelling, Y. Xu, W. Zhang, J. W. Andreasen, C. R. Snyder, L. J. Richter, M. J. Bird, I. McCulloch, G. Costantini, J. M. Frost and J. Nelson, Perpendicular Crossing Chains Enable High Mobility in a Noncrystalline Conjugated Polymer, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(37), e2403879121,  DOI:10.1073/pnas.2403879121.
5. J. Mun, Y. Ochiai, W. Wang, Y. Zheng, Y.-Q. Zheng, H.-C. Wu, N. Matsuhisa, T. Higashihara, J. B.-H. Tok, Y. Yun and Z. Bao, A Design Strategy for High Mobility Stretchable Polymer Semiconductors, Nat. Commun., 2021, 12(1), 3572,  DOI:10.1038/s41467-021-23798-2.
6. S. Moro, N. Siemons, O. Drury, D. A. Warr, T. A. Moriarty, L. M. A. Perdigão, D. Pearce, M. Moser, R. K. Hallani, J. Parker, I. McCulloch, J. M. Frost, J. Nelson and G. Costantini, The Effect of Glycol Side Chains on the Assembly and Microstructure of Conjugated Polymers, ACS Nano, 2022, 16(12), 21303–21314,  DOI:10.1021/acsnano.2c09464.
7. Z. Cao, S. A. Tolba, Z. Li, G. T. Mason, Y. Wang, C. Do, S. Rondeau-Gagné, W. Xia and X. Gu, Molecular Structure and Conformational Design of Donor–Acceptor Conjugated Polymers to Enable Predictable Optoelectronic Property, Adv. Mater., 2023, 35(41), 2302178,  DOI:10.1002/adma.202302178.
8. R. Noriega, J. Rivnay, K. Vandewal, F. P. V. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, A General Relationship between Disorder, Aggregation and Charge Transport in Conjugated Polymers, Nat. Mater., 2013, 12(11), 1038–1044,  DOI:10.1038/nmat3722.
9. S. Fratini, M. Nikolka, A. Salleo, G. Schweicher and H. Sirringhaus, Charge Transport in High-Mobility Conjugated Polymers and Molecular Semiconductors, Nat. Mater., 2020, 19(5), 491–502,  DOI:10.1038/s41563-020-0647-2.
10. D. Venkateshvaran, M. Nikolka, A. Sadhanala, V. Lemaur, M. Zelazny, M. Kepa, M. Hurhangee, A. J. Kronemeijer, V. Pecunia, I. Nasrallah, I. Romanov, K. Broch, I. McCulloch, D. Emin, Y. Olivier, J. Cornil, D. Beljonne and H. Sirringhaus, Approaching Disorder-Free Transport in High-Mobility Conjugated Polymers, Nature, 2014, 515(7527), 384–388,  DOI:10.1038/nature13854.
11. M. Nikolka, K. Broch, J. Armitage, D. Hanifi, P. J. Nowack, D. Venkateshvaran, A. Sadhanala, J. Saska, M. Mascal, S.-H. Jung, J. Lee, I. McCulloch, A. Salleo and H. Sirringhaus, High-Mobility, Trap-Free Charge Transport in Conjugated Polymer Diodes, Nat. Commun., 2019, 10(1), 2122,  DOI:10.1038/s41467-019-10188-y.
12. X. Yan, M. Xiong, X.-Y. Deng, K.-K. Liu, J.-T. Li, X.-Q. Wang, S. Zhang, N. Prine, Z. Zhang, W. Huang, Y. Wang, J.-Y. Wang, X. Gu, S. K. So, J. Zhu and T. Lei, Approaching Disorder-Tolerant Semiconducting Polymers, Nat. Commun., 2021, 12(1), 5723,  DOI:10.1038/s41467-021-26043-y.
13. V. Rühle, J. Kirkpatrick and D. Andrienko, A Multiscale Description of Charge Transport in Conjugated Oligomers, J. Chem. Phys., 2010, 132(13), 134103,  DOI:10.1063/1.3352568.
14. N. E. Jackson, K. L. Kohlstedt, B. M. Savoie, M. Olvera De La Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, Conformational Order in Aggregates of Conjugated Polymers, J. Am. Chem. Soc., 2015, 137(19), 6254–6262,  DOI:10.1021/jacs.5b00493.
15. L. Wilbraham, E. Berardo, L. Turcani, K. E. Jelfs and M. A. Zwijnenburg, High-Throughput Screening Approach for the Optoelectronic Properties of Conjugated Polymers, J. Chem. Inf. Model., 2018, 58(12), 2450–2459,  DOI:10.1021/acs.jcim.8b00256.
16. P. Friederich, A. Fediai, S. Kaiser, M. Konrad, N. Jung and W. Wenzel, Toward Design of Novel Materials for Organic Electronics, Adv. Mater., 2019, 31(26), 1808256,  DOI:10.1002/adma.201808256.
17. D. Abbaszadeh, A. Kunz, N. B. Kotadiya, A. Mondal, D. Andrienko, J. J. Michels, G.-J. A. H. Wetzelaer and P. W. M. Blom, Electron Trapping in Conjugated Polymers, Chem. Mater., 2019, 31(17), 6380–6386,  DOI:10.1021/acs.chemmater.9b01211.
18. M. Matta, R. Wu, B. D. Paulsen, A. J. Petty, R. Sheelamanthula, I. McCulloch, G. C. Schatz and J. Rivnay, Ion Coordination and Chelation in a Glycolated Polymer Semiconductor: Molecular Dynamics and X-Ray Fluorescence Study, Chem. Mater., 2020, 32(17), 7301–7308,  DOI:10.1021/acs.chemmater.0c01984.
19. V. Lemaur, J. Cornil, R. Lazzaroni, H. Sirringhaus, D. Beljonne and Y. Olivier, Resilience to Conformational Fluctuations Controls Energetic Disorder in Conjugated Polymer Materials: Insights from Atomistic Simulations, Chem. Mater., 2019, 31(17), 6889–6899,  DOI:10.1021/acs.chemmater.9b01286.
20. W. Michaels, Y. Zhao and J. Qin, Atomistic Modeling of PEDOT:PSS Complexes I: DFT Benchmarking, Macromolecules, 2021, 54(8), 3634–3646,  DOI:10.1021/acs.macromol.1c00351.
21. N. Siemons, D. Pearce, C. Cendra, H. Yu, S. M. Tuladhar, R. K. Hallani, R. Sheelamanthula, G. S. LeCroy, L. Siemons, A. J. P. White, I. McCulloch, A. Salleo, J. M. Frost, A. Giovannitti and J. Nelson, Impact of Side-Chain Hydrophilicity on Packing, Swelling, and Ion Interactions in Oxy-Bithiophene Semiconductors, Adv. Mater., 2022, 34(39), 2204258,  DOI:10.1002/adma.202204258.
22. T. Sedghamiz, A. Y. Mehandzhiyski, M. Modarresi, M. Linares and I. Zozoulenko, What Can We Learn about PEDOT:PSS Morphology from Molecular Dynamics Simulations of Ionic Diffusion?, Chem. Mater., 2023, 35(14), 5512–5523,  DOI:10.1021/acs.chemmater.3c00873.
23. R. Alessandri and J. J. De Pablo, Prediction of Electronic Properties of Radical-Containing Polymers at Coarse-Grained Resolutions, Macromolecules, 2023, 56(10), 3574–3584,  DOI:10.1021/acs.macromol.3c00141.
24. H. Makki, C. A. Burke and A. Troisi, Microstructural Model of Indacenodithiophene- Co -Benzothiadiazole Polymer: π-Crossing Interactions and Their Potential Impact on Charge Transport. J. Phys, Chem. Lett., 2023, 14(39), 8867–8873,  DOI:10.1021/acs.jpclett.3c02305.
25. G. LeCroy, R. Ghosh, P. Sommerville, C. Burke, H. Makki, K. Rozylowicz, C. Cheng, M. Weber, W. Khelifi, N. Stingelin, A. Troisi, C. Luscombe, F. C. Spano and A. Salleo, Using Molecular Structure to Tune Intrachain and Interchain Charge Transport in Indacenodithiophene-Based Copolymers, J. Am. Chem. Soc., 2024, 146(31), 21778–21790,  DOI:10.1021/jacs.4c06006.
26. N. Siemons, D. Pearce, H. Yu, S. M. Tuladhar, G. S. LeCroy, R. Sheelamanthula, R. K. Hallani, A. Salleo, I. McCulloch, A. Giovannitti, J. M. Frost and J. Nelson, Controlling Swelling in Mixed Transport Polymers through Alkyl Side-Chain Physical Cross-Linking, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(35), e2306272120,  DOI:10.1073/pnas.2306272120.
27. A. Wadsworth, H. Chen, K. J. Thorley, C. Cendra, M. Nikolka, H. Bristow, M. Moser, A. Salleo, T. D. Anthopoulos, H. Sirringhaus and I. McCulloch, Modification of Indacenodithiophene-Based Polymers and Its Impact on Charge Carrier Mobility in Organic Thin-Film Transistors, J. Am. Chem. Soc., 2020, 142(2), 652–664,  DOI:10.1021/jacs.9b09374.
28. H. Bronstein, Z. Chen, R. S. Ashraf, W. Zhang, J. Du, J. R. Durrant, P. Shakya Tuladhar, K. Song, S. E. Watkins, Y. Geerts, M. M. Wienk, R. A. J. Janssen, T. Anthopoulos, H. Sirringhaus, M. Heeney and I. McCulloch, Thieno[3,2- b]thiophene−Diketopyrrolopyrrole-Containing Polymers for High-Performance Organic Field-Effect Transistors and Organic Photovoltaic Devices, J. Am. Chem. Soc., 2011, 133(10), 3272–3275,  DOI:10.1021/ja110619k.
29. T. Lei, J.-Y. Wang and J. Pei, Design, Synthesis, and Structure–Property Relationships of Isoindigo-Based Conjugated Polymers, Acc. Chem. Res., 2014, 47(4), 1117–1126,  DOI:10.1021/ar400254j.
30. A. Giovannitti, C. B. Nielsen, D.-T. Sbircea, S. Inal, M. Donahue, M. R. Niazi, D. A. Hanifi, A. Amassian, G. G. Malliaras, J. Rivnay and I. McCulloch, N-Type Organic Electrochemical Transistors with Stability in Water, Nat. Commun., 2016, 7(1), 13066,  DOI:10.1038/ncomms13066.
31. K. J. Thorley and C. B. Nielsen, Conformational Analysis of Conjugated Organic Materials: What Are My Heteroatoms Really Doing, ChemPlusChem, 2024, 89(6), e202300773,  DOI:10.1002/cplu.202300773.
32. C. Burke, H. Makki and A. Troisi, From Chemical Drawing to Electronic Properties of Semiconducting Polymers in Bulk: A Tool for Chemical Discovery, J. Chem. Theory Comput., 2024, 20(9), 4019–4028,  DOI:10.1021/acs.jctc.3c01417.
33. T. Qin and A. Troisi, Relation between Structure and Electronic Properties of Amorphous MEH-PPV Polymers, J. Am. Chem. Soc., 2013, 135(30), 11247–11256,  DOI:10.1021/ja404385y.
34. R. P. Fornari and A. Troisi, Narrower Bands with Better Charge Transport: The Counterintuitive Behavior of Semiconducting Copolymers, Adv. Mater., 2014, 26(45), 7627–7631,  DOI:10.1002/adma.201402941.
35. R. Manurung and A. Troisi, Screening Semiconducting Polymers to Discover Design Principles for Tuning Charge Carrier Mobility, J. Mater. Chem. C, 2022, 10(38), 14319–14333,  10.1039/D2TC02527B.
36. S. Prodhan, R. Manurung and A. Troisi, From Monomer Sequence to Charge Mobility in Semiconductor Polymers via Model Reduction, Adv. Funct. Mater., 2023, 33(36), 2303234,  DOI:10.1002/adfm.202303234.
37. R. Noriega, A. Salleo and A. J. Spakowitz, Chain Conformations Dictate Multiscale Charge Transport Phenomena in Disordered Semiconducting Polymers, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(41), 16315–16320,  DOI:10.1073/pnas.1307158110.
38. P. Carbone and A. Troisi, Charge Diffusion in Semiconducting Polymers: Analytical Relation between Polymer Rigidity and Time Scales for Intrachain and Interchain Hopping, J. Phys. Chem. Lett., 2014, 5(15), 2637–2641,  DOI:10.1021/jz501220g.
39. J. Lenz and R. T. Weitz, Charge Transport in Semiconducting Polymers at the Nanoscale, APL Mater., 2021, 9(11), 110902,  DOI:10.1063/5.0068098.
40. T. Lei, J.-H. Dou, X.-Y. Cao, J.-Y. Wang and J. Pei, Electron-Deficient Poly(p-Phenylene Vinylene) Provides Electron Mobility over 1 cm² V⁻¹ s⁻¹ under Ambient Conditions, J. Am. Chem. Soc., 2013, 135(33), 12168–12171,  DOI:10.1021/ja403624a.
41. A. Onwubiko, W. Yue, C. Jellett, M. Xiao, H.-Y. Chen, M. K. Ravva, D. A. Hanifi, A.-C. Knall, B. Purushothaman, M. Nikolka, J.-C. Flores, A. Salleo, J.-L. Bredas, H. Sirringhaus, P. Hayoz and I. McCulloch, Fused Electron Deficient Semiconducting Polymers for Air Stable Electron Transport, Nat. Commun., 2018, 9(1), 416,  DOI:10.1038/s41467-018-02852-6.
42. P. W. Anderson, Absence of Diffusion in Certain Random Lattices, Phys. Rev., 1958, 109(5), 1492–1505,  DOI:10.1103/PhysRev.109.1492.
43. E. Ratcliff and N. Stingelin, Terra Incognita Unravelled, Nat. Mater., 2025, 24(1), 10–11,  DOI:10.1038/s41563-024-02047-z.
44. T. Nematiaram, D. Padula, A. Landi and A. Troisi, On the Largest Possible Mobility of Molecular Semiconductors and How to Achieve It, Adv. Funct. Mater., 2020, 30(30), 2001906,  DOI:10.1002/adfm.202001906.
45. L. Breiman, Random Forests, Mach. Learn., 2001, 45(1), 5–32,  DOI:10.1023/A:1010933404324.
46. N. Fujinuma, B. DeCost, J. Hattrick-Simpers and S. E. Lofland, Why Big Data and Compute Are Not Necessarily the Path to Big Materials Science, Commun. Mater., 2022, 3(1), 59,  DOI:10.1038/s43246-022-00283-x.
47. M. Li, A. H. Balawi, P. J. Leenaers, L. Ning, G. H. L. Heintges, T. Marszalek, W. Pisula, M. M. Wienk, S. C. J. Meskers, Y. Yi, F. Laquai and R. A. J. Janssen, Impact of Polymorphism on the Optoelectronic Properties of a Low-Bandgap Semiconducting Polymer, Nat. Commun., 2019, 10(1), 2867,  DOI:10.1038/s41467-019-10519-z.
48. S. N. Patel, A. M. Glaudell, K. A. Peterson, E. M. Thomas, K. A. O’Hara, E. Lim and M. L. Chabinyc, Morphology Controls the Thermoelectric Power Factor of a Doped Semiconducting Polymer, Sci. Adv., 2017, 3(6), e1700434,  DOI:10.1126/sciadv.1700434.
49. J. Y. Oh, S. Rondeau-Gagné, Y.-C. Chiu, A. Chortos, F. Lissel, G.-J. N. Wang, B. C. Schroeder, T. Kurosawa, J. Lopez, T. Katsumata, J. Xu, C. Zhu, X. Gu, W.-G. Bae, Y. Kim, L. Jin, J. W. Chung, J. B.-H. Tok and Z. Bao, Intrinsically Stretchable and Healable Semiconducting Polymer for Organic Transistors, Nature, 2016, 539(7629), 411–415,  DOI:10.1038/nature20102.
50. C. Burke, A. Landi and A. Troisi, The Dynamic Nature of Electrostatic Disorder in Organic Mixed Ionic and Electronic Conductors, Mater. Horiz., 2024, 11(21), 5313–5319,  10.1039/D4MH00706A.
51. L. M. J. Kroon-Batenburg, P. H. Kruiskamp, J. F. G. Vliegenthart and J. Kroon, Estimation of the Persistence Length of Polymers by MD Simulations on Small Fragments in Solution. Application to Cellulose, J. Phys. Chem. B, 1997, 101(42), 8454–8459,  DOI:10.1021/jp971717k.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00485c

---