Beyond the four core effects: revisiting thermoelectrics with a high-entropy design

Abstract

Low-exergy waste heat, which constitutes the majority of industrial-scale thermal losses, remains largely unrecoverable with conventional technologies. Thermoelectrics offer a solid-state solution for converting this hard-to-access energy into electricity, making them attractive for decentralized power generation and sensor applications. High-entropy materials (HEMs) have gained traction as a strategy for better-performing thermoelectrics, but the mechanisms driving their benefits require further exploration. This article highlights key insights for heat and electronic transport in HEMs. For heat transport, we argue that reduced, and often ultralow, lattice thermal conductivity in HEMs—with respect to ordered counterparts—can be taken for granted, emerging naturally as a fifth core effect of high-entropy systems. While band convergence is often considered beneficial for electronic transport, its impact depends strongly on the electronic structure. We summarize the scenarios where it can be detrimental to thermoelectric performance. These insights motivate strategies that align seamlessly with advancements in artificial intelligence and data-driven approaches, helping accelerate the discovery of next-generation thermoelectric materials.

---

Corey Oses

Corey Oses, an assistant professor of materials science and engineering at Johns Hopkins University, leads the Entropy for Energy laboratory focusing on the discovery of materials for clean and renewable energy. Specifically, Oses looks to leverage the stabilizing effects of disorder to innovate clean hydrogen production, waste-heat conversion, nuclear-waste immobilization, and electric grid technologies. He completed his bachelor's degree in applied and engineering physics from Cornell University in 2013 and his PhD in materials science from Duke University in 2018. More information can be found at https://entropy4energy.ai.

Tianhao Li

Tianhao Li is a PhD student in Materials Science and Engineering at the Whiting School of Engineering, Johns Hopkins University. His research centers on computational materials science, with an emphasis on high-entropy materials modeling to accelerate the discovery of next-generation materials. He develops and maintains high-throughput calculation workflows, designs and optimizes C++ algorithms for materials applications, and contributes to the construction and curation of open materials databases. Tianhao earned his BS in Materials Science and Engineering from Changsha University of Science and Technology in 2020 and his MS in the same field from Duke University in 2023.

Xiao Xu

Xiao Xu, a PhD student in materials science and engineering at the Whiting School of Engineering, Johns Hopkins University. His research interests lie in both experimentation and computation. He focuses on developing frameworks for autonomous materials design, artificial intelligence-assisted materials prediction, and synthesizing new materials for green energy. He received his bachelor's degree in materials science and engineering from Southeast University in 2020, and his master's degree in electrical and computer engineering from the University of Texas at Austin in 2023.

Guangshuai Han

Guangshuai Han, a postdoctoral researcher in civil and materials engineering at the Ralph O'Connor Sustainable Energy Institute, Johns Hopkins University. Han focuses on applying artificial intelligence to accelerate the discovery of high-performance materials for hydrogen generation, thermoelectric energy conversion, and environmental safety. His work integrates advanced sensing, computational modeling, and material design to tackle pressing challenges in infrastructure resilience and clean energy. He earned his bachelor's degree from Harbin Institute of Technology and both his master's and PhD in civil engineering from Purdue University.

Guotao Qiu

Guotao Qiu received his PhD in Applied Physics and Materials Engineering from the University of Macau in 2023. He is currently a postdoctoral researcher at Johns Hopkins University, working under the supervision of Prof. Corey Oses. His research focuses on computational materials science, particularly in magnetic materials and high-entropy materials.

Jonathan R. Owens

Jonathan R. Owens received a BSc (2011) in Mathematics from the University of Texas at Austin and MSc (2012) and PhD (2015) degrees in Physics from Rensselaer Polytechnic Institute. Since 2019, after a few years as a software engineer, he has been a scientist at GE Vernova Advanced Research (formerly General Electric Research). His research interests include applications of computational methods for material discovery and characterization, including CO2 and H2O sorbents, thermal barrier coatings, and thermoelectric materials. He is also interested in emerging techniques to enable more accurate computational approaches, such as machine learning and quantum computing.

---

Thermoelectrics are solid-state materials that can convert heat to electricity without moving parts, making them attractive for waste-heat recovery. However, conventional waste-heat recovery is most effective for high-temperature sources, which possess substantial exergy—a measure of usable energy relative to the surroundings.¹ High-temperature industrial systems, such as those in natural-gas combined-cycle power plants, already operate close to thermodynamic limits, leaving little room for thermoelectric integration. Instead, thermoelectrics offer a promising approach to harnessing low-grade waste heat, the majority (>80%) of which remains below 200 °C in industrial settings.^2,3 While less efficient than high-temperature recovery technologies, their scalability and reliability make them ideal for decentralized energy harvesting.

Low-power sensors that need to monitor a power-generation system hold promise as one useful application. For example, the combustor in a natural-gas power plant has acoustic sensors that monitor the combustion process, analyzing the signal for problematic anomalies.^4,5 A sensor attached to the combustor that is self-powering could be beneficial. Adding a component to a well-established, hardened system requires that the sensor exhibit high reliability. Thermoelectric devices are particularly attractive in this context due to their solid-state nature and lack of moving parts, making them well-suited for long-term deployment with minimal maintenance.

Another application proposed by the authors is thermoelectric integration in semiconductor switches for power conversion devices, such as high-voltage direct-current (HVDC) converters. These switches operate at high frequencies and, despite active cooling, maintain a temperature gradient of around 100 °C between the semiconductor junction and the heat sink.⁶ By placing a thermoelectric device at the base plate, some of this energy can be recovered. In gigawatt-scale systems, even modest conversion efficiencies could yield up to a half megawatt of reclaimed power.

These potential applications underscore the need for continuous advancements in thermoelectric materials to enhance their efficiencies and integration feasibility. In this context, high-entropy strategies have gained attention as a promising approach to thermoelectric materials design, offering low thermal conductivity and tunable electronic properties. However, common assumptions about high-entropy thermoelectrics often overlook the underlying mechanisms that govern their transport behavior. This work is structured as follows: it begins with a brief introduction to high-entropy materials and their thermoelectric properties. The merits of high-entropy strategies are then examined through the lens of heat and electronic transport. Finally, key insights are summarized, motivating potential directions for future research and materials discovery (Fig. 1).

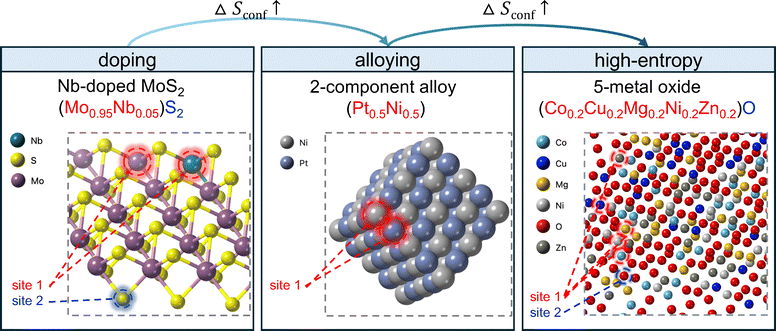Fig. 1 A schematic representation of doping,⁷ alloying,⁸ and high-entropy⁹ approaches in materials design. The transition from doping to alloying to high-entropy materials corresponds to an increase in configurational entropy (ΔS_conf). As additional elements are incorporated into equivalent lattice sites, the system's entropy rises, stabilizing multi-element solid solutions and enhancing chemical disorder. Doping also has context-specific definitions: e.g., in semiconductors, doping serves the purpose of changing the charge carrier concentrations and shifting energy bands.

Definitions

High-entropy materials (HEMs)

Materials with (near-)equimolar mixing of multiple elements sharing crystallographic sites are defined as high-entropy materials (HEMs).^10–13 The random distribution of multiple components raises configurational entropy, contributing to materials formation and stabilization.¹⁴ Consequently, a stable phase is obtained that couples long-range structural order with localized compositional complexity. Entropy stabilization gives rise to new and sometimes counter–intuitive mixtures that would otherwise phase separate, providing a flexible platform for compositional engineering.¹⁰ Intriguing properties emerge, such as high mechanical strength,^15,16 enhanced chemical stability,^10,16,17 low thermal conductivity,^18–21 and high energy storage capability.²²

Thermoelectrics

Thermoelectrics are remarkable solid-state materials that directly convert heat into electricity,^23–26 offering a unique solution for growing clean energy demands.^27–31 The dimensionless figure of merit, which is used to evaluate the performance of thermoelectric materials, is defined as:^28,32where S, σ, κ_l, κ_e and T are the Seebeck coefficient, electrical conductivity, lattice thermal conductivity, electronic thermal conductivity, and absolute temperature, respectively. Commercialized thermoelectric materials include alloys such as Cu–Ni³³ and semiconductors such as Bi₂Te₃.^34,35 Their maximum zT value at room temperature is ∼1.^33,34,36,37 According to eqn (1), a high zT can be obtained by enhancing S and σ while decreasing κ_l and κ_e. The charge carrier's mobility, concentration, and effective mass decide S and σ, and the material's phonon properties dominate κ_l. To improve zT, these factors are manipulated using band engineering,^36,38–42 quantum confinement,^43–45 defect engineering,^46–49 and nano-structuring.^50–53 These efforts aim to develop a material that is an excellent electrical conductor and poor heat conductor, accomplished by simultaneously promoting phonon scattering and inhibiting electron scattering. Unfortunately, electronic and thermal conductivities are positively correlated and present an inherent trade-off for achieving high zT. Therefore, decoupling phonon thermal conductivity from electronic transport while optimizing carrier band structures remains the central objective for thermoelectric materials design.

Understanding phonon transport in HEMs

HEMs are widely recognized for their low thermal conductivities, making them promising candidates for thermoelectric applications.^14,22,54 We propose that this advantage can often be assumed when employing high-entropy design strategies, emerging naturally as another core effect of HEMs. In fact, the four original core effects^55,56 can also contribute to enhanced thermoelectric performance, revealing a powerful platform for novel high-zT materials:

1. High-entropy effect. The high-entropy effect stabilizes a simple solid–solution phase rather than decomposing into multiple intermetallic compounds, a phenomenon attributed to the entropy-driven lowering of the free energy.^15,54 This enhanced phase stability favors higher lattice-symmetry structures,^57–59 which in turn influences electronic structure by creating more opportunities for band degeneracy—potentially augmenting the Seebeck coefficient.⁶⁰

2. Sluggish diffusion. Sluggish diffusion has been regarded as a core effect of HEMs, but its validity has been challenged and remains a topic of debate.⁵⁶ While it does not directly alter phonon scattering mechanisms, sluggish diffusion can indirectly reduce thermal conductivity by stabilizing metastable phases, restricting grain growth (Fig. 2a (ref. 61 and 62)), and preserving defect structures, all of which contribute to increased phonon scattering.^18,63,64

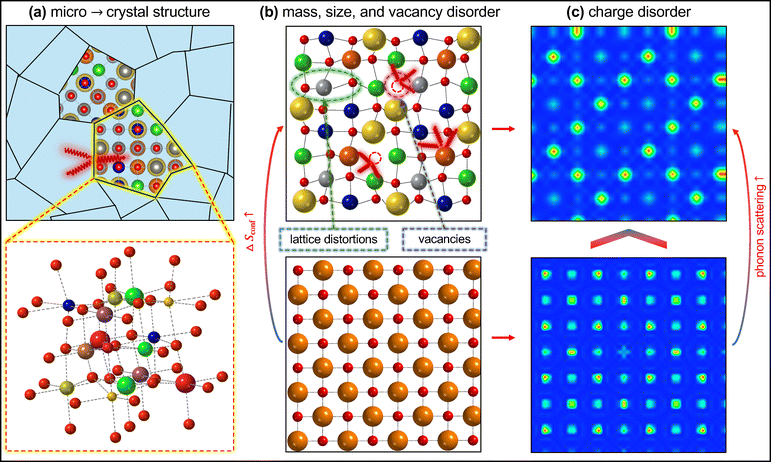Fig. 2 Phonon scattering mechanisms in high-entropy materials. (a) Microstructural complexity in high-entropy materials leading to scattering at the grain boundaries.^61,62 (b) Schematic of the lattice framework illustrating phonon scattering from various types of defects, including atomic mass/size fluctuations and vacancies.⁶⁵ ΔS_conf is the configurational entropy. (c) Electron density map depicting charge disorder—stemming from variations in electronegativity and bonding characteristics among constituent elements—also contributes to localized strain fields and fluctuations in interatomic force constants. Charge disorder plays an important role in phonon scattering, significantly reducing lattice thermal conductivity.¹⁸

3. Severe lattice distortions. Large variations in atomic size, bonding energy, and electronic character among constituents induce severe lattice distortions, enhancing phonon scattering.^54,66,67 This effect arises due to local strain fields caused by the heterogeneous atomic environments in HEMs, leading to fluctuations in interatomic force constants. Such distortions and their effect on thermal conductivity have been demonstrated in studies of (YGdHoErYb)₂Ti₂O₇⁶⁸ and (HfZrTaNbTi)C,⁶⁹ among others.¹⁰

4. Cocktail effect. The cocktail effect refers to synergistic interactions among multiple elements, where their combined influence and indirect microstructural effects (Fig. 2a (ref. 61 and 62)) also enhance phonon scattering.^15,70–72

5. Reduced lattice thermal conductivity. We propose reduced, and often ultralow, lattice thermal conductivity as another core effect of HEMs, arising not as a feature of any particular composition but instead as an emergent property of (high) chemical disorder. The origin of this behavior is discussed in detail in subsequent sections.

Computational investigation of HEMs revealed key mechanisms behind the low thermal conductivity of HEMs.¹⁹ Phonon broadening and scattering have been reported and studied in high-entropy alloys,⁷³ high-entropy oxides,¹⁸ and high-entropy carbides,¹⁹ and are driven by mass and force constant disorder (Fig. 2b). First-principles calculations can isolate these mechanisms by averaging over the masses and force constants separately and analyzing their impact on broadening, scattering, and ultimately the thermal conductivity. Mass disorder plays the dominant role in the phonon-broadening observed in high-entropy alloys and carbides. Both studies echo that force constant disorder also plays an important role in broadening and cannot be ignored. Computational analyses of high-entropy oxides analyzed the impact of different scattering mechanisms with thermal conductivity directly: they resolved the dominant effect to be force constant disorder—not mass disorder—which is induced by local ionic charge variations (Fig. 2b). Experiments confirm that these effects help drive the thermal conductivity toward its theoretical minimum limit.¹⁸ In high-entropy carbides, charge disorder is also found to influence structural features such as the lattice constants and magnitudes of the anion-sublattice distortions accommodating the different metal cations.¹⁹

The influence of force constant disorder—and likewise, charge disorder—in HEMs is a departure from canonical phonon-scattering theory of alloys. Klemens theory considers scattering mechanisms from mass and force constant fluctuations as a function of the differences in atomic mass and radius, respectively, between the host atom and the substitutional defects.^65,74 The mass disorder typically dominants, capturing most of the compositional-dependence of the thermal conductivity without needing to invoke other scattering mechanisms.⁶⁵ The strain effect (per atomic radii differences) is often ignored, as large volume differences are energetically unfavorable and its functional form relies on a wide-varying fitting parameter, making it difficult to estimate. Charge disorder—also inducing localized strain fields—is not usually considered as substitutional disorder typically replaces sites of one component for another of the same charge. While HEMs can be seen as related to—and an extreme case of—solid–solution alloys,⁷⁵ they constitute a new domain with high entropy stabilizing traditionally unfavorable mixtures, giving rise to heterodesmic structures achieving new levels of force constant disorder. These features, coupled with their core effects, distinguish HEMs from lower-entropy counterparts, offering new pathways for high-zT thermoelectrics.

Mass and charge disorder are inherent characteristics of high-entropy, multi-element systems. Even small variations in mass (elements within the same period) or charge (elements from the same group) still increase phonon scattering compared to ordered counterparts. Given that this effect has been observed across different chemistries, we propose reduced lattice thermal conductivity as a fifth core effect of high-entropy materials. We will suggest pathways to leverage this insight toward the design of a more effective search workflow for high-zT thermoelectrics.

Band convergence in HEMs: opportunities and challenges

Given that HEMs inherently exhibit low lattice thermal conductivity, enhancing electronic transport must become the focus for improving thermoelectric performance. Band convergence offers one of the most effective strategies:^76,77 aligning the energies of multiple electronic-band extrema increases the density of states near the Fermi level, boosting charge carrier transport and improving both electrical conductivity and the Seebeck coefficient.⁷⁸

Achieving band convergence in conventional materials typically requires complex band engineering techniques, which can be difficult to fine-tune.^79,80 In contrast, HEMs offer a unique platform for enhanced band convergence through compositional engineering, as illustrated in Fig. 3a. Compared with ordered materials, where band extrema tend to be well-separated, high-entropy systems exhibit band thickening and new band emergence, creating opportunities for band convergence and contributing to a more favorable electronic structure for thermoelectric applications. Band thickening occurs due to the breaking of periodicity in disordered systems, where spectral broadening results from the coexistence of multiple local environments.⁸¹ Band thickening increases the density of states, enhancing carrier concentration and transport efficiency.⁸² New bands emerge with the incorporation of additional components (electrons) into the system, promoting degeneracy and overlap.⁸³

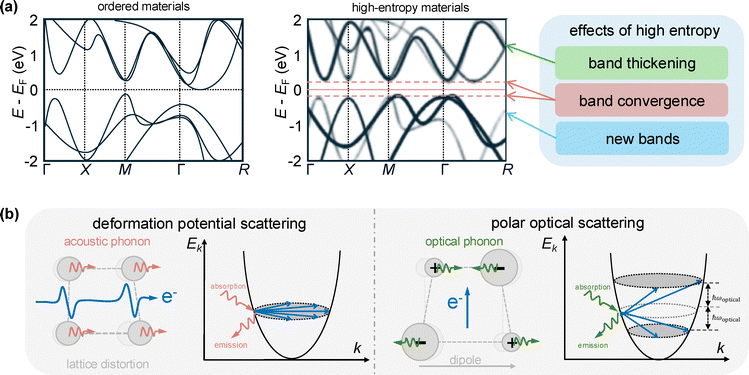Fig. 3 Electronic structure features of high-entropy materials (HEMs) and their impact on band convergence. (a) Comparison between ordered materials and HEMs, where high-entropy effects can induce band thickening, the emergence of new bands, and band convergence at distant k-points rather than at the same k-point, mitigating detrimental interband scattering. An example of band convergence occurs in the illustration near k = Γ, where k is the electron wavevector. The effective band structure illustration is inspired by ref. 78, 81 and 84. (b) Two primary electron–phonon scattering mechanisms—deformation potential scattering and polar-optical scattering—illustrating how phonon interactions can either enhance or limit carrier mobility in the event of band convergence. Achieving favorable band convergence in HEMs requires careful control over electronic structure, balancing enhanced carrier transport with minimized scattering effects. The dispersion illustrations are inspired by Fig. 2.8 in ref. 85. ω is the phonon mode frequency.

While band convergence can occur in HEMs, its impact on thermoelectric performance is more complex compared to their consistently beneficial low lattice thermal conductivity. Park, Snyder, and Jain systematically challenged the assumption that band convergence universally enhances thermoelectric properties.⁸⁶ Computational analysis of the CaMg₂Sb₂–CaZn₂Sb₂ Zintl system demonstrates that when bands converge to the same k-point, interband electron–phonon scattering can intensify, suppressing power factor (S²σ in eqn (1)), reducing carrier mobility, and negating expected benefits of band convergence. In contrast, band convergence at distant k-points—exemplified by full-Heusler Sr₂ SbAu—minimizes such scattering effects, preserving high electrical conductivity and improving overall thermoelectric performance.

As illustrated in Fig. 3b, two primary electron–phonon scattering mechanisms govern the impact of band convergence on transport properties.

• Deformation potential scattering (DPS) arises from phonon-driven lattice distortions that shift electrons to new states.^87,88 While both acoustic (neighbors oscillating in phase) and optical phonons (out-of-phase oscillations) can induce DPS, the original theory⁸⁷ is built on acoustic phonons, which are assumed to dominant, and is routinely calculated using first-principles software packages.^89–92 When band convergence occurs at a single k-point, zone–center acoustic phonons can drive interband transitions, enhancing DPS and thereby reducing carrier mobility and the Seebeck coefficient.⁸⁶ In contrast, if convergence occurs at distant k-points, only higher-energy and sparsely-populated zone–boundary phonons can couple them; interband DPS thus remains weak, preserving both mobility and the Seebeck coefficient.⁸⁶

• Polar–optical scattering (POS) occurs from electrons interacting with the polarization field generated by optical phonons of ionically-bonded atoms.^88,93,94 The general interaction between a charged particle and a polarizable medium constitutes a polaron.⁹⁵ This type of scattering is also routinely calculated using first-principles software packages.^89–92 As bands converge to the same k-point, POS characteristically intensifies since scattering rates ∝ |k − k′|⁻².⁸⁶ Conversely, POS coupling is negligible between states at distant k-points and transport properties are largely preserved.

Zunger's work on random alloys provides additional support for this conclusion,⁸¹ as the effective band structure method revealed that excessive electronic scattering in highly disordered systems can counteract the benefits of increased density of states. If band convergence occurs within a highly disordered HEM, the resulting electronic localization and enhanced scattering can degrade carrier mobility rather than enhance it, further reinforcing the need for careful electronic structure design in high-entropy thermoelectrics. Meanwhile, experimental studies confirm that high-entropy strategies can effectively enhance thermoelectric performance, achieving significant zT improvements through band convergence and entropy-driven phonon scattering.^78,96,97 For instance, Pb- and Ge-based systems have achieved remarkable zT values as high as 2.7—a 30% enhancement over low-entropy counterparts—demonstrating the potential of entropy engineering in thermoelectrics.^14,39,97,98 However, it remains unclear whether current designs represent the optimal utilization of high-entropy features for thermoelectric applications.

Perspectives on future strategies for high-entropy thermoelectrics

Thermoelectric materials offer promising solutions for energy harvesting, waste heat recovery, and power generation. However, low thermoelectric figures of merit remains a fundamental challenge. High-entropy strategies introduce a new design paradigm, offering significant tunability in carrier transport/scattering and band structure.

To further optimize high-entropy thermoelectrics, several key research directions should be prioritized:

• Quantifying the roles of phonon transport contributions. Lattice thermal conductivity in HEMs is inherently reduced with respect to ordered counterparts, arising from the complex local chemical environments in multi-element systems. It has been shown that, in high-entropy oxides, charge disorder plays the dominant role in driving lattice thermal conductivity to near-theoretical minima.¹⁸ This observation is both intriguing and surprising, given that mass disorder typically dominants in conventional scattering theory of alloys.^65,74 More studies are needed across other high-entropy chemistries to clarify the mechanisms responsible for their low thermal conductivities. Correlations between compositional features and thermal conductivity can be resolved quantitatively using data-driven approaches.^99–101 Mass disorder is easily captured by the mass-fluctuation phonon scattering parameter.⁷⁴ We suggest the development of similar parameters quantifying local charge fluctuations, deriving from elemental properties such as electronegativity, valence electron count, oxidation state, and ionic radius. Metrics such as the compositionally-weighted standard deviation and range, along with more complex functional forms,^102,103 can be encoded into compact scalar features capturing the complex bonding in HEMs.

• Employing the fifth core effect. Current search workflows for high- zT thermoelectrics typically calculate and filter by the lattice thermal conductivity. The challenge is that HEMs demand high-fidelity modeling frameworks: e.g., the virtual crystal approximation proved ineffective across studies.^18,73 Instead, supercell-based models are required^75,104,105 that, when integrated with phonon-Boltzmann workflows for the lattice thermal conductivity,^106–109 become prohibitively expensive. A more effective strategy would prioritize enhancing electron transport instead and, among top candidates, further filter for those that offer the widest ranges of elemental masses and electronegativities to minimize phonon transport.

• Electronic band structure descriptors. Resolving the HEM effective band structure⁸¹ is computationally expensive and rarely done in practice.^96,110,111 Moreover, the vast chemical space of HEMs is far too large for rigorous electron-Boltzmann calculations within a density functional theory framework.^89,91,112 This underscores the need for the development of descriptors enabling rapid screening of new HEM compositions. For example, proven computational descriptors such as the entropy-forming-ability (EFA) and disordered enthalpy–entropy descriptor (DEED) have validated formabilities of 60+ compositions and delivered 19 new high-entropy ceramics since 2018.^15,113,114 Similar descriptors can be designed to capture the electronic structure and transport of HEMs that, when combined with EFA and DEED, form a uniquely powerful framework for discovery. Such an approach would map theoretical performance limits to promising chemical configurations, guiding experimental synthesis and accelerating the discovery of next-generation thermoelectric materials.

• Carrier-transport databases. The establishment of large-scale databases¹¹⁵ focused on phonon and electron transport properties will facilitate machine learning modeling of thermoelectric materials. By integrating computational and known experimental data, these models can significantly accelerate materials design while also having broader utility beyond thermoelectrics, benefiting fields such as catalysis, batteries, and functional ceramics.¹⁴

• Synthesis scalability and practical deployment. Experimental validation is essential for the proposed materials design workflows. Scalable synthesis methods for HEMs—including co-precipitation, aerosol/spray pyrolysis, electrochemical techniques, and microwave-assisted synthesis—have advantages in rapid processing, cost-effectiveness, and high yield.¹¹⁶ While there are also scalable techniques for disordered thermoelectric materials such as direct sintering, they produce lower zT values than lab-scale samples, likely due to unwanted oxidation.¹¹⁷ Future research should build on existing scalable and general-synthesis approaches¹¹⁸ to improve phase homogeneity and optimize electron transport across grain boundaries. Moreover, multiscale hierarchical modeling—spanning first-principles simulations¹⁰⁴ to device design^117,119—will be crucial for predicting stable configurations, guiding synthesis strategies, and ultimately facilitating their practical deployment.

Data availability

All data can be obtained from the corresponding references.

Author contributions

C. O. conceived the study and developed the manuscript outline. T. L., X. X., and G. H. performed the literature review. All authors (C. O., T. L., X. X., G. H., G. Q., and J. R. O.) contributed to the writing of the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors thank Rama Venkatasubramanian (JHU Applied Physics Laboratory), Bill McNamara (JHU), A. J. Donelson (JHU), Chip Cotton (JHU), Jaehyung Lee (JHU), Rajib Datta (GE Vernova Advanced Research; GEVAR), Naveenan Thiagarajan (GEVAR), Paul Glaser (GEVAR), Jinbo Cao (GEVAR), and G. Jeffrey Snyder (Northwestern University) for helpful discussions. Research was sponsored by the Advanced Research Projects Agency-Energy (ARPA-E) (DE-AR0001787). X. X. acknowledges support from the Institute for Data-Intensive Engineering and Science (IDIES) at JHU. C. O. acknowledges support from the Ralph O'Connor Sustainable Energy Institute (ROSEI) at JHU and the Advanced Research Computing at Hopkins (ARCH).

References

1. Y. Zhao, W. Li, X. Zhao, Y. Wang, D. Luo, Y. Li and M. Ge, Energy and exergy analysis of a thermoelectric generator system for automotive exhaust waste heat recovery, Appl. Therm. Eng., 2024, 239, 122180.
2. A. C. Thekdi and S. U. Nimbalkar, Industrial Waste Heat Recovery: Potential Applications, Available Technologies and Crosscutting R&D Opportunities, Tech. Rep. ORNL/TM-2014/622, Oak Ridge National Laboratory ( 2014).
3. K.-T. Lee, D.-S. Lee, W.-H. Chen, Y.-L. Lin, D. Luo, Y.-K. Park and A. Bandala, An overview of commercialization and marketization of thermoelectric generators for low-temperature waste heat recovery, iScience, 2023, 26, 107874.
4. Y. Shi, Y. Wang, Y. Deng, H. Gao, Z. Lin, W. Zhu and H. Ye, A novel self-powered wireless temperature sensor based on thermoelectric generators, Energy Convers. Manage, 2014, 80, 110–116.
5. N. Docquier and S. Candel, Combustion control and sensors: a review, Prog. Energy Combust. Sci., 2002, 28, 107–150.
6. A. Giampieri, Z. Ma, J. L. Chin, A. Smallbone, P. Lyons, I. Khan, S. Hemphill and A. P. Roskilly, Techno-economic analysis of the thermal energy saving options for high-voltage direct current interconnectors, Appl. Energy, 2019, 247, 60–77.
7. M. R. Laskar, D. N. Nath, L. Ma, E. W. Lee, C. H. Lee, T. Kent, Z. Yang, R. Mishra, M. A. Roldan, J.-C. Idrobo, S. T. Pantelides, S. J. Pennycook, R. C. Myers, Y. Wu and S. Rajan, p-type doping of MoS₂ thin films using Nb, Appl. Phys. Lett., 2014, 104, 092104.
8. W.-J. Zeng, C. Wang, Q.-Q. Yan, P. Yin, L. Tong and H.-W. Liang, Phase diagrams guide synthesis of highly ordered intermetallic electrocatalysts: separating alloying and ordering stages, Nat. Commun., 2022, 13, 7654.
9. A. Mao, H.-Z. Xiang, Z.-G. Zhang, K. Kuramoto, H. Yu and S. Ran, Solution combustion synthesis and magnetic property of rock-salt (Co_0.2 Cu_0.2 Mg_0.2 Ni_0.2 Zn_0.2)O high-entropy oxide nanocrystalline powder, J. Magn. Magn. Mater., 2019, 484, 245–252.
10. C. Oses, C. Toher and S. Curtarolo, High-entropy ceramics, Nat. Rev. Mater., 2020, 5, 295–309.
11. Y. Sun and S. Dai, High-entropy materials for catalysis: A new frontier, Sci. Adv., 2021, 7, eabg1600.
12. M. Brahlek, M. Gazda, V. Keppens, A. R. Mazza, S. J. McCormack, A. Mielewczyk-Gryn, B. Musico, K. Page, C. Rost, S. B. Sinnott, C. Toher, T. Z. Ward and A. Yamamoto, What is in a name: Defining “high entropy” oxides, APL Mater., 2022, 10, 110902.
13. S. S. Aamlid, M. Oudah, J. Rottler and A. M. Hallas, Understanding the role of entropy in high entropy oxides, J. Am. Chem. Soc., 2023, 145, 5991–6006.
14. G. Qiu, T. Li, X. Xu, Y. Liu, M. Niyogi, K. Cariaga and C. Oses, High entropy powering green energy: hydrogen, batteries, electronics, and catalysis, npj Comput. Mater., 2025 DOI:10.1038/s41524-025-01594-6.
15. P. Sarker, T. Harrington, C. Toher, C. Oses, M. Samiee, J.-P. Maria, D. W. Brenner, K. S. Vecchio and S. Curtarolo, High-entropy high-hardness metal carbides discovered by entropy descriptors, Nat. Commun., 2018, 9, 4980.
16. A. Calzolari, C. Oses, C. Toher, M. Esters, X. Campilongo, S. P. Stepanoff, D. E. Wolfe and S. Curtarolo, Plasmonic high-entropy carbides, Nat. Commun., 2022, 13, 5993.
17. S. Schweidler, M. Botros, F. Strauss, Q. Wang, Y. Ma, L. Velasco, G. C. Marques, A. Sarkar, C. Kübel, H. Hahn, J. Aghassi-Hagmann, T. Brezesinski and B. Breitung, High-entropy materials for energy and electronic applications, Nat. Rev. Mater., 2024, 9, 266–281.
18. J. L. Braun, C. M. Rost, M. Lim, A. Giri, D. H. Olson, G. N. Kotsonis, G. Stan, D. W. Brenner, J.-P. Maria and P. E. Hopkins, Charge-Induced Disorder Controls the Thermal Conductivity of Entropy-Stabilized Oxides, Adv. Mater., 2018, 30, 1805004.
19. M. Esters, C. Oses, D. Hicks, M. J. Mehl, M. Jahnátek, M. D. Hossain, J.-P. Maria, D. W. Brenner, C. Toher and S. Curtarolo, Settling the matter of the role of vibrations in the stability of high-entropy carbides, Nat. Commun., 2021, 12, 5747.
20. Y. Zhang, M. Xie, Z. Wang, X. Song, R. Mu, F. Zhou, J. Bao, J. Gao and W. Pan, Exploring the increasing behavior of thermal conductivity for high-entropy zirconates at high temperatures, Scr. Mater., 2023, 228, 115328.
21. F. Li, L. Zhou, J.-X. Liu, Y. Liang and G.-J. Zhang, High-entropy pyrochlores with low thermal conductivity for thermal barrier coating materials, J. Adv. Ceram., 2019, 8, 576–582.
22. W.-L. Hsu, C.-W. Tsai, A.-C. Yeh and J.-W. Yeh, Clarifying the four core effects of high-entropy materials, Nat. Rev. Chem., 2024, 8, 471–485.
23. Q. Chen, J. Chen, X. Xu, Z. Wang, Y. Ding, L. Xiong, B. Zhu and L. Tao, Morphology optimization of Bi₂Se₃ thin films for enhanced thermoelectric performance, Cryst. Growth Des., 2021, 21, 6737–6743.
24. B. Zhu, Q. Chen, S. Jiang, M. Holt, W. Zhu, D. Akinwande and L. Tao, Thermoelectric effect and devices on IVA and VA Xenes, InfoMat, 2021, 3, 271–292.
25. H. Wu, Y. Zhang, S. Ning, L.-D. Zhao and S. J. Pennycook, Seeing atomic-scale structural origins and foreseeing new pathways to improved thermoelectric materials, Mater. Horiz., 2019, 6, 1548–1570.
26. W. Zhong, Y. Zhao, B. Zhu, J. Sha, E. S. Walker, S. Bank, Y. Chen, D. Akinwande and L. Tao, Anisotropic thermoelectric effect and field-effect devices in epitaxial bismuthene on Si (111), Nanotechnology, 2020, 31, 475202.
27. C. Gayner and K. K. Kar, Recent advances in thermoelectric materials, Prog. Mater. Sci., 2016, 83, 330–382.
28. X.-L. Shi, J. Zou and Z.-G. Chen, Advanced thermoelectric design: from materials and structures to devices, Chem. Rev., 2020, 120, 7399–7515.
29. C. Han, Z. Li and S. Dou, Recent progress in thermoelectric materials, Sci. Bull., 2014, 59, 2073–2091.
30. I. Siloi, P. Gopal, S. Curtarolo, M. B. Nardelli, P. Vaqueiro and M. Fornari, Thermoelectric properties of minerals with the mawsonite structure, ACS Appl. Energy Mater., 2019, 2, 8068–8078.
31. J. Chen, B. Zhu, L. Zhong, X. Xu, D. Kang, P. Shen, J. Nie, B. Xu, J. Bai, F. Xue and L. Tao, Tuning Thermoelectric and Mechanical Properties of Zinc-Cupronickel via Hot Rolling Deformation, J. Elec. Mater., 2022, 51, 7113–7121.
32. L. Chen, B. Zhu, J. Chen, S. Xing and L. Tao, 2D Bi₂ Te₃/Si heterostructure with high thermoelectric power factor enabled by interface regulated carrier injection, Nanotechnology, 2023, 34, 255201.
33. C. Jia, X. Xu, L. Zhong, D. Kang, P. Shen, B. Xu, J. Bai, F. Xue, K. Yin, B. Zhu and L. Tao, Multi-Interface-Induced Thermal Conductivity Reduction and Thermoelectric Performance Improvement in a Cu–Ni Alloy, ACS Appl. Energy Mater., 2022, 5, 5044–5052.
34. Q. Zhang, M. Yuan, K. Pang, Y. Zhang, R. Wang, X. Tan, G. Wu, H. Hu, J. Wu, P. Sun, G.-Q. Liu and J. Jiang, High-performance industrial-grade p-type (Bi,Sb)₂ Te₃ thermoelectric enabled by a stepwise optimization strategy, Adv. Mater., 2023, 35, 2300338.
35. N. Chen, H. Zhu, G. Li, Z. Fan, X. Zhang, J. Yang, T. Lu, Q. Liu, X. Wu, Y. Yao, Y. Shi and H. Zhao, Improved figure of merit (z) at low temperatures for superior thermoelectric cooling in Mg₃ (Bi,Sb)₂, Nat. Commun., 2023, 14, 4932.
36. Y. Shtern, A. Sherchenkov, M. Shtern, M. Rogachev and D. Pepelyaev, Challenges and perspective recent trends of enhancing the efficiency of thermoelectric materials on the basis of PbTe, Mater. Today Commun., 2023, 37, 107083.
37. J. Feng, J. Li and R. Liu, Low-temperature thermoelectric materials and applications, Nano Energy, 2024, 126, 109651.
38. E. Witkoske, Z. Tong, Y. Feng, X. Ruan, M. Lundstrom and N. Lu, The use of strain and grain boundaries to tailor phonon transport properties: A first-principles study of 2H-phase CuAlO₂. II, Jpn. J. Appl. Phys., 2020, 127, 115108.
39. B. Jiang, W. Wang, S. Liu, Y. Wang, C. Wang, Y. Chen, L. Xie, M. Huang and J. He, High figure-of-merit and power generation in high-entropy GeTe-based thermoelectrics, Science, 2022, 377, 208–213.
40. C. Chang, M. Wu, D. He, Y. Pei, C.-F. Wu, X. Wu, H. Yu, F. Zhu, K. Wang, Y. Chen, L. Huang, J.-F. Li, J. He and L.-D. Zhao, 3D charge and 2D phonon transports leading to high out-of-plane ZT in n-type SnSe crystals, Science, 2018, 360, 778–782.
41. G. Tan, F. Shi, S. Hao, L.-D. Zhao, H. Chi, X. Zhang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Non-equilibrium processing leads to record high thermoelectric figure of merit in PbTe--SrTe, Nat. Commun., 2016, 7, 12167.
42. Y. Zhong, F. Lv, X. Zhao, Q. Deng, X. An, Z. He, L. Gan and R. Ang, Extraordinary role of resonant dopant vanadium for improving thermoelectrics in n-type PbTe, Mater. Today Phys., 2023, 30, 100955.
43. Q. Tang, B. Jiang, K. Wang, W. Wang, B. Jia, T. Ding, Z. Huang, Y. Lin and J. He, High-entropy thermoelectric materials, Joule, 2024, 8, 1641–1666.
44. H. Han, L. Zhao, X. Wu, B. Zuo, S. Bian, T. Li, X. Liu, Y. Jiang, C. Chen, J. Bi, J. Xu and L. Yu, Advancements in thermoelectric materials: optimization strategies for enhancing energy conversion, J. Mater. Chem. A, 2024, 12, 24041–24083.
45. R. Chen, Y. Wang, L. Jiang, R. Min, H. Kang, Z. Chen, E. Guo, X. Yang, X. Jiang and T. Wang, Enhancing thermoelectric properties of MCoSb-based alloys by entropy-driven energy-filtering effects and band engineering, Mater. Today Phys., 2023, 30, 100957.
46. Y. Jiang, J. Dong, H.-L. Zhuang, J. Yu, B. Su, H. Li, J. Pei, F.-H. Sun, M. Zhou, H. Hu, J.-W. Li, Z. Han, B.-P. Zhang, T. Mori and J.-F. Li, Evolution of defect structures leading to high ZT in GeTe-based thermoelectric materials, Nat. Commun., 2022, 13, 6087.
47. Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z.-Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Defect engineering in thermoelectric materials: what have we learned?, Chem. Soc. Rev., 2021, 50, 9022–9054.
48. Z. Li, C. Xiao, H. Zhu and Y. Xie, Defect chemistry for thermoelectric materials, J. Am. Chem. Soc., 2016, 138, 14810–14819.
49. Y. Zhang, Z. Li, S. Singh, A. Nozariasbmarz, W. Li, A. Genç, Y. Xia, L. Zheng, S. H. Lee, S. K. Karan, G. K. Goyal, N. Liu, S. M. Mohan, Z. Mao, A. Cabot, C. Wolverton, B. Poudel and S. Priya, Defect-engineering-stabilized AgSbTe₂ with high thermoelectric performance, Adv. Mater., 2023, 35, 2208994.
50. M. Li, H. Zhao, X. Qu, Z. Ding, L. Shan, C. Qu, F. Gao, Y. Li, B. Yao, H. Ma and Y. Lan, Enhanced thermoelectric performance of n-type Bi₂ (Se,Te)₃ bulk nanocomposites through Ti doping, Ceram. Int., 2024, 50, 16301–16308.
51. Y. Zheng, Q. Zhang, X. Su, H. Xie, S. Shu, T. Chen, G. Tan, Y. Yan, X. Tang, C. Uher and G. J. Snyder, Mechanically robust BiSbTe alloys with superior thermoelectric performance: a case study of stable hierarchical nanostructured thermoelectric materials, Adv. Energy Mater., 2015, 5, 1401391.
52. A. Sherchenkov, N. Borgardt, M. Shtern, Y. Zaytseva, Y. Shtern, M. Rogachev, V. Sazonov, A. Yakubov and D. Pepelyaev, The role of nanostructuring strategies in PbTe on enhancing thermoelectric efficiency, Mater. Today Energy, 2023, 37, 101416.
53. C. Gayner, L. T. Menezes, Y. Natanzon, Y. Kauffmann, H. Kleinke and Y. Amouyal, Development of nanostructured Bi₂ Te₃ with high thermoelectric performance by scalable synthesis and microstructure manipulations, ACS Appl. Mater. Interfaces, 2023, 15, 13012–13024.
54. J.-W. Yeh, Alloy design strategies and future trends in high-entropy alloys, JOM, 2013, 65, 1759–1771.
55. J.-W. Yeh, S.-K. Chen, S.-J. Lin, J.-Y. Gan, T.-S. Chin, T.-T. Shun, C.-H. Tsau and S.-Y. Chang, Nanostructured High-Entropy Alloys with Multiple Principle Elements: Novel Alloy Design Concepts and Outcomes, Adv. Eng. Mater., 2004, 6, 299–303.
56. D. B. Miracle and O. N. Senkov, A critical review of high entropy alloys and related concepts, Acta Mater., 2017, 122, 448–511.
57. M. Jankousky, H. Chen, A. Novick and V. Stevanovic, All “Roads” Lead to Rocksalt Structure, J. Am. Chem. Soc., 2024, 146, 23004–23011.
58. C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Entropy-stabilized oxides, Nat. Commun., 2015, 6, 8485.
59. D. Hicks, C. Oses, E. Gossett, G. Gomez, R. H. Taylor, C. Toher, M. J. Mehl, O. Levy and S. Curtarolo, AFLOW-SYM: platform for the complete, automatic and self-consistent symmetry analysis of crystals, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 184–203.
60. R. Liu, H. Chen, K. Zhao, Y. Qin, B. Jiang, T. Zhang, G. Sha, X. Shi, C. Uher, W. Zhang and L. Chen, Entropy as a gene-like performance indicator promoting thermoelectric materials, Adv. Mater., 2017, 29, 1702712.
61. B. M. Foley, H. J. Brown-Shaklee, J. C. Duda, R. Cheaito, B. J. Gibbons, D. Medlin, J. F. Ihlefeld and P. E. Hopkins, Thermal conductivity of nano-grained SrTiO₃ thin films, Appl. Phys. Lett., 2012, 101, 231908.
62. W. Kim, Strategies for engineering phonon transport in thermoelectrics, J. Mater. Chem. C, 2015, 3, 10336–10348.
63. Z. Zhao, H. Xiang, F.-Z. Dai, Z. Peng and Y. Zhou, (La_0.2 Ce_0.2 Nd_0.2 Sm_0.2 Eu_0.2)₂ Zr₂ O₇: A novel high-entropy ceramic with low thermal conductivity and sluggish grain growth rate, J. Mater. Sci. Technol., 2019, 35, 2647.
64. S. Liu, D. Wu, M. Kong, W. Wang, L. Xie and J. He, High-Entropy Thermoelectric Materials: Advances, Challenges, and Future Opportunities, ACS Energy Lett., 2025, 10, 925–934.
65. R. Gurunathan, R. Hanus and G. J. Snyder, Alloy scattering of phonons, Mater. Horiz., 2020, 7, 1452–1456.
66. M. Widom, Modeling the structure and thermodynamics of high-entropy alloys, J. Mater. Res., 2018, 33, 2881–2898.
67. R. Moshwan, X.-L. Shi, W.-D. Liu, J. Liu and Z.-G. Chen, Entropy engineering: An innovative strategy for designing high-performance thermoelectric materials and devices, Nano Today, 2024, 58, 102475.
68. S. Zhu, J. Zhu, S. Ye, K. Yang, M. Li, H. Wang and J. He, High-entropy rare earth titanates with low thermal conductivity designed by lattice distortion, J. Am. Ceram. Soc., 2023, 106, 6279–6291.
69. X. Yan, L. Constantin, Y. Lu, J.-F. Silvain, M. Nastasi and B. Cui, (Hf_0.2 Zr_0.2 Ta_0.2 Nb_0.2 Ti_0.2)C high-entropy ceramics with low thermal conductivity, J. Am. Ceram. Soc., 2018, 101, 4486–4491.
70. J. Cai, J. Yang, G. Liu, H. Wang, F. Shi, X. Tan, Z. Ge and J. Jiang, Ultralow thermal conductivity and improved ZT of CuInTe₂ by high-entropy structure design, Mater. Today Phys., 2021, 18, 100394.
71. P.-C. Wei, C.-N. Liao, H.-J. Wu, D. Yang, J. He, G. V. Biesold-McGee, S. Liang, W.-T. Yen, X. Tang, J.-W. Yeh, Z. Lin and J.-H. He, Thermodynamic routes to ultralow thermal conductivity and high thermoelectric performance, Adv. Mater., 2020, 32, 1906457.
72. O. N. Senkov, G. B. Wilks, J. M. Scott and D. B. Miracle, Mechanical properties of Nb₂₅ Mo₂₅ Ta₂₅ W₂₅ and V₂₀ Nb₂₀ Mo₂₀ Ta₂₀ W₂₀ refractory high entropy alloys, Intermetallics, 2011, 19, 698–706.
73. F. Körmann, Y. Ikeda, B. Grabowski and M. H. F. Sluiter, Phonon broadening in high entropy alloys, npj Comput. Mater., 2017, 3, 36.
74. P. G. Klemens, The Scattering of Low-Frequency Lattice Waves by Static Imperfections, Proc. Phys. Soc. London A, 1955, 68, 1113–1128.
75. K. Yang, C. Oses and S. Curtarolo, Modeling Off-Stoichiometry Materials with a High-Throughput Ab-Initio Approach, Chem. Mater., 2016, 28, 6484–6492.
76. H. Y. Lv, W. J. Lu, D. F. Shao and Y. P. Sun, Enhanced thermoelectric performance of phosphorene by strain-induced band convergence, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085433.
77. S. Perumal, P. Bellare, U. S. Shenoy, U. V. Waghmare and K. Biswas, Low thermal conductivity and high thermoelectric performance in Sb and Bi codoped GeTe: complementary effect of band convergence and nanostructuring, Chem. Mater., 2017, 29, 10426–10435.
78. K. Li, L. Sun, W. Bai, N. Ma, C. Zhao, J. Zhao, C. Xiao and Y. Xie, High-Entropy Strategy to Achieve Electronic Band Convergence for High-Performance Thermoelectrics, J. Am. Chem. Soc., 2024, 146, 14318.
79. S. Hao, V. P. Dravid, M. G. Kanatzidis and C. Wolverton, Computational strategies for design and discovery of nanostructured thermoelectrics, npj Comput. Mater., 2019, 5, 58.
80. L. Xi, J. Yang, L. Wu, J. Yang and W. Zhang, Band engineering and rational design of high-performance thermoelectric materials by first-principles, J. Materiomics, 2016, 2, 114–130.
81. V. Popescu and A. Zunger, Effective Band Structure of Random Alloys, Phys. Rev. Lett., 2010, 104, 236403.
82. M. Hong, Z.-G. Chen, L. Yang, T. C. Chasapis, S. D. Kang, Y. Zou, G. J. Auchterlonie, M. G. Kanatzidis, G. J. Snyder and J. Zou, Enhancing the thermoelectric performance of SnSe_1−x Te_x nanoplates through band engineering, J. Mater. Chem. A, 2017, 5, 10713–10721.
83. G. Xie, Z. Li, T. Luo, H. Bai, J. Sun, Y. Xiao, L.-D. Zhao, J. Wu, G. Tan and X. Tang, Band inversion induced multiple electronic valleys for high thermoelectric performance of SnTe with strong lattice softening, Nano Energy, 2020, 69, 104395.
84. Y. Mizuguchi, H. Usui, R. Kurita, K. Takae, M. R. Kasem, R. Matsumoto, K. Yamane, Y. Takano, Y. Nakahira, A. Yamashita, Y. Goto, A. Miura and C. Moriyoshi, Glassy atomic vibrations and blurry electronic structures created by local structural disorders in high-entropy metal telluride superconductors, Mater. Today Phys., 2023, 32, 101019.
85. Y. Shinozuka, Electron-Lattice Interactions in Semiconductors, Jenny Stanford Publishing, New York, 2021.
86. J. Park, M. Dylla, Y. Xia, M. Wood, G. J. Snyder and A. Jain, When band convergence is not beneficial for thermoelectrics, Nat. Commun., 2021, 12, 3425.
87. J. Bardeen and W. Shockley, Deformation Potentials and Mobilities in Non-Polar Crystals, Phys. Rev., 1950, 80, 72–80.
88. Z. Li, P. Graziosi and N. Neophytou, Deformation potential extraction and computationally efficient mobility calculations in silicon from first principles, Phys. Rev. B, 2021, 104, 195201.
89. G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71.
90. G. K. H. Madsen, J. Carrete and M. J. Verstraete, BoltzTraP₂, a program for interpolating band structures and calculating semi-classical transport coefficients, Comput. Phys. Commun., 2018, 231, 140–145.
91. A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Efficient calculation of carrier scattering rates from first principles, Nat. Commun., 2021, 12, 1–9.
92. Hacking Materials Research Group and A. Jain, AMSET: ab initio scattering and transport, 2015, https://hackingmaterials.lbl.gov/amset/, (accessed April 20, 2025).
93. D. K. Ferry, Scattering by polar-optical phonons in a quasi-two-dimensional semiconductor, Surf. Sci., 1978, 75, 86–91.
94. H. Fröhlich, Electrons in lattice fields, Adv. Phys., 1954, 3, 325–361.
95. P. M. M. C. de Melo, J. C. de Abreu, B. Guster, M. Giantomassi, Z. Zanolli, X. Gonze and M. J. Verstraete, High-throughput analysis of Fröhlich-type polaron models, npj Comput. Mater., 2023, 9, 147.
96. X. Wang, H. Yao, Z. Zhang, X. Li, C. Chen, L. Yin, K. Hu, Y. Yan, Z. Li, B. Yu, F. Cao, X. Liu, X. Lin and Q. Zhang, Enhanced thermoelectric performance in high entropy alloys Sn_0.25Pb_0.25Mn_0.25Ge_0.25Te, ACS Appl. Mater. Interfaces, 2021, 13, 18638–18647.
97. B. Jiang, Y. Yu, H. Chen, J. Cui, X. Liu, L. Xie and J. He, Entropy engineering promotes thermoelectric performance in p-type chalcogenides, Nat. Commun., 2021, 12, 3234.
98. B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, High-entropy-stabilized chalcogenides with high thermoelectric performance, Science, 2021, 371, 830–834.
99. C. Oses, C. Toher and S. Curtarolo, Data-driven design of inorganic materials with the Automatic Flow Framework for Materials Discovery, MRS Bull., 2018, 43, 670–675.
100. A. van Roekeghem, J. Carrete, C. Oses, S. Curtarolo and N. Mingo, High-Throughput Computation of Thermal Conductivity of High-Temperature Solid Phases: The Case of Oxide and Fluoride Perovskites, Phys. Rev. X, 2016, 6, 041061.
101. O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo and A. Tropsha, Universal fragment descriptors for predicting properties of inorganic crystals, Nat. Commun., 2017, 8, 15679.
102. R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, SISSO: A compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates, Phys. Rev. Mater., 2018, 2, 083802.
103. T. A. R. Purcell, M. Scheffler and L. M. Ghiringhelli, Recent advances in the SISSO method and their implementation in the SISSO + + code, J. Chem. Phys., 2023, 159, 114110.
104. C. Oses, M. Esters, D. Hicks, S. Divilov, H. Eckert, R. Friedrich, M. J. Mehl, A. Smolyanyuk, X. Campilongo, A. van de Walle, J. Schroers, A. G. Kusne, I. Takeuchi, E. Zurek, M. Buongiorno Nardelli, M. Fornari, Y. Lederer, O. Levy, C. Toher and S. Curtarolo, aflow + +: A C + + framework for autonomous materials design, Comput. Mater. Sci., 2023, 217, 111889.
105. A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65, 353–356.
106. L. Lindsay, First Principles Peierls-Boltzmann Phonon Thermal Transport: A Topical Review, Nanosc. Microsc. Therm., 2016, 20, 67–84.
107. M. Omini and A. Sparavigna, An iterative approach to the phonon Boltzmann equation in the theory of thermal conductivity, Phys. B, 1995, 212, 101–112.
108. M. Omini and A. Sparavigna, Beyond the isotropic-model approximation in the theory of thermal conductivity, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 9064–9073.
109. J. J. Plata, P. Nath, D. Usanmaz, J. Carrete, C. Toher, M. de Jong, M. D. Asta, M. Fornari, M. Buongiorno Nardelli and S. Curtarolo, An efficient and accurate framework for calculating lattice thermal conductivity of solids: AFLOW-AAPL Automatic Anharmonic Phonon Library, npj Comput. Mater., 2017, 3, 45.
110. Z. Ma, Y. Luo, W. Li, T. Xu, Y. Wei, C. Li, A. Y. Haruna, Q. Jiang, D. Zhang and J. Yang, High Thermoelectric Performance and Low Lattice Thermal Conductivity in Lattice-Distorted High-Entropy Semiconductors AgMnSn_1−xPb_xSbTe₄, Chem. Mater., 2022, 34, 8959–8967.
111. A. Sharma and U. Singisetti, Effective electronic band structure of monoclinic β-(Al_xGa_1−x)₂ O₃ alloy semiconductor, AIP Adv., 2023, 13, 015101.
112. C. Jeong, R. Kim, M. Luisier, S. Datta and M. Lundstrom, On Landauer versus Boltzmann and full band versus effective mass evaluation of thermoelectric transport coefficients, J. Appl. Phys., 2010, 107, 023707.
113. K. Kaufmann, D. Maryanovsky, W. M. Mellor, C. Zhu, A. S. Rosengarten, T. J. Harrington, C. Oses, C. Toher, S. Curtarolo and K. S. Vecchio, Discovery of high-entropy ceramics via machine learning, npj Comput. Mater., 2020, 6, 42.
114. S. Divilov, H. Eckert, D. Hicks, C. Oses, C. Toher, R. Friedrich, M. Esters, M. J. Mehl, A. C. Zettel, Y. Lederer, E. Zurek, J.-P. Maria, D. W. Brenner, X. Campilongo, S. Filipovic, W. G. Fahrenholtz, C. J. Ryan, C. M. DeSalle, R. J. Crealese, D. E. Wolfe, A. Calzolari and S. Curtarolo, Disordered enthalpy-entropy descriptor for high-entropy ceramics discovery, Nature, 2024, 625, 66–73.
115. M. Esters, C. Oses, S. Divilov, H. Eckert, R. Friedrich, D. Hicks, M. J. Mehl, F. Rose, A. Smolyanyuk, A. Calzolari, X. Campilongo, C. Toher and S. Curtarolo, aflow.org: A web ecosystem of databases, software and tools, Comput. Mater. Sci., 2023, 216, 111808.
116. T. G. Ritter, S. Pappu and R. Shahbazian-Yassar, Scalable Synthesis Methods for High-Entropy Nanoparticles, Adv. Energy Sustain. Res., 2024, 5, 2300297.
117. L. Xie, C. Ming, Q. Song, C. Wang, J. Liao, L. Wang, C. Zhu, F. Xu, Y.-Y. Sun, S. Bai and L. Chen, Lead-free and scalable GeTe-based thermoelectric module with an efficiency of 12%, Sci. Adv., 2023, 9, eadg7919.
118. B. Wang, C. Wang, X. Yu, Y. Cao, L. Gao, C. Wu, Y. Yao, Z. Lin and Z. Zou, General synthesis of high-entropy alloy and ceramic nanoparticles in nanoseconds, Nat. Synth., 2022, 1, 138–146.
119. B. V. K. Reddy, M. Barry, J. Li and M. K. Chyu, Mathematical modeling and numerical characterization of composite thermoelectric devices, Int. J. Therm. Sci., 2013, 67, 53–63.

---