Oscillations in incident electric field enhances interfacial water evaporation

Abstract

The observed superthermal evaporation rate of water from porous hydrogels has been attributed to different reasons, such as the formation of intermediate water state with reduced latent heat, and the emission of water clusters cleaved off by photons. However, it remains unclear how the electromagnetic field interacts with the liquid–vapor interface and enhances evaporation at the molecular level. Here, we employed non-equilibrium molecular dynamics simulations to investigate interfacial evaporation from pure water and polyvinyl alcohol hydrogels. Our results show that the evaporation rate remains consistent for a given interfacial heat input, regardless of hydrogel presence, suggesting that forming different water states alone does not enhance evaporation. When an alternating electric field is applied, we observed enhanced evaporation due to the cleavage of water molecules and clusters formed in the interface region, particularly when water was confined within hydrogels.

---

New concepts

The observed superthermal evaporation rate of water from porous hydrogels has been attributed to different reasons in the literature, such as the formation of intermediate water state with reduced latent heat, and the emission of water clusters cleaved off by photons. However, it remains unclear how the electromagnetic field interacts with the liquid–vapor interface and enhances evaporation at the molecular level. Our results show that the evaporation rate remains consistent for a given interfacial heat input, regardless of hydrogel presence, suggesting that forming different water states alone does not enhance evaporation. When an alternating electric field is applied, we observed enhanced evaporation due to the cleavage of water molecules and clusters formed in the interface region, particularly when water was confined within hydrogels. We show, for the first time, the complex dynamics of water clusters during the interfacial solar evaporation, which has not been previously reported in the literature. For example, even with electric fields, large clusters in the interface region are difficult to evaporate directly, but they can break into single molecules and small clusters and evaporate. Materials and conditions can be further modified to achieve even higher evaporation rates and develop advanced water evaporation systems.

Introduction

Water scarcity remains a critical global challenge, requiring cost-effective and efficient solutions. Traditional water purification methods, such as distillation and reverse osmosis, are energy-intensive,¹ while membrane distillation, though capable of using low-grade waste heat, has low energy efficiency.² Renewable solar energy offers a sustainable alternative to fossil fuels, addressing the high energy demands of water purification.³ Among these approaches, interfacial solar evaporation has gained significant attention for its high evaporation rate. By localizing heat at the liquid–vapor interface, this technique minimizes heat loss to bulk water, enhancing overall performance and making it a promising solution for clean water production.⁴

Various interfacial materials have been developed to enhance interfacial solar evaporation, including plasmonic particles, metal–organic frameworks, and hydrogels, just to name a few.⁵ Hydrogels combined with solar absorbers have garnered significant attention due to their hydrophilic structure, which facilitates water hydration, retention, and continuous water supply at the evaporation interface. Surprisingly, the water evaporation rate from polyvinyl alcohol (PVA)–polypyrrole hydrogels is measured to be even higher than the thermal evaporation limit assuming all solar radiation is utilized for vaporizing water.⁶ Subsequent research engineering the hydrophilicity and microstructures of hydrogel has achieved even higher evaporation rates up to ∼6.3 times of the thermal evaporation limit.^7–11

The origins of the superthermal evaporation rate, however, remain unclear. One early hypothesis suggests that hydrogels enhance evaporation by reducing the latent heat of water. When confined in hydrogel pores, water might evaporate as small clusters, requiring fewer hydrogen bonds to break, thus lowering vaporization enthalpy.⁶ A later theory attributed this latent heat reduction to the formation of distinct water states in hydrogels.⁷ When water molecules are confined in the hydrogel, the network of hydrogen bonds is modified by the interaction between water and polymer. Three water states have been identified for water confined in hydrogels: bound water (non-freezing, bonded strongly to hydrogel polar functional groups), intermediate water (linked to both the polymer network and water molecules), and free water (similar to bulk water, forming strong bonds with other water molecules). Intermediate water was posited to be a state with a higher enthalpy than bulk water, requiring less energy for vaporization. Another possible mechanism of the reduced latent heat is the extra osmotic pressure when water is confined inside the hydrogel. The osmotic pressure in hydrogels is contributed not only by the ions in the solution, but also from polymer tension caused by configurational changes and network deformations. The elevated osmotic pressure drives water into the hydrogel, leading to swelling and an increase in the enthalpy of confined water states, thereby reducing the energy required to vaporize liquid water, i.e., the latent heat. However, theoretical analysis showed that the latent heat reduction due to this extra osmotic pressure is far below the required levels to explain the experimentally observed enhanced evaporation rates.¹²

The concept of lower latent heat of water confined in the hydrogel is in fact questionable. A recent study by Caratenuto and Zheng showed that enhanced evaporation rate of water confined in hydrogel and other porous materials is due to greater energy input and not due to reduced vaporization enthalpy of water.¹³ The enlarged liquid–vapor surface area in these materials primarily due to porosity leads to higher evaporative cooling effect and greater temperature difference with the environment. This results in extra heat absorption from the environment, and if the energy balance is carefully analyzed, the latent heat of water remains unchanged. Zhang's work also suggested that latent heat should not be directly calculated from the evaporation rate due to (a) the effects of natural convection flow field, water filling level, and area of evaporation surface etc. on the evaporation rate and (b) the complicated energy input into the system, such as heat absorbed from the environment.¹⁴

Recently, Chen's group discovered the photomolecular effect at liquid–vapor interfaces where incident photons can cleave off water clusters from the liquid phase.^15–17 While water itself is almost transparent to visible light, the liquid–vapor interface is found to strongly interact with photons. Tailoring the surface topology in hydrogel leads to the formation of nano-micro pores and results in many liquid–vapor interfaces.^18,19 When a hydrogel with negligible visible light absorption is partially wetted, it becomes absorptive in the visible spectra due to these interfaces. Even for a simple interface between bulk water and air without hydrogel, shifts in Raman spectra were observed when the interface was illuminated under light, suggesting the emission of water clusters from the surface. The evaporation rate is enhanced beyond the thermal evaporation limit when illuminated by light, even when the hydrogel contains no absorbers in the visible spectra.

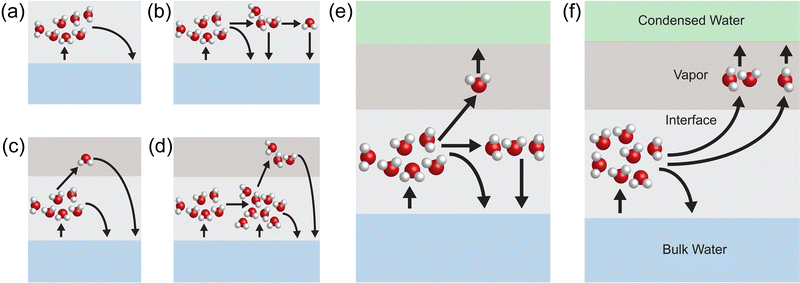
Despite these exciting advances, there has been no molecular-level understanding of how light, water states, and hydrogel interact and contribute to evaporation exceeding the thermal limit. In this work, we have performed molecular dynamics (MD) simulations to unveil the microscopic dynamics of evaporation from liquid–vapor interface with and without hydrogel, using purely thermal energy and alternating electric fields mimicking electromagnetic radiation. Our major findings are: (1) in a “dark environment” with thermal energy input alone, the evaporation rate from hydrogel is the same as that from pure water given a fixed interfacial heat input; (2) the interaction energy of intermediate water is only up to ∼12% different from that of pure water, suggesting water states would not affect vaporization enthalpy significantly; (3) evaporation rate shows significant enhancement when an alternating electric field mimicking electromagnetic radiation is applied for both pure water and water in hydrogel. The hydrogel can facilitate the formation of water clusters at the interface, but these clusters are found difficult to break using heat alone. It was under alternating electric fields that these clusters can be cleaved off from the interface and contribute to evaporation, as illustrated in Fig. 1.

Fig. 1 Illustration of evaporation of water confined in the hydrogel in a dark environment (left) and under solar radiation (right). The zoomed-in section represents the bound (orange), intermediate (brown), and free (blue and white) water states formed in the hydrogel. The disruption of water hydrogen bond network due to hydrogel's structure results in the formation of more water clusters in the interface region irrespective of the energy source. Solar radiation assists in cleaving single water molecules and clusters from the interface region, resulting in an enhanced evaporation rate.

Material & methods

Atomic structures

The PVA hydrogel structure was modeled with eight crosslinked chains, each consisting of 18 repeat units. Adjacent polymer chains were crosslinked with covalent bonds between carbons connected to the functional groups, which is the structure formed by the radiation crosslinking process.^20,21 An initial amorphous configuration of crosslinked PVA chains was generated to form a three-dimensional hydrogel network. Water molecules were introduced with an initial density of ∼1 g cm⁻³ and positioned on the bottom substrate. There was no water initially on the top substrate and the water molecules evaporating from the bottom substrate eventually condensed on the top substrate. Air was modeled as N₂ molecules for simplicity and initially placed in the vacuum region, approximating the density of air at 298 K. The bottom and top substrates were represented as copper with a face-centered cubic (FCC) lattice structure, using a lattice constant of 3.61 Å.²² Each substrate comprised seven atomic layers: a fixed base layer and six temperature-controlled layers, with a total thickness exceeding the cutoff distance.

Simulation details

MD simulations were performed using the open-source software package LAMMPS,^23,24 with periodic boundary conditions applied in all three dimensions. The simulation domain measured 50 × 170 × 50 ų with an additional 10 Å vacuum layer on both sides in the y-direction (Fig. 2(a)). In MD simulations, it is recommended to use forcefields compatible with different materials used in the simulation to avoid inconsistencies such that same Lennard-Jones (LJ) potential and mixing rules can be used.²⁵ Therefore, polymer consistent force field (PCFF) was employed for the PVA hydrogel and water.^26–31 This forcefield has been previously validated for hydrogel–water systems.^32–34 Moreover, PCFF water model, which is a flexible water model, enables the simulation of vibrational, translational, and rotational modes. The PCFF has also been used for modeling water confined in polymers, showing reasonable predictive power in evaporation thermodynamics and transport properties.^35–38 The atomic partial charges were assigned by the forcefield. Additionally, force field parameters compatible with PCFF were used to model N₂ molecules and copper substrates.^22,39 A 10 Å cutoff distance was applied for LJ and Coulombic interactions, while long-range Coulombic interactions were calculated using the particle–particle particle-mesh (PPPM) method with an accuracy of 1 × 10⁻⁶. A timestep of 0.25 fs was used to account for the presence of light hydrogen atoms.⁴⁰ Non-bonded LJ and Coulombic interactions between atoms that were permanently bonded (either directly or via one intermediate bond) were excluded using the special_bonds command with weighting factors of 0, 0, and 1.^27,28 Neighbor lists were built using the bin style with a 2 Å skin distance and updated every timestep as needed. Initial velocities were assigned to all atoms (excluding the fixed substrate layers) corresponding to a temperature of 298 K using a Gaussian distribution while ensuring zero linear and angular momentum. Three independent simulation runs were performed to determine the statistical uncertainty. The results represented as the average of three simulations such as number of water molecules evaporated can be in decimal form instead of integers.

Fig. 2 Water evaporation due to thermal energy input only. (a) MD snapshot showing the simulation domain with dimensions, containing substrates, water, PVA hydrogel and air represented as N₂ molecules. Visualization is performed in perspective display mode using the Visual Molecular Dynamics (VMD) package.⁴⁴ (b) Water density profile along y-direction for both cases, i.e., with and without hydrogel. This plot shows the results for only one simulation run. (c) The number of evaporated water molecules, N_W,E, for both with and without hydrogel cases (left panel). The heat input to the thermal source, i.e., hydrogel or dynamic water layer by the thermostat (right panel). Negative values mean the energy added to the system, i.e., the thermal source. (d) Average interaction energy of water molecules in bound, intermediate and free water states for three different cases with different numbers of water molecules in the simulation domain. (e) Tracking of evaporated water molecules to define them as bound, intermediate, or free water state before evaporating for three different cases with different numbers of water molecules in the simulation domain. The results in (c)–(e) represent average values of three independent simulations. The shaded areas in (c) and error bars in (d)–(e) represent error calculated via sample standard deviation.

The simulations consist of three stages: (1) equilibration (1.5 ns): all materials (except for the fixed substrate layers) were equilibrated at 298 K using separate Nose–Hoover thermostats; (2) preparation (1 ns): the substrates (except for the fixed substrate layers) were maintained at 298 K using separate Nose–Hoover thermostats, while the thermal source (hydrogel or dynamic water layer) was heated to the target temperature. Water and N₂ molecules were simulated in the NVE ensemble, with only their velocities and positions updated; (3) production (2 ns): conditions were identical to the preparation stage, except the thermal source was maintained at the desired temperature using a Nose–Hoover thermostat, and an electric field was applied in the y-direction to water in the liquid and interface regions if required. A damping parameter of 25 fs was used for all Nose–Hoover thermostats.

Water molecules were defined as evaporated if the oxygen atom was located within the specified region (100 Å < y_Ow < 170 Å). The number of water molecules evaporated during the production run was calculated by subtracting the number of evaporated molecules observed during the equilibration and preparation stages. The LJ interaction parameter ε between water oxygen and bottom substrate was reduced to minimize the impact of bottom substrate on water. Moreover, the number of water molecules in the simulation domain was varied in simulations under thermal energy input only and with the presence of hydrogel to confirm no size dependence (see details in ESI†).

Density profile and radial distribution function

To determine the density profile, 3 Å-wide chunks were defined along the y-direction (defined in Fig. 2(a)). The mass density of water within each chunk was calculated directly in LAMMPS, with values averaged every 100 ps using data sampled at 10 fs intervals. The reported density for each chunk represents the average of all outputted density values during the simulation production run.

The number of water molecules in each state was determined using the water density profile and the radial distribution function (RDF) between hydrogel oxygen atoms (central atoms) and water oxygen atoms (distribution atoms). Details of the water state calculations are provided in the ESI.† The RDF was computed up to the cutoff distance, divided into 1000 bins, and averaged every 100 ps using data collected at 10 fs intervals. The averaged RDF values from the production run were then used for further post-processing.

Results & discussion

Water evaporation under thermal energy

We first investigate the effect of hydrogel on water evaporation rates under thermal energy input alone, representing a “dark environment”. Our simulation setup (Fig. 2(a)) included solid substrates as boundaries, with water molecules (initial density ∼1 g cm⁻³) placed on the bottom substrate and air represented as bi-atomic nitrogen gas (for simplicity). The top substrate also acts as the condensing surface. We have conducted MD simulations of thermal water evaporation both with and without hydrogel. For the case with hydrogel, PVA hydrogel was equilibrated atop the water, absorbing water at the interface due to strong water–polymer interactions. Thermal energy was applied only to the hydrogel (maintaining the temperature at 400 K), analogous to solar-heated hydrogels with absorbers in experiments. For the pure water case, a dynamic water layer near the interface was heated and maintained at 380 K, with the rest of the system heated indirectly. The total number of water molecules was consistent across simulations.

Fig. 2(b) shows the density profile plots for with and without hydrogel cases during the production run. The liquid–vapor interface region thickness was determined using the following density limits, ρ_g + 0.01ρ_f < ρ(y) < 0.95ρ_f, where ρ_g, ρ_f, and ρ(y) represent the densities of vapor, liquid, and the local density at a distance y away from the bottom surface, respectively.⁴¹ The thickness of the liquid–vapor interface region in the without hydrogel case is 9 Å which is close to the thickness reported previously.^42,43 In the presence of hydrogel, the thickness of the liquid–vapor interfacial region doubled due to the disruption effects by the hydrogel on water structure. When equal thermal energy was input, evaporation rates (number of water molecules evaporated per unit time) were similar for both cases (Fig. 2(c)).

Some experimental studies attribute evaporation enhancement to the weaker bonding of “intermediate water”.^7,10 To investigate this, we simulated three cases with varying numbers of water molecules (case-A: 1280; case-B: 1792; case-C: 2560) with an identical hydrogel. Water states analysis (see details in ESI†) reveal that bound and intermediate water molecule counts remain consistent across cases, while free/bulk water (hereafter as free water) molecules increase with the increasing amount of water molecules. We further analyzed the average interaction energy of water molecules in different states with their surrounding hydrogel chains, substrates, and other water molecules. The interaction energy is calculated as the average potential energy between a water molecule and its neighbors. Fig. 2(d) shows that bound water molecules have the highest interaction energy due to their strong bonding with hydrophilic polymers, making them the hardest to evaporate. Interestingly, the interaction energies of intermediate water and free water are almost the same with interaction energy of the intermediate water being slightly lower. We have tracked the trajectory of evaporated water molecules and identified their water states before evaporation (Fig. 2(e)) (see details in ESI†), and found that the bound water is the most difficult to evaporate. Only for the case A with smallest number of water molecules, the evaporation of intermediate water can surpass the free water evaporation. However, the free water makes the dominant contribution to the evaporation in cases B and C potentially due to the dynamics of the process and small energy difference between intermediate and free water states. Our MD simulation of “dark evaporation” suggest that meditating water states in hydrogel cannot explain the experimental observation of enhanced dark evaporation rate.^7,14

Impact of electric field on water evaporation

Recent experiments discovered an unexpected interaction between light, i.e., electromagnetic waves, with the liquid–vapor interfaces of water.^15,16 The incident photons can cleave off water clusters from the liquid phase, resulting in an “emission” of vapor flux surpassing the thermal limit. This phenomenon is coined as the photomolecular effect, analogous of the photoelectric effect where electrons are emitted from metal surfaces under photon incidence.

As a polar liquid, water mainly interacts with the electric field oscillations of light. To provide insights into how water molecules interact with electromagnetic waves, we applied an alternating electric field on water in the y-direction (shown in Fig. 2(a)) alongside thermal energy input. The thermal energy provided by either the hydrogel or a dynamic water layer (interfacial heat input) was expected to maintain evaporation rates similar to dark experiments, while the electric field introduced additional effects to alter the rate. As illustrated in Fig. 3(a), the alternating electric field induces vibration, translation, and rotation in water molecules and clusters, facilitating their evaporation into the vapor phase. The vibrational modes in water will occur due to flexible bonds and angle in PCFF water model. As shown in Fig. 3(b), applying an alternating electric field increases the evaporation rate from both pure water and hydrogel, but the enhancement in evaporation rate is significantly higher for the case with hydrogels.

Fig. 3 Impact of electric field on water evaporation. (a) Schematic representing the solar radiation as alternating electric field applied to water in the liquid and interface regions. The sinusoidal electric field provides energy and assists in the stretching of water clusters in the liquid–vapor interface region allowing them to evaporate and resulting in evaporation rate enhancement. The same principle is also applicable to single water molecules in the interface region. (b) The number of evaporated water molecules during production run with and without hydrogel at different alternating electric field strengths. The frequency of the AC electric field is 500 GHz. (c) Total heat added/removed to/from the thermal source (hydrogel or dynamic water layer) by the thermostat at different AC electric field strengths. (d) Impact of electric field frequency at E = 0.07 V Å⁻¹ on water evaporation rate with and without hydrogel. The zero frequency indicates the DC electric field with E = 0.07 V Å⁻¹. The results in (b)–(d) represent average values of three independent simulations while the error bars are calculated via sample standard deviation.

Fig. 3(c) shows the amount of heat input by the thermostat along with the applied alternating field to keep the reservoir at the fixed temperature. As the strength of the alternating electric field increases, the thermal energy input added to water decreases, as the electric field adds energy to the system (Fig. 3(c)). In contrast, under a DC electric field even with varying strengths, the thermal energy input remains steady, aligning with the unchanged evaporation rates observed (see details in ESI†).

The cutoff electric field strength (E_cut), representing the field strength at which thermal energy input approaches zero, marks the state where evaporation is driven entirely by the electric field. Despite the hydrogel being maintained at a higher temperature, E_cut,H is 0.025 V Å⁻¹ lower for the hydrogel case than for pure water (E_cut,W), underscoring the greater impact of the electric field on hydrogel-confined water. Crucially, even at E_cut, the corresponding evaporation rate is significantly higher for water confined in the hydrogel compared to the pure water case. Specifically, the evaporation rate achieved with the electric field alone is approximately 2.30 times greater for the hydrogel case and ∼1.44 times greater for pure water compared to evaporation driven purely by thermal energy. This dramatic increase in the number of evaporated water molecules highlights the substantial role of alternating electric fields in enhancing water evaporation.

Fig. 3(d) represents the impact of alternating electric field frequency on the evaporation rate of water. No evaporation rate enhancement is observed at zero frequency which represents DC electric field. As the frequency of electric field increases, the evaporation rate increases significantly. This indicates that at much higher frequencies, similar phenomena can be observed for lower values of electric field strength. Moreover, this enhancement is much higher in the presence of hydrogel compared to when no hydrogel is present.

Clusters dynamics

While enhanced evaporation rates are observed in both cases with and without hydrogel, the much greater enhancement in evaporation in the presence of hydrogel suggest that the gel–water interaction plays a critical role in water dynamics. At the molecular scales, the polymeric chains of hydrogels can perturbate the hydrogen bond network among water molecules, which might facilitate the formation of water clusters that are susceptible to cleavage under alternating electric fields.

To investigate this, we analyzed the size distribution of water clusters in the liquid–vapor interface and vapor regions (details in ESI†). The clusters are defined as sets of water molecules interconnected by hydrogen bonds (Fig. 4(a)). The Stillinger criteria is used to determine the formation of hydrogen bonds between water molecules.^45–48 The distribution in the interface region (Fig. 4(b)) shows that the presence of the hydrogel increases both the number and size of water clusters. It is clear that the presence of hydrogel facilitates the formation of large clusters, due to the disruptive effects on the hydrogen bond network among water molecules. Several water molecules in pure water interfacial region form extended hydrogen bond network. Water molecules that were part of this extended hydrogen bond network were defined as bulk water and not considered as clusters. Same phenomenon was observed in the presence of hydrogel as well but there were relatively more isolated clusters which were not part of the extended bulk water hydrogen bond network in this case.

Fig. 4 Clusters observed in the interface and vapor regions. (a) VMD⁴⁴ snapshot representing clusters in the interface and vapor regions. Water molecules oxygen forming clusters in the interface region and vapor region are represented by purple and green colors, respectively. (b) Number and size of water clusters formed in the liquid–vapor interface region with and without hydrogel, and with and without electric field. This plot shows the results for only one simulation run. (c) Total number of water clusters present in the interface and vapor regions with and without hydrogel at different electric field strengths. (d) Average cluster size in the interface and vapor regions with and without hydrogel at different electric field strengths. The results in (c)–(d) represent average values of three independent simulations while the error bars are calculated via sample standard deviation.

Despite the increased number of clusters in the interfacial region with the presence of hydrogel, fewer clusters can be observed in the vapor region (Fig. 4(c)). This can be attributed to that the bound water molecules often participate in cluster formation and they contribute to a higher interaction energy with the surrounding than intermediate or free water. However, the number of evaporated clusters increases significantly when an alternating electric field is applied with a higher increase observed in the presence of hydrogel. The induced vibrations provide the energy required to break clusters or parts of clusters free from the interface region, facilitating their evaporation. Electric field also results in an increase in the total number of clusters in the interface region for both with and without hydrogel cases. This increase is possibly due to breaking of large clusters into a greater number of smaller clusters which are more susceptible to evaporation. Average cluster size in the interface and vapor regions indicates the impact of electric field on cluster dynamics (Fig. 4(d)). In the interface region, electric field can simultaneously (a) assist in evaporating smaller clusters such that bigger clusters can be formed, increasing the average cluster size; (b) break larger clusters into smaller clusters resulting in a reduction of average cluster size. Due to the presence of larger and more clusters in the interface region with the presence of hydrogel, there is a higher probability of evaporating more clusters with size greater than two water molecules by the electric field resulting in an increase in average cluster size in the vapor region.

Notably, while clusters larger than water trimers are present in the interfacial region, they mostly do not directly contribute to the evaporation rate. Instead, these large clusters show rich kinetic behaviors of cluster separation and recombination, and it is the fragments of the large clusters that contribute to the evaporation rate. By tracking the trajectories of water clusters (>water trimers) emitted from the liquid phase, we found and identified the following dynamic cases:

• Case 1: the emitted large cluster directly condenses back into the liquid phase (Fig. 5(a)).

Fig. 5 Dynamics of clusters formed in the interface region. (a) Case 1: cluster directly condenses into the bulk water. (b) Case 2: cluster breaks but eventually condenses into the bulk water. (c) and (d) Case 3: cluster breaks, evaporates, but eventually recondenses into the bulk water. (e) and (f) Case 4: cluster breaks, evaporates, and condenses on the condensed water side.

• Case 2: the cluster can separate or become bigger, and finally condenses back into the liquid phase (Fig. 5(b)).

• Case 3: cluster breaks, evaporates, and recondenses into the liquid phase (Fig. 5(c) and (d)).

• Case 4: cluster breaks into smaller clusters or single molecules, and some of the small clusters and single molecules evaporate and condense on the condenser side, while the rest condenses back into the liquid phase (Fig. 5(e) and (f)).

For a pure liquid–vapor interface without hydrogel, no direct evaporation of the tracked clusters into the vapor phase was observed. 100% of the emitted large clusters directly condensed back into the liquid phase (case 1) without showing any dynamical behavior for both conditions, i.e., with and without electric field.

When hydrogel is present, the percentages of clusters following cases 1–4 are ∼45%, ∼44%, ∼4%, and ∼7%, respectively. As shown in Fig. 4(b), the hydrogel disrupts water structure and favors the formation of large clusters in the interfacial region, and as a result, the large clusters are more likely to emit from the liquid phase and contribute to evaporation rate by breaking into smaller clusters or single molecules. After applying the electric field (0.1 V Å⁻¹), the percentage of cases 1–4 are ∼29%, ∼49%, ∼6% and ∼16%, respectively. Our simulation shows that hydrogel favors the formation of clusters in the interfacial region, and the electric field facilitates the “indirect” evaporation of large clusters through breaking into single molecules, or smaller clusters.

Limitations

It is important to note the limitations of our MD study. The effect of the hydrogel porosity, which is understood to play an important role in water transport and evaporation, has not been considered here due to the length scale of MD simulations. Instead, molecular interaction between hydrogel polymer chains and water molecules is the focus of this work. By simulating a simple water–gel mixed layer, we can directly probe the effect of water states on evaporation without the side-effects of porosity. PVA hydrogel, which is hydrophilic, has been considered in this work due to its simplified structure and widespread use in the experiments. However, water transport and retention will depend on wettability of the hydrogel and is bound to impact the evaporation process. For example, introducing a hydrophobic component in the solar evaporator has been reported to improve the evaporation process.⁸ Moreover, the frequency of the applied alternating electric field in MD simulations is in the THz range, lower than that of the visible photons, constrained by computational limitations in MD timesteps. Effects of electric field gradients within a wavelength are also not considered here, since the wavelength of THz electromagnetic waves is much larger than the MD simulation domain. In addition, water dynamics are treated classically using Newtonian mechanics, thereby no quantum effects or electronic responses to electromagnetism are considered here. Evaporation phenomenon at peak frequency of solar radiation (340 THz) was simulated (see details in ESI†). The results show enhancement in water evaporation when confined in hydrogel but at extremely high electric field strength possibly due to this frequency being much higher than vibrational frequency of water molecules and no spatial variations in E-field. Therefore, our MD results represent the classical low-frequency limit of the interaction between the electromagnetic field and the liquid–vapor interfaces. The low frequency of the electric field might also explain why we rarely observe evaporated clusters larger than three molecules. In principle, the energy of a ∼520 nm green photon is estimated to cleave off around 10 hydrogen bonds. However, the alternating frequency is much higher than the vibrational frequencies of atoms. Light can possibly modulate the nonlocal charge correlations across hydrogen bonds in a non-resonant but collective manner, creating some intermediate water states and then affecting the evaporation dynamics of water molecules near surfaces.^49,50 However, the quantum mechanical theory for non-resonant light–water interaction near water surfaces remains to be developed.

Conclusions

This study presents a novel perspective on the mechanisms underlying water evaporation enhancement observed in porous materials, such as hydrogels. The analyses reveal that water evaporation from hydrogels does not inherently increase under thermal energy alone (i.e., in dark environments) if the same amount of energy is applied to both hydrogel and pure water systems.

Contrary to prior hypotheses, the intermediate water state formed within the hydrogel does not exhibit significantly weaker bonding that facilitates evaporation. Instead, these water molecules in the intermediate state display almost similar (slightly lower) interaction energy compared to free water molecules, as confirmed by the tracking of evaporated water molecules in this study. This finding aligns with experimental observations, where porous materials that do not induce the formation of water states still exhibit enhanced evaporation rates.¹³ These results collectively challenge the notion that intermediate water state plays a pivotal role in evaporation rate enhancement.

The results of MD simulations strongly support the photomolecular theory. First, the application of an alternating electric field significantly increases the evaporation rate compared to thermal energy alone, as the field directly influences water clusters and single molecules in the liquid–vapor interface region, promoting their transition to the vapor phase. Second, the enhancement is markedly more pronounced when water is confined in a hydrogel, which facilitates the formation of clusters susceptible to light cleavage in the interfacial region. The lower cutoff electric field strength (E_cut) observed in hydrogel systems manifests that hydrogel polymeric chains can perturbate the hydrogen bond networks among water molecules, and facilitate the formation of clusters susceptible for cleavage under light irradiation. However, even with electric fields, large clusters in the interface region are difficult to evaporate directly, but they can break into single molecules and small clusters and evaporate.

In summary, this study provides a comprehensive molecular-level investigation into the mechanisms driving water evaporation enhancement. Using non-equilibrium molecular dynamics simulations, we critically evaluate water evaporation under dark conditions and alternating electric fields. The results support the photomolecular effect, demonstrating that solar radiation, represented by alternating electric fields, plays a crucial role in breaking water clusters at the interface, thereby increasing the evaporation rate. To solidify the findings of this work, it is crucial to experimentally evaluate the role of water states formed in the hydrogel for enhanced water evaporation by considering solar assisted evaporation from pure water, in the presence of hydrogel, and other porous materials that do not form water states. Some experimental studies indicating water evaporation enhancement using pure water under light and from sponge suggest that water states in hydrogel are not crucial for evaporation, which is consistent with the conclusion of this work.^13,16 Moreover, to confirm the role of water clusters in enhanced water evaporation, formed in the interface and vapor regions with and without the presence of hydrogel, indirect measurements using Infrared (IR) and Raman spectroscopy can be performed. Since direct visualization of clusters dynamics might be challenging, requiring in situ scanning electron microscopy (SEM)/scanning transmission electron microscopy (STEM) measurements, the results of IR and Raman spectroscopy should be carefully analyzed to confirm the presence of clusters considering the recent ambiguity regarding them.^51,52 It would also be interesting to go beyond the visible spectrum at a much lower oscillating frequency as the majority of our MD simulations are below this frequency range. This can be done, for example, by using antenna devices to induce electromagnetic (EM) field. Measuring the effect on water evaporation rate over the entire EM spectra could highlight the significance of electric field frequency. The phenomenon highlighted in this work might also occur under externally applied AC electric field,^53,54 but experiments and theoretical studies are needed to confirm this. This work emphasizes the importance of interface dynamics and structural characteristics of hydrogels. These insights provide a strong foundation for developing advanced evaporators and optimizing energy-efficient water management systems under solar radiation.

Author contributions

Project administration: X. Q. and J. L.; conceptualization: S. R., X. Q., and J. L.; methodology: S. R. and C. Y.; investigation: S. R.; visualization: S. R. and C. Y.; formal analysis: S. R.; supervision: X. Q. and J. L.; writing – original draft: S. R.; writing – review & editing: X. Q. and J. L.; funding acquisition: J. L.

Conflicts of interest

There are no conflicts to declare.

Data availability

All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.†

Acknowledgements

American Chemical Society (ACS) Petroleum Research Fund (PRF) award ND5-65609 (S. R., J. L.). Computational Resources provided by High-Performance Computing Center at North Carolina State University. Computational Resources provided by Advanced Cyberinfrastructure Coordination Ecosystem: Service & Support (ACCESS) program, supported by National Science Foundation (NSF) grants 2138259, 2138286, 2138307, 2137603, and 2138296. The authors acknowledge the fruitful discussion with Drs. Guihua Yu and Youhong (Nancy) Guo.

Notes and references

1. R. F. Service, Science, 2006, 313, 1088–1090.
2. A. Deshmukh, C. Boo, V. Karanikola, S. Lin, A. P. Straub, T. Tong, D. M. Warsinger and M. Elimelech, Energy Environ. Sci., 2018, 11, 1177–1196.
3. J. Blanco, S. Malato, P. Fernández-Ibañez, D. Alarcón, W. Gernjak and M. I. Maldonado, Renewable Sustainable Energy Rev., 2009, 13, 1437–1445.
4. C. Du, X. Zhao, X. Qian, C. Huang and R. Yang, Nano Energy, 2023, 107, 108086.
5. X. Wu, Y. Lu, X. Ren, P. Wu, D. Chu, X. Yang and H. Xu, Adv. Mater., 2024, 36, 2313090.
6. F. Zhao, X. Zhou, Y. Shi, X. Qian, M. Alexander, X. Zhao, S. Mendez, R. Yang, L. Qu and G. Yu, Nat. Nanotechnol., 2018, 13, 489–495.
7. X. Zhou, F. Zhao, Y. Guo, B. Rosenberger and G. Yu, Sci. Adv., 2019, 5, eaaw5484.
8. X. Zhang, Y. Peng, L. Shi and R. Ran, ACS Sustainable Chem. Eng., 2020, 8, 18114–18125.
9. M. Zhu, X. Liu, Y. Tian, A. Caratenuto, F. Chen and Y. Zheng, Sci. Rep., 2022, 12, 4403.
10. B. Luo, J. Wen, H. Wang, S. Zheng, R. Liao, W. Chen, O. Mahian and X. Li, Energy Environ. Mater., 2023, 6, e12353.
11. L. Cui, F. Wu, W. Wang, C. Hu, J. Zheng, Z. Zhu and B. Liu, ACS Appl. Polym. Mater., 2024, 6, 3253–3262.
12. G. Chen, Phys. Chem. Chem. Phys., 2022, 24, 12329–12345.
13. A. Caratenuto and Y. Zheng, Sci. Adv., 2024, 10, eadn6368.
14. J. H. Zhang, R. Mittapally, G. Lv and G. Chen, Energy Environ. Sci., 2025, 18, 1707–1721.
15. Y. Tu, J. Zhou, S. Lin, M. Alshrah, X. Zhao and G. Chen, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2312751120.
16. G. Lv, Y. Tu, J. H. Zhang and G. Chen, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2320844121.
17. G. Chen, Commun. Phys., 2024, 7, 330.
18. Y. Guo, F. Zhao, X. Zhou, Z. Chen and G. Yu, Nano Lett., 2019, 19, 2530–2536.
19. Q. Zhao, Y. Yang, B. Zhu, Z. Sha, H. Zhu, Z. Wu, F. Nawaz, Y. Wei, L. Luo and W. Que, Desalination, 2023, 568, 116999.
20. Y. Ikada, T. Mita, F. Horii, I. Sakurada and M. Hatada, Radiat. Phys. Chem., 1977, 9, 633–645.
21. X. Jiang, C. Wang and Q. Han, Comput. Theor. Chem., 2017, 1102, 15–21.
22. H. Heinz, R. A. Vaia, B. L. Farmer and R. R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290.
23. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
24. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In’T Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
25. H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765.
26. H. Sun, J. Comput. Chem., 1994, 15, 752–768.
27. H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987.
28. H. Sun, Macromolecules, 1995, 28, 701–712.
29. H. Sun, Macromolecules, 1993, 26, 5924–5936.
30. H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Phys. Chem., 1995, 99, 5873–5882.
31. S. P. Kadaoluwa Pathirannahalage, N. Meftahi, A. Elbourne, A. C. G. Weiss, C. F. McConville, A. Padua, D. A. Winkler, M. Costa Gomes, T. L. Greaves, T. C. Le, Q. A. Besford and A. J. Christofferson, J. Chem. Inf. Model., 2021, 61, 4521–4536.
32. S. A. Deshmukh, S. K. R. S. Sankaranarayanan and D. C. Mancini, J. Phys. Chem. B, 2012, 116, 5501–5515.
33. S. A. Deshmukh, S. K. R. S. Sankaranarayanan, K. Suthar and D. C. Mancini, J. Phys. Chem. B, 2012, 116, 2651–2663.
34. S. Wang, L. Yu, X. Jia, L. Zhang, H. Liu, E. Gao and C. Chen, Innovation Mater., 2024, 2, 100092.
35. G. Yiapanis, A. J. Christofferson, M. Plazzer, M. P. Weir, E. L. Prime, G. G. Qiao, D. H. Solomon and I. Yarovsky, Langmuir, 2013, 29, 14451–14459.
36. A. J. Christofferson, G. Yiapanis, A. H. M. Leung, E. L. Prime, D. N. H. Tran, G. G. Qiao, D. H. Solomon and I. Yarovsky, J. Phys. Chem. B, 2014, 118, 10927–10933.
37. J. He, T. Arbaugh, D. Nguyen, W. Xian, E. M. V. Hoek, J. R. McCutcheon and Y. Li, J. Membr. Sci., 2023, 674, 121498.
38. Y. Song, M. Wei, F. Xu and Y. Wang, Engineering, 2020, 6, 577–584.
39. S. Wang, K. Hou and H. Heinz, J. Chem. Theory Comput., 2021, 17, 5198–5213.
40. S. Tian, Z. Xu, S. Wu, T. Luo and G. Xiong, Int. J. Heat Mass Transfer, 2022, 195, 123134.
41. E. Bird, J. Gutierrez Plascencia, P. Keblinski and Z. Liang, Int. J. Heat Mass Transfer, 2022, 184, 122285.
42. J. Alejandre, D. J. Tildesley and G. A. Chapela, J. Chem. Phys., 1995, 102, 4574–4583.
43. L. X. Dang and T.-M. Chang, J. Chem. Phys., 1997, 106, 8149–8159.
44. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
45. F. H. Stillinger, J. Chem. Phys., 1963, 38, 1486–1494.
46. D. M. Huang and P. Attard, J. Chem. Phys., 2005, 122, 174503.
47. J. Wedekind and D. Reguera, J. Chem. Phys., 2007, 127, 154516.
48. W. Xu, Z. Lan, B. L. Peng, R. F. Wen and X. H. Ma, J. Chem. Phys., 2015, 142, 054701.
49. M. E. Tuckerman, D. Marx, M. L. Klein and M. Parrinello, Science, 1997, 275, 817–820.
50. X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373.
51. M. Ahmed and W. Lu, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2419957122.
52. G. Chen, G. Lv, J. H. Zhang and Y. Tu, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2425993122.
53. F. Hashinaga, G. P. Kharel and R. Shintani, Food Sci. Technol. Int., 1995, 1, 77–81.
54. Y. Chen, Y. Zhang, Y. Wang, X. Liu and D. He, Sens. Actuators, A, 2022, 347, 113958.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00353a

---