Enhanced performance in transparent conducting materials at the interface of a wide band gap semiconductor and a correlated metal

Abstract

Several classes of inorganic transparent conducting coatings are available (broad band wide band gap semiconductors, noble metals, amorphous oxides and correlated metals), with peak performance depending on the layer thickness. Correlated metallic transition metal oxides have emerged as potential competitive materials for small coating thicknesses, but their peak performance remains one order of magnitude below other best in class materials. By exploiting the charge transfer at the interface between a correlated metal (SrNbO₃) and a wide band gap semiconductor (SrTiO₃), we show that pulsed laser deposition-grown SrNbO₃ heterostructures on SrTiO₃ outperform correlated metals by an order of magnitude. The apparent increase in carrier concentration confirms that an electronically active interfacial layer is contributing to the transport properties of the heterostructure. The correlated metallic electrode allows the extraction of high mobility carriers resulting in enhanced conductivity for heterostructures with thicknesses up to 20 nm. The high optical absorption of the high mobility metallic interface does not have a detrimental effect on the transmission of the heterostructure due to its small thickness. The charge transfer-driven enhanced electrical properties in correlated metal – wide band gap semiconductor heterostructures offer a distinct route to high performance transparent conducting materials.

---

New concepts

This work demonstrates charge transfer between a correlated metal and a wide-gap semiconductor to form a highly conducting nanoscale region at the heterostructure interface that acts as a transparent conductor. By taking advantage of the high conductivity of the correlated metal SrNbO₃, we can extract the high mobility electrons formed at the interface with SrTiO₃. This results in only very thin films (<10 nm) of SrNbO₃ being required, and since the high conductivity interface only occupies a nanoscale region, sufficient transparency is attained to afford figures of merit superior to other transparent conducting materials competing with resource-limited ITO. Given the broad chemical tunability of both correlated metals and wide-gap semiconductors, this creates extensive opportunities to design and optimise the interface between these materials classes to generate outperforming transparent conductors by overcoming the distinct physical limitations on transparent conductivity of each class in isolation.

1. Introduction

Transparent conducting materials (TCMs) are in demand due to their widespread application in display screen technologies and photovoltaics.¹ To quantify the suitability of a TCM for specific applications, the two primary functionalities, electrical conductivity and optical transmission, are assessed and an appropriate figure of merit (FOM) can be defined depending on the targeted application.² A widely accepted performance metric is the Haacke FOM defined as³where T is the average transmittance in the visible spectrum (1.55–3.1 eV) and R_s is the sheet resistance of the coating.

Several classes of inorganic compounds have been identified as TCMs. Heavily doped, wide band gap semiconductors, often referred to as transparent conducting oxides (TCOs), are a well-established industrial technology⁴ with coating thicknesses of several hundred of nanometers required and the electronic mechanisms limiting further improvement in their overall performance are still an intense subject of academic research.⁵ The concept of doping a wide band gap crystalline semiconductor with a broad conduction band can be extended to amorphous oxide semiconductors (AOSs).⁶ Noble metal thin films, such as Ag, are also an established technology: here, to limit the opaqueness of the coating due to the strong absorption of the free electrons in the visible region of the spectrum, their thickness has to be limited to a few nanometers (<10 nm). Correlated metal (CM) thin films have also been shown to be a promising alternative with intermediate thicknesses (20–50 nm) compared to the two previous systems, taking advantage of a large carrier concentration and a reduced absorption in the infrared controlled by a renormalized effective mass 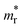(determined by the parameter where is the non-interacting electron effective mass).⁷ Strategies to optimize the FOM of such materials are emerging.⁸

Since the optimum carrier concentration in TCOs is governed by the intrinsic electronic structure of the compound through the plasma frequency position, the fundamental mechanism driving the performance of TCOs is to design impurity donors that create excess electrons in a broad s-like band leading to maximum mobilities, and thus the overall performance is mobility controlled. Conversely, in CMs the intrinsic mobility of carriers originating from the d-like band is constrained by the mass renormalization parameter Z_k and the primary mechanism to enhance the functionality of the CMs is to maximize the number of carriers, thus the overall performance is band filling controlled. Considering the difference in strategies required to optimize different classes of TCMs, it is important to identify the regime where each class of material outperforms, and where potential improvements may be made in their overall performance. Using a simple model available in the literature,⁷ the transmittance, sheet resistance and Haacke FOM for an optimized TCO (n = 1.9 × 10²¹ cm⁻³, μ = 55 cm² V⁻¹ s⁻¹)⁹ and CM (5d², n = 3.15 × 10²² cm⁻³, μ = 15 cm² V⁻¹ s⁻¹, Z_k = 0.5)⁸ as a function of the film thickness can be evaluated and is presented in Fig. 1(a).

Fig. 1 (a) Transmittance (top panel), sheet resistance (middle panel) and Haacke figure of merit (bottom panel) as a function of film thickness for an optimized wide band gap semiconductor (TCO, blue curve) and a correlated metal (CM, red curve) using the model described in the literature⁷ and the materials parameters given in the main text. The vertical grey line corresponds to the 25 nm thickness below which the correlated metals perform best and above which the wide band gap semiconductors perform best. The horizontal grey line highlights the difference in coating thickness required to achieve 10 Ω □⁻¹ for the two classes of materials (25 nm for CM and 80 nm for TCO). (b) Atomic structure of a (SrTiO₃)₆/(SrNbO₃)₆ heterostructure (light blue and purple octahedra correspond to Ti and Nb environments respectively) and the associated layer-projected density of states obtained by density functional theory (DFT). The top black line shows the total density of states. The non-zero density of states in the SrTiO₃ layer (cyan filling) at the Fermi level suggests charge transfer from the SrNbO₃.

By design, TCOs provide a high transmittance (Fig. 1(a) top panel) for all film thicknesses whereas, despite the benefit of the correlation-enhanced effective mass, CMs show finite absorption above the plasma frequency and therefore their transmission decreases rapidly in thick films and is only comparable to TCOs up to film thicknesses of around 20 nm. This CM thickness threshold is larger than the noble metal coating thickness threshold for TCM applications (<10 nm). When considering the second performance-governing property of a transparent conducting material, the sheet resistance (Fig. 1(a) middle panel), the CMs provide a lower sheet resistance for an equivalent TCO thickness because of their large carrier concentration and modest mobility. In the simple model here, to achieve a sheet resistance of 10 Ω □⁻¹, 28 nm CM and 78 nm TCO films are required. It is important to note that the model used does not include scattering mechanisms influencing the mobility in the material, thus for the TCO, this thickness is below the 100 nm threshold observed experimentally to produce the expected resistivity values and a much thicker coating (about 300 nm) is required to achieve the optimum sheet resistance. The balancing of these properties leads to two distinct FOM regions (Fig. 1(a) bottom panel) where at thickness smaller (larger) than 25 nm the CMs (TCOs) perform better than TCOs (CMs). Overall, TCOs achieve a higher FOM across the range of thicknesses considered (the maximum FOM is ≈10⁻² Ω⁻¹ for a 10 nm CM film and ≈10⁻¹ Ω⁻¹ for a 400 nm TCO film). This latter observation can be understood from the governing physics and the intrinsic properties of the respective best-in-class materials. The performance of TCOs relies on optimizing the carrier mobility in the film, thus focusing on minimizing defects and unwanted extrinsic scattering mechanisms, and intensive research has led to the achievement of theoretical limits in performance.⁵ By contrast, in the filling-controlled CMs the chemistry of the compound itself dictates its optimum performance through the carrier concentration and mobility which is predominantly governed by the strong electron correlation rather than extrinsic scattering mechanisms. Given the limitations for CMs as TCMs due to their properties, their peak performance cannot match the state-of-the-art TCO's as shown by the FOM calculated from a model described in the literature,⁷ (Fig. 1(a) bottom panel) and experimentally confirmed, e.g., CaMoO₃ FOM is 9.8 × 10⁻⁴ Ω⁻¹,⁸ and epitaxial ITO FOM is 0.08 Ω⁻¹.⁹ This perspective leads to a new strategy to design high performance transparent conducting thin films that exploits the interface between metallic and semiconducting transparent conducting materials.

To circumvent the filling control limitation of CMs and the extrinsic mobility limiting scattering mechanisms in TCOs, we explore the role of charge transfer from Nb⁴⁺ in SrNbO₃ to Ti⁴⁺ in SrTiO₃, based on the redox chemistry of these transition elements forming Nb⁵⁺ and Ti³⁺ with associated carrier generation in SrTiO₃: DFT calculations¹⁰ indicate substantial electron transfer from the Nb 4d to the Ti 3d states. Since the first experimental observation of a two-dimensional electron gas at the interface between the two insulating transition metal oxides LaAlO₃ and SrTiO₃,¹¹ several mechanisms have been identified leading to the creation of dimensionally-confined itinerant electrons in oxide heterostructures such as charge transfer due to favourable band alignment,¹² polar discontinuity¹¹ and oxygen vacancies.¹³ The electronic structure of these complex materials is often difficult to capture accurately, making it difficult to predict the nature of the interface and the large mismatch of the work functions between insulating transition metal oxides and conventional metals renders the extraction of the extra itinerant charge carriers difficult due to the formation of Schottky barriers.¹⁴ The development of metallic perovskite-based correlated oxides offers the opportunity to create all-oxide junctions where the metallic oxide can act as an effective carrier extraction layer. Theoretical and experimental studies have demonstrated the validity of this hypothesis.¹⁵ Spectroscopic evidence of a two-dimensional electron gas was observed at the BaSnO₃/SrNbO₃ interface¹⁶ and transport properties suggested interfacial superconductivity driven by charge transfer at the SrNbO₃/SrTiO₃ interface.¹⁷

In these heterostructures, the electron transfer occurs from the partially filled Nb 4d band which presents a strong effective mass renormalisation leading to high carrier concentrations (∼10²² cm⁻³) and experimental mobilities in the range 0.1–5 cm² V⁻¹ s⁻¹.¹⁸ The electron acceptor layer, in a similar strategy to the optimisation of conventional TCO materials, should possess a conduction band minimum with spatially extended s-like orbitals resulting in low effective mass and potentially high carrier mobilities. The BaSnO₃ conduction band minimum is dominated by highly dispersive Sn-5s orbitals with large room temperature mobilities (>100 cm² V⁻¹ s⁻¹) observed in high quality single crystals.¹⁹ In analogy to the conventional TCO compounds, when grown as heterostructure thin films, the observed mobilities decrease by an order of magnitude (in the range of 5–10 cm² V⁻¹ s⁻¹) due to dislocations arising from lattice mismatch.²⁰ Therefore, realising experimentally a high mobility 2-dimensional electron gas in a BaSnO₃-based heterostructure is challenging. The conduction band minimum of the other candidate material as an electron acceptor layer, SrTiO₃, is dominated by Ti-3d orbitals with a higher effective mass than BaSnO₃. Experimentally, the mobilities observed in SrTiO₃-based 2-dimensional electron gases are as high as 10 000 cm² V⁻¹ s⁻¹ at low temperature, decreasing by several orders of magnitude to 10 cm² V⁻¹ s⁻¹ at room temperature¹¹ due to the strong longitudinal optical phonon scattering.²¹

Considering the challenges in growing high quality BaSnO₃ thin films^22,23 and the availability of high quality SrTiO₃ single crystals as substrates, to test the hypothesis that the interface between correlated metal and semiconductor oxides can lead to efficient carrier extraction, we have grown hetero-epitaxial thin films of the correlated metal SrNbO₃ over a series of thicknesses on wide band gap semiconductor SrTiO₃ substrates and studied their structural characteristics, focusing on the atomic scale interface arrangement, and their electrical and optical properties.

The series of thin films prepared generate improved FOM for transparent conduction by simultaneously increasing the effective carrier concentration and mobility through charge transfer at the interface while maintaining the transparency of the coating.

2. Results and discussion

2.1. Charge transfer at the interface of SrNbO₃ and SrTiO₃

Highly (0 0 1) oriented SrNbO₃ films have been obtained with an average root mean squared (RMS) surface roughness of 0.2 nm (Fig. S1, ESI†) for a film thickness of 17 nm (Fig. S2, ESI†), up to a maximum of 0.9 nm roughness for a film thickness of 132 nm. The lattice parameters for SrNbO₃ were calculated from reciprocal space mapping (Fig. S3 and S4, ESI†) and out-of-plane diffraction with a = 3.99(3) Å, b = 4.01(3) Å in-plane and c = 4.07(1) Å suggesting a small tetragonal distortion with c/a = 1.02 Å. The in-plane lattice parameters (Fig. S5, ESI†) are close to the reported value for bulk cubic SrNbO₃ with a_bulk = 4.024 Å. The lattice mismatch between SrNbO₃ and SrTiO₃ is −2.96% and the rocking curve (Fig. S6, ESI†) presents a broad Gaussian (FWHM 1.48(5)°) and narrow Lorentzian component (FWHM 0.074(1)°), which indicates the presence of dislocations in the films.

To understand the atomic arrangement at the interface, high angle annular dark field scanning transmission electron microscopy (HAADF-STEM) has been performed. In contrast to polar discontinuity-induced charge transfer, the band alignment, or reduction–oxidation, mechanism does not require atomically sharp interfaces, therefore the samples were grown on non-chemically etched SrTiO₃ substrates and the mixed termination nature of the interface is confirmed by a “blurry” interface (Fig. S7, ESI†). The atomically resolved elemental STEM-EDX map (Fig. 2(a)), and intensity profile (Fig. 2(b); Fig. S7 and S8, ESI†) suggests a graded composition with a mixture of Nb and Ti at the interface arising from interdiffusion during growth. To extract a quantitative atomic composition of the interfacial layer, the intensity profile from the HAADF-STEM images presented in Fig. 2(c) and Fig. S10 (ESI†) was simulated with different models using QSTEM (Fig. S10–S12, ESI†) where the Ti and Nb composition of the B site is varied. The best model is comprised of a SrTi_1−xNb_xO₃ interface three atomic layers thick (approximately 12.2 Å) where x varies linearly from 0 to 1 sandwiched between SrTiO₃ and SrNbO₃ layers respectively (red line in Fig. 2(d)).

Fig. 2 (a) High magnification HAADF-STEM image and the EDX maps in atomic percent. (b) EDX profile measured perpendicular from the STO substrate up to the SNO film and averaged to the whole area. The profile shows that the Ti/Nb mixing occurs within a range of about 1 nm and goes gradually. (c) HAADF-STEM imaging of the SrTiO₃/SrNbO₃ heterostructure (left) and simulated HAADF-STEM image with the closest atomic model overlaid (right). (d) Calculated conduction band edge energy (blue line left panel) and associated carrier concentration profile across the heterostructure (black line right panel) for the heterostructure including the graded interface layer following the composition variation (red line left panel) obtained from the microscopy study. (e) Average oxidation states obtained from XANES measurements. Black dots are for reference materials (Nb⁵⁺: Nb-doped SrTiO₃ single crystal, Sr₂Nb₂O₇ (Nb⁵⁺), La_1/3NbO₃ (Nb⁵⁺) and Nb₂O₅ powder; Nb⁴⁺: NbO₂ powder), green empty stars are for SrTiO₃/SrNbO₃ heterostructures and blue empty squares are for DyScO₃/SrNbO₃ heterostructures.

To investigate the influence of this graded layer on the charge transfer predicted for an abrupt interface, we performed Schrödinger–Poisson simulations using the experimental interface structure obtained from the electron microscopy study (Fig. 2(c)). The model shows the transition of the conduction band edge across the graded interface (left panel Fig. 2(d)), allowing for the injection of the highly mobile carriers into the correlated metal. The profile of the carrier concentration in equilibrium indicates a 2DEG-like accumulation of charge carriers at the interface. The favorable band alignment between SrNbO₃ and SrTiO₃ together with the graded interface results in a situation similar to modulation doping where electrons from SrNbO₃ transfer into SrTiO₃ forming a 2-dimensional gas at the interface as illustrated by the gradual carrier concentration depletion in the SrNbO₃ and the sharp carrier concentration peak observed on the SrTiO₃ side.

The graded layer at the interface between the CM SrNbO₃ and the wide band gap semiconductor SrTiO₃ does not impede the charge transfer (Fig. S13, ESI†) and is similar to the introduction of the linearly graded channel in high mobility electron transistors which has been shown to improve the extraction of carriers with reduced scattering.²⁴ To confirm that electronic transfer from the SrNbO₃ top to the SrTiO₃ bottom layers is realized, we investigated the average Nb oxidation state using XANES for different thickness layers and substrates (Fig. 2(e); Fig. S14, ESI†). The contribution of the interface region in the 80 nm sample has minimal effect on the average oxidation state because of its small proportion of the whole system and is therefore saturated by the bulk SrNbO₃ properties in the film itself. Films of nominal thicknesses 80 nm and 20 nm on DyScO₃ substrates, in which charge transfer or cation diffusion is not expected, show an average oxidation state of 3.94(9)+ and 4.01(9)+, within error of the nominal 4+. SrNbO₃ films of nominal thicknesses 80 nm and 20 nm on SrTiO₃ substrates were measured and show average oxidation states of +4.05(9) and +4.35(9) respectively. The intermixing of B-site cations at the interface alone is not enough to produce this magnitude of increased oxidation state. For an average increase of 0.35+, there would need to be a minimum diffusion interface thickness of 7 nm of Nb⁵⁺ which is much larger than the experimentally observed 1.22 nm diffusion layer using HAADF-STEM. It can also be assumed that surface oxidation and associated Nb⁵⁺ defects in the film would not cause a significant increase solely in the 20 nm STO case when no such oxidation is seen on DSO. Considering these observations, the charge transfer in the 20 nm sample can be estimated and contributes significantly to the average oxidation state of the system, with approximately 35% Nb⁵⁺ resulting in electronically active Ti³⁺. This oxidation state change is consistent with the electron transfer from the NbO₂ layer above the interface into the TiO₂ layer beneath it observed in the partial density of states of a (SrTiO₃)₆/(SrNbO₃)₆ heterostructure (Fig. 1(b)).

2.2. Electrical properties

To investigate the effect of the charge transfer layer on the electrical properties of the heterostructure we measured the resistivity, carrier concentration and mobility as a function of film thickness and on different substrates where no (DyScO₃) or very little (LSAT) charge transfer should be observed (Table S1, ESI†). The temperature dependent resistivity is presented in Fig. 3(a) and shows that all the films prepared present a typical metallic behavior. The first observation is that for all thicknesses, the heterostructures grown on LSAT and DyScO₃ present higher resistivity compared to the heterostructures grown on SrTiO₃ with a room temperature resistivity between 40–70 μΩ cm which is similar to the values reported on films grown on LaAlO₃.¹⁸ In contrast, the room temperature resistivities of the SrNbO₃ heterostructures with thicknesses in the range of 2 to 74 nm grown on SrTiO₃ substrates, varied between 4.4(8) μΩ cm and 12.8(4) μΩ cm, lower than the lowest reported value of 28.2 μΩ cm for SrNbO₃ films grown on KTaO₃ substrates.²⁵ The residual resistivity ratio (RRR) also exhibits contrasting trends. For the heterostructures grown on DyScO₃ and LSAT, the RRR is slightly higher than 1 and comparable to SrNbO₃ single crystals^18,25 and other CM heterostructures grown by PLD.^7,8 The SrNbO₃ heterostructures grown on SrTiO₃ exhibit a much larger RRR (>1000) which is typically observed in lightly doped (10¹⁷–10¹⁸ cm⁻³) SrTiO₃ single crystals²⁶ and in SrTiO₃ based 2-dimensional electron gas system.¹⁵ Another distinct feature of the heterostructures grown on SrTiO₃ is the evolution of the room temperature resistivity as a function of thickness. Ordinarily, as the coating thickness decreases, the measured resistivity deviates from the expected constant conductivity model at a threshold thickness (50 nm for CMs and 200 nm for TCO's) and increases according to the Mayadas and Shatzkes model which includes various scattering mechanisms.⁷ Strikingly, for the heterostructures grown on SrTiO₃, with decreasing film thickness, the room temperature resistivity is observed to decrease rather than increase as observed in conventional CMs and TCOs (Fig. 3(a)). This could suggest that the single slab interpretation is not valid and that an interfacial layer with a high mobility carrier should be considered. This phenomenon is observed for thicknesses down to a nominal SrNbO₃ thickness of 2 nm below which the resistivity shows a slight increase. This is expected due to either the film thickness being reduced below the estimated electron mean free path (EMFP) of 3.5 nm in SrNbO₃ thus introducing surface scattering²⁷ or that no bulk SrNbO₃ film is formed as the nominal thickness is close to the graded layer thickness observed by HRTEM (1.2 nm).

Fig. 3 (a) Electrical resistivity as a function of temperature for various thicknesses of SrNbO₃ heterostructures grown on SrTiO₃ substrates (yellow to purple line) and thick (red line) and thin (blue line) SrNbO₃ heterostructures grown on DyScO₃ and LSAT substrates respectively. (b) Effective carrier concentration extracted from Hall effect (top panel) and associated carrier mobility (bottom panel) as function of temperature. The color scheme is the same as in (a) and the mobilities of all SrNbO₃ heterostructures grown on SrTiO₃ substrate overlap. The black line in the top panel represents the theoretical carrier concentration expected for one free electron per unit cell in SrNbO₃. (c) Effective carrier concentration obtained from Hall effect at 300 K as a function of SrNbO₃ thickness (black dots). The black line corresponds to the theoretical carrier concentration expected for one free electron per unit cell in SrNbO₃ and the red line corresponds to the carrier concentration expected with an additional interfacial charge transfer layer of 9 nm as represented in the inset.

Fig. 3(b) shows the temperature dependence of the effective carrier concentration extracted from Hall effect measurements (top panel) and the associated carrier mobility (bottom panel). All films present a nearly constant carrier concentration for all measured temperatures as expected from the temperature dependence of the resistivity. For the 17 nm heterostructures grown on LSAT and for thicknesses above 60 nm heterostructures grown on SrTiO₃, the effective carrier concentration converges towards the expected bulk value (n_th) assuming a formal Nb⁴⁺ oxidation state. For heterostructures grown on SrTiO₃ with thicknesses between 5–20 nm, the effective carrier concentration increases as the thickness decreases as expected for the additional contribution from charge transfer at the interface. The generation of high mobility carriers is confirmed by the comparison of the mobility of films grown on SrTiO₃ that exhibit mobilities reaching 3.2 × 10⁴ cm² V⁻¹ s⁻¹ at low temperature compared to 10 cm² V⁻¹ s⁻¹ for films grown on LSAT (Fig. 3(b) bottom panel). The temperature variation of the mobility for the SrNbO₃ heterostructure grown on SrTiO₃ is similar to the SrTiO₃-based 2DEG reported in the literature. The combination of increased carrier mobility and apparent increased carrier concentration suggests that both the carrier filling and mobility limitations can be circumvented in these heterostructures.

To confirm that the apparent increased effective carrier concentration originates from the creation of an additional conducting charge transfer layer, we investigate the measured effective carrier concentrations of SrNbO₃ heterostructure grown on SrTiO₃ at 2 K as a function of the thickness (Fig. 3(c)). The effective carrier concentration values (n_eff) obtained from Hall effect measurements are calculated using the film thickness t measured using X-ray reflectivity (except for the 2 nm nominal thickness which was grown using a calibrated number of pulses), which does not consider the thickness of the additional electronically active charge transfer region t_CT. The apparent increase in carrier concentration is caused by the underestimation of the total electronically active thickness, t + t_CT, where t_CT is the depth of the charge transfer into the SrTiO₃ substrate neglecting the experimentally observed compositionally graded layer. Considering this, a simple model can be used to estimate the depth of the charge transfer layer where .

In Fig. 3(c), the model (red line) shows the change of carrier concentration with film thickness if an additional electronically active thickness t_CT = 9 nm is included. This additional electronically active layer is thicker than the experimentally observed compositionally graded layer at the interface (1.22 nm) as illustrated in the inset of Fig. 3(c). Together with the measured change of Nb oxidation states on heterostructures grown on SrTiO₃ (Fig. 2(e)) which cannot solely be explained by the intermixing of Nb and Ti at the interface, this observation strongly suggests that the unconventional observed decreased room temperature resistivity as the thickness decreases is due to a charge transfer rather than possible strain or Nb-delta doping of SrTiO₃.

2.3. Improved FOM in the hybrid CM/TCO heterostructure

We have demonstrated that the extraction of high mobility carriers through charge transfer at the interface of a CM and a wide band gap semiconductor is experimentally achievable and this phenomenon could offer an attractive strategy to enhance the electrical properties of the filling-controlled CM without detrimental effect on the optical properties. The optical transmission for SrNbO₃ heterostructures grown on SrTiO₃ for various film thicknesses was measured on double-side polished SrTiO₃ substrates (Fig. S15, ESI†) and the average transmission calculated for the visible spectrum range of (1.55–3.1 eV) is presented in the top panel of Fig. 4(a). Transmittances as high as 80% are measured for film thicknesses up to 20 nm, above which they follow closely the theoretical model for a CM system (red line) introduced in Fig. 1(a), confirming that at lower thicknesses the optical transparency is not reduced drastically by the introduction of the high mobility carriers at the interface, as the absorption remains low for the 9 nm interfacial layer. The main advantage of enhancing the electrical conductivity of the heterostructure provided by the charge transfer mechanism at room temperature is clearly visible in the bottom panel of Fig. 4(a), where the room temperature sheet resistance is presented as function of film thickness. Two different regimes are identifiable; for film thickness larger than 20 nm the sheet resistances fall on a line (red line in Fig. 4(a) bottom panel) corresponding to a constant resistivity of 12 μΩ cm, whereas for film thickness smaller than 20 nm the sheet resistances fall on a line (blue line in Fig. 4(a) bottom panel) corresponding to a smaller constant resistivity of 5 μΩ cm.

Fig. 4 (a) Transmission (black circles top panel) and sheet resistance (empty black stars bottom panel) of SrNbO₃ heterostructures grown on SrTiO₃ substrates as function of film thickness. The red line in the top panel is the same transmission calculated for an optimized CM presented in Fig. 1(a). The red and blue lines in the bottom panel correspond to constant resistivities of 12 μΩ cm and 5 μΩ cm respectively. (b) Haacke FOM for the SrTiO₃/SrNbO₃ heterostructures as function of thickness (green empty stars) and LaAlO₃/SrNbO₃ for the optimum thickness (black empty star). The red and blue opaque line represents the calculated Haacke FOM for an optimized d² CM (red squares are for SrTiO₃/SrMoO₃ heterostructure from Stoner et al).⁸ and ITO respectively as presented in Fig. 1(a). Measured Haacke FOM as function of thickness for epitaxial ITO (thick blue line), d¹ SrVO₃ CM (orange line and squares), noble metals (grey line) and amorphous oxides (purple line) are reproduced from ref. 28 for comparison.

Combining the large transmittance and enhanced resistivity for various thicknesses, it is possible to calculate the Haacke FOM for the SrNbO₃ heterostructure grown on SrTiO₃ (Table S2, ESI†) which is presented in Fig. 4(b) (green empty stars) together with the FOM of other best in class materials. It shows peak performance for a thickness around 20 nm with a FOM of 0.04 Ω⁻¹, an enhancement of more than one order of magnitude compared to the optimized d¹ CM systems (orange line and full orange square for SrVO₃ and black empty star for a SrNbO₃ heterostructure grown on LaAlO₃). The hybrid CM/TCO outperforms all other classes of materials (CM, amorphous oxides, noble metals) and is close to the 0.08 Ω⁻¹ record for 400 nm epitaxial ITO.⁹

3. Conclusion

Realizing the two-dimensional electron gas at an oxide interface often presents limitations in extracting the generated carriers as they lie between two insulating layers. Here, this limitation is circumvented by the use of a correlated metallic oxide which has the dual role of providing (i) the favorable band alignment to generate charge transfer at the interface and (ii) an optically transparent efficient electrode for the extraction of the generated high mobility carriers. We have demonstrated experimentally that by bringing together the correlated metallic oxide SrNbO₃ and the wide band gap semiconductor SrTiO₃ in epitaxial heterostructures, we can enhance the electrical conductivity of this hybrid coating without detriment to the optical transmission in the visible. The combination provides a peak performance an order of magnitude better than the correlated metal on its own. This strategy opens new paths to design novel hybrid CM–TCO heterostructures with FOM exceeding the best in class materials.

4. Experimental section/methods

Thin film growth: SrNbO₃ films were deposited via pulsed laser deposition (PVD Products NanoPLD, Coherent Lambda Physik COMPex Pro 248 nm KrF Excimer laser) on SrTiO₃ (001) substrates (PI-KEM, UK). Dense ceramic targets of Sr₂Nb₂O₇ were prepared via conventional solid state synthesis. Stoichiometric amounts of SrCO₃ (>99.9% purity) and Nb₂O₅ (99.9985% purity) were weighed, ground thoroughly in an agate mortar and pestle and calcined in air at 900 °C for 12 hours, re-ground and fired again in air at 1200 °C for a further 12 hours. The resulting powder was pressed into a 32 mm diameter pellet and then pressed with a cold isostatic press at 30 kpsi before sintering at 1450 °C for 24 hours. Heating and cooling was at a rate of 5 °C per minute for all steps. Deposition was performed under chamber base pressure (∼5 × 10⁻⁷ Torr) with nominal substrate temperature of 650 °C and a laser fluence of 1.3 J cm⁻² at a rate of 1 Hz.

X-Ray diffraction: powder X-ray diffraction of the target material was performed on a Panalytical Co source (λ = 1.79 Å) instrument in Bragg–Brentano geometry. X-Ray analysis of thin films was performed on a Rigaku Smartlab diffractometer, with Cu source (λ = 1.54 Å) and a 2D Hypix detector in 1D mode for large angle θ − 2θ scans and reflectivity and 0D for rocking curve analysis. Film thicknesses ≥5 nm were determined by X-ray reflectivity and used to calibrate the growth rate per laser pulse for deposition of films with nominal thickness <5 nm.

Electron microscopy: the sample was prepared using the focused ion beam (FIB) technique. The film was covered with carbon and platinum protection layers. For the high angle annular dark field scanning transmission electron microscopy (HAADF-STEM) imaging and STEM-EDX analysis, a probe aberration corrected microscope FEI Titan operated at 300 kV and equipped with Super-X detector was used. The structure model of the film was made in CrystalMaker software by merging cubic SrTiO₃ and SrNbO₃. For the interface layer, different Ti/Nb contents were tested: 0.3Ti + 0.7Nb; 0.5Ti + 0.5Nb; 0.7Ti + 0.3Nb and a sharp interface. The simulated HAADF-STEM images were calculated using the QSTEM 2.5 software.²⁹

XANES: X-Ray absorption near edge structure was obtained at Diamond Light Source beamline B18 in reflection geometry. Niobium oxidation states was calibrated using NbO₂ (Nb⁴⁺), Nb₂O₅ (Nb⁵⁺), Sr₂Nb₂O₇ (Nb⁵⁺), La_1/3NbO₃ (Nb⁵⁺) and a 0.5 wt% Nb⁵⁺ doped SrTiO₂ single crystal substrate.

Electrical properties: resistivity measurements were obtained using a Quantum Design physical properties measurement system (PPMS) capable of a temperature range of 300 K to 2 K and applying magnetic fields up to a magnitude of 14 T. The films were contacted in Van der Pauw geometry.

Optical properties: UV-vis-NIR transmission spectra were obtained using a Agilent Cary 5000 between 2500 nm and 200 nm, with reduced slit height setting. The NIR (2500–900 nm) scan rate was 12 nm min⁻¹ and the UV-vis scan rate was 600 nm min⁻¹, with a measurement interval of 0.667 nm. Average visible transmission was calculated between 400 nm and 800 nm.

Computational details: periodic DFT calculations were performed on a twelve-layer slab model containing six layers each of SrTiO₃ and six layers of SrNbO₃. Both surfaces of the slab were terminated with SrO layers and separated by a vacuum region of 32.3 Å. All calculations were carried out using VASP³⁰ with the PAW³¹ approach to treat core electrons and a 550 eV plane-wave cutoff energy. The meta-GGA functional SCAN³² was used to reduce the overestimated delocalisation of electron density common in GGA functionals. Calculations were performed in a fixed 3.908 Å × 3.908 Å × 80 Å cell where the in-plane parameters were chosen to match those of SrTiO₃ representing growth on a fixed substrate. A dipole correction layer was placed in the vacuum region to counter the periodic dipole moment generated by the asymmetric slab. The positions of all atoms were optimized until forces fell below 0.01 eV Å⁻¹ using an 11 × 11 × 1 k-point grid. A single-point calculation of the partial density of states was then performed with a 24 × 24 × 1 k-point grid.

Data availability

All data presented in this paper can be access through the University of Liverpool Data Repository https://datacat.liverpool.ac.uk/id/eprint/2849 as soon as the paper will be published.

Conflicts of interest

A patent application GB202018825A was filed 30 November 2020.

Acknowledgements

The authors acknowledge EPSRC for funding through EP/N004884/1 and EP/V026887/1. We thank the Diamond Light Source for the award of beam time as part of the Energy Materials Block Allocation Group SP14239.

References

1. C. G. Granqvist, in Handbook of Transparent Conductors, ed. D. S. Ginley, Springer US, Boston, MA, 2011, pp. 353–423 DOI:10.1007/978-1-4419-1638-9_11.
2. A. Anand, M. M. Islam, R. Meitzner, U. S. Schubert and H. Hoppe, Adv. Energy Mater., 2021, 11, 2100875.
3. G. Haacke, J. Appl. Phys., 1976, 47, 4086–4089.
4. S. C. Dixon, D. O. Scanlon, C. J. Carmalt and I. P. Parkin, J. Mater. Chem. C, 2016, 4, 6946–6961.
5. B. A. D. Williamson, T. J. Featherstone, S. S. Sathasivam, J. E. N. Swallow, H. Shiel, L. A. H. Jones, M. J. Smiles, A. Regoutz, T.-L. Lee, X. Xia, C. Blackman, P. K. Thakur, C. J. Carmalt, I. P. Parkin, T. D. Veal and D. O. Scanlon, Chem. Mater., 2020, 32, 1964–1973.
6. J. E. Medvedeva, D. B. Buchholz and R. P. H. Chang, Adv. Electron. Mater., 2017, 3, 1700082.
7. L. Zhang, Y. Zhou, L. Guo, W. Zhao, A. Barnes, H.-T. Zhang, C. Eaton, Y. Zheng, M. Brahlek, H. F. Haneef, N. J. Podraza, M. H. W. Chan, V. Gopalan, K. M. Rabe and R. Engel-Herbert, Nat. Mater., 2016, 15, 204–210.
8. J. L. Stoner, P. A. E. Murgatroyd, M. O'Sullivan, M. S. Dyer, T. D. Manning, J. B. Claridge, M. J. Rosseinsky and J. Alaria, Adv. Funct. Mater., 2019, 29, 1808609.
9. H. Ohta, M. Orita, M. Hirano, H. Tanji, H. Kawazoe and H. Hosono, Appl. Phys. Lett., 2000, 76, 2740–2742.
10. Z. Zhong and P. Hansmann, Phys. Rev. X, 2017, 7, 011023.
11. A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423–426.
12. A. Giampietri, G. Drera and L. Sangaletti, Adv. Mater. Interfaces, 2017, 4, 1700144.
13. D. A. Muller, N. Nakagawa, A. Ohtomo, J. L. Grazul and H. Y. Hwang, Nature, 2004, 430, 657–661.
14. M. Minohara, R. Yasuhara, H. Kumigashira and M. Oshima, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 235322.
15. J. Zhang, Y.-Y. Pai, J. Lapano, A. R. Mazza, H. N. Lee, R. G. Moore, B. J. Lawrie, T. Z. Ward, G. Eres, V. R. Cooper and M. Brahlek, Small Sci., 2022, 2, 2100087.
16. S. Mahatara, S. Thapa, H. Paik, R. Comes and B. Kiefer, ACS Appl. Mater. Interfaces, 2022, 14, 45025–45031.
17. H. Wei, S. Chen, Y. Zou, Y. Wang, M. Yang, Q. Zhang, K. Zou, L. Gu, K. Jiang, E.-J. Guo and Z. G. Cheng, Phys. Rev. B, 2024, 109, 205404.
18. S. Kumar, J. Ahammad, D. Das, R. Kumar, S. Dhar and P. Johari, J. Appl. Phys., 2024, 135, 015303.
19. H. J. Kim, U. Kim, H. M. Kim, T. H. Kim, H. S. Mun, B.-G. Jeon, K. T. Hong, W.-J. Lee, C. Ju, K. H. Kim and K. Char, Appl. Phys. Express, 2012, 5, 061102.
20. P. V. Wadekar, J. Alaria, M. O’Sullivan, N. L. O. Flack, T. D. Manning, L. J. Phillips, K. Durose, O. Lozano, S. Lucas, J. B. Claridge and M. J. Rosseinsky, Appl. Phys. Lett., 2014, 105, 052104.
21. A. Verma, A. P. Kajdos, T. A. Cain, S. Stemmer and D. Jena, Phys. Rev. Lett., 2014, 112, 216601.
22. D. Pfützenreuter, M. Zupancic, Z. Galazka, R. Schewski, A. Dittmar, K. Irmscher, M. Albrecht and J. Schwarzkopf, Nanotechnology, 2021, 32, 505609.
23. K. Eom, H. Paik, J. Seo, N. Campbell, E. Y. Tsymbal, S. H. Oh, M. S. Rzchowski, D. G. Schlom and C.-B. Eom, Adv. Sci., 2022, 9, 2105652.
24. Y. J. Li, H. M. Shieh, J. S. Su, M. J. Kao and W. C. Hsu, Mater. Chem. Phys., 1999, 61, 266–269.
25. D. Oka, Y. Hirose, S. Nakao, T. Fukumura and T. Hasegawa, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 205102.
26. A. Spinelli, M. A. Torija, C. Liu, C. Jan and C. Leighton, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 155110.
27. Y. Park, J. Roth, D. Oka, Y. Hirose, T. Hasegawa, A. Paul, A. Pogrebnyakov, V. Gopalan, T. Birol and R. Engel-Herbert, Commun. Phys., 2020, 3, 102.
28. S. H. Sim, K. T. Kang, S. Lee, M. Lee, H. Taniguchi, S. Kim, S. Roh, J. H. Oh, S. A. Lee, J.-S. Bae, J. H. Jang, J. Hwang, S. Han, T. Park and W. S. Choi, Chem. Mater., 2019, 31, 8019–8025.
29. C. Koch, PhD thesis, Arizona State University, 2002.
30. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
31. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
32. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00283d

---