Inverse design of isotropic auxetic metamaterials via a data-driven strategy†
Ertai
Cao‡
a,
Zhicheng
Dong‡
b,
Ben
Jia
b and
Heyuan
Huang
 *ac
*ac
aSchool of Aeronautics, Northwestern Polytechnical University, Xi’an, 710072, China. E-mail: huangheyuan@nwpu.edu.cn
bSchool of Civil Aviation, Northwestern Polytechnical University, Xi’an, 710072, China
cDesign National Key Laboratory of Strength and Structural Integrity, Xi’an, 710072, China
First published on 10th April 2025
Abstract
Efficiently and precisely designed isotropic auxetic metamaterials present significant challenges due to the inherent uncertainties in their geometric configurations. This study introduces an innovative data-driven structural design strategy that enables accurate prediction of the mechanical properties and inverse design for isotropic auxetic metamaterials. Notably, Kolmogorov–Arnold networks (KANs) are utilized, replacing fixed activation functions with learnable functions, to successfully establish a precise mapping between design parameters and mechanical responses for classical missing rib auxetic metamaterials. The predicted mean square error (MSE) for the stress dataset is as low as 0.81%, only one-fourth of that achieved by multilayer perceptron (MLP) models of equivalent width, while computational efficiency surpasses finite element methods by more than 103 times. Building on this mapping, Model III, optimized using a genetic algorithm, achieves an average MSE of just 0.05%, significantly outperforming the original structure (Model I) and a randomly perturbed structure (Model II) with an average MSE of 2.28% and 1.79%, respectively. Experimental validation and finite element analysis further confirm the accuracy of these results, demonstrating the successful realization of isotropic mechanical response designs. This study presented a data-driven inverse design method as a powerful and efficient tool for the precise design of auxetic metamaterials with isotropic mechanical responses. It holds particular promise for applications in flexible wearable devices and tissue engineering, providing a robust foundation for future innovations in these fields.
New conceptsThis study introduces a high-efficiency, data-driven framework for designing missing-rib isotropic auxetic metamaterials with precise mechanical responsiveness. By leveraging the Kolmogorov–Arnold network (KAN) with learnable activation functions, we establish an accurate mapping between geometric parameters and mechanical behavior, surpassing existing methods in both accuracy and computational efficiency. Conventional direct inverse design often struggles to capture the intricate mechanics revealed by multiple sets of mechanical experiments or finite element simulations, forcing the use of extensive trial-and-error processes. In contrast, combining KANs with genetic algorithms significantly streamlines inverse design, enabling swift, accurate optimization of the metamaterial's geometric configuration. This innovation not only advances our ability to predict and control metamaterial performance but also deepens insights into geometry–property relationships. Consequently, the framework holds strong potential for diverse applications, from flexible wearable devices to tissue engineering, where isotropic auxetic features are crucial. |
1. Introduction
In mechanical metamaterial design, geometric architectures possess a unique capacity to modulate the mechanical functionalities of materials.1 By harnessing the strong correlation between innovative microstructure design and desired mechanical performance, mechanical metamaterials can be imparted with distinctive and extraordinary characteristics, such as negative response parameters,2 programmability,3 high stretchability,4 and ultra-stability,5 thereby exhibiting tremendous application potential in sensors,6 energy-responsive systems,7 actuators,8 tissue engineering,9 and flexible wearable devices.10 As a classic mechanical metamaterial, auxetic materials were first introduced by Lakes in 1987,11 sparking significant interest in their engineering applications. Evans coined the term “auxetic” in 1991,12 further advancing research into materials with negative Poisson's ratios.Auxetic metamaterials expand laterally when stretched axially,13 perfectly aligning with the negative Poisson's ratio effect broadly observed in biological tissues.14–16 This feature enables auxetic metamaterials seamlessly conform to the complex stress–strain responses of biological tissues,17 significantly mitigating stress concentrations.18 As a result, they meet the demand for high conformability and low-stress concentration in flexible wearable devices and bio-patches,19–21 significantly alleviating the pressure and discomfort exerted on tissues while simultaneously enhancing tissue regeneration.22–24 Recent studies have focused on the nonlinear mechanical behavior of auxetic metamaterials under large deformation, highlighting the impact of microstructural parameters and strain conditions.25–30
However, with the increasing complexity of real-world application scenarios, mechanical metamaterials, represented by auxetic metamaterials, urgently need to evolve from uniaxial to isotropic mechanical responses.31 Studies have shown that under isotropic stress conditions, structures can effectively distribute stress,32 reduce local stress concentrations, and enhance fatigue resistance and overall functional stability.33 For example, Shao et al. developed an untethered, multidirectional stretchable self-powered triboelectric electronic skin, which maintained stable open-circuit voltage and short-circuit current outputs under 100% uniaxial, 100% biaxial, and 400% isotropic strains.34 This ensured the accuracy, robustness, and reproducibility of the sensing platform, enabling high-quality pressure imaging and real-time multi-touch visualization. Similarly, Hu et al. combined chiral auxetic metamaterials with elastomer substrates, achieving consistent resistance changes across tensile directions varying from 0° to 135°.35 This approach significantly enhanced the sensitivity (by 53-fold) and omnidirectional sensing capability of the stretchable strain sensor.
The isotropic design of auxetic metamaterials has been also explored by previous works. Grima et al. proposed an isotropic auxetic model based on square lattices with a single degree of freedom.36 The Poisson's ratio for isotropic systems in various dimensions, including those for auxetic materials, was discussed by K. W. Wojciechowski,37 which helps in understanding the mechanical behavior of isotropic auxetic metamaterials under different loading conditions. Despite these advancements, current research predominantly relies on empirical forward geometric design methods for materials and structures.38–40 While being intuitive and straightforward, such methods are suitable only for design scenarios where material properties are clearly anticipated at the initial stage.41,42 In contrast, under multidirectional and complex loading conditions, the mechanical response of structures becomes increasingly intricate. This renders direct design approaches insufficient, as they lack systematic optimization processes and struggle to predict complex mechanical behaviors accurately. Consequently, achieving multi-objective and multidirectional optimization in materials remains challenging, presenting significant obstacles in designing isotropic auxetic metamaterials.
Hence, the design paradigm for mechanical metamaterials is gradually shifting from conventional direct design to intelligent inverse design.43,44 With the emergence of data-driven approaches, machine learning-based inverse design optimization has been progressively applied in mechanical metamaterial design.1,45–47 By automatically generating geometries that meet specified performance requirements, such methods reduce or even eliminate inefficient trial-and-error procedures, thereby allowing rapid identification of optimal designs.48 Related studies have also utilized data-driven approaches to optimize mechanical metamaterial design, including high-performance 3D structures,49 programmable metamaterials with negative thermal expansion and Poisson's ratio,50 and reversible, self-deploying materials with adjustable mechanical properties.51
Currently, inverse design can be categorized as either direct or indirect. Direct inverse design harnesses algorithms such as generative adversarial networks (GANs)52 and convolutional neural networks (CNNs)53 to directly produce geometries or modeling parameters that satisfy particular mechanical performance targets, thereby efficiently generating optimized shapes.54–56 However, when dealing with multiple, complex, and potentially discontinuous mechanical responses, direct inverse design often faces challenges such as insufficient accuracy and poor robustness, making it difficult to accurately replicate the inverse processes from the relationship between multiple sets of mechanical experiments or finite element simulations.57
In contrast, indirect inverse design employs deep learning models to predict the mechanical properties of existing metamaterials and subsequently utilizes metaheuristic algorithms, such as evolutionary strategies or genetic algorithms, to identify target materials meeting specified requirements. For instance, Deng et al. combined a neural network with an evolutionary strategy to inversely design the original geometry of a metamaterial composed of hinged rotating blocks, effectively capturing several predefined nonlinear mechanical responses.58 Compared to direct inverse design, this approach offers greater flexibility and generality in the evaluation of multiple response relationships and is better suited for tackling complex isotropic response designs.59 Accordingly, in this study, we adopt an indirect inverse design strategy and introduce the Kolmogorov–Arnold network (KAN) algorithm,60 based on the Kolmogorov–Arnold representation theorem, to efficiently approximate high-dimensional, complex function relationships and optimize geometric parameters that govern isotropic mechanical performance.61 Unlike conventional multilayer perceptrons (MLPs),62 which rely on fixed activation functions and linear weight matrices, a KAN employs learnable functions in place of static activations, thereby eliminating dependence on linear weight matrices. This endows a KAN with exceptional computational accuracy and interpretability in complex structural optimizations. Furthermore, by rapidly learning the forward relationship between geometry and mechanical response, a KAN substantially enhances both the efficiency and accuracy of inverse designs.63 Finally, by integrating KANs with a genetic algorithm in an optimization framework, we can effectively pinpoint optimal solutions in multi-objective design spaces while minimizing computational costs.
Therefore, to achieve the precise and efficient design of isotropic auxetic metamaterials, we focus on the classic missing-rib auxetic structure and employ a novel data-driven design framework to optimize its geometric parameters, thereby endowing the auxetic metamaterials with isotropic stress–strain responses. Specifically, we first identify and extract the various key mechanical parameters that control the mechanical responses of the missing-rib auxetic metamaterials. Subsequently, to enhance design accuracy and efficiency while reducing computational time and costs, we uniquely introduce the Kolmogorov–Arnold network (KAN) algorithm. This approach aims to establish an accurate mapping between the aforementioned design parameters and the structural mechanical responses by replacing fixed activation functions with learnable functions, enabling high-precision predictions of the generated random configuration datasets. Finally, by integrating KANs with a genetic algorithm, we continuously optimize the geometric parameters that govern mechanical performance, thereby realizing the inverse design of target auxetic metamaterials with isotropic mechanical responses. The KAN-genetic algorithm hybrid proposed in this study demonstrates significant potential for complex structural optimization, aiming to offer a novel research perspective and providing important reference directions for the design and optimization of future mechanical metamaterials.
2. Design and validation
2.1 Structural design
As a mechanical metamaterial exhibiting a negative Poisson's ratio (NPR), auxetic metamaterials have been extensively applied in bio-patches and flexible wearable devices (see Fig. 1). However, existing research predominantly focuses on the unidirectional mechanical responses of these structures, with a limited investigation into their circumferential stress–strain behaviors. In practical applications, particularly within biological soft tissue environments, it is desirable for auxetic metamaterials to exhibit similar stress–strain characteristics in multiple directions, thereby achieving quasi-isotropic mechanical responses. Therefore, this study employs the uniformity of stress–strain curves across multiple orientations as an evaluation metric, striving to ensure that the structure demonstrates isotropic performance in different loading directions. Additionally, considering the structural symmetry, it is sufficient to analyze stress–strain responses within 180°, thereby encompassing the full circumferential mechanical performance. As illustrated in Fig. 1, this study established criteria for evaluating tensile performance at every 30° within the −90° to 90° range and uniformly assessed the variations in stress–strain curves of identical structures across different directions. The ultimate design objective is to develop an isotropic auxetic metamaterial with consistent stress–strain performance throughout the entire 0°–360° circumferential range.The classic standard missing rib auxetic metamaterial comprises multiple intersecting bent ‘Z’-shaped units, exhibiting a pronounced unidirectional NPR effect.64 Consequently, this study adopts it as the fundamental structural model, named as Model I. The reason for selecting the missing rib square grid model is that its initial anisotropic characteristics provide a challenging test scenario for optimization algorithms. Through optimization, we aim to enhance its mechanical performance, potentially including improvements in isotropy or achieving other tailored properties. By contrast, if we had chosen a naturally isotropic model possessing a 6-fold axis or a 3-fold axis,65–67 the optimization results could be perceived as expected, thereby not fully highlighting the algorithm's innovation.
To further expand the design space and identify auxetic metamaterials with isotropic properties, we introduced random perturbations to the design parameters of the basic structure, thereby enhancing the variability of the resulting configurations. By adjusting multiple parameters, structures with diverse mechanical response characteristics were generated, leading to the creation of a stress–strain dataset for multi-directional auxetic structures. This dataset served as the foundation for inverse design to identify optimal configurations. Fig. 2a illustrates Model I and its modified counterpart, Model II, after random perturbations at multiple vertices. To ensure accurate replication and extension of Model I, the positions of the intersecting rib nodes remained fixed, while only the remaining vertices underwent random perturbations. It was important to note that these vertices were not entirely independent; rather, they could be regarded as four free nodes, each capable of moving freely in both the x and y directions. The specific variable parameters were  ,
, 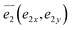 ,
, 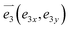 , and
, and  . To prevent the overall appearance of the auxetic metamaterial from being compromised and to avoid the creation of additional intersecting rib nodes, the variation of these parameters was restricted to no more than 40% of the distance c between intersecting rib nodes. Specifically, in Model II, the light-colored square background delineates the range of variability, while the red arrows indicate the direction of node movement. These design modifications enabled the generation of structural units with diverse mechanical responses, thereby providing a comprehensive foundation for the stress–strain relationship dataset of isotropic auxetic metamaterials.
. To prevent the overall appearance of the auxetic metamaterial from being compromised and to avoid the creation of additional intersecting rib nodes, the variation of these parameters was restricted to no more than 40% of the distance c between intersecting rib nodes. Specifically, in Model II, the light-colored square background delineates the range of variability, while the red arrows indicate the direction of node movement. These design modifications enabled the generation of structural units with diverse mechanical responses, thereby providing a comprehensive foundation for the stress–strain relationship dataset of isotropic auxetic metamaterials.
To accommodate practical applications and facilitate manufacturing as well as testing processes, this study further identified the key design parameters of the metamaterials. As shown in Fig. 2b, the distance c between intersecting rib nodes was used to measure the unit cell length, being set to 8 mm in this study. The rib width w, which influenced the structure's stiffness and energy absorption capacity, was set to 0.8 mm. By selecting different rotation angles θ, we fabricated test samples in various configurations, effectively characterizing the uniformity of the structures’ mechanical responses in multiple directions. Fig. 2c displays the test samples of Model I and Model II after being rotated by 60°.
2.2 Simulations and experiments
To evaluate the impact of random perturbations and rotation angles on the mechanical performance of missing rib auxetic metamaterials, we employed COMSOL Multiphysics for structural modeling and simulation analysis. Initially, we constructed the unit cell according to Model I and generated new unit cell models by randomly adjusting eight directional parameters. To create auxetic metamaterial models with uniform rotation angles and similar shape ranges within a specified rectangular region, we rotated the unit cells and replicated them into a 10 × 10 array, as shown in Fig. 3a. Subsequently, we utilized the Box Selection command to trim the array, retaining the desired range. Specifically, to ensure the integrity of the geometric morphology, the box selection function included the portions intersecting with the solid structure (see Fig. 3b). After completing the unit cell model construction, we thickened the structure to ensure its strength and stiffness for practical applications. Through boolean operations, we combined the thickened structure with the clamping ends, thereby completing the final two-dimensional metamaterial model. 2D modeling was based on the plane stress assumption (see Fig. 3c). | ||
| Fig. 3 Finite element modeling process of isotropic auxetic metamaterials: (a) rotation array random structure; (b) target range selection; (c) final two-dimensional metamaterial model. | ||
Fig. 4a illustrates the boundary conditions for mechanical loading, where the lower end was fixed, and a displacement dy was applied to the upper end to achieve stretching until the patch reached a nominal strain of 20%. During the simulation process, the displacement dy ranged from 0 to 9.6 mm, with sampling intervals of 0.48 mm. Fig. 4b and c respectively depict the mesh discretization of the model and the independence test process. Specifically, five different mesh densities were employed, resulting in mesh dimensions of 1493, 2192, 3472, 4775, and 6245 elements. The results indicated that when the mesh element was 3472 (Mesh 3), the model achieved high computational efficiency and convergence, while accurately simulating the tensile deformation process of the auxetic metamaterial. Therefore, to balance computational accuracy and efficiency, we ultimately selected the preset regular mesh density (Mesh 3) for the overall mesh discretization of subsequent structures.
To further validate the accuracy of the simulation analysis results, five test specimens were fabricated using 3D printing with the polycaprolactone (PCL) material, followed by tensile testing. The PCL material employed in this study was sourced from Sigma-Aldrich (New Jersey, USA), renowned for its excellent biocompatibility, and is widely utilized in the field of bio-patches.68–70 To assess the mechanical properties of this 3D-printed material, including ultimate tensile strength, modulus, and Poisson's ratio, we first fabricated specimens in accordance with the ASTM D638 standard and conducted uniaxial tensile tests using an MTS E45 testing machine.71 The resulting tensile stress–strain curves are presented in Fig. 5a, and the parameters of the PCL material used in this study are provided in the ESI†Table 1.
| C 10 (MPa) | C 01 (MPa) | ρ (kg m−3) |
|---|---|---|
| −83.976 | 109.877 | 1146 |
Due to the nonlinear characteristics of the stress–strain response during the elastic phase of the tensile tests, we fitted the experimental data using the Mooney–Rivlin hyperelastic constitutive model,72 which describes the mechanical behavior of flexible polymer materials within the medium to large strain range,73 and its expressions are:
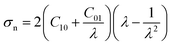 | (1) |
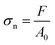 | (2) |
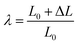 | (3) |
Here, σn represents the nominal stress, λ denotes the stretch ratio, F is the applied load, A0 is the original equivalent cross-sectional area, L0 is the original length, and ΔL is the elongation length. The true stress σt is defined as:
| σt = λσn | (4) |
Subsequently, we fabricated structural samples of the basic missing rib auxetic metamaterial and those subjected to random perturbations in eight parameters and rotation angle variations using fused deposition modeling (FDM) technology.74,75 Five specimens were printed for each structural variant, followed by uniaxial tensile testing using an MTS E45 universal testing machine (see Fig. 5b), and the resulting tensile stress–strain curves are presented in Fig. 5c and d. The stress–strain curves demonstrated that the experimental results closely align with the parameter trends and stress–strain responses observed in the simulation analysis, further validating the accuracy of the simulation model.
By comparing the scanning electron microscope (SEM) results of the PCL particles and the final printed models, as shown in Fig. 6, it was proved that the 3D printing in this paper successfully represents the designed model. The surface was smoother after 3D printing, and the material accumulation and defects generated during the printing process were not sufficient to affect its macroscopic mechanical properties and performance in practical applications.
 | ||
| Fig. 6 (a) Appearance of PCL particles, 3D printed Model I and Model II samples. SEM of (a) PCL particles, (b) 3D printed Model I and (c) Model II samples at different scales. | ||
3. KAN prediction
3.1 Characterization of mechanical performance under random design parameters
The study randomly generated eight design parameter vectors , after which the results are shown in Fig. 7. Using COMSOL Multiphysics and MATLAB in tandem, the parameter vectors
, after which the results are shown in Fig. 7. Using COMSOL Multiphysics and MATLAB in tandem, the parameter vectors 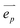 were passed to the complete tensile-expansive metamaterial model introduced in Section 2.2, and rotation angles were controlled in seven directions. Through computational analysis, a total of 2500 sets of nominal stress data per direction (17
were passed to the complete tensile-expansive metamaterial model introduced in Section 2.2, and rotation angles were controlled in seven directions. Through computational analysis, a total of 2500 sets of nominal stress data per direction (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 entries in total across all seven directions) were obtained. Fig. 7b–h illustrate the distribution of these 2500 sets of results for each direction ranging from −90° to 90°. The dashed lines represent the mean value in each direction, serving as the foundation for subsequent training and optimization.
500 entries in total across all seven directions) were obtained. Fig. 7b–h illustrate the distribution of these 2500 sets of results for each direction ranging from −90° to 90°. The dashed lines represent the mean value in each direction, serving as the foundation for subsequent training and optimization.
Fig. 7i consolidates the average stress–strain curves across the seven directions. The figure shows that tilting the structure at an angle often leads to a lower modulus, and most structures exhibit nonuniform stress–strain responses in multiple directions. Nevertheless, as shown in Fig. 7b–h, there is still some overlap in the stress–strain results among different angles, implying that it is indeed possible, via inverse design methods, to identify metamaterials whose stress–strain responses remain relatively isotropic across all directions.
Overall, by adjusting the initial design parameters to alter the geometry, the stress–strain curves of the target auxetic metamaterial could be successfully manipulated. Therefore, the central challenge addressed in this study was determining how to modify these design parameters to achieve the desired target structure. A common approach involves using datasets obtained through finite element simulations for direct inverse design. Alternatively, one can train a neural network on the finite element results to generate a larger dataset and then iteratively perform forward estimation coupled with genetic algorithms to accomplish indirect inverse design. In this work, the concentration degree of stress–strain curves under different loading directions cannot be used as input (due to the fact that it generally has only one individual value). Therefore, since neural network training requires both the design parameters and the stress–strain curves as input–output data, we adopt the latter (indirect inverse design) approach.
3.2 KAN-based prediction of isotropic mechanical performance
The Kolmogorov–Arnold network (KAN), as a novel neural network architecture based on the Kolmogorov–Arnold approximation theorem,60 can efficiently approximate continuous multivariate functions by employing functional decomposition and specialized neurons, which demonstrates that any multivariate continuous function can be decomposed into a combination of univariate functions. Specifically, for any continuous function f(x1, x2,…, xn), it can be expressed in the following form: | (5) |
In this formulation, both φq,p and Φq are univariate continuous functions. By leveraging this decomposition, the KAN can reduce the complexity arising from high-dimensional inputs and thereby theoretically improve function approximation efficiency. Historically, directly applying this decomposition in practical machine learning has been deemed impractical. However, Liu et al. overcame these limitations by integrating modern deep learning optimization methods, rendering the Kolmogorov–Arnold theorem applicable in constructing more efficient and interpretable neural networks than the traditional multilayer perceptron (MLP).61 Consequently, this study utilizes KANs to predict the isotropic mechanical performance of structures, while making the necessary adjustments following the specific output requirements.
As illustrated in Fig. 8, the KAN is designed to replace the traditional MLP module in the training process. The training pipeline, built using the PyTorch library76 and the Pykan library,61 began by standardizing the input vector  with Scikit-learn's StandardScaler to ensure a uniform distribution of input data. The main body of the network consisted of three intermediate layers, each containing 32 neurons. Before the output layer, there were two fully connected layers, expanding to widths of 64 and 7 × 21 nodes, respectively, thus guaranteeing that the final output dimension and accuracy meet the requirements of the prediction task. The target output dimension is 7 × 21, corresponding to a two-dimensional matrix of nominal stress values for each of the seven directions at strain levels ranging from 0 to 0.2 (with an interval of 0.01). Through this design, the KAN model could effectively capture the complex relationship between the eight-dimensional input vector
with Scikit-learn's StandardScaler to ensure a uniform distribution of input data. The main body of the network consisted of three intermediate layers, each containing 32 neurons. Before the output layer, there were two fully connected layers, expanding to widths of 64 and 7 × 21 nodes, respectively, thus guaranteeing that the final output dimension and accuracy meet the requirements of the prediction task. The target output dimension is 7 × 21, corresponding to a two-dimensional matrix of nominal stress values for each of the seven directions at strain levels ranging from 0 to 0.2 (with an interval of 0.01). Through this design, the KAN model could effectively capture the complex relationship between the eight-dimensional input vector  and the seven sets of stress–strain curve values Y. Given that some data points in the mechanical response dataset deviated significantly from the average values, we employ the Smooth L1 Loss function during the training phase,77 which was less sensitive to outliers and helped stabilize the training process. The Smooth L1 Loss function is defined as follows:
and the seven sets of stress–strain curve values Y. Given that some data points in the mechanical response dataset deviated significantly from the average values, we employ the Smooth L1 Loss function during the training phase,77 which was less sensitive to outliers and helped stabilize the training process. The Smooth L1 Loss function is defined as follows:
 | (6) |
Simultaneously, we employed the mean square error (MSE) loss as a metric to evaluate the predictive performance. Compared with the Smooth L1 Loss function used during training, the MSE provided a more precise assessment of whether our prediction algorithm met the required accuracy standards. Specifically, the MSE was a classic loss function for regression tasks, calculated by squaring the difference between predicted and true values to assess the accuracy of the model's predictions. Its formulation is as follows:
 | (7) |
Additionally, we adopted the AdamW optimizer, an adaptive learning rate optimization algorithm, for the training process, integrating weight decay and employing an early stopping mechanism to mitigate overfitting. Moreover, we introduced the OneCycleLR learning rate scheduler to adjust the learning rate during training dynamically.
Using the previously generated dataset of 2500 samples per direction (with 80% as the training set and 20% as the test set), we evaluated the network performance. As shown in Fig. 9a, the KAN rapidly converges toward the target values, ultimately achieving a test-set MSE of 0.81%, which is below 1%. To examine whether the KAN offered an accuracy advantage over the conventional MLP, we additionally constructed two MLPs, each with three hidden layers, with widths of 32 and 256, respectively (see Fig. 9b). The MSE for the 32-wide MLP on the training set is 3.57%, whereas the 256-wide MLP yields an MSE of 2.65%. In contrast, the KAN approach approximated the target more efficiently, with the training-set error approximately one-quarter that of the equally wide MLP. Fig. 9c compares the finite element (FE) simulation results and KAN predictions for a newly generated set of parameters  across seven directions, yielding an MSE of about 0.1337%. Furthermore, forward predictions with the KAN took only about 0.005 seconds each, which was 4200 times faster than the roughly 21 seconds required by direct FE calculations. These findings demonstrated that the KAN can replace FE simulations in this problem with minimal error and significantly higher computational speed, paving the way for large-scale computations in subsequent inverse design processes.
across seven directions, yielding an MSE of about 0.1337%. Furthermore, forward predictions with the KAN took only about 0.005 seconds each, which was 4200 times faster than the roughly 21 seconds required by direct FE calculations. These findings demonstrated that the KAN can replace FE simulations in this problem with minimal error and significantly higher computational speed, paving the way for large-scale computations in subsequent inverse design processes.
4. Inverse design
4.1 Inverse design combining the KAN and genetic algorithm
As illustrated in Fig. 10a, this study employs a genetic algorithm (GA) in conjunction with the KAN to achieve inverse optimization for isotropic stress–strain responses. Genetic algorithms are used to explore the design space, while the KAN acts as a predictive model to help us predict the stress–strain response based on the given design parameters. With this combination, we can evaluate a large number of design alternatives in a short period of time without the need for extensive finite element analyses, thus greatly improving computational efficiency. This approach references the framework of the joint deep learning and genetic algorithm proposed by Wang et al. and is improved according to the KAN algorithm.78We constructed the GA framework using the DEAP library,79 setting the average mean square error (MSE) as the fitness function to quantify discrepancies between predicted results and target values. Concretely, we calculated the MSEi between the stress output Y in seven directions and the corresponding average stress row vector, and then computed the row-wise mean as:
 | (8) |
 is the j-th value of the average stress row vector.
is the j-th value of the average stress row vector.
During implementation of the algorithm, an initial population of 500 individuals was generated, each represented by an 8-dimensional floating-point vector  confined to the range [−2.0, 2.0]. In each iteration of the optimization process, the pre-trained KAN was used to predict the output Y of each individual based on standardized inputs, thereby performing fitness evaluation. To enhance efficiency, a tournament selection with a tournament size of three was employed to propagate individuals to the next generation, retaining high-quality solutions while preserving population diversity. During population evolution, the crossover operator adopted the Blend strategy, linearly combining two individuals to produce new offspring. Simultaneously, Gaussian mutation was applied with a probability of 0.2 to adjust genetic parameters randomly, thus improving the algorithm's exploration capability. To maintain feasibility, all individuals underwent a clipping operation that constrained gene values to [−2.0, 2.0] after mutation and crossover. Moreover, an elitism strategy was implemented to further improve solution quality, whereby the best-performing individuals were directly carried over to the next generation, ensuring no loss of critical information. Over the course of 100 generations, the optimal fitness value was recorded in each generation to monitor convergence trends and assess algorithm performance. After completing the optimization, the best solution yielded by the genetic algorithm was extracted as the final design, named as Model III. As illustrated in Fig. 10c, the calculation converged rapidly within the first 10 generations.
confined to the range [−2.0, 2.0]. In each iteration of the optimization process, the pre-trained KAN was used to predict the output Y of each individual based on standardized inputs, thereby performing fitness evaluation. To enhance efficiency, a tournament selection with a tournament size of three was employed to propagate individuals to the next generation, retaining high-quality solutions while preserving population diversity. During population evolution, the crossover operator adopted the Blend strategy, linearly combining two individuals to produce new offspring. Simultaneously, Gaussian mutation was applied with a probability of 0.2 to adjust genetic parameters randomly, thus improving the algorithm's exploration capability. To maintain feasibility, all individuals underwent a clipping operation that constrained gene values to [−2.0, 2.0] after mutation and crossover. Moreover, an elitism strategy was implemented to further improve solution quality, whereby the best-performing individuals were directly carried over to the next generation, ensuring no loss of critical information. Over the course of 100 generations, the optimal fitness value was recorded in each generation to monitor convergence trends and assess algorithm performance. After completing the optimization, the best solution yielded by the genetic algorithm was extracted as the final design, named as Model III. As illustrated in Fig. 10c, the calculation converged rapidly within the first 10 generations.
To evaluate the isotopic stress–strain response of the optimized structure, we employed the trained KAN to predict outcomes based on the standardized Model III design parameters. Concurrently, we utilized these same parameters for finite element simulations and for testing 3D-printed specimens. Fig. 10b compares the stress–strain relationships of Model III under multiple orientations (from −90° to 90° at 30° intervals) in terms of predictions, simulations, experiments, and the stress dataset. The three sets of results exhibit a high degree of consistency, and the appearance of their experimental and simulation processes is also highly similar (see Fig. 11). Within the linear strain range from 0 to 0.2, the agreement between predicted and experimental data is especially strong, underscoring the reliability of the KAN-based predictions. Furthermore, the negligible discrepancy between simulation and experimental data confirms that the finite element model could accurately replicate the actual mechanical behavior of the designed structure.
To evaluate whether Model III met the targets of inverse design, Fig. 12a assesses its isotropic stress–strain responses from a uniformity perspective. By comparing the mean stress values in multiple directions with the corresponding actual responses, the resulting error distributions were obtained. The outcomes indicate that the mean square errors (MSEs) of the predicted, simulated, and experimental data are below 0.05%, confirming that Model III achieved a highly uniform and isotropic stress distribution across multiple directions.
Fig. 12b presents the isotropic stress distributions at strains of 0.1 and 0.2, derived from the original training dataset. Shown in polar coordinates, these distributions visualize how stress varies by direction under random conditions. The figure reveals that classical missing-rib auxetic metamaterials exhibit markedly uneven stress in all directions, forming a cross-shaped distribution with a degree of rotational symmetry at −90°, 0°, and 90°, with the appearance of elevated stresses. This observation aligns with the findings of Zhu et al., who reported a corresponding hexagram-like distribution at strains of 0.2 or higher in six-missing-rib auxetic structures.80 In Fig. 12c, Model I and Model II conform to the same trend at a strain of 0.2, showing pronounced directional unevenness, especially in specific directions where stress values deviate substantially from the mean. By contrast, the predicted, simulated, and experimental stress distributions of Model III, as shown in Fig. 12c, are nearly circular across all directions, demonstrating that it achieves a more uniform isotropic response.
When strain varied from 0 to 0.2, the corresponding stress distribution results further corroborated the above observations. As shown in Fig. 13a, Model III exhibits a more uniform, nearly isotropic stress distribution within the strain range throughout the entire loading process. In contrast, the yellow-highlighted regions at the centers of Model I and Model II form a cross-shaped distribution, opposite to the pattern shown in Fig. 12c, indicating localized stress concentration or uneven distribution in certain directions. If a structure's stress value is higher at a specific strain, it appears as a larger value in the single-point stress plot of Fig. 12c and as a deeper color in the stress distribution plot of Fig. 13a. This finding demonstrated that Model III, optimized by the KAN coupled with a genetic algorithm, maintained highly uniform mechanical performance throughout the loading process. Fig. 13b–d respectively give the MSE of each angle and the average for Model I, Model II, and Model III. It can be seen intuitively that the inverse design process reduces the error at any two angles of the auxetic metamaterials. Fig. 13e visually compares the average MSE of the three models in a bar chart, revealing differences in their error levels. The results show that the average MSE of Model III, with only 0.0443%, is significantly lower than those of the other models, compared with 2.2837% for Model I and 1.7894% for Model II. These outcomes indicated that the optimized design substantially enhanced uniformity in isotropic stress–strain responses, thus underscoring the outstanding performance of the combined KAN and genetic algorithm in the inverse design of isotropic auxetic metamaterials.
4.2 Analysis of the negative Poisson's ratio effect in Model III
Model III, which can achieve uniform isotropic stress–strain responses, was selected to further investigate whether it retained its negative Poisson's ratio characteristics. While the structures presented in this study do exhibit some auxetic behavior, they were not fully auxetic in the strictest sense. This distinction was explained by Branka et al.,81 who discussed the difference between structures with the partial auxetic and fully auxetic material. For convenience, the simplified expression of auxetic and negative Poisson's ratio was still used in the analysis.Fig. 14a illustrates how displacements at specific points were measured using digital image correlation (DIC) to determine the Poisson's ratio variation of the missing-rib auxetic metamaterial across different orientations. In the experiments, we chose transverse strain εx which is perpendicular to the loading direction and longitudinal εy which is parallel to the loading direction as characterization parameters. We also incorporated DIC markers in multiple orientations to capture the displacement distribution under complex mechanical loading. In the conventional research orientation of missing-rib auxetic metamaterials (e.g., −90°), this point-selection method can readily capture a rectangle or square in which three points are measured, allowing a relatively direct assessment of Poisson's ratio at small strains. However, for non-horizontal or non-vertical angles (e.g., −60°), Poisson's ratio here serves primarily as an approximate indicator. Fig. 14b depicts changes in the Poisson's ratio of Model III as strain increases from 0.01 to 0.2, encompassing orientations from −90° to 90°. The curves demonstrate that Model III maintains a pronounced negative Poisson's ratio at −90°, −30°, 0°, 60°, and 90°, while exhibiting values near zero at −60° and 30°. Nevertheless, the overall parameters remain within controllable ranges, and all Poisson's ratio variations stabilize without marked fluctuations. These results confirmed that while Model III achieved uniform isotropic stress–strain performance, it still retained auxetic properties characterized by negative or near-zero Poisson's ratios.
To explore the underlying principle by which Model III attained isotropic stress–strain responses, we visualized and compared the stress distributions and load-transfer paths of Model I, Model II, and Model III under different loading angles (0°, 30°, 60°, and 90°) through FEM. As illustrated in Fig. 15, Model I exhibits a clear, high-stress load-transfer path at 0° and 90°, whereas at 30° and 60°, the load-transfer paths are significantly shorter and non-uniform. Moreover, the load-transfer pattern differs noticeably between 30° and 60°. Model II shows a more evenly distributed load-transfer path at 0° and improved uniformity at 60°, but non-uniformity remains at 30°, and the stress at 90° is still considerably higher than in other directions. Model III, by contrast, demonstrates a highly uniform stress distribution and uniform load-transfer paths across all loading angles. This is especially evident at 30° and 60°, where the stress-transfer patterns are notably homogeneous, while at 0° and 90°, the stress distribution remains moderate rather than excessively concentrated. Such an isotropic stress distribution in Model III may arise because parameter optimization leads the internal angles of the four-missing-rib auxetic metamaterial to approximate a 60° configuration, somewhat akin to six-missing-rib auxetic designs. This indicates that the present study has effectively expanded the design boundaries of the classic four-missing-rib auxetic metamaterial, uncovering previously untapped potential within its fundamental architecture.
 | ||
| Fig. 15 Comparison of stress distributions and load-transfer paths among (a) Model I, (b) Model II, and (c) Model III. | ||
5. Conclusion
In summary, this study proposed a novel data-driven framework, combining the Kolmogorov–Arnold network (KAN) with genetic algorithms to overcome the limitations of conventional direct and empirical forward design methods in mechanical metamaterials. In forward predictions using the KAN, the test-set error was merely 0.81%, a quarter of that achieved by a multilayer perceptron (MLP) of equivalent width. Furthermore, each prediction took only about 0.005 seconds, which was 4200 times faster than direct finite element analysis, underscoring its significant advantages for optimizing isotropic mechanical metamaterials via inverse design. By combining the forward prediction efficiency of the KAN with the global optimization capability of genetic algorithms, the proposed auxetic metamaterial (Model III) exhibited highly consistent and isotropic stress–strain responses across all orientations. The final stress response of Model III achieved an average mean square error (MSE) below 0.05%, corresponding to a marked reduction, by at least an order of magnitude, relative to Model I (2.28%) and Model II (1.79%). Also, Model III exhibited a more uniform and continuous stress-transfer network, particularly mitigating stress concentration issues that often arise in the original structure at 30° and 60°. Overall, the KAN-genetic algorithm framework we developed in this study can not only advance the development of auxetic metamaterials from uniaxial to isotropic mechanical response but also pave the way for the design of next-generation metamaterials for fields ranging from tissue engineering to flexible wearable devices.Data availability
The data supporting this article have been included as part of the ESI.† The KAN algorithm utilized in this study was based on the work of Ziming Liu et al.61 The implementation of the algorithm, along with usage examples, is publicly available. Codes can be accessed at https://github.com/KindXiaoming/pykan and can also be conveniently installed via pip install pykan.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 12141203), the Fundamental Research Funds for the Central Universities (No. D5000230052), the Shaanxi Innovation Ability Support Plan Project Funds (No. 2024RS-CXTD-29), and the Northwestern Polytechnic University Doctoral Dissertation Innovation Foundation (No. CX2023083).References
- P. Jiao, J. Mueller, J. R. Raney, X. Zheng and A. H. Alavi, Nat. Commun., 2023, 14, 6004 CrossRef CAS PubMed.
- X. Yu, J. Zhou, H. Liang, Z. Jiang and L. Wu, Prog. Mater. Sci., 2018, 94, 114–173 CrossRef.
- P. Sinha and T. Mukhopadhyay, Mater. Sci. Eng., R, 2023, 155, 100745 CrossRef.
- X. Zhang, Q. Sun, X. Liang, P. Gu, Z. Hu, X. Yang, M. Liu, Z. Sun, J. Huang, G. Wu and G. Zu, Nat. Commun., 2024, 15, 392 CrossRef CAS PubMed.
- T. Frenzel, M. Kadic and M. Wegener, Science, 2017, 358, 1072–1074 CrossRef CAS PubMed.
- Y. Jiang, Z. Liu, N. Matsuhisa, D. Qi, W. R. Leow, H. Yang, J. Yu, G. Chen, Y. Liu, C. Wan, Z. Liu and X. Chen, Adv. Mater., 2018, 30, 1706589 CrossRef PubMed.
- C. Ma, S. Wu, Q. Ze, X. Kuang, R. Zhang, H. J. Qi and R. Zhao, ACS Appl. Mater. Interfaces, 2021, 13, 12639–12648 CrossRef CAS PubMed.
- S. Bonfanti, R. Guerra, F. Font-Clos, D. Rayneau-Kirkhope and S. Zapperi, Nat. Commun., 2020, 11, 4162 CrossRef CAS PubMed.
- J. Chen, J. Chen, H. Wang, L. He, B. Huang, S. Dadbakhsh and P. Bartolo, Int. J. Extreme Manuf., 2025, 7, 12001 CrossRef CAS.
- Y. Deng, X. Guo, Y. Lin, Z. Huang and Y. Li, ACS Nano, 2023, 17, 6410–6434 CrossRef PubMed.
- R. Lakes, Science, 1987, 235, 1038–1040 CrossRef CAS PubMed.
- K. E. Evans, Endeavour, 1991, 15, 170–174 CrossRef CAS.
- X. Zhou, L. Ren, Z. Song, G. Li, J. Zhang, B. Li, Q. Wu, W. Li, L. Ren and Q. Liu, Composites, Part B, 2023, 254, 110585 CrossRef CAS.
- C. Wiebe and G. W. Brodland, J. Biomech., 2005, 38, 2087–2094 CrossRef PubMed.
- L. H. Timmins, Q. Wu, A. T. Yeh, J. E. Moore and S. E. Greenwald, Am. J. Physiol. Heart Circ. Physiol., 2010, 298, H1537–H1545 CrossRef CAS PubMed.
- R. Gatt, M. Vella Wood, A. Gatt, F. Zarb, C. Formosa, K. M. Azzopardi, A. Casha, T. P. Agius, P. Schembri-Wismayer, L. Attard, N. Chockalingam and J. N. Grima, Acta Biomater., 2015, 24, 201–208 CrossRef PubMed.
- Y. Ma, X. Feng, J. A. Rogers, Y. Huang and Y. Zhang, Lab Chip, 2017, 17, 1689–1704 RSC.
- S. Jiang, X. Liu, J. Liu, D. Ye, Y. Duan, K. Li, Z. Yin and Y. Huang, Adv. Mater., 2022, 34, 2200070 CrossRef CAS PubMed.
- J. Yu, L. Chen, X. Hou, J. Mu, J. He, W. Geng, X. Qiao and X. Chou, J. Materiomics, 2022, 8, 247–256 CrossRef.
- Z. Dong, X. Ren, B. Jia, X. Zhang, X. Wan, Y. Wu and H. Huang, Mater. Today Bio, 2024, 26, 101098 CrossRef PubMed.
- Q. Pan, S. Chen, F. Chen and X. Zhu, Sci. China: Technol. Sci., 2020, 63, 2518–2526 CrossRef.
- P. Mardling, A. Alderson, N. Jordan-Mahy and C. L. Le Maitre, Biomater. Sci., 2020, 8, 2074–2083 RSC.
- H. Huang, Z. Dong, X. Ren, B. Jia, G. Li, S. Zhou, X. Zhao and W. Wang, Nano Res., 2023, 16, 3475–3515 CrossRef.
- B. Jia, H. Huang, Z. Dong, X. Ren, Y. Lu, W. Wang, S. Zhou, X. Zhao and B. Guo, Chem. Soc. Rev., 2024, 53, 4086–4153 RSC.
- H. Reda, N. Karathanasopoulos, K. Elnady, J.-F. Ganghoffer and H. Lakiss, Mater. Des., 2018, 147, 134–145 CrossRef.
- H. Reda, K. Elnady, J. F. Ganghoffer and H. Lakiss, Compos. Struct., 2018, 184, 860–871 CrossRef.
- H. Reda, K. Elnady, J. F. Ganghoffer and H. Lakiss, Int. J. Non-Linear Mech., 2018, 99, 1–12 CrossRef.
- K. El Nady, F. Dos Reis and J. F. Ganghoffer, Compos. Struct., 2017, 170, 271–290 CrossRef.
- F. Dos Reis and J.-F. Ganghoffer, Comput. Mater. Sci., 2012, 51, 314–321 CrossRef.
- F. Dos Reis and J. F. Ganghoffer, Comput. Struct., 2012, 112, 354–363 CrossRef.
- H. M. A. Kolken and A. A. Zadpoor, RSC Adv., 2017, 7, 5111–5129 RSC.
- H. Ma, K. Wang, H. Zhao, Y. Hong, Y. Zhou, J. Xue, Q. Li, G. Wang and B. Yan, Compos. Struct., 2023, 304, 116410 CrossRef CAS.
- X. Liang, G. Chen, S. Lin, J. Zhang, L. Wang, P. Zhang, Y. Lan and J. Liu, Adv. Mater., 2022, 34, 2107106 CrossRef CAS PubMed.
- B. Shao, M.-H. Lu, T.-C. Wu, W.-C. Peng, T.-Y. Ko, Y.-C. Hsiao, J.-Y. Chen, B. Sun, R. Liu and Y.-C. Lai, Nat. Commun., 2024, 15, 1238 CrossRef CAS PubMed.
- T. Hu, T. Pan, D. Guo, Y. Xiao, F. Li, M. Gao, Z. Huang, J. Zhu, T. Cheng and Y. Lin, ACS Nano, 2023, 17, 22035–22045 CrossRef PubMed.
- J. N. Grima and K. E. Evans, J. Mater. Sci. Lett., 2000, 19, 1563–1565 CrossRef CAS.
- K. W. Wojciechowski, J. Phys. Soc. Jpn., 2003, 72, 1819–1820 CrossRef CAS.
- S. Shan, S. H. Kang, Z. Zhao, L. Fang and K. Bertoldi, Extreme Mech. Lett., 2015, 4, 96–102 CrossRef.
- G. Carta, M. Brun and A. Baldi, Mech. Mater., 2016, 97, 67–75 CrossRef.
- I. Shufrin, E. Pasternak and A. V. Dyskin, Int. J. Solids Struct., 2012, 49, 2239–2253 CrossRef.
- Y. Zhu, S. Jiang, F. Lu and X. Ren, Eng. Struct., 2022, 262, 114399 CrossRef.
- A. Montazeri, E. Bahmanpour and M. Safarabadi, Int. J. Mech. Sci., 2023, 260, 108670 CrossRef.
- X. Zheng, X. Zhang, T.-T. Chen and I. Watanabe, Adv. Mater., 2023, 35, 2302530 CrossRef CAS PubMed.
- J. Chen, S. Hu, S. Zhu and T. Li, Interdiscip. Mater., 2023, 2, 5–29 Search PubMed.
- C. S. Ha, D. Yao, Z. Xu, C. Liu, H. Liu, D. Elkins, M. Kile, V. Deshpande, Z. Kong, M. Bauchy and X. Zheng, Nat. Commun., 2023, 14, 5765 CrossRef CAS PubMed.
- J. Feng, J. Qiao, Q. Xu, G. Zhang and L. Li, Int. J. Mech. Sci., 2025, 287, 109920 CrossRef.
- M. W. Cho, K. Ko, M. Mohammadhosseinzadeh, J. H. Kim, D. Y. Park, D. S. Shin and S. M. Park, Mater. Horiz., 2024, 11, 2615–2627 RSC.
- X.-L. Peng and B.-X. Xu, Int. J. Mech. Sci., 2024, 265, 108900 CrossRef.
- H. Yao, X. Zhao, K. Shi, W. Sun and S. Mi, Mater. Horiz., 2024, 11, 4689–4704 RSC.
- M. W. Cho, K. Ko, M. Mohammadhosseinzadeh, J. H. Kim, D. Y. Park, D. S. Shin and S. M. Park, Mater. Horiz., 2024, 11, 2615–2627 RSC.
- W. Yan, T. Jones, C. L. Jawetz, R. H. Lee, J. B. Hopkins and A. Mehta, Mater. Horiz., 2024, 11, 3805–3818 RSC.
- I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Commun. ACM, 2020, 63, 139–144 CrossRef.
- Z. Li, F. Liu, W. Yang, S. Peng and J. Zhou, IEEE Trans. Neural Netw. Learn. Syst., 2021, 33, 6999–7019 Search PubMed.
- Y. Mao, Q. He and X. Zhao, Sci. Adv., 2020, 6, eaaz4169 CrossRef PubMed.
- Z. Yang, Y. C. Yabansu, D. Jha, W. Liao, A. N. Choudhary, S. R. Kalidindi and A. Agrawal, Acta Mater., 2019, 166, 335–345 CrossRef CAS.
- D. K. Pokkalla, L. H. Poh and S. T. Quek, Int. J. Mech. Sci., 2021, 193, 106169 CrossRef.
- A. Zunger, Nat. Rev. Chem., 2018, 2, 121 CrossRef CAS.
- B. Deng, A. Zareei, X. Ding, J. C. Weaver, C. H. Rycroft and K. Bertoldi, Adv. Mater., 2022, 34, 2206238 CrossRef CAS PubMed.
- T. Meier, R. Li, S. Mavrikos, B. Blankenship, Z. Vangelatos, M. E. Yildizdag and C. P. Grigoropoulos, npj Comput. Mater., 2024, 10, 3 CrossRef CAS.
- A. N. Kolmogorov, Dokl. Akad. Nauk SSSR, 1957, 114, 953–956 Search PubMed.
- Z. Liu, Y. Wang, S. Vaidya, F. Ruehle, J. Halverson, M. Soljačić, T. Y. Hou and M. Tegmark, arXiv:2404.19756 DOI:10.48550/arXiv.2404.19756.
- M.-C. Popescu, V. E. Balas, L. Perescu-Popescu and N. Mastorakis, WSEAS Trans. Circuits Syst., 2009, 8, 579–588 Search PubMed.
- Z. Liu, P. Ma, Y. Wang, W. Matusik and M. Tegmark, arXiv:2408.10205 DOI:10.48550/arXiv.2408.10205.
- C. W. Smith, J. N. Grima and K. Evans, Acta Mater., 2000, 48, 4349–4356 CrossRef CAS.
- K. W. Wojciechowski, Mol. Phys., 1987, 61, 1247–1258 CrossRef CAS.
- K. W. Wojciechowski, J. Phys. A: Math. Gen., 2003, 36, 11765 CrossRef.
- K. W. Wojciechowski, Prop. Appl. Nanocrystalline Alloys Amorph. Precursors, 2005, 184, 241–252 Search PubMed.
- J. H. Park, H.-J. Park, S. J. Tucker, S. R. Rutledge, L. Wang, M. E. Davis and S. J. Hollister, Adv. Funct. Mater., 2023, 33, 2215220 CrossRef CAS.
- D. Liu, W. Nie, D. Li, W. Wang, L. Zheng, J. Zhang, J. Zhang, C. Peng, X. Mo and C. He, Chem. Eng. J., 2019, 362, 269–279 CrossRef CAS.
- V. Trakoolwannachai, P. Kheolamai and S. Ummartyotin, Composites, Part B, 2019, 173, 106974 CrossRef CAS.
- ASTM International, 2014.
- A. P. S. Selvadurai, J. Mech. Phys. Solids, 2006, 54, 1093–1119 CrossRef.
- B. Kim, S. B. Lee, J. Lee, S. Cho, H. Park, S. Yeom and S. H. Park, Int. J. Precis. Eng. Manuf., 2012, 13, 759–764 CrossRef.
- O. A. Mohamed, S. H. Masood and J. L. Bhowmik, Adv. Manuf., 2015, 3, 42–53 CrossRef CAS.
- K. Rajan, M. Samykano, K. Kadirgama, W. S. W. Harun and Md. M. Rahman, Int. J. Adv. Manuf. Technol., 2022, 120, 1531–1570 CrossRef.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga, in Advances in Neural Information Processing Systems 32, MIT Press, Vancouver, Canada, 2019 Search PubMed.
- R. Girshick, in 2015 IEEE International Conference on Computer Vision (ICCV), IEEE Computer Society, Santiago, Chile, 2015, pp. 1440–1448 Search PubMed.
- L. Wang, Appl. Math. Comput., 2005, 170, 1329–1343 CrossRef.
- F.-A. Fortin, F.-M. De Rainville, M.-A. G. Gardner, M. Parizeau and C. Gagné, J. Mach. Learn. Res., 2012, 13, 2171–2175 Search PubMed.
- Y. Zhu, S. Jiang, L. H. Poh, Y. Shao and Q. Wang, Smart Mater. Struct., 2020, 29, 45030 CrossRef.
- A. C. Brańka, D. M. Heyes and K. W. Wojciechowski, Phys. Status Solidi B, 2011, 248, 96–104 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00154d |
| ‡ These authors contributed equally to this manuscript. |
| This journal is © The Royal Society of Chemistry 2025 |













