Experiment-in-loop interactive optimization of polymer composites for “5G-and-beyond” communication technologies

Abstract

“Fifth-generation-and-beyond” communication technologies have sparked considerable demand for polymer composite materials with low coefficients of thermal expansion (CTE) and low dielectric loss at high operation frequencies. However, the complexity of process parameters and the lack of knowledge about fabrication procedures hinder this goal. In this study, state-of-the-art experiment-in-loop Bayesian optimization (EiL-BO) was developed to optimize a composite of a perfluoroalkoxyalkane matrix with silica fillers. The Gaussian process equipped with an automatic relevance determination kernel that automatically adjusts the scaling parameters of individual dimensions effectively enhances EiL-BO's ability to search for candidates in a complex and anisotropic multidimensional space. This addresses the critical challenge of handling problems with high-dimensional parameters and is capable of managing eight-dimensional parameters, including filler morphology, surface chemistry, and compounding process parameters. The obtained optimal composite shows a low CTE of 24.7 ppm K⁻¹ and an extinction coefficient of 9.5 × 10⁻⁴, outperforming the existing polymeric composite, revealing exceptionally effective and versatile EiL-BO that accelerates the development of advanced materials.

---

New concepts

In this study, Bayesian optimization using an ARD kernel was employed to facilitate an interactive experiment-in-loop optimization process for the fabrication of polymer composites for applications in the field of “5G and beyond” communication technologies. While machine learning approaches, including Bayesian optimization, have proven effective in optimizing material structures and processing parameters in material fabrication, the fabrication of complex composites with anisotropic and high-dimensional parameter spaces remains challenging. The efficiency of the as-developed optimization methodology is notable: composite materials with superior performance, surpassing that reported in previous studies, were achieved in only few iterations. The resulting materials concurrently exhibit both low thermal expansion and low dielectric loss at high operational frequencies, up to the GHz range, addressing one of the most critical issues in packaging materials for “5G and beyond” communication technologies.

This work demonstrates a proof of concept for an interactive, experiment-in-loop optimization process equipped with an ARD kernel. The significance of this approach in handling high-dimensional and anisotropic candidate spaces was validated, showing promise for accelerating advancements in materials science, even when fundamental knowledge and experience are limited.

Introduction

With the advent of fifth-generation (5G) wireless technology, there is a growing demand for polymer materials as packaging materials and device components such as printed circuit boards.^1,2 Owing to the utilization of high-frequency micro-/millimeter-wave bands, materials with low dielectric permittivity (ε) and loss tangent (tan δ) at high frequencies are required to facilitate rapid and high-quality signal transmission. However, high heat intensity due to elevating device power may lead to thermal deformation. Since polymers typically exhibit a coefficient of thermal expansion (CTE) that is far higher than that of other parts of the device, the difference in the CTE can thus degrade the device and affect its operation. Therefore, polymeric materials with low CTEs are in high demand.

Fluororesins, such as perfluoroalkoxyalkane (PFA) and polytetrafluoroethylene (PTFE), are among the most promising candidates because the C–F bond has an ultralow dipole moment and electronic susceptibility, which is the key to low ε and tan δ. Moreover, the strong electronegativity of fluorine is effective in reducing ion and electron polarizability, which is beneficial for low dielectric loss. However, the CTEs of fluororesins are relatively high. This issue can be addressed by compositing fluororesins with ceramic fillers such as silica,³ TeO₂,⁴ perovskite (Ca, Li, and Sm)TiO₃,⁵ and 0.7Ba(Co_1/3Nb_2/3)O₃–0.3Ba(Zn_1/3Nb_2/3)O₃ (BCZN).⁶

In polymer composites, the CTE and dielectric properties are highly sensitive to various factors. These include the shape and volume fraction of fillers, their surface chemistry, and processing parameters. Liu et al. performed surface functionalization for a silica filler using methyltriethoxysilane to enhance the compatibility between the silica filler and the PTFE matrix. Enhanced compatibility not only improves the dispersion of the filler but also promotes interaction at the interface, which can confine the movement of the PTFE chain and thus reduce the CTE and dielectric loss.³ A similar approach involving surface functionalization was adopted by Jin et al.,⁷ Yuan et al.,⁸ and Wang et al.,⁶ where reduction in the CTE and dielectric loss was achieved. Ren et al. studied the effect of the filler shape by comparing spherical and fibrous silica and reduced ε and tan δ using fibrous silica. They attributed this to the high aspect ratio, which hindered chain relaxation.⁹ Alhaji et al. studied the effect of the size of spherical silica fillers and realized that a smaller filler size can effectively reduce the CTE but lead to higher ε and tan δ.¹⁰ This conclusion is supported by the work of Chen et al., who claimed that dielectric-performance degradation is caused by interfacial polarization because of the higher interface density in the case of the smaller filler size.¹¹ However, contradictory conclusions were drawn in the theoretical study conducted by Qin et al.¹² and the experimental study conducted by Ibrahim et al.¹³ In these cases, rather than the interfacial polarization, the effect that interface limit the orientation and the movement of dipoles and the polymer chain is more predominant in the interfacial region. The effect decreases the ε and tan δ. The competition between these two effects is affected by the interfacial structures, which are determined by the filler dispersion and the interfacial compatibility.¹⁴ Overall, owing to the complexity of the fabrication parameters and the resulting filler dispersion and interfacial effect, fabricating the desired polymer composites with a low CTE and high-frequency dielectric loss is a challenge, and requires time- and labor-intensive tasks.

Recently, machine learning-driven optimization has emerged as a valuable tool in materials science. Bayesian optimization (BO), one of the commonly used machine learning methods, has proven to be useful for various applications, particularly those combining high-throughput computational methods for data acquisition. Ju et al. optimized the thermal conductivity of a Si/Ge superlattice structure and achieved the optimized structure by 438 data, only 3.4% of the total candidates.¹⁵ In the study by Yamawaki et al., BO could identify the top 0.5% structures using less than half the amount of data required in a random search for optimizing the thermoelectric figure of merit (FOM) of a holey graphene nanoribbon structure.¹⁶ Okazawa et al. optimized the structure of binary alloy catalysts for the dissociation of the nitrogen bond using BO and realized a minimal surface energy of ∼0.2 eV Å⁻² within only one iteration, significantly outperforming the random search strategy.¹⁷ Tsuji et al. optimized nanocluster catalysts for efficient ammonia synthesis, where BO significantly accelerated the search for the optimal catalyst within two or three iterations.¹⁸ Takahashi et al. achieved a far higher efficiency in exploring dielectrics with a high dielectric constant using BO compared with a random search.¹⁹ BO has also been utilized in the polymer materials, including machining process optimization,²⁰ porous media analysis,²¹ and laser material processing.²² These studies demonstrate the effectiveness of BO in experiments searching for optimal process parameters for polymers. In these studies, a kernel involving simple Gaussian process regression (GPR) with a fixed length scale was proven to be sufficiently effective for the BO of an isotropic data space. However, in practical investigations aimed at fabricating ready-to-use materials, the transition from simulation-based optimization to experiment-in-loop optimization is critical. Although there has been an increasing number of studies on experiment-in-loop optimization,^23–26 researchers typically avoid complicating the variety of input parameters to reduce the required number of experiments, because the acquisition of experimental data is far more costly than simulation data. This has motivated the development of high-throughput robot-assisted experimental approaches specialized for a particular purpose.^23–26 However, neither manual nor automated experimental-in-loop optimization has been realized for polymer compounds because of the large dimensions in the material and process parameters and the complexity of processes such as compounding and hot pressing, which are difficult to fully automate.

To increase the efficiency of BO, recent efforts have focused on improving the surrogate model. Herbol et al. increased the efficiency of structure optimization for hybrid organic–inorganic perovskites by applying a custom GPR kernel that used the underlying knowledge of this material system.²⁷ Similar approaches were adopted by Khatamsaz et al., who used physics-informed GPR to optimize the design of NiTi shape-memory alloys via a thermal treatment process.²⁸ Nevertheless, these approaches typically require an in-depth understanding of the underlying mechanisms, which are not applicable to the fabrication of polymer composites for 5G. Automatic relevance determination (ARD) kernel is an alternative approach that can automatically adjust the “weights” of individual input dimensions to accurately capture and balance the unique influence of each input feature on the objective.^29,30 The ARD kernel may be a valuable tool for optimizing the fabrication process for the proposed polymer-based composite with a low CTE, ε, and tan δ.

In this study, we employed experiment-in-loop BO for fabricating a PFA polymer/silica composite via a compounding process. We used five types of silica fillers, which differed in shape, size, surface functionalization, and volume fraction. In addition to the compounding process parameters, an eight-dimensional parameter space was defined as the input parameter. To manage this high-dimensional space, the weights of the individual dimensions are automatically adjusted using an ARD kernel. The application of the ARD kernel increases the efficiency of BO, by quickly targeting the parameters for fabricating composites. The obtained optimal composite shows a low CTE of 24.7 ppm K⁻¹ and an extinction coefficient of 9.5 × 10⁻⁴, superior to polymers for 5G wireless technology reported in previous studies. We also systematically examined the structural improvement during the BO process and found that the topological structure is crucial for achieving a low CTE. We found a three-phase composite consisting of voids, fillers, and a matrix, with a specific distribution, shape, and volume fraction, which can lead to the relaxation of inward bending deformation by the collective movement of the silica filler and PFA may be responsible for the strongly suppressed thermal expansion.

Results and discussion

Fabrication of PFA/silica composites

To realize a high CTE and low dielectric loss, we composed a PFA resin (HS-230, Daikin) with silica fillers of various shapes, sizes, and surface functionalization via a compounding process (filler details are presented in Table S1, ESI†). A dual-screw cycling-type compounding machine (MC15HT, Xplore Instruments) was used, which allowed flexible control of the compounding time and rotation speed. The compounding temperature was fixed at 380 °C, which was higher than the melting point of PFA at 310 °C. The process temperature was fixed according to a pre-experiment, which revealed that the CTE decreased with the increase in compounding temperature and saturated above 370 °C (Fig. S1, ESI†). Following the compounding process, we used a hot-press machine to mold the sample from the filament shape into a thin film at 360 °C. The hot-pressing temperature was selected to achieve an appropriate thickness for subsequent measurements. The film was then cut to a specific size and assessed through dielectric measurements and thermomechanical analysis to obtain the CTE, ε, and tan δ values.

Evaluation of the PFA composite

The dielectric properties including ε and tan δ were measured by a cavity resonator method at a frequency of 10 GHz. The measurement was conducted using a Microstrip Line Dielectric Resonator System (AET Japan), which ensures high precision in high-frequency dielectric property characterization. The system operates in the transverse electric (TE) mode, where the electric field is primarily transverse to the propagation direction, minimizing conductor losses and enhancing the measurement accuracy. This method provides high sensitivity to dielectric properties, making it particularly suitable for characterizing low-loss polymer composites.

The coefficient of thermal expansion (CTE) was measured using a NETZSCH TMA 402 thermomechanical analyzer in a nitrogen (N₂) atmosphere. The measurement was conducted over a temperature range of 20 °C to 150 °C, with both heating and cooling rates set at 5 K min⁻¹. The CTE was determined from the cooling curve by calculating the average expansion rate, i.e., the total change in length divided by the total temperature change.

Bayesian optimization

To efficiently optimize the experimental parameters for the fabrication of the PFA/silica composite, we employed BO with an ARD kernel GPR model using the PHYSBO package.³¹ The common kernel setting for the GPR model is the radius basis function (RBF), which is also called the squared exponential kernel. The RBF kernel between two points x′ and x in the input space is defined as follows:where σ is the variance parameter, which controls the overall variability, l is the length-scale parameter, which controls how fast the correlation for two points decays with distance, and is the Euclidean distance between the two points. For the ARD kernel, the RBF kernel is modified to allow an independent length scale for each input dimension as follows:where D represents the number of dimensions in the input space, x_i and represent the ith-dimension input, and l_i is the length-scale parameter for the ith-dimension input.³² The ARD kernel automatically adjusts the relevance of individual dimensions of distinct physical factors, which was proved to be more effective than the RBF kernel in handling tasks with complexities as high as eight dimensions.¹⁰ In the ARD kernel, l_i was adjusted by maximizing the marginal log-likelihood (MLE) of the Gaussian process mode. For this process, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method, which efficiently estimates the inverse Hessian approximation by storing only the most recent gradient information, was used. Notably, in the PHYSBO package, all these hyperparameters were adjusted automatically.

A schematic of the BO-driven experimental loop is shown in Fig. 1. In the first round of BO, we conducted six experiments and used the datasets to train a GPR model, aiming to predict the mean of the target yield μ(x) and the standard deviation σ(x), where x represents the input parameters. These experiments were conducted using randomly selected experimental parameters, which included the material parameters determined by the materials added to the compounding machine and the process parameters for compounding, such as the compounding time and rotation speed. The definitions of each dimension and the range of the input parameters are listed in Table 1. We allowed the mixing of different filler shapes owing to the synergistic effect observed in previous studies, where a mixture of fillers with varying shapes and sizes significantly improved both the CTE and dielectric properties.^33,34 Although the underlying mechanism has not been well established, this strategy was helpful for achieving the desired properties. Moreover, this setting allowed us to determine the optimal filler type.

Fig. 1 Schematic of the experiment-in-loop BO process for the fabrication of the “5G-and-beyond” PFA composite with low dielectric loss and thermal expansion. An experiment involving (a) compounding and hot pressing was conducted for the fabrication of (b) the PFA/silica composite, followed by (c) performance evaluation of the FOM based on measurements of the CTE and dielectric properties. (d) Collected experimental data were then fed to (e) the ARD kernel to train the model to suggest experimental parameters of candidates in the next iteration.

Table 1 Definitions of descriptors for the input parameters

Process parameters		Plate filler condition	Spherical filler condition		Filament filler condition		Filler weights^a
Time (min)	Rotation (rpm)	Surface treatment	Surface treatment	Diameter	Surface treatment	Diameter	Weight of plate filler (g)	Weight of spherical filler (g)	Weight of filament filler (g)
a Maximum 7 g in total.
5	50	With (1)	With	Small (2.2 μm)	With	Small (0.7–2.1 μm)	0	0	0
7	100	Without (0)	Without	Large (20 μm)	Without	Large (7.5 μm)	1	1	1
9	150						2	2	2
	200						3	3	3
	250		Small diameter and without surface function (0)				4	4	4
			Small diameter and with surface function (1)				5	5	5
			Large diameter and without surface function (2)				6	6	6
			Large diameter and with surface function (3)				7	7	7

---

Furthermore, since the 5G-and-beyond wireless technology requires a low CTE and low dielectric loss simultaneously, we defined a figure of merit (FOM) as the target function, as follows:

FOM = (e_max − e)/e_range − (d − d_min)/d_range, (3)

where e represents the CTE, and d represents the dielectric extinction coefficient, which is given by . The subscripts max, min, and range represent the maximum, minimum, and range of either e or d. Herein, e_max represents the highest CTE achievable in the composite, which corresponds to the CTE of pure PFA. d_min refers to the lowest achievable dielectric extinction coefficient, which is the extinction coefficient of pure silica. Both parameters were obtained through experimental measurements. The FOM formulation was designed to ensure balanced optimization of CTEs and extinction coefficients by normalizing both terms. This prevents the BO process from disproportionately prioritizing one parameter over the other due to differences in their absolute variation ranges. This FOM describes the normalized variation rate of the CTE and the extinction coefficient; a larger FOM corresponds to a lower CTE and extinction coefficient.

After the GPR was trained with the initial datasets, the acquisition functions based on the trained GPR model can output several new data points corresponding to the experimental parameters that are likely to yield a high FOM and the corresponding x via the expected improvement (EI), as follows:

EI(x) = (μ(x) − FOM_{current_max})ϕ(z) + σ(x)ϕ(z), (4)

We then conducted experiments following the sets of parameters of the top five candidates predicted by the EI function and repeated the procedure for 11 rounds. All hyperparameters and scaling parameters of the individual dimensions were automatically adjusted in each round.

BO process analysis

Fig. 2(a) illustrates the results of the BO process, showing a rapid increase in the FOM, which peaked in the fourth round, as indicated by the gray spots. We also compared the predicted values and variances of the FOM before each round to assess the divergence between the experimental results and the GPR model prediction, which helps us to evaluate the impact of the BO process and verify its effect. The predicted values vary similarly to the experimental results, peaking in the fourth round, and the variance decreased as the predicted values increased. During the third and fourth rounds, the predicted values closely matched the experimental results with a small variance, demonstrating the effectiveness of the ARD-GPR surrogate model in capturing the relationship between input parameters and target material properties. This consistency suggests that the BO process effectively guided the optimization towards high-FOM candidates. After reaching the maximum FOM in the fourth round, predictions with a larger variance were observed, indicating that the BO process exploited the search space with higher uncertainty. Conversely, predictions with smaller variances aim to further explore the maximum FOM in search regions with lower uncertainty, as the model was trained with a more densely distributed dataset. The selection between exploration and exploitation is automatically determined by auto-adjusted hyperparameters in PHYSBO.

Fig. 2 Evolution of the properties of the PFA/silica composite fabricated during the BO process. (a) Evolution of the prediction/variance in the BO process and the experimental results. (b) Evolution of the ARD scaling parameters of individual dimensions during the BO process. (c) CTE, (d) ε and tan δ variations during BO. The dots indicate the value at each iteration, and the lines represent the present best value during BO.

To further analyze the prediction accuracy of the surrogate model throughout the BO process, a series of parity plots were made (Fig. S5, ESI†). The results indicated that the coefficient of determination (R²) reached its highest value (∼0.73) around iteration 4, aligning well with the optimization peak observed in Fig. 2(a). However, after iteration 6, R² declines, indicating an increase in prediction variance. This can be attributed to the shift from exploitation to exploration, the uneven distribution of data points leading to reduced model accuracy in unexplored regions, and the increasing complexity of the objective function. These findings highlight the limitations of the surrogate model in later iterations, suggesting potential improvements in BO strategies.

Further analysis of the scaling parameters of the ARD kernel during BO (Fig. 2(b)) revealed the most critical dimensions for determining the FOM across the BO rounds. Herein, smaller scaling parameters indicate the dimensions that are more important for determining the output value. As the optimization progressed, these parameters initially fluctuated significantly. Here, we focused on the fourth round, in which the BO prediction value peaked with a small variance. We found that the top three critical dimensions were the weight of the plate filler, the condition (size/surface chemistry) of the plate filler, and the weight of the filament filler. These scaling parameters provide valuable insights into the most critical parameters for designing polymer composites with low CTE and dielectric losses. Notably, they can be either positive or negative for the FOM. As discussed later, the sample with high FOM (sample #D) usually consists of a large amount of filament fillers, whereas the lower-FOM filler samples (sample #A) consist of more plate fillers without surface functionalization. The insights from the scaling parameters align with the analysis of the sample parameters, indicating the effect of the ARD kernel in capturing the critical dimensions. Herein, although the scaling parameters eventually stabilized as more datasets were used in the BO process, they were less valuable because a large number of predictions after the fourth round exhibit large variance.

Performance of PFA/silica composites

Fig. 2(c) and (d) illustrate the variation in CTE, ε, and tan δ during the BO. As the optimization progresses, the CTE decreases, reaching a minimum after four rounds of BO. The CTE aligns well with the FOM, which also reaches its optimal value in the fourth round. In comparison, tan δ decreases more rapidly. After just one round of BO, it reaches 5.75 × 10⁻⁴, which is close to the minimum value (5.47 × 10⁻⁴) among all the acquired data. After the first iteration, tan δ remains relatively constant, with only a few data points exhibiting relatively high values. In contrast, ε does not exhibit a clear trend in the BO process, fluctuating slightly around an average of 2.44, with a standard deviation within 6% and a maximum fluctuation of only 18% (Fig. S2, ESI†). This makes the extinction coefficient follow the trend of tan δ, rapidly reduced by in the first iteration by approximately 400% and remain relatively constant within a standard deviation of 60% for the remainder of the BO process. The reduction in the CTE is relatively slow; the CTE is minimized in the fourth round, which indicates the required number of rounds for maximizing the FOM.

After the fourth round of BO, a PFA/silica composite (sample #D) with excellent properties was fabricated, featuring a CTE of 24.76 ppm K⁻¹, ε of 2.56, and tan δ of 6 × 10⁻⁴ (extinction coefficient of 9.5 × 10⁻⁴). This sample consists only of filament fillers, with no surface functionalization and small diameters (details of the sample #D parameters are provided in Table 2). In contrast, the low-FOM samples typically include spherical and plate fillers (the parameters and performance of all samples are presented in Table S2, ESI†). Moreover, the rotation speed and time are less important in determining the FOM (samples #D and #E). As stated above, these results are consistent with the conclusions drawn from the scaling parameters of the ARD kernel.

Table 2 Fabrication parameters and properties of Sample #A–#E

Sample no.	Sample properties					Fabrication parameters
	CTE (ppm K^−1)	ε	tan σ	Extinction coefficient	FOM	Time (min)	Rotation (rpm)	Plate filler condition	Spherical filler condition	Filament filler condition	Weight of the plate filler (g)	Weight of the spherical filler (g)	Weight of the filament filler (g)
#A	121.3	2.26	5.64 × 10^−3	8.46 × 10^−3	−0.802	5	50	1	0	3	5	0	1
#B	122.3	2.25	5.75 × 10^−4	8.62 × 10^−4	0.141	5	250	1	2	0	0	7	0
#C	49.9	2.43	8.27 × 10^−4	1.28 × 10^−3	0.572	5	250	0	2	0	0	1	6
#D	24.8	2.56	5.97 × 10^−4	9.50 × 10^−4	0.782	7	50	0	0	0	0	0	7
#E	28.5	2.50	6.42 × 10^−4	1.01 × 10^−3	0.750	5	100	0	0	0	0	0	7

---

Fig. 3(a) and (b) present the comparisons of the CTE/dielectric extinction coefficient and FOM of the present study with those of previous studies, whose FOM values were calculated based on eqn (3). The CTE of 24.76 ppm K⁻¹ is almost the lowest, except for the silica/PTFE and silica/PEEK composite fabricated by Jiang et al.³³ and Xue et al.,³⁵ respectively, while their extinction coefficients are more than one order of magnitude higher than those in the present study. Despite showing a slightly higher CTE than the composites reported by Jiang et al. and Xue et al., the composite fabricated in this study shows a better performance overall considering a combination of both CTE and extinction coefficient values, which achieved a record-high FOM of 0.782, surpassing not only the fluor resin/silica composite but also composites with other components such as polystyrene (PS)/silica,³⁴ polyetheretherketone (PEEK)/silica,³⁵ and epoxy resin/boron nitride nanotube (BNNT).³⁶ Details regarding the component of these samples and their CTE, dielectric properties are presented in Table S3 (ESI†). The highly efficient process for the fabrication of the practical PFA composite with excellent performance highlights the superiority of combining the ARD kernel with experiment-in-loop optimization.

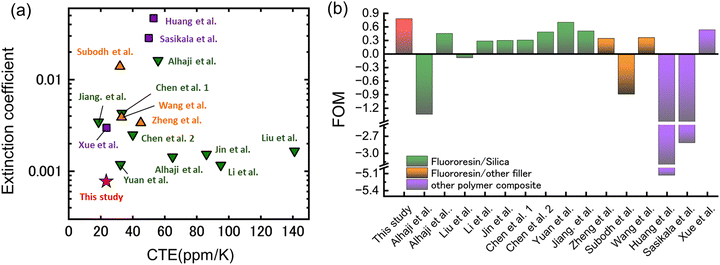Fig. 3 Excellent performance compared with previous studies. Comparison of the (a) CTE, dielectric extinction coefficient, and (b) FOM of the PFA/silica composite with those of previously reported polymer composites;^{3–8,10,11,34–38} different colors indicate materials with different chemical components (green: fluor resin/silica composite; orange: fluorresin/other filler composite; purple: composite of other polymers). The red star/column corresponds to the PFA/silica composite in the present study.

Chemical components and structure of PFA/silica composites

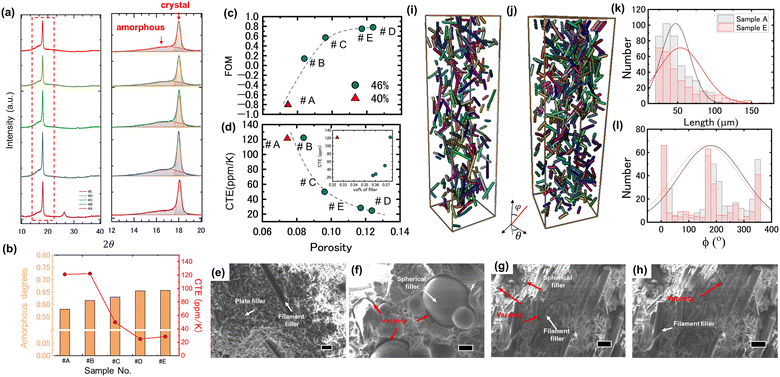
We systematically investigated the chemical components and structure of the PFA composite to gain insights into the enhanced performance, particularly focusing on the CTE, which is primarily optimized during the BO process. We analyzed five representative samples, labeled #A to #E selected from the BO process. The fabrication parameters and properties are presented in Table 2. According to the effective medium theory (EMT),^39–41 the CTE of composite materials is determined by the CTE and the mechanical properties (Young's modulus and shear modulus) of individual components of the composite, including the polymer matrix, fillers, and voids. The properties of the filler and the matrix are affected by their chemical properties. The silica filler is stable during the compounding process because of its high melting point and mechanical strength. Consequently, the CTE and mechanical properties remain unchanged, and were considered identical for all the samples.

However, because the compounding temperature is higher than the melting point of PFA, chemical properties such as the concentration of the amorphous component in PFA are assumed to differ under different compounding parameters. In this study, we focused on the amorphous degree of PFA, as a high amorphous degree typically leads to a high CTE⁴² and low mechanical strength,⁴³ yielding a high CTE of the composite. We investigated the PFA matrix using X-ray diffraction (XRD) analysis. Fig. 4(a) shows the XRD patterns of samples #A–#E. The broad peak at 2θ = 17° corresponds to the amorphous component (I_a), and the sharp peak at 2θ = 18° signifies the crystal component (I_c). Therefore, we can evaluate the amorphous degree by I_a/(I_a + I_c). As displayed in Fig. 4(b), the samples with a lower CTE exhibit a higher amorphous degree. This trend is opposite to the aforementioned trend that a higher amorphous degree typically leads to a higher CTE; therefore, it is unlikely that the strongly suppressed CTE is caused by the change in the amorphous degree of the PFA matrix.

Fig. 4 Amorphous component analysis and microstructure characterization of the PFA/silica composite. (a) XRD results for samples #A–#E. The XRD peaks of amorphous and crystal components are fitted by the Gaussian function and are indicated by the shadowed areas. (b) Amorphous degrees obtained from XRD and the corresponding CTEs (red) for samples #A–#E. (c) FOM and (d) CTE of samples #A–#E with respect to porosity; the dashed curve is for visual guidance; the inset in (d) shows the CTE under different volume fractions of fillers. SEM images of (e) sample #A, (f) sample #B, (g) sample #C, and (h) sample #E (scale bar = 10 μm). XCT results for (i) sample #A and (j) sample #E and the derived (k) length distribution and (l) orientation of filament silica fillers. The curves represent a Gaussian fit of the histogram.

Because the volume fraction of voids and fillers can influence the effective CTE of the composite according to the EMT, we investigated the concentration of voids by measuring the density of the composite using Archimedes’ method and calculated the practical volume fractions of the individual components. The densities of the samples #A–#E are presented in Table S4 (ESI†) and are lower than the theoretical density of a 100% dense composite due to the presence of voids. Therefore, we can consider the sample as a three-phase composite consisting of voids, silica fillers, and a PFA matrix. Fig. S3 (ESI†) shows the EMT calculation of the CTE for a three-phase composite along with the theoretical CTE values for samples #A–#E (see ESI† for details). According to the EMT calculation, although both voids and fillers can result in a lower CTE, the CTE is less sensitive to voids because their elastic and shear moduli are negligibly small. However, in the actual experiments, as indicated by Fig. 4(d), although the changes in the volume fraction of voids are within a limited range of 7.5–14.2% for samples #A–#E, the CTE varies by up to 97.5 ppm K⁻¹, which significantly increased the FOM, from –0.802 to 0.782 (Fig. 4(c)). Moreover, although the EMT predicts a reduction in the CTE with an increase in the filler volume fraction, the experimental results do not exhibit such a reduction. In fact, there is no clear correlation between the CTE and the volume fraction of the filler, as shown in the inset of Fig. 4(d).

This suggests that the low CTE achieved here may arise from a more complex mechanism than the simple weighted average of the CTE. One possible mechanism is the topology effect proposed by Sigmund et al., where a three-phase composite consisting of a matrix, fillers, and voids can substantially reduce the CTE, even to a negative value, under specific topological conditions.^44,45 In such a structure, the difference in CTE between the filler and the matrix leads to anisotropic expansion upon heating, potentially causing internal bending deformation and macroscopic shrinkage. Voids are critical for providing the necessary physical space for internal movement or deformation upon heating, which relaxes the thermal expansion within the composite and significantly reduces its CTE. In this context, apart from the specific topological design of the composite, a higher porosity, larger interface area, and larger difference in the CTE between the filler and the matrix are likely to enhance the topological effect, reducing the CTE. This conclusion aligns with the trends observed in the present study, where samples #D and #E, which have higher porosity and larger interfacial area owing to the high surface-to-volume ratio of the filament fillers, exhibit a low CTE.

Although drawing a conclusion on how the structural variations affect the CTE is a challenge without systematically varying the topological design to investigate the impact on the CTE, we can gain valuable insights into the character of the topology in achieving a low CTE by analyzing the specific structures of the composites. Scanning electron microscopy (SEM) was used to analyze the microscopic topologies of the fillers and voids. Fig. 4(e)–(h) present the cross-sectional SEM images of representative samples #A, #B, #C, and #E (additional SEM images of other samples at both high and low magnifications are shown in Fig. S4, ESI†). In sample #A, which contains both filament and plate fillers, these components are uniformly dispersed and exhibit minimal voids, which corresponds to its low porosity. In contrast, sample #B exhibits large voids, primarily between the filler and the PFA matrix. In sample #C, which features a mix of spherical and filament fillers, vacancies were observed near both the spherical and filament fillers, and the vacancies near the spherical fillers are larger. Samples #D and #E, characterized by the highest porosity, exhibit small voids close to the filament filler, with sizes ranging from tens to hundreds of nanometers. These SEM observations indicate that the void topology differs among samples and is related to the type of filler used. In addition, low-CTE samples typically consist of filament fillers, which not only affect the topology and volume fraction of the voids but also results in the characterized topology of fillers.

To further characterize the topology of the fillers, we investigated samples #A and #E using X-ray computed tomography (XCT) (nano3DX, Rigaku). To achieve sufficient contrast in the data with a high silica volume fraction, we used a voxel size of 0.66 μm, which is smaller than the thickness of the plate filler. As a result, only the filament filler in sample #A could be analyzed. Fig. 4(i) and (j) show the filament fillers in samples #A and #E, respectively. The filament in sample #A was shorter (51.5 μm) than that in sample #E (58.6 μm), as shown in Fig. 4(k). Moreover, the filament fillers are aligned along the plane of the film, with better alignment in sample #E than in sample #A, indicating that the fillers form a continuous network in the in-plane direction (Fig. 4(l)). This characteristic of the filler topology is similar to the optimal structure that exhibited a negative CTE in the previous study,⁴⁵ where the continuous phase of the filler was characterized.

With the above-mentioned analysis of these representative samples, correlating the fabrication process, microstructural topology, and the resulting CTE, we can summarize key insights for optimizing the PFA composite. For instance, increasing the filament filler content enhances the porosity, facilitating thermal expansion relaxation, while filament alignment, influenced by rotation speed, may contribute to anisotropic structural effects. Additionally, untreated fibers tend to form interconnected networks, which effectively suppress CTE. However, it should be noted that while our analysis provides valuable insights into future sample design, the BO approach does not systematically vary each parameter, and the process inherently involves some degree of bias. Therefore, certain interactions may not be fully decoupled, and the conclusions are primarily applicable to local optimization.

Conclusions

We employed an ARD-GPR kernel in experiment-in-loop BO to optimize the multidimensional experimental parameters for the compounding process of PFA/silica composites, targeting a low CTE, ε, and tan δ for applications in the 5G-and-beyond telecommunications. Exceptional results were achieved, including a CTE of 24.7 ppm K⁻¹ and an extinction coefficient of 9.5 × 10⁻⁴. The main feature of the optimal sample is the large amount of small-diameter filament fillers. With the inaugural machine learning-driven experimental endeavour in fabricating polymer composites with low CTE, ε, and tan δ, our outcomes surpassed those of previous studies that relied on conventional empirical approaches. Moreover, the predicted values/variances agree well with the experimental results. Before reaching the maximum FOM in the fourth round of the BO, the experimental results closely follow the predictions, with the variance decreasing and exhibiting minimum values at the data point with maximum FOM. This indicates that the maximum FOM achieved experimentally was derived from the BO and not obtained by chance. Moreover, the most critical dimensions, as reflected by the scaling parameters of the ARD kernel, align with the analysis of the characteristics of samples with either a high or a low FOM. This consistency verifies the effectiveness of the ARD-GPR surrogate model for accelerating the BO process with multiple anisotropic dimensions.

Further analysis of the chemical components and structures of several representative samples revealed that the microstructural topologies of the composite, particularly the voids and fillers, are highly correlated with the resulting low CTE. We attribute the significant reduction in the CTE to the topological effect, which is typically functional in composites with specifically designed topologies. In such structures, a mismatch in the CTE between the filler and the matrix can lead to uneven heating, causing bending and shrinkage. These effects can be mitigated by the spaces provided by the voids, leading to a CTE far lower than that predicted via EMT.

The fabricated polymer composite with ultralow CTE, ε, and tan δ values is expected to influence the 5G-and-beyond applications by providing a generic and lossless transmission electronic base material. Furthermore, the demonstrated material informatics methodology employing the ARD kernel in experiment-in-loop BO with multiple anisotropic dimensions showcased a useful approach for accelerating the development of composite materials for practical applications in various fields.

Author contributions

J. S. conceived and supervised the research; B. X. and T. A. S. performed the sample fabrication; B. X., T. A. S., and T. S. performed the sample characterization and analysis; B. X. performed machine learning and model analysis with the help of K. K., J. G., R. M., and T. K.; B. X. and J. S. wrote the manuscript with input from all the authors.

Data availability

All data generated or analyzed during this study are included in this published article. Additional raw data supporting the figures are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The authors acknowledge Takayuki Yamada for the discussions on the thermal expansion of composite materials. The XCT measurements were supported by the Tokushima Prefectural Industrial Technology Center.

References

1. R. Li, X. Yang, J. Li, Y. Shen, L. Zhang, R. Lu, C. Wang, X. Zheng, H. Chen and T. Zhang, Mater. Today Phys., 2022, 22, 100594.
2. N. Saba and M. Jawaid, J. Ind. Eng. Chem., 2018, 67, 1–11.
3. F. Liu, Y. Jin, J. Li, W. Jiang and W. Zhao, Compos. Sci. Technol., 2023, 241, 110142.
4. G. Subodh, M. Joseph, P. Mohanan and M. T. Sebastian, J. Am. Ceram. Soc., 2007, 90, 3507–3511.
5. L. Zheng, J. Zhou, J. Shen, W. Chen, Y. Qi, S. Shen and S. Li, J. Mater. Sci.: Mater. Electron., 2017, 28, 11665–11670.
6. H. Wang, F. Zhou, J. Guo, H. Yang, J. Tong and Q. Zhang, Ceram. Int., 2020, 46, 7531–7540.
7. W. Jin, A. Li, Y. Li, Y. Yu, J. Shen, J. Zhou and W. Chen, Ceram. Int., 2022, 48, 28512–28518.
8. Y. Yuan, H. Lin, D. Yu, Y. Yin and B. Tang, J. Mater. Sci.: Mater. Electron., 2017, 28, 8810–8817.
9. L. Ren, K. Pashayi, H. R. Fard, S. P. Kotha, T. Borca-Tasciuc and R. Ozisik, Composites, Part B, 2014, 58, 228–234.
10. I. A. Alhaji, Z. Abbas, M. H. Mohd Zaid and A. M. Khamis, Polymers, 2021, 13, 2449.
11. Y.-C. Chen, H.-C. Lin and Y.-D. Lee, J. Polym. Res., 2003, 10, 247–258.
12. H. Qin, K. Liu, M. Tian, J. Mi and L. Zhang, Polymer, 2022, 256, 125199.
13. I. A. M. Ibrahim, A. A. F. Zikry, M. A. Sharaf, J. E. Mark, K. Jacob, I. M. Jasiuk and R. Tannenbaumn, IOP Conf. Ser.: Mater. Sci. Eng., 2012, 40, 012011.
14. L. Wang, J. Yang, W. Cheng, J. Zou and D. Zhao, Front. Mater., 2021, 8, 1–16.
15. S. Ju, T. Shiga, L. Feng, Z. Hou, K. Tsuda and J. Shiomi, Phys. Rev. X, 2017, 7, 021024.
16. M. Yamawaki, M. Ohnishi, S. Ju and J. Shiomi, Sci. Adv., 2018, 4, 1–8.
17. K. Okazawa, Y. Tsuji, K. Kurino, M. Yoshida, Y. Amamoto and K. Yoshizawa, ACS Omega, 2022, 7, 45403–45408.
18. Y. Tsuji, Y. Yoshioka, K. Okazawa and K. Yoshizawa, ACS Omega, 2023, 8, 30335–30348.
19. A. Takahashi, K. Terayama, Y. Kumagai, R. Tamura and F. Oba, Sci. Technol. Adv. Mater.: Methods, 2023, 3(1), 2261834.
20. H. Sun, S.-Q. Zhao, F.-Y. Peng, R. Yan and X.-W. Tang, Adv. Manuf., 2024 DOI:10.1007/s40436-024-00520-1.
21. M. Delpisheh, B. Ebrahimpour, A. Fattahi, M. Siavashi, H. Mir, H. Mashhadimoslem, M. A. Abdol, M. Ghorbani, J. Shokri, D. Niblett, K. Khosravi, S. Rahimi, S. M. Alirahmi, H. Yu, A. Elkamel, V. Niasar and M. Mamlouk, J. Mater. Chem. A, 2024, 12, 20717–20782.
22. J. J. Patil, C. T.-C. Wan, S. Gong, Y.-M. Chiang, F. R. Brushett and J. C. Grossman, ACS Nano, 2023, 17, 4999–5013.
23. M. Saeidi-Javash, K. Wang, M. Zeng, T. Luo, A. W. Dowling and Y. Zhang, Energy Environ. Sci., 2022, 15, 5093–5104.
24. R. Tamura, T. Osada, K. Minagawa, T. Kohata, M. Hirosawa, K. Tsuda and K. Kawagishi, Mater. Des., 2021, 198, 109290.
25. Z. Hou, Y. Takagiwa, Y. Shinohara, Y. Xu and K. Tsuda, ACS Appl. Mater. Interfaces, 2019, 11, 11545–11554.
26. K. Homma, Y. Liu, M. Sumita, R. Tamura, N. Fushimi, J. Iwata, K. Tsuda and C. Kaneta, J. Phys. Chem. C, 2020, 124, 12865–12870.
27. H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, npj Comput. Mater., 2018, 4, 51.
28. D. Khatamsaz, R. Neuberger, A. M. Roy, S. H. Zadeh, R. Otis and R. Arróyave, npj Comput. Mater., 2023, 9, 1–11.
29. C. E. Rasmussen, Gaussian Processes in Machine Learning, in Advanced Lectures on Machine Learning, ed. O. Bousquet, U. von Luxburg and G. Rätsch, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 63–71.
30. T. Paananen, J. Piironen, M. R. Andersen and A. Vehtari, npj Comput. Mater., 2017, 7, 188.
31. Y. Motoyama, R. Tamura, K. Yoshimi, K. Terayama, T. Ueno and K. Tsuda, Comput. Phys. Commun., 2022, 278, 108405.
32. T. Paananen, J. Piironen, M. R. Andersen and A. Vehtari, AISTATS 2019 - 22nd Int. Conf. Artif. Intell. Stat., 2020, 89, 1743–1752.
33. Z. Jiang and Y. Yuan, Mater. Res. Express, 2018, 5, 066306.
34. T. S. Sasikala, B. P. Nair, C. Pavithran and M. T. Sebastian, Langmuir, 2012, 28, 9742–9747.
35. P. J. Xue, S. L. Liu and J. J. Bian, J. Adv. Dielectr., 2021, 11, 1–8.
36. X. Huang, C. Zhi, P. Jiang, D. Golberg, Y. Bando and T. Tanaka, Adv. Funct. Mater., 2013, 23, 1824–1831.
37. Y. Li, J. Zhou, J. Shen, Q. Li, Y. Qi and W. Chen, J. Mater. Sci.: Mater. Electron., 2022, 33, 10096–10103.
38. Y.-C. Chen, H.-C. Lin and Y.-D. Lee, J. Polym. Res., 2004, 11, 1–7.
39. Z. Hashin, J. Mech. Phys. Solids, 1991, 39, 745–762.
40. B. W. Rosen and Z. Hashin, Int. J. Eng. Sci., 1970, 8, 157–173.
41. J. D. Eshelby, Proc. R. Soc. London, Ser. A, 1957, 241, 376–396.
42. S. X. Lu, P. Cebe and M. Capel, Polymer, 1996, 37, 2999–3009.
43. L. Chevalier, C. Linhone and G. Regnier, Plast., Rubber Compos., 1999, 28, 393–400.
44. O. Sigmund and S. Torquato, J. Mech. Phys. Solids, 1997, 45, 1037–1067.
45. O. Sigmund and S. Torquato, Appl. Phys. Lett., 1996, 69, 3203–3205.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01606h

‡ These authors contributed equally (B. Xu and T. A. Sultana).

---