 Open Access Article
Open Access ArticleBulk thermally conductive polyethylene as a thermal interface material†
Gangchen
Ren
 a,
Zhongtong
Wang
a,
Xinzhu
Huang
a,
Zhongtong
Wang
a,
Xinzhu
Huang
 b,
Daniel
Hur
b,
Daniel
Hur
 a,
Mark A.
Pfeifer
c,
Meredith N.
Silberstein
a and
Zhiting
Tian
*a
a,
Mark A.
Pfeifer
c,
Meredith N.
Silberstein
a and
Zhiting
Tian
*a
aSibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, New York 14853, USA. E-mail: zt223@cornell.edu
bDepartment of Materials Science and Engineering, Cornell University, Ithaca, New York 14853, USA
cCornell Center for Materials Research, Cornell University, Clark Hall, 627, 142 Sciences Dr, Ithaca, New York 14850, USA
First published on 15th January 2025
Abstract
As the demand for high-power-density microelectronics rises, overheating becomes the bottleneck that limits device performance. In particular, the heterogeneous integration architecture can magnify the importance of heat dissipation and necessitate electrical insulation between critical junctions to prevent dielectric breakdown. Consequently, there is an urgent need for thermal interface materials (TIMs) with high thermal conductivity and electrical insulation to address this challenge. In this work, we synthesized thermally conductive polyethylene (PE) bars with vertically aligned polymer chains via a solid-state drawing technique to achieve a thermal conductivity of 13.5 W m−1 K−1 with a coverage area of 2.16 mm2. We utilized wide-angle X-ray scattering to elucidate the molecular structural changes that led to this thermal conductivity enhancement. Furthermore, we conducted a device-cooling experiment and showed a 39% hot spot temperature reduction compared to a commercial ceramic-filled silicone thermal pad under a heating power of 3.6 W. Thus, this bulk-scale thermally conductive PE bar with nanoscale structural refinement demonstrated superior cooling performance, offering potential as an advanced thermal interface material for thermal management in microelectronics.
New conceptsWe demonstrate a pure polyethylene (PE) bar that achieved a record-high thermal conductivity of 13.5 W m−1 K−1 with an applicable coverage area of 2.16 mm2. Previous studies have shown that PE could be engineered from thermal insulation to thermally conductive materials by disentangling and aligning polymer chains. However, most previous research mainly focused on increasing thermal conductivity, with practicality constrained by the nano- and micro-scale coverage areas. To attain a large cross-section as the end product, a large preform is required. Yet, the primary challenge lies in securely gripping and uniformly drawing larger preforms. We overcome this challenge by developing a novel and reliable drawing method that leverages carefully selected crosshead speed, chamber temperature, and preform geometry. This new approach enabled uniform drawing of thick preforms, achieving high thermal conductivity while retaining a substantial coverage area. This innovation enabled us to perform the first device-level cooling test using aligned PE, demonstrating superior cooling performance with a 39% hot spot temperature reduction compared to a commercial ceramic-filled silicone thermal pad under 3.6 W heating power, showcasing its potential as a thermal interface material (TIM). Our approach opens new avenues for polymer-based TIM development, addressing the growing demands of thermal management in microelectronics. |
Introduction
Thermal management in microelectronics is a critical challenge for next-generation electronic devices. Adverse temperature rises are exacerbated by high power density and heterogeneous or 3D integrated architectures, with consequences of reduced signal quality, shortened device lifetime, and even catastrophic failure.1–6 Thus, effective heat dissipation is a vital task to conquer. Thermal interface materials (TIMs) are the critical junctions between the die and the heat spreader (TIM1) and can also be placed between the heat spreader and the heat sink (TIM2) to bridge the air gap formed from the imperfect contact due to the asperities on each of the meeting surfaces.7,8In general, an ideal TIM should possess high thermal conductivity to minimize thermal resistance, thereby achieving optimal heat dissipation. Meanwhile, excellent electrical insulation is vital for TIMs to prevent dielectric breakdown, which can cause short-circuit failure and threaten the safety of both devices and users.9–11 Therefore, thermally conductive and electrically insulated TIMs are needed for effective heat dissipation while avoiding electrical failure.
There is always a tradeoff between high thermal conductivity, mechanical compliance, and electrical insulation for conventional TIMs. Metal-based TIMs such as solders,12,13 sinters,14,15 and liquid metals16,17 offer high thermal conductivity but are electrically conducting and suffer from thermomechanical stress due to the rigidly connected surfaces with different thermal expansion coefficients, which could gradually crack the TIMs.8,18,19 Due to their fluid nature, liquid metals may leak or overflow, leading to contamination of device components and electrical short-circuit failure in applications requiring electrical insulation.18,19 Polymer nanocomposite TIMs, such as thermal greases and pads, are composed of a polymer matrix integrated with highly thermally conductive fillers. They are mechanically compliant and typically electrically insulating but exhibit much lower thermal conductivity compared to metal-based TIMs.20 Although a higher filler loading ratio enhances thermal conductivity, it also causes a problematic increase in the viscosity of greases and hardened pads, resulting in reduced compliance and increased contact thermal resistance.21,22 Pure polymer TIMs with high thermal conductivity are desirable, yet are out of reach so far.23,24
One way to achieve the high thermal conductivity of a pure polymer is to engineer the molecular structures and morphology. Polyethylene (PE) appears to be a promising candidate for enhancing the intrinsic polymer thermal conductivity with an excellent electrical insulation property.23,25 Previous numerical predictions showed that aligned PE chains could exhibit thermal conductivity several orders of magnitude higher than amorphous PE.26–28 Experimental fabrication of the thermally conductive PE fibers (∼104 W m−1 K−1) and films (∼62 W m−1 K−1)29,30 demonstrated two-orders-of-magnitude higher thermal conductivity than the bulk PE (0.2–0.5 W m−1 K−1). Despite the high thermal conductivity, their limiting dimension is in the nano and micro scale, which is impractical for real-world applications.29–32
Inspired by previous works, we leveraged polymer chain alignment for thermal conductivity enhancement. In this work, we synthesized a thermally conductive PE bar with a thermal conductivity of 13.5 W m−1 K−1 while preserving an applicable coverage area of 2.16 mm2 with the smallest dimension larger than 1 mm. A device-cooling experiment was done to demonstrate the practicability and high performance of the fabricated PE bar. To the best of our knowledge, this is the record-high thermal conductivity for a pure polymer at this bulk scale. Our findings open up new avenues to engineer polymer TIMs for the thermal management of microelectronics.
Methods
Thermally conductive polyethylene bar fabrication
We started by preparing a PE preform by solution-casting. 2 wt% ultra-high molecular weight polyethylene (UHMWPE) powders (Sigma-Aldrich) were homogenously mixed in 100 g xylene (Beantown Chemical) for 1 hour using an ultrasonic processor (Fig. 1a). Then, the well-mixed solution was submerged in an oil bath (IKA HBR 4 control) and heated at 125 °C while stirring at 400 RPM until the Weissenberg effect was observed. The polymer solution was kept at 125 °C without stirring for 2 hours to dissolve the UHMWPE powers into xylene completely (Fig. 1b). The dissolved polymer solution was then poured into a cylindrical mold (diameter ∼ 36 mm and height ∼ 310 mm) (Fig. 1c). A cylindrical-shaped polymer gel was initially formed by cooling the solution in the mold at room temperature for approximately 12 hours. Once the shape of the polymer gel was temporarily created, providing sufficient stability to support its own weight, the gel was transferred into a flat-bottom container (diameter ∼ 165 mm and depth ∼ 75 mm) for a more efficient drying and further shaping process. Finally, the polymer gel was periodically flipped to gradually form the PE preform with a rectangular cross-section, which was favored in the solid-state drawing process (Fig. 1d). Too small preforms would not be able to result in a large enough coverage area while excessively large preforms were prone to fracture during the drawing process due to the stress developed from the significant volume deformation around the gripping area. Therefore, meticulously selecting a sufficiently large rectangular-shaped preform is important.A two-stage solid-state drawing technique was implemented to align the polymer chains uniaxially. The PE preforms were approximately 10–11 mm in width, 6–7 mm in thickness, and ∼30 mm in height. Two-millimeter interval markings were labeled on the preform to indicate the initial drawing ratio. As Fig. 1e shows, the PE preform was held and heated at 125 °C in the temperature chamber attached to the tensile tester (ZwickRoell Z010) for 20 min to ensure spatially uniform temperature distribution of the preform. This softened the preform to facilitate the drawing process without causing it to melt. A constant crosshead speed of 10 mm min−1, and a chamber temperature of 125 °C were applied to complete drawing stage I. At a lower draw ratio, we need a higher drawing rate to apply sufficient force to initiate the necking process in the bulk preform. At a higher draw ratio (around 20), we lowered the crosshead speed to 5 mm min−1 to avoid fracture failure and increased the chamber temperature to 130–135 °C for drawing stage II. This elevated temperature could further soften the drawn PE, which has gained enhanced strength from the previous drawing stage. For each drawing stage, the optimal crosshead speed and chamber temperature were determined through a series of controlled experiments to ensure successful drawing while preventing fractures in the large cross-section of the samples. Drawn samples were held and cooled to room temperature after the drawing was completed to preserve the aligned and disentangled polymer chains (Fig. 1f). The drawing ratio was calculated by dividing the length of the after-drawn interval by the length of the initial interval.
Characterization of thermal and mechanical properties
The steady-state thermal conductivity measurement method was applied by using the Physical Property Measurement System (PPMS) equipped with the Thermal Transport option (TTO) from Quantum Design. Drawn PE bars were cut into 10 mm sections for measurement. As illustrated in Fig. 2a, the sample was connected to the PPMS by the gold-plated copper leads assembly. Copper leads were attached to the sample for heating, cooling, and data acquisition by silver epoxy (EPO-TEK H20E). A high-vacuum condition (∼10−4 torr) was maintained during the measurement to minimize convection heat transfer. Radiation heat transfer was minimized by covering the sample with a radiation shield. The samples were prepared by trimming them into suitable dimensions and attaching the necessary parts as required in the system operation manual.33 | ||
| Fig. 2 (a) Measured thermal conductivity of PE bars as a function of draw ratio with their coverage area. Thermal conductivity measurement of a PE bar with leads attached for connecting TTO to PPMS. (b) Sample dimension comparison with previous research work, nanodiamond (ND) and graphene (GN).29–32 | ||
The sample was heated by an electrical heater and cooled by a heat sink. The temperature difference across the sample was measured as a function of the heating power. Thus, the thermal conductance C was determined using eqn (1) below,
 | (1) |
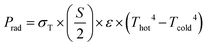 | (2) |
 | (3) |
To investigate the thermal limit of the fabricated PE bars, we characterized the melting temperature (Tm) and degradation temperature (Td) of the PE samples by utilizing a differential scanning calorimeter (DSC) (TA Instruments DSC Auto 2500) and thermogravimetric analyzer (TGA) (TA Instruments 5500), respectively. Undrawn PE and samples at a draw ratio of 37 were used for both analyses. For DSC experiments, we ran the heat–cool–heat experiment with a heating rate of 10 °C min−1 and a cooling rate of 5 °C min−1. For TGA experiments, we set the heating rate to 5 °C min−1, and the furnace environment to nitrogen to avoid the influence of oxidation. Tm was determined from the heat flow versus temperature graph output by the DSC (shown in Fig. S3a and b, ESI†). The initial degradation temperature (Td1) and degradation temperature at the maximum weight loss (Td2) were extracted from the weight loss versus temperature graph produced by the TGA (shown in Fig. S3c and d, ESI†). Due to the measurement device limitation, we were unable to measure the thermal conductivity of the PE bars as a function of increasing temperatures, but the information can be inferred from a prior work.34
To understand the mechanical response of the thermally conductive PE bars, we measured Young's modulus and coefficient of thermal expansion (CTE). We performed tensile experiments (ZwickRoell Z010) for samples at draw ratios of 0 (PE preform), 25, and 40 along the drawing direction under room temperature. Young's modulus was determined by fitting the slope of the stress versus strain curve shown in Fig. S1 (ESI†). We conducted thermal expansion experiments (TA Instruments Q400EM Thermomechanical Analysis) to acquire the dimension change of material as a function of temperature for samples at draw ratios of 0 (PE preform), 25, and 37 (see Fig. S2 in the ESI†). CTE value was calculated based on eqn (4),
 | (4) |
Polymer morphology characterization
To capture and visualize the molecular structure evolution process resulting from the solid-state drawing, a scanning electron microscope (ZEISS Geminis 500 SEM) was used. Wide-angle X-ray scattering (WAXS) from Bruker D8 General Area Detector Diffraction System (GADDS) with cobalt (Co) radiation source was utilized to investigate the molecular structure of the polymer samples. Crystallite orientation was quantified by analyzing the azimuthal intensity distribution along the {110} peak using Herman's orientation factor (HOF) calculation, as shown in eqn (5) and (6),35 | (5) |
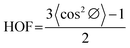 | (6) |
 | (7) |
Prototype device-cooling testing
We in-house manufactured a heater and heat sink assembly to mimic the real-world microelectronic operational environment. The drawn PE bar was used as the thermal interface material bridging the heater and heat sink, as presented in Fig. 5a. Transient infrared images (Fotrio 618 C) were taken throughout the heating process to capture the surface temperature of the heater. The heater was constructed by soldering nichrome resistive wire between two copper plates with a surface area of 2 mm by 2 mm. Heating power was controlled by the DC voltage power supply. The heat sink was maintained at 20 °C and continuously cooled by a recirculating chiller (Buchi F-105) with ethylene glycol and water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio) as the coolant. The upper surface of the heat sink was coated with a graphite coating (GRAPHIT 33 from KONTAKT CHEMIE) to reach black-body radiation conditions, optimizing the accuracy of captured temperature from the IR images. Interfaces between the heater, thermal interface materials, and heat sink were filled with silver epoxy (EPO-TEK H20E) to secure the stability of the assembly. Undrawn PE preforms, commercial ceramic-filled silicone thermal pads, and PE bars with a draw ratio of 35 were tested under the same heating and cooling conditions. All samples were trimmed to similar widths, thicknesses, and heights to ensure the consistency of the comparison.
1 volume ratio) as the coolant. The upper surface of the heat sink was coated with a graphite coating (GRAPHIT 33 from KONTAKT CHEMIE) to reach black-body radiation conditions, optimizing the accuracy of captured temperature from the IR images. Interfaces between the heater, thermal interface materials, and heat sink were filled with silver epoxy (EPO-TEK H20E) to secure the stability of the assembly. Undrawn PE preforms, commercial ceramic-filled silicone thermal pads, and PE bars with a draw ratio of 35 were tested under the same heating and cooling conditions. All samples were trimmed to similar widths, thicknesses, and heights to ensure the consistency of the comparison.
Results
The thermal conductivity of the fabricated PE bars was plotted as a function draw ratio, as presented in Fig. 2a. The PE preform was labeled as a draw ratio of 0. We measured the undrawn sample to have a thermal conductivity of 0.375 W m−1 K−1, which matched the literature result,30 thus validating that our measurement method was adequate for this type of polymer sample. As the trendline indicated, the thermal conductivity of PE increased almost linearly with increasing draw ratio. At a draw ratio of 35, the thermal conductivity reached 13.5 W m−1 K−1, which was significant for a pure polymer. Moreover, the coverage area was retained at 1.8 mm by 1.2 mm, orders of magnitude higher than in previous works,29–32 as illustrated in Fig. 2b. This area falls in the ballpark of the required TIM dimensions for practical applications. Thermal conductivity would increase with higher draw ratios. However, further increasing the draw ratio presented a tradeoff between increasing thermal conductivity and shrinking coverage area.29,30 To balance these factors and enhance practical applicability, a larger coverage area was prioritized. Most commercial polymer-based TIMs rely on thermally conductive fillers, such as ceramic, boron nitride, or diamond powder, to reach thermal conductivities of 1 to 10 W m−1 K−1. Remarkably, our pure PE bar without any fillers achieved a thermal conductivity of 13.5 W m−1 K−1, surpassing these products.T m, Td1, and Td2 are summarized in Table 1. From the DSC results, the melting temperature was ∼136 °C for the undrawn PE preform and ∼145 °C for the PE at a drawn ratio of 37. The alignment of polymer chains seems to increase the melting temperature of the PE, which is better for high operating temperatures. From the TGA results, the initial degradation temperature was ∼432 °C for the undrawn PE preform and ∼434 °C for the PE at a draw ratio of 37. The degradation temperature at the maximum weight loss was ∼484 °C for the undrawn PE preform and ∼478 °C for the PE at a draw ratio of 37. The degradation temperatures of the preform and drawn PE exhibited negligible deviation, indicating the polymer chain alignment did not affect the degradation temperature of PE.
| Sample | T m (°C) | T d1 (°C) | T d2 (°C) |
|---|---|---|---|
| Undrawn PE | 136.02 | 431.83 | 484.26 |
| DR 37 | 144.99 | 434.18 | 478.35 |
Both Young's modulus and CTE for samples at various draw ratios are shown in Fig. 3. The Young's modulus along the alignment direction increased with increasing draw ratio. CTE decreased with increasing draw ratio, indicating that the alignment of polymer chains minimizes thermal expansion. The CTE of drawn PE more closely matched that of inorganic mating surfaces, such as copper, alumina, silicon, and sapphire, than it matched undrawn PE. Therefore, the drawn PE bar could greatly reduce the thermal stress developed between the interface of the TIM and the chip during the heating and cooling cycles, thereby strengthening the reliability of the devices.
In order to verify the alignment of polymer chains from the drawing mechanism, we used SEM to visualize the drawn PE bar at different draw ratios and compared them with the undrawn polymer preform. As depicted in Fig. 4a–c, there was a clear transition from the randomly orientated polymer blocks to unidirectionally orientated polymer chain bundles. For the undrawn sample (Fig. 4a), the randomly orientated fiber blocks acted as phonon scattering points, significantly impeding phonon transport and thus lowering the thermal conductivity. At a lower draw ratio (DR 17, Fig. 4b), polymer chain bundles started to show a trend of alignment but still had the randomly distributed interconnecting chain bundles between each aligned chain bundles, which hindered the thermal transport along the chains. At a higher draw ratio (DR 35, Fig. 4c), polymer chain bundles were much more uniformly aligned toward the drawing direction, as indicated. The number of interconnecting chain bundles was significantly minimized compared to the sample with a lower draw ratio, thus improving the phonon transport along this direction and enhancing thermal conductivity.
To uncover the thermal transport physics behind this enhancement in thermal conductivity, we implemented WAXS to analyze the crystallite orientation factor and the degree of crystallinity. The WAXS pattern presented in Fig. 4d and e showed the comparison between the preform (DR 0) and drawn PE bar (DR 35), revealing an obvious transition from concentric arcs to discrete dots that indicated the orientation preference of the initially randomly orientated crystallites resulting from solid-state drawing. Specifically, the peaks of the undrawn sample (Fig. 3d) at {110} and {200} groups evolved from isotropic arcs to concentrated dots (DR 35, Fig. 4e) along the drawing direction (chain alignment direction). The orientation preference of the crystallites was quantified by using Herman's orientation factor, as shown in Fig. 4f. Herman's orientation factor quickly increased from 0 for the solution-casted preform to 0.95 for the solid-state drawn PE bar. This drastic increase in crystallite orientation matched the thermal conductivity enhancement, which increased from 0.375 W m−1 K−1 (DR 0) to 13.5 W m−1 K−1 (DR 35). Crystallinity also increased with the increasing draw ratio, from 0.55 for the PE preform to 0.73 for the PE bar with a draw ratio of 35, as plotted in Fig. 4f. Therefore, the escalation of thermal conductivity could be revealed to correlate with the rise in polymer crystallite orientation preference and crystallinity through the drawing mechanism.29,30,36,37
To demonstrate the practicability of the PE bar in thermal management, we conducted a prototype device-cooling test (Fig. 5a). As shown in Fig. 5b, IR images were taken as the heating progressed to track the heater surface temperature so that the cooling effect from different thermal interface materials could be visually observed. The surface temperature of the heater ranged from lowest to highest when bridged to the heat sink by using a PE bar (DR 35), the commercial ceramic-filled silicone thermal pad (k ∼ 1.2 W m−1 K−1), and undrawn PE. The result clearly demonstrated that our PE bar (DR 35) was significantly more capable of removing the heat from the heater to the sink. Quantitatively, Fig. 5c and d showed the time-dependent temperature plot extracted from the IR images for different thermal interface materials at different heating powers. At the steady state of the 1.6 W heating, we observed a 7 °C heater surface temperature reduction between the PE bar (DR 35) and the commercial ceramic-filled silicone thermal pad, and a 21 °C reduction between the PE bar (DR 35) and the undrawn PE. For the 3.6 W heating, the heater surface temperature was lowered by 20 °C using the PE bar (DR 35) as the thermal interface material compared to the commercial ceramic-filled silicone thermal pad. The substantial heater temperature reduction convincingly demonstrated the superior cooling performance of our PE bar. This advantage would be amplified if the device operated at an even higher power. In addition, the success of conducting this proof-of-concept experiment has brought pure polymer TIM one step closer to real-world microelectronic cooling applications.
Conclusions
In conclusion, we developed a fabrication method to achieve a record-high thermal conductivity for an electrically insulated pure polymer at an mm2 coverage area. More specifically, we produced a thermally conductive polyethylene (PE) bar (∼13.5 W m−1 K−1) with a millimeter-scale coverage area (∼2.16 mm2), which was orders of magnitude larger than the coverage area in previous works. The high thermal conductivity combined with the large coverage area made our PE bar possible for device-scale cooling testing. We demonstrated the correlation between the boost in thermal conductivity of the PE bar and the molecular structure change from the solid-state drawing by utilizing wide-angle X-ray scattering. Furthermore, we performed prototype device-cooling tests to compare the cooling capability of the PE bar, commercial ceramic-filled silicon thermal pad, and undrawn PE. The heater hotspot temperature was reduced by 7 °C at 1.6 W heating power and 20 °C at 3.6 W heating power when using the PE bar (DR 35) to bridge the thermal interface between the heater and heat sink, compared to the commercial ceramic-filled silicon thermal pad. Therefore, this excellent cooling performance made our PE bar a promising candidate as a thermal interface material in the thermal management of microelectronics.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by CHIMES, one of the seven centers in JUMP 2.0, a Semiconductor Research Corporation (SRC) program sponsored by DARPA under Award No. HR0011-23-3-0002 (2023-JU-3136). Z. Wang was supported by the United States National Air Force Office of Scientific Research (AFOSR) under Contract No. FA9550-22-1-0030. The authors acknowledge that the work made use of the Cornell Center for Materials Research shared instrumentation facility.References
- A. L. Moore and L. Shi, Emerging challenges and materials for thermal management of electronics, Mater. Today, 2014, 17, 163 CrossRef CAS.
- M. M. Waldrop, The chips are down for Moore's law, Nature, 2016, 530, 144 CrossRef CAS PubMed.
- P. Ball, Computer engineering: Feeling the heat, Nature, 2012, 492, 174 CrossRef CAS PubMed.
- R. Warzoha, et al., Applications and Impacts of Nanoscale Thermal Transport in Electronics Packaging, J. Electron. Packag., 2020, 143, 020804 CrossRef.
- P. K. Schelling, L. Shi and K. E. Goodson, Managing heat for electronics, Mater. Today, 2005, 8, 30 CrossRef CAS.
- Semiconductor Industry Association. International Technology Roadmap for Semiconductors (ITRS) 2.0: Executive Report, 2015.
- R. Prasher, Thermal Interface Materials: Historical Perspective, Status, and Future Directions, Proc. IEEE, 2006, 94, 1571 CAS.
- X. Hu, L. Jiang and K. E. Goodson, Thermal Characterization of Eutectic Alloy Thermal Interface Materials with Void-like Inclusions, in Twentieth Annual IEEE Semiconductor Thermal Measurement and Management Symposium (IEEE Cat. No. 04CH37545) ( 2004), pp. 98–103.
- M. T. Demko, J. E. Yourey, A. Wong, P.-Y. Lin, G. S. Blackman, G. C. Catlin and M. Yahyazadehfar, Thermal and Mechanical Properties of Electrically Insulating Thermal Interface Materials, 2017 16th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm) ( 2017), pp. 237–242 Search PubMed.
- J. Chen, X. Huang, B. Sun and P. Jiang, Highly Thermally Conductive Yet Electrically Insulating Polymer/Boron Nitride Nanosheets Nanocomposite Films for Improved Thermal Management Capability, ACS Nano, 2019, 13, 337 CrossRef CAS PubMed.
- L. Alexis, J. Lee, G. A. Alvarez, S. Awale, D. S. Jesus, M. Lizcano and Z. Tian, Significantly Enhanced Thermal Conductivity of hBN/PTFE Composites: A Comprehensive Study of Filler Size and Dispersion, ACS Appl. Mater. Interfaces, 2024, 16, 29042 CrossRef CAS PubMed.
- C. Deppisch, T. Fitzgerald, A. Raman, F. Hua, C. Zhang, P. Liu and M. Miller, The material optimization and reliability characterization of an indium-solder thermal interface material for CPU packaging, JOM, 2006, 58, 67 CrossRef CAS.
- R. Zhang, J. Cai, Q. Wang, J. Li, Y. Hu, H. Du and L. Li, Thermal Resistance Analysis of Sn-Bi Solder Paste Used as Thermal Interface Material for Power Electronics Applications, J. Electron. Packag., 2014, 136, 011012 CrossRef.
- S. Deng, X. Zhang, G. Xiao, K. Zhang, X. He, S. Xin, X. Liu, A. Zhong and Y. Chai, Thermal interface material with graphene enhanced sintered copper for high temperature power electronics, Nanotechnology, 2021, 32, 315710 CrossRef CAS PubMed.
- M. Li, Y. Xiao, Z. Zhang and J. Yu, Bimodal Sintered Silver Nanoparticle Paste with Ultrahigh Thermal Conductivity and Shear Strength for High Temperature Thermal Interface Material Applications, ACS Appl. Mater. Interfaces, 2015, 7, 9157 CrossRef CAS PubMed.
- Y. Gao and J. Liu, Gallium-based thermal interface material with high compliance and wettability, Appl. Phys. A, 2012, 107, 701 CrossRef CAS.
- C. K. Roy, S. Bhavnani, M. C. Hamilton, R. W. Johnson, J. L. Nguyen, R. W. Knight and D. K. Harris, Investigation into the application of low melting temperature alloys as wet thermal interface materials, Int. J. Heat Mass Transfer., 2015, 85, 996 CrossRef CAS.
- J. S. Lewis, T. Perrier, Z. Barani, F. Kargar and A. A. Balandin, Thermal interface materials with graphene fillers: review of the state of the art and outlook for future applications, Nanotechnology, 2020, 32, 142003 CrossRef PubMed.
- W. Xing, H. Wang, S. Chen, P. Tao, W. Shang, B. Fu, C. Song and T. Deng, Gallium-Based Liquid Metal Composites with Enhanced Thermal and Electrical Performance Enabled by Structural Engineering of Filler, Adv. Eng. Mater., 2022, 24, 2101678 CrossRef CAS.
- W. Xing, Y. Xu, C. Song and T. Deng, Recent Advances in Thermal Interface Materials for Thermal Management of High-Power Electronics, Nanomaterials, 2022, 12, 3365 CrossRef CAS PubMed.
- D. P. R. Thanu, B. Liu and M. A. Cartas, Thermal Interface Materials and Cooling Technologies in Microelectronic Packaging—A Critical Review, J. Microelectron. Electron. Packag., 2018, 15, 63 CrossRef.
- F. Sarvar, D. C. Whalley and P. P. Conway, Thermal Interface Materials – A Review of the State of the Art, in 2006 1st Electronic Systemintegration Technology Conference, Vol. 2 ( 2006), pp. 1292–1302.
- X. Wei, Z. Wang, Z. Tian and T. Luo, Thermal Transport in Polymers: A Review, J. Heat Transfer, 2021, 143, 072101 Search PubMed.
- C.-P. Feng, L.-Y. Yang, J. Yang, L. Bai, R.-Y. Bao, Z.-Y. Liu, M.-B. Yang, H.-B. Lan and W. Yang, Recent advances in polymer-based thermal interface materials for thermal management: A mini-review, Compos. Commun., 2020, 22, 100528 CrossRef.
- S. Z. Ahmed Dabbak, H. A. Illias, B. C. Ang, N. A. Abdul Latiff and M. Z. H. Makmud, Electrical Properties of Polyethylene/Polypropylene Compounds for High-Voltage Insulation, Energies, 2018, 11, 1448 CrossRef.
- X. Wang, M. Kaviany and B. Huang, Phonon coupling and transport in individual polyethylene chains: a comparison study with the bulk crystal, Nanoscale, 2017, 9, 18022 RSC.
- H. Ma and Z. Tian, Toward Enhancing Thermal Conductivity of Polymer-Based Thin Films for Microelectronics Cooling, in 2017 16th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm) ( 2017), pp. 390–393.
- H. Ma, Y. Ma and Z. Tian, Simple Theoretical Model for Thermal Conductivity of Crystalline Polymers, ACS Appl. Polym. Mater., 2019, 1, 2566 CrossRef CAS.
- S. Shen, A. Henry, J. Tong, R. Zheng and G. Chen, Polyethylene nanofibres with very high thermal conductivities, Nat. Nanotechnol., 2010, 5, 251 CrossRef CAS PubMed.
- Y. Xu, et al., Nanostructured polymer films with metal-like thermal conductivity, Nat. Commun., 2019, 10, 1771 CrossRef PubMed.
- X. Pan, L. Shen, A. P. H. J. Schenning and C. W. M. Bastiaansen, Transparent, High-Thermal-Conductivity Ultradrawn Polyethylene/Graphene Nanocomposite Films, Adv. Mater., 2019, 31, 1904348 CrossRef CAS PubMed.
- X. Yu, et al., Dielectric polymer composites with ultra-high thermal conductivity and low dielectric loss, Compos. Sci. Technol., 2022, 229, 109695 CrossRef CAS.
- Quantum Design. 2002. Physical Property Measurement System: Thermal Transport Option User's Manual, n.d Search PubMed.
- X. Wang, V. Ho, R. A. Segalman and D. G. Cahill, Thermal conductivity of high-modulus polymer fibers, Macromolecules, 2013, 46, 4937 CrossRef CAS.
- N. S. Murthy, X-Ray Diffraction from Polymers, Polym. Morphol., 2016, 14–36 CAS.
- B. Poulaert, J.-C. Chielens, C. Vandenhende, J.-P. Issi and R. Legras, Thermal conductivity of highly oriented polyethylene fibres, Polym. Commun., 1990, 31, 148 CAS.
- C. L. Choy, Y. Fei and T. G. Xi, Thermal conductivity of gel-spun polyethylene fibers, J. Polym. Sci., Part B:Polym. Phys., 1993, 31, 365 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01419g |
| This journal is © The Royal Society of Chemistry 2025 |




