Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reweighting configurations generated by transferable, machine learned models for protein sidechain backmapping†
Jacob I.
Monroe

University of Arkansas, Fayetteville, AR, USA. E-mail: jacob.monroe@uark.edu
First published on 5th February 2025
Abstract
Multiscale modeling requires the linking of models at different levels of detail, with the goal of gaining accelerations from lower fidelity models while recovering fine details from higher resolution models. Communication across resolutions is particularly important in modeling soft matter, where tight couplings exist between molecular-level details and mesoscale structures. While multiscale modeling of biomolecules has become a critical component in exploring their structure and self-assembly, backmapping from coarse-grained to fine-grained, or atomistic, representations presents a challenge, despite recent advances through machine learning. A major hurdle, especially for strategies utilizing machine learning, is that backmappings can only approximately recover the atomistic ensemble of interest. We demonstrate conditions for which backmapped configurations may be reweighted to exactly recover the desired atomistic ensemble. By training separate decoding models for each sidechain type, we develop an algorithm based on normalizing flows and geometric algebra attention to autoregressively propose backmapped configurations for any protein sequence. Critical for reweighting with modern protein force fields, our trained models include all hydrogen atoms in the backmapping and make probabilities associated with atomistic configurations directly accessible. We also demonstrate, however, that reweighting is extremely challenging despite state-of-the-art performance on recently developed metrics and generation of configurations with low energies in atomistic protein force fields. Through detailed analysis of configurational weights, we show that machine-learned backmappings must not only generate configurations with reasonable energies, but also correctly assign relative probabilities under the generative model. These are broadly important considerations in generative modeling of atomistic molecular configurations.
Design, System, ApplicationComputational design of biological molecules and materials requires modeling and simulation methods that bridge multiple length and time scales. Probabilistic backmappings represent a way to facilitate such multiscale simulations through rigorous coupling of atomistic models to the results of less computationally demanding coarse-grained models. This promises to enable the efficiency of lower-resolution models while exactly recovering ensembles associated with a finer resolution. In this work, we explore the use of probabilistic backmapping models for recovering atomistic details of proteins from coarse-grained simulations. Specifically, we design transferable models for backmapping protein sidechains that are sensitive the local environment of the coarse-grained bead. Our models are amenable to reweighting generated configurations into atomistic ensembles defined by modern protein force fields. We focus our analysis on conditions for which these methods will be efficient, and hence of practical utility. Such methods will facilitate the exploration of conformational ensembles of large biomolecules, as well as the self-assembly behaviors of collections of biomolecules, which currently require coarse-grained simulations that, out of computational necessity, neglect important atomistic details. |
1 Introduction
Models at multiple resolutions have become a crucial component in molecular-level simulations of biological and soft-matter systems. These range from simulations involving quantum-level details to classical representations of individual atoms to “coarse-grained” (CG) models in which atoms, or entire molecules, are treated as individual particles. To capture self-assembly phenomena, such as protein aggregation, simulations must include large numbers of macromolecules interacting over long time scales, which necessitates CG representations. While an emphasis has been placed on the development of accurate CG models,1,2 the reintroduction of atomic-level details, or “backmapping”, remains a significant challenge.Most approaches to backmap to all-atom (AA) configurations from CG representations have been deterministic.3–6 However, this ignores the inherent many-to-one mapping involved in coarse-graining that inevitably leads to a loss of information. Instead, there exists an ensemble of fine-grained configurations related to any one low-dimensional representation. More formally, any backmapping from a CG configuration R to an AA configuration r can be represented by a conditional probability density P(r|R). To enhance sampling, a CG model can be used to access low-dimensional configurations at a longer time and length scales than accessible to an AA model. Once free energy barriers insurmountable to the AA system are crossed in CG simulations, atomic detail may be restored by sampling from P(r|R).
Two primary complications arise in typical backmapping approaches. The first lies in the implicit assumption that the CG model perfectly captures the low-dimensional behavior of the AA ensemble. If this is not the case, an accurate sampling of the true AA ensemble may only be achieved through redistribution of backmapped configurations across state space during further simulations. This would require crossing of free energy barriers that, based on the decision to utilize a CG model, were established as too high for an AA system to cross in a reasonable amount of compute time. Strategies to rigorously sample the AA ensemble, despite deficiencies in the CG model, have been established in the form of “resolution exchange”.7–9 While a cheaper Hamiltonian, such as a CG model, enhances sampling by proposing configurations that are accepted or rejected in the atomistic ensemble, such techniques suffer from the necessity of simultaneously simulating many intermediate states.10,11
The second complication stems from the failure of a learned backmapping to perfectly capture the true P(r|R). Clearly this is rarely true for deterministic backmappings, where P(R|r) = δ(R − M(r)) for a mapping function M(r). Recently, machine learned models have benefited both the development of CG models12–16 and backmappings.17–26 Most notably, a number of backmapping strategies predict ensembles of AA structures rather than single configurations.27–32 Any trained model, however, will be imperfect, both in its prediction of real molecular structures and configurations of high likelihood in an AA ensemble derived from molecular dynamics (MD) or Monte Carlo (MC) simulation with a specific force field. Specifically, machine learned models do not automatically satisfy the constraints imposed by a well-defined thermodynamical ensemble (i.e., a Boltzmann distribution).
A number of approaches, all based on metropolization or reweighting, have been established to rigorously sample a thermodynamic ensemble given imperfect samples from a machine-learned model. Boltzmann generators33 learn to approximately convert a simple probability density, such as a standard normal distribution, to a Boltzmann ensemble via normalizing flows.34,35 While amenable to either metropolization36,37 or reweighting,33 no dimensionality reduction is applied. Instead of mapping from an analytical ensemble, related techniques38 learn to transform between Boltzmann ensembles at different temperatures. Variational autoencoder-based MC (VAE-based MC)39 also learns a model probability density, but does so by learning both a low-dimensional ensemble and a probabilistic backmapping. Though VAE-based MC proposes new AA configurations by first transitioning through a CG space, the moves can be configured to exactly satisfy detailed balance in the target ensemble. It is important to highlight that all of the above models are only amenable to metropolization or reweighting due to explicit learning of a function to predict probabilities of configurations under the learned probability density. A notable deficiency lies in the system-specific training that is required for all of these techniques, which precludes transferability to new molecules.
In this work, we focus on developing general, transferable backmappings to transition between CG and AA representations of proteins. Specifically, we learn a probabilistic backmapping for each amino acid type. Our approach is similar in spirit to that of Jones et al.29 in that the resulting model is autoregressive and relies on the local environment around a CG beads during backmapping. Unlike their work, which is based on denoising diffusion models, the probability density of a configuration under our models is readily calculable. Another key difference is the use of internal, or bond-angle-torsion (BAT), coordinates in this work instead of Cartesian coordinates, which is in line with a recent publication by Yang and Gómez-Bombarelli.31 Those authors also do not supply closed-form probability densities as part of their model, with stochastic sampling only occurring on a reduced-dimensional space of atomic coordinates rather than the full set. As we will demonstrate, working in an internal coordinate system makes for interpretable probability densities, leads to simple loss functions, and renders the application of bond constraints trivial.
Unlike both of the works discussed above,29,31 our model predicts not only heavy-atom coordinates, but also the positions of hydrogens. While bonds involving hydrogens are typically constrained in biomolecular force fields, flexibility in their angles and dihedrals is essential for hydrogen bonding. As such, it is also important to probabilistically sample hydrogen degrees of freedom as well during backmapping. Transferable backmappings including hydrogens have been reported for polystyrene based on its backbone and monomer building blocks.23,40 In those works, however, the predicted probability density for atom locations is discretized on a fine spatial grid. This not only complicates sampling of realistic molecular structures (the authors instead generate atom locations as averages over the probability density), but also limits transferability across system densities or pressures. Shmilovich et al.30 applied the same discretization scheme, including hydrogens, to develop non-transferable backmapping models of specific proteins. However, the models are not only conditioned on the generated CG sample, but also an atomistic configuration from a previous time step, further complicating metropolization or reweighting.
Reweighting has previously been reported for probabilistic backmappings (including hydrogens) trained for specific proteins,28 but the resulting models lack the transferability of this work or those discussed above. Specifically, Chennakesavalu et al.28 independently trained models on MD data for each protein studied. The same authors recently developed a transferable backmapping strategy using a transformer to globally couple sampling of sidechain configurations,27 but did not assess reweighting for that process. We instead train on data from the Protein Data Bank41 and demonstrate that configurations with reasonable energies may be generated for a chosen AA force field. Though architectures capable of backmapping multiple CG representations42 have recently been presented, our models depend explicitly on a single chosen representation. In this work, this is the entire backbone, with center-of-mass beads representing the sidechains, whereas other authors, for example, have used learned mappings27 or only alpha carbons.29,31 This complicates direct comparisons of model performance, but is a necessary aspect of selecting a CG representation on which to condition AA coordinates.
A description of our model, including fine details of our chosen CG resolution, is contained within Methods. We also describe therein the details of the reweighting performed in this work, highlighting a previously unappreciated subtlety involving probabilistic backmappings. In Results and discussion, we present the performance of our model. While our results are at or above the state-of-the-art in terms of previously derived metrics,29,31 we highlight difficulties in producing energetically favorable protein structures that can be used to sample a Boltzmann ensemble defined by a typical AA force field. While energy minimization is common in many machine-learning based methods for backmapping sidechain positions,24,25,43 it does not yield samples from a well-defined probability density that can be metropolized or reweighted. This point is eloquently discussed by Lyman and Zuckerman9 and is not treated at length here.
2 Methods
2.1 Coarse-grained representation
Our CG representation is inspired by the Rosetta centroid representation44 and is shown schematically in Fig. 1. All backbone heavy atoms are included in the CG configuration, as well as the β-carbon of the sidechain and the hydrogen bonded to the backbone nitrogen. Rather than a centroid representing the sidechain, however, we place a single bead at the center of mass of all of the sidechain atoms. The trained backmapping model can produce all-atom structures for any identical topology, regardless of the CG force field or exact mapping function. Results will be best, however, for CG models that most accurately represent the structural ensemble of CG configurations observed in the training set.2.2 Backmapping model
We independently train a backmapping model using Tensorflow45 (version 2.13 or later) for each sidechain residue type in the canonical set of amino acids. This includes alternative protonation states and alternative forms of histidine, but excludes the standard capping groups (ACE, NHE, and NME) and cysteine residues involved in disulfide bonds. It is assumed that termini are uncapped and carry positive and negative charge on the N-terminus and C-terminus, respectively. A single model is trained to backmap hydrogen atoms for all N-terminal residues except for proline, which requires a separate model to be trained due to the different number of hydrogen atoms. A full list of residue types considered and the number of training samples for each are provided in Table 1.| Residue type | Unique PDBs | Training examples | Training epochs |
|---|---|---|---|
| Conditional models | |||
| ALA | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853 853 |
605![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911 911 |
20 |
| ARG | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676 676 |
376![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
40 |
| ASH | 81 | 311 | 2000 |
| ASN | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 365 365 |
321![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
20 |
| ASP | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 499 499 |
442![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 164 164 |
30 |
| CYM | 0 | 0 | N/A |
| CYS | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 239 |
100 |
| GLH | 80 | 389 | 2000 |
| GLN | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266 266 |
297![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 947 |
20 |
| GLU | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 609 |
508![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
30 |
| HID | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 613 613 |
135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058 058 |
30 |
| HIE | 9595 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 159 |
300 |
| HIP | 2195 | 8640 | 2000 |
| HYP | 0 | 0 | N/A |
| ILE | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 627 627 |
425![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 069 069 |
20 |
| LEU | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 990 |
707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 399 399 |
20 |
| LYN | 0 | 0 | N/A |
| LYS | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809 809 |
447![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 455 |
30 |
| MET | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 976 |
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222 |
30 |
| PHE | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 272 272 |
302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 636 636 |
40 |
| PRO | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 376 376 |
348![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
30 |
| SER | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888 888 |
495![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 184 |
20 |
| THR | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 594 594 |
428![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 342 |
20 |
| TRP | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 425 425 |
100 |
| TYR | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 041 041 |
271![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 049 049 |
40 |
| VAL | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 734 |
541![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893 893 |
20 |
| Unconditional models | |||
| GLY | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006 006 |
546![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 274 274 |
10 |
| NPRO | 1233 | 1961 | 10 |
| Nterm | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 499 499 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 796 |
10 |
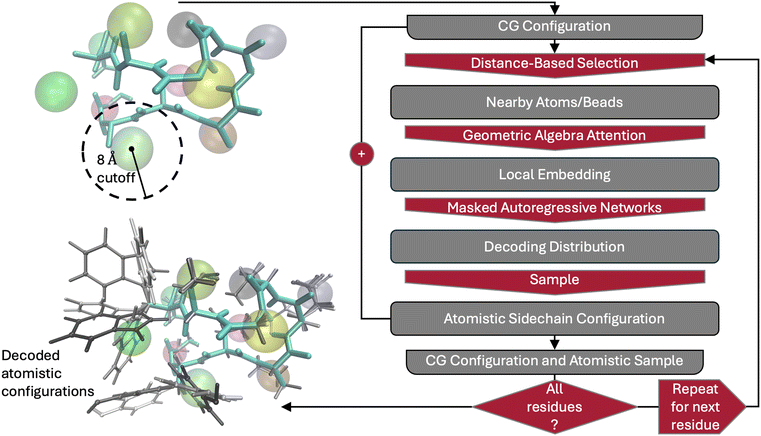
A schematic of the overall backmapping workflow is shown in Fig. 1. Each backmapping model consists of two main steps: building a description of the local environment of a sidechain bead to be backmapped and construction and sampling from a probability density for all internal (bond-angle-torsion, or BAT) sidechain coordinates. The first step is accomplished through geometric algebra attention46 acting on the relative coordinates of particles near the sidechain bead. This ensures a local description that is translationally and rotationally invariant, as well as equivariant to permutations of particle identities. Backmappings for N-terminal hydrogens and glycine do not utilize the first step, and are thus termed “unconditional” due to lack of conditioning on the local environment. In the case of glycine, a CG bead representing the center of mass of the two “sidechain” hydrogens is still present, but this information is ignored in the backmapping. The second step conditions masked autoregressive normalizing flows47 on the local description to produce a probability density of the sidechain internal degrees of freedom. A sample is drawn from this distribution and the corresponding Cartesian coordinates are added to the overall backmapped structure. Full backmappings always proceed by drawing samples from unconditional models (N-terminal hydrogens and glycine) first. Residues are then decoded from the N-terminus to the C-terminus for simplicity, as we do not expect the order to play a significant role in the results. The overall model is autoregressive due to each residue being decoded in turn, with the probability of subsequent residue configurations conditioned on those of previously decoded atoms. Each sampled sidechain configuration of residue i can be assigned a conditional probability of P(ri|R, r<i). The overall conditional probability of the entire protein AA configuration given the CG configuration is then P(r|R) = ΠiP(ri|R, r<i).
To describe the local environment, the 150 closest atoms and/or CG particles within 0.8 nm of the sidechain bead to be decoded are selected. If fewer than 150 particles are selected, the resulting set of coordinates is padded to this number, as required for input to the geometric algebra attention layer. One-hot encodings of selected particles are also provided as input to the geometric algebra attention layer. These one-hot encodings are based on all protein atom types and residue types in the AMBER14SB force field.48 Though an arbitrary choice, this only applies labels to produce one-hot encodings—any AA force field may be used in the reweighting described below. Before being passed into the geometric algebra attention layer, a dense network mapping one-hot encodings to the working dimension, or embedding dimension, is applied. Embedding dimensions depend on the residue being backmapped and are set to 10 times the number of heavy atoms in the residue's sidechain. This allows more information about the local environment and sidechain configuration to be represented for larger residues. Our geometric algebra attention layers consist of 2 blocks containing dense networkings mapping to value and score functions of a vector attention layer, followed by a layer of dense networks, as described in ref. 46. All dense networks consist of a single hidden dimension matching the embedding, or working, dimension for vector attention. Vector attention layers in both blocks utilize up to rank 2 information and do not pool over all particles, applying dense networks separately to each working-dimensional output from all 150 contributing particles. We apply a final vector attention layer that does sum contributions over all particles to yield our description of the local environment around a sidechain bead.
The local description is provided as input to a dense network that maps to the parameters of starting distributions for a normalizing flow to act on. Bonds and angles are represented by Gaussian distributions and torsions by von Mises distributions. All distributions are implemented through tensorflow-probability49 (version 0.21) and are independent of each other prior to the application of a normalizing flow. A masked autoregressive normalizing flow47 is applied to these distributions and consists of 3 blocks of rational quadratic spline flows.50 Each of the blocks takes the local description as conditional input to ensure its relevance even through a deep architecture. Within the first block, autoregressive masks apply to sidechain degrees of freedom in sequential order, while in the last block the order is reversed. Within the middle block, the order is “random”, though for reproducibility we set the random seed to 42 for all models and runs. Rational quadratic splines are constrained to the interval (−π, π), which contains the low-variance Gaussian distributions of bonds and angles when bonds are measured in Angstroms. We used 20 spline knots and dense layers, each containing a single hidden layer of dimension 100, to produce rational quadratic spline parameters for transforming each dimension. The dense layers are masked to ensure an autoregressive distribution.51
The code supporting this work is split into two separate repositories. One provides a generic suite of tools for developing and training normalizing flows, custom probability densities, and overall variational autoencoding or backmapping models.52 The second repository53 includes all of the specific implementations of models, as well as code for generating the training data, performing simulations, and analyzing the full decoding model.
2.3 Datasets
Training samples were pulled from structures in the Protein Data Bank (PDB).41 We consider all protein structures with fewer than 10 distinct proteins and less than 5000 atoms deposited before August 12, 2023. We cluster sequences based on 50% sequence similarity, with only the structure with the highest combined resolution saved for each cluster. Since some PDB entries with multiple sequences appeared multiple times, the results are pruned to only include a given PDB identifier only once. For structures with multiple models, such as from NMR experiments, we utilize only the first model. This resulted in 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524 PDB structures, which includes protein complexes.
524 PDB structures, which includes protein complexes.
To prepare data for training, we pass every raw PDB structure through the pdbfixer tool.54 This removes non-protein atoms, such as bound drug molecules or waters, then identifies missing atoms, including hydrogens, before adding them to the structure based on geometric criteria. Structures are immediately removed if they contain non-standard residues, have more than 10% of residues missing, or have more than 1% of their included residues missing heavy atoms. We exclude all residues with atoms other than hydrogens added by this tool from backmapping targets of subsequent training sets. However, we include all atoms in the resulting structures in the portion of training sets used to condition the backmapping (i.e., for determining the local environment of a CG bead). Residues completely missing from PDB structures are not filled in by the pdbfixer tool and are excluded from the training dataset in every sense. This mainly excludes terminal residues or those along highly flexible loops appearing in low-resolution structures. The resulting set of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 structures is the “clean” dataset. The “energy minimized” dataset contains the 20
327 structures is the “clean” dataset. The “energy minimized” dataset contains the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 clean dataset structures that were energy minimized without errors for 1000 steps in OpenMM55 using the AMBER14SB force field48 in vacuum.
325 clean dataset structures that were energy minimized without errors for 1000 steps in OpenMM55 using the AMBER14SB force field48 in vacuum.
2.4 Training
Inputs for each training example include the Cartesian coordinate of the sidechain bead to decode, positions of all atoms and sidechain beads in the CG structure, positions of atoms for a random set of sidechains, and a one-hot encoding specifying the atom or sidechain bead types. Random selection of residues for including sidechain atoms emulates the process of backmapping residues in a random order. The AMBER14SB force field48 is used to assign atom types for the purpose of defining the one-hot encoding, while one-hot encodings of sidechain beads correspond to the residue type in the same force field. Targets of a training example are the BAT coordinates of the atoms in the sidechain to be decoded. The output of a backmapping model is actually a tensorflow-probability distribution object, which enables either sampling or computation of its log-probability over a sample. For training purposes, we simply maximize the log-probability of targets under the predicted backmapping distribution. For generation of new structures, we instead sample from the predicted backmapping distribution.Numbers of training examples for each residue type are displayed in Table 1. Backmapping models for all residue types are trained for varying numbers of epochs (shown in Table 1) based on the size of the training data set and complexity of the sidechain. We use 10 epochs for all unconditional models. For all models, we use an ADAM optimizer56 with the default settings in Tensorflow45 (version 2.13 or later) and a batch size of 64. Training data is split 90/10 into training and validation sets. We only save the model weights for the epoch yielding the lowest loss on the validation set to avoid overfitting. Training typically took between 24 and 72 hours using 40 GB NVIDIA A100 GPUs for training conditional models. NVIDIA T1000 GPUs on a desktop workstation were sufficient for training all unconditional models in less than a day.
2.5 Simulations
OpenMM55,57–59 (version 8.0) serves as the engine for all-atom simulations of 1UAO (chignolin). We use the AMBER14SB forcefield with the gbn2 (ref. 60) (igb8 in AMBER) implicit solvent model. There is no cutoff and all bonds involving hydrogens are constrained.61 We perform a simulations of the unrestrained protein as well as one with the atoms involved in the CG representation harmonically restrained. For the unrestrained protein, we enhance sampling through temperature replica exchange implemented through OpenMMTools.62,63 Langevin dynamics with a timestep of 2 fs and collision frequency of 1 ps maintains the temperature of each replica and propagates dynamics. Six replicas at temperatures assigned exponentially between 300 and 450 K are run in parallel with configurations swapped every 1 ps. We equilibrate each replica for 1 ns before a production run of 1 μs, only using configurations saved every 10 ps from the lowest temperature replica at 300 K for further analysis. Restrained simulations occur at fixed temperature of 300 K and also with Langevin dynamics, but with a reduced timestep of 1 fs to accommodate the strong harmonic restraints. Spring constants are 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2 and applied to each CG atom position in the energy minimized configuration of the most dominant model in the PDB. Equilibration is also for 1 ns before a production run of 100 ns with configurations saved every 10 ps.
000 kJ mol−1 nm−2 and applied to each CG atom position in the energy minimized configuration of the most dominant model in the PDB. Equilibration is also for 1 ns before a production run of 100 ns with configurations saved every 10 ps.
2.6 Coarse-grained models
To generate simulations of only the CG representation, we use three different methods. The first two are based on clustering 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations sampled every 100 ps from the MD simulations of chignolin described above. We computed root-mean-squared distances (RMSDs) between alpha carbons for all pairs of aligned structures using MDTraj,64 then perform hierarchical clustering through scipy.65 Each configuration is assigned to a cluster such that its alpha carbon RMSD to all other members of the cluster is less than 2.0 Å. To probabilistically generate CG structures, a cluster is selected randomly, followed by uniformly sampling a configuration belonging to that cluster. Random cluster selection occurs either proportional to the cluster population, or uniformly. The former is termed the “cluster by population” CG model, while the latter is the “cluster uniform” CG model. Clearly, these models only sample a reduced set of the CG phase space of chignolin. However, they yield CG configurations observed in the all-atom simulations with known probabilities, which allows reweighting.
000 configurations sampled every 100 ps from the MD simulations of chignolin described above. We computed root-mean-squared distances (RMSDs) between alpha carbons for all pairs of aligned structures using MDTraj,64 then perform hierarchical clustering through scipy.65 Each configuration is assigned to a cluster such that its alpha carbon RMSD to all other members of the cluster is less than 2.0 Å. To probabilistically generate CG structures, a cluster is selected randomly, followed by uniformly sampling a configuration belonging to that cluster. Random cluster selection occurs either proportional to the cluster population, or uniformly. The former is termed the “cluster by population” CG model, while the latter is the “cluster uniform” CG model. Clearly, these models only sample a reduced set of the CG phase space of chignolin. However, they yield CG configurations observed in the all-atom simulations with known probabilities, which allows reweighting.
To allow full sampling of CG phase space and include CG configurations not observed in the AA chignolin simulations, we also developed a CG model by training a normalizing flow. This model reproduces the internal degrees of freedom (bonds, angles, and torsions) of the CG representation of chignolin observed during the AA simulations. Details for normalizing flows are identical to those described for sidechain backmappings, except that we instead use 5 blocks of masked autoregressive rational quadratic spline flows. To enable learning internal coordinates only, we treat sidechain beads as bonded to beta carbons. We train the CG flow model for 100 epochs with a batch size of 256 and 10% of configurations reserved for validation. To demonstrate successful training, marginal distributions of all CG degrees of freedom are shown in Fig. S1.†
2.7 Reweighting
To rigorously sample AA configurations in a specific thermodynamic ensemble and according to an AA potential energy function, reweighting of backmapped configurations is necessary. Generally, an average of a quantity X(r) that depends on configuration r under one ensemble may be written in terms of samples from another ensemble through reweighting | (1) |
 | (2) |
| 〈X〉1 = ∫XP1(r)dr | (3) |
| = ∫∫XP1(r)P1(R|r)dRdr | (4) |
 | (5) |
| = 〈Xw〉2 | (6) |
 | (7) |
 | (8) |
 | (9) |
In the above, it is interesting to consider the presence of the encoding, or CG mapping, probability P1(R|r) in w. Its presence derives from the necessity of writing P1(r) = ∫P1(r, R)dR. From Bayes' theorem, we can choose from P1(r, R) = P1(r)P1(R|r) or P1(r, R) = P1(R)P1(r|R). We have chosen the former due to our assumption that, typically, the potential energy, and hence the Boltzmann weight proportional to P1(r) in the AA ensemble, is known, along with some mapping, R = M(r), to the CG representation. If the CG representation is deterministic, however, P1(R|r) = δ(R − M(r)). While the typical choice in most coarse-graining schemes, this will make reweighting effectively impossible unless the backmapping is designed so that all configurations sampled through P2(r|R) map to the same CG configuration. If this is not the case, the delta function in the numerator will effectively always be zero for continuous degrees of freedom. If probabilistic backmappings are desired, the above motivates consideration of stochastic encodings during the training and implementation of CG models.
Practically, however, P1(R|r) may be chosen arbitrarily if a fixed CG mapping is provided. This follows from integrating out the R degrees of freedom in eqn (4). More appropriate choices will lead to improved weights and better use of generated configurations. In ref. 28, a uniform distribution was implicitly selected, as this yields a constant that need not be considered when reweighting unnormalized distributions. In this work, we will use delta functions for atoms already present in the CG representation, since these will be unchanged in the mapping or backmapping process, and Laplace distributions for sidechain beads. While an optimal choice for P1(R|r) is unclear, we hypothesize that P2(R|r) will perform well as it will correctly account for the distribution of M(r) observed when drawing from P2(r|R). We approximate P2(R|r) by fitting Laplace distributions to the deviations between the location of the CG bead being backmapped and the center of mass of sidechain samples over the entire dataset (Fig. S2†). Scale parameters (related to the variance) come from fitting for each residue type, while the center of the distributions of deviations are fixed to zero. This effectively acts to penalize configurations that deviate too significantly from the backmapped CG configuration.
Though it is not pursued here, we prove that reweightings are also possible through stochastic backmappings with unknown probability densities, as long as a probability may be assigned to the path used to generate a given configuration. This is the case in denoising diffusion models66 as well as stochastic normalizing flows.37 For these cases, it is useful to introduce an additional stochastic variable z representing the “noised” or transformed space of r. Following ref. 37, the backward and forward path probabilities, implicitly conditioned on CG configuration R, are given by Pb(r → z) and Pf(z → r). Their ratio is defined as
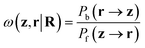 | (10) |
| 〈X〉1 = ∫∫∫XPb(r → z)P1(r)P1(R|r)dzdRdr | (11) |
 | (12) |
 | (13) |
| = 〈Xŵ〉2 | (14) |
 | (15) |
 | (16) |
 | (17) |
3 Results and discussion
3.1 Per-residue model performance
As shown in Fig. 2, trained models generate distributions of sidechain dihedral angles that match the training dataset. Models trained for all residue types produce probability densities for sidechain degrees of freedom that match similarly well. For the key dihedrals shown in Fig. 2, the maximum Jensen–Shannon (JS) divergence between training data and model-generated marginal distributions is 0.017 for dihedral 1 of tryptophan. The JS divergence ranges from 0 to ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 with lower values indicating more closely matching distributions. While this does not guarantee matching of higher-dimensional probability densities over all sidechain degrees of freedom, we expect the autoregressive nature of our model to capture such correlations. In later sections, we will test this further by examining energies of generated configurations, which are highly sensitive to correlations between degrees of freedom.
2 with lower values indicating more closely matching distributions. While this does not guarantee matching of higher-dimensional probability densities over all sidechain degrees of freedom, we expect the autoregressive nature of our model to capture such correlations. In later sections, we will test this further by examining energies of generated configurations, which are highly sensitive to correlations between degrees of freedom.
Crucially, Fig. 2 demonstrates that the local environment of a residue directly impacts the distribution of its degrees of freedom. To assess this, we draw many samples from probability distributions generated from a small set of randomly selected training configurations. Especially for charged residues, like aspartic acid, the resulting distributions are sharp, indicating a strong influence of the local environment on the predicted probability density. Bulkier residues, like tryptophan, demonstrate weaker dependence on the local environment, typically exhibiting broader distributions. Difficulties are most pronounced for long, flexible, sidechains, like lysine and arginine, due to the highly collective nature of dihedral angles in determining an orientation of the amine groups. While performance likely depends on the distance and nearest neighbors cutoffs employed (8 Å from the decoded CG bead), it may also suggest a limit to the number of degrees of freedom that may be backmapped successfully, with additional CG beads required to represent these residues.
Another measure of the sensitivity of a model to the input local environment is the distribution of center-of-mass CG bead locations of generated all-atom configurations. Fig. S2† shows distributions of deviations from the reference CG bead location in all three Cartesian coordinates, which are identical, as expected, revealing no bias based on the local orientational reference frame. Broader distributions of CG bead locations are observed for bulkier and more flexible sidechains. Interestingly, we observe the largest deviations for arginine, which also showed the most insensitivity of its backmapping distributions to the provided training examples. This corroborates our assessment that the model for arginine more poorly utilizes information concerning the local environment. Examination of these distributions is also key when considering the encoding distribution during reweighting. A tighter distribution is indicative of better adherence to the imposed deterministic encoding. Generated configurations are then expected to be of higher probability in the original ensemble.
3.2 Evaluation on protein test set
To assess the ability of our sidechain backmapping models to collectively generate entire AA protein structures from CG representations, we utilize the same protein test set of ref. 29, excluding the 4 proteins in the set with disulfide bonds. For consistency with the training set, the protein structures are prepared by the same methods as the training data. This involves addition of all missing atoms, including hydrogens, as well as energy minimization. For each test set structure, 100 independent AA configurations are sampled and compared to the reference structure used for generating the CG model input.Table 2 demonstrates that our model, trained on the energy minimized dataset, performs at a similar level to those developed in ref. 29 and 31 under the same evaluation metrics used by Jones et al.29 As expected, bond scores, which assess the percentage difference of backmapped bond lengths from the reference structure, exhibit excellent performance. Our model performs slightly better than that of Jones et al.,29 though this could be anticipated by our model's direct prediction of internal bond-angle-torsion coordinates instead of Cartesian. Our model performs better than that of Yang and Gómez-Bombarelli,31 which also uses internal coordinates but backmaps from a more minimal CG representation. A number of differences hinder comparisons to these other models with respect to all metrics. For instance, we backmap all hydrogens, whereas ref. 29 and 31 only backmap heavy atoms. As such, we also provide all metrics computed without consideration of hydrogens (or bonds involving hydrogens), which negligibly impacts our bond score.
| Bond score (%) (higher better) | Clash score (%) (lower better) | Diversity score (lower better) | |
|---|---|---|---|
| All atoms | 99.84 ± 0.04 | 12.30 ± 3.23 | −0.132 ± 0.013 |
| No hydrogens | 99.68 ± 0.08 | 2.52 ± 0.86 | −0.210 ± 0.018 |
The diversity score introduced by Jones et al.29 measures the variability (via root-mean-squared distance (RMSD) of all atoms) between generated structures compared to the RMSD of generated structures to the reference (see eqn (1)–(3) in ref. 29). Our model consistently produces negative values of this metric, which indicates greater RMSD between generated structures than their RMSD from the reference. While this is indicative of outstanding diversity in generated structures, it also implies that the average of the generated structures does not coincide with the reference. This might be expected due to prediction of BAT coordinates. Small shifts in torsions can lead to large shifts in Cartesian distances, and hence RMSD, between atoms, resulting in an enhanced diversity score.
Our clash score performance is significantly worse when including hydrogen atoms, but falls in between that of ref. 29 and 31 when considering only heavy atoms. The clash score measures the fraction of residues with any sidechain atoms overlapping (within 0.12 nm) with atoms of another sidechain. Such atoms lead to large energies and forces under standard molecular dynamics protein force fields. Improvement without hydrogens considered shows that most observed overlaps involve hydrogens. A larger clash score compared to ref. 29 is likely due to our use of BAT coordinates, though could also be associated with less expressive decoding distributions compared with denoising diffusion models. While internal coordinates significantly simplify application of bond constraints and yield reasonable distributions of bonds, angles, and torsions, both important for reweighting, their use in generative models can lead to unfavorable non-bonded interactions.39
In terms of computational time to generate new structures, Fig. S3† indicates that our overall model performs similarly to that developed by Jones et al.29 It is perhaps surprising that the normalizing flow architectures presented here are not faster than the denoising diffusion probabilistic models of ref. 29. However, we do observe 1–2 orders of magnitude speed-up for unconditional models, such as for glycine, which differ in that they do not include a geometric algebra attention layer to capture the local environment. Better optimizing the architecture for defining the local environment, or the size of the local environment considered, may be a route towards improved computational speed.
To assess the relevance of a model for producing structures consistent with a defined thermodynamic ensemble, it is important to also consider energies and forces in addition to the metrics defined above. Out of 2000 generated structures, 23 exhibited potential energies comparable to the energy minimized reference structures, with energies typically increasing with the number of residues in a protein (Fig. S4†). We explore the source of these high energies, broken down for each residue type, by comparing the median of the maximum force on a residue to both its median coordination (alpha carbons within 1 nm of the residue's alpha carbon), and distance from the reference CG bead (Fig. 3). It seems plausible that residues in more crowded environments might experience higher maximum forces upon backmapping. Surprisingly, Fig. 3 demonstrates that, even for residues that seem to ignore their local environment according to Fig. 2, there is little correlation between maximum force and coordination. Rather, residue types with large deviations from the CG bead reference also exhibit large forces. To account for differences in propensities of residues to exist on the interior or exterior of a protein, we also plot the median max force (over 100 backmapped samples) for each residue in all test set proteins against their coordination (Fig. S5†). No correlations arise, even across widely varying coordinations for the same residue type. These results point to a sensitivity of backmappings to their local environment. However, larger, more flexible molecules are more difficult to backmap. As a result, these residues are less precisely backmapped and deviate more from their reference CG bead locations, resulting in steric clashes regardless of their proximity to other residues.
3.3 Detailed study with chignolin: backmapping
For an in depth analysis of our backmapping models, we apply them to all-atom MD trajectories of chignolin (PDB ID 1UAO) in implicit solvent (see Methods) that have been mapped to their CG configurations. All model-generated distributions capture the dominant modes from MD simulation, but sample additional modes (Fig. 4 and S6†) that are observed in the full training dataset. The best match with simulation occurs for dihedral 1 of threonine residues, which shows strong orientational preferences due to hydrogen bonds. The JS divergence is 0.004 for both threonines, approximately an order of magnitude lower than the JS divergences of other residue sidechain dihedrals. In most cases, the generated configurations differ from the training dataset. To isolate the effect of changes in the backbone configuration, we have also generated configurations from a trajectory with the CG atoms (which here includes beta carbons) restrained to the native configuration. Restraints on all backbone atoms involved in the CG representation are tight to effectively keep the backbone atoms in a single configuration. As such, only the sidechain CG bead positions change in the restrained simulation. Fig. S7† demonstrates that there is little difference in the performance compared to backmapping of the unrestrained trajectory in Fig. 4 and S6.† Overall, however, backmapped configurations cover the phase space of dihedral angles sampled from MD simulations, which bodes well for reweighting. | ||
| Fig. 4 For representative residues in chignolin, distributions of the first and fourth dihedrals are compared between the MD simulation (blue), generated configurations from models trained on energy-minimized PDB structures (orange) or trajectory-trained models (red), and the training data set (black-dashed). See Fig. 2 for a description of sidechain dihedrals 1 and 4. Distributions for all residues are shown in Fig. S6.† | ||
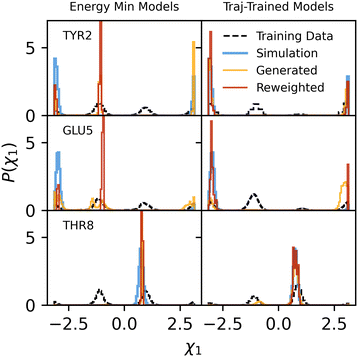
Fig. 5 reveals that total energy distributions of backmapped configurations also exhibit significant overlap. Unfavorable, high-energy configurations are most typically due to atomic overlaps that lead to large nonbonded (Lennard-Jones and electrostatic) energies. The observed bimodal distribution of nonbonded energies is likely due to localized distributions of torsion angles in sidechains—for two nearby sidechains, some combinations of key dihedral angles will lead to overlaps with near certainty, while others make overlaps nearly impossible. Overall, though, total energies are lower than observed in simulations. It is clear from Fig. 5 that this is due to too-favorable bonded energies offsetting unfavorable nonbonded (Lennard-Jones and electrostatic) energies. Energies of bonds, angles, and torsions are lower in generated configurations due to the use of energy-minimized training data. For comparison, the MD simulation data is used to train additional sidechain backmapping models for all residue types (excluding glycine) in chignolin. The same unconditional models trained on energy-minimized PDB data are used for glycine and N-terminal hydrogens. As expected, “trajectory-trained” models overlap nearly perfectly with the dihedral distributions from simulations shown in Fig. 4 and S6† (maximum JS divergence of 0.016 for dihedral 1 of TRP9). Since configurations from the temperature of interest, rather than energy minimized, are used to train these models, they also produce distributions of bond, angle, and torsion energies that overlap well with those from MD simulations (Fig. 5). Models trained on trajectories also produce lower nonbonded energies. We attribute this to the removal of spurious dihedral modes causing atomic overlaps, but note that trajectory-trained models are not transferable to proteins other than chignolin.
Notably, both models trained on energy-minimized data and chignolin trajectories produce populations of bonds and angles with very high energies. High energies for bonds and angles are possible due to normalizing flows leaving small amounts of probability density outside the set of favorable bond and angle values. This is inevitable since the flows are bijective and fixed to the domain [−π, π], while the Gaussian distributions used to model bonds and angles contain highly improbable regions outside this domain. For most bonds and angles, the probability of sampling a value outside the minimum or maximum of the training data set values is around 0.01%. While this seems small, the probability of sampling any bond or angle outside the favorable energy range, assuming independent sampling, is  , which grows quickly with the size of the sidechain. This explains the unexpectedly large populations of high bond and angle energies in Fig. 5. It also explains the increase in potential energy with protein size, though with longer sequences the probability of atomic overlaps will increase as well. Since distributions of bonds and angles are well-approximated by Gaussian distributions, our results suggest that these degrees of freedom should be excluded from normalizing flows, which may only be necessary for dihedral angles. For torsions, no high-energy population is observed due to the use of von Mises distributions, which keep all torsions within a fixed domain exactly matching their possible values.
, which grows quickly with the size of the sidechain. This explains the unexpectedly large populations of high bond and angle energies in Fig. 5. It also explains the increase in potential energy with protein size, though with longer sequences the probability of atomic overlaps will increase as well. Since distributions of bonds and angles are well-approximated by Gaussian distributions, our results suggest that these degrees of freedom should be excluded from normalizing flows, which may only be necessary for dihedral angles. For torsions, no high-energy population is observed due to the use of von Mises distributions, which keep all torsions within a fixed domain exactly matching their possible values.
3.4 Detailed study with chignolin: reweighting
Due to overlap of dihedral and potential energy distributions, we would expect reweighting to prove successful for chignolin. Around 40% and 65% of configurations generated by energy-minimized-trained and trajectory-trained models, respectively, have lower energy than the maximum energy observed in the MD simulation of chignolin. To assess reweighting, we require CG models. While the centroid representation force field of Py-Rosetta67 is a natural choice, we found that the phase space of CG configurations under this model overlaps poorly with that generated by the all-atom AMBER14SB force field. With little overlap in CG space, there is little hope of producing relevant AA structures, regardless of the performance of the backmapping.To ensure overlap of CG configurations, we examined three different methods for probabilistically generating CG configurations, which are described in Methods. Briefly, the first two “CG models” are based on clustering a reduced set of MD simulation configurations, which results in reduced coverage of CG phase space but ensures that all generated CG configurations are observed in the AA trajectory. We sample from clusters either proportional to their population or uniformly. As observed in Fig. 6a, the former preserves the locations and relative probabilities of free energy basins, while the latter flattens the free energy landscape. A normalizing flow trained to generate BAT coordinates of the CG representation of chignolin fully covers CG phase space and preserves most features of the free energy landscape shown in Fig. 6a, but produces some configurations that are highly unlikely in a MD simulation.
Successful reweighting of configurations generated through sequential sampling of the CG and backmapping distributions should recover the AA free energy landscape in the 2D space of end-to-end distance of terminal alpha carbons and root-mean-squared deviation (RMSD) from the folded structure (Fig. 6a). Using eqn (9), we can reweight generated configurations to the AA ensemble of the AMBER14SB force field at 300 K, even correcting relative sampling of coordinates only involving CG configurations, such as those shown in Fig. 6a. However, Table 3 demonstrates that, out of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 AA configurations generated by any combination of CG and backmapping models, very few effectively contribute to the calculation. In other words, only a small fraction of the weights computed from eqn (9) are appreciably greater than zero. This means that effectively only these configurations will contribute to any calculations of molecular properties. Well-converged results might require hundreds of independent samples all contributing significant weight, hence requiring on the order of hundreds of millions of generated configurations. This is surprising given that configurations generated through our protocols still exhibit substantial dihedral and potential energy overlap with the MD simulations (Fig. S8–S10†). While cluster-based CG sampling changes potential energy distributions by small amounts (Fig. S8 and S9†), sampling from the normalizing flow CG model results in higher potential energies (Fig. S10†), likely due to CG coordinates themselves not matching the CG model. Even so, energy-minimized-trained models generate 13% and the trajectory-trained models generate 21% of configurations below the maximum energy sampled in the MD simulation.
000 AA configurations generated by any combination of CG and backmapping models, very few effectively contribute to the calculation. In other words, only a small fraction of the weights computed from eqn (9) are appreciably greater than zero. This means that effectively only these configurations will contribute to any calculations of molecular properties. Well-converged results might require hundreds of independent samples all contributing significant weight, hence requiring on the order of hundreds of millions of generated configurations. This is surprising given that configurations generated through our protocols still exhibit substantial dihedral and potential energy overlap with the MD simulations (Fig. S8–S10†). While cluster-based CG sampling changes potential energy distributions by small amounts (Fig. S8 and S9†), sampling from the normalizing flow CG model results in higher potential energies (Fig. S10†), likely due to CG coordinates themselves not matching the CG model. Even so, energy-minimized-trained models generate 13% and the trajectory-trained models generate 21% of configurations below the maximum energy sampled in the MD simulation.
| CG model or residue | Energy min models | Traj-trained models |
|---|---|---|
| Full protein backmappings | ||
| Cluster by pop | 1.0 × 10−0.6 | 1.0 × 10−0.6 |
| Cluster uniform | 1.0 × 10−0.6 | 1.0 × 10−0.6 |
| Flow | 3.1 × 10−0.6 | 2.5 × 10−0.6 |
| Individual residue backmappings | ||
| GLY1 | 2.2 × 10−0.4 | 2.4 × 10−0.4 |
| TYR2 | 6.4 × 10−0.5 | 1.8 × 10−0.4 |
| ASP3 | 1.6 × 10−0.5 | 3.5 × 10−0.4 |
| PRO4 | 1.1 × 10−0.5 | 8.7 × 10−0.5 |
| GLU5 | 6.6 × 10−0.5 | 1.6 × 10−0.4 |
| THR6 | 2.5 × 10−0.5 | 3.0 × 10−0.4 |
| GLY7 | 1.7 × 10−0.4 | 8.0 × 10−0.4 |
| THR8 | 4.2 × 10−0.5 | 2.9 × 10−0.4 |
| TRP9 | 2.9 × 10−0.5 | 6.3 × 10−0.5 |
| GLY10 | 3.8 × 10−0.4 | 5.5 × 10−0.5 |
Clearly, overlap of potential energies is necessary for reweighting, but is not sufficient. Fig. 6b demonstrates that the unnormalized probability of the generated configurations, approximately provided by  , is not well-correlated with the probability in the desired ensemble P1(r) ∝ e−βU. Many low-energy configurations are assigned low probability in the generative ensemble, with the primary contribution coming from the backmapping probability P2(r|R). Indeed, low energy configurations can be assigned a wide range of probabilities by our generative models—nearly the full width of all assigned probabilities. As a result, the only contributing configurations are those that are high probability in the AA ensemble of the force field yet low probability in the generative ensemble, removing many low energy configurations.
, is not well-correlated with the probability in the desired ensemble P1(r) ∝ e−βU. Many low-energy configurations are assigned low probability in the generative ensemble, with the primary contribution coming from the backmapping probability P2(r|R). Indeed, low energy configurations can be assigned a wide range of probabilities by our generative models—nearly the full width of all assigned probabilities. As a result, the only contributing configurations are those that are high probability in the AA ensemble of the force field yet low probability in the generative ensemble, removing many low energy configurations.
Are low correlations between generated and target ensemble probabilities due to a lack of coordination between models for each sidechain? Despite the autoregressive nature of the backmapping, the independent training protocol lends plausibility to individual backmapping distributions being improperly conditioned on previously backmapped atoms. Fig. 7 displays dihedral distributions obtained by backmapping select residues of chignolin independently from a single energy minimized structure. Distributions for all other residues backmapped in the same way are shown in Fig. S11.† All other sidechain atoms except that being backmapped are present and all CG degrees of freedom are held fixed. Again we find that a larger phase space of dihedral angles are sampled by our models compared to AA TREMD simulations with all atoms restrained tightly to their energy minimized positions, except for those of the sidechain to be backmapped, which are restrained to their center-of-mass position (CG bead site). At least for the trajectory-trained models, however, reweighting of these dihedral distributions is possible and results in overlap with distributions from simulations (Fig. 7 and S11†). Reweighting improves JS divergences between trajectory-trained models and simulations from 0.41 to 0.08 for dihedral 1 of GLU5 and from 0.22 to 0.08 for dihedral 1 of TRP9, whereas no improvement is observed when reweighting models trained on energy-minimized data. Despite a 1–2 order of magnitude increase in effective fractions of contributing samples compared to backmapping an entire protein (Table 3), reweighting backmappings of individual residues in a static configuration remains challenging. Partly, this is due to additional difficulties associated with P1(R|r) when backmapping a single configuration. In this case, P2(R) is rigorously 1 since only a single CG configuration is used, meaning that P1(R|r) = δ(R − M(r)) exactly. We cannot choose this distribution arbitrarily since we only want to include those configurations consistent with the CG configuration to be decoded. We approximate this by using sharply peaked Laplace distributions for all residues, with the scale parameter set to 0.01. The resulting restraint is consistent with our use of a tight harmonic restraint on the CG bead position in our restrained MD simulations, but diminishes the number of useable backmapped samples.
While a sharper P1(R|r) does make reweighting more difficult, Fig. 8 shows that probabilities under the generative model still lack correlation with probabilities under the ensemble of interest (results for all residues in chignolin are shown in Fig. S12†). Lack of correlation for individual sidechain backmapping models propagates to backmappings of the full chignolin peptide, keeping fractions of effectively contributing samples low. This suggests that the largest improvements to reweighting full proteins will come from improving component sidechain models, particularly by ensuring that configurational probabilities assigned by the generative model correspond to Boltzmann weights in the ensemble of interest.
A related conclusion could be that reweighting is difficult because the phase spaces of model-generated and MD ensembles subtly lack overlap. Excellent overlap of bond, angle, and torsion energies with only partial overlap of non-bonded energies provides evidence for this interpretation (Fig. 5). While reasonable on their own, the specific combinations of bonds, angles, and torsions generated are not consistent with the MD ensemble since they do not produce low non-bonded energies. Due to the high dimensionality of configurational space, such subtle differences in probability densities are hard to diagnose. However, we would then expect fewer issues for smaller sidechains, such as threonine or aspartic acid. The lack of correlation observed in Fig. 8 and S12† suggests this is not the case and that future efforts should focus on better aligning configurational probabilities under the model with those of simulations.
4 Conclusions
We have presented a machine-learning approach for probabilistic backmapping of protein sidechains that may be applied to any sequence of canonical amino acids. The primary goal of the trained models is to generate structures consistent with the distribution of atomistic configurations conditioned on their local environment of both CG and AA particles. Direct access to learned conditional probabilities is a distinguishing feature of these models, as it allows for reweighting of generated structures. Reweighting allows for computation of average properties under other ensembles, such as those defined by different force fields at specific state conditions (e.g., temperatures or pressures). Classical protein force fields represent the current standard for understanding configurational ensembles of proteins at atomistic resolution. It is critical, then, to evaluate whether machine-learned models generate structures with distributions that match potential energies produced by molecular simulations utilizing modern protein force fields. To reach parity with MD or MC simulations, as well as enable reweighting of their generated structures, machine-learned models must demonstrate overlap in both configurational and potential energy space. Excitingly, our backmapping models do produce ensembles of configurations with significant potential energy overlap with molecular simulations of chignolin.However, our analysis demonstrates that generating low potential energy configurations across the entire configurational space is not enough to allow reweighting of AA configurations generated by machine-learned models. Such models must also correctly assign probabilities such that generated configurations are correctly ranked according to their probability in the desired ensemble. Previous sidechain backmapping models that exclude hydrogens29,31 have not been able to evaluate potential energies in the AA ensemble of popular modern atomistic force fields, and hence have not performed reweighting. In the work of Chennakesavalu et al.,28 reweighting of chignolin is performed after short stochastic dynamics runs to relax configurations, followed by empirical reweighting of configurations based on potential energy histograms. While this ensures overlap of potential energy distributions and large contributions from all generated configurations, it assumes that generation probabilities of all configurations within a histogram bin are equal. In our models, this approximation is not appropriate and may lead to incorrect weights because similar potential energy configurations display widely varying generative probabilities. While our models are competitive based on recently developed metrics for assessing backmapping performance (Table 2), and we observe significant potential energy overlap for small proteins, we have crucially demonstrated that the probabilities under the model must also correspond to the desired ensemble.
While they do not enable reweighting to modern protein force fields, our trained models may have utility in other applications. Though it remains to be investigated, these models could be used as highly collective MC move generators for protein sidechains. This might prove particularly useful for more efficiently performing alchemical mutations of residues. Alternatively, the conformational ensembles of small subsets of sidechains at protein–protein interfaces could be quickly explored with our methods. In these proposed applications, detailed balance, and hence proper sampling in the desired ensemble of interest, could be maintained due to the accessibility of generational probabilities. Though difficulties with reweighting suggest that MC acceptance rates will also be low, we plan to explore the use of our models within MC simulations in future work. Understanding how well-defined thermodynamic ensembles can be generated from machine-learned models is of vital importance for meaningfully incorporating these models into molecular simulations.
Data availability
Trained models, as well as code to create training data sets, train models, perform described analyses, and perform simulations is available at https://github.com/Monroe-Molecular-Simulation-Group/sidechain-decoding. This code makes use of a more general software package available at https://github.com/Monroe-Molecular-Simulation-Group/vae-mol-sim. Trajectories, as well as large training and analysis data sets, are available upon request.Author contributions
J. I. M. assumed all roles in performing this research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Materials Science and Engineering under Award Number DE-SC0024312. Computational resources were provided by the Arkansas High Performance Computing Center, which is funded through multiple National Science Foundation grants and the Arkansas Economic Development Commission.Notes and references
- W. G. Noid, J. Chem. Phys., 2013, 139, 090901 CrossRef CAS PubMed.
- M. S. Shell, Adv. Chem. Phys., 2016, 161, 395–441 CrossRef CAS.
- C. Peter and K. Kremer, Soft Matter, 2009, 5, 4357 RSC.
- A. E. Badaczewska-Dawid, A. Kolinski and S. Kmiecik, Comput. Struct. Biotechnol. J., 2020, 18, 162–176 CrossRef CAS PubMed.
- V. A. Harmandaris, N. P. Adhikari, N. F. A. van der Vegt and K. Kremer, Macromolecules, 2006, 39, 6708–6719 CrossRef CAS.
- T. A. Wassenaar, K. Pluhackova, R. A. Böckmann, S. J. Marrink and D. P. Tieleman, J. Chem. Theory Comput., 2014, 10, 676–690 CrossRef CAS PubMed.
- P. Bandyopadhyay, Chem. Phys. Lett., 2013, 556, 341–345 CrossRef CAS.
- E. Lyman, F. M. Ytreberg and D. M. Zuckerman, Phys. Rev. Lett., 2006, 96, 028105 CrossRef PubMed.
- E. Lyman and D. M. Zuckerman, J. Chem. Theory Comput., 2006, 2, 656–666 CrossRef CAS PubMed.
- Y. Liu, W. Pezeshkian, J. Barnoud, A. H. de Vries and S. J. Marrink, J. Chem. Theory Comput., 2020, 16, 5313–5322 CrossRef CAS PubMed.
- J. Spiriti and D. M. Zuckerman, J. Chem. Theory Comput., 2014, 10, 5161–5177 CrossRef CAS PubMed.
- W. G. Noid, J. Phys. Chem. B, 2023, 127, 4174–4207 CrossRef CAS PubMed.
- M. Chakraborty, C. Xu and A. D. White, J. Chem. Phys., 2018, 9 Search PubMed.
- B. E. Husic, N. E. Charron, D. Lemm, J. Wang, A. Pérez, M. Majewski, A. Krämer, Y. Chen, S. Olsson, G. de Fabritiis, F. Noé and C. Clementi, J. Chem. Phys., 2020, 153, 194101 CrossRef CAS PubMed.
- W. Wang and R. Gómez-Bombarelli, npj Comput. Mater., 2019, 5, 1–9 CrossRef.
- W. Wang, M. Xu, C. Cai, B. K. Miller, T. Smidt, Y. Wang, J. Tang and R. Gómez-Bombarelli, arXiv, 2022, preprint, arXiv:2201.12176 [physics], DOI:10.48550/arXiv.2201.12176.
- Y. An and S. A. Deshmukh, Chem. Commun., 2020, 56, 9312–9315 RSC.
- S. Hunkler, T. Lemke, C. Peter and O. Kukharenko, J. Chem. Phys., 2019, 151, 154102 CrossRef PubMed.
- W. Li, C. Burkhart, P. Polińska, V. Harmandaris and M. Doxastakis, J. Chem. Phys., 2020, 153, 041101 CrossRef CAS PubMed.
- T. D. Loeffler, H. Chan, B. Narayanan, M. J. Cherukara, S. Gray and S. K. R. S. Sankaranarayanan, J. Phys. Chem. B, 2018, 122, 7102–7110 CrossRef CAS PubMed.
- A. H. Mahmoud, M. Masters, S. J. Lee and M. A. Lill, J. Chem. Inf. Model., 2022, 62, 1602–1617 CrossRef CAS PubMed.
- J. Peng, C. Yuan, R. Ma and Z. Zhang, J. Chem. Theory Comput., 2019, 15, 3344–3353 CrossRef CAS PubMed.
- M. Stieffenhofer, T. Bereau and M. Wand, APL Mater., 2021, 9, 031107 CrossRef CAS.
- M. McPartlon and J. Xu, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2216438120 CrossRef CAS PubMed.
- M. Misiura, R. Shroff, R. Thyer and A. B. Kolomeisky, Proteins: Struct., Funct., Bioinf., 2022, 90, 1278–1290 CrossRef CAS PubMed.
- E. R. Crabtree, J. M. Bello-Rivas, A. L. Ferguson and I. G. Kevrekidis, Multiscale Model. Simul., 2023, 21, 1122–1146 CrossRef.
- S. Chennakesavalu and G. M. Rotskoff, J. Phys. Chem. B, 2024, 128, 2114–2123 CrossRef CAS PubMed.
- S. Chennakesavalu, D. J. Toomer and G. M. Rotskoff, J. Chem. Phys., 2023, 158, 124126 CrossRef CAS PubMed.
- M. S. Jones, K. Shmilovich and A. L. Ferguson, J. Chem. Theory Comput., 2023, 19, 7908–7923 CrossRef CAS PubMed.
- K. Shmilovich, M. Stieffenhofer, N. E. Charron and M. Hoffmann, J. Phys. Chem. A, 2022, 126, 9124–9139 CrossRef CAS PubMed.
- S. Yang and R. Gómez-Bombarelli, Chemically Transferable Generative Backmapping of Coarse-Grained Proteins, arXiv, 2023, preprint, arXiv:2303.01569 [cs.LG], DOI:10.48550/arXiv.2303.01569.
- S. Zheng, J. He, C. Liu, Y. Shi, Z. Lu, W. Feng, F. Ju, J. Wang, J. Zhu, Y. Min, H. Zhang, S. Tang, H. Hao, P. Jin, C. Chen, F. Noé, H. Liu and T.-Y. Liu, Towards Predicting Equilibrium Distributions for Molecular Systems with Deep Learning, arXiv, 2023, preprint, arXiv:2306.05445 [physics.chem-ph], DOI:10.48550/arXiv.2306.05445.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Science, 2019, 365, eaaw1147 CrossRef PubMed.
- G. Papamakarios, E. Nalisnick, D. J. Rezende, S. Mohamed and B. Lakshminarayanan, J. Mach. Learn. Res., 2021, 22, 1–64 Search PubMed.
- D. J. Rezende and S. Mohamed, arXiv, 2016, preprint, arXiv:1505.05770 [cs, stat], DOI:10.48550/arXiv.2002.02428.
- M. Gabrié, G. M. Rotskoff and E. Vanden-Eijnden, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2109420119 CrossRef PubMed.
- H. Wu, J. Köhler and F. Noé, arXiv, 2020, preprint, arXiv:2002.06707 [physics, stat], DOI:10.48550/arXiv.2002.06707.
- M. Invernizzi, A. Krämer, C. Clementi and F. Noé, J. Phys. Chem. Lett., 2022, 13, 11643–11649 CrossRef CAS PubMed.
- J. I. Monroe and V. K. Shen, J. Chem. Theory Comput., 2022, 18, 3622–3636 CrossRef CAS PubMed.
- M. Stieffenhofer, M. Wand and T. Bereau, Mach. Learn.: Sci. Technol., 2020, 1, 045014 Search PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, H. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- Y. Liu, M. Chen and G. Lin, A Diffusion Model for Generalized Transferable Protein Backmapping, arXiv, 2023, preprint, arXiv:2310.01768 [q-bio.QM], DOI:10.48550/arXiv.2310.01768.
- G. Xu, Q. Wang and J. Ma, Briefings Bioinf., 2022, 23, bbab529 CrossRef PubMed.
- A. Leaver-Fay, M. Tyka, S. M. Lewis, O. F. Lange, J. Thompson, R. Jacak, K. W. Kaufman, P. D. Renfrew, C. A. Smith, W. Sheffler, I. W. Davis, S. Cooper, A. Treuille, D. J. Mandell, F. Richter, Y.-E. A. Ban, S. J. Fleishman, J. E. Corn, D. E. Kim, S. Lyskov, M. Berrondo, S. Mentzer, Z. Popović, J. J. Havranek, J. Karanicolas, R. Das, J. Meiler, T. Kortemme, J. J. Gray, B. Kuhlman, D. Baker and P. Bradley, in Methods in Enzymology, ed. M. L. Johnson and L. Brand, Academic Press, 2011, vol. 487 of Computer Methods, Part C, pp. 545–574 Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/ Search PubMed.
- M. Spellings, Geometric Algebra Attention Networks for Small Point Clouds, arXiv, 2022, preprint, arXiv:2110.02393 [cs.LG], DOI:10.48550/arXiv.2110.02393.
- G. Papamakarios, T. Pavlakou and I. Murray, Masked Autoregressive Flow for Density Estimation, arXiv, 2018, preprint, arXiv:1705.07057 [cs, stat], DOI:10.48550/arXiv.1705.07057.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- J. V. Dillon, I. Langmore, D. Tran, E. Brevdo, S. Vasudevan, D. Moore, B. Patton, A. Alemi, M. Hoffman and R. A. Saurous, TensorFlow Distributions, arXiv, 2017, preprint, arXiv:1711.10604 [cs, stat], DOI:10.48550/arXiv.1711.10604.
- C. Durkan, A. Bekasov, I. Murray and G. Papamakarios, Neural Spline Flows, arXiv, 2019, preprint, arXiv:1906.04032 [cs, stat], DOI:10.48550/arXiv.1906.04032.
- M. Germain, K. Gregor, I. Murray and H. Larochelle, MADE: Masked Autoencoder for Distribution Estimation, arXiv, 2015, preprint, arXiv:1502.03509 [cs, stat], DOI:10.48550/arXiv.1502.03509.
- Monroe-Molecular-Simulation-Group, Monroe-Molecular-Simulation-Group/Vae-Mol-Sim: Initial Release – Version 0.1.0, Zenodo, 2024, https://www.zenodo.org/doi/10.5281/zenodo.14419199 Search PubMed.
- Monroe-Molecular-Simulation-Group, Monroe-Molecular-Simulation-Group/Sidechain-Decoding: Initial Release – Version 0.1.0, Zenodo, 2024, https://www.zenodo.org/doi/10.5281/zenodo.14419026 Search PubMed.
- Openmm/Pdbfixer, OpenMM, 2024, https://www.github.com/openmm/pdbfixer Search PubMed.
- P. Eastman, R. Galvelis, R. P. Peláez, C. R. A. Abreu, S. E. Farr, E. Gallicchio, A. Gorenko, M. M. Henry, F. Hu, J. Huang, A. Krämer, J. Michel, J. A. Mitchell, V. S. Pande, J. P. Rodrigues, J. Rodriguez-Guerra, A. C. Simmonett, S. Singh, J. Swails, P. Turner, Y. Wang, I. Zhang, J. D. Chodera, G. De Fabritiis and T. E. Markland, J. Phys. Chem. B, 2024, 128, 109–116 CrossRef CAS PubMed.
- D. P. Kingma and J. Ba, arXiv, 2017, preprint, arXiv:1412.6980 [cs], DOI:10.48550/arXiv.1412.6980.
- P. Eastman and V. S. Pande, J. Comput. Chem., 2010, 31, 1268–1272 CrossRef CAS PubMed.
- P. Eastman and V. Pande, Comput. Sci. Eng., 2010, 12, 34–39 CAS.
- M. S. Friedrichs, P. Eastman, V. Vaidyanathan, M. Houston, S. Legrand, A. L. Beberg, D. L. Ensign, C. M. Bruns and V. S. Pande, J. Comput. Chem., 2009, 30, 864–872 CrossRef CAS PubMed.
- J. Mongan, C. Simmerling, J. A. McCammon, D. A. Case and A. Onufriev, J. Chem. Theory Comput., 2007, 3, 156–169 CrossRef CAS PubMed.
- P. Eastman and V. S. Pande, J. Chem. Theory Comput., 2010, 6, 434–437 CrossRef CAS PubMed.
- J. D. Chodera and M. R. Shirts, J. Chem. Phys., 2011, 135, 194110 CrossRef PubMed.
- A. Rizzi, J. D. Chodera, L. N. Naden, P. Grinaway, K. A. Beauchamp, J. Fass, B. Rustenburg, G. Ross, D. W. H. Swenson and H. Bruce Macdonald, OpenMMTools v0.20.0, 2021, https://www.github.com/choderalab/openmmtools Search PubMed.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. Van der Plas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- J. Ho, A. Jain and P. Abbeel, Denoising Diffusion Probabilistic Models, arXiv, 2020, preprint, arXiv:2006.11239 [cs.LG], DOI:10.48550/arXiv.2006.11239.
- S. Chaudhury, S. Lyskov and J. J. Gray, Bioinformatics, 2010, 26, 689–691 CrossRef CAS PubMed.
- L. Kish, Survey Sampling, Wiley, New York, 1995 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional supporting figures. See DOI: https://doi.org/10.1039/d4me00198b |
| This journal is © The Royal Society of Chemistry 2025 |