A practical guide for the assay-dependent characterisation of irreversible inhibitors

Abstract

Irreversible targeted covalent inhibitors, in the past regarded as inappropriately reactive and toxic, have seen a recent resurgence in clinical interest. This paradigm shift is attributed to the exploitation of the two-step mechanism, in which a high affinity and selectivity (i.e., low K_I) scaffold binds the target and only then does a pendant low intrinsic reactivity warhead react with the target (moderate k_inact). This highlights the importance of evaluating inhibitors by deriving both their K_I and k_inact values. The development of methods to evaluate these inhibitors by accounting for their time-dependent nature has been crucial to the discovery of promising clinical candidates. Herein, we report all the practical kinetic methods available to date to derive k_inact and K_I values. These methods include direct observation of covalent modification, continuous assay (Kitz & Wilson) evaluation, and discontinuous incubation and pre-incubation time-dependent IC₅₀ assays. We also provide practical guidelines and examples for performing these assays, comparison of their utility, and perspectives for their extended applications. This review aims to provide clarity about the use of these methods for reporting complete inhibitor kinetic profiles, guiding irreversible drug development towards increased target affinity and selectivity, while modulating in vivo stability and on-target reactivity.

---

Introduction

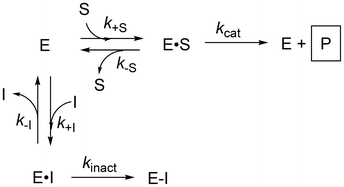
Inhibitors featuring an electrophilic moiety (warhead) that covalently reacts with a nucleophilic amino acid side chain on a protein of interest are commonly referred to as targeted covalent inhibitors (TCIs). TCIs are further divided into two common subclasses: irreversible and reversible, depending on the nature of the reaction of the warhead. Irreversible inhibitors, which are the focus of this review, distinctively offer several potential advantages over a traditional reversible non-covalent approach. Most notably, irreversibility enables prolonged on-target residence times and the possibility for rapid clearance of excess drug, as there is no need to maintain high drug concentrations in circulation once enough of the target is engaged.^1–3 Although irreversible inhibitors have been studied for many decades, they have been the topic of much debate in the medicinal chemistry community with concerns arising from irreversible off-target side-effects.⁴ However, recent advances in the development of warheads with low intrinsic reactivity coupled with structural scaffolds conferring high on-target affinity has led to many promising clinical candidates.^5–7 The scaffold acts as a target-selective platform for an otherwise weakly reactive but potentially non-specific electrophile, in the embodiment of a two-step inhibition mechanism (Fig. 1). This approach has led to a resurgence in the interest in irreversible inhibitors from industry and academia alike.⁴

Fig. 1 Two-step inhibition mechanism of irreversible covalent inhibitors, highlighting the properties influenced by inhibitor scaffold and warhead.

A crucial aspect of this paradigm shift has been the development of methods to rigorously evaluate these inhibitors, while accounting for the additional complexity of covalent reaction kinetics.^8–10 The inclusion of an irreversible reaction in the mechanism of action, reflected by rate constant k_inact, makes the inhibition time-dependent, in contrast to traditional non-covalent inhibition (i.e., rapid binding and reversible).¹¹ Methods that do not explicitly account for time-dependence, such as measuring an IC₅₀ value at a single time point and converting to a K_i value, are very popular among medicinal chemists at all levels of research, in part due to the historical popularity of reversible inhibition.¹² However, such methods can only be used for coarse screening of irreversible inhibitors as they do not provide a complete picture of efficiency, which is only obtained by measuring both the inactivation constant (K_I) and reaction rate constant (k_inact) with a given target.¹¹ In general, the relative potencies obtained in these types of screening campaigns reflect an overall efficiency ratio of k_inact/K_I and can still be useful for identifying hit compounds,¹³ but it should be noted that comparison of IC₅₀ values between different campaigns is often inappropriate as they can vary significantly depending on assay conditions (i.e., substrate concentrations and measurement time).^14,15 Moreover, if one does not measure the time dependence of inhibition, it is difficult to distinguish between an inhibitor that binds strongly and reacts slowly (low K_I, low k_inact) from one that binds weakly and reacts quickly (high K_I, high k_inact), the latter of which is not appropriate for drug development.

We must note however, that while k_inact does provide the best measure of warhead reactivity with a given target, this term includes factors other than intrinsic reactivity, such as orientation/distance relative to the protein's nucleophile, which are in turn influenced by initial non-covalent binding. Also, in the ESI we show that K_I = (k_−I + k_inact)/k_+I derives from the steady state approximation applied to Scheme 1, providing an inhibition constant that is a collection of rate constants, including k_inact. Therefore, K_I is not simply a measure of initial non-covalent binding affinity (which could be defined as K_I = k_−I/k_+I); however, it does include information about this binding and is the parameter that is most often used to assess ‘binding affinity’. In principle, these nuances are similar to the derivations and definitions of the Michaelis constant, K_M, and the catalytic constant, k_cat, that describe substrate binding and reaction with an enzyme. Nevertheless, individual characterization of these parameters provides invaluable information for guiding structure–activity relationships through optimization of binding and reactivity.

Scheme 1 Kinetic scheme for direct observation of protein modification. k_+I denotes the rate constant for inhibitor binding and k_−I denotes the rate constant for inhibitor dissociation.

The approach to develop irreversible inhibitors has resurged only recently, and since some techniques in this field have only very recently been developed, medicinal chemists may be less familiar with choosing, performing, and analyzing methods required to distinguish between the affinity and reactivity of irreversible inhibitors. Hence, in this article we describe in detail and practicality all the kinetic methods available to derive k_inact and K_I values from both continuous and discontinuous activity assays, along with all the equations for analysis and derivations thereof, included in the ESI.† We also provide practical guidelines for experimental conditions for performing these experiments, comparison of their utility, and perspectives for their extended application to reversible covalent inhibition as well as in vitro and in vivo models.

Kinetic evaluations are assay dependent

The kinetic evaluations that can be used to characterize an irreversible inhibitor will depend on the target activity assay employed, which in turn depends largely on the class of enzyme targeted (i.e., the type of reaction it catalyzes and hence the type of assays available) and the equipment and material on hand.^14,15 It is important to keep in mind that specific assay conditions such as buffer composition, co-solvents, source of recombinant enzyme, and the specific substrate used can influence kinetic evaluations for an inhibitor. Therefore, it is important to review these conditions carefully while assessing the literature or designing one's own assay for library screening.¹⁶

Theoretically, the most direct way to monitor the reaction between a target and an irreversible inhibitor is to quantify the amount of protein that is covalently modified by that inhibitor over time. This method is not dependent on enzymatic activity, but requires detection of the modified protein, in a nearly continuous fashion, typically by specialized mass spectrometry techniques such as RapidFire MS, as first demonstrated by Campuzano et al. in 2016.¹⁷ This technique, herein referred to as a ‘direct observation method’ is especially useful if there is no convenient activity assay available for the target of interest. In this case, quantifying the reaction with a covalent inhibitor is much easier than detecting the binding of a non-covalent inhibitor, as the mass increase accompanying covalent bond formation can be monitored more easily than a reversible non-covalent interaction. However, this method requires specialized and expensive instruments.

More commonly, activity assays that report the concentration of uninhibited enzyme, in a reaction mixture containing enzyme, inhibitor, and substrate, are used to indirectly monitor covalent modification over time. These assays can be continuous or discontinuous in nature, depending on the enzyme, substrate, and method of detection used.^9,15,18 Continuous assays rely on near simultaneous, real-time monitoring of product formation or substrate disappearance, typically on the scale of seconds. Enzymes that have substrates or reaction products that can be detected by absorbance or fluorescence spectrophotometry in a cuvette or microtiter plate, including proteases, hydrolases, and transaminases, lend themselves well to continuous assays.^19–21 However, in principle, any technique that allows rapid detection of product/substrate is applicable, and many have been recently developed as technology becomes more powerful. For example, another commonly targeted class of enzyme, kinases, can be monitored for their phosphorylation activity by rapid sampling coupled with mobility shift assay techniques, such as capillary electrophoresis,^22,23 or by using chelation-enhanced fluorescence to monitor phosphorylation in real-time.^24–26 Irreversible inhibitor evaluation by continuous detection in the simultaneous presence of inhibitor and substrate is often also referred to as ‘Kitz & Wilson evaluation’ after the authors who first demonstrated the kinetic treatment of an acetylcholinesterase inhibitor evaluated in this fashion, in 1964.²⁷ More robust mathematical treatments of this type of data were later shown by Tian & Tsou and Stone & Hofsteenge, in the 1980s.^28,29

If a continuous assay that allows enzyme activity to be monitored over a convenient time scale is not available, it may be too labour- and time-intensive to take many time-based aliquots that mimic ‘continuous’ conditions, in order to perform a Kitz & Wilson evaluation. In such case, discontinuous assays, also referred to as ‘end-point’ assays, may be much more practical to perform. In these assays, the enzymatic reaction is effectively quenched or is so slow that the measurement time does not significantly impact the reading, and the concentration of formed product/consumption of substrate is measured by any means available. The instrumentation options for these are vast, including but not limited to: absorbance, fluorescence, NMR, HPLC, and LC–MS. These types of assays are most effectively used in time-dependent IC₅₀ measurements and can be performed by either incubating enzyme, inhibitor, and substrate all together before measuring an end-point, or by pre-incubating the enzyme with inhibitor for a given period of time, before adding substrate and then measuring an end-point after an additional assay incubation time.^10,30 Herein these two techniques will be discussed individually as ‘incubation time-dependent IC₅₀s’ and ‘pre-incubation time-dependent IC₅₀s’, as their kinetic treatments are quite different. The evaluation of incubation time-dependent IC₅₀ values can be performed using what some refer to as the Krippendorff equation, derived in 2009.³⁰ However, pre-incubation IC₅₀ data could not be conveniently used to characterize k_inact and K_I values, until a recent method, EPIC-Fit, was developed in our lab, in 2024.¹⁰ This illustrates that advancements in methodology in this field are still in current progress. Historically, pre-incubation experiments required removal of inhibitor from the assay solution, either by jump dilution or dialysis, prior to measuring residual enzyme activity by either a continuous or discontinuous assay.¹¹ This requires the enzyme to be stable and monitorable after dilution or lengthy dialysis procedures and in general is highly impractical. The utility of this experiment in recent times has been limited to simple demonstrations of irreversibility (i.e., no recovered enzyme activity after a long incubation with at least one equivalent of inhibitor).^11,31 As such, this jump dilution/washout technique is beyond the scope of this article, which focuses on the most practical assay approaches being implemented today.

The key kinetic schemes and equations, expected data output, and treatment thereof are presented below for all of the aforementioned methods. The derivations of critical equations are included in the ESI.† We also discuss practical guidelines for designing these experiments to generate the most robust data for each evaluation method. Note that in this manuscript, for activity assay-based methods, we explicitly discuss equations for monitoring product formation, as this is commonplace. However, all of these methods can be applied while monitoring substrate consumption as well. The analogous equations for this approach can be found in the ESI.†

Direct observation methods

The irreversible formation of covalent enzyme-inhibitor complexes by TCIs makes them ideal candidates for direct evaluation by intact protein mass spectrometry. As this method requires only enzyme and inhibitor, without the need for a reporter substrate, it is the most straightforward method of kinetic analysis. Advances in mass spectrometry techniques, most notably RapidFire MS, have led to the development of high throughput systems for screening and kinetically evaluating TCIs by intact protein mass spectrometry. A comprehensive work flow for this method has been previously discussed by Campuzano et al.,¹⁷ and generally includes a rapid sampling technique coupled to an ESI LC-MS/MS analysis. In this method, a fixed concentration of enzyme is incubated with different concentrations of inhibitor (such that [I] ≫ [E]), and samples taken at different time points are rapidly analyzed by mass spectrometry to determine the proportion of covalently modified enzyme. As this assay is performed in the absence of a substrate, the rate of covalent modification depends directly on the degree of binding (K_I) and rate constant of inactivation (k_inact) of the inhibitor with the enzyme (Scheme 1).

The resulting mass spectrum is analyzed for the proportions of the unmodified enzyme and the enzyme-inhibitor adduct. As derived in the ESI,† the equation for the time-dependent concentration of modified enzyme indicates a mono-exponential association (increase) (eqn (S1)) whose first order rate constant (k_obs) shows hyperbolic dependence on inhibitor concentration (eqn (S2)).^11,32

[E–I] = [E]₀(1 − e^−k_obst) (S1)

The percentage of protein that has been modified can be determined by comparing the intensity of the peak for modified enzyme against the intensity of a standard control containing a known concentration of protein. By plotting the percentage of modified protein against time (Fig. 2A), the observed rate constant (k_obs) can be obtained for each specific enzyme concentration by fitting the curves to eqn (S1). The k_obs values can then be plotted against the inhibitor concentration (Fig. 2B) to obtain K_I and k_inact by using nonlinear regression to fit to eqn (S2).

Fig. 2 Direct observation of protein modification. (A) Modified enzyme is detected directly as a function of time, providing observed rate constants of modification (k_obs). (B) These modification rate constants show hyperbolic dependence on the concentration of inhibitor at which they were obtained, allowing for k_inact and K_I to be fitted. The slope of the linear portion of this curve (dashed red line) gives the ratio k_inact/K_I. The curves shown here were generated using k_inact = 1 min⁻¹ and K_I = 1 μM.

At very low inhibitor concentrations ([I] ≪ K_I), eqn (S2) reduces to and k_obs shows a linear dependence on [I] with an approximate slope of k_inact/K_I (Fig. 2B). This means that with only a few low concentrations, inhibitors can be screened and in the very least analyzed according to their k_inact/K_I values.

As the inhibitor concentration increases ([I] ≫ K_I), the value of k_obs plateaus at an asymptotic value equal to k_inact.¹¹ If an inhibitor that likely follows a two-step inactivation mechanism does not show a hyperbolic relationship between k_obs and [I], and is rather linear, this is likely due to the inhibitor being tested at concentrations that are lower than K_I. Ideally, inhibitors should be evaluated in concentrations in the range of (0.5 × K_I) ≤ [I] ≤ (5 × K_I) and data points should be collected at times ranging from before the first half-life, where t_1/2 = ln(2)/k_obs, to 3 times the half-life, for each inhibitor concentration. This allows sufficient time for both the curvature and upper plateau of the exponential curve to be well defined (see Fig. 2A), as well as ensuring that both the initial linear region and the upper plateau of the hyperbolic curve (see Fig. 2B) are clearly defined and accurately fitted. When fitting k_obs to eqn (S1), the value at time zero should be constrained to zero and the pre-exponential term can be constrained to 100% if the reaction between enzyme and inhibitor goes to completion.

Inhibitors having poor solubility may be very difficult to test at sufficiently high concentrations to achieve a clearly defined hyperbolic relationship between k_obs and [I]. In the rare case where the enzyme may be more soluble than the inhibitor, it may be possible to use a low, constant concentration of inhibitor and to increase the excess concentration of enzyme up to saturation, as reported by Hansen et al. for a series of KRAS^G12C inhibitors.³² Even under conditions where [E] ≫ [I], covalent modification still proceeds in a first-order fashion, and k_obs shows a hyperbolic dependence on [E], similar to the graph shown in Fig. 2B. (The kinetic treatment, equations, and guidelines for this type of analysis are essentially the same as described when enzyme concentration is fixed, where all the [I] terms in eqn (S1)–(S3) are replaced by [E] and vice versa.) While this is a clever technique, it is rarely applicable since it relies on the use of high concentrations of highly soluble enzyme.²⁸

Alternatively, the double reciprocal version of eqn (S2) can be fitted by linear regression with a few data points (eqn (S3)).

By plotting 1/k_obs against 1/[I], a linear relationship is obtained with a slope of K_I/k_inact, a y-intercept of 1/k_inact, and an x-intercept of −1/K_I (see Fig. S1†).¹¹ However, the linearization of eqn (S2) can often mask the fact that a data set does not demonstrate saturation (Fig. S2†). Fitting this kind of incomplete data set to eqn (S3) introduces the most error in the fitted values of parameters k_inact and K_I, as the data obtained at the highest and lowest inhibitor concentrations often disproportionately skew the line of best fit. The individual values of k_inact and K_I obtained by this method tend to be unreliable (see Table S1†), and this approach should therefore only be used as a last resort, keeping in mind that for an inhibitor with such low solubility and poor affinity (high K_I relative to its solubility limit), substantial structural modification will probably be required.

Despite being the most direct method of kinetic evaluation, intact protein mass spectrometry alone is not necessarily the most convenient characterization method.²⁸ A high throughput and time-dependent sampling system, like RapidFire, makes kinetic characterization by mass spectrometry much more convenient,^17,33 but requires expensive, specialized equipment. Therefore, this method is not usually the first choice of researchers in the academic field for kinetic evaluation and is often reserved for thorough analysis of promising clinical candidates or special cases in which an enzyme's inhibition kinetics are highly influenced by the substrate used in other types of assays (discussed below) due to enzymatic hysteresis.³⁴ However, as technology advances and costs of equipment decrease, we foresee this method becoming more accessible and widely used.

Continuous activity assays (Kitz & Wilson evaluation)

If an appropriate continuous activity assay exists for the enzyme of interest, a Kitz & Wilson evaluation is the most convenient approach available for complete characterization of an irreversible inhibitor. It allows for enzyme modification to be measured indirectly, in the simultaneous presence of both substrate and inhibitor, through the application of an enzyme activity assay (Scheme 2).

Scheme 2 Kinetic scheme for evaluation of irreversible inhibition with concomitant continuous activity assay (aka ‘Kitz & Wilson conditions’). k_+I denotes the rate constant for inhibitor binding and k_−I denotes the rate constant for inhibitor dissociation, while k_+S denotes the rate constant for substrate binding and k_−S denotes the rate constant for substrate dissociation.

In this approach, the activity assay is generally initiated by addition of enzyme to a solution of substrate and different concentrations of inhibitor, making sure to include a control reaction without inhibitor, and a blank reaction without enzyme. The blank can be subtracted to account for any background reaction of substrate. Formation of product is then observed over time from the reaction of enzyme with substrate. The rate of formation of product (P) during the assay is proportional to the concentration of free enzyme (E) remaining in the reaction mixture, that is .^9,11 Therefore, inactivation of the enzyme due to binding and reacting with the inhibitor is manifested as time-dependent decrease in the rate of product formation (i.e., a curve), relative to the uninhibited control, which reflects a decrease in free enzyme concentration over time as shown in Fig. 3A. Under conditions where [I] ≫ [E], the final slope for product formation will be zero (i.e., the enzyme is completely inhibited), and the product formation curves can be fitted to a mono-exponential equation. The derivation of the equations describing this time-dependent inactivation are shown in the ESI:†

[E]_cat(t) = [E]₀e^−k_obs·t (S4)

where

Fig. 3 Monitoring enzyme inactivation by a continuous activity assay. (A) The reaction of enzyme with substrate, in the presence of inhibitor, leads to time-dependent inactivation curves that can be fitted to provide rate constants of inactivation (k_obs). (B) These inactivation rate constants show hyperbolic dependence on the concentration of inhibitor at which they were obtained, allowing for k_inact and K_I to be fitted. The slope of the linear portion of this curve (dashed red line) gives the ratio k_inact/K_I. These curves were generated using k_inact = 1 min⁻¹, K_I = 1 μM, at [S] = 100 μM and K_M = 10 μM (α = 11).

These equations resemble those described above for direct observation methods. However, enzyme depletion/modification is not monitored directly; rather, inactivation is monitored indirectly by its effect on product formation. Inactivation can therefore be expressed in terms of product concentration observed over time, with the plateau reaching a maximum value of the ratio between the initial inhibited rate (V_I) and k_obs, (eqn (S6)).

In practice, initial rates are measured over the first 10% of conversion and it is very difficult to measure the instantaneous initial rate of inhibited reactions accurately, especially at high inhibitor concentrations where the enzyme is rapidly depleted. For these reasons, it is often impractical to include V_I as an independent constraint for the fitting of each reaction curve, and this constraint is commonly removed, allowing the final plateau to be fitted as an independent parameter. Empirically, this upper plateau is the simply the final product concentration after the reaction between the enzyme and inhibitor is complete.

[P]_I(t) = [P]_I(∞)·(1 − e^−k_obst) (S7)

This mono-exponential or ‘one phase’ association equation is commonly preprogrammed into fitting software such as GraphPad Prism (see ESI† for a plain text version). Fitting each reaction curve to this equation gives a k_obs value at each inhibitor concentration. Now, as described for the direct observation method, these k_obs values can be plotted against the inhibitor concentration, ideally revealing their hyperbolic relationship (Fig. 3B). The hyperbola can then be fitted to eqn (S5), to obtain k_inact and K_I^app, where K_I^app = K_I (1 + [S]/K_M).

Optionally, since a library of compounds is often tested under the same conditions (i.e., at the same [S]), it may be more convenient to plot k_obs against [I]/(1 + [S]/K_M). In this way the fitted parameter is directly equal to the K_I value since competition with the substrate has already been accounted for on the x-axis. Also, at [I] ≪ K_I^app, eqn (S5) simplifies to (see above). Therefore, the slope of the linear region of the curve, at low inhibitor concentrations, can be fitted to simple linear regression to provide an approximation of the ratio of k_inact/K_I^app (Fig. 3B). This analysis can be useful for confirming the ratio obtained from fitting the parameters individually. Hence, it is important to make sure that sufficiently low inhibitors concentrations (i.e. well below K_I^app) are tested as well.

If an inhibitor that likely follows a two-step inactivation mechanism shows a relationship between k_obs and [I] that is not hyperbolic, but rather linear, this is likely due to the inhibitor concentrations tested being much lower than the apparent K_I. As mentioned above, it is generally advisable to test inhibitor concentrations ranging from (0.5 × K_I^app) ≤ [I] ≤ (5 × K_I^app). Practically speaking, one may be limited in the concentrations that can be tested due to solubility constraints. In this case, it may be possible to lower the amount of competitive substrate used in the assay, which would also lower K_I^app, and hence the range of concentrations required. However, it should be noted that the uninhibited reaction must be strictly linear for the period of observation to ensure that any curvature in the inhibited reactions is only due to inhibition and not due to substrate depletion or enzyme degradation.⁸ This is generally accomplished by using [S] > (5 × K_M), but will also depend on the concentration of enzyme used and its k_cat value for its substrate. Ultimately, a balance is required between using enough enzyme and substrate to provide a linear region for a long duration, while still observing enough inhibition to be able to fit a plateau for each reaction reliably.

Ideally, each inhibited enzyme reaction should be run for at least three half-lives of the reaction, as described above for direct observation methods. However, for higher [I], this plateau may be reached very quickly, within a minute or less. In this case it can be difficult to fit these data sets that comprise many data points on the final upper plateau, and relatively few data points over the initial period where the reaction is still taking place. Statistically this resembles a straight line more than an exponential curve, which may result in the fitting providing artefactually low k_obs values. For these kinetic runs it may be necessary to truncate the dataset to a pre-determined number of half-lives (e.g., 3) and refit the data, such that the plateau is not overemphasized in the fitting. This will often also correlate with a better fitting overall (i.e., higher R² value).

As a last resort, for the case of an ill-defined hyperbolic graph required for the final fitting, the data may be fit by linear regression to the double reciprocal version of eqn (S5), as described for the direct observation method. However, we must caution that this fitting method is subject to much higher error (see Fig. S1 and S2†), and it may be more reliable to simply use this inhibitor's k_inact/K_I ratio (derived from the slope of the linear region of the k_obsvs. [I] plot) as a measure of its relative potency for screening purposes. If worth pursing further, another evaluation method, such as direct observation or pre-incubation time-dependent IC₅₀s can be used, as these are performed, at least in part, in the absence of substrate and may allow for lower concentrations of inhibitor to be used.

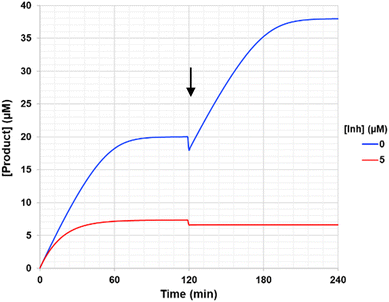
Interestingly, the availability of a continuous activity assay also allows for a quick, yet effective demonstration of irreversibility, referred to as a ‘substrate spike test’.³⁵ This is particularly useful when attempting to distinguish between irreversible inhibition and time-dependent reversible inhibition.³⁶ Only two reactions are required - a positive control (without inhibitor) and an inhibited reaction using [I] ≈ (5 × K_I^app) (i.e., a concentration that allows the upper plateau of the reaction progress curve to be established completely). Both reactions are run until the upper plateau is reached. In the positive control, this plateau is due to substrate depletion, whereas in the inhibited reaction, it is due to complete enzyme depletion. Additional substrate is then added to both reaction mixtures, such that its final concentration is the same as at the beginning of the assay, and the reactions are monitored again. The rate of the positive control should then rise to its previous initial rate, while the inhibited reaction would still show no activity (no increase in product signal) (Fig. 4). This can be contrasted to the case of reversible inhibition, where an increase in enzyme activity would also be observed, but to a lesser extent than the positive control. The positive control is crucial here to ensure that enzyme activity is not lost due to degradation.

Fig. 4 Simulated substrate spike test. Both the inhibited and uninhibited reactions are allowed to proceed until a clearly defined plateau is reached. Additional substrate is then added (arrow, 120 min) and the uninhibited reaction regains enzymatic activity while the inhibited reaction does not. These curves were generated using k_inact = 0.5 min⁻¹, K_I = 10 μM, at initial and final [S] = 20 μM and K_M = 5 μM (α = 5).

A Kitz & Wilson evaluation is the fastest, cheapest, and least materially consumptive method available, as it can provide k_inact and K_I values in just a few kinetic runs, with the same time, effort and material that would provide only a single IC₅₀ curve (see discontinuous assays, below). As such, when a continuous assay is available, the Kitz & Wilson method is highly recommended, especially for promising clinical candidates. But despite its obvious prowess, many inhibitors are still characterized using IC₅₀ values, even when a continuous assay is available.³⁷ This may be in part due to lack of knowledge about how to optimize conditions. Nevertheless, many examples of promising inhibitors evaluated in this way are available and may be used as reference or guides. These include the pivotal BTK inhibitor ibrutinib and its derivatives,³⁸ the TG2 inhibitor AA9,³⁹ and many SARS-CoV-2 main protease inhibitors.⁴⁰

Discontinuous (end-point) activity assays

In the common situation where a continuous activity assay is not available to measure enzymatic activity, it is much more labour intensive to measure rate constants of inactivation as shown in the preceding section. If the only assay available is a discontinuous one, measuring a rate constant would require taking several aliquots of reaction mixture at various times, quenching the reaction (if necessary) and then measuring the concentration of product formed, by any means available. This may also require a significant amount of material, depending on the sensitivity of the detection method. For these reasons, it is often deemed to be too impractical to measure rate constants by a discontinuous assay.

On the other hand, end-point assays are often used to generate IC₅₀ curves. In this experiment, the target enzyme is allowed to react with substrate and varied concentrations of inhibitor, and after a certain amount of time, the end-point product concentration is measured (Scheme 2). This approach is identical to that taken with reversible inhibitors and is probably the most commonly applied method for evaluation of inhibition in the drug discovery process. The IC₅₀ value measured in this way has been rigorously shown by Miyahisa et al. to be proportional to the specificity constant (k_inact/K_I ratio) of an irreversible inhibitor.¹³ This approach thus allows for the relative efficiencies of similar inhibitors to be compared to each other, within the same study. In this regard, it may be appropriate for the coarse screening (triage) of inhibitors in the earliest stages of drug discovery.⁴¹ Further, Miyahisa et al. have shown that the k_inact/K_I ratio of an unknown inhibitor can be determined from IC₅₀ curves obtained in the presence of varying concentrations of a known inhibitor (probe) in a competition experiment. However, IC₅₀ curves obtained at a single time point do not account for the time-dependence of the inhibition, and therefore they do not allow for the parameters of k_inact and K_I to be measured independently.

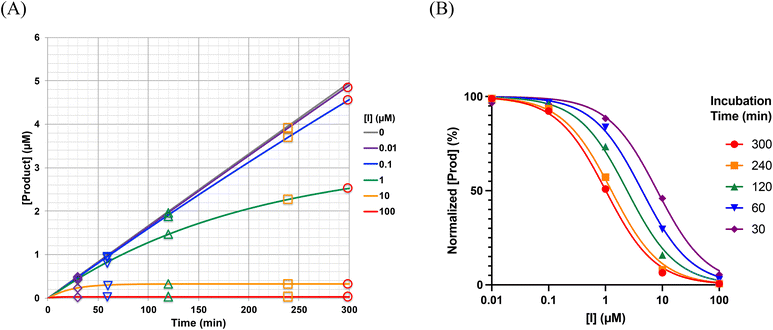
That being said, it is possible to measure IC₅₀ curves for a given inhibitor at several different incubation times, and to fit the ensemble of the time-dependent IC₅₀ data to arrive at independent values for k_inact and K_I. In general, this can be done by two different approaches, involving either ‘incubation’ end-point assays, or ‘pre-incubation’ end-point assays (see below). In an ‘incubation’ end-point assay, reactions are typically initiated by the addition of enzyme to a solution of inhibitor and substrate and allowed to proceed for a defined period of incubation, prior to quenching the reaction (if necessary) and determining the end-point product concentration. IC₅₀ curves can be measured at different incubation times, and the ensemble of time-dependent IC₅₀ data values can be fitted to provide k_inact and K_I.³⁰ In a ‘pre-incubation’ end-point assay, the enzyme is first allowed to react with inhibitor for a defined ‘pre-incubation’ period, after which the assay substrate is added and the assay reaction is allowed to proceed, until the end-point is measured. Recently we have shown the data from these pre-incubation time-dependent IC₅₀ experiments can also be fitted to provide values for k_inact and K_I.¹⁰

Incubation time-dependent IC₅₀ data. As mentioned above, an incubation end-point IC₅₀ curve is constructed by running a reaction of an enzyme in the presence of its substrate and various concentrations of a test inhibitor (Scheme 2). This will result in product formation profiles such as those simulated in Fig. 5A; however, these curves cannot be observed in a continuous manner. Rather, after a defined incubation time, the end-point concentration of formed product will be measured (symbols in Fig. 5A). These end-point concentrations are then normalised against those of the uninhibited reaction and plotted against log inhibitor concentration, resulting in incubation time-dependent end-point IC₅₀ curves (Fig. 5B). The inhibition of CYP450 enzymes is often characterised by incubation time-dependent IC₅₀ methods.³⁰

Fig. 5 A) Simulated reaction progress curves, with simultaneous inhibition, for the reaction of 2 nM enzyme (k_cat = 10 min⁻¹) with 50 μM substrate (K_M = 10 μM) in the presence of varying concentrations (0–100 μM) of inhibitor (k_inact = 0.3 min⁻¹, K_I = 10 μM). The symbols represent the endpoint product concentrations measured after varied times of incubation (30 min (diamond), 60 min (inverted triangle), 120 min (triangle), 240 min (square), 300 min (circle)). B) The endpoint concentrations from panel A were normalized against those of the uninhibited reaction and plotted against inhibitor concentration to generate standard IC₅₀ curves. The data points in panel B can be identified in panel A by the colour and shape of their symbols. Note how the measured IC₅₀ values shift to lower values at longer incubation times.

In general, the IC₅₀ value of an irreversible inhibitor shifts to a lower value over longer exposure to irreversible inhibition. The time dependency of IC₅₀ curves has been studied previously. It should be noted that while Maurer et al. derived a simple equation for how enzymatic reaction rate changes as a function of the concentration of an irreversible inhibitor and incubation time,⁴² this equation is not appropriate for application to most time-dependent IC₅₀ curves, which are typically constructed by measuring end-point product formation, rather than by measuring reaction rates. Instead, the rate of enzymatic product formation must be integrated up to the time of measurement, resulting in an equation that is more complex, but nevertheless very tractable. Krippendorff et al. first discussed this in 2009,³⁰ providing an equation that relates IC₅₀ values derived from end-point product formation to the incubation time at which they were measured (see ESI† for derivation).

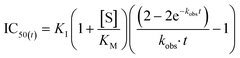Although eqn (S8) is an implicit equation, it can be entered into most fitting software, to allow the fitting of IC₅₀ values, measured at varied incubation times, to provide independent values for k_inact and K_I (see ESI† for a plain text version). By way of example, the fitting of the IC₅₀ values from Fig. 5B, according to eqn (S8), is shown in Fig. 6.

Fig. 6 The IC₅₀ values from Fig. 5B were fitted to the implicit equation eqn (S8), using GraphPad prism.

Of note, the y-axis intercept of Fig. 6 (i.e. the value of IC₅₀ at infinitely short incubation times) is K_I^app, or K_I(1 + [S]/K_M). This can be shown by applying L'Hôpital's rule to determine the lower limit of eqn (S8) (see derivation of Eqn. S9, ESI†). The different panels of Fig. 7 also illustrate how the appearance of an IC₅₀vs. incubation time curve may vary, as a function of different values of k_inact and K_I. For example, the acuteness of these curves, or the degree of time-dependence, varies according to k_inact, while the absolute values of IC₅₀ (along the y-axis) scale linearly with K_I. From a practical point of view, we have found that it is important to measure IC₅₀ values at incubation times less than 10/k_inact, where IC₅₀ values increase markedly, in order to ensure convergence during the fitting process.

Fig. 7 Effect of k_inact and K_I on the incubation time-dependency of IC₅₀ values. These simulated curves were generated using the values of k_inact indicated in the legend, at K_I values of (A) 10 μM, and (B) 0.1 μM, for [S] = 100 μM and K_M = 10 μM (α = 11). It is evident that the y-axis scales linearly with K_I, while the acuteness of the curves depends on k_inact.

Pre-incubation time-dependent IC₅₀ data. In practice, IC₅₀ values are often measured according to a pre-defined protocol, in which the concentrations of enzyme and substrate are fixed, as is the ‘incubation’ time of the assay, after which end-point product concentrations are measured. When such a standard protocol exists, the time-dependence of inhibition is often interrogated by adding an additional ‘pre-incubation’ phase to this experiment, in which the enzyme is allowed to react with the inhibitor, prior to the addition of substrate, for varied periods of time. After this initial ‘pre-incubation’ phase, assay substrate is added, and the standard activity assay is performed, ultimately leading to end-point product measurements. Scheme 3 represents the biphasic nature of this experiment, essentially combining the experimental conditions of Scheme 1 during the pre-incubation phase, and the experimental conditions of Scheme 2 during the incubation phase.

Scheme 3 Kinetic scheme for a biphasic ‘pre-incubation’ experiment. During the first phase (‘pre-incubation’), enzyme is incubated with inhibitor alone. The addition of substrate initiates the second phase (‘incubation’), during which enzyme reacts with either substrate or inhibitor.

When a standard activity assay to be applied during the incubation phase has been highly optimised, or automated, or will be used in high-throughput applications, one may not want to alter the time component of the assay conditions. Rather, it may be preferable to probe the time-dependence of inhibition by performing pre-incubation time-dependent IC₅₀ experiments, by simply adding a variable pre-incubation phase before the standard incubation assay. Many kinase inhibitors are characterised by this approach, with varied pre-incubation periods added before the addition of substrate and detection of product, such as phosphorylated peptide or ADP.^41,43

However, the biphasic nature of this experiment (Scheme 3) makes it impossible to apply a single equation to relate IC₅₀ values to k_inact or K_I. This is illustrated more explicitly in Fig. 8. During the pre-incubation phase (e.g. 20 min in Fig. 8A), enzyme reacts rapidly with inhibitor, in the absence of substrate, consuming both enzyme and inhibitor according to their relative concentrations and the resulting rate of inactivation. Then substrate is added, resulting in a slight dilution of both enzyme and inhibitor. This initiates the incubation phase, during which enzyme continues to be inactivated by inhibitor, but more slowly, as the reaction of enzyme with inhibitor is now in competition with the reaction of enzyme with substrate. The latter reaction results in the formation of product, which is ultimately measured as an end-point value at the end of the incubation phase (e.g. 20 min later, as shown by the circles in Fig. 8A).

Fig. 8 A) Simulated reaction progress curves, for the pre-incubation of 2 nM enzyme with varying concentrations (0.1–10 μM) of inhibitor (k_inact = 0.3 min⁻¹, K_I = 10 μM) for 20 min, followed by the addition of 50 μM substrate (k_cat = 10 min⁻¹, K_M = 10 μM). The orange circles represent the end-point product concentrations measured after an additional 20 min of incubation, representing a typical standard activity assay. B) End-point product concentrations are then normalized against those of the uninhibited reaction and plotted against inhibitor concentration to generate IC₅₀ curves, as a function of varied pre-incubation times. The orange data points in panel B are those shown in panel A, at a pre-incubation time of 20 min. Note how the measured IC₅₀ values shift to lower values at longer pre-incubation times.

We have recently shown that this biphasic process can be simulated numerically,¹⁰ by first dividing the different phases into fine time periods, and then calculating, for each of those time periods, the ‘instantaneous’ changes in the concentrations of inhibitor, enzyme, substrate and product according to their differential equations (Table S2, ESI†). These calculations are based on known experimental parameters of the assay, including enzyme concentration, substrate concentration, their k_cat and K_M values, and the dilution resulting from addition of substrate. These calculations also include the concentration of inhibitor and estimated values of k_inact and K_I. At the end of each finely divided time-period, new concentrations can be calculated, based on the instantaneous change of each species over that time period. These calculations are then repeated iteratively, up to the final end-point, at which the product concentration at the end of the incubation time is reported (see ESI† for the code that accomplishes this numerical modelling). This final predicted end-point value can then be compared to the measured experimental value, recorded in the pre-incubation time-dependent IC₅₀ data set. This simulation, calculation and comparison can then be performed for every data point, in multiple IC₅₀ data sets, measured at varied pre-incubation times. A difference (residual) can then be calculated, between each observed product concentration data point and the corresponding concentration that was predicted according to the estimated k_inact and K_I values. The sum of the squares of the residuals can then be minimised, by modifying the values of k_inact and K_I. In this way, k_inact and K_I can be fitted globally, to the ensemble of the pre-incubation time-dependent IC₅₀ data points, by least-squares regression. This entire simulation and fitting process has been embodied in a Microsoft Excel spreadsheet driven by macros (see ESI†), and in a Python-coded algorithm, both of which are freely available.¹⁰

The IC₅₀ data sets used as input for the EPIC-Fit method typically cover a broad range of inhibitor concentrations (e.g. 12 concentrations corresponding to 3-fold serial dilution). On a practical note, we have found that successful fitting also requires data sets covering a wide range of pre-incubation times, over which the time-dependence of inhibition becomes obvious.¹⁰ Typically, if pre-incubation times can be varied from zero, to 1/k_inact, 2/k_inact and 5/k_inact, the IC₅₀ values will also vary by an order of magnitude, and the ensemble of data points will allow for robust fitting. Our EPIC-Fit spreadsheet also allows for initial estimates of k_inact and K_I to be adjusted manually, to determine the quality of fit, prior to launching least-squares regression. However, initial estimates of K_I = 1 μM and k_inact = 1 min⁻¹ are appropriate for many different irreversible inhibitors.³¹

Perspectives

In the drug development process it is likely that many or all of the techniques discussed above will have a role to play in the critical path to a clinical candidate.⁴⁴ While many drug development campaigns will employ similar techniques, determining which technique is most appropriate will depend largely on the type of enzyme (type of assay available) and properties of the inhibitor (i.e., solubility, intrinsic reactivity). Importantly, all types of assays (continuous, incubation and pre-incubation discontinuous, and direct observation) can now be used to determine discrete values for k_inact and K_I, due to recent advances in the field. Recently, we have also shown that each of these methods can provide precise, reliable, and consistent k_inact and K_I values when compared to each other.¹⁰

At the beginning of a campaign, when thousands of compounds are being screened, discontinuous IC₅₀ experiments, either incubation or pre-incubation, at one time point may be suitable for eliminating compounds above a certain threshold of potency in a given assay (i.e., IC₅₀ > 1 μM). Then, if a continuous assay is available, hit compounds may be tested to determine their k_inact/K_I ratios, using a few low inhibitor concentrations, to obtain general structure–activity relationship information and further narrow the search to compounds with high overall efficiency.^45,46

Top compounds should then be subjected to thorough measurement of their separate k_inact and K_I values, to identify pre-clinical leads. If a continuous assay is available, this can be performed easily by a Kitz & Wilson evaluation. However, if only discontinuous assays are available, the analysis of time-dependent IC₅₀ experiments should be performed. In most laboratories where these experiments are done by hand, the most convenient approach is to perform incubation time-dependent IC₅₀ experiments, and subsequent analysis by the Krippendorff equation (eqn (S8)), as it requires less material and labour than a pre-incubation experiment. However, in laboratories that may employ automated pre-defined assay protocols featuring optimised (fixed) incubation times, analysis of pre-incubation time-dependent IC₅₀ values, using EPIC-Fit, may be more appropriate. A pre-incubation experiment may also be more useful for lower solubility compounds or slow reacting compounds, as the IC₅₀ values resulting from this experiment will be lower due to the substrate-free pre-incubation phase.

While it is obvious that direct observation of protein modification is the most powerful and robust method of evaluation, as it directly provides k_inact and K_I values without requiring extensive assay optimization or quantities of material, this method is currently somewhat inaccessible to many academic and industrial laboratories, due to the high cost of instrumentation. We recommend this evaluation for late-stage clinical candidates, either for confirmation of kinetic parameters or if it is suspected that kinetics may be affected by assay interference or by enzymatic hysteresis in the presence of different substrates.³⁴ We must also note the caveat that the high concentrations of enzyme typically used in MS experiments are often orders of magnitude higher than those encountered in vivo. Further, the binding/reactivity information (i.e., inactivation and rate constants) obtained from these experiments may not translate directly to sufficient inhibition of biological activity, which should be validated in the early stages of drug discovery.

Irreversible inhibitors make up a large majority of covalent inhibitors on the market and in the literature, but in recent years time-dependent reversible covalent inhibitors, which react reversibly with their target, have been gaining much momentum as well.^47–49 The complete kinetic evaluation of these types of inhibitors is even more complicated due to an additional rate constant and multiple equilibria. In principle they can be screened in similar ways to irreversible inhibitors. While a Kitz & Wilson type of evaluation does exist for these types of inhibitors,⁸ no methods for the analysis of incubation or pre-incubation time-dependent IC₅₀ values to determine rate and equilibrium constants have yet been presented. With the emerging interest in this field, a need for developing evaluation methods for reversible covalent inhibitors is pertinent as well, especially as reversible inhibitors with long residence times could potentially be mistaken as irreversible.²⁴ We have ongoing projects that address this challenge, which will be presented in due course.

While significant advances have been made in deriving theoretical mathematical models for irreversible inhibitor evaluation, enzymatic assays that allow for convenient in cellulo monitoring of enzyme modification and/or activity are still underdeveloped for many key enzyme targets. Any continuous or discontinuous assay performed in cells can be used to derive k_inact and K_I values, by the methods discussed above, and would be more relevant to the enzyme's native biological environment (including protein–protein interactions) and native state (including conformation). In addition to characterizing inhibitors, determining protein re-synthesis rates can be crucial to the in vivo application of irreversible inhibitors. Unlike reversible inhibitors whose target engagement and dosing depends on bioavailability and clearance, for irreversible inhibitors the rate of target engagement and subsequent dosing requirements are dictated by C_max, k_inact, K_I, and target concentration (i.e., turnover rate, including biosynthesis and degradation). Knowing these values can help model dosing regimens that effectively inhibit the target at the lowest possible concentration, while still allowing for sufficient clearance to improve safety margins, as shown by Chaudhry.³

In conclusion, the field of irreversible inhibitors has seen many advancements in mathematical models and types of assays used to manifest them, in order to distinguish k_inact and K_I values. Today, both continuous and discontinuous assays, with or without substrate, with or without pre-incubation, can be used to monitor and kinetically evaluate irreversible protein inactivation. Given these extensive options, there is no need to limit inhibitor characterisation to simple IC₅₀ values, especially for advanced clinical candidates. We hope this review provides clarity and encouragement about the use of these methods, and supports a shift towards reporting the complete kinetic profiles of inhibitors.⁵⁰ Only with this complete knowledge can one guide drug design towards increased target affinity and selectivity (low K_I), while modulating intrinsic stability and on-target reactivity (k_inact) - the very approach that led to the paradigm shift in favour of irreversible inhibitors.

Data availability

No primary research results, software or code have been included and no genuine data were generated or analysed as part of this review. Simulated data are available upon request from the authors.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

J. W. K. thanks the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Canadian Institutes of Health Research (CIHR) for funding. L. K. M. thanks NSERC for a CGS-D Award.

References

1. T. A. Baillie, Targeted Covalent Inhibitors for Drug Design, Angew. Chem., Int. Ed. Engl., 2016, 55(43), 13408–13421.
2. R. A. Copeland, The drug–target residence time model: a 10-year retrospective, Nat. Rev. Drug Discovery, 2016, 15(2), 87–95.
3. C. Chaudhry, Mathematical Model for Covalent Proteolysis Targeting Chimeras: Thermodynamics and Kinetics Underlying Catalytic Efficiency, J. Med. Chem., 2023, 66(9), 6239–6250.
4. J. Singh, R. C. Petter, T. A. Baillie and A. Whitty, The resurgence of covalent drugs, Nat. Rev. Drug Discovery, 2011, 10(4), 307–317.
5. D. Schaefer and X. Cheng, Recent Advances in Covalent Drug Discovery, Pharmaceuticals, 2023, 16(5), 663.
6. N. Shindo and A. Ojida, Recent progress in covalent warheads for in vivo targeting of endogenous proteins, Bioorg. Med. Chem., 2021, 47, 116386.
7. L. Hillebrand, X. J. Liang, R. A. M. Serafim and M. Gehringer, Emerging and Re-emerging Warheads for Targeted Covalent Inhibitors: An Update, J. Med. Chem., 2024, 67(10), 7668–7758.
8. E. Mons, S. Roet, R. Q. Kim and M. P. C. Mulder, A Comprehensive Guide for Assessing Covalent Inhibition in Enzymatic Assays Illustrated with Kinetic Simulations, Curr. Protoc., 2022, 2(6), e419.
9. C. McWhirter, Kinetic mechanisms of covalent inhibition, Annual Reports in Medicinal Chemistry, Academic Press, 2021, pp. 1–31.
10. L. K. Mader and J. W. Keillor, Fitting of k_inact and K_I Values from Endpoint Pre-incubation IC₅₀ Data, ACS Med. Chem. Lett., 2024, 15, 731–738.
11. R. A. Copeland, Irreversible Enzyme Inactivators, Evaluation of Enzyme Inhibitors in Drug Discovey, John Wiley & Sons, 2013, pp. 345–382.
12. G. V. Paolini, R. A. Lyons and P. Laflin, How desirable are your IC50s? A way to enhance screening-based decision making, J. Biomol. Screening, 2010, 15(10), 1183–1193.
13. I. Miyahisa, T. Sameshima and M. S. Hixon, Rapid Determination of the Specificity Constant of Irreversible Inhibitors (kinact/KI) by Means of an Endpoint Competition Assay, Angew. Chem., Int. Ed., 2015, 54(47), 14099–14102.
14. R. A. Copeland, Assay Considerations for Compound Library Screening, Evaluation of Enzyme Inhibitors in Drug Discovery, John Wiley & Sons, 2013, pp. 123–168.
15. P. J. Tonge, Quantifying the Interactions between Biomolecules: Guidelines for Assay Design and Data Analysis, ACS Infect. Dis., 2019, 5(6), 796–808.
16. K. W. Hoyt, D. A. Urul, B. C. Ogboo, F. Wittlinger, S. A. Laufer, E. M. Schaefer, E. W. May and D. E. Heppner, Pitfalls and Considerations in Determining the Potency and Mutant Selectivity of Covalent Epidermal Growth Factor Receptor Inhibitors, J. Med. Chem., 2024, 67(1), 2–16.
17. I. D. G. Campuzano, T. San Miguel, T. Rowe, D. Onea, V. J. Cee, T. Arvedson and J. D. McCarter, High-Throughput Mass Spectrometric Analysis of Covalent Protein-Inhibitor Adducts for the Discovery of Irreversible Inhibitors: A Complete Workflow, J. Biomol. Screen., 2016, 21(2), 136–144.
18. C. Bénard and Y. Gibon, Measurement of Enzyme Activities and Optimization of Continuous and Discontinuous Assays, Curr. Protoc. Plant Biol., 2016, 1(2), 247–262.
19. E. Vuorinen, S. Valtonen, N. Hassan, R. Mahran, H. Habib, M. Malakoutikhah, K. Kopra and H. Härmä, Protease Substrate-Independent Universal Assay for Monitoring Digestion of Native Unmodified Proteins, Int. J. Mol. Sci., 2021, 22(12), 6362–6375.
20. R. J. Kazlauskas, Quantitative Assay of Hydrolases for Activity and Selectivity Using Color Changes, Enzyme Assays, Wiley VCH, 2005, pp. 15–39.
21. A. Leblanc, C. Gravel, J. Labelle and J. W. Keillor, Kinetic Studies of Guinea Pig Liver Transglutaminase Reveal a General-Base-Catalyzed Deacylation Mechanism, Biochemistry, 2001, 40(28), 8335–8342.
22. J. F. Dawson, M. P. Boland and C. F. Holmes, A capillary electrophoresis-based assay for protein kinases and protein phosphatases using peptide substrates, Anal. Biochem., 1994, 220(2), 340–345.
23. D. Perrin, C. Frémaux and A. Shutes, Capillary microfluidic electrophoretic mobility shift assays: application to enzymatic assays in drug discovery, Expert Opin. Drug Discovery, 2010, 5(1), 51–63.
24. M. Jin, B. A. Petronella, A. Cooke, M. Kadalbajoo, K. W. Siu, A. Kleinberg, E. W. May, P. C. Gokhale, R. Schulz, J. Kahler, M. A. Bittner, K. Foreman, J. A. Pachter, R. Wild, D. Epstein and M. J. Mulvihill, Discovery of Novel Insulin-Like Growth Factor-1 Receptor Inhibitors with Unique Time-Dependent Binding Kinetics, ACS Med. Chem. Lett., 2013, 4(7), 627–631.
25. X. Zhai, R. A. Ward, P. Doig and A. Argyrou, Insight into the Therapeutic Selectivity of the Irreversible EGFR Tyrosine Kinase Inhibitor Osimertinib through Enzyme Kinetic Studies, Biochemistry, 2020, 59(14), 1428–1441.
26. D. E. Heppner, F. Wittlinger, T. S. Beyett, T. Shaurova, D. A. Urul, B. Buckley, C. D. Pham, I. K. Schaeffner, B. Yang, B. C. Ogboo, E. W. May, E. M. Schaefer, M. J. Eck, S. A. Laufer and P. A. Hershberger, Structural Basis for Inhibition of Mutant EGFR with Lazertinib (YH25448), ACS Med. Chem. Lett., 2022, 13(12), 1856–1863.
27. R. Kitz and I. B. Wilson, Esters of Methanesulfonic Acid as Irreversible Inhibitors of Acetylcholinesterase, J. Biol. Chem., 1962, 237(10), 3245–3249.
28. W. X. Tian and C. L. Tsou, Determination of the rate constant of enzyme modification by measuring the substrate reaction in the presence of the modifier, Biochemistry, 1982, 21(5), 1028–1032.
29. S. R. Stone and J. Hofsteenge, Specificity of activated human protein C, Biochem. J., 1985, 230(2), 497–502.
30. B. F. Krippendorff, R. Neuhaus, P. Lienau, A. Reichel and W. Huisinga, Mechanism-based inhibition: deriving K(I) and k(inact) directly from time-dependent IC(50) values, J. Biomol. Screen., 2009, 14(8), 913–923.
31. R. A. Copeland, A. Basavapathruni, M. Moyer and M. P. Scott, Impact of enzyme concentration and residence time on apparent activity recovery in jump dilution analysis, Anal. Biochem., 2011, 416(2), 206–210.
32. R. Hansen, U. Peters, A. Babbar, Y. Chen, J. Feng, M. R. Janes, L. S. Li, P. Ren, Y. Liu and P. P. Zarrinkar, The reactivity-driven biochemical mechanism of covalent KRAS(G12C) inhibitors, Nat. Struct. Mol. Biol., 2018, 25(6), 454–462.
33. F. Pu, S. A. Ugrin, A. J. Radosevich, D. Chang-Yen, J. W. Sawicki, N. N. Talaty, N. L. Elsen and J. D. Williams, High-Throughput Intact Protein Analysis for Drug Discovery Using Infrared Matrix-Assisted Laser Desorption Electrospray Ionization Mass Spectrometry, Anal. Chem., 2022, 94(39), 13566–13574.
34. E. W. J. Gates, A. Prince-Hallée, Y. Heidari, A. Sedighi and J. W. Keillor, High-Affinity Fluorogenic Substrate for Tissue Transglutaminase Reveals Enzymatic Hysteresis, Biochemistry, 2023, 62(21), 3085–3095.
35. L. Mader, S. K. I. Watt, H. R. Iyer, L. Nguyen, H. Kaur and J. W. Keillor, The war on hTG2: warhead optimization in small molecule human tissue transglutaminase inhibitors, RSC Med. Chem., 2023, 14(2), 277–298.
36. R. A. Copeland, Slow Binding Inhibitors, Evaluation of Enzyme Inhibitors in Drug Discovery, John WIley & Sons, 2013, pp. 203–244.
37. C. Büchold, M. Hils, U. Gerlach, J. Weber, C. Pelzer, A. Heil, D. Aeschlimann and R. Pasternack, Features of ZED1227: The First-In-Class Tissue Transglutaminase Inhibitor Undergoing Clinical Evaluation for the Treatment of Celiac Disease, Cells, 2022, 11, 1667–1686.
38. M. Hopper, T. Gururaja, T. Kinoshita, J. P. Dean, R. J. Hill and A. Mongan, Relative Selectivity of Covalent Inhibitors Requires Assessment of Inactivation Kinetics and Cellular Occupancy: A Case Study of Ibrutinib and Acalabrutinib, J. Pharmacol. Exp. Ther., 2020, 372(3), 331–338.
39. A. Akbar, N. M. R. McNeil, M. R. Albert, V. Ta, G. Adhikary, K. Bourgeois, R. L. Eckert and J. W. Keillor, Structure-Activity Relationships of Potent, Targeted Covalent Inhibitors That Abolish Both the Transamidation and GTP Binding Activities of Human Tissue Transglutaminase, J. Med. Chem., 2017, 60(18), 7910–7927.
40. D. Yamane, S. Onitsuka, S. Re, H. Isogai, R. Hamada, T. Hiramoto, E. Kawanishi, K. Mizuguchi, N. Shindo and A. Ojida, Selective covalent targeting of SARS-CoV-2 main protease by enantiopure chlorofluoroacetamide, Chem. Sci., 2022, 13(10), 3027–3034.
41. A. Thorarensen, P. Balbo, M. E. Banker, R. M. Czerwinski, M. Kuhn, T. S. Maurer, J.-B. Telliez, F. Vincent and A. J. Wittwer, The advantages of describing covalent inhibitor in vitro potencies by IC50 at a fixed time point. IC50 determination of covalent inhibitors provides meaningful data to medicinal chemistry for SAR optimization, Bioorg. Med. Chem., 2021, 29, 115865.
42. T. S. Maurer, M. A. Tabrizi-Fard and H. L. Fung, Impact of mechanism-based enzyme inactivation on inhibitor potency: implications for rational drug discovery, J. Pharm. Sci., 2000, 89(11), 1404–1414.
43. M. Schröder and A. Chaikuad, Assessing reversible and irreversible binding effects of kinase covalent inhibitors through ADP-Glo assays, STAR Protoc., 2021, 2(3), 100717.
44. C. M. Harris, S. E. Foley, E. R. Goedken, M. Michalak, S. Murdock and N. S. Wilson, Merits and Pitfalls in the Characterization of Covalent Inhibitors of Bruton's Tyrosine Kinase, SLAS Discovery, 2018, 23(10), 1040–1050.
45. J. W. Keillor, N. Chabot, I. Roy, A. Mulani, O. Leogane and C. Pardin, Irreversible inhibitors of tissue transglutaminase, Adv. Enzymol. Relat. Areas Mol. Biol., 2011, 78, 415–447.
46. J. C. Powers, J. L. Asgian, Ö. D. Ekici and K. E. James, Irreversible Inhibitors of Serine, Cysteine, and Threonine Proteases, Chem. Rev., 2002, 102(12), 4639–4750.
47. T. D. Owens, K. A. Brameld, E. J. Verner, T. Ton, X. Li, J. Zhu, M. R. Masjedizadeh, J. M. Bradshaw, R. J. Hill, D. Tam, A. Bisconte, E. O. Kim, M. Francesco, Y. Xing, J. Shu, D. Karr, J. LaStant, D. Finkle, N. Loewenstein, H. Haberstock-Debic, M. J. Taylor, P. Nunn, C. L. Langrish and D. M. Goldstein, Discovery of Reversible Covalent Bruton's Tyrosine Kinase Inhibitors PRN473 and PRN1008 (Rilzabrutinib), J. Med. Chem., 2022, 65(7), 5300–5316.
48. Y. B. Kim, L. M. Kopcho, M. S. Kirby, L. G. Hamann, C. A. Weigelt, W. J. Metzler and J. Marcinkeviciene, Mechanism of Gly-Pro-pNA cleavage catalyzed by dipeptidyl peptidase-IV and its inhibition by saxagliptin (BMS-477118), Arch. Biochem. Biophys., 2006, 445(1), 9–18.
49. A. Y. Howe and S. Venkatraman, The Discovery and Development of Boceprevir: A Novel, First-generation Inhibitor of the Hepatitis C Virus NS3/4A Serine Protease, J. Clin. Transl. Hepatol., 2013, 1(1), 22–32.
50. D. E. Heppner, B. C. Ogboo, D. A. Urul, E. W. May, E. M. Schaefer, A. S. Murkin and M. Gehringer, Demystifying Functional Parameters for Irreversible Enzyme Inhibitors, J. Med. Chem., 2024, 67, 14693–14696.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4md00707g

---