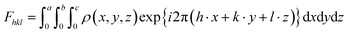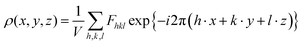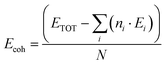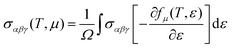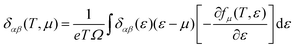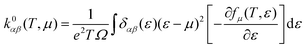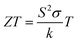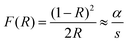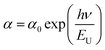DOI:
10.1039/D5MA00928F
(Paper)
Mater. Adv., 2025,
6, 9051-9063
Experimental optical analysis and DFT study of the electronic, thermoelectric and optical characteristics of a co-doped perovskite system
Received
19th August 2025
, Accepted 10th October 2025
First published on 24th October 2025
Abstract
Experimental and theoretical investigations of the electronic, thermoelectric and optical properties of Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic are presented via density functional theory (DFT) calculations performed using the generalized gradient approximation (GGA) with a plane-wave pseudopotential approach. This interesting combined analysis provides valuable insights into the potential of the material for advanced functional applications. The electronic structure analysis reveals that Ba0.85Sr0.15Ti0.85Zr0.15O3 exhibits a semiconducting behavior with a band gap energy of approximately 2.52 eV. The partial density of states analysis reveals that the O “p” orbitals dominate the valence band, while the Ti and Zr “d” orbitals primarily contribute to the conduction band. The thermoelectric properties examined between 300–1200 K show a consistently positive Seebeck coefficient, confirming p-type conduction. The material also demonstrates a notable dimensionless figure of merit at 300 K, indicating excellent thermoelectric performance near room temperature. These features suggest that Ba0.85Sr0.15Ti0.85Zr0.15O3 is a promising candidate for ambient-temperature thermoelectric energy conversion, optoelectronic devices, and multifunctional oxide-based electronics. Experimentally, UV-visible spectroscopy yielded a direct band gap of 2.419 eV and an Urbach energy of 0.784 eV, reflecting a moderate level of localized states within the band gap. The extinction coefficient spectrum reveals pronounced wavelength-dependent features, with enhanced absorption extending from the UV to the visible-red region (650–720 nm), indicating the formation of defect-related and polaronic states that effectively narrow the optical band gap.
1. Introduction
Barium titanate oxide (BaTiO3) stands out as a key ferroelectric oxide material widely recognized for its pivotal role in electronic technologies.1–3 BaTiO3 represents a fundamental and widely encountered motif in solid-state inorganic chemistry.1–3 This perovskite system exhibits excellent dielectric, piezoelectric, and ferroelectric properties, making it highly suitable for a wide range of applications, including electromechanical actuators, sensors, and ceramic capacitor dielectrics.4 Moreover, BaTiO3 holds promise in optoelectronic systems, particularly in photo-galvanic and energy-harvesting devices.5–7 Barium titanate undergoes a phase transition from a high-temperature cubic perovskite structure, characteristic of its paraelectric phase, to a ferroelectric tetragonal structure at approximately 130 °C.8 This transition is marked by pronounced dielectric anomalies, indicating the emergence of ferroelectricity accompanied by a macroscopic polarization oriented along the [001] crystallographic direction.9 Upon further cooling, BaTiO3 undergoes a polymorphic transition to an orthorhombic phase at around 0 °C, followed by a second transition to a rhombohedral phase at approximately −90 °C.10 The electronic structure of BaTiO3 has been extensively investigated through both experimental and theoretical approaches.11 Significant progress has been made in understanding its lattice dynamics and the fundamental origin of ferroelectricity, particularly through first-principles total energy calculations.11 In the literature, it has been demonstrated that Ti–O hybridization plays a crucial role in driving the ferroelectric instability in BaTiO3.12 However, discrepancies remain between the theoretical and experimental results, particularly concerning the calculated band gap, conduction band structure, and the effective mass of n-type carriers in the insulating phase. Accurately predicting the band gap of semiconductors and insulators remains a well-known challenge in ab initio calculations. Despite being well recognized, these limitations continue to pose significant challenges in ab initio band-gap engineering.11 Nevertheless, several theoretical efforts have been undertaken to overcome these issues.11 However, applying these advanced theoretical methods to practical calculations for materials, such as the BaTiO3 system, remains a significant challenge.11–14 As a result, many computational studies adopt adjustable parameters to approximate the experimentally observed band gaps more accurately.11–14 However, the introduction of a dopant within the BaTiO3 can drastically alter the properties of the material, making ab initio simulations considerably more complex and computationally demanding.14 Doping titanate perovskites like BaTiO3 with various transition metals or rare earth elements is a common practice, as it enables the tuning of a wide range of unique properties across diverse fields, including electrical, optical, structural, and mechanical domains.14 Recently, Caixia Li et al.15 conducted a detailed investigation of the structural, electronic and optical properties of A-site multi-element (Be2+, Mg2+, Ca2+, Sr2+, and Ra2+) doping of BaTiO3 ceramics using first-principles calculations based on density functional theory implemented in the Vienna ab initio Simulation Package. By calculating the band structures, density of states, dielectric functions, reflectivity, refractive indices, optical absorption coefficients, and extinction coefficients, the study demonstrated that A-site doping with Ca2+ or Sr2+ provides a theoretical basis for the development of high-frequency filters.15 In the same context, M. Maraj et al.13 have observed that doping BaTiO3 changed the optical behavior of this system, making the material more useful for optoelectronic applications. In the same context, Vu Tien Lam et al.14 demonstrated that the Zr doping of Ti leads to notable alterations in the band structure and density of states of BaTiO3. This modification results in the formation of new energy levels within the band gap, offering deeper insights into the electronic behavior of both pure and Zr-doped BaTiO3. These findings contribute to advancing the potential of the material for future electronic and optoelectronic device applications. Additionally, Haolei Shen et al.16 demonstrated that in Zr-doped BaTiO3, strong hybridization occurs not only between Ti-3d and O-2p orbitals but also between Zr-4d and O-2p orbitals. Despite these important insights, theoretical investigations into the underlying mechanisms of Zr-site doping in BaTiO3 remain relatively scarce. Within this framework, it is well established that doping significantly alters the crystal structure of ferroelectric systems, thereby playing a crucial role in determining the physical behavior of perovskite materials.16 Accordingly, Alveena Z. Khan et al.17 have examined the impact of crystal structure on the thermoelectric properties of n-type perovskites, CaTiO3, SrTiO3 and BaTiO3. Through first-principles investigations of the electrical and thermal transport properties, as well as the thermoelectric figure of merit (ZT), of SrTiO3 in its orthorhombic (Pnma), tetragonal (I4/mcm), and cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) phases, it was found that all three phases exhibit significant heat transport dominated by glass-like intra-band tunneling mechanisms.17 Moreover, it was found that the cubic and orthorhombic phases exhibit superior n-type electrical conductivity, primarily due to the weaker polar-optic phonon scattering and longer electron lifetimes compared to the tetragonal phase.17 Moreover, they find that materials with cubic and orthorhombic phases reveal superior n-type conductivity, since the significantly stronger polar-optic phonon scattering and shorter electron lifetimes in the materials with the tetragonal phase.17 Given its superior electrical properties, materials with the Pm
m) phases, it was found that all three phases exhibit significant heat transport dominated by glass-like intra-band tunneling mechanisms.17 Moreover, it was found that the cubic and orthorhombic phases exhibit superior n-type electrical conductivity, primarily due to the weaker polar-optic phonon scattering and longer electron lifetimes compared to the tetragonal phase.17 Moreover, they find that materials with cubic and orthorhombic phases reveal superior n-type conductivity, since the significantly stronger polar-optic phonon scattering and shorter electron lifetimes in the materials with the tetragonal phase.17 Given its superior electrical properties, materials with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase are expected to achieve a high-temperature ZT that is 25% greater than that of the I4/mcm phase. However, the highest ZT is predicted for the Pnma phase, owing to its advantageous electrical characteristics and low lattice thermal conductivity.
m phase are expected to achieve a high-temperature ZT that is 25% greater than that of the I4/mcm phase. However, the highest ZT is predicted for the Pnma phase, owing to its advantageous electrical characteristics and low lattice thermal conductivity.
The aim of the present study is to investigate the optical, electronic and thermoelectronic properties of the co-doped Ba0.85Sr0.15Ti0.85Zr0.15O3 system. Such a study is conducted based on a combination of experimental analysis and theoretical calculations via the density functional theory (DFT). UV-vis absorption spectroscopy is employed to experimentally investigate the optical properties of the material, enabling the determination of absorption and extinction spectra, band gap and Urbach energy using the Tauc and Urbach models. In addition, we present DFT-first-principles calculations of parameters governing the optical and electronic properties of the compound. Band gap, electrical and optical conductivities, total and partial density of states, Seebeck coefficient, and the thermoelectric figure of merit are determined. Given these considerations, investigating the electronic, optical, and thermoelectric properties of Ba0.85Sr0.15Ti0.85Zr0.15O3 is of significant technological relevance. The partial substitution of Ba2+/Ti4+ by Sr2+/Zr4+ is expected to tailor the band structure and enhance carrier transport, making this composition a promising candidate for multifunctional device applications. In particular, the tunable band gap and stable p-type semiconducting nature of Ba0.85Sr0.15Ti0.85Zr0.15O3 highlight its potential for ambient-temperature thermoelectric energy conversion, optoelectronic, and photovoltaic applications. Therefore, the present study aims to provide a comprehensive experimental and theoretical understanding of this material system to support its future integration into energy-efficient and multifunctional oxide-based technologies.
2. Experimental techniques and computational details
2.1. Experimental techniques
The compound Ba0.85Sr0.15Ti0.85Zr0.15O3 is prepared through the solid-state reaction technique, utilizing BaCO3, SrCO3, TiO2, and ZrO2 as the initial reactants. The specific composition Ba0.85Sr0.15Ti0.85Zr0.15O3 was selected because 15% Sr and Zr co-substitution has been reported to be an effective range for tuning the structural, optical, and electronic properties of BaTiO3-based perovskites while maintaining phase stability.18,19 Partial replacement of Ba2+ with Sr2+ reduces the tolerance factor and helps stabilize the tetragonal perovskite structure, whereas Zr4+ substitution at the Ti4+ site modifies lattice distortion and contributes to band gap engineering. Previous studies have shown that compositions within the 10–20% substitution range optimize dielectric, ferroelectric, and optical responses without inducing unwanted secondary phases or severely suppressing ferroelectricity.18,19 Therefore, the 15% doping level was chosen as a representative composition that balances structural stability and property enhancement, allowing a systematic investigation of the influence of co-doping on the optical, electronic, and optoelectronic performance of BaTiO3. After fixing the specific Sr and Zr doping concentration levels, the starting powders are precisely weighed and thoroughly mixed using an agate mortar to ensure uniformity. The resulting mixture is then subjected to calcination at 1150 °C for 15 hours, with a controlled heating rate of 5 °C min−1. Following calcination, the powder is pressed into pellets with an 8 mm diameter and sintered in air at 1470 °C for 4 hours to achieve the desired perovskite phase. The phase purity and crystal structure of the synthesized system were evaluated using X-ray diffraction (XRD) analysis, as detailed in our previously published work.20 Using the output refined XRD data in the G-Fourier program, we determined the two- and three-dimensional electron density maps of the prepared Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic. The optical properties of the studied system are obtained via UV-visible absorption spectroscopy by analyzing the absorption and extinction spectra over a large wavelength range from 200–800 nm.
2.2. Computational details
Theoretical study using DFT is proposed to investigate the electronic, transport, and thermoelectric characteristics of the Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic. Herein, the DFT calculations are achieved via the GGA approximation according to the hybrid method with full potential linearized-augmented plane wave + lo potential included in the Wien2k program.21 For the exchange–correlation potential, we employed the generalized gradient approximation PBE–GGA (Perdew–Burke–Ernzerhof).22 To modulate perfectly the electronic, transport, and thermoelectric responses of the Ba0.85Sr0.15Ti0.85Zr0.15O3 system, a 4 × 2 × 5 supercell that comprises 34 Ba and 6 Sr atoms on the A-sites (Ba0.85Sr0.15), 34 Ti and 6 Zr atoms on the B-sites (Ti0.85Zr0.15) and 120 oxygen atoms was utilized (Fig. 1). This perfectly reproduces the intended stoichiometry Ba0.85Sr0.15Ti0.85Zr0.15O3. Importantly, no oxygen vacancies were taken into account in the structure. The structural parameters employed as input in the calculations were derived from a Rietveld refinement of the experimental diffraction data. The optimized lattice constants are a = b = 4.02753 Å and c = 4.02273 Å. In the same context, the Tran–Blaha modified Becke–Johnson (DFT-mBJ) potential is used to determine the theoretical value of the band gap and compared with the deduced experimental value.23 The study of the transport characteristics of the Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic was performed via Boltzmann theory (semi-classical) through a WIEN2k platform using the Boltz Trap code.24 For this study, we have selected, in the irreducible Brillouin zone, a number of 1000 k-points. To ensure that the remaining force of every atom is fewer than 0.02 eV Å−1, each structure must undergo a complete relaxation. In this work, the structural optimization for Ba0.85Sr0.15Ti0.85Zr0.15O3 is performed by investigating the total energy as a function of the supercell volume, as presented in Fig. 2. The curve exhibits a clear parabolic behavior, characteristic of a stable crystalline phase where the total energy reaches a minimum at the equilibrium volume. This minimum corresponds to the most energetically favorable configuration of the lattice, indicating the optimized structural parameters obtained from the energy-volume optimization process.22,25 The symmetric nature of the curve around the minimum confirms the mechanical stability of the system and validates the convergence of total energy with respect to volume relaxation. The steep increase in total energy on both the compression and expansion sides signifies the high energetic cost associated with deviating from the equilibrium lattice constant, reflecting the resistance of the material to volume deformation. Such an energy-volume relationship is typically fitted using the Birch–Murnaghan or Murnaghan equation of state to accurately determine the equilibrium lattice constant, bulk modulus, and its pressure derivative.25 The obtained trend highlights that the partial substitution of Ba2+ by Sr2+ and Ti4+ by Zr4+ does not destabilize the perovskite framework, suggesting that Ba0.85Sr0.15Ti0.85Zr0.15O3 maintains a robust structural stability comparable to that of pure BaTiO3, while allowing tunability of its elastic and ferroelectric properties. In addition, the calculations resulted in the total energy being converged to 10−4 eV per atom as well.
 |
| | Fig. 1 4 × 2 × 5 supercell crystal structure of the Ba0.85Sr0.15Ti0.85Zr0.15O3 compound. | |
 |
| | Fig. 2 Variation in the total energy as a function of supercell volume. | |
3. Results and discussion
3.1. The energy-dispersive X-ray analysis
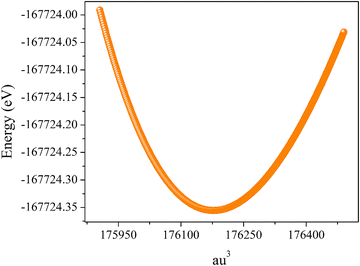
Energy-dispersive X-ray spectroscopy (EDX) is a powerful analytical technique widely employed to determine the elemental composition of materials, including complex oxide compounds. In this work, EDX spectroscopy is proposed to confirm that the cation ratios correspond to the nominal composition of Ba0.85Sr0.15Ti0.85Zr0.15O3. This spectroscopy allows for a direct, quantitative assessment of the relative amounts of each cation present in the material, providing experimental evidence that the synthesized compound maintains the intended stoichiometry. By comparing the measured elemental ratios with the theoretical values, we can validate the synthesis procedure and ensure the reliability of subsequent property measurements. For the prepared Ba0.85Sr0.15Ti0.85Zr0.15O3 perovskite, EDX results are shown in Fig. 3. The obtained EDX pattern of the studied Ba0.85Sr0.15Ti0.85Zr0.15O3 reveals the presence of peaks at specific positions. The observed peaks confirm the presence of all the used Ba, Sr, Ti, Zr, and O elements in the prepared structure and the good homogeneous mixing state of the powder. This examination confirms again that there are no missing components or external contaminants present during the synthesis procedure, thereby verifying the chemical purity of the sample. To confirm that the cation ratios match the nominal composition, a comprehensive overview of the atomic percent (atom%) and weight percent (weight%) of elements in Ba0.85Sr0.15Ti0.85Zr0.15O3 is summarized in Table 1. The atomic percent allows direct comparison of the cation ratios with the nominal stoichiometry, confirming whether the synthesis process achieved the intended chemical formula. The weight percent, on the other hand, reflects the mass contribution of each element and is particularly useful for validating the quantitative agreement with theoretical calculations or for comparison with complementary techniques, such as X-ray fluorescence. Together, the results shown in Table 1 verify the stoichiometry and ensure sample homogeneity.
 |
| | Fig. 3 Energy dispersive X-ray (EDX) spectrum of Ba0.85Sr0.15Ti0.85Zr0.15O3. | |
Table 1 Detailed elemental analysis by EDX for the studied compound
| Element |
Weight% |
Atom% |
| O |
20.81 |
58.97 |
| Ti |
17.56 |
17.63 |
| Sr |
5.50 |
3.39 |
| Zr |
5.78 |
3.49 |
| Ba |
50.35 |
16.52 |
| Total |
100.00 |
100.00 |
3.2. Electron density analysis
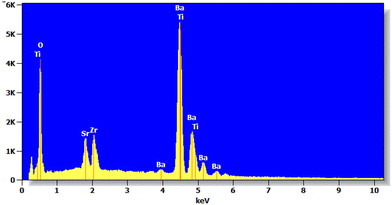
To get an idea about the areal electron density (ED) and the structural uniformity of the material, two-dimensional (2D) and special three-dimensional (3D) electron density maps of Ba0.85Sr0.15Ti0.85Zr0.15O3 were determined using the output refined XRD data in the G-Fourier program.26 In both planar (YZ-plane) and special (3D) electron density ρ(r) representation maps, the complex Fast Fourier Transform (FFT) available in the G-Fourier program and ρ(x, y, z) functions are related to each other by the following expressions:| |  | (1) |
| | 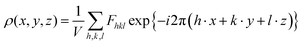 | (2) |
The parameters h, k, l and x, y, z represent the reciprocal lattice vector and the cell vector position, respectively. Fig. 4(a and b) show the planar two-dimensional and special three-dimensional Fourier maps for the ED of Ba0.85Sr0.15Ti0.85Zr0.15O3. 2D and 3D contours are produced using the Origin software from the Fourier map data of the Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic. In both plotted maps, the variation of the ED is represented by colors rising as a red–yellow–green–blue sequence. The presence of peak elevations and contours indicates an elevated ED gradient around Zr atoms compared to Ti atoms, which is related to the better atomic number of the Zr atom compared to the atomic number of Ti. The oxygen element, with fewer electrons, appears as green contours, representing a diffuse electron density. Along y/b and z/c (x = 0, y, and z), the 2D contours revealed that the crystal structure of Ba0.85Sr0.15Ti0.85Zr0.15O3 is symmetric in space, as there is no bifurcation in the ED gradient of the upper and lower bounds and both are found to overlap each other.
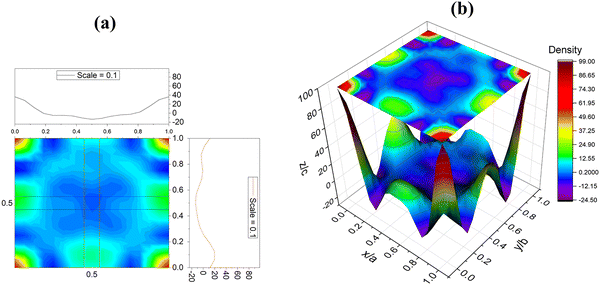 |
| | Fig. 4 2-Dimentional (2D) (a) and three-dimensional (3D). (b) Fourier map of the electron density of Ba0.85Sr0.15Ti0.85Zr0.15O3. | |
3.3. Electronic properties
To examine the electronic properties of Ba0.85Sr0.15Ti0.85Zr0.15O3, the structural stability was first assessed through phonon analysis and by evaluating the cohesive energy per atom (Ecoh), which was calculated using the following relation:27| | 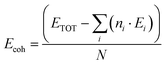 | (3) |
ETOT represents the total energy of the Ba0.85Sr0.15Ti0.85Zr0.15O3 supercell, ni denotes the atoms of the species “i” in a given supercell, and Ei is the free energy of the isolated atom of the ith species. The calculated cohesive energy was –2 eV per atom, indicating that the compound is thermodynamically stable. A negative cohesive energy suggests that the formation of the compound from its constituent atoms is energetically favorable, supporting its potential feasibility for experimental synthesis.
In this section, we also investigate the electronic band structure of the Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic using the PBE–GGA approach. Initially, the band structure was calculated within the framework of PBE–GGA. To obtain a more accurate description of the electronic structure and a better estimation of the band gap, we also performed calculations using the Tran–Blaha modified Becke–Johnson (TB-mBJ)23 potential in addition to PBE–GGA. Fig. 5(a and b) presents the calculated band structure of the Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic along the selected high-symmetry path R − Γ − X – M − Γ. Within the PBE–GGA framework, the obtained band gap is around 1.6 eV (Fig. 5(a)), which is significantly underestimated, as commonly observed in standard DFT calculations. However, when the Tran–Blaha modified Becke–Johnson (TB-mBJ) potential is employed, the band gap increases to 2.52 eV (Fig. 5(b)), confirming that the studied compound exhibits semiconducting behavior with a direct band gap. This result provides a more accurate description of the electronic structure. Moreover, the obtained value is in good agreement with the experimental data, highlighting the reliability of the TB-mBJ approach for predicting the electronic properties of perovskite oxides. Compared with bulk BaTiO3, which typically exhibits a wide indirect band gap of about 3.2 eV and thus limits its absorption mainly to the UV region, the co-doped Ba0.85Sr0.15Ti0.85Zr0.15O3 system demonstrates enhanced electronic and optical properties, making it a stronger candidate for optoelectronic applications, such as photovoltaic devices and photodetectors.28 The incorporation of Sr2+ and Zr4+ ions modifies the crystal lattice and electronic structure in a synergistic way. Substitution of Ba2+ by the smaller Sr2+ ion induces lattice contraction and local structural distortion, which in turn alters the Ti–O–Ti bond angles and Ti–O bond lengths. This modification increases orbital overlap between the Ti 3d and O 2p states, thereby narrowing the band gap and improving light absorption in the visible region.29 On the other hand, partial replacement of Ti4+ by the larger Zr4+ ion expands the lattice locally and introduces strain, which modifies the crystal field environment and redistributes the density of states near the band edges.29 These combined effects of Sr and Zr co-doping lower the effective band gap, enhance orbital hybridization, and increase the probability of electronic transitions under solar illumination. Consequently, Ba0.85Sr0.15Ti0.85Zr0.15O3 exhibits superior light-harvesting efficiency and improved charge carrier dynamics compared to undoped BaTiO3, making it a more efficient material for converting sunlight into electrical energy.
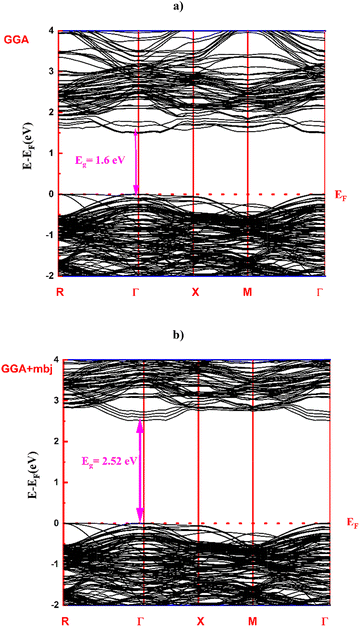 |
| | Fig. 5 Band structure of the Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic calculated using the GGA (a) as well as GGA + TB-mBJ (b) approximations. | |
To gain more information about the electronic properties of the prepared Ba0.85Sr0.15Ti0.85Zr0.15O3 ceramic, an analysis of the density of states (DOS), which aligns with the findings of the band structure, is reported in this work. This kind of analysis is employed to examine the quantity of available electronic states at various energy levels, permitting us to quantify the electronic levels per unit volume per unit energy. Explicitly, both partial and total density of states (PDOS and TDOS) of Ba0.85Sr0.15Ti0.85Zr0.15O3 are shown in Fig. 6. PDOS illustrates the contribution of subshells, including the p, s, and d orbitals, to the density of states of a specific atom, whereas the total density TDOS indicates the comprehensive density of states of the material, incorporating the contributions from each element within it. The PDOS projection revealed that the valence band is formed mainly from the O “p” orbitals, while the conduction band showed a predominant contribution from the Ti, Zr “d” orbitals, and a minor contribution from the O “p” orbitals. Interestingly, Ba and Sr did not contribute significantly to the maximum and the minimum of valence and conduction bands, respectively.
 |
| | Fig. 6 Total density of states (TDOS) (a) and partial density of states (PDOS) of the Ba (b), Sr (c), Ti (d), Zr (e) and O (f) elements calculated using the GGA + TB-mBJ approximation. | |
3.4. Thermoelectric properties
The thermoelectric performance of the investigated Ba0.85Sr0.15Ti0.85Zr0.15O3 oxide is evaluated using a semi-classical framework derived from the Boltzmann transport theory.24 Specifically, the Boltzmann transport equation is solved within the relaxation time approximation (RTA), as implemented in the Boltz–Trap computational package.24,30 This method enables the calculation of key transport parameters by assuming that the system remains close to thermal equilibrium and that charge carriers scatter with a characteristic, energy-independent relaxation time. To simplify the evaluation, the rigid band approximation is employed, which assumes that the electronic band structure remains unchanged with variations in carrier concentration. In addition, the constant scattering time approximation (CSTA) is used, assuming a fixed relaxation time across all energies. These combined assumptions simplified the estimation of critical thermoelectric parameters, including the Seebeck coefficient, electrical conductivity, and electronic contribution to thermal conductivity for the Ba0.85Sr0.15Ti0.85Zr0.15O3 perovskite. This approach provides a reliable prediction of thermoelectric behavior, particularly for identifying promising doping levels and temperature ranges for enhanced performance. The primary expressions for transport coefficients, such as the Seebeck coefficient, electrical conductivity, and electronic thermal conductivity, can be derived as functions of chemical potential (μ) and temperature by performing energy integrals of the transport distribution function (TDF) under the assumption of a zero external electric field.31 These integrals capture the contributions of all thermally accessible electronic states near the Fermi level and are weighted by their velocities and scattering probabilities. The calculations rely on the semi-classical Boltzmann transport formalism within the relaxation time approximation, ensuring that the carrier dynamics are accurately modeled under thermal equilibrium conditions. In this context, the temperature and chemical potential dependences of electrical conductivity, electronic part of the thermal conductivity and Seebeck coefficient tensors are given by the following relations32:| | 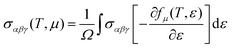 | (4) |
| | 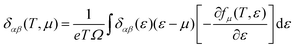 | (5) |
| | 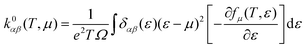 | (6) |
In this work, the temperature dependence of the Seebeck coefficient is calculated from the above-cited equations:32
| | | Sαβ(T,μ) = σαβ(T,μ)−1δαβ(T,μ) | (7) |
The function fμ(T,ε) is the Fermi–Dirac distribution. In this work, the carrier relaxation time (denoted as τ) is assumed constant, following the constant relaxation time approximation (CRTA).33 Under this assumption, both the electrical and thermal conductivities are directly proportional to τ, meaning their absolute values depend on the specific value chosen for τ. On the other hand, the Seebeck coefficient is independent of τ because τ cancels out during the derivation. This makes the Seebeck coefficient a particularly reliable parameter for comparing the thermoelectric performance of materials, even when τ is not precisely known.32
Fig. 7(a) shows the variation of electrical conductivity divided by relaxation time (σ/τ) versus temperature in the range between 300 K and 1200 K for the studied Ba0.85Sr0.15Ti0.85Zr0.15O3 sample. In this analysis, the relaxation time (τ) is assumed to be a constant, independent of temperature, following the CRTA.33 First, it can be observed that the conductivity σ/τ values of the studied system increase significantly with the temperature increase. At room temperature, the computed σ/τ value is approximately 3.44 × 1019 S m−1 s−1, which is more significant than the electrical conductivity of other oxide systems, such as Ba2FeMoO6, which reveals a low conductivity value of σ/τ = 7.12 × 109 S m−1 s−1.34 The obtained value of σ/τ is nearly close to the electrical conductivity value of the NaNbO3 perovskite, which exhibits a σ/τ of around 8.56 × 1018 S m−1 s−1.35 Over the studied temperature domain, the temperature increase is accompanied by a sharp rise in the conductivity σ/τ. This trend suggests enhanced carrier excitation and mobility with increasing temperature, which is characteristic of thermally activated conduction processes in semiconductor systems. Obviously, the increase in electrical conductivity σ/τ versus increasing temperature from 300 K to 1200 K can be attributed to the increased free charge carrier density and the improved hopping motion between potential barriers of the material. In assessing the thermoelectric performance of materials, the thermal conductivity divided by the relaxation time (k/τ) is a critical parameter as it directly affects the efficiency of energy conversion. In solids, heat is transported through two primary mechanisms: electronic thermal conductivity (ke), which arises from the motion of charge carriers (typically electrons or holes), and lattice thermal conductivity (kph), which results from the propagation of lattice vibrations or phonons. The total thermal conductivity is thus the sum of these two contributions:
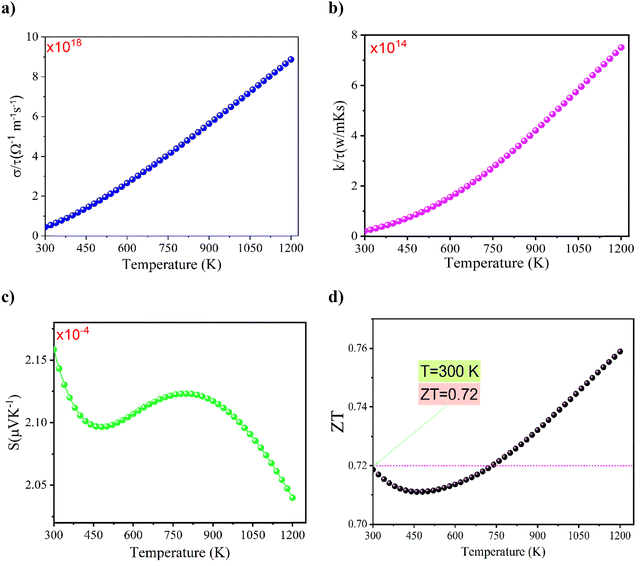 |
| | Fig. 7 Temperature dependence of σ/τ for the as-prepared Ba0.85Sr0.15Ti0.85Zr0.15O3 sample (a). Variation in the electronic contribution of thermal conductivity (k/τ) versus temperature for Ba0.85Sr0.15Ti0.85Zr0.15O3 (b). Temperature dependence of the Seebeck coefficient (c). Temperature dependence of the merit factor ZT for Ba0.85Sr0.15Ti0.85Zr0.15O3 (d). | |
Fig. 7(b) shows the variation in thermal conductivity (k/τ) versus temperature for the studied Ba0.85Sr0.15Ti0.85Zr0.15O3 system. In the literature, it has been found that thermal conductivity (k/τ) is sensitive to both photonic and electronic contributions, though in the Boltz–Trap code, the phonon part is ignored, and only the thermal conductivity linked to the electronic contribution is considered. Below 400 K, the thermal conductivity k/τ of the studied system shows a weak temperature dependence. After that, the reported results indicate that the thermal conductivity increased with rising temperature, consistent with the rise of the electrical component of the total thermal conductivity. Similar behavior has been observed in the Ba2FeMoO6 compound, in which the thermal conductivity k/τ attains a maximum value of around 1.44 × 1014 W (m K s)−1.34
To obtain information about the induced thermoelectric voltage effect in the prepared Ba0.85Sr0.15Ti0.85Zr0.15O3 material, the temperature dependence of the positive Seebeck coefficient (S) is plotted in Fig. 7(c) over a large temperature domain from 300 K to 1200 K. Over the studied temperature domain, it is observed that the Seebeck coefficient is affected by the temperature increase. In addition, our results indicate that the conduction phenomena within the studied system are governed by the contribution of holes, the charge carriers. Accordingly, it is demonstrated that the Seebeck coefficient S of the studied Ba0.85Sr0.15Ti0.85Zr0.15O3 system is positive, demonstrating p-type conduction in the material, where holes are the principal charge carriers. At around room temperature (T = 300 K), a low Seebeck coefficient value of S = 2.16 × 10−4 μV K−1 is observed, which is due to the high carrier concentration contribution, as often found for high band gap semiconductors. Dissimilar behavior is observed in the Ba2FeMoO6 oxide that reveals negative and elevated Seebeck coefficient values, indicating n-type conduction and the low carrier concentration of the material.34 Based on the calculated values of the Seebeck coefficient (S), electrical conductivity (σ/τ), and thermal conductivity (k/τ), we have determined the dimensionless figure of merit (ZT) for the investigated Ba0.85Sr0.15Ti0.85Zr0.15O3 oxide system. The temperature dependence of the ZT parameter is defined by the following relation:36,37
| | 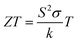 | (9) |
It quantitatively evaluates the thermoelectric efficiency of a material at a given temperature value. A higher ZT value indicates better potential for thermoelectric applications, as it reflects a favorable balance between the high power factor (S2σ) and low thermal conductivity.36,37 For the studied Ba0.85Sr0.15Ti0.85Zr0.15O3 oxide, the evolution of the merit factor ZT as a function of temperature is shown in Fig. 7(d) between 300 K and 1200 K. From this representation, it is possible to evaluate the performance of the material for TE applications. Versus the temperature increase, the plotted curve indicates that ZT increases significantly and reaches a maximum value of around 0.72. Such behavior is attributed to the enhanced Seebeck coefficient and the decreased thermal conductivity. The ZT elevated value indicates that this system can be considered a potential candidate for the fabrication of room-temperature thermoelectric devices.
3.5. Optical investigation
3.5.1. The UV-visible absorption analysis.
The optical characteristics of the synthesized Ba0.85Sr0.15Ti0.85Zr0.15O3 sample are systematically investigated through the UV-visible absorption spectroscopy at room temperature, as illustrated in Fig. 8(a). This analysis provides insights into the light absorption (α) behavior of the material, which is crucial for understanding its electronic structure and potential applicability in optoelectronic devices. The reported results show that Ba0.85Sr0.15Ti0.85Zr0.15O3 exhibits notable absorptions at 212, 342 and 640 nm. Explicitly, the absorption spectrum of Ba0.85Sr0.15Ti0.85Zr0.15O3 shows a steep absorption edge in the ultraviolet region, indicating a strong band-to-band electronic transition characteristic of perovskite oxides with wide band gaps. The high-energy absorption band values at shorter wavelengths reflect efficient UV light absorption within the studied material. Around 212 nm, the important “α” value can be associated with charge transfer transitions from the oxygen O2− 2p orbitals to Ti4+ or Zr4+ cations (O2− → Ti4+/Zr4+).38 It represents a strong metal–oxygen charge transfer and is commonly observed in perovskite oxides containing transition metals. The gradual decrease toward the visible region suggests a tailing effect related to localized defect states and co-doping-induced energy levels. Accordingly, the observed peak, around 342 nm, can be attributed to localized defect states or sub-bandgap transitions, likely involving oxygen vacancies or structural distortions in the perovskite lattice.39 It might also result from intermediate states between the valence and conduction bands, introduced by the substitution of Ba2+ with Sr2+ or Ti4+ with Zr4+, which slightly modifies the electronic structure. Around 640 nm, the observed lower-energy peak falls within the visible region and may be linked to the d–d transitions of transition metal ions (especially Ti3+ formed via oxygen vacancies or partial reduction), or possibly to defect-induced states within the band gap.40 It might also indicate localized electronic states that facilitate visible-light absorption, enhancing the photocatalytic or optoelectronic potential of the material. Compared with undoped BaTiO3, the spectrum indicates a slight red shift of the absorption edge, consistent with band gap narrowing due to Sr and Zr substitution.41 This shift, together with the enhanced sub-band-gap absorption, implies that the co-doped system possesses improved light-harvesting properties and modified electronic transitions, making it more favorable for optoelectronic and photocatalytic applications.41
 |
| | Fig. 8 Variation in the absorption coefficient (α) as a function of wavenumber (a). Variation in diffuse reflectance versus wavelength (b). Evolution of (F(R) hν) vs. photon energy (optical band via UV-vis spectrum study) (c). Variation in ln (F(R)) as a function of photon energy (d). | |
3.5.2. The Kubelka–Munk (K–M) technique.
To estimate the optical band gap (Eg) of the material, the Kubelka–Munk (K–M) function is applied, which relates the diffuse reflectance data to the absorption characteristics of the material through the following equation42:| | 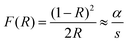 | (10) |
Here, F(R) represents the Kubelka–Munk function, which is proportional to the absorption coefficient (α), where R denotes the reflectance. The parameter “s” denotes the scattering coefficient. The modified Kubelka–Munk expression is given by [F(R)·hν]1/n (hν is the photon energy and n is a parameter that depends on the nature of the electronic transition).43 For the studied system, the diffuse reflectance spectrum, which is used to extract the experimental value of the gap energy, is shown in Fig. 8(b). The measurement is recorded over the wavelength range of 200–800 nm (in the photon energy range of 1.5–6.0 eV). The optical band gap (Eg) and the type of electronic transition of a defined material are mainly determined using the well-known Tauc relation:44
B is a constant dependent on the material. The parameter
h is Planck's constant,
ν is the frequency of the incident light, and
n is the exponent related to the nature of the electronic transition. According to Tauc's relation, the optical band gap
Eg can be estimated from the linear portion of the plot by fitting the aforementioned expression. The Tauc plot for Ba
0.85Sr
0.15Ti
0.85Zr
0.15O
3 is shown in
Fig. 8(c). To determine the experimental optical band gap, the linear portion of the curve was extrapolated to the energy axis, yielding an intercept at approximately
Eg = 2.419 eV, which is in line with the value previously calculated from the band structure. This suggests that the proposed DFT approximation is valid to investigate the electronic and thermoelectric characteristics of Ba
0.85Sr
0.15Ti
0.85Zr
0.15O
3. As compared with BaTiO
3,
45 SrTiO
3,
46 BaZrO
3,
47 and SrZrO
3,
48 which exhibit band gap energies of 3.76 eV, 3.22 eV, 3.55 eV, and 5.658 eV, a reduced band gap value is reported for Ba
0.85Sr
0.15Ti
0.85Zr
0.15O
3. In this case, we found that the substitution of BaTiO
3 by Sr and Zr ions facilitates greater electron excitation from the valence band to the conduction band, thereby increasing the overall electron concentration and enhancing the electronic properties of the material. This makes Ba
0.85Sr
0.15Ti
0.85Zr
0.15O
3 a promising material for optoelectronic devices.
3.5.3. The disorder-induced Urbach tails.
To gain deeper insight into the optical properties of the Ba0.85Sr0.15Ti0.85Zr0.15O3 system, the disorder-induced Urbach tails are analyzed.49,50 These tails correspond to the width of localized states within the optical band gap and reflect the degree of structural or electronic disorder. The Urbach energy (EU), which quantifies this width, is associated with an exponential tail in the density of states near the band edges and can be evaluated using the following relation:49,50| | 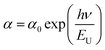 | (12) |
The parameter α0 is a pre-exponential factor. For Ba0.85Sr0.15Ti0.85Zr0.15O3, the band tail energy, also known as the Urbach energy (EU), is determined from the slope of the linear region in the plot of ln(α) versus photon energy (hν). Fig. 8(d) presents the variation of ln(α) as a function of hν for the studied sample. The deduced value of the Urbach energy is approximately EU = 0.784 eV. Mainly, this parameter reveals an inverse relationship with the optical band gap of materials.
3.5.4. The UV-visible extinction analysis.
For the studied system, the evolution of the extinction coefficient (k) versus the wavelength is presented in Fig. 9. The extinction parameter “k” shows a clear wavelength-dependent evolution, reflecting the optical absorption processes in the material. Accordingly, we found the presence of optical features (shoulder/peaks) that suggest different absorption mechanisms or transitions. At short wavelengths in the UV region, “k” starts with relatively low values and increases progressively from 200 to around 400 nm, indicating the onset of higher-energy electronic transitions. As the wavelength extends into the visible range, a shoulder appears around 380–420 nm, often seen when two processes overlap. The observed behavior suggests the contribution of defect-related (shallow defect band plus a wider transition) or excitonic states, as commonly observed in perovskite oxides.51 With further increase in wavelength, “k” continues to rise and reaches a broad maximum in the visible-red region (about 650–720 nm), which is often associated with sub-band-gap absorption mechanisms, such as defect levels, transitions involving oxygen-vacancy-related states, polaronic effects (small/large polaron absorption), or d–d transitions.52 Beyond this peak, “k” shows a slight decrease toward the near infrared (IR) region, pointing to a reduction in absorption.
 |
| | Fig. 9 Evolution of the extinction coefficient (k) versus wavelength for the studied system. | |
Compared with undoped BaTiO3, which has a wide indirect band gap of about 3.2 eV and therefore shows negligible extinction coefficient (10−5 < k < 10−4) values in the visible region, the co-doped Ba0.85Sr0.15Ti0.85Zr0.15O3 exhibits a clear enhancement in the extinction coefficient k across the UV-visible range (k ∼ 10−3).41 The substitution of Ba2+ by the smaller Sr2+ ion contracts the lattice and modifies the Ti–O–Ti bond angles, while the replacement of Ti4+ by the larger Zr4+ ion introduces local strain and changes the crystal field environment. These combined effects narrow the effective band gap, enhance orbital hybridization, and introduce defect-related or polaronic states inside the gap. As a result, k shows measurable values (of about 10−3) throughout the visible spectrum, with distinct shoulders and a broad maximum in the red region (650–720 nm), indicating stronger absorption processes than in pure BaTiO3. This improvement means that the co-doped compound can harvest a broader portion of sunlight and achieve higher optical absorption efficiency, making it more promising for optoelectronic applications than undoped BaTiO3.
4. Conclusion
The electronic, optical and thermoelectric properties of the Ba0.85Sr0.15Ti0.85Zr0.15O3 perovskite are investigated based on density functional theory and experimental optical measurements. Electronic structure calculations reveal that Ba0.85Sr0.15Ti0.85Zr0.15O3 exhibits a semiconductor character with a direct bandgap Eg = 2.52 eV, which is particularly promising for thermoelectric applications. Analysis of the projected density of states (PDOS) confirms that the valence band is predominantly composed of oxygen p orbitals. In contrast, the conduction band is mainly governed by the d orbitals of Ti and Zr, with only a minor contribution from the O p states. The Ba and Sr elements exhibit negligible influence on the formation of the band edges, indicating their limited role in the electronic transitions near the Fermi level. To evaluate its thermoelectric performance, we employed the Boltzmann transport theory as implemented in the Boltz–Trap code. The thermoelectric properties are assessed as a function of temperature in the range of 300–1200 K. Our findings indicate that Ba0.85Sr0.15Ti0.85Zr0.15O3 achieves a motivating dimensionless figure of merit (ZTmax) of 0.72 around 300 K, highlighting the potential of the material for thermoelectric energy conversion and waste-heat recovery applications. The optical properties of the studied Ba0.85Sr0.15Ti0.85Zr0.15O3 material are investigated using UV-visible spectroscopy. The co-doping of BaTiO3 with Sr2+ and Zr4+ ions enhances the extinction coefficient across the UV-visible range through lattice distortion and defect formation, resulting in stronger sub-band-gap absorption and improved light-harvesting capability for potential optoelectronic applications. The observed optical band gap and Urbach energy values suggest that this compound could be suitable for optoelectronic and photovoltaic devices, where controlled band structure and defect states are advantageous for light absorption and carrier transport. Overall, the findings position Ba0.85Sr0.15Ti0.85Zr0.15O3 as a promising multifunctional perovskite oxide for future applications in energy harvesting, environmental sensing, and electronic component design.
Conflicts of interest
The authors declare no conflicts of interest.
Data availability
All data relevant to this study are available from the corresponding author upon reasonable request.
References
- J. Zhang, Ch Li, C. Lv, H. Yu, W. Ma, M. Lei, X. Chen, M. Liu and X. Zhang, Ultra-soft, foldable, wearable piezoelectric sensor based on the aligned BaTiO3 nanoparticles, Mater. Today Phys., 2025, 50, 101606 CrossRef CAS.
- X. Kong, L. Yang, F. Meng, T. Zhang, H. Zhang, Y.-H. Lin, H. Huang, S. Zhang, J. Guo and C.-W. Nan, High-entropy engineered BaTiO3-based ceramic capacitors with greatly enhanced high-temperature energy storage performance, Nat. Commun., 2025, 16(1), 885 CrossRef CAS PubMed.
- M. S. Alkathy, A. Othman, H. A. Kassim, M. K. Gatasheh and J. A. Eiras, The influence of microstructural evolution and phase structure on ferroelectric properties of La modified BaTiO3 ceramics synthesized via sol-gel and solid-state reaction methods, Appl. Phys. A: Mater. Sci. Process., 2025, 131(4), 329 CrossRef CAS.
- J. Du, B. Sun, Ch Yang, Z. Cao, G. Zhou, H. Wang and Y. Chen, Ferroelectric memristor and its neuromorphic computing applications, Mater. Today Phys., 2025, 50, 101607 CrossRef CAS.
- V. B. Parmar, D. Raval, S. K. Gupta, P. N. Gajjar and A. M. Vora, BaTiO3 perovskite for optoelectronics application: A DFT study, Mater. Today: Proc., 2023 DOI:10.1016/j.matpr.2023.01.410.
- L. Wu, A. R. Akbashev, A. A. Podpirka, J. E. Spanier and P. K. Davies, Infrared-to-ultraviolet light-absorbing BaTiO3-based ferroelectric photovoltaic materials, J. Am. Ceram. Soc., 2019, 102(7), 4188–4199 CrossRef CAS.
- R. Vamsi, D. K. Harshitha, K. Manojkumar, D. Sateesh, R. R. Kumar, J. Boominathan, S. Hajra, S. Panda, H. J. Kim and V. Vivekananthan, Unraveling the Energy-Harvesting Performance of Antimony-Doped BaTiO3 Toward Self-Powered on-Body Wearable Impact Sensor, Energy Technol., 2025, 2500047 CrossRef CAS.
- W. Han, J. Zhu, S. Zhang, H. Zhang, X. Wang, Q. Wang, Ch Gao and Ch Jin, Phase transitions in nanoparticles of BaTiO3 as functions of temperature and pressure, J. Appl. Phys., 2013, 113, 19 Search PubMed.
- J. J. Gong, C. F. Li, Y. Zhang, Y. Q. Li, S. H. Zheng, K. L. Yang, R. S. Huang, L. Lin, Z. B. Yan and J.-M. Liu, Interactions of charged domain walls and oxygen vacancies in BaTiO3: a first-principles study, Mater. Today Phys., 2018, 6, 9–21 CrossRef.
- Y.-J. Hao, X.-Q. Gao, Y.-Ch Tang, L.-T. Xie, H.-Y. Xu, X.-X. Zhou, J.-H. Hu, H. Liu, He-Z. Li and B.-P. Zhang, Enhanced strain of BiFeO3-BaTiO3 relaxor ferroelectrics ceramics: domain structure evolution induced by electric-fields and temperature, Rare Met., 2025, 1–11 Search PubMed.
- H. K.-Naciri, M. Rguiti, A. Mabrouk, Ch Courtois, M. A. Ben Achour, Y. Lorgouilloux, R. Amrousse, N. Faska and A. Bachar, DFT-based and experimental study on Sr-doped BaTiO3: Impacts on piezoelectric and ferroelectric performance, Ceram. Int., 2025 DOI:10.1016/j.ceramint.2025.03.069.
- F. Corà, The performance of hybrid density functionals in solid-state chemistry: the case of BaTiO3, Mol. Phys., 2005, 103(18), 2483–2496 CrossRef.
- M. Maraj, A. Fatima, S. S. Ali, U. Hira, M. Rizwan, Z. Usman, W. Sun and A. Shaukat, Taming the optical response via (Ca: Zr) co-doped impurity in c-BaTiO3: A comprehensive computational insight, Mater. Sci. Semicond. Process., 2022, 144, 106573 CrossRef CAS.
- V. T. Lam, N. H. Lam, D. Q. Van, N. H. Thoan, N. N. Trung and D. D. Dung, Role of substitution Zr-site on the electronic structure and magnetic properties of BaTiO3 materials: A first principles calculation, Comput. Theor. Chem., 2025, 1243, 114989 CrossRef CAS.
- C. Li, T. Li, Ch Li, N. Ji, P. Lu and S. Ren, First-principles calculation study on influence of the influence mechanisms of A-site multi-element doping on the structure and optical properties of BaTiO3 ceramics, Research Square, 2025 DOI:10.21203/rs.3.rs-6653343/v1.
- H. Shen, K. Xia, P. Wang and R. Tan, The electronic, structural, ferroelectric and optical properties of strontium and zirconium co-doped BaTiO3: First-principles calculations, Solid State Commun., 2022, 355, 114930 CrossRef CAS.
- A. Z. Khan, J. M. Flitcroft and J. M. Skelton, First-principles modelling of the thermoelectric properties of n-type CaTiO3, SrTiO3 and BaTiO3, Mater. Adv., 2024, 5(2), 652–664 RSC.
- Q. Tang, Z. Shi, S. Xia, X. Bie, Y. Yang, D. Bian, D. Xu and R. Fan, Enhanced dielectric properties of Sr2+ and Zr4+ doped BaTiO3 colossal permittivity metamaterials, EPJ Appl. Metamat., 2024, 11, 13 CrossRef.
- Y. Li, H. Cheng, H. Xu, Y. Zhang, P. Yan, T. Huang, Ch Wang, Z. Hu and J. Ouyang, Electromechanical properties of (Ba, Sr)(Zr, Ti) O3 ceramics, Ceram. Int., 2016, 42(8), 10191–10196 CrossRef CAS.
- Y. Moualhi, H. Rahmouni and F. Bahri, Doublet doped titanate ferroelectric system for capacitors and NTC thermistor applications, Sens. Actuators, A, 2024, 377, 115596 CrossRef CAS.
- J. C. Slater, Wave Functions in a Periodic Potential, Phys. Rev., 1937, 51, 846–851 CrossRef CAS.
- P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- D. Koller, F. Tran and P. Blaha, Improving the modified Becke-Johnson exchange potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(15), 155109 CrossRef.
- G. K. H. Madsen and D. J. Singh, Boltztrap. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- F. Birch, Finite elastic strain of cubic crystals, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- W. Gao and J. R. Chelikowsky, Accuracy of Partial Core Corrections Using Fourier Transforms in Pseudopotential−Density Functional Theory, J. Chem. Theory Comput., 2018, 14, 6515–6520 CrossRef CAS PubMed.
-
M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, 1954 Search PubMed.
- M. G. Elmahgary, A. M. Mahran, M. Ganoub and S. O. Abdellatif, Optical investigation and computational modelling of BaTiO3 for optoelectronic devices applications, Sci. Rep., 2023, 13(1), 4761 CrossRef CAS PubMed.
- R. Malik, P. Dahiya, Priya, A. Hooda and S. Khasa, Effect of Sr2+ doping on structural, dielectric, electrical, and optical properties of BaTiO3 ceramics, J. Mater. Sci.: Mater. Electron., 2025, 36(8), 499 CrossRef CAS.
- S. Park, S. Woo, E. J. Mele and H. Min, Semiclassical Boltzmann transport theory for multi-Weyl semimetals, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 161113(R) CrossRef.
- Y. Wang, Y.-J. Hu, B. Bocklund, S.-L. Shang, B.-C. Zhou, Z.-K. Liu and L.-Q. Chen, First-principles thermodynamic theory of Seebeck coefficients, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98(22), 224101 CrossRef CAS.
- G. Sansone, A. Ferretti and L. Maschio, Ab initio electronic transport and thermoelectric properties of solids from full and range-separated hybrid functionals, J. Chem. Phys., 2017, 147, 114101 CrossRef PubMed.
- I. Mili, H. Latelli, Z. Charifi, H. Baaziz and T. Ghellab, A simple formula for calculating the carrier relaxation time, Comput. Mater. Sci., 2022, 213, 111678 CrossRef CAS.
- O. Sahnoun, H. Bouhani-Benziane, M. Sahnoun and M. Driz, Magnetic and thermoelectric properties of ordered double perovskite Ba2FeMoO6, J. Alloys Compd., 2017, 714, 704–708 CrossRef CAS.
- A. Mabrouki, A. Bougoffa, A. Trabelsi, E. Dhahri and K. Khirouni, Optical and thermoelectric properties of NaNbO3 thin film deposed by spray pyrolysis: experimental and DFT study, Eur. Phys. J. Plus, 2022, 137(6), 1–8 Search PubMed.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Biswas, High-performance bulk thermoelectrics with all-scale hierarchical architectures, Nature, 2012, 489(7416), 414–418 CrossRef CAS PubMed.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Convergence of electronic bands for high performance bulk thermoelectrics, Nature, 2011, 473(7345), 66–69 CrossRef CAS PubMed.
- G.-H. Pan, L. Zhang, H. Wu, X. Qu, H. Wu, Z. Hao, L. Zhang, X. Zhang and J. Zhang, On the luminescence of Ti4+ and Eu3+ in monoclinic ZrO2: high performance optical thermometry derived from energy transfer, J. Mater. Chem. C, 2020, 8(13), 4518–4533 RSC.
-
L. A. Wills, The defect structure of barium titanium oxide thin films, Diss. Northwestern University, 1994 Search PubMed.
- J. L. H. Clabel, G. Nicolodelli, G. C. Lozano, V. A. G. Rivera, S. O. Ferreira, A. H. Pinto, M. S. Lia and E. Marega Jr., The extrinsic nature of double broadband photoluminescence from the BaTiO3 perovskite: generation of white light emitters, Phys. Chem. Chem. Phys., 2021, 23(34), 18694–18706 RSC.
- G. O. Okonkwo, M. S. Rahman, S. Ahmed and M. A. Islam, Effect of Zr and Sr co-doping on structural, optical, and dielectric properties of BaTiO3 ceramics, Ceram. Int., 2021, 47, 19734–19744 Search PubMed.
- P. Kubelka and F. Munk, Ein Beitrag zur Optik der Farbanstriche, Z. Tech. Phys., 1931, 12, 593 Search PubMed.
- A. B. Murphy, Modified Kubelka–Munk model for calculation of the reflectance of coatings with optically rough surfaces, J. Phys. D: Appl. Phys., 2006, 39, 3571–3581 CrossRef CAS.
- P. R. Jubu, O. S. Obaseki, D. I. Ajayi, E. Danladi, K. M. Chahrour, A. Muhammad, S. Landi Jr., T. Igbawua, H. F. Chahul and F. K. Yam, Considerations about the determination of optical bandgap from diffuse reflectance spectroscopy using the Tauc plot, J. Opt., 2024, 53(5), 5054–5064 CrossRef.
- M. Fakhar-e-Alam, S. Saddique, N. Hossain, A. Shahzad, I. Ullah, A. Sohail, M. J. I. Khan and M. Saadullah, Synthesis, Characterization, and Application of BaTiO3 Nanoparticles for Anti-Cancer Activity, J. Cluster Sci., 2023, 34, 1745–1755 CrossRef CAS.
- N.-H. Parka, F. Dang, C. Wan, W.-S. Seo and K. Koumoto, Self-originating two-step synthesis of core–shell structured La-doped SrTiO3 nanocubes, J. Asian Ceram. Soc., 2013, 1, 35–40 CrossRef.
- S. Parida, S. K. Rout, L. S. Cavalcante, E. Sinha, M. S. Li, V. Subramanian, N. Gupta, V. R. Gupta, J. A. Varela and E. Longo, Structural refinement, optical and microwave dielectric properties of BaZrO3, Ceram. Int., 2012, 38, 2129–2138 CrossRef CAS.
- Y. Li, Y. Bai, Z. Li, Y. Gao and W. Ma, Infrared radiation and thermo-physical properties of small band gap Cu-doped SrZrO3 perovskite ceramic, Ceram. Int., 2024, 50, 40993–41002 CrossRef CAS.
- M. F. Plass, C. Popov, B. Ivanov, S. Mändl, M. Jelinek, L. M. Zambov and W. Kulisch, Correlation between photoluminescence, optical and structural properties of amorphous nitrogen-rich carbon nitride films, Appl. Phys. A: Mater. Sci. Process., 2001, 72, 21–27 CrossRef CAS.
- D. Souri, A. R. Khezripour, M. Molaei and M. Karimipour, ZnSe and copper-doped ZnSe nanocrystals (NCs): Optical absorbance and precise determination of energy band gap beside their exact optical transition type and Urbach energy, Curr. Appl. Phys., 2017, 17, 41–46 CrossRef.
- M. A. Peña and J. L. G. Fierro, Chemical structures and performance of perovskite oxides, Chem. Rev., 2001, 101, 1981–2017 CrossRef PubMed.
- C. Kormann, D. W. Bahnemann and M. R. Hoffmann, Preparation and characterization of quantum-size titanium dioxide, J. Phys. Chem., 1988, 92, 5196–5201 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
A.
Mabrouki
b,
H.
Rahmouni
*a,
A.
Mabrouki
b,
H.
Rahmouni
 a and
E.
Dhahri
a and
E.
Dhahri
 b
b
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) phases, it was found that all three phases exhibit significant heat transport dominated by glass-like intra-band tunneling mechanisms.17 Moreover, it was found that the cubic and orthorhombic phases exhibit superior n-type electrical conductivity, primarily due to the weaker polar-optic phonon scattering and longer electron lifetimes compared to the tetragonal phase.17 Moreover, they find that materials with cubic and orthorhombic phases reveal superior n-type conductivity, since the significantly stronger polar-optic phonon scattering and shorter electron lifetimes in the materials with the tetragonal phase.17 Given its superior electrical properties, materials with the Pm
m) phases, it was found that all three phases exhibit significant heat transport dominated by glass-like intra-band tunneling mechanisms.17 Moreover, it was found that the cubic and orthorhombic phases exhibit superior n-type electrical conductivity, primarily due to the weaker polar-optic phonon scattering and longer electron lifetimes compared to the tetragonal phase.17 Moreover, they find that materials with cubic and orthorhombic phases reveal superior n-type conductivity, since the significantly stronger polar-optic phonon scattering and shorter electron lifetimes in the materials with the tetragonal phase.17 Given its superior electrical properties, materials with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase are expected to achieve a high-temperature ZT that is 25% greater than that of the I4/mcm phase. However, the highest ZT is predicted for the Pnma phase, owing to its advantageous electrical characteristics and low lattice thermal conductivity.
m phase are expected to achieve a high-temperature ZT that is 25% greater than that of the I4/mcm phase. However, the highest ZT is predicted for the Pnma phase, owing to its advantageous electrical characteristics and low lattice thermal conductivity.