 Open Access Article
Open Access ArticleGraphitized cornstarch as a high-performance biomass-derived electrode for sustainable capacitive deionization
Nasser A. M.
Barakat
 *a,
Ahmed
Khalid
a,
Tamer
Melegy
b and
Marwa M.
Abdel-Aty
a
*a,
Ahmed
Khalid
a,
Tamer
Melegy
b and
Marwa M.
Abdel-Aty
a
aChemical Engineering Department, Faculty of Engineering, Minia University, El-Mynia 61516, Egypt. E-mail: nasbarakat@mu.edu.eg
bTechnical Research Center, Cairo, Egypt
First published on 9th October 2025
Abstract
The use of graphitized cornstarch, a biomass-derived carbon material, was explored as a high-performance electrode for capacitive deionization (CDI). Cornstarch was thermally treated at 1000 °C to produce a graphitic carbon structure with a high surface area (332.28 m2 g−1, BET), excellent electrical conductivity, and residual functional groups. The electrochemical performance of the graphitized cornstarch electrode was evaluated using cyclic voltammetry (CV), chronoamperometry, and electrosorption capacity measurements in NaCl solutions. The results demonstrate a specific capacitance of 1088.7 F g−1 at 1 mV s−1, significantly higher than that of conventional activated carbon (73.5 F g−1). The CDI cell assembled with graphitized cornstarch electrodes achieved an electrosorption capacity of 11.3 mg g−1 at 1.2 V in 0.03 M NaCl, compared to only 0.3 mg g−1 for activated carbon. Furthermore, the graphitized cornstarch electrode exhibited excellent stability and reversibility, with a consistent performance over multiple adsorption–desorption cycles. The presence of residual functional groups, as confirmed by FTIR analysis, contributed to pseudocapacitive behavior, enhancing the overall ion adsorption capacity. These findings highlight the potential of biomass-based electrodes, such as graphitized cornstarch, to address the challenges of water scarcity through sustainable and efficient CDI technology. This study provides valuable insights into the design and optimization of biomass-derived carbon materials for next-generation desalination systems.
1. Introduction
Water scarcity is one of the most pressing global challenges of the 21st century, affecting billions of people worldwide. According to the United Nations, over 2 billion people live in countries experiencing high water stress, and this number is expected to rise due to population growth, urbanization, and climate change. Freshwater resources are becoming increasingly scarce, with agriculture, industry, and domestic use competing for limited supplies. In this context, desalination has emerged as a critical solution to address water scarcity by converting abundant seawater and brackish water into potable water.Several desalination technologies have been developed to address water scarcity, each with its own advantages and limitations.1 Thermal desalination methods (e.g., multi-stage flash distillation, multi-effect distillation) rely on heating water to produce steam, which is then condensed to obtain freshwater.2 While effective, they are energy-intensive and require large infrastructure, making them costly and environmentally unsustainable.1 RO is the most widely used desalination technology, relying on semi-permeable membranes to separate salts from water. However, RO faces challenges such as membrane fouling, high energy consumption, and the disposal of concentrated brine, which can harm marine ecosystems.3,4 Electrodialysis (ED) uses ion-exchange membranes and an electric field to remove ions from water. While energy-efficient for brackish water, it is less effective for seawater desalination and suffers from membrane fouling and scaling issues.5,6
These challenges have driven the search for alternative desalination technologies that are energy-efficient, cost-effective, and environmentally friendly. Electrochemical desalination techniques, such as capacitive deionization (CDI) and battery-based desalination, have gained significant attention due to their low energy consumption, scalability, and environmental sustainability.7,8 Unlike conventional methods, electrochemical desalination relies on electrostatic adsorption or faradaic reactions to remove ions from water, offering several advantages including low operating voltages. Electrochemical systems typically operate at voltages below 2 V, reducing energy consumption. Moreover, compared to RO, electrochemical methods do not require high-pressure pumps, lowering operational costs. These systems can be easily scaled up or down, making them suitable for both large-scale and decentralized applications.9,10
Capacitive deionization (CDI) is a promising electrochemical desalination technology that uses porous electrodes to adsorb ions from water under an applied electric field. The basic principle of CDI involves the formation of an electrical double layer (EDL) at the electrode–electrolyte interface, where ions are electrostatically adsorbed and stored. CDI can be classified into several types, including (1) conventional CDI, which uses carbon-based electrodes to adsorb ions through EDL formation,11 (2) membrane CDI (MCDI), which incorporates ion-exchange membranes to enhance ion selectivity and efficiency,12 and (3) flow-electrode CDI (FCDI), which uses flowing carbon slurry as electrodes, enabling continuous operation.13
CDI offers several advantages, including low energy consumption, high ion removal efficiency, and minimal environmental impact. However, its performance heavily depends on the properties of the electrode materials, which play a critical role in determining the efficiency, capacity, and durability of the system. The electrode is the most critical component of a CDI cell, as it directly influences the ion adsorption capacity, charge efficiency, and cycle stability. Ideal electrode materials for CDI should possess high surface area (to provide abundant adsorption sites for ions), good electrical conductivity, controlled pore structure (to ensure optimal ion accessibility and diffusion), extreme corrosion resistance and non-toxicity characteristics.14,15 Commonly used electrode materials include activated carbon (AC), carbon aerogels,16 graphene,17,18 carbon nanofibers19,20 and carbon nanotubes.21 However, these materials often face challenges such as limited specific capacitance, high cost, and complex synthesis processes.
Biomass-based electrodes have emerged as a sustainable and cost-effective alternative to conventional carbon materials. They are derived from renewable sources such as agricultural waste, plant residues, and industrial byproducts, and offer several advantages including low cost, sustainability, tunable properties, high performance, high surface area, good electrical conductivity, and excellent ion adsorption capacity, making them suitable for CDI applications. However, the most important feature is the presence of various surface functional groups (oxygenated, nitrous, etc.) which distinctly enhance the performance.22–24
Recent advancements in CDI technology have focused on improving electrode materials, system design, and operational strategies to enhance desalination performance. For example, the incorporation of pseudocapacitive materials (e.g., metal oxides, conductive polymers) and functionalized carbon materials has been shown to significantly improve ion removal efficiency and energy efficiency.25–27 Additionally, the development of hybrid CDI systems, which combine CDI with other desalination technologies, offers new opportunities for addressing the limitations of conventional methods.28,29
In this study, we explore the use of graphitized cornstarch as a biomass-based electrode material for CDI. Cornstarch, a widely available and low-cost biomass, is transformed into a high-performance carbon material through thermal treatment and graphitization. The resulting material is characterized by its high surface area, excellent electrical conductivity, and residual functional groups, which enhance its ion adsorption capacity and pseudocapacitive behavior. We investigate the electrochemical performance of the graphitized cornstarch electrode in CDI applications, comparing it to conventional activated carbon electrodes. Our findings demonstrate the potential of biomass-based electrodes to address the challenges of water scarcity through sustainable and efficient desalination technologies.
2. Experimental
2.1. Electrode material preparation
The graphitized cornstarch was prepared through a two-step process involving drying and high-temperature calcination. Raw cornstarch (obtained from local market) was first dried in a convection oven at 200 °C for 30 hours to remove moisture and volatile components. This step ensured the complete dehydration of the cornstarch, providing a stable precursor for the subsequent calcination process. The dried cornstarch was then subjected to calcination under an inert atmosphere in a tube furnace. The calcination process was carried out at three different temperatures, 800, 1000, and 1100 °C, to investigate the effect of temperature on the structural and electrochemical properties of the resulting material. These samples will be coded as S-800, S-1000 and S-1100. For each temperature, the cornstarch was heated at a ramping rate of 3 °C min−1 and held at the target temperature for 5 hours to ensure complete carbonization and graphitization. After calcination, the furnace was allowed to cool naturally to room temperature under an argon atmosphere to prevent oxidation of the carbon material.2.2. CV measurements
Cyclic voltammetry (CV) was performed using a three-electrode cell to evaluate the electrochemical performance of the graphitized cornstarch electrodes. The setup consisted of the following components: counter electrode (a graphite rod), reference electrode (an Ag/AgCl (3 M KCl) electrode) and working electrode (a glassy carbon electrode (GCE) coated with the functional material (graphitized cornstarch)). To prepare the working electrode, a homogeneous dispersion was prepared by mixing 0.002 g of the functional material (graphitized cornstarch) with 20 μL of Nafion solution (5 wt%) and 400 μL of isopropanol. The mixture was ultrasonicated for 30 minutes to ensure uniform dispersion. The dispersion was drop-cast onto the surface of the glassy carbon electrode in three successive layers, with each layer consisting of 5 μL of the ink. After each deposition, the electrode was allowed to dry naturally for 10 minutes before applying the next layer. Following the final deposition, the electrode was dried in an oven at 80 °C for 30 minutes to remove residual solvents and ensure good adhesion of the material to the electrode surface.CV measurements were conducted using a potentiostat/galvanostat (Biologic, SP-50 Potentiostat) in different NaCl solutions at scan rates ranging from 1 mV s−1 to 100 mV s−1. The potential window was set between −0.2 V and 1.0 V (vs. Ag/AgCl) to avoid water splitting and ensure stable electrochemical performance.
2.3. CDI cell assembly and electrode fabrication
The CDI electrodes were prepared by mixing the active material with polyvinylidene fluoride (PVDF, ∼10 wt% of the total solids) in N,N-dimethyl formamide (DMF) to form a homogeneous slurry, which was cast onto carbon cloth sheets. The resulting mass loading was ∼1.0 mg cm−2, calculated from the active material per geometric electrode area. After drying at 80 °C to remove most of the solvent, the electrodes were subjected to a brief heating step at 350 °C to improve adhesion and remove residual DMF. This step was applied for a short duration under controlled conditions, ensuring electrode stability. The electrodes exhibited good mechanical integrity and reproducible performance in CDI testing, indicating that the procedure did not compromise binder functionality or electrode porosity.Typically, 1 g of PVDF was dissolved in 8 mL of DMF under continuous stirring at room temperature until a homogeneous binder solution was obtained. 0.5 g of the functional material was added to the binder solution, and the mixture was stirred vigorously to form a uniform ink. The prepared ink was coated onto carbon cloth electrodes (3.5 × 3.5 cm) using a blade-coating technique to ensure a uniform and controlled thickness. The coated electrodes were dried at 80 °C for 5 hours in an oven to remove excess solvent and improve adhesion. The electrodes were heated at a controlled rate of 2 °C min−1 to a final temperature of 350 °C, at which point they were held for 3 hours. After heat treatment, the electrodes were allowed to cool naturally to room temperature.
The CDI cell was assembled using the fabricated electrodes and a porous separator. Two identical electrodes (coated carbon cloth) were placed on either side of a 100 μm thick highly porous membrane (e.g., polypropylene or polyethylene) to serve as a spacer and prevent electrical shorting. The electrodes and the membrane were tightly pressed together to form a sandwich-like structure, ensuring good contact and minimal internal resistance. The assembled electrode–membrane stack was placed in a custom-designed CDI cell made of non-conductive materials (acrylic) to hold the components in place and provide electrical connections. Chronoamperometry measurements were conducted to evaluate the electrosorption performance of the CDI cell under different operating conditions. The CDI cell was operated in batch mode, where it was immersed in 150 mL of saline solution (NaCl) with varying concentrations (e.g., 0.02 M, 0.03 M, and 0.04 M). A potentiostat/galvanostat was used to apply a constant voltage across the electrodes and measure the resulting current. Chronoamperometry measurements were performed at different applied voltages (e.g., 0.8 V, 1.0 V, 1.2 V, 1.5 V, and 2.0 V) to investigate the effect of voltage on the electrosorption capacity. The cell was operated in a cyclic mode, where the voltage was reversed periodically to facilitate adsorption and desorption of ions. The current response was recorded over time, and the electrosorption capacity was calculated based on the charge transferred during the adsorption phase. The solution was kept well-mixed using a magnetic stirrer at 300 rpm, ensuring uniform concentration and minimizing diffusion limitations. Since the reactor operated in batch mode, there was no defined flow rate or residence time; instead, the entire 150 mL volume was subject to adsorption/desorption during each charging–discharging cycle.
2.4. Characterization
FTIR analysis was performed to identify the functional groups present in the graphitized cornstarch samples before and after calcination using a PerkinElmer Spectrum Two FTIR spectrometer. The samples were mixed with potassium bromide (KBr) and pressed into transparent pellets. The FTIR spectra were recorded in the range of 400–4000 cm−1 with a resolution of 4 cm−1. Each spectrum was averaged over 32 scans to ensure high signal-to-noise ratio. X-ray diffraction (XRD) analysis was conducted to investigate the crystallinity and phase composition of the graphitized cornstarch samples using a Bruker D8 Advance X-ray diffractometer. The samples were scanned using Cu Kα radiation (λ = 1.5406 Å) at a voltage of 40 kV and a current of 40 mA. The diffraction patterns were recorded in the 2θ range of 10°–80° with a step size of 0.02° and a scan rate of 2° min−1. Scanning electron microscopy (SEM) was used to examine the surface morphology and microstructure of the graphitized cornstarch samples using a FEI Quanta FEG 250 scanning electron microscope. The samples were mounted on aluminum stubs using conductive carbon tape and coated with a thin layer of gold–palladium to enhance conductivity. Images were acquired at an accelerating voltage of 10 kV and a working distance of 10 mm. The magnification was adjusted to capture the surface features and pore structure of the samples. Thermogravimetric analysis (TGA) was performed to evaluate the thermal stability and decomposition behavior of the cornstarch precursor and the graphitized samples. The analysis was conducted using a PerkinElmer TGA 4000 thermogravimetric analyzer. The samples were heated from room temperature to 800 °C at a rate of 10 °C min−1 under a nitrogen atmosphere (flow rate: 20 mL min−1). The weight loss of the samples was recorded as a function of temperature, and the data were analyzed to determine the thermal decomposition profile.Raman spectroscopy was performed on a Horiba LabRAM HR Evolution spectrometer equipped with a 532 nm diode-pumped solid-state laser and a 50× long-working-distance objective. The laser power was maintained below 1 mW to minimize heating, and spectra were collected in the 800–3200 cm−1 range using a 1200 lines·mm−1 grating, with integration times of 10–15 s and 3–5 accumulations per spot. Calibration was carried out against the Si reference peak at 520.7 cm−1. Transmission electron microscopy (TEM) was conducted using a JEOL JEM-2100, 200 kV instrument. For sample preparation, powders were ultrasonically dispersed in absolute ethanol and a drop of the suspension was deposited onto holey carbon-coated copper grids (300 mesh), followed by air drying at room temperature. Both bright-field and high-resolution images were obtained, and selected area electron diffraction (SAED) patterns were recorded under parallel beam conditions. Electrochemical impedance spectroscopy (EIS) was carried out using a Bio-Logic VMP3 electrochemical workstation in a three-electrode configuration, with the carbon-coated glassy carbon electrode (GCE) as the working electrode, a platinum wire as the counter electrode, and an Ag/AgCl (3 M KCl) electrode as the reference. Measurements were performed in a 0.5 M NaCl aqueous electrolyte over the frequency range of 100 kHz to 0.01 Hz, applying a sinusoidal perturbation of 5–10 mV (rms). Prior to each test, the system was stabilized under open-circuit potential for 5 min to ensure steady-state conditions.
3. Results and discussion
3.1. Electrode structure and composition
The broad peak at approximately 24.5° is attributed to the (002) diffraction plane of graphitic carbon, indicating the presence of turbostratic or disordered graphite. This feature reflects the stacking of graphene layers with partial alignment but lacking long-range crystalline order, a typical structure resulting from the carbonization of biomass precursors. This behavior is consistent with the structural fingerprint of disordered graphitic carbon as reported in ICDD PDF No. 75-1621 and ICDD PDF No. 41-1487.
The second broad diffraction peak observed near 43.5° corresponds to the (100) or (101) planes, which represent the in-plane ordering of sp2-bonded carbon atoms within the graphitic domains. The relatively low intensity and broad nature of this peak further confirm that the material comprises small, defect-rich graphitic domains embedded within an amorphous carbon matrix. This structural configuration is typical for bio-derived carbon materials subjected to pyrolysis or high-temperature treatment.
The absence of sharp, well-defined peaks in the XRD spectrum confirms that the synthesized material is predominantly non-crystalline, containing a mixture of amorphous carbon and short-range ordered graphitic structures. These structural features are advantageous for capacitive deionization applications, as they can enhance the accessible surface area and improve the electrochemical double-layer formation, thereby promoting higher electrosorption capacity.
Raman spectroscopy was conducted to further investigate the structural ordering of the graphitized cornstarch (Fig. 2). The spectrum displays two dominant peaks: the D-band located near 1329 cm−1 and the G-band centered around 1587 cm−1, which are typical vibrational modes associated with carbon-based materials. The D-band corresponds to the breathing modes of sp2 carbon atoms in disordered graphitic domains, while the G-band arises from the stretching vibrations of the sp2-hybridized carbon lattice in graphitic structures.
The relative intensity ratio of the D- to G-band (ID/IG) is commonly employed as an indicator of the degree of disorder and crystallite size in carbonaceous materials. For the present sample, the ID/IG ratio was estimated to be approximately 1.06, indicating a moderate degree of disorder: small, defect-rich graphitic domains embedded in an amorphous carbon matrix. This structural picture is consistent with the broad (002)/(100) reflections in XRD and is advantageous for CDI: (i) defects/edge planes increase the density of electrochemically accessible sites for ion adsorption, while (ii) the retained graphitic ordering preserves electronic conductivity for efficient charge transport. The balance reflected by ID/IG thus explains the observed electrochemical behavior—high electrosorption capacity and low polarization losses—because ion storage benefits from abundant defect sites, whereas charge transfer is supported by percolating sp2 networks.
The presence of a moderate ID/IG ratio indicates that the graphitized cornstarch retains a significant number of defect sites and edge planes, which are highly beneficial for electrochemical applications. Defects and disorder enhance the density of electrochemically active sites, improve ion adsorption, and facilitate charge storage during CDI operation. At the same time, the partial graphitic ordering contributes to good electronic conductivity, enabling efficient charge transfer within the electrode. The synergy between structural disorder and graphitic domains therefore plays a crucial role in boosting the electrosorption capacity of the electrodes, as confirmed by the electrochemical performance measurements.
The FTIR spectrum of the dried corn starch shows significant changes compared to the original starch, indicating partial decomposition and loss of functional groups due to the thermal treatment. The intensity of the O–H stretching peak is decreased, indicating the loss of adsorbed water and partial dehydration of the starch molecules. Moreover, the C–H stretching peak also shows reduced intensity, suggesting the breakdown of some CH2 groups during drying. The decrease in the intensity of the peak at 1645 cm−1 (O–H bending of adsorbed water) further confirms the removal of water. The broad peaks at 1420 cm−1 and 1372 cm−1 are still observed but with reduced intensity, indicating that some C–H bending vibrations persist despite the thermal treatment. The C–O–C stretching peak (at 1163 cm−1) of the glycosidic linkages shows reduced intensity, suggesting partial breakdown of the starch polysaccharides. The C–O and C–C stretching peaks (at 1081 cm−1 and 1018 cm−1) also show reduced intensity, consistent with the degradation of the glucose ring structure.
The FTIR spectrum of the graphitized cornstarch shows a dramatic decrease in the intensity of most functional groups, reflecting the near-complete transformation of the material into a carbonaceous structure after high-temperature treatment at 1000 °C. The observed changes in the spectrum are consistent with the thermal decomposition of starch and the formation of graphitic carbon. The O–H stretching peak, which was broad and intense in the original and dried cornstarch, has become small and less pronounced in the graphitized sample. This indicates the removal of combined water and the dehydration of the starch molecules during the high-temperature treatment. The remaining small peak at 3440 cm−1 can be attributed to physical moisture adsorbed on the surface of the carbonaceous material, as the graphitization process eliminates most of the hydroxyl groups originally present in the starch. The C–H stretching peak, which was prominent in the original and dried cornstarch (at 2930 cm−1), has become very small in the graphitized sample. This indicates the breakdown of most CH2 groups and the loss of organic components during the graphitization process. The small residual peak at 2920 cm−1 suggests that only trace amounts of aliphatic carbon species remain in the material.
A very small peak at 1731 cm−1, corresponding to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration of carbonyl groups, is observed in the graphitized sample.33 This peak likely arises from residual oxygen-containing functional groups (e.g., esters, aldehydes, or ketones) that were not completely eliminated during the high-temperature treatment. The presence of these groups indicates that some surface oxidation or partial decomposition of organic components may have occurred during graphitization. A very small peak at 1520 cm−1, attributed to the C
O stretching vibration of carbonyl groups, is observed in the graphitized sample.33 This peak likely arises from residual oxygen-containing functional groups (e.g., esters, aldehydes, or ketones) that were not completely eliminated during the high-temperature treatment. The presence of these groups indicates that some surface oxidation or partial decomposition of organic components may have occurred during graphitization. A very small peak at 1520 cm−1, attributed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration of aromatic or conjugated carbon structures, is observed in the graphitized sample. This peak reflects the formation of polyaromatic carbon structures during the graphitization process, which is consistent with the development of a graphitic carbon network.
C stretching vibration of aromatic or conjugated carbon structures, is observed in the graphitized sample. This peak reflects the formation of polyaromatic carbon structures during the graphitization process, which is consistent with the development of a graphitic carbon network.
The FTIR spectrum of the graphitized cornstarch is dominated by a featureless baseline with only a few low-intensity peaks, indicating the near-complete loss of organic functional groups and the formation of a highly conjugated carbon structure. The residual peaks (e.g., O–H, C–H, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and C
O, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) are very small and can be attributed to surface groups. These groups are likely present in negligible amounts and do not significantly affect the overall carbonaceous nature of the material. However, these groups can provide distinct improvement to the surface activity.
C) are very small and can be attributed to surface groups. These groups are likely present in negligible amounts and do not significantly affect the overall carbonaceous nature of the material. However, these groups can provide distinct improvement to the surface activity.
As aforementioned, the raw cornstarch displayed broad absorption bands associated with O–H stretching (≈3400 cm−1) and C–H stretching vibrations (≈2920 cm−1), typical of polysaccharide structures. After graphitization, these bands became markedly attenuated, indicating a substantial loss of hydroxyl and aliphatic groups during carbonization. Low-intensity residual peaks were observed in the fingerprint region (<1000 cm−1), but given the limited diagnostic power of FTIR for carbonaceous materials, no detailed assignments were made. Instead, the data are interpreted only as evidence for the general reduction of oxygenated functional groups. The decrease in surface functionalities is consistent with the formation of more conductive carbon domains, as corroborated by Raman spectroscopy, HRTEM/SAED, and the low resistance values observed in EIS in the coming characterization.
The thermogravimetric analysis (TGA) of the initial and dried cornstarch samples reveals distinct thermal decomposition behaviors, which are consistent with the structural changes observed in the FTIR spectra; the results are displayed in Fig. 4. The small weight loss observed in both samples, around 100 °C, corresponds to the evaporation of adsorbed water from the cornstarch.
For the initial cornstarch, no significant weight loss is detected up to around 290 °C. This indicates that the cornstarch is thermally stable up to 290 °C, with no major decomposition occurring. The FTIR spectrum of the initial cornstarch shows characteristic peaks of starch (e.g., C–H, C–O–C, and O–H vibrations), confirming the presence of intact polysaccharide structures.
The sharp weight loss (290–345 °C) corresponds to the thermal decomposition of the starch polysaccharides (amylose and amylopectin). The breakdown of glycosidic linkages (C–O–C) and the loss of hydroxyl (O–H) and C–H groups are consistent with the FTIR results, which show a reduction in the intensity of these peaks after drying.
A gradual decrease in weight is observed in the temperature range of 345–800 °C. This corresponds to the further decomposition of carbonaceous residues and the formation of stable carbon structures. The FTIR spectrum of the graphitized sample shows the near-complete disappearance of organic functional groups, supporting this interpretation. Later on, no further weight loss is detected above 800 °C. This indicates the formation of a stable carbonaceous material with minimal residual organic content. The residual weight corresponds to the carbonized product of the starch.
For the dried cornstarch sample, after the initial weight loss due to evaporation of the adsorbed water, a very small rate of weight loss is observed up to 300 °C. This indicates the slow decomposition of residual organic components and the breakdown of some polysaccharide structures. The FTIR spectrum of the dried cornstarch shows reduced intensities of C–H (2940 cm−1) and C–O–C (1067 cm−1) peaks, supporting this interpretation. Then, within the temperature range of 300–750 °C, a gradual decrease in weight is observed, without the sharp decomposition stage seen in the initial cornstarch. This suggests that the dried cornstarch undergoes continuous decomposition of its carbonaceous residues, rather than a distinct two-stage process. The FTIR spectrum of the dried cornstarch shows the formation of oxidized species (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 1720 cm−1) and polyaromatic structures (e.g., C
O at 1720 cm−1) and polyaromatic structures (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C at 1610 cm−1), which is consistent with the gradual decomposition behavior.
C at 1610 cm−1), which is consistent with the gradual decomposition behavior.
Lastly, no further weight loss is detected above 750 °C. This indicates the formation of a stable carbonaceous material, similar to the initial cornstarch. However, the slightly lower residual weight in the dried sample suggests that more organic components were decomposed during the drying process.
Overall, the TGA results for the initial and dried cornstarch samples reveal distinct thermal decomposition behaviors, which are consistent with the structural changes observed in the FTIR spectra. The initial cornstarch undergoes a sharp decomposition stage followed by gradual weight loss, reflecting the breakdown of polysaccharides and the formation of a carbonaceous material. In contrast, the dried cornstarch shows a continuous decomposition process, with a slightly lower residual weight, indicating greater thermal stability and more extensive decomposition of organic components. These findings provide valuable insights into the thermal behavior of cornstarch and its transformation into a carbonaceous material during drying and graphitization.
The graphitized cornstarch exhibits a flake-like morphology with a warped or wrinkled appearance. These flakes are several micrometers in size and have a relatively uniform thickness. This flake-like structure is typical of graphitic carbon materials formed during high-temperature pyrolysis or graphitization. The warping or wrinkling of the flakes is attributed to the thermal stress and volume contraction that occur during the decomposition of the organic precursor (cornstarch) and the subsequent rearrangement of carbon atoms into graphitic structures. During the initial stages of heating, the cornstarch undergoes thermal decomposition, losing volatile components such as water, CO2, and other gases. This process leads to the breakdown of the polysaccharide structure and the formation of carbon-rich intermediates. As the temperature increases, the carbon-rich intermediates undergo carbonization, forming amorphous carbon. This stage is characterized by the loss of heteroatoms (e.g., oxygen and hydrogen) and the formation of a disordered carbon network. At high temperatures (1000 °C), the amorphous carbon undergoes graphitization, where the carbon atoms rearrange into ordered graphitic structures. The warped flake-like morphology arises due to the stacking of graphene layers and the thermal stress induced during the high-temperature treatment.
The thickness of the flakes is influenced by the precursor material and the graphitization conditions. Cornstarch, as a biopolymer, contains long-chain polysaccharides that decompose into carbon-rich intermediates. During graphitization, these intermediates form layered structures, with the thickness determined by the extent of stacking and the thermal history of the material (Fig. 5).
The morphology and microstructural features of the graphitized cornstarch were further examined by transmission electron microscopy (TEM), as shown in Fig. 6. At lower magnification (Fig. 6A), the sample displays a triangular particle with sharp edges, suggesting that the graphitization process yielded carbonaceous structures with well-defined boundaries. The higher magnification image (Fig. 6B) reveals that the particle edges consist of nanostructured layers, indicating partial graphitic ordering at the surface. This layered nature is in agreement with the XRD results, which demonstrated broad (002) and (100) peaks corresponding to turbostratic graphite domains.
 | ||
| Fig. 6 Low (A) and high (B) normal TEM images, HRTEM (C) and SAED pattern (D) for the graphitized cornstarch at 1000 °C. | ||
The high-resolution TEM (HRTEM) image (Fig. 6C) shows well-resolved lattice fringes with an interlayer spacing of approximately 0.39 nm, which is slightly larger than the ideal graphite (002) spacing of 0.34 nm. The expanded d-spacing reflects the presence of lattice distortions and structural defects, consistent with the Raman spectrum that showed an ID/IG ratio of 1.06, indicative of defect-rich graphitic carbon. These defects enhance the electrochemical activity of the electrode by providing additional adsorption sites for ions during capacitive deionization.34
The selected area electron diffraction (SAED) pattern (Fig. 6D) exhibits diffuse concentric rings rather than sharp diffraction spots, further confirming the polycrystalline and partially amorphous nature of the carbon material. This observation is in excellent agreement with the XRD and Raman results, both of which pointed to the coexistence of ordered graphitic regions and amorphous carbon.
Table 1 summarizes the surface area measurement parameters. The surface area and pore structure of the graphitized cornstarch and commercial activated carbon were characterized using Brunauer–Emmett–Teller (BET), Barrett–Joyner–Halenda (BJH), and density functional theory (DFT) methods. The results reveal significant differences in the porosity and surface area of the two materials.
| S BET (m2 g−1) | S DFT (m2 g−1) | S BJH (m2 g−1) | Pour radius (DvI) (nm) | V meso (cm3 g−1) | V micro (cm3 g−1) | V total (cm3 g−1) | |
|---|---|---|---|---|---|---|---|
| AC | 603.42 | 617.55 | 150.36 | 1.914 | 0.3073 | 0.5345 | 0.56145 |
| Graphitized cornstarch | 332.28 | 231.44 | 115.76 | 1.933 | 0.2112 | 0.3182 | 0.33392 |
As shown in the table, the BET surface area of the graphitized cornstarch and activated carbon is 332.28 and 603.42 m2 g−1, respectively. The BET is used to estimate the total surface area of a material by analyzing nitrogen adsorption isotherms at low relative pressures. The BET surface area includes contributions from both micropores and mesopores. The activated carbon has a significantly higher BET surface area than the graphitized cornstarch, indicating a more developed porous structure. This is typical of activated carbon, which is specifically designed to have a high surface area for adsorption applications.
The measured DFT surface area for the graphitized cornstarch and activated carbon is 231.44 and 617.55 m2 g−1, respectively. The DFT method provides a more detailed analysis of the surface area by considering the pore size distribution and the adsorption mechanism in different pore sizes. DFT is particularly useful for materials with a wide range of pore sizes, as it accounts for the heterogeneity of the pore structure. The DFT surface area of the activated carbon is higher than that of the graphitized cornstarch, consistent with the BET results. However, the DFT surface area is generally more accurate for materials with complex pore structures, as it accounts for the specific adsorption behavior in different pore sizes.35
The BJH method estimates the surface area of mesopores (2–50 nm) by analyzing the desorption branch of the nitrogen adsorption isotherm. It does not account for micropores (<2 nm), which are typically the dominant contributors to the total surface area in porous materials. The BJH surface area is 115.76 and 150.36 m2 g−1 for the graphitized cornstarch and activated carbon, respectively. The BJH surface area of the activated carbon is higher than that of the graphitized cornstarch, indicating a greater contribution from mesopores. However, the BJH surface area is significantly lower than the BET and DFT surface areas for both materials, as it excludes micropores.35
The estimated pore radius (DvI) for the graphitized cornstarch and activated carbon was 1.933 and 1.914 nm, respectively. The pore radius represents the average size of the pores in the material. Both materials have similar average pore radii, indicating that their pore structures are dominated by micropores and small mesopores.36
The measured mesopore volume was 0.2112 and 0.3073 cm3 g−1 for the graphitized cornstarch and activated carbon, respectively. The mesopore volume is higher in the activated carbon, reflecting its more developed mesoporous structure. This is consistent with the higher BJH surface area of the activated carbon. On the contrary, in the same sequence, the micropore volume is 0.3182 and 0.5345 cm³ g−1 for activated carbon and graphitized cornstarch, respectively, indicating that the graphitized material possesses a greater percentage of fine pores available for ion electrosorption and charge storage. The micropore volume is significantly higher in the activated carbon, indicating a greater contribution from micropores to the total surface area. This is consistent with the higher BET and DFT surface areas of the activated carbon. Consequently, the total pore volume of the activated carbon (0.56145 cm3 g−1) is higher than that of the graphitized cornstarch (0.33392 cm3 g−1), reflecting its more extensive porous structure. It is worth mentioning that the high surface parameters of the activated carbon are mainly attributed to the chemical or physical activation processes which are used to treat the AC. However, these activation steps were not utilized on the proposed graphitized cornstarch to maintain the residual surface functional groups.
The N2 adsorption–desorption isotherms at 77 K provide further insights into the pore structures of the studied electrodes (Fig. 7A–B). The activated carbon exhibits a typical Type IV isotherm with H4 hysteresis, characteristic of a micro–mesoporous material with slit-shaped pores. The steep uptake at low relative pressures (P/P0 < 0.1) indicates the presence of micropores, while the gradual increase at higher pressures reflects mesopore filling. In comparison, the graphitized cornstarch also displays a Type IV isotherm with H4 hysteresis, but with a noticeably higher adsorbed volume, consistent with its larger specific surface area and more developed hierarchical porosity. The combination of micropores and mesopores in the cornstarch-derived carbon ensures both a high density of ion storage sites and facile ion transport pathways, which is in agreement with the superior salt adsorption capacity and fast kinetics observed in CDI measurements. The pore characteristics extracted from QSDFT analysis (Table 1) confirm that the graphitized cornstarch has a balanced micro–mesoporous structure, supporting efficient electrosorption and enhanced electrochemical performance relative to AC.
The pore size distribution (PSD) curves derived from the N2 adsorption data provide additional evidence of the hierarchical porosity of the studied electrodes (Fig. 7C and D). The activated carbon displays a primary contribution from micropores (<2 nm), consistent with its steep N2 uptake at low relative pressures, and only a modest mesopore contribution in the 2–50 nm range. In contrast, the graphitized cornstarch shows a more balanced micro–mesoporous distribution, with a significant micropore fraction for ion storage and an extended mesopore network that enhances electrolyte accessibility. This hierarchical structure is highly advantageous for capacitive deionization: micropores provide abundant adsorption sites, while mesopores act as transport channels that reduce diffusion limitations. The larger mesopore contribution observed for graphitized cornstarch compared with AC aligns with its higher salt adsorption capacity and faster adsorption kinetics (SAR) reported earlier, confirming the close relationship between pore architecture and CDI performance.
3.2. Electrode electrochemistry
The combination of low Rs, negligible Rct, and a capacitive/Warburg tail points to fast charging/discharging of the electric double layer which results in a higher desalination rate. Moreover, the efficient ion transport through accessible pores leads to greater salt electrosorption at a given potential. Furthermore, lower polarization/energy consumption during cycling improves the energy efficiency and stability.
Overall, the EIS response corroborates the structural picture from XRD/Raman: defect-rich, turbostratic sp2 carbon provides abundant adsorption sites (enhanced Cdl) while maintaining electronic pathways that minimize resistive losses, thereby supporting the strong CDI activity observed experimentally.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (carbonyl) and C–OH (hydroxyl), introduce pseudocapacitive behavior in addition to the double-layer capacitance typically observed in carbon-based materials. The pseudocapacitive contribution arises from faradaic reactions involving the redox activity of these surface groups, which cause the CV cycles to deviate from the ideal rectangular shape. In contrast, the AC electrode, which lacks significant functional groups, exhibits a nearly horizontal rectangular CV shape characteristic of pure double-layer capacitance, where the current response is primarily driven by the electrostatic adsorption/desorption of ions without faradaic reactions.
O (carbonyl) and C–OH (hydroxyl), introduce pseudocapacitive behavior in addition to the double-layer capacitance typically observed in carbon-based materials. The pseudocapacitive contribution arises from faradaic reactions involving the redox activity of these surface groups, which cause the CV cycles to deviate from the ideal rectangular shape. In contrast, the AC electrode, which lacks significant functional groups, exhibits a nearly horizontal rectangular CV shape characteristic of pure double-layer capacitance, where the current response is primarily driven by the electrostatic adsorption/desorption of ions without faradaic reactions.
The current density increases with increasing scan rate for both electrodes. At higher scan rates, the rate of ion adsorption/desorption at the electrode–electrolyte interface increases, leading to a higher current response. However, at very high scan rates, the ions may not have sufficient time to fully access the pores of the electrode material, leading to a decrease in specific capacitance.
The specific capacitance values were analyzed at different scan rates, revealing trends in electrochemical performance. The specific capacitance (Csp) is derived from CV curves using the following equation:38,39
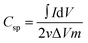 | (1) |
The graphitized cornstarch has a high surface area (332.28 m2 g−1, BET) and a balanced pore structure (micropores and mesopores), as evidenced by the BET, BJH, and DFT results. This allows for efficient ion adsorption and access to active sites. The micropore volume (0.3182 cm3 g−1) of the graphitized cornstarch is higher than that of AC, contributing to its higher specific capacitance. The graphitized cornstarch exhibits high electrical conductivity due to the formation of graphitic carbon during the high-temperature treatment (1000 °C). This facilitates efficient charge transfer and enhances the capacitive performance.
The significantly higher specific capacitance of the graphitized cornstarch, compared to activated carbon, despite its lower surface area, can be partially attributed to the presence of residual functional groups on its surface. During the graphitization process, some oxygen-containing functional groups (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–OH, and COOH) may remain on the surface of the graphitized cornstarch, as evidenced by the numerous small peaks in the FTIR spectrum. These functional groups can introduce pseudocapacitive behavior, where faradaic reactions occur at the surface, enhancing the overall charge storage capacity. Additionally, these groups can improve the wettability of the material, facilitating better electrolyte penetration and ion adsorption. In contrast, AC, despite its higher surface area, may lack such functional groups, leading to a lower specific capacitance due to the absence of pseudocapacitive contributions.40 Thus, the combination of double-layer capacitance from the graphitic structure and pseudocapacitance from residual functional groups likely contributes to the superior electrochemical performance of the graphitized cornstarch.41 The warped flake-like structure observed in the SEM images provides a high surface area and mechanical flexibility, which are beneficial for charge storage and electrode stability. The mesoporous structure of the graphitized cornstarch allows for better electrolyte penetration and ion diffusion compared to AC, leading to higher capacitance.42
O, C–OH, and COOH) may remain on the surface of the graphitized cornstarch, as evidenced by the numerous small peaks in the FTIR spectrum. These functional groups can introduce pseudocapacitive behavior, where faradaic reactions occur at the surface, enhancing the overall charge storage capacity. Additionally, these groups can improve the wettability of the material, facilitating better electrolyte penetration and ion adsorption. In contrast, AC, despite its higher surface area, may lack such functional groups, leading to a lower specific capacitance due to the absence of pseudocapacitive contributions.40 Thus, the combination of double-layer capacitance from the graphitic structure and pseudocapacitance from residual functional groups likely contributes to the superior electrochemical performance of the graphitized cornstarch.41 The warped flake-like structure observed in the SEM images provides a high surface area and mechanical flexibility, which are beneficial for charge storage and electrode stability. The mesoporous structure of the graphitized cornstarch allows for better electrolyte penetration and ion diffusion compared to AC, leading to higher capacitance.42
The specific capacitance decreases with increasing scan rate for both materials. At low scan rates, ions have sufficient time to access the entire pore structure of the electrode material, including deep micropores, leading to higher specific capacitance. At high scan rates, ions can only access the outer surface and larger pores due to time constraints, resulting in a decrease in specific capacitance. This phenomenon is known as rate limitation or diffusion limitation.43
The specific capacitance of graphitized cornstarch is highly dependent on the calcination temperature, as evidenced by the results in Fig. 10. The specific capacitance values for dried cornstarch graphitized (in 0.5 M NaCl) at 800, 1000, and 1100 °C are 125, 1088, and 690 F g−1, respectively. This trend indicates that 1000 °C is the optimum calcination temperature for achieving the highest specific capacitance. The observed behavior can be explained by the interplay between surface active groups, structural ordering, and electrical conductivity at different graphitization temperatures.
 | ||
| Fig. 10 Effect of calcination temperature on the specific capacitance (in 0.5 M NaCl) of the graphitized cornstarch. | ||
At 800 °C, the cornstarch undergoes partial carbonization, but the graphitization process is incomplete. The material retains a significant amount of oxygen-containing functional groups (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–OH) and disordered carbon structures, as indicated by the FTIR spectrum. While these functional groups can introduce pseudocapacitive behavior, the lack of sufficient graphitic ordering and electrical conductivity limits the overall charge storage capacity.44 The low surface area and poor ion accessibility at this temperature further contribute to the low specific capacitance.
O, C–OH) and disordered carbon structures, as indicated by the FTIR spectrum. While these functional groups can introduce pseudocapacitive behavior, the lack of sufficient graphitic ordering and electrical conductivity limits the overall charge storage capacity.44 The low surface area and poor ion accessibility at this temperature further contribute to the low specific capacitance.
At 1000 °C, the cornstarch undergoes complete carbonization and partial graphitization, resulting in a well-balanced structure with both graphitic domains and residual functional groups. The graphitic domains provide high electrical conductivity and facilitate efficient charge transfer, while the residual functional groups introduce pseudocapacitive behavior, enhancing the overall specific capacitance. The material also develops a porous structure with a high surface area (332.28 m2 g−1, BET) and a balanced distribution of micropores and mesopores, as evidenced by the BET and BJH results. This allows for efficient ion adsorption and electrolyte penetration. The combination of double-layer capacitance (from the graphitic structure) and pseudocapacitance (from surface functional groups) results in the highest specific capacitance at this temperature.
At 1100 °C, the cornstarch undergoes extensive graphitization, leading to the formation of highly ordered graphitic carbon with minimal residual functional groups. While the electrical conductivity of the material increases, the loss of surface-active groups reduces the pseudocapacitive contributions, leading to a decrease in specific capacitance compared to the sample graphitized at 1000 °C. Additionally, the pore structure may collapse or become less accessible at such high temperatures, further reducing the ion adsorption capacity and specific capacitance.
The specific capacitance of graphitized cornstarch is influenced by the ionic concentration of the electrolyte, as demonstrated by the results in Fig. 11. At a scan rate of 1 mV s−1, the specific capacitance values for 0.1, 0.3, 0.5, 0.7, and 1.0 M NaCl solutions are 1161.2, 1365.3, 1088.7, 1047, and 1470.8 F g−1, respectively. This non-linear dependence of specific capacitance on NaCl concentration can be attributed to the interplay between ionic conductivity, ion accessibility, and electrode–electrolyte interactions. Additionally, the 0.7 M NaCl solution exhibits the highest specific capacitance at higher scan rates, which can be explained by its optimal balance between ionic mobility and ion size.
 | ||
| Fig. 11 Effect of NaCl solution concentration on the specific capacitance of the graphitized cornstarch prepared at 1000 °C. | ||
The specific capacitance does not increase linearly with NaCl concentration. At low NaCl concentrations (e.g., 0.1 M), the ionic conductivity of the electrolyte is relatively low, limiting the number of ions available for adsorption at the electrode surface. This results in a lower specific capacitance. As the concentration increases (e.g., 0.3 M), the ionic conductivity improves, leading to a higher specific capacitance due to better ion accessibility and adsorption. At intermediate concentrations (e.g., 0.5 M), the specific capacitance may decrease slightly due to ion crowding or steric hindrance, where the increased number of ions competes for adsorption sites, reducing the efficiency of ion adsorption. At higher concentrations (e.g., 0.7 M and 1.0 M), the specific capacitance increases again due to the higher ionic strength and improved ion mobility, which enhance the charge storage capacity.
The non-linear trend may also be influenced by the interaction between the electrolyte ions and the electrode surface. At certain concentrations, the ions may form a more efficient double layer, leading to higher capacitance, while at other concentrations, the interactions may be less favorable. The 0.7 M NaCl solution exhibits the highest specific capacitance at higher scan rates. At higher scan rates, the rate of ion adsorption/desorption becomes critical. The 0.7 M NaCl solution provides an optimal balance between ionic concentration and ion mobility, allowing for rapid ion transport and efficient charge storage even at high scan rates. Compared to the 1.0 M NaCl solution, the 0.7 M solution has a lower ion concentration, which reduces the risk of ion crowding and steric hindrance at the electrode surface. This ensures that ions can access the pores more efficiently, even at high scan rates. Higher NaCl concentrations (e.g., 1.0 M) may increase the viscosity of the electrolyte, slowing down ion diffusion and reducing the specific capacitance at high scan rates. The 0.7 M solution strikes a balance between ionic strength and viscosity, enabling better performance.
3.3. CDI cell performance
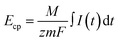 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), m is the mass of the active material in the two electrodes, I(t) is the measured current as a function of time, and
485 C mol−1), m is the mass of the active material in the two electrodes, I(t) is the measured current as a function of time, and 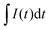 represents the total charge transferred (Coulombs) during ion adsorption.
represents the total charge transferred (Coulombs) during ion adsorption.
Additionally, the cyclic nature of chronoamperometry mimics the real-world operation of CDI systems, making it a reliable method for evaluating the durability, reversibility, and kinetics of the electrode material.
The chronoamperometry results for the CDI cells assembled using graphitized cornstarch and activated carbon electrodes (Fig. 12) reveal significant differences in their ion adsorption/desorption behavior, which can be attributed to their distinct specific capacitances, structural properties, and electrochemical performance. The graphitized cornstarch electrode (Fig. 12A) exhibits significantly higher starting currents during both the adsorption and desorption phases compared to the AC electrode. For example, in the first cycle, the starting positive current for the graphitized cornstarch (75.9 mA) is 10 times higher than that for the AC electrode (Fig. 12B, 7.53 mA). This is consistent with the much higher specific capacitance of the graphitized cornstarch, which allows for a larger amount of ions to be adsorbed and desorbed rapidly. The higher starting currents in the graphitized cornstarch electrode are attributed to its well-developed porous structure, high electrical conductivity, and residual functional groups, which enhance both double-layer capacitance and pseudocapacitance.
 | ||
| Fig. 12 Chronoamperometry with switching polarity at 1.2 V for CDI cells using graphitized cornstarch (1000 °C sample) (A) and pristine AC (B) electrodes using a 0.03 M NaCl solution. | ||
The higher absolute value of the starting negative current after polarity reversal is due to the rapid release of adsorbed ions under the reversed electric field. The starting positive current in the second cycle is higher than in the first cycle because the electrode has been conditioned during the first cycle, improving ion accessibility and adsorption kinetics. The increase in the absolute starting negative current in the second cycle is less pronounced because most of the adsorbed ions have already been released during the first desorption phase. The fixed currents in the second cycle are nearly identical to those in the first cycle because the electrode has reached a stable adsorption/desorption equilibrium, where the rates of ion adsorption and desorption are balanced.
The fixed currents for the graphitized cornstarch electrode (27.8 mA and -29.3 mA) are orders of magnitude higher than those for the AC electrode (∼0.25 mA and ∼-0.26 mA). This reflects the superior steady-state ion adsorption/desorption rates of the graphitized cornstarch, which is again attributed to its higher specific capacitance and better ion accessibility. The AC electrode, despite its high surface area, exhibits much lower fixed currents, indicating slower ion adsorption/desorption kinetics and lower ion storage capacity.
Both electrodes exhibit a similar decline rate in the current after the initial sharp decrease, with a current dropping rate of 5 × 10−4 mA s−1. This indicates that the kinetics of ion adsorption/desorption are similar for both materials once the initial rapid process is complete. However, the magnitude of the current is much higher for the graphitized cornstarch, reflecting its greater ion storage capacity and superior electrochemical performance.
The specific capacitance of the graphitized cornstarch (1088.7 F g−1) is 15 times higher than that of the AC electrode (73.5 F g−1). This difference is directly reflected in the current response during chronoamperometry, where the graphitized cornstarch exhibits much higher currents during both the adsorption and desorption phases. The higher specific capacitance of the graphitized cornstarch is attributed to its well-developed porous structure, high electrical conductivity, and residual functional groups, which enhance both double-layer capacitance and pseudocapacitance.45
The graphitized cornstarch electrode demonstrates superior electrosorption performance compared to the AC electrode, making it a promising candidate for CDI applications. Its high specific capacitance and efficient ion adsorption/desorption kinetics enable faster and more effective removal of ions from solution. The residual functional groups on the graphitized cornstarch surface enhance its pseudocapacitive behavior, further contributing to its high performance.
The high maximum electrosorption capacity of the graphitized cornstarch electrode (11.3 mg g−1, Fig. 13) is consistent with its high specific capacitance, which reflects its ability to store a large amount of charge through double-layer capacitance and pseudocapacitance. The well-developed porous structure of the graphitized cornstarch, with a balanced distribution of micropores and mesopores, allows for efficient ion adsorption and electrolyte penetration. The residual functional groups (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–OH) on the surface of the graphitized cornstarch enhance its pseudocapacitive behavior, contributing to the high electrosorption capacity. The low maximum electrosorption capacity of the AC electrode (0.3 mg g−1) is consistent with its low specific capacitance, which limits its ability to adsorb ions effectively. Although AC has a high surface area, its pore structure may not be optimized for ion adsorption in CDI applications, leading to lower performance. The absence of significant pseudocapacitive contributions further limits the electrosorption capacity of the AC electrode. In addition to salt adsorption capacity, the salt adsorption rate (SAR) was calculated to evaluate the kinetics of ion removal. At 0.03 M NaCl, the graphitized cornstarch electrode exhibited a SAC of ∼11 mg g−1 within 280 s, corresponding to a SAR of 2.36 mg g−1 min−1. In contrast, the commercial activated carbon electrode showed only ∼0.4 mg g−1 over the same time, giving a SAR of 0.086 mg g−1 min−1. The nearly 30-fold higher SAR of graphitized cornstarch highlights the fast ion adsorption kinetics, which can be attributed to the synergistic effect of hierarchical porosity and the conductive turbostratic graphitic domains that reduce ion-transport resistance. These results further confirm the superior CDI performance of graphitized cornstarch compared to conventional carbons.
O, C–OH) on the surface of the graphitized cornstarch enhance its pseudocapacitive behavior, contributing to the high electrosorption capacity. The low maximum electrosorption capacity of the AC electrode (0.3 mg g−1) is consistent with its low specific capacitance, which limits its ability to adsorb ions effectively. Although AC has a high surface area, its pore structure may not be optimized for ion adsorption in CDI applications, leading to lower performance. The absence of significant pseudocapacitive contributions further limits the electrosorption capacity of the AC electrode. In addition to salt adsorption capacity, the salt adsorption rate (SAR) was calculated to evaluate the kinetics of ion removal. At 0.03 M NaCl, the graphitized cornstarch electrode exhibited a SAC of ∼11 mg g−1 within 280 s, corresponding to a SAR of 2.36 mg g−1 min−1. In contrast, the commercial activated carbon electrode showed only ∼0.4 mg g−1 over the same time, giving a SAR of 0.086 mg g−1 min−1. The nearly 30-fold higher SAR of graphitized cornstarch highlights the fast ion adsorption kinetics, which can be attributed to the synergistic effect of hierarchical porosity and the conductive turbostratic graphitic domains that reduce ion-transport resistance. These results further confirm the superior CDI performance of graphitized cornstarch compared to conventional carbons.
 | ||
| Fig. 14 Chronoamperometry with switching polarity at 1.0 V for CDI cells using graphitized cornstarch (1000 °C sample) electrodes for three successive cycles using a 0.02 M NaCl solution. | ||
The starting current in the first cycle (25.7 mA) is relatively low compared to subsequent cycles. This is because the electrode is in its initial state, and the ion adsorption process is limited by the lack of conditioning. The electrode surface and pores are not yet fully accessible to the ions, leading to a lower initial current. The starting current in the second cycle (44.7 mA) is significantly higher than in the first cycle. This is due to the conditioning effect, where the electrode undergoes structural and surface modifications during the first cycle, improving ion accessibility and adsorption kinetics. The electrode becomes more efficient at adsorbing ions, leading to a higher starting current. The starting current in the third cycle (46.4 mA) is very close to that in the second cycle, indicating that the electrode has reached a stable conditioned state. The ion adsorption process is now optimized, and the electrode exhibits consistent performance in subsequent cycles. In the fourth and subsequent cycles (data are not shown), the starting current remains almost constant, confirming that the electrode has achieved a steady-state condition. The electrode surface and pores are fully accessible, and the ion adsorption process is highly efficient.
The constant current region represents the steady-state ion adsorption rate after the initial rapid adsorption process. The value of ∼6.3 mA indicates the rate at which ions are continuously adsorbed onto the electrode surface under the applied voltage. This steady-state current is maintained as long as the electrode is not saturated and the electrolyte concentration remains constant. After reversing the polarity, the constant negative current of ∼−0.7 mA represents the steady-state ion desorption rate. The lower absolute value compared to the positive constant current indicates that the desorption process is slower than the adsorption process. This is because the desorption process is driven by the reversed electric field, which may not be as efficient as the initial adsorption process.
 | ||
| Fig. 15 Chronoamperometry with switching polarity at different voltages for CDI cells using graphitized cornstarch (1000 °C sample) electrodes using a 0.03 M NaCl solution. | ||
A high jump in the starting current is observed when the applied voltage is increased from 1.5 V to 2.0 V. Numerically, the starting current increases from 105.3 mA cm−2 at 1.5 V to 236.2 mA cm−2 at 2.0 V. At 2.0 V, the electric field strength is significantly higher, leading to a much faster and more efficient ion adsorption process. This results in a sharp increase in the starting current. Moreover, at higher voltages, faradaic reactions (e.g., water splitting, redox reactions) may begin to occur, contributing additional current to the system. These reactions are non-linear and can cause a sudden increase in the observed current. Furthermore, the higher voltage may also lead to further activation of the electrode surface, improving ion accessibility and adsorption kinetics.
The linear increase in starting current with applied voltage in the range of 0.8 V to 1.5 V suggests that this is the optimal voltage range for CDI operation. Within this range, the ion adsorption process is efficient and controlled, with minimal risk of faradaic reactions or electrode degradation. The high jump in the starting current at 2.0 V indicates that this voltage may be approaching the upper limit for safe and efficient CDI operation. At this voltage, the risk of faradaic reactions and electrode degradation increases, which could negatively impact the long-term performance of the CDI system.
The starting currents observed in this experiment are consistent with the conditioning effect observed in previous chronoamperometry results. The electrode exhibits higher starting currents as it becomes more conditioned and efficient at adsorbing ions. The steady-state current (after the initial sharp decrease) follows a similar trend with applied voltage, increasing linearly at lower voltages and exhibiting a high jump at 2.0 V. This reflects the steady-state ion adsorption rate, which is proportional to the applied voltage.
The electrosorption capacity of the graphitized cornstarch electrode was evaluated at different applied voltages (0.8 V, 1.0 V, 1.2 V, 1.5 V, and 2.0 V) in a CDI cell fed by a 0.03 M NaCl solution. The results, Fig. 16, indicate that the electrosorption capacity increases with increasing applied voltage as follows: 0.8 V: 7.1 mg g−1, 1.0 V: 9.2 mg g−1, 1.2 V: 11.3 mg g−1, 1.5 V: 14.8 mg g−1 and 2.0 V: 19.6 mg g−1. The electrosorption capacity increases with increasing applied voltage following a non-linear trend. The increase is more pronounced at higher voltages, particularly when the voltage is increased from 1.5 V to 2.0 V. The increase in electrosorption capacity with applied voltage is primarily driven by the strength of the electric field, which enhances the ion adsorption process at the electrode surface. A higher voltage creates a stronger electric field, attracting more ions to the electrode and increasing the electrosorption capacity. At lower voltages (e.g., 0.8 V to 1.5 V), the increase in electrosorption capacity is relatively gradual, reflecting the Ohmic behavior of the electrode–electrolyte system. The ion adsorption process is efficient and controlled within this voltage range. The electrosorption capacity exhibits a high jump when the applied voltage is increased from 1.5 V to 2.0 V, with the capacity increasing from 14.8 mg g−1 to 19.6 mg g−1. At 2.0 V, the electric field strength is significantly higher, leading to a much faster and more efficient ion adsorption process. This results in a sharp increase in the electrosorption capacity. Moreover, faradaic reactions may begin to occur, contributing additional charge storage capacity. These reactions are non-linear and can cause a sudden increase in the electrosorption capacity. The electrosorption capacity results are consistent with the chronoamperometry results, showing a linear increase in starting current with applied voltage in the range of 0.8 V to 1.5 V and a high jump at 2.0 V. This reflects the Ohmic response of the electrode–electrolyte system at lower voltages and the onset of faradaic reactions at higher voltages.
 | ||
| Fig. 16 Electrosorption capacitance for the graphitized cornstarch (1000 °C) in CDI cells working at different applied voltages and fed by a 0.03 NaCl solution. | ||
SAR was further analyzed at different applied voltages to evaluate the kinetics of ion removal. The graphitized cornstarch electrode achieved SAC values of ∼6, 9, 12, 15, and 20 mg g−1 within 280 s under 0.8, 1.0, 1.2, 1.5, and 2.0 V, respectively. These correspond to SAR values of 1.28, 1.93, 2.57, 3.21, and 4.28 mg g−1 min−1, showing a clear voltage-dependent enhancement in adsorption kinetics. The progressive increase in SAR with applied voltage is attributed to the stronger electric field driving ion transport into micropores, supported by the conductive turbostratic domains that reduce resistance and facilitate rapid double-layer charging. Importantly, no bubble formation or visible gas evolution was observed even at the maximum applied voltage of 2.0 V, confirming that the adsorption process is dominated by capacitive electrosorption rather than parasitic faradaic reactions.46
 | ||
| Fig. 17 Electrosorption capacitance for the graphitized cornstarch (1000 °C) in CDI cells working at 1.2 V and fed by different NaCl solutions. | ||
The electrosorption capacity exhibits a high jump when the NaCl concentration is increased from 0.03 M to 0.04 M, with the capacity increasing from 11.3 mg g−1 to 32.6 mg g−1. At 0.04 M, the ionic strength of the electrolyte is significantly higher, leading to a much faster and more efficient ion adsorption process. This results in a sharp increase in the electrosorption capacity. The higher NaCl concentration improves the ion mobility in the electrolyte, allowing for more efficient ion transport to the electrode surface and enhancing the adsorption process. The higher ionic strength may also lead to more favorable electrode–electrolyte interactions, improving ion accessibility and adsorption kinetics.
The gradual increase in electrosorption capacity with NaCl concentration in the range of 0.02 M to 0.03 M suggests that this is the optimal concentration range for CDI operation. Within this range, the ion adsorption process is efficient and controlled, with minimal risk of ion crowding or steric hindrance. The high jump in electrosorption capacity at 0.04 M indicates that this concentration may be approaching the upper limit for efficient CDI operation. At this concentration, the risk of ion crowding and steric hindrance increases, which could negatively impact the long-term performance of the CDI system. Operating the CDI cell at lower NaCl concentrations (e.g., 0.02 M to 0.03 M) is more energy-efficient, as the electrosorption capacity increases gradually with concentration, and the risk of ion crowding is minimized. At higher concentrations (e.g., 0.04 M), the energy efficiency may decrease due to the increased risk of ion crowding and the associated energy losses.
The effect of electrolyte concentration on the CDI performance was investigated. At 0.02, 0.03, and 0.04 M NaCl, the graphitized cornstarch electrode achieved SAC values of ∼8, 12, and 33 mg g−1 within 280 s, corresponding to SAR values of 1.71, 2.57, and 7.07 mg g−1 min−1, respectively. These results demonstrate a strong dependence of CDI performance on electrolyte concentration: higher initial salt concentration increases the number of available ions and enhances the driving force for electrosorption, resulting in significantly higher SAC and SAR. The excellent rate capability at elevated concentrations further highlights the efficient ion transport in the hierarchical pore structure of graphitized cornstarch, supported by its high conductivity and defect-rich graphitic domains.
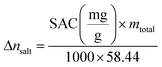 | (3) |
| Cell parameters | SAC (mg g−1) | SAR (mg g−1 min−1) | Δnsalt (mol g−1) | ΔC (mM g−1) | Cons. power (Wh mol−1) | Λ | ||
|---|---|---|---|---|---|---|---|---|
| Conc. (M) | Volt | Elec. | ||||||
| 0.03 | 1.2 | AC | 0.32 ± 0.02 | 0.09 ± 0.001 | 1.16 ± 0.05 × 10−6 | 7.76 × 10−3 ± 0.6 | 24.2 ± 2.3 | 1.33 ± 0.3 |
| 0.03 | 1.2 | Starch | 11.33 ± 0.7 | 2.57 ± 0.21 | 3.2 ± 0.11 × 10−5 | 0.213 ± 0.007 | 33.2 ± 3.5 | 0.97 ± 0.02 |
| 0.02 | 1.2 | Starch | 7.39 ± 0.6 | 1.71 ± 0.13 | 2.33 ± 0.15 × 10−5 | 0.155 ± 0.002 | 29.7 ± 2.7 | 1.08 ± 0.03 |
| 0.04 | 1.2 | Starch | 32.65 ± 1.2 | 7.07 ± 0.85 | 9.6 ± 0.91 × 10−5 | 0.64 ± 0.05 | 31.8 ± 2.9 | 1.01 ± 0.03 |
| 0.03 | 0.8 | Starch | 6.21 ± 0.45 | 1.28 ± 0.10 | 1.75 ± 0.21 × 10−5 | 0.116 ± 0.003 | 22.2 ± 1.9 | 0.967 ± 0.03 |
| 0.03 | 1.0 | Starch | 7.85 ± 0.51 | 1.93 ± 0.12 | 2.62 ± 0.21 × 10−5 | 0.175 ± 0.007 | 23.4 ± 1.9 | 1.15 ± 0.04 |
| 0.03 | 1.5 | Starch | 11.76 ± 0.72 | 3.21 ± 0.15 | 4.36 ± 0.37 × 10−5 | 0.291 ± 0.09 | 31.5 ± 2.6 | 1.28 ± 0.05 |
| 0.03 | 2.0 | Starch | 19.58 ± 1.01 | 4.28 ± 0.36 | 5.82 ± 0.11 × 10−5 | 0.388 ± 0.09 | 52.4 ± 4.7 | 1.02 ± 0.04 |
Energy consumption is a decisive parameter for practical applications, as it reflects the cost per mole of salt removed and allows benchmarking against state-of-the-art CDI electrodes. It can be calculated from the following equation:48
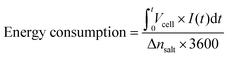 | (4) |
The results show that the graphitized cornstarch electrode achieves significantly higher Δnsalt and ΔC/g compared with commercial activated carbon, confirming its superior desalination capacity under identical conditions. Moreover, Δnsalt increases systematically with applied voltage and with feed concentration, in agreement with the enhanced SAC and SAR discussed earlier, demonstrating the electrode's ability to operate effectively under both low- and high-driving-force scenarios. Importantly, the energy consumption values remain in a moderate range (≈22–52 Wh mol−1 under all tested conditions) despite the high SAC values, which highlights the electrode's efficiency. At fixed voltage (1.2 V), the nearly constant energy consumption across different feed concentrations (≈30–32 Wh mol−1) further demonstrates stable energy performance, while the absence of visible gas evolution up to 2.0 V confirms the predominance of non-faradaic ion storage. Taken together, these parameters underscore the balance between high capacity, fast kinetics, and reasonable energy cost achieved by graphitized cornstarch, positioning it as a competitive sustainable electrode material for CDI.
The calculated charge efficiencies (Λ) (Λ = z × Δnsalt × F/Qcharge, where z = 1) for the different operating conditions are also summarized in Table 2.49 For the comparison between activated carbon and graphitized cornstarch electrodes, Λ values were 1.33 and 0.97, respectively. Although the AC electrode exhibited a value slightly above unity, this can be attributed to experimental uncertainties in charge integration and concentration calibration, which are commonly reported in the CDI literature. Importantly, the graphitized cornstarch electrode showed a Λ value close to unity, confirming that nearly all of the applied charge directly contributed to ion electrosorption.
At different NaCl concentrations (0.02–0.04 M), Λ values ranged from 1.01 to 1.08, demonstrating that the electrode maintains highly efficient charge utilization across a wide range of salinity. Similarly, the voltage series yielded Λ values between 0.97 and 1.45, with the highest values observed at elevated voltages. The slight overestimation above unity at 1.5–2.0 V is most likely due to capacitive charging dynamics and unavoidable experimental uncertainties, rather than true excess efficiency. Nevertheless, the overall results consistently indicate that the CDI process is dominated by non-faradaic double-layer electrosorption with minimal parasitic reactions.
These findings are in agreement with the electrochemical diagnostics (rectangular CVs, negligible Rct from EIS, absence of gas evolution up to 2.0 V), which collectively support the high reliability and efficiency of the graphitized cornstarch electrode for CDI applications.
The performance metrics reported in Table 2 represent the mean of at least three independent measurements (n ≥ 3), with standard deviations included. The low variability (generally <10% of the mean) confirms the reproducibility of electrode preparation and CDI testing. Minor deviations are attributed to expected differences in electrode coating thickness and electrode/electrolyte contact, but these do not affect the observed performance trends or the overall conclusions.
Although the CDI literature reports a wide range of performance metrics for electrodes such as activated carbons, graphene-based materials, CNTs, and MOF-derived carbons, a direct numerical comparison is complicated due to differences in experimental conditions, including salt concentration, cell architecture, applied voltage, and regeneration protocols. In this work, we selected commercial activated carbon as an internal benchmark because it was tested under identical conditions, ensuring a fair and scientifically valid comparison. The graphitized cornstarch electrode demonstrated a competitive salt adsorption capacity and stable cycling performance, which fall within the range of values reported for advanced carbonaceous electrodes. These results confirm that despite its lower surface area, the defect-rich turbostratic domains, favorable micro/mesoporosity, and high conductivity of the biomass-derived carbon enable efficient ion storage and transport. Thus, the material offers a sustainable and low-cost alternative to conventional high-performance carbons without compromising CDI efficiency.
The observed CDI performance of the graphitized cornstarch electrode can be attributed to a combination of structural and electrochemical factors. The micropores act as primary ion storage sites through non-faradaic electric double-layer formation, while the mesopores provide transport pathways that facilitate rapid ion diffusion into the microporous network, thereby reducing mass-transfer resistance and enhancing utilization of the internal surface. The presence of turbostratic graphitic domains, confirmed by XRD and Raman (ID/IG = 1.06), ensures efficient electronic conductivity, lowering resistive losses during charge–discharge processes. In addition, the defect-rich carbon regions identified by Raman and HRTEM introduce edge planes and adsorption sites, further improving ion accessibility. These features are supported by the EIS results, which reveal a small ohmic intercept, negligible charge-transfer resistance, and a predominantly capacitive response. Together, these mechanisms explain the favorable salt adsorption capacity, charge efficiency, and regeneration stability of the biomass-derived electrode.
The CDI performance of the graphitized cornstarch electrode compares favorably with a wide range of reported carbon-based materials. Typical SAC values for commercial activated carbons fall in the range of 2–8 mg g−1 at 10–50 mM NaCl and 1.2 V, with charge efficiencies (Λ) often below 0.8–0.9 due to co-ion expulsion. Biomass-derived carbons such as wood or coconut shell typically achieve 5–15 mg g−1 under similar batch conditions,50,51 while heteroatom-doped carbons can reach 10–20 mg g−1 but often at the expense of higher energy consumption.52,53 More advanced 2D materials such as MXenes and MOF-derived carbons have reported SAC values up to 20–25 mg g−1, yet usually require optimized flow configurations and ion-exchange membranes to maintain high Λ and energy efficiency. In contrast, the present graphitized cornstarch electrode delivered 11.3 mg g−1 at 0.03 M NaCl and 1.2 V in a simple batch-immersion cell without membranes, together with Λ ≈ 1.0, SAR ≈ 2.6 mg g−1 min−1, and moderate energy consumption (∼30 Wh mol−1). These results situate graphitized cornstarch among the best-performing biomass-derived carbons reported to date, demonstrating its promise as a sustainable and cost-effective CDI electrode.
4. Conclusions
This study demonstrates the potential of graphitized cornstarch as a sustainable and high-performance electrode material for capacitive deionization (CDI). Through thermal treatment at 1000 °C, cornstarch was transformed into a carbonaceous material with a well-developed porous structure, high electrical conductivity, and residual functional groups. The resulting electrode exhibited a specific capacitance of 1088.7 F g−1 and an electrosorption capacity of 11.3 mg g−1 in 0.03 M NaCl, significantly outperforming conventional activated carbon. The presence of residual functional groups contributed to pseudocapacitive behavior, enhancing ion adsorption and overall performance. The CDI cell assembled with graphitized cornstarch electrodes showed excellent stability and reversibility over multiple cycles, making it a promising candidate for practical desalination applications. The influence of applied voltage and NaCl concentration on electrosorption capacity was systematically studied, revealing that higher voltages and concentrations improve performance but may also increase energy consumption. These findings highlight the potential of biomass-derived carbon materials, such as graphitized cornstarch, to address water scarcity through sustainable and efficient CDI technology. Future work should focus on scaling up production and optimizing cell design for real-world applications.Declaration of AI use
We have used ChatGPT AI-assisted technology to improve the language.AI tool use disclosure
During the preparation of this work, the authors used ChatGPT (OpenAI) to improve grammar, clarity, and language expression. The authors reviewed and edited the content and take full responsibility for the final publication.Conflicts of interest
We declare we have no competing interests.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Acknowledgements
No funding has been received for this article.References
-
M. Thimmaraju, D. Sreepada, G. S. Babu, B. K. Dasari, S. K. Velpula and N. Vallepu, Desalination and water treatment, IntechOpen, 2018 Search PubMed
.
- D. S. Likhachev and F.-C. Li, Desalin. Water Treat., 2013, 51, 2836–2849 CrossRef
.
- M. Al-Abri, B. Al-Ghafri, T. Bora, S. Dobretsov, J. Dutta, S. Castelletto, L. Rosa and A. Boretti, NPJ Clean Water, 2019, 2, 2 CrossRef CAS
.
- L. F. Greenlee, D. F. Lawler, B. D. Freeman, B. Marrot and P. Moulin, Water Res., 2009, 43, 2317–2348 CrossRef CAS PubMed
.
- S. Al-Amshawee, M. Y. B. M. Yunus, A. A. M. Azoddein, D. G. Hassell, I. H. Dakhil and H. A. Hasan, Chem. Eng. J., 2020, 380, 122231 CrossRef CAS
.
- R. A. Kadhim, B. H. Khudhair and M. S. Jaafar, J. Eng., 2023, 29, 61–77 CrossRef
.
- L. Wang, Y. Zhang, K. Moh and V. Presser, Curr. Opin. Electrochem., 2021, 29, 100758 CrossRef CAS
.
- T. Kim, C. A. Gorski and B. E. Logan, Environ. Sci. Technol. Lett., 2017, 4, 444–449 CrossRef CAS
.
- P. Srimuk, X. Su, J. Yoon, D. Aurbach and V. Presser, Nat. Rev. Mater., 2020, 5, 517–538 CrossRef CAS
.
- M. Torkamanzadeh, C. Kök, P. R. Burger, P. Ren, Y. Zhang, J. Lee, C. Kim and V. Presser, Cell Rep. Phys. Sci., 2023, 4, 101661 CrossRef CAS
.
- L. Wang, J. Dykstra and S. Lin, Environ. Sci. Technol., 2019, 53, 3366–3378 CrossRef CAS PubMed
.
- Q. Wu, D. Liang, S. Lu, H. Wang, Y. Xiang, D. Aurbach, E. Avraham and I. Cohen, Desalination, 2022, 542, 116043 CrossRef CAS
.
- C. He, B. Lian, J. Ma, C. Zhang, Y. Wang, H. Mo and T. D. Waite, Water Res., 2021, 203, 117498 CrossRef CAS PubMed
.
- X. Zhao, H. Wei, H. Zhao, Y. Wang and N. Tang, J. Electroanal. Chem., 2020, 873, 114416 CrossRef CAS
.
- Y. Cheng, Z. Hao, C. Hao, Y. Deng, X. Li, K. Li and Y. Zhao, RSC Adv., 2019, 9, 24401–24419 RSC
.
- W. Wang, K. Li, G. Song, M. Zhou and P. Tan, Processes, 2022, 10, 2330 CrossRef CAS
.
- B. Jia and L. Zou, Carbon, 2012, 50, 2315–2321 CrossRef CAS
.
- A. Kalfa, T. R. Penki, I. Cohen, N. Shpigel, E. Avraham, D. Aurbach, D. Liang, Q. Wu, H. Wang and Y. Xiang, Desalination, 2020, 492, 114599 CrossRef CAS
.
- A. G. El-Deen, N. A. Barakat, K. A. Khalil and H. Y. Kim, J. Mater. Chem. A, 2013, 1, 11001–11010 RSC
.
- A. G. El-Deen, N. A. Barakat, K. A. Khalil and H. Y. Kim, New J. Chem., 2014, 38, 198–205 RSC
.
- J. Yang, L. Zou and N. R. Choudhury, Electrochim. Acta, 2013, 91, 11–19 CrossRef CAS
.
- S. Saini, P. Chand and A. Joshi, J. Energy Storage, 2021, 39, 102646 CrossRef
.
- Z. Xie, X. Shang, J. Yan, T. Hussain, P. Nie and J. Liu, Electrochim. Acta, 2018, 290, 666–675 CrossRef CAS
.
- J. Elisadiki, T. E. Kibona, R. L. Machunda, M. W. Saleem, W.-S. Kim and Y. A. Jande, Biomass Convers. Biorefin., 2020, 10, 1327–1356 CrossRef CAS
.
- S. Santangelo, F. Pantò, C. Triolo, S. Stelitano, P. Frontera, F. Fernández-Carretero, I. Rincon, P. Azpiroz, A. García-Luis and Y. Belaustegui, Electrochim. Acta, 2019, 309, 125–139 CrossRef CAS
.
- I. Siriwardane, N. Rathuwadu, D. Dahanayake, C. Sandaruwan, R. M. de Silva and K. N. de Silva, Nanoscale Adv., 2021, 3, 2585–2597 RSC
.
- Y. Jiang, S. I. Alhassan, D. Wei and H. Wang, Water, 2020, 12, 3030 CrossRef CAS
.
- S. Dahiya, A. Singh and B. K. Mishra, Chem. Eng. J., 2021, 417, 128129 CrossRef CAS
.
- W. Chen, X. He, Z. Jiang, B. Li, X.-Y. Li and L. Lin, Chem. Eng. J., 2023, 451, 139071 CrossRef CAS
.
- C. Pozo, S. Rodríguez-Llamazares, R. Bouza, L. Barral, J. Castaño, N. Müller and I. Restrepo, J. Polym. Res., 2018, 25, 1–8 CrossRef CAS
.
- Y. Ma, Z. Chen, Z. Wang, R. Chen and S. Zhang, Carbohydr. Polym., 2023, 310, 120737 CrossRef CAS PubMed
.
- C. W. Gee, J. Andersen-Ranberg, E. Boynton, R. Z. Rosen, D. Jorgens, P. Grob, H.-Y. N. Holman and K. K. Niyogi, Nat. Commun., 2024, 15, 5456 CrossRef CAS PubMed
.
- W. E. Richter, A. F. Silva, L. N. Vidal and R. E. Bruns, Phys. Chem. Chem. Phys., 2016, 18, 17575–17585 RSC
.
- O. Maslova, M. Ammar, G. Guimbretière, J.-N. Rouzaud and P. Simon, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134205 CrossRef
.
- R. Bardestani, G. S. Patience and S. Kaliaguine, Can. J. Chem. Eng., 2019, 97, 2781–2791 CrossRef CAS
.
- W. Zhang, Y. Liu, G. Lu, Y. Wang, S. Li, C. Cui, J. Wu, Z. Xu, D. Tian and W. Huang, Adv. Mater., 2015, 27, 2923–2929 CrossRef CAS PubMed
.
- S. R. Taylor and E. Gileadi, Corrosion, 1995, 51, 664–671 CrossRef CAS
.
- X. Ning, W. Zhong, S. Li, Y. Wang and W. Yang, J. Mater. Chem. A, 2014, 2, 8859–8867 RSC
.
- N. A. Barakat, A. G. El-Deen, G. Shin, M. Park and H. Y. Kim, Mater. Lett., 2013, 99, 168–171, DOI:10.1016/j.matlet.2013.03.034
.
- Y. Jiang and J. Liu, Energy Environ. Mater., 2019, 2, 30–37 CrossRef
.
- S. Aderyani, P. Flouda, S. Shah, M. Green, J. Lutkenhaus and H. Ardebili, Electrochim. Acta, 2021, 390, 138822 CrossRef CAS
.
- F. Xu, R. Cai, Q. Zeng, C. Zou, D. Wu, F. Li, X. Lu, Y. Liang and R. Fu, J. Mater. Chem., 2011, 21, 1970–1976 RSC
.
- B. Conway and W. Pell, J. Power Sources, 2002, 105, 169–181 CrossRef CAS
.
- M. Mirzaeian, Q. Abbas, M. R. Hunt and P. Hall, Energies, 2020, 13, 5577 CrossRef CAS
.
- X. Fan, Y. Lu, H. Xu, X. Kong and J. Wang, J. Mater. Chem., 2011, 21, 18753–18760 RSC
.
- A. Hassanvand, G. Q. Chen, P. A. Webley and S. E. Kentish, Water Res., 2018, 131, 100–109 CrossRef CAS PubMed
.
- C. Zhang, L. Wu, J. Ma, M. Wang, J. Sun and T. D. Waite, Water Res., 2020, 173, 115580 CrossRef CAS PubMed
.
- Y. Zhao, Y. Wang, R. Wang, Y. Wu, S. Xu and J. Wang, Desalination, 2013, 324, 127–133 CrossRef CAS
.
- T. Kim, J. Dykstra, S. Porada, A. van Der Waals, J. Yoon and P. Biesheuvel, J. Colloid Interface Sci., 2015, 446, 317–326 CrossRef CAS PubMed
.
- C. Jinitha, P. Abisha, S. Sonia and G. Bharath, Biomass Convers. Biorefin., 2025, 15, 16273–16306 CrossRef CAS
.
- N. H. Dan and T. Le Luu, Electrochim. Acta, 2024, 489, 144228 CrossRef CAS
.
- M. Gao, Y. Chen, W. Xiao, L. Miao, H. Kong, W. Liang, T. Ao, H. Mou and W. Chen, Sep. Purif. Technol., 2025, 359, 130803 CrossRef CAS
.
- Z. Wang, M. Gao, J. Peng, L. Miao, W. Chen and T. Ao, Int. J. Biol. Macromol., 2023, 241, 124596 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2025 |









