Unraveling the electronic control of hydride-ion diffusivity in oxyhydrides from model studies on BaTiO_3−2xH_x□_x

Abstract

Mixed hydride–electronic conductors are technologically important materials, but the mechanism of hydride-ion diffusivity is generally not fully understood. The diffusivities of hydride-ions and oxygen vacancies are closely related because hydride-ions are accommodated in oxygen vacancies, and a neighbouring oxygen vacancy is required for the inter-site migration of a hydride-ion. Here, we investigate the impact of electron localization in the hydride-ion-accepting oxygen vacancy on the inter-site hydride-ion migration dynamics in the perovskite-type oxyhydride BaTiO_3−2xH_x□_x (where □ denotes oxygen vacancies) using density functional theory (DFT). Supercell calculations were designed to model two (), one , and zero electrons localized in the hydride-ion-accepting site and correspondingly, zero, one, and two electrons delocalized in the conduction band formed from the Ti⁴⁺ 3d orbitals. 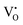It is found that the trapping of electrons causes the activation energy for inter-site migration to increase from 0.29 eV for , to 0.39 eV for , to 0.60 eV when turns into during the migration, and to 0.83 eV for . In an analogous way, the mobility of oxygen vacancies becomes increasingly hindered with increased electron occupation in the vacancies. This suggests that the tailoring of the degree of electron localization by, e.g., bandgap engineering or the introduction of electron trapping impurity states may be effective in tuning the hydride-ion conductivity in oxyhydrides, not limited to BaTiO_3−2xH_x□_x.

---

1 Introduction

Perovskite-type oxyhydrides (BaTiO_3−x−yH_x□_y, x < 0.6) represent a novel class of mixed-anion materials in which hydride-ions (H⁻) and oxide-ions (O²⁻) share the same anion sub-lattice.¹ BaTiO_3−x−yH_x□_y (x < 0.6) displays a mixed electron and H⁻ conductivity, which may be exploited for diverse applications in e.g., catalysis, topochemical synthesis, and electrochemistry.^2–5 A striking example is the high catalytic activity for ammonia synthesis when using BaTiO_3−x−yH_x□_y as a support for catalytic Fe and Ru nanoparticles.^2,6 This high catalytic activity is attributed to the H⁻ mobility through the BaTiO_3−x−yH_x□_y support as well as the donation of electrons from this support to the catalytic nanoparticles.² Therefore, both H⁻ and electronic conductivities are key to the performance of BaTiO_3−x−yH_x□_y in catalytic applications, and potentially in many other applications as well.

The H⁻ conductivity in BaTiO_3−x−yH_x□_y occurs, in part, through the hopping (migration) of H⁻ into adjacent vacant sites in the O²⁻ sub-lattice (V_O), as demonstrated by both experimental⁷ and theoretical studies.^4,8 Therefore, the formation of percolation pathways enabling H⁻ conduction throughout the material inherently depends on the diffusion of within the O²⁻ sub-lattice, which occurs via the migration of adjacent O or H⁻ into the . The electron conductivity, on the other hand, is due to the presence of H⁻ and/or in the sub-lattice, which act as n-type dopants of the empty 3d states of titanium (Ti).^9,10 When O²⁻ is replaced by H⁻ or when a forms, the valence electrons originally associated with , referred to as doping electrons, can adopt two possible states. They may either localize in the or near a Ti⁴⁺ ion, as an electron polaron, which results in a singly charged defect or a neutral defect (). This implies a semiconductor-like behavior of the material. Alternatively, they may delocalize across the Ti⁴⁺ sub-lattice and populate the conduction band (CB) as a band state, which results in a doubly charged defect . This implies a metal-like behaviour of the material.^11–14

Previous studies of BaTiO_3−x−yH_x□_y with y in the range of 0.1–0.31, combining DFT with experimental techniques such as inelastic neutron scattering (INS)¹⁵ and nuclear magnetic resonance (NMR),¹⁶ showed that the doping electrons form a band state. However, in ref. 15 it is shown that the energy difference between the two scenarios, electron polaron vs. band state, is low and lies in the range of −0.15 to 0.12 eV, depending on the H⁻ concentration and the DFT settings used. Similarly, in ref. 16 it is concluded that band states are prevalent but the existence of polarons cannot be ruled out. Therefore, the conclusion that the doping electrons always form band states cannot simply be generalized to all compositions of BaTiO_3−x−yH_x□_y (x, y < 0.6). In fact, both metal-like and semiconductor-like behaviors have been reported in various experimental studies.^1,9,11,17

Crucially, as observed in various transition metal oxide cathode materials, such as LiV₃O₈,¹⁸ LiV₂O₅,¹⁹ and LiFePO₄,²⁰ electron polarons can significantly influence the activation energy for ion conductivity. Nonetheless, for BaTiO_3−x−yH_x□_y, the H⁻ and electron conductivities have, to the best of our knowledge, been studied only independently, and the localization effects of the doping electrons were not explicitly taken into account.^4,8,21,22 As a result, the influence of electron localization on H⁻ conductivity remains unclear. Yet, elucidating the mechanisms underlying mixed hydride–electronic conductivity in BaTiO_3−x−yH_x□_y is essential for the rational design of new oxyhydrides and related technologies. Notably, electron localization engineering has been used to enhance catalytic activity, such as in CO₂ reduction, through dopant incorporation and nanostructuring.^23–25 These studies highlight the potential of controlling electron localization in the design of advanced catalysts.

Towards this aim, we build upon previous DFT studies by explicitly modeling the localization of doping electrons in BaTiO_3−2xH_x□_x and assessing its effect on H⁻ migration. We consider three cases with two (), one , and zero electrons localized in the hydride-ion-accepting site and correspondingly, zero, one, and two delocalized electrons in the conduction band. For each, we calculate the activation energy (E_a) for H⁻ migration to a neighboring oxygen vacancy. Rather than attempting to predict whether the doping electrons are localized or delocalized in BaTiO_3−2xH_x□_x, our aim is to establish a physical understanding of how their degree of localization influences H⁻ transport behavior.

2 Methodology

The DFT calculations were conducted using a plane wave basis set as implemented in the Vienna ab initio simulation package (VASP)^26–28, used with the projector augmented-wave method.²⁹ We used supercells containing 2 × 2 × 2 and 3 × 3 × 3 conventional unit cells of BaTiO₃ (39 and 134 atoms, respectively) and one H⁻ and one inserted next to each other, which correspond to BaTiO_2.75H_0.125□_0.125 and BaTiO_2.93H_0.037□_0.037. Another 2 × 2 × 2 supercell of composition BaTiO_2.75H_0.125□_0.125 was arranged in a channel geometry in such a way that the H⁻ and the form a linear chain along the crystallographic a axis. Additionally, the hydrogen-free but oxygen-vacancy containing material BaTiO_2.75□_0.25 and the fully stoichiometric material BaTiO₃ were modeled using a 2 × 2 × 2 supercell. All supercells are depicted in Fig. S1 of the Supporting Information (SI). Brillouin zones were sampled over Monkhorst–Pack grids of 5 × 5 × 5 points for the 2 × 2 × 2 supercells and 3 × 3 × 3 points for the 3 × 3 × 3 supercell. Spin-polarized calculations were conducted, where a cut-off energy of 500 eV was applied to the plane wave basis set and electronic structures were converged to energy changes less than 10⁻⁷ eV. Prior to calculating the electronic properties and E_a, every structure was optimized to relax inter-atomic forces below 10⁻⁴ eV Å⁻¹. Minimum energy paths and E_a were calculated using the nudged elastic band with a climbing image method.³⁰ The doping electrons are introduced in the system as a consequence of , as confirmed by calculations on BaTiO₃ and BaTiO_2.75□_0.25 (see the SI). Specifically, since charge neutrality is maintained in the calculations, introducing one in the supercell provides two doping electrons, while substituting one oxygen atom with a hydrogen atom yields one doping electron and one H⁻ ion . This results in a net total of three doping electrons, which can be found either localized near the , forming (high localization) or (partial localization), or delocalized over the Ti sub-lattice, forming (full delocalization).

Different combinations of exchange–correlation (XC) functionals and supercells are employed to investigate the impact of varying degrees of electron localization on H⁻ mobility. The functionals employed include the Perdew–Burke–Ernzerhof (PBEsol) functional, suitable for metallic bulk and surface systems,³¹ and the PBE functional³² within the DFT+U framework (further referred to as PBE+U).³³ They are summarized in Table 1 and further described in the following.

Table 1 Summary of the computational details and configurations of the doping electrons as considered in the calculation of E_a for inter-site migration of a H⁻ with a neighbouring . The charge state of was monitored at the initial state (I.S.) or at the transition state (T.S.)

Label	Setting	Composition	State of		E a (eV)
			I.S.	T.S.
a E a is given without zero-point vibrational energy correction.
(1) High localization	2 × 2 × 2 + PBE+U	BaTiO2.75H0.125□0.125			0.83
(2) Partial localization	2 × 2 × 2 + PBEsol	BaTiO2.75H0.125□0.125			0.60
(3) Partial localization	Channel + PBEsol	BaTiO2.75H0.125□0.125			0.39
(4) Full delocalization	3 × 3 × 3 + PBEsol	BaTiO2.93H0.037□0.037			0.29

---

(1) High localization () of the doping electrons was modeled using the PBE+U functional with the 2 × 2 × 2 supercell. The Hubbard correction (U = 3.3 eV) is applied here as a means to localize the doping electrons near Ti⁴⁺ ions, thereby compensating for the over-delocalization that is characteristic of standard XC functionals.³⁴ This approach has previously proven successful in modeling polarons in BaTiO_2.875H_0.125,¹⁵ a composition closely matching that of the 2 × 2 × 2 supercell used in this study, i.e., BaTiO_2.75H_0.125□_0.125. In ref. 15, the U parameter was tuned to reproduce a linear dependence of the total energy on the occupation of the polaronic level – a known property of the exact XC functional³⁵ – resulting in a calibrated value of U = 3.3 eV.

Fig. 1(a) shows the electronic band structure and the partial density of states (PDOS), revealing two defect (localized) states in the bandgap, close to the CB edge. The Fermi level is found above the CB edge, which indicates the presence of delocalized electrons in CB states, referred to as band states.

Fig. 1 Electronic band structure and orbital-decomposed (s, p, d) PDOS for each calculation setup. (a) High localization of doping electrons, (b) partial localization of doping electrons, (c) partial localization of doping electrons in the channel geometry, and (d) full delocalization of doping electrons. The PDOS of H is scaled 10× in (a)–(c) and 100× in (d). The dashed line represents the Fermi level. The orange and purple colors in the electronic band structures indicate localized (loc.) and delocalized (deloc.) states, respectively.

Fig. 2(a) shows real-space charge densities in the energy range of −2 to 0 eV, which, when integrated, account for a total of three doping electrons. One doping electron is delocalized over the whole Ti sub-lattice, occupying Ti orbitals of local t_2g symmetry, i.e. 3d_xz, 3d_xy, and 3d_yz orbitals [Fig. 2(a3)], which correspond to the occupied band states in the PDOS. Two doping electrons are localized near the [Fig. 2(a1 and a2)], which correspond to the two defect states in the PDOS. The defect state of lowest energy is localized around Ti3 and occupies a Ti orbital of t_2g symmetry, i.e. 3d_yz [Fig. 2(a1)], while the defect state of highest energy is shared between Ti1 and Ti3 orbitals of e_g symmetry, i.e. 3d_z² [Fig. 2(a2)]. Overall, two doping electrons reside near the , which results in . We note that H contributes in the valence band (VB) through its 1s orbital [Fig. 1(a) and Fig. S2]. Its hydridic character is confirmed by a Bader charge analysis,³⁶ showing an excess of ∼0.6 electrons, in agreement with a previous study on BaTiO_2.82H_0.1□_0.08.¹⁵

Fig. 2 Band-decomposed electron density isosurfaces at 10% for each calculation setup. (1) High localization of doping electrons, (2) partial localization of doping electrons, (3) partial localization of doping electrons in the channel geometry, and (4) full delocalization of doping electrons. Each row represents the three most populated bands in the energy range of −2 to 0 eV.

(2) Partial localization of the doping electrons was modeled using the PBEsol functional with a 2 × 2 × 2 supercell. Removing the Hubbard correction restores the over-delocalization characteristic of the XC functional and, consequently, more doping electrons are expected to form band states. However, one localized defect state remains in the bandgap, making this setting useful for studying a partially localized case [Fig. 1(b)]. This unexpected defect state is attributed to the periodic boundary conditions used in our supercell calculations, which result in the close ordering of along the Ti–□–Ti direction, leading to spurious □–□ interactions and causing electron localization. The real-space charge density shows two delocalized doping electrons occupying Ti t_2g orbitals [Fig. 2(b2 and b3)], which correspond to band states in the PDOS [Fig. 1(b)], and one localized doping electron occupying Ti1 and Ti3 e_g orbitals, corresponding to the defect state in the PDOS. Overall, only one doping electron resides near the , which results in .

(3) Partial localization in a channel. In the 2 × 2 × 2 supercell with PBEsol (2), the partial localization is due to spurious □–□ interactions. In the channel geometry, the are more closely packed along the □–H–□ direction, with a separation of 5.6 Å compared to 8 Å in the 2 × 2 × 2 supercell, thereby exacerbating the spurious interaction effects. At the initial state, the electronic structure in the channel geometry is similar to that of the 2 × 2 × 2 supercell with PBEsol (2). We observe one defect state in the band gap touching the CB edge, as well as occupied band states. Overall, one doping electron resides near the , resulting in [Fig. 1(c) and Fig. 2(c)]. However, due to the channel geometry, the degree of localization may differ from that of the 2 × 2 × 2 supercell during H⁻ migration, making this geometry an additional case of electron localization.

(4) Full delocalization of the doping electrons was modeled using the PBEsol functional with a 3 × 3 × 3 supercell. Given that the 2 × 2 × 2 supercell and the channel geometry cause electron localization due to spurious □–□ interactions, the 3 × 3 × 3 supercell was employed in order to mitigate the effect of periodic boundary conditions and obtain only delocalized electrons. Consequently, only band states are observed, as indicated by the band structure [Fig. 1(d)] and the real-space charge density [Fig. 2(d1–d3)]. Overall, no doping electron resides near the , which results in .

3 Results and discussion

After having established different degrees of electron localization, we now turn to investigate how this impacts the inter-site migration of a H⁻ with a neighbouring , which is also commonly referred to as the localized diffusion of H⁻. In previous studies, two H⁻ migration pathways were proposed. The first involves protonic species diffusing through interstitial sites and subsequently swapping positions with neighboring H⁻.^21,22 The second consists of H⁻ hopping into an adjacent while preserving its hydridic character.^4,7,8,16 Experimental studies have indicated that H⁻ migration occurs via the second pathway,^7,16 as no interstitial protonic species have been observed,³⁷ whereas the presence of has been confirmed.^10,37 Based on this, we modeled H⁻ migration according to the second pathway, where a H⁻ undergoes vacancy-mediated hopping. In order to identify the saddle point for the inter-site migration, the minimum energy path (MEP) was first calculated with 5 intermediate positions of the H⁻ in addition to the initial and final positions. This was done using the less computationally demanding setup PBEsol with a 2 × 2 × 2 supercell. Importantly, a Bader charge analysis at each configuration revealed an excess charge of approximately 0.6 electrons around the hydrogen atom, consistent with the value at the initial state, indicating that the hydrogen does not dissociate into a proton but retains its hydridic character throughout the migration process. The saddle point, further referred to as the transition state, is found exactly in the middle of the migration path, and the energy barrier is found to be symmetric around the transition state (Fig. 3). In our further calculations, only the transition state was thus calculated to save computational time.

Fig. 3 Schematic illustration of the H⁻ migration between two neighbouring together with the energy barrier for each calculation setup (the red points represent the calculated energies, and blue lines are polynomial fits). (a) High localization of doping electrons, (b) partial localization of doping electrons, (c) partial localization of doping electrons in the channel geometry, and (d) full delocalization of doping electrons. H⁻ is shown at the initial state (I.S.), transition state, and final state (F.S.), and part (b) shows, additionally, H⁻ at 5 intermediate states used for the MEP calculation. In yellow are overplotted isosurfaces at 10% of the maximum electronic density for bands in the energy range of −2 to 0 eV at the transition state.

At the transition state, two are symmetrically arranged around Ti3, thus constraining a doping electron localized in the initial to delocalize over both . As a result, the symmetry of the Ti3 3d_z² orbital is violated and cannot handle the doping electron at the transition state. Instead, the Ti3 3d_x²−y² and 3d_yz orbitals, initially well separated in the VB and CB, respectively, become mixed and accommodate the doping electron near Ti3. This band mixing affects the band structure and raises the energy levels of the defect states (see the SI). The position of the mixed bands, either in the band gap or in the CB, defines the degree of localization at the transition state, and therefore E_a. The main results are compiled in Table 1 and summarized in the following.

(1) For high localization of the doping electrons, the mixed states are located within the bandgap and are localized near Ti3 [Fig. 3(a)]. Because the electrons are confined near the jump path of H⁻, E_a increases as a result of an increase in Pauli repulsion between e⁻ and H⁻, and takes the value E_a = 0.83 eV.

(2) For partial localization of the doping electrons, the mixed states are located in the CB as band states (see the SI). In other words, at the initial state becomes at the transition state [Fig. 3(b)], which indicates that the localized electron uses the CB to swap position with H⁻. In this case, we calculate E_a = 0.60 eV, which reflects the energy cost to pump the doping electron to the CB.

(3) For partial localization in a channel geometry, one mixed state is a defect state, maintaining at the transition state, whereas the others are band states (see the SI). Interestingly, the doping electron, which was initially localized in the , relocates near Ti2 at the transition state [Fig. 3(c)]. This relocation is facilitated by the close periodic arrangement of along the □–H–□ direction, resulting in a lower E_a of 0.39 eV compared to (2) partial localization. Moreover, E_a is also found to be significantly lower than that of (1) high localization, at E_a = 0.83 eV, despite the presence of a localized doping electron. This reduction is due to the H⁻ and the localized electron migrating together in the same direction, whereas for (1) high localization, they must move against each other, intensifying their interaction.

(4) For full delocalization of the doping electrons, the electronic structure remains unchanged, that is, the three doping electrons form band states and is conserved during the H⁻ migration, which results in E_a = 0.29 eV [Fig. 3(d)]. Note that this value is very similar to E_a = 0.28 eV, as previously calculated⁸ in an equally large supercell, but using DFT+U instead of PBEsol. Since we find the same value with PBEsol, we conclude that in such low concentrations of H⁻ and , in spite of the Hubbard correction, doping electrons always tend to delocalize or are readily displaced. Such consistency among different calculation settings strongly indicates that we are accurately modeling the actual states of doping electrons in BaTiO_2.93H_0.037□_0.037, namely, band states. Another important observation is that the hydridic character is preserved at the transition state, as indicated by the Bader charge analysis showing an excess charge of ∼0.55 electrons, and that only the electrons forming H⁻ are displaced during the migration, with the rest of the doping electrons residing in the CB.

By combining the results from the four different degrees of localization, we observe that when a doping electron forming or must migrate against H⁻, it entails an additional cost in energy. This cost in energy depends on the degree of localization of the doping electron. When the electron is delocalized as a band state forming , which is favored by a lower concentration of H⁻ and , E_a is reduced. Conversely, when the doping electron remains localized during migration, as favored by the presence of an electron polaron, E_a increases. Interestingly, even in the presence of a localized doping electron, we find that E_a can still be reduced if the electron migrates in the same direction as H⁻, as enabled by the periodic arrangement of within the channel geometry.

To further assess the role of electron localization in H⁻ migration, we systematically depleted the doping electrons in our calculations and monitored the resulting changes in E_a. For both the PBEsol and PBE+U functionals, a consistent decrease in E_a was observed with increasing electron depletion. When all localized doping electrons were removed, E_a reached a minimum of approximately 0.4 eV, closely approaching the value of E_a = 0.28 eV obtained for case (4). These results confirm that the presence of localized electrons significantly hinders H⁻ migration (see details in the SI).

To verify that these results are not accidental nor dependent on the choice of the XC functional, we also carried out calculations using the hybrid functional HSE06.³⁸ The HSE06 calculations yielded one localized electron at both the initial and transition states, similar to case (1), and a comparable migration barrier of E_a = 0.89 eV (see details in the SI). The agreement in both activation energies and localization behavior confirms that this correspondence reflects the similar impact of both approaches on the system. This suggests that U parametrization offers a robust and transferable description of localization effects, providing a reliable framework for this material. This understanding provides an explanation for variations in E_a derived in previous DFT studies on H⁻ migration in BaTiO_3−x−yH_x□_y. On one hand, E_a was found to have a value of 0.28 eV,⁸ which approximates our case (4) of full electron delocalization. On the other hand, an E_a of 1 eV was derived⁴ close to our case (1) of high localization of the doping electrons. These varying results should be due to differences in the computational settings. While ref. 8 employed a 3 × 3 × 3 supercell, which is comparable to case (4), effectively modeling delocalized doping electrons, ref. 4 used a 2 × 2 × 2 supercell with a DFT+U functional, similar to case (1), thereby modeling localized doping electrons.

The present study also clarifies a fundamental distinction between proton and hydride migration by examining the influence of vibrational zero-point energy (ZPE) correction on E_a (see the SI for details on the calculation of the ZPE correction). For proton migration, ZPE corrections typically reduce E_a, as observed in various systems.^39–41 In contrast, we find that ZPE corrections increase E_a by approximately 0.01 eV in BaTiO_2.75H_0.125□_0.125. A comparison of the vibrational density of states between the initial/final states and the transition state reveals that one of the three H⁻ normal modes becomes imaginary at the transition state, while the other two exhibit an upward energy shift, resulting in the observed positive ZPE correction. The stiffening of these vibrational modes is interpreted as evidence of enhanced binding of H⁻ to the host lattice at the transition state and indicates that the H⁻ does not migrate on a single, adiabatic potential energy surface (PES) as a proton would,⁴² but instead follows a non-adiabatic path involving breaking and forming bonds governed by transitions between intersecting PESs associated with the initial and final states. This finding suggests that the migration barrier is predominantly electronic in origin, governed by non-adiabatic coupling between the initial and final state PES, in contrast to proton migration, where the barrier is primarily determined by ion–ion interactions.

It is also interesting to compare our calculated E_a with the values obtained for localized H⁻ diffusion from quasielastic neutron scattering (QENS) experiments. QENS studies on BaTiO_2.3H_0.04 reported an activation energy of E_a = 0.094 ± 0.002 eV,⁷ which aligns most closely with the value obtained for case (4) of full delocalization of the doping electrons. This consistency aligns with a previous combined DFT and INS study on BaTiO_2.82H_0.1□_0.08, which demonstrated that the doping electrons form a band state.¹⁵ Similarly, QENS studies on the oxyhydrides SrVO₂H and LaSrCoO₃H_0.7 – where H⁻ ions are incorporated into a perovskite lattice, occupying sites that share the corners of oxygen octahedra – have shown that migration proceeds via the same nearest-neighbor hopping mechanism observed in BaTiO_2.3H_0.04. These studies reported activation energies of E_a = 0.20 ± 0.035 eV⁴³ and E_a = 0.23 ± 0.045 eV,⁴⁴ respectively. These values are in closest agreement with the activation energy obtained for case (4), corresponding to full delocalization of the doping electrons. Interestingly, these materials are Mott insulators,^45–48 characterized by high electron localization on the V and Co ions, respectively. Our data thereby indicate that the doping electrons introduced in SrVO₂H and LaSrCoO₃H_0.7 by H⁻ and do not form localized states within the V_O but are instead localized near V and Co ions, or form band states. These observations suggest that H⁻ migration is a local feature, independent of whether the oxyhydride material as a whole is a Mott insulator or a conductor, as evidenced by the fact that no electrons, except those forming the H⁻ ion, are displaced during the migration in case (4) of full delocalization.

Finally, we compare our results to other classes of mixed electronic–ionic conductors, such as transition metal oxide cathode materials, where the interplay between electron polarons and ionic conductivity has been extensively studied.^{18–20,49–52} In these materials, the ionic charge carrier is a lithium cation (Li⁺), which interacts attractively with negatively charged electron polarons, leading to different outcomes compared to our findings. For example, in LiV₃O₈, LiV₂O₅, and LiCoO₂, it has been observed that the presence of electron polarons lowers E_a for Li⁺ diffusion, and their simultaneous migration with Li⁺ may be the driving force for Li⁺ diffusion.^18,19,49 Notably, E_a in these materials is generally around 0.3 eV, which is comparable to our determined E_a = 0.29 eV for case (4) – full delocalization of doping electrons. This suggests that our results cannot be generalized to all mixed electronic–ionic conductors and that the diffusing ionic species drastically affects the effect of electron polarons.

4 Conclusions

To conclude, we have shown that the degree of electron localization has a considerable impact on the activation energy E_a for the inter-site migration of a H⁻ in BaTiO_3−2xH_x□_x. Specifically, we find that E_a exhibits a systematic decrease with less localization of the doping electrons. Since the degree of electron localization is an intrinsic material property, this may open up avenues for the rational design of oxyhydrides with tailored H⁻ conductivity, e.g., by reducing the bandgap via cation substitutions to the Ti site^53,54 to promote the delocalization of doping electrons into the conduction band. Additionally, we have highlighted the application of vibrational zero-point energy corrections as a conceptual tool to distinguish between proton and H⁻ transport mechanisms in oxyhydride materials.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

Data from this study are openly available from the Swedish National Data Service (SND) at https://doi.org/10.71870/x76p-bp52.

Supplementary information (SI): additional band structure, PDOS, and real-space electron density plots. See DOI: https://doi.org/10.1039/d5ma00521c.

Acknowledgements

M. K. acknowledges the support from the Swedish Research Council (Grant No. 2021-04807 and 2016-06958) and the Swedish Energy Agency (Grant No. 48712-1). M. K. and M. M. K. acknowledge the support from the ILL (Grant No. ILL-1880.1). The computational resources were provided by the Swedish National Infrastructure for Computing (SNIC) in the C3SE center, Gothenburg, and by the ILL.

References

1. Y. Kobayashi, O. J. Hernandez, T. Sakaguchi, T. Yajima, T. Roisnel, Y. Tsujimoto, M. Morita, Y. Noda, Y. Mogami and A. Kitada, et al., An oxyhydride of BaTiO₃ exhibiting hydride exchange and electronic conductivity, Nat. Mater., 2012, 11, 507–511.
2. Y. Tang, Y. Kobayashi, N. Masuda, Y. Uchida, H. Okamoto, T. Kageyama, S. Hosokawa, F. Loyer, K. Mitsuhara, K. Yamanaka, Y. Tamenori, C. Tassel, T. Yamamoto, T. Tanaka and H. Kageyama, Metal-Dependent Support Effects of Oxyhydride-Supported Ru, Fe, Co Catalysts for Ammonia Synthesis, Adv. Energy Mater., 2018, 8, 1801772.
3. Y. Kobayashi, Y. Tang, T. Kageyama, H. Yamashita, N. Masuda, S. Hosokawa and H. Kageyama, Titanium-Based Hydrides as Heterogeneous Catalysts for Ammonia Synthesis, J. Am. Chem. Soc., 2017, 139, 18240–18246.
4. Y. Tang, Y. Kobayashi, K. Shitara, A. Konishi, A. Kuwabara, T. Nakashima, C. Tassel, T. Yamamoto and H. Kageyama, On Hydride Diffusion in Transition Metal Perovskite Oxyhydrides Investigated via Deuterium Exchange, Chem. Mater., 2017, 29, 8187–8194.
5. T. Sakaguchi, et al., Oxyhydrides of (Ca,Sr,Ba)TiO₃ Perovskite Solid Solutions, Inorg. Chem., 2012, 51, 11371–11376.
6. Y. Goto, M. Kikugawa, K. Kobayashi, Y. Manaka, T. Nanba, H. Matsumoto, M. Matsumoto, M. Aoki and H. Imagawa, Facile Formation of Barium Titanium Oxyhydride on a Titanium Hydride Surface as an Ammonia Synthesis Catalyst, RSC Adv., 2023, 13, 15410–15415.
7. C. Eklöf-Österberg, R. Nedumkandathil, U. Häussermann, A. Jaworski, A. J. Pell, M. Tyagi, N. H. Jalarvo, B. Frick, A. Faraone and M. Karlsson, Dynamics of Hydride Ions in Metal Hydride-Reduced BaTiO₃ Samples Investigated with Quasielastic Neutron Scattering, J. Phys. Chem. C, 2019, 123, 2019–2030.
8. X. Liu, T. S. Bjørheim and R. Haugsrud, Formation and migration of hydride ions in BaTiO_3−xH_x oxyhydride, J. Mater. Chem. A, 2017, 5, 1050–1056.
9. H. Guo, A. Jaworski, Z. Ma, A. Slabon, Z. Bacsik, R. Nedumkandathil and U. Häussermann, Trapping of different stages of BaTiO₃ reduction with LiH, RSC Adv., 2020, 10, 35356–35365.
10. R. Nedumkandathil, A. Jaworski, J. Grins, D. Bernin, M. Karlsson, C. Eklöf-Österberg, A. Neagu, C.-W. Tai, A. J. Pell and U. Häussermann, Hydride Reduction of BaTiO₃ – Oxyhydride Versus O Vacancy Formation, ACS Omega, 2018, 3, 11426–11438.
11. G. Bouilly, T. Yajima, T. Terashima, W. Yoshimune, K. Nakano, C. Tassel, Y. Kususe, K. Fujita, K. Tanaka, T. Yamamoto, Y. Kobayashi and H. Kageyama, Electrical Properties of Epitaxial Thin Films of Oxyhydrides ATiO_3−xH_x (A = Ba and Sr), Chem. Mater., 2015, 27, 6354–6359.
12. M. Schrader, D. Mienert, T.-S. Oh, H.-I. Yoo and K. D. Becker, An optical, EPR and electrical conductivity study of blue barium titanate, BaTiO_3−δ, Solid State Sci., 2008, 10, 768–775.
13. R. Scharfschwerdt, A. Mazur, O. F. Schirmer, H. Hesse and S. Mendricks, Oxygen vacancies in BaTiO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 15284–15290.
14. D. D. Cuong and J. Lee, Electronic structure of oxygen deficient BaTiO₃, Integr. Ferroelectr., 2006, 84, 23–30.
15. E. J. Granhed, A. Lindman, C. Eklöf-Österberg, M. Karlsson, S. F. Parker and G. Wahnström, Band vs. polaron: vibrational motion and chemical expansion of hydride ions as signatures for the electronic character in oxyhydride barium titanate, J. Mater. Chem. A, 2019, 7, 16211–16221.
16. R. Aleksis, R. Nedumkandathil, W. Papawassiliou, J. P. Carvalho, A. Jaworski, U. Häussermann and A. J. Pell, Probing the Electronic Structure and Hydride Occupancy in Barium Titanium Oxyhydride through DFT-assisted Solid-State NMR, Phys. Chem. Chem. Phys., 2022, 24, 28164–28173.
17. T. Yajima, A. Kitada, Y. Kobayashi, T. Sakaguchi, G. Bouilly, S. Kasahara, T. Terashima, M. Takano and H. Kageyama, Epitaxial thin films of ATiO_3−xH_x (A = Ba, Sr, Ca) with metallic conductivity, J. Am. Chem. Soc., 2012, 134, 8782–8785.
18. M. Chotsawat, L. Ngamwongwan, P. Komen, P. Falun, S. Jungthawan, A. Junkaew and S. Suthirakun, Insight into the Effect of Oxygen Vacancies on Ion Intercalation and Polaron Conduction in LiV₃O₈ Cathodes of Li-Ion Batteries, J. Phys. Chem. C, 2022, 126, 18216–18228.
19. S. Suthirakun, A. Genest and N. Rösch, Modeling Polaron-Coupled Li Cation Diffusion in V₂O₅ Cathode Material, J. Phys. Chem. C, 2018, 122, 150–157.
20. T. Maxisch, F. Zhou and G. Ceder, Ab initio study of the migration of small polarons in olivine Li_xFePO₄ and their association with lithium ions and vacancies, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104301.
21. J. Zhang, G. Gou and B. Pan, Study of Phase Stability and Hydride Diffusion Mechanism of BaTiO₃ Oxyhydride from First-Principles, J. Phys. Chem. C, 2014, 118, 17254–17259.
22. Y. Iwazaki, T. Suzuki and S. Tsuneyuki, Negatively charged hydrogen at oxygen-vacancy sites in BaTiO₃: Density-functional calculation, J. Appl. Phys., 2010, 108, 083705.
23. W. Lyu, Y. Liu, D. Chen, F. Wang and Y. Li, Engineering the electron localization of metal sites on nanosheets assembled periodic macropores for CO₂ photoreduction, Nat. Commun., 2024, 15, 10589.
24. Y. Zhou, et al., Dopant-induced electron localization drives CO₂ reduction to C₂ hydrocarbons, Nat. Chem., 2018, 10, 974–980.
25. S. Yan, C. Peng, C. Yang, Y. Chen, J. Zhang, A. Guan, X. Lv, H. Wang, Z. Wang, T.-K. Sham, Q. Han and G. Zheng, Electron Localization and Lattice Strain Induced by Surface Lithium Doping Enable Ampere-Level Electrosynthesis of Formate from CO₂, Angew. Chem., 2021, 133, 25945–25949.
26. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
27. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
28. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
29. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
30. G. Henkelman, B. P. Uberuaga and H. Jónsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904.
31. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Erratum: Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces [Phys. Rev. Lett. 100, 136406 (2008)], Phys. Rev. Lett., 2009, 102, 039902.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. V. I. Anisimov, J. Zaanen and O. K. Andersen, Band Theory and Mott Insulators: Hubbard U Instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
34. H. J. Kulik, Perspective: Treating Electron over-Delocalization with the DFT+U Method, J. Chem. Phys., 2015, 142, 240901.
35. J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy, Phys. Rev. Lett., 1982, 49, 1691–1694.
36. G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36, 354–360.
37. C. Eklöf-Österberg, L. Mazzei, E. J. Granhed, G. Wahnström, R. Nedumkandathil, U. Häussermann, A. Jaworski, A. J. Pell, S. F. Parker, N. H. Jalarvo, B. Lars and M. Karlsson, The role of oxygen vacancies on the vibrational motions of hydride ions in the oxyhydride of barium titanate, J. Mater. Chem. A, 2020, 8, 6360–6371.
38. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals, J. Chem. Phys., 2006, 125, 224106.
39. P. G. Sundell, M. E. Björketun and G. Wahnström, Density-functional calculations of prefactors and activation energies for H diffusion in BaZrO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 094301.
40. M. G. Wardle, J. P. Goss and P. R. Briddon, First-Principles Study of the Diffusion of Hydrogen in ZnO, Phys. Rev. Lett., 2006, 96, 205504.
41. J. A. Ryder, A. K. Chakraborty and A. T. Bell, Density Functional Theory Study of Proton Mobility in Zeolites: Proton Migration and Hydrogen Exchange in ZSM-5, J. Phys. Chem. B, 2000, 104, 6998–7011.
42. M. Björketun, P. Sundell, G. Wahnström and D. Engberg, A Kinetic Monte Carlo Study of Proton Diffusion in Disordered Perovskite Structured Lattices Based on First-Principles Calculations, Solid State Ion, 2005, 176, 3035–3040.
43. R. Lavén, U. Häussermann, A. Perrichon, M. S. Andersson, M. S. Targama, F. Demmel and M. Karlsson, Diffusional Dynamics of Hydride Ions in the Layered Oxyhydride SrVO₂H, Chem. Mater., 2021, 33, 2967–2975.
44. C. A. Bridges, F. Fernandez-Alonso, J. P. Goff and M. J. Rosseinsky, Observation of Hydride Mobility in the Transition-Metal Oxide Hydride LaSrCoO₃H_0.7, Adv. Mater., 2006, 18, 3304–3308.
45. T. Katayama, A. Chikamatsu, K. Yamada, K. Shigematsu, T. Onozuka, M. Minohara, H. Kumigashira, E. Ikenaga and T. Hasegawa, Epitaxial growth and electronic structure of oxyhydride SrVO₂H thin films, J. Appl. Phys., 2016, 120, 085305.
46. T. Yamamoto, D. Zeng, T. Kawakami, V. Arcisauskaite, K. Yata, M. A. Patino, N. Izumo, J. E. McGrady, H. Kageyama and M. A. Hayward, The role of π-blocking hydride ligands in a pressure-induced insulator-to-metal phase transition in SrVO₂H, Nat. Commun., 2017, 8, 1217.
47. C. A. Bridges, G. R. Darling, M. A. Hayward and M. J. Rosseinsky, Electronic Structure, Magnetic Ordering, and Formation Pathway of the Transition Metal Oxide Hydride LaSrCoO₃H_0.7, J. Am. Chem. Soc., 2005, 127, 5996–6011.
48. M. A. Hayward, E. J. Cussen, J. B. Claridge, M. Bieringer, M. J. Rosseinsky, C. J. Kiely, S. J. Blundell, I. M. Marshall and F. L. Pratt, The Hydride Anion in an Extended Transition Metal Oxide Array: LaSrCoO₃H_0.7, Science, 2002, 295, 1882–1884.
49. S. Ahn, J. Kim, B. Kim and S. Kim, First-principles study on small polaron and Li diffusion in layered LiCoO₂, Phys. Chem. Chem. Phys., 2023, 25, 27848–27853.
50. K. M. Bui, V. A. Dinh and T. Ohno, Diffusion Mechanism of Polaron–Li Vacancy Complex in Cathode Material Li₂FeSiO₄, Appl. Phys. Express, 2012, 5, 125802.
51. F. Amano, M. Nakata, A. Yamamoto and T. Tanaka, Effect of Ti³⁺ Ions and Conduction Band Electrons on Photocatalytic and Photoelectrochemical Activity of Rutile Titania for Water Oxidation, J. Phys. Chem. C, 2016, 120, 6467–6474.
52. V. A. Dinh, J. Nara and T. Ohno, A New Insight into the Polaron–Li Complex Diffusion in Cathode Material LiFe_1−yMn_yPO₄ for Li Ion Batteries, Appl. Phys. Express, 2012, 5, 045801.
53. S. Mukherjee, D. Phuyal, C. U. Segre, S. Das, O. Karis, T. Edvinsson and H. Rensmo, Structure and Electronic Effects from Mn and Nb Co-doping for Low Band Gap BaTiO₃ Ferroelectrics, J. Phys. Chem. C, 2021, 125, 14910–14923.
54. R. B. Comes, P. V. Sushko, S. M. Heald, R. J. Colby, M. E. Bowden and S. A. Chambers, Band-Gap Reduction and Dopant Interaction in Epitaxial La,Cr Co-doped SrTiO₃ Thin Films, Chem. Mater., 2014, 26, 7073–7082.

---