Open Access Article
Open Access ArticleSemiconducting ferromagnetism and thermoelectric performance of Rb2GeMI6 (M = V, Ni, Mn): a computational perspective
Mudasir Younis
Sofi
,
Mohd. Shahid
Khan
and
M. Ajmal
Khan
*
Department of Physics, Jamia Millia Islamia, New Delhi-110025, India. E-mail: majkhan@jmi.ac.in
First published on 4th March 2025
Abstract
We present a comprehensive first-principles investigation into the structural, electronic, magnetic, and transport properties of halide double perovskites Rb2GeMI6 (M = V, Mn, Ni) utilizing density functional theory (DFT). Structural stability is rigorously validated through geometric optimization, mechanical stability criteria, and tolerance factor analysis, confirming the feasibility of these compounds in the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. Total energy calculations based on the Birch–Murnaghan equation of state establish a robust ferromagnetic ground state, further corroborated by positive Curie–Weiss constants of 98 K (Rb2GeVI6), 90 K (Rb2GeMnI6), and 95 K (Rb2GeNiI6), underscoring their intrinsic ferromagnetic behavior. Electronic structure analyses performed using both the generalized gradient approximation (GGA) and the Tran–Blaha modified Becke–Johnson (TB-mBJ) potential reveal that these materials exhibit semiconducting ferromagnetism, characterized by a significant spin-splitting gap. The underlying mechanism is traced to the crystal field effects influencing the d-orbitals of the transition metal atoms. Magnetic moment calculations indicate values of 3μB, 5μB, and 2μB for the V-, Mn-, and Ni-based compounds, respectively, underscoring the pivotal role of transition metals in governing their magnetic properties. Furthermore, Curie temperature estimations of 530.39 K (Rb2GeVI6), 580.72 K (Rb2GeMnI6), and 440.47 K (Rb2GeNiI6) significantly exceed room temperature, reinforcing their potential for spintronic applications. A rigorous thermodynamic analysis, incorporating vibrational contributions to internal energy, Helmholtz free energy, entropy, and specific heat, confirms the stability of these materials across a broad temperature range. Finally, an in-depth investigation of transport properties, considering both temperature and chemical potential dependence of the Seebeck coefficient, electrical conductivity, and figure of merit (zT), highlights their exceptional thermoelectric potential. Notably, the materials exhibit remarkably low thermal conductivities of 3.10 W m−1 K−1 (Rb2GeVI6), 2.05 W m−1 K−1 (Rb2GeMnI6), and 1.57 W m−1 K−1 (Rb2GeNiI6), translating into impressive zT values of 1.00, 0.99, and 0.97 at room temperature. Overall, this study demonstrates that Rb2GeMI6 halide perovskites exhibit a unique synergy of structural stability, ferromagnetic semiconducting behavior, and high thermoelectric efficiency, positioning them as promising candidates for next-generation spintronic devices, thermoelectric energy harvesting, and sustainable energy technologies.
m phase. Total energy calculations based on the Birch–Murnaghan equation of state establish a robust ferromagnetic ground state, further corroborated by positive Curie–Weiss constants of 98 K (Rb2GeVI6), 90 K (Rb2GeMnI6), and 95 K (Rb2GeNiI6), underscoring their intrinsic ferromagnetic behavior. Electronic structure analyses performed using both the generalized gradient approximation (GGA) and the Tran–Blaha modified Becke–Johnson (TB-mBJ) potential reveal that these materials exhibit semiconducting ferromagnetism, characterized by a significant spin-splitting gap. The underlying mechanism is traced to the crystal field effects influencing the d-orbitals of the transition metal atoms. Magnetic moment calculations indicate values of 3μB, 5μB, and 2μB for the V-, Mn-, and Ni-based compounds, respectively, underscoring the pivotal role of transition metals in governing their magnetic properties. Furthermore, Curie temperature estimations of 530.39 K (Rb2GeVI6), 580.72 K (Rb2GeMnI6), and 440.47 K (Rb2GeNiI6) significantly exceed room temperature, reinforcing their potential for spintronic applications. A rigorous thermodynamic analysis, incorporating vibrational contributions to internal energy, Helmholtz free energy, entropy, and specific heat, confirms the stability of these materials across a broad temperature range. Finally, an in-depth investigation of transport properties, considering both temperature and chemical potential dependence of the Seebeck coefficient, electrical conductivity, and figure of merit (zT), highlights their exceptional thermoelectric potential. Notably, the materials exhibit remarkably low thermal conductivities of 3.10 W m−1 K−1 (Rb2GeVI6), 2.05 W m−1 K−1 (Rb2GeMnI6), and 1.57 W m−1 K−1 (Rb2GeNiI6), translating into impressive zT values of 1.00, 0.99, and 0.97 at room temperature. Overall, this study demonstrates that Rb2GeMI6 halide perovskites exhibit a unique synergy of structural stability, ferromagnetic semiconducting behavior, and high thermoelectric efficiency, positioning them as promising candidates for next-generation spintronic devices, thermoelectric energy harvesting, and sustainable energy technologies.
1. Introduction
The progression of modern technology necessitates the optimization of information processing and storage with maximum efficiency. Future research in this domain is anticipated to focus on spintronics, which utilizes electron spin as an additional degree of freedom, distinguishing it from conventional charge-based electronics.1,2 Compared to conventional electronics, spintronic devices promise lower power consumption, ultrafast operation, and non-volatility, making them essential for next-generation applications such as magnetoresistive random-access memory (MRAM), spin valves, and magnetic sensors.3–5 The successful realization of spintronics, however, relies on the development of materials that exhibit both robust ferromagnetism and semiconducting behavior, known as magnetic semiconductors.6 Over the years, various materials, including Eu- and Mn-based chalcogenide,7–9 spinel oxides,10,11 and Mn-doped II–VI and III–V semiconductors,12–15 have been explored for their potential to integrate spin functionality with semiconductor properties. While these materials have demonstrated promising spin-dependent transport properties, their low Curie temperatures, weak spin polarization, and limited structural stability hinder their practical application. To overcome these limitations, researchers have turned their attention to perovskite-based materials, a class known for their structural tunability, strong electron correlation effects, and exceptional charge transport properties.16 Within the perovskite family, oxide perovskites have been widely studied for spintronic applications due to their well-established synthesis and integration into microelectronic devices. However, halide perovskites, initially investigated for their superior optoelectronic performance, have recently attracted significant interest as potential candidates for magnetic and spintronic applications.17 The first indication of weak magnetism in Mn-doped methylammonium lead iodide (CH3NH3PbI3) by Náfrádi et al.18 provided early evidence of the feasibility of halide perovskites as magnetic semiconductors. Despite this breakthrough, their low Curie temperatures (<15 K), small spin splitting (<0.2 eV), and phase instability significantly limit their utility in practical spintronic devices. Given these challenges, there has been a growing interest in intrinsic magnetic semiconductors—materials that naturally exhibit ferromagnetism without external doping. In this context, double perovskite oxides (DPOs) have garnered attention due to their structural simplicity, tunable electronic states, and chemical versatility.19 However, their halide counterparts, double perovskite halides (DPHs), remain largely unexplored, despite their potential to bridge the gap between structural stability and strong magnetic interactions. Recent studies, such as those by Cai et al.,20 have demonstrated ferromagnetism in lead-free Cs2GeB′X6-type halide perovskites, opening new avenues for the development of stable, high-performance spintronic materials.Beyond advancements in spintronics, the increasing global demand for sustainable energy solutions and efficient waste heat recovery has intensified the search for high-performance thermoelectric materials capable of directly converting heat into electricity. To date, a plethora of materials have been reported to exhibit promising thermoelectric performance;21–25 however, many of them suffer from inherent limitations that hinder widespread practical application. Conventional inorganic thermoelectric materials, such as Bi2Te3 and PbTe,21,22 demonstrate excellent efficiency but are burdened by high material costs, complex fabrication processes, and the scarcity or toxicity of constituent elements. Organic thermoelectric materials, while offering low-cost processing and mechanical flexibility, typically exhibit low power factors and poor long-term stability. Meanwhile, quantum dots and hybrid composites have shown potential for performance enhancement, yet their scalability and reproducibility remain significant challenges. Given these challenges, perovskites, including oxides and halides, have emerged as promising materials due to their tunable electronic properties and cost-effective processability.26–29 While oxide perovskites have been extensively studied for thermoelectric applications,26 halide perovskites have primarily been explored for their optoelectronic properties,29 with limited focus on their thermoelectric potential, despite their inherently low thermal conductivity and efficient charge transport.30 Since the first report of ultralow thermal conductivity in CH3NH3PbI3,31 extensive efforts have been directed toward understanding its thermal transport behavior, particularly phonon dynamics. Halide perovskites exhibit a unique “phonon glass, electron crystal” characteristic,32 where charge carriers move efficiently like in high-quality semiconductors, while heat transport is significantly suppressed, resembling that of glassy materials.33 Their high Seebeck coefficients and decent carrier mobilities further underscore their promise for thermoelectric applications, making them an exciting area for future exploration.30,31 If stability challenges can be addressed, halide perovskites have the potential to bridge the gap between cost-effectiveness and high thermoelectric performance, positioning them as strong candidates for next-generation energy conversion technologies.
Despite the recent progress, the intricate relationship between magnetism, electronic structure, and thermoelectric performance in halide-based double perovskites remains largely unexplored. This study seeks to bridge this gap by conducting a comprehensive first-principles investigation into the structural stability, electronic properties, magnetic interactions, and thermoelectric performance of Rb2GeMI6 (M = V, Mn, Ni) halide perovskites using advanced density functional theory (DFT) and post-DFT methods. Notably, no prior research has systematically examined these materials within this context. The findings of our study disclose that halide-based double perovskites exhibit intrinsic ferromagnetic semiconductor behavior, characterized by substantial spin-splitting gaps, alongside high Curie temperatures and strong spin polarization, making them viable candidates for spintronic applications. Additionally, their favourable thermoelectric properties underscore their potential for efficient energy conversion technologies. By unveiling these critical attributes, this study positions halide-based double perovskites as a promising class of multifunctional materials for next-generation spintronic and thermoelectric devices.
This paper is organized to predict the comprehensive physical (structural, electronic, mechanical, phonon, thermodynamic) and thermoelectric properties of these materials.
2. Computational details
The present study employs the Wien2k software suite and its associated tools for computational analysis.34 The Kohn–Sham equation is iteratively solved using the generalized gradient approximation (GGA).35 However, since GGA often fails to accurately describe the electronic structures of systems with strongly correlated d-electrons, the Tran and Blaha modified Becke–Johnson (TB-mBJ, 2009) potential is applied on top of GGA, resulting in the GGA + mBJ method for improved accuracy.36 The full-potential linearized augmented plane wave (FP-LAPW) method is used, with the computational domain divided into muffin-tin (MT) spheres centered at Wyckoff positions (4a, 4b, 8c, and 24e) to represent atomic sites, while the interstitial space accommodates the remaining volume. The radii of these MT spheres (RMT) are carefully chosen to balance charge leakage prevention and computational efficiency. Within these spheres, atomic-like wave functions are applied, whereas Bloch-like wave behavior is maintained in the interstitial regions. The angular momentum expansion inside the MT spheres extends up to lmax = 10, and the plane wave cutoff follows the condition RMT × Kmax = 7. The self-consistency criterion is defined by convergence requirements, ensuring that the integrated charge difference between consecutive iterations remains below 0.0001e, while energy fluctuations do not exceed 0.0001 Ry. The electronic and magnetic structure calculations, along with elastic constant evaluations, are conducted using a Brillouin zone mesh comprising 1000 k-points. Mechanical stability is assessed using the Thomas Charpin cubic elastic package within the GGA–PBE framework.37 Thermodynamic properties are determined using the Gibbs2 package,38 integrated with the Wien2k software. Additionally, thermoelectric properties are computed based on Boltzmann transport theory, employing the rigid-band approximation and the constant-scattering time approximation (CSTA).39 The Seebeck coefficient (S), electrical conductivity (σ), and electronic thermal conductivity (zT) are evaluated as functions of the chemical potential (μ) for the given perovskites, following established relationships: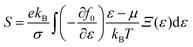 | (1) |
 | (2) |
 | (3) |
Here, Ξ(ε) is a transport distribution function specified by  where vαk represent αth component of the group velocity with wave vector k. To enhance the accuracy of thermoelectric calculations, the k-mesh density has been increased to 100
where vαk represent αth component of the group velocity with wave vector k. To enhance the accuracy of thermoelectric calculations, the k-mesh density has been increased to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 k-points, ensuring precise transport property predictions.
000 k-points, ensuring precise transport property predictions.
3. Results and discussion
The physical properties of novel halide perovskites Rb2GeMI6 (M = V, Mn, Ni) are predicted using density functional theory (DFT) with PBE–GGA and TB-mBJ approximation schemes.3.1 Structural and magnetic phase stability
To asesss the structural stability and feasibility of the given compounds, we employ the Goldschmidt tolerance factor (tdp) and the octahedral factor (μ), both of which serve as fundamental criteria for predicting the formation and stability of a cubic perovskite framework. The stability of the cubic phase is validated through the calculation of the tolerance factor, which is defined as:40 where rRb and rX represents the ionic radii of rubidium (Rb) and halide (I) atoms, respectively, while ravg denotes the average ionic radius of the B-site cations, germanium (Ge) and transition metals M (V, Mn, Ni). The octahedral factor is given by:40
where rRb and rX represents the ionic radii of rubidium (Rb) and halide (I) atoms, respectively, while ravg denotes the average ionic radius of the B-site cations, germanium (Ge) and transition metals M (V, Mn, Ni). The octahedral factor is given by:40 . The calculated tolerance factor values for the studied materials range between 0.81 and 1.11, indicating structural stability in the Fm
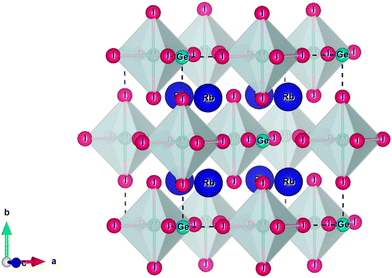
. The calculated tolerance factor values for the studied materials range between 0.81 and 1.11, indicating structural stability in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phase. Additionally, the computed octahedral factor values (0.29 ≤ μ ≤ 0.55) confirm the stability of the octahedral coordination, further supporting the cubic phase structure. Accordingly, a three-dimensional cubic crystal structure is constructed, as illustrated in Fig. 1. Within the unit cell, rubidium (Rb) atoms occupy the A-site and are coordinated by twelve iodine (I) atoms, forming a cuboctahedra environment (Fig. 1). The B-site cations, Ge and M, are octahedrally coordinated by six iodine (I) anions, forming [BX6] octahedra, which are interconnected through shared anionic vertices. This octahedral network plays a crucial role in maintaining the structural integrity and electronic properties of the material.
m cubic phase. Additionally, the computed octahedral factor values (0.29 ≤ μ ≤ 0.55) confirm the stability of the octahedral coordination, further supporting the cubic phase structure. Accordingly, a three-dimensional cubic crystal structure is constructed, as illustrated in Fig. 1. Within the unit cell, rubidium (Rb) atoms occupy the A-site and are coordinated by twelve iodine (I) atoms, forming a cuboctahedra environment (Fig. 1). The B-site cations, Ge and M, are octahedrally coordinated by six iodine (I) anions, forming [BX6] octahedra, which are interconnected through shared anionic vertices. This octahedral network plays a crucial role in maintaining the structural integrity and electronic properties of the material.
Next, we investigate the magnetic phase stability of the studied compounds by simulating various magnetic configurations using the Birch–Murnaghan equation of state, given as:41
 | (4) |
In this equation, E(V) denotes the ground state energy, V represents the unit cell volume, and B0 corresponds to the bulk modulus (and its pressure derivative), respectively. The resulting energy versus volume curves for each magnetic configuration indicate that the ferromagnetic (FM) phase has the lowest energy, suggesting its favored stability compared to other magnetic states. Fig. 2 depicts the energy optimization for the FM phase (excluding other configurations for brevity), where the energy–volume curve exhibits a distinct minimum, corresponding to the optimal equilibrium volume. At this equilibrium volume, the lattice constants are determined to be 11.74 Å for Rb2GeVI6, 11.80 Å for Rb2GeMnI6, and 11.55 Å for Rb2GeNiI6, which are consistent with values reported in the literature.20,40,42 The derived equilibrium parameters, obtained through total energy minimization, are summarized in Table 1. Furthermore, the lattice constants calculated using the generalized gradient approximation with the Perdew–Burke–Ernzerhof (GGA–PBE) functional exhibit excellent agreement with both theoretical predictions and experimental measurements, thereby reinforcing the validating of our results.
corresponds to the bulk modulus (and its pressure derivative), respectively. The resulting energy versus volume curves for each magnetic configuration indicate that the ferromagnetic (FM) phase has the lowest energy, suggesting its favored stability compared to other magnetic states. Fig. 2 depicts the energy optimization for the FM phase (excluding other configurations for brevity), where the energy–volume curve exhibits a distinct minimum, corresponding to the optimal equilibrium volume. At this equilibrium volume, the lattice constants are determined to be 11.74 Å for Rb2GeVI6, 11.80 Å for Rb2GeMnI6, and 11.55 Å for Rb2GeNiI6, which are consistent with values reported in the literature.20,40,42 The derived equilibrium parameters, obtained through total energy minimization, are summarized in Table 1. Furthermore, the lattice constants calculated using the generalized gradient approximation with the Perdew–Burke–Ernzerhof (GGA–PBE) functional exhibit excellent agreement with both theoretical predictions and experimental measurements, thereby reinforcing the validating of our results.
 | ||
| Fig. 2 Plot of the total energy against unit cell volume for Rb2GeMI6 (M = V, Mn, Ni,) determined via GGA–PBE functional scheme. | ||
To evaluate the feasibility of synthesizing the given compounds and to predict their thermodynamic stability, the enthalpy of formation (ΔH) is determined using density functional theory (DFT) calculations. The expression employed for these calculations is given as:42
 | (5) |
 represents the equilibrium energy of the unit cell, and ERb + EGe + EM + 6EI represent the DFT-calculated energies of rubidium (Rb), germanium (Ge), transition metal (M = V, Mn, Ni), and iodine (I) in their stable elemental crystalline forms. The calculated enthalpy values, summarized in Table 1, reveal negative formation enthalpies, implying that these materials are thermodynamically stable and synthetically viable.
represents the equilibrium energy of the unit cell, and ERb + EGe + EM + 6EI represent the DFT-calculated energies of rubidium (Rb), germanium (Ge), transition metal (M = V, Mn, Ni), and iodine (I) in their stable elemental crystalline forms. The calculated enthalpy values, summarized in Table 1, reveal negative formation enthalpies, implying that these materials are thermodynamically stable and synthetically viable.
To further confirm the robustness of the given compounds, cohesive energy (ΔE) is evaluated. This metric provides insight into the degree of interatomic bonding and structural stability of these materials. The cohesive energy is defined as:42
 | (6) |
 is the equilibrium energy of the unit cell, and ERb, EGe, EM, and EI are the energies of the isolated atoms Rb, Ge, M (V, Mn, Ni), and I, respectively. The computed cohesive energies, which are strictly positive (Table 1), further validate the interatomic binding strength and structural integrity of the compounds. High cohesive energy values indicate strong interactions among constituent atoms, minimizing the risk of spontaneous decomposition.
is the equilibrium energy of the unit cell, and ERb, EGe, EM, and EI are the energies of the isolated atoms Rb, Ge, M (V, Mn, Ni), and I, respectively. The computed cohesive energies, which are strictly positive (Table 1), further validate the interatomic binding strength and structural integrity of the compounds. High cohesive energy values indicate strong interactions among constituent atoms, minimizing the risk of spontaneous decomposition.
To support experimental efforts in material synthesis, simulated X-ray diffraction (XRD) patterns are generated using DFT calculations. The simulated diffraction spectra for Rb2GeMI6 compounds are obtained assuming a cubic crystal structure with an Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group symmetry (Fig. 3). The characteristic peak positions and intensities derived from these theoretical XRD patterns serve as reference data for experimental validation, aiding in phase identification and structural characterization.
m space group symmetry (Fig. 3). The characteristic peak positions and intensities derived from these theoretical XRD patterns serve as reference data for experimental validation, aiding in phase identification and structural characterization.
3.2 Vibrational thermodynamic properties
The study of vibrational thermodynamic functions provides critical insights into the temperature dependence of various properties, including vibrational internal energy (E), vibrational Helmholtz free energy (A), vibrational entropy (SV), and specific heat at constant volume (CV). These properties play a fundamental role in understanding the thermodynamic behavior of materials. A widely used approach for modelling vibrational contributions is the quasi-harmonic Debye model,43,44 which accounts for the influence of volume and temperature on vibrational states. Within this framework, the expressions governing key thermodynamic properties are as follows:Vibrational Helmholtz free energy (A)
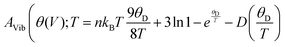 | (7) |
Debye temperature (θD)
 | (8) |
Vibrational entropy (SV):
 | (9) |
Specific heat at constant volume (CV):
 | (10) |
In these expressions, n denotes the number of atoms per formula unit, kB is the Boltzmann constant, and D refers to the Debye integral, while Bs represents the adiabatic bulk modulus, M is the molecular mass per unit cell.
The temperature dependence of these functions provides valuable information about lattice dynamics and thermal properties of materials. By analyzing variations in vibrational internal energy, Helmholtz free energy, entropy, and heat capacity with temperature, it becomes possible to predict material behavior under different thermodynamic conditions.
Vibrational internal energy (E) exhibits a direct correlation with temperature (T), primarily due to the continuous absorption of thermal energy, which enhances atomic kinetic energy and increases vibrational amplitudes. The temperature-dependent evolution of vibrational internal energy (E), as illustrated in Fig. 4(a), exhibits a linear increase with temperature (T), signifying a proportional enhancement in the system's enthalpy. This linearity further implies that system enthalpy also rises proportionally with increasing temperature, reinforcing the direct contribution of vibrational excitations to the overall thermodynamic state of the material.
The Helmholtz free energy (A), depicted in Fig. 4(b), exhibits a decreasing trend with increasing temperature. This decline is observed across all considered compounds, signifying that the thermal energy available for useful work diminishes as T rises. The uniformity of this behavior suggests that variations in the transition metal have a minimal impact on the overall vibrational structure, as the halide ion remains unchanged. Since the vibrational internal energy is fundamentally governed by the phonon spectrum, comprising both acoustic and optical modes, the preservation of the halide ion ensures the stability of the primary lattice vibrations. While differences in transition metal properties influence local vibrational frequencies through changes in atomic mass and bond stiffness, the broader phonon density of states remains relatively unaffected. Consequently, Helmholtz free energy trends remain consistent across the series, indicating that global vibrational characteristics are largely dictated by the halide lattice framework.
Vibrational entropy (SV), a measure of configurational and vibrational disorder, follows a systematic temperature-dependent increase, as shown in Fig. 4(c). Across all studied compounds, SV exhibits similar behavior, with only marginal variations, further supporting the dominant role of the halide ion in maintaining lattice stability. The limited influence of the transition metal substitution on entropy arises from its minor effect on the overall vibrational spectrum, ensuring that the density of accessible vibrational states remains largely unchanged. The observed increase in SV with rising temperature reflects the expansion of accessible vibrational states, leading to enhanced phonon population and greater configurational disorder. This temperature-dependent growth in vibrational entropy is consistent with the fundamental principles of statistical thermodynamics, where higher thermal energy levels facilitate broader phonon excitation and distribution.
In thermodynamics and statistical analysis,45,46 heat capacity (CV) plays a crucial role in examining the vibrational dynamics of lattice structures. The temperature dependence of CV follows two distinct regimes, as shown in Fig. 4(d). At low temperatures (T ≪ θD), CV follows Debye's model, exhibiting a cubic dependence on temperature:  . This arises because only long-wavelength acoustic phonons contribute significantly to heat capacity at low T. In contrast, at high temperatures (T ≫ θD), CV approaches the Dulong–Petit limit:47CV ≅ 3nR where R is the universal gas constant (8.314 J mol−1 K−1). This occurs because, at such temperatures, all phonon modes are fully excited, and energy equipartition ensures that each degree of freedom contributes equally, resulting in a constant heat capacity. Table 2 presents the calculated Debye temperature (θD), zero-point energy (E0 in kJ mol−1), and Grüneisen parameter (γ), with comparisons to literature values that confirm the accuracy of our results.
. This arises because only long-wavelength acoustic phonons contribute significantly to heat capacity at low T. In contrast, at high temperatures (T ≫ θD), CV approaches the Dulong–Petit limit:47CV ≅ 3nR where R is the universal gas constant (8.314 J mol−1 K−1). This occurs because, at such temperatures, all phonon modes are fully excited, and energy equipartition ensures that each degree of freedom contributes equally, resulting in a constant heat capacity. Table 2 presents the calculated Debye temperature (θD), zero-point energy (E0 in kJ mol−1), and Grüneisen parameter (γ), with comparisons to literature values that confirm the accuracy of our results.
The computed heat capacity profiles for Rb2GeMnI6 (M = V, Mn, Ni), illustrated in Fig. 4(d), conform to the above-mentioned regimes. At low temperatures, CV follows a T3 dependence, confirming Debye's law, while at higher T, it flattens toward the Dulong–Petit limit, reinforcing the accuracy of our computational outcomes with the classical thermodynamics.47 The Debye temperatures (θD) listed in Table 2 show minimal variation across compounds, attributed to the conserved crystal structure and bonding environment due to the constant halide ion. Substituting the transition metal primarily affects atomic mass without significantly altering phonon spectra, resulting in nearly identical θD values. Furthermore, anharmonic effects are analyzed using the Grüneisen parameter (γ), defined as 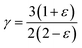 . The uniform values of γ across the compounds suggest a consistent thermal response, reinforcing the dominant role of the halide lattice in governing vibrational thermodynamics in Rb2GeMnI6 perovskites.
. The uniform values of γ across the compounds suggest a consistent thermal response, reinforcing the dominant role of the halide lattice in governing vibrational thermodynamics in Rb2GeMnI6 perovskites.
3.3 Phonon stability
The vibrational stability and phonon transport characteristics of crystalline solids depend on their phonon dispersion behavior. Using density functional perturbation theory (DFPT) within the Quantum Espresso framework,48 this study examines the phonon spectra to determine dynamic stability of the given perovskites. A material remains stable when all phonon frequencies are real and positive throughout the Brillouin zone, while negative (imaginary) frequencies indicate instability. The phonon dispersion curves in Fig. 5 show no imaginary modes, confirming the structural integrity of the studied materials. Each primitive unit cell contains ten atoms, resulting in three acoustic and twenty-seven optical phonon modes. At the Γ-point, the longitudinal acoustic (LA) and transverse acoustic (TA) phonons converge to zero frequency, as expected for stable crystalline lattices. The optical phonon modes, which include Raman-active, infrared-active, and silent branches, exhibit finite frequencies and contribute less significantly to heat transport. The phonon group velocity, defined as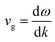 , determines the efficiency of heat conduction by representing the slope of the phonon dispersion branches. A steeper slope corresponds to a higher group velocity, enabling faster phonon propagation and greater thermal conductivity. Acoustic modes, particularly the longitudinal acoustic (LA) branch, exhibit a near-linear dispersion with a significant slope, making them the dominant contributors to heat transport. In contrast, optical modes display flatter dispersion curves, resulting in lower group velocities and minimal contributions to thermal conduction. The material's thermal transport properties, therefore, primarily depend on the behavior of the acoustic phonons, which govern its potential applications in thermal engineering and thermoelectric devices.
, determines the efficiency of heat conduction by representing the slope of the phonon dispersion branches. A steeper slope corresponds to a higher group velocity, enabling faster phonon propagation and greater thermal conductivity. Acoustic modes, particularly the longitudinal acoustic (LA) branch, exhibit a near-linear dispersion with a significant slope, making them the dominant contributors to heat transport. In contrast, optical modes display flatter dispersion curves, resulting in lower group velocities and minimal contributions to thermal conduction. The material's thermal transport properties, therefore, primarily depend on the behavior of the acoustic phonons, which govern its potential applications in thermal engineering and thermoelectric devices.
3.4 Mechanical stability
The mechanical stability of a material is inherently tied to its atomic arrangement, which dictates its ability to resist external forces. This structural integrity determines its suitability for various technological and industrial applications. Understanding these properties requires an in-depth examination of how the material deforms and responds to mechanical stress. To assess the mechanical stability of Rb2GeMI6 halide perovskites, elastic constants are calculated using the energy–strain method, incorporating tetrahedral and rhombohedral distortions within the cubic elastic framework.37 The results presented in Table 3 illustrates that all elastic constants are positive and comply with Born's stability criteria49 (C11 > 0, C12 > 0, C44 > 0, and C11 + 2C12 > 0), thereby substantiating the mechanical stability of the compounds. By analyzing the elastic constants, we obtain essential mechanical parameters, including bulk, shear, and Young's moduli, which clarify the material's response to stress.50–53 The bulk modulus (B), which quantifies resistance to uniform compression, is inversely related to volumetric deformation, influencing the material's ability to withstand structural collapse. The shear modulus (G) describes resistance to shape deformation, where lower values indicate greater plasticity and flexibility. Young's modulus (Y), a fundamental measure of stiffness, reveals the material's ability to resist elongation under tensile stress. The computed values follow the trend Y > B > G, indicating that these perovskites resist shape deformation more than volumetric changes, showcasing their structural rigidity and resilience. The ability of these materials to resist bond bending and angular distortions is evaluated through the Kleinman coefficient (ζ).53 A lower value of ζ signifies a stronger preference for bond stretching over angular distortion, suggesting that these perovskites maintain their structural integrity even under stress.| Parameter | C 11 | C 12 | C 44 | B | G | Y | v | B/G | C 12–C44 | ξ | A Z | A U |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rb2GeVI6 | 27.21 | 11.23 | 7.12 | 16.55 | 7.45 | 19.44 | 0.30 | 2.22 | 4.11 | 0.54 | 0.89 | 0.016 |
| Rb2GeMnI6 | 32.44 | 12.79 | 6.03 | 19.34 | 7.33 | 19.54 | 0.33 | 2.63 | 6.76 | 0.53 | 0.61 | 0.29 |
| Rb2GeNiI6 | 34.58 | 12.98 | 7.98 | 20.18 | 9.00 | 23.52 | 0.30 | 2.23 | 5.01 | 0.51 | 0.73 | 0.11 |
Ductility and brittleness are key mechanical properties that define how a material deforms under external forces. To classify these perovskites, several mechanical indicators are examined, including Cauchy's pressure, Pugh's ratio, and Poisson's ratio.53–55 A positive Cauchy's pressure indicates a ductile nature, while negative values suggest brittleness. Pugh's ratio, which is the ratio of the bulk modulus to the shear modulus (B/G), serves as another critical measure, where values greater than 1.75 classify a material as ductile. Poisson's ratio (ν) further supports this classification, as values above 0.26 are characteristic of ductile materials, while lower values imply brittleness. The computed values, summarized in Table 3, consistently confirm that Rb2GeMI6 perovskites exhibit strong ductile behavior, making them suitable for applications requiring mechanical flexibility, toughness, and resistance to fracture.
The mechanical behavior of crystalline materials is often influenced by their anisotropy, which determines variations in mechanical responses along different crystallographic directions. To assess the anisotropic character in Rb2GeMI6 halide perovskites, we evaluate two key anisotropy parameters: the Zener anisotropy ratio (AZ) and the Universal anisotropic factor (AU) using the expressions as:56,57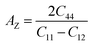 ,
,  , where the symbols have their usual meanings. These parameters provide insight into the deviation from isotropic behavior, where A = 1 represents a perfectly isotropic material. The results, presented in Table 3, indicate significant anisotropy in the studied compounds, as reflected in the deviation of both AZ and AU from unity. This anisotropic nature suggests that the mechanical response of these perovskites varies with direction, which could influence their structural applications.
, where the symbols have their usual meanings. These parameters provide insight into the deviation from isotropic behavior, where A = 1 represents a perfectly isotropic material. The results, presented in Table 3, indicate significant anisotropy in the studied compounds, as reflected in the deviation of both AZ and AU from unity. This anisotropic nature suggests that the mechanical response of these perovskites varies with direction, which could influence their structural applications.
Beyond anisotropy, evaluating mechanical constants enables the estimation of critical dynamic properties such as average sound velocity (Vav). This parameter, which reflects the propagation of acoustic waves within a material, is derived from the transverse (Vt) and longitudinal (Vl) sound velocities using density-dependent relations:53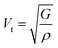 and
and  , where ρ represents the material's density. The average sound velocity (Vav) is then determined using the expression:53
, where ρ represents the material's density. The average sound velocity (Vav) is then determined using the expression:53 . Table 4 illustrates a clear decrease in Vav from the V-based compound to the Ni-based one, a trend that correlates with the progressive increase in density (V > Mn > Ni). The observed variations in sound velocity are critical for applications in phononic and thermoelectric materials, where acoustic wave interactions play a vital role in energy transport.
. Table 4 illustrates a clear decrease in Vav from the V-based compound to the Ni-based one, a trend that correlates with the progressive increase in density (V > Mn > Ni). The observed variations in sound velocity are critical for applications in phononic and thermoelectric materials, where acoustic wave interactions play a vital role in energy transport.
| Parameter | V t | V l | V av | G/B | μ m | (HV)Teter | (HV)Tian | T m ± 300 |
|---|---|---|---|---|---|---|---|---|
| Rb2GeVI6 | 1311 | 2471 | 2335 | 0.45 | 2.32 | 1.12 | 1.54 | 713.83 |
| Rb2GeMnI6 | 1308 | 2607 | 2044 | 0.38 | 3.20 | 1.08 | 1.25 | 744.75 |
| Rb2GeNiI6 | 1436 | 2716 | 1925 | 0.44 | 2.52 | 1.36 | 1.74 | 757.40 |
To further explore the mechanical resilience and industrial feasibility of these perovskites, we compute additional material parameters, including Vickers hardness (HV), machinability factor (μm), Frantsevich's ratio (G/B), and melting temperature (Tm), using empirical relations from the literature:53,58–61
| (HV)Teter = 0.151G, (HV)Tian = 0.92 (G/B)1.137G0.708 | (11) |
 | (12) |
| Tm (K) = [553 (K) + (5.911)C11]GPa ± 300 | (13) |
The hardness values, estimated using the models proposed by Teter et al.58 and Tian et al.,59 consistently produce positive results across all examined materials, indicating their intrinsic resistance to plastic deformation. Meanwhile, the machinability factor (μm) suggests that these perovskites possess favourable machining characteristics, including reduced cutting forces and mild lubricating properties, which are beneficial for industrial processing.
Another crucial parameter, melting temperature (Tm), is estimated using a correlation involving elastic stiffness constants. The high Tm values obtained reinforce the thermal stability of these compounds, positioning them as viable candidates for high-temperature applications. Furthermore, the relatively small G/B ratio suggests that these materials exhibit a balance between stiffness and plasticity, which is essential for structural durability. Collectively, the data compiled in Table 4, comprising high Vickers hardness, favourable machinability, elevated melting temperatures, and a relatively small G/B ratio, demonstrate that these materials might be promising candidates for advanced thermoelectric applications, especially under high-temperature conditions. Overall, the combination of strong anisotropy, high hardness, favourable machinability, and superior thermal stability underscores the potential of Rb2GeMI6 perovskites for advanced technological applications.
3.5 Electronic structure
The electronic profile of Rb2GeMI6 (M = V, Mn, Ni) halide perovskites is systematically investigated through spin-polarized band structure (BS) and density of states (DOS) calculations. The band structures, computed using both GGA and GGA + mBJ approximations, are systematically analyzed and presented in Fig. 6(a)–(c). The GGA-derived band structure shows an unoccupied Fermi level in both spin orientations, with the up-spin channel grazing the valence band maximum, while the spin-down counterpart remains completely unoccupied. This confirms the presence of a finite band gap in both spin states, a hallmark of ferromagnetic semiconducting behavior. The band gap, a fundamental determinant of electronic transitions, is systematically evaluated using both computational frameworks. While GGA tends to underestimate band gaps due to the intricate correlation effects of d-electrons in transition metals, the mBJ correction refines these estimations, yielding values in strong agreement with prior literature,20,40,42 as tabulated in Table 5. A refined analysis of the energy band dispersion reveals a stark contrast between spin channels. The spin-up states exhibit significant delocalization, leading to a reduced charge carrier effective mass and enhanced transport properties. In contrast, the spin-down states are more localized, resulting in a higher effective mass, which directly impacts carrier mobility and conductivity. This disparity in effective mass plays a crucial role in enhancing the transport dynamics of these compounds.| Parameter | Band gap | Spin-splitting gap | ||||||
|---|---|---|---|---|---|---|---|---|
| Approximation | GGA | GGA + mBJ | GGA | GGA + mBJ | ||||
| Spin channel | Up | Down | Up | Down | ΔECBM | ΔEVBM | ΔECBM | ΔEVBM |
| a These results were computed using the GGA + Ueff method, as reported by Cai et al.20 | ||||||||
| Rb2GeVI6 | 0.35 | 2.09 | 1.86 | 2.76 | −0.73 | 0.85 | −0.25 | 0.64 |
| Rb2GeMnI6 | 0.61 | 1.70 | 1.22 | 2.41 | −0.34 | 0.74 | −0.33 | 0.92 |
| Rb2GeNiI6 | 0.88 | 0.46 | 1.19 | 1.22 | 0.88 | 0.46 | 0.74 | 0.77 |
| Cs2GeVI620 | — | — | — | — | — | — | −0.21a | 0.01a |
| K2GeMnI642 | 0.61 | 1.71 | 1.21 | 2.45 | −0.34 | 0.78 | −0.32 | 0.98 |
| K2GeNiI640 | — | — | 1.16 | 1.22 | — | — | 0.72 | 0.79 |
Beyond the conventional band gap analysis, the spin splitting gap, defined as the energy difference between the valence band maximum (VBM) or conduction band minimum (CBM) and the Fermi level across both spin states, is quantitatively evaluated. The computed spin splitting values, summarized in Table 5, are substantial and align well with those of similar materials,20,40,42 highlighting the intrinsic potential of these halide perovskites for spintronic applications. The strong spin polarization and band engineering flexibility make these materials promising for next-generation spintronic applications.
| Material | Method | Rb (μB) | Ge (μB) | M (μB) | I (μB) | Interstitial (μB) | Total (μB) |
|---|---|---|---|---|---|---|---|
| Rb2GeVI6 | GGA + mBJ | 0.00 | −0.00 | 2.71 | 0.00 | 0.25 | 3.00 |
| Rb2GeMnI6 | GGA + mBJ | 0.00 | 0.06 | 4.55 | 0.02 | 0.22 | 5.00 |
| Rb2GeNiI6 | GGA + mBJ | 0.00 | 0.08 | 1.60 | 0.03 | 0.08 | 2.00 |
The Curie temperature (TC), the threshold at which a ferromagnetic material undergoes a transition to a paramagnetic state, is determined for the Rb2GeMI6 compounds using the mean field approximation (MFT) within the Heisenberg model. This calculation follows the relation:20,62 , where ΔE represents the energy difference between the ferromagnetic (FM) and antiferromagnetic (AFM) states, kB denotes the Boltzmann constant, and x corresponds to the concentration of magnetic ions. The parameter ΔE is obtained from first principles density functional theory (DFT) calculations, wherein the total energies of FM and AFM/NM configurations are derived from total energy versus volume curves. The energy difference, expressed as: ΔE = EAFM/NM − EFM, signifies the energy required to stabilize the ferromagnetic state. Given that each compound contains a single magnetic ion (V, Mn, or Ni), x assumes a value of 1. The computed values of ΔE are 0.137 eV for Rb2GeVI6, 0.150 eV for Rb2GeMnI6, and 0.114 eV for Rb2GeNiI6. Substituting these values into the equation yields Curie temperatures of 530.39 K, 580.72 K, and 440.47 K, respectively. These values significantly surpass those typically observed in double perovskite oxides, revealing the strength of the ferromagnetic interactions present in these materials. The remarkably high Curie temperatures indicate the exceptional stability of their magnetic ordering and suggest their viability for advanced spintronic applications, where robust ferromagnetism at elevated temperatures is imperative.
, where ΔE represents the energy difference between the ferromagnetic (FM) and antiferromagnetic (AFM) states, kB denotes the Boltzmann constant, and x corresponds to the concentration of magnetic ions. The parameter ΔE is obtained from first principles density functional theory (DFT) calculations, wherein the total energies of FM and AFM/NM configurations are derived from total energy versus volume curves. The energy difference, expressed as: ΔE = EAFM/NM − EFM, signifies the energy required to stabilize the ferromagnetic state. Given that each compound contains a single magnetic ion (V, Mn, or Ni), x assumes a value of 1. The computed values of ΔE are 0.137 eV for Rb2GeVI6, 0.150 eV for Rb2GeMnI6, and 0.114 eV for Rb2GeNiI6. Substituting these values into the equation yields Curie temperatures of 530.39 K, 580.72 K, and 440.47 K, respectively. These values significantly surpass those typically observed in double perovskite oxides, revealing the strength of the ferromagnetic interactions present in these materials. The remarkably high Curie temperatures indicate the exceptional stability of their magnetic ordering and suggest their viability for advanced spintronic applications, where robust ferromagnetism at elevated temperatures is imperative.
To elucidate the origin of the elevated Curie temperatures in these halide double perovskites compared to their oxide counterparts, we conduct a comparative analysis between Rb2GeMI6 and Bi2CrOsO6. The findings indicate that the remarkably high TC in halide perovskites arises from an indirect exchange coupling mechanism mediated by Ge-I6 octahedral units, facilitating interactions between transition metal ions. As depicted in Fig. 7, a strong hybridization is observed between M (V, Mn, Ni)-3d and I-4p orbitals, attributed to a 90° quasi-super exchange interaction between M-3d and the Ge-I6 σs–p* orbitals. This contrasts sharply with the exchange mechanism in double perovskite oxides, where a 180° super exchange interaction involving Cr(d)–O(p)–Os(d) orbitals predominates. The 90° exchange pathway proves to be significantly more effective in stabilizing ferromagnetism, consistent with the Pauli exclusion principle.
 | ||
| Fig. 8 Plot of magnetic susceptibility (χ) and its reciprocal (χ−1) against temperature for Rb2GeMI6 (M = V, Mn, Ni) halide perovskites. | ||
The ferromagnetic ground state, established through total energy vs. volume graphs (Fig. 2), is further validated by magnetic susceptibility calculations. Using the BoltzTraP code,39 which employs semiclassical Boltzmann theory, we compute susceptibility as a function of temperature and extract the Curie–Weiss model parameters by fitting the equation  .63 In this equation, χ represents the magnetic susceptibility, C is the Curie constant, a material-specific parameter related to the magnetic moment, T is the absolute temperature in Kelvin, and Θ is the Weiss temperature, which characterizes the nature of magnetic interactions—where a positive Θ signifies predominant ferromagnetic interactions, while a negative Θ suggests antiferromagnetic ordering. The Curie constant (C) is determined from the slope of the linear fit in the high-temperature paramagnetic region of the 1/χ vs. T plot, while the Weiss temperature (Θ) is obtained as the intercept where 1/χ extrapolates to zero. As illustrated in Fig. 8, the inverse susceptibility curves yield positive Θ values of approximately 98 K for Rb2GeVI6, 90 K for Rb2GeMnI6, and 95 K for Rb2GeNiI6. These positive values unequivocally confirm the dominance of ferromagnetic interactions, in full agreement with Curie–Weiss behavior.63 Consequently, we establish that the ground state of Rb2GeMI6 (M = V, Mn, Ni) is intrinsically ferromagnetic, reinforcing the robustness of their magnetic ordering and highlighting their potential for applications in advanced spintronics.
.63 In this equation, χ represents the magnetic susceptibility, C is the Curie constant, a material-specific parameter related to the magnetic moment, T is the absolute temperature in Kelvin, and Θ is the Weiss temperature, which characterizes the nature of magnetic interactions—where a positive Θ signifies predominant ferromagnetic interactions, while a negative Θ suggests antiferromagnetic ordering. The Curie constant (C) is determined from the slope of the linear fit in the high-temperature paramagnetic region of the 1/χ vs. T plot, while the Weiss temperature (Θ) is obtained as the intercept where 1/χ extrapolates to zero. As illustrated in Fig. 8, the inverse susceptibility curves yield positive Θ values of approximately 98 K for Rb2GeVI6, 90 K for Rb2GeMnI6, and 95 K for Rb2GeNiI6. These positive values unequivocally confirm the dominance of ferromagnetic interactions, in full agreement with Curie–Weiss behavior.63 Consequently, we establish that the ground state of Rb2GeMI6 (M = V, Mn, Ni) is intrinsically ferromagnetic, reinforcing the robustness of their magnetic ordering and highlighting their potential for applications in advanced spintronics.
3.6 Electron charge density distribution
The electronic charge density analysis offers valuable insights into the chemical stability and bonding characteristics of materials. In Fig. 9, we present the spin-polarized charge density plot of Rb2GeVI6 along the (111) plane, with similar patterns observed in other compounds, thus omitting them for brevity. The graphical plot highlights concentrated electron cloud density at atomic positions, a key indicator of bonding interactions within the lattice. Following Pauling's theory, a chemical bond is formed when the bonding force between atoms is particularly strong. The electron clouds around Rb and I atoms are predominantly spherical, suggesting an ionic bonding character, with Rb as the electropositive donor and I as the electronegative acceptor. In contrast, the bonding between Ge/V and I atoms demonstrates clear covalent characteristics, as evidenced by the dumbbell-shaped electron clouds along the Ge/V–I bonds, indicating charge sharing between the atoms. This covalent interaction is further confirmed by the overlapping electron density contours. The overall bonding analysis reveals a distinct hybridization of ionic and covalent bonds, highlighting the material's polar covalent bonding nature, which plays a crucial role in its structural and chemical stability.3.7 Thermoelectric coefficients
The thermoelectric effect, enabling the seamless interconversion of thermal and electrical energy, is governed by the dimensionless figure of merit (zT), defined by: where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the temperature. This equation highlights the dual strategy for maximizing thermoelectric performance—boosting the power factor (S2σ) while suppressing heat flow (κ). Herein, we applied semi-classical Boltzmann transport theory under the rigid band and constant relaxation time (τ) approximations, using BoltzTraP code39 to extract these parameters. The relaxation time, τ, a measure of the interval between electron scattering events, assumes minimal variation across the thermal energy range, simplifying the expressions for electrical conductivity (σ/τ), electronic thermal conductivity (κe/τ), and figure of merit (zT).
where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the temperature. This equation highlights the dual strategy for maximizing thermoelectric performance—boosting the power factor (S2σ) while suppressing heat flow (κ). Herein, we applied semi-classical Boltzmann transport theory under the rigid band and constant relaxation time (τ) approximations, using BoltzTraP code39 to extract these parameters. The relaxation time, τ, a measure of the interval between electron scattering events, assumes minimal variation across the thermal energy range, simplifying the expressions for electrical conductivity (σ/τ), electronic thermal conductivity (κe/τ), and figure of merit (zT).
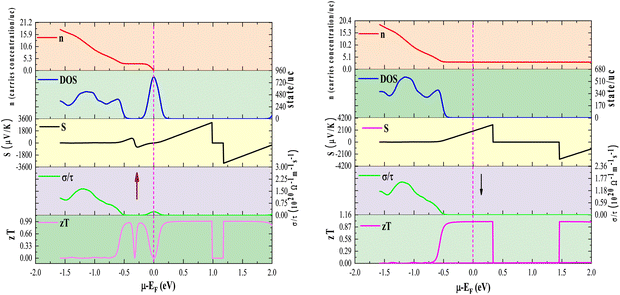
In this study, we analyzed the thermoelectric coefficients as functions of temperature and chemical potential, as illustrated in Fig. 10(a)–(d) and 11(a)–(c). Given the intrinsic ferromagnetism of the investigated materials, a spin-polarized perspective is essential, as charge and heat transport arise from distinct contributions of spin-up (↑) and spin-down (↓) states. To quantify the net effect, we employed the two-current model, a widely adopted framework for describing spin-dependent transport in ferromagnetic materials. Within this formalism, the total electrical conductivity is expressed as: σ = σ(↑) + σ(↓). Similarly, the electronic thermal conductivity follows: κe = κe(↑) + κe(↓), the net Seebeck coefficient, incorporating contributions from both spin states, is given as:42 . Here, S(↑), S(↓) denote the Seebeck coefficients for spin-up and spin-down states, respectively, κe(↑) and κe(↓) correspond to the thermal conductivity for the up and down spin directions, respectively, and σ(↑) and σ(↓) represent the corresponding electrical conductivities.
. Here, S(↑), S(↓) denote the Seebeck coefficients for spin-up and spin-down states, respectively, κe(↑) and κe(↓) correspond to the thermal conductivity for the up and down spin directions, respectively, and σ(↑) and σ(↓) represent the corresponding electrical conductivities.
The detailed analysis of thermoelectric coefficients in relation to temperature (200 K to 800 K) and chemical potential (−2 eV to 2 eV) is provided below.
The variation of S with temperature for Rb2GeVI6, Rb2GeMnI6, and Rb2GeNiI6 is depicted in Fig. 10(a). At lower temperatures (100 K), these materials exhibit remarkably high S values, recorded at 600 μV K−1, 550 μV K−1, and 450 μV K−1, respectively. However, with increasing temperature, the coefficients decline, reducing to approximately 275 μV K−1, 260 μV K−1, and 250 μV K−1 by 750 K. This reduction stems from the temperature-driven excitation of electrons. As thermal energy increases, electrons transition from the valence band to the conduction band, creating electron–hole pairs. Consequently, the increased carrier concentration reduces S. The relationship between S and carrier concentration (n) can be represented as:42 where m* is the effective carrier mass, kB is Boltzmann's constant, and T is the temperature. At absolute zero, semiconductors lack free carriers, theoretically resulting in an infinite S. However, as temperature rises, thermal excitation generates carriers, diminishing S.
where m* is the effective carrier mass, kB is Boltzmann's constant, and T is the temperature. At absolute zero, semiconductors lack free carriers, theoretically resulting in an infinite S. However, as temperature rises, thermal excitation generates carriers, diminishing S.
In addition to temperature, we also examine the chemical potential dependency of the Seebeck coefficient. The chemical potential (μ) is a crucial factor in influencing both the magnitude and the polarity of the Seebeck coefficient, as it determines the distribution of charge carriers at elevated temperatures (S). Fig. 11(a) examines the behavior of S across a range of chemical potentials for various temperatures. Positive S values signify p-type conduction (hole carriers), whereas negative values indicate n-type behavior (electron carriers). Peaks in S emerge in regions of low carrier concentration, typically between 0–1.5 eV, where the density of states (DOS) is sparse. Conversely, high DOS regions, where carrier concentration is substantial, show diminished S. For instance, at room temperature, S reaches values of ±3000 μV K−1 for Rb2GeVI6, ±2000 μV K−1 for Rb2GeMnI6, and ±700 μV K−1 for Rb2GeNiI6. The superior performance of Rb2GeVI6 is attributed to its larger band gap, which sustains high S values by limiting carrier generation. The computed values of the Seebeck coefficient (S) are presented in Table 7 alongside data for similar materials,27,30 with these compounds exhibiting higher S values than those previously reported, thereby underscoring their superior thermoelectric performance.
| Material | Thermoelectric parameters (300 K) | Optical parameters (0–5 eV) | ||
|---|---|---|---|---|
| Seebeck coefficient (μV K−1) | Figure of merit (zT) | Real part ε1(ω) | Imaginary part ε2(ω) | |
| Rb2GeVI6 | 3000 | 1.00 | 8.0 | 6.0 |
| Rb2GeMnI6 | 2000 | 0.99 | 8.4 | 4.9 |
| Rb2GeNiI6 | 700 | 0.97 | 8.6 | 5.5 |
| Rb2ScAuBr627 | 150 | 0.61 | 5.028 | 3.028 |
| Rb2ScAuI627 | 165 | 0.82 | 4.928 | 2.528 |
| Cs2AgBiCl630 | 236 | 0.74 | 5.2 | 3.5 |
| Cs2AgBiBr630 | 234 | 0.73 | 7.0 | 5.5 |
To gain further insight, we analyze the variations of the Seebeck coefficient in conjunction with the density of states (DOS) and carrier concentration as functions of chemical potential for Rb2GeVI6. This analysis distinctly focuses on the spin-up and spin-down channels, as depicted in Fig. 12, while similar trends in other compounds are omitted for clarity. The spin-up channel displays prominent peaks in the Seebeck coefficient between 0 and 1.0 eV, while the spin-down channel shows significant peaks within the narrower range of 0 to 0.5 eV. This behavior arises from the reduced electronic population (DOS) in these specific regions, which limits the number of charge carriers, intensifies the energy dependence of transport, and consequently enhances the Seebeck coefficient. These peaks illustrate the critical interplay between electronic band structure and carrier transport properties. At elevated temperatures (800 K), the peak Seebeck coefficients decline to ±1000 μV K−1 for Rb2GeVI6, ±900 μV K−1 for Rb2GeMnI6, and ±300 μV K−1 for Rb2GeNiI6. This reduction aligns with the Mott relation, which links Seebeck coefficient to chemical potential and temperature:64 . As temperature rises, both types of carriers (electrons and holes) are thermally activated, leading to a bipolar effect that reduces S. However, due to the relatively large band gaps (>0.64
. As temperature rises, both types of carriers (electrons and holes) are thermally activated, leading to a bipolar effect that reduces S. However, due to the relatively large band gaps (>0.64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV), these materials avoid complete cancellation of S, maintaining non-zero values even at high temperatures. This makes them highly promising for applications in thermoelectric generators, coolers, thermocouples, and temperature sensors.
eV), these materials avoid complete cancellation of S, maintaining non-zero values even at high temperatures. This makes them highly promising for applications in thermoelectric generators, coolers, thermocouples, and temperature sensors.
The effect of chemical potential on electrical conductivity across different temperatures is visualized in Fig. 11(b), which maps σ/τ at 300 K, 600 K, and 800 K. Across all three perovskites, conductivity peaks are prominent in the energy range of approximately −2 to 2 eV, aligning with electronic states near the Fermi level. However, a notable distinction arises in Rb2GeVI6, where the conductivity peaks shift slightly away from the Fermi level, reflecting its wider band gap and the correspondingly higher energy required for charge carrier excitation. Despite this displacement, states at the Fermi level, especially those from spin-up electrons contribute significantly to the material's overall electrical transport. Furthermore, secondary conductivity peaks appearing on both sides of the Fermi level highlight contributions from electronic states in both spin channels, reinforcing the role of band structure asymmetry in charge transport mechanisms.
A comparative analysis of Fig. 11(a) and (b) unveils a striking inverse relationship between electrical conductivity and the Seebeck coefficient. This interplay is governed by their fundamental dependence on carrier concentration: while σ scales proportionally with n, the Seebeck coefficient exhibits an inverse dependence.42 Consequently, regions exhibiting conductivity peaks correspond to minima in the Seebeck coefficient, and vice versa.
To gain deeper insight into the interplay between electrical conductivity and chemical potential, we map the variations of total electrical conductivity (σ/τ), carrier concentration (n), and volumetric density of states (DOS) as functions of chemical potential at 300 K, with a focused examination of Rb2GeVI6 for clarity. As shown in Fig. 12, these plots reveal that carrier concentration sharply decreases near the pseudo-gap in the band structure, a phenomenon that significantly contributes to the observed peaks in the Seebeck coefficient. Conversely, conductivity peaks materialize at chemical potentials where the DOS is highest, indicating that densely packed electronic bands provide an ample supply of charge carriers, thereby enhancing conduction efficiency.
Slack's theoretical framework describes κl as a function of structural and anharmonic properties, encapsulated in the expression:65,66 where θD denotes the Debye temperature, γ represents the Gruneisen parameter, V is the molar volume, m is the average molar mass per atom, N is the number of atoms in the unit cell, and T is the absolute temperature. The parameter A, which depends on the anharmonicity of the lattice, is given by:65
where θD denotes the Debye temperature, γ represents the Gruneisen parameter, V is the molar volume, m is the average molar mass per atom, N is the number of atoms in the unit cell, and T is the absolute temperature. The parameter A, which depends on the anharmonicity of the lattice, is given by:65 . The model indicates that κl is influenced by structural properties such as atomic masses, lattice geometry, and anharmonic phonon interactions. As shown in Fig. 10(c)–(e), the decrease in κl with temperature can be attributed to enhanced phonon scattering at higher thermal energies. At 300 K, Rb2GeVI6, Rb2GeMnI6, and Rb2GeNiI6 exhibit lattice thermal conductivity values of 3.10 W m−1 K−1, 2.05 W m−1 K−1, and 1.57 W m−1 K−1, respectively. These relatively low κl values are attributed to the complex structural frameworks of these materials, characterized by ten atoms per unit cell and cage-like geometries. These structures facilitate significant phonon scattering, often referred to as the “phonon rattling effect”, resulting in lower lattice thermal conductivity.32,33 Below 300 K, κl is the dominant contributor to total thermal conductivity. However, as the temperature rises toward 800 K, κl diminishes sharply, while κe increases due to the enhanced thermal energy of carriers. Consequently, at elevated temperatures, κt becomes primarily governed by the electronic contribution. The overall low thermal conductivity values of these Rb-based double perovskites highlight their suitability for thermoelectric applications. Their ability to maintain low κt, even at high temperatures, makes them highly promising candidates for waste heat recovery and energy harvesting technologies.
. The model indicates that κl is influenced by structural properties such as atomic masses, lattice geometry, and anharmonic phonon interactions. As shown in Fig. 10(c)–(e), the decrease in κl with temperature can be attributed to enhanced phonon scattering at higher thermal energies. At 300 K, Rb2GeVI6, Rb2GeMnI6, and Rb2GeNiI6 exhibit lattice thermal conductivity values of 3.10 W m−1 K−1, 2.05 W m−1 K−1, and 1.57 W m−1 K−1, respectively. These relatively low κl values are attributed to the complex structural frameworks of these materials, characterized by ten atoms per unit cell and cage-like geometries. These structures facilitate significant phonon scattering, often referred to as the “phonon rattling effect”, resulting in lower lattice thermal conductivity.32,33 Below 300 K, κl is the dominant contributor to total thermal conductivity. However, as the temperature rises toward 800 K, κl diminishes sharply, while κe increases due to the enhanced thermal energy of carriers. Consequently, at elevated temperatures, κt becomes primarily governed by the electronic contribution. The overall low thermal conductivity values of these Rb-based double perovskites highlight their suitability for thermoelectric applications. Their ability to maintain low κt, even at high temperatures, makes them highly promising candidates for waste heat recovery and energy harvesting technologies.
A deeper examination of the exceptional thermoelectric properties of Rb2GeVI6, along with strategies for further optimization, necessitates a comparative analysis of its density of states (DOS), carrier concentration (n), and zT at 300 K, considering both spin-up and spin-down channels, as illustrated in Fig. 12. Given the consistent trends observed across all three studied materials, we present a representative plot for Rb2GeVI6, while omitting the others for brevity. Notably, distinct peaks in the thermoelectric figure of merit (zT) are consistently observed within the energy ranges of approximately −0.5 to 1 eV for the up-spin channel and −0.5 to 0.5 eV for the down-spin channel, an outcome intrinsically linked to the modulation of electronic states in the density of states (DOS). This suppression of electronic states leads to a concomitant reduction in carrier concentration within this energy regime, a phenomenon that plays a pivotal role in enhancing thermoelectric efficiency. A diminished p(n)-type carrier concentration contributes to an amplified Seebeck coefficient (S), a key determinant of thermoelectric voltage, which directly influences the elevation of zT values. Despite these remarkable thermoelectric properties, additional enhancement remains within reach through strategic material engineering approaches. The application of external strain or the refinement of hole-doping methodologies, as previously proposed in the literature,67 presents compelling avenues for further optimization. By tailoring these factors, it is possible to fine-tune the electronic band structure, thereby reinforcing the Seebeck coefficient while concurrently maintaining low thermal conductivity. Such advancements would unlock even greater thermoelectric efficiency, solidifying halide perovskites as frontrunners in next-generation energy conversion technologies.
3.8 Dielectric optical properties
The optical response of a material is fundamentally governed by its band structure and dielectric function, ε(ω) = ε1(ω) + iε2(ω), where ε1(ω) represents the real component dictating dispersion and charge screening, while ε2(ω) corresponds to the imaginary component associated with optical absorption. These components adhere to the Kramer's–Kronig relations, ensuring their interdependence.61 The static dielectric constant, a key parameter influencing charge transport, is directly affected by the band gap. The analysis of the real dielectric function ε1(ω) as a function of photon energy, as shown in Fig. 13(a), indicates that Rb2GeNiI6 exhibits a higher static dielectric constant, primarily due to its lower band gap. A reduced band gap lowers the energy barrier for charge transport, thereby enhancing carrier screening and mitigating defect-induced scattering. The spectral variation of ε1(ω) shows an increasing trend with photon energy. Notably, Rb2GeNiI6 attains a peak dielectric constant of ∼8.6 at 1.0 eV, whereas Rb2GeMnI6 and Rb2GeVI6 reach maxima of 8.0 and 8.4 at 2.0 eV and 2.5 eV, respectively. The absorptive behavior characterized by ε2(ω) provides insights into electronic transitions, as depicted in Fig. 13(b). The spectra of ε2(ω) against photon energy for Rb2GeMI6 reveal distinct peaks attributed to inter-band transitions, predominantly from I-5p valence states to M-d conduction states within the visible range. A secondary set of transitions, occurring between 3.5–5.0 eV, is associated with excitations from I-5p valence bands to Ge-p conduction bands, positioned away from the Fermi level. Rb2GeNiI6 exhibits a strong absorption peak (∼5.5) at 1.5 eV, indicating efficient visible-light interaction, while Rb2GeVI6 and Rb2GeMnI6 show peaks at 3.0 eV and 2.5 eV, respectively, at higher photon energies due to their larger band gaps, with corresponding maximum values of 6.0 and 4.9. Table 7 compiles all data related to the dielectric constant, along with results from similar compounds for comparison. Our findings demonstrate superior performance compared to previous studies,28,30 highlighting the potential of inorganic Rb2GeMI6 perovskites as promising alternatives to lead-halide perovskites in optoelectronic and photovoltaic applications, owing to their favourable dielectric properties and strong visible-light absorption.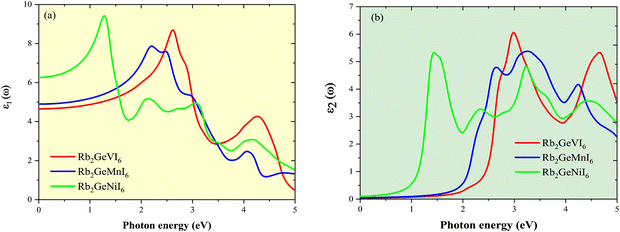 | ||
| Fig. 13 Plot of the dielectric constant (a) real part (ε1(ω) and (b) imaginary part (ε2(ω) against photon energy for Rb2GeMI6 halide perovskites. | ||
4. Conclusion
To conclude, we conducted a comprehensive evaluation of the structural, electronic, magnetic, and thermoelectric properties of Rb2GeMI6 (M = V, Mn, Ni) halide perovskites. Structural optimization confirms the stability of these compounds in the ferromagnetic phase, corroborated by positive Curie–Weiss constants. Mechanical stability evaluations, tolerance factor analyses, and negative enthalpy of formation further substantiate the robustness of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phase. Thermodynamic vibrational analyses, encompassing vibrational internal energy, Helmholtz free energy, entropy, and specific heat, indicate stability over a broad temperature range. Phonon dispersion calculations elucidate the dynamic behavior and stability of these perovskite structures. Electronic structure calculations employing the TB-mBJ functional indicate that all three compounds exhibit ferromagnetic semiconducting behavior, with notable spin-splitting energy gap. The compounds display integer magnetic moments of 3μB for Rb2GeVI6, 5μB for Rb2GeMnI6, and 2μB for Rb2GeNiI6, confirming their ferromagnetic ordering and potential for spintronic and magneto-electronic applications. The Curie temperatures, calculated to be 530.39 K (Rb2GeVI6), 580.72 K (Rb2GeMnI6), and 440.47 K (Rb2GeNiI6), demonstrate their magnetic phase phase stability well above room temperature. Electronic charge density analyses indicate a predominantly polar covalent bonding nature within these compounds. Thermoelectric evaluations reveal substantial Seebeck coefficients and diminished thermal conductivity, culminating in high thermoelectric figure of merit (zT) values of 1.00, 0.99, and 0.97 for Rb2GeVI6, Rb2GeMnI6, and Rb2GeNiI6, respectively. These findings underscore the promising potential of these perovskite materials in renewable energy technologies. Overall, this comprehensive study establishes Rb2GeMI6 (M = V, Mn, Ni) perovskites as promising candidates for spintronic devices, magneto-electronic systems, and high-efficiency thermoelectric materials, offering significant potential for next-generation solid-state and renewable energy technologies.
m cubic phase. Thermodynamic vibrational analyses, encompassing vibrational internal energy, Helmholtz free energy, entropy, and specific heat, indicate stability over a broad temperature range. Phonon dispersion calculations elucidate the dynamic behavior and stability of these perovskite structures. Electronic structure calculations employing the TB-mBJ functional indicate that all three compounds exhibit ferromagnetic semiconducting behavior, with notable spin-splitting energy gap. The compounds display integer magnetic moments of 3μB for Rb2GeVI6, 5μB for Rb2GeMnI6, and 2μB for Rb2GeNiI6, confirming their ferromagnetic ordering and potential for spintronic and magneto-electronic applications. The Curie temperatures, calculated to be 530.39 K (Rb2GeVI6), 580.72 K (Rb2GeMnI6), and 440.47 K (Rb2GeNiI6), demonstrate their magnetic phase phase stability well above room temperature. Electronic charge density analyses indicate a predominantly polar covalent bonding nature within these compounds. Thermoelectric evaluations reveal substantial Seebeck coefficients and diminished thermal conductivity, culminating in high thermoelectric figure of merit (zT) values of 1.00, 0.99, and 0.97 for Rb2GeVI6, Rb2GeMnI6, and Rb2GeNiI6, respectively. These findings underscore the promising potential of these perovskite materials in renewable energy technologies. Overall, this comprehensive study establishes Rb2GeMI6 (M = V, Mn, Ni) perovskites as promising candidates for spintronic devices, magneto-electronic systems, and high-efficiency thermoelectric materials, offering significant potential for next-generation solid-state and renewable energy technologies.
Data availability
The data sets generated and thereafter analysed would be available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no competing interest.Acknowledgements
Mudasir Younis Sofi, a recipient of the Prime Minister Research Fellowship (PMRF) award (Letter No. 3302522), wishes to express sincere gratitude to the PMRF agency (Ministry of Education (MoE), Govt. of India) for the financial support.References
- I. Žutić, J. Fabian and S. D. Sarma, Spintronics: Fundamentals and applications, Rev. Mod. Phys., 2004, 76(2), 323 Search PubMed.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. V. Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Spintronics: a spin-based electronics vision for the future, Science, 2001, 294, 1488 CrossRef CAS PubMed.
- P. Dey, J. N. Roy, P. Dey and J. N. Roy, Spintronics Applications, Spintronics: Fundamentals and Applications, 2021, pp. 223–267 Search PubMed.
- S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami and S. N. Piramanayagam, Spintronics based random access memory: a review, Mater. Today, 2017, 20(9), 530–548 CrossRef.
- K. L. Wang, J. G. Alzate and P. K. Amiri, Low-power non-volatile spintronic memory: STT-RAM and beyond, J. Phys. D:Appl. Phys., 2013, 46, 074003 CrossRef CAS.
- A. Telegin and Y. Sukhorukov, Magnetic semiconductors as materials for spintronics, Magnetochemistry, 2022, 8(12), 173 CrossRef CAS.
- A. Mauger and C. Godart, The magnetic, optical, and transport properties of representatives of a class of magnetic semiconductors: The europium chalcogenides, Phys. Rep., 1986, 141(2–3), 51–176 CrossRef CAS.
- X. Hao, J. S. Moodera and R. Meservey, Spin-filter effect of ferromagnetic europium sulfide tunnel barriers, Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 42(13), 8235 Search PubMed.
- T. Story, R. R. Gałazka, R. B. Frankel and P. A. Wolff, Carrier-concentration–induced ferromagnetism in PbSnMnTe, Phys. Rev. Lett., 1986, 56(7), 777 CrossRef CAS PubMed.
- U. Lüders, M. Bibes, K. Bouzehouane, E. Jacquet, J. P. Contour, S. Fusil, J. F. Bobo, J. Fontcuberta, A. Barthélémy and A. Fert, Spin filtering through ferrimagnetic NiFe2O4 tunnel barriers, Appl. Phys. Lett., 2006, 88(8), 082505 CrossRef.
- U. Lüders, A. Barthelemy, M. Bibes, K. Bouzehouane, S. Fusil, E. Jacquet, J. P. Contour, J. F. Bobo, J. Fontcuberta and A. Fert, NiFe2O4: a versatile spinel material brings new opportunities for spintronics, Adv. Mater., 2006, 18(13), 1733–1736 CrossRef.
- H. Ohno, A. Shen, F. Matsukura, A. Oiwa, A. Endo, S. Katsumoto and Y. Iye, (Ga, Mn) As: a new diluted magnetic semiconductor based on GaAs, Appl. Phys. Lett., 1996, 69(3), 363–365 CrossRef CAS.
- H. Munekata, H. Ohno, S. Von Molnar, A. Segmüller, L. L. Chang and L. Esaki, Diluted magnetic III–V semiconductors, Phys. Rev. Lett., 1989, 63(17), 1849 CrossRef CAS PubMed.
- A. Haury, A. Wasiela, A. Arnoult, J. Cibert, S. Tatarenko, T. Dietl and Y. M. d'Aubigné, Observation of a ferromagnetic transition induced by two-dimensional hole gas in modulation-doped CdMnTe quantum wells, Phys. Rev. Lett., 1997, 79(3), 511 CrossRef CAS.
- D. Ferrand, J. Cibert, A. Wasiela, C. Bourgognon, S. Tatarenko, G. Fishman, T. Andrearczyk, J. Jaroszyński, S. Koleśnik, T. Dietl and B. Barbara, Carrier-induced ferromagnetism in p-Zn1−xMnxTe, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 63(8), 085201 CrossRef.
- C. Moure and O. Peña, Recent advances in perovskites: Processing and properties, Prog. Solid State Chem., 2015, 43(4), 123–148 CrossRef CAS.
- Y. Lu, Q. Wang, L. Han, Y. Zhao, Z. He, W. Song, C. Song and Z. Miao, Spintronic Phenomena and Applications in Hybrid Organic–Inorganic Perovskites, Adv. Funct. Mater., 2024, 1, 2314427 CrossRef.
- B. Náfrádi, P. Szirmai, M. Spina, H. Lee, O. Yazyev, A. Arakcheeva, D. Chernyshov, M. Gibert, L. Forró and E. Horváth, Optically switched magnetism in photovoltaic perovskite CH3NH3(Mn: Pb) I3, Nat. Commun., 2016, 7, 13406 Search PubMed.
- M. Caid, Y. Rached, D. Rached and H. Rached, First principles study of the structural, elastic, magneto-electronic and thermoelectric properties of double perovskite Ba2ZrFeO6 in ferrimagnetic phase, Comput. Condens. Matter, 2023, e00847 CrossRef.
- B. Cai, X. Chen, M. Xie, S. Zhang, X. Liu, J. Yang, W. Zhou, S. Guo and H. Zeng, A class of Pb-free double perovskite halide semiconductors with intrinsic ferromagnetism, large spin splitting and high Curie temperature, Mater. Horiz., 2018, 5, 961 Search PubMed.
- J. Pei, B. Cai, H. L. Zhuang and J. F. Li, Bi2Te3-based applied thermoelectric materials: research advances and new challenges, Natl. Sci. Rev., 2020, 7(12), 1856–1858 Search PubMed.
- Y. Shtern, A. Sherchenkov, M. Shtern, M. Rogachev and D. Pepelyaev, Challenges and perspective recent trends of enhancing the efficiency of thermoelectric materials on the basis of PbTe, Mater. Today Commun., 2023, 9, 107083 Search PubMed.
- B. Russ, A. Glaudell, J. J. Urban, M. L. Chabinyc and R. A. Segalman, Organic thermoelectric materials for energy harvesting and temperature control, Nat. Rev. Mater., 2016, 1(10), 1–4 Search PubMed.
- S. Kee, M. A. Haque, D. Corzo, H. N. Alshareef and D. Baran, Self-healing and stretchable 3D-printed organic thermoelectrics, Adv. Funct. Mater., 2019, 29(51), 1905426 CrossRef CAS.
- J. Mao, H. Zhu, Z. Ding, Z. Liu, G. A. Gamage, G. Chen and Z. Ren, High thermoelectric cooling performance of n-type Mg3Bi2-based materials, Science, 2019, 365(6452), 495–498 Search PubMed.
- S. Hayat, M. A. Khan, M. A. Ali, A. Khan, R. A. Alshgari, S. Mohammad and S. Al-Qaisi, Investigating optical, electronic, and thermoelectric properties of X2ScIO6 (X = K, Rb, and Cs) double perovskite semiconductors for green energy applications, Comput. Theor. Chem., 2025, 1243, 114992 Search PubMed.
- A. Ayyaz, Q. Mahmood, G. Murtaza, A. A. Abd El-Moula, S. Al-Qaisi, N. Sfina and A. S. Alshomrany, Study of mechanical, optoelectronic, and thermoelectric properties of Rb2ScAuZ6 (Z = Br, I) for energy harvesting applications, Inorg. Chem. Commun., 2024, 165, 112520 Search PubMed.
- M. Caid, D. Rached, Y. Rached and H. Rached, Comprehensive exploration of halide double perovskites Cs2B′GeCl6 (B′: Zn, Cd) for affordable energy technologies: a high-throughput investigation, Opt. Quantum Electron., 2024, 56(6), 980 Search PubMed.
- M. Caid, D. Rached, S. Al-Qaisi, Y. Rached and H. J. Rached, DFT calculations on physical properties of the lead-free halide-based double perovskite compound Cs2CdZnCl6, Solid State Commun., 2023, 369, 115216 CrossRef CAS.
- E. Haque and M. A. Hossain, Origin of ultra-low lattice thermal conductivity in Cs2BiAgX6 (X = Cl, Br) and its impact on thermoelectric performance, J. Alloys Compd., 2018, 748, 63 Search PubMed.
- A. Pisoni, J. Jacimovic, O. S. Barisic, M. Spina, R. Gaál, L. Forró and E. Horváth, Ultra-low thermal conductivity in organic–inorganic hybrid perovskite CH3NH3PbI3, J. Phys. Chem. Lett., 2014, 5(14), 2488–2492 CrossRef CAS PubMed.
- K. Miyata, T. L. Atallah and X. Y. Zhu, Lead halide perovskites: Crystal-liquid duality, phonon glass electron crystals, and large polaron formation, Sci. Adv., 2017, 3(10), e1701469 Search PubMed.
- M. Beekman, D. T. Morelli and G. S. Nolas, Better thermoelectrics through glass-like crystals, Nat. Mater., 2015, 14(12), 1182–1185 CrossRef CAS PubMed.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowsk, F. Tran, L. Marks and L. Marks, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Techn. Universitat, Vienna, Austria, 2019, p. 287 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 Search PubMed.
- D. Koller, F. Tran and P. Blaha, Improving the modified Becke–Johnson exchange potential, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85(15), 155109 Search PubMed.
- T. Charpin, A Package for Calculating Elastic Tensors of Cubic Phases Using WIEN: Laboratory of Geometrix F-75252 (Paris, France) ( 2001).
- A. tero-de-la-Roza, D. Abbasi-Pérez and V. Luaña, Gibbs2: A new version of the quasi-harmonic model code. II. Models for solid state thermodynamics, features and implementation, Comput. Phys. Commun., 2011, 182(10), 2232–2248 Search PubMed.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 Search PubMed.
- M. Y. Sofi, M. S. Khan, J. Ali and M. A. Khan, Unlocking the role of 3d electrons on ferromagnetism and spin-dependent transport properties in K2GeNiX6 (X = Br, I) for spintronics and thermoelectric applications, J. Phys. Chem. Solids, 2024, 192, 112022 Search PubMed.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244–247 Search PubMed.
- M. Y. Sofi, M. S. Khan and M. A. Khan, Control of spin on ferromagnetism and thermoelectric properties of K2GeMnX6 (X = Cl, Br, I) halide perovskites: emerging candidates for semiconductor spintronics and thermoelectric applications, Mater. Adv., 2024, 5(11), 4913–4931 RSC.
- M. Blanco, E. Francisco and V. Luaña, GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef CAS.
- Q. Chen and B. Sundman, Calculation of Debye temperature for crystalline structures case study on Ti, Zr, and Hf, Acta Mater., 2001, 49, 947–961 CrossRef CAS.
- D. V. Schroeder and J. K. Pribram, An Introduction to Thermal Physics, Am. J. Phys., 1999, 67, 1284–1285 CrossRef.
- P. Debye, Zur Theorie der spezifischen Warmen, Ann. Phys., 1912, 344, 789–839 CrossRef.
- A. T. Petit and P. L. Dulong, Study on the measurement of specific heat of solids, Ann. Chim. Phys., 1819, 10, 395 Search PubMed.
- P. Giannozzi, et al., QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 Search PubMed.
- M. Born, On the stability of crystal lattices, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160 CrossRef CAS.
- W. Voigt Textbook of Crystal Physics (G.B. Teubner, 1928).
- A. Reuss, Berechnung Der Fließgrenze von Mischkristallen Auf Grund Der Plastizitätsbedingung Für Einkristalle, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, Te elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- M. Y. Sofi, M. S. Khan and M. A. Khan, Harnessing the half-metallicity and thermoelectric insights in Cs2AgMBr6 (M = V, Mn, Ni) double halide perovskites: A DFT study, Mater. Sci. Semicond. Process., 2025, 186, 109023 CrossRef CAS.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., 1954, 45, 823–843 Search PubMed.
- I. N. Frantsevich; F. F. Voronov and S. A. Bakuta, Elastic Constants and Moduli of Elasticity of Metals and Nonmetals, Naukova Dumka, Kiev, 1982 Search PubMed.
- W. Hume-rothery, Elasticity and anelasticity of metals, Nature, 1949, 164(4159), 84–85 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101(5), 055504 CrossRef PubMed.
- D. M. Teter, Computational alchemy: The search for new superhard materials, MRS Bull., 1998, 23(1), 22–27 CrossRef CAS.
- Y. Tian, B. Xu and Z. Zhao, Microscopic theory of hardness and design of novel superhard crystals, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- E. Fine, L. D. Brown and H. L. Marcus, Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18, 951–956 CrossRef.
- M. Y. Sofi, A. Ramzan, M. S. Khan, A. Kumar, M. R. Rather, S. A. Sofi, S. A. Khandy and M. A. Khan, Pioneering computational insights into the structural, magnetic, and thermoelectric properties of A3XN (A = Co, Fe; X = Cu, Zn) anti-perovskites for advanced material applications, Mater. Sci. Semicond. Process., 2025, 185, 108925 CrossRef CAS.
- J. Kudrnovsky, et al., Exchange interactions in III-V and group-IV diluted magnetic semiconductors, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 115208 CrossRef.
- Y. Takahashi, On the origin of the Curie-Weiss law of the magnetic susceptibility in itinerant electron ferromagnetism, J. Phys. Soc. Jpn., 1986, 55(10), 3553–3573 CrossRef.
- M. Jonson and G. D. Mahan, Mott's formula for the thermopower and the Wiedemann-Franz law, Phys. Rev. B:Condens. Matter Mater. Phys., 1980, 21, 4223–4229 CrossRef CAS.
- G. A. Slack, Non-metallic crystals with high thermal conductivity, J. Phys. Chem. Solids, 1973, 34(2), 321–335 CrossRef CAS.
- G. Qin, A. Huang, Y. Liu, H. Wang, Z. Qin, X. Jiang, J. Zhao, J. Hu and M. Hu, High-throughput computational evaluation of lattice thermal conductivity using an optimized Slack model, Mater. Adv., 2022, 3(17), 6826–6830 RSC.
- C. W. Wu, X. Ren, G. Xie, W. X. Zhou, G. Zhang and K. Q. Chen, Enhanced High-Temperature Thermoelectric Performance by Strain Engineering in BiOCl, Phys. Rev. Appl., 2022, 18(1), 014053 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |