Ion concentration polarization focusing at a millimeter-scale microbead junction: towards higher volumetric throughput

Abstract

Ion concentration polarization focusing (ICPF) is an electrokinetic technique that has shown promise in achieving even billion-fold preconcentration factors. However, increasing the volumetric throughput of ICPF is challenging because disruptive processes that reduce preconcentration efficiency worsen as the channel cross-section extends beyond the microscale. We previously introduced an approach for mitigating the above challenges in a microfluidic regime. However, in that system, the flow rate was limited to less than 1.0 μL min⁻¹. Herein, we report a high throughput and scalable ICPF of charged analytes in a millimeter-scale channel. Using 3D-printed channels of 4.0 mm² cross-section, we achieve preconcentration factors above 200-fold within 10 min at a flow rate of 30 μL min⁻¹. In this system, ICP is accomplished by ion permselective transport through a packed bed of commercially available cation exchange microbeads (30 μm and 200 μm). We investigate the scalability of the approach by comparing the ICPF performance of channels with four distinct cross-sectional areas. While ICPF occurs in all four cases, the degree of preconcentration drops below 100-fold (per 10 min) in channels with cross-sections beyond 4.0 mm². This drop in efficiency is attributed to dispersion associated with Joule heating. Therefore, by improving the device design to dissipate heat more effectively, we anticipate that this approach can be scaled up further for applications that demand high volumetric throughput electrokinetic focusing.

---

Introduction

Lab-on-a-chip (LOC) platforms continue to attract interest in chemical, bioanalytical, and biomedical applications due to inherent advantages like portability, less reagent consumption, rapid sample processing and analysis, compartmentalization, and automation.^1,2 Within the analytical workflow, sample preparation plays a crucial role.^3–5 Therefore, integrating purification, preconcentration, and separation steps into LOC analytical platforms is critical, especially when the target of interest is present in significantly low concentrations along with other interferents.^6,7 In these platforms, the preconcentration step is especially important since the sample volume on chip is small and only a fraction of the analyte molecules may interact with the detection or sensing mechanism. Therefore, concentrating the analyte before detection is needed to improve sensitivity and accuracy.⁸ Analyte preconcentration in μTASs is often achieved by stacking or focusing through isotachophoresis (ITP) and field amplified sample stacking (FASS), gradient focusing methods like isoelectric focusing (IEF), electric field gradient focusing (EFGF), and temperature gradient focusing (TGF).^9–13 Although well established, these techniques have their own drawbacks, which make their applications limited. For example, ITP requires at least two electrolytes with distinct mobilities (the leading and the trailing electrolyte), and the analyte of interest is focused between them. In IEF, a pH gradient is required to stack ampholytic targets according to their isoelectric points.¹⁴ TGF needs an appropriate buffer/mixture of buffers capable of generating an electric field gradient when a temperature gradient is applied along the microfluidic channel.¹⁵

In contrast to the above preconcentration techniques, ion concentration polarization focusing (ICPF) leverages electric field gradients but does not require multiple and/or specific electrolytes and sample preparation steps. Several researchers have demonstrated ICPF using nanochannels and nanomembranes integrated in microchannels.¹⁶ For example, Zhang and Timperman showed 300-fold preconcentration of fluorescein within 40 min, using ICPF.¹⁷ They used a PDMS microfluidic channel integrated with a track-etched polycarbonate nanocapillary array. Wang et al.¹⁸ achieved million-fold preconcentration of proteins and peptides by trapping the analytes in an extended space charge region near a nanofluidic filter. Unlike in ITP where the sample is trapped between two electrolytes, ICPF allows for a continuous supply of sample and perpetual maintenance of the steep electric field gradient, thus permitting high preconcentration factors.¹³

ICP is an electrokinetic transport phenomenon associated with ion permselective structures such as nanochannels and nanoporous membranes.¹⁹ When a voltage bias is applied across the ion permselective structure, concentration gradients arise at both ends of it due to preferential transport of counter-ions (ions of opposite charge to that of the nanochannel or the nanoporous membrane) and exclusion of co-ions. Due to this preferential transport of ions, the local concentration of both anions and cations at one end of the ion permselective structure decreases, giving rise to an ion depletion zone (IDZ). Simultaneously, the local concentration of both types of charges increases at the opposite end, resulting in an ion enrichment zone (IEZ). It is notable that ICP occurs even when there is partial charge selectivity, as long as the majority of the current through the nanostructure is carried through the electrical double layer (EDL).²⁰ Thus, the primary parameter that governs the ICP phenomenon is the ratio of surface conductance to bulk conductance (Dukhin number, Du).²¹ Due to localized depletion of ions of the background electrolyte (BGE), the ionic conductivity of the IDZ is extremely low. Therefore, a significant amount of the applied voltage drops across the IDZ, resulting in a steep electric field gradient at its boundary. It is the migration of charged analytes within this steep gradient that facilitates focusing in the presence of opposing fluid flow. Faradaic ion concentration polarization (fICP) is an analogous technique that accomplishes localized depletion of BGE ions by charge transfer reactions at electrodes, not preferential charge transport through nanoporous membranes or nanochannels as in ICP. In both ICP and fICP-based preconcentrators, focusing of a specific analyte occurs at a distinct location where the electrophoretic velocity of the analyte balances with its opposing convective velocity (Fig. 1a), which is usually driven by a combination of pressure-driven flow and electroosmosis.

Fig. 1 (a) Focusing of a negatively charged analyte at the boundary of the IDZ when the electrophoretic velocity (v_ep) of the analyte counterbalances the convective velocity (v_c). (b) Illustration of the device architecture: the 3D-printed bottom thermoplastic layer with the main channel and the auxiliary channel, the top PDMS layer with channel inlets, bead inlets, and electrode reservoirs. (c) Image of the assembled dual-channel device with the packed bead beds. A schematic is included for clear visualization of the arrangement of the bead beds.

It is important to recognize that concentration polarization is not a recent discovery; it has been a well-established phenomenon in classical membrane systems such as electrodialysis, reverse osmosis, and fuel cells.²² In the context of micro and nanofluidics, ICP (and fICP) has been demonstrated not only for analyte preconcentration but also for applications such as separating nucleic acids from serum,²³ separating microparticles,²⁴ seawater desalination,^25,26 and droplet-based microextraction applications.^27,28 However, most ICP-based preconcentrators, similar to other electrokinetic preconcentration techniques like ITP, are limited by the volume of sample they can process within a reasonable amount of time.²⁹ Higher volumetric throughput is vital when the preconcentrated plug must be sent for downstream analysis such as by mass spectrometry.^29,30 Moreover, the required volumetric throughput for certain microfluidic applications, such as nucleic acid and protein detection is in the range of 1–2.5 μL min⁻¹, whereas it can be as high as 100–1000 μL min⁻¹ for separation of circulating tumor cells and purification of ionic radioisotopes.³⁰ Therefore, to successfully adapt ICPF for such applications that demand high flow rates, increasing the volumetric throughput is equally important as improving the preconcentration factor.

Kwak et al. addressed the challenge of improving volumetric throughput in ICPF by developing a continuous-flow ICP concentrator.²⁹ Their device consisted of a main channel of 15 μm height and a bifurcated microchannel integrated with a Nafion nanoporous membrane (a cation permselective membrane) to continuously elute the preconcentrated plug through the bifurcation. With an applied voltage of 80 V, they were able to achieve maximum enrichment factors up to 200-fold for a model fluorescent tracer (fluorescein sodium salt) flowed at 5 μL min⁻¹ in a channel of 15 μm height and 980 μm width. In continuous flow ICPF reported by Papadimitriou et al., the electric field was applied perpendicular to the sample flow for the continuous focusing, separation, and extraction of three anionic fluorescent tracers.³⁰ The focused tracers were extracted continuously through a comb-like array of channels. They reported a concentration factor of 10-fold in blood plasma flowing at 15 μL min⁻¹. Ouyang et al. reported a staged ICP preconcentrator to enrich nucleic acids and proteins up to 10⁹-fold in 30 min by processing several milliliters of sample, with applied voltages ranging from 200–600 V.³¹ Their device consisted of 4 stages of massively parallelized (over 38 000) microchannels interconnected by a nanoporous membrane.

It is notable that in the above examples, the microchannel height was below 100 μm. Moving to larger channel heights (and cross-sections) is a straightforward strategy for increasing the volumetric throughput, yet challenging in ICP-based systems. This challenge stems from two scenarios that decrease the preconcentration efficiency: (i) in most work, the ion-permselective structure is a planar nanoporous membrane, and therefore the IDZ is not distributed across the entire channel cross-section, leading to “leaking” of focused analytes over the IDZ, (ii) steep electric field and concentration gradients at the boundary of the IDZ lead to strong electroconvective vortices, which results in unwanted re-mixing of focused analytes and the disruption of the boundary of the IDZ.

Approaches with varying degrees of sophistication and design have been developed to overcome these problems. MacDonald et al. used an “out-of-plane” nanoporous membrane, oriented vertically within the channel wall. They were able to generate a stable IDZ boundary that spanned over the entire channel height at flow rates up to 20 μL min⁻¹ with an applied voltage of just 20 V.³² To mitigate the fluidic instability arising from electroconvective vortices, Kim and co-workers incorporated PDMS microfins next to the nanoporous membrane.³³ These micro fins, which were spaced 100 μm from each other across the entire width of the microchannel, acted as geometrical constrictions that minimized merging of primary vortices into larger secondary vortices. Thus, a stable preconcentrated plug and a uniform IDZ boundary were maintained. In addition, the micro fins facilitated the surface conduction of cations through the IDZ towards the nanoporous membrane to circumvent slow bulk transport, thereby supporting overlimiting current without the need for electroconvective mixing. In another work from the same group, it was shown that surface conduction can be augmented by protruding the nanoporous membrane further into the nanochannel to create an alternate path for the ionic current.³⁴ Other strategies to minimize vortex flow are to decrease the current density at the permselective membrane by increasing its surface area, and minimizing the size and the lateral motion of vortices using microstructured membranes.^35,36

Inspired by the above work, our group introduced out-of-plane fICP as a means of improving volumetric throughput in fICPF.³⁷ The device comprised two microbead beds: (i) a silver bead bed that acted as a 3D flow-through electrode to generate an IDZ distributed across the entire channel cross-section, thus minimizing the “leaking” of the focused analyte plug, (ii) a polystyrene carboxylate bead bed that aided in stable focusing of analytes by geometrically obstructing the growth of smaller vortices into larger ones.

In this paper, we demonstrate that the above packed bed approach can be scaled up further for stable focusing of charged analytes in millimeter-scale channels. We first studied the electrokinetic behavior of the packed bed device using current–voltage (I–V) curves to see if the system exhibits the three-regime I–V curves characteristic of ICP. After identifying a voltage suitable for ICPF based on these I–V curves, we performed ICPF experiments in millimeter-scale channels of four distinct cross-sectional areas to investigate the scalability of the packed-bed approach. To understand the effect of the size of the cation-permselective beads on ICPF, we carried out ICPF experiments with two distinct bead diameters.

Using commercially available ion exchange resin as the ion-selective structure in 3D printed microchannels, we were able to achieve ICPF even at a flow rate of 60 μL min⁻¹. Although “packed bed ICP” has been reported previously by Syed et al.³⁸ and Ouyang et al.,³⁹ they involved nanoscale beads (100–500 nm) and therefore required more complex device fabrication procedures, such as reactive ion etching, and device architectures that are not readily scaled up. The significance of our approach is that we were able to generate ICP using a combination of 30 μm and 200 μm cation exchange microspheres. Because of the larger size of the beads, we did not require lithography to fabricate bead retention structures. Instead, larger (1 mm-tall and 4 mm-wide) 3D-printed channels containing an array of 100 μm-wide bead retention structures were sufficient. Further, bead handling and packing were more straightforward. Therefore, this approach can be used as a user-friendly sample preparation technique that can be integrated with LOC applications.

Experimental

Chemicals

The charged fluorophore, BODIPY²⁻ (4,4-fluoro-1,3,5,7,8-pentamethyl-4-bora-3a,4a-diaza-S-indacene-2,6-disulfonic acid, disodium salt) was obtained from Invitrogen (Carlsbad, CA). All other solutions were prepared using reagent-grade chemicals (Fisher Scientific, Waltham, MA) and diluted with double deionized water (18.2 MΩ cm, Sartorius Arium Pro, Göttingen, Germany) to the desired concentration. Clear Microfluidic Resin V7.0a was obtained from CADworks3D (Concord, ON, Canada). Poly(dimethylsiloxane) (PDMS) (Sylgard 184 elastomer kit) was obtained from Dow Corning Corp. (Midland, MI). Cation exchange beads of 30 μm (DOWEX® 50WX8, 200–400 mesh, strongly acidic hydrogen form) and 200 μm (DOWEX® 50WX8, 50–100 mesh, strongly acidic hydrogen form) were purchased from Sigma (St. Louis, MO). Both these bead types are styrene divinylbenzene beads with surface sulfonic acid groups (DVB-SO₃⁻). Acid-washed glass beads (200 μm) were obtained from Sigma (St. Louis, MO). Epoxy adhesive (Double/Bubble®) was purchased from Royal Adhesives & Sealants (Wilmington, CA).

Device fabrication

The devices consisted of two layers (Fig. 1b): (i) the bottom thermoplastic layer comprising the main channel and the auxiliary channel and (ii) the top PDMS layer with punch-holes for fluid inlets and outlets and reservoirs to accommodate the electrodes. The main channel was 30 mm long, 4.0 mm wide, and 1.0 mm tall, while the auxiliary channel was 2.0 mm wide, 8.5 mm long, and 1.0 mm tall unless otherwise specified in the results and discussion section (see ESI† for the .stl files of the 3D design). Each channel consisted of three 2.0 mm-wide bead beds defined by four rows of rectangular pillars (200 μm by 200 μm spaced 100 μm apart). The thermoplastic layer was 3D printed using Clear Microfluidic Resin V7.0a (Miicraft Ultra 50 3D Printer, CADworks3D, Concord, ON, Canada). After printing, the chips were thoroughly rinsed with 2-propanol and UV-cured (CureZone MKII LED Light Cure Box, Creative CADWORKS, Toronto, ON, Canada) according to the manufacturer's instructions. For the top layer, 10 parts of PDMS monomer were mixed with 1 part of crosslinker and cured at 65 °C for 3–4 h. After curing, punch holes were made for channel inlets, bead inlets, and electrode reservoirs. Both layers were treated with air plasma (PDC-001, Harrick Plasma, Ithaca, NY) for 60 s and bonded together, followed by incubation at 65 °C for at least 4 h.

Bead packing

The bead bed closest to the main channel outlet and the bead beds on either side of the central bead bed of the auxiliary channel were filled with a suspension (50 μL, w/v ∼300 mg mL⁻¹) of 200 μm cation exchange beads using a micropipette. The bead bed furthest away from the main channel outlet was filled with a suspension of 200 μm glass beads. The bead inlets were sealed with a drop of epoxy adhesive. Finally, the central bead bed, which interconnects the main channel and the auxiliary channel, was filled with 30 μm cation exchange beads, and the bead inlets were secured with epoxy adhesive.

I–V characteristics

To facilitate filling, the devices were evacuated for 30 min–1 h prior to the experiments. Then, a solution of 10.0 mM NaCl was introduced through the main channel outlet using a pipette. Gentle pressure was applied using the pipette such that all the bead beds and both the main channel and auxiliary channel were wetted with the solution. A fluorescence image was taken, which was later used for background subtraction. Pt electrodes (1.0 mm diameter) were inserted into the main channel and auxiliary channel reservoirs. Then, 10.0 mM NaCl spiked with 0.1 μM BODIPY²⁻ was infused through the main channel inlet at a flow rate of 30–60 μL min⁻¹ (as described in the results and discussion section) and withdrawn from the outlet with the aid of two 5 mL BD plastic syringes attached to two syringe pumps. Once the channel was fully filled with the electrolyte containing the fluorescent tracer, a DC voltage sweep was applied (0–120 V, 0.1 V s⁻¹) between the main channel and the auxiliary channel, using a power supply (2450 SourceMeter®, Keithley Instruments, Cleveland, OH). The I–V curves were recorded using KickStart software (Keithley Instruments, Cleveland, OH). While running the voltage sweep, a fluorescence image was recorded every 10 s using an SMZ800N stereoscope (Nikon Industries, New York, NY) equipped with a Sola Lumencor Light Engine (Lumencor, Beaverton, OR) and Photometrics Cool Snap Dyno camera (Tucson, Arizona).

Focusing an anionic tracer within the glass bead bed

The same procedure used for device filling in the I–V curve experiments was followed in focusing experiments as well. Once the flow was established, a DC voltage bias was applied between the main channel and the auxiliary channel for 10 min. Current transients were recorded using the KickStart software. A fluorescence image was recorded every 10 s to visualize the IDZ formation and subsequent focusing of BODIPY²⁻. Fluorescence intensities used for enrichment factor calculation were background subtracted and analyzed using NIS-Elements 4.6 software (Nikon), and ImageJ.

Results and discussion

I–V characteristics

Before conducting ICPF experiments, we characterized the 1.0 mm-tall, packed bed device in terms of its current response to an applied DC voltage sweep. Fig. 2a shows the I–V curves obtained in four distinct device configurations. The first configuration had three bead beds: 200-μm glass beads, 30 μm DVB-SO₃⁻ beads, and 200 μm DVB-SO₃⁻ beads (green curve). The second configuration also had three bead beds: a bed of 200 μm glass beads and two beds of 200 μm DVB-SO₃⁻ beads (blue curve). The third configuration had only two bead beds, 200 μm glass beads and 200 μm DVB-SO₃⁻ beads with the downstream bed left empty (red curve). The final configuration contained only one bead bed; 200 μm DVB-SO₃⁻ with the two upstream beds left empty (black curve). In each case, the electrolyte consisted of 10.0 mM NaCl spiked with 0.1 μM BODIPY²⁻, and a flow rate of 30 μL min⁻¹ was maintained while recording the I–V curves.

Fig. 2 (a) Current–voltage curves obtained in 1.0 mm-tall channels with four distinct bead bed configurations. Background electrolyte: 10.0 mM NaCl, flow rate: 30 μL min⁻¹. Fluorescence micrographs recorded (b) before and (c), (d) during (at 80 V and 110 V) current–voltage curve. Channels contain 0.1 μM BODIPY²⁻ in 10.0 mM NaCl.

According to Fig. 2a, the three configurations that do not incorporate the 30 μm DVB-SO₃⁻ beads (black, red and blue curves) exhibit the three-regime I–V curve characteristic to ICP: (i) ohmic region – current increased linearly with increasing voltage, (ii) limiting region – current plateaued (80–88 V in the black curve, 86–91 V in the red curve, and 81–84 V in the blue curve) due to reaching mass-transfer limitation as the IDZ expanded, (iii) over-limiting region: current increased again due to the formation of electroconvective vortices. A shift in the onset of limiting behavior to higher voltages occurs with addition of the glass beads (red curve), which increase ohmic resistance (evidenced by a shallower slope of the I–V curve), decreasing the current that drives depletion. Addition of a second bed of sulfonated beads (blue curve) improves the permselectivity of ion transport, thereby lowering the onset voltage for the limiting regime, despite the high ohmic resistance of this configuration.

For the device configuration with smaller, 30 μm DVB-SO₃⁻ beads between the 200 μm DVB-SO₃⁻ beads and 200 μm glass beads (green curve), there is no limiting region in the I–V curve. Nevertheless, the fluorescence micrographs obtained during the voltage sweep indicate BODIPY²⁻ depleting downstream of the bead beds at 80 V (Fig. 2c), and accumulation of BODIPY²⁻ on the glass bead bed (Fig. 2d). Therefore, these observations suggest that even though the characteristic three-regime I–V curve is not observed in the three-bead bed configuration, ICP still occurs. We have reported a similar observation in our previously published work on out-of-plane fICP, where we attributed the smoother transition from the limiting to over-limiting regime to the enhanced surface conduction of cations through the IDZ by the upstream bead bed.³⁷ In our current system the upstream bed comprises larger 200 μm glass beads (with low zeta potential), and the effect of surface conduction is less pronounced. However, the 30 μm beads enhance surface conduction towards the 200 μm DVB-SO₃⁻ beads. With hydrodynamic instabilities suppressed by the upstream coarse glass beads, this configuration enables faster and more efficient enrichment.

Focusing an anionic tracer on the glass bead bed

Since we observed depletion of BODIPY²⁻ downstream of the bead bed starting from 70 V during the voltage sweep, ICP preconcentration experiments were conducted at several distinct voltages (data shown only for 90 V and 100 V, see Fig. S3† for 110 V data) at a flow rate of 30 μL min⁻¹, in the 1 mm tall channel. In all these experiments, 0.1 μM BODIPY²⁻ in 10 mM NaCl was used as the model analyte.

Fig. 3a shows a series of fluorescence micrographs obtained in one such experiment where 100 V was applied to drive ICP. The device consisted of three bead beds in the main channel; 200 μm glass, 30 μm DVB-SO₃⁻, and 200 μm DVB-SO₃⁻. We observed that the dye slowly starts to focus within the glass bead bed after about 30 s of voltage application. Within 5 min, a stable focused plug is formed. Meanwhile, the fluorescence intensity downstream of the bead beds started to decrease due to the fluorescent tracer being retained upstream of the cation permselective bead bed. Interestingly, we also noticed that the fluorescence intensity of the entire upstream segment of the bead beds starts to decrease after about 8 min of voltage application. This effect was more visible at 110 V (see the fluorescence micrograph at 10 min in Fig. S3a†). This decrease in intensity can be due to one or both of two reasons: pH changes quenching the tracer molecule or the tracer undergoing thermal bleaching because of Joule heating.

Fig. 3 (a) Series of fluorescence micrographs showing the focusing of 0.1 μM BODIPY²⁻ in 1.0 mm-tall channel consisting of three bead beds; 200 μm glass, 30 μm DVB-SO₃⁻, and 200 μm DVB-SO₃⁻. The background electrolyte is 10.0 mM NaCl. Flow rate: 30 μL min⁻¹, voltage: 100 V. (b) Plot showing the evolution of maximum enrichment factor and (c) percent dye leakage over time, at two distinct voltages. Flow rate: 30 μL min⁻¹. (d) Variation of conductance downstream of the bead bed with time before, during and after application of 100 V to drive ICP. 10.0 mM NaCl, 30 μL min⁻¹, n = 3.

Fig. 3b shows the evolution of the maximum enrichment factor with time, at 30 μL min⁻¹, under 90 and 100 V. The enrichment factor increases with time, reaching more than 100-fold at 90 V and 150-fold at 100 V within 10 min. This rate of enrichment is comparable with that achieved by Ouyang et al. (∼95-fold in 10 min) for ICPF of the fluorescent tracer Alexa fluor 488 in 1× BSA, in a microfluidic channel containing a nanoporous membrane and a packed bed of bioconjugated nanospheres.³⁹ At 110 V (Fig. S3b†), the enrichment factor first increases and then starts to decrease towards the end of the experiment. This decrease is mainly due to the decreased quantum efficiency of BODIPY²⁻ as described earlier.

Apart from the maximum enrichment factor, a rough estimate of the overall enrichment factor can be made using the total volume swept and the volume of the enriched plug. Considering the fluorescence micrograph at 5 min (Fig. 3b), the volume of the plug was approximately 1.48 μL, and the volume swept in 5 min is 150 μL. Therefore, the enrichment factor achieved within 5 min at 100 V is roughly 100-fold.

Fig. 3c shows the percent leakage of the model analyte through the cation-selective bead bed. This result provides insight into how well the IDZ can repel the negatively charged analyte. At both 90 V and 100 V, the percent dye leakage reaches below 10% within 3 min. That is, more than 90% of the analyte is retained upstream of the cation-selective bead bed due to repulsion from the IDZ.

However, at 90 V, the percent dye leakage increases with time to more than 20% due to the bursting of the focused plug. This suggests that 100 V performs better than 90 V in preventing leaking of the focused analyte through the cation permselective bead bed at this flow rate.

Fig. 3d shows the variation of the conductance downstream of the bead beds before, during, and after the application of 100 V to drive ICP in the system. The current downstream of the bead bed was measured at 1.0 V using a custom-made circuit board, and the current was converted to conductance. This experiment provides information on how well the overall charged species in the electrolyte (analytes + electrolyte ions) are repelled from the IDZ/ retained upstream of the bead bed. We observed that the downstream current reduces to 92% of its initial value 2 min after the initiation of ICP. This result indicates that more than 90% of ions in the electrolyte are repelled from the IDZ. After turning off the voltage that drives ICP, the focused analyte and electrolyte ions leak through the bead bed, thus, increasing the conductivity again.

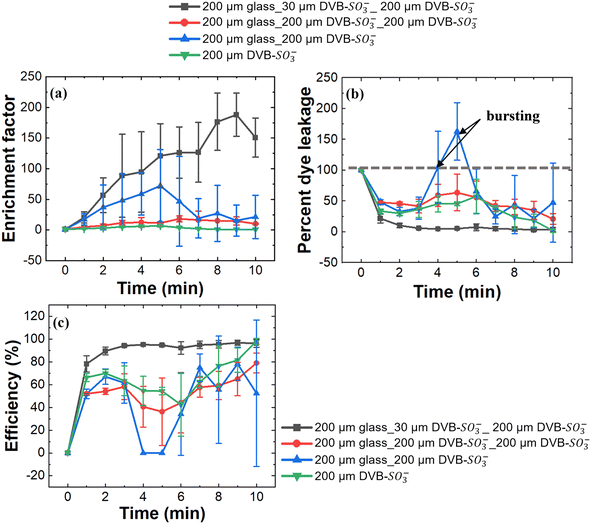
To investigate the effect of bead diameter and the length of the cation permselective bed on the enrichment factor (and therefore, the preconcentration efficiency), we performed control experiments. In the first control (Fig. 4a–c, red curve), the main channel consisted of three bead beds; one 200 μm glass bead bed, and two 200 μm DVB-SO₃⁻ bead beds (no 30 μm beads). The second control (Fig. 4a–c, blue curve) consisted of two bead beds; one 200 μm glass bead bed and one 200 μm DVB-SO₃⁻ bead bed, with the downstream bead bed left empty. The final control (Fig. 4a–c, green curve) consisted of only a 200 μm DVB-SO₃⁻ bead bed. All experiments were performed in 10.0 mM NaCl at 30 μL min⁻¹, and 100 V. As shown in Fig. 4a, none of these configurations produced enrichment factors ≥100, unlike in the configuration with the 200 μm glass, 30 μm DVB-SO₃⁻, and 200 μm DVB-SO₃⁻ bead beds (black curve). The percent dye leakage through the cation-selective bed (Fig. 4b) is higher than that of the configuration which incorporates the 30 μm DVB-SO₃⁻ beads. Note that the spikes in the percent dye leakage in the blue curve (above 100%) is because of the bursting of the enriched plug, which introduces a concentrated plug of analyte downstream the bead bed with a concentration higher than the initial analyte concentration before the application of voltage. Based on the percent dye leakage, the efficiency at which the analyte is retained at the boundary of the IDZ was also calculated and is shown in Fig. 4c (when calculating the efficiency, dye leakage ≥100% was considered as 0% efficiency, and dye leakage of 0% was considered as 100% efficiency). This efficiency is lower in all the controls than that of the configuration which incorporates the 30 μm DVB-SO₃⁻ beads.

Fig. 4 Plots showing the evolution of (a) maximum enrichment factor with time and (b) percent dye leakage (c) efficiency of dye retention upstream of the bead beds with time in four device configurations under an applied voltage of 100 V at 30 μL min⁻¹. 10.0 mM NaCl, 0.1 μM BODIPY²⁻, n = 3.

These finer cation-selective beads are strategically placed in our device design to drive ICP through enhanced surface conduction, which can be attributed to the increased Dukhin number in the system. The size of the interstitial spaces in the cation-selective bead bed decreases ∼6-fold (from ∼31 μm to ∼5 μm) when moving from 200 μm beads to 30 μm beads. That is, the critical dimension of the system decreases. The surface area-to-void volume ratio similarly increases by 6.67-fold, which is expected to enhance surface conductivity effects and contribute to a higher Dukhin number, improving cation selectivity. Furthermore, suppressed flow instabilities in the IDZ, due to the presence of a region of coarser glass beads upstream, ensure more stable and efficient preconcentration. Consequently, this two-region configuration is critical for achieving high preconcentration performance and flow stability.

Scalability of the packed bed ICPF

With the aim of testing the scalability of the packed bed approach, we then conducted focusing experiments in a 2.0 mm-tall channel. In the 2.0 mm-tall channel, the bead diameters, bead bed lengths and other channel dimensions remained the same as in the 1.0 mm tall channel, except the channel height. And, the pillars that defined the bead beds were replaced by a mesh structure (see the .stl file provided in ESI†), since the reduced aspect ratio of the pillars made them unsteady. Our hypothesis was that if the approach is scalable, the channel-cross section and the volumetric throughput can be doubled without significantly sacrificing the enrichment factor even though the applied voltage is the same as the voltage used for focusing in a 1.0 mm-tall channel.

Fig. 5a is a series of fluorescence micrographs showing the extent of BODIPY²⁻ enrichment within the glass bead bed in a 2.0 mm-tall channel at 60 μL min⁻¹, under an applied voltage of 100 V. Similar to the focusing experiments in the 1.0 or of roughly 100-fold, which was the same value estimated for the 1.0 mm-tall channel at 30 μL min⁻¹. However, after 5 min, we observed quenching of BODIPY²⁻ in the 2.0 mm channel, indicated by the distribution of the plug at t = 10 min (Fig. 5a) which covers only half of the main channel width. pH measurements (using pH paper) at the anodic reservoir before and after voltage application showed that pH drops from ∼7 to ∼2 due to the voltage application. This observation suggests that pH changes resulted in decreased quantum yield of BODIPY²⁻ in the channel.

Fig. 5 Fluorescence micrographs showing the focusing of 0.1 μM BODIPY² in a 2.0 mm-tall channel at a flow rate of 60 μL min⁻¹, under an applied voltage of 100 V, when the background electrolyte is (a) 10.0 mM NaCl, (b) 10.0 mM Tris·HClO₄.

To test this hypothesis, we performed ICPF experiments in 10.0 mM Tris·HClO₄ (pH 8.3), instead of in 10.0 mM NaCl. We hypothesized that if pH changes in the system affect the quantum yield of the fluorescent tracer, the use of a buffered system like Tris·HClO₄ would minimize those effects. Fig. 5b are fluorescence micrographs obtained during ICPF of 0.1 μM BODIPY²⁻ in 10.0 mM Tris·HClO₄ (pH 8.3) in a 2.0 mm-tall channel at 60 μL min⁻¹, under an applied voltage was 100 V. It is clear from these fluorescence micrographs that the fluorescence intensity upstream of the bead beds does not drastically decrease as in the experiment shown in Fig. 4a (1.0 mm-tall channel) and Fig. 5a (2.0 mm-tall channel), where 10.0 mM NaCl was used as the background electrolyte. This observation supports our hypothesis that pH changes that occur during ICPF in 10.0 mM NaCl affect the quantum yield of BODIPY²⁻, and thus, the enrichment factor as well. Therefore, 10.0 mM Tris·HClO₄ (pH 8.3) buffer was used as the background electrolyte in subsequent experiments.

To better understand the system's scalability, we compared the performance of channels with four distinct channel heights: 0.5 mm, 1.0 mm, 1.5 mm, and 2.0 mm, while maintaining other channel dimensions and bead dimensions the same throughout. All the experiments were performed in 10.0 mM Tris·HClO₄ (pH 8.3), and the flow rate was maintained at 15, 30, 45, and 60 μL min⁻¹, respectively, while the applied voltage was 100 V. Fig. 6a shows the variation of maximum enrichment factor with time for the four channel heights. Both 0.5 mm- and 1.0 mm-tall devices reach maximum enrichment factors of above 200-fold within 10 min. However, in the 1.5 mm-tall channel, the maximum enrichment factor reached within 10 min is about 150-fold, and in the 2.0 mm-tall channel, the enrichment factor reaches only about 75-fold. The rate of enrichment plotted in Fig. 6b shows that the performance of 0.5 mm-, 1.0 mm-, and 1.5 mm-tall devices is not statistically significantly different from each other. However, there is a significant difference in the device performance when comparing the 0.5 mm and 1.0 mm-tall channels (rates of enrichment reaching 30-fold per min) with the 2.0 mm-tall channel (rate of enrichment less than 10-fold per min). That is, after a certain threshold height, the efficiency of preconcentration drops. This drop can arise mainly due to two reasons: leaking of the focused analyte over the IDZ and broadening of the focused plug due to diffusional dispersion. According to Fig. 6c, the percent analyte (dye) leakage over the IDZ in the 1.5 mm- and 2.0 mm-tall channels is relatively higher than that of the 0.5 mm- and 1.0 mm-tall channels before t = 5 min. This significant leakage of analyte explains the low enrichment factors of 1.5 mm- and 2.0 mm-tall channels during the first 5 min of voltage application.

Fig. 6 Plot of (a) evolution of enrichment factor with time, (b) rate of enrichment, (c) percent dye leakage, (d) area of focused plug at the 10th minute in devices with four distinct channel heights: 0.5, 1.0, 1.5, and 2.0 mm. Flow rate was 15, 30, 45, and 60 μL min⁻¹ respectively. Background electrolyte is 10 mM Tris·HClO₄. Applied voltage: 100 V. In (b), the statistical differences of the means were analyzed with one-way ANOVA, followed by Tukey′s multiple comparison test (n = 3, α = 0.05).

After 5 min, the percent dye leakage in all four channel heights reaches less than 15%, and therefore, leakage no longer has a significant influence on enrichment. However, as shown in Fig. 6d, for the 1.5 mm- and 2.0 mm-tall channels, the area of the focused analyte plug is approximately as twice that observed for the smaller channel heights. This broadening explains the low enrichment factors and the slower rate of enrichment in the taller channels. We attribute this broadening to Joule heating, which becomes more detrimental when the channel height increases, due to increased current and poor heat dissipation (see Fig. S1† for current transients obtained during the focusing experiments). Therefore, further optimization of the device design is required to efficiently dissipate the heat generated at the bed during these experiments.

Conclusions

We have demonstrated high volumetric throughput preconcentration of charged analytes using ICPF at a packed microbead bed junction in 3D-printed millimeter-scale channels. Specifically, we used commercially available 30 μm cation exchange microbeads as the ion-selective structure to generate ICP. I–V characteristics of the system showed the typical ohmic, limiting, and over-limiting regimes when 200 μm cation exchange microbeads were used. When 30 μm cation exchange microbeads were used, the I–V characteristic was smoother with a direct transition from ohmic to an overlimiting regime, indicating that the finer beads aid in better surface conduction of cations. During ICPF experiments in a channel 1.0 mm-tall by 4.0 mm-wide, we achieved enrichment factors over 200-fold at a flow rate of 30 μL min⁻¹, within 10 min. Importantly, this result was obtained using 30 μm cation-selective beads, which allow for more facile device fabrication than nanometer-scale beads. Larger cation selective beads did not produce such high enrichment factors, indicating that the bead size cannot be scaled further. A 2.0 mm-tall channel supported 60 μL min⁻¹, but increased current led to localized pH changes due to water electrolysis, which were mitigated when a buffer was introduced. ICPF experiments in four channels with distinct cross-sectional areas, under the same applied voltage, show that after a threshold cross-section of 6.0 mm², the enrichment factor drops, mainly due to dispersion arising from Joule heating. Therefore, features that mitigate Joule heating should be incorporated into the channel for the successful scalability of the channel cross-section above 6.0 mm², without compromising the preconcentration efficiency.

Data availability

A subset of data may be included as supplementary material within the manuscript. For further data access, please contact the corresponding author.

Author contributions

Umesha Peramune: conceptualization, methodology, investigation, validation, formal analysis, writing – original draft. Zisun Ahmed: conceptualization, methodology, investigation, writing – review & editing. Robbyn K. Anand: funding acquisition, supervision, conceptualization, writing – review and editing.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

Funding for this research was provided by an NSF CAREER grant awarded by the Chemistry Directorate Chemical Measurement and Imaging Program under award number 1849109. Additionally, this work was supported by the National Science Foundation Convergence Accelerator Program under Grant No. 2344398.

References

1. B. Sharma and A. Sharma, Microfluidics: Recent Advances Toward Lab-on-Chip Applications in Bioanalysis, Adv. Eng. Mater., 2022, 24, 2100738,  DOI:10.1002/adem.202100738.
2. S. F. Berlanda, M. Breitfeld, C. L. Dietsche and P. S. Dittrich, Recent Advances in Microfluidic Technology for Bioanalysis and Diagnostics, Anal. Chem., 2021, 93, 311–331,  DOI:10.1021/acs.analchem.0c04366.
3. Y. He, P. Miggiels, B. Wouters, N. Drouin, F. Guled, T. Hankemeier and P. W. Lindenburg, A High-Throughput, Ultrafast, and Online Three-Phase Electro-Extraction Method for Analysis of Trace Level Pharmaceuticals, Anal. Chim. Acta, 2021, 1149, 338204,  DOI:10.1016/j.aca.2021.338204.
4. E. Turiel and A. Martín-Esteban, Molecularly Imprinted Polymers for Sample Preparation: A Review, Anal. Chim. Acta, 2010, 668, 87–99,  DOI:10.1016/j.aca.2010.04.019.
5. J. Park, D. H. Han and J. K. Park, Towards Practical Sample Preparation in Point-of-Care Testing: User-Friendly Microfluidic Devices, Lab Chip, 2020, 20, 1191–1203,  10.1039/d0lc00047g.
6. M. Sonker, V. Sahore and A. T. Woolley, Recent Advances in Microfluidic Sample Preparation and Separation Techniques for Molecular Biomarker Analysis: A Critical Review, Anal. Chim. Acta, 2017, 986, 1–11,  DOI:10.1016/j.aca.2017.07.043.
7. S. Battat, D. A. Weitz and G. M. Whitesides, An Outlook on Microfluidics: The Promise and the Challenge, Lab Chip, 2022, 22(3), 530–536,  10.1039/d1lc00731a.
8. J. H. Lee, Y. A. Song and J. Han, Multiplexed Proteomic Sample Preconcentration Device Using Surface-Patterned Ion-Selective Membrane, Lab Chip, 2008, 8(4), 596–601,  10.1039/b717900f.
9. S. Song, A. K. Singh and B. J. Kirby, Electrophoretic Concentration of Proteins at Laser-Patterned Nanoporous Membranes in Microchips, Anal. Chem., 2004, 76(15), 4589–4592,  DOI:10.1021/ac0497151.
10. S. J. Kim, Y. A. Song and J. Han, Nanofluidic Concentration Devices for Biomolecules Utilizing Ion Concentration Polarization: Theory, Fabrication, and Applications, Chem. Soc. Rev., 2010, 39(3), 912–922,  10.1039/b822556g.
11. A. T. K. Perera, D. T. Phan, S. Pudasaini, Y. Liu and C. Yang, Enhanced Sample Pre-Concentration by Ion Concentration Polarization on a Paraffin Coated Converging Microfluidic Paper Based Analytical Platform, Biomicrofluidics, 2020, 14(1), 014103,  DOI:10.1063/1.5133946.
12. B. C. Giordano, D. S. Burgi, S. J. Hart and A. Terray, On-Line Sample Pre-Concentration in Microfluidic Devices: A Review, Anal. Chim. Acta, 2012, 17, 11–24,  DOI:10.1016/j.aca.2011.12.050.
13. B. Berzina and R. K. Anand, Tutorial Review: Enrichment and Separation of Neutral and Charged Species by Ion Concentration Polarization Focusing, Anal. Chim. Acta, 2020, 1128, 149–173,  DOI:10.1016/j.aca.2020.06.021.
14. M. R. Pergande and S. M. Cologna, Isoelectric Point Separations of Peptides and Proteins, Proteomes, 2017, 5, 4,  DOI:10.3390/proteomes5010004.
15. D. Ross and L. E. Locascio, Microfluidic Temperature Gradient Focusing, Anal. Chem., 2002, 74(11), 2556–2564,  DOI:10.1021/ac025528w.
16. J. G. Shackman and D. Ross, Counter-Flow Gradient Electrofocusing, Electrophoresis, 2007, 556–571,  DOI:10.1002/elps.200600592.
17. Y. Zhang and A. T. Timperman, Integration of Nanocapillary Arrays into Microfluidic Devices for Use as Analyte Concentrators, Analyst, 2003, 128(6), 537–542,  10.1039/b300102d.
18. Y. C. Wang, A. L. Stevens and J. Han, Million-Fold Preconcentration of Proteins and Peptides by Nanofluidic Filter, Anal. Chem., 2005, 77(14), 4293–4299,  DOI:10.1021/ac050321z.
19. Z. Ahmed, Y. Bu and L. Yobas, Conductance Interplay in Ion Concentration Polarization across 1D Nanochannels: Microchannel Surface Shunt and Nanochannel Conductance, Anal. Chem., 2020, 92(1), 1252–1259,  DOI:10.1021/acs.analchem.9b04417.
20. M. Li and R. K. Anand, Recent Advancements in Ion Concentration Polarization, Analyst, 2016, 141, 3496–3510,  10.1039/c6an00194g.
21. T. A. Zangle, A. Mani and J. G. Santiago, Theory and Experiments of Concentration Polarization and Ion Focusing at Microchannel and Nanochannel Interfaces, Chem. Soc. Rev., 2010, 39, 1014–1035,  10.1039/b902074h.
22. S. Khudhur, A. Al-Amshawee, M. Y. Bin and M. Yunus, Electrodialysis Membrane with Concentration Polarization-A Review, Chem. Eng. Res. Des., 2024, 201, 645–678.
23. W. Ouyang, Z. Li and J. Han, Pressure-Modulated Selective Electrokinetic Trapping for Direct Enrichment, Purification, and Detection of Nucleic Acids in Human Serum, Anal. Chem., 2018, 90(19), 11366–11375,  DOI:10.1021/acs.analchem.8b02330.
24. C. D. Davies and R. M. Crooks, Focusing, Sorting, and Separating Microplastics by Serial Faradaic Ion Concentration Polarization, Chem. Sci., 2020, 11(21), 5547–5558,  10.1039/d0sc01931c.
25. S. J. Kim, S. H. Ko, K. H. Kang and J. Han, Direct Seawater Desalination by Ion Concentration Polarization, Nat. Nanotechnol., 2010, 5(4), 297–301,  DOI:10.1038/nnano.2010.34.
26. J. Yoon, H. J. Kwon, S. K. Kang, E. Brack and J. Han, Portable Seawater Desalination System for Generating Drinkable Water in Remote Locations, Environ. Sci. Technol., 2021, 56(10), 6733–6743,  DOI:10.1021/acs.est.1c08466.
27. S. Kim, B. Ganapathysubramanian and R. K. Anand, Concentration Enrichment, Separation, and Cation Exchange in Nanoliter-Scale Water-in-Oil Droplets, J. Am. Chem. Soc., 2020, 142(6), 3196–3204,  DOI:10.1021/jacs.9b13268.
28. A. Krishnamurthy and R. K. Anand, Recent Advances in Microscale Extraction Driven by Ion Concentration Polarization, TrAC, Trends Anal. Chem., 2022, 148, 116537,  DOI:10.1016/j.trac.2022.116537.
29. R. Kwak, S. J. Kim and J. Han, Continuous-Flow Biomolecule and Cell Concentrator by Ion Concentration Polarization, Anal. Chem., 2011, 83(19), 7348–7355,  DOI:10.1021/ac2012619.
30. V. A. Papadimitriou, L. I. Segerink and J. C. T. Eijkel, Free Flow Ion Concentration Polarization Focusing (FF-ICPF), Anal. Chem., 2020, 92(7), 4866–4874,  DOI:10.1021/acs.analchem.9b04526.
31. W. Ouyang and J. Han, Universal Amplification-Free Molecular Diagnostics by Billion-Fold Hierarchical Nanofluidic Concentration, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(33), 16240–16249,  DOI:10.1073/pnas.1904513116.
32. B. D. MacDonald, M. M. Gong, P. Zhang and D. Sinton, Out-of-Plane Ion Concentration Polarization for Scalable Water Desalination, Lab Chip, 2014, 14(4), 681–685,  10.1039/c3lc51255j.
33. K. Kim, W. Kim, H. Lee and S. J. Kim, Stabilization of Ion Concentration Polarization Layer Using Micro Fin Structure for High-Throughput Applications, Nanoscale, 2017, 9(10), 3466–3475,  10.1039/c6nr08978j.
34. J. Kim, I. Cho, H. Lee and S. J. Kim, Ion Concentration Polarization by Bifurcated Current Path, Sci. Rep., 2017, 7(1), 1–12,  DOI:10.1038/s41598-017-04646-0.
35. G. Yossifon, P. Mushenheim, Y. C. Chang and H. C. Chang, Eliminating the Limiting-Current Phenomenon by Geometric Field Focusing into Nanopores and Nanoslots, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81(4), 046301,  DOI:10.1103/PhysRevE.81.046301.
36. J. De Valença, M. Jõgi, R. M. Wagterveld, E. Karatay, J. A. Wood and R. G. H. Lammertink, Confined Electroconvective Vortices at Structured Ion Exchange Membranes, Langmuir, 2018, 34(7), 2455–2463,  DOI:10.1021/acs.langmuir.7b04135.
37. B. Berzina, S. Kim, U. Peramune, K. Saurabh, B. Ganapathysubramanian and R. K. Anand, Out-of-Plane Faradaic Ion Concentration Polarization: Stable Focusing of Charged Analytes at a Three-Dimensional Porous Electrode, Lab Chip, 2022, 22(3), 573–583,  10.1039/d1lc01011e.
38. A. Syed, L. Mangano, P. Mao, J. Han and Y. A. Song, Creating Sub-50 Nm Nanofluidic Junctions in a PDMS Microchip via Self-Assembly Process of Colloidal Silica Beads for Electrokinetic Concentration of Biomolecules, Lab Chip, 2014, 14(23), 4455–4460,  10.1039/c4lc00895b.
39. W. Ouyang, J. Han and W. Wang, Enabling Electrical Biomolecular Detection in High Ionic Concentrations and Enhancement of the Detection Limit Thereof by Coupling a Nanofluidic Crystal with Reconfigurable Ion Concentration Polarization, Lab Chip, 2017, 17(22), 3772–3784,  10.1039/c7lc00722a.

---

Footnote

† Electronic supplementary information (ESI) available: Current transients obtained during ICPF experiments at 100 V in the four devices (0.5, 1.0, 1.5, and 2.0 mm-tall channels). ICPF experiments carried out in a single-channel device at 100 V. ICPF experiments carried out in a dual-channel device at 110 V. Calculating the enrichment factor, percent dye leakage and downstream conductance. The .stl files of the design of the dual-channel millimeter-scale device (0.5 and 2.0 mm tall). See DOI: https://doi.org/10.1039/d5lc00183h

---