Mechanistic understanding of carbon mineralization in fracture systems using microfluidics

Abstract

Carbon mineralization in mafic and ultramafic rocks presents an opportunity for permanent carbon storage in the Earth's subsurface. However, due to their lower permeability, pre-existing fracture networks are key for mineralization to occur. Therefore, to fully develop this technology, a mechanistic understanding of the mineralization behavior in fractures with the consideration of hydrodynamic components is required. We use high-pressure microfluidics to investigate key mechanisms influencing dissolution–precipitation in a fracture network. The experiments were conducted in micromodels made of natural rocks with a comb-shaped flow channel to mimic a fracture network. This enabled studying the effect of injection rate on coupled dissolution–precipitation in advection and diffusion-dominated flow paths. We used gypsum carbonation as an analog reaction to allow for realistic experimental time frames due to its rapid reaction kinetics. The experimental work is coupled with high-fidelity numerical simulations to enhance our understanding of the parameters affecting the mineralization reaction. Our results demonstrate the importance of flow rate on the rate and nature of the gypsum carbonation reaction revealing that higher flow rates enable deeper penetration of the mineral precipitation front into the dead-end channels. This is an important finding since for sustained mineralization in a fracture network, precipitation in dead-ends while still allowing for flowing fractures is critical. Detailed characterization of the precipitates showed that lower flow rates led to porous and loose precipitates in the form of aragonite while higher flow rates mimicked supersaturation behavior leading to the formation of calcite. The reactive transport simulations further demonstrated the significance of flow velocity in advection-dominated channels to influence the efficiency of carbon mineralization in diffusion-dominated channels, potentially clogging of dead-end channels. These findings highlight the need for coupling chemical, mechanical, and hydrodynamic processes to evaluate the nature and extent of carbon mineralization in fractured media critical for permanent storage in mafic and ultramafic formations. This research further highlights the need for more investigation in potential subsurface fracture generation techniques to aid carbon mineralization.

---

1. Introduction

Geologic carbon sequestration (GCS) has long been considered a technique for reducing anthropogenic carbon dioxide (CO₂) from the atmosphere.¹ Various trapping mechanisms have been proposed during GCS including 1) structural trapping, when CO₂ is immobilized by an impermeable layer; 2) residual trapping, when CO₂ is trapped in the pore space by capillary forces; 3) solubility trapping, as CO₂ is dissolved into pore water; and 4) mineral trapping, where CO₂ is incorporated into mineral structures.² Each subsequent mechanism increases CO₂ storage security whereby the mineral trapping mechanism provides a long-term permanent storage. This method involves injecting CO₂ into a suitable subsurface reservoir, such as saline aquifers or mafic/ultramafic rocks, where the coupled dissolution of the host rock by the acidified CO₂-rich brine and the subsequent precipitation of carbonate minerals leads to permanent storage. The reaction rate of this coupled dissolution–precipitation process is governed by a variety of parameters including (1) the reservoir pressure and temperature, which dictates the thermophysical properties of the injected CO₂ phase; (2) the reservoir properties (e.g., porosity, permeability, rock composition, and surface area affecting reactivity); (3) the injecting and resident fluid compositions; and (4) the injection rate.³

Recent pilot studies have shown that mineralization can occur at a significantly faster rate in mafic and ultramafic rocks (i.e., 2–3 years; at the CarbFix and Wallula Basalt project sites).^2–6 However, unlike traditionally considered depleted oil and gas and saline aquifers, many mafic/ultramafic formations have low porosity and permeability, limiting storage volumes and reactive surface areas to the preexisting pore network.⁷ Understanding reaction and flow dynamics within these fractured systems is complicated. While in situ observations can provide necessary insight, the reaction of mafic/ultramafic rocks is typically too slow for such techniques.⁸ To address this issue, surrogate systems can be employed.

Studies have shown that when basalts come into contact with CO₂-rich and sulfate-bearing seawater, gypsum and anhydrite readily precipitate.⁹ Thus, it is important to evaluate the effect of the reaction between gypsum, anhydrite, and calcium carbonate for carbon storage projects in basalts. Gypsum is also one of the primary components of evaporite formations which are considered to be potential caprocks.¹⁰ Hence, evaluating the extent and rate of gypsum carbonation can help to assess the viability of evaporite formations as potential caprocks. To date, it is unknown how processes such as passivation, clogging, or mineralization-induced fracturing could affect long-term CO₂ sequestration in reactive, fractured systems. For example, passivation will reduce the reactivity of surfaces, inhibiting further dissolution and precipitation, while reaction-driven fracturing could create more reactive surface area for mineralization to occur. It is thus critical to understand the complex dissolution–precipitation reactions that occur during GCS. Fast-reacting surrogate systems, such as gypsum, allow us to explore these dynamics in a laboratory setting. To this end, we have employed gypsum as a surrogate reactive mineral, allowing us to observe dissolution–precipitation dynamics with reasonably fast kinetics while capturing calcium-carbonate-specific behaviors.

While it is challenging to probe the geochemical and geomechanical reactions occurring in the subsurface during injection, in situ laboratory experiments can provide a controlled environment to identify key mechanistic processes. To date, the majority of experiments aimed at investigating dissolution–precipitation reactions during carbon mineralization have been conducted in static systems, where hydrodynamic processes are not considered. In contrast, experimental efforts to identify the fluid dynamic processes that occur during flow through fractures frequently exclude chemical reactions or only investigate one reaction (e.g. dissolution or precipitation). Previous experimental studies suggest that dissolution is favored in advection-dominated zones, while precipitation is favored in diffusion-dominated zones such as dead-end channels. This was demonstrated through high-temperature, high-pressure core-flooding experiments in basalt rocks, where dissolution preferentially occurred in the primary flow paths, and mineralization occurred in dead-end zones.¹¹ Andreani et al. (2009)¹² showed similar results from percolation experiments through sintered dunite. The authors found that mineralization preferentially occurred in diffusion-controlled zones of the experiment, and that dissolution in advection-dominated zones resulted in the formation of a Si-rich passivating layer which eventually inhibited olivine dissolution. However, natural examples of carbon mineralization, such as in Oman's ophiolite complex, depict widespread mineralization, including within primary fractures.¹³ Additionally, these previous experiments do not have the capability for in situ observations, and the long time required for the reaction of mafic/ultramafic rocks limits the variable space that can be explored.

Several recent investigations have employed microfluidic platforms to explore microscale physico-chemical processes relevant to GCS. A recent review by Ratanpara et al. (2025)¹⁴ summarizes various microfluidic system designs and methodologies used to study CO₂ adsorption, mineralization kinetics, trapping behavior, and mass transfer relevant to carbon capture and storage. Song et al. (2018)¹⁵ were among the first to develop a biogenically calcite-functionalized microfluidic device to investigate reactive transport in the context of GCS. Their study demonstrated that CO₂ released from mineral dissolution reactions locally inhibits further dissolution and potentially generate leakage pathways. Zhang et al. (2020)¹⁶ introduced a multilayered microfluidic platform to investigate in situ calcium carbonate nucleation kinetics. They found that nucleation occurred more slowly in microcavities compared to bulk solution, and that the presence of inorganic impurities such as magnesium ions further influenced the process. Ho et al. (2021)¹⁷ conducted a microfluidic study to examine CO₂ mass transfer in water under different thermodynamic phase states. They observed enhanced mass transfer at the micro-pore scale under supercritical CO₂ conditions, highlighting a potential benefit for storage efficiency. Xiao et al. (2024)¹⁸ compared mineral precipitation dynamics under similar conditions by evaluating microbially induced carbonate precipitation (MICP) versus chemically induced carbonate precipitation (CICP). While CICP yielded faster crystal growth, MICP resulted in more heterogeneous mineral textures. More recently, Liu et al. (2025)¹⁹ employed MICP to fabricate a calcite-functionalized micromodel with crystals of controlled morphology to study microbe–fluid–rock interactions during subsurface gas storage. Their work validated the micromodel's relevance for both CO₂ and hydrogen storage systems, where mineral dissolution–precipitation and biogeochemical reactions critically influence storage performance and biological losses.

In addition to experimental approaches, geochemical modeling provides unique insights into the coupled effects of dissolution, precipitation, and fluid flow. For instance, Chen et al. (2014)²⁰ performed sensitivity analyses on precipitation–dissolution patterns in 2-D systems under varying parameters such as reaction rate constants, mineral molar volumes, and mineral growth modes. In the work of Kang et al. (2010),²¹ the dynamic processes of calcite dissolution and dolomite precipitation induced by the injection of excess CO₂ during carbon storage were simulated. More recently, Wang et al. (2024)²² modeled potential dissolution–precipitation patterns under varying Péclet number (Pe) and Damköhler number (Da_I) in rock slices categorizing them into wormhole dissolution with clustered precipitation, dissolution-dominant patterns, and compact dissolution–precipitation. These prior studies highlight the complexity of coupling dissolution, precipitation, advection, diffusion, and chemical reactions as well as the intriguing outcomes that emerge from their interactions. However, many models lack the experimental validation needed to make actionable predictions for sustainable GCS operations.

While progress has been made in the literature in understanding coupled dissolution––precipitation reactions, the role of localized hydrodynamic conditions with particular emphasis on flow rate variations in advective versus diffusive zones of fractures remains insufficiently explored in the context of carbon mineralization. This research addresses that gap by using a high-pressure microfluidic platform^23,24 and natural rock samples to systematically investigate the impact of flow rate on mineral reactions. We employ the gypsum–calcium carbonate system as an analog due to its fast kinetics, enabling real-time experimental observation of reactive transport processes. The use of pure gypsum as a model material provides a system with well-characterized, rapid reaction kinetics, which is essential for resolving the coupling between fluid flow and mineral transformation processes.^25,26 This approach allows us to isolate and systematically study the impact of hydrodynamic conditions on dissolution–precipitation mechanisms which would be far more complex in chemically heterogeneous substrates like basalt or peridotite. By working with a homogeneous, reactive phase, we can draw specific inferences that serve as a foundation for understanding a more complex system. Moreover, we quantitatively interpret the experimental phenomena using a geochemical simulator coupled with a 3-D multicomponent transport simulator using the lattice Boltzmann method (LBM). We demonstrate the importance of flow rate in affecting the extent and nature of mineral precipitation in dead-end flow channels critical for carbon mineralization in fractured systems such as mafic and ultramafic rocks.

2. Methods

2.1. Description of the microfluidic experiments

We carried out microfluidic experiments to investigate the effects of flow rate and fracture geometry during coupled dissolution–precipitation of gypsum to calcium carbonate. A schematic of the assembled micromodel is shown in Fig. 1. The micromodels were created by cutting crystalline gypsum (gypsum, Wards Scientific) into rectangular chips along the natural cleavage plane. The chips were approximately 5 cm × 2.5 cm × 1 cm in dimension, with 010 faces on the top and bottom of the chip. A comb-shaped flow path was defined by a laser-cut Teflon film, which was placed on the top surface of the chip. The channel consisted of a primary flow path with four dead-ends of different widths (0.5 mm and 1 mm) and lengths (5 mm and 9 mm) with an approximate pore volume of 4–5 mm³. A design of the channel is provided in the ESI† (Fig. S1). This design was chosen to observe the different impacts of diffusion (dead-ends) versus advection (flow channel) in the reacting system. The entire micromodel was sandwiched between two acrylic sheets and sealed on the edges using a strong epoxy (J-B Weld steel reinforced epoxy). Four ports, an inlet, an outlet, and two pressure ports (differential pressure transmitter, DPT) were installed with epoxy on the top surface of the micromodel and attached to the PEEK tubing. A detailed description on sample preparation is provided in the ESI† in section II and Fig. S2 and S3). The pressure flow lines were attached to the DPT (Validyne) to measure the differential pressure across the sample during the experiment.

Fig. 1 Schematic of the micromodel used in the flow-through experiments.

The micromodel assembly was placed inside a custom-designed high-pressure and temperature vessel (Ni–Cr-based metal alloy) equipped with a sapphire window to allow real-time visualization into the micromodel. An Olympus DP74 camera was mounted on an Olympus MVX10 microscope to record the experiment. The experiments were conducted at ambient temperature (∼25 °C) and a pore pressure of 1500 kPa, maintained by a backpressure ISCO pump. The cell was held under a confining pressure of 3000 kPa using deionized water (DI). Water acted as the confining medium, ensuring a pressure seal such that flow occurred only through the micromodel. Two high-precision, high-pressure pumps (ISCO) injected the carbonated fluid through the micromodel at a set flow rate. The fluid was composed of 0.5 M sodium carbonate (Na₂CO₃) and 1 M sodium chloride (NaCl) to facilitate the carbonation of gypsum via the following reaction:²⁶

CaSO_4(s)·2H₂O + HCO₃⁻ ⇌ CaCO_3(s) + H⁺ + SO₄²⁻ + 2H₂O, (1)

which is a combination of gypsum dissolution:

CaSO_4(s)·2H₂O ⇌ Ca²⁺ + SO₄²⁻ + 2H₂O, (2)

and calcite precipitation:

HCO₃⁻ + Ca²⁺ ⇌ CaCO_3(s) + H⁺. (3)

The injection brine containing 0.5 M Na₂CO₃ provides carbonate ions into the solution making the solution alkaline. Under alkaline conditions, the bicarbonate concentration would be low but non-negligible with the following equilibrium reactions:²⁷

CO₃⁻ + H₂O ⇌ HCO₃⁻ + OH⁻, (4)

HCO₃⁻ + H₂O ⇌ H₂CO₃ + OH⁻ (5)

H₂CO₃ ⇌ CO₂ + H₂O, (6)

HCO₃⁻ ⇌ CO₂ + OH⁻. (7)

The pressure and temperature conditions selected here do not represent true subsurface conditions owing to experimental limitations. Nevertheless, the chosen surrogate conditions enable us to closely mimic dissolution–precipitation reaction central to the mineralization-driven GCS process. Similarly, the use of Na₂CO₃ and NaCl solutions served as a simplified proxy for CO₂-induced carbonate chemistry, allowing us to isolate and study key mineral–fluid interactions. Although the use of Na₂CO₃ solution differs from CO₂-saturated brine, this simplification was necessary due to experimental constraints of room temperature and under a confining pressure of 3 MPa, which limited our ability to directly simulate subsurface CO₂-rich conditions and handle supercritical or gaseous CO₂ safely. To address this limitation, we designed our system to replicate the resultant carbonate chemistry and physical processes while maintaining experimental control. Experiments were conducted at 10 μL min⁻¹ and 60 μL min⁻¹ to investigate the effects of flow rate on the above reaction and were run for 5 h. Additional experiments were conducted at 1 μL min⁻¹ and 100 μL min⁻¹, but only the geochemistry was examined for these experiments due to fluid leaking from the flow path. For post-experiment analysis, the chip was disassembled by softening the epoxy on the edges using a hot plate and peeling it off. Surface profilometry (Keyence VK-X150) scans were performed on the sample surfaces after the experiment to characterize changes in the surface morphology due to the dissolution and precipitation reactions. Scanning electron microscopy (SEM) was also used to identify the mineralogy and morphology of the precipitates.

2.2. Numerical simulations

High-fidelity simulations using LBM were performed in a lattice mimicking the experimental micromodel domain for quantitative analysis of the reactive transport behavior. The Lattice Boltzmann pore-scale model for multicomponent reactive transport (Kang et al. 2006, 2007, 2010)^21,28,29 was extended to three-dimensional (3D) space and utilized for the numerical simulation. The fluid model (D3Q19) utilized the incompressible model proposed by He and Luo (1997),³⁰ while the D3Q7 model was used for solute transport. Homogeneous chemical reactions in the bulk fluid were considered to be in instantaneous equilibrium, while heterogeneous reactions occurring at solid surfaces were treated kinetically and implemented through fluid–solid boundary conditions. The evolution of the solid phase due to dissolution or precipitation was achieved using the volume-of-voxel method, which ensures mass conservation between the solid and fluid phases. Additional details about this model can be found in Kang et al. (2006, 2007, 2010).^21,28,29 The constant pressure boundary condition developed by Zou and He (1997)³¹ was applied at the upstream and downstream boundaries. To improve computational efficiency, the computer code was highly parallelized for high-performance computing. The numerical simulations were performed on the Chicoma high-performance computing clusters at Los Alamos National Laboratory.

In previous studies, the reported dissolution rates of gypsum under standard temperature and pressure conditions (25 °C and 1 atm) vary widely, ranging from 1.3 × 10⁻³ to 3 × 10⁻⁸ mol m⁻² s⁻¹.^26,32–35 This wide range can be attributed to factors such as variations in reaction kinetics for different cleavage planes of gypsum crystals, differences in sample purity, grain size, experimental methods, and the influence of hydrodynamic conditions.²⁶ Since reaction rates were not known, we set the dissolution rate to 1.1 × 10⁻⁶ mol m⁻² s⁻¹, and the precipitation rate to 3.42 × 10⁻⁷ mol m⁻² s⁻¹ (ref. 36) after testing different values to ensure that simulation results were representative of our experiments. Although the experiments observed the precipitation of a significant amount of calcium carbonate polymorphs (such as vaterite and minor aragonite) alongside calcite precipitation, our simulations simplified the chemical system by using only the thermodynamic parameters of calcite, the most stable carbonate phase.

The simulation domain (Fig. 2) consists of a grid with dimensions of 15 (thickness) × 585 (width) × 1440 (length) lattice units, where each cubic grid cell has a size of 20 μm. To balance computational tractability with flow resolution, the main channel thickness was assigned five lattice nodes (100 μm), while the dead-end channels used one lattice node (20 μm), matching the experimental thickness. This minor deviation ensures accurate velocity profile resolution in advective regions without significantly impacting flow behavior, given either thickness is much smaller than the channel width (1.9 mm). This choice is also based on a priori that reactant transport in dead-end channels is diffusion-dominated without the necessity to resolve the full velocity profile. The left boundary applied a constant concentration condition consistent with the experiment, where a 0.5 M sodium carbonate and 1 M sodium chloride solution was injected. The right boundary adopted a zero-gradient extrapolation to represent an open-flow boundary.

Fig. 2 3-D geometry of the gypsum chip (uncolored) with the flow path (blue).

3. Results

3.1. Effect of flow rate on the dissolution–precipitation reaction

We begin with the discussion of experimental observations for the effect of flow rate on the precipitation process. We also discuss mechanisms guiding the mineralization process. Finally, we discuss numerical results from the reactive transport LBM modeling.

Previous studies have investigated the carbonation of gypsum under static, unconfined systems, and have identified reaction products at varying solution compositions. However, surface reactions are governed not only by the solute concentration of the injected solution and relative rates of dissolution and precipitation, but also by advection and diffusion, which in turn are affected by the surface geometry and velocity profile of the solution.^37,38 Post-experiment optical images of the micromodel are shown in Fig. 3. It was found that the flow rate strongly influenced the extent and spatial distribution of mineralization. At both 10 and 60 μL min⁻¹, precipitation was observed within the main channel within 5 minutes. A closer inspection of the optical images, however, shows distinct differences in the mineralization patterns for the two flow rate cases. At 10 μL min⁻¹, the precipitation primarily concentrated in the main channel and exhibited a “porous” texture, particularly closer to the inlet. Less precipitation was found in the dead-end channels, where a penetrating mineralization front is only observed in the first and second dead-ends, despite their narrower shape. In the larger channels, the precipitation appeared to be randomly dispersed. At 60 μL min⁻¹, however, more mineralization was visible in both the main channel and the dead-ends, with precipitation in the main channel appearing more uniform compared with the slower flow case as also seen in the literature.³⁹ Mineralization within the dead-ends was higher in the 3rd and 4th (wider channels), and in contrast to the 10 μL min⁻¹ case, the mineralization front was visible within each of the dead-end channels.

Fig. 3 Optical images and surface profilometry scans obtained from microfluidic experiments conducted at different flow rates after 5 h of reaction.

To aid the visualization of the carbonation reaction, surface profilometry scans were acquired on the reacted samples (Fig. 3). The scans depict whether the surface height increased (yellow to red) or decreased (blue), in reference to the unreacted surface outside of the channel. Despite a considerable amount of calcium carbonate precipitation observed from the optical images, the relative alteration in the heights in the flow channel in both experiments was less substantial. At both flow rates, the majority of the channel showed either a decrease in surface heights or little-to-no change. However, the scan for the 60 μL min⁻¹ experiment shows variability in the extent of mineralization within the channel, with a pronounced decrease in surface heights near the inlet and along the edges of the channel. Moreover, the dead-end channels show an increase in surface height in the second, third, and fourth channels, next to a decrease in surface height at the end of the mineralization front. In contrast, the pattern in surface height appears to be more uniform for the 10 μL min⁻¹ experiment. The observation of a lack of increase in surface height agreed with the differential pressure measurements which also did not show an increase indicating that the precipitates were loose and porous (see Fig. S4 in the ESI† for the differential pressure measurements for the different experiments).

Our experimental results indicate that the flow rate has a significant impact on the carbonation of gypsum. Significant carbonation of gypsum occurred within minutes, especially for higher flow rate cases. The faster flow rates also resulted in more mineralization in the dead-end channels, specifically in the wider dead-ends further down the flow path. Due to the relatively rapid reaction rate, it is suspected that the dissolution of gypsum and precipitation of calcium carbonate are coupled in space and time, whereby the dissolution of gypsum leads to the supersaturation in the interfacial fluid of calcium carbonate and its subsequent nucleation on the surface. The carbonation dependence on flow rate is expected, at least in part, due to the fact that the dissolution of gypsum is transport-controlled, meaning that the reaction rate is only restricted by the rate of the mass transport of species.⁴⁰ Thus, at faster flow rates, more dissolution and faster transport of dissolved species will facilitate a faster rate of precipitation of reaction products. A faster advection rate results in greater penetration of the solute-bearing solution into the dead-ends, promoting more dissolution and the transport of ions to precipitate within these dead-ends. While it is likely that diffusion would be the dominant process occurring within the dead-ends, the greater penetration can promote faster diffusion and lead to mineralization further in the channel.

3.2. Effect of flow rate on the nature of mineralization

To study the mineralogical changes due to the precipitation reaction, the precipitates that formed on the gypsum micromodels were analyzed using scanning electron microscopy (SEM). A series of representative SEM images of the mineralogical differences observed for the 10 μL min⁻¹ experiment are shown in Fig. 4. The predominant mineral that precipitated in the main channel was vaterite, a polymorph of calcite, identified by its cauliflower or spheroidal morphology. The precipitates varied in size between ∼1 and 50 μm. Calcite was also present in minor quantities as euhedral-to-subhedral rhombohedral dispersed on the surface of the vaterite. No other calcium carbonate precipitate was identified, though we cannot exclude that amorphous calcium carbonate was present, as has been observed in gypsum carbonation experiments by Fernandez-Diaz et al. (2009).²⁵ The morphology of the precipitates varied throughout the channel. In the main channel, vaterite and calcite mineralization formed a thick crust with a cauliflower-like texture. Cracks were also observed in the precipitate in different places. A marked difference in vaterite texture and grain size was observed within the dead-ends and on the outside corner edges of the main channel (see Fig. 4b and e), where the mineralization was more compact and had less of a branching texture.

Fig. 4 Representative SEM images of the textural and mineralogical observations for the 10 μL min⁻¹ experiment showing a) mineralization of calcium carbonate filled the main channel; b) a decrease in grain size in the outside corners of the main channel; c) vaterite texture in the main channel with a fanning texture; d) calcite, taking the shape of euhedral-to-subhedral rhombohedral, was found dispersed on top of the vaterite precipitation; e) grain size of the precipitates decreased in the dead-ends; f) vaterite had a more compact, and less sprawling texture within the dead-ends.

SEM images taken for the micromodel for the 60 μL min⁻¹ experiment are shown in Fig. 5. The most noticeable difference in the mineralization was the more compact and less “porous” texture compared to the 10 μL min⁻¹ case. Upon closer investigation, it appeared that there was a base layer of vaterite consisting of large fan-like crystals, topped by smaller grains. Calcite rhombohedra were also present throughout the channel, especially in the first dead-end channel. A similar shift in size and morphology of vaterite was observed in the dead-ends and the outside corners; however, this is less apparent than for the 10 μL min⁻¹ experiment. Cracks were also found throughout the precipitation. In both experiments, the dissolution of gypsum was observed in the dead-ends of the micromodels at the edge of the precipitation front, and along the outside edges of the channel, where cross-sections of gypsum layers were visible (Fig. 4 and 5). Calcite was found to be more abundant, and vaterite displayed a more compact texture.

Fig. 5 Representative SEM images of the textural and mineralogical observations for the 60 μL min⁻¹ experiment showing a) the main channel was filled with calcium carbonate precipitates, displaying fractures in the precipitate; b) a decrease in grain size was observed in the outside corners of the main channel; c) vaterite texture in the main channel; d) vaterite and calcite in the main channel; e) a reduced grain size of the calcium carbonate precipitate observed in the dead-end channels and a dissolution pit near the end of each mineralization front; f) calcite and vaterite in the dead-end channels.

Two additional experiments performed at 1 and 100 μL min⁻¹ were analyzed for their mineralogy using SEM to investigate the effect of flow rate on the extent of precipitation and the mineralogy. These are shown in Fig. 6 and 7 for the 1 μL min⁻¹ and 100 μL min⁻¹ experiments, respectively.

Fig. 6 Representative SEM images of the textural and mineralogical observations for the 1 μL min⁻¹ experiment showing: a) precipitation of calcium carbonate was limited; b) vaterite transformed into calcite throughout the sample; c) acicular blades of aragonite observed only in this experiment; d) vaterite transformation to calcite.

Fig. 7 Representative SEM images of the textural and mineralogical observations for the 100 μL min⁻¹ experiment showing a) significant and widespread mineralization; b) vaterite and calcite were both abundant; c) vaterite had a more compact texture compared to the slower flow rate experiments; d) calcite was more abundant at this flow rate.

At 1 μL min⁻¹, after 6 h, mineralization was sparse and did not form a continuous layer on the surface as observed in 10 μL min⁻¹ and 60 μL min⁻¹ experiments. The predominant mineral was vaterite, having a bulbous and irregular shape. Moreover, throughout the sample, glimpses of vaterite transitioning to calcite were observed, where the irregular shape of vaterite was being replaced by squared edges. This was also the only sample where aragonite, taking the shape of fan-like blades (sometimes in a radial pattern), was found among the precipitates. Aragonite was also observed in the literature using batch experiments and its prevalence was strongly tied with the extent of supersaturation, as discussed below in more detail.²⁵ For 100 μL min⁻¹, significant mineralization occurred after only 1 h, resulting in a thick coating of calcium carbonate on the gypsum surface. Vaterite was the predominant precipitant, forming compact, dumbbell-like shapes. Significant calcite was also found as subhedral to euhedral rhombohedral, generally dispersed on top of the vaterite. Dissolution textures of gypsum can be seen in gaps of mineralization on the surface.

Our results show a clear effect of flow rate on the nature of mineralization, demonstrating the significance of advection on the mineralization process. Similar mechanistic and mineralogical differences have also been reported in the literature. For example, Fernandez-Diaz et al. (2009)²⁵ found varying pathways for calcium carbonate polymorph formation under varying degrees of supersaturation of calcium carbonate solution. Although investigating the same gypsum carbonation reaction, their focus was on the effect of brine composition as opposed to the flow rate. The authors varied Na₂CO₃ concentrations for up to 15 days, focusing on the 010 face of gypsum. They found that ACC formed first on the gypsum surface, followed by crystalline calcium carbonate polymorphs (vaterite, calcite, or aragonite). Moreover, they observed different polymorph evolutions at different concentrations. At higher concentrations (0.25 and 0.5 M Na₂CO₃), the solution was supersaturated with respect to the crystalline calcium carbonate phases after the formation of ACC on the gypsum surface. This favored the precipitation of vaterite initially, with calcite precipitation becoming more favorable as the degree of supersaturation decreased. In contrast, at lower concentrations (0.05 and 0.1 M Na₂CO₃), calcite precipitation was preferred. The authors also observed a decrease in carbonation over time due to the thick layer of precipitated carbonate, which likely precluded the ability of cations to react with the surface.²⁵ Similarly, Yu et al. (2019)²⁶ studied gypsum carbonation using Na₂CO₃ and NaHCO₃ solutions under ambient conditions for up to 336 h. They also found that calcium carbonate formed almost immediately on the gypsum surface. The polymorph vaterite was found to form first followed by calcite in close proximity, signifying a coupled process.

In view of these literature findings, we suspect that the flow rate has a similar effect to increasing the initial carbonate concentration, whereby a higher flow rate induces faster dissolution of gypsum, resulting in a localized high degree of supersaturation, favoring the formation of vaterite prior to calcite within the channel. Moreover, Fernandez-Diaz et al. (2009)²⁵ only observed aragonite in experiments using lower concentrations of Na₂CO₃, which aligns with our experimental observations where aragonite was observed only at the lowest flow rate of 1 μL min⁻¹.

While qualitative, the post-experiment 3D profilometry scans provide excellent comparative assessment of the distribution and relative volume of the precipitates. Given the small size of the microfluidic samples and the modest extent of precipitation observed, quantitative information such as post-experiment weight measurements was deemed unlikely to yield meaningful comparison. Moreover, because dissolution and precipitation occurred simultaneously within our system, it was challenging to isolate the net mass/volume changes attributable solely to precipitation. This made it difficult to accurately quantify precipitation using either post-experiment weight measurements or integrated 3D profilometry information.

3.3. Simulation results

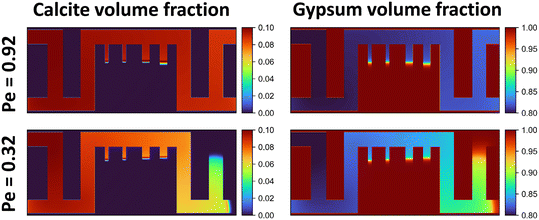
Numerical simulations were carried out to understand the experimentally observed impact of flow rate on the precipitation patterns within the channels of the micromodel. Multiple simulations were repeated, varying only the injection velocity, to simulate different values of the Pe, defined as u_avgL/D, where u_avg is the average velocity in the main channel, L is the main channel thickness, and D is the diffusivity of water molecules. Two Pe values of 0.32 and 0.92 corresponding to u_avg of 0.023 and 0.069 LB units were chosen to be representative of the low (10 μL min⁻¹) and high (60 μL min⁻¹) flow rate cases. These were chosen to demonstrate the behavior of flow velocity on carbon mineralization. It should be noted that the Pe values in the experiments and simulations are not matched one-to-one, but rather, the choice of Pe aims to accurately reflect the mechanisms of carbon mineralization within the available simulation conditions. Pure water was first injected into the simulated micromodel until the velocity profile reached a steady state. Next, the sodium carbonate solution was injected under the same pressure difference. After 0.6 days of injecting the solution, it was found that the concentrations of key ions such as calcium, carbonate, and sulfate approached a steady state. The mineral volume fractions and the distributions of key ion concentrations and pH within the flow channel are presented in Fig. 8 and 9, respectively.

Fig. 8 Calcite and gypsum volume fraction on a sidewall at 0.6 days for Pe = 0.92 and 0.32.

Fig. 9 Concentration profile of calcium, carbonate, and sulfate ions and pH in the micromodel channels at 0.6 days for Pe = 0.92 and 0.32.

From Fig. 8, the simulation results reveal partial calcite precipitation within the dead-end channels, similar to the experimental observations presented in Fig. 3. Interestingly, the dissolution pattern of gypsum within the dead-end channels aligns closely with the calcite precipitation pattern, e.g., very little dissolution and precipitation occurs further into the dead ends, rather than exhibiting uniform dissolution and precipitation along the channel.

The observed phenomena can be explained by the change in ionic concentration profiles with depth into the dead-end channels, which is plotted in Fig. 10. At the intersection of the dead-end channels and the main flow channel, diffusion is relatively high, and the ion concentrations and alkalinity of the solution are similar to those in the main channel, promoting gypsum-to-calcite transformation. Thus, the coupled dissolution–precipitation reactions effectively mirror the reactions in the main channel. However, further into the dead-end channels, the concentration of CO₃²⁻ ions becomes insufficient, and the pH shifts to near neutral. As such, calcite precipitation is restricted. Meanwhile, high calcium ion and high sulfate ion concentrations are observed in the deeper regions of the dead-ends, which inhibits gypsum dissolution. Hence, the cessation of both precipitation and dissolution is witnessed inside of the dead-end channel.

Fig. 10 Concentrations of calcium ion, sulfate ion, and carbonate ion; ion product and K_sp profile in the right most dead-end channel for calcite (top) and gypsum (bottom) at 0.6 day for Pe = 0.92.

Contrary to the dissolution of gypsum in the dead-ends, which decreases with distance, the precipitation of calcite behind the precipitation front first increases and then decreases (Fig. 8). The monotonic decrease in gypsum dissolution can be explained by the calcium ion and sulfate ion concentrations shown in Fig. 9 and 10(bottom), where both concentrations increase monotonically with distance into the channel, suggesting that gypsum dissolution becomes less favorable the further into the dead-ends.

The peak in calcite precipitation behind the precipitation front of the dead-ends results from the monotonically increasing calcium ion concentration and the monotonically decreasing carbonate ion concentration with distance into the channel, leading to a maximum of the concentration product of these two ions behind the precipitation front, as shown in Fig. 10(top). The logarithmic profiles of calcium and carbonate ion concentrations, sampled along the centerline of the rightmost dead-end channel at Pe = 0.92, show that their ion product reaches a peak near the reaction front when compared with the solubility product constant (K_sp) of calcite at 25 °C. This indicates that calcite has the strongest precipitation tendency behind the precipitation front in the dead-ends. In our experiments (Fig. 3), particularly for the 60 μL min⁻¹ case, more calcium carbonate precipitation was observed behind the precipitation front within the dead-end channels.

Moreover, a significant reduction in solid volume is observed in the region preceding the precipitation front within the dead-end channels, as indicated by the blue areas in the surface profilometry scan for the 60 μL min⁻¹ case in Fig. 3 and by the dissolution pits in SEM images in Fig. 5(e). By comparing the upper and lower figures in Fig. 10, it can be seen that the locations of the precipitation front and the dissolution front differ. This discrepancy arises because the ion product of calcium and carbonate ions matches the solubility product constant (K_sp) of calcium carbonate at ∼2.1 mm into the dead-end channel, whereas the ion product of calcium and sulfate ions aligns with the K_sp of gypsum at around 2.3 mm. Consequently, within the 2.1 mm to 2.3 mm range, only the dissolution of gypsum occurs.

To study the effect of injection rate, we reduced the injection rate by approximately threefold, lowering Pe to 0.32. The mineral volume fractions at 0.6 days are also shown in Fig. 8. The key difference between the two Pe cases lies in the uniformity of dissolution and precipitation rates in the main channel. Under high flow rates, the reaction rates are more uniform, whereas, under low flow rates, mineral volume fractions exhibit a pronounced gradient. Furthermore, under low flow rates, the penetration of the reaction front is the longest in the dead-end channels near the inlet. In contrast, under high flow rates, the penetration of precipitation is deepest in the dead-end channels farthest from the inlet. These results align with the experimental findings shown in Fig. 3.

Our simulations depicted the reaction fronts within the dead-end channels remained nearly stationary over time. Despite the negative volume effect that occurs during gypsum carbonation, the porous nature and irregular shape of the precipitate (Fig. 4–7) may result in a significantly larger actual molar volume. This implies that over time, calcium carbonate precipitations could reduce the effective cross-sectional area of dead-end channels and not in the main channel where the precipitation tendency was low suggesting that dead-end channels could be more prone to clogging. Additionally, the stationary reaction front within the dead-end channels over time, also observed in the experiments and in the simulations, indicates that the carbon sequestration efficiency within dead-end channels may be relatively low. Specifically, for the Pe = 0.92 case, the ratios of average carbon mineralization efficiency per unit surface area in the dead-end channels (from left to right) and the main channel are 54.2%, 53.9%, 27.0%, and 28.8%, respectively. For the Pe = 0.32 case, the mineralization efficiency ratios are reported lower at 42.9%, 19.7%, 35.4%, and 16.3%, respectively. There is significantly higher mineralization efficiency in shorter dead-end channels. However, the width of the dead-end channels do not have a notable effect on the mineralization efficiency. Meanwhile, the overall low mineralization efficiency in the dead-end channels may imply that the connectivity of lateral fractures is also critical. Once the lateral fractures establish connectivity, fluid convection could occur within them, potentially enabling more extensive reactions, similar to those in the main flow channels.

Combining the results of the experiments and the numerical simulations, a plausible explanation for our observations is that under higher flow rates, the dispersion diffusivity in dead-end channels is greater, leading to relatively sufficient ion transport. Overall, increasing the flow rate enhances carbon sequestration efficiency in both the main channel and dead-end channels due to the deeper penetration of the reaction front.

4. Conclusion

In this paper, high-pressure microfluidic experiments were carried out on gypsum micromodels to understand coupled dissolution–precipitation reaction mechanisms during carbon mineralization in fractured rock at varying flow rates. A simple comb-shaped flow channel was designed to study mineralization in advection-dominant and diffusion-dominant flow environments to simulate various zones within a fracture network. Real-time optical images, differential pressure measurements, and detailed scanning electron microscopy images were analyzed. In addition, numerical modeling was performed on a similar flow set-up to corroborate experimental findings and enhance the mechanistic understanding. The following conclusions were reached under the constraints of this study:

• The flow rate strongly influenced the carbonation reactions in the flow channels. The lower flow rate (10 μL min⁻¹) experiment yielded sparser and less uniform calcium carbonate precipitation compared to the higher flow rate experiment (60 μL min⁻¹). This was most pronounced in the dead-end channels, which showed limited mineral precipitation at the lower flow rate due to limited solute transport into the channels. As such, optimizing flow conditions will be critical to maximize storage.

• The texture and mineralogy of the calcium carbonate precipitation varied at different flow rates. At lower flow rates, calcium carbonate primarily precipitated in the form of vaterite which exhibited a porous, branching texture. At the higher flow rates, vaterite exhibited a more compact texture. Calcite (most stable form) was more prevalent at higher flow rates due to the high degree of supersaturation of the solution while aragonite (less stable form) was only observed at the lowest flow rate (1 μL min⁻¹).

• Numerical simulations demonstrated that the location behind the precipitation front within dead-end channels exhibited the highest tendency for calcium carbonate precipitation. This suggests that the effective reactive surface area, and thus the potential capacity of a dead-end fracture to mineralize CO₂ could be significantly reduced due to clogging.

• Experimental and simulation results showed that the reaction front within dead-end channels rapidly became stationary, indicating that the carbon sequestration efficiency within dead-end fractures could be relatively low in similar chemical systems. Moreover, shorter dead-end channels exhibit significantly higher mineralization efficiency. This implies that short dead-end channels and their connectivity to the main channel are critical in determining overall storage potential. As such, careful subsurface stimulation design will be required for optimal storage.

Future studies will focus on incorporating the different textures and mineralogy of calcium carbonate polymorphs observed under different flow rates in our experiments. This can be particularly important as the precipitate molar volume and secondary layer density will be different and can further impact fracture clogging. In addition, we intend to conduct sensitivity analyses on the critical dimensionless numbers (Pe and Da) to characterize the reaction rates of gypsum and calcium carbonate relative to flow velocity, the ratio of dead-end channel size to the main channel size, and the ratio of the height of the dead-end channel to its hydraulic radius to quantitatively evaluate their impact on the penetration depth of the reaction front and the amount of calcium carbonate precipitation within dead-end fractures. This will allow us to expound optimal parameters that enable maximal storage via mineralization.

Nomenclature

ACC	Amorphous calcium carbonate
D	Diffusivity of water molecules [m^2 s^−1]
Da	Damköhler number [−]
GCS	Geologic carbon sequestration
Ksp	Solubility product constant
L	Main channel thickness [m]
LBM	Lattice Boltzmann method
uavg	Average velocity in the main channel [m s^−1]
Pe	Péclet number, [−]

Data availability

All experimental- and simulation-based data discussed in the manuscript is available within the manuscript. Details for the simulator are available in the manuscript and in the published literature (Kang et al. 2006, 2007, 2010).^21,28,29 Any additional inquiries can be directed to the corresponding author.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The research was supported as part of the Center on Geo-process in Mineral Carbon Storage, an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under award # DE-SC0023429 and by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project number 20220809PRD4. This article has been designated with the Los Alamos Unlimited Release number LA-UR-25-20305. Computing resources have been provided by LANL's Institutional Computing Program. This work was supported by the U.S. Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). The views expressed in the article do not necessarily represent the views of the U.S. Department of Energy or the United States Government.

References

1. A. Bashir, M. Ali, S. Patil, M. S. Aljawad, M. Mahmoud, D. Al-Shehri, H. Hoteit and M. S. Kamal, Comprehensive review of CO₂ geological storage: Exploring principles, mechanisms, and prospects, Earth-Sci. Rev., 2024, 249, 104672.
2. S. Ó. Snæbjörnsdóttir, B. Sigfússon, C. Marieni, D. Goldberg, S. R. Gislason and E. H. Oelkers, Carbon dioxide storage through mineral carbonation, Nat. Rev. Earth Environ., 2020, 1, 90–102.
3. R. Xu, R. Li, J. Ma, D. He and P. Jiang, Effect of mineral dissolution/precipitation and CO₂ exsolution on CO₂ transport in geological carbon storage, Acc. Chem. Res., 2017, 50(9), 2056–2066.
4. D. E. Clark, E. H. Oelkers, I. Gunnarsson, B. Sigfússon, S. Ó. Snæbjörnsdóttir, E. S. Aradóttir and S. R. Gíslason, CarbFix2: CO₂ and H₂S mineralization during 3.5 years of continuous injection into basaltic rocks at more than 250 °C, Geochim. Cosmochim. Acta, 2020, 279, 45–66.
5. S. K. White, F. A. Spane, H. T. Schaef, Q. S. Miller, M. D. White, J. A. Horner and B. P. McGrail, Quantification of CO2 Mineralization at the Wallula Basalt Pilot Project, Environ. Sci. Technol., 2020, 54, 14609–14616.
6. J. M. Matter, M. Stute, S. Ó. Snæbjörnsdottir, E. H. Oelkers, S. R. Gislason, E. S. Aradottir, B. Sigfusson, I. Gunnarsson, H. Sigurdardottir, E. Gunnlaugsson, G. Axelsson, H. A. Alfredsson, D. Wolff-Boenisch, K. Mesfin, D. F. Taya, J. Hall, K. Dideriksen and W. S. Broecker, Rapid carbon mineralization for permanent disposal of anthropogenic carbon dioxide emissions, Science, 2016, 352, 1312–1314.
7. H. Nisbet, G. Buscarnera, J. W. Carey, M. A. Chen, E. Detournay, H. Huang, J. D. Hyman, P. K. Kang, Q. Kang, J. F. Labuz, J. Matter, C. W. Neil, G. Srinivasan, M. R. Sweeney, V. R. Voller, W. Yang, Y. Yang and H. S. Viswanathan, Carbon mineralization in fractured mafic and ultramafic rocks: A review, Rev. Geophys., 2024, 62, e2023RG000815.
8. C. W. Neil, Y. Yang, H. Nisbet, U. C. Iyare, L. O. Boampong, W. Li, Q. Kang, J. D. Hyman and H. S. Viswanathan, An integrated experimental–modeling approach to identify key processes for carbon mineralization in fractured mafic and ultramafic rocks, PNAS Nexus, 2024, 3(9), 388.
9. M. Voigt, C. R. Pearce, A. Baldermann and E. H. Oelkers, Stable and radiogenic strontium isotope fractionation during hydrothermal seawater-basalt interaction, Geochim. Cosmochim. Acta, 2018, 240, 131–151.
10. R. J. Spencer, Sulfate Minerals in Evaporite Deposits, Rev. Mineral. Geochem., 2000, 40(1), 173–192.
11. A. H. Menefee, D. E. Giammar and B. R. Ellis, Permanent CO₂ Trapping through Localized and Chemical Gradient-Driven Basalt Carbonation, Environ. Sci. Technol., 2018, 52, 8954–8964.
12. M. Andreani, L. Luquot, P. Gouze, M. Godard, E. Hoisé and B. Gibert, Experimental Study of Carbon Sequestration Reactions Controlled by the Percolation of CO₂-Rich Brine through Peridotites, Environ. Sci. Technol., 2009, 43, 1226–1231.
13. P. B. Kelemen and J. Matter, In situ carbonation of peridotite for CO ₂ storage, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17295–17300.
14. A. Ratanpara, Y. Li and M. Kim, A review of microfluidic approaches for carbon capture and storage research, Lab Chip, 2025 10.1039/D5LC00208G.
15. W. Song, F. Ogunbanwo, M. Steinsbø, M. A. Fernø and A. R. Kovscek, Mechanisms of multiphase reactive flow using biogenically calcite-functionalized micromodels, Lab Chip, 2018, 18(24), 3881–3891.
16. Z. Zhang, Y. Gao, F. C. Meldrum, L. Shui, Z. Wang, S. Li and G. Li, Investigating the nucleation kinetics of calcium carbonate using a zero-water-loss microfluidic chip, Cryst. Growth Des., 2020, 20(4), 2787–2795.
17. T. M. Ho, J. Yang and P. A. Tsai, Microfluidic mass transfer of CO2 at elevated pressures: implications for carbon storage in deep saline aquifers, Lab Chip, 2021, 21(20), 3942–3951.
18. Y. Xiao, X. He, G. Ma, C. Zhao, J. Chu and H. Liu, Biomineralization and mineralization using microfluidics: A comparison study, J. Rock Mech. Geotech. Eng., 2024, 16(2), 661–669.
19. N. Liu and M. A. Fernø, Calcite-functionalized microfluidic chip for pore scale investigation of biogeochemical interactions in porous media, Lab Chip, 2025, 25(10), 2320–2324.
20. L. Chen, Q. Kang, W. Carey and W. Tao, Pore-scale study of diffusion–reaction processes involving dissolution and precipitation using the lattice Boltzmann method, Int. J. Heat Mass Transfer, 2014, 75, 483–496.
21. Q. Kang, P. C. Lichtner, H. S. Viswanathan and A. I. Abdel-Fattah, Pore scale modeling of reactive transport involved in geologic CO₂ sequestration, Transp. Porous Media, 2010, 82, 197–213.
22. Z. Wang, M. Hu and C. Steefel, Pore-scale modeling of reactive transport with coupled mineral dissolution and precipitation, Water Resour. Res., 2024, 60, e2023WR036122.
23. P. Nguyen, G. D. Guthrie and J. W. Carey, Experimental validation of self-sealing in wellbore cement fractures exposed to high-pressure, CO2-saturated solutions, Int. J. Greenhouse Gas Control, 2020, 100, 103112.
24. M. L. Porter, J. Jiménez-Martínez, R. Martinez, Q. McCulloch, J. W. Carey and H. S. Viswanathan, Geo-material microfluidics at reservoir conditions for subsurface energy resource applications, Lab Chip, 2015, 15(20), 4044–4053.
25. L. Fernandez-Diaz, C. M. Pina, J. M. Astilleros and N. Sanchez-Pastor, The carbonatation of gypsum: Pathways and pseudomorph formation, Am. Mineral., 2009, 94, 1223–1234.
26. L. Yu, L. M. Daniels, J. A. Mulders, G. D. Saldi, A. L. Harrison, L. Liu and E. H. Oelkers, An experimental study of gypsum dissolution coupled to CaCO₃ precipitation and its application to carbon storage, Chem. Geol., 2019, 525, 447–461.
27. K. P. Zeller, P. Schuler and P. Haiss, The hidden equilibrium in aqueous sodium carbonate solutions − evidence for the formation of the dicarbonate anion, Eur. J. Inorg. Chem., 2005, 1, 168–172.
28. Q. Kang, P. C. Lichtner and D. Zhang, Lattice Boltzmann pore-scale model for multicomponent reactive transport in porous media, J. Geophys. Res.: Atmos., 2006, 111, B05203.
29. Q. Kang, P. C. Lichtner and D. Zhang, An improved lattice Boltzmann model for multicomponent reactive transport in porous media at the pore scale, Water Resour. Res., 2007, 43, W12S14.
30. X. He and L. S. Luo, Lattice Boltzmann model for the incompressible Navier–Stokes equation, J. Stat. Phys., 1997, 88, 927–944.
31. Q. Zou and X. He, On pressure and velocity boundary conditions for the lattice Boltzmann BGK model, Phys. Fluids, 1997, 9(6), 1591–1598.
32. A. A. Jeschke, K. Vosbeck and W. Dreybrodt, Surface controlled dissolution rates of gypsum in aqueous solutions exhibit nonlinear dissolution kinetics, Geochim. Cosmochim. Acta, 2001, 65(1), 27–34.
33. P. Feng, A. S. Brand, L. Chen and J. W. Bullard, In situ nanoscale observations of gypsum dissolution by digital holographic microscopy, Chem. Geol., 2017, 460, 25–36.
34. L. O. Boampong, J. D. Hyman, W. J. Carey, H. S. Viswanathan and A. Navarre-Sitchler, Characterizing the combined impact of nucleation-driven precipitation and secondary passivation on carbon mineralization, Chem. Geol., 2024, 663, 122256.
35. J. Colombani, Measurement of the pure dissolution rate constant of a mineral in water, Geochim. Cosmochim. Acta, 2008, 72(23), 5634–5640.
36. Ö. Nilsson and J. Sternbeck, A mechanistic model for calcite crystal growth using surface speciation, Geochim. Cosmochim. Acta, 1999, 63(2), 217–225.
37. P. Feng, S. Ye, N. S. Martys and J. W. Bullard, Hydrodynamic factors influencing mineral dissolution rates, Chem. Geol., 2020, 541, 119578.
38. W. Yang, M. A. Chen, S. H. Lee and P. K. Kang, Fluid inertia controls mineral precipitation and clogging in pore to network-scale flows, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(28), e2401318121.
39. H. Deng, C. Steefel, S. Molins and D. DePaolo, Fracture evolution in multimineral systems: The role of mineral composition, flow rate, and fracture aperture heterogeneity, ACS Earth Space Chem., 2018, 2, 112–124.
40. A. M. Barton and N. M. Wilde, Dissolution rates of polycrystalline samples of gypsum and orthorhombic forms of calcium sulphate by a rotating disc method, Trans. Faraday Soc., 1971, 67, 3590–3597.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lc00178a

---