Unveiling microbial single-cell growth dynamics under rapid periodic oxygen oscillations

Abstract

Microbial metabolism and growth are tightly linked to oxygen (O₂). Microbes experience fluctuating O₂ levels in natural environments; however, our understanding of how cells respond to fluctuating O₂ over various time scales remains limited due to challenges in observing microbial growth at single-cell resolution under controlled O₂ conditions and in linking individual cell growth with the specific O₂ microenvironment. We performed time-resolved microbial growth analyses at single-cell resolution under a temporally controlled O₂ supply. A multilayer microfluidic device was developed, featuring a gas supply above a cultivation layer, separated by a thin membrane enabling efficient gas transfer. This platform allows microbial cultivation under constant, dynamic, and oscillating O₂ conditions. Automated time-lapse microscopy and deep-learning-based image analysis provide access to spatiotemporally resolved growth data at the single-cell level. O₂ switching within tens of seconds, coupled with precise microenvironment monitoring, allows us to accurately correlate cellular growth with local O₂ concentrations. Growing Escherichia coli microcolonies subjected to varying O₂ oscillation periods show distinct growth dynamics characterized by response and recovery phases. The comprehensive growth data and insights gained from our unique platform are a crucial step forward to systematically study cell response and adaptation to fluctuating O₂ environments at single-cell resolution.

---

Introduction

Microbes in natural habitats are exposed to external environmental changes and have evolved strategies to adapt to the surrounding conditions.¹ They proliferate in fluctuating environments on different time scales with different parameters, such as the availability of molecular oxygen (O₂),² nutrients,³ pH,⁴ temperature,⁵ and light.⁶ These fluctuating environmental conditions are pervasive, including the ocean³ and soil,⁵ as well as in animal hosts, such as in the nasal passage,⁴ lung,⁷ and intestine.⁸ The timescale of fluctuation ranges from seasons (drying and wetting cycles in tropical forests),⁹ days (day/night cycles),^5,6 and even minutes to seconds. In aquatic environments, for instance, microbes encounter new microenvironments in the time scale of seconds to minutes due to changes in surrounding conditions, displacement caused by fluid flow, and microbes' motility in the case of chemotactic bacteria.¹⁰ The phycosphere, the nutrient and O₂ hotspot created by a phytoplankton cell, can dissipate in minutes or even faster due to diffusion and turbulence in fluid.^11,12 Fluctuating environments are also prevalent in biotechnological cultivation setups. Industrial large-scale bioreactors, for instance, stir large volumes of culture broth, often resulting in inefficient mixing and heterogeneous distribution of O₂ and nutrients, which could potentially lead to yield losses.^13–15 Investigating microbial behavior in fluctuating environments will, therefore, improve our understanding of microbial adaptation to external environmental changes and may offer insights into enhancing efficiency in industrial biotechnology.

Among the various environmental conditions, the availability of O₂ is one of the most critical for microbial growth and physiology. O₂ is intricately linked with a multitude of microbial processes, including iron homeostasis,¹⁶ oxidative stress,¹⁷ the development of pathogenic infections¹⁸ and biofilm growth.¹⁹ In addition to these microbial processes associated with O₂ availability, O₂ is also valuable as a primary electron acceptor for aerobic respiration in many microorganisms. In particular, facultative anaerobes, which are capable of growing under both aerobic and anaerobic conditions, adapt to changing O₂ environments by switching their metabolic pathways between aerobic respiration and anaerobic respiration/fermentation.^20,21 This ability of facultative anaerobes to adapt to different O₂ environments has been extensively studied under single-shift O₂ environments. Previous studies have primarily focused on examining intracellular adaptation, such as transcriptome,²⁰ protein synthesis,²² metabolome,²³ flux balance,²⁴ and phenotypic adaptation like growth fitness.²⁵ These studies have primarily been conducted in conventional cultivation setups, including microtiter plates, shaking flasks, and bioreactors. However, there is a lack of understanding regarding the cellular capability to adapt to rapidly fluctuating O₂ environments. Recent studies indicate that microbial behavior in fluctuating environments, where conditions shift within seconds to minutes, can differ significantly from behaviors observed in single-shift experiments.^26,27 Investigating the impact of O₂ fluctuations on microbial growth would facilitate a more comprehensive understanding of adaptation processes that remain to be elucidated.

The study of microbial responses to O₂ fluctuations has been hindered by several constraints. Conventional cultivation techniques do not facilitate rapid and precise changes in O₂ concentrations on the timescale of seconds to minutes, nor do they allow for simultaneous, high-resolution data acquisition. Environmental control in conventional laboratory cultivation setups is typically slow, with limited precision in maintaining homogeneity, temporal consistency, and resulting O₂ microenvironments. Additionally, these setups are often incompatible with fully resolving growth physiology under fluctuating O₂ conditions, as repetitive sampling is impractical without disrupting the culture. Consequently, it has been challenging to analyze the cellular response in terms of microbial growth and physiology caused by rapid O₂ fluctuations.

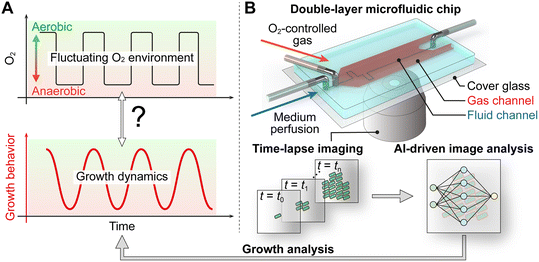
Today, microfluidic devices with precise environmental control and imaging at single-cell resolution are gaining attention as novel tools for creating oscillating environments on-chip and extracting microbial growth data with high temporal resolution. Previously reported microfluidic devices integrated O₂ control based on gas diffusion through air-permeable polydimethylsiloxane (PDMS) membrane.^28–32 Although some microfluidic systems have been developed to mimic oscillating conditions for pH, nutrients, and O₂,^27,33,34 detailed analysis linking microbial growth dynamics to fluctuating O₂ environments remains limited. To better understand microbial adaptation processes under rapid O₂ fluctuations, a platform is needed that allows for high-resolution, single-cell analysis of microbial growth, explicitly correlated with well-defined O₂ fluctuations (Fig. 1A).

Fig. 1 Conceptual illustration of on-chip microbial growth analysis under rapidly oscillating O₂ environments. (A) Conceptual sketch of the proposed analysis of microbial growth dynamics in direct correspondence with external oscillating O₂ conditions. (B) Analytical platform comprising a double-layer microfluidic chip, time-lapse microscopy, and deep-learning-based image analysis, facilitating high spatiotemporal resolution in characterizing microbial growth under oscillating O₂ environments.

In this work, we investigated, for the first time, the growth dynamics of the facultative anaerobe Escherichia coli (E. coli) MG1655 under O₂ oscillations occurring within minutes. To address the aforementioned limitations, we developed a double-layer microfluidic chip to facilitate rapid gas exchange within the cultivation chambers and frequent data acquisition accompanied by time-lapse microscopy to analyze cell division at the single-cell resolution (Fig. 1B). The PDMS microfluidic chip comprises two layers: an upper layer for gassing and a lower layer with multiple chambers for microbial cultivation. A thin intermediate PDMS membrane (65 μm) separates the two layers, facilitating rapid gas diffusion from the upper to the lower layer. The performance of the microfluidic chip was evaluated by spatially resolved O₂ imaging in the fluid channel using fluorescence lifetime imaging (FLIM) microscopy and a fluorescent O₂-sensitive dye. The microfluidic chip, automated time-lapse microscopy, and following deep-learning-based image analysis compose a versatile platform to analyze microbial growth and its correlation to applied O₂ oscillations. The platform was employed to cultivate E. coli under well-defined O₂ oscillating environments with varying oscillation periods, to examine cellular adaptation in a time-resolved manner. Here, we report periodically oscillating microbial growth dynamics composed of several adaptation phases and synchronized with applied O₂ oscillations.

Results

On-chip O₂ control with the double-layer chip

The double-layer chip was fabricated by molding the upper and the lower layers separately and subsequently assembling them as shown in Fig. 2A. The fabricated chip is depicted in Fig. 2B. For visualization purposes, the top gas-layer channels (red) and bottom fluid-layer channels (blue) were filled with colored dyes. The SEM image (Fig. 2B (i)) depicts a series of cultivation chambers (50 μm × 30 μm × 1 μm) in which cells are trapped, and their growth can be observed over time via time-lapse imaging during cultivation. Each growth chamber is connected to two parallel medium supply channels (w = 100 μm, h = 10 μm), enabling continuous medium perfusion but mass transfer inside the chamber solely by diffusion. The cross-sectional photograph of the device (Fig. 2B (ii and ii′)) shows the PDMS membrane, which has a thickness of approximately 65 μm (fluid layer in the figure), physically separating the upper gas channel from the lower fluid channel.

Fig. 2 Double-layer PDMS microfluidic chip enabling rapid gas control and single-cell imaging. (A) Schematic of the microfluidic chip fabrication process. (B) Fabricated microfluidic chip, with (i) an SEM image of the cultivation chambers and (ii and ii′) a cross-sectional view. (C) Measured O₂ level in the in-flow (plots) and simulated O₂ level at the center of the fluid channel (solid lines) following an O₂ shift from 21% to 0% at mass flow rates of 20, 100, and 600 mL min⁻¹. (D) Measured O₂ level in the fluid channel following an O₂ shift between 21% and 0%, with a zoomed view (marked with a red box). Data are expressed as mean ± S.D. (n = 3 measurements).

For gas control optimization, the on-chip gassing performance was simulated using computational fluid dynamics with experimentally determined gas-inflow concentration profiles resulting from interconnected mass flow controllers. Therefore, the O₂ concentration was measured inside the supply tubing outlet under different gas-supply flow rates (100, 300, 600 mL min⁻¹) when no chip was installed (Fig. 2C). This was necessary because likely dead volumes in the mass flow controller setup were affecting the resulting switching performance, mostly when O₂ flow was fully switched off, and residual O₂ remained inside the non-perfused tubing and connectors. The residual O₂ was depleted relatively slowly by diffusion and delayed on-chip switching performance. When switching to higher O₂ levels, this problem was not observed since all interconnections were continuously perfused, and no controller was switched off. As depicted in Fig. 2C, the simulated O₂ level in the fluid channel exhibits a corresponding change from 21% to 0% when the O₂ level in the inlet gas is changed from 21% O₂ to 0% O₂ at t = 0 min. The simulation results indicated that the gas-supply volume flow rate was the limiting factor in our design, mostly impacting the exchange time of O₂ in the fluid channel rather than diffusion across the PDMS membrane. Based on the simulation results, the maximum total flow rate of N₂ and O₂ at 600 mL min⁻¹ was applied to achieve rapid modulation of O₂ within the fluid channel.

With the determined total flow rate, the O₂ switching performance was experimentally validated by imaging the fluorescence lifetime of the O₂-sensitive dye (tris(2,2′-bipyridyl)dichlororuthenium(II)hexahydrate, RTDP) inside the fluid channel with FLIM. Fig. 2D depicts O₂ concentration measured in the fluid channel after the gas exchange from 21% to 0% and vice versa. The supply gas diffused into the fluid rapidly, achieving 99% of the aimed conditions (corresponding to a residual O₂ concentration of 0.21% when switching from 21% to 0%) within 15 seconds in both switching directions. The O₂ level in the gas supply was also switched between 21% and 0% at various oscillation half-periods T′ (T′ = 60, 30, 10, 5, 2, 1, 0.5 min), showing the robust experimental O₂-level data when toggling between 21% and 0% at various T′, as shown in Fig. S1.† These device characterization results ensure a fast gas exchange in the order of seconds in the developed microfluidic device.

E. coli growth in constant and homogeneous O₂ environments

The fabricated double-layer cultivation device was first employed to cultivate E. coli MG1655 under a range of constant O₂ levels, between 0% and 21%, to determine whether the impact of various O₂ levels on microbial growth can be spatiotemporally resolved at the single-cell level. E. coli is a facultative anaerobic bacterium that can grow under aerobic, microaerobic, and anaerobic conditions. As known, the O₂-limited growth is slower compared to the growth under O₂-rich environments.²²

Fig. 3A and B show representative time series of phase contrast images of E. coli cultivated under aerobic (21% O₂) and anaerobic (0% O₂) conditions. Both cultivations started with a single cell at 00:00 h, with a resulting larger colony area at 21% O₂ after 03:00 h cultivation time.

Fig. 3 E. coli cultivation under steady O₂ conditions. (A) Phase-contrast images of E. coli cultivated with a 21% O₂ supply (scale bars 5 μm). (B) Phase-contrast images of E. coli cultivated with a 0% O₂ supply (scale bars 5 μm). (C) Growth curves based on colony area (A_colony) under various O₂ levels. (D) Exponential growth rate (μ) under different O₂ levels, with the adapted Monod kinetic model fit shown by the blue line. (E) Single-cell area (A_{single cell}) across various O₂ levels at t = 2 h. Gray dots represent individual cell data, and red dots indicate mean values. The total numbers of analyzed cells are shown in the plot. In (C) and (D), data are expressed as mean ± S.D. n = 35 colonies (0%), 27 (0.1%), 21 (0.5%), 16 (1%), 13 (5%), 13 (10%), 29 (21%).

To further investigate whether various O₂ concentrations also result in a corresponding decrease in cell growth in the microfluidic growth chambers, we cultured E. coli under constant O₂ concentrations at 0%, 0.1%, 0.5%, 1%, 5%, 10%, and 21% O₂ in separate experiments. As shown in Fig. 3C, the colony areas (A_colony), the sum of the individual cell areas, are quantified from the phase contrast time-lapse images. As evident from the plot, A_colony exhibits exponential growth, with the lowest rate being observed at 0% O₂.

In Fig. 3D, the exponential growth rates μ were quantified based on A_colony in the exponential growth phase, showing comparable growth at O₂ concentrations between 21% and 1%. The aerobic growth rate of around 2 fits the growth rate suggested in previous literature.³⁵ Conversely, μ strongly decreases when the O₂ level is below 0.5%. The relation of growth rate and O₂ concentration was modeled by an adapted Monod kinetic, which resulted in K_O2 of 0.07 ± 0.02%. As K_O2 describes the O₂ concentration in percentage at which the growth rate is reduced to half of the maximum growth under sufficient O₂, the low K_O2 indicates a strong decrease in growth rate at very low O₂ levels. These results indicate that an O₂ concentration of at least below 0.5% is required to observe a measurable change in the growth rate of E. coli within our device. Based on the gas exchange characterization shown in Fig. 2D, the minimum switching time, t_min, necessary to decrease O₂ concentration below 0.5% and observe a detectable change between aerobic and anaerobic growth was approximately 15 seconds. The slower growth observed at low O₂ concentration is in agreement with the Pasteur point (1% of the present atmospheric O₂ level), below which is thought to inhibit heterotrophic aerobic respiration.³⁶

Beyond colony growth, our data also provide insights at the single-cell level. In Fig. 3E, each gray plot represents the area of an individual cell (A_{single cell}) measured at t = 2 h, with red plots representing the mean values. These mean values increase as oxygen concentration rises, which is consistent with the observation that cells with higher growth rates generally exhibit larger sizes.^37–39 Interestingly, A_{single cell} displayed considerable variation, ranging up to 14 μm². This wide distribution suggests cell size heterogeneity within the population. Such heterogeneity in cell size might arise from a mixture of cells at different stages: smaller cells immediately post-division, larger cells just before division, and extensively sized cells with fewer division cycles. Such intra-population diversity can be effectively resolved using microfluidic cultivation combined with single-cell, time-lapse imaging.

E. coli growth in periodically oscillating O₂ environments

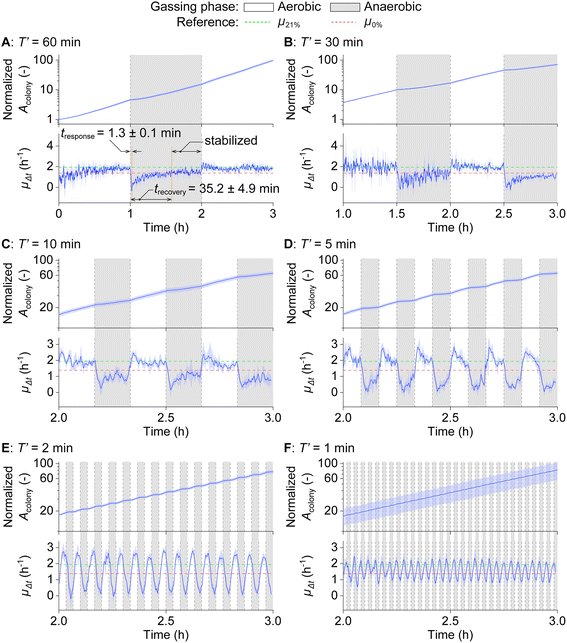
We then cultivated E. coli in oscillating O₂ environments to investigate how these oscillations affect bacterial growth. Experiments were conducted with various oscillation half-periods (T′ = 60, 30, 10, 5, 2, and 1 min), and the results are presented in Fig. 4A–F (top: A_colony, bottom: instantaneous growth rate μ_Δt). In Fig. 4A (top), the distinct growth rates during aerobic and anaerobic phases for each T′ = 60 min cycle are observable from A_colony. The rate of change in A_colony was further quantified by μ_Δt, calculated as the first derivative of ln A_colony. In Fig. 4A (bottom), a distinctive growth pattern under oscillating conditions emerges, where μ_Δt decreases directly after switching from aerobic to anaerobic conditions. A 1.2 fold decrease compared to growth at constant 0% O₂ conditions (μ_0% = 1.38 ± 0.06 h⁻¹) occurs, followed by a gradual increase up to around μ_0%. We determined t_response, the time to hit the lowest μ_Δt, and t_recovery, the time required to recover up to μ_0%, both counting from the switch from aerobic to anaerobic gassing phase. t_response and t_recovery are determined to be 1.3 ± 0.1 minutes and 35.2 ± 4.9 minutes, respectively. After t_recovery, the growth was stabilized around μ_0% till the end of the anaerobic gassing phase. After the switch from anaerobic to aerobic gassing phase, in contrast, A_colony increased rapidly, reaching the growth rate at constant 21% O₂ concentration (μ_21% = 1.95 ± 0.03 h⁻¹) within a minute.

Fig. 4 E. coli cultivation under oscillating O₂ supplies. (A–F) Growth curves based on colony area (A_colony, top) and instantaneous growth rate (μ_Δt, bottom) over time under various oscillation half-periods (T′ = 60, 30, 10, 5, 2, and 1 min). Dashed lines represent growth rates under constant 21% (μ_21%) and 0% O₂ (μ_0%) conditions for comparison. Data are expressed as mean ± S.D. n = 5 colonies (60 min), 3 (30 min), 4 (10 min), 4 (5 min), 4 (2 min), 5 (1 min).

At T′ = 30 min, μ_Δt shows a growth tendency similar to T′ = 60 min, characterized by the steep decrease right after the switch from aerobic to anaerobic conditions, and the following growth recovery till the end of the anaerobic gassing phase, as shown in Fig. 4B. At T′ = 10, 5, and 2 min, we observe μ_Δt hitting the lowest value, and the following gradual recovery phase, but never reaching μ_0%, simply due to insufficient time for recovery and adaptation, as shown in Fig. 4C–E. In the case of T′ = 2 min, only a brief recovery phase is observed after the response phase. At T′ = 1 min, the steep decrease after the switch from aerobic to anaerobic conditions is observed without a recovery phase, followed by a fast increase right after the switch from anaerobic to aerobic conditions, as shown in Fig. 4F. As a result, the μ_Δt line plots at T′ = 2 min and 1 min represent simpler waveforms (monotonous up and down) compared to the other cases.

The single-cell area also exhibited a distinct increase under aerobic and anaerobic gassing phases. Fig. S2A–F† are plotted with A_{single cell} obtained from individual cells growing in a representative chamber of each oscillation condition. Fig. S2† allows us to speculate how individual cells increase their cell size by following neighboring plots without needing cell tracking that requires more complicated analytical setups. As for overall tendencies, the plots show a faster area increase rate under aerobic than anaerobic gassing phases, similar to colony-area analysis. A rapid increase/decrease in A_{single cell} was observed immediately after each gassing switch across all oscillation conditions. Notably, a clear recovery in A_{single cell} was observed when the oscillation half-periods were sufficiently longer than t_response (T′ = 60, 30, and 10 min).

Periodic growth synchronized with applied O₂ oscillations

To compare and examine further the periodic growth behavior induced by different O₂ oscillations, growth data is averaged over periods and plotted over the period fraction, as shown in Fig. 5A. Growth data with more than three periods (T′ = 10, 5, 2, and 1 min) were analyzed.

Fig. 5 Periodic growth dynamics synchronized with applied O₂ oscillations at various T′. (A) μ_Δt plotted over fractions of the oscillation period (2T′). Data are expressed as mean ± S.D. across periods. n = 6 (10 min), 12 (5 min), 30 (2 min), 60 (1 min). (B) Frequency spectrum of μ_Δt at T′ = 10, 5, 2, and 1 min, obtained through fast Fourier transform (FFT).

The periodical comparison suggests that μ_Δt line plots from T′ = 2 and 1 min have simpler waveforms compared to the other T′ that are sufficiently longer than t_response. To examine the waveform complexity of μ_Δt line plots at various T′, the frequency spectrum of μ_Δt line plots were analyzed using the fast Fourier transform (FFT) as shown in Fig. 5B. There are several frequency peaks at T′ = 10 and 5 min. These several peaks imply the complicated waveform of μ_Δt line plots due to the existence of response and recovery phases. In contrast, there is only one frequency peak at T′ = 2 and 1 min. The single peaks imply the simpler μ_Δt line plots, representing only the response phase. Notably, the highest peaks from FFT corresponded to applied O₂ oscillation half-periods T′, showing that the periodic growth dynamics were synchronized with applied O₂ oscillation periods (T′ = 10 min: 7.8 × 10⁻⁴ Hz, T′ = 5 min: 1.8 × 10⁻³ Hz, T′ = 2 min: 4.1 × 10⁻³ Hz, T′ = 1 min: 8.4 × 10⁻³ Hz).

Distinct growth behavior dependent on aerobic/anaerobic gassing phases

To further analyze the O₂-oscillation-dependent growth behavior, we determined phase-averaged growth rates under aerobic and anaerobic gassing phases ([small mu, Greek, macron]_aerobic, [small mu, Greek, macron]_anaerobic) by calculating the growth rate for each T′, as illustrated in Fig. 6A.

Fig. 6 Comparison of phase growth data across different T′. (A) Phase-averaged growth rates for each T′, calculated for aerobic gassing phases ([small mu, Greek, macron]_aerobic) and anaerobic gassing phases ([small mu, Greek, macron]_anaerobic). (B) [small mu, Greek, macron]_aerobic and [small mu, Greek, macron]_anaerobic across different T′, with data taken from periods starting at t = 2 h. For T′ = 60 min, growth rate values are taken from half-periods beginning at t = 1 h (anaerobic) and 2 h (aerobic). Dashed lines represent growth rates under constant 21% (μ_21%) and 0% O₂ (μ_0%) conditions for comparison. (C) Time course of [small mu, Greek, macron]_aerobic and [small mu, Greek, macron]_anaerobic over multiple periods, illustrating robust growth behavior under oscillatory conditions. (B and C) Data are expressed as mean ± S.D. n = 5 colonies (60 min), 3 (30 min), 4 (10 min), 4 (5 min), 4 (2 min), 5 (1 min).

In Fig. 6B, [small mu, Greek, macron]_aerobic and [small mu, Greek, macron]_anaerobic for each T′ are summarized. At T′ = 60 min, [small mu, Greek, macron]_aerobic and [small mu, Greek, macron]_anaerobic are comparable to μ_21% and μ_0% respectively, indicating the sufficient recovery time and growth stabilization after the gassing phase shift. At T′ = 30 and 10 min, [small mu, Greek, macron]_aerobic is comparable to μ_21%, whereas [small mu, Greek, macron]_anaerobic is below μ_0%. This is due to insufficient recovery time under the anaerobic phases (t_response < T′ < t_recovery), resulting in an overall lower growth rate over anaerobic phases. This trend became more obvious at T′ = 5 and 2 min, with lower [small mu, Greek, macron]_anaerobic because of less time for growth recovery. Interestingly, [small mu, Greek, macron]_aerobic was higher than μ_21% at T′ = 5 and 2 min. This high [small mu, Greek, macron]_aerobic is the result of the steep increase in growth rate right after the switch from anaerobic to aerobic gassing phases and insufficient time to adjust the growth rate to around μ_21%, as shown in Fig. 4D and E. Lastly, [small mu, Greek, macron]_aerobic and [small mu, Greek, macron]_anaerobic at T′ = 1 min were close to each other, implying the growth adaptation attempt back and forth between aerobic and anaerobic phases, although insufficient time to adapt to either of gassing phases (T′ < t_response). These results demonstrate a phase- and oscillation-period-dependent growth behavior that can be classified into several cases by growth characteristic values, t_response and t_recovery.

Furthermore, we investigated the difference in phase-averaged growth rate over periods to examine the growth robustness under repeated O₂ oscillations. Growth data with more than 3 periods were analyzed (T′ = 10, 5, 2, and 1 min). As shown in Fig. 6C, [small mu, Greek, macron]_aerobic and [small mu, Greek, macron]_anaerobic plotted over periods exhibit robust and steady trends, even with repetitive 60 periods at T′ = 1 min. This result indicates the versatility of the developed platform to stably create O₂ oscillating conditions and analyze microbial growth under such conditions.

Discussion

The objective of this study was to investigate the growth dynamics of E. coli under oscillating O₂ environments. Previous research on microbial growth response to gaseous changes has been extensively conducted, but predominantly focused on single shifts in O₂ availability. This restriction has resulted in our limited understanding of microbial growth response to O₂ fluctuations. To facilitate further investigation, we developed the double-layer microfluidic platform for the time-lapse monitoring of microbes under rapidly oscillating O₂ environments. The platform enabled the cultivation of microbes under well-defined on-chip O₂ oscillating environments and simultaneous observation of microbial behavior at high spatiotemporal resolution. Our platform enabled the thorough analysis of the growth dynamics of E. coli based on growth rates in different time scales (μ, [small mu, Greek, macron], μ_Δt). While single-cell analysis is known for its high workload required to extract biological information such as growth rates at the single-cell level, it turned out to be crucial to establish fully automated image analysis and data extraction prior to the development of the microfluidic device. Based on these analysis procedures, we quickly iterated and adapted our microfluidic chip prototypes and directly verified the effects based on the biological outputs with only overnight delay. This high walkaway time and high throughput experimentation allowed us to primarily focus on optimizing the microfluidic chip design and experiment preparation while biological insights were automatically extracted. Such a single-cell analysis of continuous microbial growth under oscillating O₂ environments with high temporal resolution was impossible with conventional analytical platforms.

The thorough growth analysis presented here demonstrates distinct growth dynamics induced by O₂ oscillations, which are characterized by an immediate decrease in μ_Δt after the switch from aerobic to anaerobic gassing phases (response), followed by gradual increase (recovery), and later stabilized state. These distinguished cell behaviors occur depending on oscillation half-periods T′. This is reasonable, considering that the change from one metabolic pathway to another requires a series of biological events, such as signal transduction (in milliseconds), enzymatic reaction (in seconds), transcription (in minutes), and translation (in minutes), occurring at different time scales.^26,40,41 For example, the O₂ oscillation with T′ = 1 min was sufficient to rapidly and strongly decrease the E. coli growth rates in the respective anaerobic gassing phase (Fig. 4F). This observation could be explained by the rapid depletion of the ATP pool under O₂ limitation, which occurs within the time scale of microbial responses to environmental fluctuations associated with enzymatic reactions and metabolite turnover under minute.²⁶ A recurring increase in the E. coli growth rates were observed when T′ > t_response (Fig. 4A–D). This adaptation to prolonged anaerobic phases is most likely the result of specific regulatory processes that alter gene expression patterns, leading to a gradual change in cell metabolism in minutes.²⁵ Under the switch from anaerobic to aerobic gassing phases, the initial peak and the subsequent gradual decrease of μ_Δt was also observed. This temporal change in growth rate may be attributed to transient accumulation or excretion of metabolites as a result of maintaining homeostasis upon the gaseous transition in minutes.^23,42 Lastly, the FFT and phase-averaged growth rate analyses revealed periodic and robust growth dynamics synchronized with the applied O₂ oscillation periods. This result implies the cellular capability to respond and adapt to corresponding extracellular O₂ environments and highlights the importance of O₂ in determining cellular growth behavior. Regarding the metabolic switching under aerobic and anaerobic conditions, hybrid metabolism has been reported under microaerobic conditions, where both aerobic and anaerobic metabolisms are utilized.^25,43 Therefore, metabolic switching is a continuous process that may not be clearly divided into aerobic and anaerobic states. Rather, the switching time of E. coli can be characterized and determined by various biological events, as mentioned earlier. For instance, the timescales of enzymatic reaction, transcription, and translation would fit our study. Follow-up studies would be valuable to further investigate the correlation between the biological timescales and O₂ fluctuation timescales.

The demonstrated experiment and analysis platform can be strengthened with further improvements. In our platform, we measured the fluorescence lifetimes at 0% and 0.1% O₂, which can be distinguished from each other. However, we have not yet made any further measurements in the range below 0.1%. Obviously, O₂ sensing with the O₂ indicator and FLIM has its limits in terms of sensitivity, which is a complex technical issue that depends on several parameters. For example, the measurement may be affected by the accuracy and resolution of the O₂ control. A set of mass flow controllers connected to pure N₂ and O₂ gas supply was used in our setup, which also has limitations in resolution, especially at lower O₂ concentrations below 0.1%, where the mass flow rate has to be set very low compared to an ideal operating range. A follow-up study should consider using a gas supply with a lower O₂ concentration (for instance, 1%) instead of pure O₂ gas so that the mass flow controller can operate in the recommended flow range when controlling O₂ concentrations below 0.1%. FLIM and the O₂ sensing dye can be characterized with such an improved setup for O₂ control. Finally, sensitivity can be determined with finer resolution at low O₂ concentrations. Another factor is the two-point calibration at known O₂ availability. This calibration was done by flushing synthetic air containing either 0% or 21% O₂. While controlling the O₂ availability to 21% was credible, achieving a strict O₂ control at 0% remained challenging due to potential disturbances from high air permeability and the possibility of residual air remaining within the PDMS. By improving the calibration method to ensure strict 0% O₂ availability, such as by using chemical O₂ scavengers^44–46 compatible with the O₂-sensitive chemical or by using a mini-incubator that allows flushing O₂ depleted gas around the PDMS chip,⁴⁷ more precise on-chip O₂ control and sensing under anaerobic conditions may be possible to achieve.

The developed device and the finding regarding microbial behavior under O₂ oscillation have the potential to be applied to a wide range of research fields. In terms of practical applications, the findings are useful in characterizing and improving industrial bioprocesses. The fluctuating environments resulting from heterogeneous conditions in large-scale bioreactors have been widely reported, which result in unexpected inefficiency and yield losses.^13–15 Such fluctuations in industrial bioreactors, specifically O₂ fluctuations, can occur under minutes.⁴⁸ To address this issue, it is of the utmost importance to gain a further understanding of microbial behavior under rapid fluctuating environments. The developed device provides an on-chip environment that mimics rapid O₂ fluctuations inside bioreactors. This enables the analysis of O₂ fluctuation-specific microbial behavior, including the emerging phenotypic heterogeneity at single-cell resolution, which was previously not possible.

A comparable approach to recreate fluctuating O₂ environments and live-cell imaging could also prove beneficial in fundamental biology and biomedicine. For instance, it is of interest to investigate pathogenic microorganisms (for example, Salmonella typhimurium) and their mechanism on virulence expression and host-cell infection. It has been recognized that pathogens use O₂ as a signal to trigger their virulence, yet the underlying mechanism is elusive.^18,49 Our analysis platform provides an optimal environment for such a study, where microbial behavior can be resolved at single-cell resolution under a well-defined O₂ environment. Another example is to study the interaction of gastrointestinal host cells and microbial communities under fluctuating O₂ environments. There has been growing evidence that O₂ dynamics play a pivotal role in maintaining intestinal homeostasis.^50,51 The intricate regulatory mechanisms at the interface of host cells and the microbiome and the role of O₂ are of great interest since these interactions are linked to various diseases.⁵¹ Moreover, several reports imply the existence of O₂ fluctuations in the intestine and the intestinal epithelial–microbiome interface that arise from periodic ingestion of nutrients or intermittent changes in O₂ availability in the blood.^52–54 Based on these previous reports, it is reasonable to assume that the timescale of O₂ fluctuations for gut microbiome would be in the range of hours. In fact, previous research reported fluctuating bacterial abundance in wild meerkats throughout the day, with the relative abundance of aerobic (Cellulomonas) and anaerobic microbes (Clostridium) varying due to changes in O₂ availability during that time.⁵⁵ The presented device and analysis could be applied to study the interplay between host epithelial cells and microbiomes by emulating such an O₂ fluctuating environment.

Materials and methods

Microfluidic device fabrication

The double-layer microfluidic device, comprising an upper and a lower layer, was fabricated by molding PDMS in separate molds and by assembling (Fig. 2A).⁵⁶ Firstly, the mold for the upper layer was prepared by 3D printing with stereolithography (Form 3B, Formlabs, US). The mold was filled with a mixture of pre-cured PDMS solution (10 : 1) and heated to 80 °C for 20 minutes to initiate the first curing step. A silicon wafer with a two-layer SU-8 photoresist was fabricated by photolithography as described in a previous paper⁵⁷ at Helmholtz Nano Facility, Germany⁵⁸ and employed as the mold for the lower layer. The PDMS was spin-coated onto the SU-8 mold at 1000 rpm for 60 seconds (SPIN150i, APT Automation, Germany) and subsequently heated at 80 °C for 10 minutes to initiate the first curing step. Then, the upper layer was peeled off from the mold, cut into chips, and inlets were punched (punching tool φ = 0.75 mm, World Precision Instruments, US). The lower layer was not peeled off at this step. The upper layer was then placed onto the lower layer and heated at 80 °C for a minimum of one hour. This constituted the second curing step, whereby the upper and lower layers were irreversibly bonded together through the full curing process. Once fully cured, the chip was peeled off from the wafer, holes were punched (φ = 0.50 mm, World Precision Instruments, US), and bonded to a glass substrate (D263®Bio, 39.5 mm × 34.5 mm × 0.175 mm; Schott AG, Germany) by O₂ plasma treatment for 25 seconds (Femto Plasma Cleaner, Diener Electronics, Germany). The bonded chip was heated at 80 °C for one minute to increase the stability of the bonding.

Computational simulations

The gas distribution in the PDMS chip was simulated using a finite element method (COMSOL Multiphysics 6.0, COMSOL). A three-dimensional geometrical model was built comprising three distinct subdomains, a PDMS block, a fluid channel, and a gas channel (Fig. S3†). A hexahedral mesh was generated for the fluid channel, while a tetrahedral mesh was generated for the remaining geometry. The physical phenomena of fluid flow and gas flow were numerically analyzed by solving the time-dependent Navier–Stokes equations for laminar and incompressible flow. O₂ transport was determined by diffusion and convection, as well as by the ratios between O₂ concentration and O₂ solubility at the different material boundaries. Further details regarding the simulation setup are described in the ESI.†

Microscopy

An inverted microscope (Nikon Eclipse Ti-E 2, Nikon, Japan), equipped with a CMOS camera (DS-Qi2, Nikon, Japan) for phase-contrast image acquisition and a FLIM camera (550 kHz frequency domain; pco.flim, PCO AG, Germany), was utilized for the experiments. The FLIM camera was connected to a modulated excitation laser (445 nm, 100 mW; pco.flim laser, Omicron-Laserage Laserprodukte GmbH, Germany). The microscopy setup was customized with a perfect focus system (PFS, Nikon, Japan) and a temperature incubator (Okolab, Italy) to facilitate automated live-cell imaging during cell cultivation on the microscope. Phase-contrast observation for biological cultivation was conducted with a 100× objective (Plan Apo λ Oil, Nikon, Japan). FLIM imaging was conducted with a 20× objective (Plan Apo λ, Nikon, Japan). To perform FLIM, a customized filter cube was used, which was composed of an excitation filter (440/40, F47-440), a long-pass dichroic mirror (495LP, F48-495), and an emission filter (605/70, F47-605). All the filter components were purchased from AHF analysentechnik AG, Germany. A custom-made chip holder was used to mount the chip on the microscope stage. The FLIM was calibrated using a reference fluorescent slide with a known lifetime (lifetime = 3.75 ns, UMM-SFG, Starna Scientific, UK) as a standard. Further details are described in a previously published paper.⁴⁷

Gas control and O₂ sensing

Three interconnected mass flow controllers were utilized to continuously deliver the synthetic air mixture with the desired concentrations of N₂, O₂, and CO₂ (red-y, Vögtlin Instruments GmbH, Switzerland). For on-chip gas control, the inlet of the gas channel was connected to the mass flow controllers. The desired O₂ concentrations in the gas supply were achieved by automatically adjusting the corresponding volume flow rates for O₂ and N₂ while maintaining the total flow rate constant at 600 mL min⁻¹ throughout the oscillations. 0.4 mL min⁻¹ of CO₂ was always added to the synthetic air to facilitate reproducible growth of E. coli.⁵⁹ A tubing with a low gas permeability (N₂: 1.2 barrer, O₂: 2.2 barrer; Tygon®F-4040-A, Saint-Gobain, France) was used to connect the mass flow controller and the hole on the upper layer of the chip. To measure O₂ concentrations of in-flow coming out of the tubing, a fiber O₂ microsensor was used and inserted directly in the tubing (OXR50, pyroscience, Germany).

The O₂ level in the chip was measured by fluorescence lifetime imaging (FLIM) and an O₂-sensitive dye, tris(2,2′-bipyridyl)dichlororuthenium(II)hexahydrate (RTDP). The fluorescence of RTDP is quenched in the presence of O₂, which can be quantified as a change in fluorescence lifetime (τ). The fluorescence quenching is described by the Stern–Volmer equation, as follows.

τ₀ is the fluorescence lifetime under 0% O₂, and K_q is the quenching constant. K_q was derived by a two-point calibration, whereby τ₀ and τ at a known O₂ concentration were measured. Here, τ at 21% O₂ (τ₂₁) was used to derive K_q. The gaseous conditions of 0% and 21% O₂ were set by adjusting the mass flow rate of N₂ and O₂. The parameters were determined from the measurement as follows; τ₀ = 481 ns, τ₂₁ = 307 ns, K_q = 2.71.

Cell preparation

E. coli MG1655 was stored in a ROTI Store cryo vial (ROTI®Store cryo vial, Carl Roth, Germany). All microbial cultivations were conducted using a lysogeny broth (LB) complex medium, comprising 10 g L⁻¹ peptone, 5 g L⁻¹ yeast extract, and 10 g L⁻¹ NaCl. The pH of the LB medium was adjusted to 7.0 with NaOH, autoclaved at 121 °C for 20 minutes, and stored at 4 °C. All the aforementioned chemicals were purchased from Carl Roth, Germany. A single bead from the cryo vial was transferred to a 20 mL LB medium in a shaking flask and cultured at 37 °C, 150 rpm, for around 16 hours. The subsequent culture was initiated by inoculation from the previous culture, with an initial optical density (OD₆₀₀) of 0.3 or 0.0001, and cultivated until it reached the exponential growth phase.

Microfluidic cultivation and time-lapse imaging

The inoculation in the microfluidic chip was performed with the cell solution containing exponentially growing cells, with OD₆₀₀ = 0.5. The cell solution was introduced into the fluid channel of the chip with a syringe (Omnifix®-F 1 mL, Braun, Germany). Following the successful inoculation, the syringe was replaced with a new one containing a fresh medium. The remaining cells within the channel were then flushed by manually pushing the syringe. The medium was perfused at a constant rate of 100 nL min⁻¹ using a syringe pump (neMESYS, CETONI, Germany). The chip cultivation continued for three hours before the colony reached the chamber size. The time-lapse imaging was performed, with an image acquisition interval Δt = 1 min for all the cultivation under constant O₂ environments, and Δt = 10 seconds for all the cultivation under oscillating O₂ environments.

Image analysis

The acquired FLIM image data in nd2 format was saved as OME.TIFF files and processed using Fiji⁶⁰ to measure the lifetime in a rectangular ROI (h 500 pixels × w 100 pixels). A median filter (pixel size = 5) was employed to remove noise.

The details of the image analysis from cultivation experiments are described in previously published papers.^47,61 Briefly, the acquired image data in nd2 format was exported as TIFF files and pre-processed using Fiji, which included rotation, alignment (Correct 3D Drift⁶²), and cropping. The pre-processed TIFF files were then uploaded to an OMERO server⁶³ for subsequent analysis. For the automated image analysis, we developed Jupyter Notebooks and Python to perform deep-learning-based cell segmentation (Omnipose⁶⁴) followed by filtering artifacts and extracting single-cell sizes. These Jupyter Notebooks are designed for a single time-lapse recording and provide video rendering to guarantee and document sufficient cell segmentation quality. We repeatedly apply the same Jupyter Notebook to all our timelapse images (scaling analysis), leading to fully automated image processing such that experiment results are obtained overnight. The codes for cell segmentation and analysis are openly available at https://github.com/JuBiotech/Supplement-to-Kasahara-et-al.-2025.

Growth analysis

Colony area (A_colony) was used for growth analysis because A_colony provides us with continuous values as opposed to cell number, which is beneficial for further calculations. A_colony was normalized by the colony area at the start of cultivation to compare different chambers and conditions. Exponential growth rates, μ, were quantified based on A_colony in the exponential growth phase, as follows.

The relation of growth rate and O₂ concentration was modeled by a Monod kinetic⁶⁵ including a growth offset for anaerobic growth, C (h⁻¹) at 0% O₂, as follows.

μ′ + C (h⁻¹) is the growth rate under high O₂ availability, and K_O2 is the so-called Michaelis–Menten constant.

Instantaneous growth rates, μ_Δt, the first derivative of A_colony, were calculated as follows.

Phase-averaged growth rates under aerobic and anaerobic gassing phases ([small mu, Greek, macron]_aerobic and [small mu, Greek, macron]_anaerobic), were determined by averaging obtained values from the same periods in all the analyzed colonies. t_response was determined as the time to hit the lowest μ_Δt. t_recovery was determined as the time for the linear regression slope of μ_Δt in a shrinking window to reach zero.

The fast Fourier transform (FFT) was performed using the Data Analysis Tools in Excel. The sample size was adjusted to 2ⁿ prior to FFT. For all the growth analysis, growth data between 0 h ≤ t < 1 h were omitted since growth data at the beginning of the cultivation was occasionally affected by high noise due to a low initial cell number. Datasets with Δt = 10 seconds were smoothed by a centered moving average (window size = 5) before calculating μ_Δt to reduce noise.

Data availability

The codes for image analysis are available at https://github.com/JuBiotech/Supplement-to-Kasahara-et-al.-2025. Microscopy image data are available at https://doi.org/10.5281/zenodo.13982747.

Author contributions

K. K. and D. K. designed the study. K. K. conducted the experiments and data analyses. K. K., T. D., and D. K. interpreted the results. J. S. and K. N. contributed to the automated image workflows and data management. B. S. and E. L. conducted the numerical simulation. K. K., T. D., and D. K. wrote the paper. All authors contributed to the article and approved the submitted version.

Conflicts of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgements

K. K. was supported by the Japan Student Services Organization (JASSO) Student Exchange Support Program (G2130401003N). K. K. is an associate member of the SFB 1535 MibiNet “Microbial networking – from organelles to cross-kingdom communities” funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation, 458090666/CRC1535/1). J. S. was supported by the President's Initiative and Networking Funds of the Helmholtz Association of German Research Centres (EMSIG ZT-I-PF-04044). J. S. and K. N. acknowledge the inspiring scientific environment provided by the Helmholtz School for Data Science in Life, Earth and Energy (HDS-LEE). The authors would like to thank Agnes Müller-Schröer (Forschungszentrum Jülich) for her assistance in cell culture and Nadja Glöck (Forschungszentrum Jülich) for her assistance in SU-8 mold fabrication.

References

1. A. Lalejini, A. J. Ferguson, N. A. Grant and C. Ofria, Front. Ecol. Evol., 2021, 9, 715381.
2. M. Fusi, S. Rigaud, G. Guadagnin, A. Barausse, R. Marasco, D. Daffonchio, J. Régis, L. Huchet, C. Camin, L. Pettit, C. Vina-Herbon and F. Giomi, Biogeosciences, 2023, 20, 3509–3521.
3. R. Stocker, Science, 2012, 338, 628–633.
4. S. Dedrick, M. J. Akbari, S. K. Dyckman, N. Zhao, Y.-Y. Liu and B. Momeni, Front. Microbiol., 2021, 12, 613109.
5. Y. Zhang, J.-T. Li, X. Xu, H.-Y. Chen, T. Zhu, J.-J. Xu, X.-N. Xu, J.-Q. Li, C. Liang, B. Li, C.-M. Fang and M. Nie, Nat. Ecol. Evol., 2023, 7, 205–213.
6. E. Cohen Susan and S. Golden Susan, Microbiol. Mol. Biol. Rev., 2015, 79, 373–385.
7. F. Formenti, N. Bommakanti, R. Chen, J. N. Cronin, H. McPeak, D. Holopherne-Doran, G. Hedenstierna, C. E. W. Hahn, A. Larsson and A. D. Farmery, Sci. Rep., 2017, 7, 1–10.
8. C. A. Lozupone, J. I. Stombaugh, J. I. Gordon, J. K. Jansson and R. Knight, Nature, 2012, 489, 220–230.
9. D. J. Lodge, W. H. McDowell and C. P. McSwiney, Trends Ecol. Evol., 1994, 9, 384–387.
10. S. Smriga, V. I. Fernandez, J. G. Mitchell and R. Stocker, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1576–1581.
11. N. Blackburn, T. Fenchel and J. Mitchell, Science, 1998, 282, 2254–2256.
12. J. R. Taylor and R. Stocker, Science, 2012, 338, 675–679.
13. S. O. Enfors, M. Jahic, A. Rozkov, B. Xu, M. Hecker, B. Jürgen, E. Krüger, T. Schweder, G. Hamer, D. O'Beirne, N. Noisommit-Rizzi, M. Reuss, L. Boone, C. Hewitt, C. McFarlane, A. Nienow, T. Kovacs, C. Trägårdh, L. Fuchs, J. Revstedt, P. C. Friberg, B. Hjertager, G. Blomsten, H. Skogman, S. Hjort, F. Hoeks, H. Y. Lin, P. Neubauer, R. van der Lans, K. Luyben, P. Vrabel and A. Manelius, J. Biotechnol., 2001, 85, 175–185.
14. R. Takors, J. Biotechnol., 2012, 160, 3–9.
15. J. Bisgaard, M. Muldbak, T. Tajsoleiman, T. Rydal, T. Rasmussen, J. K. Huusom and K. V. Gernaey, Chem. Eng. Res. Des., 2021, 174, 471–485.
16. M. Miethke and M. A. Marahiel, Microbiol. Mol. Biol. Rev., 2007, 71, 413–451.
17. E. Cabiscol, J. Tamarit and J. Ros, Int. Microbiol., 2000, 3, 3–8.
18. A. C. André, L. Debande and B. S. Marteyn, Cell. Microbiol., 2021, 23, e13338.
19. A. J. Martín-Rodríguez, Trends Microbiol., 2023, 31, 120–134.
20. J. D. Partridge, C. Scott, Y. Tang, R. K. Poole and J. Green, J. Biol. Chem., 2006, 281, 27806–27815.
21. T. Ren, X. Jin, S. Deng, K. Guo, Y. Gao, X. Shi, L. Xu, X. Bai, Y. Shang, P. Jin and X. C. Wang, J. Cleaner Prod., 2024, 434, 140332.
22. O. N. Murashko and S. Lin-Chao, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E8025–E8034.
23. N. A. Yasid, M. D. Rolfe, J. Green and M. P. Williamson, R. Soc. Open Sci., 2016, 3, 160187.
24. J. von Wulffen, RecogNice-Team, O. Sawodny and R. Feuer, PLoS One, 2016, 11, e0158711.
25. L. Pedraz, N. Blanco-Cabra and E. Torrents, FASEB J., 2020, 34, 2912–2928.
26. J. Nguyen, J. Lara-Gutiérrez and R. Stocker, FEMS Microbiol. Rev., 2021, 45, 1–16.
27. J. Nguyen, V. Fernandez, S. Pontrelli, U. Sauer, M. Ackermann and R. Stocker, Nat. Commun., 2021, 12, 3662.
28. M. Skolimowski, M. W. Nielsen, J. Emnéus, S. Molin, R. Taboryski, C. Sternberg, M. Dufva and O. Geschke, Lab Chip, 2010, 10, 2162–2169.
29. G. Mauleon, C. P. Fall and D. T. Eddington, PLoS One, 2012, 7, e43309.
30. M. L. Rexius-Hall, G. Mauleon, A. B. Malik, J. Rehman and D. T. Eddington, Lab Chip, 2014, 14, 4688–4695.
31. S. M. Grist, S. S. Nasseri, L. Laplatine, J. C. Schmok, D. Yao, J. Hua, L. Chrostowski and K. C. Cheung, Sci. Rep., 2019, 9, 17782.
32. R. Koens, Y. Tabata, J. C. Serrano, S. Aratake, D. Yoshino, R. D. Kamm and K. Funamoto, APL Bioeng., 2020, 4, 016106.
33. S. Täuber, C. Golze, P. Ho, E. von Lieres and A. Grünberger, Lab Chip, 2020, 20, 4442–4455.
34. Q. Tang, D. Wang, J. Cui, Y. Zhang, J. Mei, J. Du, A. Xia, Q. Sun, D. Luo, B. Han, M. Gan and P. Liu, Nano Today, 2024, 54, 102067.
35. A. R. Tuttle, N. D. Trahan and M. S. Son, Curr. Protoc., 2021, 1, e20.
36. C. Goldblatt, T. M. Lenton and A. J. Watson, Nature, 2006, 443, 683–686.
37. M. Schaechter, O. Maaloe and N. O. Kjeldgaard, J. Gen. Microbiol., 1958, 19, 592–606.
38. S. Taheri-Araghi, S. Bradde, J. T. Sauls, N. S. Hill, P. A. Levin, J. Paulsson, M. Vergassola and S. Jun, Curr. Biol., 2015, 25, 385–391.
39. F. Bertaux, J. von Kügelgen, S. Marguerat and V. Shahrezaei, PLoS Comput. Biol., 2020, 16, e1008245.
40. J. D. Partridge, G. Sanguinetti, D. P. Dibden, R. E. Roberts, R. K. Poole and J. Green, J. Biol. Chem., 2007, 282, 11230–11237.
41. J. von Wulffen, A. Ulmer, G. Jäger, O. Sawodny and R. Feuer, Genes, 2017, 8, 90.
42. N. A. Beauchene, E. L. Mettert, L. J. Moore, S. Keleş, E. R. Willey and P. J. Kiley, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12261–12266.
43. M. D. Rolfe, A. Ocone, M. R. Stapleton, S. Hall, E. W. Trotter, R. K. Poole, G. Sanguinetti, J. Green and SysMO-SUMO Consortium, Open Biol., 2012, 2, 120091.
44. W. Sun, Y. Chen, Y. Wang, P. Luo, M. Zhang, H. Zhang and P. Hu, Analyst, 2018, 143, 5431–5437.
45. W. Wang, L. Li, M. Ding, G. Luo and Q. Liang, BioChip J., 2018, 12, 93–101.
46. H. M. Wu, T. A. Lee, P. L. Ko, W. H. Liao, T. H. Hsieh and Y. C. Tung, Analyst, 2019, 144, 3494–3504.
47. K. Kasahara, M. Leygeber, J. Seiffarth, K. Ruzaeva, T. Drepper, K. Nöh and D. Kohlheyer, Front. Microbiol., 2023, 14, 1198170.
48. E. K. Nauha, Z. Kálal, J. M. Ali and V. Alopaeus, Chem. Eng. J., 2018, 334, 2319–2334.
49. B. Marteyn, F. B. Scorza, P. J. Sansonetti and C. Tang, Cell. Microbiol., 2011, 13, 171–176.
50. M. A. Henson and P. Phalak, BMC Syst. Biol., 2017, 11, 145.
51. R. Singhal and Y. M. Shah, J. Biol. Chem., 2020, 295, 10493–10505.
52. J. B. J. Ward, S. J. Keely and S. J. Keely, J. Physiol., 2014, 592, 2473–2489.
53. L. Zheng, C. J. Kelly and S. P. Colgan, Am. J. Physiol., 2015, 309, C350–C360.
54. I. Moreno-Indias, M. Torres, J. M. Montserrat, L. Sanchez-Alcoholado, F. Cardona, F. J. Tinahones, D. Gozal, V. A. Poroyko, D. Navajas, M. I. Queipo-Ortuño and R. Farré, Eur. Respir. J., 2015, 45, 1055–1065.
55. A. Risely, K. Wilhelm, T. Clutton-Brock, M. B. Manser and S. Sommer, Nat. Commun., 2021, 12, 6017.
56. M. Polinkovsky, E. Gutierrez, A. Levchenko and A. Groisman, Lab Chip, 2009, 9, 1073–1084.
57. A. Grünberger, N. Paczia, C. Probst, G. Schendzielorz, L. Eggeling, S. Noack, W. Wiechert and D. Kohlheyer, Lab Chip, 2012, 12, 2060–2068.
58. W. Albrecht, J. Moers and B. Hermanns, JLSRF, 2017, 3, A112.
59. C. Merlin, M. Masters, S. McAteer and A. Coulson, J. Bacteriol., 2003, 185, 6415–6424.
60. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.
61. J. Seiffarth, T. Scherr, B. Wollenhaupt, O. Neumann, H. Scharr, D. Kohlheyer, R. Mikut and K. Nöh, SoftwareX, 2024, 26, 101638.
62. A. Parslow, A. Cardona and R. J. Bryson-Richardson, J. Visualized Exp., 2014, e51086.
63. C. Allan, J.-M. Burel, J. Moore, C. Blackburn, M. Linkert, S. Loynton, D. MacDonald, W. J. Moore, C. Neves, A. Patterson, M. Porter, A. Tarkowska, B. Loranger, J. Avondo, I. Lagerstedt, L. Lianas, S. Leo, K. Hands, R. T. Hay, A. Patwardhan, C. Best, G. J. Kleywegt, G. Zanetti and J. R. Swedlow, Nat. Methods, 2012, 9, 245–253.
64. K. J. Cutler, C. Stringer, T. W. Lo, L. Rappez, N. Stroustrup, S. Brook Peterson, P. A. Wiggins and J. Mougous, Nat. Methods, 2022, 19, 1438–1448.
65. O. Couvert, M.-L. Divanac'h, A. Lochardet, D. Thuault and V. Huchet, Food Microbiol., 2019, 77, 21–25.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lc00065c

---