Geometry of obstructed pathway regulates upstream navigational pattern of sperm population

Abstract

Sperm navigation through the complex microarchitecture of the fallopian tube is essential for successful fertilization. Spatiotemporal structural alteration due to folded epithelium or muscle contractions in the fallopian tube changes the geometry of the sperm pathways. The role of structural complexity in sperm navigational patterns has been investigated for single sperm cells but has not been fully addressed at the population level. Here, we studied the dynamics of the navigation of a bull sperm population through obstructed pathways mimicking the architecture of the female reproductive tract. We observed that slightly tapered barriers enhance navigation by 20% compared to straight pathway; however, tapered barriers with a 90° angle restrict sperm passage. We demonstrated sperm cooperation while passing through a tapered pathway in a low-viscosity medium under elevated shear rates. These findings propose a fresh perspective on how sperm move through the fallopian tube, suggesting that the convoluted pathways' shape influences sperm navigation locally.

---

1. Introduction

To reach the fertilization zone, sperm embark on a challenging journey through the female reproductive tract (FRT).¹ In mammals, after insemination of millions of sperm in the vagina, only a few thousand of them can pass the uterotubal junction and enter the fallopian tube.^2,3 These sperm interact with the environment, and with each other, as they pass each other as they move through the narrow junctures of the FRT.^4–6 The lumen of the fallopian tube is surrounded by folded ciliated epithelial surfaces which create contracted regions as narrow as 100 μm.⁷ Adding to this complexity, dynamic muscular contractions continuously alter the geometry of the fallopian tube.⁸ The fallopian tube contractility and the spatial variability of the confinement size along the tube length create a variable pathway for sperm.^1,8,9 In addition to geometrical variation, the secretion rate and viscoelasticity of the medium in the lumen of the fallopian tube changes during the menstrual cycle.^10,11 Slight temperature gradients along the oviducts in mammals induce thermotaxis in sperm.^12,13 Altogether, anatomical and physiological changes create a spatiotemporal pathway in the fallopian tube for sperm. There is evidence that the sperm count and distribution in the fallopian tube across different regions and time frames are highly variable.² Understanding the mechanisms driving these variations as well as the complexities of sperm–surface–flow interactions remains an ongoing challenge in reproductive biology.

The fertilization process is impacted by how and when sperm physically interact with their surrounding microenvironment.⁶ In proximity of surfaces, microswimmers including sperm and Escherichia coli are found to be hydrodynamically attracted to, and accumulate on, rigid walls.^14,15 Mammalian sperm convert their flagella waveform from three-dimensional in bulk swimming to two-dimensional on rigid walls.¹⁶ Sperm also exhibit boundary-following behavior in the presence and absence of fluid flow, which provides them with a preferential pathway toward the fertilization zone.^7,17,18 Curvature was also found to modulate the sperm interaction with surfaces; smaller curvature in the fallopian tube may lead to prolonged contact with epithelial surfaces.¹⁹ Additionally, if a minimum shear rate is provided mammalian sperm exhibited rheotaxis – a flow-induced reorientation to swim upstream.^20–25 This was found to be a passive mechanism facilitating guidance of sperm to the fertilization zone. In the presence of fluid flow with high shear rates, bull sperm decreased their flagella curvature, while increased viscoelasticity resulted in reduced amplitude of head oscillation.^26,27 Also, sperm exhibited a butterfly-shaped motion near a stricture under different flow conditions creating a competitive passage and blocking modes.²⁸ Overall, studying how the sperm interacts with its environment, particularly the folded structure of the fallopian tube, is critical for understanding the sperm journey in the female reproductive tract.

Microfluidics has been used extensively to reconstruct the micropatterns within the FRT and to analyze sperm motion, specifically their hydrodynamic interaction within confined environments.²⁹ This technology, coupled with high-speed imaging, has been used for two- and three-dimensional analysis of hydrodynamic, chemotactic, and thermotactic behavior of sperm in confined microenvironments.^29,30 Based on these studies, several microfluidic devices have been developed to simulate sperm navigation and the natural selection process in the FRT.^31–34

Mammalian sperm cooperation and collective motion is a phenomenon where sperm cells interact and form cooperative groups to assist each other in reaching the egg for fertilization.³⁵ This behavior has been observed in various mammalian species, particularly rodents.³⁶ The cooperative motion can occur due to sperm cells' physical attachment to each other due to sperm morphology and cell–surface interactions^37,38 or hydrodynamic interactions.^5,16,37–39 Sperm may benefit from swimming at a higher velocity when they are bundled together or dynamically clustered.^40–42 Hydrodynamic interactions between adjacent sperm influences the population's flagella waveform promoting flagellum synchronization and sperm pairing, depending on the properties of the surrounding medium as well as other hydrodynamic factors. Bull sperm cooperation is promoted by increasing the viscoelasticity of the surrounding fluid which results in an increase in the probability of sperm clustering.⁴³ Clustering provides sperm with enhanced trajectory linearity as well as protection against strong flow, therefore reducing the rate at which sperm can be swept downstream.⁴⁴ In addition, human sperm exhibit unexpected cooperation by forming groups to migrate more efficiently through high-viscosity environments in the FRT, enhancing swimming velocity.⁴⁵ Although these studies reported the cooperative motion of sperm population in high-viscosity mediums in the absence and presence of shear rate, it remains unclear whether sperm have any significant cooperation in normal low-viscosity mediums in localized shear rate zones.

Gate-like behavior of strictures with large port angles has been used to study the passage of individual sperm.²⁸ Similarly, shear rate barriers with smaller angles for selection of sperm from a raw semen sample containing a huge sperm population has also been reported.³⁴ However, it is unknown how the localized shear rate barriers with variable angle and port size affect the navigation of the sperm population in the presence of low-viscosity fluid flow.

Therefore, to simulate the geometrical variation found in the fallopian tube, we used microfabricated barriers with different geometries (Fig. S1a and b†) to simulate obstructed pathways with different geometries for a sperm population interacting with its environment and with adjacent sperm. Two types of barrier designs, straight and tapered, were used to investigate upstream navigation of a bull sperm population (Fig. 1a and b).

Fig. 1 Obstructed pathways with (a) straight and (b) tapered barriers, simulating sperm navigation through the female reproductive tract. w₁ is the gap size, L is the barrier length, and β is the angle between two side walls. The sperm trajectory in the straight barrier (c and f), tapered barrier with β = 45° (d and g), and β = 45° (e and h) at the average shear rates of 8 and 12 s⁻¹ inside the barrier gap. The trajectories are colorized based on the grayscale intensity. Scale bar is 100 μm.

We found that in the presence of fluid flow, the straight barrier blocks the sperm passage by 50% and creates a storage zone. In contrast, tapered barriers effectively enhance sperm navigation against the flow as well as restrict the passage by creating a competition resulting from localized shear-rate zones. The angle of the tapered barriers affected their function, either facilitating sperm navigation through the barriers or completely blocking their passage. Increasing the angle of the taper caused a decrease in upstream navigation and local accumulation within the barrier under the same portal shear rate. We assigned this change in barrier functionality to scattering angles of sperm from port corners which affects their ability to reorient and swim upstream. Ultimately, we discovered that in tapered barriers, sperm temporarily align in cooperative trains to pass the shear-rate portal. They take advantage of this cooperation to reduce exerting hydrodynamic forces and increase their velocity. Ultimately, we concluded that the sperm navigation in the fallopian tube is influenced by the geometry of the pathway and the spatiotemporal geometry alteration creates temporary storage, blockage, or facilitated navigation depending on the geometry of the obstructed pathway.

2. Results and discussion

2.1 Visualization of sperm navigation in an obstructed pathway

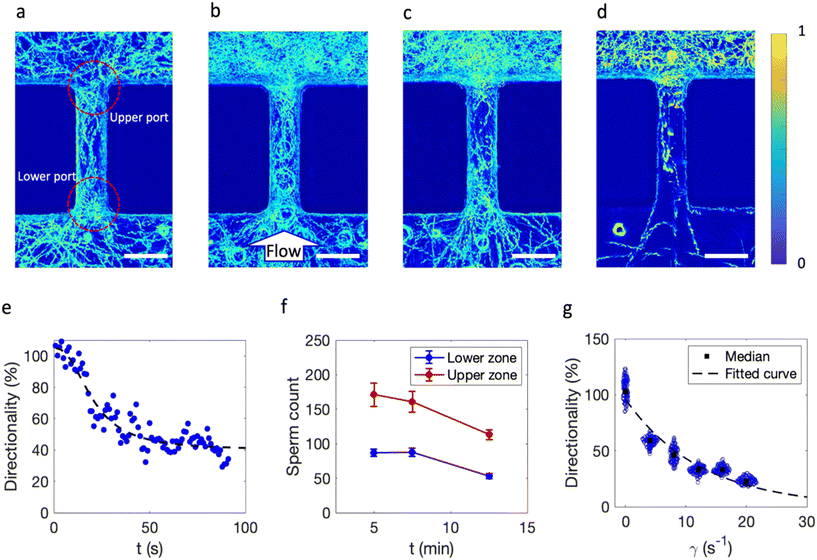
To simulate the sperm navigation through a straight obstructed pathway, an array of identical barriers with dimension of Y = 400 μm and spacing of w₁ = 95 μm are placed at the center of a microfluidic channel with width and height of 5 mm and 210 μm, respectively (Fig. S1a†). A population of sperm is established in proximity to the straight (Fig. 1a) and tapered (Fig. 1b) barriers by initially filling the chip with bull semen and washing the semen with medium from the left side with a specific flow rate which corresponds to specific shear rates in each of the obstructed pathways. The sperm locomotion and distribution were observed using a phase-contrast microscope coupled with a digital camera.

The processed images resulting from overlaying the frames of each video captured at different shear rates for 5 s represent the sperm presence and in the specific region of pathway (for more information on image processing, see ESI† Fig. S2). Depending on the taperness of the barrier, navigational pattern changes. At a portal shear rate of 8 s⁻¹, the straight barrier restricted the upstream navigation (Fig. 1c). Upon adding a 45° taper, a higher number of sperm passed the barrier (Fig. 1d). With a 90° taper, however, the number of sperm passing the barrier was decreased (Fig. 1e). Increasing the shear rate further to 12 s⁻¹ resulted in less sperm passing the barriers for all barriers (Fig. 1f–h).

2.2 Dynamics of sperm distribution in barriers

The physical aspects of navigation were initially studied using the straight barrier at shear rates of 0, 4, 8, and 12 s⁻¹ (Fig. 2a–d). Under zero flow conditions, sperm randomly move in the vicinity of the barrier; however, the straight-lined navigational patterns in upper and lower ports show that the obstructed pathway organizes the sperm movement direction due to boundary following behavior with a balanced distribution between the two sides.⁷

Fig. 2 Dynamic analysis of sperm locomotion in the proximity of a straight barrier under shear rates of (a) 0 s⁻¹, (b) 4 s⁻¹, (c) 8 s⁻¹, and (d) 12 s⁻¹. Lower port indicates upstream of sperm navigation. Sperm navigate from upper to lower zone as a result of rheotactic motion. Images are obtained from colorizing grayscale intensity overlays of sperm motion for 5 s. The color bar shows the intensity of pixels. Scale bar indicates 100 μm. (e) Transition of directionality under shear rate of 8 s⁻¹. An average total number of 203 sperm were counted. The fluid flow rate was applied at t = 0 s. Data are fitted to a four-parameter logistic equation (dashed line). (f) Effect of longer exposure to the same shear rate of 8 s⁻¹ on the sperm count on the upper (red) and lower (blue) zones of the barrier time averaged over 5 s carried out in triplicate for each barrier; error bars show standard deviation. Although the sperm counts experienced a decay over longer run time, the directionality stayed constant. (g) Dependence of shear rate on the directionality of the straight barrier. Blue circles show the data over 5 s for each barrier and black squares indicate the median values. Each data point indicates the directionality in each time step. The total number of cells counted for directionality measurement was 314, 325, 270, 211, 223, and 206 for shear rates of 0, 4, 8, 12, 16, and 20 s⁻¹, respectively. All the measured sperm were from the same biological sample. An exponential decay function (black dashed line) was fitted to the median directionalities.

Once fluid flows, shear is applied; however, this balance is broken because sperm start to exhibit rheotactic behavior once the shear rate exceeds 3.03 s⁻¹, the critical value.²⁰ Lower and upper ports of the obstruction serve as transient regions where sperm either change their orientation or are dragged away due to fluid flow. In the lowest shear rate, flow direction from lower port to upper port, sperm are capable of rheotaxis to the lower port. Hence, some sperm are swept away by flow and some sperm navigate to the lower zone via rheotaxis.

To quantify the function of the obstructed pathway and the flow effects on sperm navigation, we counted the sperm in the upper (N_up) and the lower (N_low) regions of barriers over 100 consecutive frames; directionality (sperm concentration on either side of the barrier) was defined as N_low/N_up × 100, representing the percent asymmetry of sperm distribution on the lower side due to fluid flow.

First, the dynamics of sperm navigation and balance establishment were studied by calculating the directionality of the barrier in the transient mode from no flow to flow condition for a sample shear rate (γ = 8 s⁻¹). The percent directionality of the system over 90 s (flow is connected at t = 0 s) was calculated, and at zero flow, the % directionality averaged close to 100%; once the flow is connected, directionality gradually decreases until it reaches a plateau after approximately 40 s (Fig. 2e and Movie S1†). The decay pattern of directionality suggests that the data fit a four-parameter logistic function with a lag time and steady-state time of 10 and 40 s (more information in Material section S3†).

This model resembles the response of a first-order system to a unit step change in input. Although the system navigationally stabilizes after approximately 40 s and remains constant at 40% after 12.5 min, the average sperm count on both upper and lower zones decreases by 34% (Fig. 2f). This could be attributed to sperm exhaustion or because they are swept away by high shear rates.⁴⁶

The scattered plot of directionality over a 5-s period under different shear rates reveals that increasing shear rate decreases directionality due to both hydrodynamic restriction on sperm passage from confined areas and competitive motion maintenance in proximity of the barrier resulting from the variability in intrinsic sperm velocities (Fig. 2g and S3 and Movie S2†).

Finally, we found an exponential-decay correlation (with a decay correlation of −0.1) between directionality and shear rate (more information in Material section S3†). This decay constant depends on the quality of the semen sample and thus could potentially be used as a new single parameter representing sperm motility and quality similar to RHEOLEX.³⁴

The suggested mechanism behind the difference in the number of sperm at the lower and upper ports (% directionality) when shear rate is changed is due to the interactions of the sperm with the surfaces, corners and fluid flow. At far distances from surfaces, >50 μm for bull sperm, sperm can be modeled as a force dipole resulting in an opposing flow field around the cell.⁴⁷ In proximity of surfaces, sperm are hydrodynamically aligned with the surface (Fig. 3ai). In case of multiple sperm on the surface (a sperm population) and assuming that each sperm is a force dipole, incoming sperm with attraction angle (θ_a) less than 35.3° would be hydrodynamically attracted to the surface; otherwise, the velocity components of flow generated by surface-accumulated sperm may turn into repulsion.¹⁴ Hydrodynamic interaction with the surface generates a velocity gradient near the wall, causing reorientation and surface attraction of sperm. Once sperm reach the surfaces, they follow the boundaries due to the propulsive force generated by sperm moving toward the surfaces. During flagellar beating, sperm heads may drift away from the surface due to rotational diffusion, potentially escaping the boundary after two-dimensional swimming on surfaces.^14,16,48 Sperm closely follow the boundary until they encounter a corner, at which point they veer away from the surface (Fig. 3aii and iii for upper and lower ports, respectively). In the absence of fluid flow, a strong correlation was observed between the ability of sperm to navigate corners and the DNA integrity: sperm with the ability to turn corners had higher DNA integrity.⁴⁹ The scattering angle (θ_s) of the sperm was found to be negative due to the interaction of the flagella with the surface which resulted in turning the sperm toward the boundary preferentially.⁵⁰ This prevents the sperm from escaping slightly curved surfaces. θ_s depends on flagella oscillation frequency and amplitude which is influenced by temperature (Movie S3†).

Fig. 3 Analysis of shear rate effect on sperm navigation by analyzing scattering angle at corners. (a) Hydrodynamic attraction of sperm to surfaces with an angle of θ_a (i). Scattering of sperm from corners of upper (ii) and lower (iii) barrier ports. Scattering angle of sperm at the corners of upper (a) and lower (b) zones under different shear rates measured for 57, 53, 80, 62, 66, and 52 cells for shear rates of 0, 4, 8, 12, 16, and 20 s⁻¹, respectively. The boxplots indicate the median with lower and upper quartiles (c). Increasing the shear rate deviates the scattering angle from its normal value under no flow conditions. Sperm rheotactic navigation depends on the angle of the sperm head with flow direction (d). The head orientation determines the stability of sperm navigation upstream. A bifurcation point exists at θ = −90° where sperm navigation becomes unstable. The closer the angle to zero, the more stable the navigation.

The average scattering angle in the corners of the barrier was measured at different temperatures in the absence of fluid flow by tracking the sperm up to 50 μm from the corners. The absolute scattering angle (|θ_s|) at 30 °C was 14° ± 1.2° (average ± CV), which is close to the reported value of 12.6° ± 0.7 at 29 °C.⁵⁰ Elevating the temperature to 37 and subsequently 44 °C leads to larger scattering angles of 26° ± 0.6°, and 29° ± 0.5°, respectively (more information in ESI† Section S4). The difference in the scattering angles is attributed to the change in oscillatory behavior of the flagella due to increased motor activity.⁵¹

Applying fluid flow to the sperm population changes the scattering angle in the corners of the barrier due to external hydrodynamic forces. The scattering angle, of a minimum of 20 sperm, in the corners of the upper and lower zones changes with increasing shear rates at a constant temperature of 37 °C (Fig. 3b and c).

Sperm navigation in the presence of fluid flow and neglecting rotary diffusion can be described by eqn (1)

where θ is the angle of the sperm head with respect to the upstream direction, ω is the angular velocity of sperm created due to chirality, γ is the shear rate, and ν is a constant related to the microswimmer geometry (Fig. 3d). A minimum shear rate of 3.03 s⁻¹ needs to be met for rheotaxis, and it was found to lead to a hydrodynamic transition in sperm head reorientation by breaking the circling bias and changing the sperm head's direction upstream.²⁰ The stability of sperm navigation refers to the ability to maintain a consistent and directed movement against the flow. To have a stable navigation, θ must be in the range of −90° and 0°. At θ = 90°, which occurs when we exert the critical shear rate, navigation is unstable and is dominated by Gaussian noise due to head oscillation.⁵² We suspect that at corners of the upper side of the barrier, sperm direction would be perpendicular to the flow direction (θ_s = 0° or θ = −90°, which is called the bifurcation point); thus, sperm navigation through an obstructed straight pathway is dominated by Gaussian noise. Hydrodynamic forces caused by fluid flow, however, cause deviations in sperm direction toward the upper zone. Hence, % directionality should decrease by introducing a minimum shear rate; however, it should always slightly exceed 50%. This is because at a low shear rate, sperm motion is dominated by randomness, but the drag force moves some sperm to the upper zone, therefore the % directionality should always be slightly above randomness.

As expected, the scattering angle in the upper port was 0° ± 0.6° for a shear rate of 4 s⁻¹. The experimentally determined % directionality at this shear rate was 60% which is close to the expected value from the equation. Fluid flow resulted in a concentration of sperm count in the upper zone due to partial blocking of sperm passage. Increasing the shear rate increases the scattering angle until a stable value is reached at approximately +34° at higher shear rates. At high shear rates and a high scattering angle >+34°, the sperm passage is significantly decreased due to the inability of sperm to enter the upper port and navigate by rheotactic swimming to the lower zone.

The scattering angle in the lower port is elevated by increasing the shear rate due to higher drag force exerted on sperm. In low shear rates, the sperm depart from lower ports with an angle of −43° ± 0.3 which is in the range of stable navigation (Fig. 3d). Hence, the sperm reorient upstream and reach the inner wall of the pathway. The consecutive departure from and attraction to the side walls generate a transition zone which gives the sperm the chance to change orientation upstream and pass through the obstruction (Fig. 2b and c). This surface–flow interaction phenomenon was also observed in sperm accumulation in proximity to channel strictures.²⁸ Higher shear rates put the sperm in an unsuitable orientation which reduces the probability of upstream navigation. Overall, increasing shear rate suppresses and magnifies the scattering angle in upper and lower ports; therefore, sperm tend to accumulate near the upper port.

2.3 Geometry of barrier alters the sperm navigational pattern

Because the sperm pathway is convoluted and obstructed with spatiotemporal geometrical changes in the FRT, we studied the effect of pathway shape on the navigational pattern of a sperm population. We fabricated barriers, with straight sides and tapered sides, with similar port sizes of w₁ = 85 μm ± 10 μm and vertical height of Y = 400 μm. The flow rate was adjusted to have the same average portal shear rate of 8 s⁻¹ in the lower ports. The degree of taperness (β) is defined as the angle of the barrier between two side walls of the taper (Fig. 1b). The sides were tapered with angles of 45° and 90° and navigation was observed under a shear rate of 8 s⁻¹ (Fig. 4a–c and Movie S4†). The navigational pattern is altered by adding a taper to the barrier and % directionality increased by approximately 20% with a 45° taper, further increasing the angle to 90°, resulting in a significant decrease in the % directionality (p < 0.0001) (Fig. 4d).

Fig. 4 Changing barrier geometry by adding taperness to the ports. Snapshots of sperm locomotion in (a) straight, 180°, (b) 45°-tapered, and (c) 90°-tapered (c) barriers under the same portal shear rate. Arrows indicate the direction of fluid flow. (d) Comparing average directionality for three types of barriers (triplicate measurement) under the same flow conditions (p < 0.0001 from one-way ANOVA analysis). Taper = 0° represents a straight barrier. Error bars indicate standard deviation. (e) Sperm scattering at corners of barriers with a 45° (i) and 90° (ii) taper. The taper of the barrier enhances the stability of sperm upstream navigation by putting closer to stable point. (f) Accumulation index of tapered barriers decreased with increasing taperness from β = 45° to β = 90° (triplicate measurement). Scale bars indicate 100 μm. Corresponding images show the overlaid pictures of sperm motion inside the barrier captured for 5 s of videos. Blue pixels indicate the sperm presence in the barrier. (g) Shear rate profiles along the y-axis of the barrier for β = 45° to β = 90°. Black and red dashed lines show the critical rheotaxis shear rate (y_c) and barrier length (Y).

Previously, we proved that the shear rate alteration causes a change in sperm scattering angle at corners which affects the stability of navigation through the barrier. Based on the same principle, we manipulated the scattering angle by changing the geometry and studied the sperm navigation under the same portal shear rate. At the corners of the lower ports, a small taper (β = 45°) in the barrier induced a scattering angle close to zero (a stable fixed point), resulting in a facilitated upstream navigation through the shear rate portal (Fig. 4e). The overlaid image of sperm locomotion as they exit the barrier port also confirms the close to zero scattering angles (Fig. S5a and b†). Larger tapers (β = 90°) increase the sperm scattering angle (θ_s); therefore, as the angle gets farther from the stable fixed point of eqn (1), the barrier acts as a block to navigation. Therefore, sperm in less tapered barriers, angles below 90°, are more likely to quickly reorient upstream and swim to the lower zone, resulting in a higher sperm count in the lower zone of the barrier.

To further investigate the effect of changing taper of the barrier, we calculated the accumulation index for the two barriers by performing image analysis and comparing the intensities in the absence and presence of fluid flow. The accumulation index is defined as the ratio of normalized intensity inside the barrier (Fig. S2e†) in the presence and absence of fluid flow. This factor indicates the magnitude of sperm present and the accumulation within the tapered barrier as well as the effect of adding external fluid flow on the sperm accumulation. The accumulation index of the two barriers with tapers of 45° and 90° under the same flow conditions as well as corresponding processed images as measured in triplicate was 2.8 for the 45° and 1.8 for the 90° tapered barriers (Fig. 4f). The lower accumulation index indicates that the barrier with the larger angle has accumulated fewer sperm; therefore these barriers do not capture and allow sperm to reorient upstream well (p < 0.05 from t-test).

Navigation in the presence of fluid flow strongly depends on sperm rheotactic swimming which is dependent on shear rate. Straight-pathway barriers have the same shear rate along the flow direction; however, tapered barriers create a gradient of shear rate. The shear rate gradient induces a gradual change in navigation of the sperm toward the high-shear rate port instead of exposing them to a constant shear rate. Hence, sperm in tapered barriers are more likely to reorient and swim upstream. Comparing the shear rate profiles along the y-axis under the same conditions, the distance at which the barrier induces rheotaxis is twice as high as for the 45° barrier compared to the 90° barrier (Fig. 4g; shear rate profiles of tapered barriers are shown in Fig. S6b and c†). Hence, more sperm are attracted to the barrier port when β is 45°, resulting in a higher accumulation index.

To further investigate the effect of geometry, we increased the port size from 85 μm to 130 and 230 μm. Then, under the same inlet flow conditions, the % directionality and accumulation index were calculated for a 45° tapered barrier (Fig. S7 and Movie S5†). Increasing the port size reduces the portal shear rate from 8 s⁻¹ to 5 s⁻¹ and 3 s⁻¹ for 130 and 230 μm port sizes, respectively. Despite this reduction, the rates are still above the minimum required shear rate for rheotaxis. The smaller rheotaxis zone, however, in larger port sizes results in a decrease in the accumulation index. Meanwhile, the % directionality increases due to reduced passage selectivity resulting from a lower shear rate at the lower portal; directionality and accumulation index decreased by 2.5-fold for the 85 μm port size, while for the 230 μm port size it decreased by 1.7-fold. The change in port size can represent temporary muscle contractions in the fallopian tube, which controls the local sperm passage by reducing tube diameter.⁸ Overall, the geometry of the obstructed pathway impacted the navigation of the sperm population by changing the navigation and accumulation patterns.

2.4 Sperm cooperate to pass high-shear-rate zones

In the previous section, we observed that tapered barriers facilitate the upstream navigation by modulating the sperm scattering angle at portal corners. Given the high concentration of sperm in proximity to the barrier port, it is highly probable that sperm within the small area hydrodynamically interact with each other. Additionally, the presence of sperm inherently alters the fluid streamlines on the surface due to the velocity field around them.⁵³ To study this phenomenon, we tracked a spherical particle as it passed through the 45°-tapered barrier port in the presence of fluid flow and swimming sperm (Fig. 5a). The oscillatory motion of the sperm caused the particle to interact with the sperm tails when in close proximity. This interaction changed the particle's trajectory from the expected streamline-following motion (Fig. 5b). The consecutive interaction with other sperm resulted in an oscillating trajectory for the particle.

Fig. 5 Sperm hydrodynamic interaction and cooperation. (a) Tracking a spherical particle (yellow) passing through the 45°-tapered barrier port in the presence of fluid flow (= 8 s⁻¹) and swimming sperm (red). (b) Deviation of the particle's trajectory due to interactions with oscillating sperm tails, resulting in an oscillatory motion. The black dot shows a particle with approximately the same location with respect to port location. Scale bar and color bar indicate 100 μm and wall shear rate. White arrows show the fluid flow streamline. (c) Different stages of sperm cooperation: phase 1: initial alignment induced by the tapered barrier, phase 2: formation of a cooperative train through the high-shear-rate port, and phase 3: dispersal into the upstream reservoir.

Hydrodynamic interactions between sperm is a phenomenon that enhances movement efficiency in fluid flows by increasing swimming velocity.⁴³ We observed that sperm interact and cooperate with each other while passing the barrier port, forming cooperative groups in the shape of a train (Movie S6†). There are three phases of sperm cooperation as they move upstream (Fig. 5c). First the tapered barrier induces a temporary alignment of sperm at the entrance of the barrier port which is facilitated by the change in scattering angle, setting the stage for cooperative behavior (phase 1: initial alignment). As the sperm enter the high-shear-rate port, they form a cooperative group in the shape of a train. The sperm synchronize their flagella, enhancing their swimming efficiency to navigate the high-shear environment effectively (phase 2: formation of cooperative train). After exiting the high-shear-rate port, the sperm disperse into the upstream reservoir. The removal of the shear rate constraint causes the cooperative group to disband, illustrating the transient nature of this cooperation (phase 3: dispersal). The counting of cells for a period of 5 s indicated that 83% of sperm cooperate while passing through the taper.

To quantify sperm cooperation, we calculated the distance between the sperm heads (Δr) and the orientation difference (Δθ) of all possible pairs over the course of a cooperation event involving six representative sperm (Fig. 6a). During the period of cooperation, most sperm had considerable alignment (cos(Δθ) close to 1). Also, higher numbers of points at smaller distances show that sperm are more aligned to each other at shorter distances (higher cos(Δθ)). Dynamic analysis of orientation difference cos(Δθ) and distance Δr during the period of observation confirmed the three distinct phases, namely initial alignment, formation of cooperative train, and dispersal (Fig. 6b and c). During initial alignment, sperm reorient slightly to become focused, getting closer together, so the alignment decreased. Consequently, sperm enter the cooperation course and synchronize their flagella, therefore increasing alignment to an average cos(Δθ) of 0.9. While staying in the cooperative train, sperm swim close to each other (Δr ≤ 17.5 μm). Upon reaching the upstream reservoir where the shear is minimal, sperm start to disperse from the train, and we observe an increase in Δr and a decrease in Δθ. The correlation function C(r) over varying distances (r) and time (t) provides insights into the spatial and temporal dynamics of sperm interactions (Fig. 6d). The average swimming velocity of sperm during the cooperative train phase (phase 2) is 17% faster than phase 1 and 33% faster than phase 3. This observation is consistent with a previous study where sperm paired in cooperative groups had higher persistence against the higher shear rate.⁴⁴

Fig. 6 Analysis of sperm cooperation dynamics. (a) Orientation difference (cos(Δθ)) plotted against the relative distance (Δr) between sperm heads, (b) time evolution of cos(Δθ), (c) average relative distance (Δr) between sperm pairs over time and (d) heatmap depicting the correlation function C(r) across distances and time points t. Phase transitions: phase 1, initial alignment; phase 2, cooperative train; and phase 3, dispersal. Error bars indicate standard error among sperm pairs, and the color bar indicates correlation function value.

The physical attachment of sperm heads, agglutination, is found to occur in several mammalian species.^36,40 Agglutinated bull sperm are reported to possess higher motility and remain viable longer in vitro compared to individual sperm.⁵⁴ We observed agglutinated sperm under the different shear rates induced by changing port size for barriers with a 45° taper (Fig. 7a–c). Due to different shear rates caused by changes in the port sizes (w₁), we suspected that shear rate might induce agglutination in addition to hydrodynamic cooperation through flagella synchronization. To test this hypothesis, we counted the number of sperm passing in an agglutinated cluster with distinct cluster sizes and individual sperm under different shear rates (Fig. 7d).

Fig. 7 Hydrodynamic cooperation of agglutinated sperm in barrier port with a 45° taper with port sizes (a) 85 μm, (b) 130 μm, and (c) 230 μm. Scale bars indicate 100 μm. Yellow boxes are the counting zone. (d) Probability of agglutinated cluster size of sperm under variable port sizes corresponding to 8, 5, and 3 s−1. Exponential decay functions were fitted to the data (dashed lines). (e) Cooperation of individual and agglutinated sperm while passing barrier port. (f–i) Inter-cluster hydrodynamic cooperation of sperm in the barrier outlet port for a 45° barrier with port size of 85 μm. Scale bars indicate 20 μm.

The distribution of cluster size follows a power-law function with an average decay constant of 49 ± 12; however, the distributions are not significantly different for various shear rates (p > 0.05). We also observed that irrespective of agglutinated cluster size, sperm participate in cooperation (Fig. 7e). Hydrodynamic cooperation between individual and agglutinated sperm in the outlet of the barrier port was observed (Fig. 7f to i). We observed that despite cluster size, sperm form hydrodynamic cooperative groups to pass the high shear rate zone. Since agglutinized sperm have higher swimming velocity, they are more capable of overcoming the high shear rate zone. Therefore, hydrodynamic cooperation between agglutinized sperm and individual sperm may be another mechanism that helps the single sperm to pass the port without being swept away by fluid flow.

2.5 Sperm locomotion model in the fallopian tube

There are two prevailing models for explaining the sperm movement in the fallopian tube toward the fertilization zone: the guidance model and the competitive-race model.⁴ In the competitive-race model countless sperm race toward the fertilization zone and fertilize the egg once it enters the fallopian tube. A guidance model suggests that sperm are actively guided toward the egg by various mechanisms, particularly geometric guidance and rheotactic movement, within the fallopian tube.^4,21 This model assigns a guiding role to the microarchitecture of the fallopian tube aiding the sperm to reach the fertilization zone. Regardless of model, it has been shown that only a small fraction of ejaculated sperm actually manage to reach the fallopian tube and the fertilization zone.^2,3 The prevailing competitive-race model proposes that rather than solemnly guiding sperm in the fallopian tube, a selection process occurs, with only the fittest sperm reaching the egg first and winning the race.^1,28 In the competitive-race model, sperm count should gradually decrease along the fallopian tube due to the filter-like behavior of convoluted geometry of the fallopian tube keeping less motile sperm from reaching the egg. Sperm count and distribution along the fallopian tube are highly variable with respect to space and time.² In addition, mammalian sperm can be stored in the FRT prior to ovulation, suggesting the involvement of chemical signals that increase muscle contractions that can change the FRT geometry.^55,56

Based on our findings, the geometry of obstructed pathways change the navigational pattern of sperm, imposing temporary storage, facilitated cooperative navigation, or selective passage modes depending on the geometry. These results may suggest a new model for sperm locomotion in the fallopian tube, explaining that the geometry of convoluted pathways determines the local sperm navigation. Since the epithelial surfaces are folded randomly, local sperm–surface–flow interactions are altered stochastically.

3. Conclusion

The process of fertilization hinges on the journey of the sperm to meet the egg in mammals. During this journey, sperm interact hydrodynamically with the complex microstructured pathways created by the epithelial surfaces of the fallopian tubes. Spatial heterogeneity and temporal muscle contractions create spatiotemporal geometry alterations. Several studies have been performed to simulate the FRT using simple sperm passage channels; however, there is no study clarifying the effect of geometry alteration on the upstream navigation of sperm. We systematically studied the effect of changing geometry of the barrier on the navigational pattern of a sperm population, mimicking the structure of the fallopian tube. We found that 45°-tapered barriers increased navigation by 20%. However, when tapering is increased to 90°, it obstructs sperm passage. Additionally, enlarging the barrier port decreases shear rate within the barrier, leading to reduced selectivity in sperm passage. As a result of shear rate, the velocity also decreases in the barrier. Hence, the sperm with lower velocities can also pass, while at higher shear rates, only the fastest sperm can pass. Furthermore, we observed sperm cooperation when they pass through a tapered pathway in a low-viscosity environment under increased shear rates. In addition to viscoelasticity, localized shear rate focusing structures can promote hydrodynamic cooperation in sperm.⁴³ Also, we concluded that the presence of confined boundaries suffice to induce rheotactic cooperative motion in bovine sperm.

Overall, the results reveal the significant role of the geometry of obstructed pathways on sperm upstream navigation affecting the sperm journey in the FRT. This new navigation model may shed light on how nature modulates several critical sperm navigation processes, guiding, selecting, and storage, by tuning the sperm–surface–flow interaction. The results also indicate that even in normal viscosity medium, sperm can exhibit hydrodynamic cooperation to aid each other to pass the shear rate challenge. The results of this study can be used to analyze and study the locomotion of other swimmers while passing obstructed pathways with variable geometries as well as to design microfluidic systems for controlled selection of sperm in assisted reproduction.

4. Materials and methods

4.1 Bovine sperm sample and medium preparation

Cryopreserved milk-extended semen straws from a bull were thawed and maintained in a water bath at 37 °C before being used in experiments within 2 h. The raw semen sample contained approximately 100 million sperm per milliliter with 30% motility. For sperm navigation analysis, a low-viscosity medium (BO-SemenPrep, IVF Bioscience, Falmouth, England) containing added 0.2% (w/w) bovine serum albumin (BSA) was used. BSA was added to prevent sperm head tethering to the surface of microchannels. The medium was prewarmed at 37 °C before being introduced to the chip.

4.2 Device fabrication and experimental procedure

To model obstructed segments within the fallopian tube, we used an array comprising identical confinements with specific geometric configurations (ESI† Section S1). This array facilitated the monitoring of multiple replicates of the same geometry, ensuring robust and reliable experiments. Positioned within a wide channel equipped with both inlet and outlet, the array sustained a distributed fluid flow throughout the pathways. The structures were fabricated from polydimethylsiloxane (PDMS) by conventional soft lithography.⁵⁷ We used a heated microscope stage (Carl Zeiss) to maintain the temperature at a specific temperature (37 °C in main experiments). To establish a stable population of sperm in the proximity of barriers, we initiated the process by filling the chip with a semen sample. Subsequently, thorough washing with medium was conducted until the barriers were devoid of any extraneous particles or debris, ensuring an unobstructed experimental environment. The fluid flow of medium injection was controlled by a syringe pump (Chemyx Fusion 200).

4.3 Sperm imaging and image processing

Sperm motion in the proximity of barriers was monitored by a phase-contrast microscope (Nikon Eclipse TE300) integrated with a digital camera (Andor Zyla 4.2) for movie acquisition at 20 frames per second using a 10× objective lens. The consecutive frames for each obstruction were then processed using ImageJ (version 1.54 g). To extract the sperm movement and presence in specific zones, we used a multi-step image processing (ESI† Section S2). For all frames of the same video at each pixel location, we assigned the lowest intensity among all frames, showing the sperm presence in that location. Then, the same process was applied by considering the median intensity value for each pixel. By applying a standard deviation among these two images, we would have a single image in which the intensity of different regions indicates sperm presence in that specific location over a constant time window. The grayscale images were colorized using a code in MATLAB (version R2024a) software for enhanced visualization. Grayscale images were converted to black and white for calculating the accumulation index of barriers.

4.4 Navigation and accumulation analysis

To quantify directionality, sperm numbers in the upper and lower zones of a set of three barriers over 5 s of video were counted using the particle analysis module in ImageJ software (version 1.54 g). Directionality was calculated by dividing the number of sperm in the lower zone by the upper zone in each frame. For long run figures, the number of frames were reduced to 1 frame per second. For calculating the accumulation index, overlaid images of sperm motion in the absence and presence of fluid flow were first set to black and white to show all pixels containing sperm in the highest intensity (white). Accumulation index is calculated bywhere I and I′ are average intensities inside the barrier in the absence and presence of fluid flow, respectively. A and A′ are the area inside each barrier in square pixels. Intensities are normalized to exclude the confounding effect of sperm concentration in each experiment.

Shear rate (τ) profile in barrier is estimated by assuming Poiseuille flow for a Newtonian, incompressible fluid and calculating wall shear rate by

where Q, w, and h are fluid flow rate, barrier port width, and barrier port height, respectively. Eqn (4) describes the correlation of shear rate with the degree of barrier taperness (β).where Y and w₁ are the distance from the barrier port and the port size of the barrier, respectively.

In addition to eqn (4), we used numerical simulation techniques to visualize the shear rate profile in a single barrier by using the laminar flow module in COMSOL Multiphysics software (version 6.1). The density and viscosity of fluid were 1000 kg m⁻³ and 1 mPa s, respectively.

The shear rate profile was plotted in a cut-plane placed at a distance of 10 μm from the surface of the lower channel wall.

4.5 Sperm cooperation analysis

High-speed video recordings captured sperm motion as they passed through a port of barrier under controlled experimental conditions. Recorded video frames were processed using ImageJ to track the location (x_i, y_i) and orientation θ of sperm heads for each frame. The Euclidean distance between pairs of sperm heads i and j was computed as:The alignment between pairs of sperm heads i and j was quantified using the cosine of the orientation difference:

cos(Δθ_ij) = cos(θ_i − θ_j) (6)

Sperm pairs were considered aligned if |Δθ_ij| was within 20°.

The correlation function C(r) was computed to quantify the spatial arrangement and alignment of sperm pairs across different distances r and time points t. Pairs of sperm were considered for C(r) calculation if the distance Δr_ij was within a defined threshold δ, which is 17.5 μm for bull sperm, indicating the distance where the sperms are considered to be involved in cooperative events.⁴³ For each distance r, cos(Δθ_ij) values from all qualifying pairs were averaged to obtain C(r):

where N_r is the number of pairs contributing to the average at distance r.

Forward difference method was used for calculating the sperm swimming velocity during the cooperation event.

4.6 Statistical analysis

For statistical analysis, JMP 16.0 and MATLAB softwares were used. All error bars indicate standard deviation unless indicated. Significance levels below 0.05 were considered significant differences. The Kolmogorov–Smirnov (K–S) test was used for comparing distributions of scattering angles at different temperatures. Student t-test was used to compare means. Curve fitting of % directionality data was performed in MATLAB software using least squares method. One-way ANOVA analysis with a significance level of 5% was performed for the effect of taperness on directionality. To evaluate whether the distribution of agglutinated cluster sizes differs significantly between different shear rates, we performed a chi-square (χ²) test. The observed frequencies of cluster sizes for each shear rate were compared against the expected frequencies, which were calculated as the average frequency across all conditions.

Generative AI statement

The authors certify that generative AI was not used in preparing this article. Non-generative AI, such as spelling and grammar checkers in Office 365 and Google Docs, and citation managing software, was used. All instances when non-generative AI was used were reviewed by the authors and editors.

Data availability

All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.† Raw data are available at https://doi.org/10.5281/zenodo.13520196.

Author contributions

A. K. conceived and designed the experiments, performed the experiments, analyzed the data, wrote the first draft, and edited and reviewed later drafts. M. Y. conceived and designed the experiments and reviewed and edited the manuscript. A. A. supervised the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Select Sires, Inc. (Plain City, OH, USA) for generously providing the frozen bovine semen samples. We extend our gratitude to Dr. Kelley Donaghy for her assistance in editing the manuscript. This work was conducted in part at the Cornell NanoScale Facility, a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (Grant NNCI-20252).

References

1. S. S. Suarez and A. A. Pacey, Hum. Reprod. Update, 2005, 12, 23–37.
2. M. Williams, C. J. Hill, I. Scudamore, B. Dunphy, I. D. Cooke and C. L. R. Barratt, Hum. Reprod., 1993, 8, 2019–2026.
3. C. R. Austin and R. V. Short, Reproduction in Mammals: Volume 1, Germ Cells and Fertilization, Cambridge University Press, 1972.
4. M. Eisenbach and L. C. Giojalas, Nat. Rev. Mol. Cell Biol., 2006, 7, 276–285.
5. Y. Yang, J. Elgeti and G. Gompper, Phys. Rev. E, 2008, 78, 061903.
6. S. S. Suarez, Cell Tissue Res., 2016, 363, 185–194.
7. P. Denissenko, V. Kantsler, D. J. Smith and J. Kirkman-Brown, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8007–8010.
8. E. M. Coutinho, J. Maia and C. E. R. Mattos, Gynecol. Invest., 2010, 6, 146–161.
9. S. S. Suarez, K. Brockman and R. Lefebvre, Biol. Reprod., 1997, 56, 447–453.
10. D. P. Wolf, L. Blasco, M. A. Khan and M. Litt, Fertil. Steril., 1978, 30, 163–169.
11. R. H. F. Hunter, P. Coy, J. Gadea and D. Rath, J. Assist. Reprod. Genet., 2011, 28, 191–197.
12. A. Bahat, I. Tur-Kaspa, A. Gakamsky, L. C. Giojalas, H. Breitbart and M. Eisenbach, Nat. Med., 2003, 9, 149–150.
13. W. Xiao, M. Yu, Y. Yuan, X. Liu and Y. Chen, Mol. Hum. Reprod., 2022, 28(8) DOI:10.1093/molehr/gaac027.
14. A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102.
15. Rothschild, Nature, 1963, 198, 1221–1222.
16. R. Nosrati, A. Driouchi, C. M. Yip and D. Sinton, Nat. Commun., 2015, 6, 8703.
17. C. Tung, L. Hu, A. G. Fiore, F. Ardon, D. G. Hickman, R. O. Gilbert, S. S. Suarez and M. Wu, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5431–5436.
18. C. Tung, F. Ardon, A. G. Fiore, S. S. Suarez and M. Wu, Lab Chip, 2014, 14, 1348–1356.
19. M. R. Raveshi, M. S. Abdul Halim, S. N. Agnihotri, M. K. O'Bryan, A. Neild and R. Nosrati, Nat. Commun., 2021, 12, 3446.
20. C. Tung, F. Ardon, A. Roy, D. L. Koch, S. S. Suarez and M. Wu, Phys. Rev. Lett., 2015, 114, 108102.
21. Z. Zhang, J. Liu, J. Meriano, C. Ru, S. Xie, J. Luo and Y. Sun, Sci. Rep., 2016, 6, 23553.
22. K. Miki and D. E. Clapham, Curr. Biol., 2013, 23, 443–452.
23. V. Kantsler, J. Dunkel, M. Blayney and R. E. Goldstein, eLife, 2014, 3, e02403.
24. C. K. Tung and S. S. Suarez, Cells, 2021, 10 DOI:10.3390/cells10061297.
25. K. Ishimoto and E. A. Gaffney, J. R. Soc., Interface, 2015, 12(106), 20150172.
26. F. Yazdan Parast, A. S. Gaikwad, R. Prabhakar, M. K. O'Bryan and R. Nosrati, Cell Rep. Phys. Sci., 2023, 4, 101646.
27. D. J. Smith, E. A. Gaffney, H. Gadêlha, N. Kapur and J. C. Kirkman-Brown, Cell Motil. Cytoskeleton, 2009, 66, 220–236.
28. M. Zaferani, G. D. Palermo and A. Abbaspourrad, Sci. Adv., 2019, 5, eaav2111.
29. R. Nosrati, P. J. Graham, B. Zhang, J. Riordon, A. Lagunov, T. G. Hannam, C. Escobedo, K. Jarvi and D. Sinton, Nat. Rev. Urol., 2017, 14, 707–730.
30. E. T. Y. Leung, C.-L. Lee, X. Tian, K. K. W. Lam, R. H. W. Li, E. H. Y. Ng, W. S. B. Yeung and P. C. N. Chiu, Nat. Rev. Urol., 2022, 19, 16–36.
31. M. Zaferani, S. H. Cheong and A. Abbaspourrad, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8272–8277.
32. R. Nosrati, M. Vollmer, L. Eamer, M. C. San Gabriel, K. Zeidan, A. Zini and D. Sinton, Lab Chip, 2014, 14, 1142–1150.
33. F. Yazdan Parast, M. K. O'Bryan and R. Nosrati, Adv. Mater. Technol., 2022, 7, 2101291.
34. M. Yaghoobi, A. Abdelhady, A. Favakeh, P. Xie, S. Cheung, A. Mokhtare, Y. L. Lee, A. V. Nguyen, G. Palermo, Z. Rosenwaks, S. H. Cheong and A. Abbaspourrad, Lab Chip, 2024, 24, 210–223.
35. S. Wigby, S. S. Suarez, B. P. Lazzaro, T. Pizzari and M. F. Wolfner, Curr. Top. Dev. Biol., 2019, 135, 287–313.
36. H. S. Fisher and H. E. Hoekstra, Nature, 2010, 463, 801–803.
37. B. J. Walker, K. Ishimoto and E. A. Gaffney, Phys. Rev. Fluids, 2019, 4, 093101.
38. S. F. Schoeller and E. E. Keaveny, J. R. Soc., Interface, 2018, 15, 20170834.
39. N. Taketoshi, T. Omori and T. Ishikawa, Phys. Fluids, 2020, 32(10) DOI:10.1063/5.0022107.
40. H. Moore, K. Dvoráková, N. Jenkins and W. Breed, Nature, 2002, 418, 174–177.
41. H. D. M. Moore and D. A. Taggart, Biol. Reprod., 1995, 52, 947–953.
42. T. Pizzari and K. R. Foster, PLoS Biol., 2008, 6, e130.
43. C. Tung, C. Lin, B. Harvey, A. G. Fiore, F. Ardon, M. Wu and S. S. Suarez, Sci. Rep., 2017, 7, 3152.
44. S. Phuyal, S. S. Suarez and C.-K. Tung, Front. Cell Dev. Biol., 2022, 10 DOI:10.3389/fcell.2022.961623.
45. S. Xiao, J. Riordon, A. Lagunov, M. Ghaffarzadeh, T. Hannam, R. Nosrati and D. Sinton, Commun. Biol., 2023, 6, 495.
46. S. Tasoglu, H. Safaee, X. Zhang, J. L. Kingsley, P. N. Catalano, U. A. Gurkan, A. Nureddin, E. Kayaalp, R. M. Anchan, R. L. Maas, E. Tüzel and U. Demirci, Small, 2013, 9, 3374–3384.
47. T. J. Pedley and J. O. Kessler, Annu. Rev. Fluid Mech., 1992, 24, 313–358.
48. A. Guidobaldi, Y. Jeyaram, I. Berdakin, V. V. Moshchalkov, C. A. Condat, V. I. Marconi, L. Giojalas and A. V. Silhanek, Phys. Rev. E, 2014, 89, 032720.
49. L. Eamer, M. Vollmer, R. Nosrati, M. C. San Gabriel, K. Zeidan, A. Zini and D. Sinton, Lab Chip, 2016, 16, 2418–2422.
50. V. Kantsler, J. Dunkel, M. Polin and R. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(4) DOI:10.1073/pnas.1210548110.
51. I. H. Riedel-Kruse, A. Hilfinger, J. Howard and F. Jülicher, HFSP J., 2007, 1, 192–208.
52. B. M. Friedrich and F. Jülicher, Phys. Rev. Lett., 2009, 103, 068102.
53. J. Elgeti, U. B. Kaupp and G. Gompper, Biophys. J., 2010, 99, 1018–1026.
54. K. Umezu, S. Kurata, H. Takamori, T. Numabe, Y. Hiradate, K. Hara and K. Tanemura, Cell, 2020, 9(8) DOI:10.3390/cells9081865.
55. T. J. Orr and M. Zuk, Curr. Biol., 2012, 22, R8–R10.
56. W. V. Holt and A. Fazeli, Annu. Rev. Anim. Biosci., 2016, 4, 291–310.
57. Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Res., 1998, 28, 153–184.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00797b

---