Comparative high spatial resolution measurements of Sr isotopic composition in bio-apatite using different LA-MC-ICPMS configurations: application to faunal (sub)seasonal mobility studies

Abstract

The effects of isobaric interferences on the precision and accuracy of in situ Sr isotopic composition measurements in bio-apatite were investigated using different plasma conditions, interface configurations and instrumentation. Analysis of modern shark enameloid via laser ablation MC-ICPMS (LA-MC-ICPMS) Neptune and Neoma using H-type cones show similar long-term ⁸⁷Sr/⁸⁶Sr reproducibilities of 0.709194 ± 0.000034 and 0.709189 ± 0.000027 (2SD), respectively. Neither instrument showed detectable interference from matrix-generated ⁴⁰Ca³¹P¹⁶O or Ca dimer/argide isobars. The ratios agree with solution-based MC-ICPMS and TIMS analyses, yielding an average ⁸⁷Sr/⁸⁶Sr of 0.709176 ± 0.000008 (2SD). The use of a Jet sampler and a X-type skimmer cone with Neoma increases the sensitivity 2–3 times while maintaining the same level of accuracy. The formation of ⁴⁰Ca³¹P¹⁶O polyatomic clusters can be avoided by tuning the plasma to a low oxide level. An inherent feature of high-sensitivity cones is the production of Ca dimers/argides, which affects ⁸⁴Sr/⁸⁶Sr, additionally suffering from ⁶⁸Zn¹⁶O isobars readily generated at higher oxide levels owing to the ubiquitously high Zn concentration in bio-apatite. The mass bias of ⁸⁷Sr/⁸⁶Sr analysis follows the exponential law across all instrument configurations, which is interpreted as being due to a small average mass difference between normalised and normalising ratios. We demonstrate the benefit of high-sensitivity cones by analysing the highly compositionally zoned enamel of a woolly mammoth. Higher ion beam intensity allowed improved spatial resolution down to 40 μm diameter, revealing compositional variability obscured by larger spots. Improved counting statistics allowed for shorter integration times, resulting in <10 days of temporal resolution for >10 years of enamel formation. Increased sensitivity is of particular value for analysing organisms with low Sr uptake, such as humans, and in slowly mineralizing bioapatite tissues. Another benefit is the enhanced ability to distinguish early in vivo enamel formation from subsequent maturation, which is crucial for reconstructing the palaeoecology of large mammals and human life histories.

---

Introduction

Strontium isotopes have been widely used since the development of the modern mass spectrometer in the early 1950s.¹ Their immediate application was in earth and planetary sciences, where they have become a fundamental petrogenetic tracer and geochronometer using a ⁸⁷Rb–⁸⁷Sr radioactive decay scheme.² However, owing to the relative ease of perturbation, Sr isotopes have played a subordinate role compared with more robust, immobile element-based systems such as ¹⁴⁷Sm–¹⁴³Nd or later ¹⁷⁶Lu–¹⁷⁶Hf.^3–6 The high abundance of Sr and its compositional diversity in the natural environment, together with its common uptake by plants and animals, make Sr isotopes widely used in forensics, (palaeo)environmental studies, palaeoanthropology, (bio)archaeology and food or medical sciences. The development of laser ablation (LA) coupled with multi-collector inductively coupled plasma mass spectrometry (MC-ICPMS)⁷ has revitalized the application of Sr isotopes, enabling high spatial resolution analyses that reveal details obscured by bulk analyses. The quest to analyse minimum sample volume with maximum precision led to the development of various strategies in hardware, instrumental parameters and data reduction.^8–14 Apart from technological improvements such as the reaction cell permitting chemical separation of the most problematic isobar ⁸⁷Rb from ⁸⁷Sr^14,15 or the application of special geometry cones enhancing instrument sensitivity, tuning conditions have been identified as an important factor in reducing or eliminating the effects impeding the accuracy of LA (MC) ICPMS measurements.¹⁶ The flexibility of the ICP source allows for a wide range of conditions influencing ionisation, isotopic and elemental fractionation, polyatomic cluster formation and doubly charged ions or oxide formation, which can be adjusted according to the properties of the element(s) of interest and the type of matrix. Bioapatite, the main compound of skeletal tissues, is one of the most commonly targeted matrices. Its composition can be approximated as a hydroxyapatite Ca₅(PO₄)₃(OH) with CO₃ substitutions. Although apatite is surprisingly flexible in incorporating various elements at the trace level, bio-mineralisation imposes some limitations, and relative abundances are linked to habitat, diet or trophic level. High Sr uptake is accompanied by modest Rb uptake and virtually no REE, whose doubly charged ions (particularly Er and Yb) interfere with Sr isotopes. The absence of doubly charged REE isobars makes bioapatite particularly suitable for the quantification of matrix effects such as Ca-argide and dimer or ⁴⁰Ca³⁰P¹⁶O formation, whose influence on the accuracy of Sr isotopic composition measurements is debated.^{8,9,11,13,17–19} Some studies have shown a large magnitude of these effects, albeit correctable to a minor level,^9,18 while others have not observed them at all.¹¹ An additional factor comes from the use of high-sensitivity cones, together with the increased ion beam results in different isotopic fractionation, mass bias or oxide production.^14,20–27 In this study, we investigated the influence of plasma conditions, matrix effects and instrumental mass bias on the precision, accuracy and reproducibility of Sr isotopic composition measurements of bioapatite by LA-MC-ICPMS using dental enameloids of modern shark teeth. We quantify the influence of Ca dimer/argide, ⁴⁰Ca³¹P¹⁶O isobar, and Zn oxides on the accuracy of Sr isotopic ratio measurements. We present a decade-long record of analyses performed with the MC-ICPMS Neptune and compare it with data obtained using the newer generation MC-ICPMS Neoma. Additional experiments were performed using high-sensitivity cones. Except for ⁸⁷Sr/⁸⁶Sr, we provide analyses of the rarely investigated ⁸⁴Sr/⁸⁶Sr ratio,^9,13 whose accuracy commonly serves as the data quality check and is a sensitive monitor of robust Ca dimer/argide and Kr isobaric interference corrections. The LA-MC-ICPMS data were compared with a long-term record of solution-based analyses under wet and dry plasma conditions. In addition, we tested the current limitations of high-precision, high-spatial-resolution analyses using the dental enamel of a woolly mammoth molar. We demonstrate precise and accurate measurements at spatial resolution of 100 to 40 μm laser beam diameter and <10 days temporal resolution of Sr isotopic composition variations in about 11 year-long formation of a single dental plate. Enhanced sensitivity and spatial resolution demonstrate a much improved ability to separate the in vivo record in the earliest formed enamel from the later maturation stage, which is critical for reconstructing the palaeoecology of large mammals and the life histories of the humans.

Material and methods

Solution analyses were performed on the SRM 987 Sr standard, which is most commonly used to monitor the performance of the analytical set-up and for interlaboratory comparisons. Periodically, modern shark enameloid was measured after the full chemical preparation procedure from digestion to ion exchange column separation as an additional quality check.²⁸ In situ laser ablation MC-ICPMS analyses were performed on modern shark teeth. An example of the application of the in situ LA-MC-ICPMS methodology is demonstrated on an approximately 30-ka-old woolly mammoth molar tooth from Torske, Chortkiv district, Ternopil region in Western Ukraine. The specimen (number D-14) was provided by the Lviv State Museum of Natural History, Ukraine. Sample preparation is described in ref. 29.

Solution mode MC ICPMS analyses

Analyses were performed using MC ICPMS Neptune with collectors connected to amplifiers equipped with 10¹¹ Ω resistors. The collector setup and the main analytical parameters are summarised in ESI Table S1 (S# – ESI†). Two introduction systems were used: (1) Stable Introduction System (SIS), which is a quartz glass dual-pass cyclonic spray chamber with ESI 100 μL min⁻¹ microconcentric, pneumatic PFA nebuliser; (2) Aridus II desolvating nebuliser fitted with the same type of PFA pneumatic nebulizer with either 50 or 100 μL min⁻¹ flow rate. Free aspiration was applied in both cases. The instrument was tuned in the hot plasma range (RF power = 1250–1300 W) to achieve a compromise between signal stability, sensitivity and low oxide production, monitored with the ¹⁴⁰Ce¹⁶O⁺/¹⁴⁰Ce⁺ ratio. For SIS, about 3–5% oxide was a typical value, but some measurements were made with an oxide level of about 10%. The Aridus II was tuned to an oxide level below 0.2%. The spray chamber and membrane temperatures were set to 160 °C and 120 °C, respectively. The flow rate of nitrogen used with the Aridus II was 4–8 mL min⁻¹.

The desolvating nebulisation increased the sensitivity of the mass spectrometers by about 4–8 times with respect to the SIS. For both introduction systems, SRM 987 was at a concentration providing 10–15 V of ⁸⁸Sr. The standard Ni sampler and H-type skimmer cones (hereafter jointly referred to as H-type cones) were used. The isotope ratios were measured in static mode. A single run consisted of 50 cycles of 4.048 s integration. The collector gains were measured prior to each analytical session using the factory setup. The peak centering was performed during tuning and verified every few hours. The baseline was measured on the masses of interest, “on peak zeroes” (OPZ), performed on 2% HNO₃. Washouts between samples were conducted using 3% HNO₃. The total integration time of the baseline was similar to that of the sample. Krypton isobaric interferences associated with trace level contamination of the Ar plasma gas have been reported as an obstacle to accurate Sr isotopic composition measurements, and various correction methods have been proposed.^{7,10,13,30,31} In our setup, we observe less than 0.5 mV of ⁸⁴Kr, with a typical level of <0.2 mV, and ordinary gas blank subtraction efficiently removes Kr isobars from Sr isotopes. In solution-based analyses, the ⁸⁷Rb isobar is also a minor problem as samples are highly purified by ion exchange chromatography. The ⁸⁵Rb/⁸⁷Rb correction value was estimated from Rb–Sr mixed solutions as 0.38557, which is slightly lower than the natural reference value of 0.38571 due to the difference in mass bias between Rb and Sr. For the correction, the estimated ratio was de-normalised using the exponential mass bias law and within run ⁸⁸Sr/⁸⁶Sr ratio. After subtraction of the interfering isobars, the final ratios were normalized to ⁸⁶Sr/⁸⁸Sr = 0.1194, applying the exponential law.³² The data were filtered at a 2σ level.

Laser ablation MC ICPMS analyses

Spatially resolved (in situ) Sr isotopic composition measurements were conducted using an excimer laser (ArF, 193 nm) RESOlution by Resonetics (now Applied Spectra) equipped with the M-50 double-volume sample cell, later replaced by the larger S-155 two-volume cell, both by Laurin Technic. Modern shark teeth serve as a standard for bioapatite treatment. Nearly all analyses were conducted with the preferred energy density of about 7–8 J cm⁻², but the data include experiments with energy down to 5 J cm⁻². The laser pulse frequency was varied from 5 to 30 Hz. Ablation was conducted as a line scan with spot size diameter varying from 40 to 130 μm and stage speed of either 0.5 or 1.0 mm min⁻¹. Ablation occurred when He was mixed in the internal funnel with the Ar sample gas. The laser-generated aerosol was delivered to the MC-ICPMS source after passing through a signal smoothing manifold. To enhance MS sensitivity, 4 to 8 mL per min nitrogen was added to the sample carrier gas (Table S1†). The sensitivity determined on the NIST 614 glass standard varied from 0.8 to 1.5 mV ppm⁻¹ of ⁸⁸Sr for the 60 μm diameter spot and 5 Hz repetition rate, and depended largely on the set of cones used (same type but different sets). Solution analyses were performed using a standard sampler and H-type skimmer cones. The analyses were conducted using Neptune, followed¹¹ by the modifications described below. Additional analyses were performed using MC ICPMS Neoma coupled with the same laser ablation system. The experiments were conducted in two modes: (1) with the H-type cones and (2) with the X-type skimmer cone and Jet sampler cone (hereafter referred to as Jet-X cones). The collector setup and the main instrument parameters for both modes are presented in Table S1.† Data reduction was analogous to that performed for the solution-based analyses, with the difference confined to ⁸⁷Rb correction. Due to the differing properties of Rb and Sr ablation, this was corrected for elemental fractionation using the fractionation factor ⁸⁵Rb/⁸⁶Sr of 1.155 for Neptune¹¹ and 1.138 estimated for Neoma with the Jet-X cones by ablation of BHVO-2G glass standard. The polyatomic isobaric interferences related to the ablation of the apatite matrix, such as Ca-dimers, Ca-argides, or ⁴⁰Ca³¹P¹⁶O, vary depending on the instrumental setup, and their treatment is discussed below.

Results and discussion

Solution-based MC ICPMS analyses under wet and dry plasma conditions

The isotope ratios determined by thermal ionisation mass spectrometry (TIMS) are commonly used as target values for MC-ICPMS measurements. This is chiefly due to much reduced problems related to baseline corrections, the considerably smaller mass bias, and the lack of matrix effects. In the classic paper by ref. 33, the long-term reproducibility of SRM 987 was determined as ⁸⁷Sr/⁸⁶Sr = 0.710248 ± 0.000011 and ⁸⁴Sr/⁸⁶Sr = 0.056492 ± 0.000016 (uncertainties are 2SD). Our more limited dataset obtained with TIMS Triton gave ⁸⁷Sr/⁸⁶Sr = 0.710244 ± 0.000007 and ⁸⁴Sr/⁸⁶Sr = 0.056493 ± 0.000005 (n = 32, 2SD), which agrees well with the above values (ratios normalised to ⁸⁶Sr/⁸⁸Sr = 0.1194 using exponential law³²). Although the published range of ⁸⁷Sr/⁸⁶Sr is much broader, the aforementioned ratios have long been used as reference values and are preferred in this study.

Data obtained by MC ICPMS Neptune for SRM 987 shows long-term reproducibility expressed as 2SD (standard deviation) for >10 years period of ⁸⁷Sr/⁸⁶Sr = 0.710260 ± 0.000011 (n = 213) and 0.710251 ± 0.000013 (n = 107) for the wet and dry plasma, respectively (Fig. 1a). The external precision is similar to the internal precision of an individual run in both cases, which is expressed as 2SE (standard error). Notably, the dry plasma conditions provide slightly more accurate data (relative to TIMS values), although, in a strict sense, within uncertainties, the wet and dry plasma results are indistinguishable. The corresponding ⁸⁴Sr/⁸⁶Sr ratios are 0.056492 ± 0.000023 and 0.056499 ± 0.000030, which are also accurate. The internal precision of ⁸⁴Sr/⁸⁶Sr is nearly three times better (absolute error) than that of long-term reproducibility. Although the latter values are practically the same and agree well with the TIMS ratio, the long-term reproducibility of data obtained using Aridus II is worse than that of SIS. This is interpreted as being due to a low ⁸⁴Sr signal (17 to 170 mV) and the higher importance of accurate baseline correction. In the case of the desolvating nebuliser, it requires a lot of patience due to the excessively long washout time, and thus, incomplete washout likely affected some measurements. Some contribution to lowering the precision could be associated with ⁸⁴Kr and ⁸⁶Kr interferences. However, as mentioned above, the Kr content in our analyses is minor, and the baseline subtraction practically corrects it to zero (mean measured ⁸³Kr/⁸⁶Sr = 0.000001 ± 0.000007). In the absence of any major isobaric interferences, the main factor potentially affecting the accuracy of isotope ratio determination is the mass bias correction, if it departs from the exponential law of ref. 32, as demonstrated for Nd isotopes e.g. ref. 34–37. Ionisation in the ICP source generates approximately 10 times larger isotope fractionation than the thermal source of TIMS, but unlike TIMS, the bias is relatively stable throughout a single measurement. The prediction of an exponential mass bias law is that log natural ⁸⁸Sr/⁸⁶Sr versus ⁸⁷Sr/⁸⁶Sr ratios corrected for baseline and interferences form a linear trend with a gradient equal to 0.50359 (Fig. 1b and c). The linear regression parameters estimated for ratios in LN(⁸⁷Sr/⁸⁶Sr)_m vs. LN(⁸⁷Sr/⁸⁶Sr)_m coordinates yield 0.50382 ± 0.00049 (MSWD = 0.8) and 0.50362 ± 0.00054 (MSWD = 1.0) for wet and dry plasma conditions, respectively (Fig. 1c and d). Both values are in excellent agreement with the theoretical prediction, demonstrating that the exponential law perfectly describes the mass discrimination of Sr isotopes during MC-ICPMS measurements. This remarkable agreement makes the Sr isotope system unique. However, in our view, this relationship arises from the small average mass difference between the normalised ⁸⁷Sr/⁸⁶Sr and the normalising ⁸⁸Sr/⁸⁶Sr ratios. As shown for Nd isotopes, the smaller the mass difference, the closer the agreement with the exponential law; conversely, larger mass differences result in greater deviation from the exponential law.^35–37 Our data suggest that this model is also valid across lower mass ranges. Analogous assessment for ⁸⁴Sr/⁸⁶Sr gave −1.028 ± 0.010 (MSWD = 3.6) and −1.052 ± 0.019 (MSWD = 9.3) gradients for the wet and dry plasma, respectively (Fig. 1d). Both values approximate the expected −1.023 gradient, however, the lower precision of the ⁸⁴Sr/⁸⁶Sr measurements limits a more detailed assessment of mass bias effects. Nonetheless, under wet and dry plasma conditions, the short- and long-term reproducibility of Sr isotope ratios is accurate at high precision.

Fig. 1 Results of SRM 987 Sr standard measurements under wet (SIS) and dry (Aridus II) plasma conditions: (a) ⁸⁷Sr/⁸⁶Sr vs.⁸⁴Sr/⁸⁶Sr; (b) ⁸⁷Sr/⁸⁶Sr vs. beta fractionation factor; (c) natural logarithm of the measured (amplifier gain-, baseline- and interference-corrected) ⁸⁷Sr/⁸⁶Sr_m vs. natural log of the raw ⁸⁸Sr/⁸⁶Sr_m ratio; (d) natural logarithm of the measured ⁸⁴Sr/⁸⁶Sr_m vs. natural log of raw ⁸⁸Sr/⁸⁶Sr_m ratio. Plots (c) and (d) compare the estimated gradients for wet and dry plasma conditions, with the slope predicted using the exponential mass bias law. Uncertainties are expressed as 2SD. See main text for details.

Laser ablation MC-ICPMS of bioapatite

LA-MC-ICPMS Neptune. The teeth of contemporary sharks are an ideal material for the quality control of laser ablation MC ICPMS Sr isotopic composition analyses of dental enamel. They have a high Sr concentration (about 1750 ppm, as determined by LA ICPMS) and a homogenous isotopic composition that reflects that of sea water. Some variations may arise depending on the shark's origin. From the batch of 50 purchased teeth, we randomly selected 9 whose dental enameloid was micro-sampled (using a microdrill) and subjected to the solution mode analyses. Measurements were performed using MC-ICPMS Neptune and Neoma. To compensate for the slight variations in reproducibility of SRM 987 at different instruments, the obtained ⁸⁷Sr/⁸⁶Sr shark values were normalised to the preferred SRM 987 value of ⁸⁷Sr/⁸⁶Sr = 0.710248.³⁸ The measurements ranged from 0.709164 ± 0.000005 to 0.709186 ± 0.000008 with an average of 0.709173 ± 0.000014 (2SD) (weighted average 0.709172 ± 0.000006). This value was additionally verified by 5 replicate analyses using TIMS Triton, which gave a mean value of ⁸⁷Sr/⁸⁶Sr = 0.709178 ± 0.000010 (2SD). The results are in perfect agreement with the average Sr isotopic composition of the present-day sea water of 0.709175 ± 0.000019 (ref. 39) and with the solution-based MC-ICPMS analyses of bull shark (0.709205 ± 0.000035) and spot-tail shark (0.709170 ± 0.000025) determined by ref. 40.

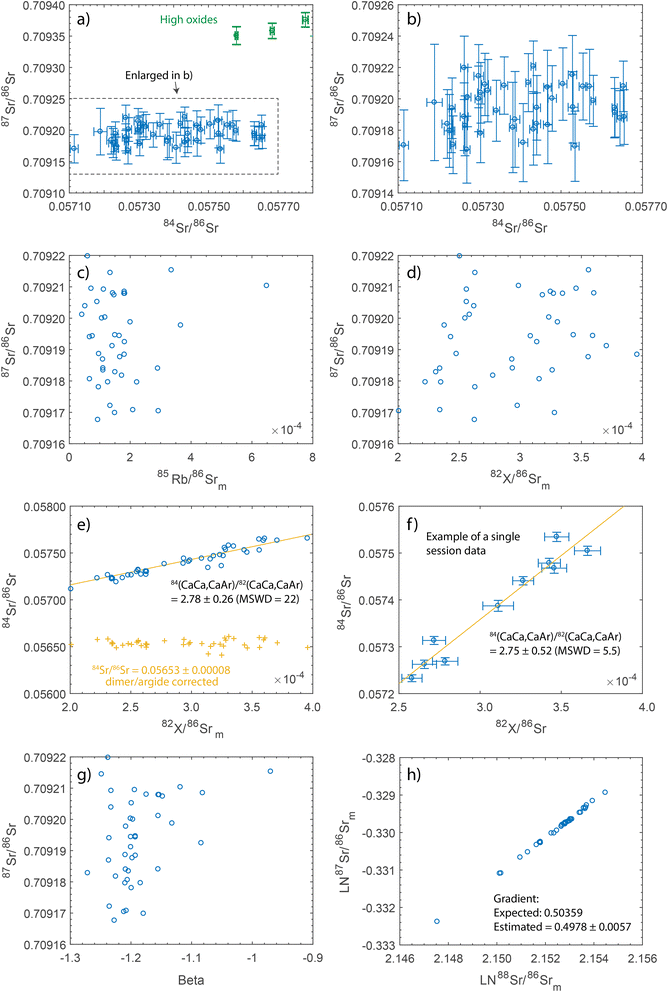
In Fig. 2, we compiled the LA MC ICPMS analyses of shark dental enameloid collected over 10 years. An individual analysis represents a mean ratio for the integration time between 60 and 600 seconds, with the vast majority lasting from 150 to 250 s (Fig. 2a and b). The intensity of ⁸⁸Sr varied from ca. 1 to 20 V, indicating variable spot size, laser pulse repetition rate, and, to a lesser degree, MC-ICPMS settings. The ⁸⁷Sr/⁸⁶Sr ranges from 0.70915 to 0.70922, with the internal precision expressed as 2RSE (relative standard error) ranging from 120 ppm for signals ≤1 V of ⁸⁸Sr to approximately 20 ppm for signals >10 V. It is noteworthy that low-intensity measurements, although less precise, remain accurate. The internal precision well approaches or occasionally even matches that achieved for the SRM 987 solution-based measurements (ca. 15 ppm 2RSE) for comparable integration time and intensities > ca. 10 V of ⁸⁸Sr. However, the long-term reproducibility (0.709195 ± 0.000025; 2SD) is approximately two times lower than that of the solution analyses. This is attributed to the instability of the transient signal and imperfections of natural solid materials (defects, zonation, etc.). Overall, the long-term reproducibility, expressed as arithmetic mean with 2SD (standard deviation) uncertainty for all data, yielded ⁸⁷Sr/⁸⁶Sr = 0.709194 ± 0.000034 (Fig. 2a and b), which is satisfactory for resolving compositional differences in a broad range of applications requiring high spatial resolution.

Fig. 2 Summary of LA-MC-ICPMS Neptune measurements of the Sr isotopic composition of a modern shark enameloid: (a) ⁸⁴Sr/⁸⁶Sr vs. ⁸⁷Sr/⁸⁶Sr. (b) Close-up of the dataset highlighted by the black rectangle in (a); (c) 2RSE (relative standard error) as a function of ⁸⁸Sr ion beam intensity; (d) ⁸⁷Sr/⁸⁶Sr vs. measured ⁸⁵Rb/⁸⁶Sr_m (m denotes ratios corrected for amplifier gain, baseline, and interferences); (e) ⁸⁷Sr/⁸⁶Sr vs. beta fractionation factor; (f) natural logarithm of measured ⁸⁷Sr/⁸⁶Sr_m vs. natural logarithm of raw ⁸⁸Sr/⁸⁶Sr_m, comparing the observed slope to the gradient predicted using the exponential mass bias law. The error bars in (a) and (b) represent 2SE (standard error).

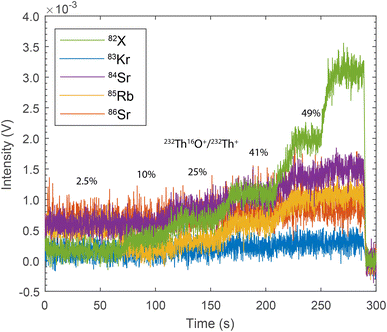
Sr isotope analyses of shark teeth are unaffected by isobars of doubly charged REE ions simply because there is no detectable uptake of these elements during the animals' lives. The Kr level in our setup is the same as that in the solution mode analyses; thus, ordinary gas blank subtraction efficiently strips the interference from the peaks. Thus, the primary concerns are the ⁸⁷Rb and matrix-related isobars. The Rb concentration in shark tooth is negligible. The measured ⁸⁵Rb/⁸⁶Sr (Fig. 2d) normalized using Sr mass bias spanned from below the detection limit of Rb to 0.0004 with the average 0.000088 ± 0.000103 (2σ outliers rejected). Such small interference can be effectively corrected using the standard peak stripping method. Some of the data are slightly overcorrected (negative ⁸⁵Rb/⁸⁶Sr values, Fig. 2d) due to a “more intense washout” of ⁸⁵Rb and contrasting cone memory effects affecting Rb vs. Sr such that ⁸⁵Rb can drop below the corresponding baseline level observed in some runs. This is illustrated in Fig. 3, which shows a decrease in the ⁸⁵Rb signal below the blank level during ablation. Such inadequate baseline correction may change the ⁸⁷Sr/⁸⁶Sr ratio by as much as 15 ppm. This effect is undetectable in materials with higher Rb abundance because the baseline correction does not lead to negative values. Only long pre-conditioning of the cones with apatite matrix seems to prevent more intense Rb washout during the ablation.

Fig. 3 Isotopic composition measurement of shark enameloid demonstrating intense washout of ⁸⁵Rb during ablation, dropping below the corresponding gas blank and leading to inaccurate ⁸⁷Rb isobaric interference correction.

A debated obstacle in obtaining accurate ⁸⁷Sr/⁸⁶Sr ratio is the ⁴⁰Ca³¹P¹⁶O isobar generated during the ablation of apatite matrix.^9,18,41,42 This, however, seems specific to the instrument or setup, as some studies essentially do not observe the formation of this compound.¹¹ The production of this cluster is strongly linked to the oxide level in the plasma.^9,18 We de-tuned the torch position and gas flows to achieve ²³²Th¹⁶O/²³²Th of approximately 10%, but we observed no detectable effect on the accuracy of ⁸⁷Sr/⁸⁶Sr ratio determination, indicating that even relatively high oxide production is insufficient to generate enough ⁴⁰Ca³¹P¹⁶O ions to affect ⁸⁷Sr/⁸⁶Sr ratio within the obtained precision, which agrees with the observation of ref. 11. Other apatite matrix-related isobars include Ca-dimers and argides.^{9,13,31,43,44} The Ca dimers and argides affect all Sr isotopes, but due to the low abundance of ⁸⁴Sr (ca. 0.59%), the ⁸⁴Sr/⁸⁶Sr ratio is a particularly sensitive indicator of these interferences. This is well illustrated with the anomalous group of ⁸⁴Sr/⁸⁶Sr ratios showing values from 0.0568 to 0.0578 (Fig. 2a). They show a clear positive linear correlation with mass ⁸²X used as a monitor of Ca argide/dimer (⁴²Ca⁴⁰Ca, ⁴²Ca⁴⁰Ar) (Fig. S1a and b†). The measured intensity of ⁸²X was 20–120 μV, with the majority of measurements ranging from 20 to 60 μV, which translates into max. 0.2 mV of ⁴⁴Ca interference on ⁸⁴Sr ref. 13 report about 100 mV of total Ca-argide/dimer signal and shift in ⁸⁴Sr/⁸⁶Sr ratios similar to those in our study. The anomalous ⁸⁴Sr/⁸⁶Sr ratios show a positive correlation with ⁸²X/⁸⁶Sr_m (Fig. S1a and b†). Linear regression defines a zero intercept at 0.05658 ± 0.00018, which agrees with the reference value of 0.05650 (both ratios normalized using Sr mass bias). The slope of the regression defines ⁸⁴(CaCa, CaAr)/⁸²(CaCa, CaAr) as 3.2 ± 1.1 (MSWD = 6.3), which broadly agrees with the expected value of ca. 3.2241 for ⁴⁴Ca/⁴²Ca. The data scatter may be due to the small instability of the plasma conditions that change the dimer/argide production or the contribution from other isobar(s) affecting ⁸²X/⁸⁶Sr ratio (Fig. S1a†). Although it is impossible to differentiate between the Ca dimer and argide clusters, as pointed out by ref. 13, the relative abundances of key isotopes are similar, and the same correction will accommodate both interfering compounds. The group of inaccurate ⁸⁴Sr/⁸⁶Sr data was generated by a single user during several consecutive sessions. We investigated all the operator-controlled parameters of laser ablation and MC-ICPMS, but no correlation was found with the anomalous data. Moreover, we did not intentionally tune the MC-ICPMS to stimulate the Ca-dimer/argide production to a visible level. The accidental use of the X-type skimmer cone is the most probable cause of the observed systematics. Nonetheless, even such significant dimer/argide production does not affect the corresponding ⁸⁷Sr/⁸⁶Sr ratio, which, uncorrected for dimer/argide isobars, is 0.709181 ± 0.000032 (2SD, n = 28) and perfectly agrees with the reference value. All the remaining ⁸⁴Sr/⁸⁶Sr measurements, uncorrected for dimer/argide, yielded an accurate mean value of 0.056501 ± 0.000049 (2SD, n = 328). The small positive correlation with ⁸²X/⁸⁶Sr (Fig. S1b†) is certainly not because of the dimers/argides, as the relationship in the ⁸²X/⁸⁶Sr and ⁸⁴Sr/⁸⁶Sr coordinates does not follow the argide/dimer trend (Fig. S1a†). A potential reason could be a “residual”, uncorrected by blank subtraction, Kr interference. However, assuming that all mass 82 is ⁸²Kr, the performed correction reduces the slope of the observed trend from 0.96 ± 0.14 (2SD, MSWD = 6.2) to 0.52 ± 0.17 (2SD, MSWD = 6.7). This changes the mean ⁸⁴Sr/⁸⁶Sr ratio to 0.056496 ± 0.000053, resulting in a negligible difference in accuracy and precision.

The determination of the mass bias trajectory, as for the SRM 987 (Fig. 2f and S1c, d†), in the case of ⁸⁷Sr/⁸⁶Sr ratio, shows a gradient of 0.050337 ± 0.000054 (MSWD = 0.96), which closely follows the exponential mass bias law (Fig. 2f). In the case of the ⁸⁴Sr/⁸⁶Sr ratio, the fractionation trajectory with a slope of −0.999 ± 0.010 (data affected by dimer/argide interferences excluded) significantly deviates from the expected value of −1.048 (Fig. S1d†) and the data obtained in solution mode (Fig. 2d). This discrepancy is likely due to the low precision of the measurements (0.1% 2RSD), which limits the detection of mass bias effects. Nevertheless, from a practical perspective, the measured ⁸⁴Sr/⁸⁶Sr ratio agrees with the TIMS value within uncertainty, indicating that any deviation from the exponential law did not significantly distort the results.

MC-ICPMS Neoma, H-type cones

The experiments conducted with H-type cones are analogous to the Neptune measurements. At the same RF plasma power set to 1250 or 1300 W, we typically achieve about 2% of oxide production (²³²Th¹⁶O/²³²Th), and exceptionally, about 0.5%, which was accompanied by ²³²Th/²³⁸U fractionation of ca. 0.8 (determined ablating NIST 612 glass standard). On Neptune, achieving low oxide levels (ca. 0.5%) was rather effortless. However, in the case of Neoma, oxide levels are typically higher, and their reduction is often at the expense of a higher loss of sensitivity. As demonstrated above, a very low oxide level is not a prerequisite for precise and accurate Sr isotope measurements. Similar to Neptune, the Kr level was essentially negligible, with ⁸⁴Kr gas blank below 0.2 mV and the mean gas blank corrected ⁸³Kr/⁸⁶Sr_m = 0.000009 ± 0.000020. We verified the ⁸⁵Rb/⁸⁷Rb ratio applied to the ⁸⁷Rb isobar correction using solution Rb–Sr mixtures. Dry plasma was achieved using a desolvating nebuliser, the Aridus II introduction system. The resultant ⁸⁵Rb/⁸⁷Rb ratio normalized to ⁸⁸Sr/⁸⁶Sr was 0.38573. The elemental fractionation was determined by ablation of BHVO-2G ⁸⁵Rb/⁸⁶Sr = 1.148, which is similar to that observed with Neptune.¹¹ The quality of data obtained for shark teeth over 4 months is comparable to that of Neptune data. The internal precision was 20 to 60 ppm (2RSE) for the ⁸⁸Sr ion beam, ranging from 2 to 9 V and 150–200 s integration time (Fig. S2a†). The accuracy of ⁸⁷Sr/⁸⁶Sr = 0.709189 ± 0.000027 (2SD, n = 57) and ⁸⁴Sr/⁸⁶Sr = 0.056513 ± 0.000027 (2SD, one gross outlier rejected) was almost identical to that of the Neptune data. The Neoma data has long-term reproducibility, which may be due to the shorter data acquisition period. The normalized ratios showed no correlation with the isobaric interference monitors (⁸²X and ⁸⁵Rb) or with the changes in the instrumental mass bias (Fig. S2c and d†). The extent of the instrumental mass bias expressed as a beta factor is similar to that observed for Neptune for the H-type cones and follows the exponential law as indicated by the estimated gradient 0.5019 ± 0.0037 (MSWD = 0.7), which within uncertainty follows the predicted trajectory (Fig. 2e, f and 5e, f). Matrix-generated ion clusters, such as Ca dimers/argides or ⁴⁰Ca³¹P¹⁶O, were not detected within the obtained precision.

The internal precision achieved for LA-MC-ICPMS shark analyses approaches that of SRM 987 solution-based analyses when comparing data acquired with signals of similar intensity and integration time. For ⁸⁸Sr >6 V, ⁸⁷Sr/⁸⁶Sr ratios show an internal precision of 35 to 20 ppm 2RSE and yield a mean ratio of 0.709182 ± 26 (36 ppm, 2RSD). The solution mode analyses have similar internal and external precision at the level of approximately 15 ppm (for measurements at about 15 V of ⁸⁸Sr). Lower external precision is expected in the case of transient signal analyses of a natural standard with small-scale heterogeneities, local mechanical defects, or zonation in element concentration, matrix effect, etc. Nonetheless, the long-term reproducibility of LA-MC-ICPMS at the level presented in this study is satisfactory for most applications and can certainly be improved.

MC-ICPMS Neoma and Jet-X cones

The jet sampler cone and X-type skimmer cone enhance the sensitivity of MC-ICPMS but also oxide formation, polyatomic interferences, and changes in isotopic fractionation.^{20–22,24–26,45} While keeping the plasma conditions similar to those described above for the H-type cones, oxides increase to several tens of percent, resulting in elevated ⁸⁷Sr/⁸⁶Sr ratios due to ⁴⁰Ca³⁰P¹⁶O formation (Fig. 4a). Additional contribution to deteriorating Sr isotope ratio accuracy is from Ca dimers/argides. Applying near-cold plasma conditions (RF power ca. 1020 W) and reducing oxide formation by adjusting Ar gas flows and sampling depth appears sufficient, if not to eliminate, then at least to suppress the ⁴⁰Ca³⁰P¹⁶O isobar to a negligible level, while maintaining approximately 2–3 times signal enhancement relative to H-type cones. Although considerably reduced, the oxide level was still high, up to approximately 14%. Bringing the ²³²Th¹⁶O/²³²Th ratio down to approximately 0.5% had no detectable benefit regarding ⁸⁷Sr/⁸⁶Sr ratio accuracy, and further reduction was at the cost of a large loss of sensitivity, making the use of Jet-X cones worthless. Despite lower, in comparison to the H-type cones, short-term signal stability (ca. 3% 2RSE for ⁸⁸Sr), the benefit of higher signal allows to obtain internal precision improved by at least a factor of 2 (20–30 ppm 2RSE) for the same laser ablation parameters as used with the H-type cones (Table S1†). Because of the appearance of invisible effects with H-type cones, the correction parameters used for ⁸⁷Rb interference for the Jet-X cones and low RF power were verified on Rb/Sr standard solution mixtures using an Aridus II desolvating nebuliser. Tune parameters were selected to closely resemble those of LA data acquisition as closely as possible. The estimated ⁸⁵Rb/⁸⁷Rb = 0.38572 is practically the same as for the H-type cones, while the elemental fractionation determined on the BHVO-2G glass standard was ⁸⁵Rb/⁸⁶Sr = 1.138, which is slightly lower than that observed for the H-type cones. The reproducibility for data collected over 4 months, ⁸⁷Sr/⁸⁶Sr = 0.709193 ± 0.000028 (2SD, n = 51), is the same as that obtained with the H-type cones for much larger sample volumes (Fig. 4b and c). Although accurate within uncertainty, the ratio is slightly higher than the TIMS or MC-ICPMS solution-based value. Although we cannot exclude some minor production of ⁴⁰Ca³¹P¹⁶O, its contribution to mass 87 seems unlikely at low oxide levels. We did not find any interference that could be attributed to the slight “excess” of the ⁸⁷Sr/⁸⁶Sr ratio. Calcium dimers/argides do not have a detectable effect on this ratio, as supported by the lack of correlation between the ⁸²X/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr (Fig. 4d). A similar conclusion was reached in the studies of ref. 42, 44 and 46. Naturally, at this minor level of “inaccuracy,” small details play an important role. Incomplete or extra washouts for ⁸⁵Rb will affect the baseline correction and hence the accuracy of the ratio estimate, especially when the measurements are at low signal intensities. We observed a small deterioration in the data quality when the cones were not well coated with the apatite matrix, which is probably a prerequisite for accurate high-precision analyses. Although the ⁸⁷Sr/⁸⁶Sr ratio remains accurate within uncertainty, it tends to be slightly higher. Larger magnitude changes are occasionally observed during long runs for the ⁸⁴Sr/⁸⁶Sr ratio, which also tends to be higher at the beginning of the run and reaches the reference ratio at a later stage. We observed such behaviour only with the Jet-X cones. This suggests that some minor discharge occurs between the plasma and the sampler cone, which enhances the dimer/argide production. Adjusting the plasma parameters does not eliminate dimers/argides, which appear to be an inherent feature of the cone geometry. The uncorrected mean for matrix-generated isobars ⁸⁴Sr/⁸⁶Sr = 0.05728 ± 0.00028 is inaccurate but notably, the data scatter is smaller than that in the “accidental dataset” produced with Neptune (Fig. 4e). The relationship is linear with a gradient in normalized ⁸²X/⁸⁶Sr vs. ⁸⁴Sr/⁸⁶Sr coordinates 2.78 ± 0.26 (MSWD = 22). Over a single session (Fig. 4f), the relationship remains the same with the slope defining ⁸⁴(CaCa, CaAr)/⁸²(CaCa, CaAr) ratio as 2.75 ± 0.52 (MSWD = 5.5). This is lower than the expected ⁴⁴Ca/⁴²Ca ratio of 3.22,⁴⁷ which is likely due to a large difference in the mass bias between Sr and Ca, but possibly also due to the contribution of other, yet unrecognized sources of interferences (see below). The inference of the latter observation is that the correction ratio will vary with varying plasma conditions and possibly also compositional variations in trace elements in sharks' enameloid. Correction with the use of the estimated ratio (Fig. 4e) yields ⁸⁴Sr/⁸⁶Sr = 0.05653 ± 0.00008 (2SD).

Fig. 4 Summary of laser ablation MC-ICPMS Neoma measurements of Sr isotopic composition of a modern shark enameloid with Jet-X cones: (a) ⁸⁷Sr/⁸⁶Sr vs. ⁸⁴Sr/⁸⁶Sr; (b) enlarged view of the region highlighted in (a); (c) measured ⁸⁵Rb/⁸⁶Sr_m vs. ⁸⁷Sr/⁸⁶Sr; (d) ⁸⁷Sr/⁸⁶Sr vs. ⁸²X/⁸⁶Sr (Ca dimer/argide monitor); (e) ⁸⁴Sr/⁸⁶Sr vs. ⁸²X/⁸⁶Sr; (f) example of ⁸⁷Sr/⁸⁶Sr vs. ⁸²X/⁸⁶Sr behaviour over a course of a single session; (g) ⁸⁷Sr/⁸⁶Sr vs. beta fractionation factor; (h) natural logarithm of measured ⁸⁴Sr/⁸⁶Sr_m vs. natural logarithm of measured ⁸⁸Sr/⁸⁶Sr_m, comparing the observed gradient with that predicted by the exponential mass bias law. Uncertainty on the gradient is given as 2SD. Subscript m denotes ratios corrected for amplifier gain, baseline, and interferences.

The effect of Zn oxide on Sr isotopes has rarely been explored and was found to be insignificant in solution-based work with Zn/Sr ratios up to approximately 1.⁴⁴ Dental tissues are rich in Zn, especially in the outer enamel,^48,49 and their abundance and Zn/Sr ratio are typically strongly zoned. In sharks, the Zn concentration is on the order of several hundred ppm, reaching even ca. 0.2 wt%, approaching the Sr concentration. Oxygen and zinc form a range of interfering isobars on masses 83, 84, 85, 86, 87 and 88. The most abundant ⁶⁶Zn and the most abundant oxygen isotope ¹⁶O form the highest interference, making mass 82 a sensitive monitor of ZnO isobars. The most significant consequence is on ⁸⁴Sr due to the formation of ⁶⁸Zn¹⁶O, which is the second most abundant Zn isotope (18.5%). The accurate ⁸⁴Sr/⁸⁶Sr ratio measured with H-type cones, both with Neptune and Neoma, indicates that ZnO oxide, if present, is negligible in such a configuration. In the case of high-sensitivity cones, where minor ⁸⁴Sr isotope and mass 82 are additionally affected by Ca-dimer/argide, assessing the potential effect of superposed ZnO isobars is more difficult. Hence, we performed experiments in solution mode, aspirating only the NIST 683 Zn standard using Aridus II connected with Neoma. Experiments were conducted for different oxide levels controlled by lowering the sampling depth while keeping all other parameters unchanged (Fig. 5). At ²³²Th¹⁶O/²³²Th of ca. 2–3% or lower, the ion beams at 82 and 84 masses are at the acid blank level (or the effect is too small to be detected with a Faraday collector). Increasing oxides to about 10% causes a significant rise at mass 82 (⁶⁶Zn¹⁶O) and a smaller rise at mass 84 (⁶⁸Zn¹⁶O). This also changed the signal on mass 85 to the level below the corresponding blank, yet had no effect on masses 86 and 83, the latter being the most reliable Kr interference monitor. Higher oxides caused the rise of interferences in all monitored isotopes, with the biggest change for masses 82 (⁶⁶Zn¹⁶O) and 84 (⁶⁸Zn¹⁶O). A further increase in the number of oxide magnifies the effect, which is best manifested by the changes in mass 82 (Fig. 5). Noteworthy, the effect of ⁷⁰Zn¹⁶O isobars on mass 86, although present, is negligible as ⁷⁰Zn constitutes only 0.6% of total Zn. The effect of ⁷⁰Zn¹⁷O, involving a minor oxygen isotope, on mass 87 is even smaller. Hence, the effect of ZnO is expected to be minor or even negligible on the ⁸⁷Sr/⁸⁶Sr ratio. However, it is important for the ⁸²X/⁸⁶Sr ratio used for argide/dimer correction, if Zn concentration or oxide level is high. A complementary test for potential ZnO interferences was directly performed on the dental enamel. High Zn enrichment in the outer enamel layer is an expression of amelogenesis.^48,50,51 We measured the invariant in nature, the ⁸⁴Sr/⁸⁶Sr ratio, as a line scan from the inner to outer enamel of a woolly mammoth (see below). Subsequently, we measured the intensity of ⁶⁶Zn as a measure of element concentration along the same line. The estimated Zn/Sr ratio changes from approximately 0.2 in the inner enamel to nearly 4 in the outer enamel. The first scan was conducted with an oxide level of ca. 2%. We observe a strong increase in ⁸²X/⁸⁶Sr and ⁸⁴Sr/⁸⁶Sr in the outer enamel layer, where the zinc concentration abruptly rises. A small effect is also visible on ⁸³Kr/⁸⁶Sr ratios (Fig. 6a and b). Applying only the correction for dimers, the ⁸⁴Sr/⁸⁶Sr ratio is accurate, but notably, it gently rises in the Zn-rich zone, and the data is more scattered. Setting up oxides to a very high level of approximately 50% did not reveal any extra features and resulted only in the magnification of the changes observed for the low oxide production (Fig. 6c and d). Under such conditions, the final ⁸⁴Sr/⁸⁶Sr ratio becomes highly inaccurate. A “by-product” of our experiments is the observation of a rise in the ⁸²X/⁸⁶Sr ratio across the enamel, even when the Zn content gently decreases. We did not observe any chemical change in the studied profile that could explain this observation, which certainly deserves further investigation. Overall, our experiments show that even at fairly low oxide levels, ZnO is a significant obstacle in obtaining accurate ⁸⁴Sr/⁸⁶Sr ratios in materials with elevated Zn/Sr ratios.

Fig. 5 Contribution of ZnO polyatomic isobars on Sr, Rb and Kr masses in dependence on the oxide level using MC-ICPMS Neoma with a Jet sampler cone and an X-type skimmer cone. A NIST 683 Zn standard solution was aspirated using Aridus II, and the oxide level was increased by lowering the sampling depth, while all other parameters were kept constant.

Fig. 6 Laser ablation MC-ICPMS line scans from inner to outer enamel in a mammoth molar showing the ⁸⁴Sr/⁸⁶Sr ratio along with ⁸²X/⁸⁶Sr, ⁸³Kr/⁸⁶Sr isobaric monitors, compared with zinc concentration measured along the same line and expressed as ⁶⁶Zn ion beam intensity. Experiments were conducted with ²³²Th¹⁶O/²³²Th = 2% (a and b) and 50% (c and d).

Better plasma sampling and ion extraction with the Jet-X cones also results in smaller isotopic fractionation, which was also observed for the wet plasma, solution mode Sr isotopic composition analyses.²⁰ The latter authors also reported a good agreement between the fractionation trend and the exponential law. Our data show a narrow range of the beta factors from −1.25 to −1.08 for nearly all our measurements (Fig. 4g). The fractionation trend has a gradient of 0.4978 ± 0.0057 (MSWD = 0.6) and deviates from the expected exponential law prediction by 1.15% but overlaps with it within uncertainty and does not have any bearing on the accuracy of ⁸⁷Sr/⁸⁶Sr measurements (Fig. 4h). The higher error of the estimated gradient is due to the smaller amount of data and the smaller range of isotope fractionation. Smaller isotopic fractionation is also reflected in the slightly smaller elemental fraction between Rb and Sr, with ⁸⁵Rb/⁸⁶Sr = 1.138.

Spatial and temporal resolution of seasonal Sr isotopic composition record in woolly mammoth enamel

Unlike sharks, a marine open-sea water animal living in an environment with virtually no variation in Sr isotopes, the variability of bioavailable Sr in terrestrial animals is considerable. This is the foundation of the application of Sr isotopes in studies of animal or human mobility.^52–55 A woolly mammoth molar, with its prolonged mineralisation time (>10 years), large size and structure that helps to better withstand diagenetic changes, provides an insight into a significant period of an animal's life recorded in a single dental plate.^29,56–58 A single molar comprises several dental plates, whose formation in the mesio-distal direction is slightly displaced in time, but adjacent plates reflect the uptake of virtually the same Sr, and their measured isotopic composition should show differences only related to different enamel formation rates. The details of the tooth enamel histology are beyond the scope of this article. For a practical summary in the context of Sr isotopic measurements, the reader is referred to e.g. ref. 11, 29, 48, 56 and 58–60. In this study, we used a woolly mammoth molar from the Torske region of Western Ukraine and compared its remarkable compositional variation in adjacent plates to test the limits of spatial and temporal resolution, along with the precision and accuracy of LA-MC-ICPMS analyses.

The analyses were performed with the setups described above, namely, MC-ICPMS Neptune with H-type cones and MC-ICPMS Neoma with (1) the H-type and (2) the high sensitivity (Jet-X) cones for different laser beam diameters. As the S-155 laser sample cell was large enough to fit an entire dental plate of a mammoth molar, the measurements were taken as a single line scan (Fig. 7a). The ablation lines were placed near the enamel–dentine junction (EDJ) and proceeded from the cusp (early forming enamel) to the cervix (late forming enamel). The results obtained with the Neptune for the longest centrally located tooth plate (Fig. 7a), summarised in Fig. 7b–d, show twelve cyclic changes in the ⁸⁷Sr/⁸⁶Sr ratio ranging from 0.7099 to 0.7119 and invariant ⁸⁴Sr/⁸⁶Sr with a mean value of 0.056507 ± 0.000010 (2SD). The latter ratio is accurate and indicates the absence of significant dimer production, with the mean of the interference monitor ratio ⁸²(Kr + CaCa + CaAr)/⁸⁶Sr_m = 0.000025 ± 0.000014 (2SD). The accurate ⁸⁷Sr/⁸⁶Sr ratio obtained for the accompanying matrix-matched shark tooth analyses proves ⁴⁰Ca³¹P¹⁶O to be negligible, as expected for low-oxide plasma. This leaves ⁸⁷Rb as the only significant isobaric interference. The ⁸⁵Rb/⁸⁶Sr ratio in the shark (≤0.0001) is more than an order of magnitude lower than that observed in terrestrial animals (Fig. 7c), and the shark tooth cannot serve as an optimal verification of the accuracy of the ⁸⁷Rb interference correction. Instead, we relied on the reference ratio determined using the Rb–Sr mixed solutions, which demonstrates the reliability of the ⁸⁵Rb isobar correction well above ⁸⁵Rb/⁸⁶Sr_m of 0.025. Even a slightly higher interference can be accurately corrected.^9,11

Fig. 7 Cusp to cervix Sr isotopic composition of the dental enamel of a woolly mammoth from the Torske region of Western Ukraine. Measurements performed with the LA-MC-ICPMS Neptune using H-type cones; (a) scan of a molar tooth fragment with a marked ablation line (blue colour) within the internal enamel layer; (b) ⁸⁷Sr/⁸⁶Sr, (c) ⁸⁴Sr/⁸⁶Sr, and (d) measured ⁸⁵Rb/⁸⁶Sr_m. Individual 1 s integration is shown in grey. The red lines represent smoothed data using a moving average with a span of 50 s. The line thickness corresponds to ±2SE uncertainty.

The cusp to cervix variations along the EDJ in Sr concentration show an ⁸⁸Sr ion beam from 3.5 to 8.2 V. Smoothing the ⁸⁷Sr/⁸⁶Sr data using a moving average with a span of 50 seconds, corresponding to 0.8 mm of ablated enamel, gives an internal precision of 40 to 280 ppm (2RSE), with the vast majority of data (about 90%) falling within the range of 40 to 120 ppm (excluding locally mechanically damaged zones). The precision varies greatly depending on the compositional gradient of the Sr isotopic composition (Fig. 7b–d). Our histomorphometric record, with a close-to-a-week resolution chronology of enamel secretion, suggests that the observed compositional cyclicity reflects 12 annual cycles interpreted as diet changes during the cold and warm seasons. The decreasing ‘wavelength’ of the cycles towards the cervix represents the slowing down of the recruitment rate of new ameloblasts in the secretion front along the EDJ with time. At each stage of enamel formation, the precision obtained is more than satisfactory for resolving temporal variations in ⁸⁷Sr/⁸⁶Sr at the sub-seasonal level.

The results obtained using Neoma with the H cone for different dental plates from the same tooth are in excellent agreement with the data obtained using Neptune. The compositional details can be easily followed and correlated with the analyses of both instruments (Fig. 7 and 8). The non-radiogenic ⁸⁴Sr/⁸⁶Sr ratio is also accurate and shows no indication of the presence of polyatomic Ca dimer/argide interferences. The internal precision obtained for the time equivalent fragments of dental enamel is comparable for both instruments, ranging from 70 to 110 ppm (2RSE). Measurements of contemporaneously mineralised enamel on the opposite side of the same tooth plate, with the same laser parameters but using Jet-X high-sensitivity cones, are in perfect agreement with the H-type cones (Fig. 8c). Higher sensitivity (4.5 to 8.0 V of ⁸⁸Sr) led to improved internal precision (50–90 ppm 2RSE). However, the normalised ⁸⁴Sr/⁸⁶Sr ratio fluctuates strongly throughout a run, ranging from approximately 0.060 to 0.062 (Fig. 8c and d). An additional correction for Ca dimer/argide isobars gives a stable and accurate ⁸⁴Sr/⁸⁶Sr = 0.056472 ± 0.000005 (2SE). A small region at the beginning of the scan deviates from this value because of intense fracturing, which also affects the corresponding ⁸⁷Sr/⁸⁶Sr ratio (Fig. 8d). Reducing the spot size to 40 μm reduces the ablated sample volume almost 7 times. The intensity of ⁸⁸Sr ranged from approximately 1.0 to 2.5 V. Despite the lower internal precision, all compositional details are visible (Fig. 8e and f). The lower precision did not obscure the high spatial resolution advantage. As expected, it revealed more compositional details. This is well illustrated by magnifying the same peak measured with the 3 different settings (Fig. 9a–c). The region with the highest ⁸⁷Sr/⁸⁶Sr ratio, visible in the 40 μm spot measurement, is only detected as a sharp peak in the 104 μm spot measurements. Similarly, smaller peaks are much better defined in the regions of less radiogenic Sr when scanned with a smaller ablation spot diameter (Fig. 9c). Despite some loss of precision, the increased spatial resolution is certainly beneficial in terms of obtaining a more detailed reconstruction of the temporal changes in the mineralised enamel. The increased sensitivity provided by the Jet-X cones not only allows the use of a smaller laser beam diameter but also reduces the integration time owing to the improved counting statistics, resulting in improved spatial and temporal resolution of measurements even with a larger laser beam. Reducing the integration region from 50 to 25 seconds, which represents 0.4 mm of ablated enamel, corresponding to approximately 10 days of enamel growth, reveals much more detail, similar to analyses using the smaller laser spot (Fig. 9e). The same reduction of the integration region in the case of the 40 μm beam gives no improvement, which is simply a consequence of the poorer counting statistics. Reducing the integration region even further, to 10 seconds (0.17 mm of mineralised enamel = 4 days), does not bring any improvement, although the major compositional changes can still be depicted and might still be useful for mobility studies. Although the high spatial and temporal resolution obtained cannot generally be interpreted with the same level of detail when reconstructing migratory paths (the regional coverage of Sr isotopic composition is not known in sufficient detail), such high-resolution data provide additional insight into the habits of the animals, especially when combined with other techniques such as dental histology, stable isotope, trace element data and isoscapes. The use of high-sensitivity Jet-X cones will be even more appreciated in the analysis of enamel with low extension (formation) rates and in the analysis of higher trophic level animals, particularly humans, whose dental enamel contains considerably less Sr. The reduced laser beam diameter also allows the separation of different stages of enamel formation and the recovery of the least disturbed in vivo record of bio-apatite mineralisation.

Fig. 8 Cusp to cervix Sr isotopic composition measurements of woolly mammoth enamel performed using LA-MC-ICPMS Neoma. Measurements were conducted with the H-type cones (a and b) and high-sensitivity Jet-X cones on the opposite side of the same dental plate (c and d). A shorter dental plate was analysed using Jet-X cones with a 40 μm laser beam diameter (e and f). Green rectangles show equivalent regions mineralized at approximately the same time (see also Fig. 9).

Fig. 9 Comparison of measurement precision using LA-MC-ICPMS Neoma with H-type (a) and Jet-X cones (b and c) in an enamel region corresponding to approximately 1 year of mineralization. Laser beam diameters of 104 μm (a and b) and 40 μm (c) were applied. Precision is shown for 50, 25, and 10 s integrations corresponding to enamel mineralization times of approximately 20 (a–c), 10 (d–f) and 4 (g–i) days, respectively. The optimal compromise between precision and highest temporal resolution is represented by the analyses with Jet-X cones, 104 μm diameter and 25 seconds integration time (e). The highest spatial resolution was achieved with a 40 μm diameter and 50 second integration time (c). The selected region is marked with a green rectangle in Fig. 8a, c and d. The heavy red line represents the moving average, and the light red lines represent ± 2SE uncertainty.

Conclusions

The long-term measurements of SRM 987 using MC-ICPMS Neptune demonstrate the high accuracy and reproducibility of ⁸⁷Sr/⁸⁶Sr and ⁸⁴Sr/⁸⁶Sr under both wet and dry plasma conditions, with the dry plasma values more closely matching the TIMS reference data. Solution-based analyses of contemporary shark dental enameloid, used as a bioapatite reference material for LA MC-ICPMS, yield an ⁸⁷Sr/⁸⁶Sr ratio of 0.709176 ± 0.000008 (2SD), consistent with present-day seawater. Laser ablation MC-ICPMS analyses of shark enameloids using the Neptune and Neoma instruments with H-type cones yielded consistent ⁸⁷Sr/⁸⁶Sr ratios, with internal precision ranging from 50 to 25 ppm (2RSE) and long-term reproducibility of ∼50 ppm for Neptune and ∼40 ppm (2RSD) for Neoma cones. Mean ⁸⁷Sr/⁸⁶Sr values were 0.709194 ± 0.000034 (Neptune) and 0.709189 ± 0.000027 (Neoma, 2SD), which agreed well with the solution-based reference data. No significant interferences from ⁴⁰Ca³¹P¹⁶O or Ca-dimer/argides were observed. The use of a Jet skimmer and X-type sampler cones on Neoma increases oxide production, introducing ⁴⁰Ca³¹P¹⁶O interference. This can be effectively suppressed by plasma tuning while preserving a 2–3 times signal enhancement, improving ⁸⁷Sr/⁸⁶Sr precision by at least a factor of two. Elevated Ca dimer/argide species bias the ⁸⁴Sr/⁸⁶Sr ratio but are correctable to an accurate value. Minor ⁶⁸Zn¹⁶O interference on ⁸⁴Sr is minimized at low oxide levels (<2% ²³²Th¹⁶O/²³²Th). A notable feature of ⁸⁷Sr/⁸⁶Sr analysis by MC-ICPMS is its mass bias behaviour, which follows the exponential law across all instrument configurations. This is attributed to the small average mass difference between the normalised and normalising ratios, as also seen for isotopic measurements of Nd.^35,36

We tested different LA-MC-ICPMS configurations to examine seasonal variations in Sr isotopic composition in woolly mammoth enamel, obtaining high-precision measurements with sub-monthly resolution. The use of Jet-X cones enhanced the sensitivity, enabling improved spatial resolution. Reducing the laser spot diameter to 40 μm results in lower precision, yet still sufficiently high, allowing for the detection of finer compositional details that would otherwise be averaged out with a larger beam size. Similarly, shortening the integration time at higher signal intensities resulted in a resolution of <10 days for moderate enamel extension rates. Enhanced instrument sensitivity, leading to higher spatial and temporal resolution, is vital for analysing organisms at higher trophic levels, incorporating much lower amounts of Sr, such as humans, and bio-apatite tissues mineralizing at a slower pace. Another advantage is the improved ability to separate the in vivo record in the earliest formed enamel from the later maturation overprint, which is critical for reconstructing the palaeoecology of large mammals and the life histories of humans.

Data availability

Data for this article are available at https://database.ing.pan.pl/ and https://dataportal.ing.pan.pl.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was funded by the National Science Centre, Poland, grant no. UMO-2023/49/B/ST10/02100 awarded to R. Anczkiewicz. We also acknowledge the instrument funding by EPOS PL+ grant no. POIR DIR/PMIB/2020/89. We are grateful to the two anonymous reviewers for their helpful comments and Charlie Palmer for the editorial handling of the manuscript.

References

1. E. G. Johnson and A. O. Nier, Phys. Rev., 1953, 91, 10–17.
2. O. Hahn, F. Straßmann, J. Mattauch and H. Ewald, Chem.-Ztg., 1943, 67, 55–56.
3. S. B. Jacobsen and G. J. Wasserburg, Earth Planet. Sci. Lett., 1980, 50, 139–155.
4. D. J. DePaolo, Nature, 1981, 291, 193–196.
5. P. Patchett and M. Tatsumoto, Contrib. Mineral. Petrol., 1981, 75, 263–267.
6. S. Duchêne, J. Blichert-Toft, B. Luais, P. Télouk, J. M. Lardeaux and F. Albarède, Nature, 1997, 387, 586–589.
7. J. N. Christensen, A. N. Halliday, D.-C. Lee and C. M. Hall, Earth Planet. Sci. Lett., 1995, 136, 79–85.
8. A. Buzenchi, H. Moreira, O. Bruguier, D. Bosch and B. Dhuime, J. Anal. At. Spectrom., 2023, 38, 2113–2126.
9. M. S. A. Horstwood, J. A. Evans and J. Montgomery, Geochim. Cosmochim. Acta, 2008, 72, 5659–5674.
10. J. G. Konter and L. P. Storm, Chem. Geol., 2014, 385, 26–34.
11. W. Müller and R. Anczkiewicz, J. Anal. At. Spectrom., 2016, 31, 259–269.
12. L. Rey, T. Tacail, F. Santos, S. Rottier, G. Goude and V. Balter, Chem. Geol., 2022, 587, 120608.
13. J. Woodhead, S. Swearer, J. Hergt and R. Maas, J. Anal. At. Spectrom., 2005, 20, 22–27.
14. P. Télouk and V. Balter, J. Anal. At. Spectrom., 2024, 39, 879–887.
15. D. Bevan, C. D. Coath, J. Lewis, J. Schwieters, N. Lloyd, G. Craig, H. Wehrs and T. Elliott, J. Anal. At. Spectrom., 2021, 36, 917–931.
16. J. Fietzke and M. Frische, J. Anal. At. Spectrom., 2016, 31, 234–244.
17. J. Lewis, C. D. Coath and A. W. G. Pike, Chem. Geol., 2014, 390, 173–181.
18. A. Simonetti, M. R. Buzon and R. A. Creaser, Archaeometry, 2007, 50, 371–385.
19. P. Z. Vroon, B. van der Wagt, J. M. Koornneef and G. R. Davies, Anal. Bioanal. Chem., 2008, 390, 465–476.
20. T. Ariga, K.-C. Shin and T. Narukawa, Spectrochim. Acta, Part B, 2025, 225, 107134.
21. Z. Hu, Y. Liu, S. Gao, W. Liu, W. Zhang, X. Tong, L. Lin, K. Zong, M. Li, H. Chen, L. Zhou and L. Yang, J. Anal. At. Spectrom., 2012, 27, 1391–1399.
22. S. Lauwens, M. Costas-Rodríguez, H. Van Vlierberghe and F. Vanhaecke, J. Anal. At. Spectrom., 2017, 32, 597–608.
23. R. Nakada, N. Asakura and K. Nagaishi, Geochem. J., 2019, 53, 293–304.
24. K. Newman, J. Anal. At. Spectrom., 2012, 27, 63–70.
25. N. Shirai and M. Humayun, J. Anal. At. Spectrom., 2011, 26, 1414–1420.
26. M. A. Vaughan and G. Horlick, Spectrochim. Acta, Part B, 1990, 45, 1289–1299.
27. L. Yang, L. Zhou, Z. Hu and S. Gao, Anal. Chem., 2014, 86, 9301–9308.
28. A. A. Anczkiewicz and R. Anczkiewicz, Chem. Geol., 2016, 427, 1–16.
29. R. Anczkiewicz, A. Nava, L. Bondioli, W. Müller, C. Spötl, M. Koziarska, M. Boczkowska, P. Wojtal and J. Wilczyński, Quat. Sci. Rev., 2023, 313, 108191.
30. M. G. Jackson and S. R. Hart, Earth Planet. Sci. Lett., 2006, 245, 260–277.
31. T. Waight, J. Baker and D. Peate, Int. J. Mass Spectrom., 2002, 221, 229–244.
32. W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090.
33. M. F. Thirlwall, Chem. Geol. Isot. Geosci., 1991, 94, 85–104.
34. E. Frères, D. Weis, K. Newman, M. Amini and K. Gordon, Geostand. Geoanal. Res., 2021, 45, 501–523.
35. D. Vance and M. Thirlwall, Chem. Geol., 2002, 185, 227–240.
36. M. F. Thirlwall and R. Anczkiewicz, Int. J. Mass Spectrom., 2004, 235, 59–81.
37. Y. Yu, E. Hathorne, C. Siebert, M. Gutjahr, J. Fietzke and M. Frank, Chem. Geol., 2024, 662, 122220.
38. J. M. McArthur, R. J. Howarth and G. A. Shields, in The Geologic Time Scale, 2012, pp. 127–144,  DOI:10.1016/b978-0-444-59425-9.00007-x.
39. J. M. McArthur, R. J. Howarth and T. R. Bailey, J. Geol., 2001, 109, 155–170.
40. S.-G. Yim, M.-J. Jung, Y.-J. Jeong, Y. Kim and A. C.-s. Cheong, J. Anal. Sci. Technol., 2021, 12, 10.
41. S. R. Copeland, M. Sponheimer, J. A. Lee-Thorp, P. J. le Roux, D. J. de Ruiter and M. P. Richards, J. Archaeol. Sci., 2010, 37, 1437–1446.
42. J. Irrgeher, P. Galler and T. Prohaska, Spectrochim. Acta, Part B, 2016, 125, 31–42.
43. M. Bizzarro, A. Simonetti, R. K. Stevenson and S. Kurszlaukis, Geochim. Cosmochim. Acta, 2003, 67, 289–302.
44. F. C. Ramos, J. A. Wolff and D. L. Tollstrup, Chem. Geol., 2004, 211, 135–158.
45. L.-F. Gou, Z.-D. Jin, L. Deng, M.-Y. He and C.-Y. Liu, Spectrochim. Acta, Part B, 2018, 146, 1–8.
46. Z. Yang, B. J. Fryer, H. P. Longerich, J. E. Gagnon and I. M. Samson, J. Anal. At. Spectrom., 2011, 26, 341–351.
47. K. J. R. Rosman and P. D. P. Taylor, Pure Appl. Chem., 1998, 70, 217–235.
48. W. Müller, A. Nava, D. Evans, P. F. Rossi, K. W. Alt and L. Bondioli, Geochim. Cosmochim. Acta, 2019, 255, 105–126.
49. F. Brudevold, L. T. Steadman, M. A. Spinelli, B. H. Amdur and P. Gron, Arch. Oral Biol., 1963, 8, 135–144.
50. B. Reynard and V. Balter, Palaeogeogr. Palaeoclimatol. Palaeoecol., 2014, 416, 4–16.
51. M. Yamaguchi, K. Inamoto and Y. Suketa, Res. Exp. Med., 1986, 186, 337–342.
52. T. D. Price, in Isotopic Proveniencing and Mobility: the Current State of Research, ed. T. D. Price, Springer International Publishing, Cham, 2023, pp. 1–27,  DOI:10.1007/978-3-031-25722-3_1.
53. W. Müller, F. Lugli, J. McCormack, D. Evans, R. Anczkiewicz, L. Bondioli and A. Nava, in Treatise on Geochemistry (Third Edition), ed. A. Anbar and D. Weis, Elsevier, Oxford, 2025, pp. 281–328,  DOI:10.1016/B978-0-323-99762-1.00105-4.
54. J. E. Ericson, J. Hum. Evol., 1985, 14, 503–514.
55. M. J. Wooller, C. Bataille, P. Druckenmiller, G. M. Erickson, P. Groves, N. Haubenstock, T. Howe, J. Irrgeher, D. Mann, K. Moon, B. A. Potter, T. Prohaska, J. Rasic, J. Reuther, B. Shapiro, K. J. Spaleta and A. D. Willis, Science, 2021, 373, 806–808.
56. N. Kowalik, R. Anczkiewicz, W. Müller, C. Spötl, L. Bondioli, A. Nava, P. Wojtal, J. Wilczynsk, M. Koziarska and M. Matyszczak, Quat. Sci. Rev., 2023, 306, 108036.
57. W. Dirks, T. G. Bromage and L. D. Agenbroad, Quat. Int., 2012, 255, 79–85.
58. J. Z. Metcalfe and F. J. Longstaffe, Quat. Res., 2012, 77, 424–432.
59. C. Robinson, J. Kirkham, S. J. Brookes, W. Bonass and R. Shore, Int. J. Dev. Biol., 1995, 39, 145–152.
60. M. P. Ferretti, Acta Palaeontol. Pol., 2003, 48, 383–396.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ja00146c

---