 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dual-field multicollector LG-SIMS analysis of mixed U–Pu reference particles†
Evan E.
Groopman
 *a,
Todd L.
Williamson
*a,
Todd L.
Williamson
 a,
Kyle M.
Samperton
a,
Kyle M.
Samperton
 b,
Spencer M.
Scott
b,
Bryan J.
Foley
b,
Michael G.
Bronikowski
b,
George S.
King
b,
Spencer M.
Scott
b,
Bryan J.
Foley
b,
Michael G.
Bronikowski
b,
George S.
King
 b and
Matthew S.
Wellons
b
b and
Matthew S.
Wellons
b
aMaterials Measurement Science Division, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA. E-mail: evan.groopman@nist.gov
bSavannah River National Laboratory, Aiken, SC 29808, USA
First published on 6th June 2025
Abstract
In this study, we demonstrate a new dual-field multicollector protocol for magnetic sector large-geometry secondary ion mass spectrometry (LG-SIMS) that enables concurrent analysis of U and Pu isotopes. We apply this analysis protocol to recently produced mixed U–Pu microparticle reference materials, called UPu-100A. These particles, loaded on a Si substrate, show highly reproducible U and Pu isotopic and U/Pu assay results, with particle-to-particle molar variability typically less than 1% relative, and down to 0.1% for 235U/238U and less than 0.3% for 240Pu/239Pu. We demonstrate the impact of surface and primary beam sputter chemistry on the acquisition and interpretation of mixed-actinide particle analyses. We show that, in general, consuming most of each particle within a single analysis yields the most reproducible results. Using O3− primary ions reduces sputter chemistry artifacts during particle depth profiling on Si relative to O− primary ions, which further enhances reproducibility. The Pu/U relative sensitivity factors for O3− and O− primary ions on Si were 2.036 ± 0.016 (1 standard deviation, SD) and 2.142 ± 0.034 (1 SD), respectively. This work highlights how integration of novel analytical protocols and fit-for-purpose reference materials can push the boundaries of particle-scale material characterization.
Introduction
Since the 1990s, the International Atomic Energy Agency (IAEA) has conducted environmental sampling of member states' nuclear facilities to help maintain Nuclear Safeguards.1–3 Environmental uranium and plutonium can be chemically and isotopically analyzed at the bulk (>nanogram) and particle (<nanogram) scale to infer the operational history of nuclear facilities. Nuclear forensics investigations employ similar types of analyses on interdicted nuclear materials, e.g., Kristo (2020)4 and references therein. The IAEA Department of Safeguards has identified “isotopic characterization of Pu containing particles using large-geometry secondary ion mass spectrometry (LG-SIMS)”, to be a “top priority Research and Development (R&D) need” and looks to improve the capability “to perform mixed U–Pu particle analysis, including screening, isotopic and elemental composition analysis”.5–7 The IAEA emphasizes the development and characterization of reference materials to support this R&D. Elementally and isotopically homogeneous particle reference materials address several needs within the International Nuclear Safeguards community, including quality assurance and quality control (QA/QC), which are important aspects of any regulatory framework. In addition, common reference materials are necessary for quantitatively comparing the performance of different mass spectrometry techniques and for developing new techniques and protocols. This applies to mainstay techniques of Nuclear Safeguards,8 such as Secondary Ion Mass Spectrometry (SIMS)9–15 and Thermal Ionization MS (TIMS),16–23 and to emerging techniques that may enhance future actinide particle analyses, such as Laser Ablation (LA) Inductively Coupled Plasma MS (ICP-MS) and other ICP-MS modalities,22,24,25 Resonance Ionization MS (RIMS),26,27 and Atom Probe Tomography (APT).28 Widespread distribution of well-characterized particle reference materials will enable a better understanding of the quantitative performance of different techniques and help drive better analyses and investments in future Safeguards-related technology.Savannah River National Laboratory (SRNL), which is part of the IAEA's Network of Analytical Laboratories (NWAL) qualified for the production of particle reference materials, including ISO/IEC 17025:2017 accredited (A2LA – 3750-01) methods for uranium and plutonium assay, recently produced a batch of monodisperse, mixed U–Pu particle reference materials (called “UPu-100A”) for use in operational QA/QC procedures and for related microparticle R&D.29 Prior to the production and certification of the SRNL UPu-100A particles, there were few, if any, monodisperse U–Pu particle reference materials that were characterized by (1) wide availability, (2) homogeneous U and Pu isotopics, and (3) verified U/Pu assay amounts. One well-known material used previously was the PNL-2 clay beads, made at Pacific Northwest Laboratory in the early 1990s.30 These consisted of micrometer-scale aluminosilicate spheres loaded with minor concentrations of U and Pu from a feedstock solution. While the U and Pu isotopics were shown to be homogeneous, the particles were never individually assayed for total U and Pu concentration by mass spectrometry. Instead, an electron microprobe was used to characterize the elemental composition, but the Pu concentration had a large relative uncertainty due to an average mass fraction of approximately 0.001, which was near the limit of sensitivity for a particulate. Stoffel et al. (1994)30 and others identified a SIMS relative sensitivity factor (RSF) of approximately 2.9 for Pu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U from clay particles loaded with U and Pu on a carbon substrate, however, there may be a systematic offset due to uncertainty on the Pu
U from clay particles loaded with U and Pu on a carbon substrate, however, there may be a systematic offset due to uncertainty on the Pu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U assay amount per particle. In this paper we show that the RSF is closer to 2.0 to 2.1 on a Si substrate, with the acknowledgement that substrate and primary ion beam chemistry can affect the RSF values during particle analysis.9,15 Ranebo et al. (2010)31 created mixed U–Pu particles using an aerosol-based method and found a Pu
U assay amount per particle. In this paper we show that the RSF is closer to 2.0 to 2.1 on a Si substrate, with the acknowledgement that substrate and primary ion beam chemistry can affect the RSF values during particle analysis.9,15 Ranebo et al. (2010)31 created mixed U–Pu particles using an aerosol-based method and found a Pu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U RSF of approximately 2.3.31 However, their particles were deposited on carbon tape on a carbon planchet, which can result in large hydride backgrounds (UH+/U+ > 10−3) and other molecular interferences. Several other studies have been made on various mixed U–Pu particles produced at different institutions, but these are not generally widely available or certified at the level of rigor required for modern International Nuclear Safeguards applications, e.g.17,32,33
U RSF of approximately 2.3.31 However, their particles were deposited on carbon tape on a carbon planchet, which can result in large hydride backgrounds (UH+/U+ > 10−3) and other molecular interferences. Several other studies have been made on various mixed U–Pu particles produced at different institutions, but these are not generally widely available or certified at the level of rigor required for modern International Nuclear Safeguards applications, e.g.17,32,33
SRNL manufactured UPu-100A reference particles using the engineered aerosol-based production platform called THESEUS, for THermally Evaporated Spray for Engineered Uniform particulateS.29,34 While a full description is given in Foley et al. (2025),29 we briefly describe the process here. The THESEUS platform uses a monodisperse aerosol generator to make droplets out of the feedstock solution, followed by calcination with an inline heater, and deposition onto a substrate (the UPu-100A particles were electrostatically precipitated onto Si planchets). Online aerodynamic particle sizing (APS) provides in situ particle size information and a particle density estimate when compared to scanning electron microscopy (SEM) images of the deposited particles' size distribution. The production had a target nominal particle size of 1 μm with elemental and isotopic target values of: 238U/239Pu atomic ratio of 100, atomic concentration enrichment of 5% 235U, 236U concentration of 10 to 20 μmol mol−1 U, and a 240Pu/239Pu atomic ratio of 0.3. The UPu-100A feedstock was prepared by quantitative mixing in solution of New Brunswick Laboratory (NBL) uranium certified reference materials (CRMs) C112A, U970, and U930D and in-house SRNL plutonium stock materials Pu-239-79-2021 and Pu-240-98-2021. Particle morphologies and sizes were characterized by SEM and compared to APS measurements, indicating an approximate mean particle size of 1.08 μm and an approximate density of 6.0 g cm−3 (6.0 pg μm−3). Both feedstock and bulk particle elemental and isotopics compositions were measured using multicollector (MC)-ICP-MS (Table 1) and quadrupole (Q)-ICP-MS.
| Atomic concentration or ratio | Value | Uncertainty (k = 2) |
|---|---|---|
| a Pu aliquot contained 241Am. See Foley et al. (2025). | ||
| 234U/235U | 0.011877 | 0.000070 |
| 234U/238U | 0.0006201 | 0.0000030 |
| 235U/238U | 0.05221 | 0.00019 |
| 236U/238U | 0.00001972 | 0.00000017 |
| 238U/239Pu | 103.3 | 1.2 |
| (235U + 238U)/(239Pu + 240Pu) | 84.66 | 0.99 |
| 240Pu/239Pu | 0.28381 | 0.00095 |
| 241Pua/239Pu | 0.00447 | 0.00022 |
| 242Pu/239Pu | 0.00888 | 0.00014 |
| 234U (at. conc. U%) | 0.05889 | 0.00028 |
| 235U (at. conc. U%) | 4.959 | 0.017 |
| 236U (at. conc. U%) | 0.001873 | 0.000016 |
| 238U (at. conc. U%) | 94.980 | 0.017 |
| 239Pu (at. conc. Pu%) | 77.091 | 0.058 |
| 240Pu (at. conc. Pu%) | 21.880 | 0.057 |
| 241Pua (at. conc. Pu%) | 0.344 | 0.017 |
| 242Pu (at. conc. Pu%) | 0.685 | 0.011 |
The National Institute of Standards and Technology (NIST) conducts mass spectrometry metrology related to actinide particle reference materials and analytical method development.9,13–15,35–39 One of the primary characterization challenges for actinide particle analyses by SIMS is isobaric interferences from both molecules and peak tailing (abundance sensitivity), particularly when quantifying minor and trace isotope components. For mixed U–Pu particle analyses, the molecular isobaric interferences of 238U1H+ on 239Pu+ and 238U1H2+ and 239Pu1H+ on 240Pu+ are the greatest challenges. This problem can be especially acute if the U/Pu atomic ratio were much greater than about 10.40,41 Molecular hydride interferences are typically many orders of magnitude larger than the effects of peak tailing from a major isotope, such as 238U, which is on the order of 10−7 to 10−9 times the 238U intensity at mass-to-charge ratios, m/z, between 239 and 240, respectively. Peak tailing is always present, however, it may be corrected for using external measurements under identical instrument conditions. In contrast, the magnitude of molecular interferences varies, depending upon the substrate and sample compositions, including the U/Pu atomic ratio, the relative abundances of 239Pu and 240Pu, and the U isotope abundances. The mass resolving power (MRP, M/ΔM or peak width at 10% peak height) required to separate UH molecular isobars from U and Pu isotopes is very large (>37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and would result in insufficient ion transmission for atom-limited samples, such as micrometer-scale particles. For U-only particles, it is typical to correct the 235U1H+ molecular isobar on 236U+ by monitoring the atomic ratio of 238U1H+/238U+.13 However, for mixed U–Pu particles, the relative abundances of 235U and 236U may preclude this type of correction being used to infer the abundance of 238U1H+ interfering with 239Pu+. In addition, it is not well understood how similar the UH+/U+ and PuH+/Pu+ formation rates are from particles since there do not exist appropriate particulate reference materials for these measurements to be made easily. One potential solution to the hydride interference problem is the use of combined SIMS – accelerator mass spectrometer (AMS) instruments, such as the Notre Dame University (formerly US Naval Research Laboratory) NAUTILUS,41,42 which accelerates secondary ions from the SIMS through a stripping gas, dissociating molecular isobars. However, these instruments are not widespread or commercially available. Therefore, some internal corrections must be made based upon the evolution of different isotope signals, or the comparison of measurements of unknown samples with known reference materials (such as SRNL UPu-100A). However, there may be limits to the accuracy and precision of U–Pu isotopic and assay analyses by SIMS based upon the available substrate and composition of the sample. To date, TIMS has been the mainstay technique for mixed U–Pu analyses because of the inter-element selectivity achieved with the thermal ionization process.21–23,43 Different actinides evaporate and ionize at different filament temperatures, though there can be some overlap. Combined with a magnetic sector, these two processes allow for the discrimination of many isobars. As an additional benefit, hydride abundances are typically lower on TIMS than on SIMS, likely due to the filament heating driving off H. However, other molecular isobars can still cause interferences. Due to some elemental overlap in the thermal evaporation process, redeposition of neutrals, and other particle- and protocol-related effects, it can be challenging for TIMS to produce precise and accurate U/Pu assays on a per-particle basis, especially those with large U/Pu ratios. SIMS and TIMS could therefore be complementary when measuring similar particles from a known single source: TIMS can better resolve U and Pu isotopic ratios, which can then be used to estimate hydride interferences on SIMS to get a more accurate and precise U/Pu assay. In this study, we measured the well-characterized UPu-100A particles, treating them as unknowns, with the goal of making the most precise and accurate measurements using only the LG-SIMS before comparing them to bulk elemental and isotopic values.
000) and would result in insufficient ion transmission for atom-limited samples, such as micrometer-scale particles. For U-only particles, it is typical to correct the 235U1H+ molecular isobar on 236U+ by monitoring the atomic ratio of 238U1H+/238U+.13 However, for mixed U–Pu particles, the relative abundances of 235U and 236U may preclude this type of correction being used to infer the abundance of 238U1H+ interfering with 239Pu+. In addition, it is not well understood how similar the UH+/U+ and PuH+/Pu+ formation rates are from particles since there do not exist appropriate particulate reference materials for these measurements to be made easily. One potential solution to the hydride interference problem is the use of combined SIMS – accelerator mass spectrometer (AMS) instruments, such as the Notre Dame University (formerly US Naval Research Laboratory) NAUTILUS,41,42 which accelerates secondary ions from the SIMS through a stripping gas, dissociating molecular isobars. However, these instruments are not widespread or commercially available. Therefore, some internal corrections must be made based upon the evolution of different isotope signals, or the comparison of measurements of unknown samples with known reference materials (such as SRNL UPu-100A). However, there may be limits to the accuracy and precision of U–Pu isotopic and assay analyses by SIMS based upon the available substrate and composition of the sample. To date, TIMS has been the mainstay technique for mixed U–Pu analyses because of the inter-element selectivity achieved with the thermal ionization process.21–23,43 Different actinides evaporate and ionize at different filament temperatures, though there can be some overlap. Combined with a magnetic sector, these two processes allow for the discrimination of many isobars. As an additional benefit, hydride abundances are typically lower on TIMS than on SIMS, likely due to the filament heating driving off H. However, other molecular isobars can still cause interferences. Due to some elemental overlap in the thermal evaporation process, redeposition of neutrals, and other particle- and protocol-related effects, it can be challenging for TIMS to produce precise and accurate U/Pu assays on a per-particle basis, especially those with large U/Pu ratios. SIMS and TIMS could therefore be complementary when measuring similar particles from a known single source: TIMS can better resolve U and Pu isotopic ratios, which can then be used to estimate hydride interferences on SIMS to get a more accurate and precise U/Pu assay. In this study, we measured the well-characterized UPu-100A particles, treating them as unknowns, with the goal of making the most precise and accurate measurements using only the LG-SIMS before comparing them to bulk elemental and isotopic values.
Experimental
For particle characterization at NIST, we used both an AMETEK CAMECA IMS-1270E7 (upgraded to IMS-1280 equivalence) LG-SIMS and an AMETEK CAMECA IMS-1300 LG-SIMS (CAMECA Instruments, Inc., Fitchburg, WI, USA). Both instruments were equipped with Oregon Physics Hyperion-II RF plasma ion sources (Oregon Physics, Inc., Beaverton, OR, USA). We will refer to the instruments as the “1280” and the “1300” when the distinction is necessary. Qualitatively, the instruments are similar; however, there are a couple of differences that can have an impact on measurement protocols. On the 1280, the RF source (model H200), produces a much larger O3− beam intensity (>20×) than the RF source on the 1300 (model H201), though the underlying reason for this difference remains unknown. The higher O3− beam current make the 1280 source more suitable for using Köhler illumination during analysis.9 On the 1300, when we used O3−, we employed a focused primary beam that was rastered across the particle of interest. In contrast, the 1300 RF source produces >50% higher beam currents of O− and O2− than the RF source on the 1280. On the 1280, the multicollector (MC) slit size options are 150 μm, 250 μm, and 500 μm. On the 1300, the MC slit sizes are 250 μm, 350 μm, and 400 μm. The 250 μm slit is typically required for uranium particle age dating, though the narrowness of the slit can make it difficult to keep the MC detectors aligned when peak jumping the magnet between analyses for age dating and uranium isotopics.14,37,38 The 500 μm or 400 μm slits are suitable for the measurement of uranium isotopics alone, but they do not provide enough mass resolving power to discriminate some molecular interferences for 234U–230Th particle age dating. Unfortunately, the mechanical movement between selected slit sizes is not highly reproducible on the micrometer-scale, which causes misalignment of the apparent MC trolley positions. Therefore, it is not practical to switch between slit sizes for different types of measurements (e.g., age dating and uranium isotopics) during a measurement campaign since it would require MC realignment after each switch. The 1300 also utilizes a newer version of CAMECA's CIPS software (version R1.1.2 at the time of this writing), which allows for the control of additional Optional Instrument Parameters (OIP) relative to the 1280 that can be specified for each magnetic field during analysis. Some of these instrument parameters can be used to control the mass dispersion and spectrometer focusing properties, which allow for better alignment of the MC trolleys while peak hopping the magnet.In this study we used both LG-SIMS instruments to make isotopic and U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pu assay measurements of UPu-100A particles on Si planchets. Unless otherwise stated, all isotope concentrations and isotopes ratios are reported by atomic concentration, not mass concentration. Table 2 shows a summary of instrument analysis conditions. On the 1280, we measured particles using a 50 μm Köhler O3− primary beam (1 to 2 nA), peak hopping the single-collector to measure 234U+ (4 s count time per cycle), 235U+ (3 s), 236U+ (4 s), 238U+ (2 s), 239Pu+ (4 s), 240Pu+ (4 s), 241Pu+ (4 s), and 242Pu+ (4 s). The raw signals at m/z = 236, 239, 240, 241, and 242 contain both atomic and molecular hydride ions. We also used the MC on the 1280 to measure particles using either O− (4 nA) or O3− (2 nA) primary ions with the five electron multiplier (EM) detectors centered on L2: 235U+, L1: 238U+, C: 239Pu+, H1: 240Pu+, H2: 242Pu+, with cycles 12 s long. On the 1300, we measured the UPu-100A particles using a focused O3− (1 nA) primary ion beam rastered over a 25 μm square. However, due to a lower maximum ion current of O3− on the 1300, the spot size was relatively large (estimated between 15 μm and 20 μm), so the sputtered area of the planchet was larger than 25 μm and filled most of the field-apertured imaged area. We developed a MC protocol using the five detectors to measure most of the U and Pu isotopes at two magnetic fields using the 350 μm exit slit: B-field #1: L2: 234U+, L1: 235U+, C: 236U+, H1: 238U+, H2: 239Pu+; and B-field #2: L2: 238U+, L1: 239Pu+, C: 240Pu+, H1: 242Pu+, H2: 242Pu1H+, with 10 s cycle lengths each. We did not measure 241Pu here due to the isobaric interference of its decay product, 241Am, since Am and Pu have different relative sensitivity factors (RSFs), and we did not have a certified 241Pu
Pu assay measurements of UPu-100A particles on Si planchets. Unless otherwise stated, all isotope concentrations and isotopes ratios are reported by atomic concentration, not mass concentration. Table 2 shows a summary of instrument analysis conditions. On the 1280, we measured particles using a 50 μm Köhler O3− primary beam (1 to 2 nA), peak hopping the single-collector to measure 234U+ (4 s count time per cycle), 235U+ (3 s), 236U+ (4 s), 238U+ (2 s), 239Pu+ (4 s), 240Pu+ (4 s), 241Pu+ (4 s), and 242Pu+ (4 s). The raw signals at m/z = 236, 239, 240, 241, and 242 contain both atomic and molecular hydride ions. We also used the MC on the 1280 to measure particles using either O− (4 nA) or O3− (2 nA) primary ions with the five electron multiplier (EM) detectors centered on L2: 235U+, L1: 238U+, C: 239Pu+, H1: 240Pu+, H2: 242Pu+, with cycles 12 s long. On the 1300, we measured the UPu-100A particles using a focused O3− (1 nA) primary ion beam rastered over a 25 μm square. However, due to a lower maximum ion current of O3− on the 1300, the spot size was relatively large (estimated between 15 μm and 20 μm), so the sputtered area of the planchet was larger than 25 μm and filled most of the field-apertured imaged area. We developed a MC protocol using the five detectors to measure most of the U and Pu isotopes at two magnetic fields using the 350 μm exit slit: B-field #1: L2: 234U+, L1: 235U+, C: 236U+, H1: 238U+, H2: 239Pu+; and B-field #2: L2: 238U+, L1: 239Pu+, C: 240Pu+, H1: 242Pu+, H2: 242Pu1H+, with 10 s cycle lengths each. We did not measure 241Pu here due to the isobaric interference of its decay product, 241Am, since Am and Pu have different relative sensitivity factors (RSFs), and we did not have a certified 241Pu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241Am or Pu
241Am or Pu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Am standard. However, m/z ≈ 241 could be trivially added with a third magnetic field jump. We found that if we used trolley H1 as the axial detector for each B-field, respective OIP settings of DSP2 S1 = 1300 DAC bits (−188 V), HC1 Stig = −77 DAC bits (−28 V), and DSP2 S1 = 1520 DAC bits (−220 V), HC1 Stig = −82 DAC bits (−30 V) resulted in alignment of all of the MC detectors with minimal peak shape distortions. Using trolley C as the axial detector makes the alignment much more difficult due to the nature of the mass dispersion effects. Note, the CAMECA user manual states that a DSP2 S1 value of 1070 DAC bits corresponds to an increase in mass dispersion of 10%. The tuning modes “CIRC” and “XY” for the LG-SIMS refer to slight variations in the focusing of the stigmatic secondary ion beam. CIRC refers to the traditional tuning where the beam is both stigmatic and isotropic (magnification in the magnet's radial plane, X, and the transfer plane, Y, are identical). In the XY mode, aberrations can be reduced and transmission and MRP improved by increasing the transverse beam magnification. However, the XY mode can only be used with the axial single-collector EM detector; CIRC mode can be used with either the single-collector or MC detectors. For off-axis MC EMs, aberrations can result in tilt of the magnet focal plane, especially at large DSP2 S1 values, which can cause clipping of the ion beams when the XY tuning mode is used.
Am standard. However, m/z ≈ 241 could be trivially added with a third magnetic field jump. We found that if we used trolley H1 as the axial detector for each B-field, respective OIP settings of DSP2 S1 = 1300 DAC bits (−188 V), HC1 Stig = −77 DAC bits (−28 V), and DSP2 S1 = 1520 DAC bits (−220 V), HC1 Stig = −82 DAC bits (−30 V) resulted in alignment of all of the MC detectors with minimal peak shape distortions. Using trolley C as the axial detector makes the alignment much more difficult due to the nature of the mass dispersion effects. Note, the CAMECA user manual states that a DSP2 S1 value of 1070 DAC bits corresponds to an increase in mass dispersion of 10%. The tuning modes “CIRC” and “XY” for the LG-SIMS refer to slight variations in the focusing of the stigmatic secondary ion beam. CIRC refers to the traditional tuning where the beam is both stigmatic and isotropic (magnification in the magnet's radial plane, X, and the transfer plane, Y, are identical). In the XY mode, aberrations can be reduced and transmission and MRP improved by increasing the transverse beam magnification. However, the XY mode can only be used with the axial single-collector EM detector; CIRC mode can be used with either the single-collector or MC detectors. For off-axis MC EMs, aberrations can result in tilt of the magnet focal plane, especially at large DSP2 S1 values, which can cause clipping of the ion beams when the XY tuning mode is used.
| Parameter | 1280 monocollection (M/ΔM = 3500) | 1280 multicollection (M/ΔM = 3500) | 1300 multicollection (M/ΔM = 3000) |
|---|---|---|---|
| Köhler spot/raster size (μm) | 50 (Köhler) | 50 (Köhler) | 25 (raster) |
| Primary L4 aperture (μm) | 200 | ||
| Accelerating voltage (kV) | −13 | ||
| Sample voltage (kV) | +10 | ||
| Impact energy (keV) | 23 | ||
| Field of view | 50 μm × 50 μm | ||
| Entrance slit (μm) | 175 | 150 | 150 |
| Field aperture (μm) | 6000 | ||
| Contrast aperture (μm) | 400 | ||
| Energy slit (eV) | 50 | ||
| Exit slit (μm) | 250 | 250 | 350 |
| Tuning mode | XY | CIRC | CIRC |
| Axial detector | EM | C | H1|H1 |
| HC1 stig | 30 | −73 | −77|−82 |
| DSP2 S1 | 0 | 1500 | 1300|1520 |
| Detector(s) | EM | L2/L1/C/H1/H2 | L2/L1/C/H1/H2 |
| Detector dead time (ns) | 27.5 | 72.0/70.0/71.7/71.4/71.5 | 64.0/64.1/63.6/64.9/64.3 |
| Discriminator threshold (−mV) | 75 | 75/75/75/75/75 | 150/150/150/150/150 |
| Isotope species | 234U+, 235U+, 236U+, 238U+, 239Pu+, 240Pu+, 241Pu+, 242Pu+ | 235U+, 238U+, 239Pu+, 240Pu+, 242Pu+ | 234U+, 235U+, 236U+, 238U+, 239Pu+|238U+, 239Pu+, 240Pu+, 242Pu+, 242Pu1H+ |
| B-field wait time per cycle (s) | 2, 1, 1, 1, 1, 1, 1, 1 | 0 | 2|2 |
| B-field count time per cycle (s) | 4, 3, 4, 2, 4, 4, 4, 4 | 12 | 10|10 |
| Application | U, Pu isotopes | U, Pu profiling behavior | U, Pu isotopes |
For all measurements, NIST/NBL CRM U900 on Si was used for mass bias and MC yield balance corrections. Typically, we use the pulse height distributions (PHD) for each EM to set their high voltages for a target efficiency of approximately 92% at the desired discriminator threshold level. On the NIST 1280, the thresholds were set to −75 mV, where the minima of the differentiated PHDs were located at approximately −40 mV. This choice reduces the EM dark current, which is useful for particle radiochronometry.15 On the NIST 1300, however, the differentiated PHDs were broadened by approximately a factor of 2 relative to the 1280, which may indicate the presence of higher gain amplifiers in the pulse counting electronics. A discriminator threshold level of −75 mV on the 1300 resulted in higher levels of noise being counted relative to the 1280. Therefore, we selected thresholds of −150 mV on the 1300 and adjusted the EM voltages for efficiencies of approximately 92%. After this, the noise levels on both instruments were comparable, on the order of 0.001 counts per s. Subsequently on each instrument, 235U+ from CRM U900 was cyclically peak hopped onto each EM to make fine scale yield balance adjustments. Uranium isotope ratio measurements were made on CRM U900 using the B-field #1 setup. Additionally, 235U+ can be peak hopped onto the H1 detector, interleaved with the B-field #1 setup, in order to get an independent measurement of the mass bias using the 235U/238U ratio from the same detector.
Results and discussion
Hydride correction
For mixed U–Pu samples, there is no guarantee of a clean ion channel at one mass unit higher than a major isotope that can be monitored to infer the hydride signal during a measurement. The presence of intrinsic 236U complicates the measurement of 235U1H, 239Pu overlaps with 238U1H, and monitoring the mass-to-charge ratio m/z = 243 u (charge +1) for 242Pu1H is not typically viable due to the usually minor abundance of 242Pu and the potential presence of isobaric 243Am. There are several potential hydride corrections that could be made, such as by measuring the UH+/U+ ratio from pure U particles in a given session and extrapolating this factor to infer PuH+/Pu+ in unknown mixed U–Pu or pure Pu particles.44 However, it is unlikely that any single correction scheme will work ideally for all potential U–Pu compositions. This emphasizes the importance of having certified U–Pu reference materials from which the hydride signals can be deconvolved and potentially applied to unknown samples. However, for this study, we initially treated the UPu-100A particles as unknowns and developed a defensible correction without using the bulk reference values as a guide.Fig. 1 (left panel) shows the 238U1H+/238U+ ratios from measurements of CRM U900 on the 1300 used for mass bias correction. These measurements had minimal sputter cleaning done before analysis (only enough to locate and center on a particle). Therefore, the hydride signals were relatively high at the start of the measurements. The light grey traces show individual measurements, and the black dashed trace shows the Tukey biweight location and scale (robust mean and standard deviation) of the measurement traces. We found that the average characteristic behavior of these traces could be fit well using a least-squares algorithm by the sum of two exponential curves (individual exponentials shown in dark red, sum in red) of the form:
 | (1) |
 | (2) |
 | ||
| Fig. 1 (Left panel) Average hydride atomic ratios from CRM U900 can be characterized as the sum of two exponential curves (see eqn (1)). Individual exponentials shown as dashed dark red lines, sum as solid red line. Grey curves show measured hydride evolution for individual CRM U900 particles. (Right panel) Estimated hydride evolution in UPu-100A particles by fitting eqn (1) to the measured (235U1H + 236U)+/235U+ ratio. | ||
For the first version of the hydride correction (v.1), we found that fitting the (236U + 235U1H)+/235U+ ratio with the τi and Ai parameters fixed based on the U900 decay yielded reasonable results without adding too much variance to the corrected values. This method appeared defensible for analyzing an unknown sample set. Fig. 1 right panel shows the estimated hydride evolution from the UPu-100A particles using this exponential fit. For a second method (v.2) we allowed τ1 to vary within a ±100% range of its value from U900, in addition to the S and C free parameters. In this case, the correction tended to overestimate the hydride contribution on some particles, resulting in more variance in the corrected population. However, the ensemble of C values from the particle fits (intrinsic 236U/235U ratio) had an average value that more closely matched the true 236U/235U composition than in correction v.1. We therefore performed an iterative series of fits, the first to establish an ensemble C value that was then fixed as a constant (with uncertainty), after which S and τ1 were allowed to vary for each particle. Naturally, this method required a suite of particle measurements (assumed or known a priori to be from the same source), but it was successful in minimizing the variance induced by different hydride levels and behaviors between particles and planchets.
We considered other potential hydride corrections, such as using the evolution of the 239Pu+/238U+, 240Pu+/238U+, and/or 240Pu/239Pu ratios. However, the Pu+/U+ interelement ratios were affected by both the hydride evolution and sputter chemistry effects, which are described later. These combined to make it difficult to resolve the pure hydride contribution for each particle. Using the evolution of 240Pu/239Pu resulted in a more complicated hydride relationship that was not as robust in recovering the true UPu-100A composition. Fitting to the derivatives of several ratios was successful, but this method relied on assumptions regarding the initial or final hydride abundances upon solving the coupled set of differential equations for each particle. We therefore chose the correction method described above as straightforward and defensible methods that required minimal external input about each particle's hydride background. For these corrections, we assumed that the relative hydride formation rate for PuH+/Pu+ and UH+/U+ were equivalent. Other experiments with appropriate reference materials would be required to verify this assumption. We also assumed that the 238U1H2+ interference on 240Pu+ had an abundance that followed the square of the monohydride formation rate, i.e., that 238U1H2+/238U+ = (238U1H+/238U+).2 This correction for the UPu-100A particles is small, however, it may be more important for particles with U/Pu ratios >1000 and smaller 240Pu/239Pu ratios. This square relationship has been qualitatively observed on other samples, though it can be somewhat difficult to measure, and it remains unknown whether it holds over a wide range of hydride abundances. However, given the number of potential free parameters in the system, some assumptions were necessary to simplify the analysis. As a caveat, the corrections described here may not be as successfully applied to particles with larger 236U and lower 235U abundances, for example, since the hydride evolution would be masked by the underlying 236U signal earlier in the profile. In general, working to minimize the hydride background before measurement, such as by substrate selection and/or sample baking, will reduce the magnitude and complexity of corrections needed to recover the true isotopic composition.
Isotopic results
Isotopic analyses were performed by consuming approximately 90% of each particle. We measured 40 particles on the 1300 MC using O3− (two sessions of 20 particles two weeks apart), 17 on the 1280 single-collector using O3−, and 22 on the 1280 MC (11 each using O− and O3−). Fig. 2 shows the isotopic results from the 40 particles on the 1300 uncorrected for hydride interferences, which would predominantly affect the measurement of 236U, 239Pu, and 240Pu. The grey bands show the bulk MC-ICP-MS values (Table 1).29 The weighted arithmetic mean (WM) and 95% expanded uncertainty on the standard error (SE) of the weighted mean are also shown. The data weights, wi, are taken to be the inverse variances of each measurement, 1/σi2. The unbiased, expanded 95% uncertainty on the WM is calculated by multiplying the standard error of the weighted mean by the Student's t-value given the effective number of degrees of freedom (Neff) and by the square root of the mean squares of the weighted deviates statistic (MSWD, also known as the reduced chi-squared value).9,45,46 The effective degrees of freedom is calculated as: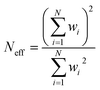 | (3) |
 | (4) |
The plots in Fig. 2 show highly consistent measurements using the two-B-field MC setup, with no discernible evidence for isotopic heterogeneity between particles. The ratios for isotopes unaffected by hydride interferences were in good agreement with the bulk isotopic values. After performing either hydride correction, the isotope ratios were all in good agreement (Fig. 3 and 4). The iterative nature of the v.2 correction resulted in a much tighter 236U/238U ratio estimate for the population and for individual particles. For the Pu isotope ratios, the two methods yielded nominal differences that were much smaller than the 1 SD uncertainties. However, without a true blind unknown sample, potentially with more challenging isotopic composition (e.g., more 236U and less 235U), it remains inconclusive as to which correction would perform better in more situations. Qualitatively from Fig. 3 and 4, we can conclude that both corrections were successful in removing a significant fraction of the hydride interference and recovering the true composition.
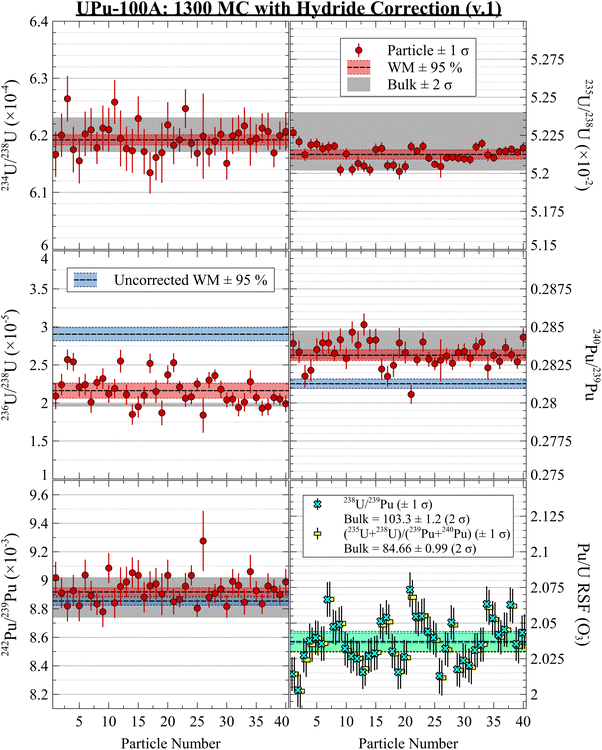 | ||
| Fig. 3 UPu-100A isotopic results using 1300 dual MC setup with hydride correction v.1. Uncorrected WM values shown in blue. | ||
 | ||
| Fig. 4 UPu-100A isotopic results using 1300 dual MC setup with hydride correction v.2 (iterative fit to 236U/235U). Uncorrected WM values shown in blue. | ||
Table 3 shows the isotope ratio WM and the unbiased weighted standard deviation (SD) for the set of 40 particles measured on the 1300.9,45 An Neff near 40 would indicate that all of the uncertainties were approximately equal, whereas a lower number would indicate that the weighted mean and its uncertainty were most dependent on fewer of the particle data. The Neff values for the ratios were between 32 and 33, indicating a high degree of consistency between the different ratio measurements. Variations in absolute uncertainty on individual measurements were likely driven by the number of integrated U and Pu counts per particle and were the primary reason for Neff < 40. The relative uncertainties for each isotope ratio were generally less than 1%, and down to 0.1% for 235U/238U. The exception was 236U/238U, which was highly influenced by variable hydride abundance spot-to-spot and could not be cleanly corrected given the presence of Pu in the sample. Comparing the 236U/235U ratios in the particles to the bulk 236U/235U ratio allowed us to estimate the hydride contribution for each particle analysis. On average, the particles on Si showed a UH+/U+ level of (1.8 ± 0.3) × 10−4 (1 SD), which was slightly higher than U900 particles on Si using O3− (although the latter were measured after significant pre-sputtering).35
| Method | Ratio | WM | ±1 SD | % unc | N eff | MSWD | ζ | ζ (RMS) |
|---|---|---|---|---|---|---|---|---|
| Uncorrected | 234U/238U (×10−4) | 6.192 | 0.025 | 0.41 | 32.4 | 0.57 | −0.31 | 3.38 |
| 235U/238U (×10−2) | 5.2124 | 0.0054 | 0.10 | 32.5 | 2.56 | −0.79 | ||
| 236U/238U (×10−5) | 2.904 | 0.135 | 4.65 | 32.6 | 3.22 | 6.89 | ||
| 240Pu/239Pu | 0.28126 | 0.00071 | 0.25 | 32.2 | 1.53 | −2.98 | ||
| 242Pu/239Pu (×10−3) | 8.855 | 0.081 | 0.91 | 32.1 | 0.87 | −0.24 | ||
| Corrected (v.1) | 234U/238U (×10−4) | 6.192 | 0.025 | 0.41 | 32.4 | 0.57 | −0.31 | 0.71 |
| 235U/238U (×10−2) | 5.2124 | 0.0054 | 0.10 | 32.5 | 2.56 | −0.79 | ||
| 236U/238U (×10−5) | 2.162 | 0.178 | 8.25 | 32.7 | 2.47 | 1.06 | ||
| 240Pu/239Pu | 0.28314 | 0.00080 | 0.28 | 32.4 | 1.57 | −0.72 | ||
| 242Pu/239Pu (×10−3) | 8.918 | 0.082 | 0.92 | 32.2 | 0.88 | 0.36 | ||
| Corrected (v.2) | 234U/238U (×10−4) | 6.192 | 0.025 | 0.41 | 32.4 | 0.57 | −0.31 | 0.78 |
| 235U/238U (×10−2) | 5.2124 | 0.0054 | 0.10 | 32.5 | 2.56 | −0.79 | ||
| 236U/238U (×10−5) | 2.057 | 0.061 | 2.99 | 32.6 | 0.75 | 1.37 | ||
| 240Pu/239Pu | 0.28339 | 0.00071 | 0.25 | 32.2 | 1.43 | −0.49 | ||
| 242Pu/239Pu (×10−3) | 8.927 | 0.079 | 0.89 | 32.2 | 0.83 | 0.44 |
The ζ score, which describes the relative deviation of a measurement from the reference value with respect to the combined measurement and reference uncertainty, is defined as:
 | (5) |
We calculated Pu/U RSF values for the corrected and uncorrected 1300 particle measurements by comparing the measured 238U+/239Pu+ and (235U + 238U)+/(239Pu + 240Pu)+ ratios to their bulk values (Table 4). The RSFs calculated from both bulk ratios showed near-identical agreement, although their uncertainties are also highly correlated. We found an average RSF value using O3− on Si of 2.036 ± 0.016 (1 SD). Based on the MSWD values for the measured 238U+/239Pu+ and (235U + 238U)+/(239Pu + 240Pu)+ ion ratios, we observed approximately 8× more scatter in the U/Pu contents than could be explained by counting statistics. However, the spread remained fairly small, with a weighted SD of only 0.75% relative. These results indicate a tight tolerance of U/Pu contents in each of the aerosol droplets. When we calculated the RSF from each particle and then their WM, the resulting MSWDs were close to one, indicating that the additional uncertainty from the bulk value explained nearly all of the excess variance in the particle data. When using the bulk ratios divided by the WMs of the particle ionic ratios, the calculated RSFs were 0.1% to 0.2% higher, which was well within the uncertainty of the RSFs shown in Table 4. The particle data weights were slightly different if the bulk uncertainty were propagated into each particle measurement before taking their WM. However, the resulting differences were effectively negligible. In either case, we demonstrated that the combination of spot-to-spot variation in the LG-SIMS measurements and the random sampling of the feedstock solution when producing particles yielded U/Pu variation on the order of less than 1% and that different statistical treatments did not introduce significant bias. In addition, the impact of potential Pu polymerization on the distribution of particle-level U/Pu ratios appears to be minimal, a further indicator of successful U–Pu feedstock preparation.48
| Method | 238U+/239Pu+ | ±1 SD | ±95% SE | MSWD | (235U+238U)+/(239Pu+240Pu)+ | ±1 SD | ±95% SE | MSWD |
|---|---|---|---|---|---|---|---|---|
| a Note: RSF uncertainties between methods and from different bulk ratios are highly correlated. | ||||||||
| Uncorrected | 50.27 | 0.39 | 1.17 | 70.38 | 41.28 | 0.31 | 1.01 | 84.02 |
| Corr. (v.1) | 50.63 | 0.38 | 1.09 | 64.62 | 41.52 | 0.30 | 0.95 | 77.91 |
| Corr. (v.2) | 50.68 | 0.37 | 1.07 | 62.97 | 41.55 | 0.30 | 0.94 | 76.65 |
| Method | RSF from 238U+/239Pu+ | ±1 SD | ±95% SE | MSWD | RSF from (235U + 238U)+/(239Pu + 240Pu)+ | ±1 SD | ±95% SE | MSWD |
|---|---|---|---|---|---|---|---|---|
| Uncorrected | 2.0515 | 0.0167 | 0.0074 | 1.90 | 2.0476 | 0.0162 | 0.0069 | 1.77 |
| Corr. (v.1) | 2.0371 | 0.0162 | 0.0070 | 1.80 | 2.0362 | 0.0157 | 0.0065 | 1.69 |
| Corr. (v.2) | 2.0352 | 0.0159 | 0.0067 | 1.74 | 2.0347 | 0.0155 | 0.0064 | 1.64 |
As a point of comparison, Fig. 5 shows deviations of LG-SIMS (1280 single-collector) isotope ratio measurements of CRM U900 particles from their certificate values. The 236U can be cleanly corrected since U900 is nearly pure U3O8, although it's uncertainty is larger than that of 234U, which only differs in concentration by approximately a factor of 2, due to the propagation of uncertainties from the hydride correction. Overall, the deviations from the certificate values were all much smaller than 1% relative, on average. The U900 particles tended to be much larger than the UPu-100A particles in this study, so the comparison should reflect extremely well on the quality and consistency of the UPu-100A particles as reference materials.
 | ||
| Fig. 5 LG-SIMS single-collector measurements of CRM U900 showing isotope ratio deviations from the certificate values. | ||
Fig. 6 shows single-collector measurements of the UPu-100A particles, with and without the same hydride corrections used above. Note: the peak centering on 235U was slightly misaligned for the first few particle measurements, so the 235U/238U ratios for these particles were omitted. Overall, the data were in good agreement with the bulk values, but the precision was lower than the MC measurements. For a single element, such as U, using the single-collector with count times appropriate to each isotope's abundance does not result in a dramatic loss of precision on materials like the NIST/NBL U-series CRMs. However, the additional measurement of Pu isotopes more than halved the duty cycle of each species, resulting in a noticeable decrease in precision compared to the MC results above. At the time of the measurements, the 241(Am + Pu)+/239Pu+ ratio appeared to be in agreement with the bulk value, which did not distinguish between 241Am and 241Pu. However, Am tends to ionize more easily than Pu (the RSF is greater than 1), so it is not surprising that the measured ratio was on the higher end of the bulk value. We did not perform any decay or RSF corrections to these values. The v.1 hydride correction, which worked well for the MC data, appeared to add increased variance to the corrected isotopes ratios, such as 236U/238U and 240Pu/239Pu, despite the use of time-interpolation. The iterative version of the hydride correction (v.2) appeared to overestimate the correction applied to the Pu isotope ratios, despite less fully correcting the measured 236U/238U ratio compared to the 1300 MC data. Overall, the MC version of the analysis protocol is highly superior to the single-collector version, improving the internal and external precisions and the efficacy of our hydride correction algorithm.
Surface and sputter chemistry
Substrate and primary beam chemistry can play an important role in actinide particle analysis. The substrate and primary beam species can affect the hydrogen background, useful yields, and RSFs.9,35 Both silicon and carbon planchets are commonly used in nuclear safeguards-related analyses, with the former resulting in much lower hydride backgrounds.13,35 Other substrates, such as Au, resulted in much lower useful yields.49 However, Si can be challenging to use for single-collector measurements when using an O− primary beam due to the phase and sputtering behavior change than occurs while profiling.9,15,36 Here, the UPu-100A particles were deposited on Si to reduce the hydride background. With the MC on the 1280 we compared the sputtering behavior of UPu-100A particles using both O− and O3−, which precludes the need to time-interpolate signals during the substrate phase change. Fig. 7 shows side-by-side characteristic profiles of the UPu-100A particles measured with a 4.5 nA O− beam (left) and a 2 nA O3− beam (right). The top panels show the instantaneous isotope signals, the middle panels show instantaneous isotope ratios, and the bottom panels show the integrated RSF value up to each cycle using the bulk (235U + 238U)/(239Pu + 240Pu) ratio of 84.66 ± 0.99 (k = 2) (note: since we did not measure 236U, we did not perform a hydride correction on these data). The most prominent features in the O− profiles were the initial transient from ion implantation (a byproduct of sputtering with a reactive ion beam) and the sharp drop in instantaneous yield at approximately cycle 25, where a phase shift occurred in the Si.9,36,50 The U and Pu signals did not decline by the same relative amount, as evidenced by the drop in the Pu+/U+ ratios shown in the middle panel. Of particular note was the relative profiling behavior of the U and Pu isotopes after approximately cycle 60. The elemental profiles began to diverge from parallel trajectories, with the U signals falling more rapidly than the Pu signals. This can be seen in the increasing Pu/U ratio after cycle 60 in the middle O− panel. The intra-elemental isotope ratios were otherwise uniform across the particle profiles (discounting small initial variations in the Pu isotope ratios due to the decay of the hydride background). The profiles using O3− also showed the initial transient sputtering behavior, however, the Pu/U ratios remained fairly constant for nearly the entire profile. The Pu/U ratios did not start to increase again until approximately cycle 190, at which point more than 98% of the particle had been consumed. Comparing these profiles highlights the importance of substrate and sputter chemistry on the interpretation of mixed actinide particle analyses. In the O− profiles, the varying Pu/U ratios throughout might be misinterpreted to be due to intraparticle heterogeneity. However, by using O3−, the particles appeared to be elementally and isotopically homogeneous to within the limits of the spatial resolution employed here.The lower panels of Fig. 7 show the sputter chemistry and substrate effects on the inferred Pu/U RSF from each particle profile. The statistical uncertainties on the RSF SEs were expanded to ±95% by taking into account the amount of preceding variation in the Pu/U ratios (applying a factor of √MSWD and the Student's t-value). For the O− profile, the Pu/U ratios were never constant, so the integrated RSF value varied throughout the profile and the corresponding uncertainty was larger. In contrast, the integrated RSF for O3− showed initial variation before plateauing less than halfway through the full consumption of the particle (note: these RSF values were not hydride-corrected). We have shown previously that consuming most of a particle would result in the most consistent inter-element actinide particle analyses, such as U–Th.14,15 However, for the U–Pu system, the resulting RSF from the reference material and inferred U–Pu composition of an unknown using O− (at least on Si) would be highly sensitive to the amount of each particle consumed. This would introduce extra variance into the U/Pu assay amount, especially for particles with a wider range of sizes where consistently consuming the same fraction of each particle would be challenging.
For the 1280 MC data, we did not perform a hydride correction because we did not measure 236U. Without a hydride correction, the apparent RSFs on Si were 2.080 ± 0.020 (95% SE; or ±0.024 1 SD) for O− and 1.977 ± 0.019 (95% SE; or ± 0.034 1 SD) for O3−. If we scale the uncorrected O3− RSF to match the average corrected 1300 MC value of 2.036 ± 0.016 (1 SD), it would imply a corrected O− RSF of 2.142 ± 0.034 (1 SD). This value generally agrees with the RSF value of 2.241 ± 0.063 (k = 2) from Foley et al. (2025)29 with an absolute ζ score of 1.40. Interestingly, the relative difference in Pu/U RSF between O− and O3− on Si was approximately 5%, which was much smaller than the difference observed for Th/U on Si, where the O− RSF was approximately 26% larger than O3−.9 In contrast, the O− and O3− Th/U RSFs on C were identical, within uncertainties. Future work could explore surface and sputter chemistry effects on other actinides and substrates, including their relative and absolute useful yields.
Approximate useful yield
Using the average size (1.07 μm ± 0.27 μm, 1 SD) and estimated density (6.0 g cm−3) of the particles, we attempted to estimate the useful yields of U and Pu ions in the LG-SIMS with the measurement conditions shown in Table 2. There was no uncertainty given with the density estimate, and it's plausible that on a per-particle basis density, porosity, and size would be correlated. If the size uncertainty were propagated into particle volume and mass, the average mass estimate per particle would be 3.8 pg ± 2.9 pg (1 SD), with a relative uncertainty of 76% (the uncertainty expands rapidly due to the volume's cubic dependence on size). However, we observed a relative standard deviation of approximately 42% for both the total U counts and total Pu counts per particle from LG-SIMS measurements. Using a mean particle mass of 3.8 pg of U3O8 with a 42% relative uncertainty and a U/Pu ratio of 84.66, we calculated the approximate U and Pu useful yields for each particle. These resulted in estimated average useful yields of 6.2% ± 2.6% for U and 12.6% ± 5.3% for Pu. The distribution of observed particle sizes may have included some doublet particles.29 These useful yield values were not highly precise, but they agreed with previous findings for the yield of U using O3− (ref. 9) and with the more precise RSF measurements made here.Conclusions
The development and characterization of actinide particle reference materials remains an important need for International Nuclear Safeguards.5–7 In particular, mixed actinide systems, such as U–Pu and U–Th, have unique analytical challenges that can be best addressed using elementally and isotopically homogeneous particles of specific tailored compositions. In this study, we demonstrated that internal corrections can be made on mixed U–Pu microparticle measurements by LG-SIMS to mitigate the effects of hydride interferences on 236U, 239Pu, and 240Pu. We developed a new MC protocol that allowed for the analysis of most U and Pu isotopes of interest, and which could be modified to include other isotopes, as needed. Combining these two developments allowed us to achieve highly accurate and precise analyses of the SRNL UPu-100A U–Pu microparticles.29 Our measurements were in excellent agreement with bulk MC-ICP-MS values, and in most cases showed comparable particle-to-particle reproducibility to the certificate reference uncertainties. Isotopically, UPu-100A showed comparable precision particle-to-particle as CRM U900, despite lower mass-per-particle, on average. Depending on the hydride correction method used, the RMS ζ scores for all displayed isotope ratios were 0.71 (correction v.1) and 0.78 (correction v.2), while the maximum ζ score for each set was from the 236U/238U ratio, with values of 1.06 (v.1) and 1.37 (v.2). We demonstrated the effects of sputtering and substrate chemistry on the U–Pu system and showed how these surface chemical effects could be misinterpreted as resulting from particle heterogeneity. The UPu-100A particles were not monodisperse enough to be used for precise useful yield evaluation, however, the estimated U+ and Pu+ yields agreed with previous measurements. Using O3−, we estimated a highly precise Pu/U RSF of 2.036 ± 0.016 (1 SD, less than 1% relative uncertainty) for particles on Si, which can be used to perform U/Pu assay measurements on unknown particle samples. The highly reproducible particle-to-particle results indicate that effectiveness of the analytical protocol and the quality of the feedstock and particle preparation. Interestingly, the estimated RSF for analysis with O− primary ions was only about 5% higher, 2.142 ± 0.034 (1 SD), which contrasts with a larger difference in Th/U RSF observed on Si.9 We conclude that the UPu-100A particles are both elementally and isotopically homogeneous to within the combined analytical precision of bulk and microparticle mass spectrometry techniques. These are high-quality particle reference materials and are suitable for both QA/QC and R&D applications.Disclaimer
Certain commercial equipment, instruments, software, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identifications are not intended to imply recommendation or endorsement by NIST, nor it is intended to imply that the materials or equipment identified are necessarily the best available for the purpose. This is an Official contribution of the National Institute of Standards and Technology; not subject to copyright in the United States.Data availability
The data supporting this article have been included as part of the ESI.† Data for this article, including spreadsheets, are also available at https://doi.org/10.18434/mds2-3693.Author contributions
EEG: wrote paper, developed methods, collected data, wrote software, performed analyses. TLW: developed methods, collected data, performed analyses. KMS, SMS, BJF, MGB, GSK, WSM: made and bulk-characterized UPu-100A particles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding for development and production of the UPu-100A mixed U–Pu microparticles was provided by the Office of International Nuclear Safeguards (NA-241) of the Department of Energy National Nuclear Security Administration. This work was produced in conjunction with Battelle Savannah River Alliance, LLC under Contract No. 89303321CEM000080 with the U.S. Department of Energy. We thank Travis Tenner (LANL), Ben Naes (LANL), and David Simons (MELE Associates) for helpful discussions. We thank the NIST Editorial Review Board and anonymous external reviewers for their reviews.References
- A. Axelsson, D. M. Fischer and M. V. Peńkin, J. Radioanal. Nucl. Chem., 2009, 282, 725–729 CrossRef CAS.
- D. L. Donohue, J. Alloys Compd., 1998, 271, 11–18 CrossRef.
- D. L. Donohue and R. Zeisler, Anal. Chem., 2012, 65, 359A–368A CrossRef.
- M. J. Kristo, in Handbook of Radioactivity Analysis, ed. M. F. L'Annunziata, Academic Press, 4th edn, 2020, vol. 2, pp. 921–951, doi: DOI:10.1016/B978-0-12-814395-7.00013-1.
- Research and Development Plan: Enhancing Capabilities for Nuclear Verification, Report STR-385, IAEA Safeguards, Vienna, Austria, 2018 Search PubMed.
- Enhancing Capabilities for Nuclear Verification: Resource Mobilization Priorities, Report STR-399, IAEA Safeguards, Vienna, Austria, 2022 Search PubMed.
- Development and Implementation Support Programme for Nuclear Verification 2024–2025, Report STR-405, IAEA Safeguards, Vienna, Austria, 2024 Search PubMed.
- S. Boulyga, S. Konegger-Kappel, S. Richter and L. Sangély, J. Anal. At. Spectrom., 2015, 30, 1469–1489 RSC.
- E. E. Groopman, T. L. Williamson and D. S. Simons, J. Anal. At. Spectrom., 2022, 37, 2089–2102 RSC.
- P. M. L. Hedberg, P. Peres, F. Fernandes, N. Albert and C. Vincent, J. Vac. Sci. Technol. B, 2018, 36, 03F108 CrossRef.
- P. M. L. Hedberg, P. Peres, F. Fernandes and L. Renaud, J. Anal. At. Spectrom., 2015, 30, 2516–2524 RSC.
- Y. Ranebo, P. Hedberg, M. Whitehouse, K. Ingeneri and S. Littmann, J. Anal. At. Spectrom., 2009, 24, 277–287 RSC.
- D. S. Simons and J. D. Fassett, J. Anal. At. Spectrom., 2017, 32, 393–401 RSC.
- C. Szakal, D. S. Simons, J. D. Fassett and A. J. Fahey, Analyst, 2019, 144, 4219–4232 RSC.
- E. E. Groopman, T. L. Williamson, T. R. Pope, M. Bronikowski, S. M. Scott and M. Wellons, Analyst, 2025 10.1039/D5AN00249D.
- E. L. Callis and R. M. Abernathey, Int. J. Mass Spectrom. Ion Processes, 1991, 103, 93–105 CrossRef CAS.
- D. Suzuki, F. Esaka, Y. Miyamoto and M. Magara, Appl. Radiat. Isot., 2015, 96, 52–56 CrossRef CAS PubMed.
- M. Kraiem, S. Richter, H. Kühn and Y. Aregbe, Anal. Chim. Acta, 2011, 688, 1–7 CrossRef CAS PubMed.
- S. Richter and S. A. Goldberg, Int. J. Mass Spectrom., 2003, 229, 181–197 CrossRef CAS.
- S. Richter, H. Kühn, Y. Aregbe, M. Hedberg, J. Horta-Domenech, K. Mayer, E. Zuleger, S. Bürger, S. Boulyga, A. Köpf, J. Poths and K. Mathew, J. Anal. At. Spectrom., 2011, 26, 550–564 RSC.
- R. Jakopič, S. Richter, H. Kühn, L. Benedik, B. Pihlar and Y. Aregbe, Int. J. Mass Spectrom., 2009, 279, 87–92 CrossRef.
- F. Esaka, K. Yasuda, D. Suzuki, Y. Miyamoto and M. Magara, Talanta, 2017, 165, 122–127 CrossRef CAS PubMed.
- J. D. Inglis, J. Maassen, A. Kara, R. E. Steiner, W. S. Kinman and D. Lopez, J. Radioanal. Nucl. Chem., 2017, 312, 663–673 CrossRef CAS.
- B. T. Manard, C. D. Quarles Jr, V. C. Bradley, T. L. Spano, N. A. Zirakparvar, B. W. Ticknor, D. R. Dunlap, P. Cable-Dunlap, C. R. Hexel and H. B. Andrews, J. Am. Chem. Soc., 2024, 146, 14856–14863 CrossRef CAS PubMed.
- J. Wimpenny, K. M. Samperton, P. Sotorrio, M. S. Wellons, S. M. Scott, D. Willingham and K. Knight, J. Anal. At. Spectrom., 2023, 38, 827–840 RSC.
- M. R. Savina, D. Z. Shulaker, B. H. Isselhardt and G. A. Brennecka, J. Anal. At. Spectrom., 2023, 38, 1205–1212 RSC.
- M. R. Savina, R. Trappitsch, A. Kucher and B. H. Isselhardt, Anal. Chem., 2018, 90, 10551–10558 CrossRef CAS PubMed.
- F. Meisenkothen, M. McLean, I. Kalish, D. V. Samarov and E. B. Steel, Anal. Chem., 2020, 92, 11388–11395 CrossRef CAS PubMed.
- B. J. Foley, S. M. Scott, M. G. Bronikowski, W. W. Kuhne, K. M. Samperton, A. R. Swindle, G. S. King, T. C. Shehee, J. H. Christian, B. E. Naes, T. J. Tenner and M. S. Wellons, J. Anal. At. Spectrom., 2025 10.1039/d5ja00114e.
- J. J. Stoffel, J. K. Briant and D. S. Simons, J. Am. Soc. Mass Spectrom., 1994, 5, 852–858 CrossRef CAS PubMed.
- Y. Ranebo, N. Niagolova, N. Erdmann, M. Eriksson, G. Tamborini and M. Betti, Anal. Chem., 2010, 82, 4055–4062 CrossRef CAS PubMed.
- C.-G. Lee, D. Suzuki, Y. Saito-Kokubu, F. Esaka, M. Magara and T. Kimura, Int. J. Mass Spectrom., 2012, 314, 57–62 CrossRef CAS.
- K. Raptis, G. Duhamel, R. Ludwig, S. Balsley, S. Bürger, V. Mayorov, A. Koepf, S. Hara, Y. Itoh, K. Yamaguchi, T. Yamaguchi and J. Ninagawa, J. Radioanal. Nucl. Chem., 2012, 296, 585–592 CrossRef.
- B. E. Naes, S. Scott, A. Waldron, S. Lawson, M. G. Bronikowski, L. I. Gleaton, R. J. Smith, K. N. Wurth, T. J. Tenner and M. Wellons, Analyst, 2023, 148, 3226–3238 RSC.
- E. E. Groopman, T. L. Williamson and D. S. Simons, Recent Advances in Uranium Particle Analyses by LG-SIMS, in Proceedings of the INMM & ESARDA Joint Annual Meeting, Vienna, Austria, 2023 Search PubMed.
- N. Sharp, J. D. Fassett and D. S. Simons, J. Vac. Sci. Technol., B:Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2016, 34, 03H115 Search PubMed.
- T. Williamson, E. Groopman and D. Simons, Dual Chronometer Measurements of Uranium Particles by LG-SIMS, in Proceedings of the INMM & ESARDA Joint Annual Meeting, Vienna, Austria, May 22–26, 2023 Search PubMed.
- T. L. Williamson, D. S. Simons and J. D. Fassett, Multi-Collector Configuration Considerations And Substrate Relative Sensitivity Factor Effects for Age-dating Measurements of Particles by Large Geometry Secondary Ion Mass Spectrometry, in Proceedings of the INMM & ESARDA Joint Virtual Annual Meeting, 2021 Search PubMed.
- A. J. Fahey, N. W. M. Ritchie, D. E. Newbury and J. A. Small, J. Radioanal. Nucl. Chem., 2010, 284, 575–581 CrossRef CAS.
- M. Aleshin, T. Tanpraphan, O. Bildstein, L. Sangely, U. Repinc, A. Bosko, J. Poths, S. Vogt and Y. Kuno, Isotopic Analysis of UPu Mixed Particles Using Large-Geometry Secondary Ion Mass Spectrometer (LG-SIMS), Vienna, 2018 Search PubMed.
- D. Willingham, E. Groopman and L. Sangely, J. Am. Soc. Mass Spectrom., 2020, 31(8), 1647–1655 CrossRef CAS PubMed.
- E. E. Groopman, D. G. Willingham, A. J. Fahey and K. S. Grabowski, J. Anal. At. Spectrom., 2020, 35, 600–625 RSC.
- J. Maassen, J. D. Inglis, A. Wende, T. M. Kayzar-Boggs, R. E. Steiner and A. Kara, J. Radioanal. Nucl. Chem., 2019, 321, 1073–1080 CrossRef CAS.
- A. Diacre, A. L. Faure, M. Cornaton, F. Pointurier and O. Evrard, Talanta, 2023, 252, 123848 CrossRef CAS PubMed.
- J. Kirchner, Weighted Averages and Their Uncertainties, http://seismo.berkeley.edu/%7Ekirchner/toolkits.html, 2006 Search PubMed.
- K. Ludwig, Berkley Geochronological Centre, Special Publication, 2012 Search PubMed.
- I. Wendt and C. Carl, Chem. Geol., 1991, 86, 275–285 Search PubMed.
- V. L. Schuelein, Parameters for Plutonium Polymer Formation in Nitric Acid, United States, 1975 Search PubMed.
- A. J. Fahey, Work performed at the National Institute of Standards and Technology, 2011.
- K. Wittmaack, Surf. Interface Anal., 1996, 24, 389–398 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary data spreadsheet. See DOI: https://doi.org/10.1039/d5ja00115c |
| This journal is © The Royal Society of Chemistry 2025 |



