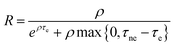Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A throughput model explaining non-linearity in discrete ion counters used in mass spectrometry
Stefaan
Pommé
 *a and
Sergei F.
Boulyga
b
*a and
Sergei F.
Boulyga
b
aEuropean Commission, Joint Research Centre (JRC), Geel, Belgium. E-mail: stefaan.pomme@ec.europa.eu; Tel: +32 (0)14 571 289
bInternational Atomic Energy Agency (IAEA), Vienna, Austria
First published on 25th June 2025
Abstract
A mathematical model is presented to calculate the expected throughput rate in a discrete ion counter with imposed non-extending dead time. The count loss mechanism consists of a combined effect of the imposed dead time, interfered with pulse pileup owing to the finite time resolution of the electronic pulses generated in the ion counter. This model may be applicable to mass spectrometers making use of discrete ion counters, thus providing a means to reproduce counting-rate dependency of observed atomic abundance ratios.
Introduction
Mass spectrometry is a powerful analytical technique that is used to identify and quantify atoms or molecules based on their mass-to-charge ratio.1 The atomic abundance ratio within a sample can be derived either from a current ratio, acquired through an ion beam impacting a Faraday cup, or from a count ratio measured by a discrete ion counter, such as an electron multiplier (Secondary Electron Multipliers (SEM), Channel Electron Multipliers (CEM), Microchannel Plates (MCP)) or a photomultiplier (Daly detector). The perfect ion detector would be linear with no electronic noise and constant yield. Overall, the linearity of current measurement in a Faraday cup is typically more straightforward compared to the counting process in a discrete ion counter, which is susceptible to count loss resulting from pulse pileup and dead time. The advantage of the electron multiplier in pulse counting mode is the extremely low electronic baseline (referred to as ‘dark noise’, typically less than 1 s−1), allowing quantification of low-current ion beams (<10−18 A).1The linearity of the ion counter can be assessed experimentally by measuring reference materials with certified relative isotopic abundances across various beam intensities.2–7 As the count rate escalates, a correction is needed for dead time, during which the electronic system cannot register subsequent pulses. A significant dead-time component is the non-extending dead time electronically imposed on the pulse amplifier, factory-set and typically lasting a few tens of nanoseconds.6,7 At high input rates, the dead-time effect on measured isotope ratios becomes more apparent due to the increased probability of quasi-coincident ion impacts. While a straightforward live-time correction formula can mitigate count loss over a broad range of input rates, experiments indicate that this approach may falter at exceptionally high input rates.3,5,6,8–10
High ion input rates can be produced, for instance, by single nanoparticles or by ablated aerosol particles in inductively coupled plasma mass spectrometry (ICPMS). Hirata et al.8 pointed out that event rates obtained from large particles can exceed 107 s−1, leading to incomplete count-loss correction and resulting in erroneous elemental or isotopic ratios. Recently, several research groups have reported developments of high time-resolution data acquisition systems for recording transient signals from nanoparticles by using quadrupole ICPMS9,11,12 and by MC-ICPMS.8,13,14 Strenge and Engelhard9 observed that dead-time-related count losses are the main cause of nonlinearity in millisecond and microsecond time-resolved single-particle ICPMS of microdroplets and nano-particles. They cautioned that traditional dead-time correction methods may yield slightly distorted results. Duffin et al.10 identified pulse pileup as a significant challenge in measuring rapid transient signals from nanoparticles.
This paper presents a more advanced throughput formula aimed at facilitating dead-time correction over a wide range of beam intensities. It is based on a cascade model of extending and non-extending dead time, drawing upon mathematical models established in the realm of radionuclide metrology15–19 and fast photon counting.20 Implementation of this improved model has the potential to improve our understanding of non-linearity in mass spectrometry and enhance the attainable accuracy in critical applications involving particle analysis, such as nuclear safeguards21,22 and climate research.23,24
Throughput model
The concepts of pulse pileup, extending dead time (EDT), and non-extending dead time (NEDT) are well-established in the literature of nuclear counting, with their effects on counter throughput extensively documented.16–18,20,25–40 It can be argued that theories developed for radioactivity measurements are equally applicable to ion counting in mass spectrometry. A fundamental requirement is that the input process is a “stationary Poisson process”. This implies that a measurement is conducted over a period in which the input rate ρ of events (ions impacting the sensitive area of the ion counter) remains constant, and the time-interval distribution between successive events is exponentially distributed. This means that ions arrive randomly in time, independently of each other.It is assumed that the pulses generated in the detector have a characteristic width, τe, that is relatively consistent. When two coincident pulses merge into a single sum pulse, it results in the loss of the second signal and an extension of the dead-time period, as depicted in Fig. 1. This pileup process, in the absence of a pileup rejection mechanism, can be classified as EDT, with the associated throughput formula following an exponential rate-dependency:16,17
| R = ρe−ρτe | (1) |
On the other hand, the primary source of dead time is assumed to be the factory-set NEDT of duration τne imposed on ‘detected’ events from the pulse amplifier. This dead time is triggered when the leading edge of a pulse surpasses the discriminator threshold set well above the electronic noise level. Any subsequent pulse arriving within the NEDT is not counted and, ideally, should have no effect on the duration of the dead time. The throughput formula for a purely NEDT-based counter is:16,17
 | (2) |
Mathematically, this process can be modelled as a Poisson process passing through a sequential cascade of EDT and NEDT.16–18,20,25,26,36 A mathematical solution exists for the time-interval distribution of counted events, the expected throughput rate, and the variance of counts over a fixed time interval.16–18 The throughput formula for such system is:
 | (3) |
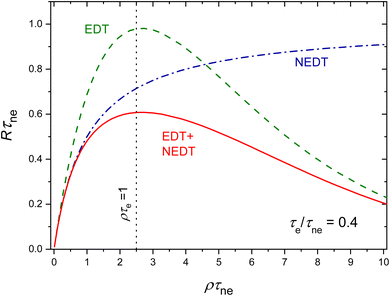
The eqn (3) simplifies to an exponential function as seen in eqn (1) when τne ≤ τe (EDT), and approaches the shape of eqn (2) when τe ≪ τne (NEDT). The relative importance of the two terms in the denominator varies with the input rate ρ. The system primarily follows NEDT behaviour at low count rates, while the exponential term from EDT becomes more significant at higher input rates. Fig. 3 shows a typical throughput curve calculated from eqn (3), comparing it with the models for EDT (eqn (1)) and NEDT (eqn (2)). Fig. 4 shows a similar graph on a semi-logarithmic scale, highlighting the transition from NEDT behaviour towards EDT. The count rate R reaches its maximum at ρτe = 1, where the first derivative of eqn (3) equals zero:
 | (4) |
In the obvious case where the imposed non-extending dead time purposely exceeds the pulse width (τne > τe), the output rate in the ion counter can be approximated by the following series expansion:
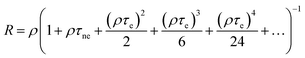 | (5) |
For small input rates (ρτe ≪ 1), the linear term 1 + ρτne dominates, and the throughput formula closely follows that of a NEDT counter (eqn (2)). However, at high input rates (ρτe > 1), significant deviations arise due to the higher-order terms of ρτe. Fig. 5 illustrates the ratio between the expected output rate R for τe/τne = 0.4 (eqn (3)) and that of a purely NEDT counter with the same τne value, but τe = 0 (eqn (2)).
 | ||
| Fig. 5 Ratio of the throughput formula for an EDT-NEDT cascade (eqn (3), for τe/τne = 0.4) to that of a purely NEDT counter (eqn (2)), presented on a semi-logarithmic scale. The curve highlights the growing fraction of counts lost due to pulse pileup. | ||
Inverse throughput
When observing a count rate R, inversion of the throughput formula is required to calculate a best estimate![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) of the original input rate. In the case of NEDT, inversion of eqn (2) is easily achieved:16
of the original input rate. In the case of NEDT, inversion of eqn (2) is easily achieved:16 | (6) |
Eqn (6) is commonly used in mass spectrometry to compensate for the main count loss component due to NEDT.
The case of EDT is less straightforward; the recursive relationship16
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) < = Re < = Re![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) τe τe | (7) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) < ≤ 1/τe, using, for example, as a first approximation:
< ≤ 1/τe, using, for example, as a first approximation: | (8) |
Another convenient approach for EDT is to use a series expansion:17
 | (9) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) < ≤ 1/τe. Since the throughput curve takes the shape of an asymmetric bell (Fig. 3), for each R value there are two solutions: one for ρτe ≤ 1 and a second for ρτe ≥ 1. The following series expansion is designed to obtain both solutions,
< ≤ 1/τe. Since the throughput curve takes the shape of an asymmetric bell (Fig. 3), for each R value there are two solutions: one for ρτe ≤ 1 and a second for ρτe ≥ 1. The following series expansion is designed to obtain both solutions, ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) < and
< and ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) >, by changing the sign in the formula:17,28
>, by changing the sign in the formula:17,28 | (10) |
 and some numerical values of the coefficients cj are provided in Refs. 17 and 28. To achieve the required precision, one can use the first values (c0 = 1, c1 = −1/3, c2 = 1/36, c3 = 1/270, c4 = 1/4320) as a starting point in eqn (10), and then continue with a Newton–Raphson iteration:
and some numerical values of the coefficients cj are provided in Refs. 17 and 28. To achieve the required precision, one can use the first values (c0 = 1, c1 = −1/3, c2 = 1/36, c3 = 1/270, c4 = 1/4320) as a starting point in eqn (10), and then continue with a Newton–Raphson iteration: | (11) |
Of particular interest to mass spectrometry is the inverse of the throughput formula in eqn (3), which relates to EDT and NEDT in series. This can be solved iteratively through the following recursion formula:16,18
 | (12) |
At moderate input rates (ρτe ≤ 1), eqn (6) can be applied as a first approximation for ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) on the right-hand side of eqn (12), with an accurate result typically obtained after 1 to 3 iterations.
on the right-hand side of eqn (12), with an accurate result typically obtained after 1 to 3 iterations.
Since the throughput curve in Fig. 3 passes through a maximum, there are two possible solutions to the inversion of eqn (3): one for ρτe ≤ 1 and another for ρτe ≥ 1. Some elaborate inversion formulas have been derived by Libert.29 In this work, a Newton–Raphson iteration method is proposed to find the solutions:
 | (13) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) τe +
τe + ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (τne−τe) and the starting value for the second solution (
(τne−τe) and the starting value for the second solution (![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ≫ 1/τe) is inspired by a series expansion of the Lambert W function:
≫ 1/τe) is inspired by a series expansion of the Lambert W function: | (14) |
Convergence is typically achieved in a few iterations. Eqn (13) is also applicable at low count rates, where eqn (6) can be used for the starting value. The most challenging region lies near the maximum of the throughput curve, where the derivative approaches zero.
Pulse width and dead time
Best estimates of the pulse width and dead time can be obtained by conducting a linearity test at different input rates and using a least squares fitting procedure to identify the parameter values that optimally restore linearity.An additional test can be considered by comparing two measurements with the same input rate, but different values of the NEDT: measurement 1 with the NEDT shorter than the pulse width, τne < τe, and measurement 2 with a longer NEDT, τne > τe. The first measurement is equivalent to an EDT counter with exponential throughput (eqn (1)), 1/R1 = ρ−1eρτe, whereas the second has an EDT-NEDT throughput (eqn (3)), 1/R2 = ρ−1eρτe + (τne − τe). Then a simple relationship holds between the dead-time values and the inverse count rates:
 | (15) |
If τne > τe in both measurements, one obtains the difference between the NEDT values:
 | (16) |
Live-time counting
There are more effective alternatives for compensating rate-related count loss than inverting the throughput curve. The simplest method of dead-time correction is “live-time counting”, which uses a live-time clock, where an accurately timed pulse train (“virtual pulser”) is counted only during the time intervals when the measuring system is free to accept or record events.16,17 In this particular case, the dead-time region corresponds to a logical OR of the imposed NEDT and the pulse widths of all events, both “valid” and “invalid”. A schematic representation is shown in Fig. 6.The live-time technique works effectively in a steady regime, for a so-called “stationary Poisson process”. The input rate can be calculated from the output rate by correcting with the ratio of real time (TR = TL + TD) to live time (TL):
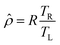 | (17) |
Implementing this technique in mass spectrometry could resolve the dead-time issues to a satisfactory level, particularly when the input rate remains constant. In radionuclide metrology, additional measures are taken to correct for correlation effects between input rate and dead time, which mostly affect short-lived nuclides compared to long-lived ones. These corrections include formulas,16,17,40 “loss-free counting” techniques41–46 to manage rapidly varying dead times, and pileup-rejection mechanisms to avoid sum pulses that distort the energy spectrum.38,39,47 Some of these measures may also be of interest to mass spectrometry, especially when analysing transient signals.
Uncertainty
The distribution of the number of events N recorded during a fixed-real-time measurement generally exhibits underdispersion relative to a Poisson process, resulting in a smaller standard deviation than the square root of N:16,18 | (18) |
However, the variation in the dead-time corrected number of counts, Nc, is always overdispersed.16 The degree of overdispersion depends on the method used to compensate for dead time. The most accurate method involves a live-time counting technique, assuming a sufficiently long measurement time to accurately establish the correction factor TR/TL. The resulting relative uncertainty in the dead-time corrected number of counts is then (at least):
 | (19) |
In the less favourable case where no live-time information is available, the dead-time corrected counts must be calculated by inverting the throughput formula (eqn (12) or (13)), which introduces a higher variance. The resulting uncertainty equation is (Fig. 7):16,18
 | (20) |
 | ||
| Fig. 7 Uncertainty propagation factor (i.e., “overdispersion” relative to Poisson statistics, using eqn (20)) for the EDT-NEDT (τe/τne = 0.4) corrected number of counts, derived from the inverse throughput formulas (eqn (12) or (13)). | ||
The additional uncertainty factor in eqn (20) depends only on ρ and τe, not on τne. Therefore, this type of uncertainty cannot be reduced by imposing a longer NEDT. Where the throughput formula in eqn (3) reaches a maximum, the uncertainty in eqn (20) approaches infinity. In this region, a more realistic uncertainty value can be estimated by performing the inversion for two different output rates, R1,2 = R ± σ(R)/2. The input rate of the major isotope can also be verified by comparing it with the rate from a minor isotope with lower abundance and, consequently, lower count loss.
In addition to the count rate uncertainty, the uncertainty on the characteristic dead time parameters τne and τe must be propagated into the uncertainty budget of the estimated input rate.16 The associated sensitivity factors are calculated from σ2(ρ) ≈ (∂R/∂ρ)−2(∂R/∂τ)2σ2(τ), which results in:
 | (21) |
A graphical illustration is shown in Fig. 8 for τe/τne = 0.4. At relatively low count rate (ρτe < 0.4), the propagation factor for NEDT is larger than for pileup and approximates the sensitivity factor ρτne typical of a NEDT counter.16 Both sensitivity factors go well beyond unity at high input rates (ρτe > 0.5), where e.g. 1% error in pulse width can result in several % error in the estimated count rate. Uncertainty budgets that do not incorporate dead-time propagation may be severely incomplete.
 | ||
| Fig. 8 Propagation factor (eqn (21)) of relative uncertainty on the NEDT τne and the pulse width τe with respect to the reverse throughput rate for sequential EDT-NEDT with τe/τne = 0.4. A sensitivity factor of 1 translates a 1% error in τne or τe into a 1% error in atomic abundance. | ||
Amount ratio
The amount ratio of two isotopes, r = n1/n2, is assumed to be proportional to the intensities of their respective ion beams in the mass spectrometer, and thus also to the rate of ions impinging on the ion counter, r = ρ1/ρ2. Current practice involves calculating the ratio of the measured count rates, R1 and R2, corrected for the expected count loss due to NEDT only (eqn (8)). The approximate isotope ratio estimate is then: | (22) |
However, an unbiased calculation of the isotope ratio should use the more complete throughput formula from eqn (3):
 | (23) |
The error associated with the approximation in eqn (22) can be calculated as:
 | (24) |
This error cancels out when both isotopes have equal concentrations, n1/n2 = ρ1/ρ2 = 1, and increases progressively as the isotope ratio moves away from unity.
Numerical example
Numerical examples are provided in Tables 1 and 2 and visualised in Fig. 9–11. An ion counter is modelled with a characteristic pulse width of τe = 20 ns and an imposed NEDT of τne = 50 ns. The material consists of major and minor isotopes with an abundance ratio of n1/n2 = 30. Table 1 contains representative data regarding the expected count rates and throughput factors, before and after corrections for the count loss due to NEDT. Fig. 9 shows the corresponding throughput curves in a log–log scale. Mass spectrometry will result in biased atom ratios where the count rates for both isotopes are no longer parallel. Correcting for NEDT viaeqn (6) extends the linearity region by an order of magnitude. Linearity can be fully restored by using the inverse throughput formulas in eqn (12) and (13). Table 2 shows the results from the first iteration steps. The Newton–Raphson method (eqn (13)) converges faster and is applicable over the full range.| Input | Uncorrected throughput | Corrected for NEDT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ 1 τ e | ρ 1 | R 1 | R 2 | X 1 | X 2 | X 1/X2 | |||||
| 0.0004 | 2 104 | 2.00 104 | 6.67 102 | 0.9990 | 1.0000 | 0.9990 | 2.00 104 | 6.67 102 | 1.0000 | 1.0000 | 1.0000 |
| 0.01 | 5 105 | 4.88 105 | 1.67 104 | 0.9756 | 0.9992 | 0.9764 | 5.00 105 | 1.67 104 | 0.9999 | 1.0000 | 0.9999 |
| 0.1 | 5 106 | 3.98 106 | 1.65 105 | 0.7967 | 0.9917 | 0.8033 | 4.97 106 | 1.67 105 | 0.9949 | 1.0000 | 0.9949 |
| 0.4 | 2 107 | 9.56 106 | 6.45 105 | 0.4781 | 0.9677 | 0.4940 | 1.83 107 | 6.67 105 | 0.9159 | 0.9999 | 0.9160 |
| 1 | 5 107 | 1.19 107 | 1.54 106 | 0.2371 | 0.9226 | 0.2570 | 2.91 107 | 1.67 106 | 0.5820 | 0.9994 | 0.5823 |
| 2 | 1 108 | 9.63 106 | 2.85 106 | 0.0963 | 0.8555 | 0.1125 | 1.86 107 | 3.33 106 | 0.1856 | 0.9977 | 0.1860 |
| 6 | 3 108 | 7.27 105 | 6.57 106 | 0.0024 | 0.6573 | 0.0037 | 7.55 105 | 9.79 106 | 0.0025 | 0.9790 | 0.0026 |
| Input | Eqn (12) with starting value from eqn (6) | Eqn (13) with starting values from eqn (6) or (14) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ρτ e | X | X (0)/X | X (1)/X | X (2)/X | X (3)/X | X (4)/X | X (0)/X | X (1)/X | X (2)/X | X (3)/X | X (4)/X |
| 0.0004 | 0.9990 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 0.01 | 0.9756 | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 0.1 | 0.7967 | 0.9949 | 0.9981 | 1.0000 | 1.0000 | 1.0000 | 0.9949 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 0.4 | 0.4781 | 0.9159 | 0.9338 | 0.9885 | 0.9979 | 0.9996 | 0.9159 | 0.9952 | 1.0000 | 1.0000 | 1.0000 |
| 1 | 0.2371 | 0.5820 | 0.5997 | 0.7111 | 0.7712 | 0.8096 | 1.8037 | 1.3052 | 1.1381 | 1.0660 | 1.0323 |
| 2 | 0.0963 | 0.1856 | 0.1892 | 0.2007 | 0.2027 | 0.2031 | 1.0735 | 1.0011 | 1.0000 | 1.0000 | 1.0000 |
| 6 | 0.0024 | 0.0025 | 0.0025 | 0.0025 | 0.0025 | 0.0025 | 0.9455 | 0.9938 | 0.9999 | 1.0000 | 1.0000 |
 | ||
| Fig. 9 (Top) Output rate from an ion counter with τe = 20 ns and τne = 50 ns for major and minor isotopes in a material with an atom ratio n1/n2 = 30, as a function of the major input rate. When both curves run in parallel, the mass spectrometry result is unbiased; (Middle) Same output rates after correction for NEDT using eqn (6). The linearity region has been extended by an order of magnitude; (Bottom) Throughput ratio for both isotopes, before and after NEDT correction. Deviation from unity indicates the non-linear working region of the mass spectrometer. | ||
Fig. 10 and 11 illustrate the non-linearity as a function of the output rate of the main isotope, which may be viewed as the experimenter's perspective. At high input rates (ρ1τe ≈ 1), the user may observe quite excessive variations in the atomic ratio as a function of the output rate. Fig. 11 shows the throughput ratio for various atom ratios at typical output rates used in linearity tests. The graph reveals a rather flat region at low count rates, followed by a bend, and a sharp deviation from linearity. This pattern resembles experimental linearity plots published in literature, however the sign is opposite.3,5
Experiment
Previous studies on ion counter linearity in mass spectrometry were generally limited to relatively low count rates (below 10−6 s−1), where pulse pileup effects are minimal and difficult to measure accurately, but where other effects might cause apparent non-linearity, such as a high-frequency transient oscillations (“ringing”),48 drift and aging effects,49etc. Thus, linearity tests published in 2001 (ref. 3) and 2009 (ref. 5) show the opposite behaviour as expected from the throughput model. With increasing input rate, the output rate of the major isotope was higher than predicted from the NEDT model, resulting in seemingly lower isotopic abundances for the minor isotopes. One plausible explanation would be that excess counts were generated by afterpulses from multiple ions arriving at the detector in rapid succession. This can lead to amplifier-overload events, potentially causing a “ringing” effect in the electronic circuitry. The resulting electronic oscillations may generate spurious afterpulses that are erroneously counted as additional ions. These afterpulses would disproportionately affect the measurements of the most abundant isotope. Consequently, this would inflate the count rate for the major isotope relative to the minor isotopes, leading to an apparent decrease in the abundance of minor isotopes. This problem was eventually solved with the introduction of a new generation of SEMs with improved linearity via a lower operating voltage and modified last dynode electronics.5,48In 2016,7 static linearity tests were performed on a multi-collector inductively coupled plasma mass spectrometer (MC-ICP-MS) at the IAEA, using IRMM-072 reference material from the JRC. The results revealed that the dead-time effect aligned with that of a NEDT counter, and no additional count loss due to pileup was observed up to count rates of 8 105 s−1. While the observed dead time closely approximated the nominal value specified by the manufacturer, notable deviations up to about 3 ns were identified. Measurement of the dead time is therefore mandatory for accurate mass spectrometry. The authors posit that the dead time of any type of secondary electron multiplier detector is much shorter than the NEDT of τne = 20–70 ns, possibly at the level of τe < 10 ns, and therefore can be disregarded as a source of count loss.
Within the framework of the throughput model presented in this work, the latter statement holds only partially true. Assuming an EDT-NEDT model with τne = 20 ns and τe = 10 ns, the serial expansion of the throughput formula in eqn (5) can be further simplified to a first order approximation:
 | (25) |
At an input rate of ρ = 106 s−1; the NEDT term is ρτne = 0.02 and the EDT term is much smaller at just 0.00005. In this region, NEDT dominates and the pileup introduces only a minimal deviation of 0.005% to the count rate. Increasing the input rate by an order of magnitude to ρ = 107 s−1 leads to the respective terms of 0.2 for NEDT and 0.005 for EDT. At this rate, neglecting pileup introduces a significant error of 0.43% in X. This could be partially mitigated by adopting a slightly higher τne value. At even higher count rates, accurate mass spectrometry results become unattainable within the NEDT model. For ρ = 108 s−1, the NEDT term is ρτne = 2.0 and the sum of the pileup terms in eqn (5) amount up to 0.718, inducing 19% error on X.
In a recent study, Siegmund et al.50 suggested an approach for investigating high intensity transient signals under controlled conditions by generating 200 μs ion beam pulses in MC-ICPMS with a liquid sample introduction to demonstrate the effect of intensity spikes that normally occur in laser ablation or nano-particle analysis. They performed a linearity test of secondary electron multipliers (SEM) subjected to a 233U/235U beam at input fluxes from ca. 104 to about 3 × 107 ions per second, and found that the investigated ion counters reveal some non-linearity beyond that caused solely by the dead time (whereas it was a valid approach for data acquired up to 2 × 105 s−1 ion count range). The diminishing response of the ion detection system at ion fluxes above 2 × 106 s−1 is compatible with additional count loss originating from pulse pile-up. In fact, the throughput curve up to 3 × 107 s−1 looks indeed as predicted in Fig. 3, and by applying the correction formula in eqn (12) they could fix the biased amount ratio. This is currently the most compelling direct evidence supporting the applicability of the model presented here to discrete ion counting in mass spectrometry. A more comprehensive experimental study is currently ongoing.51
For future tests, especially those involving transient signals, it is important to recognise a second, subtle form of non-linearity related to input rate variability. When the input rate varies significantly during measurement, an additional correction term must be included in the throughput formula to account for the non-proportionality between average input and output rates. This correction is proportional to the input rate variance and half the second derivative of the throughput function.52
Conclusion
The presented throughput model predicts rate-related non-linearity in mass spectrometry when using a discrete ion counter. In current practice, count rates are corrected for count loss due to the imposed non-extended dead time, but not for the additional extending dead time generated by pileup of detector pulses. However, the NEDT model breaks down at extremely high count rates. Formulas have been provided for the true throughput rate (eqn (3)) in the counter, the inverse throughput to correct for count loss (eqn (6) and (12)–(14)), the resulting counting uncertainty (eqn (20)), the error propagation of the characteristic dead time and pulse width (eqn (21)), and the error made by incomplete dead-time correction when ignoring pileup (eqn (24)). As a result, this approach enables extending the linearity of the ion counter across the full range of input rates, thus eliminating rate-related bias in mass spectrometry.Data availability
All data in Tables and graphs have been generated using the formulas presented in this paper.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Prof. Dr Oana-Alexandra Dumitru from the University of Florida is gratefully acknowledged for being a source of inspiration to accomplish this work.References
- N. S. Lloyd, J. Schwieters, M. S. A. Horstwood and R. R. Parrish, Particle detectors Used in Isotope Ratio Mass Spectrometry, with Applications in Geology, Environmental Science and Nuclear Forensics, in Handbook of Particle Detection and Imaging, ed. C. Grupen and I. Buvat, Springer-Verlag, Berlin Heidelberg, 2012 Search PubMed.
- A. Held and P. D. P. Taylor, A calculation method based on isotope ratios for the determination of dead time and its uncertainty in ICP-MS and application of the method to investigating some features of a continuous dynode multiplier, J. Anal. At. Spectrom., 1999, 14, 1075–1079 RSC.
- S. Richter, S. A. Goldberg, P. B. Mason, A. J. Traina and J. B. Schwieters, Linearity tests for secondary electron multipliers used in isotope ratio mass spectrometry, Int. J. Mass Spectrom., 2001, 206, 105–127 CrossRef CAS.
- U. Nygren, H. Ramebäck, M. Berglund and D. C. Baxter, The importance of a correct dead time setting in isotope ratio mass spectrometry: Implementation of an electronically determined dead time to reduce measurement uncertainty, Int. J. Mass Spectrom., 2006, 257, 12–15 CrossRef CAS.
- S. Richter, A. Alonso, Y. Aregbe, R. Eykens, F. Kehoe, H. Kühn, N. Kivel, A. Verbruggen, R. Wellum and P. D. P. Taylor, A new series of uranium isotope reference materials for investigating the linearity of secondary electron multipliers in isotope mass spectrometry, Int. J. Mass Spectrom., 2009, 281, 115–125 CrossRef CAS.
- U. Nygren, H. Ramebäck, A. Vesterlund and M. Berglund, Consequences of and potential reasons for inadequate dead time measurements in isotope ratio mass spectrometry, Int. J. Mass Spectrom., 2011, 300, 21–25 CrossRef CAS.
- S. Richter, S. Konegger-Kappel, S. F. Boulyga, G. Stadelmann, A. Koepf and H. Siegmund, Linearity testing and dead-time determination for MC-ICP-MS ion counters using the IRMM-072 series of uranium isotope reference materials, J. Anal. At. Spectrom., 2016, 31, 1647–1657 RSC.
- T. Hirata, S. Niki, S. Yamashita, H. Asanuma and H. Iwano, Uranium-lead isotopic analysis from transient signals using high-time resolution-multiple collector-ICP-MS (HTR-MC-ICP-MS), J. Anal. At. Spectrom., 2021, 36, 70–74 RSC.
- I. Strenge and C. Engelhard, Single particle inductively coupled plasma mass spectrometry: investigating nonlinear response observed in pulse counting mode and extending the linear dynamic range by compensating for dead time related count losses on a microsecond timescale, J. Anal. At. Spectrom., 2020, 35, 84–99 RSC.
- A. M. Duffin, E. D. Hoegg, R. I. Sumner, T. Cell, G. C. Eiden and L. S. Wood, Temporal analysis of ion arrival for particle quantification, J. Anal. At. Spectrom., 2021, 36, 133–141 RSC.
- I. Strenge and C. Engelhard, Capabilities of fast data acquisition with microsecond time resolution in inductively coupled plasma mass spectrometry and identification of signal artifacts from millisecond dwell times during detection of single gold nanoparticles, J. Anal. At. Spectrom., 2016, 31, 135–144 RSC.
- D. Mozhayeva and C. Engelhard, A critical review of single particle inductively coupled plasma mass spectrometry – A step towards an ideal method for nanomaterial characterization, J. Anal. At. Spectrom., 2020, 35, 1740–1783 RSC.
- T. Hirata, S. Yamashita, M. Ishida and T. Suzuki, Analytical Capability of High-Time Resolution-Multiple Collector-Inductively Coupled Plasma-Mass Spectrometry for the Elemental and Isotopic Analysis of Metal Nanoparticles, Mass Spectrom. , 2020, 9, A0085 CrossRef CAS PubMed.
- S. Yamashita, M. Ishida, T. Suzuki, M. Nakazato and T. Hirata, Isotopic analysis of platinum from single nanoparticles using a high-time resolution multiple collector Inductively Coupled Plasma - Mass Spectroscopy, Spectrochim. Acta, Part B, 2020, 169, 105881 CrossRef CAS.
- S. Pommé, Radionuclide metrology: confidence in radioactivity measurements, J. Radioanal. Nucl. Chem., 2022, 331, 4771–4798 CrossRef.
- S. Pommé, R. Fitzgerald and J. Keightley, Uncertainty of nuclear counting, Metrologia, 2015, 52, S3–S17 CrossRef.
- International Commission on Radiation Units and Measurements (ICRU), Particle counting in radioactivity measurements, ICRU Report, Maryland, USA, 1994, vol. 52 Search PubMed.
- S. Pommé, Cascades of pile-up and dead time, Appl. Radiat. Isot., 2008, 66, 941–947 CrossRef PubMed.
- S. Pommé, When the model doesn’t cover reality: examples from radionuclide metrology, Metrologia, 2016, 53, S55–S64 CrossRef.
- J. A. Williamson, M. W. Kendall-Tobias, M. Buhl and M. Seibert, Statistical evaluation of dead time effects and pulse pileup in fast photon counting. Introduction of the sequential model, Anal. Chem., 1988, 60, 2198–2203 CrossRef CAS.
- R. Jakopič, K. Toth, J. Bauwens, R. Buják, C. Hennessy, F. Kehoe, U. Jacobsson, S. Richter and Y. Aregbe, 30 years of IRMM-1027 reference materials for fissile material accountancy and control: development, production and characterisation, J. Radioanal. Nucl. Chem., 2021, 330, 333–345 CrossRef.
- S. Boulyga, S. Konegger-Kappel, S. Richter and L. Sangély, Mass spectrometric analysis for nuclear safeguards, J. Anal. At. Spectrom., 2015, 30, 1469–1489 RSC.
- O. A. Dumitru, J. Austermann, V. J. Polyak, J. J. Fornós, Y. Asmerom, J. Ginés, A. Ginés and B. P. Onac, Constraints on global mean sea level during Pliocene warmth, Nature, 2019, 574, 233–236 CrossRef CAS PubMed.
- P. T. Spooner, T. Chen, L. F. Robinson and C. D. Coath, Rapid uranium-series age screening of carbonates by laser ablation mass spectrometry, Quat. Geochronol., 2016, 31, 28–39 CrossRef.
- I. De Lotto, P. F. Manfredi and P. Principi, Counting statistics and dead-time losses, Energ. Nucl., 1964, 11, 599–611 ( Energ. Nucl. , 1964 , 11 , 557–564 ) Search PubMed.
- J. W. Müller, Sur l’arrangement en série de deux temps morts de types différents, Internal Report BIPM, Sèvres, France, BIPM-73/9, 1973 Search PubMed.
- J. W. Müller, Dead-time problems, Nucl. Instrum. Methods, 1973, 112, 47–57 CrossRef.
- J. W. Müller, Stastiques de comptage, Internal Report BIPM, Sèvres, France, BIPM-82/13, 1982 Search PubMed.
- J. Libert, Détermination du taux de comptage en amont de deux temps morts classiques en série et de types différents, Nucl. Instrum. Methods Phys. Res., Sect. A, 1989, 274, 319–323 CrossRef.
- S. Pommé, B. Denecke and J.-P. Alzetta, Influence of pileup rejection on nuclear counting, viewed from the time-domain perspective, Nucl. Instrum. Methods Phys. Res., Sect. A, 1999, 426, 564–582 CrossRef.
- S. Pommé, Time-interval distributions and counting statistics with a non-paralysable spectrometer, Nucl. Instrum. Methods Phys. Res., Sect. A, 1999, 437, 481–489 CrossRef.
- S. Pommé and G. Kennedy, Pulse loss and counting statistics with a digital spectrometer, Appl. Radiat. Isot., 2000, 52, 377–380 CrossRef PubMed.
- S. Pommé and J. Uyttenhove, Statistical precision of high-rate spectrometry with a Wilkinson ADC, J. Radioanal. Nucl. Chem., 2001, 248, 263–266 CrossRef.
- S. Pommé, Dead time, pile-up and counting statistics, in Applied Modeling and Computations in Nuclear Science, ACS Symposium Series, 2007, vol. 945, pp. 218–233 Search PubMed.
- S. Pommé and J. Keightley, Count rate estimation of a Poisson process - Unbiassed fit versus central moment analysis of time interval spectra. In: Applied Modeling and Computations in Nuclear Science, ACS Symp. Ser., 2007, 945, 316–334 CrossRef.
- C. Michotte and M. Nonis, Experimental comparison of different dead-time correction techniques in single-channel counting experiments, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 608, 163–168 CrossRef.
- S. Cheng, B. Pierson, S. Pommé and M. Flaska, Time interval distributions of nuclear events in a digital spectrometer, Nucl. Instrum. Methods Phys. Res., Sect. A, 2024, 1063, 169218 CrossRef CAS.
- S. Pommé and K. Pelczar, A simplified approach to counting statistics with an imperfect pileup rejector, Nucl. Instrum. Methods Phys. Res., Sect. A, 2025, 1070, 170067 CrossRef.
- S. Cheng, B. Pierson, S. Pommé, B. Archambault and M. Flaska, Time-interval distributions in a digital gamma multi-channel analyzer at extreme input rates, Nucl. Instrum. Methods Phys. Res., Sect. A, 2025, 1073, 170260 CrossRef CAS.
- R. Fitzgerald, Corrections for the combined effects of decay and dead time in live-timed counting of short-lived radionuclides, Appl. Radiat. Isot., 2016, 109, 335–340 CrossRef CAS PubMed.
- G. P. Westphal, Review of loss-free counting in nuclear spectroscopy, J. Radioanal. Nucl. Chem., 2008, 275, 677–685 CrossRef CAS.
- S. Pommé, J.-P. Alzetta, J. Uyttenhove, B. Denecke, G. Arana and P. Robouch, Accuracy and precision of loss-free counting in γ-ray spectrometry, Nucl. Instrum. Methods Phys. Res., Sect. A, 1999, 422, 388–394 CrossRef.
- S. Pommé, How pileup rejection affects the precision of loss-free counting, Nucl. Instrum. Methods Phys. Res., Sect. A, 1999, 432, 456–470 CrossRef.
- S. Pommé, Experimental test of the 'zero dead time' count-loss correction method on a digital gamma-ray spectrometer, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 474, 245–252 CrossRef.
- S. Pommé, A plausible mathematical interpretation of the 'variance' spectra obtained with the DSPECPLUS TM digital spectrometer, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 482, 565–566 CrossRef.
- S. Pommé, On the statistical control of 'loss-free counting' and 'zero dead time' spectrometry, J. Radioanal. Nucl. Chem., 2003, 257, 463–466 CrossRef.
- J. Bartošek, J. Mašek, F. Adams and J. Hoste, The use of a pileup rejector in quantitative pulse spectrometry, Nucl. Instrum. Methods, 1972, 104, 221–223 CrossRef.
- S. R. Noble, J. Schwieters, D. J. Condon, Q. G. Crowley, N. Quaas and R. R. Parish, TIMS Characterization of a New Generation Secondary Electron Multiplier, AGU Fall Meeting, 2006, session V11E-06 Search PubMed.
- P. M. L. Hedberg, P. Peres, F. Fernandes and L. Renaud, Multiple ion counting measurement strategies by SIMS– a case study from nuclear safeguards and forensics, J. Anal. At. Spectrom., 2015, 30, 2516–2524 RSC.
- H. Siegmund, S. Konegger-Kappel and S. Boulyga, Analysis of ultra-fast transient signals by LA-MC-ICPMS – overcoming instrumental limitations, European Workshop on Laser Ablation, Ghent, Belgium, 2024 Search PubMed.
- H. Siegmund, S. Konegger-Kappel, S. Boulyga, M. Kilburn and S. Pommé, Recording High-Intensity Transient Signals with Secondary Electron Multipliers in MC-ICPMS: Dead-Time Correction and Non-linearity Effects, 2025, in preparation.
- S. Pommé, Non-linearity correction for variable signal analysis in mass spectrometry using discrete ion counters, 2025, in preparation.
| This journal is © The Royal Society of Chemistry 2025 |