Open Access Article
Open Access ArticleChallenges in measuring nanoparticles and microparticles by single particle ICP-QMS and ICP-TOFMS: size-dependent transport efficiency and limited linear dynamic range†
Madeleine
Lomax-Vogt
 ab,
Lucas M.
Carter
ab,
Lucas M.
Carter
 a,
Jonas
Wielinski
a,
Jonas
Wielinski
 d,
Stanislav
Kutuzov
d,
Stanislav
Kutuzov
 ac,
Gregory V.
Lowry
ac,
Gregory V.
Lowry
 d,
Ryan
Sullivan
d,
Ryan
Sullivan
 e,
Paolo
Gabrielli
f and
John W.
Olesik
e,
Paolo
Gabrielli
f and
John W.
Olesik
 *ac
*ac
aTrace Element Research Laboratory, School of Earth Sciences, The Ohio State University, Columbus, OH 43210, USA. E-mail: olesik.2@osu.edu
bDepartment of Chemistry and Biochemistry, The Ohio State University, Columbus, OH 43210, USA
cByrd Polar and Climate Research Center, The Ohio State University, Columbus, OH 43210, USA
dDepartment of Civil and Environmental Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
eCenter for Atmospheric Particle Studies, Carnegie Mellon University, Pittsburgh, PA 15213, USA
fHoneybee Robotics, Blue Origin, Altadena, CA 91001, USA
First published on 5th February 2025
Abstract
While spICP-MS has been used mainly to measure nanoparticles, it can also be used to measure microparticles. The transport efficiency of nanoparticles is typically independent of their size. However, the transport efficiency of microparticles can be particle size (mass) dependent as well as being dependent on the sample uptake rate and sample introduction system used. To measure both nanoparticles and microparticles a very large linear dynamic range (where signal intensity is linearly proportional to the measured analyte(s) mass within a very short measurement time (∼300 to 500 µs, the width of signals produced by an individual particle)) is needed. Deviations from linearity could occur due to incomplete particle vaporization or from signals that are beyond the instrument's ion detection system linear dynamic range. To characterize and determine the cause of nonlinearity we measured sets of nearly monodisperse engineered SiO2 particles with diameters from 500 to 5000 nm and Au particles with diameters from 60 to 1500 nm. We found that by reducing the sensitivity (up to a factor of 269×) the upper end of the linear dynamic range, in particle size that produced signal intensities that were linearly proportional to the particle (analyte) mass, could be greatly extended. Not surprisingly, reducing the sensitivity increased the minimum size detectable particle. The results are consistent with SiO2 particles as large as 5000 nm being completely vaporized in the ICP.
1 Introduction
The use of single particle Inductively Coupled Plasma-Mass Spectrometry (spICP-MS) to determine particle number concentration, size (mass equivalent diameter) and elemental chemical composition continues to grow rapidly.1–5 However, the vast majority of the applications reported to date using spICP-MS have focused on engineered nanoparticles, sometimes including their fate in the environment6–20 and biological21–23 systems.When measuring engineered nanoparticles (diameters ≤ 100 nm): (1) the transport efficiency into the ICP does not depend on size; (2) typically the elemental composition of the particles is known and includes only one or two elements; (3) it is reasonable to assume that the nanoparticles are completely vaporized in the plasma under optimum conditions for analysis of solutions; and (4) the required linear dynamic range (for signal intensities), while wide, is typically within the range provided by most modern ICP-MS instruments capable of single particle detection (especially if analog rather than pulse counting measurements are used).
Measuring both polydisperse nanoparticles and microparticles with a wide range of unknown, highly variable elemental compositions is much more challenging. The transport efficiency from the sample to the nebulizer through the spray chamber and into the ICP may be dependent on the microparticle mass and/or size, complicating measurement of particle number concentrations as a function of size. For example, Ebdon et al.24–26 showed that refractive particles larger than about 2000 nm may not be transported through a nebulizer/spray chamber into an ICP-OES. Using a high efficiency single cell spICP-MS introduction system27 with an uptake rate of 10 µL min−1 resulted in 100% transport efficiency of cells up to ∼3000 nm and but lower transport efficiency for ∼6400 nm cells.28 However, cells have a lower density than most particles.
If the microparticles are too large, they may not be completely vaporized, atomized, and ionized in the plasma which would lead to an underestimate of the total mass and size of the particle.29,30 Olesik and Gray reported29 that ICP-MS Si+ signal intensity was linearly related to the mass of Si in SiO2 particles with diameters only up to about 1 µm, consistent with particles larger than 1 µm not being completely vaporized in the plasma. However, Ebdon and Collier24 provided evidence that refractory particles as large as 8 µm were completely vaporized in ICP-OES when using a 3 mm inner diameter (i.d.) injector (center tube of the ICP torch).
Measurement of both nanoparticles (diameter ≤ 100 nm) and fine microparticles (100 nm ≤ d ≤ 2500 nm or more) requires a huge signal intensity dynamic range. The mass of a particle depends on the cube of its diameter. Therefore, the dynamic range (in mass or signal intensity) to measure particles with diameters from 10 nm to 2500 nm is at least 1.6 × 107 (2503). To measure particles with diameters from 10 nm to 5000 nm the dynamic range needs to be at least 1.3 × 108 (5003). In addition, because the sensitivity (counts per fg) is element dependent, an even larger linear dynamic range may be required. Furthermore, although some current ICP-Quadupole MS instruments are said to have a linear dynamic range up to ∼1010 (∼1011 on some instruments) it is important to remember that is for a measurement time of at least one second.31 For spICP-MS, typically dwell times of 2 ms or less are used, and the signal from ions produced from a single particle typically lasts for only ∼0.3 to 0.5 ms.5,29
The linear dynamic range provided by ICP-TOFMS instruments is typically32 ∼106 (for a 1 second measurement time). Therefore, the dynamic range for 2 ms may be ∼2000 (and that assumes a constant intensity during the 2 ms). In reality, the signal from a vaporized, ionized particle typically has a roughly Gaussian shape (with a somewhat longer trailing tail due to diffusion of the ion cloud as it travels in the ICP to the sampling cone33–35) so the peak intensity will be larger than the average intensity.
Data illustrating the challenges due to particle size dependent transport efficiencies and a limited dynamic range, where signal intensity is linearly proportional to the particle analyte mass when measuring nanoparticles and microparticles, are discussed below. Sets of nearly monodisperse engineered particles (SiO2 with diameters from 500 to 5000 nm and Au particles with diameters from 60 to 1500 nm) were used to explore particle transport efficiency from the nebulizer to the ICP and the linear dynamic range. Measurements at optimum and reduced sensitivity were used to distinguish nonlinearity due to incomplete particle vaporization from limited ion detection system linear dynamic range.
2 Experimental
2.1 Engineered nanoparticle and microparticle suspensions
Commercially available citrate-capped engineered Au and bare SiO2 nanoparticle and microparticle suspensions were purchased from BBI Solutions (Crumlin, United Kingdom), Nancomposix (California, USA), ThermoFisher Scientific (Waltham, Massachusetts, USA), or Bangs Laboratories (Indiana, USA) (details including densities of the engineered Au and SiO2 (ref. 36 and 37) particles are in Table S1†). Suspensions were prepared by serial dilution (Table S1†) in deionized water (18.2 MΩ cm, produced by a ThermoFisher Scientific/Barnstead Smart2Pure Pro UV/UF 16 LPH system). Stock suspensions were placed in an ultrasonic bath for 10 minutes before dilution and then repeatedly inverted until settled particles were resuspended in an attempt ensure a homogeneous and agglomerate-free suspension. Each suspension was diluted 12× to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640
640![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× to contain a known number of particles (∼100
000× to contain a known number of particles (∼100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to ∼250
000 to ∼250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles per mL). The mean particle diameter and the mass concentration of Au or Si in the original stock suspension (provided by each manufacturer) or the particle number concentration (provided by the manufacturer) were used to calculate the number of particles per mL in the diluted particle suspensions. All particle suspensions were made gravimetrically using an electronic analytical balance (Mettler-Toledo XSR304, Greifensee, Switzerland).
000 particles per mL). The mean particle diameter and the mass concentration of Au or Si in the original stock suspension (provided by each manufacturer) or the particle number concentration (provided by the manufacturer) were used to calculate the number of particles per mL in the diluted particle suspensions. All particle suspensions were made gravimetrically using an electronic analytical balance (Mettler-Toledo XSR304, Greifensee, Switzerland).
2.2 Single particle inductively coupled plasma-mass spectrometers
Three commercially available spICP-MS instruments were used in this study: a PerkinElmer NexION 350D spICP-QMS (Thornhill, Ontario, Canada), a TOFWERK icpTOF-R spICP-TOFMS (Thun, Switzerland), and a Nu Instruments Vitesse spICP-TOFMS (Wrexham, United Kingdom). The NexION 350D and TOFWERK icpTOF-R used a 1.8 mm i.d. Meinhard (Golden, Colorado, USA) sapphire injector, an Elemental Scientific Inc. (Omaha, Nebraska, USA) 47 mm PFA barrel spray chamber with O-ring-free endcap, and an Elemental Scientific Inc. self-aspirating PFA-50 nebulizer without probe to deliver freely aspirated solutions and suspensions to the instrument with minimal joints in which particles may become stuck. An Elemental Scientific Inc. self-aspirating PFA-20 nebulizer without probe was also used for some measurements during spICP-QMS analysis. In one set of NexION 350D measurements, an Elemental Scientific Inc. PFA-ST nebulizer was used at an uptake rate of 340 µL min−1 with the suspension delivered to the nebulizer using a peristaltic pump. The Nu Instruments Vitesse used a cyclonic spray chamber and a glass, concentric nebulizer with sample pumped at 400 µL min−1. Sample uptake rates on the NexION 350D and icpTOF-R were measured gravimetrically. Instrument parameters are listed in Table 1.| PerkinElmer NexION 350D | Nu instruments Vitesse | TOFWERK icpTOF-R | |
|---|---|---|---|
| a Mass spectrum collected every 30 µs and then spectra summed over each 2000 µs. b Peak shape may be distorted at mass resolution of 0.2 or 0.15; as a result, the sensitivity reduction factor may be smaller for what is estimated to provide a smaller mass resolution. c PerkinElmer NexION 350D. d Nu Instruments Vitesse. e TOFWERK icpTOF-R. | |||
| Instrument type | spICP-QMS | spICP-TOFMS | spICP-TOFMS |
| Plasma power (W) | 1600 | 1300 | 1500 |
| Plasma gas (L min−1) | 18 | 13 | 17 |
| Auxiliary gas (L min−1) | 1.2 | 2.0 | 1.0 |
| Injector i.d. (mm) | 1.8 | 1.8 | 1.8 |
| Nebulizer gas flow (L min−1) | 1.09 | 1.00 | 1.00 |
| Sample uptake rate (µL min−1) | 22, 60, or 340 | ∼400 | 60 |
| Sampling depth (mm) | 11 | 12 | 5 |
| Integration time, single particle (µs) | 100 | 80 | 2000a |
The nebulizer gas flow rate on each spICP-MS instrument was optimized to achieve maximum 115In+ sensitivity while maintaining a cerium oxide to cerium (140Ce16O+/140Ce+) ratio less than 3% using a multi-element solution standard containing 1 µg L−1 each of Be, Co, Ce, ln, and U (on the NexION 350D) or 1 µg L−1 each of Co, In, Ce and U (on the TOFWERK icp TOF-R and Nu Instruments Vitesse). Decreasing the nebulizer gas flow rate and/or increasing the sampling depth would increase the time the sample spends in the hot plasma prior to the reaching the sampling orifice, potentially increasing the maximum particle size that could be completely vaporized in the plasma. However, the data discussed in this paper were always acquired at the optimum nebulizer gas flow rate for analysis of solutions (using the sampling depth listed in Table 1). No changes in the nebulizer gas flow rate or sampling depth were made to increase the time particles spent in the plasma.
The NexION 350D Quadrupole Ion Deflector (QID) was optimized for maximum sensitivity at low-, mid-, and high-masses. The Autolens function was then used for measurements. The icpTOF-R Extraction Lens 2 was optimized daily for maximum 115In+ sensitivity.
Si+ intensity produced by SiO2 particles was determined using m/z 28. The Au+ intensity produced by Au particles was determined using m/z 197.
 | (1) |
While a mass dependent compound Poisson distribution may be more appropriate for spICP-TOFMS measurements,42 the instrument software version we had did not include it.
Transport efficiency is commonly determined using the Particle Frequency (Particle Number) method or the Particle Size (Solution/Nanoparticle) method, described in detail by Pace et al.38 The Particle Number method is the ratio of the number of detected particles to the number delivered to the nebulizer (known # per mL in engineered particle suspension × uptake rate × measurement time). The Solution/Nanoparticle method estimates transport efficiency from the ratio of the solution sensitivity (in counts per fg delivered to the nebulizer) to the particle sensitivity (not affected by transport efficiency) in average counts per fg of analyte in the particle. The Solution/Nanoparticle method cannot be used to determine the size (or mass) dependent transport efficiency because it determines the transport efficiency of elements dissolved in the solution, not of the particles. Therefore, the Particle Frequency (Particle Number) method was used here.
3 Results and discussion
3.1 Mass/size-dependent transport efficiency of nanoparticles and microparticles
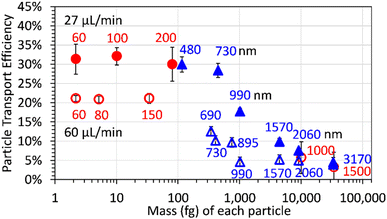
Engineered Au and SiO2 particles with masses between 2 and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 fg (diameters between 60 and 3170 nm) were measured by spICP-QMS using uptake rates of 27 and 60 µL min−1. Fig. 1 shows the particle transport efficiencies as a function of particle mass; the efficiencies are plotted as a function of particle diameter in Fig. S1.†
358 fg (diameters between 60 and 3170 nm) were measured by spICP-QMS using uptake rates of 27 and 60 µL min−1. Fig. 1 shows the particle transport efficiencies as a function of particle mass; the efficiencies are plotted as a function of particle diameter in Fig. S1.†
Au particles with diameters up to at least 200 nm and SiO2 particles with diameters up to about 730 nm had similar transport efficiencies (∼30%) when an uptake rate of 27 µL min−1 was used. The particle transport efficiency decreased dramatically for SiO2 particles with diameters of 990 nm (∼1100 fg) or more. The transport efficiency for SiO2 particles with diameters larger than 2000 nm was more than five times smaller than for SiO2 particles with diameters of 730 nm or smaller.
The particle transport efficiencies measured with an uptake rate of 60 µL min−1 are consistently lower than at 27 µL min−1. This is likely because aerosol droplets can evaporate more extensively during their travel through the spray chamber when a lower uptake rate is used (resulting in smaller, more efficiently transported droplets) and the probability of droplet–droplet collisions/coagulation (resulting in larger, less efficiently transported droplets) is less likely at the lower uptake rate.44 At an uptake rate of 60 µL min−1, the decrease in particle transport efficiency also appears to begin for particles with a smaller mass (diameter). For example, the transport efficiency of 690 nm SiO2 particles was about half of the transport efficiency of 150 nm Au particle at an uptake rate of 60 µL min−1 while the transport efficiency of 730 nm SiO2 particles was similar to the transport efficiency of 200 nm Au particles or 480 nm SiO2 when the uptake rate was 27 µL min−1. The particle transport efficiencies will also be dependent on the sample introduction system used.
The implication of the behavior shown in Fig. 1 is that to measure both nanoparticles and microparticles in a sample, it is necessary to determine the particle size/mass-dependent transport efficiencies over the particle size/mass range of interest. A transport efficiency determined using nanoparticles (e.g. 60 nm Au) cannot be used to calculate the particle number concentration of particles larger than some uptake rate dependent mass or size. For example, using the 60 nm Au particle transport efficiency at sample uptake rates of 60 or 27 µL min−1, 22% and 31% respectively, to determine the number concentration of 3170 nm SiO2 particles (transport efficiencies of ∼4%) of would result in an underestimation of the particle number concentration by more than 80%.
The particle transport efficiency is also dependent on the particle mass (or size) when a much higher sample uptake rate (340 µL min−1) is used (Fig. S2†). As expected, the transport efficiency when the higher sample uptake rate is used is lower for all particle sizes than when lower sample uptake rates (such as 27 or 60 µL min−1) are used.
3.2 Signal intensity versus particle (analyte) mass
There are at least two possible causes of a deviations from a linear relationship between signal intensity and particle analyte mass. Signal intensities would not be proportional to particle analyte mass if the particles are too large to be completely vaporized, atomized, and ionized in the plasma prior to reaching the sampling orifice.29,30,45–48 Another possibility is that particles larger than some size (which may depend on the instrument, analyte element, and isotopic abundance) produce a signal outside of the instrument's ion detection system linear dynamic range (i.e. the analyte signal is not linearly related to the number of analyte ions produced in the plasma or the number of ions that reach the detector).Typically, for nanoparticles (diameter ≤ 100 µm), the signal intensity is proportional to the mass of an analyte element, especially when using analog detection.49–51 Non-linear behavior has been reported when measuring Au particles larger than 200 nm using an analog detector52,53 and silica (SiO2) microparticles29,30,45–48 larger than about 1 µm.
It is possible to somewhat extend the pulse-counting linear dynamic range by applying a “dead-time” correction.52 In this case, the maximum accurately detectable Au particle size was increased from 40 nm to 60 nm.52 An alternative way to extend the largest size (mass) particle that can be accurately measured is to use another ion that contains the analyte element but that produces a smaller signal (e.g. a minor isotope of the element or a polyatomic ion containing the analyte element). For example, measuring AuAr+ instead of Au+ can also enable the measurement of larger Au particles (increasing from the maximum size within the linear dynamic range from 100 nm to 400 nm53) in pulse counting mode. The signal intensity of AuAr+ ions produced by particles was four orders of magnitude smaller than the intensity of Au+ elemental ions from the same size particle. These results show that Au particles as large as 400 nm in diameter are completely vaporized in the ICP so that the initially observed 40 nm limit was due a decrease in the ratio of analyte ions detected (counts) to analyte ions reaching the detector, not incomplete vaporization of 40 nm Au particles. However, when the sensitivity is reduced (by using AuAr+ or a minor isotope of an element that is not monoisotopic) means that smaller particles may not be detectable, thus increasing the low-end of the linear dynamic range.
Using optimized sensitivity (e.g., obtained by optimizing the nebulizer gas flow rate to produce the maximum 115In+ signal intensity from a solution standard containing In and Ce while keeping the CeO+/Ce+ signal ratio below 3%), 500, 690, and 895 nm SiO2 particles produce a signal that increases proportionally (linearly) with the mass of Si in those particles, as shown in Fig. 2a, while the signal produced from 1050 nm SiO2 particles was slightly less than linearly proportional to the mass of Si. Signals produced from SiO2 particles with average diameters of 1050, 2060, and 3170 nm were about 15%, 35%, and 51%, respectively, smaller than expected from the linear regression line based on the signals produced by the 500, 690, and 895 nm SiO2 particles (Fig. 2b). The ratio of Si+ intensities produced by 2060 nm and 895 nm SiO2 particles (8100 counts/1100 counts = 7.36) is smaller than the ratio of Si mass in each particle standard (4270 fg/350 fg = 12.2).
Interestingly, Olesik and Gray also reported29 a linear relationship between signal intensity and the particle mass for SiO2 particles smaller than 1 µm using an analog current amplifier and a digital oscilloscope for analog to digital conversion and similar deviations from linearity for particles as large as ∼2000 nm. They concluded that SiO2 particles larger than 1 µm diameter may be incompletely vaporized in the plasma prior to reaching the sampling orifice. They did not consider the possibility of nonlinearity due to the ion detection system.
Because very short dwell times (0.1 ms) were used with the NexION 350D, the signal in units of counts per second is very large even when the total number of counts in the dwell times summed across the “particle event” may only be 2000 counts, as shown in the right y-axes of Fig. 2a and b. The approximate signals in units of counts per second were estimated by dividing the average Si+ intensity (summed across the peak in signal versus time for each detected particle) by the width of the particle event (∼300 µs), not the maximum counts per second during the particle event signal. The Si+ signal produced from a 3170 nm SiO2 particle would be about 160 million counts per s if the signal was on the same linear regression line as the 500, 690, and 895 nm SiO2 particles.
Subsequently, we made another set of measurements with SiO2 particles from 690 to 5000 nm (Fig. S3†). The results are consistent with those shown in Fig. 2; particles with diameters of 1050 nm or more produce signals that are less than proportional to the mass of Si in the particle. The deviation from linearity increases for 2060 nm, 3170 nm, and 5010 nm SiO2 particles.
When particles produce signal outside of the linear dynamic range of the instrument, it is impossible to accurately determine the particle mass equivalent diameter using a linear calibration. For example, the mass equivalent diameter of 3170 nm SiO2 particles would be underestimated by 25%, 61%, and 51%, respectively, on the NexION (Fig. 2b), icpTOF-R (Fig. 3b), and Vitesse (Fig. 3d) when the optimized sensitivity is used. Furthermore, different sized particles that produce signals outside of the instrument linear dynamic range may produce similar signals. For example, the average Si+ signal produced by 3170 nm SiO2 particles (∼3200 counts) using the Vitesse was smaller than the average Si+ signal produced by smaller (2060 nm) SiO2 particles (∼3300 counts) (Fig. 3d).
By reducing the NexION 350D Si+ sensitivity by 269× (using Δm = 0.2 amu instead of 0.7 amu) the 2060 nm and 3170 nm SiO2 particles produce Si+ signals (47 counts and 169 counts, respectively) that are linear and proportional to the average mass of Si (4272 fg and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567 fg of Si, respectively) in those particles (Fig. 4). The ratio of the average Si+ signal produced by 3170 nm particles to the average Si+ signal produced by 2060 nm SiO2 particles (169 counts/47 counts = 3.60) is almost the same as the ratio of the Si masses in 3170 nm and 2060 nm SiO2 particles (15
567 fg of Si, respectively) in those particles (Fig. 4). The ratio of the average Si+ signal produced by 3170 nm particles to the average Si+ signal produced by 2060 nm SiO2 particles (169 counts/47 counts = 3.60) is almost the same as the ratio of the Si masses in 3170 nm and 2060 nm SiO2 particles (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567 fg/4272 fg = 3.62). This is consistent with complete vaporization of the particles.
567 fg/4272 fg = 3.62). This is consistent with complete vaporization of the particles.
Reducing the sensitivity to measure larger particles within the linear dynamic range of the ion detection system increases the minimum size particle that can be accurately measured. As a result, the average Si+ intensities produced by the 895 and 1050 nm SiO2 particles (Fig. 4) were larger than expected (based on the linear regression line fit to the 2060 and 3170 nm particles). The average Si+ signals of 895 nm (∼18.7 counts) and 1050 nm (∼19.4 counts) SiO2 particles are above the linear regression line using 269× reduced sensitivity because many of the particles in the suspensions produce signals that are below the detection limit. The manufacturer specifies54 the relative standard deviation (RSD) of the particle diameters to be 10% (corresponding to a 33% RSD in the particle masses). Fig. 5 shows the detected distribution of Si+ intensities produced from the particles with four different average diameters. As shown in Fig. 5a, the expected average Si+ signal intensity produced by 895 nm SiO2 (based on the counts per fg calculated from the sensitivity (counts per s) determined from the 3170 nm average intensity) is below the detection limit. As a result, only particles on the very upper end of the particle size distribution were detected, resulting in a higher than expected average signal.14,55 Only 1% as many 895 nm SiO2 particles were detected when the sensitivity was reduced 269× as when the optimum sensitivity was used. Only 14% as many 1050 nm particles were measured when the sensitivity was reduced 269× as when the optimized sensitivity was used. For the 2060 nm particles, less than 20% of the particles on the lower end of the particle size were below the detection limit, having little effect on the average signal intensity.
SiO2 particles with an average diameter greater than about 895 nm were beyond the linear dynamic range when the optimum sensitivity was used (Fig. 2) while SiO2 particles smaller than around 2000 nm were too small to be accurately measured when the sensitivity was reduced by 269×. Therefore, an intermediate sensitivity is needed to accurately measure these particles. Fig. S3† shows the measured Si+ signal intensities as a function of the mass of Si in the particles when the sensitivity is reduced by 13×. SiO2 particles with diameters from 690 to 990 nm are linearly related to the Si mass in the particle. Average Si+ signals produced by SiO2 particles larger than 990 nm are smaller than expected for a linear, proportional relationship between signal and mass of Si in the particle. Therefore, the sensitivity must be reduced by more than 13× to extend the linear dynamic range to particles up to 2000 nm.
It is possible to extend the linear dynamic range of the instrument by combining measurements made with different sensitivities. The sensitivity reduction factors (determined from the ratio of the slopes of each linear regression line) can be used to transform the signals made at reduced sensitivity to the same scale as the optimized sensitivity so that all the measured intensities can be plotted on a single line (Fig. 6). This approach is analogous to the dual detector calibration used to produce a single calibration line from signals measured following the final dynode (resulting in the highest gain) by pulse counting and by analog measurement of the detector current about mid-way through the set of dynodes (resulting in a lower gain).
The data in Fig. 4 and 6 are consistent with SiO2 particles with diameters of 3170 nm or less being completely vaporized in the ICP. In a subsequent set of measurements, we investigated SiO2 particles as large as 5010 nm in diameter (Fig. S3† shows data with optimized sensitivity, Δm = 0.7 amu). When the sensitivity was reduced, the largest SiO2 particle that still produced a signal that was linearly proportional to the mass of Si in the particle increased. Reducing the sensitivity by 13× (using Δm = 0.5), SiO2 particles as large as 990 nm produced signals that were linearly proportional to the mass of Si in the particle (Fig. S4†). Larger particles (diameters ≥ 1570 nm) produced smaller signals than expected.
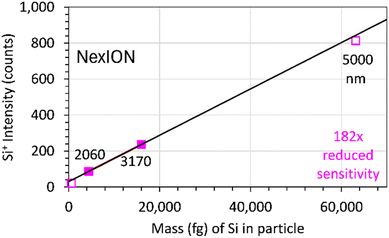
Reducing the sensitivity by 182× (using Δm = 0.15), provides results that are consistent with SiO2 particles nearly as large as 5010 nm being completely vaporized in the ICP (Fig. 7). However, SiO2 particles with diameters ≤ 1050 nm produced signals that were too small to accurately measure.
The Nu Instruments Vitesse spICP-TOFMS has an ion beam attenuator56 that uses grids to attenuate the ion beam current by ∼30× or ∼1000×, independent of m/z. Using optimized conditions (no attenuation), only the 500 nm, 690 nm, and 895 nm SiO2 particles produced Si+ signals that were linearly proportional to the mass of each particle (Fig. 3c and d). Using reduced sensitivity, the 895 nm, 1050 nm, and 2060 nm SiO2 particles produced average Si+ signals within the linear dynamic range of the instrument (Fig. 8c and d). The average Si+ intensities of the 500 nm and 690 nm SiO2 particles were overestimated due to the threshold cutting off lower intensity particle signals from the average intensity (similar to the data shown in Fig. 4). Using the ratio of particle number concentration measured using reduced sensitivity to optimized sensitivity, ∼96% and 66% of 500 nm and 690 nm SiO2 particles, respectively, were below the threshold. Further reducing sensitivity of both the icpTOF-R and Vitesse could ensure that all large SiO2 particles that are completely vaporized produce Si+ signal within the linear dynamic range. However, using reduced sensitivity, smaller SiO2 particles may not produce enough signal above the threshold to be accurately measured. It may be necessary to measure particle suspensions using both optimized sensitivity (for smaller particles) and one or more reduced sensitivities.
Au particles with diameters from 60 nm to 1500 nm were also measured with optimized sensitivity (Fig. S5a and b†) and 22× reduced sensitivity (Fig. S5c and d†) using the TOFWERK icpTOF-R. With optimized sensitivity only particles up to 150 nm in diameter produced signals that were linearly proportional to the Au mass in the particles (Fig S5a and b†). The signals for Au particles with diameters from 150 nm to 1000 nm increase nonlinearly. Even though the ion detection system could measure more than 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts, the relationship between Au mass and signal intensity became nonlinear at around 1400 counts. Perhaps a non-linear calibration function could be used to measure particles that produced signals greater than ∼1400 counts but less than ∼10
000 counts, the relationship between Au mass and signal intensity became nonlinear at around 1400 counts. Perhaps a non-linear calibration function could be used to measure particles that produced signals greater than ∼1400 counts but less than ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts; this requires further investigation. The average signal intensity from 1000 nm Au particles was larger than the signal produced from 1500 nm Au particles. The largest Au particle within the linear range was 300 nm when the sensitivity was reduced by 22×. The signals produced from 400 to 1500 nm Au particles were smaller than expected (Fig. S2b and S3d†) but closer to the expected signals than when optimized sensitivity was used. Further reduction in sensitivity, or perhaps a nonlinear calibration, would be needed to obtain the correct Au particle diameter based on the measured signal intensities.
000 counts; this requires further investigation. The average signal intensity from 1000 nm Au particles was larger than the signal produced from 1500 nm Au particles. The largest Au particle within the linear range was 300 nm when the sensitivity was reduced by 22×. The signals produced from 400 to 1500 nm Au particles were smaller than expected (Fig. S2b and S3d†) but closer to the expected signals than when optimized sensitivity was used. Further reduction in sensitivity, or perhaps a nonlinear calibration, would be needed to obtain the correct Au particle diameter based on the measured signal intensities.
4 Conclusions
The particle transport efficiency may be dependent on the particle size when a nebulizer/spray chamber sample introduction system is used. For the sample introduction system used in this study, the transport efficiency for SiO2 particles larger than 700 to 800 nm fell off dramatically as the particle diameter increased. The transport efficiency cannot be measured using nanoparticles (such as 60 nm Au) to accurate estimate the transport efficiency of particles larger than 700 to 800 nm. Therefore, the transport efficiency of larger particles must be experimentally determined as a function of particle size (mass). Furthermore, the Particle Frequency (Particle Number) based method must be used. The Particle Size (Solution/Nanoparticle) method measures the particle transport efficiency of elements dissolved in the solution and therefore cannot be used to determine the particle transport efficiency as a function of particle size (mass). The particle transport efficiency is also strongly dependent on the sample uptake rate when a nebulizer/spray chamber sample introduction system is used.44We have presented evidence that SiO2 particles as large as 5000 nm in diameter are completely vaporized in the ICP. The linear dynamic range for particle measurement using spICP-QMS or spICP-TOFMS is limited more by the ion detection system than by incomplete particle vaporization for SiO2 particles. Reducing instrument sensitivity (while keeping plasma conditions the same) can extend the upper end of the linear dynamic range enough to accurately measure engineered SiO2 particles at least large as 5000 nm (the largest size tested in this study).
The development of commercial spICP-TOFMS instruments is an important step forward in single particle analysis. This technique has the potential to, with important considerations and limitations, quickly measure the elemental compositions, mass equivalent size distributions, and number concentrations of thousands of individual nanoparticles and microparticles in minutes using small (less than 10 mL) sample volumes in a variety of environmental and industrial suspensions containing polydisperse, multi-element nanoparticles and microparticles. However, the particle size (mass) dependent particle transport efficiency of microparticles and the limited linear dynamic range of spICP-QMS and spICP-TOFMS must be accounted for to obtain accurate microparticle number concentrations, sizes, and elemental compositions.
Other considerations, including element and sample dependent detection limits and the effect of sample dependent background signal intensities (the quasi-continuous background that particle signals need to be distinguished from) must also be considered to accurately measure and compare measured particle number concentrations, the elemental compositions of particles, and the particle mass equivalent diameters. Some of these considerations will be the subject of a future publication.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
JWO and MLV conceived and planned this research. MLV and LMC made most of the measurements. PG was the original PI on the NSF grant that partially funded this research. SK provided Coulter counter measurements to confirm the particle number concentrations in some of the engineered particle suspensions. The first draft of this manuscript was taken in part from MLV's thesis. JWO wrote the final manuscript with editing input from MLV, LMC, and PG. JW was involved in key discussions about the results from the TOFWERK spICP-TOFMS and provided help in troubleshooting the instrument. RS and GVL allowed us to use the TOFWERK spICP-TOFMS in their laboratory. All authors provided input on the manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Funding support for JWO, MLV, LMC, and SK was provided in part by NSF Award 1744961. PerkinElmer is thanked for providing the NexION 350 ICP-MS and for partial funding support for JWO, MLV, and LMC. The Carnegie Mellon University Center for Atmospheric Particle Studies and Department of Civil and Environmental Engineering is thanked for use of the TOFWERK spICP-TOFMS instrument. Lukas Schlatt of Nu Ametek is thanked for making the measurements on the Vitesse spICP-TOFMS and sharing the data with us. JW acknowledges the Swiss National Science Foundation for funding this research under the Postdoctoral Mobility program (Project No. P500PN_202844).References
- F. Laborda, E. Bolea and J. Jiménez-Lamana, Single Particle Inductively Coupled Plasma Mass Spectrometry: A Powerful Tool for Nanoanalysis, Anal. Chem., 2014, 86, 2270–2278 CrossRef CAS PubMed.
- D. Mozhayeva and C. Engelhard, A critical review of single particle inductively coupled plasma mass spectrometry – A step towards an ideal method for nanomaterial characterization, J. Anal. At. Spectrom., 2020, 35, 1740–1783 RSC.
- X. Tian, H. Jiang, L. Hu, M. Wang, W. Cui, J. Shi, G. Liu, Y. Yin, Y. Cai and G. Jiang, Simultaneous multi-element and multi-isotope detection in single-particle ICP-MS analysis: Principles and applications, Trends Anal. Chem., 2022, 157, 116746 Search PubMed.
- J. Olesik, Single Particle ICP-MS: From Engineered Nanoparticles to Natural Nanoparticles, Spectroscopy, 2020, 35, 20–22 Search PubMed.
- M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Single Particle ICP-MS: Advances toward routine analysis of nanomaterials, Anal. Bioanal. Chem., 2016, 408, 5053–5074 CrossRef PubMed.
- J. Vidmar, T. Zuliani, R. Milačič and J. Ščančar, Following the Occurrence and Origin of Titanium Dioxide Nanoparticles in the Sava River by Single Particle ICP-MS, Water, 2022, 14, 959 CrossRef CAS.
- L. Hendriks and D. M. Mitrano, Direct Measurement of Microplastics by Carbon Detection via Single Particle ICP-TOFMS in Complex Aqueous Suspensions, Environ. Sci. Technol., 2023, 57, 7263–7272 CrossRef CAS PubMed.
- M. D. Montaño, C. W. Cuss, H. M. Holliday, M. B. Javed, W. Shotyk, K. L. Sobocinski, T. Hofmann, F. v. d. Kammer and J. F. Ranville, Exploring Nanogeochemical Environments: New Insights from Single Particle ICP-TOFMS and AF4-ICPMS, ACS Earth Space Chem., 2022, 6, 943–952 CrossRef PubMed.
- H. Karkee and A. Gundlach-Graham, Characterization and Quantification of Natural and Anthropogenic Titanium-Containing Particles Using Single-Particle ICP-TOFMS, Environ. Sci. Technol., 2023, 57, 14058–14070 CrossRef CAS PubMed.
- L. N. Rand, Using Single Particle ICP-MS to Study Occurrence and Behavior of Engineered, Natural, and Incidental Nanoparticles in Freshwater Streams, Colorado School of Mines, Arthur Lakes Library, 2019 Search PubMed.
- J. Xu, C. Chen, X. Hu, D. Chen, G. Bland, J. Wielinski, R. Kaegi, D. Lin and G. V. Lowry, Particle-Scale Understanding of Arsenic Interactions with Sulfidized Nanoscale Zerovalent Iron and Their Impacts on Dehalogenation Reactivity, Environ. Sci. Technol., 2023, 57, 21917–21926 CrossRef CAS PubMed.
- S. Bevers, M. D. Montaño, L. Rybicki, T. Hofmann, F. von der Kammer and J. F. Ranville, Quantification and Characterization of Nanoparticulate Zinc in an Urban Watershed, Front. Environ. Sci., 2020, 8 DOI:10.3389/fenvs.2020.00084.
- Y. Huang, A. A. Keller, P. Cervantes-Avilés and J. Nelson, Fast Multielement Quantification of Nanoparticles in Wastewater and Sludge Using Single-Particle ICP-MS, ACS ES&T Water, 2021, 1, 205–213 Search PubMed.
- A. J. Goodman, A. Gundlach-Graham, S. G. Bevers and J. F. Ranville, Characterization of nano-scale mineral dust aerosols in snow by single particle inductively coupled plasma mass spectrometry, Environ. Sci.: Nano, 2022, 9, 2638–2652 RSC.
- G. D. Bland, P. Zhang, E. Valsami-Jones and G. V. Lowry, Application of Isotopically Labeled Engineered Nanomaterials for Detection and Quantification in Soils via Single-Particle Inductively Coupled Plasma Time-of-Flight Mass Spectrometry, Environ. Sci. Technol., 2022, 56, 15584–15593 CrossRef CAS PubMed.
- G. D. Bland, M. Battifarano, A. E. Pradas del Real, G. Sarret and G. V. Lowry, Distinguishing Engineered TiO2 Nanomaterials from Natural Ti Nanomaterials in Soil Using spICP-TOFMS and Machine Learning, Environ. Sci. Technol., 2022, 56, 2990–3001 CrossRef CAS PubMed.
- G. D. Bland and G. V. Lowry, Multistep Method to Extract Moderately Soluble Copper Oxide Nanoparticles from Soil for Quantification and Characterization, Anal. Chem., 2020, 92, 9620–9628 CrossRef CAS PubMed.
- J. Xu, G. D. Bland, Y. Gu, H. Ziaei, X. Xiao, A. Deonarine, D. Reible, P. Bireta, T. P. Hoelen and G. V. Lowry, Impacts of Sediment Particle Grain Size and Mercury Speciation on Mercury Bioavailability Potential, Environ. Sci. Technol., 2021, 55, 12393–12402 CrossRef CAS PubMed.
- T. Erhardt, C. M. Jensen, O. Borovinskaya and H. Fischer, Single Particle Characterization and Total Elemental Concentration Measurements in Polar Ice Using Continuous Flow Analysis-Inductively Coupled Plasma Time-of-Flight Mass Spectrometry, Environ. Sci. Technol., 2019, 53, 13275–13283 CrossRef PubMed.
- S. E. Szakas, K. Menking-Hoggatt, T. Trejos and A. Gundlach-Graham, Elemental Characterization of Leaded and Lead-Free Inorganic Primer Gunshot Residue Standards Using Single Particle Inductively Coupled Plasma Time-of-Flight Mass Spectrometry, Appl. Spectrosc., 2023, 77, 873–884 CrossRef CAS PubMed.
- L. Hendriks, V. M. Kissling, T. Buerki-Thurnherr and D. M. Mitrano, Development of single-cell ICP-TOFMS to measure nanoplastics association with human cells, Environ. Sci.: Nano, 2023, 10, 3439–3449 RSC.
- S. Rodrigues, A. Avellan, G. D. Bland, M. C. R. Miranda, C. Larue, M. Wagner, D. A. Moreno-Bayona, H. Castillo-Michel, G. V. Lowry and S. M. Rodrigues, Effect of a Zinc Phosphate Shell on the Uptake and Translocation of Foliarly Applied ZnO Nanoparticles in Pepper Plants (Capsicum annuum), Environ. Sci. Technol., 2024, 58, 3213–3223 CAS.
- M. Baccaro, M. D. Montaño, X. Cui, A. Mackevica, I. Lynch, F. von der Kammer, R. W. Lodge, A. N. Khlobystov and N. W. van den Brink, Influence of dissolution on the uptake of bimetallic nanoparticles Au@Ag-NPs in soil organism Eisenia fetida, Chemosphere, 2022, 302, 134909 CrossRef CAS PubMed.
- L. Ebdon and A. R. Collier, Particle size effects on kaolin slurry analysis by inductively coupled plasma-atomic emission spectrometry, Spectrochim. Acta, Part B, 1988, 43, 355–369 CrossRef.
- L. Ebdon, M. E. Foulkes and S. Hill, Direct atomic spectrometric analysis by slurry atomisation. Part 9. Fundamental studies of refractory samples, J. Anal. At. Spectrom., 1990, 5, 67–73 RSC.
- P. Goodall, M. E. Foulkes and L. Ebdon, Slurry nebulization inductively coupled plasma spectrometry-the fundamental parameters discussed, Spectrochim. Acta, Part B, 1993, 48, 1563–1577 CrossRef.
- A. S. Groombridge, S.-i. Miyashita, S.-i. Fujii, K. Nagasawa, T. Okahashi, M. Ohata, T. Umemura, A. Takatsu, K. Inagaki and K. Chiba, High Sensitive Elemental Analysis of Single Yeast Cells (Saccharomyces cerevisiae) by Time-Resolved Inductively-Coupled Plasma Mass Spectrometry Using a High Efficiency Cell Introduction System, Anal. Sci., 2013, 29, 597–603 CrossRef CAS PubMed.
- S.-i. Miyashita, A. S. Groombridge, S.-i. Fujii, A. Minoda, A. Takatsu, A. Hioki, K. Chiba and K. Inagaki, Highly efficient single-cell analysis of microbial cells by time-resolved inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2014, 29, 1598–1606 RSC.
- J. W. Olesik and P. J. Gray, Considerations for measurement of individual nanoparticles or microparticles by ICP-MS: determination of the number of particles and the analyte mass in each particle, J. Anal. At. Spectrom., 2012, 27, 1143 RSC.
- W.-W. Lee and W.-T. Chan, Calibration of single-particle inductively coupled plasma-mass spectrometry (SP-ICP-MS), J. Anal. At. Spectrom., 2015, 30, 1245–1254 RSC.
- PerkinElmer, NexION 5000 Multi-Quadrupole ICP Mass Spectrometer, https://www.perkinelmer.com/product/final-assy-nexion-5000-n8160010.
- L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, Characterization of a new ICP-TOFMS instrument with continuous and discrete introduction of solutions, J. Anal. At. Spectrom., 2017, 32, 548–561 RSC.
- M. P. Dziewatkoski, L. B. Daniels and J. W. Olesik, Time-Resolved Inductively Coupled Plasma Mass Spectrometry Measurements with Individual, Monodisperse Drop Sample Introduction, Anal. Chem., 1996, 68, 1101–1109 CrossRef CAS PubMed.
- J. W. Olesik, Investigating the Fate of Individual Sample Droplets in Inductively Coupled Plasmas, Appl. Spectrosc., 1997, 51, 158A–175A CrossRef CAS.
- I. I. Stewart, C. E. Hensman and J. W. Olesik, Influence of Gas Sampling on Analyte Transport within the ICP and Ion Sampling for ICP-MS Studied Using Individual, Isolated Sample Droplets, Appl. Spectrosc., 2000, 54, 164–174 CrossRef CAS.
- V. Masalov, N. Sukhinina, E. Kudrenko and G. Emelchenko, Mechanism of formation and nanostructure of Stöber silica particles, Nanotechnology, 2011, 22, 275718 CrossRef CAS PubMed.
- K. Nozawa, H. Gailhanou, L. Raison, P. Panizza, H. Ushiki, E. Sellier, J. P. Delville and M. H. Delville, Smart Control of Monodisperse Stöber Silica Particles: Effect of Reactant Addition Rate on Growth Process, Langmuir, 2005, 21, 1516–1523 CrossRef CAS PubMed.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Determining Transport Efficiency for the Purpose of Counting and Sizing Nanoparticles via Single Particle Inductively Coupled Plasma Mass Spectrometry, Anal. Chem., 2011, 83, 9361–9369 CrossRef CAS PubMed.
- M. Tanner and D. Günther, Short transient signals, a challenge for inductively coupled plasma mass spectrometry, a review, Anal. Chim. Acta, 2009, 633, 19–28 CrossRef CAS PubMed.
- L. A. Currie, Limits for qualitative detection and quantitative determination. Application to radiochemistry, Anal. Chem., 1968, 40, 586–593 CrossRef CAS.
- L. A. Currie, Nomenclature in evaluation of analytical methods including detection and quantification capabilities (IUPAC Recommendations 1995), Pure Appl. Chem., 1995, 67, 1699–1723 CrossRef CAS.
- A. Gundlach-Graham and R. Lancaster, Mass-Dependent Critical Value Expressions for Particle Finding in Single-Particle ICP-TOFMS, Anal. Chem., 2023, 95, 5618–5626 CrossRef CAS PubMed.
- P. A. Freedman and K. Newman, Detection arrangements in mass spectrometers, US Pat., 8084751, 2011 Search PubMed.
- J. W. Olesik, J. A. Hartshorne, N. Casey, E. Linard and J. R. Dettman, Further insight into analyte transport processes and water vapor, aerosol loading in ICP-OES and ICP-MS, Spectrochim. Acta, Part B, 2021, 176, 106038 CrossRef CAS.
- S. G. Bevers, C. Smith, S. Brown, N. Malone, D. H. Fairbrother, A. J. Goodman and J. F. Ranville, Improved methodology for the analysis of polydisperse engineered and natural colloids by single particle inductively coupled plasma mass spectrometry (spICP-MS), Environ. Sci.: Nano, 2023, 10, 3136–3148 RSC.
- K.-S. Ho, K.-O. Lui, K.-H. Lee and W.-T. Chan, Considerations of particle vaporization and analyte diffusion in single-particle inductively coupled plasma-mass spectrometry, Spectrochim. Acta, Part B, 2013, 89, 30–39 CrossRef CAS.
- A. Laycock, N. J. Clark, R. Clough, R. Smith and R. D. Handy, Determination of metallic nanoparticles in biological samples by single particle ICP-MS: a systematic review from sample collection to analysis, Environ. Sci.: Nano, 2022, 9, 420–453 RSC.
- D. Ojeda, E. Bolea, J. Pérez-Arantegui and F. Laborda, Exploring the boundaries in the analysis of large particles by single particle inductively coupled plasma mass spectrometry: application to nanoclays, J. Anal. At. Spectrom., 2022, 37, 1501–1511 RSC.
- J. Liu, K. E. Murphy, R. I. Maccuspie and M. R. Winchester, Capabilities of Single Particle Inductively Coupled Plasma Mass Spectrometry for the Size Measurement of Nanoparticles: A Case Study on Gold Nanoparticles, Anal. Chem., 2014, 86, 3405–3414 CrossRef CAS PubMed.
- S. Yamashita, M. Nakazato and T. Hirata, Size Analysis of Small Metal Nanoparticles Using Single Particle ICP Mass Spectrometry, Anal. Sci., 2021, 37, 1637–1640 CrossRef CAS PubMed.
- C. Degueldre, P. Y. Favarger and S. Wold, Gold colloid analysis by inductively coupled plasma-mass spectrometry in a single particle mode, Anal. Chim. Acta, 2006, 555, 263–268 CrossRef CAS.
- I. Strenge and C. Engelhard, Single particle inductively coupled plasma mass spectrometry: investigating nonlinear response observed in pulse counting mode and extending the linear dynamic range by compensating for dead time related count losses on a microsecond timescale, J. Anal. At. Spectrom., 2020, 35, 84–99 RSC.
- S. Yamashita, A. Miyake and T. Hirata, Size analysis of large-sized gold nanoparticles using single particle ICP-mass spectrometry, J. Anal. At. Spectrom., 2020, 35, 2834–2839 RSC.
- TechNote 104 Silica Microspheres, Bangs Laboratories, Inc., 2013, https://bangslabs.com/wp-content/uploads/BLI_TN104_SilicsMicrospheres.pdf.
- A. C. Gimenez-Ingalaturre, K. Ben-Jeddou, J. Perez-Arantegui, M. S. Jimenez, E. Bolea and F. Laborda, How to trust size distributions obtained by single particle inductively coupled plasma mass spectrometry analysis, Anal. Bioanal. Chem., 2023, 415, 2101–2112 CrossRef CAS PubMed.
- P. Warburton, A. Donard, L. Schlatt, P. Shaw and J. Cottle, Presented in Part at the Goldschmidt, 2023 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00425f |
| This journal is © The Royal Society of Chemistry 2025 |