Influence of the distance between the focused point and Al surface on atomic and molecular emission spectra in air
Huihui
Zhu
ab,
Bowen
Fan
c,
Yubo
Zhang
ab,
Zhuo
Wu
ab,
Fuli
Chen
ab,
Xiaohui
Su
d and
Tao
Lü
 *ab
*ab
aSchool of Automation, China University of Geosciences, Wuhan, 430074, China. E-mail: lvtaohn@126.com
bHubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems, Wuhan, 430074, China
cSchool of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China
dSchool of Future Technology, China University of Geosciences, Wuhan 430074, China
First published on 3rd December 2024
Abstract
The focused position of the lens relative to the sample surface affects the density, temperature, and dynamic characteristics of laser-induced plasma, which are important for improving the spectral intensity, minimizing self-absorption, and improving stability of laser-induced breakdown spectroscopy (LIBS). The emission intensities of the Al atomic line and the AlO B2Σ+–X2Σ+(0,0) band, using nanosecond pulse laser ablation of an aluminum target in air, at three different focused point-to-sample distances were investigated. The Al atomic line was optimal when the focus was 1 cm above the sample surface, which is attributed to the low density and high temperature of the plasma. Conversely, the AlO B2Σ+–X2Σ+(0,0) band emission spectrum is superior when the focused point is 1 cm below the Al surface, with the spectral intensity enhancing as the number of laser shots increases. A time-resolved pump–probe shadowgraph technique was employed to record dynamic snapshots of the ablation plume at different focused point-to-sample distances to account for the enhancement mechanism of the spectral intensity. The intensity variations in the atomic and molecular spectra are related to the shock wave propagation velocity in the longitudinal and radial directions, providing insights into the enhancement mechanism of the spectral signals. Moreover, the morphology of craters was analyzed by using a scanning electron microscope and a profilometer, revealing that the depth-to-diameter ratio and ablation amount correlated with different spectral intensity variations at focused point-to-sample distances of −1 and 0 cm. These results will assist in choosing optimal strategies for quantifying elements using LIBS atomic or molecular spectrometry.
1. Introduction
Laser-induced breakdown spectroscopy (LIBS) can detect the composition and content of elements in various physical states (solid, liquid, and gas).1–3 The basic principle involves focusing high-energy laser pulses to form plasma on the sample surface, which emits characteristic spectral lines. The sample components can be determined by analyzing the emission spectrum.4,5 In principle, LIBS can simultaneously detect multiple elements in a sample, making it widely applicable in fields such as geology, environmental monitoring, space exploration, and nuclear material monitoring.6–8In LIBS, varying the acquisition delay allows the capture of spectra corresponding to different stages of plasma evolution.9–12 Initially, during the earliest times of expansion (≲1 μs), the plumes are hotter and denser, with emission dominated by ions. As the plasma cools (∼0.5–10 μs), atomic emissions become more prominent. At later times (∼2–50 μs), molecular species are generally formed due to atomic collisions and recombination, which occur more frequently as the plasma temperature decreases.13,14 Therefore, LIBS is used not only to analyze the characteristic spectra of atoms and ions in substances, but also to analyze the characteristic spectral bands of molecules. The spectral emission of molecules is important for halogen detection (e.g., F, Cl…), whose atomic and ionic lines are significantly weaker compared to some of the diatomic molecular emissions of halogens with alkali earth elements15,16 or for elements interesting for isotopic analysis (laser ablation molecular isotope spectroscopy (LAMIS)).12,17,18 Harilal et al. reported the formation mechanisms of molecules during the complex interactions of a laser-produced plasma plume. Their study found that early in plasma expansion, the shock wave (SW) generated at the plume edge acts as a barrier to the combustion process, with molecular formation becoming prevalent after the SW collapse.13 Zhao et al. studied the atomic and molecular emissions from the plasma of laser-ablated nitromethane in Ar or N2 atmospheres. They found that the fragmentation of nitromethane molecules was the dominant mechanism for early CN formation following plasma formation.19
Aluminum exhibits high chemical reactivity and readily reacts with oxygen in the air, which helps us better understand and explore the physical mechanisms underlying the formation of Al plasma and AlO by laser ablation of Al targets. Many studies have reported on the ablation of Al or AlO plasma,20–22 which facilitates the comparison and validation of our experimental results with existing studies. However, the stability, repeatability, and accuracy of quantitative analysis using LIBS are lower than those of traditional spectral analysis methods. Therefore, enhancing the analytical performance of LIBS has become the primary focus of current research.18–20 Strategies for enhancing the spectral quality include double-pulse excitation,13,23 spatial confinement,24 and magnetic confinement.25 However, these enhancement methods not only increase the complexity of optical setups but also increase experimental costs. Moreover, the settings and parameters of the experimental equipment, including the laser energy, pulse width, and wavelength, can significantly affect the spectral intensity in LIBS.26–30 Zhang et al. investigated the effect of laser pulse energy on Al atomic and AlO molecular spectra. Their results showed that the Al atom and AlO molecule exhibited different sensitivities to the laser pulse energy. As the laser pulse energy increased, the intensity of the Al atoms increased, whereas the emission of the AlO molecules first increased and then remained unchanged.30
In addition, to consider the impact of the experimental parameters on the spectral signals, studying the impact of the distance between the focused point and the target surface is also an important issue when analyzing solid samples. Harilal et al. studied the effect of spot size on the extreme ultraviolet conversion efficiency of CO2 laser-produced Sn plasma. It was discovered that the focus position is not the best place to optimize the conversion efficiency.31 Xu et al. investigated the influence of the distance between the focusing lens and target sample by femtosecond LIBS. The results indicate that by changing the distance between the focusing lens and the target surface, high-temperature and low-density plasma with strong spectral intensity can be obtained in femtosecond LIBS. This plasma, with its high temperature and low density, can be used to improve the LIBS sensitivity.32 Wang et al. studied the variations in the line intensity, background noise intensity, signal-to-background ratio, detection sensitivity, and limit of detection (LOD) of an element as a function of the lens-to-sample distance (LTSD). Their results show that when the LTSD was 94 mm, both the intensity of the analytical line and the background noise reached a maximum. When the LTSD changed from 93 to 99 mm, the LOD value of Si, Mn, and Cr remained small.33 Chen et al. used a picosecond laser to ablate a pure copper plate to generate a plasma spectrum and studied the effect of the focusing distance on the characteristics of the copper plasma. Studies have demonstrated that variations in the focal length and pulse energy result in differences in the beam irradiance as the lens-to-copper surface distance increases. Both the beam irradiance and size of the ablation spot changed the geometric structure of the plasma and particle density inside the plasma.34
Changes in the focused point-to-sample distance result in variations in the coupling efficiency between the laser pulse and sample surface, thereby affecting the morphology of the ablation crater formed after material removal.34 The morphology of the ablation craters also affected the spectral signals. Corsi et al. evaluated the effect of crater depth on the plasma properties (temperature, density, and emission characteristic spectrum). They found that the confinement effect produced by the crater enhanced the LIBS signal from laser-induced plasma.35 Li et al. studied the changes in the spectral line intensities of Fe and Cr during crater formation. They found that when a crater developed, the intensities of the ion lines decreased and those of the atomic lines increased. This is because the plasma generated in the crater had a higher initial emission intensity and cooled more easily as the crater deepens.34 Currently, these studies primarily investigate the impact of the distance between the focused point and the target sample, as well as the formation of an ablation crater, on the characteristic ions and atomic spectral lines. However, further investigations are required to understand the influence of these factors on the molecular spectrum.
Therefore, this study compares the trend of spectral line intensity changes with the number of laser shots for the Al I 396.15 nm and the (0,0) band of the AlO B2Σ+–X2Σ+ emission spectrum resulting from the distances of the focused point relative to the Al surface: −1 cm, 0 cm, and +1 cm, which are represented by L−1, L0, and L1. We examined the influence of the ablation crater morphology, diameter-to-depth ratio, and ablation amount on the evolution of the laser-induced plasma during this process. In addition, the temperature and density of the laser-induced plasma were calculated. We also used a CCD to capture laser-induced SWs to elucidate the influence of the focused point-to-sample distance on the characteristic spectra of the Al atoms and AlO molecules.
2. Materials and methods
Fig. 1 shows the experimental setup. A Q-switched Nd:YAG laser operating at a fundamental wavelength of 1064 nm was used as the ablation laser. Both the half-wave plate and Glan laser polarizer attenuated the laser energy to the desired value of 80 mJ. A focusing lens (focal length = 150 mm) converged the laser beam on the Al target (99% purity, the roughness is 4.30 ± 1.34 μm and the thickness is 1 cm), forming an Al plasma, and the lens was fixed on a translation stage to obtain different focused point-to-sample distances. L0 denotes that the focal position coincides with the sample surface, whereas L1 and L−1 indicate that the focal position is 1 cm above and below the sample surface, respectively. The plasma emission was transmitted to a spectrometer (SR-750-B1, Andor) equipped with an ICCD detector (iStar 334T, Andor). The slit width of the spectrometer was set to 10 μm. When collecting the spectrum, the collector is positioned at an angle of about 30° to the sample surface aligned with the focal point direction, and is approximately 2 mm away from the sample surface. The gate width of the ICCD for collecting the atomic spectrum is 5 μs, and for collecting the molecular spectrum of AlO, the gate width is 50 μs. A digital delay generator (DG645, Stanford Research Systems) was used to control the delay of the spectrometer relative to that of the nanosecond laser. The acquisition delay time was adjusted, the atomic spectrum was set to 500 ns, and the molecular emission was set to 10 μs. The cumulative number of the spectrum was 10 times to enhance the signal-to-noise ratio. Additionally, the pump–probe shadowgraphy technique was employed to capture the evolution of the SW generated at different focal positions. A CCD camera (Genie Nano XL, Teledyne DALSA) and nanosecond probe beam (Nanosecond-Flashlamps) are placed on both sides of the sample stage. The exposure time of the CCD is set to the millisecond level, which completely covers the duration of the laser-induced plasma. The pulse width of the Nanosecond-Flashlamps is 11 ns (which is also the gate width), which is parallelly irradiated on the plasma through a lens and then transmitted to the CCD camera. The delay of the probe beam relative to the ns laser was controlled using a digital delay generator. The spectral data were collected three times, and the average values were calculated to reduce errors.3. Results and discussion
3.1 Spectral characteristics under the conditions of L1, L0, and L−1
Emission spectroscopy can be used to identify various excited species (atoms, ions, and molecules) in a laser ablation plume and evaluate the fundamental plasma properties. This section focuses on the characteristics of the atomic and molecular spectra when the focus is on the Al surface (L0), 1 cm above (L1), and 1 cm below (L−1) the Al surface. Spectra in the wavelength range of 300–600 nm obtained from the Al plasma recorded for L0 at various times after the onset of plasma formation are shown in Fig. 2. As shown in Fig. 2(a) and (b), during the initial stages, Al I and Al II dominated the emission. As time progressed, Al I was enhanced and Al II was weakened, as shown in Fig. 2(c). At later times (≥6 μs), the atomic spectrum weakened and AlO B2Σ+–X2Σ+ emission appeared (Fig. 2(d)). Therefore, we chose a delay time of 500 ns for atomic spectrum collection and 10 μs for molecular spectrum collection. | ||
| Fig. 2 Time-resolved plasma spectrum recorded at L0. The acquisition delays: 50 ns, 500 ns, 6 μs, and 10 μs and gain: 2000. | ||
The self-absorption can influence the intensity of the spectrum.36,37 The atomic spectral lines collected at L0 (red line), L−1 (black line) and L1 (blue line) are shown in Fig. 3(a). The full width at half maximum (FWHM) of the atomic spectrum at L1 is 1.25 Å, much smaller than the values at L0 and L−1, which are 4.21 Å and 3.91 Å respectively. Then, we calculate the self-absorption coefficient (SAC) to reflect the degree of self-absorption of the spectrum.38 The specific calculation formula is as follows:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ablation pulses.
000 ablation pulses.
 | ||
Fig. 4 The AlO molecular spectrum at L−1 (black line), L0 (red line), and L1 (blue line) after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pulses. The gate time: 50 μs and acquisition delays: 10 μs. 000 pulses. The gate time: 50 μs and acquisition delays: 10 μs. | ||
We statistically analyzed the evolution of Al I 396.15 nm and the (0,0) band of AlO B2Σ+–X2Σ+ emission spectral intensity with the number of ablation pulses at L−1, L0, and L1. In Fig. 5(a), the intensity of Al I 396.15 nm initially increases and then decreases with the number of laser shots at L0 and L−1. The trend in the atomic spectral intensity at L0 is consistent with the results of Nagli et al.41 At L−1, as the number of laser shots increases, the emission of the Al atomic line first increases and then remains unchanged. This was related to the depth-to-diameter ratio of the ablation crater, as discussed in Section 3.4. It can be seen from Fig. 5(b) that the molecular spectrum intensity collected at L−1 and L0 is significantly stronger than that at L1. In addition, the intensity of the molecular spectrum was less affected by the number of ablation pulses than that of the atomic lines. Consequently, altering the focused point-to-sample distance has a significant impact on the intensity trends of the atomic and molecular spectra.
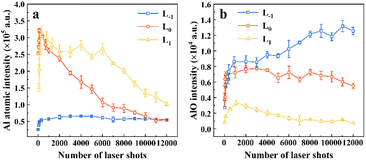 | ||
| Fig. 5 Pulse-resolved Al I 396.15 nm (a) and AlO B2Σ+–X2Σ+ (0,0) band emission (b) at three focal positions, L−1, L0 and L1. | ||
3.2 Plasma temperature and density
Temperature Te and electron density Ne are the characteristic properties of plasma that influence its spectral emissions.42Fig. 6 presents an example of the Al atomic line collected at L1 under 100 pulses, and the AlO B2Σ+–X2Σ+ (Δν = 0) emission spectrum collected at L−1 under 800 pulses. These characteristic spectra were used to calculate temperature and density. The plasma temperature was determined using the Boltzmann plot method. For plasma in local thermodynamic equilibrium (LTE), the population of excited states conforms to the Boltzmann distribution function as follows:32 | (1) |
The electron density is typically determined using the FWHM of the spectral lines to measure the Stark broadening by neglecting the contributions of ion impact broadening and Doppler broadening. This is expressed as follows:43
 | (2) |
In addition, the McWhirter criterion (a necessary condition) should be satisfied for the validity of LTE:44
| Ne ≥ 1.6 × 1012Te1/2(ΔE)3 | (3) |
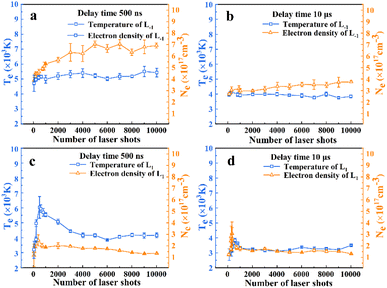 | ||
| Fig. 7 The evolution of plasma temperature Te (blue line) and electron number density Ne (orange line) with the number of ablations. | ||
Fig. 7 shows that the plasma temperature collected at 10 μs is significantly lower than that at 500 ns. The AlO molecular spectrum arises primarily from the molecular vibrations and rotations. High temperatures tend to disrupt the molecular bonds, thereby impeding the formation of AlO molecules.5 In Fig. 7(a) and (c), the plasma density is lower at L1, which explains why high-resolution atomic spectra were obtained. Simultaneously, at L1, the temperature was more easily affected by the number of ablation pulses; the temperature first increased and then decreased with an increase in the number of ablation pulses, as shown in Fig. 7(c). Meanwhile, at L−1, the plasma temperature first increases and then remains constant. In addition, as shown in Fig. 7(b) and (d), the evolution of the plasma temperature remained relatively stable with the number of laser shots. These results are consistent with the observed evolution of the Al atomic spectral intensity.
3.3 Relationship between shock wave propagation and spectral intensity
To elucidate the impact of the focused point-to-sample distance on the intensity of the Al atomic and AlO emission spectra, we employed the shadowgraph technique to record the SW generated by the Al plasma at three different distances, as illustrated in Fig. 8. The recorded snapshots show the emergence of a gourd-shaped SW front at L1, which comprises the first pear-shaped SW and the second hemispheric SW resulting from air breakdown and dielectric breakdown, respectively.45 This is because the ionization front of the air forms instantaneously, expands acutely, and compresses the surrounding air, causing a difference in the propagation speed of the SW in the radial and longitudinal directions.The distance and velocity of the SW in the longitudinal and radial directions were investigated, as shown in Fig. 9. The SW induced by the laser can be approximated as an instantaneous, massless point explosion (blast wave). The radius, R, of the blast wave depends on the energy converted into the plasma state, E. An analytical expression between R and E can be provided by the Sedov–Taylor formula:46
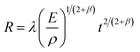 | (4) |
Once the energy value of the hemispherical blast wave (E) is estimated, the instantaneous propagation velocity of the spherical shock can be calculated by differentiating eqn (4) with respect to time. The radial wave propagation speed was always higher than the longitudinal speed at L−1 and L0, as shown in Fig. 9(a) and (b), respectively. As illustrated in Fig. 9(c), the longitudinal wave propagates faster than the radial wave at L1 (the velocity of the longitudinal wave decays rapidly from 8086 m s−1 at 157 ns to 976 m s−1 at 2066 ns and the radial velocity decreased from 5150 m s−1 at 157 ns to 967 m s−1 at 2066 ns).
In view of the above analysis, we found that SW propagation is directly related to spectral characteristics. For atomic spectra, as shown in Fig. 3 and 5(a), compared with that at L−1, the FWHM is narrower and the intensity is stronger at L1. This is because the plasma volume is larger at L1 (plasma images at L1 and L−1), which reduces the plasma density and narrows the FWHM. The plasma generated from gas breakdown at the L1 position absorbs and scatters part of the laser energy, resulting in a lower energy density at L1 compared to L0 and L−1, and thus the energy density distribution follows the pattern of L0 > L−1 > L1. Additionally, the air expansion and displacement caused by the gas breakdown create a low-pressure region, which alters the gas dynamics near the sample surface, and it is beneficial for the upward expansion of the Al plasma. This principle is similar to the enhancement of preheating in dual-beam laser-induced breakdown spectroscopy.47 In contrast, at L−1 radial velocity propagates faster than the longitudinal velocity in Fig. 9(a). It is compressed by the air, which weakens the propagation velocity of the Al plasma, making the atomic spectrum weak at L−1 in Fig. 5(a).
For molecular spectra, as shown in Fig. 4 and 5(b), the intensity of the molecular spectrum collected at L−1 is stronger than that at L1. According to the formation process of the excited-state AlO radical proposed by Kasatani et al.,48
| Al + O2 → AlO(X2Σ) + O, |
| Al + O + O2 → AlO3 → AlO(B2Σ) + O2. |
It can be observed that the reaction between Al and O2 only generates AlO in the ground state (X2Σ). To acquire AlO in the excited state (B2Σ), Al and O require a subsequent collision with O2, which leads to the formation of the intermediate state AlO3. This study demonstrates the significant role of O2 in the atmosphere in the formation of AlO. At the same time, according to the research of Harilal et al.,13 the availability of O2 in the plasma, which is controlled by the SW, develops at the plasma–gas interface. Consequently, at L1, the longitudinal wave propagated faster than the radial wave, confirming that the nanosecond laser first induces air breakdown. Air plasma is instantly formed, rapidly expands, and compresses the surrounding air. This prevents O2 in the air from combining with the highly excited state of Al; therefore, the intensity of the AlO molecular spectrum at L1 was relatively weaker. In addition, Ran et al. showed that the SW generated during the laser ablation of a sample formed a vortex near the sample surface, causing the surrounding air to flow into and diffuse into the bottom of the plasma to promote the formation of AlO molecules.22 At L−1, owing to the compression of air, the radial wave propagated faster than the longitudinal wave in Fig. 9(a), distributing the Al plasma near the sample surface, which was more conducive to the formation of the molecular spectrum. This is also related to the heat transfer during the ns laser ablation process. In discussing the impact of heat transfer on the ablation process, the contact area between the ablation plume and the surrounding air is a key factor. At the L−1 position, the plume has a larger contact area with the air, which promotes rapid heat dissipation. However, at the L1 position, the heat exchange between the plume and the surrounding air is less efficient due to the presence of a low-pressure region, resulting in slower cooling. This slower cooling is unfavourable for the formation of oxides like AlO, as their formation typically requires rapid cooling to facilitate the bonding of oxygen and Al. Therefore, differences in heat transfer efficiency directly affect the formation of molecules such as AlO, making this a crucial point in the discussion of heat transfer in ablation plumes.
3.4 The influence of ablation crater morphology on spectral intensity
The spectral intensity exhibits different evolutions at different focused positions. To elucidate the reason for this, we used a scanning electron microscope (SEM: MIRA3, TESCAN) and a 3D optical profilometer (NewView 9000, ZYGO) to measure the morphology of ablation craters and statistically calculated the depth-to-diameter ratio of the ablation crater and ablation amount under different ablation pulses. As shown in Fig. 10, the diameter of the crater is 750 μm at L0, which is smaller than the diameter of 1400 μm measured at L−1. This was caused by the different laser energy densities of the laser beam reaching the sample surface owing to the different focusing positions. We also found that multiple focuses appeared at L1 causing the laser beam to breakdown the air and subsequently interact with the sample surface. Here, we only measure the depth at L−1 and L0, employing a profilometer. Fig. 11(a) and (c) illustrate the morphology of the ablative crater, and Fig. 11(b) and (d) provide statistical data on the depth of the ablative crater under different laser shots. It is clear that the central area at L−1 is less smooth compared to that at L0. This difference arises from insufficient ablation, indicating that the central temperature at L−1 is lower than that at L0. Also, the occurrence of a phase explosion results in a smoother surface of the ablation crater. This phenomenon occurs when the energy density exceeds approximately 15 J cm−2. After a rough calculation, the energy density at L−1 and L0 is 5.16 J cm−2 and 18 J cm−2, respectively. At L0, the high laser energy density caused a phase explosion, resulting in a smoother central area of the ablation crater.49 Conversely, at L−1, the energy is inadequate to induce a phase explosion, leading to insufficient ablation and a rougher central area. The depth-to-diameter ratios of the ablation craters are listed in Table 1. What can be confirmed is that the spectral intensity depends on the ratio of depth to diameter,35,50–52 but the optimal ratio depends on the specific experimental conditions. At L0, after approximately 100 ablation pulses, the ratio reached 0.16, coinciding with the peak intensity of the atomic lines. However, the spectral intensity initially increases and then remains constant at L−1. After 1000 ablation shots, the intensity begins to stabilize, corresponding to a depth-to-diameter ratio of 0.03.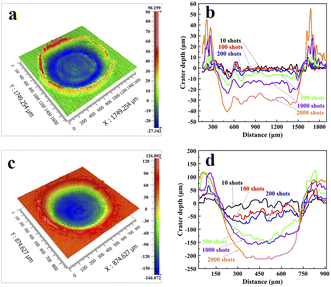 | ||
| Fig. 11 The 3D morphology of the Al ablation crater measured under 500 pulses at (a) L−1 and (c) L0. The crater depth at (b) L−1 and (d) L0 under different laser shots. | ||
| Number of laser shots at L−1 | 100 | 300 | 500 | 1000 | 2000 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|---|---|---|---|---|---|---|
| Depth (μm) | 17.41 | 22.08 | 30.96 | 54.24 | 96.51 | 344.56 |
| Depth to diameter | 0.0116 | 0.0139 | 0.0188 | 0.0321 | 0.0568 | 0.1974 |
| Volume (mm3) | 0.0026 | 0.0077 | 0.0119 | 0.0231 | 0.0404 | 0.1826 |
| Ablation amount (mg) | 0.007 | 0.0208 | 0.0322 | 0.0623 | 0.109 | 0.4931 |
| Number of laser shots at L0 | 100 | 300 | 500 | 1000 | 2000 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|---|---|---|---|---|---|---|
| Depth (μm) | 117.19 | 165.22 | 273.6 | 274.92 | 329.76 | 861.55 |
| Depth to diameter | 0.1643 | 0.2056 | 0.3244 | 0.3298 | 0.3864 | 0.9863 |
| Volume (mm3) | 0.0139 | 0.0222 | 0.038 | 0.0441 | 0.0681 | 0.1414 |
| Ablation amount (mg) | 0.0375 | 0.0599 | 0.103 | 0.1189 | 0.1838 | 0.3817 |
The variation in the spectral intensity was also influenced by the interaction between the plasma and crater wall. This can be observed from the change in the amount of ablation with the number of laser shots, as shown in Fig. 12. The formula of the ablation amount is m = ρV (the sample density ρ = 2.7 mg mm−3). The program calculates the volume of the ablation crater by fitting the data points on its surface. First, the program reads laser measurement data on a 2D grid and then uses the least squares method to fit a plane as a reference baseline. The fitting equation is z = k0 × x + k1 × y + k2. Next, the program calculates the height difference of each data point on the ablation crater surface relative to the fitted plane and accumulates all pixels with negative height differences to calculate the volume of the ablation area. Finally, due to the height data used in the program being based on normalized non-physical units, it is necessary to convert the actual units according to specific scaling factors, and the volume of the ablation crater is output. Fig. 12 illustrates the relationship between the volume of the material removed and the number of laser shots. The amount of ablation at L0 is greater than that at L−1, but its ablation diameter is much smaller than that at L−1, which indicates that the intensity is not significantly related to the amount of ablation. This is due to the large diameter of the ablation crater, which increases the contact area between the ablation plume and the surrounding air. Additionally, the laser has a Gaussian beam profile, resulting in lower plasma temperatures at the edges of the crater, which is farther from the beam center, thereby facilitating the formation of AlO. In Fig. 12(a), the removal material increases linearly with the number of laser shots at L−1. However, it increases nonlinearly at L0, as shown in Fig. 12(b). As the number of laser shots increased, the initial interaction between the plasma and crater wall strengthened, resulting in more material-forming plasma. However, as the crater depth increased, the shielding effect of the laser within the crater intensified, reducing the laser energy reaching the bottom of the crater. Consequently, the laser ablates slightly less material at the bottom of the crater. This leads to a weakening of the spectral intensity at L0 as the number of shots increases.
4. Conclusions
In this paper, the evolution of Al I 396.15 nm and AlO B2Σ+–X2Σ+(0,0) band emission spectra was dependent on focused point-to-sample distances. The atomic spectrum obtained at L1 was preferable because of its high temperature and low plasma density, which weakened the self-absorption effects. However, a superior AlO emission spectrum is observed at L−1 and the spectral intensity continues to increase as the number of laser shots increases. We compared the plume hydrodynamics at three different focal positions and found that the longitudinal wave propagated faster than the radial SW at L1 because the air expansion and displacement caused by the gas breakdown create a low-pressure region, which alters the gas dynamics near the sample surface. It is beneficial to the subsequent expansion of Al plasma, thereby enhancing the Al atomic line. However, at L−1, the velocity of the radial wave is faster than that of the longitudinal wave, and the SW is compressed by the surrounding air, causing the Al plasma to concentrate near the sample surface. Additionally, the morphology of the ablation crater at L−1 indicates a larger contact area between the plume and the surrounding air, promoting rapid cooling and creating a low-temperature environment, which is conducive to the formation of the molecular spectrum. Moreover, the depth-to-diameter ratio and ablation amount were measured at L0 and L−1, which can help to better understand the spectral intensity variation with ablation pulses. These results further explain the enhancement mechanism of the atomic lines and the formation of the molecular spectra. Therefore, high-resolution atomic lines and high-intensity molecular spectra were obtained by changing the focused point-to-sample distance. These results can help us choose an appropriate focus strategy for application-oriented LIBS analysis.Data availability
All data relevant to this study are available. For further information or special data requests, please contact the corresponding author. All requests will be processed in accordance with the relevant data-sharing policies.Author contributions
Huihui Zhu: conceptualization, investigation, data analysis and discussions, and writing – original draft. Bowen Fan: writing – review & editing. Yubo Zhang, Zhuo Wu, Fuli Chen and Xiaohui Su: validation. Tao Lü: funding acquisition, writing – review & editing, and supervision. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Key Research and Development Program of Hubei Province (2023BAB063); National Key Research and Development Program of China (2024YFF0728300); National Key Scientific Instrument and Equipment Development Projects of China (41927803); National Natural Science Foundation of China (12372212).References
- D. Zhang, R. Yang, H. Ge, Z. Feng, G. Wang, J. Hou, W. Tian and J. Zhu, Spectrochim. Acta, Part B, 2023, 204, 106670 CrossRef CAS.
- Z. Feng, J. Zhang, X. Li, Q. Gao and B. Li, J. Phys. D Appl. Phys., 2022, 55, 505206 CrossRef CAS.
- S. Li, R. Zheng, Y. Deguchi, W. Ye, Y. Tian, J. Guo, Y. Li and Y. Lu, Plasma Sci. Technol., 2023, 25, 045510 CrossRef.
- D. M. Wong, A. A. Bol'shakov and R. E. Russo, Encycl. Spectrosc. Spectrom., 2016, 18, 533–538 Search PubMed.
- D. W. Hahn and N. Omenetto, Appl. Spectrosc., 2012, 66, 347–419 CrossRef CAS.
- S. U. Choi, S. C. Han, J. Y. Lee and J. Il Yun, J. Anal. At. Spectrom., 2021, 36, 1287–1296 RSC.
- P. K. Srungaram, K. K. Ayyalasomayajula, F. Yu-Yueh and J. P. Singh, Spectrochim. Acta, Part B, 2013, 87, 108–113 CrossRef CAS.
- R. Gaudiuso, M. Dell'Aglio, O. De Pascale, G. S. Senesi and A. De Giacomo, Sensors, 2010, 10, 7434–7468 CrossRef CAS PubMed.
- C. Méndez-López, L. J. Fernández-Menéndez, C. González-Gago, J. Pisonero and N. Bordel, Opt. Laser Technol., 2023, 164, 109536 CrossRef.
- A. A. Bol'Shakov, X. Mao, J. J. González and R. E. Russo, J. Anal. At. Spectrom., 2016, 31, 119–134 RSC.
- M. Weiss, Z. Gajarska, H. Lohninger, M. Marchetti-Deschmann, G. Ramer, B. Lendl and A. Limbeck, Anal. Chim. Acta, 2022, 1195, 339422 CrossRef CAS PubMed.
- R. E. Russo, A. A. Bol'Shakov, X. Mao, C. P. McKay, D. L. Perry and O. Sorkhabi, Spectrochim. Acta, Part B, 2011, 66, 99–104 CrossRef.
- S. S. Harilal, B. E. Brumfield, B. D. Cannon and M. C. Phillips, Anal. Chem., 2016, 88, 2296–2302 CrossRef CAS.
- N. R. Glavin, C. Muratore, M. L. Jespersen, J. Hu, T. S. Fisher and A. A. Voevodin, J. Appl. Phys., 2015, 117, 165305 CrossRef.
- M. Weiss, Z. Gajarska, H. Lohninger, M. Marchetti-Deschmann, G. Ramer, B. Lendl and A. Limbeck, Anal. Chim. Acta, 2022, 1195, 339422 CrossRef CAS.
- L. Nagli, M. Gaft and Y. Raichlin, Spectrochim. Acta, Part B, 2020, 166, 105813 CrossRef CAS.
- H. Niki, T. Yasuda and I. Kitazima, J. Nucl. Sci. Technol., 1998, 35, 34–39 CrossRef CAS.
- R. E. Russo, X. Mao, J. J. Gonzalez, V. Zorba and J. Yoo, Anal. Chem., 2013, 85, 6162–6177 CrossRef CAS PubMed.
- Y. L. Zhao, G. G. Li, H. M. Hou, J. C. Shi and S. N. Luo, J. Hazard. Mater., 2020, 393, 122396 CrossRef CAS.
- H. Hou, X. Mao, V. Zorba and R. E. Russo, Anal. Chem., 2017, 89, 7750–7757 CrossRef CAS.
- K. Yahiaoui and S. Messaoud Aberkane, Spectrochim. Acta, Part B, 2021, 180, 106197 CrossRef CAS.
- P. Ran, H. Hou and S. N. Luo, J. Anal. At. Spectrom., 2017, 32, 2254–2262 RSC.
- S. Zhao, C. Song, X. Gao and J. Lin, Results Phys., 2019, 15, 102736 CrossRef.
- H. Li, C. Wang, Y. Wang, S. Fu and L. Fang, Meas. Sci. Technol., 2023, 34, 095204 CrossRef CAS.
- A. Hussain, G. Xun, H. Asghar, M. Azam, Q. - Ain and Z. Nawaz, Opt. Spectrosc., 2021, 129, 452–459 CrossRef CAS.
- X. Li, Z. Wang, Y. Fu, Z. Li and W. Ni, Plasma Sci. Technol., 2015, 17, 621–624 CrossRef CAS.
- M. S. Afgan, Z. Hou, W. Song, J. Liu, Y. Song, W. Gu and Z. Wang, Chemosensors, 2022, 10, 350 CrossRef CAS.
- D. Díaz, A. Molina and D. Hahn, Spectrochim. Acta, Part B, 2018, 145, 86–95 CrossRef.
- A. L. Krüger, G. Nicolodelli, P. R. Villas-Boas, A. Watanabe and D. M. B. P. Milori, Plasma Chem. Plasma Process., 2020, 40, 1417–1427 CrossRef.
- Y. Zhang, Q. Wang, A. Chen and X. Gao, Laser Phys., 2023, 33, 076003 CrossRef CAS.
- S. S. Harilal, R. W. Coons, P. Hough and A. Hassanein, Appl. Phys. Lett., 2009, 95, 3–5 CrossRef.
- W. Xu, A. Chen, Q. Wang, D. Zhang, Y. Wang, S. Li, Y. Jiang and M. Jin, J. Anal. At. Spectrom., 2019, 34, 1018–1025 RSC.
- J. Wang, X. Li, H. Li, X. Li and Z. Li, J. Phys. D Appl. Phys., 2020, 53, 255203 CrossRef CAS.
- L. Chen, H. Deng, Z. Wu, Z. Xiong, J. Guo, Q. Liu, A. D. Samuel and L. Shang, Adv. High Energy Phys., 2022, 2022, 4885924 Search PubMed.
- M. Corsi, G. Cristoforetti, M. Hidalgo, D. Iriarte, S. Legnaioli, V. Palleschi, A. Salvetti and E. Tognoni, Appl. Spectrosc., 2005, 59, 853–860 CrossRef CAS PubMed.
- K. Grant, G. Paul and J. O'Neill, Appl. Spectrosc., 1991, 45, 701–705 CrossRef CAS.
- C. G. Parigger, D. M. Surmick and G. Gautam, J. Phys.:Conf. Ser., 2017, 810, 12012 CrossRef.
- A. M. El Sherbini, T. M. El Sherbini, H. Hegazy, G. Cristoforetti, S. Legnaioli, V. Palleschi, L. Pardini, A. Salvetti and E. Tognoni, Spectrochim. Acta, Part B, 2005, 60, 1573–1579 CrossRef.
- C. G. Parigger, D. M. Surmick, G. Gautam and A. M. El Sherbini, Opt. Lett., 2015, 40, 3436–3439 CrossRef CAS PubMed.
- X. N. He, W. Hu, C. M. Li, L. B. Guo and Y. F. Lu, Opt. Express, 2011, 19, 10997 CrossRef CAS PubMed.
- L. Nagli, A. Prosnyakov, M. Gaft and Y. Raichlin, Spectrochim. Acta, Part B, 2021, 183, 106246 CrossRef CAS.
- H. Shakeel, S. Arshad, S. U. Haq and A. Nadeem, Phys. Plasmas, 2016, 23, 53504 CrossRef.
- E. Mal, R. Junjuri, M. K. Gundawar and A. Khare, J. Anal. At. Spectrom., 2019, 34, 319–330 RSC.
- Y. Zhang, Z. Zhao, T. Xu, G. Niu, Y. Liu and Y. Duan, Appl. Opt., 2016, 55, 2741–2747 CrossRef CAS PubMed.
- H. Hu, X. Wang, H. Zhai, N. Zhang and P. Wang, Appl. Phys. Lett., 2010, 97, 061117 CrossRef.
- T. Lű, Y. Hu, Z. Li, J. Meng, C. Zhang and E. Tuyizere, Spectrochim. Acta, Part B, 2018, 147, 43–50 CrossRef.
- N. Li, E. Harefa and W. Zhou, Plasma Sci. Technol., 2022, 24, 115507 CrossRef CAS.
- K. Kasatani, H. Higashide, H. Shinohara and H. Sato, Chem. Phys. Lett., 1990, 174, 71–74 CrossRef CAS.
- Y. Cao, X. Zhao and Y. C. Shin, J. Laser Appl., 2013, 25, 032002 CrossRef.
- X. Zeng, X. Mao, S. S. Mao, J. H. Yoo, R. Greif and R. E. Russo, J. Appl. Phys., 2004, 95, 816–822 CrossRef CAS.
- X. Su, W. Zhou and H. Qian, Opt. Express, 2014, 22, 28437–28442 CrossRef PubMed.
- L. Ren, X. Hao, H. Tang and Y. Sun, Results Phys., 2019, 15, 102798 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |








