Methanol-based thermoelectric conversion device with high power

Abstract

A liquid thermoelectric conversion device (LTE) converts environmental heat into electric power via the electrochemical Seebeck coefficient α. The maximum power (W_max) is expressed as , where ΔT and R′ are the temperature difference between electrodes and device resistance in operation, respectively. Here, we systematically investigated the resistance components of LTEs composed of aqueous, methanol (MeOH) and acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. We found that the charge transfer resistance R_ct of the MeOH LTE is the smallest among the three LTEs. We demonstrated that the W_max of the MeOH LTE is slightly larger than or comparable with that of the corresponding aqueous LTE. We further discussed the effects of the convection of an electrolyte on R′.

Keywords: Liquid thermoelectric conversion; Methanol; Resistivity components; Coated electrode.

---

1 Introduction

Energy harvesting devices are extensively investigated from the viewpoint of achieving the sustainable development goals (SDGs). Among the devices, liquid thermoelectric conversion devices (LTEs)^1–5 have a simple device structure in which a redox-dissolved electrolyte is sandwiched between two electrodes. LTEs utilize the thermogalvanic effect (electrochemical Seebeck coefficient α) at each electrode to convert temperature differences ΔT between the electrodes into thermal voltage or electric power W. The research of LTE is increasingly active with significant progress.^6–23 The performance of LTE is determined by α, effective electric conductivity σ, and effective thermal conductivity κ of the electrolyte. The term “effective” is used because the convection of the electrolyte due to gravity affects σ and κ in an actual LTE in operation.^24–26 The maximum power (W_max) is expressed as , where R′ is the device resistance in operation. To increase W_max, it is effective to increase α or to decrease R′. α is expressed as , where ΔS and e (>0) are the entropy change at the reduction reaction of the redox couple and elementary charge.

In a non-operating LTE at ΔT = 0 K without electrolyte convection, the device resistance (R) can be decomposed into solution resistance R_s, charge transfer resistance R_ct, and diffusion resistance R_dif.²⁷ Similar to the resistance in a solid, R_s is determined by the balance between the electric force and frictional force. Then, R_s is proportional to the electrode distance d.²⁸ On the other hand, R_ct and R_dif are governed by the redox reaction kinetics in the vicinity of the electrode, and are independent of d. As the reaction progresses, the concentration of reactants/products at the electrode surface changes in a way that prevents further reaction. The resultant concentration gradient drives the diffusion of reactants from (products into) the bulk region, causing R_dif. In a LTE in operation, R′ is further influenced by the electrolyte convection driven by ΔT,^25,26 which causes mass transfer and tends to make the concentration in the electrolyte uniform.

Aqueous solutions containing Fe²⁺/Fe³⁺ are most extensively investigated as electrolytes for LTE, because Fe²⁺/Fe³⁺ is inexpensive and aqueous LTE shows high σ. Kim et al.²⁰ reported that α and σ of Fe²⁺/Fe³⁺ aqueous solutions become larger when ClO₄⁻ is the counter anion. Buckingham et al.²¹ demonstrated that α of Fe²⁺/Fe³⁺ aqueous solutions can be optimized by the pH of the electrolyte. Jung et al.²² reported that FeCN coated carbon cloth shows small R_ct in Fe²⁺/Fe³⁺ aqueous solution. Aiba et al.²⁸ reported that R of graphite-dispersing coated electrodes steeply decreases as the electrode thickness t increases below t ≤ 100 μm. On the other hand, Wake et al.,^18,19 systematically investigated α and σ of organic solutions containing Fe(ClO₄)₂/Fe(ClO₄)₃. They found that the σ (= 34.6 mS cm⁻¹ at 0.7 M) of methanol (MeOH) solution is the highest among those of 11 organic solutions. In addition, the α values of MeOH (1.85 mV K⁻¹ at 0.5 M) and acetone (2.88 mV K⁻¹ at 0.1 M) are much higher than the α (= 1.56 mV K⁻¹ at 0.5 M) of aqueous solution. Therefore, MeOH and acetone LTEs are alternative LTE candidates with high W_max.

In this paper, we systematically investigated the resistance components of LTEs composed of aqueous, MeOH and acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. We found that the R_ct of the MeOH LTE is the smallest among the three LTEs. We demonstrated that the W_max of the MeOH LTE is slightly larger than or comparable with that of the corresponding aqueous LTE. We further discussed the effects of the electrolyte convection on R′.

2 Results and discussion

2.1 Resistance components against temperature

Fig. 1a shows the current I–voltage V plots at ΔT = 0 K in (a) aqueous, (b) MeOH, and (c) acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ at different temperatures T. s and d were 42 mm² and 10 mm, respectively. At all temperatures, V increases in proportion to I. R was evaluated from the slope of the plot, as indicated by straight lines. R steeply decreases as T increases.

Fig. 1 Voltage V against current I in (a) aqueous, (b) MeOH, and (c) acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ at different temperatures T. The electrode area s and distance d were 42 mm² and 10 mm, respectively. The straight lines are the results of least-squares fits.

Fig. 2 shows the Cole–Cole plots of complex impedance in (a) aqueous, (b) MeOH, and (c) acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ at different T. s and d were 42 mm² and 10 mm, respectively. The Cole–Cole plot in (a) aqueous solution at 293 K shows a prototypical shape. The plot shows a semicircle at the left side and a straight line with an inclination of 45 degrees at the right side. The resistances at the left and right sides of the semicircle correspond to R_s and R_s + R_ct, respectively. Solid curves are the results of least-squares fits with a Randles equivalent circuit composed of R_s, R_ct, electric double layer capacitance C_d, and Warburg impedance Z_W. Z_W is expressed as Z_W = A_W(ω^−1/2 − iω^−1/2), where A_W is the Warburg coefficient. The feature of the observed impedance is reproduced by the Randles equivalent circuit model. Similar behaviors are also observed at difference T and in different solutions. One may notice that the observed semicircle in (a) aqueous solution is slightly flattened as compared with the calculated one. The deviation between them can be improved if we replace C_d with constant phase element (CPE) Q, as shown in Fig. S4.†Q is expressed as 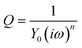where ω is the angular velocity. Y₀ and n are frequency-independent constants. Q becomes pure capacitance at n = 1. We note that there is little change in R_s and R_ct between the C_d and CPE models (Table S1†).

Fig. 2 Cole–Cole plots of complex impedance in (a) aqueous, (b) MeOH, and (c) acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ at different temperatures T. s and d were 42 mm² and 10 mm, respectively. Solid curves are the results of least-squares fits with a Randles equivalent circuit composed of R_s, R_ct, C_d, and Z_W. The vertical axis is shifted for each plot.

Fig. 3 shows R (filled circles), R_s (open squares), and R_ct (open circles) against in (a) aqueous, (b) MeOH, and (c) acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. In (a) aqueous solution, R, R_s, and R_ct increase as increases. We evaluated the activation energy Δ_i (i = s and ct) by least-squares fits with activation-type functions, [solid curves in Fig. 3a]. The activation energies are determined as Δ_s = 1550 K and Δ_ct = 1730 K. Similar behaviors are observed in (b) MeOH and (c) acetone solutions even though R_ct is scattered at higher temperatures. In (b) MeOH solution, the activation energies are Δ_s = 1380 K and Δ_ct = 1360 K. In (c) acetone solution, the activation energies are Δ_s = 1830 K and Δ_ct = 2420 K.

Fig. 3 Device resistance R (filled circles), solution resistance R_s (open squares), and charge-transfer resistance R_ct (open circles) against the reciprocal of temperature T in (a) aqueous, (b) MeOH, and (c) acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. s and d were 42 mm² and 10 mm, respectively. The solid curves are the results of least-squares fits with activation-type functions, (i = s and ct), where Δ_i is the activation energy.

Here, let's consider the solution dependence of the resistance components. The magnitudes of R and R_s gradually increase in the order aqueous, MeOH, and acetone solutions. We note that R_ct in MeOH solution is the smallest among the three solutions.

Here, we recall that the magnitude of R_s is proportional to d (ref. 28) and can be reduced by reducing d. Then, it may be possible to make the R of the MeOH LTE comparable to or smaller than that of the aqueous LTE. Thus, the MeOH LTE with small d is a promising LTE candidate with high W_max.

2.2 Scaling relation between R_s and viscosity η

Now, let us discuss the solution parameter that governs the magnitude of R_s. In bulk solution, the j-th ion feels both the electric force (= |z_j|eE, where |z_j|, e, and E are the charge number of the j-th ion, elementary charge, and electric field, respectively) and frictional force proportional to the velocity v_j of the j-th ion. According to Stokes' law, the frictional force is given as 6πηr_jv_j, where η and r_j are the viscosity of the solution and effective radius of the j-th ion, respectively. Then, the mobility of the j-th ion is given as 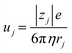. On the other hand, R_s⁻¹ is expressed as ,²⁷ where F and c_j are the Faraday constant and molar concentration of the j-th ion, respectively. By substituting , we obtain . Note that c_j and z_j are fixed in the present investigation. If the solution dependence of r_j can be ignored, R_s is proportional to η.

Fig. 4(a) shows η against T in aqueous (open squares), MeOH (open circles), and acetone (open triangles) solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. The T-dependence of η was evaluated using a sine-wave vibro viscometer (SV-10; A&D Company Limited) equipped with a heat bath. In all solutions, η steeply decreases with T. Fig. 4b shows the correlation between η and R_s. Open squares, circles, and triangles represent the η of aqueous, MeOH and acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃, respectively. As shown by the straight line, R_s increases almost linearly with η regardless of the solvent type. This observation indicates that the magnitude of R_s is governed by the η of the solution. In other words, the development of low-η solution would lead to a reduction in R_s. We note that the scaling relationship between η and R_s does not hold in the dilute solution. The η of the solvent increases in the order acetone (0.32 mPa s), MeOH (0.62 mPa s) and water (1.01 mPa s). Nevertheless, R is the smallest in aqueous solution even at 0.1 M.¹⁸

Fig. 4 (a) Viscosity η against temperature T in aqueous (open squares), MeOH (open circles), and acetone (open triangles) solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃; (b) correlation between η and R_s. Open squares, circles, and triangles represent the η of aqueous, MeOH and acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃, respectively. s and d were 42 mm² and 10 mm, respectively. The straight line in (b) is the result of least-squares fits.

2.3 Resistance components of MeOH solution against t

Fig. 4a shows the I–V plots at different t in 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ MeOH solution at 298 K. s and d were 42 mm² and 10 mm, respectively. For all electrodes, V increases in proportion to I. R was evaluated from the slope of the plot. Importantly, R decreases as t increases. Fig. 4b shows the Cole–Cole plots of complex impedance at different t in 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ MeOH solution at 298 K. s and d were 42 mm² and 10 mm, respectively. Solid curves are the results of least-squares fits with a Randles equivalent circuit composed of R_s, R_ct, C_d, and Z_ω. The observed impedance is well reproduced by the Randles equivalent circuit model.

Fig. 6a shows R⁻¹ against t. R⁻¹ slightly increases as t increases in the small t region (t ≤ 60 μm), and then is saturated to about 0.014 Ω⁻¹. Fig. 5b shows R_s⁻¹ against t. R_s⁻¹ (= 0.021 Ω⁻¹) is almost independent of d, because the macroscopic electric force between the electrodes is independent of the electrode structure. A similar t-independent behavior of R_s is observed in 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ aqueous solution.²⁸

Fig. 5 (a) Voltage V against current I in 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ MeOH solution at 298 K at different electrode thicknesses t; (b) Cole–Cole plots of complex impedance in 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃ MeOH solution at 298 K at different t. s and d were 42 mm² and 10 mm, respectively. Straight lines in (a) are the results of least-squares fits. Solid curves in (b) are the results of least-squares fits with a Randles equivalent circuit composed of R_s, R_ct, C_d, and Z_ω. The vertical axis in (b) is shifted for each plot.

Fig. 6c shows R_ct⁻¹ against t. In the small t region (t ≤ 50 μm), R_ct⁻¹ increases as t increases. In the large t region (t ≥ 50 μm), however, R_ct⁻¹ is seriously scattered. This is probably because the degree of dispersion of the graphite particles varies from electrode to electrode, causing the scattering if the data were plotted against t. On the other hand, R_ct⁻¹ is expected to increase in proportion to the electrochemically active surface area (EASA), which is usually evaluated by the C_d of the electrode.^29–31 We investigated a correlation between C_d and t [Fig. S5a†] and correlation between C_d and R_ct⁻¹ [Fig. S5b†]. We found that the correlation between C_d and t is poor, supporting our idea that the degree of dispersion varies from electrode to electrode. Nevertheless, we found a good correlation between C_d and R_ct⁻¹, indicating that R_ct⁻¹ is proportional to the EASA.

Fig. 6 Reciprocal of (a) R, (b) R_s, and (c) R_ct against electrode thickness t at 298 K. s and d were 42 mm² and 10 mm, respectively. The solid red straight line in (b) is the result of least-squares fits.

2.4 Output characteristics of MeOH LTE

First, let us investigate the effect of the LTE orientation on output power W. Fig. 7a shows the output characteristics of MeOH whose d is 2 mm. The high (T_H) and low (T_L) electrodes were 298 K and 328 K, respectively. ΔT was fixed at 30 K. The electrolyte is MeOH solution containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. The circles were the data of horizontally oriented LTEs (denoted as “side”). The triangles and inverted triangles were the data of vertically oriented LTEs whose T_H-electrode is at the top and bottom, respectively. In both the LTEs, does not show any orientation dependence. The α values of the MeOH (aqueous) LTE are 1.48 (1.22), 1.48 (1.25), and 1.48 (1.22) mV K⁻¹ in the side, top, and bottom configurations, respectively. This is because α is governed by the entropy change at the reduction reaction and is not affected by the electrolyte convection. On the other hand, W shows significant orientation dependence. We evaluated the V₀ and R′ of the LTE in operation by least-squares fit of the I–V plot. steeply decreases in the order side (0.52 W m⁻²), top (0.45 W m⁻²), and bottom (0.42 W m⁻²) configurations. A similar orientation effect is also observed in the aqueous LTE whose d is 2 mm (Fig. 7b). W_max steeply decreases in the order side (0.51 W m⁻²), top (0.46 W m⁻²), and bottom (0.40 W m⁻²) configurations.

Fig. 7 Output voltage V and power density W against current density I of (a) MeOH (t = 115 μm) and (b) aqueous (t = 110 μm) LTEs at ΔT = 30 K. s and d were 42 mm² and 2 mm, respectively. The electrolytes were MeOH and aqueous solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. The circles are the data of horizontally oriented LTEs. The triangles and inverted triangles are the data of vertically oriented LTEs whose T_H-electrode is at the top and bottom, respectively. Solid straight lines are the results of least-squares fits of the I–V plots. Broken curves are the results of least-squares fits with quadratic function.

The observed orientation effect can be ascribed to the convection of the electrolyte caused by gravity. Yang et al.²⁵ investigated the convection effect on W through fluid simulations. In a horizontally oriented LTE, the direction of temperature difference is perpendicular to that of gravity. Then, the electrolyte near the T_H-electrode rises, and then moves to the T_L-electrode when it reaches the top of the electrode. The electrolyte near the T_L-electrode descends, and moves to the T_H-electrode when it reaches the bottom of the electrode. The resultant uniform convection throughout the electrolyte effectively carries consumed redox ions to the respective electrode and promotes the redox reaction there. In a vertically oriented LTE, the direction of temperature difference is parallel to that of gravity, and hence, uniform convection throughout the electrolyte is difficult. Then, the redox reaction at the electrode is not promoted as much, because consumed ions are not sufficiently supplied by the electrolyte convection. Consistent with our observation, their simulation²⁵ showed that W decreases in the order side, top, and bottom configurations.

Next, let us compare the W_max of (a) MeOH LTE with that of (b) aqueous LTE. In the side configuration, the W_max (= 0.52 W m⁻²) of the MeOH LTE is comparable with the W_max (= 0.51 W m⁻²) of the corresponding aqueous LTE. In the top configuration, the W_max (= 0.45 W m⁻²) of the MeOH LTE is comparable with the W_max (= 0.46 W m⁻²) of the corresponding aqueous LTE. In the bottom configuration, the W_max (= 0.42 W m⁻²) of the MeOH LTE is 5% larger than the W_max (= 0.40 W m⁻²) of the corresponding aqueous LTE. Thus, we demonstrated that the W_max of the MeOH LTE is slightly larger than or comparable with that of the corresponding aqueous LTE. The large W_max of the MeOH LTE is ascribed to the large α and small R_ct, because the former causes high V₀ and the latter causes small R′. In Table 1, we compare the obtained W_max of the MeOH LTE with those of aqueous LTEs containing Fe²⁺/Fe³⁺ reported in the literature. We note that the effective electric conductivity σ strongly depends on d and ΔT, reflecting that R_ct and R_dif are independent of d and the convection effect is driven by ΔT. Therefore, a direct comparison of W_max evaluated at different d and ΔT is difficult. Roughly speaking, however, the W_max of the MeOH LTE is comparable with those of aqueous LTEs reported so far.

Table 1 Output characteristics of LTEs containing Fe²⁺/Fe³⁺. ΔT, d, s, and W_max are the temperature difference, electrode distance, electrode area, and maximum output, respectively

Solvent	ΔT (K)	d (mm)	s (mm^2)	W max (W m^−2)	Ref.
H2O	25	8	64	0.60	20
H2O	20	7	200	0.07	21
H2O	30	10	13	0.50	22
H2O	30	2	42	0.51	This work
MeOH	30	2	42	0.52	This work

---

The dimensionless figure of merit is a significant parameter of LTE, since ZT determines the thermal efficiency η. Nishitani et al.³² reported the κ of several solutions containing Fe₂(ClO₄)₂/Fe₃(ClO₄)₃. The κ values at 0.8 M are 0.23 and 0.46 W m⁻¹ K⁻¹ in the MeOH and aqueous solutions. of the MeOH and aqueous LTEs can be evaluated from Fig. 7: α = 1.48 and 1.22 mV K⁻¹, respectively. of the MeOH and aqueous LTEs can be evaluated from Table 2: σ = 0.213 and 0.280 S cm⁻¹ in the side configuration. We obtained ZT = 0.040 and 0.018 in the MeOH and aqueous LTEs, respectively. The larger ZT in the MeOH LTE is ascribed to the smaller κ of MeOH solution.

Table 2 Device resistance (R′) of LTEs in operation (ΔT = 30 K) together with the device resistance (R) of the non-operating LTE (ΔT = 0 K). s and d were 42 mm² and 2 mm, respectively. The electrolytes were MeOH and aqueous solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. The high (T_H) and low (T_L) electrodes were 298 K and 328 K, respectively. R was measured at T_L and T_H. Side means that the LTE was oriented horizontally. Top and bottom means that the LTE was oriented vertically with the T_H-electrode located at the top and bottom, respectively

	R′ (Ω)			R (Ω)
	Side	Top	Bottom	T L	T H
MeOH	22.4	25.9	27.7	27.3	20.8
H2O	17.0	18.2	20.2	18.6	13.5

---

2.5 Resistance components of LTE in operation

Table 2 shows the R′ of the operating LTEs (ΔT = 30 K) and the R of the non-operating LTE. We carefully performed a series of measurements using the same LTE. Looking at Table 2, one may notice a significant orientation dependence of R′; R′ decreases in the order side, top, and bottom configurations. As discussed in the previous subsection, the orientation effect can be ascribed to the electrolyte convection driven by ΔT. We further investigated the ΔT dependence of R′ in the side configuration with fixing T_L at 298 K (Fig. S6†). In the MeOH and aqueous LTEs, R′ decreases as ΔT increases: R′ = 26.8 (20.3), 24.4 (18.2), and 22.4 (15.6); Ω at ΔT = 10, 20 and 30 K, respectively. It is reasonable that the convection effect becomes stronger (R′ becomes smaller) as ΔT increases. We further performed EIS measurements of the operating and non-operating LTEs. The Cole–Cole plot of the operating LTE is almost the same as that of the non-operating LTE at (Fig. S7†). In the MeOH and aqueous LTEs, R_s = 6.4–6.6 (3.4) Ω and R_ct = 3.2–3.5 (4.8) Ω, respectively. Therefore, the convection effect in the operating LTE mainly affects R_dif, but has little effect on R_s and R_ct.

Finally, let us compare R′ with the average value of R at T_L and T_H. In the MeOH LTE, R′ in the top and bottom configurations is larger than the average (= 24.1 Ω). In the aqueous LTE, R′ in the top and bottom configurations is larger than the average (= 16.1 Ω). This means that the electrolyte convection has an enhancing effect on R_dif, in addition to the aforementioned suppressing effect.²⁵ As the redox reaction progresses, the concentration of reactants/products at the electrode surface changes in a way that prevents further reaction. The resultant concentration gradient drives the diffusion of reactants from (products into) the bulk region, causing R_dif. The electrolyte convection also enhances the mass transfer of the reactants/products, causing the suppressing effect on R_dif. On the other hand, the electrolyte convection tends to make the concentration in the electrolyte uniform and to suppress the concentration gradient in the vicinity of the electrode. This may be the origin of the enhancing effect on R_dif.

3 Conclusions

In conclusion, we systematically investigated the resistance components of LTEs composed of aqueous, MeOH and acetone solutions containing 0.8 M Fe(ClO₄)₂/Fe(ClO₄)₃. We found that the R_ct of the MeOH LTE is the smallest among the three LTEs. We demonstrated that the W_max of the MeOH LTE (d = 2 mm) is slightly larger than or comparable with that of the corresponding aqueous LTE. The MeOH LTE with small d is a promising LTE candidate with high W_max.

4 Experimental section

4.1 Coated electrode and electrolyte

Graphite powder (CAS RN: 7782-42-5, Wako Special Grade) was purchased from FUJIFILM Wako Corp. and used as received. The Raman scattering spectrum (Fig. S1†) at room temperature shows two characteristic bands at 1350 cm⁻¹ and 1580 cm⁻¹. The former and the latter bands are ascribed to the disorder (D) and graphene (G) bands, respectively. The intensity of the D band is much smaller as compared with that of the G band, indicating a small content of the defects.

The graphite powder and polyvinylidene difluoride (PVDF) were mixed thoroughly in a ratio of 9 : 1 with N,N-dimethylformamide (DMF).²⁸ The mixture was coated onto stainless steel foil (SUS304, 10 μm) with the use of a coating machine. Then, the electrode was dried in vacuum at 60 °C. The electrode thickness t, which was evaluated with a micrometer, was controlled by the roll height of the machine. Except for the measurement of the t-dependence of the resistance components, t was fixed at ≈ 100 μm. Fig. S2† shows the cross sectional and surface scanning electron microscopy (SEM) images of the electrode (t = 131 μm). The electrode consists of graphite particles with uneven surfaces. The size distribution of the particles was determined to be 19 ± 12 μm from 40 particles.

The electrolytes were aqueous, MeOH, and acetone solutions containing 0.8 M Fe(ClO₄)₂·6.0H₂O and 0.8 M Fe(ClO₄)₃·7.1H₂O. The solutes and solvent were purchased from FUJIFILM Wako Corp. and used as received. The solute concentration (= 0.8 M) was selected because the W_max of the aqueous LTE shows a maximum around 0.8 M.⁹

4.2 Fabrication of LTE

Resistance and output characteristics of LTE were investigated with a specially-designed two-pole cell (Fig. S3†).³³ The cell consists of a cylindrical electrolyte tank and two electrode plates. The electrolyte tank was a 7.3 mm ϕ polytetrafluoroethylene (PTFE) cylinder. The electrode plate was a Pt disk, whose inner surface was completely covered with the coated electrodes. An aluminum base is attached to the outside of each Pt electrode, and a Peltier element and a cooling fan are attached to the base. The temperatures of the high (T_H) and low (T_L) electrodes were independently controlled with the Peltier element and cooling fan. T_H and T_L were monitored with T-type thermocouples. The electrode area s was 42 mm². The electrode distance d was 10 mm or 2 mm.

4.3 Device resistance and resistance components

Device resistance, i.e., R at ΔT = 0 and R′ at finite ΔT, was evaluated from the current I–voltage V relation. In the measurement of R, T_L and T_H were fixed at T. The slope of the I–V plot corresponds to R. The measurement of R was performed with horizontally oriented LTE (side configuration). In the measurement of R′, T_L was fixed at 298 K. With the open circuit voltage V₀ as the reference, V changed in proportion to I. The slope of the I–V plot corresponds to R′. We further investigated the orientation and ΔT dependence of R′.

Resistance components, i.e., R_s and R_ct, were evaluated by electrochemical impedance spectroscopy (EIS) with the use of a potentiostat (Vertex.One.EIS, Ivium Technologies). In the EIS measurement, an alternative electric field is applied, and the induced current component is sensitively detected. The frequency range was from 1 Hz to 20 kHz, and the amplitude was 10 mV. The EIS data were analyzed with a Randles equivalent circuit,²⁷ which consists of R_s, R_ct, C_d, and Z_W. Z_W is expressed as Z_W = A_W(ω^−1/2 − iω^−1/2), where A_W and ω are the Warburg coefficient and angular velocity, respectively. Unless otherwise stated, measurement was performed at ΔT = 0 K and in the side configuration.

4.4 Output characteristics of LTE

Output characteristics of LTE were investigated with fixing T_L at 298 K. The voltage V was measured against current I (≤ 1.0 mA). W is expressed as IV. V₀ and R′ were evaluated by least-squares fitting of the I–V plot. W_max is expressed as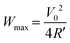 . To accurately evaluate the convection effect on V₀, R′ and W_max, we carefully investigated their orientation dependence using the same LTE.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Touya Aiba: data curation; formal analysis; investigation. Haruka Yamada: data curation; formal analysis; investigation (resistance components of MeOH solution against t). Yutaka Moritomo: conceptualization; supervision; writing – original draft; writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Yazaki Memorial Foundation for Science and Technology, the Iwatani Naoji Foundation, and the joint research with Taisei Rotec Corporation.

References

1. T. Ikeshoji, Thermoelectric conversion by thin-layer thermogalvanic cells with soluble redox couples, Bull. Chem. Soc. Jpn., 1987, 60, 1505–1514.
2. I. Quickenden and Y. Mua, A review of power generation in aqueous thermogalvanic cells, J. Electrochem. Soc., 1995, 142, 3985.
3. Y. Mua and T. I. Quickenden, Power conversion efficiency, electrode separation, and overpotential in the ferricyanide/ferrocyanide thermogalvanic cell, J. Electrochem. Soc., 1996, 143, 2558.
4. J. Kawamura, M. Shimoji and H. Hoshino, The ionic conductivity and thermoelectric power of the superionic conductor Ag₃SBr, J. Phys. Soc. Jpn., 1981, 50, 194–200.
5. A. Schiraldi, E. Pezzati and P. Baldini, Thermoelectric power of the high ionic conductivity glasses silver iodide AgI:Ag₂O·B₂O₃, J. Phys. Chem., 1985, 89, 1528–1531.
6. Y. Liang, J. K.-H. Hui, M. Morikawa, H. Inoue, T. Yamada and N. Kimizuka, High positive seebeck coefficient of aqueous I⁻/I³⁻ thermocells based on host-guest interactions and LCST behavior of PEGylated α-cyclodextrin, ACS Appl. Energy Mater., 2021, 4, 5326–5331.
7. B. Yu, J. Duan, H. Cong, W. Xie, R. Liu, X. Ahuang, H. Wang, B. Qi, M. Xu and L. Wan, Thermosensitive crystallization-boosted liquid thermocells for low-grade heat harvesting, Science, 2020, 370, 342–346.
8. Y. Xaing, X. Guo, H. Zhu, Q. Zhang and S. Zhu, Aqueous biphase-boosted liquid-state thermocell for continuous low-grade heat harvesting, Chem. Eng. J., 2023, 461, 142013.
9. J. H. Kim, J. H. Lee, E. E. Palen, M.-S. Suh, H. H. Lee and R. J. Kang, Iron (II/III) perchlorate electrolytes for electrochemically harvesting low-grade thermal energy, Sci. Rep., 2019, 9, 8706.
10. J. Duan, G. Feng, B. Yu, J. Li, M. Chen, P. Yang, J. Feng, K. Liu and J. Zhou, Aqueous thermogalvanic cells with a high Seebeck coefficient for low-grade heat harvest, Nat. Commun., 2018, 9, 5146.
11. T. Kim, J. S. Lee, G. Lee, H. Yoon, J. Yoon, T. J. Kangd and Y. H. Kim, High thermopower of ferri/ferrocyanide redox couple in organic-water solutions, Nano Energy, 2017, 31, 160.
12. M. Sindhuja, B. Lohith, V. Sudha, G. R. Manjunath and S. Harinipriya, Low grade thermal energy harvester using graphene-based Thermocells, Mater. Res. Express, 2017, 4, 075513.
13. H. Im, T. Kim, H. Song, J. Choi, J. S. Park, R. Ovalle-Robles, H. D. Yang, K. D. Kihm, R. H. Baughman, H. H. Lee, T. J. Kang and Y. H. Kim, High-efficiency electrochemical thermal energy harvester using carbon nanotube aerogel sheet electrodes, Nat. Commun., 2016, 7, 10600.
14. H. Zhou, T. Yamada and N. Kimizuka, Supramolecular thermo-electrochemical cells: Enhanced thermoelectric performance by host-guest complexation and salt-induced crystallization, J. Am. Chem. Soc., 2016, 138, 10502–10507.
15. A. H. Kazim and B. A. Cola, Electrochemical characterization of carbon nanotube and poly (3,4-ethylenedioxythiophene)-poly(styrenesulfonate) composite aqueous electrolyte for thermo-electrochemical cells, J. Electrochem. Soc., 2016, 163, F867.
16. S. W. Lee, Y. Yang, H.-W. Lee, H. Ghasemi, D. Kraemer, G. Chen and Y. Cui, An electrochemical system for efficiently harvesting low-grade heat energy, Nat. Commun., 2014, 5, 3942.
17. Y. Tanaka, A. Wake, D. Inoue and Y. Moritomo, Concentration gradient effect in liquid thermoelectric device composed of organic-solvent-added aqueous solution containing K₄[Fe(CN)₆]/K₃[Fe(CN)₆], Jpn. J. Appl. Phys., 2024, 63, 014002.
18. A. Wake, D. Inoue and Y. Moritomo, A liquid thermoelectric device composed of organic solution, Appl. Phys. Express, 2022, 15, 054002.
19. A. Wake, D. Inoue and Y. Moritomo, Liquid thermoelectric conversion devices composed of several organic solvents, Jpn. J. Appl. Phys., 2023, 62, 014002.
20. K. Kim, S. Hwang and H. Lee, Unravelling ionic speciation and hydration structure of Fe(III/II) redox couples for thermoelectrochemical cells, Electrochim. Acta, 2020, 335, 135651.
21. M. A. Buckingham, F. Marken and L. Aldous, The thermoelectrochemistry of the aqueous iron(II)/iron(III) redox couple: significance of the anion and pH in thermogalvanic thermal-to-electrical energy conversion, Sustainable Energy Fuels, 2018, 2, 2717–2726.
22. S.-M. Jung, S.-Y. Kang, B.-J. Lee, J. Kwon, D. Lee and Y.-T. Kim, Fe-N-C electrocatalyst for enhancing Fe(II)/Fe(III) redox kinetics in thermo-electrochemical cells, Adv. Funct. Mater., 2023, 33, 2304067.
23. B. Yu, H. Xiao, Y. Zeng, S. Liu, D. Wu, P. Liu, J. Guo, W. Xie, J. Duan and J. Zhou, Cost-effective n-type thermocells enabled by thermosensitive crystallizations and 3D multi-structured electrodes, Nano Energy, 2022, 93, 106795.
24. J. Duan, B. Yu, L. Huang, B. Hu, M. Xu, G. Feng and J. Zhou, Liquid-state thermocells: Opportunities and challenges for low-grade heat harvesting, Joule, 2021, 5, 768–779.
25. W. Yang, L. Sun, J. Bao, Z. Mo, M. Du, Y. Xu and J. Zhang, Multiphysics modeling of mass and heat transfer in a thermo-electrochemical cell, Ind. Eng. Chem. Res., 2023, 62, 12345.
26. P. F. Sadazar, S. Kumar and B. A. Cola, Design and optimization of thermo-electrochemical cells, J. Appl. Electrochem., 2014, 44, 325–336.
27. A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical Methods, Wiley, West Sussex, 2022.
28. T. Aiba, D. Inoeu and Y. Moritomo, Coated electrodes for liquid thermoelectric conversion devices to enhance Fe²⁺/Fe³⁺ redox kinetics, Sustainable Energy Fuels, 2024, 8, 2138–2143.
29. P. Connor, J. Schuch, B. Kaiser and W. Jaegermann, The determination of electrochemical active surface area and specific capacity revisited for the system MnO_x as an oxygen evolution catalyst, Z. Phys. Chem., 2020, 234, 979–994.
30. R. Martínez-Hincapié, J. Wegner, M. U. Anwar, A. Raza-Khan, S. Franzka, S. Kleszczynski and V. Čolič, The determination of the electrochemically active surface area and its effects on the electrocatalytic properties of structured nickel electrodes produced by additive manufacturing, Electrochim. Acta, 2024, 476, 143663.
31. H. Tian, C. Chen, Z. Yu, W. Luo, X. Yu, Z. Chang, S. Li, X. Cui and J. Shi, Controlled construction of core-shell structured prussian blue analogues towards enhanced oxygen reduction, ChemSusChem, 2024, 17, e202301265.
32. K. Nishitani and Y. Moritomo, Thermal conductivity of organic solutions against solute concentration, J. Phys. Soc. Jpn., 2024, 93, 045002.
33. Y. Fukuzumi, Y. Hinuma and Y. Moritomo, Configuration entropy effect on temperature coefficient of redox potential of P2-Na_xCoO₂, Jpn. J. Appl. Phys., 2019, 58, 065501.

---

Footnote

† Electronic supplementary information (ESI) available: Raman scattering spectrum of graphite powder, SEM images of the coated electrode, picture of LTE, Cole–Cole plots analyzed with a CPE model, correlation between C_d and t (C_d and R_ct⁻¹), I–V plots of LTE against ΔT, and Cole–Cole plots of LTE against ΔT and orientation. See DOI: https://doi.org/10.1039/d4im00113c

---