Two-step hybrid photo-thermochemical looping process, using metallic clusters on metal oxide carriers, for very efficient green hydrogen production

Abstract

In this work, we demonstrate a sustainable method for producing high-purity hydrogen through a two-step water-splitting process that leverages reducible oxides to store and release oxygen independently of hydrogen. Unlike conventional solar thermochemical (STCH) water-splitting techniques, which require extremely high temperatures exceeding 1000 °C, our approach operates at significantly lower temperatures—below ≈600 °C—thanks to a sunlight-driven photocatalyst composed of silver metal clusters (Ag₅) supported on ceria and Ce–Zr oxygen storage materials. This lower-temperature operation not only reduces the demand for high-performance materials for the design of the process but also enhances safety, simplifies system design, and improves the long-term stability of both materials and equipment. Overall, this green technology offers an energy-efficient and environmentally responsible pathway for clean hydrogen production. Density-functional-theory calculations show that Ag₅ clusters (1) enhance the photo-absorption, especially in the visible range, by increasing the gap states of the CeO₂ surface, and decrease the oxygen vacancy formation energy (E_VO) in certain positions around the clusters dramatically, and (2) create active sites in the Ag-CeO₂ interface possessing lower reaction energy and activation barrier for the hydrogen evolution reaction. Guided by these studies, we demonstrate a cleaner and more energy-efficient hydrogen production process, achieving an average output of ≈55 mL per cycle (≈435 μmol g⁻¹ h⁻¹). This corresponds to an oxygen vacancy parameter δ ≈ 0.26 per cycle—about 51% of the theoretical maximum—significantly surpassing the performance of traditional high-temperature STCH methods. Notably, our process reaches a solar-to-hydrogen (STH) conversion efficiency of ≈9.7%, placing it at the upper end of the typical STCH range (1–10%) while operating at much lower, intermediate temperatures. These results highlight the strong potential of this greener approach to hydrogen production, offering high efficiency due to the utilization of a broader wavelength range of the solar light and a smaller environmental footprint. Additionally, the use of methane in the reduction cycle promotes the formation of oxygen vacancies, while selectively generating carbon monoxide. The two-step concept has the potential to convert biomethane into a higher-value syngas product, with the added benefit of producing extra hydrogen. This allows for the adjustment of the CO/H₂ ratio, enabling subsequent Fischer–Tropsch processing for liquid fuel production.

---

Green foundation

1. Advancement in green chemistry: our work reduces the temperature for water splitting, enhancing hydrogen production efficiency while lowering energy consumption compared to traditional high-temperature SCTH methods, making the process more sustainable.

2. Green chemistry achievement: we achieved an hydrogen production at 600 °C using a photo-catalyst (silver pentamers on ceria based oxides), improving light absorption and reaction efficiency. This process yields high-purity hydrogen with a solar-to-hydrogen conversion rate of 9.7%.

3. Further research for greener impact: to make this process even greener, future research could focus on improving efficiencies using other supporting metal oxides and optimizing it using renewable methane. This could further minimize the environmental impact.

1. Introduction

Hydrogen is one of the most promising green energy carriers for today's energy transition. Hydrogen that is produced from renewable energies and without the use of fossil raw materials is generally referred to as green hydrogen, as these production methods are not associated with the emission of greenhouse gases, especially CO₂.¹ In the established processes that use fossil raw materials, CO₂ is inevitably produced and emitted in a stoichiometric ratio to the hydrogen produced, which is then referred to as grey hydrogen. However, a detailed analysis of the processes for the production of green hydrogen by LCA (life-cycle assessment) also shows significant contributions to eco-indicators such as GWP (global warming potential), consumption of scarce resources or land use for these processes.² These contributions arise primarily from the manufacture of equipment for the generation of renewable energy, e.g. PV (Photovoltaic) panels, or their conversion into hydrogen in electrolysers with precious metal electrodes. For photocatalysis, such LCAs show great potential for more efficient use of resources, as readily available materials are essentially used.^3,4 In the Ag clusters investigated in this work, for example, significantly lower quantities of metals are used than in the nanoparticles of the catalysts in the electrolyzers.

Photocatalytic processes utilize the energy provided by the sun to split water into its hydrogen and oxygen constituents. Since hydrogen and oxygen are the main products, the near-zero global and air emissions from these processes are a big advantage.^5–7 However, currently, their low efficiencies and the lack of suitable separation of hydrogen and oxygen with sufficient purity make this process unsuitable for application at an industrial scale.⁸

To separate the release of hydrogen and oxygen in the same device photocatalytic hydrogen evolution is often operated in the presence of a sacrificial agent that is oxidized instead of the water, avoiding the oxygen evolution.⁹ Although this mode of hydrogen production is possible at ambient conditions it is economically not as attractive as it appears, due to the cost and energy demand of the sacrificial agents. The same holds for thermochemical water splitting at room temperature where a metal-water reaction can be operated in apparently catalytic mode, but also only at the expense of another sacrificial agent. For example, in ref. 10 this role is taken by tungsten carbide that is oxidized to tungsten oxide. For economic reasons, these systems will only be interesting on an academic level.

Electrochemical methods, which are the most advanced ones to provide alternatives to the currently used industrial chemical methods, can provide hydrogen and oxygen separately at the cathode and anode, respectively.^11–13 However, they suffer from several disadvantages, including dependence on the electric grid, low durability, usage of noble metals as catalysts, and subsequently high capex costs.¹⁴ Although one can increase the efficiencies of these processes, using electricity coupled with light in the photoelectrochemical methods, the drawbacks remain.¹⁵

Another well-established method to separately produce hydrogen and oxygen is the thermal looping process or solar thermochemical (STCH) water-splitting.^16–18 This process uses stable metal oxides from which oxygen can be released in the first step of the loop and a subsequent step in which water is split using an appropriate catalyst attached to the oxides. In the latter step, pure hydrogen is generated, and the oxygen replaces the oxygen vacancies (V_O) created in the oxide during the first step. The main drawback of this method is the high temperatures needed for the process, which are ≈1800 K for the creation of oxygen vacancies (V_O) in the first step and ≈1120 K for the water splitting.^19,20 Such high temperatures result in handling issues of the catalysts, because of rapid quenching rates for volatile materials. This fact and the high temperatures needed are the biggest impediments to this technology being industrially viable. Although the high temperatures needed can be provided using solar concentrators, the handling of the catalysts makes it industrially not viable.²¹ Therefore, green efficient alternatives to the above processes are urgently needed.

Metal clusters of small atomicity, also known as atomic quantum clusters (AQCs), display unique properties due to their strong quantum confinement effects, which drive their catalytic activities for different reactions.²² Furthermore, because they possess several atoms to interact with the reactants, they provide many more degrees of freedom than single-atom catalysts. This allows fine-tuning of their catalytic properties, which can be further expanded by selecting the appropriate supports.²³ At the same time, the excitonic behavior of AQCs, can be further exploited for photocatalytic processes,²⁴ alongside the above-mentioned thermo-catalytic applications.

In this work, our density functional theory (DFT) calculations show that Ag₅ clusters: (1) enhance photoabsorption—particularly in the visible range—by introducing gap states in the CeO₂ surface and significantly lowers the oxygen vacancy formation energy (E_VO) at certain positions around the clusters, and (2) create interfacial sites with lower reaction energy and activation barriers for the hydrogen evolution reaction. Driven by these studies and a commitment to advancing sustainable hydrogen production, we present an environmentally friendly and energy-efficient solution based on a hydrogen evolution looping (HEL) two-step water-splitting process. This green approach achieves efficiencies comparable to—or better than—the conventional solar thermochemical hydrogen (STCH) methods, while operating at significantly lower temperatures. Our method utilizes silver pentamers (Ag₅ AQCs) supported on metal oxides, serving as both thermal and photocatalysts in the initial low-temperature (≈773 K) generation of oxygen vacancies (V_O), and as thermal catalysts in the subsequent hydrogen production step. The entire process is designed to minimize energy input and maximize sustainability, making it a promising pathway for green hydrogen production, as shown schematically in Fig. 1.

Fig. 1 Looping scheme of the HEL water-splitting process.

Overall, by operation of this photocatalytic reaction in a chemical looping mode, no other resources than water and solar light are consumed for the production of hydrogen. This justifies considering it as Green Hydrogen according to the International Energy Agency's definition.²⁵

This process concept can also be considered as a contribution to Green Chemistry because it avoids fossil raw materials, emission of greenhouse gases, and hazardous chemicals by using catalysts for a by-product-free production of hydrogen in a safe and well-controllable process according to the principles of Green Chemistry.²⁶

We will also show that this HEL concept can be extended by using CH₄ in the reduction cycle to facilitate the formation of V_O. Through this extension, the amount of H₂ per cycle was increased by a factor of ≈60, thereby allowing the production of syngas, with an adjustable CO/H₂ ratio, which could be used for the production of liquid fuels through a Fischer–Tropsch process.

2. Results and discussion

2.1. Preliminary results

First, photocatalytic water splitting was carried out with TiO₂/Cu₅ AQCs deposited onto TiO₂ nanoparticle supports. It was observed that H₂ evolved, but O₂ was missing as a product (Fig. S1†). The amount of evolved H₂ decreased over time until it disappeared, and the colour of the catalyst changed. Since the TiO₂ nanoparticles possess oxygen vacancies and O₂ could not be detected as a significant product, we speculate that V_O present in the TiO₂ nanoparticles must play a crucial role in the observed reaction, which resembles thermochemical water splitting, but at much lower temperatures. We could then assume that Ag₅ AQCs also catalyse the H₂O splitting, generating H₂, and the O from H₂O eliminates the V_O of the TiO₂ nanoparticles. Therefore, oxygen is trapped within the TiO₂ and could not be detected as a product after the reaction. To continue the H₂ production, the metal oxide needs to be regenerated, creating new V_O in the material. We further observed that the Ag₅ AQCs could also catalyse the regeneration of the V_O at 773 K (increasing the amount using light irradiation – see later), confirming the dual catalytic/photocatalytic activity of such clusters. To carry out further studies, we choose CeO₂, which is an oxide with higher oxygen storage capacity than TiO₂.

Fig. S2† shows the feasibility of the hydrogen evolution looping (HEL) process as a photocatalytic modified thermochemical approach. For this purpose, the production of H₂, where H₂O was introduced as steam during the second step of the HEL, was carried out at the same temperature (773 K) used for the V_O formation in the first step of the HEL. Although the hydrogen production in this preliminary experiments was small (≈ at 1.5 μmol per cycle or ≈10 μmol g⁻¹ h⁻¹) it indicates the potentialities of the process. To get inside into the HEL looping process and enhance the understanding of the whole process, and with the aim of optimizing the whole process we first carried out more experiments and in-depth simulations based on DFT for the two thermal/photocatalytic steps.

2.2. Step 1: oxygen vacancies’ formation

2.2.1. DFT calculations. In the DFT calculations, two types of Ag₅ isomers (trapezoid/2d and bipyramid/3d) are taken into consideration and deposited on a CeO₂ slab (Fig. 2B and C).²⁷ It is found that all the Ag atoms prefer to bind to the surface oxygens in both 2d and 3d Ag₅ AQCs and the 3d Ag₅ deforms to a new pyramidal shape, which is more stable energetically by 0.79 eV (see the table in Fig. 2A) lower than the 2d isomer on the substrate. To understand the effect of AQCs on the V_O formation, one surface or subsurface V_O is created by removing one oxygen atom on the surface or subsurface. 10 positions around the 2d and 3d AQCs are taken into consideration (surface V_O: green highlighted sites; subsurface V_O: purple highlighted sites, Fig. 2B and C). Since 3d Ag₅ on the substrate shows more stability, the following discussions are mainly based on this 3d isomer.

Fig. 2 Results of DFT-calculation of trapezoidal (2d) and bipyramidal (3d) Ag₅ on CeO₂ in the absence and presence of V_O. (A) Energetical stability of a 2d and 3d Ag₅ deposited on pristine CeO₂ surface. (B) Geometries and oxygen vacancy positions of a trapezoidal Ag₅ AQC adsorbed on CeO₂. (C) Geometries and oxygen vacancy positions of a bipyramidal Ag₅ AQC adsorbed on CeO₂. (D) Related oxygen vacancy formation energy (E_VO) of the different positions around AQCs. (E) The density of states and wavefunctions of the polaron of the 3d Ag₅ on a pristine CeO₂ surface. (F) Density of states of the 3d Ag₅ on reduced CeO₂ surface with V_O on site 1. (G) Density of states of the 3d Ag₅ on reduced CeO₂ surface with V_O on site 6.

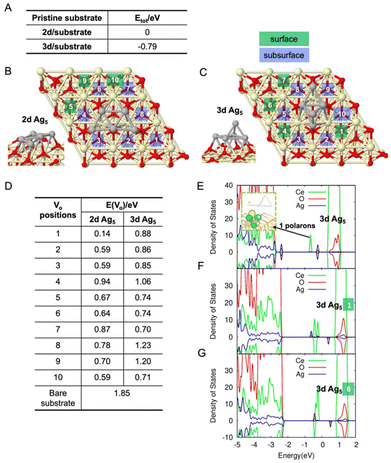
First, we find that the AQCs could enhance the photon absorption, especially in the visible range, by increasing the gap states of the CeO₂ surface, which is in line with previous results.^28,29 Compared to the bare surface (Fig. S3†), Fig. 2E shows some electronic states (blue peaks) originating from the Ag atoms and the polaronic state (green peak) stemming from charge transfer from Ag₅ to the substrate in the ∼3.1 eV band gap. The inset picture displays the polaronic state localized on the surface Ce near the Ag₅ at an energy of 1 eV below the conduction band, due to the 0.6 electron transfer from the AQC. This excess electron reduces the particular Ce⁴⁺ to Ce³⁺. More polaronic states are observed in the presence of V_O. Fig. 2F and G (V_O on site 1 and 6 of 3d geometry) each show four polarons created by the two excess electrons due to the one V_O and the 1.0 electron transfers (forming two excess electrons) from the Ag₅ depicted by the green peaks in the band gap. Similar phenomena can be found for 2d isomers in Fig. S4.† The detailed localization of Ce atoms can be found in Fig. S5.† In addition, based on the case of 3d Ag₅ on the pristine surface in Fig. 3E, one further electron is transferred from the AQC to the ceria substrate. Therefore, we conclude that V_O and Ag₅ AQCs reinforce each other since the polaronic states caused by Ag₅ could not only coexist, but also be enhanced by those generated by V_O (the charge transfer from AQCs is enhanced by V_O). Also, two spin-polarized states (blue peaks in the band gap) are observed and attributed to the states sitting on the Ag₅ cluster. Since the unoccupied state above the Fermi energy (0 eV) could accept an excited electron from the valence band, while the electron on the other occupied state could be excited to the conduction band, the AQCs are expected to enhance the separation of electron–hole pairs by absorbing the photons in the visible range.^30,31

Fig. 3 In situ XRD of (A) CeO₂ and (B) CeO₂/Ag₅ AQCs, with the insights showing a magnification of the CeO₂(202) reflection. For both experiments, the initial black patterns were obtained in (Step-1), rt-723 K under Ar : H₂ = 2 : 2 mL min⁻¹; alternating red and blue patterns were obtained at the end of the respective Ar : H₂ = 2 : 2 mL min⁻¹ (red) or Ar : O₂ = 2 : 2 mL min⁻¹ (blue) segments of 2 min.

Secondly, we predict a decrease in the E_VO by depositing Ag₅ AQCs on the surface of CeO₂. Table D in Fig. 2 demonstrates that the E_VO is dramatically decreased in some positions around the AQCs (e.g., 0.14 eV, 0.59 eV) compared to the bare substrate 1.85 eV (more details could be found in Fig. S6†). It should be noted that these values depend on the parameters chosen in the DFT calculations, especially the value of Hubbard U.³² The dependence is further confirmed and demonstrated in Fig. S7:† 2.6 eV is predicted at Hubbard U = 4.5 eV for the bare substrate which agrees well with the cited literature. Some lattice distortions around the AQCs are observed, which are speculated to be the main factor leading to a decreasing oxygen vacancy formation energy together with the injection of electrons to the substrate from the AQCs destabilizing the lattice. This means that the bond energy between the Ce atoms and the lattice oxygen atom on the surface is decreased, thereby facilitating oxygen vacancy formation.

2.2.2. Experimental formation of oxygen vacancies. Guided by the above theoretical results, we expose CeO₂/Ag₅ AQCs to a reducing atmosphere (H₂) at 773 K. A change in color from yellow to grey can be observed immediately (see Fig. S8†). With CeO₂ by itself, the time to change the color from yellow to grey is increased. As the whole catalyst changes its color, this clearly indicates that it is not limited to a surface effect, as the whole bulk is exposed to the reducing atmosphere, reducing Ce⁴⁺ to Ce³⁺.

Time-resolved in situ XRD measurements also confirm the formation of a higher amount of oxygen vacancies V_O in the CeO₂ lattice when Ag₅ AQCs are deposited on CeO₂ compared to pure commercial CeO₂, meaning Ag₅ AQCs catalyze oxygen vacancy formation. Fig. 3 shows in situ XRD analysis of both the CeO₂ commercial material (A, left) and the CeO₂/Ag₅ AQCs (B, right) (see ESI, Note 1†). An inset in each graph displays a magnified view of the CeO₂(202) reflection at 2Θ angles of approximately 14.8°. The patterns are stacked and progress with TOS (time on stream) from bottom to top. All along the experiment shown, both materials maintain the fluorite Fm3̄m structure, without the appearance of side phases, which can be better fitted to a PDF 96-434-3162. Initially, during heating under Ar : H₂=1 : 1 (black patterns), the position of the reflections shifts to lower 2Θ angles. This shift is caused by the expansion of the unit cell volume, due to thermal expansion and potentially, a contribution caused by the reduction of Ce⁴⁺ to Ce³⁺ and the associated formation of V_O.^33,34 To disentangle these contributions, alternating cycles of 2 min of H₂ and O₂ in Ar are applied: the graphs display the last acquired pattern of the H₂ (red) and O₂ (blue) cycles. On the one hand, the commercial CeO₂ material reflections position barely shifts during the alternating cycles, as shown in the magnification insight of panel 3.A.1. On the other hand, the CeO₂/Ag₅ material reflections position significantly shift during the cycles (see Fig. 3B.2). At the end of the H₂-rich periods, the unit cell has expanded (decrease of the 2Θ angle). This expansion is caused by the generation of V_O,^34,35 which reaches the bulk of the material (powder XRD is inherently a bulk characterization technique). At the end of the O₂-rich periods, the peak maximum position is recovered, meaning that the V_O is reoccupied. We note that such processes are relatively fast and occur within 2 minutes of exposure to the gas phase. Upon cooling, the peak position shifts back to higher angles due to unit cell thermal contraction.

We conducted a Rietveld refinement analysis on the XRD data to make a quantitative analysis of the oxygen vacancies. The results indicate that the lattice parameter of fluorite-type CeO₂ in the initial CeO₂/Ag₅ sample (a = 5.4129 ± 0.0001 Å) is larger than that of bare CeO₂ (a = 5.4107 ± 0.0001 Å). The higher lattice parameter of CeO₂ in the CeO₂/Ag₅ is attributed to the partial reduction of smaller Ce⁴⁺ cations to larger Ce³⁺ in the fluorite structure [r(Ce³⁺) = 1.143 Å, r(Ce⁴⁺) = 0.970 Å; all cations are 8-fold coordinated]³⁶ and the associated formation of V_O. Fig. 4A shows the lattice parameter of CeO₂ in both samples as a function of time and gas atmosphere at an isothermal temperature of 723 K. The reduction and oxidation periods are marked in green and red, respectively. The lattice parameter of the fluorite structure in the CeO₂ sample remains constant, regardless of the atmosphere. In contrast, the CeO₂/Ag₅ sample exhibits a significant increase in its lattice parameter over time when the atmosphere is switched to H₂. This increase is followed by a return to the initial value during the subsequent oxidation cycle. The mole fraction x of Ce³⁺ in the reduced fluorite phases, described as Ce^III_x Ce^IV_1−xO_2−δ and the oxygen vacancies parameter δ (i.e. x/2) were also determed using the following relationship:³³

Fig. 4 (A) Lattice and (B) oxygen vacancy parameters (δ) for pure CeO₂ and CeO₂/Ag₅ AQCs as a function of time and gas atmosphere at 723 K. Reduction (green) and oxidation (red) periods are highlighted.

Fig. 4B shows δ as a function of time and gas atmosphere at an isothermal temperature of 450 °C. Reduction and oxidation periods are represented in green and red, respectively. As shown, the V_O increases from about 0.004 to 0.02 over time when the atmosphere is switched to H₂ and decreases back to the initial value when the atmosphere is switched to O₂. Notably, the maximum level of V_O during the reduction step decreases with each cycle, dropping from 0.02 in the first cycle to ≈0.016 in the last reduction cycle (this fact could be related to the increase in crystallite size of CeO₂ observed in the CeO₂/Ag₅ sample see ESI, Note 2†). In contrast, the lattice parameter, the V_O and the crystallite size in the bare CeO₂ sample remain constant. These results demonstrate that the presence of Ag₅ on the surface of CeO₂ enables the formation of V_O in the bulk of the support at the operating conditions tested, as theoretically predicted in the previous section, whereas the lack of Ag₅ results in a material showing no significant bulk appearance of vacancies.

Finally, to analyze the influence of light, we show in Fig. 5 the XPS results of the used catalyst before and after irradiation. The comparison of the XPS Ce 3d spectra clearly shows that there is an increase in the relative ratio of the Ce³⁺ features u₀ and v₀ at ∼903.0 and 885 eV, respectively.^37,38 The deconvolution of both before and after irradiation samples is included in Fig. 5, with quantitative results displayed in Table S1† and indicating an increase of the surface atomic concentration of %Ce³⁺ from 26.0 to 40.4%. Following XRD, the XPS results further prove that Ag₅ clusters photocatalyze the reduction of Ce⁴⁺ and the formation of oxygen vacancies, confirming the dual catalytic/photo-catalytic role played by the clusters.

Fig. 5 XPS Ce3d from CeO₂/Ag₅ AQCs system before and after irradiation (top) and deconvoluted spectra.

To further explain the experimental results, we can use the Gibbs free energy change for the thermal transformation 2CeO₂ → Ce₂O₃ + 0.5 O₂, represented in Fig. 6 (we also include in the figure the transformation in H₂ and CH₄ atmospheres, corresponding to the reactions 2CeO₂ + H₂ → Ce₂O₃ + H₂O and 2CeO₂ + CH₄ → Ce₂O₃ + CO + H₂, respectively). From this figure, the temperature at which this is a spontaneous reaction can be estimated. It is observed that the thermal reduction needs very high temperatures, but the reduction of CeO₂ by H₂ (red line) has a more negative value of ΔG compared to the thermal reduction of CeO₂ (black continuous line), indicating that the reduction is facilitated in a H₂ atmosphere. At 773 K, although there is a significant reduction of ΔG° (≈205 kJ mol⁻¹), H₂ alone cannot transform CeO₂ into Ce₂O₃, suggesting that it could not produce V_O at 773 K (ΔG° ≈ 75 kJ mol⁻¹ > 0). However, one has to consider that the energy needed for vacancy formation is smaller than for transforming CeO₂ into a new thermodynamic phase (Ce₂O₃). Indeed, it is reported that at 0 K bulk CeO₂ can be transformed into CeO_2−x with E_VO ≈ 251 kJ mol⁻¹ (2.6 eV at Hubbard U = 4.5 eV shown in Fig. S7†), which is smaller than the value observed in Fig. 6 for the transformation of CeO₂ into Ce₂O₃ (E_VO at 0 K ≈ 380 kJ mol⁻¹) implying a reduction of ≈130 kJ mol⁻¹. Assuming a similar thermodynamic dependence of E_VO with temperature for values of x < 0.5 than for x = 0.5 (a similar behavior was calculated by Wang et al.⁴⁰ for SrFeO₃), then the calculated E_VO at T = 773 K in a H₂ atmosphere should be reduced to ≈75 kJ mol⁻¹–130 kJ mol⁻¹ ≈ −55 kJ mol⁻¹, indicating that H₂ alone could produce V_O at 773 K. On the other hand, the experimental results show that without clusters, the formation of vacancies is negligible, probably because of the large activation energy involved in the process, requiring the use of a catalyst to overcome the energy barrier.

Fig. 6 Gibbs free energy change for CeO₂ and CeO₂ reacting with CH₄ and H₂ to Ce₂O₃ (entropy and enthalpy taken from ref. 39).

As it was seen above, Ag₅ AQCs can also reduce the energy of vacancy formation. According to DFT, there is a reduction in ΔG° (at 0 K) for the vacancy formation of about 170 kJ mol⁻¹ (≈1.76 eV) in some positions⁴¹ (see Fig. 2). Considering the reduction noted above of E_VO for x < 0.5, ΔG° at 773 K for pure CeO₂ ≈ 150 kJ mol⁻¹ (280 kJ mol⁻¹–130 kJ mol⁻¹). Then, for CeO₂/Ag₅ AQCs, the predicted value of ΔG° at 773 K ≈ 150 kJ mol⁻¹–170 kJ mol⁻¹ ≈ −20 kJ mol⁻¹, indicating that the reaction is thermodynamically possible and at the same time, Ag₅ AQCs can catalyze the reaction, which explains the experimental results that the formation of V_O is spontaneous at this temperature. Of course, the use of a H₂ atmosphere with CeO₂/Ag₅ AQCs should imply a much larger driving force for the production of vacancies, so that the process of vacancy formation takes place in only 2 minutes in a H₂ atmosphere, as it was noted above (results shown in Fig. 3).

We now proceed to look into the second step of the HEL looping process in more detail. For this purpose, we carried out DFT calculations and more experiments for the water-splitting step.

2.3. Step 2: water splitting

2.3.1. DFT calculations. Using DFT calculation, we investigated the energetics and kinetics of the hydrogen evolution reaction (HER) on the reduced CeO₂ surface in the absence and presence of the Ag₅ AQCs.

In practice, there are V_O on the surface and even in the bulk of ceria, and water splitting occurs on these V_O^31,32. Therefore, the effect of an oxygen vacancy, but in different positions is considered (Fig. 7). For the reduced surface in the absence of Ag₅, it is found the water prefers the V_O site, and no energy activation barrier is found for the water dissociation process, which is consistent with the reports of Wu, et al. and Li, et al. mentioned above. The dissociated [OH] group fills the V_O and the [H] binds to the neighbor O, forming two –OH groups. However, a huge energy barrier of around 4.3 eV is calculated for the breaking of two O–H bonds and formation of the H₂ molecule, which is the rate-determining step of HER. This feature agrees well with the above literature. The configuration of the transition state and the reaction path for H₂ forming from separate H are shown in Fig. S9A.† This shows that one O–H bond breaks first and the dissociated H moves towards the other activated O–H, leading to a H⋯H distance of 0.85 Å. The next step involves the desorption of H₂ molecules from the ceria surface, which is an exothermic process. In contrast, two reaction paths corresponding to V_O positions 1 and 6 in Fig. 2C are shown as pink and blue plots in Fig. 7 and reveal that the Ag₅ not only provides active sites on the surface of the AQC, but also the deposition of Ag₅ induces some active sites in the interface of AQC and substrate. The corresponding reaction free energy diagrams for hydrogen evolution reaction at 773 K are shown in Fig. 7. In the case of vacancy 6 (blue path), we find a spontaneous water dissociation process which means no intact adsorbed water around AQC on the substrate can be found above vacancy site 6. For the following H₂ formation process, it is found the reaction energy decreases by 0.64 eV and the activation energy decreases by 1.32 eV compared to the bare reduced substrate (black reaction path; see the definition of activation and reaction energies in Fig. S9C†). As a consequence, the 3d Ag₅ AQC creates at least two positions at the interface (the symmetric position on the right side of AQC) possessing lower reaction and activation energies which improve the catalytic activity for HER. In the case of vacancy 1 (pink path), the adsorption free energy of a water molecule is 0.35 eV. For the subsequent step, a 1.2 eV activation energy is found for the water dissociation, which is an exothermic reaction where one H binds to AQC and the remaining [OH] fills the O vacancy site 1. However, a zero-activation energy is obtained for H₂ formation from the intermediate where one [H] binds to Ag₅ and the other binds to the oen oxygen on CeO₂ surface. And the energy barrier of this H₂ formation step (reaction energy of 1.81 eV) is suppressed by around 1 eV compared to that of the blue path (activation energy of 2.83 eV; site 6: reduced surface with Ag₅) and by 2.34 eV compared to that of the black path (activation energy of 4.15 eV; reduced bare surface). Therefore, the path corresponding to vacancy 1 (pink) shows further improvement for HER. More details about transition states for water splitting and H₂ formation can be found in Fig. S9 and S10.† In the final desorption step, one H₂ desorption process remains exothermic but has a low free energy of less than 0.1 eV (blue path), while the other becomes endothermic with a free energy of 0.3 eV (pink path) in the presence of AQCs. This represents a significant deviation from the free energy of 0.77 eV on the bare surface, which is attributed to the extra coupling from Ag₅ compared to the bare substrate. In conclusion, the AQCs could provide active sites in the H₂ formation step, which means the deposition of Ag₅ AQC increases the catalytic activity in this thermochemical process. Overall, the doping or deposition of Ag₅ AQCs works better than the metal atom doping in the ceria system reported by Li et al., where the HER process is inhibited.³¹

Fig. 7 Reaction free energy diagrams for H₂ generation on the reduced CeO₂ surface in the absence (black path) and presence (site 1: pink path and site 6: blue path) of pyramidal Ag₅ AQC at 773 K.

2.3.2. Optimized experimental results. Taking into account the previously reported DFT calculations and experiments, we report now not only the improvement of the preliminary experiments, but also other important extensions of the HEL looping concept. We have seen that the use of a H₂ atmosphere with CeO₂/Ag₅ AQCs imply a much larger driving force for the production of vacancies. Therefore we envisaged the possibility of scaling up the looping process (with a larger amount of sample) using part of the produced H₂ in each cycle, in the first step to favor the V_O production. At the same time, to accelerate the vacancy diffusion through the bulk phase, we increased the temperature to 600 °C. In order to avoid the sintering of the CeO₂ particles at this higher temperature (see above), we used a Zr-doped (50%) oxide (CZO) as a carrier oxide, which at the same time favors (at least at high temperatures) the vacancy formation, although at expenses that are more unfavorable thermodynamics compared to pure ceria.¹⁷ Fig. 8 shows the H₂ net production (after subtracting the H₂ introduced during the first step, 20 mL) per cycle (2 h) using a light intensity of 2.5 suns. The average H₂ net production is ≈55 mL per cycle (≈2.46 mmol per cycle or 0.89 mg g⁻¹ per cycle or 440 μmol g⁻¹ h⁻¹). This corresponds to a value of δ ≈ 0.26 per cycle (≈52% of the theoretical maximun number of vacancies), which is higher than the one obtained in STCH at high temperatures (28% for this CZO compound¹⁷⁾. A STH of ≈9.7% is obtained (see ESI, Note 3†) demonstrating the potentialities of this new route at intermediate temperatures. Fig. S11† shows that the production at the same conditions but without light is ≈18 mL per cycle or ≈9 mL h⁻¹. This implies that the process is ≈68% photocatalytic driven and ≈32% is catalytic driven, confirming the dual catalytic role of the Ag clusters (for comparison a CZO sample without clusters do not produce H₂ at this temperature). Fig. S12† shows the results obtained at different temperatures, from which one can get that the activation energy for the whole termal-photo-catalytic process is ≈40 kJ mol⁻¹. It is remarkable that the sample was stable for more than 370 h employed for the optimization of this procedure (see Fig. S13†).

Fig. 8 Net H₂ evolution per cycle with the optimized HEL looping method with Ce_0.5Zr_0.5O₂/Ag₅ AQCs (0.5%). Reaction conditions: T = 873 K, m Ce_0.5Zr_0.5O₂ = 2.727 g.

It is noteworthty that the results obtained by the HEL procedure surpass all previously reported results for ceria-based compounds in high temperature STCH, as shown in Table S2.† As indicated in the same table, our results are comparable even to the STCH outcomes obtained with other Ce-based oxides, perovskites and high entropy oxides at high temperatures, showing that a much greener procedure for the H₂ production can be achieved by this procedure.

These results clearly indicate that the lower temperatures used in our looping process are due to the photo-catalytic activity of clusters overcoming the thermal instabilities observed in different materials, with better performances than the Ce-based compounds (such as single and double-oxide substituted ABO₃ perovskites, iron aluminate-based spinels or high entropy oxides¹⁶), which is a major drawback for their application in STCH.

2.4. Further experiments using the HEL looping concept: oxygen vacancy regeneration with CH₄

To further show the versatility of the HEL looping concept, we studied the introduction of methane in the first step of oxygen vacancy formation. We can observe in Fig. 6 that at 773 K, the difference between the Gibbs free energy change in H₂ as a reducing agent and CH₄ as a reducing agent is 40 kJ mol⁻¹. This highlights the possibility that CH₄ could act as a reducing agent at 773 K to facilitate the formation of V_O. It is known that doping can increase oxygen ion conductivity. With increased oxygen ion conductivity, the number of V_O formed by Ag₅ AQCs could be increased, resulting in a higher entropy and thus, a larger gradient/slope. Since vacancies affect the catalyst's band gap, a reversible color change already points to the formation of V_O (Fig. S8†). Fig. 9 shows the DRS spectra of CeO₂/Ag AQCs after reduction in CH₄/light, after impregnation (original state), and after oxidation in air. It has been observed that the optical properties depend on the catalyst's oxygen vacancy density. A higher amount of V_O inside the material results in enhanced optical properties in the light's visible spectrum.

Fig. 9 DRS spectra of CeO₂/Ag₅ AQCs after impregnation, reduction with light/CH₄ and its oxidized state.

Fig. 10 shows the XRD of CeO₂/Ag₅ AQCs after different catalyst treatments. As can be seen, shifts in the characteristic peaks occurred compared to the catalyst's oxidized state. When the catalyst is irradiated, reduced by methane, or after impregnation (so that the support material already has V_O), the characteristic peaks are shifted to lower 2θ angles compared to the catalyst's oxidized state. Therefore, it can be concluded that with Ag AQCs deposited on CeO₂ the oxygen vacancy formation with CH₄ or light is no longer a surface effect, since a change in the bulk phase can be observed. This can be explained by the enhanced interaction between Ag and Ce species, as the oxygen mobility and activation are facilitated, similar to Ag-supported manganese catalysts for the oxidation of toluene⁴². The peaks shift to lower 2θ angles and are associated with an expansion of the unit cell caused by the oxygen extraction from the lattice.³⁵

Fig. 10 XRD spectra of CeO₂/Ag₅ AQCs with different treatments.

By looking at the XPS spectra of the Ce 3d (Fig. 11A), it can be observed that reducing the catalyst with CH₄/light results in an increase of the typical features associated to Ce³⁺ at ≈885 eV and ∼903 eV. Deconvolution leads to a surface atomic concentration of Ce³⁺ of 42.6% (see Table S1†). Fig. 11B depicts the Ag 3d XPS spectra of the sample after reduction with CH₄/light and the oxidized state of the catalyst. There is no shift of the characteristic peak for the sample exposed to light, hinting that the silver clusters remain in the same oxidation state in both steps of the looping process. Using CH₄ as a reducing agent, CeO₂ with Ag₅ AQCs deposited on the surface can be recovered at 773 K for the following oxidation cycle, even without light. As light can induce V_O, exposing the catalyst to light in a CH₄ environment can accelerate the oxide regeneration. The following reaction is proposed since H₂ and CO were identified as products with V_O, while formed V_O caused the catalyst's color change:

2Ce⁴⁺ + O²⁻ + CH₄ → 2H₂ + CO + Ce³⁺ + V_O

Fig. 11 XPS spectra of CeO₂/Ag₅ AQCs. Ce3d (left) Ag3d (right) after reduction with CH₄/light and in the oxidized state.

If CH₄ can be used as a reducing agent, then CeO₂/Ag₅ AQCs should be able to be reoxidized by H₂O to produce H₂, as we have already seen before. By curing the CH₄/light-induced vacancies, the final gas should only contain H₂ after reoxidation. Since the oxidation and reduction of the catalyst are reversible, the amount of H₂ per cycle should not decrease after several cycles. Fig. 12 shows the amount of H₂ evolved per cycle during 16 cycles. Each experiment is performed under the same conditions with the same catalyst, only with a different irradiation source. The average amount of H₂ produced per cycle is shown on the right.

Fig. 12 HEL loop with CeO₂/Ag₅ AQCs (0.5 wt% Ag₅) and CH₄ as reducing agent, reaction conditions: m CeO₂ = 50 mg, A_irradiation = 19.6 cm², dV/dt = 15 ml min⁻¹ with 2 : 1 Ar : CH₄ for the reduction cycle, dV/dt = 13 ml min⁻¹ with 10 : 3 Ar : H₂O, T = 773 K, irradiation source: no light, 200 W Hg (Xe) lamp/1000 W Xe lamp, λ < 1450 nm, t_oxidation = 0.5 h, t_reduction = 0.5 h.

It is observed that with light, the average amount of H₂ evolved per cycle is higher compared to the experiment in which the catalyst was not exposed to light during the reduction cycle. With higher intensity, the amount per cycle even increased to ≈35% with 1000 W intensity. Looking at the m/z = 2 signal from the mass spectrometer (Fig. S14†) it can be concluded that the oxidation cycle time is too short to consume all the vacancies formed during the reduction cycle. This means that the reaction rate for the oxidation cycle at 773 K is not high enough to oxidize the catalyst completely. Since the amount of H₂ generated per cycle depends on the light source used, the reaction rate for the oxidation cycle does not follow a zero-order kinetic. With a higher amount of available V_O formed in the reduction cycle, the reaction rate of the oxidation cycle is increased, resulting in an amount of evolved H₂ of 600 μmol g⁻¹ h⁻¹, which corresponds to a δ ≈ 0.10, and represents ≈20% of the theoretical maximun number of vacancies. The proposed reaction for the HEL with CH₄ can be described similarly to that proposed by Wang et al. for the Rh-CeO₂/Al₂O₃ catalyst⁴³ with r_oxidation < r_reduction.

These results clearly show the possibility of extending our HEL concept to transform biomethane into a more added-value syngas product, with the possibility to obtain separately more hydrogen, so that the CO/H₂ ratio could be adjusted to carry out subsequently a Fischer–Tropsch process to produce liquid fuels.

The comparison of different hydrogen technologies is very challenging, due to the utilization of different reaction feedstocks (water, methane, biomass) and auxiliaries (catalysts, microorganisms, electrodes).⁴⁴ Due to the huge research activities in this field, there are many new developments on very different technology readiness levels.⁴⁵ A comparison of technologies is only possible if performance or economic indicators can be determined within the same system boundaries.⁴⁶ Therefore, often the same technology is assessed with some variations, for example, the combination of photovoltaic electricity production and electrolysis for hydrogen production.⁴⁷ But even here, different boundary conditions cause a huge variation, e.g. in the production cost of a kg of hydrogen for €6 to €15 per kg.⁴⁸ Another interesting case for comparison is thermochemical water splitting, using the thermal energy of the sun to drive reduction-oxidation cycles of redox systems, especially metal oxides at high temperatures.³⁴ Due to the very different TRLs (technology readiness levels) and integration in value chains, a direct comparison is only possible using key indicators like solar-to-hydrogen efficiency, land use expressed in the hydrogen yield per m² and year, and the production costs. Even without being able to make a quantitative comparison between STCH and HEL technology, there are clear advantages to the HEL concept. (1) Through photocatalysis, HEL utilizes a significantly larger proportion of the spectrum of sunlight, as the UV/VIS range is used in addition to infrared radiation. (2) Due to the lower process temperature of approx. 600 °C, the pressure drop in the product gas stream is lower than at the temperature of the STCH process at about 1200 °C and thus requires less compression energy for feeding the hydrogen into the downstream processes. Together with point #1 this results in a more efficient utilization of the available solar energy at a given area. (3) Evaluations of technologies for the use of solar energy that performed TEAs (Techno-economic analysis) and LCAs for high-temperature processes such as STCH, that requires so-called solar towers or heliostats, and technologies that use parabolic mirrors to collect sunlight have repeatedly come to the conclusion that the investment costs for the parabolic mirror systems are significantly lower.^49–51 The main reason for this is the lower demands on the materials used, which only have to withstand temperatures of up to 600 °C.^29,31 For PV/electrolysis, the STH efficiency is about 15%, which yields 5 to 7 kg H₂ per m² and year resulting in production costs in a range of €5 to €10 per kg.⁴⁵ The same indicator of STCH is STH = 2 to 10%, hydrogen yield of 0.3 to 0.75 kg m⁻² years, (which represents the target value of the EU Green Deal), and production costs of €10 to €15 per kg H₂.⁵² For a comparison of the presented results, the obtained experimental data were converted into macroscopic units and a scale-up scenario was used. A solar concentrator is assumed to focus the sunlight with 10-fold intensity on a receiver tube. This is coated with 100 g m⁻² of AQC/CeO₂. Assuming the same utilization of 50% of the oxygen of the oxide, as in the optimized procedure, in each redox cycle would produce ≈ 87 × 2 (assuming only a moderate increase with the light intensity as we saw above, Fig. 12) = 174 mg per m² of reactor surface and cycle. With 4 cycles per hour and 2000 sun hours per year, this would yield 1.39 kg H₂ m⁻² of reactor surface and year, with an STH efficiency of ≈10% which clearly competes with the other mentioned methods. Due to the high purity of the hydrogen, no purification is required. For light collection parabolic mirror should be sufficient for providing the intensity and temperature for the proposed process, keeping the design rather simple and inexpensive.

3. Conclusions

Building huge photoreactors to harvest the energy for H₂ would explode the CAPEX costs (photoreactor⁵³ €1000 per m² vs. parabolic solar collector⁵⁴ €220 per m²), resulting in uneconomically high H₂ production costs. One approach is to concentrate the light using parabolic mirror systems as an example. Concentrating the light increases the photon density and the operating temperature. Photocatalysts with a core–shell structure have been studied in the literature, which can split water with a total quantum efficiency of close to 100%.⁵⁵ A disadvantage that occurs is that H₂ and O₂ are formed in a ratio of 2 : 1 without any spatial separation.

Here we demonstrated an alternative approach for producing H₂ is a two-step hybrid thermochemical cycle called Hydrogen Evolution Looping (HEL). DFT calculations were performed, predicting that the Vo formation energy is reduced by depositing Ag₅ AQCs on CeO₂. The operating temperature of the Vo reduction cycle was lowered by exposing the catalytic system (CeO₂/Ag AQCs) to light compared to pure CeO₂. Pure CeO₂ required 1670 K–1870 K for its reduction.⁵⁶ With CeO₂/Ag AQCs at 773 K, V_O were already formed on the catalyst's surface. DFT calculations also show that Ag₅ AQCs create active sites in the interface possessing lower reaction energy and an activation barrier for the hydrogen evolution reaction. H₂ production via HEL was stopped by preventing the exposure to light of the catalyst. Light-induced oxygen vacancy formation was identified as a surface effect under the investigated reaction conditions, which confirms the latest results from the literature.³¹ By creating a metal–ceria interface, the oxygen ion conductivity can be increased, facilitating the transfer of bulk oxygen to the surface.⁵⁷ Using the H₂-assisted method under optimized conditions, with Ce_0.5Zr_0.5O₂/Ag AQCs (under 2.5 suns and at 873 K), we can generate approximately half of the theoretical maximun number of vacancies per cycle. This results in a production rate of 435 μmol g⁻¹ h⁻¹ (≈10 mL g⁻¹ h⁻¹), which surpasses all previously reported results for ceria-based compounds in high temperature STCH, as shown in ESI, Table 1.† As indicated in the same table, our results are comparable to the STCH outcomes obtained with other Ce-based oxides, perovskites and high entropy oxides at high temperatures. This suggest the potential to further enhance the efficiency of our method by using such compounds while also reducing the risk of the oxide deterioration by lowering the operating temperature. CH₄ can be used at 773 K as an educt to create vacancies in CeO₂/Ag AQCs for the reduction cycle. In this case, this is no longer a surface effect as the vacancies are formed throughout the bulk phase. The reduction can be accelerated by exposing the catalyst to light. Higher intensity leads to higher reaction rates, but the dependence is non-linear. By using CH₄ in the reduction cycle to facilitate the formation of V_O, the amount of H₂ per cycle is increased, resulting in an amount of evolved H₂ of 600 μmol g⁻¹ h⁻¹ (10% of the maximum number of vacancies per cycle) and allowed the production of syngas with an adjustable CO/H₂ ratio, which could be used for the production of liquid fuels through a Fischer–Tropsch process.

4. Experimental

4.1. Chemicals

The following chemicals/materials were used as purchased: silver foils (99.95% purity) were purchased from Goodfellow, UK. Sandpaper (1000 grit) was supplied by Wolfcraft España S.L, Madrid, Spain. All aqueous solutions were prepared with MilliQ-grade water using a Direct-Q8UV system from Millipore (Millipore Ibérica S.A., Madrid, Spain). Commercially available Titanium oxide (P25, Evonic), Cerium oxide (>99.5%, Alfa Aesar) and Ce_0.5Zr_0.5O₂ (Sigma Aldrich) were used as supports. Argon (99.999%, Air Liquide Deutschland GmbH & Sigma Aldrich), Methane (99.5%, Linde Gas GmbH), Hydrogen (99.999%, Air Liquide Deutschland GmbH & Sigma Aldrich).

4.2. Catalyst preparation

4.2.1. Ag₅ AQCs synthesis. The synthesis of Ag₅ AQCs was performed using a modified version of a previously reported method⁵⁸ to enhance the monodispersity of the clusters, switching from potentiostatic (constant voltage) to galvanostatic (constant current) conditions using a Biologic VMP300 potentiostat (Seyssinet-Pariset, France). A thermally insulated Methrom three-electrode electrochemical cell, deoxygenated just before synthesis, was employed. A hydrogen electrode served as the reference, while two Ag foils (17.5 cm² surface area) were used as the counter and working electrodes. Before synthesis, both silver electrodes were polished with P1200 sandpaper, thoroughly rinsed with MilliQ® water, and sonicated. The electrodes were then activated for 5 minutes at 250 mA. The synthesis procedure involved applying six galvanostatic steps: 250 μA for 60 minutes, 480 μA for 60 minutes, 1 mA for 60 minutes, 2 mA for 60 minutes, followed by two final steps of 4 mA for 30 minutes each. Between each step, the electrodes were polished, sonicated, and washed as previously described. An ion-selective electrode was used to confirm that the concentration of residual Ag⁺ ions was below 3 mg L⁻¹ after precipitation with NaCl. Finally, the samples were concentrated at 40 °C using a rotary evaporator (Buchi Rotavapor R-210 at 2 mbar) (Massó Analítica S.A., Barcelona, Spain) to a final concentration of approximately 30 mg L⁻¹, as determined by flame atomic absorption spectroscopy.

4.2.2. Ag₅ AQCs deposition. Ag₅ AQCs were deposited onto Ce oxides by a wet impregnation method. First the oxides were calcinated at 473 K for 2 h with a heating rate of 5 K min⁻¹ to remove adsorbed water and solvents on the surface. The appropriate amount of calcinated oxides were transferred to a Teflon beaker and the required amount of cluster solution was added to the Teflon beaker and dried in air.

4.2.3. Catalyst characterization. UV-vis and fluorescence spectroscopy of AQCs were performed at room temperature using 1 cm path-length Hellma quartz cuvettes (Hellma GmbH & Co. KG., Müllheim, Germany). To obtain the crystallinity and phases of the photocatalysts X-ray diffraction measurements were done in a Bruker D8 Advance diffractometer in reflection geometry with a Cu Kα as an anode (λ = 1.5418 Å) operating at 40 kV and 40 mA. XPS spectra were acquired.

There is a well-established correlation between the emission energy (E_em) of clusters and the number of atoms (N) they contain, as predicted by the spherical jellium model: E_em ≈ E_HOMO–LUMO = E_F/N^1/3, where E_HOMO–LUMO gap is the energy gap between the highest occupied and lowest unoccupied molecular orbitals, and E_F is the Fermi energy of the bulk metal.⁵⁹ The fluorescence spectra can therefore be used to determine the size distribution of clusters, which is consistent with other characterization techniques, such as Mass Spectrometry (see ref. 58 for further details). Fig. S15† shows the emission spectra of the cluster samples used in this study, featuring a single peak at λ ≈ 409 nm (3.1 eV). Using the jellium model and assuming E_F ≈ 5.3 eV for Ag, it can be inferred that the clusters primarily consist of five atoms [N_jellium ≈ 5.3], which aligns with the sizes previously reported for clusters with a similar emission peak.⁵⁶

X-ray Photelectron Spectroscopy (XPS) measurements were carried out using a K-Alpha system (Thermo Fisher Scientific, USA) equipped with a monochromatic Al Kα source. Samples were prepared on carbon pads. Spectra were acquired in constant analyzer energy mode with a pass energy of 50 eV, a step size of 0.1 eV, and a spot size of 400 μm. All XPS spectra were calibrated using the C 1s core level at a binding energy of 284.8 eV. The spectra were deconvoluted using Fityk software,⁶⁰ with assigned peaks according to literature^37,38 : Ce⁺⁴ (v = ∼882.0 eV, v′′ = ∼888.2 eV, v′′′ = ∼898.0 eV, u = ∼900.8 eV, u′′ = ∼907.3 eV, u′′′ = ∼916.6 eV) and Ce³⁺ (v₀ = ∼885.0 eV, v′ = ∼880.0 eV, u₀ = ∼903.0 eV, u′ = ∼898.3 eV). The background signal was removed using the Shirley method⁶¹ and the different peaks were fitted using Pseudovoigt functions. The FWHM (Full width at half maximum) for the Ce³⁺ and Ce⁺⁴ groups was fixed, separately. The atomic surface concentrations of Ce³⁺, Ce⁴⁺ were calculated from peak areas according to eqn (X), where A_Ce³⁺ is the sum of the areas of the features described above.

4.2.4. In situ X-ray diffraction (XRD). In situ X-ray diffraction (XRD) was performed in the 12.2.2 beamline of the Advanced Light Source synchrotron of the Lawrence Berkeley National Laboratory in Berkeley, California, USA. The setup and cell are described in detail elsewhere.^62,63 Briefly, around 1 mg of the powder material is placed inside a 0.7 mm diameter capillary made of amorphous quartz, with an inner concentrical thinner tungsten capillary that delivers the gas mixture to the sample. The desired flow rate of the individual gases is adjusted using mass flow controllers. The tip of the capillary containing the sample is placed inside a SiC tube that acts as a furnace by being illuminated using two infrared lamps, both controlled using an S-type thermocouple. Two holes done on the SiC furnace allow for the X-rays (25 keV, 10–30 μm spot size) to interact with the sample and travel toward the 2D detector (Dectris Pilatus 1 M). A mild random wobble was applied using the stage motors to improve statistics over the 30 seconds of acquisition for each individual pattern. Each sample was analyzed as follows: Step-1, heating from rt to 723 K at 60 K min⁻¹, under Ar: 2 mL min⁻¹ and H₂: 2 mL min⁻¹, hold for 2 min; Step-2, 773 K, under Ar: 2 mL min⁻¹ and H₂: 2 mL min⁻¹, hold for 2 min; Step-3, 773 K, under Ar: 2 mL min⁻¹ and O₂/air: 2 mL min⁻¹, hold for 2 min; repetition of (2 + 3) × 7 times (i.e. cycling of H₂-rich and O₂-rich steps); Step-18, cooling from 773 K to rt at 60 K min⁻¹, under Ar: 2 mL min⁻¹. The 2D detector images were processed using Dioptas software⁶⁴ with the sample to detector distance as determined using a LaB₆ NIST 660b standard. Rietveld refinement of the XRD data was performed using FullProf Suite software⁶⁵ and fitting using a Thompson–Cox–Hastings pseudo-Voigt convoluted with axial divergence asymmetry function (Function 7)⁶⁶

4.2.5. Hydrogen evolution looping experiments. Hydrogen evolution looping (HEL) experiments were performed in a self-built stainless-steel reactor containing heat cartridges to control the temperature

The reactor is connected to a 3-way valve, which can introduce dry argon or water-saturated argon into the reactor. Fig. S16a† (reduction cycle) and Fig. S16b† (oxidation cycle) show the flow charts of the used setup to perform HEL experiments. First, the catalyst (m_cat = 50–400 mg) was added to 10–40 mL of pure water followed by an ultrasonication for 5 min. Afterward, the suspension was added on top of an Erlenmeyer flask containing a stainless-steel sinter plate surrounded by a hollow cylinder of Teflon. The flask is connected to a vacuum pump and by evacuating, the catalyst is deposited on the top of the sinter plate. The deposited catalyst is then dried overnight in an oven at 333 K. After putting the sintered plate into the reactor, the pipes and the reactor are evacuated and purged with Ar four times, followed by purging the water saturator with Ar for 30 min with a volume flow of 200 mL min⁻¹ to remove air in the pipes. After heating up the reactor to the required temperature with a ramp of 3.3 K min⁻¹. For some experiments, the sample was pretreated with H₂ or CH₄. The cyclic experiment contains 2 phases characterized by their duration time: an irradiation phase (t_irradation) for the creation of V_O and an oxidation phase (t_oxidation) for the formation of hydrogen. While irradiating, dry Ar passes the reactor. By introducing water vapor in the oxidation phase, H₂ is evolving. Switching between dry Ar and with water-saturated Ar is conducted by a 3-way valve controlled by a servo motor. The outgoing gas was analyzed once every 30 min by gas chromatography. (7890A, Agilent Technologies, Porapak-N column). The reaction was performed at 673 K–773 K with an intensity of 4000 W m⁻² supplied by a 200 W Hg lamp/40 000 W m⁻² supplied by a 1000 W Xe lamp.

The optimized HEL experiments were performed in a quartz reactor with an internal diameter of 9 mm and length of 50 cm

The sample is supported by quartz wool in the irradiation zone of the reactor, heated with an oven (Hobersal HTF), irradiated with an intensity of 2500 W m⁻² supplied by a 1000 W Xe lamp (Quantum Design). Set up and measure conditions were similar to ones described in 5.1. The outgoing gas was analyzed once every 15 min by gas chromatography (Clarus 580, PerkinElmer) and every second by a MS spectrometer (OmniStar GSD 350, Pfeiffer vacuum).

4.3. Theoretical methods

The periodic slab model CeO₂(111) (Ce atoms: 48; O atoms: 96) is composed of 15.58 Å × 15.58 Å unit cells arranged in three O–Ce–O trilayers with a 15 Å vacuum layer above the surface. The geometrical and electrical properties for pristine or reduced CeO₂(111) surface and Ag₅ deposited on pristine or reduced CeO₂(111) were calculated by density functional theory (DFT) based simulation package Vienna Ab initio simulation package (VASP). The periodic boundary condition method and spin-polarized DFT were adopted. The projector augmented wave (PAW) method was performed to describe the interaction between valence electrons and the ion cores and the generalized-gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE)⁶⁷ was utilized for the exchange–correlation functionals. A plane-wave basis set with a 500 eV cut-off energy was used to expand the Kohn–Sham wave functions. Hubbard U term⁶⁸ U = 6.3 eV to correct on-site coulombic interactions of cerium 4f electrons was adopted for the lattice relaxation.^69,70 More specifically, the results presented in Fig. 3 and 7 were obtained by using U = 6.3 eV while U = 4.0, 4.5, 5, 5.5, 6, 6.5 were utilized to optimize the unit cell of CeO₂ to build each surface slab respectively and the dependence of Hubbard U for the V_O formation energy was finally characterized and shown in Fig. S7.† In all cases, the Brillouin zone was sampled at the Γ point due to the large unit cell (15.576 Å × 15.576 Å) in the two directions with periodic boundary conditions (x and y directions). The Becke-Jonson (BJ) damping function in Grimme's D3 method⁷¹ was adopted to include van der Waals corrections due to the accuracy for reproducing the binding or adsorption energies on metal oxide surfaces.

The electronic structures (wavefunctions and density of states) of the CeO₂(111) substrate, and Ag₅ AQCs deposited on CeO₂(111) in the absence and presence of O vacancy were performed with spin-polarized HSE06 calculations based on the optimized configurations in the earlier DFT+U with D3 (BJ) performance since HSE06 is really time-consuming.^72–74 In the HSE06 hybrid exchange–correlation functional, the exchange potential consists of a short-range PBE part mixed with an HF exchange and a long-range PBE part. Bader analysis method⁷⁵ is applied to the results of spin-polarized HSE06 calculation for atomic charge distributions. The V_O formation energy is defined below:

E_VO = 1/xE(CeO_2−x) + 1/2E(O₂) − 1/xE(CeO₂)

To find transition states (TS), a damped molecular dynamics algorithm was combined with the climbing-image nudged elastic band (CI-NEB) method.^76,77 During the CI-NEB calculation, the structural optimization would be completed when the maximum forces on all atoms were smaller than 0.04 eV Å⁻¹. Finally, a check was made to confirm that only one imaginary frequency is present for the transition state. All the optimized structures were visualized by VESTA.⁷⁸

Free energy diagrams display the free energy variation (ΔG) along the hydrogen evolution reaction from the reactants to the final products through various intermediate states. The Free energy was calculated by

G = E_DFT + E_ZPE − TS

where ZPE is the zero-point energies, S is the entropy, and T is temperature (773 K).

Author contributions

Anh Dung Nguyen designed and conducted the photocatalytic experiments and contributed to writing the manuscript. David Buceta designed and supervised the synthesis and deposition of the Ag₅ AQCs, and collaborates in the overall conception and discussions of the photocatalytic experiments. Qingqing Wu and Moteb Alotaibi conducted the theoretical calculations and wrote the corresponding part of the manuscript. Iria R. Arias synthesised and purified the Ag₅ AQCs, prepared the deposited AQCs in the substrates and collaborates in the discussion and analysis of the optimized HEL experiments. Julian Müller and Albert Gili contributed with the in situ XRD investigation of the catalysts. Maged F. Bekheet performed Rietveld refinement analysis on the obtained in situ XRD data, and contributed to the discussion of the results. Martin Dieste and Nerea Davila-Ferreira conducted the optimized HEL experiments and collaborate in their overal conception, discussion and analyis. Fatimah Alhawiti contributed to the discussion and examination of the V_O calculations. Colin Lambert designed and supervised the theoretical results, and collaborated in the overall conception and discussion of the manuscript. M. Arturo López-Quintela, supervised the results and contributed to the overall conception, discussion, and writing the manuscript. Reinhard Schomäcker supervised the results and contributed to the overall conception, discussion, and writing the manuscript. Review and editing were done by all co-authors.

Conflicts of interest

Anh Dung Nguyen, David Buceta, Qingqing Wu, Colin Lambert, M. Arturo López Quintela and Reinhard Schomäcker are co-inventors of a patent filed, which is related to the looping process described in the manuscript.

Data availability

Data for this article are available at: (1) Experimental data can be uploaded from the following link: https://doi.org/10.14279/depositonce-19490. (2) Theoretical data can be uploaded from the following link: https://www.dropbox.com/scl/fo/t65j2xo9njcrm1e69jvh2/AJrSMnzyd9epuEWaV-MyZyM?rlkey=zxi0i7tlukzc7dkbetf2nz03o&dl=0. (3) HEL optimized results can be uploaded from the following link: data optimized HEL (https://nubeusc-my.sharepoint.com/:f:/g/personal/malopez_quintela_usc_es/Ek4qcGJoQNVGkfgh_DzyLEoBKgeqj03RnPkNGOsQXhcD9A?e=WtVXei).

Acknowledgements

This research was partially supported by the Consellería de Educación (Xunta de Galicia), Grants No. Grupos Ref. Comp. ED431C-2021/16; Spanish Ministerio de Ciencia e Innovación (MICIU) PID2022-142334OB-I0, financed by MICIU/AEI/10.13039/501100011033 and European Union (ERDF/EU); and TED2021-131899B-I00, financed by MICIU/AEI /10.13039/501100011033 and EU Next Generation (EU/PRTR). CJL and QW acknowledge support from the EPSRC Program grant “Quantum Engineering of Energy-Efficient Molecular Materials”. A. Gili acknowledges support by the German Federal Ministry of Education and Research in the framework of the project Catlab (03EW0015A). JTM and MFB thank the Advanced Light Source, which is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the US Department of Energy under Contract No. DE-AC02-05CH11231, and where the in situ XRD measurements where conducted at beamline 12.2.2 in the framework of the AP proposals (ALS-11921).

References

1. J. Incer-Valverde, A. Korayem, G. Tsatsaronis and T. Morosuk, Energy Convers. Manage., 2023, 291, 117294.
2. D. Alghool, M. Haouari and P. Trucco, Int. J. Hydrogen Energy, 2024, 81, 214–224.
3. J. Maurya, E. Gemechu and A. Kumar, Int. J. Hydrogen Energy, 2023, 48, 20077–20095.
4. C. Nelson, M. M. Gui and P. K. J. Robertson, Adv. Energy Sustainability Res., 2025, 6, 2400337.
5. H. Nishiyama, T. Yamada, M. Nakabayashi, Y. Maehara, M. Yamaguchi, Y. Kuromiya, Y. Nagatsum, H. Tokudome, S. Akiyama, T. Watanabe, R. Narushima, S. Okunaka, N. Shibata, T. Takata, T. Hisatomi and K. Domen, Nature, 2021, 598, 304–318.
6. A. Gupta, B. Likozar, R. Jana, W. C. Chanu and M. K. Singh, Int. J. Hydrogen Energy, 2022, 47, 33282–33307.
7. M. J. Molaei, Fuel, 2024, 365, 131159.
8. S. Alsayegh, J. R. Johnson, B. Ohs and M. Wessling, J. Cleaner Prod., 2019, 208, 1446e1458.
9. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80.
10. T. Yamamoto, S. Ashida, N. Inubuse, S. Shimizu, Y. Miura, T. Mizutani and K.-ichi Saitow, J. Mater. Chem., 2024, 12, 30906–30918.
11. B. You and Y. Sun, Acc. Chem. Res., 2018, 51, 1571–1580.
12. X. Xiao, L. Yang, W. Sun, Yu Chen, H. Yu, K. Li, B. Jia, L. Zhang and T. Ma, Small, 2022, 18, 2105830.
13. D. T. Tran, P. K. L. Tran, D. Malhotra, T. H. Nguyen, T. T. An Nguyen, N. T. A. Duong, N. H. Kim and J. H. Lee, Nano Convergence, 2025, 12, 9.
14. Md M. Rashid, M. K. Al Mesfer, H. Naseem and M. Danishshould, Int. J. Eng. Adv. Technol., 2015, 4(3), 2249–8958.
15. Yi Yang, S. Niu, D. Han, T. Liu, G. Wang and Y. Li, Adv. Energy Mater., 2017, 7, 1700555.
16. J. T. Tran, K. J. Warren, S. A. Wilson, C. L. Muhich, C. B. Musgrave and A. W. Weimer, Wiley Interdiscip. Rev.: Energy Environ., 2024, 13, e528.
17. S. Abanades, Chem. Eng., 2019, 3, 63.
18. D. Oudejans, M. Offidani, A. Constantinou, S. Albonetti, N. Dimitratos and A. Bansode, Energies, 2022, 15, 3044.
19. F. Safari and I. Dincer, Energy Convers. Manage., 2020, 205, 112182.
20. Y. Mao, Y. Gao, W. Dong, H. Wu, Z. Song, X. Zhao, J. Sun and W. Wang, Appl. Energy, 2020, 267, 114860.
21. C. L. Muhich, B. D. Ehrhart, I. Al-Shankiti, B. J. Ward, C. B. Musgrave and A. W. Weimer, Wiley Interdiscip. Rev.: Energy Environ., 2016, 5, 261–287.
22. H. Rong, S. Ji, J. Zhang, D. Wang and Y. Li, Nat. Commun., 2020, 11, 5884.
23. L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079.
24. See e.g. Y. A. Attia, D. Buceta, C. Blanco-Varela, M. B. Mohamed, G. Barone and M. A. López-Quintela, J. Am. Chem. Soc., 2014, 136, 1182–1185; N. Vilar-Vidal, J. R. Rey and M. A. López-Quintela, Small, 2014, 10, 3632–3636; Ye Liu, Yu Wang and N. Pinna, ACS Mater. Lett., 2024, 6, 2995–3006.
25. Global Hydrogen Review 2022-Analysis, International Energy Agency, 2022, p 71, Available from: https://www.iea.org.
26. P. T. Anastas and J. C. Warner. Green chemistry: theory and practice, Oxford University Press, Oxford [England]; New York, 1998. ISBN 9780198502340.
27. M. Alotaibi, Q. Wu and C. Lambert, Appl. Surf. Sci., 2013, 613, 156054.
28. M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500.
29. P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853.
30. Yu Zhang, D. T. Payne, C. L. Pang, C. Cacho, R. T. Chapman, E. Springate, H. H. Fielding and G. Thornton, J. Phys. Chem. Lett., 2019, 10, 5265–5270.
31. R. Li, C. Wen, K. Yan, T. Liu, B. Zhang, M. Xub and Z. Zhouc, J. Mater. Chem. A, 2023, 11, 7128–7141.
32. T. Wu, Q. Deng, H. A. Hansen and T. Vegge, J. Phys. Chem. C, 2019, 123, 5507–5517.
33. M. F. Bekheet, M. Grünbacher, L. Schlicker, A. Gili, A. Doran, J. D. Epping, A. Gurlo, B. Klötzerb and S. Penner, CrystEngComm, 2019, 21, 145–154.
34. A. Gili, M. F. Bekheet, F. Thimm, B. Bischoff, M. Geske, M. Konrad, S. Praetz, C. Schlesiger, S. Selve, A. Gurlo, F. Rosowskidg and R. Schomäcker, Catal. Sci. Technol., 2024, 14, 4174.
35. M. F. Bekheet, M. Grünbacher, L. Schlicker, A. Gili, A. Doran, J. D. Epping, A. Gurlo, B. Klötzerb and S. Penner, CrystEngComm, 2019, 21, 145.
36. R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. A, 1969, 25, 925.
37. P. Burroughs, A. Hamnett, A. F. Orchard and G. Thornton, J. Chem. Soc., Dalton Trans., 1976, 17, 1686–1698.
38. E. Bêche, P. Charvin, D. Perarnau, S. Abanades and G. Flamant, Surf. Interface Anal., 2008, 40, 264–267.
39. CRC Handbook of Chemistry and Physics, ed. D. R. Lide, 76th edn, 2003, vol. 84, p. 2474.
40. X. Wang, Y. Gao, E. Krzystowczyk, S. Iftikhar, J. Dou, R. Cai, H. Wang, C. Ruan, S. Ye and F. Li, Energy Environ. Sci., 2022, 15, 1512–1528.
41. Note: 1.76 eV is obtained by the energy reduction from the oxygen vacancy formation energy 2.6 eV of CeO₂ in the absent of Ag₅ to 0.84 eV of Ag₅/CeO₂. 0.84 eV is calculated by 0.14 eV + 0.7 eV since the oxygen vacancy formation energy elevates with the decrease of Hubbard U, where 0.84 eV is a linear prediction (0.14 eV for U = 6.3; then 0.84 eV for U = 4.5) from the dependence plotting on Hubbard U of the oxygen formation energy.
42. Z. Qua, Y. Bua, Y. Qina, Yi Wanga and Q. Fub, Appl. Catal., B, 2013, 132–133, 353–362.
43. R. Wang, H. Xu, X. Liu, Q. Ge and W. Li, Appl. Catal., A, 2006, 305, 204–210.
44. I. Dincer and C. Acar, Int. J. Hydrogen Energy, 2014, 40, 11094–11111.
45. I. Dincer and C. Acar, Int. J. Hydrogen Energy, 2015, 42, 14843–14864.
46. A. J. Carrillo, J. González-Aguilar, M. Romero and J. M. Coronado, Chem. Rev., 2019, 119, 4777–4816.
47. M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling, I. Staffell, P. Balcombe, Y. Shao-Horn and H. Schäfer, Chem. Soc. Rev., 2022, 51, 4583–4762.
48. J. Collis and R. Schomäcker, Front. Energy Res., 2022, 10, 909298.
49. N. A. Jailani, A. Ahmad and N. Norazahar, J. Energy Saf. Technol., 2021, 4, 13–28.
50. F. Hosseinifard, G. R. Aghdami, M. Salimi and M. Amidpour, Fuel Process. Technol., 2025, 271, 108207.
51. L. B. Gobio-Thomas, M. Darwish and V. Stojceska, Therm. Sci. Eng. Prog., 2023, 46, 102224.
52. F. Safari and I. Dincer, Energy Convers. Manage., 2020, 205, 112182.
53. A. Cabrera Reina, S. Miralles-Cuevas, L. Cornejo, L. Pomares, J. Polo, I. Oller and S. Malato, Renewable Energy, 2020, 145, 1890–1900.
54. A. Giostri, M. Binotti, P. Silva, E. Macchi and G. Manzolini, J. Sol. Energy Eng., 2013, 135, 011001.
55. T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411–414.
56. H. S. Cho, T. Myojin, S. Kawakami, N. Gokon, T. Kodama, Y. H. Kang, S. N. Lee, K. K. Chai, H. K. Yoon and H. J. Lee, Energy Procedia, 2014, 49, 1922–1931.
57. R. J. Gorte, AIChE J., 2010, 56, 1226–1135.
58. V. Porto, D. Buceta, B. Domínguez, C. Carneiro, E. Borrajo, M. Fraile, N. Davila-Ferreira, I. R. Arias, J. M. Blanco, M. C. Blanco, J. M. Devida, L. J. Giovanetti, F. G. Requejo, J. C. Hernández-Garrido, J. J. Calvino, M. López-Haro, G. Barone, A. M. James, T. García-Caballero, D. M. González-Castaño, M. Treder, W. Huber, A. Vidal, M. P. Murphy, M. A. López-Quintela and F. Domínguez, Adv. Funct. Mater., 2022, 32, 2113028.
59. see e.g. J. Zheng, C. Zhang and R. M. Dickson, Phys. Rev. Lett., 2004, 93, 077402; B. Santiago-González and M. A. López-Quintela, in Functional Nanometer-Sized Clusters of Transition Metals: Synthesis, Properties, and Applications, ed. W. Chen and S. Chen, The Royal Society of Chemistry, 2014, ch. 2, pp. 25–50.
60. M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128.
61. D. A. Shirley, Phys. Rev. B, 1972, 5, 4709.
62. A. Gili, et al., ACS Catal., 2019, 9(8), 6999–7011.
63. L. Schlicker, et al., Rev. Sci. Instrum., 2018, 89, 033904.
64. C. Prescher and V. P. Prakapenka, High Pressure Res., 2015, 35, 223–230.
65. J. Rodriguez-Carvajal, J. Phys. B, 1993, 192, 5.
66. L. W. Finger, D. E. Cox and A. P. Jephcoat, J. Appl. Crystallogr., 1994, 27, 892–900.
67. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
68. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
69. R.K Singha, Y. Tsuji, M.H Mahyuddin and K. Yoshizawa, J. Phys. Chem. C, 2019, 123, 9788–9798.
70. Y. Jiang, J. B. Adams and M. van Schilfgaarde, J. Chem. Phys., 2005, 123, 064701.
71. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
72. P López-Caballero, A W. Hauser and M P de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074.
73. S. Dong, B. Li, X. Cui, S. Tan and B. Wang, J. Phys. Chem. Lett., 2019, 10, 4683–4691.
74. F. Alhawiti, et al., Phys. Chem. Chem. Phys., 2024, 26, 27088–27097.
75. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
76. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
77. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
78. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5gc01425e

‡ These authors are considered as co-first authors.

---