On the use of advanced scanning transmission electron microscopy and machine learning for studying multi-component materials

Abstract

The nanoscale distribution of elements in two multi-component materials is assessed by unsupervised machine learning methods. These are compared to elemental maps to highlight the potential shortcomings of simplistic compositional analyses. Quantification of the resulting microstructure components provides insight into the evolution of the microstructure and the possible reasons for misinterpretation of the traditional element maps.

---

There is a wide interest in the use of entropically stabilised materials, often referred to as high-entropy (HE) materials.^1–4 These materials exploit increased configurational entropy (ΔS_conf) available to incorporate multiple different atomic species into a single crystal lattice structure, even if they otherwise would not be stable in that structure by enthalpic driving forces alone. This provides a simple but effective method to create atomically engineered crystal structures containing elements that would ordinarily form a different crystal structure (subject solely to enthalpic driving forces). This ability to engineer new materials with novel properties is seen as an important step in the development of next-generation structural,⁵ functional^6–8 and catalytic materials.^9,10

One of the key capabilities needed for the continued development of these materials is the ability to characterise the structure and composition of the material at the nanoscale. Many publications in the area report the use of only scanning electron microscopy (SEM) and powder X-ray diffraction (PXRD) to provide evidence of chemical homogeneity.¹¹ However, the interaction volume of SEM can be tens of nanometres cubed at the typical voltages (5–30 keV) used, depending on the imaging conditions, material and the alignment of the microscope.¹² Powder X-ray diffraction is also a bulk-averaged technique which cannot distinguish nanoscale crystallites of materials, with the possibility of minority crystal phases being ‘swamped’ by large, crystalline materials.

What is evident from recent studies¹¹ is that variations of structure and composition can occur at much finer (1–10 nm) length-scales. This makes the validity of SEM data questionable if we are to be confident of truly uniform mixing of elements at the atomic scale within the materials considered. This therefore requires the use of higher spatial resolution approaches, notably scanning transmission electron microscopy (STEM). This comes with its own limitations, notably the need for more advanced sample preparation,¹³ but also the interpretation of STEM data often requires more in-depth data analysis.^14,15

Many published works use a visual comparison of measurements (often in the form of elemental maps) to imply correlations, or lack thereof, between elements; however, this can introduce user bias in terms of the elements that are selected, while the method of scaling data to form the map can also alter the relative contributions of the elements, making a rigorous comparison difficult. The direction of travel in recent years in advanced electron microscopy has been to move towards machine learning methods.^16,17 These utilise the complete spectral data recorded at each position in the scan, rather than simply considering the intensity of a single energy channel or single X-ray emission peak. Consequently, these can provide a more complete comparison of the variation of all of the elements (peaks) in the spectrum and so provide not only a clearer indication of relative chemical variations, but by analysing the ensemble data also provide the opportunity to do more quantitative comparisons.

One development in recent months has been the application of the ‘hierarchical density-based spatial clustering of applications with noise’ (HDBSCAN) algorithm.^18,19 Clustering involves grouping measurements according to a predefined metric of similarity. Usually this is done on a manifold (or low-dimensional) reprojection of the original data. HDBSCAN in particular helps to address one of the long-standing issues in machine learning segmentation, namely how many components (or clusters) to decompose the data into. By using a physical parameter (the number of measurements [or scan pixels] expected for a cluster), the algorithm determines the number of components internally, removing the need to define this as a user and in the process the number of outputs is therefore determined by the structure of the data, rather than the bias of the user.

This article will highlight this machine learning capability compared to more simplistic elemental analysis approaches and will apply them to two different multi-component materials to highlight how this can lead to a clearer understanding of the nature of the phases present in the system.

Results and discussion

For this study, two high-entropy metal sulfides were synthesised and studied. These were a 6-metal-containing material ((MnFeCuAgZnCd)S), and a 7-metal-containing material ((MnCoCuAgZnCdGa)S). The more traditional bulk analysis techniques were used on the 6-metal material, namely PXRD and SEM coupled to EDX. These are shown in Fig. 1a and b, respectively.

Fig. 1 (a) PXRD of the 6-metal-containing material (the locations of reflections expected for wurtzite are indicated) and (b) SEM-EDX elemental maps, scale bar indicates 2 µm.

The PXRD analysis of the material indicates it is primarily formed of wurtzite, as expected, but with a reasonable set of impurity peaks (particularly at 2θ of 25° and in the range 30–40°) that can be attributed to jalpaite (Ag₃CuS₂). In the SEM-EDX results, the elemental distribution appears broadly uniform except for a reasonable amount of localisation of silver (in agreement with the formation of a silver-rich jalpaite phase). Analysis of the overall spectral data gave between 8 and 10 at% for each of the metallic elements. However, the appearance of the EDX maps bears only a weak relation to the actual sample image (formed from secondary electrons).

The materials were further studied at the nanoscale via STEM-EDX. The elemental maps for the 6-cation sample are shown in Fig. 2. These have been arranged in such a way that it becomes clear that there are three very strong correlations between elemental species in the system. These are iron and copper shown in Fig. 2a and b, respectively, silver and cadmium shown in Fig. 2c and d, and manganese and zinc shown in Fig. 2e and f. This further supports the observation of silver-rich jalpaite forming in this system. The localisation of iron–copper sulfide regions also suggests the presence of chalcopyrite ((Fe/Cu)S) in the material, which agrees with other studies of this system by the authors.¹¹ However, unambiguous determination of this structure was not possible from the PXRD data; the remaining manganese-zinc sulfide regions appear to represent the expected wurtzite (ZnS) phase. It is also possible that these materials are present in an amorphous form that could not be detected by the XRD analysis. The structure and chemistry outlined here suggests that multiple phases have arisen because the enthalpic driving force for the formation of favourable structures has overridden the desired entropic stabilisation of the wurtzite phase. However, this is mostly determined by visual correlation of the elemental maps; the use of ML approaches can provide a deeper insight into the actual trends within the data, i.e., it can group the individual measurements that have a consistent EDX profile, allowing clearer spatial correlations to be identified. Furthermore, by averaging the signals across those groupings, a more complete picture of the actual composition is possible.

Fig. 2 STEM element maps for the 6-cation sample for (a) Cu, (b) Fe, (c) Ag, (d) Cd, (e) Mn and (f) Zn. The scale bar indicates 3 µm.

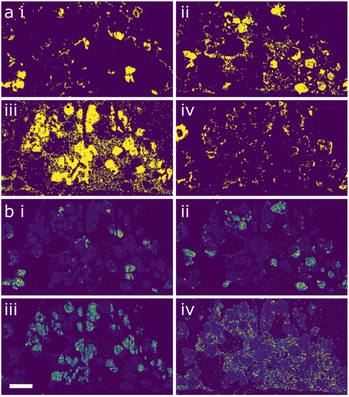
Both ML workflows applied to the data returned four major components within the region of microstructure analysed. These are shown in Fig. 3a and b, respectively, with clusters labelled (i–iv). In each case there seems to be strong agreements with the three main phases, chalcopyrite (i), jalpaite (ii) and wurtzite (iii). The presence of the fourth component suggests the need for a deeper analysis.

Fig. 3 Machine learning (clustering) outputs for the STEM-EDX data from the 6-cation system. (a) shows the spatial clustering from workflow 1 (GMM) while (b) shows the spatial clustering for workflow 2 (HBDSCAN). (i) shows chalcopyrite, (ii) jalpaite, (iii) majority wurtzite and (iv) minority wurtzite. Scale bar indicates 3 µm.

A major advantage of the ML approach is that each cluster can be used as a mask for smart segmentation of the EDX data, and the association of each measurement with that cluster can be used as a weighting to calculate a representative ‘average’ spectrum for the cluster. This has the advantage of having a significantly higher signal-to-noise ratio than any individual measurement, allowing meaningful quantitative analysis of the data. The representative compositions for the different clusters are shown in Table 1.

Table 1 Compositions of the unsupervised clustering outputs from the two workflows. (i) is chalcopyrite, (ii) jalpaite (iii) the majority wurtzite and (iv) the minority wurtzite. These are identical to the labels in Fig. 3

	i	ii	iii	iv
	Workflow 1
Ag	1.39 ± 0.17	39.0 ± 4.0	2.78 ± 0.18	10.8 ± 0.62
Cd	0.67 ± 0.10	15.8 ± 1.7	7.70 ± 0.35	7.00 ± 0.39
Cu	17.6 ± 0.96	5.06 ± 0.63	1.03 ± 0.10	8.59 ± 0.53
Fe	25.4 ± 1.3	0.71 ± 0.13	5.5 6 ± 0.32	10.5 ± 0.63
Mn	2.51 ± 0.26	0.81 ± 0.14	17.3 ± 0.76	9.45 ± 0.57
S	52.1 ± 2.4	38.5 ± 4.1	60.2 ± 2.4	51.1 ± 2.4
Zn	0.35 ± 0.08	0.11 ± 0.03	5.45 ± 0.30	2.45 ± 0.22
	Workflow 2
Ag	1.96 ± 0.14	16.6 ± 1.2	0.83 ± 0.06	6.86 ± 0.45
Cd	4.48 ± 0.32	28.5 ± 2.1	13.1 ± 0.61	15.3 ± 1.0
Cu	15.3 ± 0.79	9.50 ± 0.86	1.83 ± 0.17	8.46 ± 0.76
Fe	24.6 ± 1.29	1.83 ± 0.21	5.85 ± 0.33	10.4 ± 0.78
Mn	2.78 ± 0.22	1.83 ± 0.20	15.2 ± 0.67	8.18 ± 0.62
S	50.0 ± 2.2	41.1 ± 3.02	57.5 ± 2.3	48.4 ± 2.9
Zn	0.80 ± 0.11	0.45 ± 0.08	5.57 ± 0.31	2.32 ± 0.26

---

An immediate point is that all of the phases are considerably less phase-pure than the STEM element maps (Fig. 2) would suggest but are considerably less uniform than the SEM elements maps (Fig. 1a) suggest. Even for the jalpaite and chalcopyrite that would at first glance seem to be the enthalpically stable structures, there is considerable mixing of the metals. For the GMM approach (workflow 1) these phases contain between 5–7% of the ‘other’ elements not expected from the maps, while for the HDBSCAN (workflow 2) approach, this increases to 10–12%. The majority wurtzite phase (cluster iii) analysis in both cases shows a much higher sulfur : metal ratio than expected; for stoichiometric wurtzite this should be 1 : 1, but in both clustering cases the ratio is increased to nearly 3 : 2. The fourth minority cluster coincides with the wurtzite locations but is the only feature of the microstructure that shows a reasonably uniform composition in terms of the 6 metals.

The suggestion here is that the original 6-component wurtzite has formed with the desired broad mixture of the different cations in it. However, it has then undergone some later transformation to form a multi-phase mixture of jalpaite/chalcopyrite in equilibrium with a defective wurtzite structure. The formation of jalpaite in the system means that an excess of sulfur or a deficiency of metals must exist in another part of the microstructure, leading to a higher metal : sulfur ratio; this is evident from the quantification, but the likely explanation is that a reasonable population of vacancies now exists on the cation sublattice in the majority wurtzite cluster. Chalcopyrite, by contrast, is similar to wurtzite but with a slightly different stack order so would not cause a change in local chemistry.

The interesting feature of the quantification is that the remnant of the original wurtzite has a configurational entropy close to the theoretical limit for the system (approximately 0.85R compared to a maximum for 0.9R); however, even this does not seem to be sufficient to prevent the decomposition of the system to produce multiple phases with higher order (configurational entropies of 0.5–0.6R). In particular, the enthalpic driving force for silver (potentially acting in concert with cadmium) to form jalpaite compared to remaining in the wurtzite structure seems to be too great even for entropic stabilisation and is worthy of further study.

For the nanoscale 7-element system, the elemental maps are shown in Fig. 4. In this instance there seems to be a generally even distribution of the silver, indium, copper and gallium (Fig. 4c, d, f and g) in the system with local concentrations of cobalt, manganese and zinc (Fig. 4a, b and e) in the centre of the nanoparticles, suggesting a core–shell microstructure. As with the previous example, the ML workflows were applied to the system; in this instance there is a notable difference between the outputs, as seen in Fig. 5. Workflow 1 has segmented the data into two clusters (Fig. 5a and b), broadly representing the core and shell, respectively.

Fig. 4 STEM-EDX element maps for the 7-cation system showing (a) Mn, (b) Co, (c) Cu, (d) Ag, (e) Zn, (f) In and (g) Ga. The scale bar indicates 50 nm.

Fig. 5 Machine learning (clustering) results for the STEM-EDX data from the 7-cation system. (a) and (b) show the core and shell clusters determined by workflow 1, while (c) shows the single nanoparticle region cluster determined by workflow 2. Scale bar indicates 50 nm.

Workflow 2 did not differentiate the core and shell components, meaning that the nanoparticles were effectively segmented as a single composition. Quantification of the clusters is shown in Table 2.

Table 2 Experimental compositions of the unsupervised clustering outputs from the two workflows. For workflow 1 (i) is the core and (ii) the shell. These are equivalent to Fig. 5a and b, respectively

	Workflow 1		Workflow 2
	i	ii	i
Ag	20.90 ± 1.7	20.14 ± 1.7	19.19 ± 1.6
Co	2.88 ± 0.44	3.17 ± 0.47	3.24 ± 0.48
Cu	12.25 ± 1.1	10.36 ± 1.0	11.3 ± 1.1
Ga	3.16 ± 0.42	2.63 ± 0.37	2.88 ± 0.37
In	8.48 ± 0.77	7.98 ± 0.75	7.72 ± 0.71
Mn	1.00 ± 0.21	0.72 ± 0.17	0.90 ± 0.19
S	48.35 ± 3.9	52.50 ± 4.3	51.92 ± 4.2
Zn	2.97 ± 0.43	2.48 ± 0.38	2.84 ± 0.41

---

From this, the separation of the core and shell regions in ML workflow 1 (i and ii in both Table 2, and Fig. 5a and b) appears to have little or no relation to the segregation of cobalt, manganese, and zinc. In both clusters from workflow 1 these elements are found in similar amounts.

What is clear is that the three elements that produce maps appearing to show enhancement in the core (cobalt, manganese, and zinc) have all been weakly incorporated into the crystal structure, with ∼3% or lower concentrations for all elements. It is therefore possible that the reduction in nanoparticle thickness at the edge of the particles could lead to a sufficient reduction in signal and that noise in the data could be misinterpreted. For cobalt, manganese, and zinc, the maps all have an average of 1–2 counts per pixel, meaning that the signal-to-noise ratio is likely to be high in these cases. Compare this to the silver map, for example, with 15–20 counts per pixel; there are likely to be fewer noise-related artefacts in these elemental signals.

The clustering analysis of this data is by no means conclusive, but there is the suggestion that the core–shell morphology may be an ‘over-fitting’ of the data and so creating a microstructure that may not be present. The answer to this problem is to perform additional higher-resolution analysis of this system. Approaches such as atomic resolution STEM are time-consuming and less readily available so should be reserved for those samples that require it to unambiguously characterise the system.

Conclusions

The main takeaway from this study is that high-resolution compositional studies of multi-component materials can be considerably more complex than would be suggested by simple comparison of elemental maps. In the two cases presented in this work, the likely phase distribution suggested from the side-by-side comparison on elemental maps is shown to miss out on key details of the true microstructure as determined through statistical analysis of the collective.

In the case of the microscale 6-cation sulfide, the composition of the majority phases in the system is very hard to judge from the maps, with considerable mixing of elements in the different phases (e.g. copper in jalpaite, cadmium in chalcopyrite) and a notable variation in the metal : sulfur ratio in the majority wurtzite structure. All of which can be traced back to the decomposition of a more highly mixed parent wurtzite structure.

In the case of the nanoparticles of the 7-cation sulfide, the elemental maps suggest the occurrence of a core–shell structure, with the core being enriched in cobalt and possibly manganese and zinc. However, machine learning segregation and the resulting quantitative analysis raise the possibility that the core–shell structure may be an artefact that does not correlate with meaningful variations in composition. Higher-resolution techniques are necessary to address this issue, but the motivation for applying these comes from the outputs of the clustering techniques rather than from the elemental maps themselves.

Elemental maps on their own may not be the best way to present the distribution of different species in such complex systems. This can act two ways: in the first it can be that uniform elemental maps might be incorrectly judged to show perfect mixing of elements, while in the second, it is possible that intensity variations in an elemental map might be judged to be evidence of imperfect mixing, when they might really be smaller than the noise present in the measurements.

Regarding the two clustering workflows, variations between the clustering outputs are a result of the different approaches used in the two-step clustering process. UMAP is part of a family of approaches that model the data using graph theory (projecting the original data as a high-dimensional graph and seeking a low-dimensional version that preserves most of the original structure),²¹ while PCA is a matrix factorisation approach that looks for latent variables in the data that describe the largest amount of variance.²⁰ The low-dimensional projection of the original data will therefore differ subtly between approaches. Consequently, the grouping of measurements into clusters will differ between methods.

The clustering algorithm used will also influence the outputs; GMM assumes that points are drawn from a fixed number of Gaussian distributions, while HDBSCAN does not assume a prior statistical distribution, and instead assumes that clusters are dense regions of data separated by lower-density regions, allowing for arbitrarily shaped clusters. This leads to differences in the individual measurements incorporated into the outputs and hence the composition of the cluster.

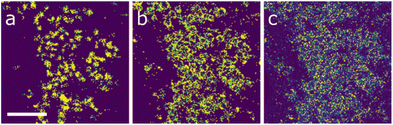
For the outputs for the 6-element system, the differences in cluster composition reflect that, in workflow 1, the first three clusters contain many extra measurements that appear to be part of the ‘background’ of the sample. In workflow 2 most of these are grouped into the fourth cluster resulting in the first three cluster maps showing material that is more tightly grouped into particles. This suggests a lower tolerance to misidentification of individual points. However, in both cases the general segmentation of the data into chemically distinct and interpretable clusters is successful and the results are broadly comparable in terms of the phases present.

A more nuanced approach is needed to interpret the 7-metal system; the major difference is that the UMAP-based (HDBSCAN) clustering method interpreted all the nanoparticle data as being similar, while the PCA-based (GMM) method separated the nanoparticle measurements into core and shell. Since the number of clusters was a user-defined parameter, there is the question of whether the core–shell morphology is an artefact imposed from the initialisation. Trusting to the data itself to determine the number of clusters needed would seem to be prudent. From prior experience the more advanced processes in this workflow seem to be a more reliable approach, and there is strong motivation to continue developing this method.

The current state-of-the-art in compositional analysis in TEM utilises machine learning approaches that can explore the wider trends in data. This is particularly important in research into complex multi-component systems where we expect statistical distributions of elements rather than highly organised chemical variations in regular crystals. The successful application of advanced STEM with cutting-edge data science to multi-element sulfides in this study suggests the opportunity exists to deepen our understanding of the wide range of multi-element and high-entropy materials currently being developed. Given the huge parameter space available for synthesis of these materials, the reproducibility, speed, and potential for automated analysis for high-throughput experiments makes data-driven analysis an appealing approach to improve the productivity of this research.

Methods and materials

STEM-EDX experiments were performed on a ThermoFisher Talos 200X (S)TEM operated at 200 kV and utilising a Super-X SDD detector. STEM-EDX data were processed using two different unsupervised clustering workflows. Both workflows took the as-recorded data and binned it by a factor of 2 (in order to reduce the size in computer memory). Subsequently the data was normalised using the RobustScaler method provided by the scikit-learn package.

Workflow 1 then used principle-component analysis (PCA) to reduce the dimensionality of the data; the final dimensionality was determined by studying the change point in the ‘Scree-plot’ of the decomposition. The reformed data was then clustered using the Gaussian mixture method (GMM) with the number of clusters manually determined. All algorithms were implemented from scikit-learn²⁰

Workflow 2 used the unified manifold and projection (UMAP) algorithm²¹ to reduce the data to four dimensions; the hierarchical density-based spatial clustering of applications with noise (HDBSCAN) algorithm²² was then used to cluster the measurements by similarity (determined from the Euclidean distance metric).

Representative spectra for each cluster were analysed using the HyperSpy²³ python libraries for quantitative EDX, with k-factors for 200 keV TEM.²⁴

The first sample used in the study was a bulk powder of a 6-element sulfide (AgCdCuFeMnZnS) produced from equal amounts of metal dithiocarbamate precursors. These were synthesized according to a known procedure described in the work of Lewis and coworkers.^11,25,26 Briefly, a metal salt, usually a nitrate or chloride, was dissolved in water before being added slowly to a methanolic solution of sodium diethyldithio-carbamate. The reaction mixture was stirred for 2 h before the solid product was removed by filtration and dried under vacuum. Equal molar amounts of the precursors were mixed and thermally decomposed to produce the samples.

The material was prepared for STEM experiments by embedding the as-made powder in resin and using a ultramicrotome to prepare 50-nm sections before floating these onto 3-mm gold TEM grids.

The nanoparticle system²⁷ of the 7-element sulfide (AgInCoCuGaMnZnS) was produced by solution-phase thermal decomposition of metal dithiocarbamate. Each desired diethyldithiocarbamate precursor was measured out (0.1 mmol) and added to oleylamine (10 mL) and dissolved under an inert atmosphere at 60 °C. Separately, a flask of oleylamine (20 mL) was heated to 200 °C under an inert atmosphere. When the precursor mixture had fully dissolved, it was injected rapidly into the second flask of oleylamine. When the temperature had returned to 200 °C, the reaction was timed for 1 h before being cooled to room temperature rapidly with a water bath. Acetone was added to precipitate the solid product, which was isolated by centrifugation at 5000g for 10 min, before being resuspended in toluene.

Samples were produced by drop-casting the as-synthesised nanoparticles onto a clean carbon film on a 3-mm gold TEM grid.

Data availability

The data and workflows used in this study can be accessed at: https://figshare.manchester.ac.uk/articles/dataset/High-entropy_sulfide_data_for_clustering_comparison/29327552/1.

Author contributions

ASE: conceptualization, formal analysis, methodology, project administration, supervision, writing – original draft. CM: investigation, data curation, methodology, writing – review & editing. MAB: investigation, data curation, methodology, writing – review & editing. ZK: data curation, methodology, software. REA: investigation. SM: formal analysis. DJL: funding acquisition, project administration, resources, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support for the electron microscopy work through EPSRC grants EP/R00661X/1, EP/S019367/1, EP/P025021/1, EP/S021531/1 and EP/P025498/1. DJL acknowledges support from EP/W033348/1 and EP/X016404/1.

Notes and references

1. B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent, Mater. Sci. Eng., A, 2004, 375–377, 213–218.
2. J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303.
3. E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534.
4. M. A. Buckingham, B. Ward-O'Brien, W. Xiao, Y. Li, J. Qu and D. J. Lewis, Chem. Commun., 2022, 58(58), 8025–8037.
5. M. A. Buckingham, J. M. Skelton and D. J. Lewis, Cryst. Growth Des., 2023, 23, 6998–7009.
6. Z. Cheng, J. Sun, X. Gao, Y. Wang, J. Cui, T. Wang and H. Chang, J. Alloys Compd., 2023, 930, 166768.
7. P. Kumari, A. K. Gupta, R. K. Mishra, M. S. Ahmad and R. R. Shahi, J. Magn. Magn. Mater., 2022, 554, 169142.
8. L. Sun and R. J. Cava, Phys. Rev. Mater., 2019, 3, 090301.
9. Y. Sun and S. Dai, Sci. Adv., 2021, 7, 1600.
10. N. K. Katiyar, K. Biswas, J.-W. Yeh, S. Sharma and C. S. Tiwary, Nano Energy, 2021, 88, 106261.
11. M. A. Buckingham, J. J. Shea, Z. Kho, P. M. E. Lo, J. Swindell, W. Xiao, D. J. Lewis, A. S. Eggeman and S. A. Hunt, Commun. Chem., 2025, 8, 65.
12. D. C. Joy and J. B. Pawley, Ultramicroscopy, 1992, 47, 80–100.
13. V. B. Özdöl, V. Srot and P. A. van Aken, Handbook for Nanoscopy, Wiley, 2012.
14. K. E. MacArthur, T. J. A. Slater, S. J. Haigh, D. Ozkaya, P. D. Nellist and S. Lozano-Perez, Microsc. Microanal., 2016, 22, 71–81.
15. D. J. Kelly, M. Zhou, N. Clark, M. J. Hamer, E. A. Lewis, A. M. Rakowski, S. J. Haigh and R. V. Gorbachev, Nano Lett., 2018, 18, 1168–1174.
16. Y. Han, et al., Nat. Mach. Intell., 2021, 3, 267–274.
17. S. V. Kalinin, Nat. Rev. Methods Primers, 2022, 2, 11.
18. J. Blanco-Portals, F. Peiró and S. Estradé, Microsc. Microanal., 2022, 28, 109–122.
19. Z. Kho, A. Bridger, K. Butler, E. C. Duran, M. Danaie and A. S. Eggeman, APL Mater., 2025, 13, 010901.
20. F. Pedregosa, et al., J. Mach. Learn. Res., 2011, 12, 2825–2830.
21. L. McInnes, et al., J. Open Source Softw., 2018, 3, 29–861.
22. L. McInnes, et al., J. Open Source Softw., 2017, 2, 11–205.
23. F. de la Peña et al., Hyperspy:v2.30, Zenodo, 2025,  DOI:10.5281/zenodo.14956374.
24. P. J. Sheridan, J. Electron Microsc. Tech., 1989, 11, 41–61.
25. B. Ward-O’Brien, et al., J. Am. Chem. Soc., 2021, 143(51), 21560–21566.
26. W. Xiao, et al., Chem. Mater., 2023, 35(19), 7904–7914.
27. B. Ward-O’Brien, et al., Nano Lett., 2022, 22(20), 8045–8051.

---