Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interaction of lipid domains originating from differential domain–monolayer contact energy
Avishai
Barnoy
ab and
Michael M.
Kozlov
 *a
*a
aDepartment of Physiology and Pharmacology, Faculty of Medical and Health Sciences, Tel Aviv University, 69978 Tel Aviv, Israel. E-mail: michk@tauex.tay.ac.il
bSchool of Chemistry, Faculty of Exact Sciences, Tel Aviv University, Israel
First published on 3rd January 2025
Abstract
We consider a flat membrane containing pure lipid domains located in the membrane monolayers and separated in the membrane plane. We assume the energy of contact along the membrane mid-surface between a domain and the underlying monolayer to be different from that between the two monolayers. We theoretically analyse the effect of the differential contact energy on the elastic deformations of tilt and splay in the membrane monolayers and the resulting interaction between two domains situated in the apposed monolayers. We demonstrate that the character of this interaction depends on the ratio, η, between the domain rigidity and that of a regular membrane monolayer. For the rigidity ratio smaller than a critical value, η < η* ≈ 3, the domain interaction is predicted to be attractive for all inter-monolayer distances. For the super-critical values of the rigidity ratio, η > η*, the interaction is repulsive for small distances and attractive for large distances with a certain equilibrium inter-domain separation corresponding to a vanishing interaction force. The predicted attractive interaction is proposed to favor the registration in the membrane plane of apposed domains as observed in most domain-containing membranes.
Introduction
Studies of the formation and organization of membrane domains whose physicochemical properties such as the lipid and protein composition and the lipid phase state differ from those of the regular membrane monolayers represent an extensive and, practically, self-standing field of membrane biophysics.1–4 In the context of cell membranes, the most familiar and extensively discussed are the domains which consist mainly of glycosphingolipids and cholesterol, contain specific proteins, and are referred to as the lipid rafts.5 In multicomponent pure lipid membranes, the domain formation results from the in-plane segregation of coexisting lipid phases, most commonly, the regions of liquid-ordered (Lo)1 or gel (Lβ)6,7 phase within the bulk of a liquid-disordered (Ld) (ref. 8 and references therein) phase.Theoretical modelling of domain formation in lipid bilayers was performed by various approaches ranging from sophisticated methods of soft matter physics9,10 to state-of-the-art numerical simulations.11 This led to understanding the molecular interactions in the lipid monolayer plane driving the domain formation.12,13 Yet, one aspect of the domain arrangement within membranes remained largely open, namely, the forces responsible for the commonly observed strong spatial correlation between domains formed in the apposed membrane monolayers. In most of the experimental studies, the domains in one membrane monolayer were observed to be in register with those in the apposed monolayer so that both the lipid rafts in cell membranes and the regions of ordered lipid phases in pure lipid membranes were mostly seen to span the whole membrane thickness (see ref. 14 for review). The origin of the trans-monolayer interactions mediating a cross-talk between domains in the apposed monolayers remained hypothetical.
The major proposal for explaining this phenomenon is that the lipid phase separation and the resulting domain formation in one membrane monolayer trigger the same process right underneath in the second monolayer due to a hypothetical trans-membrane coupling interaction.9,15,16 At the same time, it was possible to experimentally separate the trans-bilayer domains into unregistered monolayer domains by applying tangential shear forces to the top and bottom membrane surfaces.17 This implied that the trans-membrane registration was not crucial for the monolayer domain stability and that an attractive interaction must exist between laterally separated domains located in apposed monolayers favoring their mutual approach and ultimate overlapping. While an effective interaction related to the domain line tension was suggested to be responsible for fine-tuning the relative positioning of the already overlaying domains,18 an understanding of interactions between separated non-overlapping domains has remained missing.
Here we propose a mechanism leading to an attractive interaction between domains formed in the apposed membrane monolayers and stemming from the membrane deformations. We suggest that the origin of the membrane deformations and, hence, the domain interaction is the difference in the energies of contact between a monolayer and a domain and that between two regular membrane monolayers. The physical essence of the differential contact energy is equivalent to that of the domain's surface tension proposed in ref. 15 and 19 and discussed in ref. 14. The same concept of differential contact energy was recently considered in the context of the membrane shaping by caveolin discs.20 Our theoretical analysis of flat membranes shows that the propensity of a domain-containing membrane to minimize the overall differential contact energy generates the deformations of tilt and splay of the membrane monolayers, which propagate along the membrane plane and mediate an interaction of separated membrane domains. We determine the conditions under which this interaction is attractive and demonstrate the feasibility of these conditions for realistic lipid membranes.
Qualitative essence of the model
Single domain
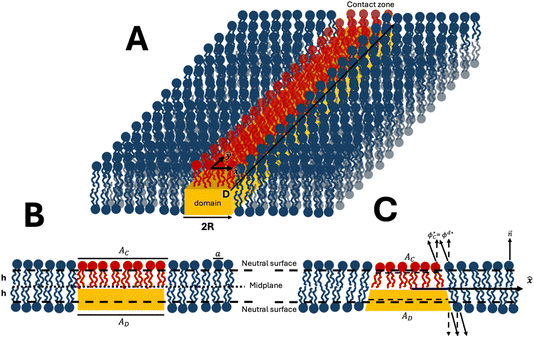
To qualitatively explain the model’s main idea, we first consider a lipid bilayer containing a single lipid domain in one of its monolayers (Fig. 1). We use the following terminology illustrated in Fig. 1A. The monolayer lipid domain will be called simply the domain. The membrane monolayer containing the domain will be referred to as the proximal monolayer. The second monolayer apposed to the proximal one will be called the distal monolayer. The fragment of the distal monolayer whose lipid molecules touch by their hydrocarbon chains the hydrophobic surface of the domain will be called the contact zone. For simplicity, we assume that the physical properties of the distal monolayer, including the contact zone, are identical to those of the proximal monolayer but differ from those of the domain. For the bilayer with multiple domains (Fig. 2), the bottom and top monolayers will be referred to as the proximal and the distal ones, respectively.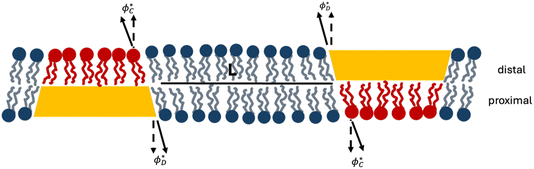 | ||
| Fig. 2 Cross-section of a membrane with two domains located in apposed monolayers. Due to symmetry, the tilt angles in equivalent sections of the apposed monolayers are identical. The color scheme follows that of Fig. 1. The inter-domain distance along the midplane is L. Dashed arrows represent the normal to the neutral surface, solid arrows represent the lipid director. | ||
The central hypothesis of the model is that the contact interaction between the lipid molecules of the distal and proximal monolayers along the bilayer mid-plane is different from that between the contact zone and the hydrophobic plane of the domain. This differential contact interaction is the origin of the domain surface tension introduced in ref. 15 and 19. To be specific, we consider the contact between the distal and proximal monolayers to be energetically more favorable than that between the distal monolayer and the domain. In the following, the energy of the contact interaction will be called the contact energy, for brevity.
To keep the computations simple, we consider the one-dimensional version of the model in which a domain has the shape of a strip of finite width, 2R, and infinite length (Fig. 1A). We choose the planar coordinates system in the bilayer mid-plane with the axes x and y directed perpendicularly and parallel to the domain’s length, respectively (Fig. 1A). For the one-domain system the origin of the x coordinate, x = 0, is chosen in the middle of the domain (Fig. 1A). For the two-domain system the domains are oriented parallel to the axis y and, hence, to each other, the distance between the domain edges is denoted by L (Fig. 2). The monolayer deformations depend only on the x-coordinate, simplifying the analysis. Despite this simplification, the predictions must also be qualitatively valid for the realistic two-dimensional distributions of deformations.
For the following, we need to briefly recall a few basic notions used to describe a lipid monolayer as an elastic surface (see for review ref. 21). While, generally, a lipid monolayer, as any interface, can be described by any surface parallel to the monolayer plane called the dividing surface,22 most conveniently it is represented by a specific dividing surface referred to as the monolayer neutral surface.23–25 The deformations of the monolayer stretching–compression determined at the neutral surface are energetically decoupled from the deformations of the monolayer bending23–25 and, hence, from the deformation of splaying the hydrocarbon chains of lipid molecules.26 According to the analysis of experimental data on lipid monolayers of different compositions, the monolayer neutral surface underlies the effective boundary between the region of the lipid polar heads and that of the hydrocarbon moieties of the lipid molecule.
The premise of our model is that the in-plane area per one lipid molecule, a, determined at the neutral surface of any of the membrane monolayers does not change upon the splaying and/or tilting of lipid molecules and/or generation of the monolayer tension. The constancy of a upon splaying is the consequence of the above-mentioned property of the neutral surface. The invariance of a upon tilting follows from the essence of the lipid tilt deformation as the transverse shear of the lipid material, which keeps constant the molecular volume and in-plane area.26,27 Finally, the background for the constancy of a upon the tension generation is the large stretching–compression modulus of a lipid monolayer whose typical value of about 100 mN m−1 (ref. 28) exceeds by a few orders of magnitude the experimentally feasible tension values of less than 1 mN m−1 (see e.g. ref. 29).
In addition, we will assume that the lipid molecular area, a, is equal for all lipid molecules of the system including those composing the regular monolayers and the domains. In real systems, the lipid molecular area at the neutral surface can vary within the range of about 30–40% depending on the lipid species and phase state.25,30–32 We neglect this variation meaning that the predictions of our modelling have qualitative rather than quantitative character.
We consider, for simplicity, the bilayer to be flat, which implies that it is subjected to a lateral tension preventing its deviations from the planar shape. We denote by AD and AC the areas of, respectively, the domain and the contact zone determined at the neutral surfaces of the corresponding monolayers (Fig. 1B). The numbers of lipid molecules constituting the domain and the contact zone are, respectively,  and
and  .
.
We consider the initial state of the bilayer to exhibit no tilt of the lipid molecules in any part of the system (Fig. 1A and B). In this state, the areas and the molecular numbers are equal for the contact zone and the domain, AC = AD, and NC = ND (Fig. 1B).
The system tends to reduce the contact energy by decreasing the number of lipid molecules, NC, and, hence, the area, AC, of the contact zone, while keeping constant the domain’s parameters, AD and ND. This can be achieved by tilting the lipid molecules26,27,33 at the domain’s boundary (Fig. 1C). A simple geometrical consideration shows that the tilting of the lipid molecules of the contact zone inward and those of the domain outward from the domain’s center reduces AC and, hence, decreases NC (Fig. 1C). The molecular tilt induced at the domain boundary propagates along the monolayer plains decaying with the distance from the boundary, which generates the splay deformation (Fig. 1C).26,27,33
Hence, the reduction of the number of molecules in the contact zone, NC, and, thus, the contact energy is accompanied by the cost of the elastic energy of the tilt and splay.26,27,33 The energetically most favorable and, therefore, equilibrium configuration of the system is characterized by a certain extent of the lipid tilt-splay that is set by the interplay between the contact energy driving the deformations and the elastic energy resisting it.
Multiple domains
In the case where the bilayer contains two (Fig. 2) or more lipid domains, the factors driving the system’s deformations are the same as those described for a single domain. Yet, an additional important factor to be considered in this case is the overlap of membrane deformations generated by neighboring domains. This overlap results in a membrane-mediated interaction between the domains, which can be either repulsive or attractive depending on the system’s parameters.Main definitions and equations
We consider a flat lipid bilayer whose monolayers contain domains. We analyse two systems: a lipid bilayer with one domain (Fig. 1), and a bilayer with two domains located in apposed monolayers (Fig. 2).For clarity, we introduce the main notions and equations for the system with one domain (Fig. 1). They can be straightforwardly used in the two-domain case (Fig. 2). In a few cases where such a direct usage is not possible, we provide additional definitions.
The system will be described by three mutually parallel flat surfaces: the bilayer’s mid-plane and the neutral surfaces of the proximal and distal monolayers separated from the bilayer’s midplane by a distance, h, approximately equal to the monolayer thickness (Fig. 1B).
The physical values of the domain and the contact zone will be denoted by the subscripts D and C, respectively, whereas those describing the distal or the proximal monolayers will be indicated by the superscripts d and p. We will use no indices by introducing notations and relationships common for all parts of the system.
The system is characterized at every point of its neutral surface by the tilt, t, and splay, ![[J with combining macron]](https://www.rsc.org/images/entities/i_char_004a_0304.gif) , of the constituent lipid molecules. The notions of tilt and splay are introduced and discussed in ref. 26, 27 and 33. In brief, for the 1D system considered here, the lipid tilt, t, is equal to t = tan
, of the constituent lipid molecules. The notions of tilt and splay are introduced and discussed in ref. 26, 27 and 33. In brief, for the 1D system considered here, the lipid tilt, t, is equal to t = tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, where ϕ is the angle between the unit vector,
ϕ, where ϕ is the angle between the unit vector,  , describing the average orientation of the lipid hydrocarbon chains and the unit normal,
, describing the average orientation of the lipid hydrocarbon chains and the unit normal,  , of the monolayer’s neutral surface (Fig. 3). We define the tilt angle, ϕ, to be positive if
, of the monolayer’s neutral surface (Fig. 3). We define the tilt angle, ϕ, to be positive if 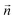 leans away from
leans away from  in the clockwise direction and negative otherwise. The values of the tilt angle in the domain, the contact zone, the proximal monolayer outside the domain, and the distal monolayer outside the contact zone will be denoted by ϕD, ϕC, ϕp, and ϕd, respectively.
in the clockwise direction and negative otherwise. The values of the tilt angle in the domain, the contact zone, the proximal monolayer outside the domain, and the distal monolayer outside the contact zone will be denoted by ϕD, ϕC, ϕp, and ϕd, respectively.
The lipid splay, ![[J with combining macron]](https://www.rsc.org/images/entities/i_char_004a_0304.gif) , quantifies the variation of the lipid chain orientation along the monolayer neutral plane (Fig. 3). For the flat 1D bilayers considered here, the splay is defined by
, quantifies the variation of the lipid chain orientation along the monolayer neutral plane (Fig. 3). For the flat 1D bilayers considered here, the splay is defined by  .
.
For simplicity, we assume the monolayer deformations in all parts of the system to be weak leading to small tilt angles, ϕ < 1, so that tilt and splay can be approximated as t = ϕ and  . The smallness of the splay is expressed by
. The smallness of the splay is expressed by  .
.
Energy of the system
Our goal is to find the equilibrium configuration of the system corresponding to the minimum of the system’s energy, F. The energy will be computed with respect to the initial state in which the tilt and, hence, the splay vanish, ϕ = 0, , in all parts of the system (Fig. 1A and B).
, in all parts of the system (Fig. 1A and B).
We consider the energy F to consist of the contact energy, Fcont, and the elastic energy of tilt-splay, Ft.
 | (1) |
The meaning of  in eqn (1) is the summation of the contributions of all parts of the system.
in eqn (1) is the summation of the contributions of all parts of the system.
To introduce the contact energy, Fcont, we first define the partial contact energies, εD and εL. The value εD is the energy of contact between the contact zone and the domain related to the unit area of the contact zone’s neutral plane. The value εL is the energy of contact between the distal and proximal monolayers related to the unit area of the neutral surface of the former. The contact energy, Fcont, is proportional to the variation in the number of lipid molecules in the contact zone, NC, resulting from the emerging tilt-splay deformations. Taking into account that in the initial state NC = ND and using the relationship  , the contact energy can be presented as
, the contact energy can be presented as
| Fcont = (AC − AD)Δε, | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14,15,19 (where kBT ≈ 4 × 10−21 joules is the product of the Boltzmann constant and the absolute temperature).
14,15,19 (where kBT ≈ 4 × 10−21 joules is the product of the Boltzmann constant and the absolute temperature).
For the one-dimensional model considered here, we will present the domain area as AD = 2·D·R, where 2R is the domain width along the x axis, as already mentioned, and D is a constant multiplier whose meaning is the length along the direction of the system’s uniformity (Fig. 1A). For estimations, we will use the minimal relevant value of the domain’s half-width, R ≈ 100 nm.
The sum of the tilt and splay energies of a monolayer related to the unit area of its neutral surface, fb + ft, can be expressed in the case considered here of small deformations as,26
 | (3) |
 | (4) |
The elastic moduli of splay and tilt of the domain denoted by κD and κtD must be, generally, larger than the corresponding moduli, κ and κt, of the regular parts of the system’s monolayers. To keep the calculations simple, we assume the splay and tilt moduli of the domains to differ from those of the regular monolayers by the same factor, η,
| κD = η·κ, κtD = η·κt | (5) |
The factor η will be referred to below as the relative rigidity of the domain and assumed to be η > 1.
Main equations
The distributions of the tilt angle, ϕ(x), and, hence, of the splay, , can be found either by minimizing the full energy (eqn (1)) or by solving the related Lagrange equation, which for a flat monolayer and a small tilt-splay deformation is
, can be found either by minimizing the full energy (eqn (1)) or by solving the related Lagrange equation, which for a flat monolayer and a small tilt-splay deformation is | (6) |
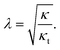 | (7) |
Based on the cited-above values of the elastic moduli, the relaxation length λ has a value in the range of 1–2 nm.
Due to the simplifying assumption (eqn (5)), the relaxation length (eqn (7)) is the same for the domain, the contact zone and all other parts of the system.
The solutions of Lagrange equations (eqn (6)) must satisfy certain boundary conditions. For simplicity, we explicitly present here the boundary conditions for the system with one domain (Fig. 1C). For the system with two domains, the boundary conditions can be found analogously. For symmetry reasons, in the middle of the domain, x = 0, the tilt angles of the domain and the contact zone must vanish,
| ϕD(x = 0) = 0, ϕC(x = 0) = 0. | (8) |
At large distances, x = ∞, the tilt angles of the proximal and distal monolayers must vanish,
| ϕp(x = ∞) = 0, and ϕd(x = ∞) = 0, | (9) |
Finally, a set of conditions has to be satisfied at the domain boundary, x = R. The geometrical characteristics at this boundary will be denoted by asterisks and referred to as the boundary values (Fig. 1C). First, the orientation of the hydrocarbon chains,  , in each leaflet must be continuous. The continuity of
, in each leaflet must be continuous. The continuity of  can be expressed through the boundary tilt angles of the domain,
can be expressed through the boundary tilt angles of the domain,  , the contact zone,
, the contact zone, 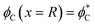 , the proximal monolayer ϕp(x = R) = ϕp*, and ϕd(x = R) = ϕd*, by
, the proximal monolayer ϕp(x = R) = ϕp*, and ϕd(x = R) = ϕd*, by
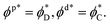 | (10) |
Using the tilt boundary values, the contact energy (eqn (2)) related to the unit length of the y axis can be expressed as
 | (11) |
Way of computations
In the following, we find the distribution of tilt and splay in each part of the system by solving the Lagrange equation (eqn (6)) with the boundary conditions (eqn (8) and (10)). Inserting the resulting functions ϕ(x) into eqn (4), performing the integration over the area of each part of the system, inserting the results into eqn (1) and summing them along with eqn (11) we obtain the full energy of the system as a function of the boundary tilt angles, and
and  . Minimizing the resulting energy with respect to
. Minimizing the resulting energy with respect to 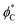 and
and 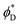 we find the equilibrium values of these angles and the energy of the equilibrium state. In the case of the two-domain system, the dependence of the equilibrium energy on the distance between the domains will enable the analysis of the domain interaction mediated by the membrane deformations.
we find the equilibrium values of these angles and the energy of the equilibrium state. In the case of the two-domain system, the dependence of the equilibrium energy on the distance between the domains will enable the analysis of the domain interaction mediated by the membrane deformations.
Because of the structure of the Lagrange equation (eqn (6)), all the results depend on the dimensionless form of the system’s variables and parameters having units of length. Specifically, the dimensionless coordinate, domain half-width, and distance between the domains are, respectively,
 | (12) |
Results
One domain
Due to the system’s symmetry with respect to the middle of the domain, x = 0, we analyse half of the system, x ≥ 0 (Fig. 1C). The distribution of the tilt angle in the domain, the contact zone, and the proximal and distal monolayers resulting from our computations are given by | (13) |
The equilibrium boundary angles in the contact zone and the domain are, respectively,
 | (14) |
 | (15) |
The energy of the equilibrium state computed with respect to the initial state is
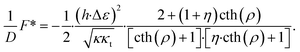 | (16) |
Taking into account that a realistic value of the dimensionless half-width of the domain is large compared to the relaxation length,  , so that cth(ρ) ≈ 1, the expressions eqn (14)–(16) can be simplified. In particular, the energy is given by
, so that cth(ρ) ≈ 1, the expressions eqn (14)–(16) can be simplified. In particular, the energy is given by
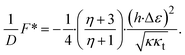 | (17) |
The dependence of the equilibrium energy on the relative rigidity is presented in Fig. 4A, and the distribution along the x-axis of the tilt angles for both the distal and proximal monolayers is shown in Fig. 4B for different values of the relative domain rigidity. The extent of tilting in the distal monolayer is independent of the relative domain rigidity. The extent of tilting in the proximal monolayer including the domain decreases with growing domain rigidity. When the rigidity of the domain is equal to the rigidity of the membrane, η = 1, the tilt angles in the distal and proximal monolayers are equal (Fig. 4B, orange and purple dashed lines). The energy relaxation is most effective if the domain is as flexible as the regular monolayers, η = 1 (Fig. 4A), but even if the domain is infinitely rigid, η → ∞, the energy relaxes to a substantial extent due to the tilting in the distal monolayer.
Two domains in apposed monolayers
Now we consider a bilayer containing two domains. If the domains are inserted into the same membrane leaflet, they induce similar tilt-splay deformations in the proximal and distal monolayers. Based on the previous work on membrane deformations by caveolin discs20 and cap-like inclusions,37 the overlap of the membrane deformations generated by the two similar domains located in the same monolayer must generate a repulsive interaction between the domains.Here we consider a bilayer containing two domains located in the apposed monolayers and separated by a distance L between the domains’ edges (Fig. 2).
Since the main goal of this section is to analyse the membrane-mediated interaction between the domains, we describe the monolayer deformations and the energy only of the mid-part of the system located between the domains’ centers and dependent on the inter-domain distance, L. Since the relevant domain size, R, substantially exceeds the nanometer-large relaxation length, R ≫ λ, the deformations and energies of the left and right peripheral parts of the system do not depend on the separation, L, and, therefore, do not contribute to the domain interaction.
Due to the system’s symmetry, the boundary tilt angles for the domain located in the distal,  , and proximal,
, and proximal,  , monolayers must be equal,
, monolayers must be equal,  (Fig. 2). The same is true for the boundary angles of the two contact zones,
(Fig. 2). The same is true for the boundary angles of the two contact zones,  .
.
For the distal monolayer of the system, the computed distributions of the tilt angle in the contact zone, the domain, and the monolayer between them (Fig. 2) are given by
 | (18) |
For the proximal monolayer, the distributions of the tilt angle are obtained by inverting the sign of the dimensionless coordinate, ξ, in eqn (18).
To present the computed expressions for the boundary tilt angles and the energy, we first define two auxiliary functions of the dimensionless inter-domain distance l = L/λ,
 | (19) |
 | (20) |
The dependences of the boundary tilt angles of the contact zone and the domain on the dimensionless distance, l, are given by
 | (21) |
 | (22) |
The energy of the middle part of the system is expressed through the boundary angles by
 | (23) |
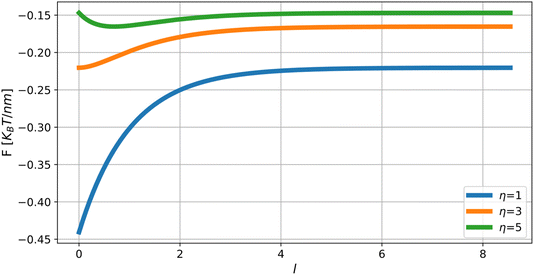
The dependence of the energy on the inter-domain distance, F*(l), determined by eqn (23) along with eqn (19)–(22) is presented in Fig. 5 for different values of the relative domain’s rigidity η.
There are two regimes of interaction. For values, η, larger than a critical value, η*, the interaction is repulsive for small inter-domain distances, and attractive for large inter-domain distances. This regime is characterized by an equilibrium distance, l*, between the domains, corresponding to the minimum of the energy (Fig. 5). For the values of the relative rigidity smaller than the critical value, η < η*, the interaction is attractive for all distances. The critical relative rigidity, η*, can be found from the approximation of the energy function (eqn (23)) valid for small distances, l ≪ 1, which is
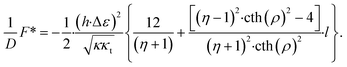 | (24) |
The corresponding interaction force,  , at a vanishing distance is given by
, at a vanishing distance is given by
 | (25) |
The critical value of the relative domain rigidity, η*, separating the two regimes of the domain interaction is that for which the force (eqn (25)) vanishes,
 | (26) |
For the realistic values of the dimensionless half-width of the domain, ρ ≫ 1, the critical value is η* ≈ 3. The dependence of the critical relative rigidity, η*, on the dimensionless domain size, ρ, is presented in the phase diagram in Fig. 6.
The dependence of the equilibrium inter-domain distance, l*, on the relative rigidity, η, is presented in Fig. 7.
The maximal inter-domain attractive force corresponds to the case in which the domain rigidity is similar to that of the regular lipid monolayer, η = 1, and is equal  .
.
Discussion
We considered a flat membrane containing lipid domains in its monolayers. We hypothesized that the partial energy of contact between a monolayer and a domain along the membrane midplane differs from that between the two membrane monolayers. Such a differential contact energy is the origin of the domain’s surface tension proposed in ref. 15 and 19. We demonstrated by computations that the differential contact energy generates the intra-membrane deformations of lipid tilt and splay which in turn give rise to a membrane-mediated interaction between the domains. The central finding of our analysis is that the character of the interaction between domains located in apposed membrane monolayers depends on the ratio between the domains’ and the monolayer’s rigidities. Assuming that the domains are more rigid than the regular monolayers we predict that domains whose rigidity is less than threefold that of a regular lipid monolayer exhibit an attractive interaction for any inter-domain separation (Fig. 6 and 7). More rigid domains are predicted to mutually repel at small and attract at large separations, and infinitely rigid domains exhibit a repulsion for all distances. The scale of the interaction energy, F0, is set, according to (eqn (24)), by the combination of the above-defined parameters of the system, . For the differential partial contact energy of Δε = 0.5kBT nm−2, and the common values of the monolayer thickness, h = 2 nm, the monolayer splay (bending) modulus κ = 10kBT, the monolayer tilt modulus, κt = 30 mN m−1, and the domain size, D = 100 nm, the energy scale is F0 ≈ 10kBT. The scale of the interaction force (eqn (25)), is set by
. For the differential partial contact energy of Δε = 0.5kBT nm−2, and the common values of the monolayer thickness, h = 2 nm, the monolayer splay (bending) modulus κ = 10kBT, the monolayer tilt modulus, κt = 30 mN m−1, and the domain size, D = 100 nm, the energy scale is F0 ≈ 10kBT. The scale of the interaction force (eqn (25)), is set by  , which for the above parameter values has a biologically reasonable value of
, which for the above parameter values has a biologically reasonable value of  . The range of the predicted inter-domain interaction is determined by the relaxation length, λ (eqn (7)), and is therefore, relatively short.
. The range of the predicted inter-domain interaction is determined by the relaxation length, λ (eqn (7)), and is therefore, relatively short.
The major limitation of the present analysis is the consideration of a flat membrane. This implies that the membrane is exposed to a stretching force generating a large lateral tension, γ ≫ Δε, and preventing, therefore, membrane bending. In loose membranes subjected to relatively small membrane tensions, γ ≪ Δε, the differential contact energy is expected to generate, in addition to the tilt and splay deformation, the curvature of the domains and, hence, of the surrounding membrane. According to our preliminary analysis, the development of the domain’s curvature considerably reinforces the domain interaction and increases the interaction range to  , which can be substantially larger than that given by eqn (7) for biologically relevant tensions, γ ≤ 0.1 mN m−1, much smaller than the tilt modulus, γ ≪ κt ≈ 10 mN m−1. A detailed analysis of the domain interaction in loose membranes will be presented in a separate article.
, which can be substantially larger than that given by eqn (7) for biologically relevant tensions, γ ≤ 0.1 mN m−1, much smaller than the tilt modulus, γ ≪ κt ≈ 10 mN m−1. A detailed analysis of the domain interaction in loose membranes will be presented in a separate article.
Finally, our model does not account for the effects of proteins present in cell membranes in general and cell membrane domains in particular. Membrane proteins can substantially influence the domain interaction in case they are localized to the boundaries of the domains and/or contact zones and modify the degree of the lipid tilting. Therefore, our model is directly applicable to the domain interaction in purely lipid membranes but may miss some protein effects as far as lipid rafts are concerned.
Conclusions
According to our model, the differential energy of the intra-membrane contact between a lipid domain and the underlying lipid monolayers generates deformations of the membrane lipid matrix and the resulting domain interactions. The deformations for flat membranes considered here are those of tilt and splay of the constituent lipid molecules. The character of the interaction between two domains located in apposed monolayers depends on the domain’s relative rigidity. Moderately rigid domains attract each other at all inter-domain distances. Domains whose rigidities are more than threefold those of regular membrane monolayers mutually repel at small distances, and attract at large distances, thus, exhibiting an equilibrium separation with a vanishing interaction force.Data availability
This study was carried out using publicly available data from the published articles (see references).Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
MMK acknowledges support from the Israel Science Foundation (Grant No. 1994/22) and holds the Joseph Klafter Chair in Biophysics.References
- T. Baumgart, S. T. Hess and W. W. Webb, Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension, Nature, 2003, 425(6960), 821–824 CrossRef CAS PubMed.
- H. A. Rinia and B. de Kruijff, Imaging domains in model membranes with atomic force microscopy, FEBS Lett., 2001, 504(3), 194–199 CrossRef CAS PubMed.
- H. A. Rinia, M. M. Snel, J. P. van der Eerden and B. de Kruijff, Visualizing detergent resistant domains in model membranes with atomic force microscopy, FEBS Lett., 2001, 501(1), 92–96 CrossRef CAS PubMed.
- E. Sezgin, I. Levental, S. Mayor and C. Eggeling, The mystery of membrane organization: composition, regulation and roles of lipid rafts, Nat. Rev. Mol. Cell Biol., 2017, 18(6), 361–374 CrossRef CAS PubMed.
- K. Simons and E. Ikonen, Functional rafts in cell membranes, Nature, 1997, 387(6633), 569–572 CrossRef CAS PubMed.
- J. H. Ipsen, G. Karlstrom, O. G. Mouritsen, H. Wennerstrom and M. J. Zuckermann, Phase equilibria in the phosphatidylcholine-cholesterol system, Biochim. Biophys. Acta, Biomembr., 1987, 905(1), 162–172 CrossRef CAS PubMed.
- B. D. Ladbrooke and D. Chapman, Thermal analysis of lipids, proteins and biological membranes. A review and summary of some recent studies, Chem. Phys. Lipids, 1969, 3(4), 304–356 CrossRef CAS PubMed.
- G. W. Feigenson, Phase diagrams and lipid domains in multicomponent lipid bilayer mixtures, Biochim. Biophys. Acta, Biomembr., 2009, 1788(1), 47–52 CrossRef CAS PubMed.
- G. G. Putzel, M. J. Uline, I. Szleifer and M. Schick, Interleaflet coupling and domain registry in phase-separated lipid bilayers, Biophys. J., 2011, 100(4), 996–1004 CrossRef CAS PubMed.
- S. Komura and D. Andelman, Physical aspects of heterogeneities in multi-component lipid membranes, Adv. Colloid Interface Sci., 2014, 208, 34–46 CrossRef CAS PubMed.
- W. F. Bennett and D. P. Tieleman, Computer simulations of lipid membrane domains, Biochim. Biophys. Acta, Biomembr., 2013, 1828(8), 1765–1776 CrossRef CAS PubMed.
- S. Garg, J. Ruhe, K. Ludtke, R. Jordan and C. A. Naumann, Domain registration in raft-mimicking lipid mixtures studied using polymer-tethered lipid bilayers, Biophys. J., 2007, 92(4), 1263–1270 CrossRef CAS PubMed.
- M. D. Collins and S. L. Keller, Tuning lipid mixtures to induce or suppress domain formation across leaflets of unsupported asymmetric bilayers, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(1), 124–128 CrossRef CAS PubMed.
- S. May, Trans-monolayer coupling of fluid domains in lipid bilayers, Soft Matter, 2009, 5(17), 3148–3156 RSC.
- M. D. Collins, Interleaflet coupling mechanisms in bilayers of lipids and cholesterol, Biophys. J., 2008, 94(5), L32–L34 CrossRef CAS PubMed.
- J. J. Williamson and P. D. Olmsted, Comment on “Elastic Membrane Deformations Govern Interleaflet Coupling of Lipid-Ordered Domains”, Phys. Rev. Lett., 2016, 116(7), 079801 CrossRef CAS PubMed.
- M. C. Blosser, A. R. Honerkamp-Smith, T. Han, M. Haataja and S. L. Keller, Transbilayer Colocalization of Lipid Domains Explained via Measurement of Strong Coupling Parameters, Biophys. J., 2015, 109(11), 2317–2327 CrossRef CAS PubMed.
- T. R. Galimzyanov, R. J. Molotkovsky, M. E. Bozdaganyan, F. S. Cohen, P. Pohl and S. A. Akimov, Elastic Membrane Deformations Govern Interleaflet Coupling of Lipid-Ordered Domains, Phys. Rev. Lett., 2015, 115(8), 088101 CrossRef PubMed.
- H. J. Risselada and S. J. Marrink, The molecular face of lipid rafts in model membranes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(45), 17367–17372 CrossRef CAS PubMed.
- A. Barnoy, R. G. Parton and M. M. Kozlov, Mechanism of membrane curvature generation and caveola formation by flat disc-like complexes of caveolin, bioRxiv, 2024, preprint, DOI:10.1101/2024.07.09.602763.
- F. Campelo, C. Arnarez, S. J. Marrink and M. M. Kozlov, Helfrich model of membrane bending: from Gibbs theory of liquid interfaces to membranes as thick anisotropic elastic layers, Adv. Colloid Interface Sci., 2014, 208, 25–33 CrossRef CAS PubMed.
- J. W. Gibbs, The Scientific Papers, New York, Dover, 1961 Search PubMed.
- M. M. Kozlov, S. L. Leikin and V. S. Markin, Elastic properties of interfaces - elasticity moduli and spontaneous geometric characteristics, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 277–292 RSC.
- M. M. Kozlov and M. Winterhalter, Elastic-Moduli and Neutral Surface for Strongly Curved Monolayers - Analysis of Experimental Results, J. Phys. II, 1991, 1(9), 1085–1100 CrossRef CAS.
- S. Leikin, M. M. Kozlov, N. L. Fuller and R. P. Rand, Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes, Biophys. J., 1996, 71(5), 2623–2632 CrossRef CAS PubMed.
- M. Hamm and M. Kozlov, Elastic energy of tilt and bending of fluid membranes, Eur. Phys. J. E, 2000, 3(4), 323–335 CrossRef CAS.
- M. Hamm and M. Kozlov, Tilt model of inverted amphiphilic mesophases, Eur. Phys. J. B, 1998, 6(4), 519–528 CrossRef CAS.
- E. Evans and R. Skalak, Mechanics and Thermodynamics of Biomembranes, CRC, Boca Raton, Florida, 1980 Search PubMed.
- B. Pontes, P. Monzo and N. C. Gauthier, Membrane tension: A challenging but universal physical parameter in cell biology, Semin. Cell Dev. Biol., 2017, 71, 30–41 CrossRef CAS PubMed.
- J. F. Nagle and S. Tristram-Nagle, Structure of lipid bilayers, Biochim. Biophys. Acta, Rev. Biomembr., 2000, 1469(3), 159–195 CrossRef CAS PubMed.
- N. Fuller and R. P. Rand, The influence of lysolipids on the spontaneous curvature and bending elasticity of phospholipid membranes, Biophys. J., 2001, 81(1), 243–254 CrossRef CAS PubMed.
- J. A. Szule, N. L. Fuller and R. P. Rand, The effects of acyl chain length and saturation of diacylglycerols and phosphatidylcholines on membrane monolayer curvature, Biophys. J., 2002, 83(2), 977–984 CrossRef CAS PubMed.
- M. M. Terzi and M. Deserno, Novel tilt-curvature coupling in lipid membranes, J. Chem. Phys., 2017, 147(8), 084702 CrossRef PubMed.
- R. Dimova, Recent developments in the field of bending rigidity measurements on membranes, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- W. Helfrich, Elastic properties of lipid bilayers: theory and possible experiments, Z. Naturforsch. C, 1973, 28(11–12), 693–703 CrossRef CAS PubMed.
- M. Doktorova, D. Harries and G. Khelashvili, Determination of bending rigidity and tilt modulus of lipid membranes from real-space fluctuation analysis of molecular dynamics simulations, Phys. Chem. Chem. Phys., 2017, 19(25), 16806–16818 RSC.
- T. R. Weikl, M. M. Kozlov and W. Helfrich, Interaction of conical membrane inclusions: Effect of lateral tension, Phys. Rev. E, 1998, 57(6), 6988–6995 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |