Advanced machine learning techniques for hyacinth bean identification using infrared spectroscopy and computer vision†
Received
11th January 2025
, Accepted 24th February 2025
First published on 17th March 2025
Abstract
The classification and quality assessment of underutilized hyacinth bean (HB) (Lablab purpureus L.) landrace accessions were systematically performed using state-of-the-art machine learning (ML) approaches. Invasive and non-invasive techniques were used to identify and evaluate the accessions via FTIR and computer vision, respectively. Regression and classification models based on FTIR achieved outstanding accuracy in chemical characterization; among these, neural network models demonstrated better performance in terms of R2, RMSE, and computational efficiency. However, sample preparation and scalability posed challenges for high-throughput applications. The non-invasive techniques fared better when a transfer learning approach was applied using the pretrained model EfficientNet_V2_S, achieving an F1 score of 98.25% for classification. These methods could also offer lower computational costs and minimal preprocessing. Comparative investigations revealed the advantages of each approach: the accuracy of chemical analysis through the FTIR technique and the scalability/resource efficiency of computer vision. The predictive accuracy was further improved in the neural network model and KNN technique employing hyperparameter tuning, highlighting the need for systematic tuning techniques. This paper highlights the need for hybrid methods that combine invasive and non-invasive strategies for the comprehensive identification of HB accessions. This study presents practical methodologies for classification and quality assessment that support sustainable agricultural practices, enhance biodiversity conservation efforts, and optimize crop management strategies while facilitating the integration of advanced ML technologies into agriculture and food research.
Sustainability spotlight
The research aims to improve sustainability by developing efficient techniques for identifying underutilized hyacinth bean accessions. It combines machine learning with both invasive and non-invasive techniques, reducing dependence on resource-intensive methods. This approach promotes sustainable agricultural practices, enhances resilience and adaptation in food and biological research, and aligns with international objectives for sustainable food systems and environmental management.
|
1. Introduction
The hyacinth bean (HB) (Lablab purpureus L.) is an increasingly popular plant owing to its remarkable versatility and multifunctional features, making it a valuable crop for addressing current demands in food security and crop resilience through its adaptability and high nutritional content.1–3 Although HB is a multipurpose legume species, it has been considered underutilized compared to other legumes, such as soybean (Glycine max), common bean (Phaseolus vulgaris), chickpea (Cicer arietinum), and pigeon pea (Cajanus cajan).4–6 It originated in Africa and was subsequently introduced to Asia and other tropical and subtropical regions of the world.1,2,7,8 HB has a rich nutritional profile, comprising protein (20–28%), carbohydrates (55–60%), crude fat (1–2%), and essential minerals (0.05%).1,2,7–9 HB species persist in a variety of environments, making them crucial for breeding initiatives and food security.4,10,11 The characterisation of these landraces is intricate due to their shared physical characteristics. Modern techniques for characterization are essential for these HB landraces. The classification and identification of HB accessions are challenging tasks because of their morphological similarities and environmental variability.9,12–15
Traditional methods rely on morphological and visual traits, which usually yield vague and inconsistent results, particularly for landrace types grown in different agroecological environments.1,16–20 Misclassification is a major problem in exploiting varieties for breeding programs, management practices, and conservation programs. The lack of research on HB accessions using advanced identification techniques exacerbates this problem. The defined characteristics are insufficient to ensure the attainment of genetic diversity and specific characteristics in HB landraces, resulting in suboptimal exploitation of their agronomic potential. The current approaches are also nonscalable, making them less viable for widespread application in the agricultural or food processing sectors. There is a critical need to develop new, accurate, and scalable methods to overcome these limitations. Technological advances, such as machine learning (ML) and computer vision (CV), offer promising solutions to solve these problems. The analysis of large datasets is made possible through automatic recognition, the detection of complex patterns, and high-precision and uniform results in classification.21,22 Non-destructive approaches, such as CV and transfer learning (TL) frameworks, are suitable for proper identification, evaluation, and conservation of HB accessions to fill in the major gaps in traditional approaches.
This research addresses the challenges of identifying HB accessions through advanced ML techniques to develop precise, scalable, and efficient classification frameworks. The 12 hyacinth bean accessions were chosen for recognition from the Maharashtra Gene Bank, India, owing to their substantial nutritional value, adaptability, and agricultural importance, despite their endangered status. This study presents a proof-of-concept methodology, which is consistent with established studies that efficiently employ small datasets for particular crops or geographical variations in food and agricultural sciences.
The primary objective of this study was to compare the performances of invasive (FTIR spectroscopy) and non-invasive (CV) methods for identifying HB accessions systematically, and assess their strengths and limitations. In this study, we also developed and optimized regression and classification models for invasive approaches by using state-of-the-art ML frameworks with high accuracy and robust performance. The trade-offs among accuracy, computational efficiency, scalability, and practicality of the evaluated strategies were also considered. We propose future-ready, data-driven solutions that promote sustainable agriculture, biodiversity conservation, and efficient crop management through accurate classification of underutilized HB landraces.
2. Materials and methods
2.1 Materials
The HBs, containing 12 landrace accessions, were obtained from different locations in the western part of India (Fig. 1). The 12 accession names are BAHB-11, BAHB-12, BAHB-14, BAHB-15, BAHB-3, BAHB-4, BAHB-6, BAHB-7, BAHB-8, BAHB-9, BJHB-9 and LAHB-39. The accession numbers and local names of these beans are presented in Table 1. In addition, all the ML models were developed and trained on a system featuring an NVIDIA GeForce RTX 4050 GPU, Intel Core i7 processor, 16 GB of RAM, and SSD storage for high-speed data handling. All analyses, including model training and evaluation, were conducted via MATLAB R2024b and Python 3.12, leveraging their advanced libraries and toolkits for ML and data processing.
 |
| | Fig. 1 Map of the selected region for hyacinth bean collection. | |
Table 1 Accession numbers and names of 12 hyacinth bean accessions with abbreviations
| Abbreviations |
Accession number |
Accession name |
| BJHB-9 |
BAIF/Jawhar/Hyacinth Bean/9 |
Bomblya wal |
| BAHB-6 |
BAIF/Akole/Hyacinth Bean/6 |
Butka ghevda |
| BAHB-8 |
BAIF/Akole/Hyacinth Bean/8 |
Gabara ghevda |
| BAHB-14 |
BAIF/Akole/Hyacinth Bean/14 |
God wal |
| BAHB-12 |
BAIF/Akole/Hyacinth Bean/12 |
Hirva lamb ghevda |
| BAHB-9 |
BAIF/Akole/Hyacinth Bean/9 |
Kadu wal |
| BAHB-3 |
BAIF/Akole/Hyacinth Bean/3 |
Kala wal |
| BAHB-15 |
BAIF/Akole/Hyacinth Bean/15 |
Lal lamb sheng ghevda |
| BAHB-11 |
BAIF/Akole/Hyacinth Bean/11 |
Lamb shiracha ghevda |
| LAHB-39 |
LP/Akole/Hyacinth Bean/39 |
Shravan ghevda |
| BAHB-7 |
BAIF/Akole/Hyacinth Bean/7 |
Tambda wal |
| BAHB-4 |
BAIF/Akole/Hctyacinth Bean/4 |
Vatana ghevda |
2.2 Invasive accession identification via FTIR spectroscopy
2.2.1 Dataset preparation.
All 12 accessions were dried in a vacuum oven at 40 °C for 6 h and thoroughly ground to obtain fine powders. The absorption spectra of these accessions were measured in triplicate using an attenuated total reflectance FTIR spectrometer (BRUKER, Alpha, Germany). The samples were scanned from 4000 to 500 cm−1. The instrument was operated at 4 cm−1 resolution with 64 scans.23–25
2.2.2 Preprocessing and feature selection.
The FTIR absorption spectrum dataset of 12 samples was pre-processed to ensure accuracy. Baseline correction was used to remove drift via polynomial fitting, and normalization was used to address variations in the accessions. A Savitzky–Golay filter smoothed the spectra retaining features, and spectral regions considered nonrelevant were excluded when the focus was 4000–500 cm−1.26 The Relief algorithm was used for the signature feature selection of spectral data that were relevant and significant for further analysis; therefore, the robust feature selection was maintained.27,28
2.2.3 Regression approach for accession identification.
Eight regression frameworks with 25 subtypes were used to develop the predictive models. The types and subtypes of the models, along with their hyperparameters, are shown in Tables 2 and S1.† These include linear regression, tree-based algorithms, support vector machines, efficient linear approaches, ensemble methods, Gaussian process regression (GPR), neural networks (NNs), and kernel-based techniques.29 Furthermore, the 5-fold cross-validation method was considered for robustness, overfitting minimization, and performance validation of the models on different splits of data.
Table 2 Regression models with hypermeters for the prediction of hyacinth bean accessions
| Models |
Presets |
Hyperparameters |
| Linear |
Linear |
Terms: linear; robust option: off |
| Stepwise linear |
Initial terms: linear; upper bound on terms: interactions; maximum number of steps: 1000 |
| Tree |
Fine tree |
Minimum leaf size: 4; surrogate decision splits: off |
| Medium tree |
Minimum leaf size: 12; surrogate decision splits: off |
| Support vector machines (SVM) |
Linear SVM |
Kernel function: linear; kernel scale: automatic; box constraint: automatic; epsilon: auto |
| Quadratic SVM |
Kernel function: quadratic; kernel scale: automatic; box constraint: automatic; epsilon: auto |
| Cubic SVM |
Kernel function: cubic; kernel scale: automatic; box constraint: automatic; epsilon: auto |
| Fine Gaussian SVM |
Kernel function: Gaussian; kernel scale: 1; box constraint: automatic; epsilon: auto |
| Medium Gaussian SVM |
Kernel function: Gaussian; kernel scale: 4; box constraint: automatic; epsilon: auto |
| Coarse Gaussian SVM |
Kernel function: Gaussian; kernel scale: 16; box constraint: automatic; epsilon: auto |
| Efficient linear |
Efficient linear least squares |
Learner: least squares; solver: auto; regularization: auto; regularization strength (lambda): auto; relative coefficient tolerance (beta tolerance): 0.0001 |
| Efficient linear SVM |
Learner: SVM; solver: auto; regularization: auto; regularization strength (lambda): auto; relative coefficient tolerance (beta tolerance): 0.0001; epsilon: auto |
| Ensemble |
Boosted trees |
Minimum leaf size: 8; number of learners: 30; learning rate: 0.1; number of predictors to sample: select all |
| Bagged trees |
Minimum leaf size: 8; number of learners: 30; number of predictors to sample: select all |
| Gaussian process regression (GPR) |
Squared exponential GPR |
Basis function: constant; kernel function: squared exponential; use isotropic kernel: yes; kernel scale: automatic; signal standard deviation: automatic; sigma: automatic; optimize numeric parameters: yes |
| Matern 5/2 GPR |
Basis function: constant; kernel function: Matern 5/2; use isotropic kernel: yes; kernel scale: automatic; signal standard deviation: automatic; sigma: automatic; optimize numeric parameters: yes |
| Exponential GPR |
Basis function: constant; kernel function: exponential; use isotropic kernel: yes; kernel scale: automatic; signal standard deviation: automatic; sigma: automatic; optimize numeric parameters: yes |
| Rational quadratic GPR |
Basis function: constant; kernel function: rational quadratic; use isotropic kernel: yes; kernel scale: automatic; signal standard deviation: automatic; sigma: automatic; optimize numeric parameters: yes |
| Neural network |
Narrow neural network |
Number of fully connected layers: 1; first layer size: 10; activation: ReLU; iteration limit: 1000; regularization strength (lambda): 0 |
| Medium neural network |
Number of fully connected layers: 1; first layer size: 25; activation: ReLU; iteration limit: 1000; regularization strength (lambda): 0 |
| Wide neural network |
Number of fully connected layers: 1; first layer size: 100; activation: ReLU; iteration limit: 1000 |
| Bilayered neural network |
Number of fully connected layers: 2; first layer size: 10; second layer size: 10; activation: ReLU; iteration limit: 1000 |
| Tri layered neural network |
Number of fully connected layers: 3; first layer size: 10; second layer size: 10; third layer size: 10; activation: ReLU; iteration limit: 1000 |
| Kernel |
SVM kernel |
Learner: SVM; number of expansion dimensions: auto; regularization strength (lambda): auto; kernel scale: auto; epsilon: auto |
| Least squares regression kernel |
Learner: least squares kernel; number of expansion dimensions: auto; regularization strength (lambda): auto; kernel scale: auto |
2.2.3.1 Evaluation metrics for regression models.
This integration of statistical and computational metrics assesses regression models by evaluating their regression outputs viaeqn (1)–(5). The total prediction error-based error metrics are the mean squared error (MSE) and root mean squared error (RMSE). Additionally, the mean absolute error (MAE) and mean absolute percentage error (MAPE) quantify the absolute and relative errors between the predictions and actual results. The explanation of model variance via the coefficient of determination is denoted by the letter R2. Model efficiency and scalability can be understood in terms of the prediction speed, training time, and size, which provide a good-quality predictor assessment and lead to computational feasibility.30,31 The formulae are defined as follows:| | 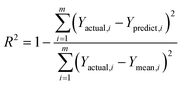 | (1) |
| |  | (2) |
| | 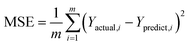 | (3) |
| |  | (4) |
| |  | (5) |
where m represents the total number of data points in the dataset, whereas Yactual,i denotes the observed or actual value for the ith data point. Similarly, Ypredict,i refers to the predicted value for the ith data point, which is generated by the model. The index i indicates the specific data point being analysed and ranges from 1 to m, encompassing all the data points in the dataset.
2.2.3.2 Model selection and optimization.
We used eight model types with 25 subtypes to obtain the best regression model, having the following criteria: R2 ≥ 0.75, MAE ≤ 0.99, MSE ≤ 0.99, RMSE ≤ 0.99, and minimal model size. This methodical filtering approach assures the selection of a robust yet concise model. Among all the models, the NN model was ultimately chosen as the best-performing model. The selected NN was then optimized via a comprehensive hyperparameter search. The search space included 1 to 3 fully connected layers, activation functions (ReLU, tanh, sigmoid, or none), standardization (yes or no), regularization strength (lambda: 2.0833 × 10−7 to 1), and layer sizes (1 to 30 for each layer). Hyperparameter tuning aims to maximize the predictive accuracy while maintaining robustness. A five-fold cross-validation was employed throughout the process to ensure model generalizability across different data splits.
2.2.4 Classification approach for accession identification.
For accession identification, eight classification model types were explored, including tree-based methods, discriminant analysis, Naive Bayes, support vector machines, k-nearest neighbors (KNNs), ensemble techniques, NNs, and kernel-based approaches. The model types and subtypes with hyperparameters are shown in Tables 3 and S1.† A total of 25 subtypes across these models were developed to ensure comprehensive evaluation. Each model was trained via pre-processed FTIR spectral data with 5-fold cross-validation.
Table 3 Classification models with hypermeters for the identification of hyacinth bean accessions
| Model type |
Preset |
Hyperparameters |
| Tree |
Fine tree |
Maximum number of splits: 100; split criterion: Gini's diversity index; surrogate decision splits: off |
| Medium tree |
Maximum number of splits: 20; split criterion: Gini's diversity index; surrogate decision splits: off |
| Coarse tree |
Maximum number of splits: 4; split criterion: Gini's diversity index; surrogate decision splits: off |
| Discriminant |
Linear discriminant |
Covariance structure: full |
| Naive Bayes |
Kernel Naive Bayes |
Distribution name for numeric predictors: kernel; distribution name for categorical predictors: not applicable; kernel type: gaussian; support: unbounded |
| Support vector machines (SVM) |
Linear SVM |
Kernel function: linear; kernel scale: automatic; box constraint level: 1; multiclass coding: one-vs-one |
| Quadratic SVM |
Kernel function: quadratic; kernel scale: automatic; box constraint level: 1; multiclass coding: one-vs-one |
| Cubic SVM |
Kernel function: cubic; kernel scale: automatic; box constraint level: 1; multiclass coding: one-vs-one |
| Fine Gaussian SVM |
Kernel function: Gaussian; kernel scale: 1; box constraint level: 1; multiclass coding: one-vs-one |
| Medium Gaussian SVM |
Kernel function: Gaussian; kernel scale: 4; box constraint level: 1; multiclass coding: one-vs-one |
| Coarse Gaussian SVM |
Kernel function: Gaussian; kernel scale: 16; box constraint level: 1; multiclass coding: one-vs-one |
|
k-nearest neighbor (KNN) |
Fine KNN |
Number of neighbors: 1; distance metric: Euclidean; distance weight: equal |
| Medium KNN |
Number of neighbors: 10; distance metric: Euclidean; distance weight: equal |
| Cosine KNN |
Number of neighbors: 10; distance metric: cosine; distance weight: equal |
| Cubic KNN |
Number of neighbors: 10; distance metric: Minkowski (cubic); distance weight: equal |
| Weighted KNN |
Number of neighbors: 10; distance metric: Euclidean; distance weight: squared inverse |
| Ensemble |
Bagged trees |
Ensemble method: bag; learner type: decision tree; maximum number of splits: 47; number of learners: 30 |
| Subspace discriminant |
Ensemble method: subspace; learner type: discriminant; number of learners: 30; subspace dimension: 8 |
| Subspace KNN |
Ensemble method: subspace; learner type: nearest neighbors; number of learners: 30; subspace dimension: 8 |
| Neural network |
Narrow neural network |
Number of fully connected layers: 1; first layer size: 10; activation: ReLU; iteration limit: 1000; regularization strength (lambda): 0 |
| Medium neural network |
Number of fully connected layers: 1; first layer size: 25; activation: ReLU; iteration limit: 1000; regularization strength (lambda): 0 |
| Wide neural network |
Number of fully connected layers: 1; first layer size: 100; activation: ReLU; iteration limit: 1000; regularization strength (lambda): 0 |
| Bilayered neural network |
Number of fully connected layers: 2; first layer size: 10; second layer size: 10; activation: ReLU; iteration limit: 1000; regularization strength: 0 |
| Tri layered neural network |
Number of fully connected layers: 3; first layer size: 10; second layer size: 10; third layer size: 10; activation: ReLU; iteration limit: 1000 |
| Kernel |
SVM kernel |
Learner: SVM; number of expansion dimensions: auto; kernel scale: auto; multiclass coding: one-vs-one; iteration limit: 1000 |
2.2.4.1 Evaluation metrics for the classification models.
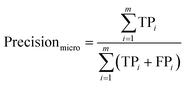
The classification models were evaluated using various methods, including accuracy, the error rate, precision, recall, the F1 score, and computational cost in terms of resources (eqn (6)–(19)). The accuracy percentage indicates the proportion of samples that were correctly classified, thereby reflecting the error rate as a fraction of misclassified samples. Precision denotes the proportion of accurate positive predictions made by the model, computed via macro, micro, and weighted average metrics. The analysis of the macro, micro, and weighted percentages assesses the model sensitivity by identifying all pertinent instances. Macro, micro, and weighted F1-scores are utilized to evaluate the overall performance of a system by integrating both precision and recall metrics. Traditional metrics have been employed to analyse loss due to misclassifications resulting from models that include the total cost. The evaluation of the computational efficiency included metrics, such as the observation rate per second, training time in seconds, and model size in bytes, facilitating a comprehensive and systematic assessment of classification models aimed at effectively identifying accessions at scale.15,32–36 The formulae are defined as follows:| |  | (6) |
| |  | (7) |
| |  | (8) |
| |  | (9) |
| |  | (10) |
| |  | (11) |
| |  | (12) |
| | 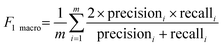 | (13) |
| |  | (14) |
| |  | (15) |
| |  | (16) |
| |  | (17) |
| |  | (18) |
| |  | (19) |
where TP (true positives): correctly predicted positive instances; TN (true negatives): correctly predicted negative instances; FP (false positives): negative instances incorrectly predicted as positive; FN (false negatives): positive instances incorrectly predicted as negative; i: index representing a specific class in multiclass classification; m: total number of observations in the dataset; w: weight for class i, defined as TPi + FNi.
2.2.4.2 Model selection and optimization.
Eight models were evaluated on the basis of the following criteria: accuracy of at least 75%, an error rate not exceeding 5%, a total cost of not more than 1, and a model size limited to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bytes. Under these criteria, the KNN and NN models emerged as the most effective options. The optimization of the KNN model involves several hyperparameters: the number of neighbors, which ranged from 1 to 24; distance metrics, which included city block, Chebyshev, correlation, cosine, Euclidean, Hamming, Jaccard, Mahalanobis, Minkowski cubic, and Spearman; and weighting methods for distances, which can be equal, inverse, or squared inverse. An optimized NN model was achieved through hyperparameter search, following the aforementioned procedure: modifications in the number of layers, activation functions, regularization strength, and layer sizes. For optimization, a 5-fold cross validation was conducted. On the basis of the enhancements in classification and the computational complexities of the models, the final models were selected.
000 bytes. Under these criteria, the KNN and NN models emerged as the most effective options. The optimization of the KNN model involves several hyperparameters: the number of neighbors, which ranged from 1 to 24; distance metrics, which included city block, Chebyshev, correlation, cosine, Euclidean, Hamming, Jaccard, Mahalanobis, Minkowski cubic, and Spearman; and weighting methods for distances, which can be equal, inverse, or squared inverse. An optimized NN model was achieved through hyperparameter search, following the aforementioned procedure: modifications in the number of layers, activation functions, regularization strength, and layer sizes. For optimization, a 5-fold cross validation was conducted. On the basis of the enhancements in classification and the computational complexities of the models, the final models were selected.
2.3 Non-invasive accession identification via CV
2.3.1 Dataset preparation.
Images of the 12 HB accessions were captured using a CV system (Fig. 2) comprising a digital microscopic camera with a lens, LED illumination, a matte black wooden enclosure to minimize reflections, and a computer for control and storage. Images were acquired in .jpg format at 2520 × 1680 pixels and 90 dpi resolution. A total of 960 images were captured per class (12 classes × 80 samples = 960 images). This setup ensured consistent image quality and provided a reliable dataset for analyzing the HB accessions.
 |
| | Fig. 2 Schematic of the computer vision system. | |
2.3.2 Image preprocessing and augmentation.
High-resolution images of the HB accessions were pre-processed using the rembg library for background removal, enhancing the image focus and reducing the noise. A pretrained segmentation model was fine-tuned to isolate beans, generating binary masks to remove background pixels, leaving only beans on transparent or uniform backgrounds. The images were then resized and normalized for uniform dimensions and pixel values. Data augmentation included resizing to the minimum required number of pixels for the models, random horizontal flipping for variability, tensor conversion for ML, and normalization using the mean and standard deviation values.
2.3.3 Transfer learning approach for accession identification.
Transfer learning was implemented via 10 pretrained models, including EfficientNet_B3, EfficientNet_V2_S, ConvNeXt_Tiny, MaxVit_T, RegNet_Y_1_6 GF, RegNet_Y_3_2 GF, DenseNet169, ShuffleNet_V2_X2_0, MobileNet_V3_Large, and RegNet_X_3_2 GF. All of the models were initialized by ImageNet weights. Fully connected layers were used as the final layers of all models with SoftMax activation functions for classification of the 12 HB accessions. All of the models used the AdamW optimizer on pre-processed images with a learning rate of 0.0001 and a weight decay of 0.01 for regularization purposes. The cross-entropy loss was used, and training was performed with 10 epochs and a batch size of 32. The accuracy, loss, macro average precision, weighted average precision, recall, and F1 score were evaluated. In addition, several additional parameters involved in computing (like GFLOPs, ROC curves, PR curves and confusion matrices) were used to compute an adequate performance report.15,34,37,38 Hence, these methods can provide significantly better accuracy in classifications with good generalization properties during the recognition of HB accessions.
2.3.4 Pretrained model selection and optimization.
The pretrained models were tested against the primary key performance metrics, which included high accuracy, F1 score, precision, recall, and fewer parameters and GFLOPs. Among all 10 models, EfficientNet_V2_S performed the best in terms of all of the evaluation criteria. Hence, it was chosen for further optimization with a systematic hyperparameter tuning process. The last fully connected layer was replaced with a 12-class output via activation functions (such as ReLU, LeakyReLU, and Swish) with various dropout rates of 0.3, 0.4, and 0.5, respectively. Experiments were performed with batch sizes of 16, 32, and 64; learning rates set at 0.0001 and 0.0005; and training epochs set at 10, 15, and 20. An AdamW optimizer with a weight decay of 0.01 combined with the cosine annealing warm restart scheduler was adopted to dynamically control the learning rate. The various metric validation accuracies, macro- and weighted precisions, recalls, F1 scores, GFLOPs, confusion matrices, ROC curves, and PR curves were computed. Training losses were analysed in comparison with validation performance to determine the best fit.22,35,39 This was the fine-tuning approach, which reached model performance at peak levels during the identification of the HB accessions.
3. Results and discussion
The HB dataset consists of 12 landrace accessions from western India. It was analyzed using invasive (FTIR spectroscopy) and non-invasive (CV) techniques. The results of these analyses are presented below. The images of the HB accessions are given in Fig. 3, and the FTIR absorption spectra for the same accessions are shown in Fig. 4.
 |
| | Fig. 3 Actual and background-removed images of hyacinth beans (12 accessions). | |
 |
| | Fig. 4 FTIR spectra of 12 hyacinth bean accessions. | |
3.1 Invasive accession identification via FTIR spectroscopy
3.1.1 Preprocessing and feature selection.
The preprocessing step improved the quality of the spectral data by removing the baseline drift, normalizing the variations, and reducing noise without the loss of important features.28,40,41 The Relief algorithm helps in the selection of dominant spectral features from the FTIR spectra, with a focus on 16 notable wavenumbers associated with differentiating accessions. The wavenumbers reported in Table 4 refer to important functional groups, thus providing insight into the chemical composition of the HB accessions and their different spectral features that are relevant for accurate classification.
Table 4 Selected features (wavenumbers in cm−1) and functional groups for the identification of hyacinth bean accessions
| Selected features (wavenumbers in cm−1) |
Functional group |
| 1543.05 |
Amide II (N–H bending, proteins) |
| 1535.34 |
| 1527.62 |
| 1558.48 |
| 1550.77 |
| 1643.35 |
Amide I (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching, proteins) O stretching, proteins) |
| 1635.64 |
| 1627.92 |
| 1550.77 |
| 1033.85 |
Amide III (C–N stretching and N–H bending, proteins) |
| 1026.13 |
| 1018.41 |
| 1010.70 |
| 1002.98 |
| 995.27 |
| 987.55 |
| 979.84 |
3.1.2 Regression model performance.
Table 5 presents the evaluation criteria for the 25 regression frameworks, which include R2, RMSE, MAE, MAPE, prediction speed, training time, and model size. It compares the FTIR spectral data analysis regression models, with the narrow NNs showing superior predictive accuracy, whereas the tree-based and Gaussian process regression models show moderate computational efficiency.26 The actual vs. predicted values of the models are presented in Fig. S1.† These evaluation metrics and graphical representations exhaustively evaluate the predictive accuracy, computational efficiency, and scalability. Therefore, they provide an exhaustive comparison of the performance of regression models in the context of HB accession identification. The plots of the actual results vs. the predicted values highlight the robustness of the model in accurately portraying the correlations of the input features with the target variables. The residual plots also support the effectiveness of the model by showing the spread and randomness of errors, thus validating the lack of significant bias in the predictions. These assessments increase the reliability of regression frameworks used for HB accession identification. Fig. 5 provides the comparative graphs of all 25 regression models that give the MAEs, MSEs, R2 values, and RMSEs. These visualizations provide a clear comparison of model performance, enabling the identification of the most accurate and efficient frameworks for identifying HB accessions.
Table 5 Regression models with evaluation metrics for the invasive approacha
| Models |
RMSE |
MSE |
R
2
|
MAE |
MAPE% |
Prediction speed (obs per s) |
Training time (s) |
Model size (bytes) |
|
SVM: support vector machines; GPR: Gaussian process regression; RMSE: root mean square error; MSE: mean square error; R2: coefficient of determination; MAE: mean absolute error; MAPE: mean absolute percent error.
|
| Linear |
1.778 |
3.161 |
0.741 |
1.381 |
46.528 |
4905.969 |
4.363 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 912 |
| Stepwise linear |
3.167 |
10.027 |
0.179 |
0.952 |
14.092 |
4390.057 |
31.361 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814 814 |
| Fine tree |
1.345 |
1.808 |
0.852 |
1.097 |
33.235 |
6223.824 |
3.077 |
5794 |
| Medium tree |
2.311 |
5.342 |
0.562 |
2.016 |
59.841 |
4947.791 |
3.891 |
4786 |
| Linear SVM |
1.921 |
3.691 |
0.698 |
1.537 |
40.981 |
4084.168 |
3.901 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
| Quadratic SVM |
1.437 |
2.064 |
0.831 |
0.950 |
26.222 |
4194.448 |
3.775 |
9895 |
| Cubic SVM |
1.519 |
2.308 |
0.811 |
1.022 |
30.319 |
4107.655 |
3.615 |
9351 |
| Fine Gaussian SVM |
1.590 |
2.529 |
0.793 |
1.031 |
38.522 |
2922.606 |
4.091 |
9891 |
| Medium Gaussian SVM |
2.202 |
4.850 |
0.603 |
1.534 |
49.614 |
5243.609 |
3.714 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843 843 |
| Coarse Gaussian SVM |
2.992 |
8.954 |
0.267 |
2.397 |
77.962 |
5754.706 |
3.574 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 795 795 |
| Efficient linear least squares |
3.351 |
11.227 |
0.080 |
2.919 |
96.360 |
4691.669 |
3.537 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
| Efficient linear SVM |
3.423 |
11.714 |
0.041 |
2.980 |
97.894 |
4718.187 |
3.556 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814 814 |
| Boosted trees |
1.599 |
2.558 |
0.790 |
1.284 |
38.864 |
2006.043 |
5.890 |
161![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301 301 |
| Bagged trees |
1.930 |
3.726 |
0.695 |
1.576 |
52.243 |
2055.851 |
5.394 |
159![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
| Squared exponential GPR |
1.476 |
2.179 |
0.822 |
0.431 |
17.788 |
7014.570 |
4.373 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 642 |
| Matern 5/2 GPR |
1.452 |
2.107 |
0.827 |
0.430 |
18.526 |
6625.442 |
4.293 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
| Exponential GPR |
1.339 |
1.792 |
0.853 |
0.368 |
17.533 |
3835.214 |
4.166 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 628 628 |
| Rational quadratic GPR |
1.431 |
2.047 |
0.832 |
0.397 |
17.810 |
4265.795 |
4.610 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673 673 |
| Narrow neural network |
0.758 |
0.574 |
0.953 |
0.228 |
4.018 |
5762.236 |
4.488 |
8508 |
| Medium neural network |
0.811 |
0.658 |
0.946 |
0.305 |
8.468 |
6592.139 |
4.218 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 668 |
| Wide neural network |
0.878 |
0.771 |
0.937 |
0.299 |
11.758 |
6770.481 |
4.341 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 468 468 |
| Bilayered neural network |
0.905 |
0.819 |
0.933 |
0.274 |
12.519 |
6666.481 |
4.328 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280 |
| Tri layered neural network |
0.764 |
0.584 |
0.952 |
0.279 |
6.239 |
6473.976 |
4.179 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052 052 |
| SVM kernel |
2.590 |
6.706 |
0.451 |
2.054 |
75.512 |
5550.609 |
4.329 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 688 |
| Least squares regression kernel |
2.121 |
4.499 |
0.632 |
1.629 |
57.789 |
2927.525 |
3.953 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618 618 |
 |
| | Fig. 5 Comparative graphs for all 25 regression models for (a) MAE, (b) MSE, (c) R2 values, and (d) RMSE. | |
The assessment of 25 regression models demonstrated notable performance disparities among the frameworks, highlighting the necessity for a model selection customized for HB accession recognition via filters. Upon using the filter criterion, the NNs continuously surpassed other model types, with the narrow NN identified as the top-performing model. The model attained a RMSE of 0.75792, an R2 of 0.95294, MAE of 0.22801, and a MAPE of 4.02%. This model demonstrated exceptional predictive accuracy while maintaining a compact model size of 8508 bytes and a prediction speed of 5762 observations per second, highlighting its efficiency for large-scale applications.
In comparison, other GPR models, of which the squared exponential GPR is a special case, demonstrate satisfactory performance, achieving an R2 value of 0.82150 and an RMSE of 1.47618, while accommodating a relatively larger modeled structure and thus exhibiting lower computational cost. The compared linear regression model was less computationally intensive, indicating relatively smaller values for R2 (0.74112), with a larger error in the metrics. This exceptional performance of NNs, with the ability to approximate complex, nonlinear relationships inherent in FTIR spectral data, points to a delicate balance between accuracy, speed, and sparseness in the narrow NN, which makes it the best choice for HB accession identification. This also aims to emphasize the importance of selection criteria concerning both the nature of the data and the type of application.
A comparison of the regression models reveals that NN outperforms the other methods in terms of R2, RMSE, MAE, and computational speed. NNs have proven capable of capturing complex nonlinear relationships in FTIR spectral data, allowing the precise identification of subtle patterns essential for accurately classifying HB accessions, as evidenced by the model's high classification accuracy and robustness in experimental results.28,42 In addition, in terms of model adaptability within the capacity to modify its hyperparameters, such as in activation functions, regularization methods, and architectural configurations, the improved aspects were predictive power and robustness. For this reason, the optimum model was NN because it further improved, with an optimal performance relative to the precise and scalable classification of HBs. In addition to achieving notable improvement over the competing models used in the pilot studies, the optimized NN was proof of the success of the optimization process (Fig. S2†).
The optimized hyperparameter of regression analysis was a compact NN structure with a single fully connected layer of 10 neurons. ReLU was used as the activation function, which bounded at 1000 iterations. Lambda was set at 0.0035, with the standardized data on all inputs having uniform input scaling. This was further optimized to produce an RMSE of 0.6918 and an R2 of 0.96, demonstrating that the optimized model was more capable of capturing patterns in the FTIR spectral data at a higher accuracy than the narrow NN model achieved initially, which was 0.7579 with an R2 of 0.9529. In terms of the computational efficiency, this fine-tuned model is not large at 8 kB, but is less than the narrow network, with 8.5 kB recorded. In addition, its training time is the same as that of the narrow NN, with a record of 5.78 seconds versus 4.49 seconds in the case of the latter. The optimized model also improved the MAE (0.32900) and MAPE (9.5%), indicating better accuracy of predictions for individual and percentage errors.
3.1.2.1 Hyperparameter tuning.
The optimization technique has advantages concerning regularisation, layer dimensions, and activation functions. This enhanced the model's performance over the entire dataset. Although the baseline models obtained high prediction speeds of 5762–6770 observations per sec, it was necessary to balance the accuracy and compactness along with the robustness of the optimized model. The optimization results suggest that the improvement in accuracy and computing speed in determining the HB accessions was greater. Hyperparameter tuning of the NN model improved its efficiency by finely tuning its architecture and training parameters. The changes included the number of layers, types of activation functions, normalization techniques, degrees of regularization, and layer dimensions, all of which improved the accuracy of the predictive model and reduced the error metrics associated with it. The robustness of the optimized model is validated via 5-fold cross-validation, which results in better performance irrespective of which segment of the data it is tested upon. The results from the optimized model further exhibit good generalizability to data that have not been previously reported, making it a reliable tool for identifying accessions and for future use.28,40
3.1.3 Classification approach for accession identification.
The performance metrics for the eight classification models and their 25 subtypes are detailed in Table 6. The classification performance metrics of the models are shown, with the fine KNN, weighted KNN, lagged trees, and NN methods achieving the highest accuracy, whereas the tree-based models have lower accuracy. Visual comparisons of the accuracy, error rate (%), overall cost, speed of prediction and training time across all these models are shown in Fig. 6. Eight classification models were tested with the following requirements: at least 75% accuracy, an upper bound on the error rate of 5%, a maximum total cost of 1, and not larger than 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bytes in model size. Upon applying the specified criteria, KNN and NN emerged as the top-performing frameworks, demonstrating high accuracy values and favorable precision–recall metrics while requiring fewer computational resources. These thus served as relevant frameworks for the utilized dataset. Compared with alternative methods, NNs consistently demonstrated superior capability in representing details of the HB accession data.
000 bytes in model size. Upon applying the specified criteria, KNN and NN emerged as the top-performing frameworks, demonstrating high accuracy values and favorable precision–recall metrics while requiring fewer computational resources. These thus served as relevant frameworks for the utilized dataset. Compared with alternative methods, NNs consistently demonstrated superior capability in representing details of the HB accession data.
Table 6 Classification models with evaluation metrics for the invasive approacha
| Preset |
Accuracy (%) |
Total cost |
Error rate (%) |
Weighted precision (%) |
Weighted recall (%) |
Weighted F1 score (%) |
Prediction speed (obs per s) |
Training time (s) |
Model size (bytes) |
|
SVM: support vector machines; KNN: k-nearest neighbor.
|
| Fine tree |
41.667 |
28 |
58.333 |
0.000 |
41.667 |
34.192 |
5400.054 |
6.243 |
9569 |
| Medium tree |
41.667 |
28 |
58.333 |
0.000 |
41.667 |
34.192 |
5085.015 |
6.811 |
9569 |
| Coarse tree |
27.083 |
35 |
72.917 |
0.000 |
27.083 |
22.747 |
3172.337 |
1.937 |
7773 |
| Linear discriminant |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
1569.392 |
3.458 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
| Kernel Naive Bayes |
64.583 |
17 |
35.417 |
0.000 |
64.583 |
57.532 |
94.207 |
9.319 |
385![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
| Linear SVM |
56.250 |
21 |
43.750 |
73.056 |
56.250 |
59.444 |
269.762 |
7.500 |
412![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 742 742 |
| Quadratic SVM |
77.083 |
11 |
22.917 |
0.000 |
77.083 |
73.439 |
312.024 |
5.464 |
446![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150 |
| Cubic SVM |
83.333 |
8 |
16.667 |
89.722 |
83.333 |
81.958 |
255.441 |
11.337 |
438![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 230 |
| Fine Gaussian SVM |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
287.392 |
8.632 |
446![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
| Medium Gaussian SVM |
72.917 |
13 |
27.083 |
73.889 |
72.917 |
73.016 |
261.808 |
7.791 |
458![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414 414 |
| Coarse Gaussian SVM |
4.167 |
46 |
95.833 |
0.000 |
4.167 |
3.333 |
222.018 |
6.042 |
480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
| Fine KNN |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
800.384 |
5.384 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762 762 |
| Medium KNN |
35.417 |
31 |
64.583 |
0.000 |
33.333 |
30.337 |
757.281 |
3.873 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762 762 |
| Cosine KNN |
31.250 |
33 |
68.750 |
0.000 |
31.250 |
26.782 |
2555.897 |
1.072 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
| Cubic KNN |
29.167 |
34 |
70.833 |
0.000 |
29.167 |
24.259 |
1630.834 |
2.067 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 778 |
| Weighted KNN |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
2043.553 |
0.770 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 780 |
| Bagged trees |
95.833 |
2 |
4.167 |
96.667 |
95.833 |
95.767 |
515.624 |
3.542 |
414![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
| Subspace discriminant |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
322.762 |
2.014 |
238![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 054 |
| Subspace KNN |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
287.669 |
2.648 |
278![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136 136 |
| Narrow neural network |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
5058.169 |
2.058 |
9633 |
| Medium neural network |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
4482.253 |
3.078 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 113 |
| Wide neural network |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
3494.442 |
0.967 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
| Bilayered neural network |
97.917 |
1 |
2.083 |
98.333 |
97.917 |
97.884 |
3422.582 |
1.709 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405 405 |
| Tri layered neural network |
89.583 |
5 |
10.417 |
91.806 |
89.583 |
89.239 |
3718.394 |
2.442 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177 177 |
| SVM kernel |
70.833 |
14 |
29.167 |
71.944 |
70.833 |
69.511 |
257.522 |
11.390 |
919![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276 276 |
 |
| | Fig. 6 Comparative graphs for all 25 classification models for (a) accuracy (%), (b) error rate (%), (c) total cost, (d) prediction speed (obs per s), and (e) training time (s). | |
The best-performing model is a narrow NNs with an accuracy of 97.91%, a weighted F1 score of 97.91%, and a compact model size of 4460 bytes at a prediction speed of 5058 observations per second. This model demonstrates exceptional equilibrium between the predicted accuracy and computational efficiency. The architecture featuring ReLU activation and single-layer networking likely accounts for its higher performance. The KNN models, particularly the weighted KNN, exhibited competitive performance, achieving an accuracy of 97.91% and comparable F1 scores. However, the training time for the KNN models was slightly greater, and the model size was larger than those of the other models, making them computationally less efficient for large applications. The SVM and ensemble models demonstrate commendable precision and recall. However, they exhibit lower accuracy and reduced computational efficiency, rendering them less suitable for this task. The comparative analysis indicates that both the NN and KNN models effectively recognize patterns within the specified dataset. The narrow NN emerged as the most robust solution, demonstrating scalability, resource efficiency, and notable accuracy. The application of predefined filters facilitates the selection of high-performance models and guarantees thorough evaluation coverage of classification frameworks. This underscores the need for customized approaches to optimize performance in accession classification tasks within the domain of HBs.
3.1.3.1 Hyperparameter optimization for the KNN and NN models.
Hyperparameter optimization for the KNN and NN models was performed, as outlined in Section 2.2.4.2. The optimized hyperparameters for KNN include six neighbors, correlation as the distance metric, and inverse distance weighting. For the NN, the best configuration consists of two fully connected layers with 10 neurons each, ReLU activation, an iteration limit of 1000, regularization (lambda = 0.000423), and standardized data.
The results indicated that NN surpassed previous methods for both regression and classification tasks because of its ability to identify complex, nonlinear relationships in the data. Unlike traditional models, the NNs leverage multiple hidden layers and activation functions to distinguish between complex patterns from the FTIR spectral data and image-based data. Their significant flexibility enables generalization across distributions, such as dropout and batch normalization, to help reduce overfitting. Moreover, their ability to achieve hierarchical representations makes NNs well suited for deep feature extraction.
The optimized KNN model achieved a significant improvement, with an accuracy of 99.52% (1.6% increase), an error rate of 0.48%, and a reduced model size of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 bytes. Additionally, its prediction speed increased to 815.91 observations per second, whereas the training time slightly decreased to 35.49 seconds, as shown in Fig. S3(a–c).† These enhancements highlight the effectiveness of optimization in improving the KNN performance and computational efficiency. Fig. S3(d–f)† displays the optimization graphs for the NN model, which results in a NN model achieving an accuracy of 98.37%, which is a 0.45% improvement, with an error rate of 1.63%. The model size was reduced to 12
200 bytes. Additionally, its prediction speed increased to 815.91 observations per second, whereas the training time slightly decreased to 35.49 seconds, as shown in Fig. S3(a–c).† These enhancements highlight the effectiveness of optimization in improving the KNN performance and computational efficiency. Fig. S3(d–f)† displays the optimization graphs for the NN model, which results in a NN model achieving an accuracy of 98.37%, which is a 0.45% improvement, with an error rate of 1.63%. The model size was reduced to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 bytes, and the prediction speed reached 4236.37 observations per second. The training duration was minimized to 2.36 seconds. The bilayer NN architecture, featuring two fully connected layers with ReLU activation functions, effectively captured complex nonlinear relationships, leading to robust performance. The KNN model, augmented by a refined distance metric and inverse weighting, exhibited elevated classification accuracy, rendering it appropriate for applications necessitating precision. Conversely, the NN model achieves a harmonious equilibrium between predictive accuracy and computational efficiency, particularly in the identification of nonlinear patterns and the ability to scale with extensive datasets. This investigation underscores the importance of hyperparameter tuning tailored to the distinctive characteristics of each model.
250 bytes, and the prediction speed reached 4236.37 observations per second. The training duration was minimized to 2.36 seconds. The bilayer NN architecture, featuring two fully connected layers with ReLU activation functions, effectively captured complex nonlinear relationships, leading to robust performance. The KNN model, augmented by a refined distance metric and inverse weighting, exhibited elevated classification accuracy, rendering it appropriate for applications necessitating precision. Conversely, the NN model achieves a harmonious equilibrium between predictive accuracy and computational efficiency, particularly in the identification of nonlinear patterns and the ability to scale with extensive datasets. This investigation underscores the importance of hyperparameter tuning tailored to the distinctive characteristics of each model.
3.1.4 Similar works.
Advances in spectroscopy and ML29 facilitate the fast and accurate classification, quantification, and authentication of diverse food and agricultural products, and provide new methodologies and increased predictive accuracies.
Classification of oils and margarines with 100% accuracy in identifying pure margarines has been achieved using ATR-FTIR spectroscopy and ML.28 KNN demonstrated excellent performance with a 97% oil classification accuracy, although the adulteration detection R2 ranged from 45–99%. Moreover, FTIR spectroscopy, ML and the use of polyphenolic antioxidants classified 270 pigmented rice samples with accuracies ranging from 93.5–100%.40 The random forest and SVM models identified critical FTIR peaks, which increased the profiling efficiency. Furthermore, the spectroscopic workflow for black tea GI discrimination achieved 100% accuracy via FTIR.43 ML models (KNNs and SVMs) have enhanced efficiency, supporting real-time, low-cost origin verification. Furthermore, the melt–stretch properties of nine starches from plant-based cheese analogues were evaluated, and the optimal additives were hydroxypropyl tapioca, waxy potato, and tapioca. ML classification was obtained with excellent efficiency, and the rheological data provided 100% predictive accuracy.44 Similarly, IR absorption profiles and chemometrics were used for the classification of milk heat treatments with an accuracy of 97% using random forest. Principal component analysis (PCA) identifies characteristic wavelengths, thereby providing a powerful quality control method.45
Similarly, ML-assisted spectroscopy was used for the non-destructive authentication of edible oils, with >0.96 AUC, and detected adulteration in 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 samples. High spectral clustering allows for the creation of a hypothesis-free, scalable database.27 Additionally, terahertz spectroscopy with SVR for the quantification of bisphenol mixtures achieved an R2 of 0.98. The absorption spectra were reconstructed accurately and showed robust applicability in industrial mixture analysis.46 Moreover, rapeseed varieties were classified via FTIR-PAS (photoacoustic spectroscopy) with PCA, which yielded 0% SVM error and 7.5% PLS-DA (partial least-squares discriminant analysis) error. SPA (successive projections algorithm) increased the accuracy; however, it reduced the number of variables, where FTIR-PAS verified its efficiency and non-destructive nature.41 Furthermore, ATR-FTIR spectroscopy with the assistance of ML models was used to quantify selenium in kefir grains. The total selenium prediction resulted in an RP (relative coefficient) of 0.97 and an RPD (relative prediction deviation) of 4.36; organic selenium prediction resulted in an RP of 0.95 and an RPD of 6.44, which enabled quick and eco-friendly detection.47 The FTIR spectroscopy and clustering results, with an accuracy of 93.9%, were more precise than those of the other methods. PCA and LDA (linear discriminant analysis) are techniques that enhance the reduction of dimensions since clustering serves as a good classification model.42
500 samples. High spectral clustering allows for the creation of a hypothesis-free, scalable database.27 Additionally, terahertz spectroscopy with SVR for the quantification of bisphenol mixtures achieved an R2 of 0.98. The absorption spectra were reconstructed accurately and showed robust applicability in industrial mixture analysis.46 Moreover, rapeseed varieties were classified via FTIR-PAS (photoacoustic spectroscopy) with PCA, which yielded 0% SVM error and 7.5% PLS-DA (partial least-squares discriminant analysis) error. SPA (successive projections algorithm) increased the accuracy; however, it reduced the number of variables, where FTIR-PAS verified its efficiency and non-destructive nature.41 Furthermore, ATR-FTIR spectroscopy with the assistance of ML models was used to quantify selenium in kefir grains. The total selenium prediction resulted in an RP (relative coefficient) of 0.97 and an RPD (relative prediction deviation) of 4.36; organic selenium prediction resulted in an RP of 0.95 and an RPD of 6.44, which enabled quick and eco-friendly detection.47 The FTIR spectroscopy and clustering results, with an accuracy of 93.9%, were more precise than those of the other methods. PCA and LDA (linear discriminant analysis) are techniques that enhance the reduction of dimensions since clustering serves as a good classification model.42
3.2 Non-invasive accession identification via CV
The preprocessing of high-quality images covered segmentation and the removal of background elements, so the model was used to focus on individual HB accessions devoid of extraneous noise. Data augmentation practices implemented, and it includes resizing, horizontal flipping, and normalization. These techniques help create more variability in the training set so that the model performs better in generalization.35,48–51 The preprocessing and augmentation techniques facilitated consistent performance across all conditions, establishing a robust basis for cross-validation and minimising errors related to variations in image quality for accurate detection of HB accessions.13
3.2.1 Comparative study of pretrained models.
An analysis of ten pretrained models was performed, which revealed large variations in performance, as shown in Table 7. Fig. 7 shows the loss and accuracy of each model converge through the number of epochs, thus establishing the validity and usability of the models. Fig. 8a shows the performance comparison plot for the given pretrained models with their required parameters, including accuracy and F1 score and other GFLOPs. The precision and F1 score plots suggest that EfficientNet_V2_S is the best model, followed closely by MaxVit_T and DenseNet169, whereas MobileNet_V3_Large has significantly lower performance. The efficiency metrics suggested that EfficientNet_V2_S offers better computational efficiency. It requires fewer GFLOPs and parameters than MaxVit_T, which requires significantly more computational resources. The precision and recall plots also emphasize the great ability of EfficientNet_V2_S to maintain high levels of precision and sensitivity, which reduces the misclassification rates (Fig. 8b). In addition, the confusion matrices for each model in Fig. S4† corroborate these findings, with EfficientNet_V2_S having the fewest number of misclassifications, confirming its reliability and robustness in HB accession identification tasks.
Table 7 Pretrained models with evaluation metrics for the non-invasive approacha
| Model |
Accuracy |
F
1-score |
Precision |
Recall |
Parameters |
GFLOPs |
|
GFLOPs: giga floating point operations per seconds.
|
| EfficientNet_B3 |
0.953 |
0.960 |
0.964 |
0.959 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714 714![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676 676 |
0.011 |
| EfficientNet_V2_S |
0.977 |
0.981 |
0.982 |
0.981 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 860 |
0.020 |
| ConvNeXt_Tiny |
0.959 |
0.953 |
0.960 |
0.959 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829 829![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356 356 |
0.028 |
| MaxVit_T |
0.971 |
0.973 |
0.977 |
0.970 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413 413![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 780 |
0.030 |
| RegNet_Y_1_6 GF |
0.953 |
0.955 |
0.959 |
0.960 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324 324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
0.010 |
| RegNet_Y_3_2 GF |
0.965 |
0.969 |
0.975 |
0.968 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 941 941![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494 494 |
0.018 |
| DenseNet169 |
0.971 |
0.972 |
0.976 |
0.971 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460 |
0.013 |
| ShuffleNet_V2_X2_0 |
0.959 |
0.957 |
0.960 |
0.956 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369 369![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 584 |
0.005 |
| MobileNet_V3_Large |
0.930 |
0.929 |
0.947 |
0.925 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 217![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 404 404 |
0.004 |
| RegNet_X_3_2 GF |
0.953 |
0.953 |
0.970 |
0.944 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299 299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
0.014 |
 |
| | Fig. 7 Training and validation graph (loss and accuracy) for the selected 10 pre-trained models. | |
 |
| | Fig. 8 Comparative graph for the selected 10 pre-trained models: (a) accuracy, F1 score, parameters, and GFLOPs; (b) precision and recall. | |
The best performance of the models tested was recorded for EfficientNet_V2_S, where an accuracy of 97.66%, an F1 score of 98.07%, a precision of 98.18%, and a recall of 98.08% were obtained. These values indicate that this approach offers the best balance between the accuracy of classification and reliability. Hence, it is the most reliable model for identifying HB accessions. The alternative models MaxVit_T and DenseNet169 yield good performance metrics, with accuracies of 97.07% and F1 scores of 97.28%, respectively. The reduced computational efficiency for MaxVit_T is 0.030414 GFLOPs, whereas that of DenseNet169 is 0.012504 GFLOPs, and EfficientNet_V2_S is 0.020193 GFLOPs. Apart from the improved classification effectiveness, EfficientNet_V2_S also retains reduced complexity in computation. This attribute is very helpful in high application scenarios or where the resources are limited. Models such as ConvNeXt_Tiny and ShuffleNet_V2_X2_0 perform well. However, they cannot provide high precision and recall because they fail to capture the tiny details that are present in the data. MobileNet_V3_Large provides a lower accuracy of 92.98% and an F1 score of 92.86%, which also indicates poor feature extraction in complex images.
EfficientNet_V2_S, the best model of those analyzed in this paper, is a highly advanced architecture that combines scalability and computational efficiency. Its ability to analyze complex patterns in HB images with fewer parameters means that it has a better design for the classification of images. Moreover, it has higher recall rates to minimize the possibility of misclassification to the greatest extent possible, a property that is essential in applications that demand high levels of reliability. Thus, its accuracy is necessarily balanced with computational efficacy and scalability. Based on the results, EfficientNet_V2_S was a good model for classifying a given accession of non-invasive HBs, with a state-of-the-art level of practical efficiency.
3.2.2 Optimization of EfficientNet_V2_S.
The hyperparameter optimization of EfficientNet_V2_S improved the validation metrics with minimal computational efficiency. With a batch size of 32, a dropout of 0.3, a learning rate of 0.0001, and 20 epochs, the ReLU activation function improves the accuracy from 97.66% to 98.25%. The F1 score increased from 98.09% to 98.25%, which means that it better represents the model's ability to strike a balance between precision and recall. The precision and recall values increase to 98.33% and 98.21%, respectively, indicating higher identification accuracy and reduced misclassifications. The optimization ensured that the number of GFLOPs remained at 0.02019, thereby retaining the efficiency with improved model performance. Hyperparameter tuning systematically enhances model design, resulting in improved accuracy while maintaining computational efficiency. EfficientNet_V2_S is a model optimized for the identification of HB accessions.
3.2.3 Similar works.
In the process of inspecting the quality of various food products, advanced techniques employing ML and CV have proven invaluable. The insights from several studies that applied similar technologies to enhance food quality inspection processes are discussed here.
In the baby corn industry, a quality inspection framework utilizing deep learning models, particularly EfficientNetB5, significantly outperforms traditional image processing methods. This automated system achieves up to 99.06% accuracy and provides a robust solution for distinguishing between pass and fail categories on the basis of visual inspection, demonstrating the efficiency and precision of ML in agricultural product sorting.52 Similarly, for rice quality, non-destructive screening methods using near-infrared spectra coupled with ML models such as logistic regression and support vector machines have shown high accuracy (94%) in classifying rice taste quality. This approach not only enhances the postharvest process but also supports the production of high-quality rice, which is potentially applicable to other food commodities.53 For yam quality detection, the development of intelligent acoustic devices employing discriminant analysis has proven effective. The technique using sound-producing software achieved an accuracy rate of approximately 82.3% in yellow yam, indicating that an ability is established using the acoustic property that is viable for quality determination without impairing the commodity.12 Furthermore, CV and ML are integrated with smart glasses and depth cameras for prawn farming. These smart devices and cameras enable frequent data capture on the growth of the prawns to optimize the feed and harvesting strategies. This method reduced the labor-intensive sampling, which is characteristic of traditional methods. Instead, it opens an avenue for automation in the quality monitoring of aquaculture.54
The tomato industry has also benefited from the development of ML and image processing techniques that have been used for disease detection. The study achieved accuracy levels of up to 99.6% by using descriptors and classifiers, such as support vector machines, k-nearest neighbours, and CNN, which demonstrate the suitability of these technologies in determining diseases at an early stage and improving crop quality.55 During the quality inspection of mushrooms, CV and ML revealed that there was a significant increase in the identification of species and classification of quality. The study mentioned limitations to the current applications, and the future scope of integrating these technologies promises mushroom production with better safety.56 In addition, the pretrained vision transformers were more accurate than traditional CNNs were even when trained with fewer samples in the case of apple and banana quality assessment. This allows ML to be applied in resource-poor settings for enhanced efficiency in the sorting and grading of agricultural products.57 A multivariate approach that included decision trees and logistic regression with ML models revealed that the predictions of beef freshness were better than those of conventional single-channel analysis in terms of color values.50 CV and ML applications in insect production may offer exciting opportunities for process automation to ensure product quality. Indeed, these technologies allow easy detection, identification, and classification of insects with high precision to optimize production efficiency and sustainability in this emerging industry trends.48 These studies have shown that the integration of ML with CV into food quality inspection processes could increase accuracy, efficiency, and scalability in a wide variety of food industries by providing a clear avenue toward more automated and accurate methods of quality control.
3.3 Comparative analysis of invasive and non-invasive approaches
In this study, the invasive FTIR technique employs regression and classification methods to identify HB accessions. Enhancing a NN regression model can achieve an R2 value of up to 0.96, with an RMSE as low as 0.69 and a minimum MAE of 0.33, indicating precise modeling of the spectra. The invasive method employed a classification approach, achieving an accuracy of 97.91% and a weighted F1 score of 97.91% within the narrow NN framework. This invasive approach yields precise chemical composition information from spectral data, making it suitable for applications that demand high accuracy. Nonetheless, the intricate sample preparation and elevated computational expenses restrict its scalability.
Non-invasive methods that utilize CV technology have demonstrated increased efficiency and feasibility. The EfficientNet_V2_S model attained a validation accuracy of 98.25% and an F1 score of 98.25%, and its precision and recall scores exceeded 98%. Limited preprocessing techniques that effectively utilize a scalable framework increase the efficacy of non-invasive methods for high-throughput applications. Although these methods may demand increased computational resources, they are capable of identifying subtle patterns in visual data, thereby providing improved and valuable solutions. The invasive approaches demonstrate significantly greater precision and require rigorous chemical testing. Non-invasive approaches offer scalability and efficiency in addressing various needs while identifying HB accessions.
4. Conclusion
This study compared two identification approaches, invasive and non-invasive methods, for HB accessions, highlighting their relative strengths and applications. The FTIR-based method demonstrates high precision in chemical composition analysis. However, it is limited in scalability and high-throughput applications because of the extensive sample preparation time needed. The non-invasive CV method demonstrates considerable versatility and requires minimal preparation, making it applicable in a wide range of situations for capturing visual patterns. This method is most effective in large-scale operations and outdoor applications within agricultural and biodiversity initiatives. Hybrid systems that integrate spectral and visual data present novel opportunities, enabling the combination of the accuracy of invasive techniques with the scalability of non-invasive approaches. Further investigation is needed to improve the computational frameworks and utilize advanced systems for ML. Enhancing datasets by integrating a broader spectrum of samples and evaluating them under varied climatic conditions can augment the robustness and applications of the models. The suggested methodologies can be modified for different underutilized legumes or crops by adjusting the feature extraction technique to accommodate differences in chemical composition and morphological characteristics. Moreover, ML models can be optimized via various datasets from many crop species, thus ensuring robust classification and forecasting precision across a wider range of agricultural applications. Real-time implementations via portable devices have the potential to transform field-level phenotyping and facilitate novel applications in sustainable agriculture and conservation science.
Data availability
The dataset used in this study, including hyacinth bean images for identification through computer vision, is publicly available on Kaggle at https://www.kaggle.com/datasets/pratikgorde/hyacinth-bean-image-dataset.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors are grateful and would like to thank the Department of Food Process Engineering, National Institute of Technology, Rourkela, Odisha, for providing the necessary facilities to carry out this work. Financial support from the Department of Science and Technology, New Delhi (DST/INSPIRE/2023/IF230002), is also gratefully acknowledged. The authors thank Rishabh Goyal for his assistance in the initial fabrication of the computer vision system.
References
- X. Huang, F. Xu, D. Yun, C. Li, J. Kan and J. Liu, Int. J. Biol. Macromol., 2023, 251, 126369 CrossRef CAS PubMed
 .
.
- M. Roy, S. Ullah, M. Alam and M. A. Islam, Legume Sci., 2021, 4, e128 CrossRef
 .
.
- A. Subagio, Food Chem., 2006, 95(1), 65–70 CrossRef CAS
 .
.
- M. S. A. Talucder, U. B. Ruba and M. A. S. Robi, J. Agric. Food Res., 2024, 16, 101116 Search PubMed
 .
.
- D. Chen, A. Ding, L. Zhu, T. Grauwet, A. Van Loey, M. Hendrickx and C. Kyomugasho, Food Chem., 2023, 404, 134531 CrossRef CAS PubMed
 .
.
- A. A. Tas and A. U. Shah, Trends Food Sci. Technol., 2021, 116, 701–711 Search PubMed
 .
.
- T. S. Naiker, H. Baijnath, E. O. Amonsou and J. J. Mellem, J. Food Process. Preserv., 2019, 44, e14334 Search PubMed
 .
.
- T. S. Naiker, H. Baijnath, E. O. Amonsou and J. J. Mellem, J. Food Process. Preserv., 2020, 44, e14430 CAS
 .
.
- S. M. Chen, F. S. Zeng, W. W. Fu, H. T. You, X. Y. Mu, G. F. Chen, H. Lv, W. J. Li and M. Y. Xie, Int. J. Biol. Macromol., 2023, 253, 127307 Search PubMed
 .
.
- Z. G. Ahmed, U. Radwan and M. A. El-Sayed, Biocatal. Agric. Biotechnol., 2020, 24, 101531 Search PubMed
 .
.
- F. Ojija and C. Ngimba, Environ. Sustain. Indic., 2021, 10, 100111 Search PubMed
 .
.
- J. Audu, R. R. Dinrifo, A. Adegbenjo, S. P. Anyebe and A. F. Alonge, Heliyon, 2023, 9, e14567 CrossRef CAS PubMed
 .
.
- M. Dogan, Y. S. Taspinar, I. Cinar, R. Kursun, I. A. Ozkan and M. Koklu, Comput. Electron. Agric., 2023, 204, 107575 CrossRef
 .
.
- O. Eric, R.-M. O. M. Gyening, O. Appiah, K. Takyi and P. Appiahene, Eng. Appl. Artif. Intell., 2023, 125, 106736 CrossRef
 .
.
- A. C. Vimal Singh and A. P. Singh, Procedia Comput. Sci., 2023, 218, 348–356 CrossRef
 .
.
- J. S. Cho, H. J. Bae, B. K. Cho and K. D. Moon, Food Chem., 2017, 220, 505–509 CrossRef CAS PubMed
 .
.
- D. Das, K. Pal, N. Sahana, P. Mondal, A. Das, S. Chowdhury, S. Mandal and G. K. Pandit, Food Chem. Adv., 2023, 2, 100164 CrossRef
 .
.
- K. Kılıç, İ. H. Boyacı, H. Köksel and İ. Küsmenoğlu, J. Food Eng., 2007, 78, 897–904 CrossRef
 .
.
- J. F. Martínez Ávalos, J. I. Gamero Barraza, E. Delgado, M. I. Guerra Rosas, C. A. Gómez Aldapa, H. Medrano Roldán, C. P. Cabrales Arellano and D. Reyes Jáquez, Food Chem. Adv., 2024, 4, 100723 CrossRef
 .
.
- R. Megias-Perez, S. Grimbs, R. N. D'Souza, H. Bernaert and N. Kuhnert, Food Chem., 2018, 258, 284–294 CrossRef CAS PubMed
 .
.
- P. M. Gorde, D. R. Dash, S. K. Singh and P. Singha, Sustain. Chem. Pharm., 2024, 39, 101619 CrossRef CAS
 .
.
-
A. Lerina, L. B. Mario, I. Martina and M. Cimitile, Presented in Part at the International Workshop on Metrology for Agriculture and Forestry, Trento, Italy, 2020 Search PubMed
 .
.
- D. R. Dash, S. K. Singh and P. Singha, Int. J. Biol. Macromol., 2024, 263, 130120 CrossRef CAS PubMed
 .
.
- M. Pavani, P. Singha, D. T. Rajamanickam and S. K. Singh, Future Foods, 2024, 9, 100286 CrossRef CAS
 .
.
- M. Pavani, P. Singha and S. K. Singh, JSFA reports, 2024, 4, 197–207 CrossRef CAS
 .
.
- R. Goyal, P. Singha and S. K. Singh, Food Chem., 2025, 477, 143502 CrossRef CAS PubMed
 .
.
- P. Deng, X. Lin, Z. Yu, Y. Huang, S. Yuan, X. Jiang, M. Niu and W. K. Peng, Food Chem., 2024, 447, 139017 CrossRef CAS PubMed
 .
.
- C. Y. E. Tachie, D. Obiri-Ananey, M. Alfaro-Cordoba, N. A. Tawiah and A. N. A. Aryee, Food Chem., 2024, 431, 137077 CrossRef CAS PubMed
 .
.
- R. Goyal, P. Singha and S. K. Singh, Trends Food Sci. Technol., 2024, 146, 104377 CrossRef CAS
 .
.
- M. M. Islam, M. A. Talukder, M. R. A. Sarker, M. A. Uddin, A. Akhter, S. Sharmin, M. S. A. Mamun and S. K. Debnath, Intell. Syst. Appl., 2023, 20, 200278 Search PubMed
 .
.
- H. Yin, Y. H. Gu, C.-J. Park, J.-H. Park and S. J. Yoo, Agriculture, 2020, 10(10), 439 Search PubMed
 .
.
- M. Razavi, S. Mavaddati, Z. Kobti and H. Koohi, Softw. Impacts, 2024, 20, 100654 CrossRef
 .
.
- P. Talukder and R. Ray, Biocatal. Agric. Biotechnol., 2024, 58, 103195 Search PubMed
 .
.
-
Y. Tew, W. Y. Lee and G. M. Tam, Presented in Part at the 2024 3rd International Conference on Digital Transformation and Applications (ICDXA), 2024 Search PubMed
 .
.
- P. Treepong and N. Theera-Ampornpunt, Curr. Res. Food Sci., 2023, 7, 100574 CrossRef PubMed
 .
.
- M. N. Wagimin, M. H. b. Ismail, S. S. M. Fauzi, C. T. Seng, Z. A. Latif, F. M. Muharam and N. A. M. Zaki, Comput. Electron. Agric., 2024, 221, 109006 CrossRef
 .
.
- Z. u. Rehman, M. A. Khan, F. Ahmed, R. Damaševičius, S. R. Naqvi, W. Nisar and K. Javed, IET Image Process., 2021, 15, 2157–2168 CrossRef
 .
.
- J. J. Tsai, C. C. Chang, D. Y. Huang, T. S. Lin and Y. C. Chen, Food Chem., 2023, 426, 136610 CrossRef CAS PubMed
 .
.
-
L. Aversano, M. L. Bernardi, M. Cimitile, M. Iammarino and S. Rondinella, Presented in Part at the 2020 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), 2020 Search PubMed
 .
.
- A. Herath, R. Tiozon Jr, T. Kretzschmar, N. Sreenivasulu, P. Mahon and V. Butardo, Food Chem., 2024, 460(3), 140728 Search PubMed
 .
.
- Y. Lu, C. Du, C. Yu and J. Zhou, Comput. Electron. Agric., 2014, 107, 58–63 CrossRef
 .
.
- X. Wu, J. Zhu, B. Wu, J. Sun and C. Dai, Comput. Electron. Agric., 2018, 147, 64–69 Search PubMed
 .
.
- Y. Li, N. Logan, B. Quinn, Y. Hong, N. Birse, H. Zhu, S. Haughey, C. T. Elliott and D. Wu, Food Chem., 2024, 438, 138029 CrossRef CAS PubMed
 .
.
- S. Yun, S. Jeong and S. Lee, Food Hydrocolloids, 2024, 157, 110456 CrossRef CAS
 .
.
- Y.-T. Wang, H.-B. Ren, W.-Y. Liang, X. Jin, Q. Yuan, Z.-R. Liu, D.-M. Chen and Y.-H. Zhang, J. Food Eng., 2021, 311, 110740 CrossRef
 .
.
- Y. Sun, J. Huang, L. Shan, S. Fan, Z. Zhu and X. Liu, Food Chem., 2021, 352, 129313 CrossRef CAS PubMed
 .
.
- M. Li, D. Shi, Y. Cheng, Q. Dang, W. Liu, Z. Wang, Y. Yuan and T. Yue, Food Chem., 2025, 465, 142056 CrossRef CAS PubMed
 .
.
- S. Nawoya, F. Ssemakula, R. Akol, Q. Geissmann, H. Karstoft, K. Bjerge, C. Mwikirize, A. Katumba and G. Gebreyesus, Comput. Electron. Agric., 2024, 216, 108503 CrossRef
 .
.
- M. M. Oliveira, B. V. Cerqueira, S. Barbon and D. F. Barbin, J. Food Compost. Anal., 2021, 97, 103771 CrossRef CAS
 .
.
- C. N. Sanchez, M. T. Orvananos-Guerrero, J. Dominguez-Soberanes and Y. M. Alvarez-Cisneros, Heliyon, 2023, 9, e17976 CrossRef PubMed
 .
.
- N. Shome, R. Kashyap and R. H. Laskar, Image Vis. Comput., 2024, 147, 105063 CrossRef
 .
.
- K. Wonggasem, P. Chakranon and P. Wongchaisuwat, Artif. Intell. Agric., 2024, 11, 61–69 Search PubMed
 .
.
- E. O. Diaz, H. Iino, K. Koyama, S. Kawamura, S. Koseki and S. Lyu, Food Chem., 2023, 429, 136907 CrossRef CAS PubMed
 .
.
- M. Xi, A. Rahman, C. Nguyen, S. Arnold and J. McCulloch, Aquacult. Eng., 2023, 102, 102339 CrossRef
 .
.
- S. S. Harakannanavar, J. M. Rudagi, V. I. Puranikmath, A. Siddiqua and R. Pramodhini, Glob. Transit. Proc., 2022, 3, 305–310 CrossRef
 .
.
- H. Yin, W. Yi and D. Hu, Comput. Electron. Agric., 2022, 198, 107015 CrossRef
 .
.
- M. Knott, F. Perez-Cruz and T. Defraeye, J. Food Eng., 2023, 345, 111401 CrossRef
 .
.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Poonam
Singha
,
Poonam
Singha
 and
Sushil Kumar
Singh
and
Sushil Kumar
Singh
 *
*
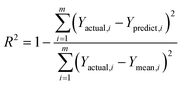

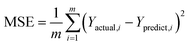









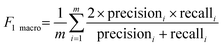






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bytes. Under these criteria, the KNN and NN models emerged as the most effective options. The optimization of the KNN model involves several hyperparameters: the number of neighbors, which ranged from 1 to 24; distance metrics, which included city block, Chebyshev, correlation, cosine, Euclidean, Hamming, Jaccard, Mahalanobis, Minkowski cubic, and Spearman; and weighting methods for distances, which can be equal, inverse, or squared inverse. An optimized NN model was achieved through hyperparameter search, following the aforementioned procedure: modifications in the number of layers, activation functions, regularization strength, and layer sizes. For optimization, a 5-fold cross validation was conducted. On the basis of the enhancements in classification and the computational complexities of the models, the final models were selected.
000 bytes. Under these criteria, the KNN and NN models emerged as the most effective options. The optimization of the KNN model involves several hyperparameters: the number of neighbors, which ranged from 1 to 24; distance metrics, which included city block, Chebyshev, correlation, cosine, Euclidean, Hamming, Jaccard, Mahalanobis, Minkowski cubic, and Spearman; and weighting methods for distances, which can be equal, inverse, or squared inverse. An optimized NN model was achieved through hyperparameter search, following the aforementioned procedure: modifications in the number of layers, activation functions, regularization strength, and layer sizes. For optimization, a 5-fold cross validation was conducted. On the basis of the enhancements in classification and the computational complexities of the models, the final models were selected.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching, proteins)
O stretching, proteins)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912
912![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814
814![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967
967![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843
843![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 795
795![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774
774![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814
814![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301
301![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705
705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642
642![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622
622![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 628
628![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673
673![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668
668![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 468
468![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280
280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052
052![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688
688![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618
618
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bytes in model size. Upon applying the specified criteria, KNN and NN emerged as the top-performing frameworks, demonstrating high accuracy values and favorable precision–recall metrics while requiring fewer computational resources. These thus served as relevant frameworks for the utilized dataset. Compared with alternative methods, NNs consistently demonstrated superior capability in representing details of the HB accession data.
000 bytes in model size. Upon applying the specified criteria, KNN and NN emerged as the top-performing frameworks, demonstrating high accuracy values and favorable precision–recall metrics while requiring fewer computational resources. These thus served as relevant frameworks for the utilized dataset. Compared with alternative methods, NNs consistently demonstrated superior capability in representing details of the HB accession data.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622
622![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418
418![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 742
742![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150
150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230
230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030
030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414
414![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590
590![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762
762![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762
762![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750
750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778
778![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780
780![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938
938![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054
054![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136
136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113
113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513
513![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405
405![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177
177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276
276
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 bytes. Additionally, its prediction speed increased to 815.91 observations per second, whereas the training time slightly decreased to 35.49 seconds, as shown in Fig. S3(a–c).† These enhancements highlight the effectiveness of optimization in improving the KNN performance and computational efficiency. Fig. S3(d–f)† displays the optimization graphs for the NN model, which results in a NN model achieving an accuracy of 98.37%, which is a 0.45% improvement, with an error rate of 1.63%. The model size was reduced to 12
200 bytes. Additionally, its prediction speed increased to 815.91 observations per second, whereas the training time slightly decreased to 35.49 seconds, as shown in Fig. S3(a–c).† These enhancements highlight the effectiveness of optimization in improving the KNN performance and computational efficiency. Fig. S3(d–f)† displays the optimization graphs for the NN model, which results in a NN model achieving an accuracy of 98.37%, which is a 0.45% improvement, with an error rate of 1.63%. The model size was reduced to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 bytes, and the prediction speed reached 4236.37 observations per second. The training duration was minimized to 2.36 seconds. The bilayer NN architecture, featuring two fully connected layers with ReLU activation functions, effectively captured complex nonlinear relationships, leading to robust performance. The KNN model, augmented by a refined distance metric and inverse weighting, exhibited elevated classification accuracy, rendering it appropriate for applications necessitating precision. Conversely, the NN model achieves a harmonious equilibrium between predictive accuracy and computational efficiency, particularly in the identification of nonlinear patterns and the ability to scale with extensive datasets. This investigation underscores the importance of hyperparameter tuning tailored to the distinctive characteristics of each model.
250 bytes, and the prediction speed reached 4236.37 observations per second. The training duration was minimized to 2.36 seconds. The bilayer NN architecture, featuring two fully connected layers with ReLU activation functions, effectively captured complex nonlinear relationships, leading to robust performance. The KNN model, augmented by a refined distance metric and inverse weighting, exhibited elevated classification accuracy, rendering it appropriate for applications necessitating precision. Conversely, the NN model achieves a harmonious equilibrium between predictive accuracy and computational efficiency, particularly in the identification of nonlinear patterns and the ability to scale with extensive datasets. This investigation underscores the importance of hyperparameter tuning tailored to the distinctive characteristics of each model.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 samples. High spectral clustering allows for the creation of a hypothesis-free, scalable database.27 Additionally, terahertz spectroscopy with SVR for the quantification of bisphenol mixtures achieved an R2 of 0.98. The absorption spectra were reconstructed accurately and showed robust applicability in industrial mixture analysis.46 Moreover, rapeseed varieties were classified via FTIR-PAS (photoacoustic spectroscopy) with PCA, which yielded 0% SVM error and 7.5% PLS-DA (partial least-squares discriminant analysis) error. SPA (successive projections algorithm) increased the accuracy; however, it reduced the number of variables, where FTIR-PAS verified its efficiency and non-destructive nature.41 Furthermore, ATR-FTIR spectroscopy with the assistance of ML models was used to quantify selenium in kefir grains. The total selenium prediction resulted in an RP (relative coefficient) of 0.97 and an RPD (relative prediction deviation) of 4.36; organic selenium prediction resulted in an RP of 0.95 and an RPD of 6.44, which enabled quick and eco-friendly detection.47 The FTIR spectroscopy and clustering results, with an accuracy of 93.9%, were more precise than those of the other methods. PCA and LDA (linear discriminant analysis) are techniques that enhance the reduction of dimensions since clustering serves as a good classification model.42
500 samples. High spectral clustering allows for the creation of a hypothesis-free, scalable database.27 Additionally, terahertz spectroscopy with SVR for the quantification of bisphenol mixtures achieved an R2 of 0.98. The absorption spectra were reconstructed accurately and showed robust applicability in industrial mixture analysis.46 Moreover, rapeseed varieties were classified via FTIR-PAS (photoacoustic spectroscopy) with PCA, which yielded 0% SVM error and 7.5% PLS-DA (partial least-squares discriminant analysis) error. SPA (successive projections algorithm) increased the accuracy; however, it reduced the number of variables, where FTIR-PAS verified its efficiency and non-destructive nature.41 Furthermore, ATR-FTIR spectroscopy with the assistance of ML models was used to quantify selenium in kefir grains. The total selenium prediction resulted in an RP (relative coefficient) of 0.97 and an RPD (relative prediction deviation) of 4.36; organic selenium prediction resulted in an RP of 0.95 and an RPD of 6.44, which enabled quick and eco-friendly detection.47 The FTIR spectroscopy and clustering results, with an accuracy of 93.9%, were more precise than those of the other methods. PCA and LDA (linear discriminant analysis) are techniques that enhance the reduction of dimensions since clustering serves as a good classification model.42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714
714![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676
676![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192
192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860
860![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829
829![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356
356![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413
413![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780
780![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324
324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098
098![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 941
941![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494
494![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504
504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460
460![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369
369![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584
584![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217
217![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 404
404![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299
299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660
660
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





