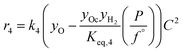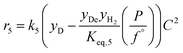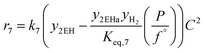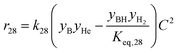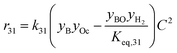Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetic and process modeling of Guerbet coupling chemistry over Cu–Mg–Al mixed oxides†
Javier E.
Chavarrio‡
 a,
Christoph
Markowitsch‡
a,
Christoph
Markowitsch‡
 ab,
Erick
Votava
a,
Markus
Lehner
ab,
Erick
Votava
a,
Markus
Lehner
 b and
George W.
Huber
b and
George W.
Huber
 *a
*a
aDepartment of Chemical and Biological Engineering, University of Wisconsin – Madison, Madison, WI 53706, USA. E-mail: gwhuber@wisc.edu
bChair of Process Technology and Industrial Environmental Protection, Montanuniversität Leoben, 8700 Leoben, Austria
First published on 20th February 2025
Abstract
Guerbet coupling chemistry is a route to oligomerize ethanol into C4+ alcohols. Long chain ethers can be obtained through bimolecular dehydration of these alcohols. Ethers generated from the dehydration of C6+ alcohols produce a fuel that satisfies diesel engine requirements, therefore selective production of C6+ alcohols is of particular interest. The desired hexanol is synthesized through ethanol and butanol coupling, accompanied by the formation of undesired products through several reaction pathways. In this work the coupling of ethanol and butanol has been studied over Cu0.01Mg2.99AlOx to produce C6+ alcohols through Guerbet coupling reactions. Two series of catalytic tests were performed at 325 °C and 300 psig by using either pure ethanol feed or a cofeed ethanol–butanol 70–30 mole%. A kinetic model was developed to predict the product distribution over a wide range of contact times. Kinetic parameters were regressed by coding a routine that included a solution of differential mole balances embedded in an optimization problem. The herein developed kinetic model was integrated in a process simulation flowsheet that models the upgrading of ethanol into C6+ oxygenates. The butanol cofeeding strategy in the simulations was approached by recycling the produced butanol into the coupling reactor. The simulation results reveal that cofeeding butanol into the Guerbet reactor enhances initial production rates of C6+ alcohols, at the expense of fostering production of byproducts from butanol self-coupling. A maximum carbon yield of 82.2% for C6+ diesel fuel precursors can be obtained by minimizing the byproduct production after introduction of a hydrogenation reactor.
Broader contextDiesel fuel demand is forecasted to increase in the upcoming decades driven by transportation of commodities and materials. Electrification of the heavy-duty transportation sector is not a promising solution to supply power to the heavy-duty fleet due to technical limitations. Thereby, investigation on synthesis of sustainable diesel fuel is critical to support economic development with low environmental burden. A technology based on catalytic upgrading of ethanol has been demonstrated as viable to produce diesel fuel. Nevertheless, the current state of this technology requires a better description of the reaction units which is achieved through development of kinetic models. These models not only provide an accurate assessment of the process's feasibility but also identify operational regimes that enhance performance. By guiding process optimization and improving efficiency, the insights from these models contribute to the development of a more sustainable diesel production route. |
1. Introduction
Ethanol is the most produced liquid biofuel in the world, with an estimated global production of 29.6 billion gallons in 2023.1 In the US, ethanol is typically blended with gasoline at ∼10% v/v, to produce a mixture that exhibits a higher octane number than gasoline, improving the engine energy efficiency.2,3 Other factors like energy security and climate protection have also served as motivation for ethanol blending.4 The electrification of vehicles has been promoted as an approach to decarbonize the fuel industry. By 2030, 11 to 63% of the total passenger car sales in the world are forecasted to be electric vehicles, with percentages climbing up to 100% by 2050.5 Unfortunately, electrification of the heavy-duty transportation fleet is not expected to occur to the same extent due to technical barriers related to the size and weight of batteries. Moreover, regulations to reduce accelerated wear and tear of roads due to transportation of heavy loads hinder the electrification of trucks in the mid-term.5 Therefore, it is imperative to find ways to produce sustainable diesel fuel surrogates to stay aligned with decarbonization of the transportation sector. The demand for gasoline is projected to decrease due to the increase of personal electric vehicles,6 reducing the consumption of bioethanol for blending and potentially creating an ethanol surplus in the market. Synthesizing heavy distillate-range fuels through ethanol upgrading represents a market opportunity that the bioethanol industry needs to maintain its participation in the energy sector.7Recently, our group developed a three-stage process to produce diesel fuel8,9 through catalytic upgrading of ethanol that encompasses the: (1) catalytic oligomerization of ethanol into longer chain alcohols through Guerbet coupling chemistry,10,11 (2) hydrogenation of byproducts generated in the first reactor (mainly esters, aldehydes, and ketones) into alcohols,12 and (3) bimolecular dehydration of the alcohols mixture over an acid catalyst to produce a blend of long-chain ethers.13,14 We initially used hydroxyapatite (HAP) as the catalyst for ethanol conversion,15,16 but later switched to a Cu/MgAlOx catalyst.10 The advantages of the Cu–Mg–Al catalyst compared to the HAP catalyst are higher product selectivity to C6+ alcohols and lower inhibition to water. Process modeling, life cycle assessment, techno-economic analysis, and fuel performance demonstrations were carried out by our collaborators to show the competitiveness of this technology.8 Despite the meaningful progress made in studying this diesel synthesis technology, there exists strong assumptions in the modeling of the process that constrains its global optimization. For instance, all our studies have contemplated the use of yield rather than kinetic reactors for each catalytic stage due to the inexistence of models applicable to our catalysts. The development of kinetic models under relevant reaction conditions for our reactors will reduce the stiffness imposed by yield reactors, allowing us to perform more realistic modeling of our synthesis process. Process design follows the hierarchical diagram depicted in Scheme S1 (ESI†), where the reaction units have the highest priority, with upstream being more important. The Guerbet coupling reactor has the highest priority in our process as it is the first reaction unit. Therefore, making efforts to describe it more accurately is imperative to continue validating the economic feasibility of our technology. As such, derivation of a kinetic model for the Guerbet coupling reactor is one of the goals of this report.
To the best of our knowledge, six previous attempts to model Guebert coupling chemistry over HAP17–20 and mixed metal oxides21,22 have been published in the literature. There are two kinetic models where the kinetic constants were derived using the initial rates method to fit experimental information to rate expressions. Ho et al.17 studied and modeled the ethanol coupling chemistry over HAP, which follows the aldol condensation mechanism. Initial rates were determined by performing reactions in the kinetic regime between 300–340 °C in flow reactors. Their rate function follows a Langmuir adsorption, where ethanol is specified as the most predominant surface species. The model presented by the authors exhibits an excellent ability to explain the observed consumption and formation rates of ethanol, acetaldehyde, and butanol within the studied range of temperature. In another study, Young et al.18 investigated the global ethanol coupling reaction to butanol over TiO2, HAP, and MgO. However, their work developed solely rate expressions for acetaldehyde consumption in the aldol condensation reaction (2 acetaldehyde → crotonaldehyde + H2O). While their model accurately describes the acetaldehyde consumption rate as a function of its partial pressure, the formulation of a rate expression for a single elementary reaction step does not provide sufficient information to model the full pathway from ethanol to butanol. Lastly, Scheid et al.21 investigated the ethanol coupling reaction over Mg–Al mixed oxides, with the Mg/Al ratio equals 5. This catalyst is the one that most resembles ours, with the caveat that ours also includes copper to facilitate (de)hydrogenation steps.10 Unlike the aforementioned studies, Scheid et al. did not focus only on studying the upgrading of ethanol into butanol, but rather on a more complex reaction network involving alcohol coupling, dehydrogenation, and dehydration reactions for ethanol and butanol. In their approach, their reaction network is composed of six reversible reactions that follow elemental reaction orders, with inclusion of adsorption, reaction, and desorption steps to yield a LHHW model. Since their study involves multiple reactions occurring simultaneously over the surface of the catalyst, Scheid et al. have approached the kinetic parameters regression problem by solving a differential-algebraic optimization problem to predict the observed mole fraction distribution of the products in the outlet of their flow reactor. Although all these three kinetic models are limited to C2–C4 chemistry, useful insights about the shape of the rate expression can be obtained for derivation of more complicated models.
Three more studies modeling a more complicated reaction network for ethanol coupling chemistry are available in the literature. In these papers the authors performed initial experiments to establish a reaction mechanism as a basis for their kinetic modeling. For instance, Tsuchida et al.20 performed studies in continuous flow to investigate the alcohol coupling chemistry of ethanol in conversions up to 80% over HAP. Their catalytic observations yielded a reaction network composed of 13 reactions and served as a basis to derive their kinetic model. In their simulations, they predict the outlet concentration of C2–C10 linear and branched alcohols and olefines by solving a differential model as a function of the residence time for temperatures ranging between 300–450 °C. Recently, Eagan et al.19 made a great effort modeling the Guerbet coupling chemistry over HAP, explaining coupling, interrupted coupling, and dehydration reactions. One of the strengths of this model is its ability to simulate the catalyst inhibition as a function of the amount of water present in the system. The authors’ model employs only nine kinetic parameters to describe 647 reactions involving 185 alcohols. Eagan et al. considered the existence of acid and basic sites following what is observed from a mechanistic point of view, which resulted in complex rate expressions that requires specialized skills to implement it in a process simulation package like Aspen. Finally, Nezam et al.22 modeled the Guerbet chemistry over Ni–La2O3/γ-Al2O3. Their study is interesting because they model the observed kinetic behavior when cofeeding ethanol and isoamyl alcohol to produce longer chain alcohols.
Besides developing kinetic models to make our process modeling more realistic, we also believe that inclusion of recycling streams to recover unreacted species is a determining factor in the feasibility of our process. In our previous work,9 we have made efforts to understand the potential benefits of recycling the unreacted ethanol and produced butanol into the Guerbet coupling reactor to foster the condensation of longer chain alcohols, primarily hexanol, produced through the apparent reaction ethanol + butanol → hexanol + water. Our preliminary results indicate that hexanol production rates increase by a factor of at least two when butanol is cofed into the reactor at a feed ratio of ethanol–butanol of 70–30% on a mole basis.9 Based on these promising results, and for the sake of developing a more robust kinetic model for our alcohol coupling reactor, herein we conducted a series of catalytic experiments over a Cu0.01Mg2.99AlO catalyst. Experiments were performed by cofeeding pure ethanol as control experiments and a blend of ethanol–butanol in a mole ratio of 70–30%. Next, a detailed kinetic model considering the most relevant reaction products was developed by employing differential mole balances and solving an optimization problem for the derivation of kinetic constants considering experimental data acquired with ethanol and ethanol–butanol feeds. Lastly, our kinetic model has been implemented within an Aspen Plus process simulation to explore in more detail the implication of recycling a blend ethanol–butanol into the coupling reactor and its impact over the global production of diesel fuel precursors.
2. Methods
2.1 Catalyst synthesis
A 0.3 wt% copper magnesium aluminum mixed metal oxide catalyst (Cu0.01Mg2.99AlO) identified previously10 as a promising catalyst for ethanol oligomerization reactions has been derived from a hydrotalcite type precursor through the co-precipitation method.10,23 Initially, three aqueous solutions were prepared as follows: (1) 240 mL of a solution containing Mg2+ 0.843 M (Mg(NO3)3·6H2O, Sigma-Aldrich 237175), Al3+ 0.282 M (Al(NO3)3·9H2O, Sigma-Aldrich 237973), and Cu2+ 0.002 M (Cu(NO3)2·3H2O, Sigma-Aldrich 61194); (2) 300 mL of a solution 0.225 M of Na2CO3 (Sigma-Aldrich 223530); and (3) 500 mL of a solution 1.35 M of NaOH (Sigma-Aldrich 795429). Solutions were prepared in such a way that in the whole synthesis the ratio (Cu + Mg)2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al3+
Al3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO=3
CO=3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OH− was 3
OH− was 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. First, solution 2 containing Na2CO3 was transferred into a 1 L beaker and heated up to 60 °C on a stir plate, while being stirred with a magnetic stir bar. Next, solution 1 and 3 were added in a dropwise fashion to the 1 L beaker by using syringe pumps. Flowrates in the syringe pumps were controlled so that the addition occurred in 1 h and the pH remained at 10 during the synthesis. Temperature and pH were monitored continuously by employing a temperature/pH probe (Ohaus ST20). After complete addition of solution 1, the mixed solution was transferred into a Schott bottle, capped, and aged over 24 h at 60 °C with magnetic stirring. The aged solution was then vacuum filtered and washed with hot deionized water to remove residual sodium and nitrate ions. Subsequently, the filtered cake was redissolved in 300 mL of a 1 M solution of Na2CO3, filtered, and washed with 500 mL of DI. Filter cake was dried overnight at 110 °C in an oven (Lab-line, 3511), crushed into a powder, and calcined for 2 h at 600 °C under a heating ramp of 4 °C min−1 in a muffle furnace under a static air atmosphere.
10. First, solution 2 containing Na2CO3 was transferred into a 1 L beaker and heated up to 60 °C on a stir plate, while being stirred with a magnetic stir bar. Next, solution 1 and 3 were added in a dropwise fashion to the 1 L beaker by using syringe pumps. Flowrates in the syringe pumps were controlled so that the addition occurred in 1 h and the pH remained at 10 during the synthesis. Temperature and pH were monitored continuously by employing a temperature/pH probe (Ohaus ST20). After complete addition of solution 1, the mixed solution was transferred into a Schott bottle, capped, and aged over 24 h at 60 °C with magnetic stirring. The aged solution was then vacuum filtered and washed with hot deionized water to remove residual sodium and nitrate ions. Subsequently, the filtered cake was redissolved in 300 mL of a 1 M solution of Na2CO3, filtered, and washed with 500 mL of DI. Filter cake was dried overnight at 110 °C in an oven (Lab-line, 3511), crushed into a powder, and calcined for 2 h at 600 °C under a heating ramp of 4 °C min−1 in a muffle furnace under a static air atmosphere.
2.2 Alcohol coupling reactions
Gas-phase alcohol coupling reactions were carried out in stainless-steel packed bed reactors (316 SS, 1/4″ O.D., 16″ length), where the catalyst mass ranged between 40–1500 mg, depending on the studied contact time. Ten catalytic runs per feed were carried out at contact times (τ) ranging between 0.21–21.6 h kgcat kmolgas−1. The synthesized Cu0.01Mg2.99AlOx catalyst was sieved to ensure a uniform particle size distribution (standard sieve mesh 30–80), packed, and held at the center of the tubing by glass wool (Acros organics) and silica beads (Sigma-Aldrich) at both ends. The tubular reactor was then confined within an aluminum heating block, equipped with a K-type thermocouple, to keep an isothermal profile along the reaction bed. An electric furnace (Thermo Fisher, Lindberg blue M Mini-Mite) was employed to heat up the reactor and control the temperature program. Prior to catalytic tests, the catalyst bed was reduced in situ at 325 °C by flowing H2 (Airgas, UHP grade) at 50 mL min−1 overnight (more than 12 h), with a heating ramp of 4 °C min−1.10 Posterior to the reduction of the bed, the tubular reactor was pressurized up to 300 psig of hydrogen atmosphere, and pressure was maintained constant by using a back pressure regulator (Equilibar, ZF0SVN8) with nitrogen as the pilot fluid. Alcohol coupling reactions were performed at 325 °C and 300 psig by pumping either pure ethanol or a blend of ethanol–butanol of composition 70–30% in mole basis at 65 µL min−1 into the reactor by using a syringe pump (Teledyne ISCO). Hydrogen was used as a carrier and co-fed into the reactor at an adjusted rate so that the mole ratio of ethanol + butanol to hydrogen in the inlet of the reactor was 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Hydrogen is cofeed into the reactor along with the alcohols to partially suppress the formation of esters and aldehydes inherent to the alcohols coupling chemistry.11 Before contacting the catalyst, the liquid feed was passed through a preheated section maintained at 260 °C to ensure complete vaporization of the alcohols. Posterior to the reaction, reaction products were crashed on 10 mL of 1-propanol (96566, Sigma-Aldrich), preloaded in a removable glass condenser (110 mL, Ace glass), submerged in a dry ice bath (dry ice/acetone). Uncondensed products left the collection vessel and were directed towards a three-way valve for online analysis in a GC (Shimadzu 2010), equipped with flame ionization and thermal conductivity detectors, or venting. Condensed products were withdrawn every 40 minutes (∼2 g of reaction product) up to the collection of four samples per catalytic run. Liquid products were then prepared for gas chromatography analysis by diluting the samples in 1-propanol and adding a known amount of 1-pentanol (∼1 wt%, Sigma-Aldrich, 138975) as the internal standard. Samples’ analysis was conducted in a GC-FID (Shimadzu 2014), equipped with an RTX-VMS (Restek) column. Identification of reaction products was helped by GC-MS (Shimadzu GCMS-QP2010) and quantification of product concentration was done by using external standards when available.
1. Hydrogen is cofeed into the reactor along with the alcohols to partially suppress the formation of esters and aldehydes inherent to the alcohols coupling chemistry.11 Before contacting the catalyst, the liquid feed was passed through a preheated section maintained at 260 °C to ensure complete vaporization of the alcohols. Posterior to the reaction, reaction products were crashed on 10 mL of 1-propanol (96566, Sigma-Aldrich), preloaded in a removable glass condenser (110 mL, Ace glass), submerged in a dry ice bath (dry ice/acetone). Uncondensed products left the collection vessel and were directed towards a three-way valve for online analysis in a GC (Shimadzu 2010), equipped with flame ionization and thermal conductivity detectors, or venting. Condensed products were withdrawn every 40 minutes (∼2 g of reaction product) up to the collection of four samples per catalytic run. Liquid products were then prepared for gas chromatography analysis by diluting the samples in 1-propanol and adding a known amount of 1-pentanol (∼1 wt%, Sigma-Aldrich, 138975) as the internal standard. Samples’ analysis was conducted in a GC-FID (Shimadzu 2014), equipped with an RTX-VMS (Restek) column. Identification of reaction products was helped by GC-MS (Shimadzu GCMS-QP2010) and quantification of product concentration was done by using external standards when available.
Liquid phase concentration of product i was calculated with eqn (1), where CvialpentOH is the concentration of the internal standard in the analysis vial, RFx,i stands for the relative response factor of compound i with respect to the internal standard, Areai corresponds to the area of peak i recorded in the gas chromatograph, mcondenserpropOH and ρpropOH are the mass and density of 1-propanol employed as the crashing solvent and preloaded in the collection condenser, mcondenserproduct and ρcondenserproduct represent the mass and liquid phase density of the reaction effluent crashed over the 1-propanol, mvialpropOH is the mass of propanol used to dilute the samples for the GC analysis, and mvialproduct and ρvialsample represent the mass and density of the sample (reaction effluent + crashing solvent) used in the GC analysis.
 | (1) |
Ethanol conversion was calculated for each experiment by using eqn (2).
 | (2) |
The carbon balance was calculated as the ratio of the carbon concentration detected in the outlet and the carbon concentration fed to the reaction setup as presented in eqn (3).
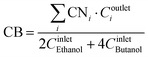 | (3) |
2.3 Kinetic modeling
The change in flow rate of component i (Fi) participating in j reactions in a packed-bed reactor is expressed by eqn (4). | (4) |
Regression of kinetic parameters for the system of 37 ordinary differential equations generated from eqn (4) has been achieved after implementation of the mathematical model in Matlab® R2022b, by following the algorithm depicted in Fig. 1. As observed, the algorithm is fed with estimated values for the kinetic constants (k0) and liquid phase concentrations of the species quantified in our experiments (Cexpi(τ)) to minimize the objective function. In the algorithm, differential balances for the gas phase flows are established and solved by using the ODE23s function. For solution of the ordinary differential equations the initial conditions were assumed to be the mole flow of each species in the inlet of the reactor. Subsequently, gas phase mole fractions are computed to be employed in the proposed rate model. A more detailed derivation of the rate expression is presented in Section S2 of the ESI.† Estimation of the liquid phase concentrations is carried out by renormalizing the gas phase mole fractions (yi) in a H2- and CO-free basis. Ultimately, profiles of liquid phase carbon concentrations are obtained and compared to experimental data to proceed with the optimization. A hybrid optimization approach was carried out to minimize the objective function, initializing the routine with the particle swarm algorithm by invoking the ‘particleswarm’ function with a swarm size of 100 particles and typically a maximum of 50 iterations and subsequent refinement of the best solution by using the ‘lsqcurvefit’ function. Determination of the parameters’ confidence intervals was carried out with the ‘nlparci’ function at 95% confidence interval, and estimation of the confidence band around the regressed model with the ‘nlpredci’ function. For clarification, experimental data obtained feeding ethanol, and the blend ethanol–butanol were used simultaneously to fit the model.
 | ||
| Fig. 1 Flowchart of the optimization algorithm employed for regression of the kinetic constants that rule the chemistry of alcohols coupling. | ||
The objective function to be minimized was formulated as a weighted combination of squared error and logarithmic squared error. While the sum of the absolute squared error tends to bias towards species with high carbon concentrations, the sum of the logarithmic squared error assigns greater weight to species with low concentrations. In our exploratory study, we found that combining both approaches helped balance the performance of our optimization problem. The values of the weights α and β were determined based on the objective function value after the optimization procedure, considering only the absolute squared error and the logarithmic squared error, respectively. In this study, α = 4.44 and β = 47.18. This approach ensures that the hybrid objective function has equal contribution from both error types, converging towards a value of two as the optimization progresses.
The rate model proposed in this work is based on a LHHW adsorption model given its proven good performance for modeling the Guerbet coupling chemistry over hydroxyapatite,17–19 Ni–La2O3/γ-Al2O3,22 and MgxAlyO.21 We have assumed that dehydrogenation and dehydrogenative coupling reactions between alcohols, aldehydes, hydrogen, and esters are ruled by reversible reactions due to the presence of copper.24,25 In this respect, the general rate expression for the reaction aA + bB ⇌ cC + dD is ruled by eqn (5). Such an expression has been applied to the set of 37 chemical reactions that model the chemistry in the reactor and the final functional shape is shown in Table 1. Our previous work elucidating the reaction chemistry running over the catalyst surface11 served as the basis for the derivation of the reaction network that rules our model.
 | (5) |
 by using thermochemical data at 325 °C. The thermochemical data used for equilibrium constant calculations were sourced from Aspen Properties. The data were validated, when possible, against thermochemical information available in the open literature, including the NIST Webbook,26,27 JANAF tables,28 and chemical properties handbooks.29,30 Details of the validation process, including supporting calculations, are provided in the ESI† (.xls file). yi is the mole fraction of species i in the gas phase, a, b, c, and d are stoichiometric coefficients and Δnj is the change in moles of the chemical reaction j, P represents the total pressure of the system, and f° is the fugacity of an ideal gas at 1 bar. The value of C is calculated by means of eqn (6).
by using thermochemical data at 325 °C. The thermochemical data used for equilibrium constant calculations were sourced from Aspen Properties. The data were validated, when possible, against thermochemical information available in the open literature, including the NIST Webbook,26,27 JANAF tables,28 and chemical properties handbooks.29,30 Details of the validation process, including supporting calculations, are provided in the ESI† (.xls file). yi is the mole fraction of species i in the gas phase, a, b, c, and d are stoichiometric coefficients and Δnj is the change in moles of the chemical reaction j, P represents the total pressure of the system, and f° is the fugacity of an ideal gas at 1 bar. The value of C is calculated by means of eqn (6). | (6) |
In eqn (6)j might be j = (alcohol, aldehyde, ketone, ester, water) and i represents the species i that belongs to group j. In our approach, we have assumed that all species belonging to a given group j share the same adsorption constant. For example, all alcohols have the same adsorption constant. Also, we have assumed that the adsorption constant of any ketone is the same as the adsorption constant of an aldehyde.
2.4 Process modeling simulations
With the aim of demonstrating the feasibility of integrating our kinetic model into a process simulation to develop routes for selective production of diesel fuel precursors (e.g., hexanol, octanol, decanol), we have embedded the kinetic model here developed for the Guerbet coupling reactor in an Aspen Plus V14 flowsheet simulation. A process flow diagram of the simulation is depicted in Fig. 2.As displayed, ethanol is pumped (P-101) from a feed-tank into a heat exchanger for its vaporization before feeding it into the Guerbet reactor (R-101). Pressure is increased in this stage from atmospheric up to 20 barg. The Guerbet reactor is simulated as a plug flow reactor (PFR) in which the set of reactions and their rate expressions derived from our kinetic model are implemented. Reaction contact time is specified by varying the mass of catalyst loaded in the reactor. The PFR is simulated as isothermal and isobaric, operating at 325 °C and 20 barg, i.e., the conditions at which the kinetic model was developed. Hydrogen is cofed to the reactor along with ethanol to obtain an inlet molar ratio of alcohol to hydrogen of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The reaction products are a mixture of linear and branched alcohols, aldehydes, esters, and ketones, whose composition depends on the amount of catalyst used in the simulation. These effluents are subsequently fed into a downstream hydrogenolysis reactor (R-102) to convert aldehydes, esters, and ketones into primary and secondary alcohols. In our simulation, this second reactor is designed as an equilibrium reactor operating at 200 °C based on our previous findings,9,12 where we observed that the maximum ester hydrogenolysis yields are achieved at high contact times, with convergence towards equilibrium composition when employing copper-based catalysts. The operating pressure of the reactor is decreased from 30 barg, as used elsewhere,12 to 19 barg to decrease the investment and operating costs required for compression. The equilibrium reactions included for modeling the hydrogenation reactor are presented in Table S1 in the ESI.†
1. The reaction products are a mixture of linear and branched alcohols, aldehydes, esters, and ketones, whose composition depends on the amount of catalyst used in the simulation. These effluents are subsequently fed into a downstream hydrogenolysis reactor (R-102) to convert aldehydes, esters, and ketones into primary and secondary alcohols. In our simulation, this second reactor is designed as an equilibrium reactor operating at 200 °C based on our previous findings,9,12 where we observed that the maximum ester hydrogenolysis yields are achieved at high contact times, with convergence towards equilibrium composition when employing copper-based catalysts. The operating pressure of the reactor is decreased from 30 barg, as used elsewhere,12 to 19 barg to decrease the investment and operating costs required for compression. The equilibrium reactions included for modeling the hydrogenation reactor are presented in Table S1 in the ESI.†
After the hydrogenolysis stage, the gaseous product is cooled and separated into a liquid and a gas phase in a flash drum (F-101). The gaseous fraction consisting mainly of hydrogen is compressed to 20 barg and recycled to the hydrogenolysis and Guerbet coupling reactors. The split ratio is adjusted to achieve the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) alcohol ratio of 1
alcohol ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 in the Guerbet coupling reactor and the desired H2
4 in the Guerbet coupling reactor and the desired H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio in the hydrogenolysis reactor. A purge gas stream is implemented to prevent accumulation of undesirable species within the process. The liquid fraction of the flash drum (F-101) is expanded with a pressure regulation valve (V-101) to atmospheric pressure and is directly fed to a first rectification column (S-101). The top product of this column contains mainly water and unconverted ethanol, as well as gaseous components that were dissolved in the liquid at higher pressure (e.g., H2, CO). A molecular sieve (S-102) is used to separate most of the water from the organic products, and a subsequent distillation column (S-103) is employed to maximize the separation efficiency of water and ethanol. The alcohol mixture is then pumped (P-102) upstream towards the Guerbet reactor.
ester ratio in the hydrogenolysis reactor. A purge gas stream is implemented to prevent accumulation of undesirable species within the process. The liquid fraction of the flash drum (F-101) is expanded with a pressure regulation valve (V-101) to atmospheric pressure and is directly fed to a first rectification column (S-101). The top product of this column contains mainly water and unconverted ethanol, as well as gaseous components that were dissolved in the liquid at higher pressure (e.g., H2, CO). A molecular sieve (S-102) is used to separate most of the water from the organic products, and a subsequent distillation column (S-103) is employed to maximize the separation efficiency of water and ethanol. The alcohol mixture is then pumped (P-102) upstream towards the Guerbet reactor.
The bottom product of the rectification column (S-101) contains oxygenates (e.g., alcohols, esters, ketones) with a carbon number of four or higher. This stream is then fed into a subsequent rectification column (S-104), where the top fraction containing primarily butanol, 2-methyl-1-butanol, and 2-pentanone is separated and pumped (P-103) upstream to the Guerbet reactor. The ratio of ethanol to 1-butanol in the Guerbet reactor feed stream is determined by this recycling stream. The bottom product of the column (S-104) contains diesel fuel precursors, mainly alcohols whose carbon number equals six or higher (A6+), and ketones (K7+) and esters (ES8+) in low concentration.
In this work we have investigated the influence of the following three process variables: (1) the residence time τ in the Guerbet coupling reactor, (2) the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio on the hydrogenolysis reactor, and (3) the discharge ratio of butanol in stream PR-2 leaving the separation column S-104 to understand its impact on the overall production of C6+ alcohols. Quantification of our results was performed by calculating carbon yields in the stream PR-1. For example, in eqn (7) we present the carbon yield to C6+ alcohols, which is defined as the ratio of the concentration of the carbon atoms contained in the C6+ alcohols in the stream PR-1 to the carbon concentration in the ethanol feed stream. Carbon yields for other species like esters, ketones, and aldehydes have been calculated in a similar way and reported as cumulated fractions.
ester ratio on the hydrogenolysis reactor, and (3) the discharge ratio of butanol in stream PR-2 leaving the separation column S-104 to understand its impact on the overall production of C6+ alcohols. Quantification of our results was performed by calculating carbon yields in the stream PR-1. For example, in eqn (7) we present the carbon yield to C6+ alcohols, which is defined as the ratio of the concentration of the carbon atoms contained in the C6+ alcohols in the stream PR-1 to the carbon concentration in the ethanol feed stream. Carbon yields for other species like esters, ketones, and aldehydes have been calculated in a similar way and reported as cumulated fractions.
 | (7) |
3. Results and discussion
3.1 Kinetic modeling
In the following paragraphs, we present the kinetic modeling for the Guerbet coupling chemistry using a fresh catalyst. The stability of this catalyst has been previously tested under prolonged time on stream, demonstrating sustained catalytic activity for up to 170 h. Coke formation, rather than metal sintering, was identified as the primary deactivation mechanism.10 Catalyst deactivation caused changes in carbon selectivities as demonstrated in the ESI† of our previous work. Comparable observations were reported by Guo et al.,31 who tested a similar catalyst under the here examined reaction conditions (except for a reaction pressure of 600 psi). Their findings indicate that carbon selectivity profiles remain relatively stable over time after reaching the steady state. Surface properties of our catalyst are summarized in Table 2 except for the number of copper surface sites or average particle size, which could not be counted successfully through N2O titration due to low copper load. Expanded discussion and detailed characterization of the fresh and spent catalysts are available in our previous publication.10| Property | Value |
|---|---|
| Cu loading (wt%) | 0.3 |
Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al molar ratio Al molar ratio |
2.9 |
| BET surface area (m2 g−1) | 172 |
| Pore volume (mL g−1) | 0.5 |
| Basic sites (µmol g−1) | 325 |
| Acid sites (µmol g−1) | 861 |
Ethanol oligomerization over copper catalysts supported on Mg–Al mixed oxides has been reported to produce more than 160 different species including alcohols, aldehydes, esters, ketones, olefins, paraffins, ethers, and acetals.10 The development of a kinetic model encompassing 160 species is challenging and might include species in trace quantities that are not meaningful to predict the main features of the reaction effluent. In our catalytic experiments, we have identified 60 species, where alcohols, aldehydes, esters, and ketones are the prominent functionalities as shown by the carbon balances presented in Fig. S1 (ESI†). A generalized reaction network outlining the formation of alcohol coupling products is presented in Scheme 1. As depicted, the alcohol coupling chemistry begins with the dehydrogenation of alcohols to aldehydes (R1), which then condense to form an α,β-alkenal (R2). The formation of this alkenal is the rate limiting step in the global alcohol coupling reaction.32,33 The alkenal is subsequently hydrogenated at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, forming an 2-alkenol, which subsequently undergoes a bond isomerization reaction to form 1-alkenol, ultimately tautomerizing into the saturated aldehyde.17,18 Our previous findings indicate the isomerization and keto–enol tautomerization occur rapidly yielding the apparent reaction that hydrogenates the alkenal into the saturated aldehyde (R3).11 Side reactions, such as dehydrogenative coupling and retro-aldol condensation, promoted by the presence of copper,34,35 lead to the formation of esters (R4) and ketones (R5),36,37 respectively. Finally, monomolecular dehydration of alcohols produces alkenes (R6), which are subsequently hydrogenated into alkanes (R7).
O bond, forming an 2-alkenol, which subsequently undergoes a bond isomerization reaction to form 1-alkenol, ultimately tautomerizing into the saturated aldehyde.17,18 Our previous findings indicate the isomerization and keto–enol tautomerization occur rapidly yielding the apparent reaction that hydrogenates the alkenal into the saturated aldehyde (R3).11 Side reactions, such as dehydrogenative coupling and retro-aldol condensation, promoted by the presence of copper,34,35 lead to the formation of esters (R4) and ketones (R5),36,37 respectively. Finally, monomolecular dehydration of alcohols produces alkenes (R6), which are subsequently hydrogenated into alkanes (R7).
For our model, we selected a set of 31 identified species plus 9 expected intermediates labelled as alcohols, aldehydes, esters, or ketones that were able to explain at least 90% of the carbon fed into the reactor. Alkanes and alkenes were excluded from the model, as they accounted for less than 1.3% of the carbon balance in the experiments. This allowed us to reduce the number of species considered in our model, while capturing the main components in the outlet stream composition. The reduction of the number of species in the model is beneficial to diminish the complexity of the mathematical problem but imposes the drawback that the experimental carbon balance of the selected species does not sum 100% as in the mathematical model. To overcome such shortcoming, we have normalized the composition of each species by the carbon balance that the modeled species can explain. We have opted to use this normalization approach for closing the experimental carbon balance, as it was previously used by Scheid et al.21 and Eagan et al.19 to compute gas phase mole fractions and successfully develop their kinetic models. While other approaches, such as attributing the missing carbon to an ‘unknown’ species or expanding the reaction network in Scheme 1 to predict unidentified but potentially expected long-chain species, could be considered, we believe these methods also rely on assumptions that may compromise the accuracy and reliability of the model. Dotted lines in Fig. S1 (ESI†) indicate the evolution of the normalization values as a function of the contact time for the pure ethanol feed (control experiments) and cofeed experiments. Raw data of the concentration of all the species identified in this research are presented in the ESI† (spreadsheet).
Fig. 3 displays the experimental (scattered data) and predicted (solid lines) liquid phase concentration profiles of the reactants and products as a function of the contact time for the Guebert coupling reactor. The set of kinetic parameters that reproduces the behavior of the chemistry over Cu0.01Mg2.99AlO at 325 °C and 300 psig for the proposed model is reported in Table 3 accompanied by their corresponding equilibrium constants when applicable. Backward rate constants can be calculated as kb = kf/Keq. As observed, the model reproduces with great agreement the experimental observations, with most of the data points lying within the confidence interval of the prediction (shaded area around solid lines). The agreement between the model and experiments is also displayed in (1) the spreadsheet in the ESI,† where we depict the experimental and predicted liquid phase concentration of all modeled species; and (2) the parity plot of Fig. S2 (ESI†), where the predicted carbon concentrations vs. the experimental ones of the modeled species spread over the 45° line, showing balanced errors for both sets of catalytic runs. To confirm that the reaction operated under a kinetic controlled regime, heat and mass transfer limitation calculations were carried out, as presented in Section S3 of the ESI.† The calculations indicate no significant internal diffusion limitations (Weisz–Prater = 0.004 ≪ 1) or internal temperature gradients (Prater = 2.2 × 10−5 ≪ 1).
| Reaction | Parameter |
k
f ± CIα![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05 0.05 |
K eq |
|---|---|---|---|
| 1 | k 1 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236 ± 1706 236 ± 1706 |
3.19 |
| 2 | k 2 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 ± 6334 219 ± 6334 |
0.88 |
| 3 | k 3 | 1.035 × 106 ± 1.4028 × 106 | 1.24 |
| 4 | k 4 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252 ± 10 252 ± 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 851 |
0.39 |
| 5 | k 5 | 123 ± 108 | 0.41 |
| 6 | k 6 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 986 ± 30 986 ± 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 720 |
1.00 |
| 7 | k 7 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 ± 43 996 ± 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 001 |
0.87 |
| 8 | k 8 | 123 ± 108 | 0.87 |
| 9 | k 9 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014 014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ± 192 500 ± 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 330 330 |
|
| 10 | k 10 | 759![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ± 138 300 ± 138![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
|
| 11 | k 11 | 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 ± 33 520 ± 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
|
| 12 | k 12 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732 732![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ± 477 700 ± 477![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
|
| 13 | k 13 | 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090 ± 172 090 ± 172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
|
| 14 | k 14 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761 761![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 779 100 ± 779![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 760 |
|
| 15 | k 15 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227 ± 36 227 ± 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 027 |
|
| 16 | k 16 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 582 ± 17 582 ± 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 638 |
|
| 17–23 | k 17–k23 | 1.5531 × 107 ± 2.0014 × 107 | |
| 24 | k 24 | 7209 ± 1688 | 5.41 |
| 25 | k 25 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955 ± 4083 955 ± 4083 |
9.11 |
| 26 | k 26 | 9016 ± 2252 | 30.47 |
| 27 | k 27 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 ± 3594 175 ± 3594 |
25.15 |
| 28 | k 28 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 ± 22 958 ± 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 391 |
12.91 |
| 29 | k 29 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 ± 10 895 ± 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171 171 |
10.45 |
| 30 | k 30 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ± 20 300 ± 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 908 908 |
7.97 |
| 31 | k 31 | 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 ± 128 400 ± 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
54.20 |
| 32 | k 32 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 582 ± 17 582 ± 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 638 |
5.71 |
| 33 | k 33 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031 ± 14 031 ± 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301 301 |
|
| 34 | k 34 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 ± 23 745 ± 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
|
| 35–37 | k 35–k37 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 582 ± 17 582 ± 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 638 |
|
| 38 | K adsalcohols | 274 ± 33 | |
| 39 | K adswater | 616 ± 230 | |
| 40 |
K
adsaldehydes![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ketones ketones
|
36 ± 56 | |
| 41 | K adsesters | 7807 ± 1900 |
Fig. 4 presents the ethanol conversion as a function of the contact time for both pure ethanol and cofeed experiments. Note that since butanol is a product and a reactant for the cofeed experiments, calculation of its conversion extent is challenging, and no attempts were made for this purpose. As displayed, experiments indicate that ethanol conversions in cofeed experiments are slightly higher than those in the control experiments within the first 5 h kgcat kmolgas−1 of contact time. This initial behavior is because the addition of butanol readily produces large amounts of butyraldehyde, which form a butanol/butyraldehyde-rich pool that enables new reaction pathways for coupling ethanol and acetaldehyde moieties. Interestingly, in both tested scenarios, ethanol conversion slows at higher contact times, reaching a maximum of ∼70%, consistent with previous observations from our group.11 This deceleration is attributed to the competitive adsorption of water, which impacts the adsorption frequency of reactive aldehydes required for the Guerbet coupling mechanism.38 Since aldehyde partial pressure is governed by its equilibrium with the parent alcohol, a reduced aldehyde consumption rate directly limits alcohol conversion.
Acetaldehyde and butyraldehyde concentration profiles are presented in Fig. 3(e) and (f). As depicted, acetaldehyde is readily formed from ethanol dehydrogenation over copper active sites. This dehydrogenation is observed to occur fast due to the rapid increase of acetaldehyde concentration in a short contact time. In contrast, the butyraldehyde concentration exhibits two different initial increasing rates for the cofeed and control experiments. In the control experiments, butyraldehyde is formed from aldol condensation followed by a hydrogenation, while in the cofeed experiments this aldehyde is formed from butanol dehydrogenation. Given that the apparent formation rate of butyraldehyde (the slope of the profile) in the control experiments at early contact times is lower than that of the cofeed experiments, it is concluded that butanol dehydrogenation is faster than acetaldehyde self-condensation. In our system, once butyraldehyde is formed, acetaldehyde and butyraldehyde react on the surface yielding C4–8 alcohols (c) and (d), and ketones and esters (g) and (h). The intermediate role of the linear aldehydes in the reaction network is also observed in the diagram, showing an increasing concentration profile at low contact times that peaks between 2–3 h kgcat kmolgas−1 and decreases afterwards. The exact position of the aldehyde peak depends on whether the precursor alcohol was fed into the reactor or not. Although other species such as butanol or hexanol can also be considered intermediates due to participation in dehydrogenative couplings to produce esters and ketones, their intermediate fashion is not evident within the tested contact times.
Panels (a) and (b) present the butanol concentration profiles for our experiments, exhibiting two different trends. In the control experiments it is observed that butanol concentration is continuously increasing, while in the cofeed experiments butanol concentration decreases from 4.4 M with an apparent convergence to a steady value of 3.4 M. The concentration of other alcohols is plotted in Fig. 3(c) and (d). As shown, the concentration of the profile of linear alcohols is higher than the one for their branched counterparts, demonstrating that our catalyst is more selective for the formation of linear alcohols when butanol was cofed into the system. Remarkably, the initial production rate of C6+ alcohols is faster at early contact times when butanol is cofed into the system, validating our motivation to cofeed butanol into the system and demonstrating the beneficial effects of cofeeding a blend of ethanol–butanol to obtain higher production rates of hexanol. The concentration profiles for species different to ethanol, butanol, and their corresponding aldehydes reach similar concentrations at high contact times regardless of butanol being cofed.
Analysis of the selectivity of the catalysts for linear and branched alcohols is presented in Fig. 5, which displays the relative concentration of C6 and C8 alcohols. The relative concentration from the model and experiments displays excellent agreement for C6 alcohols with some minor discrepancies for C8 alcohols. A major disagreement is observed for the ratio octanol/2-ethylhexanol in the cofeed experiments (Ccofeed8), where the trend at low contact times could not be captured by the model. Since octanol and 2-ethylbutanol were detected in lower quantities than their C6 counterparts, we indicate that the model fit the C6 alcohols better than the C8 ones. In the plot it is regarded that the relative concentration of hexanol to 2-ethylbutanol (C6 ratio) behaves similar in the cofeed and pure ethanol feed (control) experiments, leveling off at a ratio of 3. This finding suggests that feeding butanol does not affect nucleophilicity and/or electrophilicity roles in the condensation of acetaldehyde with butyraldehyde, and that at high contact times ∼75% of C6 alcohols will be hexanol. Nonetheless, a similar behavior is not observed for C8 alcohols in the control and cofeed experiments. As shown, the ratio of linear to branched alcohols in the control experiments converges to ∼2, while in the cofeed experiments the convergence is towards 1. This disparity in relative ratios of C8 alcohols is due to the fact that feeding butanol increases the production of 2-ethylhexanol, since this alcohol can also be formed from butyraldehyde self-condensation. The plot demonstrates that alcohols coupling over our catalysts form predominantly linear species rather than branched. This selectivity of linear over branched alcohols can also be regarded in the instantaneous selectivity calculated from the kinetic constants of our model. In Table 1 it is seen that reactions (10) and (11) modeling the formation of 2-hexenal and 2-ethyl-2-butenal, respectively, share the same reactants, which allows us to compute the instantaneous selectivity of the linear over the branched unsaturated aldehydes as the ratio of their kinetic constants, yielding a value of SHe=/2EBa= = 5.4. In further steps of the reaction network, the alkenals are hydrogenated into their respective aldehydes, which react to form new species like alcohols at rates that yield the results presented in Fig. 5.
As previously commented, the motivation of feeding butanol into the alcohol coupling reactor is to increase the production rates of longer chain alcohols, primarily hexanol produced from the net reaction ethanol + butanol → hexanol + H2O. Nevertheless, the coupling of the same reactants also yields 2-ethylbutanol, which is a less desirable product. Linear alcohols undergo preferably bimolecular dehydrations to ethers while branched alcohols dehydrate monomolecularly into olefins.13,15 As a reminder, the product of our global process is a blend of ethers produced through bimolecular dehydration of alcohols. Fig. 6 presents the ratio of the concentration of the linear and branched alcohols in the cofeed experiments with respect to the control experiments. As observed, the concentration of all alcohols is higher in the cofeed experiments at early contact times, as compared to the control ones, with a continuous decrease that converges asymptotically to values around 1. These results indicate then that cofeeding butanol fosters the condensation of linear alcohols or aldehydes at higher rates to produce longer chain alcohols. Noticeably, at high contact times the experiments show few increases in hexanol concentration if butanol is cofed into the reactor. For longer chain alcohols like octanol and decanol the experimental observations and the model lines fall below the dotted reference line, indicating that other reactions are consuming hexanal/octanal and acetaldehyde, which causes a decreased concentration of octanol and decanol in the final product compared to the control case. It is also observed that at long contact times the production of 2-ethylbutanol is virtually unaffected by the addition of butanol, however the final concentration of 2-ethylhexanol increased by 50% when 30 mol% butanol is fed into the reactor.
One of the consequences of cofeeding butanol is the promotion of dehydrogenative coupling reactions between butanol/butyraldehyde and aldehydes/alcohols. Fig. S3 (ESI†) presents a comparison of the concentration of the esters produced from ethanol and butanol coupling for the studied cofeed scenario relative to the pure ethanol feed. As observed, feeding less ethanol into the system caused a reduction of ∼50% in the mole concentration of ethyl acetate compared to the reference scenario. This is due to the lower amount of acetaldehyde generated in the cofeed experiments that limited the coupling of ethanol with acetaldehyde. In contrast, the opposite trend is observed for butyl butyrate, whose concentration in the final product increased by at least 150% due to the presence of butanol in the feed. The concentration ratio of unsymmetrical esters like butyl acetate and ethyl butyrate indicates that at early contact times there exist promotion of the dehydrogenative coupling reaction that forms additional C6 esters in the cofeed scenario. Experiments also reveal that the relative butyl acetate concentration converges towards a value slightly higher than one, which indicates that even at high contact times the production of butyl acetate is more promoted than the production of ethyl butyrate when butanol is cofed. The relative concentration of ethyl butyrate to butyl acetate in the cofeed and control experiments is presented in Fig. S4 (ESI†). As observed, ethyl butyrate is formed in higher concentration than butyl acetate in the control experiments. Nonetheless, in the cofeed experiments both esters are observed to have virtually the same concentration at most of the contact times. The explanation for this resides in the fact that butyl acetate is formed more easily in cofeed than in the control experiments. Formation of butyl acetate requires the dehydrogenative coupling of butanol and acetaldehyde, which are easily furnished in the cofeed experiments at low contact times, while for the control experiments butanol formation requires previous butyraldehyde synthesis through acetaldehyde condensation. As such, in cofeed experiments the production of butyl acetate is observed to occur at comparable rates as ethyl butyrate. Fig. S5 (ESI†) presents the ratio of the reaction quotient (Q) to the equilibrium constant (Keq) for alcohol dehydrogenation and dehydrogenative coupling, as predicted by our kinetic model. As observed, C4+ alcohols rapidly establish equilibrium with their respective aldehydes and hydrogen. In contrast, ethanol remains far from equilibrium, maintaining the driving force that favors acetaldehyde formation. Similarly, the model indicates that dehydrogenative coupling reactions of alcohols and aldehydes are also far from equilibrium, with a Q/Keq ratio lower than 0.1. This suggests that the reaction system still retains significant chemical potential for ester production.
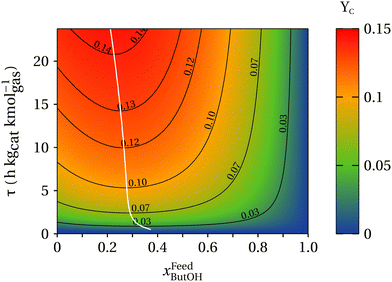
Of particular interest is understanding the effect of an ethanol–butanol cofeed for the linear alcohols and the respective aldehyde carbon yields as described by eqn (8). Fig. 7 presents a heat map of the carbon yield of linear alcohols + aldehydes as a function of the contact time and the mole fraction of butanol in the feed of the reactor. As observed, the model indicates within the analyzed range of contact times, the maximum amount of carbon atoms for the linear alcohols/aldehydes is ∼14% of the carbon fed into the system. Remarkably, it is observed that at a constant contact time the carbon yield to linear species decreases after xFeedButOH ∼ 25%, which comes from a reduction in the concentration of acetaldehyde needed to proceed with the aldol-condensation towards linear species. Fig. 7 also suggests that there exists a region between xFeedButOH = 0–30% and high contact times that maximizes the production of linear alcohols + aldehydes. Over the heat map a white line has been drawn and represents (∂YC/∂xFeedbutOH)τ = 0. This line indicates the maximum concentration of diesel fuel precursors that can be achieved at constant contact time. The trajectory of the drawn line over the heatmap indicates that cofeeding between 23–28 mole% of butanol is the optimal blend ratio to maximize the advantageous effect of butanol cofeeding, particularly in the production of linear and branched C6+ alcohols and aldehydes.
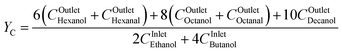 | (8) |
3.2 Process modeling
The process simulation for diesel fuel production has been carried out in previous works,8,9 where a conversion reactor was used to calculate the composition in the outlet stream of the Guerbet coupling reactor. The implementation of a conversion reactor implies that experiments must be carried out at a fixed conversion for the respective feed composition to obtain an appropriate product composition. The influence of the catalyst quantity and residence time must therefore always be determined separately and cannot be predicted by simple variations in Aspen Plus. Nevertheless, introduction of a kinetic model to simulate the reactor's behavior allows the investigation with more flexibility of the influence of variables such as residence time and feed composition on the performance of the overall system (product quantities, energy demands, etc.).In preliminary simulations, the Guerbet coupling kinetic model was implemented in a plug-flow reactor in Aspen Plus V14 as a custom model. Converged simulations were obtained for simulations feeding pure ethanol and the 70–30% ethanol–butanol cofeed, achieving the same product composition as in the model presented in the kinetic modeling section. This demonstrates the feasibility of integrating the Guerbet coupling kinetic model in a process simulation. Our kinetic model was then embedded in the simulation process presented in Fig. 2, which consists of the Guerbet reaction, a downstream hydrogenolysis reactor, and the product separation units. This simulation elucidated the impact of process variables such as the resident time and the ethanol–butanol cofeed (varying the butanol recycling ratio) in the Guerbet coupling reactor, as well as the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio in the hydrogenolysis reactor. The influence of the contact time in the coupling reactor was assessed by changing the amount of catalyst in the reactor, while the impact of the H2
ester ratio in the hydrogenolysis reactor. The influence of the contact time in the coupling reactor was assessed by changing the amount of catalyst in the reactor, while the impact of the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio fed into the hydrogenolysis reactor over the product yields is assessed by studying specific ratios of 400
ester ratio fed into the hydrogenolysis reactor over the product yields is assessed by studying specific ratios of 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 200
1, 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 100
1, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
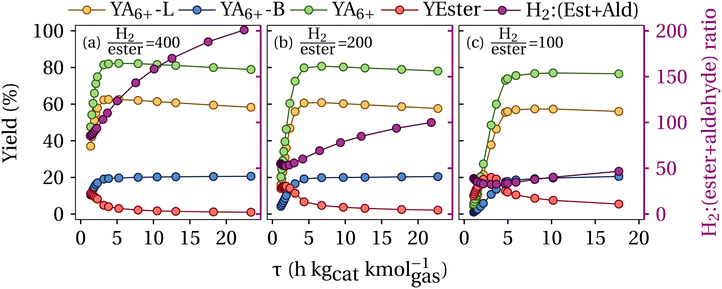
Fig. 8 shows the simulation results of the process depicted in Fig. 2. As observed in panel (a), a maximum yield of 82.2% (green circles) for C6+ alcohols in the final product of the process can be achieved when operating at a contact time of 5.23 h kgcat kmolgas−1 and a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio of 400
ester ratio of 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the Guerbet and hydrogenolysis reactors, respectively. The ester yield under such conditions is calculated as 3.6%. In our process, the ester yield needs to be lower than 5% to decrease their negative effect in the downstream etherification reactor.12,13 In Fig. 8(b) it is observed that reduction of the H2
1 in the Guerbet and hydrogenolysis reactors, respectively. The ester yield under such conditions is calculated as 3.6%. In our process, the ester yield needs to be lower than 5% to decrease their negative effect in the downstream etherification reactor.12,13 In Fig. 8(b) it is observed that reduction of the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio to 200
ester ratio to 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the hydrogenolysis reactor increases the ester yield up to 4.7% at the assessed contact time, going even higher than 5% at the 100
1 in the hydrogenolysis reactor increases the ester yield up to 4.7% at the assessed contact time, going even higher than 5% at the 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio regardless of the contact time as presented in panel (c). Remarkably, the maximum yield of C6+ alcohols also decreases with reduction of the H2
1 ratio regardless of the contact time as presented in panel (c). Remarkably, the maximum yield of C6+ alcohols also decreases with reduction of the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio, showing a maximum value of 75.6% at 6 h kgcat kmolgas−1 of contact time in the alcohol coupling reactor and a H2
ester ratio, showing a maximum value of 75.6% at 6 h kgcat kmolgas−1 of contact time in the alcohol coupling reactor and a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio of 100
ester ratio of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the hydrogenation unit.
1 in the hydrogenation unit.
Additional evaluation of the process performance is obtained by assessing the relative selectivity of linear to branched alcohols in the outlet stream of the presented technology. Fig. 9 displays the relative selectivity of linear to branched C6 and C8 alcohols. As observed in all cases, short residence times in the coupling reactor favors the production of hexanol over 2-ethylbutanol, whilst the opposite effect is seen for 1-octanol and 2-ethylhexanol. Increasing the contact time in the coupling reactor causes a decrease in the ratio of the C6 alcohols and increases the one of their C8 analogue. In general, these relative selectivities change within the first 4.5 h kgcat kmolgas−1 regardless of the assessed scenario, plateauing between 4.3–3.5 and 1.1–1.5 for the C6 and C8 ratios, respectively.
In a second process evaluation phase, the influence of the amount of catalyst and the discharging of butanol from the separation column S-104 (see Fig. 2) on the alcohol product yields is considered. The top product stream of the column S-104 is split into the stream PR-2 and the recycling stream fed back to the Guerbet coupling reactor. The split percentage was assessed between 0 and 20%, where 0 represents no flow through PR-2. YA4-PR-2 is indicated here as the yield of butanol in the discharged stream at the top product of the separation column S-104. The yields of the higher alcohols and esters, as well as the cumulated yield of alcohols higher than carbon number 6 (YA6+) and the ethanol to butanol ratio upstream of the Guerbet coupling reactor are given for a low (15 tons) and high (60 tons) catalyst load and the discharge ratio of 0 to 20% in Fig. 10, respectively.
 | ||
Fig. 10 Alcohols, esters, and aldehydes yields, calculated according to eqn (8), as well as the ethanol to butanol ratio and cumulated C6+ yield in the product stream P-103 for a catalyst load of (a) and (b) 15 tons and (c) and (d) 60 tons and a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio of 400 ester ratio of 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. YA4-PR-2: carbon yield of butanol in stream PR2, YA6+-L: carbon yield of C6+ linear alcohols, YA6+-B: carbon yield of C6+ branched alcohols, YEst: carbon yield of esters, and YA6+: carbon yield of C6+ alcohols. Scattered data represent the results from the simulated scenarios and the continuous line is drawn to guide the eyes. 1. YA4-PR-2: carbon yield of butanol in stream PR2, YA6+-L: carbon yield of C6+ linear alcohols, YA6+-B: carbon yield of C6+ branched alcohols, YEst: carbon yield of esters, and YA6+: carbon yield of C6+ alcohols. Scattered data represent the results from the simulated scenarios and the continuous line is drawn to guide the eyes. | ||
As presented in Fig. 10(b), for a low catalyst load of 15 tons the butanol discharge (between 0–20%) in the distillation column S-104 has no significant impact on the overall A6+ yield, remaining stable within 45–49% and exhibiting its maximum at a discharge ratio of 2.5%. Nevertheless, stronger variations for the ethanol–butanol feed ratio were observed, with ratios ranging between 65 and 82%. It is also observed in Fig. 10(a), that the formation of esters decreases for a higher butanol discharge ratio and undershoots the desired 5% level at a butanol discharge ratio higher than 5%.
The yields for a higher catalyst load of 60 tons are presented in Fig. 10(c) and (d). It is observed that the butanol discharge has a negative impact on the A6+ yield, resulting in a maximum of 81% without butanol discharge, and decreasing to 61% at a discharge ratio of 20%. Remarkably, the requirement of limiting the yield of esters to maximum 5% is achieved for all butanol discharge ratios. In this view, at higher contact times no butanol discharge in S-104 increases the yield of C6+ alcohols.
4. Conclusions
A model for the kinetics of alcohols coupling with Guerbet chemistry over a Cu0.01Mg2.99AlOx catalyst was developed. Catalytic experiments between 0–21.6 h kgcat kmolgas−1 were performed in a gas phase continuous flow reactor at 325 °C and 300 psig by feeding either pure ethanol or an ethanol–butanol blend under a hydrogen atmosphere. Experimentally at least 60 different chemical species were identified in the reaction pool, from which only 31 were included in our kinetic model explaining at least 90% of the identifiable carbon in the product. The generated model captures the kinetic behavior of most of the species, demonstrating its ability to represent concentration profiles for ethanol–butanol blends ranging between 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and 70
0 and 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mole% and contact times up to 21.6 h kgcat kmolgas−1. The model effectively captures the catalyst's tendency to favor the production of linear alcohols over branched ones. The linearity of alcohols is crucial in diesel fuel production, as linear alcohols preferentially undergo bimolecular dehydration to form ethers, whereas branched alcohols favor monomolecular dehydration. Maximizing the production of linear alcohol backbones enhances diesel fuel yield in this process. Cofeeding butanol accelerates the production rate of longer chain alcohols at early contact times. At higher contact times, the yield of linear alcohols resembles those obtained in the control case for a single pass Guerbet coupling reactor. Implementation of the Guerbet coupling kinetic model in Aspen Plus was feasible and allowed a more detailed process simulation of the production of diesel fuel precursors. The influence of the feed compositions and the contact time in the Guerbet reactor on the product composition of the outlet stream was investigated by means of sensitivity analyses. A hydrogenolysis reactor was modeled in the simulation to hydrogenate the esters. Investigation of the H2
30 mole% and contact times up to 21.6 h kgcat kmolgas−1. The model effectively captures the catalyst's tendency to favor the production of linear alcohols over branched ones. The linearity of alcohols is crucial in diesel fuel production, as linear alcohols preferentially undergo bimolecular dehydration to form ethers, whereas branched alcohols favor monomolecular dehydration. Maximizing the production of linear alcohol backbones enhances diesel fuel yield in this process. Cofeeding butanol accelerates the production rate of longer chain alcohols at early contact times. At higher contact times, the yield of linear alcohols resembles those obtained in the control case for a single pass Guerbet coupling reactor. Implementation of the Guerbet coupling kinetic model in Aspen Plus was feasible and allowed a more detailed process simulation of the production of diesel fuel precursors. The influence of the feed compositions and the contact time in the Guerbet reactor on the product composition of the outlet stream was investigated by means of sensitivity analyses. A hydrogenolysis reactor was modeled in the simulation to hydrogenate the esters. Investigation of the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio in the hydrogenolysis reactor and its impact on the yield of alcohols was also performed.
ester ratio in the hydrogenolysis reactor and its impact on the yield of alcohols was also performed.
The optimized operating conditions of the Guerbet coupling reactor include a contact time of 5.23 kgcat kmolgas−1, where the C6+ alcohols yield is maximized at 82.2%. Partial discharge of the butanol leaving the S-104 separation stage has no positive influence on the C6+ alcohols yield, whereby all the butanol is recycled upstream of the Guerbet reactor. A hydrogenolysis reactor needs to be incorporated and operated with a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratio of 400
ester ratio of 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to achieve an ester yield of 3.6%, which is below the permissible limit of 5%. Lower H2
1 to achieve an ester yield of 3.6%, which is below the permissible limit of 5%. Lower H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ester ratios lead to a shift in terms of higher contact times, which result in a lower C6+ alcohol yield. The kinetic model developed herein provides a good basis for future process optimization and techno-economic evaluations.
ester ratios lead to a shift in terms of higher contact times, which result in a lower C6+ alcohol yield. The kinetic model developed herein provides a good basis for future process optimization and techno-economic evaluations.
Author contributions
JEC: experiments, data interpretation, kinetic modeling programming and fitting, paper conceptualization, writing; CM: simulations, data interpretation, kinetic modeling programming and fitting, paper conceptualization, writing; EV: experiments; ML: paper conceptualization, funding acquisition, writing, project managing, GWH: paper conceptualization, funding acquisition, writing, project managing. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Data availability
All the data for this article are available in the main text and the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported and financed by the U.S. Department of Energy – Vehicle Technology Office (DOE-VTO), based upon work supported by the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under the Bioenergy Technologies Office, Co-optimization of Fuels and Engines (Co-optima) initiative award number DE-EE0008480. The views expressed in this manuscript do not necessarily represent the views of the U.S. Department of Energy or the United States Government. This work was conducted and financially supported as part of a Marshall Plan grant in cooperation between Montanuniversität Leoben (Austria) and the University of Wisconsin-Madison (U.S.A.).References
- Renewable Fuels Association, 2024 Ethanol Industry Outlook, Renewable Fuels Association, 2024.
- J. E. Anderson, U. Kramer, S. A. Mueller and T. J. Wallington, Energy Fuels, 2010, 24, 6576–6585 CrossRef CAS.
- P. Iodice and A. Senatore, Influence of ethanol-gasoline blended fuels on cold start emissions of a four-stroke motorcycle. Methodology and results, Report 0148-7191, SAE Technical Paper, 2013.
- C. Johnson, K. Moriarty, T. Alleman and D. Santini, History of Ethanol Fuel Adoption in the United States: Policy, Economics, and Logistics, National Renewable Energy Lab. (NREL), Golden, CO (United States), 2021 Search PubMed.
- M. Kah, S. Lang, J. Chiu and H. X. Wong, Forecasts of electric vehicle penetration and its impact on global oil demand, Columbia University Center on Global Energy Policy, 2022 Search PubMed.
- ExxonMobil, ExxonMobil Global Outlook: Our view to 2050, https://corporate.exxonmobil.com/what-we-do/energy-supply/global-outlook/energy-demand, (accessed 08/22/2024).
- N. M. Eagan, M. D. Kumbhalkar, J. S. Buchanan, J. A. Dumesic and G. W. Huber, Nat. Rev. Chem., 2019, 3, 223–249 CrossRef CAS.
- J.-M. Restrepo-Flórez, P. Cuello-Penaloza, E. Canales, D. Witkowski, D. A. Rothamer, G. W. Huber and C. T. Maravelias, Sustainable Energy Fuels, 2023, 7, 693–707 RSC.
- J.-M. Restrepo-Flórez, J. E. Chavarrio, E. Canales, D. Witkowski, S. Subramanian, P. Cuello-Peñaloza, D. A. Rothamer, C. T. Maravelias and G. W. Huber, Sustainable Energy Fuels, 2025, 9, 98–114 RSC.
- P. A. Cuello-Penaloza, R. G. Dastidar, S.-C. Wang, Y. Du, M. P. Lanci, B. Wooler, C. E. Kliewer, I. Hermans, J. A. Dumesic and G. W. Huber, Appl. Catal., B, 2022, 304, 120984 CrossRef CAS.
- P. A. Cuello-Penaloza, J. Chavarrio-Cañas, Y. Du, M. P. Lanci, D. A. Maedke, J. A. Dumesic and G. W. Huber, Appl. Catal., B, 2022, 318, 121821 CrossRef CAS.
- J. E. Chavarrio, K. Kirkendall-Jones, R. G. Dastidar and G. W. Huber, ACS Catal., 2024, 14, 11411–11424 CrossRef CAS.
- E. Canales, S. C. Hower, D. P. Li, A. Tambe, D. Rothamer and G. W. Huber, Sustainable Energy Fuels, 2024, 8, 3036–3047 RSC.
- E. Canales, D. Witkowski, D. Rothamer and G. W. Huber, Energy Fuels, 2024, 38, 19611–19625 CrossRef CAS.
- N. M. Eagan, B. M. Moore, D. J. McClelland, A. M. Wittrig, E. Canales, M. P. Lanci and G. W. Huber, Green Chem., 2019, 21, 3300–3318 RSC.
- N. M. Eagan, M. P. Lanci, G. W. Huber, P. A. C. Penaloza and J. S. Buchanan, US Pat., US20210363085A1, 2021 Search PubMed.
- C. R. Ho, S. Shylesh and A. T. Bell, ACS Catal., 2016, 6, 939–948 CrossRef CAS.
- Z. D. Young, S. Hanspal and R. J. Davis, ACS Catal., 2016, 6, 3193–3202 CrossRef CAS.
- N. M. Eagan, M. P. Lanci and G. W. Huber, ACS Catal., 2020, 10, 2978–2989 CrossRef CAS.
- T. Tsuchida, S. Sakuma, T. Takeguchi and W. Ueda, Ind. Eng. Chem. Res., 2006, 45, 8634–8642 CrossRef CAS.
- A. J. Scheid, E. Barbosa-Coutinho, M. Schwaab and N. P. G. Salau, Ind. Eng. Chem. Res., 2019, 58, 12981–12995 CrossRef CAS.
- I. Nezam, L. Peereboom and D. J. Miller, Reactions, 2020, 1, 102–114 CrossRef.
- P. H. Galebach, D. J. McClelland, N. M. Eagan, A. M. Wittrig, J. S. Buchanan, J. A. Dumesic and G. W. Huber, ACS Sustainable Chem. Eng., 2018, 6, 4330–4344 CrossRef CAS.
- J. T. Kozlowski and R. J. Davis, ACS Catal., 2013, 3, 1588–1600 CrossRef CAS.
- R. Burks, Jr. and H. Adkins, J. Am. Chem. Soc., 1940, 62, 3300–3302 CrossRef.
- P. J. Linstrom and W. G. Mallard, J. Chem. Eng. Data, 2001, 46, 1059–1063 CrossRef CAS.
- (a) H. Y. Afeefy, J. F. Liebman and Stephen E. Stein, Neutral Thermochemical Data, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, US, https://doi.org/10.18434/T4D303, (retrieved February 25, 2025); (b) D. R. Burgess, Jr., Thermochemical Data, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, US, https://doi.org/10.18434/T4D303, (retrieved February 25, 2025); (c) Glushko Thermocenter, Russian Academy of Sciences, Moscow, Entropy and Heat Capacity of Organic Compounds, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, US, https://doi.org/10.18434/T4D303, (retrieved February 25, 2025).
- M. W. Chase, C. A. Davies, J. R. Downey, D. J. Frurip, R. A. McDonald and A. N. Syverud, Database, 1985 Search PubMed.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, 95th edn, 2014 Search PubMed.
- Chemical Properties Handbook, ed. C. L. Yaws, McGraw-Hill Education, New York, 1st edn, 1999 Search PubMed.
- M. F. Guo, M. J. Gray, H. Job, C. Alvarez-Vasco, S. Subramaniam, X. Zhang, L. Kovarik, V. Murugesan, S. Phillips and K. K. Ramasamy, Green Chem., 2021, 23, 8030–8039 RSC.
- E. F. de Souza, H. P. Pacheco, N. Miyake, R. J. Davis and F. S. Toniolo, ACS Catal., 2020, 10, 15162–15177 CrossRef CAS.
- T. L. Jordison, C. T. Lira and D. J. Miller, Ind. Eng. Chem. Res., 2015, 54, 10991–11000 CrossRef CAS.
- J. Li, L. Lin, Y. Tan, S. Wang, W. Yang, X. Chen, W. Luo and Y.-J. Ding, ChemCatChem, 2022, 14, e202200539 CrossRef CAS.
- Z. Sun, A. Couto Vasconcelos, G. Bottari, M. C. A. Stuart, G. Bonura, C. Cannilla, F. Frusteri and K. Barta, ACS Sustainable Chem. Eng., 2017, 5, 1738–1746 CrossRef CAS.
- M. Neurock, Z. Tao, A. Chemburkar, D. D. Hibbitts and E. Iglesia, Faraday Discuss., 2017, 197, 59–86 RSC.
- M. E. Sad, M. Neurock and E. Iglesia, J. Am. Chem. Soc., 2011, 133, 20384–20398 CrossRef CAS PubMed.
- D. D. Petrolini, N. Eagan, M. R. Ball, S. P. Burt, I. Hermans, G. W. Huber, J. A. Dumesic and L. Martins, Catal. Sci. Technol., 2019, 9, 2032–2042 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: (1) Mathematical development of the kinetic model, transport limitation calculations, and comparison of experimental and modeled trends (pdf). (2) Experimental and modeled concentration profiles for alcohol coupling, reaction matrix, and physicochemical properties used in model development (spreadsheet). See DOI: https://doi.org/10.1039/d5ey00045a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |

![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) aldehyde + H2
aldehyde + H2