Novel coal fly ash–chitosan composite for highly efficient, cost-effective and stable removal of lead and chromium from industrial wastewater

Abstract

In the present study, a novel and economical adsorbent was synthesized from a coal fly ash–chitosan composite to remove Pb²⁺ and Cr⁶⁺ from aqueous solutions. The characterization of the adsorbent under optimal conditions revealed that it was mesoporous and rich in different functional groups, which enhanced its adsorption properties. The optimal conditions for the adsorption process were achieved at three levels. At the first level, the optimal conditions for fly ash calcination (300 °C for 2 h), H₃PO₄ concentration (0.4 mol L⁻¹), MFA–CS ratio (3 : 1), and effective morphology (nanopowder) for Pb²⁺ and Cr⁶⁺ removal were achieved. At the second level, response surface methodology achieved adsorption capacities of 339.27 mg g⁻¹ for Pb²⁺ removal and 242.84 mg g⁻¹ for Cr⁶⁺ removal under optimal conditions. The third level involved pH standardization, which further enhanced the adsorption capacities to 352.19 mg g⁻¹ for Pb²⁺ removal and 265.13 mg g⁻¹ for Cr⁶⁺ removal. These results were well fitted by the pseudo-second-order kinetic and Langmuir isotherm models, demonstrating that the adsorption progressed via monolayer chemisorption. Removal efficiencies of 86.78% and 67.09% were obtained for Pb²⁺ and Cr⁶⁺, respectively, during their simultaneous removal. Thermodynamic studies confirmed the spontaneity of the adsorption process. The adsorbent demonstrated reusability, retaining its performance over 15 regeneration cycles. In column studies, maximum adsorption capacities of 255.61 mg g⁻¹ for Pb²⁺ and 42.08 mg g⁻¹ for Cr⁶⁺ were achieved, described well by the Thomas model. This cost-effective adsorbent, driven by ion exchange and surface complexation mechanisms, holds significant promise for wastewater treatment.

---

Water impact

This work explores the development of a cost-effective, green, efficient and stable adsorbent composite from industrial waste (coal fly ash) to remove heavy metals from industrial waste water. This work involves dual advantages of waste valorization and environmental remediation. This study paves the way for enhanced sustainability through circular economy and water recovery.

1. Introduction

Heavy metals in industrial wastewater, such as mercury, lead, chromium, and copper, pose significant health risks, including organ damage, neurological disorders, and developmental issues, to humans when present beyond permissible limits (Fig. S1†). Lead (Pb²⁺) and chromium (Cr⁶⁺) removal was selected for this study considering their high toxicity and frequent occurrence in industrial effluents from sources such as battery manufacturing, mining, electroplating, and tanning.¹ Compared with many other heavy metals, Pb²⁺ and Cr⁶⁺ pose a greater risk to human health and the environment because of their high severe toxicological effects.² These metals are particularly harmful, and their concentrations exceeding permissible limits (0.05 mg L⁻¹ for Pb²⁺ and Cr⁶⁺) are associated with serious health issues, including neurological damage and cancer. Their widespread use, environmental persistence, and elevated health risks make them priority pollutants, underscoring the importance of their effective removal for public and environmental health.

Lead and chromium, commonly released by industries such as battery manufacturing, mining, electroplating, and tanning, are particularly harmful, with levels exceeding their permissible limits (0.05 mg L⁻¹ for Pb²⁺ and Cr⁶⁺) leading to serious health effects such as neurological damage and cancer, making their removal essential for public health and environmental protection.¹ Common methods for removing lead and chromium from wastewater include chemical precipitation and membrane filtration; however, adsorption is preferred because of its simplicity, cost-effectiveness, and high efficiency in targeting a wide range of metal ions. Unlike other methods, adsorption does not generate harmful by-products and can be easily regenerated for reuse, making it a sustainable and eco-friendly solution for heavy metal elimination.^3,4

Fly ash, a residual material from coal combustion, is widely recognized as a cost-effective and abundant adsorbent with favourable properties including high surface area and porous morphology, which enhance its suitability for wastewater treatment applications.² Chitosan, a naturally derived biopolymer from chitin, is biodegradable and possesses abundant functional groups (–NH₂, –OH, –COOH, etc.) that contribute to its strong affinity toward heavy metals via mechanisms such as ion-exchange and complexation.⁵ When combined, fly ash and chitosan form a composite that benefits from both the mechanical stability and porosity of fly ash and the functional activity of chitosan, resulting in an efficient, sustainable, and cost-effective material for the remediation of toxic metals.⁶ Recent studies have highlighted the promising capabilities of fly ash–chitosan composites in removing heavy metals from aqueous systems. For instance, a fly ash-coated chitosan composite in a ratio of 8/1 achieved a Cr⁶⁺ adsorption capacity of 36.22 mg g⁻¹, with the removal mechanism primarily driven by ion exchange between Cr⁶⁺ species and the protonated amino groups on chitosan, supported by the porous fly ash structure.⁷ In another study, an EDTA-modified fly ash–chitosan composite exhibited a maximum Pb²⁺ adsorption capacity of 2.5 mg g⁻¹, where metal removal was attributed to surface complexation facilitated by EDTA groups, although the overall capacity was limited by reduced surface accessibility.⁶ A zeolite adsorbent synthesized from coal fly ash demonstrated an exceptional Pb²⁺ adsorption capacity of 500 mg g⁻¹, suggesting that thermal activation and aluminosilicate restructuring significantly enhanced the surface functionality and facilitated monolayer chemisorption governed by specific binding interactions.⁸ In soil-contaminated water systems, a chitosan-coated fly ash-supported biochar composite in a ratio of 4/1 achieved 33.21% Cr⁶ removal⁺, with the moderate efficiency probably influenced by complexity and the presence of competing ions in the soil leachate.⁹ Furthermore, a chitosan biopolymer supported on alkali-activated fly ash achieved a Pb²⁺ removal efficiency of 98%, which was attributed to the increased surface basicity and pore development during alkali treatment that improved electrostatic attraction and metal ion diffusion.¹⁰ Chitosan coating on ceramic alumina was effective in removing Cr⁶⁺, achieving a high capacity of 153.85 mg g⁻¹ via monolayer adsorption, as indicated by Langmuir isotherm fitting, emphasizing the importance of uniform active sites for heavy metal uptake.¹¹ A chitosan–fly ash composite cross-linked with tripolyphosphate showed a maximum capacity of 165.8 mg g⁻¹ for reactive red 120 dye at 45 °C, with the Freundlich isotherm fitting indicating multilayer adsorption onto a heterogeneous surface, and chemical crosslinking was noted to enhance the mechanical stability of the composite.¹² A carbonized zeolite/chitosan composite synthesized via pyrolysis at 500 °C demonstrated adsorption capacities of 111.35 mg g⁻¹ for Cu²⁺ and 104.75 mg g⁻¹ for Cr⁶⁺, with optimal performance observed at pH 8.1 and 9.6, respectively. The kinetic data followed pseudo-second-order behaviour, suggesting chemisorption as the dominant rate-limiting mechanism.¹³ These developments highlight the potential of the fly ash–chitosan composite as an efficient and sustainable adsorbent for the removal of heavy metals from wastewater.

The majority of studies on heavy metal removal have been conducted using batch systems, which are valuable for preliminary assessments but do not accurately represent column operations relevant to industrial applications. The column studies are essential for understanding real-time adsorption performance, breakthrough behaviour, and scalability. A few researchers have investigated the column adsorption to gain insights into the removal mechanisms and regeneration behaviour. For example, the breakthrough curves for Pb²⁺, Cr²⁺, Cu²⁺, and Ni²⁺ removal using chitosan-based adsorbents were modelled using the Thomas, Adams–Bohart, and Yoon–Nelson equations, with effective regeneration achieved using 0.1 mol dm⁻³ nitric acid under dynamic conditions.¹⁴ A novel nanofiltration membrane composed of vinyl resin (VR), cellulose nanofibrils (CNF), and titanium alpha aluminate (TAAL) nanoparticles for efficient removal of methylene blue (MB) from industrial wastewater achieved a remarkable 98.6% removal efficiency for 30 ppm MB dye, with a maximum adsorption capacity of 125.8 mg g⁻¹.¹⁵ Although the study focused on dye removal, it exemplifies the growing interest in dynamic systems and the potential for developing advanced, generable materials for column applications. In another study, amidoxime chelating resin was tested at a flow rate of 1.0 mL min⁻¹, with breakthrough volumes recorded at 190 mL for Cu²⁺, 150 mL for Ni²⁺, and 80 mL for Pb²⁺. The resin retained over 85% of its initial adsorption capacity after five regeneration cycles using 0.2 M HNO₃.¹⁶ Similarly, a granular activated carbon derived from coconut shell was employed for Pb²⁺ removal. Batch studies were initially used to screen adsorbents before transitioning to column tests, which showed that breakthrough time and capacity were influenced by bed height, hydraulic loading rate, and initial concentration. The spent adsorbent was successfully regenerated using HNO₃.¹⁷ Pumice and brown coal were also examined for Cr³⁺ and Cr⁶⁺ removal, with optimum performance observed at a flow rate of 5 mL min⁻¹ and significant effects of pH, concentration, and bed height on adsorption capacity.¹⁸ Despite these valuable contributions, comprehensive studies on heavy metal removal in the column mode using low-cost, eco-friendly, and regenerated adsorbents are still limited. This highlights a significant gap and emphasizes the need for further investigation into column studies to enable practical, scalable, and sustainable water treatment solutions.

This study develops a novel H₃PO₄-modified fly ash–chitosan composite (MFA–CS) aimed at the efficient removal of Pb²⁺ and Cr⁶⁺ from wastewater, employing a hierarchical three-level optimization strategy including RSM to maximize the adsorption capacity. Comprehensive thermo-kinetic analyses using conventional and non-conventional models, column adsorption experiments with breakthrough curve modelling, and detailed mechanistic investigations were also conducted. Additionally, the composite's performance was evaluated for simultaneous removal of multiple heavy metals, reflecting real-world wastewater conditions. Cost analysis was also incorporated to assess the economic feasibility of the adsorption process, providing practical insights into scalability and application potential. The study further evaluated the adsorbent stability over 15 regeneration cycles, offering key insights into its durability and reusability. By addressing these critical aspects, this research contributes significantly to the development of an effective, robust, and sustainable adsorbent for heavy metal remediation in wastewater treatment.

2. Materials and experimental methods

2.1 Chemicals and reagents

Phosphoric acid (85% purity), lead acetate trihydrate (99% purity, AR grade), potassium dichromate (99.9% purity, AR grade), sodium hydroxide pellets (97% purity), and chitosan (high molecular weight, 90% degree of deacetylation) were procured from Sisco Research Laboratories Pvt. Ltd. (SRL). Hydrochloric acid (35–37% purity, AR grade) was procured from Finar company. Sulphuric acid (98% purity, AR grade) and acetic acid (99.5% assay) were acquired from SDFCL company. Nitric acid (70% purity, AR grade) was obtained from Qualigens company. The use of high-purity reagents ensures reproducibility and aligns with recent standardization practices reported in the literature.¹⁹

2.2 Preparation method of MFA–CS adsorbent

The coal fly ash was initially washed thoroughly and then subjected to oven drying at 110 °C to obtain dried coal fly ash. The dried fly ash was then subjected to calcination in a muffle furnace at an optimum temperature of 300 °C for 2 h, followed by washing and drying. A total of 2 g of the calcined fly ash was then soaked in a H₃PO₄ acid solution (0.4 mol L⁻¹) for 26 h followed by washing and drying. The resulting material was designated as modified fly ash (MFA). Then, 3 g of chitosan was added into 150 ml of CH₃COOH (3% v/v) solution. This solution underwent orbital shaking for 12 h to produce a uniform gel. The MFA was then incorporated into the chitosan solution at an optimum ratio of 3/1 (MFA : CS) and stirred for 24 h to ensure homogeneity. Three morphological forms of MFA–CS were synthesized, and are illustrated in Fig. 1. For the nanopowder, a NaOH solution (3.0 g per 100 mL H₂O) was added to the MFA–CS solution to induce precipitation, followed by drying and grinding. Beads were formed by introducing the MFA–CS solution dropwise into NaOH using a syringe, followed by retaining the hydrogel beads in the solution for 26 h, washing and drying. For film preparation, the homogeneous MFA–CS solution was poured into a Petri dish and left to dry at room temperature for 48 h to form a thin film. The concise synthesis protocols were referred from the study of treatment of oily produced water using coagulant mixtures.²⁰

Fig. 1 Process flow for MFA–CS production.

2.3 Analytical and characterization equipment

Heavy metal concentrations in the solution were analysed by Atomic Absorption Spectroscopy (AAS) (Shimadzu, Japan) at wavelengths of 324.8 nm for Pb²⁺ and 357.9 nm for Cr⁶⁺. The thermal stability and decomposition behaviour of the adsorbent were assessed by Thermogravimetric Analysis (TGA) (Shimadzu, Japan) at a heating rate of 5 °C min⁻¹ over a temperature range of 30–1000 °C. The pore volume, surface area, and pore diameter of the adsorbent were measured using the Brunauer–Emmett–Teller (BET) method (Microtrac Bel, Japan), which records nitrogen gas adsorption and desorption at various relative pressures to generate adsorption and desorption isotherms. Functional groups present on the adsorbent surface were identified by Fourier Transform Infrared (FTIR) spectroscopy (Jasco, Japan) within the wavenumber range of 4000–400 cm⁻¹. The surface morphology and microstructural features of the MFA–CS composite before and after adsorption were examined by field emission scanning electron microscopy (FE-SEM) (FEI, USA). The elemental composition and distribution across different surface locations were determined by energy-dispersive X-ray (EDX) spectroscopy (Oxford Instruments, UK). The phase identification and crystallite size of MFA–CS were analysed using an X-ray powder diffractometer (XRD) (Rigaku, Japan) over a 2θ range of 5° to 90°.

2.4 Batch and column studies

In the first-level optimization, the calcination of coal fly ash was performed at a temperature ranging from 250 °C to 400 °C inside a muffle furnace for 2 h to determine the optimal temperature for Pb²⁺ and Cr⁶⁺ removal. Subsequently, the calcination time was optimized by varying the duration from 1 to 3 h at a fixed temperature of 300 °C to maximize the metal removal efficiency. The molar concentration of H₃PO₄ was also optimized by adjusting it between 0.3 mol L⁻¹ and 0.5 mol L⁻¹ to achieve maximum Pb²⁺ and Cr⁶⁺ adsorption. Furthermore, the MFA–CS composite ratio was investigated at 1/1, 1/2, 1/3, and 3/1 to determine the most effective composition for metal removal. The impact of adsorbent morphology was assessed using three different forms: nanopowder, beads, and film to identify the most efficient structure for Pb²⁺ and Cr⁶⁺ adsorption. This hierarchical approach is validated and commonly employed in similar material development studies.²¹ The mathematical equations describing the adsorbent performance are provided in Table S1.†

The second-level optimization was performed using the Box–Behnken method of RSM, where trials were performed with an MFA–CS amount ranging from 1 to 10 g L⁻¹, 20 to 180 min time, and a metal load from 100 to 1000 mg L⁻¹ for 17 trials to maximize the Q_e for Pb²⁺ and Cr⁶⁺ removal. The third-level optimization focused on pH studies within the range of 2.0 to 6.0 to achieve the maximum Q_e for both the metals, and the point of zero charge (pH_pzc) was determined. The isotherm studies were performed at RSM optimal parameters for Pb²⁺ and Cr⁶⁺ by changing the metal load from 100 to 1000 mg L⁻¹ and tested against five non-linear isotherm models. Kinetic studies were carried out for 20 to 240 min under RSM optimal conditions and analysed using four non-linear kinetic models. The mathematical equations of kinetic and isotherm models are included in Table S2.† All adsorption experiments were repeated thrice, and the analysis of error was reported. The simultaneous removal of Pb²⁺ and Cr⁶⁺ was assessed at 100 mg L⁻¹ Pb²⁺ or Cr⁶⁺ concentration, 30 min time, 1 g L⁻¹ MFA–CS amount, and pH 5.0. Thermodynamic variables (ΔG°, ΔS°, and ΔH°) were calculated for both the metals at a temperature ranging from 25 °C to 50 °C to evaluate the spontaneity of the adsorption. The regeneration tendency of MFA–CS was tested using four eluting agents: HNO₃, HCl, NaOH, and H₂SO₄ at a metal concentration of 0.1–1 mol L⁻¹ to find the optimal desorption substance. The adsorption–desorption cyclic study was carried out for up to 15 cycles using H₂SO₄ (0.4 mol L⁻¹) for Pb²⁺ and 0.6 mol L⁻¹ HNO₃ for Cr⁶⁺ removal. This regeneration studies demonstrated the long-term reusability of MFA–CS, minimizing the dependence on new adsorbents and enhancing the system sustainability.

A series of column experiments were conducted to investigate the removal performance of Pb²⁺ and Cr⁶⁺ ions under varying operational conditions. The study primarily examined the effects of three parameters: inlet flow rate, initial metal concentration, and bed height. To assess the impact of flow rate, untreated metal ion solution was introduced in an upward flow direction at rates ranging from 5 to 15 mL min⁻¹, while maintaining a constant bed height of 10 cm and a fixed initial metal concentration of 500 mg L⁻¹. Effluent samples were collected at regular time intervals between 50 and 1100 min to determine the concentration ratio (C_t/C_o). Subsequently, the influence of initial metal concentration was evaluated by varying it from 250 to 1000 mg L⁻¹ at a constant flow rate of 10 mL min⁻¹ and a fixed bed height of 10 cm. Breakthrough data were similarly recorded across the same time intervals for both Pb²⁺ and Cr⁶⁺ ions. Furthermore, the effect of bed height was explored by varying the column height from 5 to 15 cm, keeping the flow rate constant at 10 mL min⁻¹. In these trials, the concentration of Pb²⁺ was maintained at 750 mg L⁻¹, while Cr⁶⁺ was kept at 500 mg L⁻¹. The experimental setup, including the configuration of the column set up, is illustrated in Fig. S2.† Breakthrough curves were plotted using the C_t/C_o values to analyse the dynamic behaviour of the column under different conditions and to determine the optimal operating parameters. The nomenclature, parameter definitions, and relevant mathematical expressions used in the analysis are provided in Table S3.† To further interpret the experimental results, the data were fitted using two widely accepted adsorption models: Yoon–Nelson and Thomas, as described in Table S4.† The presentation of column experiments was streamlined following the format and clarity previously demonstrated in the literature.²²

3. Results and discussion

3.1 Characterization of adsorbent physico-chemical properties

3.1.1 BET analysis. The best-performing adsorbent, MFA–CS nanopowder, was selected for BET analysis. Before analysis, the adsorbent samples experienced an initial treatment at 250 °C for 3 h to remove moisture. Later, nitrogen gas was introduced at 77 K to obtain adsorption–desorption isotherms, as demonstrated in Fig. 2. The observed isotherm corresponded to the type-4 classification (IUPAC norms), indicating the presence of mesopores.²³ At a relative pressure (0.019 to 0.42), micro-pores were filled, signifying single-layer adsorption. The adsorption of multilayers commenced as the pressure elevated, resulting in the development of additional nitrogen layers. At a higher relative pressure, N₂ condensation was observed in the mesopores, which demonstrated changing pore sizes.^24,25

Fig. 2 Adsorption–desorption BET studies on MFA–CS.

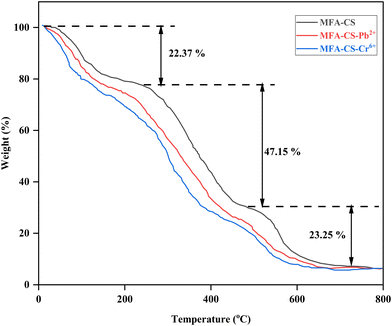
The N₂ adsorption–desorption isotherm of the MFA–CS composite displays a prominent hysteresis loop in the relative pressure range of 0.48 to 0.99, which is indicative of the mesoporous structure. This hysteresis arises from the capillary condensation of nitrogen within mesopores during adsorption, followed by delayed evaporation during desorption due to pore network effects.³ Specifically, the presence of ink-bottle-shaped pores, characterized by narrow necks connected to wider cavities, results in nitrogen being trapped during desorption until a lower relative pressure is reached, leading to the observed gap between the adsorption and desorption branches.²⁶ Such pore structures also promote the multilayer adsorption and restricted desorption pathways. Similar adsorption patterns have been reported for heavy metal ion elimination from wastewater using porous carboxymethyl chitosan beads,²⁷ nanofiltration membrane for dye removal,²⁶ and polyvinyl alcohol–chitosan composites.³ Following the adsorption of Pb²⁺ and Cr⁶⁺ on the MFA–CS adsorbent, a reduction in surface area was observed: 41.02% (from 139.84 m² g⁻¹ to 82.47 m² g⁻¹) for Pb²⁺ and 22.49% (from 139.84 m² g⁻¹ to 108.38 m² g⁻¹) for Cr⁶⁺. This could indicate that metals possibly engaged the pores and shaped a covering on the surface. A similar pattern was noticed in pore diameter reduction, with the reduction of 41.02% (from 54.31 nm to 32.03 nm) and 24.17% (from 54.31 nm to 41.18 nm) following the adsorption of Pb²⁺ and Cr⁶⁺, respectively, which signifies the effective adsorption on the adsorbent surface. A comparative surface property reported in the literature is briefed in Table S5.†

3.1.2 Surface morphology and compositional analysis. The surface morphology assessment through FE-SEM and elemental composition analysis using EDX are presented in Fig. 3 and Table S6,† respectively. These analyses were performed on pristine-modified fly ash (MFA) and on the best-performing MFA–CS nanopowder before and after Pb²⁺ and Cr⁶⁺ metal adsorption. EDX readings were captured at three different locations on the MFA–CS surface and reported the average values. The structural characteristics of pristine MFA are mentioned in Table S6† and morphology in Fig. 3(A), revealing an elemental composition of 32.08% carbon, 6.13% nitrogen, 22.65% oxygen, 4.87% phosphorus, 18.69% silicon, and 2.18% calcium. In contrast, the pristine MFA–CS nanopowder adsorbent is mentioned in Table S6† and its morphology in Fig. 3(B), which exhibited a composition of 31.61% carbon, 5.63% nitrogen, 32.49% oxygen, 3.55% sodium, 16.52% silicon, 3.74% phosphorus, and 1.92% calcium. The increased oxygen content in MFA–CS indicates the incorporation of oxygen-containing functional groups from chitosan, enhancing the adsorption capability.²⁸

Fig. 3 SEM results: (A) MFA; (B) MFA–CS (nanopowder 3 : 1); (C) MFA–CS (Pb²⁺); (D) MFA–CS (Cr⁶⁺).

After the adsorption of Pb²⁺ and Cr⁶⁺ metals, morphological changes were observed in the best-performing MFA–CS nanopowder, as shown in Fig. 3(C) and (D). The porous structure became less distinct as metal ions accumulated in the adsorption sites, resulting in the development of a smooth, film-like layer on the surface. The EDX results confirmed the effective metal adsorption, and the weight percentages of 14.96% ± 1.05 for Pb²⁺ and 7.61% ± 0.75 for Cr⁶⁺ on the adsorbent surface were observed. These values were obtained from measurements at three different locations on the adsorbent surface, and the corresponding statistical analysis, including standard deviations, is provided in Table S6.† The approach adopted for quantitative elemental analysis is in line with best practices highlighted in recent studies based on copper ion removal from wastewater using magnetic gamma alumina nanoparticles.²⁹ A reduction in carbon, nitrogen, and oxygen contents was also observed post-adsorption (Table S6†), which indicates the surface saturation and potential replacement of functional groups by metal ions.³⁰ These outcomes are aligned with the earlier studies on metal mitigation using various adsorbents, including chitosan–polyvinyl alcohol–zeolite composites,³¹ magnetic EDTA-modified chitosan–SiO₂–Fe₃O₄ adsorbents,³⁰ and carboxymethyl-chitosan composites.²⁸ The observed structural and compositional changes highlighted the effectiveness of the MFA–CS nanopowder for the Pb²⁺ and Cr⁶⁺ metal adsorption, making it a promising material for wastewater treatment.

3.1.3 Thermal stability. The thermal stability of the MFA–CS composite, before and after metal ion adsorption, was evaluated using TGA, as shown in Fig. 4. The TGA profile revealed a characteristic three-stage degradation pattern, indicative of distinct physicochemical transformations within the composite matrix. In the first stage, a weight loss of 22.37% was observed between room temperature and 150 °C. This loss is probably due to the evaporation of physically adsorbed water molecules, residual solvents, and loosely bound volatile organic compounds. This stage reflects the hydrophilic nature of the composite and indicates the presence of surface-accessible functional groups capable of hydrogen bonding.¹⁵ The second stage, occurring between approximately 150 °C and 400 °C, showed a significant weight loss of 47.15%. This degradation was associated with the thermal depolymerisation of chitosan–coal fly ash composites and separation of functional groups such as carboxyl, hydroxyl, and amine groups. These groups are crucial for metal ion binding, and their decomposition suggests substantial structural reorganization. The process probably includes the scission of glyosidic linkages in chitosan and the breakdown of chemically bonded organic moieties that interacted with metal ions during adsorption.^15,32 In the final stage, from 400 °C to 600 °C, a further 23.25% weight loss was recorded. This phase corresponds to the thermal decomposition of more stable carbonaceous residues and inorganic leftovers remaining after the earlier stages. It probably involves the collapse of cross-linked polymer networks, oxidation of carbon backbones, and volatilization or transformation of inorganic mineral content derived from coal fly ash.^3,28,33 This multistep degradation trend is consistent with the thermal behaviours reported for other composites in environmental remediation, such as polyvinyl alcohol-modified chitosan,³ chitosan–biochar composite,³⁴ and cellulose nanofibril–vinyl resin nanocomposites,¹⁵ and a comparable three-stage degradation profile during the development of nanofiltration membranes was observed. Collectively, these findings affirm the good thermal integrity of the MFA–CS composite, supporting its suitability for practical applications in aqueous-phase metal ion removal under different thermal conditions.

Fig. 4 TGA of MFA–CS.

3.1.4 Crystallinity studies. The degree of crystallinity of MFA–CS, pre- and post-metal adsorption, was studied using XRD, as represented in Fig. 5.

Fig. 5 XRD analysis: (a) MFA–CS; (b) MFA–CS–Pb²⁺; (c) MFA–CS–Cr⁶⁺.

This pattern exhibited a high degree of crystallinity, quantified at 62.47%. Upon adsorption of heavy metals, a notable decrease in the degree of crystallinity was observed, with values reduced to 40.31% for Pb²⁺ and 49.42% for Cr⁶⁺. This reduction was accompanied by a broadening of peaks and a decline in intensity, indicating structural disruptions within the composite.³⁵ The diminished crystallinity indicates that metal ions occupied the available pore spaces and interacted with the functional groups, potentially weakening hydrogen bonds and altering the lattice structure of the composite.^3,36 The XRD spectra further revealed distinct peaks associated with metal-laden phases. For Pb²⁺, diffraction peaks in the range of 27–30° corresponded to lead phosphate, suggesting the formation of insoluble lead phosphate species.^37,38 Similarly, characteristic peaks at 39.91° for chromium hydroxide and 50.98° for chromium phosphate were identified. The gradual decline in peak intensity after metal adsorption confirmed the formation of surface precipitates, likely consisting of metal hydroxides, phosphates, or complexed species.³ These observations indicated that metal removal in MFA–CS occurred predominantly via surface precipitation and complexation mechanisms, wherein Pb²⁺ and Cr⁶⁺ react with the available functional groups of phosphate, hydroxyl, etc., within the composite. Similar trends of XRD patterns have been reported for heavy metal ion removal from wastewater using fly ash-coated chitosan⁷ and orange peel biochar.³⁹

3.1.5 FTIR spectroscopy analysis. The FTIR spectra of MFA–CS before and after metal adsorption (Pb²⁺ and Cr⁶⁺), shown in Fig. 6(a–c), were recorded in the range of 4000–400 cm⁻¹. The pristine MFA–CS displayed a broad absorption band between 3942 and 3410 cm⁻¹, attributed to the O–H stretching vibrations from hydroxyl groups.⁶ Following adsorption, this band became less intense and shifted to the 3864–3345 cm⁻¹ range, suggesting hydrogen bonding and surface complexation with metal ions.²¹ A peak within 3380–3025 cm⁻¹, assigned to the N–H stretching vibration of amine groups, also showed smoothing and broadening post-adsorption, probably due to electrostatic interactions with metal ions.⁴⁰ Characteristic peaks in the 2375–1910 cm⁻¹ region, which can be associated with triple bond stretching (C≡C) or N=C=O moieties, were observed to shift toward 2305–1840 cm⁻¹ after adsorption, indicating possible coordination or electrostatic interaction.⁴⁰ Similarly, the band observed in the 1575–1385 cm⁻¹ range, ascribed to the asymmetric and symmetric C=O stretching vibrations of carboxylate (–COO–) groups, shifted to 1510–1315 cm⁻¹, implying metal–ligand complex formation.⁴¹ The C–H stretching vibration at 2973.10 cm⁻¹ in the unmodified sample showed minor shifts to 2964.37 cm⁻¹ (Pb²⁺) and 2971.98 cm⁻¹ (Cr⁶⁺), possibly due to hydrogen bonding interactions.⁴¹ A peak at 952.03 cm⁻¹, assigned to aromatic C–H bending, shifted to 943.76 and 949.38 cm⁻¹ for Pb²⁺ and Cr⁶⁺ adsorbed samples, suggesting changes in local bonding environments.⁴² Notably, strong absorption bands between 1250 and 1025 cm⁻¹ were associated with P–O and C–O–P stretching vibrations, confirming the presence of phosphorus-containing functional groups in the modified fly ash matrix.⁴³ The band near 1160 cm⁻¹, in particular, supports the incorporation of phosphate species on the surface of MFA–CS, as also suggested by similar spectral features in nanocomposite systems.²¹ These spectral shifts and intensity variations demonstrate the interaction of –OH, –COOH, and –NH₂ functional groups with Pb²⁺ and Cr⁶⁺ ions, indicative of adsorption through surface complexation, hydrogen bonding, and electrostatic attraction.

Fig. 6 FTIR analysis: (a) MFA–CS; (b) MFA–CS–Pb²⁺; (c) MFA–CS–Cr⁶⁺.

3.2 First-level optimization

3.2.1 Optimization of the calcination temperature of coal fly ash. The optimization of the calcination temperature of coal fly ash is crucial to achieving maximum adsorption capacity for heavy metal removal while minimizing energy consumption.³⁹ In this study, the calcination temperature was varied between 250 °C and 400 °C, with increment of 50 °C, for a duration of 2 h. The concentration of metals was changed from 50 mg L⁻¹ to 500 mg L⁻¹ to assess the adsorption performance of Pb²⁺ and Cr⁶⁺, as graphically represented in Fig. 7. The results specify that Q_e was increased when the temperature elevated from 250 °C to 300 °C for both the metals. This enhancement is due to the improved surface area (52.63 m² g⁻¹ to 85.63 m² g⁻¹) and carbon content (65.40% to 73.69%) of the coal fly ash, as presented in Table S7,† which enhanced the active site availability for metal adsorption.⁷ The increase in temperature facilitated the removal of volatile organic compounds and enhanced carbonization, leading to a more efficient adsorbent structure.^44,45 The Q_e showed a marginal increase for both metals at 350 °C, which indicates that the carbon content (73.69% to 76.30%) and surface area (85.63 m² g⁻¹ to 92.98 m² g⁻¹) reached the near-optimal conditions for metal binding. However, at 400 °C, Q_e declined with the increase in metal concentration, due to the excessive thermal treatment, which can cause partial structural collapse that reduced the metal binding efficiency.⁷ The optimal calcination temperature was determined as 300 °C, at which Q_m values of 188.96 mg g⁻¹ for Pb²⁺ and 117.64 mg g⁻¹ for Cr⁶⁺ were achieved at 500 mg L⁻¹ concentration. A similar trend has been observed in studies utilizing various adsorbents for the heavy metal removal, including chitosan-coated fly ash,⁷ biochar derived from poultry manure,⁴⁶ and biochar obtained from orange peel.³⁹

Fig. 7 Optimization of the fly ash calcination temperature for metal removal: (a) Pb²⁺ and (b) Cr⁶⁺ removal.

3.2.2 Optimization of calcination time of coal fly ash. Determining the optimal calcination time is critical for improving the physicochemical properties of fly ash while ensuring the energy efficiency, thereby making the thermal activation process both sustainable and economically viable.³⁹ In this work, the calcination duration was systematically varied from 1 h to 3 h at a fixed optimum temperature of 300 °C. The effect of this thermal treatment was evaluated over a wide concentration range of metal ions (50–500 mg L⁻¹) for both Pb²⁺ and Cr⁶⁺, to assess the adsorption performance of the modified fly ash. The resulting adsorption capacities (Q_e), illustrated in Fig. 8(a) for Pb²⁺ and Fig. 8(b) for Cr⁶⁺, demonstrate a significant dependence on calcination time. As the calcination duration increased from 1 h to 2 h, a substantial improvement in Q_e was observed from 171.05 mg g⁻¹ to 186.38 mg g⁻¹ for Pb²⁺ and from 96.38 mg g⁻¹ to 117.64 mg g⁻¹ for Cr⁶⁺ at 500 mg L⁻¹ metal ion concentration. This enhancement is primarily attributed to the kinetics of thermally induced surface activation. During this phase, the decomposition of surface-bound hydroxyl groups and the volatilization of organic matter occurred, along with the release of structural water.³⁹ This promotes the evolution of porous structures by opening up blocked or inaccessible pore networks.⁴⁷ At this stage, the calcination kinetics favour surface restructuring without exceeding the thermal threshold that leads to material degradation. The increased surface properties enhance the interaction between the fly ash surface and the target metal ions, thereby improving the Q_e values.⁴⁸ However, extending the calcination time to 3 h results in a decline in adsorption capacity, with Q_e decreasing to 155.03 mg g⁻¹ for Pb²⁺ and 83.06 mg g⁻¹ for Cr⁶⁺. This decline can be attributed to the onset of structural collapse.⁴⁷ Prolonged heating can cause agglomeration of fine particles, which leads to a reduction in pore accessibility.⁴⁷ Additionally, excessive thermal exposure can cause the crystallization of amorphous aluminosilicate phases into more inert, less reactive crystalline forms, thereby decreasing the number of active binding sites.³⁴ These changes are indicative of kinetic saturation, where further thermal input no longer contributes to activation but induces irreversible structural transformations that diminish adsorption performance.³⁹

Fig. 8 Optimization of the fly ash calcination time and kinetic modelling for metal removal: (a) Pb²⁺ removal; (b) Cr⁶⁺ removal. (c) Pseudo-first-order kinetic model for Pb²⁺ and Cr⁶⁺. (d) Pseudo-second-order kinetic model for Pb²⁺ and Cr⁶⁺.

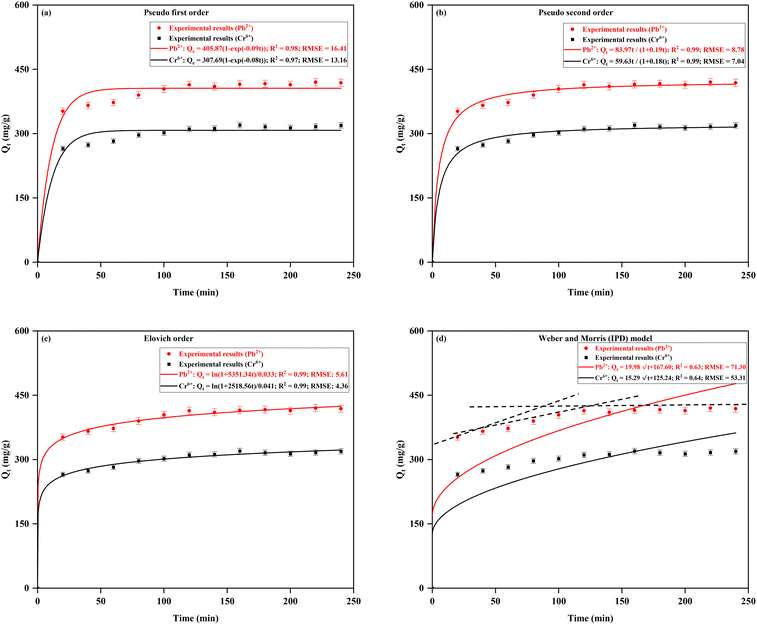
Furthermore, the kinetic studies of Pb²⁺ and Cr⁶⁺ removal using fly ash calcined at 300 °C adsorbent was investigated to assess the effect of contact time (20 min to 180 min) on Q_e and fitted using the PFO and PSO models. The corresponding model fits are shown in Fig. 8(c) and (d), respectively. The Q_e value of both metal ions showed a notable increase up to 120 min, after which a decline was observed. This trend suggests that the active sites on the adsorbent surface became saturated after 2 h, leading to a subsequent reduction in adsorption efficiency possibly due to desorption or surface rearrangements. Therefore, selecting a 2 h calcination time ensured optimal physicochemical enhancement of fly ash for maximizing the metal ion adsorption capacity. The PSO model exhibited a superior fit with the experimental data, as indicated by the high correlation coefficients (R² = 0.96 for Pb²⁺ and R² = 0.91 for Cr⁶⁺), compared to the PFO model, which indicates that the adsorption process was primarily governed by chemisorption mechanism rather than physical interactions between the metal ions and adsorbent surface.⁴⁹

3.2.3 Optimization of the phosphoric acid concentration. The optimization of phosphoric acid (H₃PO₄) concentration in modifying fly ash is crucial for obtaining enhanced heavy metal uptake using a minimum acid concentration.⁴⁰ This study investigated the impact of varying H₃PO₄ concentrations from 0.3 mol L⁻¹ to 0.5 mol L⁻¹ on the adsorption performance of calcined fly ash for Pb²⁺ and Cr⁶⁺ removal, and the outcomes are shown in Fig. 9. The data have indicated that increasing the H₃PO₄ concentration from 0.3 mol L⁻¹ to 0.4 mol L⁻¹ led to improvement in metal removal. For Pb²⁺, Q_e increased by 12.58%, from 210.49 mg g⁻¹ to 236.98 mg g⁻¹. Similarly, Cr⁶⁺ removal exhibited an increase of 22.46%, from 118.43 mg g⁻¹ to 145.03 mg g⁻¹. The enhancement in adsorption capacity can be endorsed to increased surface functionalization due to the formation of phosphate groups, which further enhanced pore development and active adsorption sites.⁴⁹

Fig. 9 Optimization of H₃PO₄ concentration for metal removal: (a) Pb²⁺ and (b) Cr⁶⁺removal.

However, a further increase in H₃PO₄ concentration to 0.5 mol L⁻¹ resulted in a decline in Q_e. The Q_e value for Pb²⁺ decreased by 11.17% (236.98 mg g⁻¹ to 210.49 mg g⁻¹), while for Cr⁶⁺, it decreased by 8.46% (145.03 mg g⁻¹ to 132.76 mg g⁻¹). This reduction can be linked to excessive phosphoric acid loading, which caused pore blockage due to the precipitation of phosphate complexes on the fly ash surface, thereby reducing the availability of active adsorption sites and limiting metal ion accessibility, ultimately diminishing the Q_e value.¹ Based on these findings, the optimum H₃PO₄ concentration for modifying fly ash to maximize Pb²⁺ and Cr⁶⁺ removal was determined to be 0.4 mol L⁻¹. Similar findings on the effect of phosphoric acid concentration on heavy metal removal have been reported in the literature using different adsorbents such as acid-treated coco peat biochar⁴⁰ and phosphoric acid-modified bentonite–chitosan composite.⁵⁰

3.2.4 Optimization of coal fly ash-to-chitosan ratio in the composite. 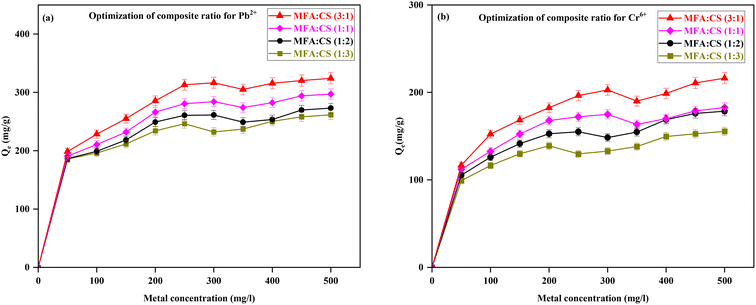The optimization of the composite ratio of modified fly ash (MFA) and chitosan (CS) is essential for maximizing Q_e, as it affects the structural properties and functional group availability, which are essential for metal ion binding and cost-effective wastewater treatment.³⁴ In this study, the adsorbent performance was analysed for four MFA : CS ratios—1/1, 1/2, 1/3, and 3/1, with results illustrated in Fig. 10 for Pb²⁺ and Cr⁶⁺ removal. The results indicated that Q_e decreased with the increase in chitosan content, with Pb²⁺ removal values of 297.12 mg g⁻¹ for the 1/1 ratio, 273.06 mg g⁻¹ for 1/2, and 261.48 mg g⁻¹ for 1/3, while the 3/1 ratio exhibited the highest Q_e value of 324.17 mg g⁻¹ at 500 mg L⁻¹ metal concentration. This trend indicates that an increased proportion of modified fly ash and decreasing chitosan content enhanced the surface properties for the metal removal. A similar pattern was observed for Cr⁶⁺ removal, with Q_e of 182.72 mg g⁻¹ for 1/1, 178.49 mg g⁻¹ for 1/2, 155.41 mg g⁻¹ for 1/3, and a significantly higher Q_e value of 216.28 mg g⁻¹ for the 3/1 MFA : CS ratio at 500 mg L⁻¹ metal concentration. The increased adsorption with a higher MFA content can be linked to its superior porosity and surface area that facilitated the metal ion retention.³⁴ Considering these findings, the optimal composite ratio of MFA : CS was determined to be 3/1 for further studies to achieve maximum metal removal. Similar results have been reported in studies on heavy metal elimination using chitosan-magnetic biochar composites,³⁴ chitosan-coated fly ash–biochar,⁹ and chitosan-coated MgO–biochar.⁵¹

Fig. 10 Optimization of the MFA–CS composite ratio for metal removal: (a) Pb²⁺ and (b) Cr⁶⁺removal.

3.2.5 Optimization of the morphology. Understanding the different morphological characteristics of the MFA–CS adsorbent is important, as the morphology directly influences the surface properties of the adsorbent for heavy metal removal.⁵² This study evaluated three distinct morphologies: nanopowder, beads, and film, and the synthesis procedure is outlined in section 2.2. The adsorption performance results, presented in Fig. 11 for Pb²⁺ (Fig. 11a) and Cr⁶⁺ (Fig. 11b), revealed that Q_e for Pb²⁺ was highest for nanopowder at 324.17 mg g⁻¹, followed by beads at 235.49 mg g⁻¹ and film at 212.76 mg g⁻¹. A similar trend was observed for Cr⁶⁺ removal, with Q_e of 216.28 mg g⁻¹ for nanopowder, 157.08 mg g⁻¹ for beads, and 132.97 mg g⁻¹ for film morphology. The superior adsorption capacity of the nanopowder can be endorsed to its higher surface area (139.84 mg g⁻¹ for nanopowder, 101.29 mg g⁻¹ for beads, and 81.95 mg g⁻¹ for film) and pore volume (0.097 cm³ g⁻¹ for nanopowder, 0.078 cm³ g⁻¹ for beads, and 0.062 cm³ g⁻¹ for film), allowing more active sites to engage with metals.^3,52 These findings highlight the importance of choosing an optimal morphology for enhancing the adsorption performance, with nanopowder showing a higher potential for heavy metal removal compared to the beads and film. Therefore, nanopowder morphology chosen in the various heavy metal removal studies involved MnOx-modified cocopeat biochar,⁵³ phosphoric acid-modified red gram biochar–MnO₂ nanocomposite,⁵⁴ polyvinyl alcohol-modified chitosan nanocomposite,³ and carboxymethyl chitosan composite.²⁸

Fig. 11 Effect of the morphology for metal removal: (a) Pb²⁺ and (b) Cr⁶⁺ removal.

3.3 Second-level optimization

The second-level optimization targeted contact time (A), MFA–CS feed dosage (B), and initial metal ion concentration (C) with the objective of maximizing adsorption capacity (Q_e), while minimizing both batch time and adsorbent dosage. The Box–Behnken design (BBD) under RSM was employed to statistically evaluate and optimize these process parameters. The experimental range was defined as contact time from 20 to 180 min, metal ion concentration from 100 to 1000 mg L⁻¹, and MFA–CS dosage from 1 to 10 g L⁻¹. A total of 17 experiments, including five replicates at the centre points, were conducted to ensure the estimation of pure error and robustness of the model. The experimental results are presented in Table S8.† The mathematical quadratic equations that describe the Q_e value for Pb²⁺ and Cr⁶⁺ are represented by eqn (1) and (2), respectively.

Pb²⁺: Q_e = 237.12 + 5.75A + 19.43B − 43.95C − 1.95AB + 14.20AC − 14.16BC − 10.70A² − 12.75B² + 37.68C²; R₁² = 0.91; p = 0.16; F = 20.25 (1)

Cr⁶⁺: Q_e = 182.66 + 6.89A + 17.60B − 32.47C − 5.71AB − 4.92AC − 11.19BC − 0.4058A² − 13.32B² + 18.74C²; R₂² = 0.87; p = 0.21; F = 13.78 (2)

The P-values for both metals were found to be less than 0.25, and the F-values exceeded 1.0, endorsing the significance of the models.^44,45 Additionally, the R² values close to 1.0 indicate a strong fit and reliable predictive ability of the models. The graphical depictions of residuals Vs forecasted Q_e and actual Vs forecasted Q_e, as displayed in Fig. S3 and S4† for both Pb²⁺ and Cr⁶⁺, respectively. Furthermore, the 3-D effects of dual factors on Q_e for both Pb²⁺ and Cr⁶⁺ are illustrated in Fig. S5 and S6.† The optimal conditions resulted from the RSM studies as 20 min contact time, 1 g L⁻¹ adsorbent dosage, and 1000 mg L⁻¹ metal ion concentration, for both Pb²⁺ and Cr⁶⁺. Under these optimal conditions, the Q_e values were obtained as 339.27 mg g⁻¹ for Pb²⁺ and 242.84 mg g⁻¹ for Cr⁶⁺, respectively. To confirm the accuracy of these optimal conditions, three experimental replicates were performed (runs 18–20), as shown in Table S8.† The assessment of the replicated experiments is summarized in Table 1, including the validation of optimum conditions.

Table 1 Analysis of variance in RSM

Run no.	Objective	σ	Variance	Average value of Qe (mg g^−1)
6, 9, 10, 12, 13	Precision check for Pb^2+ (5.5 g L^−1, 100 min, 550 mg L^−1)	3.20	10.27	236.12
6, 9, 10, 12, 13	Precision check for Cr^6+ (5.5 g L^−1, 100 min, 550 mg L^−1)	2.07	4.30	182.66
18, 19, 20	Validation of optimum conditions for Pb^2+ (1000 mg L^−1, 1 g L^−1, 20 min)	3.57	12.73	339.27
18, 19, 20	Validation of optimum conditions for Cr^6+ (1000 mg L^−1, 1 g L^−1, 20 min)	030.30	10.90	242.84

---

3.4 Third-level optimization: pH effect

The study of pH effect on the adsorbent performance is essential, as industrial effluents often exhibit significant variability in pH levels. The optimization of pH conditions can enhance the efficacy of an adsorbent in removing heavy metals, as highlighted in numerous studies.^54,55 In this study, the pH was varied from 2.0 to 6.0 at optimal parameters identified by the RSM analysis, with the results depicted in Fig. 12(a). High H⁺ ions compete with metals for adsorption location on the MFA–CS surface at low pH, leading to resistance and reduced adsorption performance.³ As the pH rises, the H⁺ ions decrease, reducing competition and improving the adsorption of heavy metals.^56,57

Fig. 12 Third-level optimization: (a) pH effect and (b) pH_pzc determination for Pb²⁺ and Cr⁶⁺.

At pH values above 6.0, the formation of metal hydroxide precipitates was observed, probably due to the decreased solubility of metal ions and the enhanced formation of metal hydroxide complexes, as reported previously.^34,58 The MFA–CS adsorbent exhibited optimal performance at pH 5.0, where the Q_e value reached 352.19 mg g⁻¹ for Pb²⁺ and 265.13 mg g⁻¹ for Cr⁶⁺. This enhanced adsorption under mild acidic conditions can be attributed to favourable electrostatic interactions between the negatively charged functional groups on MFA–CS and the metal ions.⁵⁹ To validate the influence of pH, the pH_pzc was determined, as shown in Fig. 12(b). The pH_pzc values were found to be 5.51 for Pb²⁺ and 5.62 for Cr⁶⁺. Below the pH_pzc values, the surface of MFA–CS becomes positively charged, leading to increased proton (H⁺) competition with metal cations for binding sites.⁶⁰ This ion competition significantly reduces Q_e as fewer active sites are available for metal ion binding.⁶¹ This trend is aligned to various studies on heavy metal elimination using materials such as biochar–chitosan composites and Cajanus cajan biochar.^53,61 Additionally, it is evident that at lower pH, high concentrations of H⁺ not only outcompete metal ions but also disrupt coordination interactions by protonating donor atoms on the adsorbent surface, thereby reducing the complexation efficiency.^59,60 This underscores the importance of maintaining an optimal pH range to balance ion-exchange, surface charge, and metal ion speciation for maximum adsorption efficiency.

3.5 Isotherm, kinetic, and thermodynamic studies

3.5.1 Adsorption isotherm analysis. The isotherm analysis was conducted using 5 non-linear models (Table S2†) for a Pb²⁺ or Cr⁶⁺ concentration of 100–1000 mg L⁻¹, at optimal parameters determined through the RSM analysis: 1000 mg L⁻¹ metal concentration, 1 g L⁻¹ MFA–CS feed, and 20 min contact time for both Pb²⁺ and Cr⁶⁺. The obtained isotherm profile fittings are presented in Fig. 13, with calculated variables and R² values provided in Table 2. The study indicated that the Langmuir isotherm yielded the highest R² values (0.99) for both Pb²⁺ and Cr⁶⁺, suggesting monolayer adsorption on the MFA–CS surface.^7,62 The Langmuir isotherm separation factor (R_L) was found to be less than 1.0, signifying that the adsorption was favourable and spontaneous for both the metals.³ The activation energy (E_a) values were determined from the D–R isotherm to be 28.30 kJ mol⁻¹ for Pb²⁺ and 27.58 kJ mol⁻¹ for Cr⁶⁺, suggesting that the adsorption primarily occurred through chemisorption rather than physisorption.³ The Q_m predicted by the Langmuir model were 367.65 mg g⁻¹ for Pb²⁺ and 277.52 mg g⁻¹ for Cr⁶⁺, demonstrating the capability of MFA–CS in mitigating these metals. A comparison of MFA–CS's adsorption capacity with other adsorbents is briefed in Table 3. As given in Table 3, various reported adsorbents for the removal of Pb²⁺ and Cr⁶⁺ have demonstrated a wide range of adsorption capacities influenced by their composition and surface modifications. For example, a cross-linked alginate-rice husk ash–graphene oxide–chitosan nanocomposite achieved a maximum adsorption capacity of 242.5 mg g⁻¹ for Pb²⁺ removal, which can be attributed to the combined effect of an increased surface area and abundant active sites.⁶³ Similarly, electrospun DTPA-modified chitosan–polyethylene oxide nanofibers achieved an adsorption capacity of 142.0 mg g⁻¹ for Pb²⁺ removal, benefiting from enhanced chelation properties.⁶⁴ Regarding Cr⁶⁺ removal, a phosphogypsum-distiller grain composite attained an adsorption capacity of 157.9 mg g⁻¹,⁶⁵ while the ZnO–chitosan nanocomposite reached 69.5 mg g⁻¹.⁶⁶ In comparison, the MFA–CS composite developed in this study demonstrated substantially higher adsorption capacities for both Pb²⁺ (352.19 mg g⁻¹) and Cr⁶⁺ (265.13 mg g⁻¹). This superior performance resulted from a carefully optimized H₃PO₄ modification of coal fly ash that improved the composite's surface characteristics. Furthermore, hierarchical optimization of key parameters including calcination temperature, calcination time, H₃PO₄ concentration, coal fly ash-to-chitosan ratio in the composite, and morphology was conducted to maximize the adsorption capacity. These findings highlight the outstanding adsorption capability and potential practical utility of the MFA–CS to remove Pb²⁺ and Cr⁶⁺ from the wastewater.

Fig. 13 Isotherm investigation: (a) Langmuir; (b) Freundlich; (c) Temkin; (d) Dubinin–Radushkevich (D–R); (e) Jovanovic.

Table 2 Isotherm model fitting results

Isotherm	Parameters	Pb^2+	Cr^6+
Langmuir	Qm (mg g^−1)	367.65	277.52
	KL (L mg^−1)	0.015	0.013
	RL	0.22	0.24
	R^2	0.99	0.99
Freundlich	KF (L g^−1)	104.67	73.55
	n (unitless)	5.61	5.32
	R^2	0.98	0.98
Temkin	KT (L g^−1)	0.83	0.64
	bT (J mol^−1)	46.99	60.03
	R^2	0.97	0.98
D–R	Qm (mg g^−1)	330.91	247.61
	β (mol^2 kJ^−2)	6.42 × 10^−4	6.57 × 10^−4
	Ea (kJ mol^−1)	28.30	27.58
	R^2	0.67	0.62
Jovanovic	Qm (mg g^−1)	332.81	250.11
	Kj (L mg^−1)	0.009	0.009
	R^2	0.96	0.95

---

Table 3 Comparative analysis of adsorbents for Pb²⁺ and Cr⁶⁺ elimination

Adsorbent	Qm (mg g^−1)	Target metal	References
Cucumber peel	133.60	Pb^2+	67
Wood ash amended biochar	61.50	Pb^2+	68
Banana stem	179.90	Pb^2+	69
Electrospun DTPA-modified chitosan/polyethylene oxide nanofibers	142.0	Pb^2+	64
Cross linked alginate-rice husk ash–graphene oxide–chitosan nanocomposite	242.50	Pb^2+	63
Entrapped silica nanopowder within calcium alginate	83.33	Pb^2+	70
MFA–CS	352.19	Pb^2+	This study
Carbon-coated montmorillonite nanocomposite	12.40	Cr^6+	71
ZnO–chitosan nano-biocomposite	69.50	Cr^6+	66
Fly ash coated by chitosan	36.22	Cr^6+	7
Azospirillum biofertilizer	5.58	Cr^6+	72
Phosphogypsum and distillers grains composite	157.9	Cr^6+	65
MFA–CS	265.13	Cr^6+	This study

---

3.5.2 Kinetic studies. The kinetic studies used 4 non-linear models, as outlined in Table S2,† with graphical representations of the fittings provided in Fig. 14 and model parameters summarized in Table 4. The adsorption capacity for both the metals exhibited a time-dependent increase, ultimately stabilizing at equilibrium. The kinetic analysis identified two separate phases: an initial rapid adsorption phase occurring within the first 100 min for Pb²⁺ and Cr⁶⁺, and a subsequent slower phase that gradually approached equilibrium. This trend aligned with the observed initial adsorption rate constants (h), where the relatively small value of K₂ compared to h suggests a fast initial adsorption rate that decelerated over time.^50,73 The initial fast adsorption phase was probably initiated by the abundance of available active locations on the MFA–CS surface, coupled with the high metal ion concentration in solution and minimal mass transfer resistance.³⁴ These factors facilitate the swift occupation of external adsorption sites. As adsorption progresses, the diminishing availability of adsorption sites contributed to the reduced rate, restricting the movement of metals into the pores of the MFA–CS.³⁴ The findings have specified that the pseudo-second-order (PSO) gave the best fit (R² = 0.99), implying that Pb²⁺ and Cr⁶⁺ on the MFA–CS surface predominantly occurred via chemisorption.⁶⁷

Fig. 14 Kinetic studies: (a) PFO; (b) PSO; (c) Elovich; (d) Weber and Morris (IPD) model.

Table 4 Kinetic model fitting results

Kinetic model	Parameters	Pb^2+	Cr^6+
Pseudo first order	Qe (mg g^−1)	405.87	307.69
	K1 (L min^−1)	0.09	0.08
	R^2	0.98	0.97
	RMSE	16.41	13.16
Pseudo second order	Qe (mg g^−1)	424.05	322.32
	K2 (g mg^−1 min^−1)	4.67 × 10^−4	5.74 × 10^−4
	h	83.97	59.63
	R^2	0.99	0.99
	RMSE	8.78	7.04
Elovich model	α (mg g^−1 min^−1)	162 162.08	61 428.52
	β (g mg^−1)	0.033	0.041
	R^2	0.99	0.99
	RMSE	5.61	4.36
IPD model	kW&M (mg g^−1 min^1/2)	19.98	15.29
	C	167.60	125.24
	R^2	0.63	0.64
	RMSE	71.30	53.31

---

Although the intra-particle diffusion (IPD) model yielded lower R² values (0.63 for Pb²⁺ and 0.64 for Cr⁶⁺), it revealed a three-stage adsorption process, which provides further insights into the diffusion mechanisms. The first stage, characterized by a steep slope, corresponds to primary surface adsorption. This rapid phase is driven by the availability of free binding sites on the outer surface of the adsorbent, where the metal ions are initially captured.⁷⁴ The second stage, marked by a reduced slope, signifies the intra-particle diffusion phase, where metal ions begin to penetrate the pores of the MFA–CS. During this phase, the rate of adsorption slows down due to the increased resistance to diffusion as the ions move deeper into the material.^3,74 The reduction in the slope during this stage indicates that the adsorption rate becomes more diffusion-controlled, as the metal ions struggle to diffuse further into the material's internal structure.⁵⁰ Finally, the third stage is represented by a stagnating slope, which suggests that the adsorption process is nearing equilibrium. At this point, the number of available binding sites for further adsorption is reduced, and the rate of adsorption slows significantly.⁷⁵ This progression of adsorption stages reflects the combined impact of external surface adsorption, intra-particle diffusion, and the final equilibrium attainment, all of which are governed by the diffusion mechanism within the adsorbent material.²⁸ This three-stage adsorption process aligns with the findings of similar kinetic studies on heavy metal elimination, such as using polyvinyl alcohol-impregnated chitosan,³ bentonite–chitosan composites,⁵⁰ chitosan magnetic biochar composites,³⁴ and KMnO₄-modified cocopeat biochar.⁵³

3.5.3 Thermodynamics of adsorption. The thermodynamic parameters, ΔH°, ΔS°, and ΔG°, were determined using eqn (3) and (4) for Pb²⁺ and Cr⁶⁺ at four different temperatures: 25 °C, 30 °C, 40 °C, and 50 °C. These calculations were conducted under the optimal conditions identified through the RSM for both Pb²⁺ and Cr⁶⁺. The fitness plot is shown in Fig. 15, while the relating parameter results are detailed in Table 5.

ΔG° = ΔH° − TΔS° (4)

where K_eq is the thermodynamic equilibrium constant.

Fig. 15 Thermodynamic studies for Pb²⁺ and Cr⁶⁺ removal.

Table 5 Thermodynamic parameters for Pb²⁺ and Cr⁶⁺ mitigation using MFA–CS

Target metal	Temperature (K)	ΔH° (kJ mol^−1)	ΔS° (kJ mol^−1 K^−1)	ΔG° (kJ mol^−1)
Pb^2+	298.15	2.93	0.058	−14.51
	303.15			−14.80
	313.15			−15.39
	323.15			−15.97
Cr^6+	298.15	3.29	0.057	−13.81
	303.15			−14.10
	313.15			−14.67
	323.15			−15.24

---

The results indicated that the ΔG° values were consistently negative (−13.81 to −15.97 kJ mol⁻¹), suggesting that adsorption onto the MFA–CS surface occurred spontaneously.⁷⁶ The positive ΔH° values (2.93 to 3.29 kJ mol⁻¹) validated that the adsorption was endothermic. The positive ΔS° values (57.37 to 58.53 J mol⁻¹ K⁻¹) can suggest a rise in randomness at the interphase boundary, further driving the adsorption spontaneously.⁴¹ These thermodynamic findings align with earlier studies on heavy metal elimination using the Saraca asoca bark powder,⁴¹ chitosan magnetic biochar composite,³⁴ and polyvinyl alcohol modified chitosan.⁵⁷ The methodology for the estimation of various thermodynamic parameters has been adopted from a similar study of wastewater treatment using activated carbon–nanocellulose composite.⁷⁷

3.6 Simultaneous adsorption

Multi-metal adsorption experiments were conducted using a 100 mL aqueous solution containing Pb²⁺ and Cr⁶⁺ ions at a concentration 200 mg L⁻¹ under optimized conditions: pH 5.0, contact time of 20 min, and MFA–CS dosage of 1 g L⁻¹. The composite demonstrated simultaneous removal efficiencies of 86.78% for Pb²⁺ and 67.09% for Cr⁶⁺, confirming its effectiveness in treating real effluents containing multiple metal ions. However, the observed reduction in Cr⁶⁺ removal compared to single-metal systems highlights the influence of co-existing ions and the competitive nature of the adsorption process. In multi-metal systems, metal ions compete for the same active adsorption sites, especially when the adsorbent has a limited number of functional groups such as –NH₂, –OH, and –COOH, as present in the MFA–CS composite.⁷⁸ Pb²⁺ displayed a stronger affinity for the adsorbent surface than Cr⁶⁺, which can be explained by several physicochemical factors. Pb²⁺ has a higher electronegativity (2.33) than Cr⁶⁺ (1.66), and a larger ionic radius (1.19 Å compared to 0.52 Å), both of which contribute to stronger electrostatic interactions and complexation with the active sites.⁷⁸ Additionally, Cr⁶⁺ species have a higher hydration energy, making them less likely to shed their hydration shell and interact with the adsorbent surface, thereby decreasing their overall adsorption efficiency.⁷⁹ The faster adsorption kinetics of Pb²⁺ also allows it to occupy the available adsorption sites more rapidly than Cr⁶⁺. This competitive advantage reduces the effective number of sites available for Cr⁶⁺, contributing to its lower removal in the binary system.³ These findings align with the previous studies on competitive adsorption of heavy metals including those using metal–organic frameworks,⁸⁰ chitosan-magnetic biochar composites,³⁴ and polyvinyl alcohol-modified chitosan, which also reported the preferential adsorption of metal ions based on size, charge, hydration energy, and interaction mechanism. These results emphasize the importance of accounting for competitive interactions in multi-metal systems, especially when designing adsorption-based treatment strategies for real industrial or environmental effluents.

3.7 Regeneration

Regenerating the adsorbent using an appropriate desorbing agent is crucial for enhancing the sustainability and cost-effectiveness of the adsorption process by enabling the repeated use of adsorbents while maintaining the high removal efficiency.^27,81 To determine the most suitable eluent, desorption experiments were conducted using 0.2 mol L⁻¹ solutions of HCl, H₂SO₄, HNO₃, and NaOH, with desorption efficiencies for Pb²⁺ and Cr⁶⁺ explained in Fig. 16(a). The outcomes indicated that H₂SO₄ exhibited the highest desorption efficiency (R_des) for Pb²⁺ (88.48%), whereas HNO₃ was most effective for Cr⁶⁺ (86.12%). Further optimization was performed by changing the H₂SO₄ and HNO₃ concentrations from 0.1 to 1 mol L⁻¹, as shown in Fig. 16(b). The highest R_des was attained at 0.4 mol L⁻¹ H₂SO₄ for Pb²⁺ (96.02%) and 0.6 mol L⁻¹ HNO₃ for Cr⁶⁺ (94.12%). These optimal concentrations ensure sufficient metal desorption while preventing excessive leaching of active functional groups from the adsorbent. At higher concentrations, an excessive removal of loosely bound species occurred, leading to a decline in overall R_es.^3,34,50 To evaluate the reusability of the adsorbent, cyclic regeneration tests were conducted using the optimized concentrations of 0.4 mol L⁻¹ H₂SO₄ for Pb²⁺ and 0.6 mol L⁻¹ HNO₃ for Cr⁶⁺, and the results are presented in Fig. 16(c). The MFA–CS adsorbent exhibited good stability, retaining desorption efficiencies of 85.24% and 44.71% after the 3rd and 15th cycles for Pb²⁺ and 84.36% and 37.12% after the 3rd and 15th cycles for Cr⁶⁺. The decline in R_des over multiple cycles can be linked to progressive surface saturation, partial loss of active sites, and potential structural degradation of the adsorbent.⁵⁷ However, the significant retention of desorption efficiency after the 15th regeneration cycle highlights the robustness and practical applicability of MFA–CS for repeated use in heavy metal removal processes.

Fig. 16 Regeneration studies: (a) determination of the desorbing agent. (b) Determination of the optimum concentration of the desorbing material. (c) Cyclic capability of MFA–CS.

3.8 Economic examination

The preliminary cost analysis conducted in this study (Table S9†) provides an estimate of the production cost for 1 g of MFA–CS adsorbent, which amounts to 655.95. Chitosan accounts for approximately 82.32% of the total cost, indicating that bulk-scale chitosan production and procurement optimization could significantly reduce the overall material cost. A comparative cost assessment (Table S10†) with other adsorbents reported in the literature shows that MFA–CS holds promise as a cost-effective and scalable option for wastewater remediation.

However, for real-world implementation and industrial scalability, a comprehensive techno-economic analysis (TEA) is essential. Such an analysis would not only evaluate raw material and utility costs but also include capital investment, process scale-up parameters, operational and maintenance costs, labour, waste handling, and lifecycle analysis. Furthermore, sensitivity analysis could be used to identify cost drivers and assess economic robustness under different market and operational conditions. These aspects are crucial for determining the overall economic feasibility and competitiveness of the MFA–CS adsorbent in large-scale wastewater treatment applications. A detailed TEA is proposed as a critical area for future study to support potential commercialization.

3.9 Mechanisms of adsorption

The adsorption mechanisms on the MFA–CS composite involve the simultaneous operation of surface complexation, ion-exchange, and electrostatic attraction; however, their relative contributions vary based on metal speciation, pH, and surface chemistry.⁷⁸ FTIR analysis revealed notable shifts and intensity changes in functional groups such as –NH₂, –COOH, and –OH after metal adsorption, confirming the dominance of surface complexation. These functional groups serve as electron donors, forming coordination bonds with Pb²⁺ and Cr⁶⁺ species, indicating that chemisorption governs the process.⁵⁰ The PSO kinetic model fit and the activation energy values (16–40 kJ mol⁻¹) from the D–R isotherm further support the prevalence of chemical interactions over physical ones.³⁴ Ion-exchange also played a significant role, particularly at pH 5 to 6, where protons and naturally present cations (e.g., Na⁺, Ca²⁺, Mg²⁺, and K⁺) on the adsorbent surface were replaced by the incoming heavy metal ions.^64,82 This exchange was more favourable for Pb²⁺ due to its larger ionic radius (1.19 Å) and lower hydration energy, which facilitated its replacement of surface cations and enhanced its uptake.³⁴ Cr⁶⁺, being smaller and more hydrated, exhibited a lower ion-exchange potential, which partly explains its lower removal efficiency. Electrostatic attraction primarily influenced the initial adsorption stage, especially for Cr⁶⁺ species in the form of HCrO₄⁻ or CrO₄²⁻, under acidic pH where the adsorbent surface is protonated and positively charged.⁸³ This mechanism enhanced the proximity of Cr⁶⁺ to active sites but did not govern the overall uptake. In contrast, for Pb²⁺, electrostatic effects were less influential due to the cation–cation repulsion at lower pH values. Additionally, the relatively low R² values (0.63 and 0.64) obtained from the IPD kinetic model suggest that the adsorption was largely driven by chemisorption compared to diffusion-controlled mechanisms.⁵⁰ In summary, while all three mechanisms coexisted, surface complexation was the predominant pathway, supported by ion-exchange in contributing to metal binding strength and selectivity and electrostatic attraction assisting in the initial migration of ions toward the adsorbent surface. A comprehensive illustration of the potential adsorption mechanisms occurring on the MFA–CS surface is presented in Fig. 17, emphasizing the interplay of ion-exchange, surface complexation, and electrostatic pull in the adsorption process. The pictorial representation of the mechanism has been taken from a study of methylene blue degradation using silica coated Fe₃O₄ magnetic nanoparticles.⁸⁴

Fig. 17 Potential adsorption mechanisms on the MFA–CS surface.

3.10 Column studies

3.10.1 Effect of column parameters on adsorption performance. The column setup utilized in this study is depicted in Fig. S2,† while the experimental procedure is detailed in section 2.4. The adsorption capability of the column was evaluated at different flow rates, initial metal ion concentrations, and bed heights to determine their influence on the adsorption capacity of Pb²⁺ and Cr⁶⁺. As shown in Fig. 18(a) of breakthrough curve, increasing the flow rate from 5 mL min⁻¹ to 10 mL min⁻¹ led to a significant increase of 47.41% in the Q_m value of Pb²⁺, from 65.93 mg g⁻¹ to 97.19 mg g⁻¹. However, a further increase in flow rate to 15 mL min⁻¹ resulted in only a slight increase of 8.01%, reaching 104.97 mg g⁻¹. This trend can be linked to the enhanced mass transfer of Pb²⁺ ions at higher flow rates, reducing external diffusion resistance and increasing the accessibility of adsorption sites. However, outside a certain flow rate, reduced residence time limits the adsorption efficiency due to inadequate contact time between the adsorbent and metal ions.⁴⁰ For Cr⁶⁺, a similar trend was observed initially, with the adsorption capacity increased from 31.56 mg g⁻¹ to 42.08 mg g⁻¹ when the flow rate was enhanced from 5 mL min⁻¹ to 10 mL min⁻¹. However, the adsorption capacity declined to 32.91 mg g⁻¹ at a flow rate of 15 mL min⁻¹. This reduction occurred due to the decreased residence time, which prevents Cr⁶⁺ ions from fully interacting with the adsorbent surface, leading to incomplete adsorption.⁸⁵

Fig. 18 Breakthrough curve of column studies: (a) influence of the flow rate; (b) influence of inlet metal concentration; (c) influence of the bed height.

The adsorption capacity of Pb²⁺ exhibited a nonlinear response to changes in initial metal concentration, as shown in Fig. 18(b). The maximum q_e increased from 74.54 mg g⁻¹ at 250 mg L⁻¹ to 97.19 mg g⁻¹ at 500 mg L⁻¹ and further to 128.50 mg g⁻¹ at 750 mg L⁻¹. However, at 1000 mg L⁻¹, the adsorption capacity slightly decreased to 110.62 mg g⁻¹. This behaviour can be explained by the initial rise in mass transfer driving force at higher concentrations, which enhances adsorption. However, at excessively high concentrations, the available active sites became saturated, leading to a decline in further adsorption.¹⁴ For Cr⁶⁺, maximum q_e increased from 36.07 mg g⁻¹ at 250 mg L⁻¹ to 42.08 mg g⁻¹ at 500 mg L⁻¹ but then dropped to 25.25 mg g⁻¹ at 750 mg L⁻¹ and slightly recovered to 27.65 mg g⁻¹ at 1000 mg L⁻¹. The decline at higher concentrations indicates competitive interactions among Cr⁶⁺ ions for active sites, potentially leading to saturation and reduced adsorption efficiency.⁸⁶

The variation in bed height had an impact on adsorption performance, as presented in Fig. 18(c). For Pb²⁺, the adsorption capacity was highest at 5 cm (255.61 mg g⁻¹) but decreased to 128.5 mg g⁻¹ at 10 cm and remained relatively stable at 130.47 mg g⁻¹ at 15 cm. The initial high adsorption capacity at 5 cm indicates that the adsorption sites were more readily accessible with a smaller bed height, leading to efficient adsorption. However, as the bed height increased, mass transfer limitations and increased intra-particle diffusion resistance have reduced the effectiveness of adsorption.⁸⁷ In the case of Cr⁶⁺, the Q_e initially increased from 30.07 mg g⁻¹ at 5 cm to 42.08 mg g⁻¹ at 10 cm, which indicates an optimal balance between contact time and diffusion resistance. However, at 15 cm, the capacity declined to 31.21 mg g⁻¹, possibly due to the reduced efficiency in metal ion transport through the larger bed height, leading to lower adsorption effectiveness.⁶¹ Q_m values of 255.61 mg g⁻¹ for Pb²⁺ and 42.08 mg g⁻¹ for Cr⁶⁺ were obtained in the column studies with the optimal column parameters. The breakthrough parameters at the optimum conditions of metal concentration, bed height, and flow rate are given in Table S11† for both Pb²⁺ and Cr⁶⁺ metals.

3.10.2 Breakthrough curve modelling. The results of the column studies were attempted to fit using two mathematical models: Yoon–Nelson and Thomas. The model formulae are listed in Table S4,† with fitting results depicted in Fig. 19 for the Yoon–Nelson model and Fig. 20 for the Thomas model, covering the removal of both Pb²⁺ and Cr⁶⁺ metals. The model parameters calculated for both the metals are given in Table 6. From the results, it is evident that the Thomas model demonstrated the best fit (R² = 0.99) across all variations in flow rate, bed height, and metal concentration for both Pb²⁺ and Cr⁶⁺, compared to the Yoon–Nelson model. For Pb²⁺, the Yoon–Nelson rate constant (K_YN) changed between 0.013 and 0.027 min⁻¹, while the required time for 50% breakthrough (τ) ranged from 440.18 to 870.29 min. For Cr⁶⁺, the K_YN values ranged from 0.013 to 0.02 min⁻¹, with τ values varying from 125.38 to 545.38 min. The rate constant (K_Th) for Pb²⁺ varied between 0.27 and 3.45 mL min⁻¹ mg⁻¹, while the q_o ranged from 64.12 to 250.43 mg g⁻¹. For Cr⁶⁺, the K_Th values ranged from 0.26 to 3.26 mL min⁻¹ mg⁻¹, and q_o varied between 24.38 and 41.63 mg g⁻¹. From the breakthrough curves, the Thomas model exhibited a better relationship with the experimental data than the Yoon–Nelson model, as evidenced by consistently higher R² values. This indicates that the Thomas model, which assumes Langmuir kinetics, more accurately describes the adsorption process under column operation. The superior fit of the Thomas model specified that adsorption followed a PSO kinetic behaviour, with the chemisorption mechanism.^40,61

Fig. 19 Yoon–Nelson model fittings for the column studies to remove Pb²⁺ and Cr⁶⁺: (a) change in the flow rate; (b) change in metal concentration; (c) change in the bed height.

Fig. 20 Thomas model fittings for the column studies to remove Pb²⁺ and Cr⁶⁺: (a) change in the flow rate; (b) change in metal concentration; (c) change in the bed height.

Table 6 Breakthrough curve modelling in column studies

Model parameters	Flow rate (mL min^−1)			Initial concentration (mg L^−1)				Bed height (cm)
	5	10	15	250	500	750	1000	5	10	15
Yoon–Nelson (Pb^2+)
KYN	0.017	0.013	0.013	0.027	0.013	0.021	0.013	0.017	0.02	0.03
τ	870.29	700.15	540.42	870.15	700.10	560.25	440.18	600.95	565.82	800.38
R^2	0.96	0.95	0.97	0.98	0.96	0.97	0.99	0.97	0.98	0.97
Yoon–Nelson (Cr^6+)
KYN	0.016	0.015	0.014	0.013	0.015	0.02	0.018	0.02	0.015	0.015
τ	440.25	340.55	220.85	545.38	340.45	170.92	125.38	152.62	320.87	377.18
R^2	0.96	0.97	0.99	0.98	0.95	0.97	0.96	0.98	0.95	0.97
Thomas (Pb^2+)
KTh	3.45	2.74	2.73	1.08	0.27	0.41	0.27	0.88	1.03	1.51
qo	64.12	95.48	110.98	72.48	95.87	124.38	105.73	250.43	125.37	128.68
R^2	0.99	0.99	0.98	0.99	0.99	0.99	0.98	0.99	0.99	0.99
Thomas (Cr^6+)
KTh	3.26	3.13	3.03	0.26	0.31	0.47	0.54	1.14	0.78	0.80
qo	30.47	40.97	30.15	33.68	41.07	24.38	26.37	28.37	41.63	30.58
R^2	0.99	0.98	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99

---

4. Conclusions

The MFA–CS adsorbent proved to be a highly efficient material for the mitigation of Pb²⁺ and Cr⁶⁺ from aqueous solutions. The three-level optimization studies yielded Q_m values of 352.19 mg g⁻¹ for Pb²⁺ and 265.13 mg g⁻¹ for Cr⁶⁺ in batch studies, with adsorption behaviour well defined by the Langmuir isotherm and PSO models, highlighting a chemisorption-driven monolayer adsorption process. Thermodynamic studies have proven that the adsorption occurred spontaneously and endothermically. Notably, MFA–CS confirmed reusability up to 15 regeneration cycles. In column studies, the adsorbent achieved Q_m values of 255.61 mg g⁻¹ for Pb²⁺ and 42.08 mg g⁻¹ for Cr⁶⁺, with breakthrough curves well defined by the Thomas model. The MFA–CS adsorbent offers a promising solution for wastewater treatment applications, driven primarily by the ion exchange, electrostatic attraction, and surface complexation mechanisms.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this study.

Author contributions

Khandgave Santosh Sopanrao: synthesis, characterization, experiments, data analysis, and drafting. Inkollu Sreedhar: conceptualization, methodology, supervision, validation, review, and project management.

Conflicts of interest

The authors confirm the absence of any known financial or personal conflicts of interest that could have influenced the findings of this study.

Acknowledgements

The researchers sincerely appreciate the Hyderabad campus of BITS, Pilani, for granting access to essential facilities and gratitude to all the researchers who assisted in data collection for this study. We appreciate the technical staff of Central Analytical Lab for their support.

References

1. L. Zhang, S. Tang, F. He, Y. Liu, W. Mao and Y. Guan, Chem. Eng. J., 2019, 378, 122215,  DOI:10.1016/j.cej.2019.122215.
2. N. N. A. Malek, A. H. Jawad, K. Ismail, R. Razuan and Z. A. ALOthman, Int. J. Biol. Macromol., 2021, 189, 464–476,  DOI:10.1016/j.ijbiomac.2021.08.160.
3. K. S. Sopanrao and I. Sreedhar, Sep. Purif. Technol., 2024, 340, 126731,  DOI:10.1016/j.seppur.2024.126731.
4. A. A. E. A. Elfiky, M. F. Mubarak, M. Keshawy, I. E. T. El Sayed and T. A. Moghny, Environ. Sci. Pollut. Res., 2023, 30, 79091–79105,  DOI:10.1007/s11356-023-27691-x.
5. A. U. Rajapaksha, R. Selvasembian, A. Ashiq, V. Gunarathne, A. Ekanayake, V. O. Perera, H. Wijesekera, S. Mia, M. Ahmad, M. Vithanage and Y. S. Ok, Sci. Total Environ., 2022, 809, 152055,  DOI:10.1016/j.scitotenv.2021.152055.
6. E. Osmani, I. Dimitrievska, P. Paunovik, K. Atkovska, F. Rexhepi and A. Grozdanov, Compos. Theory Pract., 2024, 24, 87–94,  DOI:10.62753/ctp.2024.02.2.2.
7. A. Adamczuk and D. Kołodyńska, Chem. Eng. J., 2015, 274, 200–212,  DOI:10.1016/j.cej.2015.03.088.
8. J. Sun, Y. Zhou, P. Hu, R. Duan, W. Wang, Y. Ye, M. Chen and X. Chen, JOM, 2025, 1–14,  DOI:10.1007/s11837-024-07103-2.
9. X. Ma, X. Zhang, Y. Li, Q. Xiong, H. Wu, J. Mei and Z. Zhang, J. Water Process Eng., 2024, 68, 106294,  DOI:10.1016/J.JWPE.2024.106294.
10. S. K. Mondal, C. Wu, F. C. Nwadire, A. Rownaghi, A. Kumar, Y. Adewuyi and M. U. Okoronkwo, Langmuir, 2022, 38, 903–913,  DOI:10.1021/acs.langmuir.1c01829.
11. V. M. Boddu, K. Abburi, J. L. Talbott and E. D. Smith, Environ. Sci. Technol., 2003, 37, 4449–4456,  DOI:10.1021/es021013a.
12. I. A. Mohammed, A. H. Jawad, A. S. Abdulhameed and M. S. Mastuli, Int. J. Biol. Macromol., 2020, 161, 503–513,  DOI:10.1016/j.ijbiomac.2020.06.069.
13. E. Hidayat, T. Yoshino, S. Yonemura, Y. Mitoma and H. Harada, Materials, 2023, 16(6), 2532,  DOI:10.3390/ma16062532.
14. Y. S. Petrova, A. V. Pestov and L. K. Neudachina, Sep. Sci. Technol., 2016, 51, 1437–1445,  DOI:10.1080/01496395.2016.1157085.
15. A. H. Ragab, N. F. Gumaah, A. A. El Aziz Elfiky and M. F. Mubarak, BMC Chem., 2024, 18, 1–15,  DOI:10.1186/s13065-024-01211-5.
16. A. F. Shaaban, D. A. Fadel, A. A. Mahmoud, M. A. Elkomy and S. M. Elbahy, J. Environ. Chem. Eng., 2014, 2, 632–641,  DOI:10.1016/j.jece.2013.11.001.
17. J. Goel, K. Kadirvelu, C. Rajagopal and V. K. Garg, J. Hazard. Mater., 2005, 125, 211–220,  DOI:10.1016/j.jhazmat.2005.05.032.
18. F. Gode and E. Moral, Bioresour. Technol., 2008, 99, 1981–1991,  DOI:10.1016/j.biortech.2007.03.026.
19. M. F. Mubarak, G. E. Khedr and H. M. El Sharkawy, J. Alloys Compd., 2024, 1000, 175151,  DOI:10.1016/j.jallcom.2024.175151.
20. R. Hosny, M. Fathy, M. Ramzi, T. Abdel Moghny, S. E. M. Desouky and S. A. Shama, Egypt. J. Pet., 2016, 25, 391–396,  DOI:10.1016/j.ejpe.2015.09.006.
21. A. K. El-Sawaf, A. A. Nassar, A. A. El Aziz Elfiky and M. F. Mubarak, Polym. Bull., 2024, 81, 12451–12476,  DOI:10.1007/s00289-024-05279-w.
22. M. Ramzi, R. Hosny, M. El-Sayed, M. Fathy and T. A. Moghny, Int. J. Chem. Sci., 2016, 14, 16–28,  DOI:10.1007/s00290-025-0972-768X.
23. S. Chen, M. Zhong, H. Wang, S. Zhou, W. Li, T. Wang and J. Li, Int. J. Environ. Sci. Technol., 2023, 20, 1551–1568,  DOI:10.1007/s13762-022-04002-4.
24. N. Esfandiar, R. Suri and E. R. McKenzie, J. Hazard. Mater., 2022, 423, 126938,  DOI:10.1016/j.jhazmat.2021.126938.
25. A. M. Zayed, B. S. Metwally, M. A. Masoud, M. F. Mubarak, H. Shendy and M. S. M. Abdel Wahed, Appl. Nanosci., 2024, 14, 21–32,  DOI:10.1007/s13204-023-02939-7.
26. A. A. E. A. Elfiky, M. F. Mubarak, M. Keshawy, I. E. T. El Sayed and T. A. Moghny, Environ. Dev. Sustainable, 2024, 26, 19935–19957,  DOI:10.1007/s10668-023-03444-1.
27. W. Luo, Z. Bai and Y. Zhu, RSC Adv., 2018, 8, 13370–13387,  10.1039/c7ra13064c.
28. P. K. Patel, L. M. Pandey and R. V. S. Uppaluri, Environ. Res., 2024, 240, 117502,  DOI:10.1016/j.envres.2023.117502.
29. A. K. El-Sawaf, S. R. El-Dakkony, M. A. Zayed, A. M. Eldesoky, A. A. Nassar, A. El Shahawy and M. F. Mubarak, Results Eng., 2024, 22, 101971,  DOI:10.1016/j.rineng.2024.101971.
30. Y. Ren, H. A. Abbood, F. He, H. Peng and K. Huang, Chem. Eng. J., 2013, 226, 300–311,  DOI:10.1016/j.cej.2013.04.059.
31. U. Habiba, A. M. Afifi, A. Salleh and B. C. Ang, J. Hazard. Mater., 2017, 322, 182–194,  DOI:10.1016/j.jhazmat.2016.06.028.
32. Z. Wang, P. Jin, M. Wang, G. Wu, J. Sun, Y. Zhang, C. Dong and A. Wu, J. Chem. Technol. Biotechnol., 2018, 93, 2691–2700,  DOI:10.1002/jctb.5624.
33. M. Monier, D. M. Ayad and D. A. Abdel-Latif, Colloids Surf., B, 2012, 94, 250–258,  DOI:10.1016/j.colsurfb.2012.01.051.
34. K. S. Sopanrao and I. Sreedhar, Environ. Sci. Pollut. Res., 2024 DOI:10.1007/s11356-024-33727-7.
35. H. Arabyarmohammadi, A. K. Darban, M. Abdollahy, R. Yong, B. Ayati, A. Zirakjou and S. E. A. T. M. van der Zee, J. Polym. Environ., 2018, 26, 2107–2119,  DOI:10.1007/s10924-017-1102-6.
36. S. S. Khandgave and I. Sreedhar, Mater. Today: Proc., 2023, 72, 19–26,  DOI:10.1016/j.matpr.2022.05.367.
37. Y. Li, Z. Zhang, X. Liu, S. Che, N. Shi, Y. Chen and M. Yan, Int. J. Biol. Macromol., 2022, 207, 760–770,  DOI:10.1016/j.ijbiomac.2022.03.133.
38. H. Xu, X. Li, M. Gao, X. Hu, X. Zhang, Y. Li, X. Xu, J. Hu, C. Tang and X. Hu, J. Environ. Chem. Eng., 2022, 10, 107101,  DOI:10.1016/J.JECE.2021.107101.
39. H. N. Tran, S. J. You and H. P. Chao, Waste Manage. Res., 2016, 34, 129–138,  DOI:10.1177/0734242X15615698.
40. S. Sireesha and I. Sreedhar, Bioresour. Technol. Rep., 2023, 22, 101486,  DOI:10.1016/j.biteb.2023.101486.
41. A. S. Lall, A. K. Pandey and J. V. Mani, Pollution, 2022, 8, 249–267,  DOI:10.22059/POLL.2021.329212.1164.
42. B. Qiu, X. Tao, H. Wang, W. Li, X. Ding and H. Chu, J. Anal. Appl. Pyrolysis, 2021, 155, 105081,  DOI:10.1016/J.JAAP.2021.105081.
43. B. O. Nardis, J. R. Franca, J. S. d. S. Carneiro, J. R. Soares, L. R. G. Guilherme, C. A. Silva and L. C. A. Melo, Sci. Total Environ., 2021, 151559,  DOI:10.1016/j.scitotenv.2021.151559.
44. M. F. Mubarak, H. Selim, H. B. Hawash and M. Hemdan, Environ. Sci. Pollut. Res., 2024, 31, 2297–2313,  DOI:10.1007/s11356-023-31240-x.
45. M. Hemdan, A. H. Ragab, H. A. El-Siaad, J. K. Kamel, N. F. Gumaah and M. F. Mubarak, Environ. Sci. Pollut. Res., 2024, 31, 66164–66183,  DOI:10.1007/s11356-024-35612-9.
46. J. Sobik-Szołtysek, K. Wystalska, K. Malińska and E. Meers, Materials, 2021, 14, 1–21,  DOI:10.3390/ma14216566.
47. A. H. Ragab, B. S. Mettwally, M. F. Mubarak, A. Al-Ghamdi and M. Hemdan, J. Inorg. Organomet. Polym. Mater., 2024, 34, 1491–1505,  DOI:10.1007/s10904-023-02851-1.
48. D. Mohan, A. Sarswat, Y. S. Ok and C. U. Pittman, Bioresour. Technol., 2014, 160, 191–202,  DOI:10.1016/j.biortech.2014.01.120.
49. F. El Mansouri, H. El Farissi, F. Cacciola, A. Talhaoui, A. El Bachiri, A. Tahani, J. C. G. E. da Silva and J. Brigui, Polym. Adv. Technol., 2022, 33, 2254–2264,  DOI:10.1002/pat.5676.
50. K. S. Sopanrao, A. Venugopal, C. M. Patel and I. Sreedhar, Environ. Sci. Pollut. Res., 2024 DOI:10.1007/s11356-024-35653-0.
51. J. Xiang, Q. Lin, X. Yao and G. Yin, Environ. Res., 2021, 195, 110650,  DOI:10.1016/j.envres.2020.110650.
52. M. Thakur, J. K. Rajput and R. Kumar, J. Hazard. Mater. Adv., 2023, 11, 100362,  DOI:10.1016/J.HAZADV.2023.100362.
53. K. Santosh, S. Sarthak, G. Sadamanti, S. Utkarsh and U. Inkollu, Biomass Convers. Biorefin., 2023, 14(18), 21939–21961,  DOI:10.1007/s13399-023-04411-6.
54. S. Siddiqui, P. Bhatnagar, S. Sireesha, K. S. Sopanrao and I. Sreedhar, Bioresour. Technol. Rep., 2023, 21, 101304,  DOI:10.1016/j.biteb.2022.101304.
55. S. Sireesha and I. Sreedhar, Mater. Today: Proc., 2023, 72, 34–40,  DOI:10.1016/J.MATPR.2022.05.454.
56. M. B. Shakoor, Z. L. Ye and S. Chen, Sci. Total Environ., 2021, 779, 146240,  DOI:10.1016/j.scitotenv.2021.146240.
57. P. K. Patel, L. M. Pandey and R. V. S. Uppaluri, Chem. Eng. J., 2023, 459, 141563,  DOI:10.1016/j.cej.2023.141563.
58. Z. H. Khan, M. Gao, W. Qiu, M. S. Islam and Z. Song, Chemosphere, 2020, 246, 125701,  DOI:10.1016/j.chemosphere.2019.125701.
59. M. Hemdan, A. H. Ragab, S. S. Elyan, M. A. Taher and M. F. Mubarak, J. Cluster Sci., 2025, 36, 2,  DOI:10.1007/s10876-024-02730-w.
60. M. F. Mubarak, A. Adaileh, I. A. Ahmed, M. A. Ali and M. Hemdan, J. Cluster Sci., 2025, 36, 27,  DOI:10.1007/s10876-024-02740-8.
61. S. Sireesha and I. Sreedhar, Environ. Sci. Pollut. Res., 2024 DOI:10.1007/s11356-024-33551-z.
62. H. Zhang, A. M. Omer, Z. Hu, L. Y. Yang, C. Ji and X. K. Ouyang, Int. J. Biol. Macromol., 2019, 135, 490–500,  DOI:10.1016/j.ijbiomac.2019.05.185.
63. A. A. Nassar, M. F. Mubarak, A. K. El-Sawaf, M. A. Zayed and M. Hemdan, Int. J. Biol. Macromol., 2025, 284, 137983,  DOI:10.1016/j.ijbiomac.2024.137983.
64. N. S. Surgutskaia, A. D. Martino, J. Zednik, K. Ozaltin, L. Lovecká, E. D. Bergerová, D. Kimmer, J. Svoboda and V. Sedlarik, Sep. Purif. Technol., 2020, 247, 116914,  DOI:10.1016/j.seppur.2020.116914.
65. G. Lian, B. Wang, X. Lee, L. Li, T. Liu and W. Lyu, Sci. Total Environ., 2019, 697, 134119,  DOI:10.1016/j.scitotenv.2019.134119.
66. N. Y. Jyoti, S. Singh, S. Das and S. Srivastava, Environ. Technol. Innovation, 2023, 32, 103310,  DOI:10.1016/j.eti.2023.103310.
67. M. Basu, A. K. Guha and L. Ray, J. Cleaner Prod., 2017, 151, 603–615,  DOI:10.1016/J.JCLEPRO.2017.03.028.
68. S. Cairns, S. Chaudhuri, G. Sigmund, I. Robertson, N. Hawkins, T. Dunlop and T. Hofmann, Environ. Technol. Innovation, 2021, 24, 101961,  DOI:10.1016/j.eti.2021.101961.
69. S. Kokate, K. Parasuraman and H. Prakash, Results Eng., 2022, 14, 100439,  DOI:10.1016/j.rineng.2022.100439.
70. R. D. C. Soltani, G. S. Khorramabadi, A. R. Khataee and S. Jorfi, J. Taiwan Inst. Chem. Eng., 2014, 45, 973–980,  DOI:10.1016/J.JTICE.2013.09.014.
71. J. Wei, C. Tu, G. Yuan, D. Bi, L. Xiao, B. K. G. Theng, H. Wang and Y. S. Ok, J. Hazard. Mater., 2019, 368, 541–549,  DOI:10.1016/J.JHAZMAT.2019.01.080.
72. K. Kulkarni, S. Dhulipudi, Y. Chendake, A. Kulkarni and C. V. Subrahmanyam, Water, Air, Soil Pollut., 2022, 233(7), 245,  DOI:10.1007/s11270-022-05707-5.
73. S. Cheng, Y. Liu, B. Xing, X. Qin, C. Zhang and H. Xia, J. Cleaner Prod., 2021, 314, 128074,  DOI:10.1016/j.jclepro.2021.128074.
74. M. F. Hussein, M. F. Mubarak, A. M. Al-Sirhani and R. Hosny, Discov. Appl. Sci., 2024, 6, 519,  DOI:10.1007/s42452-024-06176-7.
75. P. K. Patel, L. M. Pandey and R. V. S. Uppaluri, Int. J. Biol. Macromol., 2023, 242(Part 1), 124812,  DOI:10.1016/j.ijbiomac.2023.124812.
76. E. Igberase, A. Ofomaja and P. O. Osifo, Int. J. Biol. Macromol., 2019, 123, 664–676,  DOI:10.1016/j.ijbiomac.2018.11.082.
77. A. D. Adaileh, A. H. Ragab, M. A. Taher, N. F. Gumaah, M. S. S. Soliman, A. Taha and M. F. Mubarak, Inorg. Chem. Commun., 2025, 173, 113779,  DOI:10.1016/J.INOCHE.2024.113779.
78. X. Fan, X. Wang, Y. Cai, H. Xie, S. Han and C. Hao, J. Hazard. Mater., 2022, 423, 127191,  DOI:10.1016/j.jhazmat.2021.127191.
79. S. Milićević, M. Vlahović, M. Kragović, S. Martinović, V. Milošević, I. Jovanović and M. Stojmenović, Minerals, 2020, 10, 1–16,  DOI:10.3390/min10090753.
80. M. Forghani, A. Azizi, M. J. Livani and L. A. Kafshgari, J. Solid State Chem., 2020, 291, 121636,  DOI:10.1016/J.JSSC.2020.121636.
81. S. S. Gabr, M. F. Mubarak, M. Keshawy, I. E. T. El Sayed and T. A. Moghny, Appl. Water Sci., 2023, 13, 1–19,  DOI:10.1007/s13201-023-02018-w.
82. B. Li and Z. Ren, J. Polym. Environ., 2020, 28, 1811–1821,  DOI:10.1007/s10924-020-01728-5.
83. G. J. Jiao, J. Ma, Y. Li, D. Jin, Z. Ali, J. Zhou and R. Sun, Chemosphere, 2021, 278, 130377,  DOI:10.1016/j.chemosphere.2021.130377.
84. K. R. M. Oraby, A. Villalonga, F. S. M. Hassan, M. A. Zayed, M. F. Mubarak, I. Ojeda, A. Sánchez and R. Villalonga, Process Biochem., 2025, 148, 10–16,  DOI:10.1016/j.procbio.2024.11.012.
85. S. Koppula, P. Jagasia, M. K. Panchangam and S. B. Manabolu Surya, J. Solid State Chem., 2022, 312, 123168,  DOI:10.1016/j.jssc.2022.123168.
86. L. P. Lingamdinne, G. K. R. Angaru, Y. Jeon, S. Lee, J. R. Koduru, J.-K. Yang and Y.-Y. Chang, New J. Chem., 2023, 47, 11964–11975,  10.1039/d3nj01416a.
87. Z. Ding, X. Hu, Y. Wan, S. Wang and B. Gao, J. Ind. Eng. Chem., 2016, 33, 239–245,  DOI:10.1016/j.jiec.2015.10.007.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary data related to this article are available in Appendix A. See DOI: https://doi.org/10.1039/d5ew00257e

---