Open Access Article
Open Access ArticleEnhancing fault detection in wastewater treatment plants: a multi-scale principal component analysis approach with the Kantorovich distance
K. Ramakrishna
Kini
a,
Fouzi
Harrou
*b,
Muddu
Madakyaru
 *c and
Ying
Sun
b
*c and
Ying
Sun
b
aDepartment of Instrumentation and Control Engineering, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, India
bKing Abdullah University of Science and Technology (KAUST) Computer, Electrical and Mathematical Sciences and Engineering (CEMSE) Division, Thuwal, 23955-6900, Saudi Arabia. E-mail: fouzi.harrou@kaust.edu.sa
cDepartment of Chemical Engineering, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, India. E-mail: muddu.m@manipal.edu
First published on 8th March 2025
Abstract
Anomaly detection in wastewater treatment plants (WWTPs) is critical for ensuring their reliable operation and preventing system failures. This paper proposes an advanced monitoring scheme that integrates multiscale principal component analysis (PCA) with a Kantorovich distance (KD)-driven monitoring approach to enhance WWTP monitoring in noisy environments. The combination of wavelet-based multiscale filtering with PCA effectively denoises the data, while the KD-driven scheme offers a robust metric for detecting deviations from normal operating conditions. This approach does not require labeled data and employs the nonparametric Kantorovich distance (KD) test, providing a flexible and practical solution for anomaly detection. Validation using data from the COST benchmark simulation model (BSM1) demonstrates the effectiveness of the proposed methods. The study evaluates different sensor faults—bias, intermittent, and aging—at varying signal-to-noise ratio (SNR) levels and explores the impact of different wavelet bases and decomposition levels on denoising and detection performance. The results show that the proposed scheme outperforms traditional PCA and multiscale PCA-based techniques, offering improved anomaly detection capabilities in the presence of significant noise.
Water impactThis research proposes an advanced monitoring system for wastewater treatment plants (WWTPs) that combines multiscale principal component analysis (PCA) with a Kantorovich distance (KD)-based approach to improve anomaly detection in noisy environments. By using wavelet-based multiscale filtering to denoise data and a robust KD-driven metric to detect deviations, this data-driven method enhances the monitoring of WWTPs. It ensures continuous operation, prevents water pollution, protects public health, and supports sustainable development by maintaining optimal plant performance. |
1 Introduction
Wastewater treatment plants (WWTPs) are crucial in maintaining public health and protecting the environment. They treat sewage and industrial effluents to remove contaminants, ensuring that the water released into rivers, lakes, or seas meets the necessary regulatory standards. The optimal operation of WWTPs is essential for avoiding the spread of waterborne diseases, protecting aquatic ecosystems, and ensuring the availability of clean water for various uses.1 The expanding urbanization and industry demand more efficient and reliable wastewater treatment.2 Monitoring the operational characteristics of WWTPs is essential due to various factors.3 It ensures compliance with environmental requirements, optimizes the efficiency of the treatment process, and reduces the likelihood of operational failures.4,5 Regular surveillance facilitates the identification of anomalies and inefficiencies in the system, hence enabling prompt interventions to prevent expensive malfunctions and violations of environmental standards. Additionally, it assists in preserving equipment and prolonging the lifespan of the infrastructure by ensuring that all components operate within their specified limitations.Traditionally, univariate monitoring charts such as cumulative sum (CUSUM), exponentially weighted moving average (EWMA), and generalized likelihood ratio (GLR) tests have been used for process monitoring. These methods are effective in detecting shifts and trends in single-variable data. However, these traditional methods have limitations when applied to multivariate data.6 They cannot capture the interrelationships between multiple variables, which is critical in complex systems like WWTPs. This limitation makes them less effective in environments where the process is influenced by several correlated factors. To address the limitations of univariate methods, multivariate monitoring techniques such as principal component analysis (PCA), independent component analysis (ICA), and partial least squares (PLS) have been developed. While these multivariate methods offer significant advantages in handling complex data, they also have limitations.7 For instance, PCA assumes linear relationships and may not perform well with nonlinear data. ICA requires the components to be statistically independent, which may not always be the case. PLS, while powerful, can be computationally intensive and sensitive to noise in the data.
In ref. 8, various statistical control charts (Shewhart, CUSUM, EWMA) were evaluated for fault detection in wastewater treatment. The EWMA chart proved to be the most effective, particularly for drift faults, with the lowest false alarm rate and optimal detection time. Monitoring manipulated variables also reduced missed detections compared to controlled variables, leading to better fault detectability and reduced energy consumption. In ref. 9, a dynamic principal component analysis (PCA)-based method was proposed for sensor fault isolation in WWTPs, overcoming the limitations of static methods in dynamic processes. The method was validated with simulated fault scenarios, showing superior performance in sensor fault detection compared to previous approaches. The study in ref. 10 introduced a soft sensor approach combining PCA and k-nearest neighbor (KNN) to monitor and detect abnormalities in water resource recovery facilities (WRRFs). PCA reduces data dimensions and reveals interrelationships, while KNN effectively detects anomalies and handles high-dimensional data. Nonparametric thresholds from kernel density estimation enhance detection accuracy and radial visualization aids in fault analysis. Tested on real data from a WRRF in Saudi Arabia, the approach outperforms conventional PCA-based methods in detecting and diagnosing influent measurement abnormalities. In ref. 11, an adaptive process monitoring framework using incremental principal component analysis (IPCA) was proposed to address the limitations of conventional PCA in time-varying processes. The framework updates the PCA eigenspace with new data at low computational cost and uses complete decomposition contribution (CDC) for variable contributions. The empirical best linear unbiased prediction (EBLUP) method is included for imputing missing values. Simulations on benchmark model BSM2 demonstrate the framework's effectiveness in distinguishing time-varying behavior from faults and accurately isolating small sensor faults. The study in ref. 12 proposed a distributed fault detection and diagnosis method using PCA in a whole-plant monitoring scheme. The plant is divided into multiple blocks, with local PCA-based fault detection in each block. The results are then centralized for global fault detection and diagnosis. Compared to centralized PCA and other distributed PCA methods, this approach performs better in detecting faults and reducing communication costs, particularly in a WWTP. In another study,13 a Bayesian Gaussian latent variable model (Bay-GPLVM) was proposed for nonlinear process monitoring and fault diagnosis, addressing the limitations of traditional probabilistic PCA (PPCA). The Bay-GPLVM enhances robustness by obtaining posterior distributions for latent variables, outperforming PPCA-based methods in handling nonlinear processes, and improving monitoring efficiency. In ref. 14, a kernel PCA-based fault diagnosis system was developed for biological reactions in full-scale WWTPs, using common bio-chemical sensors like ORP and DO. The system targets the sequencing batch reactor (SBR) process, distinguishing between normal and abnormal operational statuses. After data preprocessing, various dimension reduction techniques (PCA, linear discriminant analysis (LDA), kernel PCA) were applied, and the combination of kernel PCA and LDA proved to be effective.14,15 Fusion data yielded higher fault recognition rates than raw sensor data, demonstrating the system's superiority in diagnosing faults. The study in ref. 16 proposed a kernel-based machine learning method using KPCA and a one-class support vector machine (OCSVM) to monitor influent conditions in WWTPs, effectively detecting anomalies in complex, non-linear data. Applied to a seven-year dataset, this approach outperforms traditional models, offering accurate anomaly detection with minimal computational cost and adaptability across different WWTPs.
Recent studies in WWTPs have explored a range of fault detection approaches, showcasing diverse strategies and notable advancements.17 Aguado et al.18 applied adaptive modeling with Hotelling's T2-statistic and fuzzy c-means clustering to detect process deviations and isolate faults, using one-year simulation data from the BSM1_LT prototype. Harrou et al.19 developed deep belief networks (DBNs) and one-class support vector machines (OCSVMs) for early anomaly detection, tested on data from a decentralized WWTP in Golden, CO, USA. Xu et al.20 proposed a CPSO–DKPCA method combining dynamic kernel principal component analysis (DKPCA) with chaotic particle swarm optimization (CPSO) and Granger causality (GC) analysis for enhanced fault detection. The approach was evaluated using BSM1 simulation data and real WWTP data from Sichuan. Yang et al.21 proposed a Wasserstein distance-based joint distribution adaptation strategy for improved abnormality detection, validated using the benchmark simulation model no. 1 (BSM1) for a WWTP. Marais et al.8 compared statistical control charts, identifying the EWMA method for its low false alarm rates and fast detection, validated using BSM1 data. Cheng et al. (2021)22 proposed a robust adaptive boosted canonical correlation analysis (Rab-CCA) method to reduce missed and false alarms in noisy environments, validated using BSM1 and real full-scale WWTP data. Chang et al. (2024)23 combined uniform manifold approximation and projection (UMAP) with support vector data description (SVDD) for improved detection and adaptability, validated using BSM1 simulation data. Lastly, Kini et al. (2024)24 enhanced fault detection using a data-driven PCA approach integrated with the Kolmogorov–Smirnov (KS) test, achieving high F1 scores for various sensor fault detections based on BSM1 simulation data. These studies collectively underscore the innovative use of statistical, machine learning, and adaptive modeling techniques to address the complex fault detection challenges in WWTPs.
Monitoring WWTPs faces significant challenges due to noisy data, arising from environmental factors, sensor malfunctions, and operational variances. This noise can obscure critical information, reducing the effectiveness of traditional and multivariate monitoring methods such as PCA, ICA, and PLS, often resulting in false alarms or missed detections. Wavelet-based multiscale filtering has been proposed as an effective solution to mitigate this issue. By decomposing signals into different frequency components, this technique isolates noise at specific scales, providing cleaner signals and enhancing the detection of meaningful patterns and anomalies. Effective anomaly detection in WWTP influents, such as irregularities in the flow rate, biochemical oxygen demand (BOD), and pollutant levels, is crucial for maintaining efficient operations and preventing system failures. Accurate detection ensures efficient system operation, optimizing resources, reducing equipment wear, and preventing costly downtime, repairs, and environmental harm. The contributions of this study are summarized as follows.
• Firstly, this study presents an effective monitoring scheme that combines multiscale PCA with Kantorovich distance (KD)-driven techniques, enhancing anomaly detection in WWTPs. Specifically, the nonparametric KS test is applied to evaluate the distribution of residuals produced by PCA. After PCA is used to model the normal operating conditions of a system, residuals—representing the difference between the observed data and the PCA-reconstructed data—are calculated. In the case of a normally operating system, these residuals should follow a certain distribution (e.g., Gaussian distribution). However, when an anomaly occurs, the residuals deviate from this expected distribution. The KS test is suitable for this because it is nonparametric and makes no assumptions about the underlying data distribution. It compares the empirical distribution of the residuals against the expected distribution, quantifying the maximum difference between the two. If the KS statistic exceeds a predefined threshold, it indicates that the residual distribution has significantly deviated, signaling the presence of an anomaly. This approach allows for flexible and robust detection of abnormalities without requiring predefined labels or assumptions about the noise structure, making it particularly suited for noisy environments like WWTPs.
• Secondly, integrating discrete wavelet transform (DWT) with PCA significantly enhances anomaly detection in noisy environments like WWTPs. The ability of DWT to decompose data into different frequency components across multiple scales allows for effective noise reduction, as high-frequency noise can be filtered out while retaining essential low-frequency signal information. Denoising the data before applying PCA makes the input cleaner, leading to more accurate modeling of normal operating conditions and reducing false positives. Additionally, DWT enhances feature extraction by allowing PCA to capture global trends and local variations, improving sensitivity to subtle anomalies that single-scale methods might miss. This multiscale approach boosts the robustness of anomaly detection, particularly in environments with low signal-to-noise ratios (SNRs), where sensor data are often noisy. As a result, the combined DWT–PCA method provides a more resilient monitoring system, ensuring early and reliable fault detection even under challenging operational conditions.
• Finally, data from the COST benchmark simulation model (BSM1) are employed to validate the proposed fault detection method, which is particularly suited for monitoring and optimizing the operation of wastewater treatment plants (WWTPs). The BSM1 model offers a realistic simulation environment, enabling comprehensive evaluation of the approach under various sensor fault conditions. In this study, different types of sensor faults—such as bias, drift, intermittent, freezing, and precision degradation—are simulated to assess the robustness and accuracy of the detection scheme. Each fault represents a common failure mode that can occur in WWTP sensors, impacting the accuracy and reliability of the data collected for operational monitoring. These faults are difficult to detect in real time, especially under noisy conditions, which makes the ability to identify them early critical for maintaining the efficiency and safety of WWTP operations. Four key metrics are adopted to evaluate the performance of the proposed fault detection method: true positive rate (TPR), false positive rate (FPR), precision, and F1-score. The results from the study demonstrate that the proposed approach—combining discrete wavelet transform (DWT) for denoising with PCA and a Kantorovich distance-driven detection scheme—outperforms traditional PCA-based techniques. The integration of multiscale filtering and advanced residual analysis not only improves fault detection sensitivity, particularly for subtle or intermittent anomalies, but also reduces the occurrence of false positives. This leads to more reliable and efficient monitoring of WWTPs, ensuring timely identification and mitigation of sensor faults, even under significant noise conditions.
The remaining sections are organized as follows. Section 2 presents the foundational concepts, including an overview of PCA and its application in anomaly detection, the key principles of wavelet-based multiscale filtering, the Kantorovich distance (KD) and its role in anomaly detection, and the proposed MSPCA-KD-based fault detection approach. Section 3 discusses the dataset used in this study and evaluates the performance of the proposed method under various scenarios, including bias, drift, and intermittent sensor faults in noisy environments. Finally, section 4 concludes the study.
2 Methodology
2.1 Principal component analysis (PCA)
Principal component analysis (PCA) transforms correlated variables into uncorrelated principal components, capturing maximum variance and reducing dimensionality while preserving the data's essential structure.25,26 This makes it a vital tool for analyzing complex, high-dimensional processes such as wastewater treatment monitoring. The method begins with data standardization to zero mean and unit variance. The covariance matrix is then computed, followed by eigenvalue decomposition to derive eigenvalues λi and eigenvectors pi, which define the principal components:| ∑P = PΛ, | (1) |
| T = XstdPk, | (2) |
 | (3) |
2.2 Wavelet-based multi-scale filtering
Wavelet-based multiscale filtering effectively handles the time–frequency characteristics of WWTP data, capturing dynamics across multiple scales such as daily fluctuations and long-term biological activities. Wavelets provide compact signal representations in the time–frequency domain, enabling decomposition into distinct frequency components for selective noise reduction while preserving critical features.29,30Mathematically, a wavelet is represented as:
 | (4) |
 | (5) |
| x(t) = SP(t) + DP(t), | (6) |
2.3 Kantorovich distance (KD) and its application in anomaly detection
The Kantorovich distance (KD), also known as the Wasserstein distance or earth mover's distance (EMD), measures the distance between two probability distributions.32 It is widely used in anomaly detection, optimal transport, and machine learning for quantifying distributional dissimilarity.33 The KD captures the minimal cost of transporting mass between distributions, considering both distance and mass.34 Recent studies highlighted the KD's effectiveness in fault detection. Sanjula and Li35 used the KD for change point detection in industrial processes, leveraging PCA-based residuals. Arifin et al.36 applied the KD to detect pipeline leaks by monitoring residual mass flow rates. Kini37 employed the KD with non-Gaussian ICA for fault detection in chemical processes. Zongyu et al.38 combined the KD with Bayesian inference and multiblock variational autoencoders to enhance detection accuracy. Li39 used a KD-based approach for detecting sensor attacks, while Wang et al.40 integrated the KD with neighborhood preserving embedding for dynamic multivariate processes.Mathematically, the KD is defined for two distributions μ and ν on a metric space (X, d) as
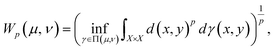 | (7) |
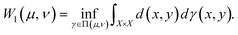 | (8) |
2.4 Proposed MSPCA-KD-based fault detection approach
Noise in WWTPs complicates fault detection and can mask critical features, leading to missed detections and increasing the risk of false alarms. When important signal components are obscured by noise, it becomes more difficult to identify abnormal behavior, resulting in delayed or missed fault identification. Additionally, excessive noise may cause the system to misinterpret normal fluctuations as faults, thus raising false alarms. This makes it essential to adopt a fault detection strategy that can accurately separate signals from noise, reducing both missed detections and false positives. Wavelet transforms have proven to be highly effective in signal processing, as they can filter out noise across both time and frequency domains. In this work, we introduce a method that leverages the combined strengths of wavelet-based multiscale filtering and PCA to enhance fault detection in noisy environments. Wavelet-based filtering excels at decomposing data into different frequency components, allowing the separation of noise from valuable signal features across multiple scales. This multiscale decomposition ensures that even subtle and localized signal changes—often masked by noise—are preserved, improving the detection of faults that might otherwise go overlooked. Additionally, we incorporate the KD, which is highly effective for measuring differences between probability distributions. Integrating the KD into the fault detection framework enhances the system's ability to handle various fault types, improving detection accuracy and robustness. This approach, referred to as the multiscale PCA-KD (MSPCA-KD), capitalizes on the noise-filtering capabilities of wavelets and the fault detection strengths of the KD, resulting in a highly effective strategy for identifying faults under noisy conditions. The proposed approach, depicted in the flowchart in Fig. 1, consists of both offline and online stages, ensuring efficient fault detection while maintaining a robust model based on historical data.The offline or training stage involves the following key steps:
• Multiscale filtering: the data are decomposed into various levels using wavelet functions, allowing effective noise reduction through multiscale denoising.
• Data preprocessing: the de-noised data are standardized to have zero mean and unit variance, ensuring uniform scaling across variables.
• PCA model development: a PCA model is then built using the denoised and standardized data. The optimal number of principal components (PCs) is selected based on the cumulative percent variance (CPV) technique, ensuring that the most informative components are retained.
• Residual generation: the residuals (Tr_Re) are calculated based on the difference between the original data (X) and the reconstructed data (![[X with combining circumflex]](https://www.rsc.org/images/entities/b_char_0058_0302.gif) ) from the PCA model. The expression used is:
) from the PCA model. The expression used is:
 | (9) |
• Threshold computation: KDE is applied to estimate the probability density function (PDF) of the Kantorovich distance (KD) based on the residuals from the training data. The process of threshold determination using KDE consists of the following steps:
1. KDE application: KDE is used to estimate the PDF of the KD statistic computed from the residuals. The density estimation is given by:41
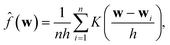 | (10) |
2. Threshold selection: the fault detection threshold is defined as the (1 − α)th quantile of the estimated distribution of the KD statistic obtained via Kernel density estimation (KDE), where α corresponds to a given probability of false alarms. In this study, α is fixed a priori at 0.05, ensuring that 95% of the KD statistics under normal conditions fall below this threshold.42 Mathematically, the threshold is expressed as:42
T = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) −1(1 − α) −1(1 − α) | (11) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) −1 is the inverse cumulative distribution function derived from KDE.
−1 is the inverse cumulative distribution function derived from KDE.
By using KDE to determine the threshold, the method becomes adaptable to different distributions and effectively reduces the chances of false alarms and missed detections in noisy environments.
The testing stage in the proposed FD based strategy consists of the following steps:
• Multi-scale filtering: the testing data are decomposed to different decomposition levels using wavelet functions to have de-noised data.
• Data pre-processing: the filtered data are pre-processed by subtracting the mean of the training data and dividing by the standard deviation of the training data to ensure consistency in the scale.
• Residual generation: similar to the training stage, residuals Te_Re are generated for the standardized data using eqn (9).
• KD statistic computation: the residuals Tr_Re and Te_Re undergo sample-wise comparison in a moving window of fixed length to generate the KD statistic.
• Final decision: the KD statistic is compared to the detection threshold. If the KD statistic exceeds the threshold, a fault is indicated; otherwise, normal operation is assumed.
3 Results and discussion
This section describes the WWTP data and evaluates the detection performance of the proposed MSPCA-KD strategy for identifying various sensor faults under noisy conditions. To quantify performance, four statistical metrics are used: fault detection rate (FDR), false alarm rate (FAR), precision, and F1-score. Detailed descriptions of these metrics can be found in ref. 24.3.1 Data description
This study evaluates the multiscale PCA-based Kantorovich distance anomaly detection method under different noisy conditions. We use data from the benchmark simulation model no. 1 (BSM1), a comprehensive wastewater treatment model developed by the European COST initiative. The BSM1 features a five-compartment activated sludge reactor with two anoxic and three aerobic tanks, designed for biological nitrogen removal (Fig. 2). Additionally, the model includes a secondary clarifier with a ten-layer non-reactive unit. The main objectives of the plant are to control dissolved oxygen and nitrate levels by adjusting the oxygen transfer coefficient and internal recycling flow rate. We assess the predictive performance of the anomaly detection method in this context.Fig. 2 shows the schematic diagram of WWTP process, with external reflux from the settler and internal reflux from the last aerated tank. Following the COST BSM1 benchmark, the simulation includes dry, storm, and rainy weather conditions.43 This study focuses on 14 days of dry weather data. The considered influent variables are listed in Table 1.
| Symbol | Definition | Unit |
|---|---|---|
| S S | Readily biodegradable substrate | g COD m−3 |
| X I | Particulate inert organic matter | g COD m−3 |
| X S | Slowly biodegradable substrate | g COD m−3 |
| X B,H | Active heterotrophic biomass | g COD m−3 |
| S NH | NH4+ + NH3 nitrogen | g N m−3 |
| S ND | Soluble biodegradable organic nitrogen | g N m−3 |
| X ND | Particulate biodegradable organic nitrogen | g N m−3 |
| Q i | Flow into the anoxic section | m3 d−1 |
Table 2 provides descriptive statistics for various variables. The distributions of most variables show varying degrees of skewness and kurtosis, indicating differences in the shape and spread of the data. Variables like SS, SND, and SNH exhibit positive skewness and leptokurtic distributions, suggesting a tendency for higher values and heavier tails. In contrast, variables like XB,H and XND show near-symmetrical distributions with platykurtic characteristics, indicating more normal-like distributions with lighter tails. The variable Qi also shows a moderate positive skew and a flatter peak compared to the normal distribution. Variables vary in skewness, with some right-skewed and others near-symmetrical.
| Variable | Mean | Std dev | Min | Q1 | Median | Q3 | Max | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| S S | 65.24 | 18.45 | 40.00 | 54.27 | 64.00 | 72.22 | 120.01 | 0.80 | 3.85 |
| X I | 45.60 | 21.79 | 14.84 | 25.62 | 45.30 | 59.93 | 109.83 | 0.43 | 2.53 |
| X S | 192.72 | 50.19 | 96.95 | 147.37 | 202.55 | 227.34 | 293.81 | −0.22 | 2.01 |
| X B,H | 26.48 | 7.81 | 13.35 | 19.51 | 27.56 | 31.59 | 42.74 | −0.09 | 2.03 |
| S NH | 30.14 | 7.01 | 20.00 | 26.41 | 29.80 | 34.46 | 50.00 | 0.64 | 3.42 |
| S ND | 6.52 | 1.84 | 4.00 | 5.43 | 6.40 | 7.22 | 12.00 | 0.80 | 3.85 |
| X ND | 9.95 | 2.93 | 5.02 | 7.33 | 10.36 | 11.88 | 16.07 | −0.09 | 2.03 |
| Q i | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448.59 448.59 |
5134.66 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.00 000.00 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610.75 610.75 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 264.00 264.00 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081.00 081.00 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.00 180.00 |
0.40 | 2.57 |
Fig. 3 shows the heatmap of the correlation matrix of the data under dry conditions. The correlation analysis of influent variables under dry weather conditions reveals several important relationships that shed light on the dynamics of the WWTP system. Firstly, a perfect correlation (1.00) between soluble biodegradable organic nitrogen (SND) and the readily biodegradable substrate (SS) suggests a direct interdependence between the availability of organic substrates and the concentration of soluble nitrogen. This is likely because both variables are closely tied to microbial nutrient processing within the system. As readily biodegradable substrates are consumed by microorganisms, the presence of soluble nitrogen is also affected, leading to their strong linear relationship.
Another notable perfect correlation (1.00) exists between particulate biodegradable organic nitrogen (XND) and active heterotrophic biomass (XB,H), indicating that nitrogenous particulate matter is highly associated with the microbial biomass responsible for organic matter decomposition. This strong link emphasizes the role of heterotrophic bacteria in processing particulate organic nitrogen, a key component of the nitrogen cycle in the WWTP.
In addition, the strong correlation (0.95) between the readily biodegradable substrate (SS) and ammonium nitrogen (SNH) reflects the interconnected nature of organic substrate availability and nitrogen levels in the influent. As organic matter degrades, nitrogen compounds such as ammonium are released, explaining their close relationship.
Furthermore, examining the correlations between the influent flow rate (Qi) and various variables under dry conditions reveals how flow impacts the system. A strong correlation (0.83) between Qi and the readily biodegradable substrate (SS) suggests that as flow increases, more organic material enters the system, likely from stable wastewater sources. Similarly, the high correlation (0.92) between Qi and particulate inert organic matter (XI) indicates a consistent influx of suspended solids with increasing flow, highlighting the presence of non-biodegradable particles in the influent stream. The moderate correlation between Qi and the slowly biodegradable substrate (XS) (0.69) implies that the influent is more concentrated with readily biodegradable materials, while the correlation with heterotrophic biomass (XB,H) (0.78) shows how flow influences microbial activity.
Finally, the strong correlations between Qi and both soluble biodegradable nitrogen (SND) (0.83) and particulate biodegradable nitrogen (XND) (0.78) suggest that nitrogenous compounds in both soluble and particulate forms increase as the flow rate rises, even under dry conditions. This pattern reflects the regular nitrogen load managed by the WWTP during normal operational states, illustrating the plant's capability to handle fluctuations in influent composition efficiently. Together, these correlations not only highlight the interplay between various chemical and biological processes in the treatment system but also emphasize the system's resilience under dry conditions. The interdependencies among influent variables suggest that the plant can maintain effective treatment performance by relying on the established relationships between organic matter, nitrogen compounds, and microbial biomass.
3.2 Monitoring results
The dataset used in this study comprises 1340 sampling instances across 8 variables, evenly divided into training and testing sets. The training data are essential for building data-driven reference models, which are then used to detect anomalies in the testing data. Both PCA and MSPCA models were developed using the training set. To determine the optimal number of principal components (PCs), the CPV criterion was employed, resulting in the selection of three PCs that captured the majority of the data variance. A moving window of size 40 was applied to calculate the KD-based fault indicator, which tracks system dynamics and identifies deviations from normal operation. For the MSPCA model, the optimal decomposition depths were determined to be 3, 3, and 4 for signal-to-noise ratio (SNR) levels of 20, 10, and 5, respectively. These varying depths reflect the model's ability to adapt to different noise levels, balancing denoising efficiency and anomaly detection sensitivity.The proposed MSPCA-KD strategy is compared with several conventional fault detection approaches, including PCA-T2, PCA-SPE, PCA-KD, MSPCA-T2, and MSPCA-SPE. These established methods serve as benchmarks to highlight the superior detection capabilities of the MSPCA-KD approach. The fault indicators' result plots display the fault indicator's time evolution using distinct color coding: the non-faulty region is marked in blue, the faulty region is in red, and the fault detection threshold is in black. This clear and intuitive visual representation effectively demonstrates the accuracy of each method in distinguishing between normal and faulty conditions over time, allowing for a straightforward assessment of their detection performance.
In this section, the monitoring performance for three distinct types of faults—bias, intermittent, and drift—is evaluated under three different noise scenarios: low noise level (SNR = 20), medium noise level (SNR = 10), and high noise level (SNR = 5). Each fault type represents a common failure mode in sensor systems, with unique characteristics that can significantly affect data quality and the accuracy of operational monitoring in WWTPs.
• Bias faults: these occur when a sensor systematically deviates from the true value, consistently over- or underestimating the measured variable. This can lead to persistent inaccuracies in the collected data, potentially causing long-term inefficiencies or suboptimal process control in the WWTP.
• Intermittent faults: these faults arise sporadically, causing sudden and temporary disruptions in sensor readings. The challenge with intermittent faults is that they can be difficult to detect due to their transient nature. If left unchecked, these faults can lead to misleading data interpretation during short intervals, affecting real-time monitoring.
• Drift Faults: drift faults occur when a sensor's readings gradually shift over time, either due to sensor aging, environmental conditions, or other factors. This slow, progressive deviation can accumulate and result in significant errors in long-term monitoring, impacting the reliability of predictive maintenance and control actions in the WWTP.
The three noise scenarios—low, medium, and high—represent different levels of external disturbances or measurement errors that can further degrade the quality of sensor data. Low noise (SNR = 20) suggests minimal interference, whereas high noise (SNR = 5) reflects substantial disturbance, making fault detection more challenging. Noise impacts the ability of fault detection algorithms to distinguish between normal variations in the data and actual faults. Therefore, it is crucial to evaluate the robustness of each fault detection method across different noise levels to ensure reliable performance under real-world conditions, where noise is often unavoidable.
For the three scenarios, the faults have been considered in the Qi as well as SNH variable of the WWTP set-up as follows:
• The bias fault which is equal to 3% of the total variation is introduced in the Qi variable between sampling time instants 250 and end of the testing data.
• An intermittent fault which is equal to 3% of the total variation is introduced in the Qi variable between sampling time instants [130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230] and [450
230] and [450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500] of the testing data.
500] of the testing data.
• A drift fault with a slope of 0.2 is introduced in the SNH variable after sampling time instants 250 and end of the testing data.
In this study, the fault detection strategies are tested under these varying noise conditions to assess their ability to maintain accuracy and sensitivity to faults in the presence of noise. This analysis is critical for designing monitoring systems that are resilient to sensor errors and capable of effectively detecting anomalies in noisy environments typical of industrial settings like wastewater treatment plants.
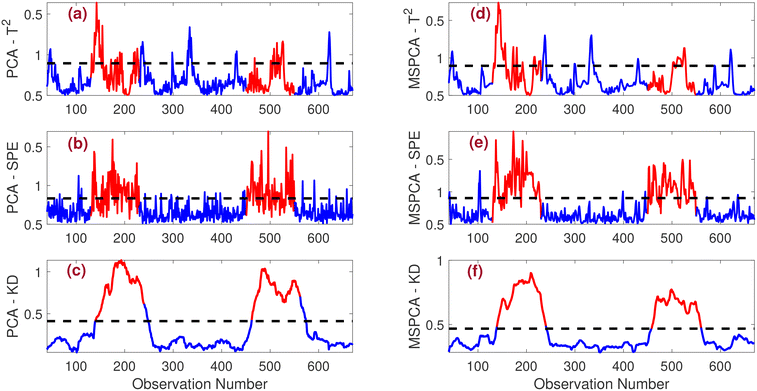
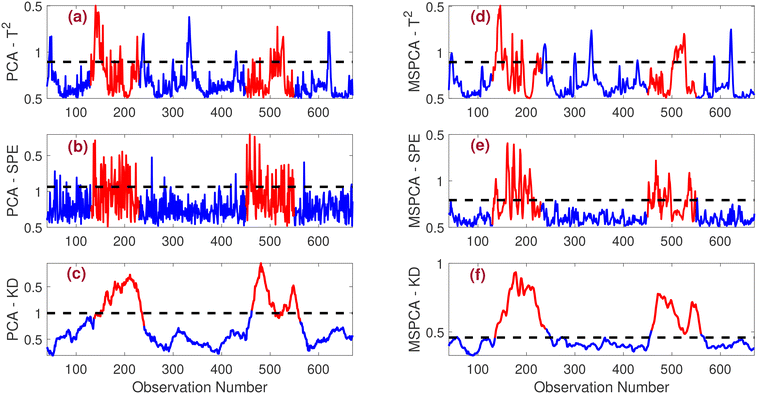
• Bias fault: the performance of PCA and MSPCA-based strategies in detecting the bias fault is shown in Fig. 4. Traditional strategies such as PCA-T2, PCA-SPE, MSPCA-T2, and MSPCA-SPE fail to detect the fault effectively. While multi-scale filtering improves detection slightly in the MSPCA-T2 and MSPCA-SPE methods, as seen in Fig. 4(d) and (e), the results remain suboptimal. Due to the lower noise level in this scenario, both PCA-KD and MSPCA-KD strategies successfully detect the bias fault. However, the proposed MSPCA-KD method has a distinct advantage: it detects the fault more quickly than the other FD schemes, providing a faster response in identifying abnormalities.
• Intermittent fault: the monitoring performance for the intermittent fault is evaluated next. Fig. 5 illustrates the effectiveness of both PCA and MSPCA-based strategies in detecting this type of fault. In Fig. 5(a) and (d), it is evident that the T2 indicator is unable to detect the fault effectively. Conversely, as shown in Fig. 5(e), the MSPCA-SPE strategy outperforms the PCA-SPE strategy depicted in Fig. 5(b) in detecting the intermittent fault. The KD-based methods demonstrate superior fault detection capabilities compared to the traditional T2 and SPE methods. Notably, the proposed MSPCA-KD strategy has a distinct advantage: it identifies faults more rapidly than the other fault detection schemes, allowing for a quicker response to anomalies in the system.
• Drift fault:Fig. 6 illustrates the performance of PCA and MSPCA-based fault detection schemes in monitoring a drift fault. The result plots indicate that all methods successfully detect the fault. However, the T2-based indicator exhibits a delay in detection, while the SPE and KD-based indicators demonstrate improved fault detection capabilities. Overall, the MSPCA-KD strategy outperforms the other approaches, demonstrating the best detection of drift faults.
Table 3 presents a comprehensive comparison of various fault indicators used for monitoring bias, drift, and intermittent faults, employing different detection metrics. The MSPCA-KD-based fault detection method exhibits a notably high F1-score, primarily due to its high FDR and zero FAR across different fault scenarios. The superior FDR achieved by the proposed MSPCA-KD approach, in contrast to traditional fault detection methods, highlights its effectiveness and underscores its advantages in accurately identifying faults while minimizing erroneous detections.
| Fault | Index | PCA-T2 | PCA-SPE | PCA-KD | MSPCA-T2 | MSPCA-SPE | MSPCA-KD |
|---|---|---|---|---|---|---|---|
| Bias | FDR | 16.67 | 47.67 | 97.62 | 28.38 | 63.29 | 99.05 |
| FAR | 6.80 | 5.60 | 0.00 | 5.20 | 0.50 | 0.00 | |
| Precision | 80.45 | 93.02 | 98.79 | 90.22 | 99.53 | 100.00 | |
| F1-score | 27.85 | 62.89 | 98.33 | 43.40 | 77.29 | 99.52 | |
| Intermittent | FDR | 24.50 | 60.00 | 97.50 | 32.50 | 80.50 | 100.00 |
| FAR | 6.52 | 5.96 | 6.00 | 5.82 | 1.77 | 0.00 | |
| Precision | 62.02 | 81.08 | 100.00 | 70.65 | 95.26 | 100.00 | |
| F1-score | 35.34 | 69.00 | 98.73 | 45.02 | 87.63 | 100.00 | |
| Drift | FDR | 73.62 | 90.62 | 92.85 | 78.81 | 93.89 | 97.23 |
| FAR | 9.20 | 4.60 | 0.00 | 7.80 | 2.80 | 0.00 | |
| Precision | 93.07 | 97.06 | 100.00 | 94.85 | 98.25 | 100.00 | |
| F1-score | 82.21 | 93.75 | 96.29 | 86.08 | 96.02 | 98.59 |
The proposed MSPCA-KD fault detection approach demonstrates superior performance under low noise conditions (SNR = 20), achieving the highest F1-score and precision while maintaining a zero false alarm rate across various fault types, including bias, intermittent, and drift faults. Its effectiveness can be attributed to the integration of MSPCA with the KD, which enhances the model's ability to capture complex data patterns while effectively tracking dynamic changes in the system. This results in improved sensitivity and specificity, enabling timely and accurate fault detection.
• Bias fault: the monitoring of the bias fault is evaluated. As shown in Fig. 7(a) and (d), the PCA-T2 and MSPCA-T2 strategies are ineffective in detecting the fault. Similarly, the PCA-SPE fault detection strategy also fails, while the MSPCA-SPE strategy exhibits slightly improved performance, as observed in Fig. 7(e). The PCA-KD successfully detects the fault but with some missed detections, evident in Fig. 7(c). In contrast, the proposed MSPCA-KD strategy clearly outperforms all the other methods, providing accurate fault detection as depicted in Fig. 7(f). This enhanced performance can be attributed to the advantages of multi-scale filtering, which allows the MSPCA-KD approach to adapt more effectively to the complexities introduced by medium noise levels.
 | ||
| Fig. 7 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-KD, (d) MSPCA-T2, (e) MSPCA-SPE, and (f) MSPCA-KD in the presence of bias faults for SNR = 10. | ||
• Intermittent fault: this section examines the monitoring of an intermittent fault. As illustrated in Fig. 8(a) and (d), both the PCA-T2 and MSPCA-T2 strategies are unable to detect the fault. The MSPCA-SPE fault detection strategy performs better than the PCA-SPE strategy, as shown in Fig. 8(b) and (e). The PCA-KD strategy detects the fault more effectively than the conventional indicators but still has a few missed detections within the fault region, as seen in Fig. 8(c). Despite the noise present in the data, the MSPCA-KD strategy utilizes multi-scale filtering to achieve clear fault detection, as demonstrated in Fig. 8(f).
 | ||
| Fig. 8 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-KD, (d) MSPCA-T2, (e) MSPCA-SPE, and (f) MSPCA-KD in the presence of intermittent faults for SNR = 10. | ||
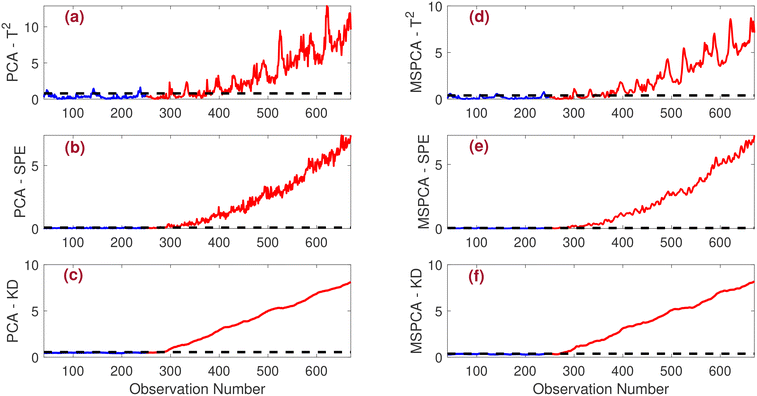
• Drift fault: the performance of PCA and MSPCA-based strategies in detecting the drift fault under medium noise conditions (SNR = 10) is illustrated in Fig. 9. The statistical plots clearly show that both PCA and MSPCA-based fault detection strategies successfully identify the drift fault. However, the MSPCA-based approaches demonstrate superior performance compared to the PCA-based methods, primarily due to the noise present in the data. Notably, the MSPCA-KD strategy has a distinct advantage, as it detects the fault more quickly and with fewer missed detections than the other approaches.
 | ||
| Fig. 9 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-KD, (d) MSPCA-T2, (e) MSPCA-SPE, and (f) MSPCA-KD in the presence of drift faults for SNR = 10. | ||
Table 4 presents a comparison of various fault detection (FD) strategies evaluated through detection metrics. The results clearly demonstrate that the MSPCA-based FD methods outperform their PCA counterparts, showcasing superior detection performance attributed to the multi-scale filtering enabled by wavelet functions. Notably, the proposed MSPCA-KD approach excels compared to the other methods, achieving a significantly high F1-score, thus highlighting its effectiveness in fault detection.
| Fault | Index | PCA-T2 | PCA-SPE | PCA-KD | MSPCA-T2 | MSPCA-SPE | MSPCA-KD |
|---|---|---|---|---|---|---|---|
| Bias | FDR | 15.71 | 32.52 | 91.67 | 21.29 | 54.58 | 96.00 |
| FAR | 7.25 | 6.00 | 0.00 | 6.40 | 0.40 | 0.00 | |
| Precision | 77.38 | 90.10 | 100.00 | 84.76 | 99.62 | 100.00 | |
| F1-score | 26.14 | 47.84 | 95.65 | 34.04 | 70.16 | 97.95 | |
| Intermittent | FDR | 23.50 | 32.45 | 82.50 | 29.00 | 44.50 | 99.25 |
| FAR | 6.35 | 3.41 | 1.20 | 6.08 | 1.15 | 1.50 | |
| Precision | 61.84 | 80.24 | 100.00 | 67.44 | 94.17 | 97.08 | |
| F1-score | 34.60 | 46.35 | 92.18 | 40.56 | 60.30 | 98.32 | |
| Drift | FDR | 71.90 | 89.32 | 90.48 | 77.12 | 91.67 | 96.02 |
| FAR | 9.50 | 8.40 | 0.00 | 8.20 | 1.80 | 0.00 | |
| Precision | 92.53 | 94.73 | 100.00 | 93.91 | 98.84 | 100.00 | |
| F1-score | 80.76 | 86.08 | 95.00 | 84.69 | 95.12 | 97.96 |
In summary, the monitoring performance of the proposed MSPCA-KD approach for fault detection at SNR = 10 demonstrates superior effectiveness in identifying bias, intermittent, and drift faults compared to traditional PCA methods. Integrating multi-scale filtering significantly enhances detection accuracy and responsiveness, resulting in high F1-scores across various fault scenarios. These findings underscore the advantages of employing MSPCA-KD for robust fault detection in sensor systems, particularly under medium-noise conditions.
 | ||
| Fig. 10 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-KD, (d) MSPCA-T2, (e) MSPCA-SPE, and (f) MSPCA-KD in the presence of bias faults for SNR = 5. | ||
 | ||
| Fig. 11 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-KD, (d) MSPCA-T2, (e) MSPCA-SPE, and (f) MSPCA-KD in the presence of intermittent faults for SNR = 5. | ||
The results of monitoring a drift fault in the presence of high noise levels are shown in Fig. 12. Due to the significant noise, both PCA-T2 and PCA-SPE perform slightly worse in detecting the drift fault than MSPCA-T2 and MSPCA-KD. While the MSPCA-T2 and MSPCA-KD strategies successfully identify the fault, there is a small detection delay. The KD-based metric stands out for its ability to accurately pinpoint the fault. Notably, the MSPCA-KD approach detects the fault faster than the PCA-KD method, providing a clear advantage. Table 5 compares the performance of different methods using key detection metrics. Due to the benefits of multi-scale wavelet filtering, MSPCA methods outperform PCA approaches under noisy conditions. The MSPCA-KD strategy demonstrates superior performance, achieving F1-scores of 97.48%, 97.98%, and 96.77% across different faults.
 | ||
| Fig. 12 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-KD, (d) MSPCA-T2, (e) MSPCA-SPE, and (f) MSPCA-KD in the presence of drift faults for SNR = 5. | ||
| Fault | Index | PCA-T2 | PCA-SPE | PCA-KD | MSPCA-T2 | MSPCA-SPE | MSPCA-KD |
|---|---|---|---|---|---|---|---|
| Bias | FDR | 10.29 | 16.97 | 41.48 | 13.42 | 38.58 | 95.52 |
| FAR | 8.00 | 5.80 | 0.00 | 5.80 | 1.20 | 0.00 | |
| Precision | 68.25 | 78.02 | 100.00 | 79.43 | 97.88 | 100.00 | |
| F1-score | 17.96 | 27.87 | 58.63 | 22.92 | 55.34 | 97.48 | |
| Intermittent | FDR | 14.50 | 17.00 | 25.50 | 16.50 | 30.50 | 96.05 |
| FAR | 5.11 | 7.41 | 0.00 | 3.83 | 0.95 | 0.00 | |
| Precision | 55.76 | 50.00 | 100.00 | 81.16 | 96.85 | 100.00 | |
| F1-score | 23.01 | 25.37 | 40.63 | 27.61 | 46.52 | 97.98 | |
| Drift | FDR | 67.38 | 85.67 | 88.81 | 76.52 | 89.52 | 93.75 |
| FAR | 10.20 | 6.00 | 0.00 | 5.20 | 1.20 | 0.00 | |
| Precision | 91.21 | 96.00 | 100.00 | 96.00 | 98.94 | 100.00 | |
| F1-score | 77.50 | 90.54 | 94.06 | 85.20 | 94.00 | 96.77 |
Overall, at a low SNR level of 5, the fault detection (FD) performance of PCA and MSPCA-based methods is significantly affected by the high noise present in the data. PCA-based approaches, including T2 and SPE, struggle to accurately detect bias, intermittent, and drift faults, often failing entirely or detecting with delay. MSPCA-based methods, on the other hand, perform better due to the advantages of multi-scale filtering offered by wavelets, particularly in the MSPCA-KD approach. Despite the noise, the MSPCA-KD strategy consistently outperforms the other methods, with higher fault detection rates and fewer missed detections. It achieves the best results with high F1-scores, demonstrating its robustness and effectiveness even under challenging noise conditions.
| Fault | Method | Depth = 2 | Depth = 3 | Depth = 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FDR | FAR | Prec | F1-sc | FDR | FAR | Prec | F1-sc | FDR | FAR | Prec | F1-sc | ||
| Bias | MSPCA-T2 | 9.95 | 3.85 | 82.14 | 17.82 | 12.19 | 4.00 | 83.60 | 21.23 | 13.42 | 5.80 | 79.43 | 22.92 |
| MSPCA-SPE | 20.00 | 1.00 | 97.10 | 33.17 | 30.61 | 0.80 | 98.06 | 46.53 | 38.58 | 1.20 | 97.88 | 55.34 | |
| MSPCA-KD | 53.19 | 0.00 | 100.00 | 69.44 | 94.38 | 0.00 | 100.00 | 97.10 | 95.52 | 0.00 | 100.00 | 97.48 | |
| Intermittent | MSPCA-T2 | 13.50 | 3.19 | 64.28 | 22.54 | 14.50 | 2.70 | 68.07 | 23.92 | 16.50 | 3.83 | 81.16 | 27.61 |
| MSPCA-SPE | 25.50 | 0.45 | 95.32 | 37.39 | 27.75 | 0.25 | 82.83 | 41.04 | 30.50 | 0.95 | 96.85 | 46.52 | |
| MSPCA-KD | 69.50 | 0.00 | 100.00 | 82.00 | 90.00 | 0.00 | 100.00 | 94.75 | 96.05 | 0.00 | 100.00 | 97.98 | |
| Drift | MSPCA-T2 | 73.72 | 3.90 | 97.19 | 83.84 | 75.01 | 2.27 | 98.13 | 84.59 | 76.52 | 5.20 | 96.00 | 85.20 |
| MSPCA-SPE | 86.69 | 0.80 | 94.79 | 90.56 | 87.88 | 0.48 | 92.14 | 89.96 | 89.52 | 1.20 | 98.74 | 94.00 | |
| MSPCA-KD | 89.45 | 0.00 | 100.00 | 94.43 | 91.88 | 0.00 | 100.00 | 95.76 | 93.75 | 0.00 | 100.00 | 96.77 | |
• Given the high level of noise in the data, a slightly larger decomposition depth facilitates more effective feature extraction and noise reduction, thus enhancing fault detection in the wastewater treatment plant. As observed, the F1-score values for the MSPCA-based fault detection strategies improve with a decomposition depth of 4, compared to depths of 2 or 3.
• Across all three fault types and decomposition depths, the MSPCA-KD fault detection (FD) strategy consistently outperforms the MSPCA-T2 and MSPCA-SPE based strategies, showing superior F1-score values. The KD indicator leverages sample-by-sample comparisons between the residuals of training and testing datasets, which improves detection performance relative to conventional FD methods. When the KD indicator is integrated with multi-scale wavelet filtering, its detection capabilities are further enhanced, especially in the presence of noise.
• For a decomposition depth of 2, the proposed MSPCA-KD FD strategy achieved F1-scores of 69.44%, 82.00%, and 94.93% for the three fault scenarios. With a decomposition depth of 3, the F1-scores improved to 97.10%, 94.75%, and 95.76%. Finally, at a decomposition depth of 4, the MSPCA-KD FD strategy exhibited F1-scores of 98.22%, 97.98%, and 96.77% for the three faults. These results indicate that a decomposition depth of 4 provides the best detection performance for bias, intermittent, and drift faults in the wastewater treatment process.
| Fault | Method | Haar | Symlet | Daubechies | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FDR | FAR | Prec | F1-sc | FDR | FAR | Prec | F1-sc | FDR | FAR | Prec | F1-sc | ||
| Bias | MSPCA-T2 | 14.71 | 7.21 | 77.50 | 24.78 | 17.21 | 8.00 | 78.26 | 28.05 | 15.71 | 7.25 | 77.38 | 26.14 |
| MSPCA-SPE | 28.57 | 0.00 | 100.00 | 44.44 | 30.61 | 3.60 | 93.41 | 46.13 | 32.52 | 6.00 | 90.10 | 47.84 | |
| MSPCA-KD | 86.90 | 0.00 | 100.00 | 93.00 | 92.38 | 0.00 | 100.00 | 96.03 | 95.52 | 0.00 | 100.00 | 97.95 | |
| Intermittent | MSPCA-T2 | 20.00 | 5.32 | 61.53 | 30.19 | 21.30 | 2.06 | 80.76 | 33.58 | 29.00 | 6.08 | 67.44 | 40.56 |
| MSPCA-SPE | 24.50 | 0.00 | 100.00 | 39.35 | 43.00 | 1.25 | 93.47 | 58.67 | 44.50 | 1.15 | 94.17 | 60.30 | |
| MSPCA-KD | 70.00 | 0.00 | 100.00 | 82.35 | 99.00 | 1.65 | 96.27 | 97.75 | 99.25 | 1.5 | 97.08 | 98.32 | |
| Drift | MSPCA-T2 | 76.12 | 5.20 | 96.50 | 85.41 | 80.45 | 6.67 | 95.93 | 88.20 | 77.12 | 8.20 | 93.91 | 84.70 |
| MSPCA-SPE | 83.29 | 3.80 | 97.87 | 90.07 | 90.48 | 1.48 | 99.05 | 94.85 | 91.67 | 1.80 | 98.84 | 95.12 | |
| MSPCA-KD | 92.45 | 0.00 | 100.00 | 96.07 | 93.88 | 0.00 | 100.00 | 96.84 | 96.02 | 0.00 | 100.00 | 97.97 | |
• The detection results for the MSPCA-T2, MSPCA-SPE, and MSPCA-KD methods demonstrate significant improvement when utilizing the Daubechies wavelet for multi-scale filtering, compared to the Haar and Symlet wavelets. The Daubechies wavelet exhibits superior scale and shift invariance properties, providing a distinct advantage in fault detection.
• The MSPCA-KD-based fault detection strategy outperforms the conventional MSPCA-T2 and MSPCA-SPE strategies, achieving higher F1-score values across all three fault scenarios. Regardless of the wavelet type used—Haar, Symlet, or Daubechies—the KD statistic consistently demonstrates better performance than the traditional indicators based on T2 and SPE. This superiority is attributed to the KD statistic's sample-by-sample comparison of residuals from both training and testing datasets, enhancing detection performance.
• The MSPCA-KD-based FD strategy yields F1-scores of 93.00%, 82.35%, and 96.07% for the three faults when employing the Haar wavelet for multi-scale filtering. When using the Symlet wavelet, the F1-scores increase to 96.03%, 97.75%, and 96.84%. Remarkably, with the Daubechies wavelet, the F1-scores reach 97.75%, 98.32%, and 97.97%. These results unequivocally highlight the superiority of the Daubechies wavelet, which significantly enhances the performance of the MSPCA-KD-based FD strategy.
In summary, the results highlight that leveraging the appropriate wavelet family can significantly enhance the effectiveness of fault detection strategies, paving the way for more reliable monitoring solutions in WWTPs.
4 Conclusion
The impact of measurement noise on fault detection approaches in WWTPs can lead to significant degradation in performance. To address this issue, this study proposed a noise-filtering fault detection approach that integrates PCA with wavelet functions. The PCA-based data-driven strategy was utilized as the modeling framework, while wavelet functions facilitated multi-scale filtering, resulting in the development of the MSPCA-based FD approach. A novel indicator based on the KD was also introduced to enhance fault detection, culminating in the MSPCA-KD strategy. This strategy assessed the residuals between training and testing data for fault detection and employed a non-parametric KDE scheme to compute the decision threshold.The performance of the proposed FD approach was rigorously evaluated by monitoring three types of faults in the WWTP setup. The results demonstrated the superiority of the multi-scale methods to conventional techniques, particularly in detecting bias, intermittent, and drift faults. The KD statistic's effectiveness in evaluating model residuals enabled the MSPCA-KD strategy to outperform all other methods in identifying different faults. Furthermore, an additional study examined the impact of varying decomposition depths on the performance. It was found that as noise levels in the data increased, larger decomposition depths facilitated effective de-noising at multiple levels, resulting in improved fault detection. Additionally, the study highlighted that utilizing the advantages of Daubechies wavelets for multi-scale filtering proved to be significantly more effective in de-noising than Haar and Symlet wavelets. Overall, this study underscores the importance of incorporating advanced noise filtering techniques and wavelet-based methodologies to enhance fault detection in complex environments like wastewater treatment plants, ultimately contributing to improved operational reliability and efficiency.
Future research could explore the synergy between the MSPCA-KD approach and advanced machine learning algorithms specifically for fault diagnosis and classification. This could involve applying techniques such as ensemble learning or deep learning to leverage the strengths of the MSPCA-KD method. By integrating these approaches, researchers could enhance fault classification accuracy and prediction capabilities, ultimately leading to improved detection rates and enabling proactive maintenance strategies.
Data availability
In the proposed research work, we have used the publicly available dataset for wastewater treatment plants (WWTPs). The data from the COST benchmark simulation model (BSM1) are employed to validate the proposed fault detection. The details of data generation can be found in the following paper. Copp J. B. The COST simulation benchmark: description and simulator manual: office for official publications of the European community. Luxembourg: ISBN 92-894-1658-0; 2002.Author contributions
K. Ramakrishna Kini: writing – original draft, methodology, software, investigation. Fouzi Harrou: writing – review and editing, methodology, software, supervision, validation. Muddu Madakyaru: formulation, writing – review & editing, conceptualization, formal analysis, project administration, supervision, validation. Ying Sun: review and editing, visualization.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors would like to thank Manipal Academy of Higher Education (MAHE), Manipal for supporting authors who wish to publish open access under the agreement between RSC (The Royal Society of Chemistry) and Manipal Academy of Higher Education (MAHE), Manipal, India.Notes and references
- S. B. Grant, J. D. Saphores, D. L. Feldman, A. J. Hamilton, T. D. Fletcher and P. L. Cook, et al. Taking the “waste” out of “wastewater” for human water security and ecosystem sustainability, Science, 2012, 337(6095), 681–686 CrossRef CAS PubMed.
- R. L. Siegrist, Decentralized water reclamation engineering. A Curriculum Workbook Charm, Springer International Publishing AG, 2017 Search PubMed.
- P. Arcano-Bea, M. Timiraos, A. Díaz-Longueira, Á. Michelena, E. Jove and J. L. Calvo-Rolle, A One-Class-Based Supervision System to Detect Unexpected Events in Wastewater Treatment Plants, Appl. Sci., 2024, 14(12), 5185 CrossRef CAS.
- F. Bellamoli, M. Di Iorio, M. Vian and F. Melgani, Machine learning methods for anomaly classification in wastewater treatment plants, J. Environ. Manage., 2023, 344, 118594 CrossRef CAS PubMed.
- H. L. Ivan and V. Zaccaria, Exploring the effects of faults on the performance of a biological wastewater treatment process, Water Sci. Technol., 2024, 90(2), 474–489 CrossRef CAS.
- F. Harrou, Y. Sun, A. S. Hering and M. Madakyaru, et al., Statistical process monitoring using advanced data-driven and deep learning approaches: theory and practical applications, Elsevier, 2020 Search PubMed.
- K. B. Newhart, M. C. Klanderman, A. S. Hering and T. Y. Cath, A holistic evaluation of multivariate statistical process monitoring in a biological and membrane treatment system, ACS ES&T Water, 2023, 4(3), 913–924 Search PubMed.
- H. L. Marais, V. Zaccaria and M. Odlare, Comparing statistical process control charts for fault detection in wastewater treatment, Water Sci. Technol., 2022, 85(4), 1250–1262 CrossRef CAS PubMed.
- C. Lee, S. Choi and I. B. Lee, Sensor fault diagnosis in a wastewater treatment process, Water Sci. Technol., 2006, 53(1), 251–257 CrossRef CAS PubMed.
- T. Cheng, F. Harrou, Y. Sun and T. Leiknes, Monitoring influent measurements at water resource recovery facility using data-driven soft sensor approach, IEEE Sens. J., 2018, 19(1), 342–352 Search PubMed.
- P. Kazemi, J. Giralt, C. Bengoa, A. Masoumian and J. P. Steyer, Fault detection and diagnosis in water resource recovery facilities using incremental PCA, Water Sci. Technol., 2020, 82(12), 2711–2724 CrossRef CAS PubMed.
- A. Sanchez-Fernández, M. J. Fuente and G. Sainz-Palmero, Fault detection in wastewater treatment plants using distributed PCA methods, in 2015 IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), IEEE, 2015, pp. 1–7 Search PubMed.
- B. Wang, Z. Li, Z. Dai, N. Lawrence and X. Yan, A probabilistic principal component analysis-based approach in process monitoring and fault diagnosis with application in wastewater treatment plant, Appl. Soft Comput., 2019, 82, 105527 CrossRef.
- B. H. Jun, J. H. Park, S. I. Lee and M. G. Chun, Kernel PCA based faults diagnosis for wastewater treatment system, in Advances in Neural Networks-ISNN 2006: Third International Symposium on Neural Networks, Chengdu, China, May 28–June 1, 2006, Proceedings, Part III 3, Springer, 2006, pp. 426–431 Search PubMed.
- I. González, A. Serrano, J. García-Olmo, M. C. Gutiérrez, A. F. Chica and M. Á. Martín, Assessment of the treatment, production and characteristics of WWTP sludge in Andalusia by multivariate analysis, Process Saf. Environ. Prot., 2017, 109, 609–620 CrossRef.
- T. Cheng, A. Dairi, F. Harrou, Y. Sun and T. Leiknes, Monitoring influent conditions of wastewater treatment plants by nonlinear data-based techniques, IEEE Access, 2019, 7, 108827–108837 Search PubMed.
- A. Khurshid and A. K. Pani, Machine learning approaches for data-driven process monitoring of biological wastewater treatment plant: A review of research works on benchmark simulation model no. 1 (bsm1), Environ. Monit. Assess., 2023, 195(8), 916 CrossRef PubMed.
- D. Aguado and C. Rosen, Multivariate statistical monitoring of continuous wastewater treatment plants, Eng. Appl. Artif. Intell., 2008, 21(7), 1080–1091 Search PubMed.
- F. Harrou, A. Dairi, Y. Sun and M. Senouci, Statistical monitoring of a wastewater treatment plant: A case study, J. Environ. Manage., 2018, 223, 807–814 CrossRef PubMed.
- B. Xu, P. Zhuang, Y. Wang, W. He, Z. Wang and Z. Liu, Fault Diagnosis of Wastewater Treatment Processes Based on CPSO-DKPCA, Int. J. Comput. Intell. Syst., 2024, 17(1), 19 CrossRef.
- D. Yang, X. Peng, C. Su, L. Li, Z. Cao and W. Zhong, Regularized Wasserstein distance-based joint distribution adaptation approach for fault detection under variable working conditions, IEEE Trans. Instrum. Meas., 2023, 73, 2510211 Search PubMed.
- H. Cheng, J. Wu, D. Huang, Y. Liu and Q. Wang, Robust adaptive boosted canonical correlation analysis for quality-relevant process monitoring of wastewater treatment, ISA Trans., 2021, 117, 210–220 CrossRef PubMed.
- T. Chang, T. Liu, X. Ma, Q. Wu, X. Wang, J. Cheng, W. Wei, F. Zhang and H. Liu, Fault detection in industrial wastewater treatment processes using manifold learning and support vector data description, Ind. Eng. Chem. Res., 2024, 63(35), 15562–15574 CrossRef CAS.
- R. K. Kini, F. Harrou, M. Madakyaru and Y. Sun, Enhanced data-driven monitoring of wastewater treatment plants using the Kolmogorov–Smirnov test, Environ. Sci.: Water Res. Technol., 2019, 10, 1464–1480 RSC.
- F. Harrou, Y. Sun, A. S. Hering, M. Madakyaru and A. Dairi, Statistical Process Monitoring Using Advanced Data-Driven and Deep Learning Approaches, Theory and Practical Applications, Elsevier, Amsterdam, The Netherlands, 2020 Search PubMed.
- J. E. Jackson and G. S. Mudholkar, Control procedures for residuals associated with principal component analysis, Technometrics, 1979, 21(3), 341–349 CrossRef.
- G. Diana and C. Tommasi, Cross-validation methods in principal component analysis: a comparison, Stat. Methods Appl., 2002, 11, 71–82 CrossRef.
- S. J. Qin, Statistical process monitoring: basics and beyond, J. Chemom., 2003, 17(8–9), 480–502 CrossRef CAS.
- F. Harrou, A. Zeroual, F. Kadri and Y. Sun, Enhancing Road Traffic Flow Prediction with Improved Deep Learning using Wavelet Transforms, Results Eng., 2024, 102342 CrossRef.
- R. Ganesan, T. K. Das and V. Venkataraman, Wavelet-based multiscale statistical process monitoring: A literature review, IIE Trans., 2004, 36(9), 787–806 CrossRef.
- S. Mallat, A theory for multi resolution signal decomposition: the wavelet representation, IEEE Trans. Pattern Anal. Mach. Intell., 1989, 11(7), 674–693 CrossRef.
- S. Kolouri, S. R. Park, M. Thorpe, D. Slepcev and G. K. Rohde, Optimal mass transport: Signal processing and machine-learning applications, IEEE Signal Process. Mag., 2017, 34(4), 43–59 Search PubMed.
- S. Kammammettu and Z. Li, Change point and fault detection using Kantorovich distance, J. Process Control, 2019, 80, 41–59 CrossRef CAS.
- K. R. Kini, M. Bapat and M. Madakyaru, Kantorovich distance based fault detection scheme for non-linear processes, IEEE Access, 2021, 10, 1051–1067 Search PubMed.
- S. Kammammettu and Z. Li, Change point and fault detection using Kantorovich distance, J. Process Control, 2019, 80, 41–59 CrossRef CAS.
- B. M. Arifin, Z. Li, G. A. Meyer and A. Colin, A novel data-driven leak detection and localization algorithm using the Kantorovich distance, Comput. Chem. Eng., 2018, 108, 300–313 CrossRef CAS.
- K. R. Kini and M. Madakyaru, Improved process monitoring strategy using Kantorovich distance-independent component analysis: An application to Tennessee Eastman process, IEEE Access, 2020, 8, 205863–205877 Search PubMed.
- Y. Zongyu, J. Qingchao and G. Xingsheng, Distributed process monitoring based on Kantorovich distance-multiblock variational autoencoder and Bayesian inference, Chin. J. Chem. Eng., 2024, 73, 311–323 CrossRef.
- D. Li and S. Martínez, High-confidence attack detection via wasserstein-metric computations, IEEE Control Syst. Lett., 2020, 5(2), 379–384 Search PubMed.
- Y. Wang, W. Yang, Y. Wang, H. Fan and Y. Zheng, Improved fault detection using kantorovich distance and neighborhood preserving embedding method, in 2021 IEEE 10th Data Driven Control and Learning Systems Conference (DDCLS), IEEE, 2021, pp. 685–690 Search PubMed.
- E. Parzen, On estimation of a probability density function and mode, Ann. Math. Stat., 1962, 33(3), 1065–1076 CrossRef.
- B. Taghezouit, F. Harrou, Y. Sun, A. H. Arab and C. Larbes, Multivariate statistical monitoring of photovoltaic plant operation, Energy Convers. Manage., 2020, 205, 112317 CrossRef.
- J. Alex, L. Benedetti, J. Copp, K. Gernaey, U. Jeppsson and I. Nopens, et al. Benchmark simulation model no. 1 (BSM1), Report by the IWA Taskgroup on benchmarking of control strategies for WWTPs, 2008, vol. 1 Search PubMed.
- C. S. Ayala, B. Laxman, V. Aaron and K. Vladik, Why Daubechies wavelets are so successful, J. Intell. Fuzzy Syst., 2022, 43(6), 6933–6938 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |