 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting aquatic toxicity of anionic hydrocarbon and perfluorinated surfactants using membrane-water partition coefficients from coarse-grained simulations†
Andrea
Gredelj
 *ab,
Jayne
Roberts
*ab,
Jayne
Roberts
 *a,
Eoin M.
Kearney
*a,
Eoin M.
Kearney
 c,
Elin L.
Barrett
c,
Elin L.
Barrett
 a,
Nicola
Haywood
a,
Nicola
Haywood
 a,
David
Sheffield
a,
David
Sheffield
 a,
Geoff
Hodges
a,
Geoff
Hodges
 a and
Mark A.
Miller
a and
Mark A.
Miller
 *c
*c
aSafety, Environmental and Regulatory Science (SERS), Unilever, Colworth Park, Sharnbrook MK44 1LQ, UK. E-mail: Jayne.Roberts@unilever.com
bDepartment of Environmental Engineering, Norwegian Geotechnical Institute (NGI), P.O. Box. 3930 Ullevål Stadion, N-0806 Oslo, Norway. E-mail: andrea.gredelj@ngi.no
cDepartment of Chemistry, Durham University, South Road, Durham DH1 3LE, UK. E-mail: m.a.miller@durham.ac.uk
First published on 18th March 2025
Abstract
Anionic surfactants are widely used in commercial and industrial applications. For assessment of their environmental fate and effects, it is highly desirable to quantify the membrane-water partition/distribution coefficient (Kmw/Dmw). Here, we further develop a computational route to Dmw for anionic surfactants based on coarse-grained molecular dynamics simulations, validating it against new and existing experimental measurements. Having parameterised molecular fragments for the coarse-grained models, the simulations are used to predict Dmw for molecules where no experimental values are available. This expanded set of simulated Dmw values is then used to derive QSARs for acute toxicity of mono-constituent anionic surfactants in daphnids and fish, allowing for extrapolation to similar compounds without experimental Dmw values. For this study, we have selected hydrocarbon-based (HC) surfactants because of their widespread use, and perfluorinated (FC) surfactants as a challenging case study. Separate daphnid and fish QSARs demonstrate good fits, robustness and predictivity, and highlight differing toxicity relationships for HC and FC surfactants in daphnids. Overall, the combined use of simulated Dmw and derived QSARs is a promising approach for ecotoxicity screening of surfactants.
Environmental significanceRegulation and screening of chemicals for environmental risk assessment often rely on the octanol–water partitioning coefficient (Kow). However, for ionogenic and charged molecules, Kow is hard to measure or predict and has limited biological relevance. The membrane-water partitioning/distribution coefficient (Kmw/Dmw) is acknowledged as a more appropriate descriptor of bioaccumulation and toxicity, especially for surfactants. Here, we address the need to reliably predict Dmw by developing, validating and applying coarse-grained methods for molecular dynamics simulations. The results are used to build QSAR models to facilitate ecotoxicity screening. We focus on families of anionic surfactants with hydrocarbon and perfluorocarbon backbones. Due to their environmental persistence and unique physicochemical properties, the latter group is both important and challenging. |
1. Introduction
Over the last decade, the chemical safety regulatory landscape has seen an accelerating shift away from a historic framework, based largely on the generation of in vivo data to fill hazard endpoints, towards a new position which supports greatly reducing or completely eliminating the use of animal testing. In the European Union, REACH Regulation1 states that testing on vertebrate animals can only be used as a last resort to fulfil data requirements for the registration of chemicals.2 In the United States, the amended Toxic Substances Control Act (TSCA) explicitly promotes the reduction and replacement of vertebrate animals in the testing of chemicals and actively encourages the development of alternative test methods.3With more than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemicals estimated to be in regular industrial use across Europe and North America alone,4 many of which have insufficient hazard data for regulatory submission, the development and acceptance of computational (in silico) approaches provide opportunities to address endpoint data requirements either directly or as part of a weight-of-evidence approach. Historically, in silico approaches established in regulations to determine aquatic toxicity endpoints have been focussed on the application of structure-based predictions using quantitative structure–activity relationship (QSAR) models coupled with well-established Modes or Mechanisms of Action (MoA/MechoA) such as that described by non-specific toxicity (narcosis).5–7 The majority of such published QSARs derived for narcosis rely on the octanol–water partition coefficient (Kow) as a proxy for the lipophilicity/hydrophobicity of chemicals.5,8–12 Since narcosis is driven by critical accumulation in tissues and phospholipid membranes,13,14 resulting in disturbance in their integrity and function, the toxicity of chemicals demonstrating this MoA/MechoA is highly correlated with lipophilicity. However, biological membranes are ordered, anisotropic three-dimensional structures. Therefore, as octanol is a homogenous isotropic medium, it cannot adequately describe the membrane interactions of chemicals such as ionisable organic compounds and surfactants.15,16
000 chemicals estimated to be in regular industrial use across Europe and North America alone,4 many of which have insufficient hazard data for regulatory submission, the development and acceptance of computational (in silico) approaches provide opportunities to address endpoint data requirements either directly or as part of a weight-of-evidence approach. Historically, in silico approaches established in regulations to determine aquatic toxicity endpoints have been focussed on the application of structure-based predictions using quantitative structure–activity relationship (QSAR) models coupled with well-established Modes or Mechanisms of Action (MoA/MechoA) such as that described by non-specific toxicity (narcosis).5–7 The majority of such published QSARs derived for narcosis rely on the octanol–water partition coefficient (Kow) as a proxy for the lipophilicity/hydrophobicity of chemicals.5,8–12 Since narcosis is driven by critical accumulation in tissues and phospholipid membranes,13,14 resulting in disturbance in their integrity and function, the toxicity of chemicals demonstrating this MoA/MechoA is highly correlated with lipophilicity. However, biological membranes are ordered, anisotropic three-dimensional structures. Therefore, as octanol is a homogenous isotropic medium, it cannot adequately describe the membrane interactions of chemicals such as ionisable organic compounds and surfactants.15,16
Hydrocarbon (HC) based surfactants are widely used around the globe in both industrial and consumer products.17 They are amphiphilic structures containing both hydrophobic and hydrophilic components17,18 and are commonly classified according to the charge of their hydrophilic “head” as anionic, non-ionic, cationic or zwitterionic. Anionic surfactants are by far the most widely used class of surfactants17 with 45 individual anionic surfactants (with hydrocarbon backbones) currently registered under the European Union's REACH legislation in volumes greater than 100 tonnes per year.19 In addition to the hydrocarbon-based surfactants, surfactants with perfluorinated carbon (FC) chains, which belong to a large group of chemicals known as poly- and perfluoroalkyl substances (PFAS), are currently used in a variety of specialist applications from electronics and textiles to fire-fighting foams.20 Perfluorinated surfactants are widely reported as an environmental and health problem, particularly due to their high environmental persistence.20–25 Their surfactant structure with fully fluorinated carbon backbone gives them unique properties (e.g., high stability), but also causes challenges when modelling the physical–chemical properties and environmental fate/partitioning parameters of PFAS.26,27 Deriving animal-based toxicity endpoints for such an abundance of compounds (currently estimated at more than 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000,24,28 many being surfactants20) is also not possible or ethical and emphasises the need for their grouping.29 Perfluorinated surfactants have a high affinity for binding to proteins27,30 and membrane phospholipids, making the membrane-water partitioning coefficient a highly relevant parameter for these compounds26,27,31,32 and a potential proxy for (eco)toxicity predictions. Hence, considering their unique properties and methodological challenges, the FC group of surfactants provide an interesting case study.
000,24,28 many being surfactants20) is also not possible or ethical and emphasises the need for their grouping.29 Perfluorinated surfactants have a high affinity for binding to proteins27,30 and membrane phospholipids, making the membrane-water partitioning coefficient a highly relevant parameter for these compounds26,27,31,32 and a potential proxy for (eco)toxicity predictions. Hence, considering their unique properties and methodological challenges, the FC group of surfactants provide an interesting case study.
The amphiphilic nature of both hydro- and perfluoro-carbon surfactants makes it difficult to accurately determine Kowvia empirical methods due to these species' tendency to accumulate at the octanol–water interface.26,33 For ionised compounds, Kow can lead to a significant underestimation of lipophilicity when used as a proxy for membrane partitioning, represented by the membrane lipid–water partitioning coefficient, Kmw.16,34 The speciation-corrected membrane lipid–water distribution coefficient (Dmw) provides a more biologically relevant and methodologically defensible alternative to Kow. It has been previously shown to perform as well as Kow for predicting the toxicity of neutral narcotics and is superior as a predictor of toxicity for ionisable chemicals,15,26,35–37 which is influenced by the degree of ionisation at environmentally relevant pH.37–39 Hence, in these cases, Dmw is considered a more appropriate descriptor than Kow26,40 and is also methodologically more robust to derive both experimentally and computationally. Previously, QSARs based on Dmw as a single predictor have shown a good correlation with baseline toxicity in different aquatic species (e.g., algae, Vibrio fischeri, daphnids and fish), for both neutral and ionisable narcotics.15,37,41,42 Despite this, QSARs based on Kmw/Dmw are much less prevalent in the literature and regulatory applications due to the limited availability of experimental membrane liposome-water partitioning coefficients, and the need for method standardisation. However, in recent years, there has been more effort to generate experimental Kmw/Dmw values for different classes of surfactants.19,26,43–45
Several in silico methods are capable of calculating Kmw/Dmw. While linear regressions based on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow,36 and poly-parameter Linear Free Energy Relationships (ppLFERs)46 work well for neutral organics, for ionisable chemicals commercial software such as COSMOtherm's COSMOmic module was shown to perform better.34,46 Still, COSMOmic has limitations for some chemical groups,47 including those containing short hydrocarbon26 or perfluorinated alkyl chains.26,27 Additionally, for long or flexible molecules, running the associated conformer generation software COSMOconf can be prohibitively slow, limiting COSMOmic's utility as a screening tool.
Kow,36 and poly-parameter Linear Free Energy Relationships (ppLFERs)46 work well for neutral organics, for ionisable chemicals commercial software such as COSMOtherm's COSMOmic module was shown to perform better.34,46 Still, COSMOmic has limitations for some chemical groups,47 including those containing short hydrocarbon26 or perfluorinated alkyl chains.26,27 Additionally, for long or flexible molecules, running the associated conformer generation software COSMOconf can be prohibitively slow, limiting COSMOmic's utility as a screening tool.
Another computational approach for calculating Kmw/Dmw is molecular dynamics (MD) simulation, where the chemical species of interest, along with the lipid membrane and water, are all represented with atomistic detail. In order to reduce the computational expense of MD simulations, coarse-graining is sometimes used, grouping sets of atoms into “beads” and simulating the movement and interaction at this slightly reduced resolution. This approach simplifies the representation, allowing rapid simulation of large systems.48 In particular, the Martini coarse-grained force field is an appealing candidate for the calculation of Dmw49,50 because the interactions between beads are derived from solvent partitioning data. Previous work by Potter et al.47 integrated the newest version of the force field, Martini 3, with an automatic procedure47 for generating coarse-grained representations of organic solutes.47 Using these tools, Dmw was calculated for a series of charged and zwitterionic molecules. That work exploited some, but not all the new features of Martini 3, leaving room for further expansion of the method to a wider chemical space. In the context of this work, the new halogenated beads included in Martini 3 are particularly relevant for PFAS. In addition, the recent increase in the availability of Kmw/Dmw surfactant data19,26,43–45 provides a timely opportunity to validate the refined Martini force field for membrane-water partitioning of a broader range of molecules.
The application of Kmw/Dmw measurements for surfactants thus far has been almost entirely focused on its potential use as a predictive proxy for assessing bioaccumulation in fish.19,44,51,52 To our knowledge, the approach has not yet been applied to developing ecotoxicity QSARs for charged surfactants.
The present study, therefore, aims to: (1) develop a general hydrocarbon-based anionic surfactant toxicity QSAR model for fish species and QSAR models for hydro- and perfluorocarbon -based anionic surfactants for daphnids, using simulated Dmw; (2) build on our previous work to further develop coarse-grained MD simulations for anionic surfactants, increasing confidence in the approach as an efficient computational method for deriving the Dmw for both hydro- and perfluorocarbon-based anionic surfactants.
2. Methods
2.1. Surfactant selection
The focus of this study is on anionic surfactants with ≥6 carbon atoms in their hydrocarbon chains or ≥4 carbon atoms in perfluorinated chains. All the selected surfactants had pKa values below 4.8. Apart from two carboxylic acid salts which are >90% ionised, all remaining surfactants are expected to be fully ionised in the environmentally relevant pH range of 6–9. A full list of all chemicals, including the representative structures, and relevant physical–chemical properties is given in Tables S1–S3 of the ESI.† Both group (sub-class-based) and individual compound abbreviations are used throughout, with naming conventions explained in Tables S1 and S2.† In brief, the majority of headgroups of hydrocarbon chain-based surfactants belong to several larger sub-classes: alkyl sulfates (AS), alkyl sulfonates, alkyl ether sulfates (AES), linear alkylbenzene sulfonates (LAS), salts of carboxylic acids (soaps), fatty acid ester sulfonates (FAES) and alkyl isethionates (AI). Most anionic perfluorocarbon-based surfactants belonged to perfluoroalkyl sulfonic acids (PFSA) and perfluorocarboxylic acids (PFCA). Other surfactant sub-classes are reported in Table S2 of the ESI,† including some branched and cyclic backbone-containing compounds.2.2. Experimental methods
To address the experimental data gaps in the structural representation of some anionic surfactant groups (mainly AES, AS and AI molecules), we have experimentally determined new empirical membrane lipid–water distribution coefficients (Dmw) values. These values were subsequently used for further development and validation of the coarse-grained simulation method. Dmw values were measured by one of two methods:(1) Liposome-water partitioning, based on the approach described by Ebert et al.27 using the extrusion method of preparation of large unilamellar liposome vesicles. Samples of the commercial mixture at 200 μM and single-component references at 50 μM and 100 μM were dosed in triplicate into wells of the rapid equilibrium dialysis (RED) plate containing phosphate buffered saline at natural pH 7.4. Incubation was carried out for 48 h for the mixture and 24 and 48 h for the single components at 37 °C. Triplicate data are reported for the C12 isethionate and duplicate for the C14 isethionates commercial mixture and the C14 single component reference standards. For the C12SO4 reference standard, triplicate data are reported for 50 μM and 100 μM after 48 h incubation (n = 6) and 50 μM and 100 μM after 24 and 48 h incubation for the C12EO3S (n = 12), respectively.
(2) Solid-supported lipid membranes (SSLM), using a commercially available pre-dosed assay as described by Timmer et al.43 Here, the analysis was carried out using acetate buffer with pH 7.4, following the manufacturer's guidance. The incubation time was optimised for each component and ranged from 0.5 to 144 h.
All other experimental Dmw values were obtained from existing literature (full list given in Table S11†). Full details of the experimental methods and a list of all newly generated values can be found in ESI Section 2.† In cases where multiple values for the same surfactant were available, an arithmetic mean was taken to give a single value.
The liposome Dmw values naturally emerge in units of L kg−1 (as do the simulation results). However, the protocol for SSLM measurements returns a dimensionless Dmw. The differing factor is the lipid density, which is close to 1 in units of kg L−1. Therefore, in practice, the two conventions are interchangeable. The equations associated with each of the methods are given in the ESI 2.†
2.3. Coarse-grained simulation method
The present work expands the automatic procedure from Potter et al.,47 to exploit the new Martini 3 halogenated bead types, re-optimise the bead assignment of some charged groups, and modify the mapping algorithm to comply with the Martini developers' latest guidance.54 In this section, we outline these developments, which are implemented in the most recent version of the cg_param script (available on GitHub at https://github.com/cgkmw-durham/cg_param_m3/tree/martini3_v3).
The automatic script assigns neutral fragments using their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values, allowing a broad range of groups to be represented without arbitrary fitting. However, charged “Q” groups partition so strongly into water that they cannot be reliably assigned on Kow values. Instead, assignments can be chosen to reproduce other properties, such as experimental Dmw values for simple species containing the charged groups. These assignments can then be transferred without further adjustment to other molecules, where experimental Dmw values might not be available.
Kow values, allowing a broad range of groups to be represented without arbitrary fitting. However, charged “Q” groups partition so strongly into water that they cannot be reliably assigned on Kow values. Instead, assignments can be chosen to reproduce other properties, such as experimental Dmw values for simple species containing the charged groups. These assignments can then be transferred without further adjustment to other molecules, where experimental Dmw values might not be available.
In line with previous work, parameterisations for charged groups have been hard-coded for carboxylate, sulfate and sulfonate functional groups before applying the general graph-based algorithm for mapping the rest of a given molecule. The beads for these groups were SQ5n, Q2, and Q3 respectively. The carboxylate SQ5n and sulfate Q2 assignments are the starting points recommended by the Martini developers.47 The sulfonate Q3 assignment has changed from the SQ4p recommendation in a previous publication47 which contained only one example of a sulfonate;47 the new assignment is derived from the larger number of experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw sulfonate values made available by the present work, as detailed in Section S3.1 of the ESI.†
Dmw sulfonate values made available by the present work, as detailed in Section S3.1 of the ESI.†
The new Martini 3 halogenated “X” beads have been added to the cg_param algorithm. Any aliphatic group containing two or more fluorine atoms is now assigned to a bead selected from the X category according to the Kow of the molecular fragment in the same way that other bead types are chosen. For PFAS molecules, where experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw values are available, the use of X beads improves the agreement between experiment and simulation, providing some confidence also for molecules where experimental log
Dmw values are available, the use of X beads improves the agreement between experiment and simulation, providing some confidence also for molecules where experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw is not known. We have not extended the use of X beads to other halogens, aromatic groups, or cases where a bead contains only one fluorine, all of which are outside the scope of this study.
Dmw is not known. We have not extended the use of X beads to other halogens, aromatic groups, or cases where a bead contains only one fluorine, all of which are outside the scope of this study.
To describe PFAS accurately, it is also necessary to recognise the influence of fluorine atoms on adjacent charged groups, even if they are not part of the same coarse-grained bead. Martini normally adopts a building-block approach where all fragments are parametrised independently. However, fluorine has such strong and complex electronic effects on adjacent moieties51 that they cannot satisfactorily be neglected. We have shifted the assignment of charged beads for the sulfonate and carboxylate groups from Q3 to Q1p, and SQ5n to SQ1p, respectively, whenever these groups are directly bonded to a bead containing at least two fluorine atoms. Detailed information on the parameterisation of PFAS is given in ESI Section S3.2.†
Another functional group requiring attention is the ester fragment in AI and FAES surfactants. In general, it is preferable for esters to be kept intact in a single bead, rather than split over adjacent beads. Furthermore, a dedicated study of esters (in preparation) shows that the optimal bead assignment is slightly different from that returned by routine matching to Kow. We therefore protect the –COO– fragment from being split by topological analysis in the spectral mapping algorithm and assign it to an SP2 bead, wherever possible. However, there are some cases where splitting the –COO– group is inevitable. Details of how these cases are handled are given in ESI Section S3.3.†
The present work tackles larger molecules than previously applied to this algorithm. Long chains with highly branched heavy-atom sites, such as sulfur in sulfate, can lead to numerical difficulties in the spectral mapping calculations56 as implemented in our coarse-graining procedure.50 In brief, the centrality scores of atoms in such molecules (which are used to determine the order in which they are grouped into beads) may span so many orders of magnitude that they cannot be accurately calculated with normal machine precision. We have introduced an adaptive weighting procedure to mitigate the problem while retaining the influence of mean mass and bonding path length as in our original algorithm. This modification is described in more detail in ESI Section S3.4.† It can alter the precise mapping of molecules in cases where more than one option is plausible.
In line with new recommendations of the Martini 3 developers,57 bead coordinates are now defined by the centre of geometry (COG) of the atoms that they represent, rather than by the centre of mass used in previous generations of the force field. The change to COG coordinates is focused on capturing molecular packing densities54 and only has a minor impact on the resulting Dmw values, as shown in ESI Section S3.5.†
Once the coarse-grained models have been derived for each surfactant, umbrella sampling molecular dynamics simulations are used to obtain the free energy profile in a 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) membrane, from which Dmw is then derived. These methods match those used in the previous work.47,50 The simulation parameters are given in ESI Section S3.6† and the connection between the free energy profiles and the calculation of Dmw (in L kg−1) is detailed in ESI Section S3.7.†
2.4. Ecotoxicity data
In addition to the bulk database search described above, an extensive review of scientific literature was conducted using both chemical and common surfactant names as keywords. Included in this were also a variety of externally available review documents originally prepared for the environmental risk assessment of surfactants.60–63 These documents contained industry-shared data which have been collated and evaluated by independent bodies. Hence, some toxicity values from those documents are from proprietary studies and full access to the study details was not possible, but the values were still considered scientifically relevant. A few additional data points were obtained from Unilever's historic proprietary (unpublished) internal studies. As a result, a small proportion of the values used in deriving the fish HC and daphnids HC QSARs (equivalent to 16% and 14%, respectively) were from proprietary studies. For the daphnid FC QSAR, proprietary study data were used only as part of averaged values for perfluorooctanoic acid (PFOA).
For all data points, quality criteria were established and applied as follows:
(1) Only values reported as 96 h LC50 s (for fish) and 48 h LC/EC/IC50 (for daphnids) were included in compliance with the current OECD Guidelines.64,65
(2) No restriction was made regarding fish species.59 Interspecies sensitivity of fish is a complex topic and is often chemical-specific with insufficient evidence to state whether one species or another would be more sensitive.66 Similarly, data for both Daphnia sp. and Ceriodaphnia have been included since it was previously demonstrated that there is no significant difference in their sensitivity to different chemicals.67 This approach, therefore, provides the broadest applicability to predicting fish and daphnids acute toxicity on the trophic level basis rather than by individual species.
(3) The solubility of surfactants is difficult to define due to the formation of micelles, which are soluble aggregates of surfactants. The critical micelle concentration (CMC) at which they form defines the maximum solubility of the single-molecule form.33 Hence, when evaluating the reported toxicity threshold concentrations against solubility considerations, we also relied on descriptive evaluation of test systems; in cases of described solubility issues in original publications or reported visible residuals of surfactants, these data points were omitted regardless of them being reported as below the solubility threshold.
(4) Data reported for the “active ingredient” were preferred to “formulation” data from the USEPA ECOTOX database.
(5) Data reported as measured concentrations were given preference to nominal concentrations. However, nominal concentrations were included in the absence of measured data.
(6) When data from ECHA's registration dossiers were used (initially accessed via eChemPortal and individually assessed afterwards), only data marked with high reliability (Klimisch scores of 1 or 2) were used.
(7) Only data for mono-constituent surfactants were used to develop the QSARs.
(8) When more than one equivalent endpoint for the same surfactant was available — either for the same or different fish/(Cerio)daphnia species — the geometric mean of these values was calculated and used.
Compilation of ecotoxicity data for PFAS chemicals classified as anionic surfactants was performed using the USEPA ECOTOX database.58 Data for all PFAS chemicals were exported based on the “organic compounds” ECOTOX classification by selecting the group of “Per- and Polyfluoroalkyl substances (PFAS)” and subsequently filtering to obtain the ecotoxicity data for PFAS chemicals for both fish and daphnids. The extracted chemicals were further evaluated based on the provided chemical identifiers to keep only those that can be classified as “anionic surfactants”. Toxicity data quality criteria were applied as described above. As the fish studies reporting 96 h LC50s were mostly limited to perfluorooctane sulfonic acid (PFOS) and perfluorooctanoic acid (PFOA), data scarcity for other perfluorinated (anionic) surfactants prevented us from developing the fish QSAR alongside the daphnids QSAR.
3. Results and discussion
3.1. Experimental and simulated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Dmw
Dmw
To further develop the coarse-grained mapping and simulation methodology47 for calculating log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw for surfactants, the simulated values were compared with measured values for selected chemical species from the existing literature and new experiments in this study (ESI 4†). This process has resulted in an expansion of the molecular fragments that can be accurately represented and consequently in an increase in the chemical space covered by the models. Simulation-generated log
Dmw for surfactants, the simulated values were compared with measured values for selected chemical species from the existing literature and new experiments in this study (ESI 4†). This process has resulted in an expansion of the molecular fragments that can be accurately represented and consequently in an increase in the chemical space covered by the models. Simulation-generated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw values and the corresponding experimental data are compared in Fig. 1, demonstrating a good fit (root mean squared error = 0.36).
Dmw values and the corresponding experimental data are compared in Fig. 1, demonstrating a good fit (root mean squared error = 0.36).
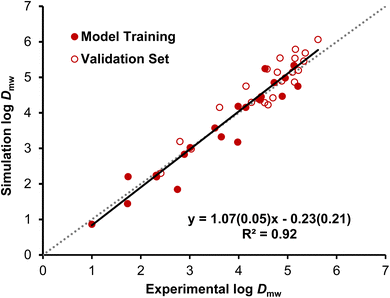 | ||
Fig. 1 Correlation of simulation log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw values with the corresponding experimental log Dmw values with the corresponding experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw values (SSLM and liposome data). When multiple experimental data points were available for the same surfactant they were averaged, with SSLM data and liposome data treated as equal quality. Solid symbols indicate molecules used to select the Martini charged bead assignments (linear sulfate, sulfonate and PFAS species given in Table S12†). Open symbols indicate predictions for chemical species that were not used in the model development. The black full line is a regression line for the entire data set; its equation is shown on the graph with standard errors of the slope and intercept (in brackets) and coefficient of determination. The dotted grey line is a line of 1 Dmw values (SSLM and liposome data). When multiple experimental data points were available for the same surfactant they were averaged, with SSLM data and liposome data treated as equal quality. Solid symbols indicate molecules used to select the Martini charged bead assignments (linear sulfate, sulfonate and PFAS species given in Table S12†). Open symbols indicate predictions for chemical species that were not used in the model development. The black full line is a regression line for the entire data set; its equation is shown on the graph with standard errors of the slope and intercept (in brackets) and coefficient of determination. The dotted grey line is a line of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlation, log 1 correlation, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw (simulation) = log Dmw (simulation) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw (experimental). Dmw (experimental). | ||
Of the 43 molecules in Fig. 1, 23 have been used to inform the selection of Martini bead types for key molecular fragments, as detailed in ESI Section S3.† These chemical species can be regarded as a training set for parametrisation of the coarse-grained models. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw values for the remaining 20 species were then produced by simulation of models constructed using the mapping and parametrisation algorithm without further adjustment. These values constitute a partial test of the method.
Dmw values for the remaining 20 species were then produced by simulation of models constructed using the mapping and parametrisation algorithm without further adjustment. These values constitute a partial test of the method.
The QSARs in this paper are based on a total of 71 unique chemicals for which relevant ecotoxicological data are available (some of which apply to both fish and daphnids). Experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw values are available for only 29 of these molecules. Hence, the coarse-grained models are supplying log
Dmw values are available for only 29 of these molecules. Hence, the coarse-grained models are supplying log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw for 42 species that could not otherwise be included in construction of the QSARs.
Dmw for 42 species that could not otherwise be included in construction of the QSARs.
While other Kmw/Dmw predictive methods exist, they are either limited to neutral organics36 or, in the case of COSMOmic, struggle to predict Dmw for both shorter anionic hydrocarbons (4–8 C atoms of alkyl sulf(on)ates)26 and molecules containing perfluorocarbon chains.26,27 Droge used COSMOmic to calculate log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw of neutral and ionisable alkyl sulf(on)ates and perfluoroalkyl acids (PFAAs), but only COSMO simulations for neutral species were able to replicate experimentally determined chain length increments, with experimental Dmw values still based on ionised species.26 Ebert et al. used the same tool and observed a similar effect for PFAAs and their industrial alternatives; for shorter chain molecules, i.e., for PFCAs with 3–6 CFx and PFBS, log
Dmw of neutral and ionisable alkyl sulf(on)ates and perfluoroalkyl acids (PFAAs), but only COSMO simulations for neutral species were able to replicate experimentally determined chain length increments, with experimental Dmw values still based on ionised species.26 Ebert et al. used the same tool and observed a similar effect for PFAAs and their industrial alternatives; for shorter chain molecules, i.e., for PFCAs with 3–6 CFx and PFBS, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw was overpredicted by COSMOmic by 0.5–2
Dmw was overpredicted by COSMOmic by 0.5–2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. Other Dmw results were varied, with perfluoroalkyl carboxylates HFPO-DA (GenX) and NaDONA overpredicted while perfluoroalkyl sulfonates PFHxS and PFOS and their (cyclic) alternative PFECHS were underpredicted.27Dmw was well captured for these compounds using coarse-grained simulations (ESI Section 4.1†). A comparison of those COSMOmic values and coarse-grained simulation log
log units. Other Dmw results were varied, with perfluoroalkyl carboxylates HFPO-DA (GenX) and NaDONA overpredicted while perfluoroalkyl sulfonates PFHxS and PFOS and their (cyclic) alternative PFECHS were underpredicted.27Dmw was well captured for these compounds using coarse-grained simulations (ESI Section 4.1†). A comparison of those COSMOmic values and coarse-grained simulation log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw for anionic surfactants against experimental data is provided in more detail and visualised in ESI Section 4.2 (Table S13 and Fig. S9).†
Dmw for anionic surfactants against experimental data is provided in more detail and visualised in ESI Section 4.2 (Table S13 and Fig. S9).†
Regardless of the good fit between the simulated and experimental Dmw values, in the specific case of alkylethoxy ethers the simulations predict an increase in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw with respect to the number of ethoxylate units (EO), in contrast to the decrease seen in experimental results35 (a trend also predicted by the ALOGPS70 neural network in log
Dmw with respect to the number of ethoxylate units (EO), in contrast to the decrease seen in experimental results35 (a trend also predicted by the ALOGPS70 neural network in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow of these molecules). The disagreement is particularly pronounced for compounds containing more than four ethoxylate units. The difficulty with alkylethoxy ethers in simulations was recognised by Rossi et al.,71 who published a custom extension to Martini 2 for polyethylene glycol. We find that, even with the extended chemical space covered by the new Martini 3 beads, we cannot capture the behaviour of both short- and long-chain polyethers with a single ether mapping and parameterisation. This class of molecule, therefore, needs dedicated attention, which is beyond the scope of this work.
Kow of these molecules). The disagreement is particularly pronounced for compounds containing more than four ethoxylate units. The difficulty with alkylethoxy ethers in simulations was recognised by Rossi et al.,71 who published a custom extension to Martini 2 for polyethylene glycol. We find that, even with the extended chemical space covered by the new Martini 3 beads, we cannot capture the behaviour of both short- and long-chain polyethers with a single ether mapping and parameterisation. This class of molecule, therefore, needs dedicated attention, which is beyond the scope of this work.
Due to this known issue, to include C12EO8S in our training set for predicting (eco)toxicity, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw was calculated using the multiple regression equation from Droge et al. derived for anionic surfactants.51 This equation uses a fragment-based approach to predict Dmw and has demonstrated a good fit for anionic surfactants, providing they are within the applicability domain and contain fragments which were initially included in the regression. Hence, it is limited to the surfactant sub-classes it was derived with and, therefore, not applicable for groups such as AI, FAES and PFAS other than perfluoroalkyl acids.
Dmw was calculated using the multiple regression equation from Droge et al. derived for anionic surfactants.51 This equation uses a fragment-based approach to predict Dmw and has demonstrated a good fit for anionic surfactants, providing they are within the applicability domain and contain fragments which were initially included in the regression. Hence, it is limited to the surfactant sub-classes it was derived with and, therefore, not applicable for groups such as AI, FAES and PFAS other than perfluoroalkyl acids.
3.2. Anionic surfactant QSARs
The full dataset of acute ecotoxicity endpoints for mono-constituent anionic surfactants is reported in ESI Section 6.† The convenience of the coarse-grained simulation method, as previously discussed, meant that log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw could be predicted for all anionic surfactants where ecotoxicity data were available, avoiding the need to eliminate data points based on a lack of experimental liposome-water partitioning values. The least-squares linear regression QSAR models were developed using logarithmic transformation of ecotoxicity endpoints for fish and daphnids correlated with log
Dmw could be predicted for all anionic surfactants where ecotoxicity data were available, avoiding the need to eliminate data points based on a lack of experimental liposome-water partitioning values. The least-squares linear regression QSAR models were developed using logarithmic transformation of ecotoxicity endpoints for fish and daphnids correlated with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw. All QSAR models are presented in Fig. 2a–c, with the regression equations and coefficients of determination presented on the corresponding graphs. Due to limitations in the number of suitable ecotoxicity data points, they were all used as a training set. All regressions for fish and daphnid toxicity demonstrated a good fit, with R2 greater than 0.7, meeting the robustness and predictivity criteria indicative of a good QSAR, with the full details of their statistical evaluation reported in ESI Section 7.†
Dmw. All QSAR models are presented in Fig. 2a–c, with the regression equations and coefficients of determination presented on the corresponding graphs. Due to limitations in the number of suitable ecotoxicity data points, they were all used as a training set. All regressions for fish and daphnid toxicity demonstrated a good fit, with R2 greater than 0.7, meeting the robustness and predictivity criteria indicative of a good QSAR, with the full details of their statistical evaluation reported in ESI Section 7.†
 | ||
Fig. 2 Fish and daphnid log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw-based QSAR models. Respective regression equations and coefficients of determination are shown for each set of chemicals (HC indicating the hydrocarbon and FC perfluorocarbon backbones) and fish/daphnids toxicity from (a) to (c). Standard errors for slopes and intercepts are reported in brackets. Inner dotted lines represent 95% confidence intervals of regression lines, while outer dotted lines represent prediction intervals of the regressions. Log Dmw-based QSAR models. Respective regression equations and coefficients of determination are shown for each set of chemicals (HC indicating the hydrocarbon and FC perfluorocarbon backbones) and fish/daphnids toxicity from (a) to (c). Standard errors for slopes and intercepts are reported in brackets. Inner dotted lines represent 95% confidence intervals of regression lines, while outer dotted lines represent prediction intervals of the regressions. Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw are simulated values, except for C12EO8S where Droge et al., 2021 method51 was used for calculations. Dmw are simulated values, except for C12EO8S where Droge et al., 2021 method51 was used for calculations. | ||
The resulting QSAR equations (with number of data points n, regression coefficient R2, standard error SE and statistical significance F) are:
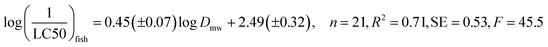 | (1) |
 | (2) |
The applicability domains for the QSAR models have been determined based on the structural and physicochemical descriptors within the training set (Table 1). To give each QSAR model the broadest level of applicability, we have included as many different headgroups as data availability allowed.
| Fish | (Cerio)daphnia | |
|---|---|---|
| Structural domain: functional groups contained (anionic surfactant sub-classes) | Sulfate | Sulfate |
| Sulfonate | Sulfonate | |
| Sulfosuccinate | Sulfosuccinate | |
| Carboxylic acid | Carboxylic acid | |
| Ester sulfonate | Isethionate | |
| Ether sulfate | Ester sulfonate | |
| Taurate | Ether sulfate | |
| Dithiophosphate | Sulfoacetate | |
Physicochemical domain: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw range Dmw range |
0.03–6.91 | 1.94–6.91 |
| Molecular weight | 158–566 | 216–619 |
The general consensus in scientific literature through multiple lines of evidence including toxic unit approaches, structure–activity analysis and both phenotypic and genotypic observations, is that anionic surfactants such as AS, AES, FAES and LAS have a narcotic mode of ecotoxic action14,62,75,76 such that toxicity is predominantly driven by adsorption, penetration and disruption of cell membranes.72,77,78 In fish, the primary target organs are the gills, where disruption of the epithelium of primary and secondary lamellae can result in hypertrophy and oedema, causing hypoxia and respiratory failure.79 Such adverse effects are well described by hydrophobicity-based descriptors and even at a gene level a cross-species transcription switch correlation with Kow is observed when an organism is exposed to chemicals with a narcotic mode of action.14,80
The additional charge that is integral to anionic surfactants, and the resulting association with headgroups of membrane lipids, have been previously proposed as a reason for observed enhanced toxicity, particularly for surfactants of lower chain length/hydrophobicity, compared to neutral compounds.9,81 As chain lengths increase, hydrophobic tendency becomes the predominant factor in toxicity causation and other factors such as biotransformation and variability in uptake kinetics as hypothesised by Droge et al. (2019)26 may influence observed regression slopes. This is reflected in eqn (1) and (2) which deviate from perfect positive correlation, the deviation being consistent with similar observations for widely used and accepted QSARs derived using log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow for both baseline and polar narcosis (for both surfactants and non-surfactants) such as those of Hodges et al. (2006),75 Könemann (1981),8 Saarikoski and Viluksela (1982)9 and Verhaar et al. (1995).11
Kow for both baseline and polar narcosis (for both surfactants and non-surfactants) such as those of Hodges et al. (2006),75 Könemann (1981),8 Saarikoski and Viluksela (1982)9 and Verhaar et al. (1995).11
Previously, Müller et al.35 applied experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kmw to derive toxicity QSARs based on a small group of alcohol ethoxylate (nonionic) surfactants. Here, we present the first membrane-water-based fish and daphnid QSAR models for anionic surfactants which are applicable to a broad range of charged moieties associated with a number of surfactant subclasses. To date, the only published QSARs that use this descriptor (and the experimentally derived ecotoxicity endpoints) while not relying on Kow–Kmw regression equations, relate to toxicity in Aliivibrio fischeri37 and the zebrafish embryo test (FET).15,41 Both studies demonstrated the applicability of log
Kmw to derive toxicity QSARs based on a small group of alcohol ethoxylate (nonionic) surfactants. Here, we present the first membrane-water-based fish and daphnid QSAR models for anionic surfactants which are applicable to a broad range of charged moieties associated with a number of surfactant subclasses. To date, the only published QSARs that use this descriptor (and the experimentally derived ecotoxicity endpoints) while not relying on Kow–Kmw regression equations, relate to toxicity in Aliivibrio fischeri37 and the zebrafish embryo test (FET).15,41 Both studies demonstrated the applicability of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kmw/Dmw for predicting baseline (narcotic) toxicity of neutral and ionisable chemicals. However, neither included surfactants. Existing published surfactant subclass-specific QSARs have so far focussed predominantly on log
Kmw/Dmw for predicting baseline (narcotic) toxicity of neutral and ionisable chemicals. However, neither included surfactants. Existing published surfactant subclass-specific QSARs have so far focussed predominantly on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow or chain length-based descriptors.73–75,82
Kow or chain length-based descriptors.73–75,82
There are advantages and drawbacks in using both descriptors when predicting surfactant toxicity. Regulatory and general acceptability of Kow as a proxy for hydrophobicity and hence toxicity of neutral, organic chemicals,83–85 coupled with readily available computational tools,86 are an important advantage of the descriptor and use of Kow-based QSARs for neutral organic chemicals. Whilst QSARs based on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow are widely used,85,87 as already mentioned, the determination of accurate and reliable log
Kow are widely used,85,87 as already mentioned, the determination of accurate and reliable log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values is highly challenging for surfactants due to their amphiphilic properties.33,87 Their tendency to aggregate at solvent interfaces and emulsify solvent phases, combined with a lack of a defined solubility limit, results in significant difficulties in determining accurate and reliable empirical values using currently available methods (e.g. OECD 123 (ref. 88)). In addition, Quantitative Structure–Property Relationships (QSPR)-predicted Kow/Dow values, with the exception of non-ionic surfactants, do not correlate well with experimental values for surfactants and also exhibit large inter- as well as intra-method-dependent variability.33 This variability has been exemplified by a study of two similar sub-classes of anionic surfactant which identified systematic differences in the log
Kow values is highly challenging for surfactants due to their amphiphilic properties.33,87 Their tendency to aggregate at solvent interfaces and emulsify solvent phases, combined with a lack of a defined solubility limit, results in significant difficulties in determining accurate and reliable empirical values using currently available methods (e.g. OECD 123 (ref. 88)). In addition, Quantitative Structure–Property Relationships (QSPR)-predicted Kow/Dow values, with the exception of non-ionic surfactants, do not correlate well with experimental values for surfactants and also exhibit large inter- as well as intra-method-dependent variability.33 This variability has been exemplified by a study of two similar sub-classes of anionic surfactant which identified systematic differences in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow calculation method when applied to the two classes.75 Despite these limitations, some Kow-based QSARs with good predictivity have been successfully derived for individual surfactant sub-classes using a range of modifications to existing QSPR methods to address some of the limitations of the existing Kow calculation methods.81,89–92 However, these QSARs are still restricted to a small range of surfactants, rather than to the general group of anionic surfactants.
Kow calculation method when applied to the two classes.75 Despite these limitations, some Kow-based QSARs with good predictivity have been successfully derived for individual surfactant sub-classes using a range of modifications to existing QSPR methods to address some of the limitations of the existing Kow calculation methods.81,89–92 However, these QSARs are still restricted to a small range of surfactants, rather than to the general group of anionic surfactants.
Surfactant chain length has also been demonstrated to be positively correlated with aquatic toxicity and simple rules relating chain length to toxicity are straightforward to apply when assessing homologues.72–74,77 However, this approach does not account for the differing polar headgroups which may exert differing levels of toxicity.93 For this reason, QSARs based on chain length are restricted to small sub-classes with the same headgroup moiety. This limitation is evident, for example, in the US EPA ECOlogical Structure–Activity Relationship Model (ECOSAR),82 developed initially to support data gaps filling under TSCA.
A total of 17 perfluorinated anionic surfactants with acute daphnid toxicity data fulfilling the quality criteria defined in Section 2.4.1 were used to generate a QSAR model (Fig. 2c and Table S16†). Initial plots indicated that fluorotelomer acids (6 individual chemicals) formed a different relationship with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw than the remaining surfactants and were consequently eliminated from the regression.
Dmw than the remaining surfactants and were consequently eliminated from the regression.
Fluorotelomer acids are known precursors of perfluoroalkyl acids and have already been associated with eco(toxicity) several orders of magnitude higher than corresponding PFAAs of the same chain lengths in different organisms.99,100 This excess toxicity was postulated to come from unsaturated and saturated fluorotelomer carboxylic acids (FTUCAs and FTCAs) releasing HF (hydrogen fluoride) as they biotransform into PFAAs (their terminal degradation product), and generally additive effects of FT(U)CAs with their metabolites.100 While more research is needed to understand the mode of action of fluorotelomer acids in aquatic organisms, vertebrates and invertebrates, this is beyond the scope of this paper.100
The resulting QSAR model equation for FC surfactants in daphnids is:
 | (3) |
The structural applicability domain includes PFCAs and PFASs of varying CFx chain lengths and their two substitutes belonging to the subclass of perfluoroalkyl ether carboxylates and cyclic PFSA, with molecular weights ranging from 213 to 613 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw 0.86 to 6.02 (Fig. 2c).
Dmw 0.86 to 6.02 (Fig. 2c).
The lower magnitude of the slope for the FC QSAR compared to that of the hydrocarbon equivalent indicates a smaller increase in toxicity to daphnids with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw increase, with higher toxicity of FC surfactants with low log
Dmw increase, with higher toxicity of FC surfactants with low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw shown in the higher intercept. Statistical comparison of the slopes and intercepts of FC and HC QSARs indicated that both parameters are statistically significantly different between the two QSARs (correlation p-values of 0.00013 and 0.003, respectively). In addition to their affinity for phospholipids,26,27,101 for some anionic PFAS (e.g. PFOS, PFOA and some other long-chain PFAAs), protein binding has been highlighted as an important mechanism in their bioaccumulation and toxicity in vertebrates30,98,102,103 due to their strong affinity for proteins. This additional consideration of binding behaviour makes understanding their mode of action and the link between their structure and “hydrophobicity” highly complex and uncertain.26,103 Despite these difficulties, and the limited available data, here we have been able to demonstrate that log
Dmw shown in the higher intercept. Statistical comparison of the slopes and intercepts of FC and HC QSARs indicated that both parameters are statistically significantly different between the two QSARs (correlation p-values of 0.00013 and 0.003, respectively). In addition to their affinity for phospholipids,26,27,101 for some anionic PFAS (e.g. PFOS, PFOA and some other long-chain PFAAs), protein binding has been highlighted as an important mechanism in their bioaccumulation and toxicity in vertebrates30,98,102,103 due to their strong affinity for proteins. This additional consideration of binding behaviour makes understanding their mode of action and the link between their structure and “hydrophobicity” highly complex and uncertain.26,103 Despite these difficulties, and the limited available data, here we have been able to demonstrate that log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dmw can not only be successfully captured by the simulation method for different perfluorinated structures but that it also provides a useful proxy for the toxicity of anionic FC surfactants to daphnids.
Dmw can not only be successfully captured by the simulation method for different perfluorinated structures but that it also provides a useful proxy for the toxicity of anionic FC surfactants to daphnids.
4. Conclusions
The advantages of replacing the octanol–water partitioning coefficient Kow by the membrane-water distribution coefficient Dmw as a bioaccumulation predictor for charged chemicals (including surfactants) have been clearly demonstrated in recent years.15,26,37,51 Accordingly, Dmw has been incorporated into regulatory guidelines for bioaccumulation.40 Reliable in silico methods to predict Dmw for surfactants with different backbones and a variety of headgroups therefore have the potential to expand the application of Dmw in environmental risk and hazard assessment. The developments in coarse-grained simulation of anionic hydrocarbon and fluorocarbon surfactants described in this paper provide advantages over other computational and predictive methods, namely applicability over a wider chemical scope and superior representation of trends for PFAS chemicals. Validation of the new simulations has been enabled in part by new experimental Dmw data, also presented here.While the application of Dmw in bioaccumulation assessments of surfactants, either directly or as an input parameter for bioaccumulation models, is now becoming established,19,51,52 the use of Dmw in aquatic toxicity assessments of surfactants has so far been limited.26,35 The use of coarse-grained Dmw values (instead of only the available experimental Dmw values) enabled the inclusion of all available ecotoxicity data in our QSARs. If restricted to experimental Dmw, the fish HC QSAR would contain only 9 data points of its current 21, and the daphnid HC QSAR only 17 of 51. We were, therefore, able to develop QSAR models for predicting aquatic toxicity of HC and FC anionic surfactants that span multiple anionic surfactant sub-classes and incorporate them into a single anionic surfactant QSAR for fish and daphnids. Ultimately, enhanced predictive capability helps to eliminate unnecessary animal testing. Derived QSARs facilitate the application of in silico New Approach Methodologies (NAMs) for aquatic toxicity screening, and hazard and risk assessment of anionic HC surfactants, which are high-tonnage, high-use substances commonly registered under REACH.
For FC surfactants, the derived daphnid QSAR model advances the ability to predict their aquatic toxicity as a group. Further work is needed to develop QSARs for other trophic levels and individual chemicals, including diverse PFAS structures and functional groups. However, even the potential of grouping some of these molecules as “anionic surfactants” is significant, given the sheer variety of PFAS chemicals in use, and current and ongoing regulatory initiatives for targeting them on a class basis.104–107
As shown in this study, coarse-grained models for new moieties can be parametrised from high-quality experimental data. The model parameters can then be transferred to related chemical species for which no experimental partitioning data are available. The strength of this modelling approach is that the full response of a molecule's conformations to the aqueous and membrane environments is then fully explored by the molecular dynamics. This approach can significantly increase the breadth of chemical coverage for future (eco)toxicity predictions over QSARs based on Kow/Dow.
Developments in coarse-grained simulation methods for deriving Dmw of surfactants are a significant step in modelling the environmental fate, behaviour and toxicity of surfactants and of ionisable chemicals in general. Further research will be directed towards expanding this approach to other ionisable chemicals including cationic and zwitterionic surfactants.
Data availability
The data supporting this article have been included as part of the ESI.† The code for coarse-grained mapping and parameterisation is available at https://github.com/cgkmw-durham/cg_param_m3/tree/martini3_v3.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Alexandre Teixeira (Unilever SERS) for his help with the analytical interpretation of data for the liposome method, and to Kathryn Gerry of Scymaris Ltd for generation of new SSLM values. MAM and EK thank Dr Thomas Potter for useful discussions on coarse-grained parameterisation. EK acknowledges the funding of the EPSRC (Grant EP/W521991/1) and Unilever. AG acknowledges the support of the basic funding to NGI from The Research Council of Norway. This research made use of the Hamilton high-performance computing (HPC) facility at Durham University.References
- European Commission, Regulation (EC) No 1907/2006 – REACH, European Union, 2006, p. 520, https://osha.europa.eu/en/legislation/directives/regulation-ec-no-1907-2006-of-the-european-parliament-and-of-the-council Search PubMed.
- ECHA, The Use of Alternatives to Testing on Animals for the REACH Regulation, Helsinki, 2023, DOI:10.2823/805454.
- USEPA, Alternative Test Methods and Strategies to Reduce Vertebrate Animal Testing, https://www.epa.gov/assessing-and-managing-chemicals-under-tsca/alternative-test-methods-and-strategies-reduce, accessed 2023-10-03.
- J. W. Firman, D. J. Ebbrell, F. J. Bauer, M. Sapounidou, G. Hodges, B. Campos, J. Roberts, S. Gutsell, P. C. Thomas, M. Bonnell and M. T. D. Cronin, Construction of an in Silico Structural Profiling Tool Facilitating Mechanistically Grounded Classification of Aquatic Toxicants, Environ. Sci. Technol., 2022, 56(24), 17805–17814, DOI:10.1021/acs.est.2c03736.
- M. T. D. Cronin, (Q)SARs to Predict Environmental Toxicities: Current Status and Future Needs, Environ. Sci.:Processes Impacts, 2017, 19(3), 213–220, 10.1039/c6em00687f.
- European Chemicals Bureau, Technical Guidance Document on Risk Assessment, Part III, Ispra, Italy, 2003, https://echa.europa.eu/documents/10162/987906/tgdpart3_2ed_en.pdf/0456c864-d696-467d-ab9d-7680f78397d6, accessed 2024-01-02 Search PubMed.
- European Chemicals Agency (ECHA), Guidance for the Implementation of REACH, Guidance on Information Requirements and Chemical Safety Assessment, Chapter R.6: QSARs and Grouping of Chemicals, 2008, https://echa.europa.eu/documents/10162/13632/information_requirements_r6_en.pdf/77f49f81-b76d-40ab-8513-4f3a533b6ac9, accessed 2024-01-02 Search PubMed.
- H. Könemann, Quantitative Structure-Activity Relationships in Fish Toxicity Studies Part 1: Relationship for 50 Industrial Pollutants, Toxicology, 1981, 19(3), 209–221, DOI:10.1016/0300-483X(81)90130-X.
- J. Saarikoski and M. Viluksela, Relation between Physicochemical Properties of Phenols and Their Toxicity and Accumulation in Fish, Ecotoxicol. Environ. Saf., 1982, 6(6), 501–512, DOI:10.1016/0147-6513(82)90032-X.
- H. J. M. Verhaar, C. J. van Leeuwen and J. L. M. Hermens, Classifying Environmental Pollutants, Chemosphere, 1992, 25(4), 471–491, DOI:10.1016/0045-6535(92)90280-5.
- H. J. M. Verhaar, W. Mulder and J. L. M. Hermens, QSARs for Ecotoxicity. In: Overview of Structure-Activity Relationships for Environmental Endpoints. Part I: General Outline and Procedure, Report Prepared within the Framework of the Project “QSAR for Prediction of Fate and Effects of Chemicals in the Environment”, ed. J. L. M. Hermens, Contract with the European Commission EV5V-CT92-0211, 1995 Search PubMed.
- C. J. Van Leeuwen, P. T. J. Van Der Zandt, T. Aldenberg, H. J. M. Verhaar and J. L. M. Hermens, The Application of QSARs, Extrapolation and Equilibrium Partitioning in Aquatic Effects Assessment for Narcotic Pollutants, Sci. Total Environ., 1991, 109–110, 681–690, DOI:10.1016/0048-9697(91)90222-Z.
- S. T. J. Droge, G. Hodges, M. Bonnell, S. Gutsell, J. Roberts, A. Teixeira and E. L. Barrett, Using Membrane-Water Partition Coefficients in a Critical Membrane Burden Approach to Aid the Identification of Neutral and Ionizable Chemicals That Induce Acute Toxicity below Narcosis Levels, Environ. Sci.:Processes Impacts, 2023, 25(3), 621–647, 10.1039/d2em00391k.
- E. K. Brockmeier, D. Basili, J. Herbert, C. Rendal, L. Boakes, A. Grauslys, N. S. Taylor, E. B. Danby, S. Gutsell, R. Kanda, M. Cronin, J. Barclay, P. Antczak, M. R. Viant, G. Hodges and F. Falciani, Data-Driven Learning of Narcosis Mode of Action Identifies a CNS Transcriptional Signature Shared between Whole Organism Caenorhabditis Elegans and a Fish Gill Cell Line, Sci. Total Environ., 2022, 849, 157666, DOI:10.1016/j.scitotenv.2022.157666.
- N. Klüver, K. Bittermann and B. I. Escher, QSAR for Baseline Toxicity and Classification of Specific Modes of Action of Ionizable Organic Chemicals in the Zebrafish Embryo Toxicity Test, Aquat. Toxicol., 2019, 207, 110–119, DOI:10.1016/j.aquatox.2018.12.003.
- B. I. Escher and R. P. Schwarzenbach, Partitioning of Substituted Phenols in Liposome−Water, Biomembrane−Water, and Octanol−Water Systems, Environ. Sci. Technol., 1996, 30(1), 260–270, DOI:10.1021/es9503084.
- C. Cowan-Ellsberry, S. Belanger, P. Dorn, S. Dyer, D. McAvoy, H. Sanderson, D. Versteeg, D. Ferrer and K. Stanton, Environmental Safety of the Use of Major Surfactant Classes in North America, Crit. Rev. Environ. Sci. Technol., 2014, 44(17), 1893–1993, DOI:10.1080/10739149.2013.803777.
- R. J. Farn, Chemistry and Technology of Surfactants, ed. R. J. Farn, Blackwell Publishing Ltd, 2006, DOI:10.1002/9780470988596.
- A. Ribbenstedt, J. M. Armitage, F. Günther, J. A. Arnot, S. T. J. Droge and M. S. McLachlan, In Vivo Bioconcentration of 10 Anionic Surfactants in Rainbow Trout Explained by In Vitro Data on Partitioning and S9 Clearance, Environ. Sci. Technol., 2022, 56(10), 6305–6314, DOI:10.1021/acs.est.1c05543.
- J. Glüge, M. Scheringer, I. T. Cousins, J. C. Dewitt, G. Goldenman, D. Herzke, R. Lohmann, C. A. Ng, X. Trier and Z. Wang, An Overview of the Uses of Per- And Polyfluoroalkyl Substances (PFAS), Environ. Sci.:Processes Impacts, 2020, 22(12), 2345–2373, 10.1039/d0em00291g.
- Z. Wang, A. M. Buser, I. T. Cousins, S. Demattio, W. Drost, O. Johansson, K. Ohno, G. Patlewicz, A. M. Richard, G. W. Walker, G. S. White and E. Leinala, A New OECD Definition for Per- and Polyfluoroalkyl Substances, Environ. Sci. Technol., 2021, 55(23), 15575–15578, DOI:10.1021/acs.est.1c06896.
- J. L. Guelfo, S. Korzeniowski, M. A. Mills, J. Anderson, R. H. Anderson, J. A. Arblaster, J. M. Conder, I. T. Cousins, K. Dasu, B. J. Henry, L. S. Lee, J. Liu, E. R. McKenzie and J. Willey, Environmental Sources, Chemistry, Fate, and Transport of Per- and Polyfluoroalkyl Substances: State of the Science, Key Knowledge Gaps, and Recommendations Presented at the August 2019 SETAC Focus Topic Meeting, Environ. Toxicol. Chem., 2021, 40(12), 3234–3260, DOI:10.1002/etc.5182.
- E. M. Sunderland, X. C. Hu, C. Dassuncao, A. K. Tokranov, C. C. Wagner and J. G. Allen, A Review of the Pathways of Human Exposure to Poly- and Perfluoroalkyl Substances (PFASs) and Present Understanding of Health Effects, J. Exposure Sci. Environ. Epidemiol., 2019, 29(2), 131–147, DOI:10.1038/s41370-018-0094-1.
- L. G. T. Gaines, G. Sinclair and A. J. Williams, A Proposed Approach to Defining Per- and Polyfluoroalkyl Substances (PFAS) Based on Molecular Structure and Formula, Integr. Environ. Assess. Manage., 2023, 19(5), 1333–1347, DOI:10.1002/ieam.4735.
- I. T. Cousins, C. A. Ng, Z. Wang and M. Scheringer, Why Is High Persistence Alone a Major Cause of Concern?, Environ. Sci.: Processes Impacts, 2019, 21(5), 781–792, 10.1039/c8em00515j.
- S. T. J. Droge, Membrane-Water Partition Coefficients to Aid Risk Assessment of Perfluoroalkyl Anions and Alkyl Sulfates, Environ. Sci. Technol., 2019, 53(2), 760–770, DOI:10.1021/acs.est.8b05052.
- A. Ebert, F. Allendorf, U. Berger, K. Goss and N. Ulrich, Membrane/Water Partitioning and Permeabilities of Perfluoroalkyl Acids and Four of Their Alternatives and the Effects on Toxicokinetic Behavior, Environ. Sci. Technol., 2020, 54(8), 5051–5061, DOI:10.1021/acs.est.0c00175.
- USEPA, CompTox list of PFAS structures - PFASSTRUCTV5 - August 2022, https://comptox.epa.gov/dashboard/chemical-lists/PFASSTRUCT, accessed 2024-03-26.
- I. T. Cousins, J. C. DeWitt, J. Glüge, G. Goldenman, D. Herzke, R. Lohmann, M. Miller, C. A. Ng, M. Scheringer, L. Vierke and Z. Wang, Strategies for Grouping Per- and Polyfluoroalkyl Substances (PFAS) to Protect Human and Environmental Health, Environ. Sci.: Processes Impacts, 2020, 22(7), 1444–1460, 10.1039/D0EM00147C.
- W. Cheng and C. A. Ng, Predicting Relative Protein Affinity of Novel Per- and Polyfluoroalkyl Substances (PFASs) by An Efficient Molecular Dynamics Approach, Environ. Sci. Technol., 2018, 52(14), 7972–7980, DOI:10.1021/acs.est.8b01268.
- S. Nouhi, L. Ahrens, H. Campos Pereira, A. V. Hughes, M. Campana, P. Gutfreund, G. K. Palsson, A. Vorobiev and M. S. Hellsing, Interactions of Perfluoroalkyl Substances with a Phospholipid Bilayer Studied by Neutron Reflectometry, J. Colloid Interface Sci., 2018, 511, 474–481, DOI:10.1016/j.jcis.2017.09.102.
- N. J. M. Fitzgerald, A. Wargenau, C. Sorenson, J. Pedersen, N. Tufenkji, P. J. Novak and M. F. Simcik, Partitioning and Accumulation of Perfluoroalkyl Substances in Model Lipid Bilayers and Bacteria, Environ. Sci. Technol., 2018, 52(18), 10433–10440, DOI:10.1021/acs.est.8b02912.
- G. Hodges, C. Eadsforth, B. Bossuyt, A. Bouvy, M.-H. Enrici, M. Geurts, M. Kotthoff, E. Michie, D. Miller, J. Müller, G. Oetter, J. Roberts, D. Schowanek, P. Sun and J. Venzmer, A Comparison of Log Kow (n-Octanol–Water Partition Coefficient) Values for Non-Ionic, Anionic, Cationic and Amphoteric Surfactants Determined Using Predictions and Experimental Methods, Environ. Sci. Eur., 2019, 31(1), 1, DOI:10.1186/s12302-018-0176-7.
- K. Bittermann, S. Spycher, S. Endo, L. Pohler, U. Huniar, K.-U. Goss and A. Klamt, Prediction of Phospholipid–Water Partition Coefficients of Ionic Organic Chemicals Using the Mechanistic Model COSMO Mic, J. Phys. Chem. B, 2014, 118(51), 14833–14842, DOI:10.1021/jp509348a.
- M. T. Müller, A. J. B. Zehnder and B. I. Escher, Liposome–Water and Octanol–Water Partitioning of Alcohol Ethoxylates, Environ. Toxicol. Chem., 1999, 18(10), 2191–2198, DOI:10.1002/etc.5620181011.
- S. Endo, B. I. Escher and K.-U. Goss, Capacities of Membrane Lipids to Accumulate Neutral Organic Chemicals, Environ. Sci. Technol., 2011, 45(14), 5912–5921, DOI:10.1021/es200855w.
- B. I. Escher, A. Baumer, K. Bittermann, L. Henneberger, M. König, C. Kühnert and N. Klüver, General Baseline Toxicity QSAR for Nonpolar, Polar and Ionisable Chemicals and Their Mixtures in the Bioluminescence Inhibition Assay with Aliivibrio Fischeri, Environ. Sci.:Processes Impacts, 2017, 19(3), 414–428, 10.1039/C6EM00692B.
- L. J. Carter, J. M. Armitage, B. W. Brooks, J. W. Nichols and S. Trapp, Predicting the Accumulation of Ionizable Pharmaceuticals and Personal Care Products in Aquatic and Terrestrial Organisms, Environ. Toxicol. Chem., 2022, 43(3), 1–11, DOI:10.1002/etc.5451.
- B. I. Escher, R. Abagyan, M. Embry, N. Klüver, A. D. Redman, C. Zarfl and T. F. Parkerton, Recommendations for Improving Methods and Models for Aquatic Hazard Assessment of Ionizable Organic Chemicals, Environ. Toxicol. Chem., 2020, 39(2), 269–286, DOI:10.1002/etc.4602.
- ECHA, Guidance on Information Requirements and Chemical Safety Assessment Chapter R.7c, Endpoint Specific Guidance, 2023, DOI:10.2823/95811.
- N. Klüver, C. Vogs, R. Altenburger, B. I. Escher and S. Scholz, Development of a General Baseline Toxicity QSAR Model for the Fish Embryo Acute Toxicity Test, Chemosphere, 2016, 164, 164–173, DOI:10.1016/j.chemosphere.2016.08.079.
- B. I. Escher and R. P. Schwarzenbach, Mechanistic Studies on Baseline Toxicity and Uncoupling of Organic Compounds as a Basis for Modeling Effective Membrane Concentrations in Aquatic Organisms, Aquat. Sci., 2002, 64, 20–35, DOI:10.1007/s00027-002-8052-2.
- N. Timmer and S. T. J. Droge, Sorption of Cationic Surfactants to Artificial Cell Membranes: Comparing Phospholipid Bilayers with Monolayer Coatings and Molecular Simulations, Environ. Sci. Technol., 2017, 51(5), 2890–2898, DOI:10.1021/acs.est.6b05662.
- A. Kierkegaard, C. Chen, J. M. Armitage, J. A. Arnot, S. Droge and M. S. McLachlan, Tissue Distribution of Several Series of Cationic Surfactants in Rainbow Trout (Oncorhynchus Mykiss) Following Exposure via Water, Environ. Sci. Technol., 2020, 54(7), 4190–4199, DOI:10.1021/acs.est.9b07600.
- A. Kierkegaard, M. Sundbom, B. Yuan, J. M. Armitage, J. A. Arnot, S. T. J. Droge and M. S. McLachlan, Bioconcentration of Several Series of Cationic Surfactants in Rainbow Trout, Environ. Sci. Technol., 2021, 55(13), 8888–8897, DOI:10.1021/acs.est.1c02063.
- K. Bittermann, S. Spycher and K.-U. Goss, Comparison of Different Models Predicting the Phospholipid-Membrane Water Partition Coefficients of Charged Compounds, Chemosphere, 2016, 144, 382–391, DOI:10.1016/j.chemosphere.2015.08.065.
- T. D. Potter, N. Haywood, A. Teixeira, G. Hodges, E. L. Barrett and M. A. Miller, Partitioning into Phosphatidylcholine–Cholesterol Membranes: Liposome Measurements, Coarse-Grained Simulations, and Implications for Bioaccumulation, Environ. Sci.:Processes Impacts, 2023, 25(6), 1082–1093, 10.1039/D3EM00081H.
- H. I. Ingólfsson, C. A. Lopez, J. J. Uusitalo, D. H. de Jong, S. M. Gopal, X. Periole and S. J. Marrink, The Power of Coarse Graining in Biomolecular Simulations, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2014, 4(3), 225–248, DOI:10.1002/wcms.1169.
- R. Menichetti, K. H. Kanekal, K. Kremer and T. Bereau, In Silico Screening of Drug-Membrane Thermodynamics Reveals Linear Relations between Bulk Partitioning and the Potential of Mean Force, J. Chem. Phys., 2017, 147(12), 125101, DOI:10.1063/1.4987012.
- T. D. Potter, E. L. Barrett and M. A. Miller, Automated Coarse-Grained Mapping Algorithm for the Martini Force Field and Benchmarks for Membrane–Water Partitioning, J. Chem. Theory Comput., 2021, 17(9), 5777–5791, DOI:10.1021/acs.jctc.1c00322.
- S. T. J. Droge, P. Scherpenisse, J. A. Arnot, J. M. Armitage, M. S. McLachlan, P. C. V. D. Ohe and G. Hodges, Screening the Baseline Fish Bioconcentration Factor of Various Types of Surfactants Using Phospholipid Binding Data, Environ. Sci.: Processes Impacts, 2021, 23(12), 1930–1948, 10.1039/D1EM00327E.
- M. S. McLachlan, A. Ebert, J. M. Armitage, J. A. Arnot and S. T. J. Droge, A Framework for Understanding the Bioconcentration of Surfactants in Fish, Environ. Sci.: Processes Impacts, 2023, 25(7), 1238–1251, 10.1039/D3EM00070B.
- S. J. Marrink, L. Monticelli, M. N. Melo, R. Alessandri, D. P. Tieleman and P. C. T. Souza, Two Decades of Martini: Better Beads, Broader Scope, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2023, 13(1), e1620, DOI:10.1002/wcms.1620.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Martini 3: A General Purpose Force Field for Coarse-Grained Molecular Dynamics, Nat. Methods, 2021, 18(4), 382–388, DOI:10.1038/s41592-021-01098-3.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations, J. Phys. Chem. B, 2007, 111(27), 7812–7824, DOI:10.1021/jp071097f.
- M. A. Webb, J. Y. Delannoy and J. J. De Pablo, Graph-Based Approach to Systematic Molecular Coarse-Graining, J. Chem. Theory Comput., 2019, 15(2), 1199–1208, DOI:10.1021/acs.jctc.8b00920.
- R. Alessandri, P. C. T. Souza, S. Thallmair, M. N. Melo, A. H. de Vries and S. J. Marrink, Pitfalls of the Martini Model, J. Chem. Theory Comput., 2019, 15(10), 5448–5460, DOI:10.1021/acs.jctc.9b00473.
- EPA, ECOTOX, https://cfpub.epa.gov/ecotox/, accessed 2023-07-29.
- ECHA, eChemPortal, https://www.echemportal.org/echemportal/, accessed 2023-07-29.
- Arthur D. Little Inc., Environmental and Human Safety of Major Surfactants, Vol. 1. Anionic Surfactants. Part 2. Alcohol Ethoxy Sulfates, Final Report to the Soap and Detergent Association, 1991, vol. 1 Search PubMed.
- Arthur D. Little Inc., Environmental and Human Safety of Major Surfactants, Volume I. Anionic Surfactants Part 3. Alkyl Sulfates, 1991 Search PubMed.
- SDA/Alkylsulfate Consortium. OECD SIDS Initial Assessment Report for SIAM 25 (2007) Category of Alkyl Sulfates, Alkane Sulfonates and α-Olefin Sulfonates, 2007, SIDS Initial Assessment Report (aciscience.org) (accessed 2023-07-29).
- BKH Consulting Engineers, Environmental Data Review of Alkyl Ether Sulfates (AES), Final Report, Dutch Soap Association (NVZ) in Cooperation with European Surfactant Industry, 1994 Search PubMed.
- OECD, Test No. 202: Daphnia Sp. Acute Immobilisation Test, OECD Guidelines for the Testing of Chemicals, Section 2, OECD, 2004, DOI:10.1787/9789264069947-en.
- OECD, Test No. 203: Fish, Acute Toxicity Test; OECD Guidelines for the Testing of Chemicals, Section 2, OECD, 2019, DOI:10.1787/9789264069961-en.
- K. Teather and J. Parrott, Assessing the Chemical Sensitivity of Freshwater Fish Commonly Used in Toxicological Studies, Water Qual. Res. J. Can., 2006, 41(1), 100–105 CrossRef CAS.
- K. A. Connors, J. L. Brill, T. Norberg-King, M. G. Barron, G. Carr and S. E. Belanger, Daphnia Magna and Ceriodaphnia Dubia Have Similar Sensitivity in Standard Acute and Chronic Toxicity Tests, Environ. Toxicol. Chem., 2022, 41(1), 134–147, DOI:10.1002/etc.5249.
- OECD, (Q)SAR Assessment Framework: Guidance for the Regulatory Assessment of (Quantitative) Structure Activity Relationship Models, Predictions, and Results Based on Multiple Predictions Series on Testing and Assessment No. 386, 2023, https://www.oecd.org/chemicalsafety/risk-assessment/qsar-assessment-framework.pdf, accessed 2024-01-09.
- L. Eriksson, J. Jaworska, A. P. Worth, M. T. D. Cronin, R. M. McDowell and P. Gramatica, Methods for Reliability and Uncertainty Assessment and for Applicability Evaluations of Classification- and Regression-Based QSARs, Environ. Health Perspect., 2003, 111(10), 1361–1375, DOI:10.1289/ehp.5758.
- I. V. Tetko and V. Y. Tanchuk, Application of Associative Neural Networks for Prediction of Lipophilicity in ALOGPS 2.1 Program, J. Chem. Inf. Comput. Sci., 2002, 42(5), 1136–1145, DOI:10.1021/ci025515j.
- G. Rossi, P. F. J. Fuchs, J. Barnoud and L. Monticelli, A Coarse-Grained MARTINI Model of Polyethylene Glycol and of Polyoxyethylene Alkyl Ether Surfactants, J. Phys. Chem. B, 2012, 116(49), 14353–14362, DOI:10.1021/jp3095165.
- S. D. Dyer, D. T. Stanton, J. R. Lauth and D. S. Cherry, Structure-Activity Relationships for Acute and Chronic Toxicity of Alcohol Ether Sulfates, Environ. Toxicol. Chem., 2000, 19(3), 608–616, DOI:10.1002/etc.5620190312.
- S. D. Dyer, J. R. Lauth, S. W. Morrall, R. R. Herzog and D. S. Cherry, Development of a Chronic Toxicity Structure-Activity Relationship for Alkyl Sulfates, Environ. Toxicol. Water Qual., 1997, 12(4), 295–303, DOI:10.1002/(SICI)1098-2256(1997)12:4<295::AID-TOX3>3.0.CO;2-3.
- S. E. Belanger, J. L. Brill, J. M. Rawlings and B. B. Price, Development of Acute Toxicity Quantitative Structure Activity Relationships (QSAR) and Their Use in Linear Alkylbenzene Sulfonate Species Sensitivity Distributions, Chemosphere, 2016, 155, 18–27, DOI:10.1016/j.chemosphere.2016.04.029.
- G. Hodges, D. W. Roberts, S. J. Marshall and J. C. Dearden, The Aquatic Toxicity of Anionic Surfactants to Daphnia Magna-A Comparative QSAR Study of Linear Alkylbenzene Sulphonates and Ester Sulphonates, Chemosphere, 2006, 63(9), 1443–1450, DOI:10.1016/j.chemosphere.2005.10.001.
- G. Hodges, D. W. Roberts, S. J. Marshall and J. C. Dearden, Defining the Toxic Mode of Action of Ester Sulphonates Using the Joint Toxicity of Mixtures, Chemosphere, 2006, 64(1), 17–25, DOI:10.1016/j.chemosphere.2005.12.021.
- G. Könnecker, J. Regelmann, S. Belanger, K. Gamon and R. Sedlak, Environmental Properties and Aquatic Hazard Assessment of Anionic Surfactants: Physico-Chemical, Environmental Fate and Ecotoxicity Properties, Ecotoxicol. Environ. Saf., 2011, 74(6), 1445–1460, DOI:10.1016/j.ecoenv.2011.04.015.
- M. J. Rosen, L. Fei, Y. P. Zhu and S. W. Morrall, The Relationship of the Environmental Effect of Surfactants to Their Interfacial Properties, J. Surfactants Deterg., 1999, 2(3), 343–347, DOI:10.1007/s11743-999-0087-2.
- D. C. Volz, S. Belanger, M. Embry, S. Padilla, H. Sanderson, K. Schirmer, S. Scholz and D. Villeneuve, Adverse Outcome Pathways during Early Fish Development: A Conceptual Framework for Identification of Chemical Screening and Prioritization Strategies, Toxicol. Sci., 2011, 123(2), 349–358, DOI:10.1093/toxsci/kfr185.
- P. Antczak, T. A. White, A. Giri, F. Michelangeli, M. R. Viant, M. T. D. Cronin, C. Vulpe and F. Falciani, Systems Biology Approach Reveals a Calcium-Dependent Mechanism for Basal Toxicity in Daphnia Magna, Environ. Sci. Technol., 2015, 49(18), 11132–11140, DOI:10.1021/acs.est.5b02707.
- D. W. Roberts and J. Costello, QSAR and Mechanism of Action for Aquatic Toxicity of Cationic Surfactants, in QSAR and Combinatorial Science, Wiley-VCH Verlag, 2003, vol. 22, pp. 220–225, DOI:10.1002/qsar.200390015.
- USEPA, Ecological Structure Activity Relationships (ECOSAR) Predictive Model, https://www.epa.gov/tsca-screening-tools/ecological-structure-activity-relationships-ecosar-predictive-model, accessed 2024-02-23.
- J. Vestel, D. J. Caldwell, L. Constantine, V. J. D'Aco, T. Davidson, D. G. Dolan, S. P. Millard, R. Murray-Smith, N. J. Parke, J. J. Ryan, J. O. Straub and P. Wilson, Use of Acute and Chronic Ecotoxicity Data in Environmental Risk Assessment of Pharmaceuticals, Environ. Toxicol. Chem., 2016, 35(5), 1201–1212, DOI:10.1002/etc.3260.
- S. P. Bradbury, C. L. Russom, G. T. Ankley, T. W. Schultz and J. D. Walker, Overview of Data and Conceptual Approaches for Derivation of Quantitative Structure-activity Relationships for Ecotoxicological Effects of Organic Chemicals, Environ. Toxicol. Chem., 2003, 22(8), 1789–1798, DOI:10.1897/01-234.
- F. N. Lambert, D. N. Vivian, S. Raimondo, C. T. Tebes-Stevens and M. G. Barron, Relationships Between Aquatic Toxicity, Chemical Hydrophobicity, and Mode of Action: Log Kow Revisited, Arch. Environ. Contam. Toxicol., 2022, 83(4), 326–338, DOI:10.1007/s00244-022-00944-5.
- D. Van Der Spoel, S. Manzetti, H. Zhang and A. Klamt, Prediction of Partition Coefficients of Environmental Toxins Using Computational Chemistry Methods, ACS Omega, 2019, 4(9), 13772–13781, DOI:10.1021/acsomega.9b01277.
- J. L. M. Hermens, J. H. M. de Bruijn and D. N. Brooke, The Octanol-Water Partition Coefficient: Strengths and Limitations, Environ. Toxicol. Chem., 2013, 32(4), 732–733, DOI:10.1002/etc.2141.
- OECD, Test No. 123: Partition Coefficient (1-Octanol/Water): Slow-Stirring Method; OECD Guidelines for the Testing of Chemicals, Section 1, OECD, 2022, DOI:10.1787/9789264015845-en.
- D. W. Roberts, QSAR Issues in Aquatic Toxicity of Surfactants, Sci. Total Environ., 1991, 109–110, 557–568, DOI:10.1016/0048-9697(91)90209-W.
- J. F. Roberts, S. J. Marshall and D. W. Roberts, Aquatic Toxicity of Ethoxylated and Propoxylated Alcohols to Daphnia Magna, Environ. Toxicol. Chem., 2007, 26(1), 68–72, DOI:10.1897/07-023R.1.
- D. W. Roberts, Aquatic Toxicity - Are Surfactant Properties Relevant?, J. Surfactants Deterg., 2000, 3(3), 309–315, DOI:10.1007/s11743-000-0134-z.
- D. W. Roberts and S. J. Marshall, Application of Hydrophobicity Parameters to Prediction of the Acute Aquatic Toxicity of Commercial Surfactant Mixtures, SAR QSAR Environ. Res., 1995, 4(2–3), 167–176, DOI:10.1080/10629369508029914.
- J. Hammer, A. M. Tukker, J. F. Postma, J. J. H. Haftka, J. L. M. Hermens, P. de Voogt and M. H. S. Kraak, Solubility Constraints on Aquatic Ecotoxicity Testing of Anionic Surfactants, Bull. Environ. Contam. Toxicol., 2018, 101(1), 99–104, DOI:10.1007/s00128-018-2361-1.
- M. Sapounidou, D. J. Ebbrell, M. A. Bonnell, B. Campos, J. W. Firman, S. Gutsell, G. Hodges, J. Roberts and M. T. D. Cronin, Development of an Enhanced Mechanistically Driven Mode of Action Classification Scheme for Adverse Effects on Environmental Species, Environ. Sci. Technol., 2021, 55(3), 1897–1907, DOI:10.1021/acs.est.0c06551.
- K. Dale, F. Yadetie, M. B. Müller, D. M. Pampanin, A. Gilabert, X. Zhang, Z. Tairova, A. Haarr, R. Lille-Langøy, J. L. Lyche, C. Porte, O. A. Karlsen and A. Goksøyr, Proteomics and Lipidomics Analyses Reveal Modulation of Lipid Metabolism by Perfluoroalkyl Substances in Liver of Atlantic Cod (Gadus morhua), Aquat. Toxicol., 2020, 227, 105590, DOI:10.1016/j.aquatox.2020.105590.
- A. D. Benninghoff, W. H. Bisson, D. C. Koch, D. J. Ehresman, S. K. Kolluri and D. E. Williams, Estrogen-Like Activity of Perfluoroalkyl Acids In Vivo and Interaction with Human and Rainbow Trout Estrogen Receptors In Vitro, Toxicol. Sci., 2011, 120(1), 42–58, DOI:10.1093/toxsci/kfq379.
- S. C. Tilton, G. A. Orner, A. D. Benninghoff, H. M. Carpenter, J. D. Hendricks, C. B. Pereira and D. E. Williams, Genomic Profiling Reveals an Alternate Mechanism for Hepatic Tumor Promotion by Perfluorooctanoic Acid in Rainbow Trout, Environ. Health Perspect., 2008, 116(8), 1047–1055, DOI:10.1289/ehp.11190.
- K. A. Houck, G. Patlewicz, A. M. Richard, A. J. Williams, M. A. Shobair, M. Smeltz, M. S. Clifton, B. Wetmore, A. Medvedev and S. Makarov, Bioactivity Profiling of Per- and Polyfluoroalkyl Substances (PFAS) Identifies Potential Toxicity Pathways Related to Molecular Structure, Toxicology, 2021, 457, 152789, DOI:10.1016/j.tox.2021.152789.
- M. M. Phillips, M. J. A. Dinglasan-Panlilio, S. A. Mabury, K. R. Solomon and P. K. Sibley, Fluorotelomer Acids Are More Toxic than Perfluorinated Acids, Environ. Sci. Technol., 2007, 41(20), 7159–7163, DOI:10.1021/es070734c.
- R. J. Mitchell, A. L. Myers, S. A. Mabury, K. R. Solomon and P. K. Sibley, Toxicity of Fluorotelomer Carboxylic Acids to the Algae Pseudokirchneriella Subcapitata and Chlorella Vulgaris, and the Amphipod Hyalella Azteca, Ecotoxicol. Environ. Saf., 2011, 74(8), 2260–2267, DOI:10.1016/j.ecoenv.2011.07.034.
- J. M. Armitage, J. A. Arnot and F. Wania, Potential Role of Phospholipids in Determining the Internal Tissue Distribution of Perfluoroalkyl Acids in Biota, Environ. Sci. Technol., 2012, 46(22), 12285–12286, DOI:10.1021/es304430r.
- C. A. Ng and K. Hungerbühler, Bioaccumulation of Perfluorinated Alkyl Acids: Observations and Models, Environ. Sci. Technol., 2014, 48(9), 4637–4648, DOI:10.1021/es404008g.
- S. E. Fenton, A. Ducatman, A. Boobis, J. C. DeWitt, C. Lau, C. Ng, J. S. Smith and S. M. Roberts, Per- and Polyfluoroalkyl Substance Toxicity and Human Health Review: Current State of Knowledge and Strategies for Informing Future Research, Environ. Toxicol. Chem., 2021, 40(3), 606–630, DOI:10.1002/etc.4890.
- BAuA (Germany), Bureau REACH RIVM (The Netherlands), Swedish Chemicals Agency (Sweden), Norwegian Environment Agency (Norway), The Danish Environmental Protection Agency (Denmark), Annex XV Restriction Report Proposal for a Restriction Substance Name(S): Per-and Polyfluoroalkyl Substances (PFASs), 2023, https://echa.europa.eu/restrictions-under-consideration/-/substance-rev/72301/term, accessed 2024-01-22 Search PubMed.
- C. F. Kwiatkowski, D. Q. Andrews, L. S. Birnbaum, T. A. Bruton, J. C. DeWitt, D. R. U. Knappe, M. V. Maffini, M. F. Miller, K. E. Pelch, A. Reade, A. Soehl, X. Trier, M. Venier, C. C. Wagner, Z. Wang and A. Blum, Scientific Basis for Managing PFAS as a Chemical Class, Environ. Sci. Technol. Lett., 2020, 7(8), 532–543, DOI:10.1021/acs.estlett.0c00255.
- A. Cordner, L. Richter and P. Brown, Can Chemical Class Approaches Replace Chemical-by-Chemical Strategies? Lessons from Recent U.S. FDA Regulatory Action on per-and Polyfluoroalkyl Substances, Environ. Sci. Technol., 2016, 50(23), 12584–12591, DOI:10.1021/acs.est.6b04980.
- I. T. Cousins, J. C. DeWitt, J. Glüge, G. Goldenman, D. Herzke, R. Lohmann, C. A. Ng, M. Scheringer and Z. Wang, The High Persistence of PFAS Is Sufficient for Their Management as a Chemical Class, Environ. Sci.:Processes Impacts, 2020, 22(12), 2307–2312, 10.1039/D0EM00355G.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4em00649f |
| This journal is © The Royal Society of Chemistry 2025 |
